Abstract
Objective
In this study, we determined efficient head model sizes relative to predicted current densities in transcranial direct current stimulation (tDCS).
Approach
Efficiency measures were defined based on a finite element (FE) simulations performed using nine human head models derived from a single MRI data set, having extents varying from 60-100% of the original axial range. Eleven tissue types, including anisotropic white matter, and three electrode montages (T7-T8, F3-right supraorbital, Cz-Oz) were used in the models.
Main results
Reducing head volume extent from 100% to 60%, that is, varying the model’s axial range from between the apex and C3 vertebra to one encompassing only apex to the superior cerebellum, was found to decrease the total modeling time by up to half. Differences between current density predictions in each model were quantified by using a relative difference measure (RDM). Our simulation results showed that RDM was the least affected (a maximum of 10% error) for head volumes modeled from the apex to the base of the skull (60-75% volume).
Significance
This finding suggested that the bone could act as a bioelectricity boundary and thus performing FE simulations of tDCS on the human head with models extending beyond the inferior skull may not be necessary in most cases to obtain reasonable precision in current density results.
Keywords: finite element simulation, tDCS, current density, segmentation
INTRODUCTION
Transcranial direct current stimulation (tDCS) is a non-invasive neuromodulation treatment that has gained attention due to its low cost compared to transcranial magnetic stimulation (TMS), yet its mechanism is not well understood [1]. Electrode montages used in tDCS treatments most commonly involve a single anode/cathode pair, with each electrode typically comprising a large (25-35 cm2 area) saline-soaked sponge placed over the scalp or hair. tDCS treatments have been found to affect motor, cognitive, language and visual function by applying either excitatory or inhibitory effects [2-6]. A maximum current of 2 mA is often used [2] to obtain these effects. However, the full scope of tDCS neuromodulation efficacy is still unclear. Stimulation currents are generally assumed to have most effect on brain regions directly underneath electrodes and it has been assumed that the influences of tDCS correlate with the concentration of electrical current in brain structures, but many other unknown factors may contribute to the effects resulting from tDCS.
At present, it is only possible to model the approximate distribution of current flow with reference to electrostatic or quasi-static electromagnetic models. A clear understanding of electric current distributions caused by tDCS therapy may enable better understanding of its mechanism. Finite element simulations using increasingly realistic human head models have become a popular tool to predict current density distributions created by tDCS treatment [7-10]. Finite element simulation software has advanced greatly in the last decade and has made these simulations more accessible. For instance, the availability of advanced segmentation tools has allowed construction of more realistic head compositions using tissue types beyond the commonly used: white matter, gray matter, cerebrospinal fluid (CSF), skull and scalp compartments [7, 10-12]. Tissue anisotropy should also be addressed when modeling white matter [7, 9, 11, 13]. While many previous studies have treated the skull as a single compartment, others have suggested that the skull should be modeled as two separate compartments because of the large differences in electrical properties between cortical and cancellous bone [14, 15]. Including a large number of tissue properties as well as tissue anisotropy increases model construction complexity and size considerably, and thus may require more computing power and time. Therefore, inclusion of tissues within a certain perimeter between the electrodes and target brain region has been suggested to improve modeling efficiency [9].
Even though many sophisticated human head tDCS simulation studies have been performed in previous studies, the head volumes used in each study have varied. For instance, some simulation studies used head models that spanned from the head apex down to the mouth and jaw areas [9], while other studies only included the head down to the base of the cerebellum [6, 8]. One previous study stated that the skull had a strong shunting effect and thus extending the field of view down to neck was important [10]. There are a number of other studies where the span of the head models could only be inferred from reported MRI data FOV and matrix size values, or figures, without explicitly stating the span of the head models being simulated [16-18]. This raises a question of simulation validity and comparability, since there has been no study to date that has clearly compared the influence of the modeled region extent on results.
To the best of our knowledge, there has not yet been a study that investigates the effect of reducing modeled head volumes to different extents on FE simulation results, specifically for tDCS simulation. Reducing the modeled head volume could presumably decrease overall simulation time since the model would involve fewer simulated regions. This would be particularly beneficial in decreasing the manual segmentation time component of model construction. For instance, a large amount of muscle tissue in the neck area is commonly segmented manually. If the neck region was not necessary to the simulation, total model construction time could be reduced. Therefore, the aims of this study were to analyze the effects of reducing modeled head volume on current density predictions, and to suggest an ‘efficient’ head volume i.e., the minimum essential head volume, to use based on these findings. The efficient volumes were selected based on brain target location, electrode configuration and specified variability limit of 5 or 10% in current density values, compared to a model with an original extent from the head apex to the C3 level. We have made only intra-model comparisons in this study because we wanted to clearly demonstrate the effect of changing model extent on results. Because we have only used one model, we consider the results only broadly indicative of the dependence of model extent on simulation validity.
MATERIALS AND METHODS
Tissue segmentation
T1-weighted, T2-weighted, and high angular resolution diffusion weighted imaging (HARDI) MRI data sets for an individual male subject were obtained using a 3T Achieva Phillips MRI system at the McKnight Brain Institute, University of Florida. T1-weighted data were acquired with a 3D fast field (in plane matrix size 256 × 256, 160 axial slices) and the T2-weighted data were acquired with a 3D turbo spin echo pulse sequence (in plane matrix size 240 × 240, 160 axial slices) with TE = 3.69 ms, TR = 8.057 ms and voxel dimension of 0.9375 × 0.9375 × 1 mm. HARDI data were collected in 70 gradient directions (6 directions were acquired at b = 100 s/mm2 and 64 directions were acquired at b = 1000 s/mm2) using a 2D multislice spin echo sequence (matrix size 112 × 112, 70 slices of 2 mm thickness) with TE = 86.0 ms and TR = 9022.8 ms. Prior to segmentation, the MRI data set was resampled using Freesurfer v5.0 (Cambridge, MA) to have voxel dimensions of 1 × 1 × 1 mm3, 256×256 in plane resolution and a total of 216 transverse slices. These 216 slices spanned from the head apex to the C3 vertebral level.
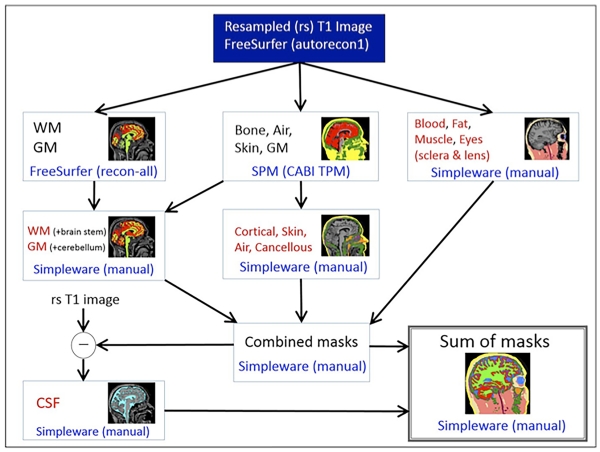
The head volume was segmented into eleven tissue types using a combination of automatic and manual segmentation techniques following a flowchart described in Figure 1. An automatic segmentation for white and gray matter was performed in Freesurfer. A bone tissue was obtained using the ‘New Segment’ module [19] in SPM8 (Wellcome Trust Centre for Neuroimaging, London, UK) based on an improved tissue probability map developed at CABI [10]. Manual corrections to Freesurfer and SPM8 segmentations, and a manual segmentation for air, blood, skin, fat, skeletal muscle, sclera and lens was performed in ScanIP v6.0 (Simpleware, Exeter, UK) with a reference to an anatomical atlas [20]. The bone compartment was further separated into cancellous and cortical parts by thresholding the resampled T1 image. Lastly, the cerebrospinal fluid (CSF) was extracted by taking the difference between the exterior volume and all previously segmented tissues (brain, bone and all other tissues).
Fig. 1.
A segmentation pipeline categorizes the head volume into eleven tissue compartments
Conductivity and tissue anisotropy assignment
Literature sourced conductivity values used for each tissue type are shown in Table 1. One conductivity value was assigned to one MRI voxel resolution of 1 mm3 consisted of six tetrahedral elements. The values chosen were empirical data measured in tissues at frequencies less than 1 kHz. Average conductivity values were used if multiple tissue conductivity values less than 1 kHz were reported. We chose this frequency because it is difficult to obtain good empirical data for many tissues at lower frequencies, and because these simulations were performed as part of a study designed to compare these simulations with current flow measured via a new MRI based method [21], wherein current pulses involving ca. 1 kHz were used.
Table 1.
Eleven tissue types and their assigned conductivities obtained from low frequency (<1kHz) data in literatures [7]. The isotropic conductivity in white matter was obtained using the formula σ=σ1 · σt where σ1 is longitudinal and σt is transverse conductivity value
| Tissue types | σ (S/m) | Reference |
|---|---|---|
| Air | 0 | - |
| Blood | 6.7×10−1 | Geddes and Baker (1967) |
| Cancellous bone | 21.4×10−3 | Akhtari et al. (2002) |
| Cortical bone | 5.52×10−3 | Akhtari et al. (2002) |
| Cerebrospinal fluid | 1.8 | Baumann et al. (1997) |
| Fat | 2.5×10−2 | Gabriel et al. (1996) |
| Gray matter | 1.0×10−1 | Gabriel et al. (1996) |
| Muscle | 1.6×10−1 | Geddes and Baker (1967) |
| Sclera, lens | 5.0×10−1 | Gabriel et al. (1996) |
| Skin | 4.3×10−1 | Holdefer et al. (2006) |
| White matter | 1.2×10−1(trans.) 1.2 (long.) |
Geddes and Baker (1967) |
The principal direction of anisotropy was calculated based on diffusion tensor image (DTI) data that was reconstructed from the HARDI image set. Each of the white matter voxel within the conductivity tensor Dw was re-oriented following the calculated DTI principal eigenvector components (V1x, V1y,V1z) such that
| (1) |
where
| (2) |
| (3) |
In case of isotropic tissue, Dw was a diagonal matrix with all entries equal to tissue isotropic conductivity values. Rx Ry Rz were the rotation matrices about z, y and x axes, respectively. For anisotropic white matter conductivity, the tensor Dw was rotated into the direction of the eigenvectors such that
| (4) |
| (5) |
where , and are the normalized values of V1x, V1y and V1z respectively. The eigenvectors corresponding to x, y and z values along with fractional anisotropy (FA) information were calculated from raw DWI, b-values and b-vectors by using the FSL FDT module [22]. We found that fractional anisotropies in white matter compartments were 0.5 and greater.
Reduced model definitions
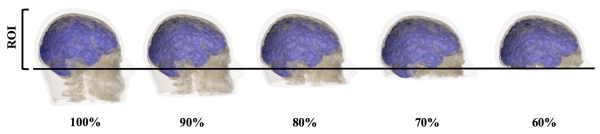
The head volume was further categorized into nine head extension models. An ‘100%’ head model with the axial slices spanning from the head apex down to the C3 vertebra, a distance of 212 mm; followed by: 95% model (to just below C2, 201 mm), 90% model (to C2, 191 mm), 85% model (to just below C1, 180 mm), 80% model (to C1, 170 mm), 75% model (to just below the inferior skull, 159 mm), 70% model (to under the pons, inferior skull open, 148 mm), 65% model (half cerebellum truncated, 138 mm), and 60% model (to the superior cerebellum, not including the pons, 127 mm), as shown in Figure 2.
Fig. 2.
Illustration of head models extension represented by (from left to right) of: 100%, 90%, 80%, 70%, and 60% volume. Region of interest (ROI) denotes the tissue regions within which intermodel comparisons were made. The images in this figure only include gray matter, bone and skin for five out of nine head extents for ease of visualization
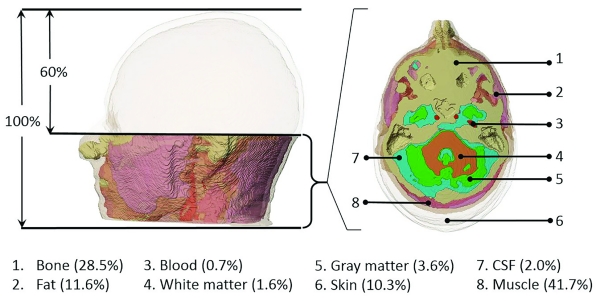
In order to demonstrate the contribution to segmentation burden in the regions outside the ROI, that is between the 100% reference and 60% models, the volume of each tissue type, Vtissue, in this region are tabulated with their conductivity values (σ) in Figure 3 below. Note that the largest volumetric contribution to this region was skeletal muscle and bone, since this region encompassed the superior cervical spine.
Fig. 3.
Volumes of tissue between 60% and 100% models shown in (left) sagittal and (right) axial views. The 8 tissues are differentiated by color, with skin being semi-transparent. The view at right shows the most inferior slice of the 60% model
Electrode configuration
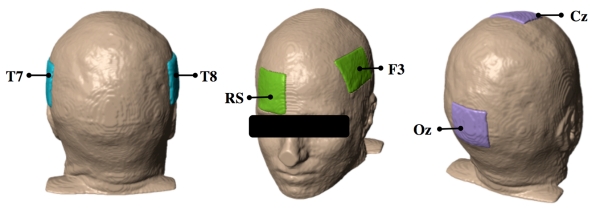
Three electrode montages, labeled following the standard 10-20 EEG electrode system, were placed in turn on each model. The three configurations were: Cz and Oz position (Cz-Oz), F3 and a right supraorbital (RS) position (F3-RS), and left (T7) and right (T8) posterior temporal cortex positions (T7-T8), as shown in Figure 4. Each rectangular electrode was approximately 1 mm in thickness and had an area of about 35 cm2. The large electrode surface area followed standard tDCS protocols used to minimize the risk of superficial burns on patients caused by current application.
Fig. 4.
Electrode placement on head models showing, from left to right: T7-T8, F3-RS and Cz-Oz montages. Electrodes were labeled using the 10-20 EEG system
Finite element modeling
All current flows were calculated using both isotropic and anisotropic white matter conditions. Head models were meshed into linear tetrahedral elements for isotropic simulations, and quadratic tetrahedral elements for anisotropic simulations. The total number of elements in each head model is shown in Table 2.
Table 2.
Numbers of elements (millions), simulation time (hours) and segmentation time (days) in each of the head volumes considered.
| Conductivity volume (%) |
Num. of elements (millions) |
Simulation time (hours) |
Segmentation time (days) |
|---|---|---|---|
| 100 | 24 | 6.0 | 6 |
| 90 | 22.2 | 4.8 | 5 |
| 80 | 19.8 | 3.5 | 4 |
| 70 | 17.4 | 3.0 | 4 |
| 60 | 14.4 | 2.6 | 3 |
Boundary Conditions
A total of 1 mA current flow, giving an average 28.6 μA/cm2 current density through each electrode area, was simulated in all nine models. Current was injected into the (first named) anode site, and removed from the second electrode.
The finite element simulation solved a mixed boundary value problem. The Laplace equation (6) was satisfied in the head volume, Ω, while the head surface, ∂Ω, had both Neumann and Dirichlet conditions, given here as
| (6) |
| (7) |
| (8) |
where σ was the tissue conductivity and ϕ was the voltage distribution inside Ω, J was the current density and n was the unit normal vector, ε+ and ε− were anode and cathode surface electrodes, respectively, and I was the total applied current. The normal component of J was only nonzero on the electrode surfaces (7). A zero voltage reference point was specified at the midpoint node of each model.
Model Solution
Stiffness and boundary condition matrices were formulated using the Galerkin equations [23] and assembled in C. Solutions to the system of matrix equations were solved in MATLAB (Mathworks, MA) by using the preconditioned conjugate gradient (pcg) method. Local voltage gradients ∇ϕ at each node were obtained from the finite element solution, and the current density J in each voxel j was calculated such that
| (9) |
Where D was a conductivity tensor with the diagonal entries equal to conductivity values defined in (1) and (2).
Current density magnitudes J were calculated as
| (10) |
Data calculation and model comparisons
Each of the reduced head volume results, for both isotropic and anisotropic cases, was compared against the 100% head model reference calculations. Since the current distributions were approximately log-normal [7], a decimal logarithm of current density values was used for comparison. A relative difference measure (RDM) was applied to quantify the difference in all nine head volumes such that
| (11) |
where Xi is the parameter under investigation (60%-95%), Xr is the reference parameter and N is the number of measurements points [24]. In using an RDM to calculate current density differences in the upper 60% regions (ROI) of all nine head volumes we therefore calculated
| (12) |
Here, dR is the resistance drop across the electrodes in the investigated volume. The subscript ‘i’ indicates the investigated volume and ‘r’ is the reference (100%) volume. RDM compares current density values between models within the upper 60% region only. We needed to adjust current density, J, by the resistance, R, in each volume because reduction of model volume alters the resistance drop across the electrodes. This adjustment was necessary to make appropriate comparisons between Js within the top 60% volume in each model version. N is the number of nodes within the ROI of all models, starting at the apex of the head. Differential RDM (DiffRDM) values, that is, differences between RDMs as model volume decreased, were calculated for each model step, such that
| (13) |
where the model volume in 2 was larger than for case 1.
Selected structure analyses
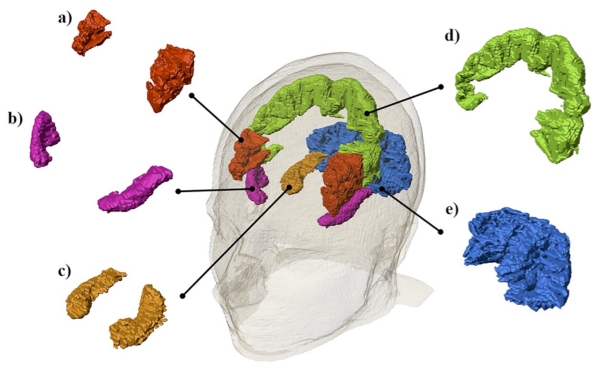
Five arbitrary brain structures, shown in Figure 5, were selected to further analyze the effects of varying model extent. The precentral gyrus was chosen to represent a cortical structure, while the hippocampus and occipital lobe were chosen to represent limbic and posterior brain structures respectively. The inferior frontal gyrus, anterior superior temporal gyrus and occipital lobe were chosen as representative tissue targets for F3-RS, T7-T8 and Cz-Oz electrode configurations, respectively. Median current density was calculated in each of the five selected structures for all head models to determine the effects of model truncation.
Fig. 5.
Illustrations of the five structures analyzed: a) the inferior frontal gyrus b) the anterior superior temporal gyrus c) the hippocampus d) the precentral gyrus and e) the occipital lobe
Efficient Head Volume
A minimum essential head model span was determined based on median current density values in the five selected structures. Percentage differences were calculated between median current densities in each volume and the 100% reference volume. A head volume was considered efficient if there was only a 5% difference between the median value in a reduced volume and the reference volume. We also considered a 10% threshold for efficiency.
RESULTS
RDM values were calculated in all nine head models for each of the three electrode configurations, under both isotropic and anisotropic white matter assumptions. Both anisotropic and isotropic simulation time was shorter by up to 50% as the head model was reduced from 100 to 60% axial extent. As expected, RDM increased as model extent was reduced from 95% to 60%. RDM values found comparing anisotropic cases were overall larger by up to 7% than RDM values in matching isotropic cases. We found no clear relationship in median current density changes between electrode configurations and their respective presumed tissue targets in all head models. Among the five specific structures analyzed using anisotropic simulations, the median current density in the precentral gyrus was found to be the least affected by model volume reduction, while the median current density in the anterior superior temporal gyrus was the most affected by reducing head volume. The inferior frontal gyrus was the structure least affected by the model volume reduction for isotropic simulations. In the sections below we present the results of each analysis in detail.
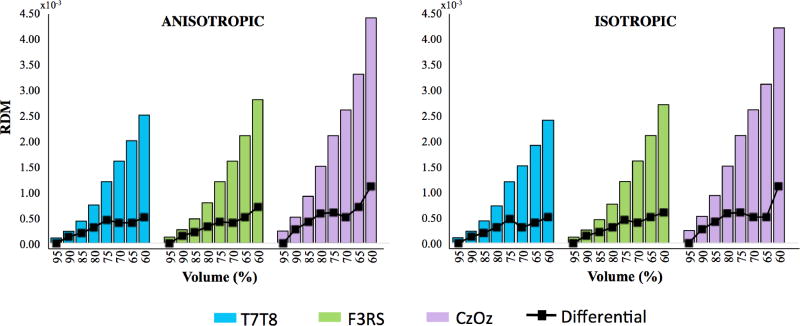
Calculated RDM in all tissue
The RDM and differential RDM values for each head volume and electrode montage, for both anisotropic and isotropic cases are shown in Figure 6. We found that RDM increased as head volume was reduced from 95% to 60% volume, regardless of whether the model was assumed isotropic or anisotropic. Comparing different montages as model extent was reduced, values for T7-T8 simulations had the smallest RDM values, while Cz-Oz had the largest overall RDM values. For instance, the RDM value for Cz-Oz at 65% model extent was approximately 3.30 while the RDM value for T7-T8 at 65% was approximately 2.00. The overall anisotropic RDM values were up to 7% greater than isotropic RDM values in matched extent models. The largest difference between anisotropic and isotropic RDM was found in the 70% volume model with the T7-T8 configuration. Anisotropic RDM values were the least and most different compared to their isotropic RDM counterparts for Cz-Oz and T7-T8 montages, respectively.
Fig. 6.
RDM results and differential RDM (black lines) for all tissues for Anisotropic (left) and Isotropic (right) cases in three electrode configurations T7-T8 (blue), F3-RS (green) and Cz-Oz (purple). The horizontal axis represents head volume models and the vertical axis represents RDM values
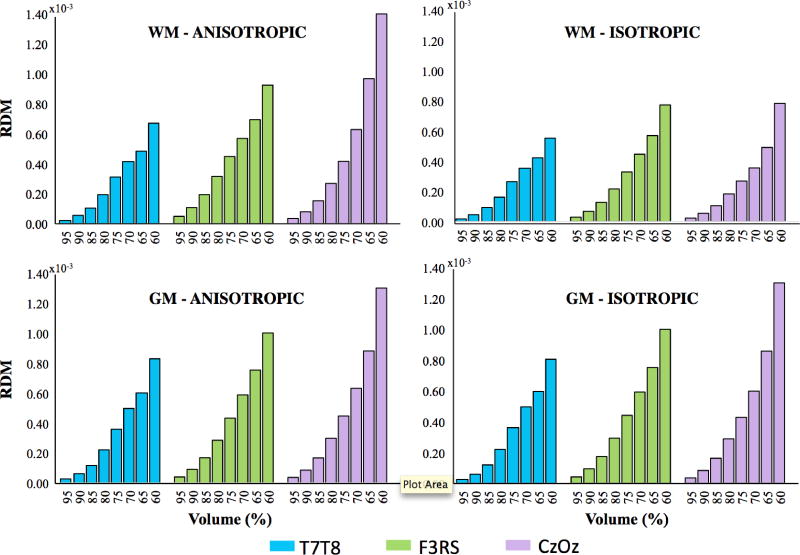
Calculated RDM values in white and gray matter
In order to further compare the effect of head model reduction on simulated current densities in anisotropic models, RDM measures were calculated separately for white and gray matter compartments, as shown in Figure 7. The differences between RDM values calculated for anisotropic and isotropic cases in gray matter were not as apparent as in those in white matter for the T7-T8 and Cz-Oz configurations. White matter and gray matter RDM in anisotropic cases for all three montages were overall larger than in isotropic cases by 14%- 97% and 0-5%, respectively.
Fig. 7.
RDM results for white matter (top) and gray matter (bottom) for Anisotropic (left) and Isotropic (right) cases in three electrode configurations T7-T8 (blue), F3-RS (green) and Cz-Oz (purple). The horizontal axis represents head volume model and the vertical axis represents RDM values
Selected structure analyses
Table 3 tabulates median current density percentage differences between each of the reduced volumes (60-95%) and reference volume (100%) models in the five focus structures. The percentage differences for the different electrode configurations and their presumed tissue targets are shaded in Table 3. We also show absolute median current densities in each structure for the reference model in this table. A graphical representation of this summary is shown in Figure 8. Negative values exemplified larger median current densities in the target of the reference volume than in the corresponding structure in reduced volumes. The smallest percentage differences for each volume were found in the precentral gyrus for each electrode configuration, regardless of whether anisotropy or isotropy was used. The largest percentage differences across all structures and electrode configurations were found in the anterior superior temporal gyrus in the anisotropic models.
Table 3.
Absolute median current density in 100% head volume and percentage differences in median current density with respect to the reference (100%) head volume for precentral gyrus, inferior frontal gyrus, anterior superior temporal gyrus, hippocampus and occipital lobe in Anisotropic (top) and Isotropic (bottom) cases for three electrode configurations. Dark shaded text denotes values in the presumed tissue target for each electrode configuration T7-T8 (blue), F3RS (green), Cz-Oz (purple). Negative values indicate the reference median current density was larger than reduced volume median current density
| ANISOTROPIC | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| %Vol. | 100 |Jmedian| (A/m2) |
95 (% diff) |
90 (% diff) |
85 (% diff) |
80 (% diff) |
75 (% diff) |
70 (% diff) |
65 (% diff) |
60 (% diff) |
| Config. | |||||||||
| Precentral gyrus | |||||||||
| T7T8 | 0.018 | 0.0 | −0.3 | −0.7 | 1.2 | −0.1 | 2.3 | 1.2 | 1.6 |
| F3RS | 0.011 | 0.0 | 3.7 | 3.4 | 2.8 | 5.8 | 4.9 | 7.3 | 9.0 |
| CzOz | 0.013 | 3.0 | 3.0 | 2.7 | 2.1 | 4.5 | 2.6 | 1.7 | −4.3 |
| Inferior frontal gyrus | |||||||||
| T7T8 | 0.012 | 3.4 | 3.1 | 2.8 | 2.4 | 4.5 | 5.8 | 8.9 | 8.2 |
| F3RS | 0.021 | 0.0 | 0.0 | 1.6 | 1.0 | 2.3 | 3.2 | 3.9 | 3.9 |
| CzOz | 0.012 | 0.0 | 0.0 | −0.3 | −0.9 | −1.5 | −3.2 | −10.0 | −15.3 |
| Anterior superior temporal gyrus | |||||||||
| T7T8 | 0.018 | 2.3 | 1.9 | 3.9 | 8.0 | 11.1 | 15.5 | 20.4 | 24.2 |
| F3RS | 0.016 | 0.0 | 0.0 | 2.3 | 4.2 | 6.1 | 10.2 | 16.4 | 21.7 |
| CzOz | 0.010 | 0.0 | 0.0 | −0.3 | −0.9 | −5.4 | −7.1 | −14.3 | −22.8 |
| Hippocampus | |||||||||
| T7T8 | 0.017 | 0.0 | 2.0 | 1.7 | 3.6 | 6.8 | 9.3 | 10.2 | 14.6 |
| F3RS | 0.012 | 0.0 | 0.0 | 3.1 | 2.5 | 5.3 | 11.2 | 13.2 | 17.9 |
| CzOz | 0.011 | 0.0 | 0.0 | 3.4 | 2.8 | 5.8 | 3.9 | −3.4 | −12.3 |
| Occipital lobe | |||||||||
| T7T8 | 0.016 | 2.6 | 2.2 | 1.9 | 4.1 | 7.8 | 8.2 | 12.0 | 19.5 |
| F3RS | 0.005 | 0.0 | 0.0 | −0.3 | −0.9 | 6.1 | 5.2 | 11.4 | 24.2 |
| CzOz | 0.018 | 0.0 | 0.0 | 1.9 | 3.4 | 4.9 | 9.4 | 11.4 | 14.4 |
| ISOTROPIC | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| %Vol. | 100 |Jmedian| (A/m2) |
95 (% diff) |
90 (% diff) |
85 (% diff) |
80 (% diff) |
75 (% diff) |
70 (% diff) |
65 (% diff) |
60 (% diff) |
| Config. | |||||||||
| Precentral gyrus | |||||||||
| T7T8 | 0.012 | 0.0 | 0.3 | 0.3 | 1.3 | 2.0 | 2.9 | 3.5 | 3.1 |
| F3RS | 0.010 | 0.0 | 3.5 | 3.5 | 2.9 | 6.1 | 5.1 | 7.6 | 9.4 |
| CzOz | 0.014 | 0.0 | 0.0 | −0.3 | −0.9 | 1.3 | −0.5 | −1.5 | −7.3 |
| Inferior frontal gyrus | |||||||||
| T7T8 | 0.011 | −0.3 | −0.3 | −0.7 | 2.7 | 1.3 | 2.9 | 3.4 | 6.6 |
| F3RS | 0.020 | 0.0 | −0.3 | −0.3 | −0.9 | 0.4 | 1.5 | 2.2 | 2.3 |
| CzOz | 0.011 | 0.0 | 0.0 | 3.4 | 2.8 | 2.1 | 0.3 | −6.8 | −12.3 |
| Anterior superior temporal gyrus | |||||||||
| T7T8 | 0.016 | −0.3 | −0.3 | 1.7 | 3.8 | 9.6 | 14.5 | 18.0 | 22.8 |
| F3RS | 0.014 | 0.0 | 2.6 | 2.6 | 4.9 | 7.2 | 12.0 | 16.4 | 22.7 |
| CzOz | 0.009 | 0.0 | 0.0 | −0.3 | −0.9 | −1.5 | −7.5 | −14.9 | −23.7 |
| Hippocampus | |||||||||
| T7T8 | 0.018 | −0.3 | 1.9 | 1.6 | 3.5 | 6.6 | 8.8 | 10.0 | 14.4 |
| F3RS | 0.011 | 0.0 | 3.3 | 3.3 | 6.2 | 9.1 | 11.6 | 13.7 | 18.5 |
| CzOz | 0.010 | 0.0 | −0.3 | 3.4 | 2.7 | 5.8 | 3.9 | −6.9 | −15.7 |
| Occipital lobe | |||||||||
| T7T8 | 0.015 | −0.3 | 2.4 | 2.0 | 4.3 | 5.6 | 8.7 | 10.6 | 19.1 |
| F3RS | 0.003 | 0.0 | −0.3 | 4.2 | 8.1 | 7.5 | 15.4 | 14.0 | 29.3 |
| CzOz | 0.017 | 0.0 | 2.3 | 2.0 | 3.7 | 5.4 | 10.3 | 12.7 | 16.3 |
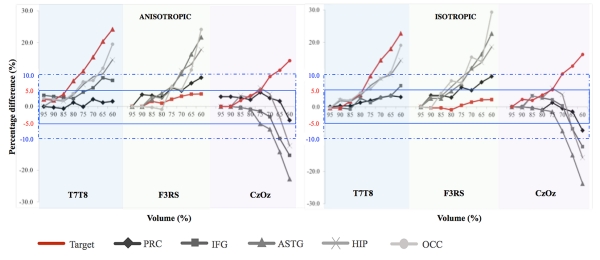
Fig. 8.
A series of plots representation of percentage differences in median current density in Anisotropic (left) and Isotropic (right) cases. Each plot corresponds to the five specific structures: precentral gyrus (PRC), inferior frontal gyrus (IFG), anterior superior temporal gyrus (ASTG), hippocampus (HIP) and occipital lobe (OCC). Light blue, green and purple shaded regions are referring to T7-T8, F3-RS and Cz-Oz electrode configurations, respectively. Red plots denote dependencies within target areas for each electrode montage. Blue solid line regions represent 5 percent error bounds and blue dashed line regions represent 10 percent error bounds
Recall that the efficient reduced volume was defined as an acceptable limit of head volume reduction. Based on the results presented in Table 3, the efficient reduced volume for each of the five structures were further categorized at 5% and 10% differences in J values based on the median current density values. Efficient reduced volume models for the different montages, targets and model types are summarized in Table 4. Among the five structures and three electrodes, an 80% extent model (to C1) produced at most 5% difference while a 60% model produced about 10% difference in target structure current densities. Effects of model truncation were less apparent in the superior and frontal structures such as the precentral gyrus and inferior frontal gyrus, than in deeper and more inferior structures such as the occipital lobe and hippocampus.
Table 4.
Efficient volume choices for 10 and 5 percent differences based on median current density comparisons to 100% models for Anisotropic (top) and Isotropic (bottom) cases volume for three electrode configurations T7-T8 (blue), F3-RS (green), Cz-Oz (purple). Dark shaded values correspond to presumed tissue targets for each electrode configuration
| Percent error (ANISOTROPIC) |
10% | 5% | ||||
|---|---|---|---|---|---|---|
| Electrode pairs | T7-T8 | F3-RS | Cz-Oz | T7-T8 | F3-RS | Cz-Oz |
| Structures | ||||||
| Hippocampus | 70% vol | 75% vol | 65% vol | 80% vol | 80% vol | 80% vol |
| Precentral gyrus | 60% vol | 60% vol | 60% vol | 60% vol | 80% vol | 60% vol |
| Occipital lobe | 70% vol | 70% vol | 70% vol | 80% vol | 80% vol | 75% vol |
| Inferior frontal gyrus | 60% vol | 60% vol | 65% vol | 75% vol | 60% vol | 70% vol |
|
Anterior superior temporal gyrus |
80% vol | 75% vol | 70% vol | 85% vol | 80% vol | 80% vol |
| Percent error (ISOTROPIC) |
10% | 5% | ||||
|---|---|---|---|---|---|---|
| Electrode pairs | T7-T8 | F3-RS | Cz-Oz | T7-T8 | F3-RS | Cz-Oz |
| Structures | ||||||
| Hippocampus | 65% vol | 75% vol | 65% vol | 80% vol | 85% vol | 80% vol |
| Precentral gyrus | 60% vol | 60% vol | 60% vol | 60% vol | 80% vol | 65% vol |
| Occipital lobe | 70% vol | 75% vol | 75% vol | 80% vol | 85% vol | 80% vol |
| Inferior frontal gyrus | 60% vol | 60% vol | 65% vol | 65% vol | 60% vol | 70% vol |
|
Anterior superior temporal gyrus |
75% vol | 75% vol | 70% vol | 80% vol | 80% vol | 75% vol |
DISCUSSION
Features considered important in realistic head models include high resolution, implementation of tissue anisotropy and use of many electrically distinct tissue types. However, inclusion of these factors can be computationally expensive. Reducing the extent of modeled head volume may increase simulation efficiency by reducing segmentation and simulation times. In this work, we used results from nine head models of different extents, using three electrode montages and two tissue anisotropy conditions, a total of 54 unique simulations. In the sections below, overall RDM results and model validity will be discussed below in terms of model construction, tissue anisotropy type and electrode montages used.
Simulation results
RDM was used as the main measure to quantify the difference between the nine reduced volumes to compare current density in each model volume against the 100% volume reference. Overall, the RDM analysis clearly showed that head model truncation affected current density distributions. The trend in the graphs shown in Figures 6 and 7 indicated that a linear relationship existed between RDM and tissue extent as models were truncated. The largest RDM was observed at 60% of the original full volume regardless of the electrode montage used and tissue anisotropy. Furthermore, the Cz-Oz RDM distribution shown in Figure 6 had the largest overall RDM magnitudes for both anisotropic and isotropic cases compared to T7-T8 and F3-RS. The Oz electrode was placed on the posterior side of the head and the electrode edge was placed close to the bottom of the 60% volume, as shown in Figure 4. Therefore, larger current densities would be expected to flow towards the inferior head near the model truncation point. This current pattern caused the Cz-Oz RDM to be much more sensitive to model truncation than the T7-T8 and F3-RS montages.
Anisotropic models showed much larger RDM magnitudes in the white matter compartment than for corresponding isotropic models (Figure 7) as expected. Overall, change in model anisotropy type had the most influence on white matter RDM curves for the Cz-Oz electrode pair. The anterior-posterior orientation of the white matter tracts lying between the Cz-Oz electrode pair [25] may have affected this large RDM change, in addition to the low Oz electrode location. Therefore, current density values calculated from the region between the electrodes that contained more longitudinal tract than transverse would have shown much larger RDM than the regions with less longitudinal tract.
The differential of RDM was calculated to assess changes in RDM for each electrode configuration as model extent was changed. As noted above, the bottom of Oz electrode was very close to the cutoff region, and thus the current surrounding the electrode was more influenced by changes in head model extent. On the other hand, F3-RS and T7-T8 electrode placements were near the head apex and further away from the cutoff site and, therefore, the current circulation between the electrode pair was less affected by the decreasing size at the bottom of the head. Overall, as truncation increased, differential RDMs increased (Figure 6) with a clear change in differential at the transition from 75-70% models. This finding was likely caused by the large change in current shunting patterns around the skull boundary at this transition. At 75% volume there was no opening in the inferior skull whereas in the 70% volume the skull was open. We speculate that current density distributions in the brain of the 70% model were affected by a lack of highly resistive bone structure in that region and consequent leakage of current into brain tissue, and thus caused a considerable increase in calculated RDM in the ROI.
Selected structure analyses could be useful to measure the effect of head model reduction directly on target structures, thus more concisely evaluating the impact of model choices. The hippocampus and precentral gyrus are commonly targeted for tDCS therapy to improve cognitive, memory and motor skills [26, 27]. Median current density changes in all five structures did not depend predictably on model extent, or montage. For instance, median current density calculated in the inferior frontal gyrus and the anterior superior temporal gyrus increased as model extent decreased from 80% to 65% volume for montages T7-T8 and F3-RS but decreased for the Cz-Oz montage. On the other hand, median current density calculated in the occipital lobe decreased as model extent decreased from 80% to 60% volume for montages T7-T8 but increased for F3-RS and Cz-Oz montages. Even though there was no clear relationship between median current density and model extent, the median currents measured in the anterior superior temporal gyrus were overall the most affected by the head reduction while those in the precentral gyrus were the least affected. The anterior superior temporal gyrus is located towards the bottom of the head, and thus was more sensitive to model truncation at the inferior edge of the model whereas the precentral gyrus was located near the head apex further away from the truncated region. Therefore, current density calculations depend on the proximity between the structures’ locations and the truncation site.
As expected, less truncated models were required to obtain 5% differences from the reference model, regardless of tissue anisotropy state and electrode configuration. The modeled volume chosen for a particular montage should be based on the structure of interest and acceptable error. For instance, if the inferior frontal gyrus was the structure of interest for a F3-RS tDCS montage, then a 60% volume model should be sufficient to obtain current density values within 5% of those found simulating the entire volume. This would cut simulation time by approximately half, as shown in Table 2.
Model validity
There are some commonly encountered shortcomings associated with model construction and simulation that are not addressed in this study. One important feature not considered here is the issue of segmentation accuracy. Segmentation accuracy is important since miscategorization of tissues in head model could presumably affect calculation outcomes [28].
Tissue segmentation errors can arise in both automatic and manual segmentation procedures. Manual segmentation of T1 data is particularly difficult to perform on tissues with low contrast such as bone, CSF and air. In addition, the presence of susceptibility artifacts nearby air-tissue interfaces in the sinus could also produce segmentation errors. In our model, we avoided the issue of segmentation error because all data was based on a single segmented head model. However, the issue of segmentation type and timing is important when considering the total time needed to perform a particular type of simulation. There are many existing automatic methods for segmenting brain tissues but fewer methods for segmenting fat, bone or skeletal muscle. A need to include tissues well below the skull creates a requirement for a much larger burden of manual processing in delineating tissues in the neck – mainly fat, bone and muscle. A clear definition of the minimum required model volume would not only save a computational time but also segmentation time. A good demarcation for minimum required model volume would also be useful when defining and standardizing MRI slice packages to be used in structural image gathering, if these images are to be used for model construction. This issue is particularly important as increasing computing power makes it possible to define individual treatment plans based on a subject’s own data.
In this study we only included white matter anisotropy. The diffusion tensor data registration with the T1-based model could possibly be incorrect. Registration and normalization of DTI data relative to T1 data was performed prior extracting eigenvectors and FA information. There have been claims that both skull and gray matter should be considered as anisotropic [11, 28], and it is possible that addition of gray matter and skull anisotropy would produce different RDM values than demonstrated here. However, there has been no empirical data to support skull anisotropy [15]. The bone was modeled as three layers tissues instead (cancellous in the center and two outside layers of cortical) according to its anatomical organization. In our models, gray matter was considered isotropic based on its FA value being less than 0.5. If this were incorrect, all models used here would therefore be uniformly incorrect. However, considering the volume of gray matter outside the 60% model volume (as shown in Figure 2, around 4%) the impact of this consideration on the RDM values would likely be very small.
Another factor that might affect this study’s outcomes could be the effect of model resolution. Our models were based on a data set with 1 mm3 resolution. A mesh refinement study may be advisable to determine the effect of changing mesh size and smoothing tissue compartments on results. All the models used in this project were meshed into tetrahedral elements. However, all six tetrahedral elements were assigned the conductivity assigned in the voxelized model. This method might be considered inaccurate [11] and thus a comparison to a smoothed tetrahedral model might be beneficial to assess the effect on model efficiency or RDM measures. We believe that voxelized models may actually provide quite similar results to those generated by tetrahedral elements modeling smoothed tissue boundaries, simply because electrical energy flow is diffuse and not particularly sensitive to sharp simulated tissue edges. Additionally, the abstractions involved in boundary smoothing may actually reduce correspondence between the model and reality. We have performed a preliminary study to determine the effect of using smoothed tissue boundaries rather than using the original voxelwise segmented compartments [29]. Comparing ‘block’ and ‘smooth’ tissue compartments based on the same source data, we found current density changes of less than 5% in target structural volumes, and less than 15% in cortical regions nearby stimulating electrodes. Therefore, a ‘block’ model pipeline (one that does not include a tissue smoothing step) could be considered sufficient to estimate current density distributions in target structures. Elimination of the need to smooth tissue compartments would further streamline the pipeline between imaging and obtaining simulation results.
Tissue conductivity values are frequency dependent [30]. For example, fat conductivity increased from 0.025S/m to 0.03S/m as frequency increased from near 1 kHz to 1MHz [30]. While conductivity characteristically increases with increasing frequency, the rate of increase is different for different tissues. Therefore increases in frequency may lead to substantially different current distributions [31]. Therefore, further study may be required to determine efficient head volume extents for stimulation performed at higher frequencies.
CONCLUSION
We investigated the effect of changing model axial extent on electrical current densities predicted in different brain tissues and structures subject to three electrode montage types. Differential RDM increased as model extent was reduced, with a clear transition when the model excluded the inferior skull. We determined ‘efficient’ model volumes where RDM values were at most 5% or 10% different from the reference model for each montage. Determination of these limits will inform choice of head extent in subsequent models, and our results here indicate that in many cases it may not be necessary to segment far below the inferior skull, greatly reducing the time required for manual segmentation of fat, bone and muscle.
This study investigated a single MRI dataset from a healthy subject. These initial intramodel results linked simulated current densities and the extent of tissue modeled, keeping other aspects of model composition constant. However, a future study could consider multiple subjects in order to determine a better and more general recommendation for efficient head extent. The effects of changing stimulation frequency, sex, handedness and inclusion of pathology in different brain regions could also be considered. Knowledge of these bounds should also prove useful in determining parameters used to gather structural MRI scans used as the source in building realistic finite element models.
While comparisons of this sort between models can help determine the relative effects of choices made when constructing computational models of therapies such as tDCS, there is a still clear need to compare these models with actual experimental data. To date no methods have allowed direct measurements of current densities within the head. We are presently executing a study using MREIT [21], an MR-based technique that makes it possible to measure current density distributions within the head. We anticipate that these studies will allow us to directly quantify current distributions in tDCS, and, further, to actually validate different modeling approaches.
ACKNOWLEDGEMENT
Research reported in this publication was supported by the National Institute Of Neurological Disorders And Stroke of the National Institutes of Health under Award Number R21NS081646 to RJS.
Footnotes
Disclosure: The authors report no conflicts of interest.
REFERENCES
- [1].Hardwick RM, Celnik PA. Cerebellar direct current stimulation enhances motor learning in older adults. Neurobiol Aging. 2014;35:2217–21. doi: 10.1016/j.neurobiolaging.2014.03.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Nitsche MA, Cohen LG, Wassermann EM, Priori A, Lang N, Antal A, Paulus W, Hummel F, Boggio PS, Fregni F, Pascual-Leone A. Transcranial direct current stimulation: State of the art 2008. Brain Stimul. 2008;1:206–23. doi: 10.1016/j.brs.2008.06.004. [DOI] [PubMed] [Google Scholar]
- [3].Kessler SK, Minhas P, Woods AJ, Rosen A, Gorman C, Bikson M. Dosage Considerations for Transcranial Direct Current Stimulation in Children: A Computational Modeling Study. Plos One. 2013;8:1–15. doi: 10.1371/journal.pone.0076112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Sadleir RJ, Vannorsdall TD, Schretlen DJ, Gordon B. Transcranial direct current stimulation (tDCS) in a realistic head model. NeuroImage. 2010;51:1310–8. doi: 10.1016/j.neuroimage.2010.03.052. [DOI] [PubMed] [Google Scholar]
- [5].Marangolo P, Fiori V, Calpagnano MA, Campana S, Razzano C, Caltagirone C, Marini A. tDCS over the left inferior frontal cortex improves speech production in aphasia. Front Hum Neurosci. 2013;7:1–10. doi: 10.3389/fnhum.2013.00539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Neuling T, Wagner S, Wolters CH, Zaehle T, Herrmann CS. Finite-element model predicts current density distribution for clinical applications of tDCS and tACS. Frontiers in Psychiatr. 2012;3:1–10. doi: 10.3389/fpsyt.2012.00083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Sadleir RJ, Vannorsdall TD, Schretlen DJ, Gordon B. Target Optimization in transcranial direct current stimulation. Frontiers in Psychiatry. 2012;3:90. doi: 10.3389/fpsyt.2012.00090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Bikson M, Datta A. Guidelines for precise and accurate computational models of tDCS. Brain Stimul. 2012;5:430–4. doi: 10.1016/j.brs.2011.06.001. [DOI] [PubMed] [Google Scholar]
- [9].Wagner S, Rampersad SM, Aydin U, Vorwerk J, Oostendorp TF, Neuling T, Herrmann CS, Stegeman DF, Wolters CH. Investigation of tDCS volume conduction effects in a highly realistic head model. J Neural Eng. 2014;11:1–14. doi: 10.1088/1741-2560/11/1/016002. [DOI] [PubMed] [Google Scholar]
- [10].Huang Y, Dmochowski JP, Su Y, Datta A, Rorden C, Parra LC. Automated MRI segmentation for individualized modeling of current flow in the human head. J of Neural Eng. 2013;10:1–13. doi: 10.1088/1741-2560/10/6/066004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Rampersad SM, Janssen AM, Lucka F, Aydin U, Lanfer B, Lew S, Wolters CH, Stegeman DF, Oostendorp TF. Simulating Transcranial Direct Current Stimulation With a Detailed Anisotropic Human Head Model. Ieee T Neur Sys Reh. 2014;22:441–52. doi: 10.1109/TNSRE.2014.2308997. [DOI] [PubMed] [Google Scholar]
- [12].Wagner T, Fregni F, Fecteau S, Grodzinsky A, Zahn M, Pascual-Leone A. Transcranial direct current stimulation: A computer-based human model study. NeuroImage. 2007;35:1113–24. doi: 10.1016/j.neuroimage.2007.01.027. [DOI] [PubMed] [Google Scholar]
- [13].Suh HS, Lee WH, Kim TS. Influence of anisotropic conductivity in the skull and white matter on transcranial direct current stimulation via an anatomically realistic finite element head model. Phys Med Biol. 2012;57:6961–80. doi: 10.1088/0031-9155/57/21/6961. [DOI] [PubMed] [Google Scholar]
- [14].Akhtari M, Bryant HC, Mamelak AN, Heller L, Shih JJ, Mandelkern M, Matlachov A, Ranken DM, Best ED, Sutherling WW. Conductivities of three-layer human skull. Brain Topography. 2000;13:29–42. doi: 10.1023/a:1007882102297. [DOI] [PubMed] [Google Scholar]
- [15].Sadleir RJ, Argibay A. Modeling Skull Electrical Properties. Annals of Biomedical Engineering. 2007;35:1699–712. doi: 10.1007/s10439-007-9343-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Datta A, Baker JM, Bikson M, Fridriksson J. Individualized model predicts brain current flow during transcranial direct-current stimulation treatment in responsive stroke patient. Brain Stimulation. 2011;4:169–74. doi: 10.1016/j.brs.2010.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Bai SW, Dokos S, Ho KA, Loo C. A computational modelling study of transcranial direct current stimulation montages used in depression. Neuroimage. 2014;87:332–44. doi: 10.1016/j.neuroimage.2013.11.015. [DOI] [PubMed] [Google Scholar]
- [18].Turkeltaub PE, Benson J, Hamilton RH, Datta A, Bikson M, Coslett HB. Left laterlizing transcranial direct current stimulation improves reading efficiency. Brain Stimul. 2012;5:201–7. doi: 10.1016/j.brs.2011.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Ashburner J, Friston KJ. Unified Segmentation. NeuroImage. 2005;26:839–51. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
- [20].Spitzer VM, Whitlock DG. Atlas of the Visible Human Male. Vol. 1. Jones and Bartlett Learning; USA: 1997. [Google Scholar]
- [21].Woo EJ, Seo JK. Magnetic resonance electrical impedance tomography (MREIT) for high-resolution conductivity imaging. Physiological Measurement. 2008;29:R1–R26. doi: 10.1088/0967-3334/29/10/R01. [DOI] [PubMed] [Google Scholar]
- [22].Behrens TE, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, Matthews PM, Brady JM, Smith SM. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn Reson Med. 2003;50:1077–88. doi: 10.1002/mrm.10609. [DOI] [PubMed] [Google Scholar]
- [23].Davies AJ. The finite element method: a first approach. Oxford University Press; New York: 1980. [Google Scholar]
- [24].Bruno P, Vatta F, Mininel S, Inchingolo P. Referenced EEG and head volume conductor model: geometry and parametrical setting; Proceedings of the 26th Annual International Conference of the IEEE EMBS; San Francisco, CA, USA: IEEE. 2004; [DOI] [PubMed] [Google Scholar]
- [25].Wedeen VJ, Rosene DL, Wang R, Dai G, Mortazavi F, Hagmann P, Kaas JH, W.I T. The Geometric Structure of the Brain Fiber Pathways. Science. 2012;335:1628–34. doi: 10.1126/science.1215280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Kwon YH, Ko MH, Ahn SH, Kim YH, Song JC, Lee CH, Chang MC, Jang SH. Primary motor cortex activation by transcranial direct current stimulation in the human brain. Neurosci Lett. 2008;435:56–9. doi: 10.1016/j.neulet.2008.02.012. [DOI] [PubMed] [Google Scholar]
- [27].Marshall L, Molle M, Hallschmid M, Born J. Transcranial direct current stimulation during sleep improves declarative memory. J Neurosci. 2004;24:9985–92. doi: 10.1523/JNEUROSCI.2725-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Shahid SS, Wen P, Ahfock T. Assessment of electric field distribuion in anisotropic cortical and subcortical regions under the influence of tDCS. Bioelectromagnetics. 2014;35:41–57. doi: 10.1002/bem.21814. [DOI] [PubMed] [Google Scholar]
- [29].Indahlastari A, Sadleir RJ. A comparison between block and smooth modeling in finite element simulations of tDCS; EMBC, 37th Annual International Conference of the IEEE; Milan. 2015; pp. 3403–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: III Parametric models for the dielectric spectrum of tissues. Physics in medicine and biology. 1996;41:2271–93. doi: 10.1088/0031-9155/41/11/003. [DOI] [PubMed] [Google Scholar]
- [31].Schmidt C, Wagner S, Burger M, van Rienen U, Wolters CH. Impact of uncertain head tissue conductivity in the optimization of transcranial direct current stimulation for an auditory target. Journal of neural engineering. 2015;12:046028. doi: 10.1088/1741-2560/12/4/046028. [DOI] [PMC free article] [PubMed] [Google Scholar]