Control Engineering Methods for the Design of Robust Behavioral Treatments

Abstract

In this paper, a robust control approach is used to address the problem of adaptive behavioral treatment design. Human behavior (e.g., smoking and exercise) and reactions to treatment are complex and depend on many unmeasurable external stimuli, some of which are unknown. Thus, it is crucial to model human behavior over many subject responses. We propose a simple (low order) uncertain affine model subject to uncertainties whose response covers the most probable behavioral responses. The proposed model contains two different types of uncertainties: uncertainty of the dynamics and external perturbations that patients face in their daily life. Once the uncertain model is defined, we demonstrate how least absolute shrinkage and selection operator (lasso) can be used as an identification tool. The lasso algorithm provides a way to directly estimate a model subject to sparse perturbations. With this estimated model, a robust control algorithm is developed, where one relies on the special structure of the uncertainty to develop efficient optimization algorithms. This paper concludes by using the proposed algorithm in a numerical experiment that simulates treatment for the urge to smoke.

I. Introduction

Proliferation of portable devices that collect patient information very frequently (i.e., intensive longitudinal data) and enable timely treatment has opened the possibility of developing effective personalized interventions [1]. These types of interventions can be behavioral or pharmacological or a combination according to the structure of the specific behavioral problem [2]. This is currently being investigated in smoking addiction, alcohol addiction, exercise behavior, and so on. Dynamical modeling of behavior is critical in developing control algorithms [3]–[6]. However, very little attention has been paid to the fact that human behavior has a significant amount of uncertainty and that this uncertainty should be addressed systematically. This paper provides an approach for modeling patient behavior and designing a robust adaptive treatment that considers both the present state of the patient and the probable perturbations to expected behavior.

Previous researchers have applied control concepts in behavioral research [3]–[5], [7]–[9], but the use of feedback is still a novel approach. In addition to feedback, additional constraints for patients’ limitations and measured disturbances can be easily addressed in controller-design-based interventions [10]. In this paper, we discuss a possible control engineering-based approach and explain how robust control tools can be used to design robust adaptive treatments. To design a robust algorithm, the first step is to define the uncertainties observed in the treatment responses. Therefore, we propose a class of uncertain affine models suitable for this task and discuss a way to identify such models using available tools, such as lasso [11]. The second step is to show that a robust control algorithm can be developed that relies on the special structure of the uncertainty in the model to develop efficient optimization algorithms.

Only simple affine models will be considered here, because very little is known about the structure of human behavior. Nevertheless, this approach can be extended to more complex models, such as nonlinear and time-varying models if one has better knowledge about the dynamics of the human behavior.

Besides the problem of choosing the right model structure, behavioral data have other remarkable challenges. The collection of behavioral data is often done over long periods of time and one cannot usually perform repeated experiments to improve the quality of the data. As a result, unlike most physical systems, behavioral data are generally more noisy, incomplete, and inconsistent. Hence, designers of treatments typically work with an incomplete, noisy data set from multiple patients [12]–[15]. Multiple participants are used to attempt to capture a more complete data set such that the gaps in one participant’s data are filled by another participant. Therefore, we also use data from several participants to determine a model that both is meaningful and can be used to design treatment for a specific group of individuals.

In this paper, we discuss a specific structure for model uncertainty that can be used for modeling human behavior. When selecting a type of uncertainty, the objective is to address: 1) differences in the behavior of different participants modeled as white Gaussian noise and 2) sparse external perturbations that can be used to model life events that affect the response to treatment. With the model structure defined earlier, lasso [11] is used for parameter identification and uncertainty quantification because it provides a way to directly estimate a model subject to sparse perturbations. Given that the models extracted from behavioral data usually have a large amount of uncertainty, there is a need for feedback and, especially, robustness. Hence, in the second part of this paper, an algorithm is proposed for a controller design that is robust with respect to the specific type of uncertainties considered.

The specific control design technique used in this paper is based on a robust model predictive controller (MPC) approach [16]. A computationally simple cost function is used, namely, a quadratic one, and the corresponding robust optimization problem is formulated. In formulating the control problem, one considers all different combinations of treatments available. The resulting robust optimization problem is then solved by relying on results from robust optimization [17]–[19] and by exploiting the specific structure of the uncertainty.

Throughout this paper, the problem of designing a treatment for smoking urge is used as our example. Although the treatment is assumed as ON/OFF (apply treatment or no treatment) in this specific example, this is not always the case. There are situations where one not only has to decide when/which treatment to apply but also the dosage (see [20] for a more detailed explanation of characteristics of behavioral problems). The presented method can be easily modified to accommodate different types (behavioral, pharmacological, or combined) and levels (dosage) of treatments. Note that in this example, the term treatment is used to refer to an intervention where text messages are sent to the subject.

A. Previous Work

Adaptive interventions are sequences of treatments that are adapted and readapted to individual circumstances and behaviors in order to achieve and maintain health behavior change [12], [13]. These interventions may be provided many times (i.e., tens, hundreds, or even thousands of treatment occasions during the entire treatment period). The interventions are often delivered via portable devices, as intensive interventions. Since these interventions adapt to individual progress, it is effective to prevent insufficient response and react immediately against the unexpected shock on behavior. Therefore, scientists in the social and behavioral sciences have been working on finding systematic ways to use portable devices such as smart phones to change health behavior or maintain healthy behavior in real time. Consequently, adaptive interventions are being developed by social and behavioral scientists for different areas, such as hypertension [14], substance abuse [15], criminal justice [21], mental health [22], and Alzheimer’s disease [23].

Engineering concepts, such as dynamical modeling, have been applied to modeling and controlling behavior [6]. References [3]–[5] present special issues that arise in applying such approaches to behavioral research. These studies employ both time-invariant and time-varying models, depending on the specific problem. Some extend studies use controller design methods to design adaptive interventions for special problems in behavioral science [7]–[9]. This paper defines uncertainties in behavior more explicitly than previous studies and discusses their effects on the robustness of the algorithm. In general, according to the intervention design problem, the MPC design method is preferred. Preliminary results of this paper were presented in [24]. More detailed explanations of modeling behavior and identification are presented in this paper. The complete proofs are also provided, along with simulations.

This paper is organized as follows. In Section II, we introduce the model that will be used to approximate patient behavior and justify its use. In Section III, we discuss a way to identify the model’s parameters from patient study data. In Section IV, an MPC formulation of the robust control problem is introduced. In Section V, a simulation of the application of the proposed approach is presented with a simulated smoking cessation treatment from [25]. In this section, some hypothetical individual results are also given to show how a control algorithm works. Finally, in Section VI, we present some concluding remarks.

II. Model

As mentioned in Section I, data on human behavior usually involve several subjects with many gaps in information over time. Moreover, behavior might change with time and vary from subject to subject. Therefore, it is very unlikely that one can accurately specify a complex model of behavior. One can use a simple model to approximate patient behavior or the main dynamics of the subject and, at the same time, highlight the fact that there is a substantial amount of uncertainty in it. Hence, a possible model for identification is a set of affine difference equations. The difference model used in this paper is of the form

$${\mathbf{y}}_{k+1}={\mathbf{a}}_f+\sum _{i=0}^{n-1}[A_i{\mathbf{y}}_{k-i}+B_i{\mathbf{T}}_{k-i}]+D{\epsilon }_k+E{\mathbf{w}}_k$$ (1)

where y_k ∞ ℝ^m is the measured output vector at time k, T_k ∞ ℝ, and T_k ∞ 𝒯 is the control input (i.e., treatment), where 𝒯 is a set of all available treatments. In many cases, this set has a finite number of elements. Unmeasurable sparse exogenous perturbations are denoted by w_k ∞ ℝ and ε_k ∞ ℝ^m, which represents uncertainty in the model. The affine term vector is a_f ∞ ℝ^m, and A_i ∞ ℝ^m×m, B_i ∞ ℝ^m, D ∞ ℝ^m×m, and E ∞ ℝ^m are coefficients matrices.

The dynamics of behavior are very complex and hard to control because of the uncertainties on behaviors. Therefore, the uncertain difference equation in (1) is used to model a large set of responses to behavioral treatment. In addition to the dynamics of behavior, which are contaminated by Gaussian noise, an unmeasured exogenous input is added to the model to represent unexpected influences.

We use as a motivating example a hypothetical study of smoking cessation. In this example, we address the problem of treatment design after quit day (i.e., day on which an individual quits smoking). Patients usually have different dynamics before and after quit day and different treatments should be designed for each of these cases. Since the objective of this paper is to develop a general design procedure, we only consider the after quit day case as an example of treatment design. The procedure developed can also be used for before quit day case.

In the smoking cessation model, there are three different variables that one can measure: smoking urge (denoted by su); negative affect, (na), which is a single scale indicating an adverse mood state; and self-efficacy, (se), which represents an individual’s belief in their ability to abstain from smoking. With these variables, the following model is proposed:

$$\begin{array}{c}\left[\begin{array}{l}{\text{su}}_{k+1}\hfill \\ {\text{na}}_{k+1}\hfill \\ {\text{se}}_{k+1}\hfill \end{array}\right]=\left[\begin{array}{l}{a}_f\hfill \\ d_f\hfill \\ g_f\hfill \end{array}\right]+\sum _{i=0}^{n-1}\left\{\left[\begin{array}{lll}{a}_i\hfill & b_i\hfill & c_i\hfill \\ d_i\hfill & e_i\hfill & f_i\hfill \\ g_i\hfill & h_i\hfill & r_i\hfill \end{array}\right]\left[\begin{array}{l}{\text{su}}_{k-i}\hfill \\ {\text{na}}_{k-i}\hfill \\ {\text{se}}_{k-i}\hfill \end{array}\right]\right\}\\ +\sum _{i=0}^{n-1}\left\{\left[\begin{array}{c}0\\ q_i\\ s_i\end{array}\right]{\mathbf{T}}_{k-i}\right\}+\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]{\mathbf{w}}_k\\ +\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{\epsilon }_k^{(\text{su})}\\ {\epsilon }_k^{(\text{na})}\\ {\epsilon }_k^{(se)}\end{array}\right].\end{array}$$ (2)

Remark 1

The signs of several of these coefficients are assumed to be known in advance for this example. For example, negative affect (na) increases smoking urge (su), whereas self-efficacy (se) decreases it. More information about the dynamics of the smoking urge can be found in [26] and [27]. This information can be used in two different ways: 1) it can be given to the identification algorithm as additional constraints or 2) it can be utilized to validate the model.

This model also shows that smoking urge cannot be directly controlled, but if the negative affect can be decreased and self-efficacy can be increased by applying treatment T, the desired smoking urge level can be achieved under the uncertainties.

One should first note that the model above is an uncertain affine model. One of the reasons why this structure was chosen was the fact that a model should not be obtained just from data, and it should also leverage characteristics determined by prior behavioral research. For instance, patients smoke cigarettes to regulate the smoking urge set point (see [3], [28] for more detailed explanation of smoking dynamics). Therefore, an affine term (constant term in the model) is added to the model to represent this set point.

The model in (1) is called a structural equation model (SEM) in social science [29]. Similar to SEM models, an affine model for smoking cessation is preferred, because the equilibrium point of the uncontrolled system is often not the origin. The model is obtained by using data from several patients and differences in patients are typically modeled as Gaussian random variables ε. The external perturbation w ∞ ℒ^∞ is motivated by a different kind of uncertainty in human behavior. The way the subjects behave is influenced by external sparse events that temporarily affect his/her response to treatment. Hence, one needs an uncertainty that is sparse, bounded in magnitude, and with limited cumulative effect. As a result, it is assumed that the segment of perturbation signal w ∞ ℒ^∞ is bounded in the ℓ₁-norm, ℓ_∞-norm, and ℓ₀-norm. For this situation, a possible signal set 𝒲, which is used in this paper, is the following. Given an MPC control window of length K and k, the set 𝒲 is

$$\mathcal{W}=\{\mathbf{w}\in {\mathcal{L}}^{\infty }:\text{for}\text{all}k,{\Vert {\mathbf{w}}_{(k:k+K-1)}\Vert }_{\infty }\le \alpha ,{\Vert {\mathbf{w}}_{(k:k+K-1)}\Vert }_1\le \gamma ,{\Vert {\mathbf{w}}_{(k:k+K-1)}\Vert }_0=K/\varsigma \}.$$ (3)

α ∞ ℕ is bound on the magnitude of the perturbation, γ ∞ ℕ is bound on cumulative effect, and ς ∞ ℕ enforces the sparsity constraint on vector w_(k:k+K−1).

III. Identification of the Model and Perturbations

To estimate the coefficients from study data, we start by noting that the model above can be taken to represent the relations among the variables as

$$Y=H\beta +\epsilon .$$ (4)

In this model, the unknown vector β contains the parameters of the model and vector w, vector Y is a function of the measurements, and matrix H is a function of the measurements and inputs (treatment). For the smoking cessation example, the structure and the dimension of the measurement vector Y, unknown vector β, and matrix H in (4) are given in Appendix A.

Algorithm 1.

Lasso Iterative Identification Algorithm

1:	Given μ, tolerance δ, iteration j = 0,1,…, β0 = 0, and randomly chosen β1 = βinitial ▷ Initialization
2:	while |βj+1 − βj| ≤ δ do
3:	${\widehat{\sigma }}^2\leftarrow \frac{{\Vert Y-H{\beta }_{j+1}\Vert }_2^2}{n}$
4:	$\widehat{\beta }\leftarrow {\text{argmin}}_{\beta ,w}\frac{{\Vert Y-H\beta \Vert }_2^2}{2n\widehat{\sigma }}+\frac{\widehat{\sigma }}{2}$
	subject to
	||w||1 ≤ μ
5:	βj+1 ← β̂
6:	end while
7:	σ ← σ̂ and β ← β̂
8:	α, γ and ς ← Parameters of set 𝒲 from statistic of vector w,

There are several ways to estimate vector β. In the examples provided in this paper, lasso [11] is used as an identification tool. Assuming ℘ is the number of the patients, N is the length of the data from each patient, and n is the order of the system, this algorithm provides a way to determine an estimate of the parameters that balances the size of the noise ε ∞ 𝒩(0, σ²) and the sparsity of the exogenous perturbation w in the model. Note that there is also a balance between the order of the system and the size of the perturbation (magnitude, sparsity, and so on). Sparsity of signal w is crucial in this context, as it represents perturbations that a patient faces infrequently

$$\{\widehat{\beta },\widehat{\sigma }\}=\underset{\beta ,\sigma ,w}{argmin}\frac{{\Vert Y-H\beta \Vert }_2^2}{2n\sigma }+\frac{\sigma }{2}\text{s.t.}{\Vert w\Vert }_1\le \mu .$$ (5)

The optimization problem in (5) is a convex minimization of a penalized joint loss function with a regularization parameter μ given for the regression coefficient, noise level, and vector w, which is a finite dimensional signal.

The design matrix H and the response vector Y are constructed from measurements from ℘ different patients (see Appendix A). Since the problem is jointly convex with respect to β and σ, if the initial estimate of β is known or given, then σ, which minimizes the objective function, can be calculated by differentiating the objective function (5) with constant β vector (step 3 in Algorithm 1). Then, the optimization problem in step 4 in Algorithm 1 is solved to estimate vector β.

The following lasso algorithm shows the identification procedure in [11], where j shows the iteration number.

The terms in the objective function (5) aim at finding the maximum likelihood estimate of the parameters of the model and the variance of the noise ε while the ℓ₁ constraint searches for a sparse exogenous input. Here, the ℓ₁-norm is used as a convex approximation of the ℓ₀-norm [30]. Thus, given the data and the order of the model n, at the end of the identification algorithm, the parameters of the model in (2), the noise levels of ε ∞ 𝒩(0, σ²), and unmeasurable exogenous input w ∞ ℝ^℘(N−n) are estimated. Then, the statistic of identified vector w ∞ ℝ^℘(N−n) is used to define signal set 𝒲 in (3).

In the smoking cessation example, since an uncertain model is searched for all ℘ individuals (patients), all observations of ${\text{su}}_k^i,{\text{na}}_k^i$ and ${\text{se}}_k^i$ (i = 1, 2, …,℘) are used to construct the regression model (4). Again the mathematical details of model (1) for smoking cessation example are defined in Appendix A.

Finally, given a time interval of length K, output vector y is a function of uncertainties w ∞ ℒ^∞, ε ∞ 𝒩(0, σ²), and the state of the system. As mentioned earlier, w is a bounded sparse uncertainty and ε is Gaussian noise that models differences between different subjects. Now, to be able to design robust controllers, we need to have a bounded support set for ε.

Remark 2

Since Gaussian distributions have unbounded support, we choose a set of high probability. More precisely, given a window of size K, the density of ε_k:k+K−1 has hyperspherical contours and we take a set of high probability of the form

$${\Vert {\epsilon }_{k:k+K-1}\Vert }_2\le \rho$$ (6)

where ρ is chosen based on the identified standard deviation of the noise. This has the added advantage of leading to a formulation of the robust treatment design that is computationally tractable. We refer the reader to [31] for a more detailed discussion of the advantages of using this approach to describe this type of noise.

IV. Robust Model Predictive Controller

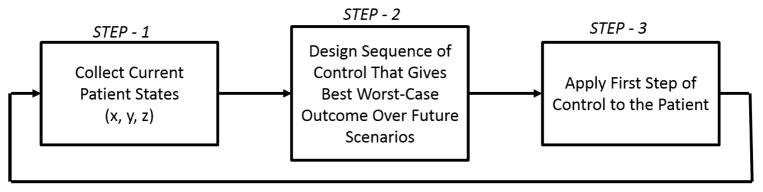
The method for controller design used in this paper is based on MPC [16]. Here, the usual approach in robust MPC is taken: one estimates the present value of the state variable and determines the value of the control variables over the horizon that minimizes a given objective function. The first of these control signals is applied, and the process is then repeated. The control algorithm is summarized in Fig. 1. In step 1, initial conditions or the information y_k−1 … y_k−n that the control algorithm will use is collected. In the smoking cessation study, this information is su_k−1 … su_k−n, na_k−1 … na_k−n, se_k−1 … se_k−n. In addition, after consultation with a practitioner in the field, the total treatment to be given to the patient is limited to an allowable set [32]–[34]. Such limitations might require the knowledge of how much treatment was given in the recent past. As a result, recent control input information T_k−1 …T_k−l (l ≥ n) is used in order to enforce the constraints on the total treatment provided.

Fig. 1.

Adaptive intervention algorithm.

Consistent with the usual MPC approach, in step 2, one minimizes a given cost function subject to constraints on the total applied control in a certain range. Then, in step 3, the result of the control algorithm is applied to the patient. Thus, in this section, a decision rule is developed that dictates whether treatment is applied to each individual at each time point under the uncertainties.

The difference equation (1) is used to determine a closed-form objective function for MPC formulation with a given receding horizon K. In the objective function, we represent 𝒴_k+1 ∞ ℝ^Km as

$${\mathcal{Y}}_{k+1}={\mathcal{A}}_f+\stackrel{\sim }{A}{\mathcal{Y}}_0+\stackrel{\sim }{B}{\stackrel{\sim }{\mathbf{T}}}_k+\stackrel{\sim }{D}\stackrel{\sim }{{\epsilon }_k}+\stackrel{\sim }{E}{\stackrel{\sim }{w}}_k$$ (7)

where 𝒴₀ ∞ ℝ^nm is the vector containing the state of the model. T̃ _k ∞ ℝ^K+n−1 is the treatment. w̃ _k ∞ ℝ^K is sparse disturbance and ε̃_k ∞ ℝ^K is noise. A_f, Ã, B̃, D̃, and Ẽ are matrices, which are calculated recursively from difference equation (1)

$$\begin{array}{ll}\hfill {\mathcal{Y}}_{k+1}& =\left[\begin{array}{c}{\mathbf{y}}_k\\ {\mathbf{y}}_{k+1}\\ ⋮\\ {\mathbf{y}}_{k+K-1}\end{array}\right],{\mathcal{Y}}_0=\left[\begin{array}{c}{\mathbf{y}}_{k-n}\\ {\mathbf{y}}_{k+1-n}\\ ⋮\\ {\mathbf{y}}_{k-1}\end{array}\right],{\stackrel{\sim }{\mathbf{T}}}_k=\left[\begin{array}{c}{\mathbf{T}}_{k-n}\\ {\mathbf{T}}_{k+1-n}\\ ⋮\\ {\mathbf{T}}_{k+K-2}\end{array}\right]\\ \hfill {\stackrel{\sim }{\mathbf{w}}}_k& =\left[\begin{array}{c}{\mathbf{w}}_{k-1}\\ {\mathbf{w}}_k\\ ⋮\\ {\mathbf{w}}_{k+K-2}\end{array}\right],{\stackrel{\sim }{\epsilon }}_k=\left[\begin{array}{c}{\epsilon }_{k-1}\\ {\epsilon }_k\\ ⋮\\ {\epsilon }_{k+K-2}\end{array}\right].\end{array}$$

Then, in this paper, the objective function of the following form is considered:

$$({\mathcal{Y}}_{k+1}-\theta )X{({\mathcal{Y}}_{k+1}-\theta )}^T$$

although more complex convex functions can be addressed by the framework presented here. For the smoking cessation example, since one minimizes smoking urge, matrix X is defined to choose smoking urge measure in vector 𝒴_k+1 as

$$X=\{\begin{array}{ll}1,\hfill & \text{if}{x}_{i,i}=k,k+m,k+2m,\dots ,k+(K-1)m\hfill \\ 0,\hfill & \text{otherwise.}\hfill \end{array}$$

Given the tuning parameter θ ∞ ℝ, approximation of desired average level of smoking urge, we aim to solve the following robust optimization problem at each step of the algorithm:

$$\underset{\mathbf{T}\in \mathcal{T}}{min}\underset{\begin{array}{l}{\Vert {\stackrel{\sim }{\epsilon }}_k\Vert }_2\le p\\ {\stackrel{\sim }{\mathbf{w}}}_k\in {\mathcal{W}}_k\end{array}}{max}({\mathcal{Y}}_{k+1}-\theta )X{({\mathcal{Y}}_{k+1}-\theta )}^T$$ (8)

which is subject to the system dynamics described in (7). We also define 𝒲_k from the set 𝒲 as

$${\mathcal{W}}_k=\{\text{vector}{\stackrel{\sim }{\mathbf{w}}}_k\in {ℝ}^K\text{satisfies}:{\Vert {\stackrel{\sim }{\mathbf{w}}}_k\Vert }_{\infty }\le \alpha ,{\Vert {\stackrel{\sim }{\mathbf{w}}}_k\Vert }_1\le \gamma ,{\Vert {\stackrel{\sim }{\mathbf{w}}}_k\Vert }_0=K/\varsigma \}.$$ (9)

The intersection of the norms in the set 𝒲_k forms convex polytopes. It should be noted that set 𝒲_k is a union of these convex polytopes; this fact is explored later when solving the robust optimization problem resulting from the MPC formulation of the control problem.

Smoking Cessation Example

We now discuss the set 𝒯 of allowable treatments used for the smoking cessation example. In this case

$$\mathcal{T}=\left\{\mathbf{T}:{\mathbf{T}}_{\eta }\in \{0,1\}\text{for}\eta =k,\dots ,k+K-1\text{and}\sum _{\eta =k-l}^{k+K-1}{\mathbf{T}}_{\eta }\le T_{\text{total}}\right\}$$ (10)

represent the fact that one can either apply or not apply treatment at each time. In addition, the number of treatments applied in the last K + l instances is constrained to be less than or equal to T_total. This constraint in the number of treatments is aimed at addressing the problem of treatment burden [32]–[34], which is decreasing effectiveness as the number of applied treatments increases. In this specific example, treatment T is binary; but in reality, it can have a different level and type of treatment.

One should note that the optimization problem described earlier is complex. Therefore, a problem equivalent to the original problem (8) is now presented that is suitable for implementation in Theorem 1. Using the results in [17]–[19] (provided in Appendix B for completeness), one can prove the following result.

Theorem 1

Consider the following semidefinite problem: min

$$\underset{\tau ,{\stackrel{\sim }{\mathbf{T}}}_k\in \mathcal{T},\lambda }{min}\tau \text{subject}\text{to}\left[\begin{array}{ccc}\tau -\lambda {\rho }^2& 0& \ast \\ 0& \lambda I& {(\stackrel{\sim }{D}X)}^T\\ ({\mathcal{A}}_f-\theta +\stackrel{\sim }{A}{\mathcal{Y}}_0+\stackrel{\sim }{B}{\stackrel{\sim }{\mathbf{T}}}_k+\stackrel{\sim }{E}{\stackrel{\sim }{\mathbf{w}}}_k)X& \stackrel{\sim }{D}X& I\end{array}\right]\ge 0$$ (11)

for all w̃ _k ∞ 𝒲_ext, where 𝒲_ext values are the extremes of the polytopes whose union is 𝒲_k.

The optimum of the problem above is an upper bound on the optimum of the original optimization problem (8) and is equal if only one of the elements in the set 𝒲_ext leads to an active constraint at the optimum.

In the LMI in (11), * is ((𝒜_f −θ+Ã𝒴₀+B̃T̃_k+Ẽw̃ _k)X)^T.

Proof

See Appendix C.

We now characterize the set of extremes, 𝒲_ext.

Theorem 2

Consider set 𝒲_k defined in (9), where α, γ, and ς define the bounds on the ℓ_∞-norm, ℓ₁-norm, and sparsity, respectively. Let n_nz = dim(w̃ _k)/ς.

1. If α ≥ γ, then 𝒲_ext is the set of all signed permutations of

   $$[\gamma \underset{K-1}{\underbrace{0\cdots 0}}].$$
2. If n_nzα ≤ γ, then 𝒲_ext is the set of all signed permutations of

   $$[\underset{n_{nz}}{\underbrace{\alpha \cdots \alpha }}\underset{K-n_{nz}}{\underbrace{0\cdots 0}}].$$
3. If γ < n_nzα < n_nzγ, then 𝒲_ext is the set of all signed permutations of

   $$[\underset{n_{+}}{\underbrace{\alpha \cdots \alpha }}h\underset{K-n_{+}-1}{\underbrace{0\cdots 0}}]$$
   where

   $$n_{+}=\lfloor \frac{\gamma }{\alpha }\rfloor \text{and}h=\gamma -n_{+}\alpha .$$

Proof

See Appendix D.

After finding the extreme points of the set 𝒲_k, a semidefinite programming or mixed integer semidefinite programming solver could be used to solve problem (11); but for a large receding horizon K, the number of extremes and, thus, the number of LMI constraints might be fairly large.

Section V presents a simulated application of the algorithm using a model that mimics data that might have been collected in smoking cessation studies, such as [25].

V. Simulation Results

A. Implementation

As an implementation of the adaptive treatment algorithm that is proposed for an intervention using portable devices, we consider individuals who wish to quit smoking, and we present a hypothetical algorithm for treatment via a smart phone. In addition, the quit day (i.e., day on which an individual quits smoking) and the time immediately following the quit day are extremely important on smoking cessation interventions and in the prevention of relapse. The simulations in this example address smoking dynamics after the quit day.

In the simulation, the participant provides information on his/her level of smoking urge, negative affect, and self-efficacy on the morning of day 1; the smart phone then provides the behavioral treatment. Robust adaptive treatment begins at midday after the participant again provides his/her level of smoking urge, negative affect, and self-efficacy. Right now, ${\text{su}}_0^i,{\text{na}}_0^i,{\text{se}}_0^i,{\mathbf{T}}_0^i$ and ${\text{su}}_1^i,{\text{na}}_1^i,{\text{se}}_1^i$ are known, where ${\mathbf{T}}_1^i$ is treatment provided in the morning. The proposed adaptive treatment algorithm is run and decides T^{i optimal} and set ${\mathbf{T}}_2^i={\mathbf{T}}^{i\text{optimal}}$. That is, if T^{i optimal} = 1, treatment is provided at midday; otherwise, it is not. Afterward, new ${\text{su}}_3^i,{\text{na}}_3^i,{\text{se}}_3^i$ are collected; then by using these new values and ${\text{su}}_2^i,{\text{na}}_2^i,{\text{se}}_2^i$, the process ${\mathbf{T}}_2^i$ is repeated to obtain ${\mathbf{T}}_3^i={\mathbf{T}}^{i\text{optimal}}$. This process is repeated throughout the entire course of treatment.

B. Identification Results

In order to test the performance of the approach presented in this paper, we emulate a real application. We develop a second-order (n = 2) model for smoking urge that approximates the behavior observed in empirical studies, such as [25]. Note that, in this paper, subjects smoke heavily. Therefore, the intervention is not expected to drive cravings to zero in this short-term program. Moreover, during the initial phase of treatment, the proposed algorithm aims to decrease smoking urge of patients as much as possible, while simultaneously reducing the amount of treatment. We aim to increase initial impact of treatment.

Here is the true model of smoking urge

$$\left[\begin{array}{c}{a}_f\\ a_0\\ a_1\\ b_0\\ b_1\\ c_0\\ c_1\end{array}\right]=\left[\begin{array}{c}1.06\\ .50\\ .35\\ .01\\ 0\\ -.12\\ -.09\end{array}\right],\left[\begin{array}{c}{d}_f\\ d_0\\ d_1\\ e_0\\ e_1\\ f_0\\ f_1\end{array}\right]=\left[\begin{array}{c}.15\\ .01\\ 0\\ .49\\ .25\\ -.05\\ 0\end{array}\right],\left[\begin{array}{c}{g}_f\\ g_0\\ g_1\\ h_0\\ h_1\\ r_0\\ r_1\end{array}\right]=\left[\begin{array}{c}.52\\ -.01\\ 0\\ -.02\\ 0\\ .49\\ .36\end{array}\right].$$

The studies mentioned earlier do not contain treatment. Hence, we augmented the model with a nonlinear effect of treatment in order to represent treatment burden. In the literature, the treatment burden is defined as increasing the level of treatment to the extent that it may cause suboptimal adherence and even negative outcomes. More information about treatment burden in social and medical sciences can be found in [32]–[34]. More precisely, the following terms were introduced:

$$\begin{array}{l}{q}_0{\mathbf{T}}_{k-1}+q_1\text{sig}\left[\sum _{u=k-44}^{u=k-2}{\mathbf{T}}_u\right]{\mathbf{T}}_{k-2}\\ s_0{\mathbf{T}}_{k-1}+s_1\text{sig}\left[\sum _{u=k-44}^{u=k-2}{\mathbf{T}}_u\right]{\mathbf{T}}_{k-2}\end{array}$$ (12)

where

$$\text{sig}(x)=\frac{1}{1+e^{-(x-17)}}.$$

sig(x) represents the sigmoid function or special case of logistic function. Then, the following parameter values are introduced:

$$[\begin{array}{cccc}{q}_0& q_1& s_0& s_1\end{array}]=[\begin{array}{cccc}-.2& .2& .2& -.2\end{array}].$$

This model for the effect of treatment is designed to emulate the case where the treatment has a positive impact, but its effectiveness decreases when the treatment is applied too frequently.

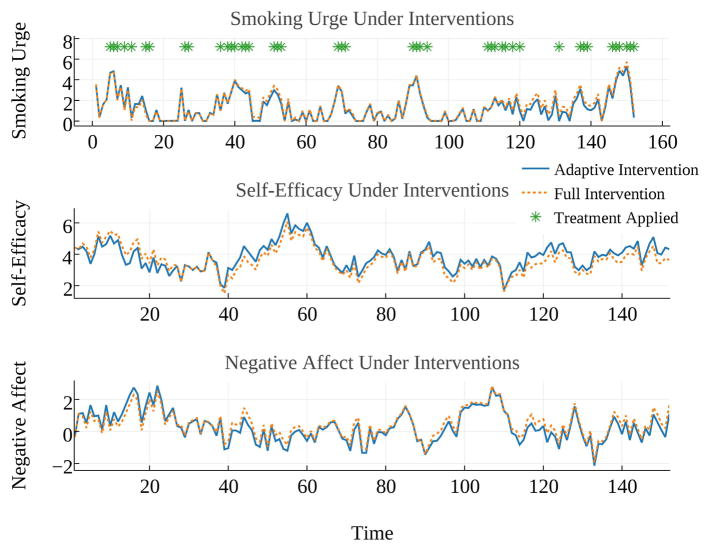
For this highly uncertain model, 500 different trajectories of the system are generated, with random initial conditions and random realizations of uncertainty. This is done to simulate the behavior of 500 subjects in a study where the treatment was provided at random times. Note that this is a reasonable surrogate for a study, since the model is designed to approximate real data, except for the influence of treatment. The model identification algorithm described in Section III is then applied, and a model to be used by the robust MPC algorithm was obtained. To validate the model, we can use the information in [26] and [27], showing that negative affect (na) increases smoking urge (se), where the sign of the coefficient of negative affect (na) is positive; self-efficacy (se) decreases smoking urge (su), where the sign of the coefficient of self-efficacy (se) is negative. These effects also can be seen in Fig. 3 and Table II. Moreover, the dynamical equations of negative affect and self-efficacy indicate that the effect of treatment is very small. This results in small improvement in smoking urge. However, this improvement is very important for heavy smokers at the beginning of the treatment process.

Fig. 3.

Smoking urge, negative affect, and self-efficacy under adaptive intervention.

TABLE II.

Intervention Performance of SDP

	Adaptive Treatment	No Robustness Treatment	Full Treatment	No Treatment
Mean(su)	1.31	1.36	1.46	1.51
Mean(se)	3.8412	3.76	3.6424	3.4863
Mean(na)	0.3096	0.3662	0.4571	0.5698
||su||2	22.55	23.32	24.48	25.15
${\sum }_{k=1}^{k=150}{\mathbf{T}}_k$	43	34	150	0

To do this, a model of the form (2) is used with order n = 2. The model coefficients obtained for a randomly chosen virtual patient are

$$\left[\begin{array}{c}{a}_f\\ a_0\\ a_1\\ b_0\\ b_1\\ c_0\\ c_1\end{array}\right]=\left[\begin{array}{c}1.11\\ .47\\ .34\\ .01\\ 0\\ -.10\\ -.08\end{array}\right],\left[\begin{array}{c}{d}_f\\ d_0\\ d_1\\ e_0\\ e_1\\ f_0\\ f_1\\ q_0\\ q_1\end{array}\right]=\left[\begin{array}{c}.13\\ .005\\ 0\\ .5\\ .24\\ -.05\\ 0\\ -0.207\\ 0.15\end{array}\right],\left[\begin{array}{c}{g}_f\\ g_0\\ g_1\\ h_0\\ h_1\\ r_0\\ r_1\\ s_0\\ s_1\end{array}\right]=\left[\begin{array}{c}.52\\ -.011\\ 0\\ -.02\\ 0\\ .49\\ .35\\ 0.202\\ -0.142\end{array}\right]$$

and the description of the uncertainty is, for robust MPC window of K = 8, the following: w̃_k has 25% nonzero terms with ||w̃_k||₁ ≤ 5 and ||w̃_k||_∞ ≤ 2.5. In order to obtain these parameters, the statistic of the identified w in Section III is used. As for Gaussian uncertainty, ε^su ∼ 𝒩(0, 1.3), ε^na ∼ 𝒩 (0, 0.78), and ε^se ∼ 𝒩 (0, 0.55) are identified. The sampling period here is 8 h and, hence, data are collected three times per day. The simulation is run for 50 days, and 150 data points are collected.

C. Experiments

We then applied the proposed controller in this paper to a nonlinear model mentioned earlier, again with randomly generated uncertainty/noise and the initial conditions given at Table I. In other words, we simulate the application of our robust MPC algorithm to a patient. The parameters used are specified as follows.

TABLE I.

Initial Condition of States and Input

su(0)	su(1)	se(0)	se(l)	na(0)	na(1)	T(0)	T(1)
3.521	0.346	4.428	4.324	−0.354	1.082	0	0

1. MPC window size: K = 8.

2. Constraints in control: T_k ∈ {0, 1} and

   $$T_{\text{total}}=\sum _{\eta =k-3}^{k+K-1}{\mathbf{T}}_{\eta }\le T_{\text{total}}=10/3.$$

   In other words, one either applies or does not apply treatment at each time point, and there is a constraint of a maximum of approximately one treatment per three sample times. Full treatment is defined as T_k = 1 for all values of k.

3. Objective function to be minimized

   $$\sum _{\eta =k+1}^{k+K}{(\text{su}(\eta )-2.2)}^2$$

   where the target value 2.2 was chosen, so that one has a significant decrease in the mean smoking value.

4. Bound on the two-norm of the Gaussian noise: ρ = 30.

5. Initial conditions of the states and input in Table I.

D. Simulations Results for a Patient

The optimization problem to be solved here is a mixed-integer, semidefinite convex problem. There are many ways to solve it, but in the simulations performed here, the requirement 𝒯 = T_k ∈ {0, 1} is relaxed to 𝒯 = T_k ∈ [0, 1] to use a general, semidefinite programming solver. The control applied is

$${\mathbf{T}}_k^{\text{applied}}=\text{round}({\mathbf{T}}_k).$$

The simulation was run for 150 time instances corresponding to a real time interval of 50 days. CVX is used with SeDuMi as the semidefinite programming solver to problem (11) [35]. The developed control law systematically improved smoking urge, since the treatment is only applied when needed. At the same time, our control law increased self-efficacy while reducing negative affect in order to reduce smoking urge. Table II represents a typical example of the results obtained.

Table II shows the performance of the adaptive treatment design in terms of objective function, average values of smoking urge, self-efficacy, negative affect, and total amount of treatment that the adaptive intervention applied. Moreover, to show the benefit of our robust adaptive intervention, the simulation is also done where controller design did not consider uncertainty (no robustness in Table II). Results indicated that the robust adaptive intervention applies the optimum amount of treatment to improve smoking urge, self-efficacy, and negative affect. The improvement in smoking urge is small, likely because this is a population of heavy smokers [25]. However, this improvement is extremely important at the beginning of the treatment process and leads to significant benefit in long term period. Note that this improvement was obtained with a minimized treatment effort. Therefore, one can see that there is a significant improvement in smoking urge not only in terms of the average but also in the fact that a consistent decrease in urge is obtained. If the treatment was more diverse than a binary signal [see the treatment set 𝒯 in (10)] (e.g., varying dosages), the controller benefits from adaptation would be greater.

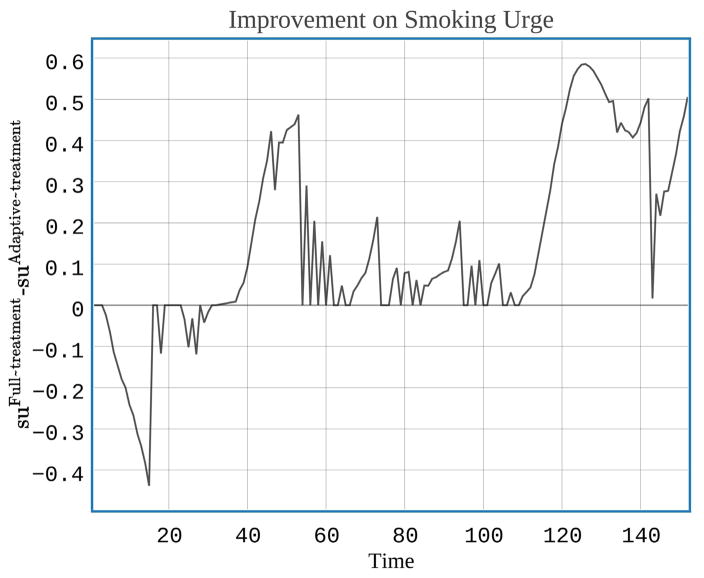
Fig. 2 shows decrease in smoking urge. In Fig. 2, su^{Full Treatment –} su^{Adaptive Treatment} is depicted, where su^{Adaptive Treatment} is smoking urge measured under the adaptive treatment and su^{Full Treatment} is smoking urge measured under the full treatment. Although the full treatment performs better than the adaptive treatment in the beginning of the treatment process, in the long term, the adaptive treatment works better, because the algorithm applies the treatment only when it is really needed, thus reducing treatment burden.

Fig. 2.

Performance of adaptive intensive intervention.

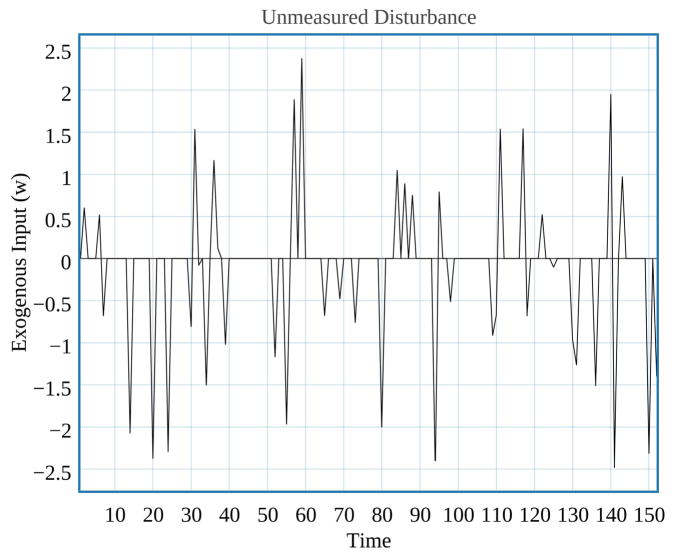
As expected, the algorithm carefully chooses when to apply treatment. It is mainly applied when external perturbations lead to a significant increasing trend in smoking urge. Finally, Fig. 3 shows the smoking urge, self-efficacy, and negative-affect measure of a virtual patient under both full treatment and adaptive intervention. Note that the responses shown in Fig. 3 are reflective of long-time, post-quit behavior. While important, this only represents a subset of the behavior stages seen in smoking cessation. Asterisks in Fig. 3 indicate when treatment is provided by the adaptive treatment algorithm. Fig. 4 shows the exogenous sparse disturbance that is applied to this particular patient for this simulation.

Fig. 4.

Sparse disturbance.

Remark 3

To be able to formulate the treatment design problem (11) as a convex optimization problem, in the simulations above, we replaced the constraint T_k ∈ {0, 1} by the relaxation T_k ∈ [0, 1]. Then, the treatment applied was round (T_k). To test the effectiveness of such relaxation, branch and bound techniques were used to solve the optimization problem under the true constraint T_k ∈ {0, 1}. The results obtained were similar and, hence, in this example, there is no advantage in solving the more complex mixed integer optimization problem.

E. SDP Results of a Population

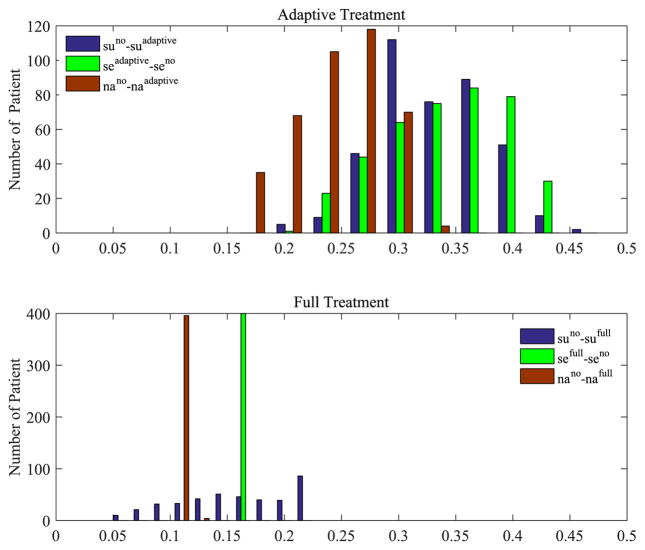
Since some of the parameters are as random in the simulation, the algorithm is run 400 times to estimate the average improvement in smoking urge, self-efficacy, and negative affect. The same parameters in Section V-C except that l = 6 in (10) are used to run the algorithm. Moreover, for the random parameters, the disturbances w̃_k are generated uniformly, such that w̃_k ∈ 𝒲_k . The Gaussian disturbances are generated under a normal distribution, such that ε^su ∼ 𝒩(0, 1.3), ε^na ∼ 𝒩 (0, 0.78), and ε^se ∼ 𝒩 (0, 0.55). For the initial conditions, su₀ ∈ 𝒰 (3.6, 0), se₀ ∈ 𝒰(4, 0), and na₀ ∈ 𝒰(2, 0) are generated. Fig. 5 shows average improvement in smoking urge (su^{No Treatment –} su^{Adaptive or Full Treatment}), self-efficacy (se^{Adaptive or Full Treatment –} se^{No Treatment}), and negative affect (na^{No Treatment –} na^{Adaptive or Full Treatment}). It is shown that the adaptive treatment increases self-efficacy while it decreases smoking urge and negative affect, even with less treatment. The average number of treatments provided is 54.6.

Fig. 5.

Adaptive and full treatment intervention results.

1. su^no, se^no, na^no: Smoking urge, self-efficiency, and negative affect without treatment.

2. su^full, se^full, na^full: Smoking urge, self-efficiency, and negative affect under full treatment.

3. su^adaptive, se^adaptive, na^adaptive: Smoking urge, self-efficiency, and negative affect with adaptive treatment.

VI. Conclusion

Behavioral and social scientists have been considering the advantages of adaptive treatments. Research has indicated that adaptive treatment strategies might give better results than fixed treatment (i.e., all patients get the same type and level of treatment) [12]. Since adaptive treatments usually provide better results than the usual methods, in this paper, we argue that control engineering methods, such as feedback or adaptation and robust optimization, can provide a systematic way to design a personalized treatment algorithm. Control engineering methods can be used to design personalized behavioral interventions while reducing treatment burden. Existing theory for adaptive treatment design is primarily qualitative and thus does not provide precise guidance regarding how much of which treatment treatment to provide to which individuals at what times. With this adaptive intervention design algorithm, treatments can be adapted and readapted in response to individuals’ progress over a long period of time. These methods hold promise for maintaining desired behavior in situations where controlling behavior is challenging due to complex dynamics. In terms of future work, effort is being put into developing more efficient numerical algorithms for solving the optimization problem for MPC. This will allow for the consideration of a larger receding horizon and, hence, better performance.

Nomenclature

ℕ

Natural numbers.

A

Matrix in ℝ^m×n.

A ≥ 0

Positive semidefinite matrix.

A^T

Transpose of the matrix A.

A_:,i

i^th column of matrix A.

I

Identity matrix in ℝ^m×m.

w

Signal in ℒ^∞.

w_k

kth element of signal w, w_k ∞ ℝ, and k = [1, 2, …, ∞].

w_(k:k+K−1)

Vector w_(k:k+K−1) ∞ ℝ^K that is segment of signal w: w_(k:k+K−1) =[w_k w_k+1 … w_k+K−1].

dim(w_(k:k+K−1))

Dimension of vector w_(k:k+K−1).

diag(w_(k:k+K−1))

Elements of vector w_(k:k+K−1) ∞ ℝ^K to the diagonal of a ℝ^K×K matrix.

⌊y⌋

Largest integer less than or equal to y.

𝒩(μ, σ²)

Standard Gaussian distribution with mean μ and variance σ².

||w_(k:k+K−1)||_p

p-norm of vector w_(k:k+K−1) that is: ${\Vert {\mathbf{w}}_{(k:k+K-1)}\Vert }_p\doteq {{}^p({\sum }_{i=k}^{k+K-1}{\mathbf{w}}_i^p)}^{1/2}$.

||w_(k:k+K−1)||₀

Number of the nonzero element of vector w_(k:k+K−1) that is ||w_(k:k+K−1) ||₀ ≐ #{i : w_i ≠ = 0}.

Biographies

Korkut Bekiroglu received the B.S. degree from the Department of Electrical and Electronics Engineering, Karadeniz Technical University, Trabzon, Turkey, in 2005, the M.S. degree from the Department of Electrical Engineering, Northeastern University, Boston, MA, USA, in 2010, and the Ph.D. degree from the Department of Electrical Engineering, The Pennsylvania State University, University Park, PA, USA, in 2010.

He is currently a Post-Doctoral Scholar with the Methodology Center, The Pennsylvania State University. His current research interests include the interface of system identification, longitudinal data analysis, robust control, robust model predictive controller design, robust interventions, adaptive treatment, discrete event dynamical systems, and robust optimization.

Constantino Lagoa received the B.S. and M.S. degrees from the Instituto Superior Técnico, Technical University of Lisbon, Lisbon, Portugal, in 1991 and 1994, respectively, and the Ph.D. degree from the University of Wisconsin-Madison, Madison, WI, USA, in 1998.

He joined the Electrical Engineering Department, The Pennsylvania State University, University Park, PA, USA, in 1998, where he is currently a Professor. His current research interests include robust optimization and control, chance constrained optimization, controller design under risk specifications, system identification, control of computer networks, and application of control approaches to the analysis and design of adaptive behavioral interventions.

Dr. Lagoa is an Associate Editor of the IEEE Transactions on Automatic Control and Automatica. He is also a member of the IFAC Technical Committee on Robust Control.

Suzan A. Murphy is currently the H.E. Robbins Distinguished University Professor of Statistics, a Professor of Psychiatry, and a Research Professor with the Institute for Social Research, Oslo, Norway. Her current research interests include improving sequential, individualized decision making in health, in particular on clinical trial design and data analysis to inform the development of mobile health treatment policies.

Ms. Susan is a fellow of the Institute of Mathematical Statistics, a fellow of The College on Problems in Drug Dependence, a Former Editor of the Annals of Statistics, a member of the U.S. National Academy of Sciences and the U.S. National Academy of Medicine, and a 2013 MacArthur Fellow.

Stephanie T. Lanza is currently a Professor of Biobehavioral Health and the Scientific Director of The Methodology Center with The Pennsylvania State University, University Park, PA, USA. She is currently involved in the areas of finite mixture modeling and time-varying effect modeling, and is devoted to disseminating cutting-edge statistical methods to applied researchers. Her current research interests include advancing analytic methods relevant for studying multidimensional and dynamic health behaviors.

Ms. Lanza is a Board Member of the Society for Prevention Research and an Associate Editor of the Prevention Science.

Appendix A. Formulation of the Identification Problem

In this section, we show how general equation (4) can be reorganized for the lasso algorithm. Start with the data set (su, na, se) of ℘ patients. Assume that for each i th patient, we have collected data set ${\text{su}}_k^i,{\text{na}}_k^i,{\text{se}}_k^i$ for k = 1, 2, . . . , N and i = 1, 2, . . . , ℘. Also assume that the order of the model n is given. Then, for each patient i , build the matrices in (13) and (14), shown at the bottom of this page.

Also, define

$$\begin{array}{ll}{\text{su}}^i\hfill & ={[\begin{array}{ll}{\text{su}}_{n+1}^i\hfill & {\text{su}}_{n+2}^i\cdots {\text{su}}_N^i\hfill \end{array}]}^T\text{where}{\text{su}}^i\in {ℝ}^{N-n}\hfill \\ {\text{na}}^i\hfill & ={[\begin{array}{ll}{\text{na}}_{n+1}^i\hfill & {\text{na}}_{n+2}^i\cdots {\text{na}}_N^i\hfill \end{array}]}^T\text{where}{\text{na}}^i\in {ℝ}^{N-n}\hfill \\ {\text{se}}^i\hfill & ={[\begin{array}{ll}{\text{se}}_{n+1}^i\hfill & {\text{se}}_{n+2}^i\cdots {\text{se}}_N^i\hfill \end{array}]}^T\text{where}{\text{se}}^i\in {ℝ}^{N-n}\hfill \end{array}$$

and

$$\text{SU}=\left[\begin{array}{c}{\text{su}}^1\\ {\text{su}}^2\\ ⋮\\ {\text{su}}^{\mathcal{P}}\end{array}\right]\text{NA}=\left[\begin{array}{c}{\text{na}}^1\\ {\text{na}}^2\\ ⋮\\ {\text{na}}^{\mathcal{P}}\end{array}\right]\text{SE}=\left[\begin{array}{c}{\text{se}}^1\\ {\text{se}}^2\\ ⋮\\ {\text{se}}^{\mathcal{P}}\end{array}\right]$$

$$X_{1,i}=\left[\begin{array}{cccccccccc}1& {\text{su}}_n^i& \mathrm{..}& {\text{su}}_1^i& {\text{na}}_n^i& \mathrm{..}& {\text{na}}_1^i& {\text{se}}_n^i& \mathrm{..}& {\text{se}}_1^i\\ 1& {\text{su}}_{n+1}^i& \mathrm{..}& {\text{su}}_2^i& {\text{na}}_{n+1}^i& \mathrm{..}& {\text{na}}_2^i& {\text{se}}_{n+1}^i& \mathrm{..}& {\text{se}}_2^i\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \\ 1& {\text{su}}_{N-1}^i& \mathrm{..}& {\text{su}}_{N-n}^i& {\text{na}}_{N-1}^i& \mathrm{..}& {\text{na}}_{N-n}^i& {\text{se}}_{N-1}^i& \mathrm{..}& {\text{se}}_{N-n}^i\end{array}\right]$$ (13)

$$X_{2,i}=\left[\begin{array}{ccccccccccccc}1& {\text{su}}_n^i& \mathrm{..}& {\text{su}}_1^i& {\text{na}}_n^i& \mathrm{..}& {\text{na}}_1^i& {\text{se}}_n^i& \mathrm{..}& {\text{se}}_1^i& T_n^i& \mathrm{..}& T_1^i\\ 1& {\text{su}}_{n+1}^i& \mathrm{..}& {\text{su}}_2^i& {\text{na}}_{n+1}^i& \mathrm{..}& {\text{na}}_2^i& {\text{se}}_{n+1}^i& \mathrm{..}& {\text{se}}_2^i& T_{n+1}^i& \mathrm{..}& T_2^i\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \\ 1& {\text{su}}_{N-1}^i& \mathrm{..}& {\text{su}}_{N-n}^i& {\text{na}}_{N-1}^i& \mathrm{..}& {\text{na}}_{N-n}^i& {\text{se}}_{N-1}^i& \mathrm{..}& {\text{se}}_{N-n}^i& T_{N-1}^i& \mathrm{..}& T_{N-n}^i\end{array}\right]$$ (14)

where SU ∈ ℝ^℘(N–n), NA ∈ ℝ^℘(N–n), and SE ∈ ℝ^℘(N–n)

$$X_1=\left[\begin{array}{c}{X}_{1,1}\\ X_{1,2}\\ ⋮\\ X_{1,\mathcal{P}}\end{array}\right]X_2=\left[\begin{array}{c}{X}_{2,1}\\ X_{2,2}\\ ⋮\\ X_{2,\mathcal{P}}\end{array}\right].$$

Finally, let

$$\begin{array}{ll}\hfill {\theta }_{\text{su}}& =[\begin{array}{llllllllllll}{a}_f\hfill & a_0\hfill & a_1\hfill & \cdots \hfill & a_n\hfill & b_0\hfill & \cdots \hfill & b_n\hfill & c_0\hfill & c_1\hfill & \cdots \hfill & c_n\hfill \end{array}]\hfill \\ \hfill {\theta }_{\text{na}}& =[\begin{array}{lllllllllllllllll}{d}_f\hfill & d_0\hfill & d_1\hfill & \cdots \hfill & a_n\hfill & e_0\hfill & e_1\hfill & \cdots \hfill & b_n\hfill & f_0\hfill & f_1\hfill & \cdots \hfill & f_n\hfill & q_0\hfill & q_1\hfill & \cdots \hfill & q_n\hfill \end{array}]\hfill \\ \hfill {\theta }_{\text{se}}& =[\begin{array}{lllllllllllllllll}{g}_f\hfill & g_0\hfill & g_1\hfill & \cdots \hfill & a_n\hfill & h_0\hfill & h_1\hfill & \cdots \hfill & b_n\hfill & r_0\hfill & r_1\hfill & \cdots \hfill & r_n\hfill & s_0\hfill & s_1\hfill & \cdots \hfill & s_n\hfill \end{array}]\hfill \\ \hfill \beta & ={[\begin{array}{cccc}{\theta }_{su}& {\theta }_{na}& {\theta }_{se}& w\end{array}]}^T\hfill \end{array}$$

where w is a w ∈ ℝ^℘(N–n) dimensional vector. Then, if all the patients satisfy the model provided in (2), we have

$$Y=H\beta$$ (15)

where Y ∈ ℝ^3℘(N–n), H ∈ ℝ^{3℘(N–n)×3(3n+1)+N}, and coefficient vector β ∈ ℝ^{(11n+3+℘(N–n))}

$$Y=\left[\begin{array}{c}SU\\ NA\\ SE\end{array}\right]H=\left[\begin{array}{cccc}{X}_1& 0& 0& I\\ 0& X_2& 0& 0\\ 0& 0& X_2& 0\end{array}\right]$$

and ε is a vector containing all noise.

Appendix B. Theorem in [17]–[19]

Theorem 3 [17]–[19]

Assume that the following problem is defined:

$$\varphi (A,b,x)\triangleq \underset{x}{min}\underset{\Vert \epsilon \Vert \le \rho }{max}{\Vert A(\epsilon )x-b(\epsilon )\Vert }_2^2.$$ (16)

Given A₀, . . . , A_p ∈ R^n×m, b₀, . . . , b_p ∈ R_n, and ε ∈ R^p, the following uncertainty structure can be defined:

$$A(\epsilon )\triangleq A_0+\sum _{i=1}^p{\epsilon }_i{A}_i,b(\epsilon )\triangleq b_0+\sum _{i=1}^p{\epsilon }_i{b}_i.$$ (17)

Then, for ρ ≥ 0, define

$$F(x)\triangleq [A_{1}x-b_1\dots A_{p}x-b_p].$$ (18)

The solution of the structured robust least square problem (16) can be calculated by solving the following semidefinite problem:

$$\underset{\tau ,x,\lambda }{min}\tau \text{s.t.}\left[\begin{array}{ccc}\tau -\lambda {\rho }^2& 0& {(A_{0}x-b_0)}^T\\ 0& \lambda I& F{(x)}^T\\ (A_{0}x-b_0)& F(x)& I\end{array}\right]\ge 0.$$ (19)

Appendix C. Proof of Theorem 1

Proof

We use the structure of 𝒴_k+1 in (7) to analyze the robustness of the optimization problem. Thus, 𝒴_k+1 in the objective function in (8) is replaced by 𝒴_k+1 in (7) as

$$\underset{\mathbf{T}\in \mathcal{T}}{min}\underset{\begin{array}{l}{\Vert {\stackrel{\sim }{\epsilon }}_k\Vert }_2\le \rho \\ {\stackrel{\sim }{\mathbf{w}}}_k\in {\mathcal{W}}_k\end{array}}{max}{\Vert ({\mathcal{A}}_f-\theta +\stackrel{\sim }{A}{\mathcal{Y}}_0+\stackrel{\sim }{B}{\stackrel{\sim }{\mathbf{T}}}_k+\stackrel{\sim }{D}\stackrel{\sim }{{\epsilon }_k}+E{\stackrel{\sim }{\mathbf{w}}}_k)X\Vert }_2^2.$$ (20)

Given objective function in (20), we can define vectors and matrix in (17) as

$$A_0=\stackrel{\sim }{B},A_i=0,b_0({\stackrel{\sim }{\mathbf{w}}}_k)={\mathcal{A}}_f-\theta +\stackrel{\sim }{A}{\mathcal{Y}}_0+\stackrel{\sim }{E}{\stackrel{\sim }{\mathbf{w}}}_k$$

and b_i = D̃_:,i .

Then, for fixed T̃_k and w̃_k, worst case residual is defined by using the methods in [18, Sec. 4] as

$$r_s{(A,b,{\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)}^2=\underset{{\Vert {\stackrel{\sim }{\epsilon }}_k\Vert }_2\le \rho }{max}{\Vert \stackrel{\sim }{B}{\stackrel{\sim }{\mathbf{T}}}_k-b(\epsilon ,{\stackrel{\sim }{\mathbf{w}}}_k)\Vert }_2^2$$

and from (18), define

$$\begin{array}{ll}\hfill M& \doteq F^{T}F,g({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)\doteq F^T(\stackrel{\sim }{B}{\stackrel{\sim }{\mathbf{T}}}_k-b_0)\hfill \\ \hfill h({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)& \doteq {\Vert \stackrel{\sim }{B}{\stackrel{\sim }{\mathbf{T}}}_k-b_0\Vert }_2^2.\hfill \end{array}$$

Then, without loss of generality, assuming ρ = 1 yields

$$r_s{(A,b,{\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)}^2=\underset{{\Vert {\stackrel{\sim }{\epsilon }}_k\Vert }_2\le 1}{max}{\left[\begin{array}{c}1\\ \epsilon \end{array}\right]}^T\times \left[\begin{array}{cc}h({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)& g{({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)}^T\\ g({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)& M\end{array}\right]\left[\begin{array}{c}1\\ \epsilon \end{array}\right].$$ (21)

Given τ ≥ 0, using the 𝒮-procedure [18, Lemma 2.1], (21) can be converted as

$${\left[\begin{array}{c}1\\ \epsilon \end{array}\right]}^T\left[\begin{array}{cc}h({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)& g{({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)}^T\\ g({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)& M\end{array}\right]\left[\begin{array}{c}1\\ \epsilon \end{array}\right]\le \tau$$ (22)

for every ε, ε^T ε ≤ 1 if and only if there exists a scalar λ ≥ 0, such that

$${\left[\begin{array}{c}1\\ \epsilon \end{array}\right]}^T\left[\begin{array}{cc}\tau -\lambda -h({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)& -g{({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)}^T\\ -g({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)& \lambda I-M\end{array}\right]\left[\begin{array}{c}1\\ \epsilon \end{array}\right]\ge 0$$ (23)

for every ε ∈ ℝ^p and fixed T̃_k and w̃_k .

Using the fact that λ ≥ 0 is implied by λI ≥ M, then the above condition can be rewritten as

$$\mathcal{F}(\tau ,\lambda ,{\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)\doteq \left[\begin{array}{cc}\tau -\lambda -h({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)& -g{({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)}^T\\ -g({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)& \lambda I-M\end{array}\right]\ge 0.$$

Then, the upper bound on the residual such that r_s (A, b, T̃_k,w̃_k)² ≤ τ can be obtained by solving the following optimization problem [18, Th. 4.1]:

$${\tau }^{\ast }=\underset{\tau ,\lambda }{min}\tau \text{s.t.}\left[\begin{array}{cc}\tau -\lambda -h({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)& -g{({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)}^T\\ -g({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)& \lambda I-M\end{array}\right]\ge 0$$ (24)

for all w̃_k ∈ 𝒲_k .

In addition, instead of checking all w̃_k ∈ 𝒲_k in LMI constraint (24), one can use the result in [36], which states that all the members of a polytope of matrices are positive semidefinite if and only if all extremes of the polytope are positive semidefinite. Furthermore, the set 𝒲_k is a union of sets bounded by polytopes. Using the same reasoning as in [36], it suffices for the LMI to be satisfied at the extremes of each of the polytopes. Therefore, we need to check all extremes of these polytopes. The LMI in (24) is satisfied in the convex hull of these extremes. It is just a consequence of the fact that an LMI is satisfied in a set of points; it is also satisfied in the convex hull of these points. Then, we have the following result:

$${\tau }^{\ast }=\underset{\tau ,\lambda }{min}\tau \text{s.t.}\left[\begin{array}{cc}\tau -\lambda -h({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)& -g{({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)}^T\\ -g({\stackrel{\sim }{\mathbf{T}}}_k,{\stackrel{\sim }{\mathbf{w}}}_k)& \lambda I-M\end{array}\right]\ge 0$$ (25)

for all w̃_k ∈ 𝒲_ext and forfixed T̃_k, where 𝒲_ext values are the extremes of the polytopes whose union is 𝒲_k . Hence, τ^* is an upper bound on the robust performance for fixed T̃_k .

For the optimality, assume that there is only one extreme w̃^* ∈ 𝒲_ext, such that one of the eigenvalues of LMI in (25) is equal to zero for some τ^* and λ^*, and LMI is positive definite for the rest of the extremes. Then, if the τ^* is not optimum, we can perturb τ^* or decrease it for this specific w̃^* ∈ 𝒲_ext while keeping the LMI still positive definite for the rest of the extreme points. This contradicts the assumption that τ^* is optimum. As a result, this optimization problem gives the optimum τ^* if only one of the extremes is an active constraint.

Thus, for every fixed T̃_k and for all w̃_k ∈ 𝒲_ext, the results in [18, Th. 4.2] or Theorem 3 can be used to convert problem (25) to (26) for ellipsoid uncertainty ||ε̃_k||₂ ≤ ρ and w̃_k ∈ 𝒲_k .

Finally, problem in (25) is modified as follows:

$$\underset{\tau ,{\stackrel{\sim }{\mathbf{T}}}_k\in \mathcal{T},\lambda }{min}\tau \text{s.t.}\left[\begin{array}{ccc}\tau -\lambda {\rho }^2& 0& \ast \\ 0& \lambda I& {(\stackrel{\sim }{D}X)}^T\\ ({\mathcal{A}}_f-\theta +\stackrel{\sim }{A}{\mathcal{Y}}_0)+\stackrel{\sim }{B}{\stackrel{\sim }{\mathbf{T}}}_k+\stackrel{\sim }{D}\stackrel{\sim }{{\epsilon }_k}+{\stackrel{\sim }{\mathbf{w}}}_k)X& \stackrel{\sim }{D}X& I\end{array}\right]\ge 0$$ (26)

for all w̃_k ∈ 𝒲_ext where again 𝒲_ext values are the extremes of the polytopes, whose union is 𝒲_k .

In this LMI, * is ((𝒜_f – θ; + Ã𝒴₀ + B̃ T̃_k + Ẽw̃_k)X)^T.

Appendix D. Proof of Theorem 2

The first two cases (α ≥ γ and n_nzα ≤ γ) are immediate, since they correspond to the cases where either ℓ₁ or ℓ_∞ is the only binding constraints. Hence, in this proof, we concentrate on the third case (γ < n_nzα < n_nzγ).

Note that, given the symmetry of the problem, we can concentrate on the subset of the elements of 𝒲_k that are positive and satisfy

$${\mathbf{w}}_{i+1}\le {\mathbf{w}}_i\text{for}\text{all}i=k:k+K-1,\text{and}{\mathbf{w}}_i\in {\stackrel{\sim }{\mathbf{w}}}_k.$$

All other extremes will be obtained from this by permutations and sign changes of the entries. Recall that, in this case, we are considering

$$\gamma <n_{nz}\alpha <n_{nz}\gamma$$

and the elements of vector w̃_k are in a nonincreasing order. Therefore, the extreme of the set is given by pushing as many of the first few elements as possible to their maximum value. Given that ||w̃_k||_∞ ≤ α and ||w̃_k||₁ ≤ γ, one can only have the first

$$n_{+}=\lfloor \frac{\gamma }{\alpha }\rfloor$$

elements of vector w̃_k equal to α. To reach the extreme and recalling that the entries of the vector w are in a nonincreasing order, the (n₊ + 1)th element of the vector must be at its maximum value. Given that ||w̃_k||₁ ≤ γ and the first N₊ terms are equal to α

$${\mathbf{w}}_{n+}+1\le \gamma -n_{+}\alpha .$$

Hence, for vectors with entries in a decreasing order, the extreme of the set is attained by a vector of the form

$$[\underset{n_{+}}{\underbrace{\alpha \cdots \alpha }}h\underset{K-n_{+}-1}{\underbrace{0\cdots 0}}].$$