Bone Remodeling as a Spatial Evolutionary Game

Abstract

Bone remodeling is a complex process involving cell-cell interactions, biochemical signaling and mechanical stimuli. Early models of the biological aspects of remodeling were non-spatial and focused on the local dynamics at a fixed location in the bone. Several spatial extensions of these models have been proposed, but they generally suffer from two limitations: first, they are not amenable to analysis and are computationally expensive, and second, they neglect the role played by bone-embedded osteocytes. To address these issues, we developed a novel model of spatial remodeling based on the principles of evolutionary game theory. The analytically tractable framework describes the spatial interactions between zones of bone resorption, bone formation and quiescent bone, and explicitly accounts for regulation of remodeling by bone-embedded, mechanotransducing osteocytes. Using tools from the theory of interacting particle systems we systematically classified the different dynamic regimes of the spatial model and identified regions of parameter space that allow for global coexistence of resorption, formation and quiescence, as observed in physiological remodeling. In coexistence scenarios, three-dimensional simulations revealed the emergence of sponge-like bone clusters. Comparison between spatial and non-spatial dynamics revealed substantial differences and suggested a stabilizing role of space. Our findings emphasize the importance of accounting for spatial structure and bone-embedded osteocytes when modeling the process of bone remodeling. Thanks to the lattice-based framework, the proposed model can easily be coupled to a mechanical model of bone loading.

1 Introduction

Bone remodeling is a complex mechano-biological process that is critical for maintenance of the healthy skeleton [1]. During bone remodeling, bone-resorbing osteoclasts remove old and damaged bone while bone-matrix producing osteoblasts generate new bone tissue to restore structural integrity, see Figure 1A. The recruitment of osteoclasts, and subsequently osteoblasts, is mediated by bone-embedded, mechano-sensing osteocytes, which translate load-induced mechanical strains into signals to control the adaptive remodeling process [2]. Disruption of the interactions between the key cellular components of remodeling can lead to pathological states. Such is the case in osteoporosis, where hormonal changes during menopause cause imbalances in the remodeling process and can lead to fracture-prone bones, and in Paget’s disease, a condition where bone undergoes cycles of uncontrolled resorption and formation [3].

Figure 1. Bone Remodeling as a Spatial Evolutionary Game.

(A) Bone remodeling is a complex multicellular process necessary for maintenance and adaptation of a healthy skeleton. Bone resorbing osteoclasts (purple) remove old and damaged bone (yellow), and osteoblasts (green, round) produce new bone matrix. Once osteoblasts have completed their task of producing new bone, they either die or become embedded in the bone tissue where they differentiate into osteocytes (green, star-shaped). Osteocytes are connected through a complex network and are thought to play an integral role in sensing bio-mechanical stimuli and translating them into chemical signals to orchestrate the remodeling process by osteoclasts and osteoblasts. (B). In the spatial setting, the expansion rate of a zone (center) is determined by the constitution of its neighbors and the corresponding interaction strengths ḡ_XY. Note that ḡ_XY quantifies the expansion rate contribution of a zone of type Y to a zone of type X. The contributions are additive, see equation (1). (C) The pay-off matrix G = (g_ij) of the non-spatial evolutionary game specifies the interaction network between resorption (R), formation (F) and quiescence (Q). Note that the expansion rate and payoff matrices are related by Ḡ = 1 + ωG.

Over the past decade, there has been a surge in quantitative modeling of the cellular processes and signaling pathways that regulate bone remodeling. The first such models, developed by Lemaire [4], Komarova [5, 6], and colleagues, focused on the temporal dynamics of remodeling at a fixed location in the bone. Based on systems of ordinary differential equations (ODE), these models successfully described the interactions between osteoclasts and osteoblasts and the resulting bone mass balance. The original ODE models have since been applied and extended by various authors, see e.g. the work by Pivonka, [7], Buenzli [8], Ji [9], and colleagues. For further references, as well as an overview of modeling studies with focus on the mechanical aspects of remodeling, we refer to the review articles [10,11].

While ODE models provide valuable insights into the complex dynamics of physiological and pathological bone turnover, they are not able to capture salient spatial features of the remodeling process [12]. In fact, the latter takes place on the complex geometries of cortical and trabecular bone, and paracrine signaling between bone cells, which is mediated by soluble chemokines, allows for non-local regulation [13]. To model such non-local phenomena, our group [14–16] and others [17, 18] previously developed partial differential equation (PDE) models of bone remodeling. In addition, discrete agent-based models of the spatial remodeling dynamics were introduced to study the dynamics of individual remodeling units [19–21]. Spatial aspects of the remodeling biology are also captured in various biomechanical models of bone adaptation [22–24].

These spatial extensions of the original ODE models are endowed with high-dimensional parameter spaces and their analyses rely on computer simulations. In consequence, to gain mechanistic insights and understand which model components are relevant to regulate and maintain physiological remodeling, systematic and extensive parameter space explorations are necessary, and a complete characterization of the dynamic regimes is generally beyond reach. Furthermore, most spatial models focus on osteoclast and osteoblast dynamics only, while treating bone as a passive constituent that is either resorbed and deposited by the two active players of the process. Based on experimental evidence [25,26] however, it has become clear that quiescent bone and embedded, mechanotransducing osteocytes play a key role in the regulation of remodeling.

In view of the above limitations of current spatial models, our objective was to develop a spatial model of bone remodeling biology that (i) is amenable to analysis and complete classification in the sense of the original, reductionist ODE model by Komarova and colleagues [5]; and (ii) treats quiescent bone and embedded osteocytes as an active part of the remodeling dynamics. We focused on trabecular remodeling and developed our model in the framework of evolutionary game theory (EGT). The latter was introduced by Maynard Smith in 1982 [27], and has since been used to study a wide range of systems in biology and ecology [28–31]. The analysis of spatial EGT models poses substantial technical difficulties and is a field of active research. Recent advances by Cox, Durrett and Perkins [32] and Durrett [33] on the weak selection limit for EGTs enabled the analyses in this article.

2 Methods

2.1 Spatial Model

We start by introducing the general idea, and then proceed to construct the formal process. To model physiological remodeling of trabecular bone (Figure 1A) in a discrete spatial setting, we partition the volume of trabecular bone into zones of bone resorption, bone formation and quiescent bone. Zones of resorption are populated by bone matrix degrading osteoclasts, and zones of formation are populated by osteoid producing osteoblasts. Quiescent zones on the other hand consist of bone matrix and embedded osteocytes. We then allow the different zones to interact in a probabilistic manner, resulting in growing and shrinking patches of resorption, formation and quiescence. For example, if a zone of formation (osteoblasts) is adjacent to a zone of quiescence (bone), then the zone of formation is expected to convert to a zone of quiescence, consisting of newly formed bone with embedded osteocytes. Conversely, if a zone of quiescence (bone) is adjacent to a zone of resorption (osteoclasts), the former is expected to vanish and be replaced by the expanding zone of resorption. The resulting process is an evolutionary competition between neighboring zones. Due to the complex interactions between cell types, the probability of each zone to invade or to be invaded depends on the make-up of its neighborhood.

To formally construct this spatial evolutionary process, we consider a fixed bone volume and partition it into a regular three-dimensional lattice with N elements. Each element is occupied by one of the three zones, and the zones are labeled as type 1 (resorption), type 2 (formation) and type 3 (quiescence). There is flexibility with respect to the physical size attributed to the lattice elements. However, the side length of each element needs to be larger than the size of individual osteoclasts because they are the largest bone cells and measure approximately 50 microns in diameter [34]. In addition, the lattice elements should be small enough to allow for sufficient spatial resolution of the process.

Following the principles of spatial EGT, see also [33], we now introduce the dynamics of the system as a continuous-time Markov process on the lattice. First, we denote by ξ_t(x) ∈ {1, 2, 3} the type occupying lattice element x at time t. Next, for each element x on the lattice and time t, we introduce an instantaneous expansion rate ψ_t(x) (referred to as its fitness in EGT), which specifies the elements’ exponentially distributed waiting time until expansion. At the time of expansion, the expanding element places an identical copy of itself onto a neighboring element, chosen uniformly at random. The instantaneous expansion rate of x is determined by the make-up of its surrounding elements,

$${\psi }_t(x)=\sum _{y~x}\overline{G}({\xi }_t(x),{\xi }_t(y)),$$ (1)

where y ~ x denotes the set of nearest neighbors of x, and Ḡ is a 3×3 matrix whose entries specify the stochastic expansion rates. In other words, Ḡ (i, j), also denoted as ḡ_ij, is the expansion rate of a type-i zone in the presence of a type-j zone, see Figure 1B. For example, ḡ₁₂ is the additive expansion rate of a resorption zone in presence of a formation zone, and ḡ₃₁ is the expansion rate conferred to a quiescent zone by a formation zone. When element x expands, one of its nearest neighbors y is chosen uniformly at random and its resident type, ψ_t(y), is replaced by the resident type ψ_t(x) at element x. Each element has its own instantaneous expansion rate, which depends on the constituency of its neighbors through (1), and elements with higher expansion rates tend to take over their neighbors, whereas less proliferative elements in turn are eliminated by their expanding neighbors.

In order to enable systematic analyses of the spatial game, the expansion rate matrix is rewritten as Ḡ ≡ 1 + ωG, where 1 is the 3 × 3 matrix consisting of all 1’s, and G = (g_ij) is a real-valued matrix with possibly negative entries. As explained in section 3.1, the resulting dynamics are a perturbation of the standard voter model, and a rigorous analysis of the system is possible in the weak selection limit as ω → 0. Finally, we point out that the matrix G corresponds to the classical pay-off matrix of the non-spatial evolutionary game; its entries capture the positive and negative interactions between the model constituents as shown in Figure 1C.

2.2 Parameter Considerations

Taking into consideration established knowledge about the biology of bone remodeling, we can make a priori restrictions on the 9-dimensional parameter space defined by the pay-off matrix G. These constraints are summarized and justified in Table 1. Furthermore, because subtracting g₁₁ from the first column in G affects neither the non-spatial replicator dynamics nor the weak selection limit of the spatial game [33], we will henceforth consider the transformed matrix G,

Table 1. Parameter Constraints.

Top: Summary of the a priori constraints on the model parameters g_ij based on published biological findings. g_ij quantifies the impact of a zone of type j on a zone of type i. Bottom: The resulting constraints for α_i and β_i.

Parameter	Constraint	Justification	References
g11	> 0	Autocrine stimulation by TNF-α, IL-1α	[35,36]
g12	∈ ℝ	Net impact depends on RANKL/OPG balance	[13,37]
g13	> 0	Release of matrix-embedded growth factors; osteocyte-derived RANKL stimulation	[25,26,38]
g21	> 0	Paracrine stimulation by TGF-β, IGF	[39,40]
g22	= 0	Presumed negligible	[14]
g23	< 0	Wnt-Sclerostin signaling, considered inhibitory.	[41,42]
g31	< 0	Osteoclasts resorb bone	[38]
g32	> 0	Osteoblasts produce bone matrix and become embedded osteoctyes	[43]
g33	= 0	Osteocytes are terminally differentiated and do not produce or resorb bone	[44]
α1	< 0	α1 = g23	-
α2	< 0	α2 = g31 − g11	-
α3	∈ ℝ	α3 = g12	-
β1	> 0	β1 = g32	-
β2	> 0	β2 = g13	-
β3	∈ ℝ	β3 = g21 − g11	-

$$G=\left(\begin{array}{ccc}0& {\alpha }_3& {\beta }_2\\ {\beta }_3& 0& {\alpha }_1\\ {\alpha }_2& {\beta }_1& 0\end{array}\right),{\alpha }_1,{\alpha }_2<0,{\beta }_1,{\beta }_2>0,{\alpha }_3,{\beta }_3\in ℝ,$$ (2)

see Table 1 for the definitions of α_i and β_i in terms of the g_ij.

2.3 Replicator Dynamics of Non-spatial Model

Spatial models are more difficult to analyze than their temporal counterparts and analyses rely on extensive simulations. Therefore, an important question in every spatial modeling study is the necessity to account for space explicitly. To address this issue, we introduce here the non-spatial version of the evolutionary game model. This version neglects spatial structure and assumes that the distinct trabecular zones are well-mixed and thus all equally likely to interact with each other. Instead of analyzing the fully stochastic system, we notice that the number of lattice elements in a bone is large (assuming a diameter of 50 – 100 microns), and hence we can study the problem in the deterministic limit as N → ∞. In this approximation, the non-spatial EGT dynamics are described by the standard replicator dynamics from EGT [27]. Formally, we denote by x(t):= (x₁(t), x₂(t), x₃(t)) ≥ (0, 0, 0) the densities of resorptive (x₁), formative (x₂) and quiescent (x₃) zones, respectively, with x₁ + x₂ + x₃ ≡ 1 at all times t ≥ 0. Then, as N → ∞, the non-spatial dynamics of the well-mixed system are described by the replicator equations

$${\stackrel{.}{x}}_1={\varphi }_G^i(x)\equiv x_i[F_i(x)-\langle F\rangle (x)],i=1,2,3,$$ (3)

where F_i(x):= (Gx)_i is the expansion rate of species i, and 〈F〉(x):= x^T Gx is the average expansion rate of the entire population [27]. The interior fixed point for the replicator dynamics (3), if it exists, is given by

$$\begin{array}{l}{\rho }_1=({\beta }_1{\beta }_2+{\alpha }_1{\alpha }_3-{\alpha }_1{\beta }_1)/D\\ {\rho }_2=({\beta }_2{\beta }_3+{\alpha }_1{\alpha }_2-{\alpha }_2{\beta }_2)/D\\ {\rho }_3=({\beta }_1{\beta }_3+{\alpha }_2{\alpha }_3-{\alpha }_3{\beta }_3)/D,\end{array}$$ (4)

where D is the sum of the three numerators. The dynamics of the replicator equation (3) are discussed in Appendix A.

2.4 Numerics

All model simulations were performed using the software MatLab (Version 8.5.0, The MathWorks Inc. 2015). The built-in Runge-Kutta solver ode45 was used to solve the deterministic replicator equations. For the fully spatial model, we used a Gillespie algorithm to simulate the stochastic process on a cubic lattice with L³ nodes and periodic boundary conditions. Initial fields were generated using a product measure as specified in the figure captions.

3 Results

In this section, we first analyze the fully spatial model, classify its dynamic regimes and identify zones in parameter space that allow for coexistence of resorption, formation and quiescence. It is important to emphasize that coexistence refers to global coexistence in the sense that all three types are present on the lattice although only one type can be present locally in one lattice element. We then study emerging spatial structure based on three-dimensional simulations of the evolutionary process. Finally, we compare the non-spatial and spatial versions of the game.

3.1 The Spatial Game

The spatial game dynamics are determined by the fitness function ψ_t(x) in equation (1), with transformed pay-off matrix Ḡ = 1 + ωG, where G is the pay-off matrix (2) and ω > 0 is small enough so that all entries of Ḡ are positive. The resulting dynamics are a perturbation of the well-studied voter model, see e.g. [45]. Thanks to recent theoretical results by Cox, Durrett and Perkins [32] and Durrett [33], the behavior of the spatial stochastic model can be analyzed in the weak selection limit. More precisely, if we let ω → 0 and simultaneously shrink space by ~ ω² and speed up time by ~1/ω, then the temporal evolution of the density of species i at location x, denoted by u_i(x, t), evolves according to the PDE

$$\frac{\partial u_i(x,t)}{\partial t}=\frac{1}{6}\mathrm{\Delta }{u}_i(x,t)+{\varphi }_H^i(u(x,t)).$$ (5)

Here, u = (u₁, u₂, u₃), Δ is the Laplace operator in ℝ³, and ${\varphi }_H^i$ is the rate of change on the right-hand side of the replicator equation (3), with the pay-off matrix G replaced by H defined as [33]

$$H_{ij}=G_{ij}+\theta (G_{ii}+G_{ij}-G_{ji}-G_{jj}).$$

The constant θ cannot be calculated exactly, but numerical simulations estimate θ ≈ 0.485 [33]. In terms of α_i and β_i, the explicit expression of the H matrix is

$$H=\left(\begin{array}{ccc}0& (1+\theta ){\alpha }_3-\theta {\beta }_3& (1+\theta ){\beta }_2-\theta {\alpha }_2\\ (1+\theta ){\beta }_3-\theta {\alpha }_3& 0& (1+\theta ){\alpha }_1-\theta {\beta }_1\\ (1+\theta ){\alpha }_2-\theta {\beta }_2& (1+\theta ){\beta }_1-\theta {\alpha }_1& 0\end{array}\right),$$ (6)

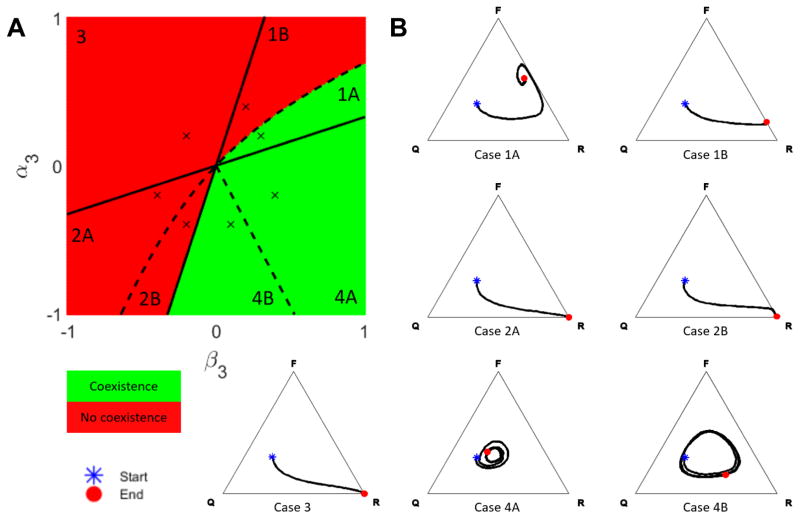
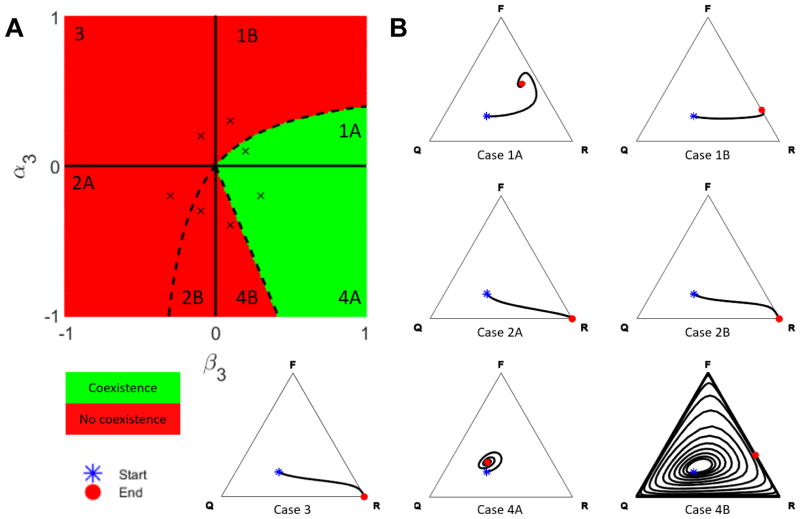
with the following constraints imposed by (2): h₁₃, h₃₂ > 0, h₂₃, h₃₁ < 0, and h₁₂, h₂₁ ∈ ℝ. In addition to the limiting behavior of the PDE (5), there are analytic coexistence results for ω finite but small enough [32]. Details of the complete analysis are found in Appendix B, and the results are summarized in Figure 2A, where the phase diagram is projected onto the (α₃, β₃)-plane, distinguishing zones of three-species coexistence (green) and lack of coexistence (red). Because we were not able to determine the qualitative behavior of all 7 scenarios based on theoretical results, we ran representative three-dimensional simulations to confirm the conjectured behavior in each case, see Figure 2B.

Figure 2. Coexistence in the Spatial Model.

(A) Phase diagram showing regions of coexistence (green) and lack of coexistence (red) in the (α₃, β₃)-plane. The (×) mark the parameter choices for the examples in panel B; the remaining model parameters were set to α₁ = −0.1, α₂ = −0.5, β₁ = 0.6, β₂ = 0.2, θ = 0.485, ω = 0.1. (B) For each case in panel A, a realization of the spatial stochastic process is simulated on a cubic lattice of side length L = 100 over 2 · 10⁹ iterations (corresponding to ≈ 2000 time units). At simulation Start, the field is seeded using a product measure with probabilities 0.2 (R), 0.3 (F) and 0.5 (Q), respectively. The resulting trajectories are visualized in ternary plots and terminate at the End symbol. The values of α₃ and β₃ are indicated by (×) in panel A, and all remaining parameters as specified above.

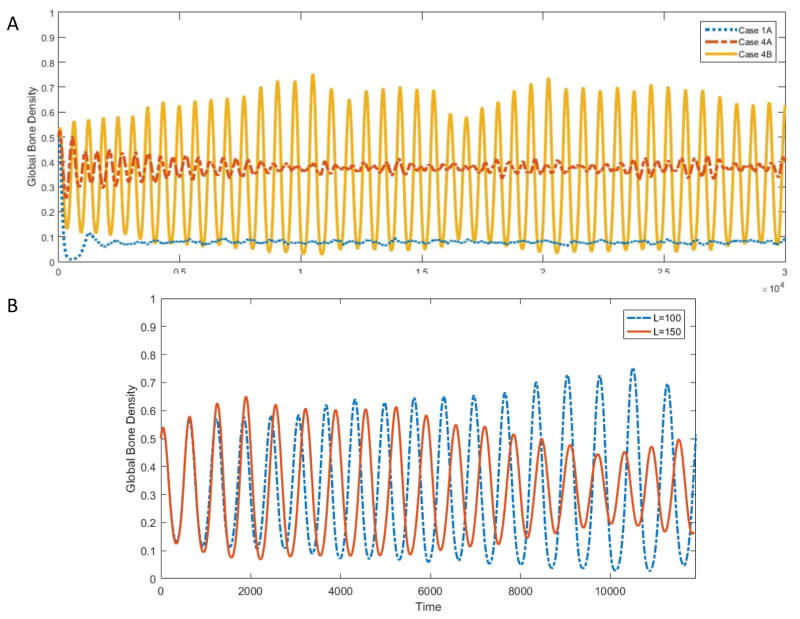
As illustrated in Figure 2A, the phase transition from no coexistence (red) to coexistence (green) occurs across the boundaries between Cases 2B and 4A, and Cases 1A and 1B, respectively. The slope of the linear boundary between Cases 2B and 4A is uniquely determined by the parameters α₃ (osteoblast-derived regulation of osteoclasts) and β₃ (difference between osteoclast-derived stimulation of osteoblasts and osteoclast-derived autocrine stimulation). In contrast, the nonlinear shape of the boundary between Cases 1A and 1B depends on all model parameters, see Appendix B for details. In the regions of no coexistence, there is either complete takeover by resorption (Cases 2A, 2B and 3) or the system converges to a stable resorption-formation equilibrium (Case 1B), see Figure 2B. Among cases with three-species coexistence, Case 1A converges to a fixed point in the interior of the simplex, whereas Cases 4A and 4B exhibit irregular oscillations that are bounded away from the edges of the simplex, see Figure 3A. Increasing the domain size was found to attenuate the oscillations in Case 4B, see Figure 3B.

Figure 3. Bone Density Evolution in Coexistence Regime.

(A) For Cases 1A, 4A and 4B, which all exhibit long-term coexistence (see Figure 2A), the evolution of the global bone density is shown over time. In Case 1A, the bone density quickly approaches its steady state value. In Case 4A and 4B, the system undergoes bounded oscillations. In all simulations, θ = 0.485, ω = 0.1, and remaining parameters as follows: Case 1A α₁ = −0.1, α₂ = −0.5, α₃ = 0.2, β₁ = 0.6, β₂ = 0.2, β₃ = 0.3; Case 4A: α₁ = −0.1, α₂ = −0.5, α₃ = −0.2, β₁ = 0.6, β₂ = 0.2, β₃ = 0.4; Case 4B: α₁ = −0.1, α₂ = −0.5, α₃ = −0.4, β₁ = 0.6, β₂ = 0.2, β₃ = 0.1. (B) For Case 4B, the process is simulated for two domain sizes, L = 100 and L = 150, respectively. Remaining parameters: θ = 0.485, ω = 0.1, α₁ = −0.1, α₂ = −0.5, α₃ = −0.4, β₁ = 0.6, β₂ = 0.2, β₃ = 0.1.

3.2 Emerging Spatial Structure

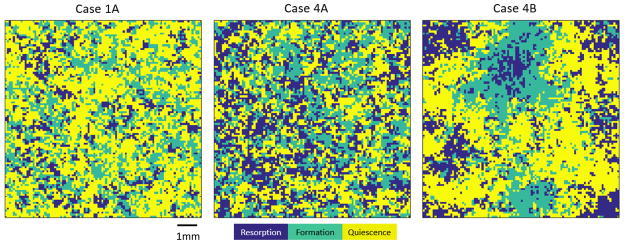
Next we sought to characterize the spatial structure of the evolutionary game in regimes that allow for three-species coexistence, i.e. Cases 1A, 4A and 4B. To this end, we performed stochastic simulations of the three-dimensional evolutionary process and visualized 2D sections as shown in Figure 4. Starting from randomly distributed initial conditions, we observed the emergence of spatial clustering of the three coexisting species. The resulting clusters of bone tissue, surrounded by zones of formation and resorption, are reminiscent of the sponge-like patterning in vertebrate trabecular bone.

Figure 4. Spatial Structure of Coexistence.

For each of the three cases that allow for coexistence in the spatial game (see Figure 2A), a realization of the stochastic process was simulated on a cubic lattice of side length L = 100. The initial field is seeded using a product measure with probabilities 0.2 (R), 0.3 (F) and 0.5 (Q), respectively, and representative 2D cross sections (size: 100 × 100 elements) of the 3D systems are shown after reaching the stationary state. The size of individual lattice elements is not directly specified (see text), but expected to be of the order of 100 microns, as indicated by the bar in the figure. All remaining model parameters as follows. Case 1A α₁ = −0.2, α₂ = −0.1, α₃ = 0.45, β₁ = 0.5, β₂ = 0.1, β₃ = 0.6; Case 4A: α₁ = −0.1, α₂ = −0.5, α₃ = −0.3, β₁ = 0.6, β₂ = 0.3, β₃ = 0.4; Case 4B: α₁ = −0.6, α₂ = −0.6, α₃ = −0.4, β₁ = 0.6, β₂ = 0.2, β₃ = 0.4.

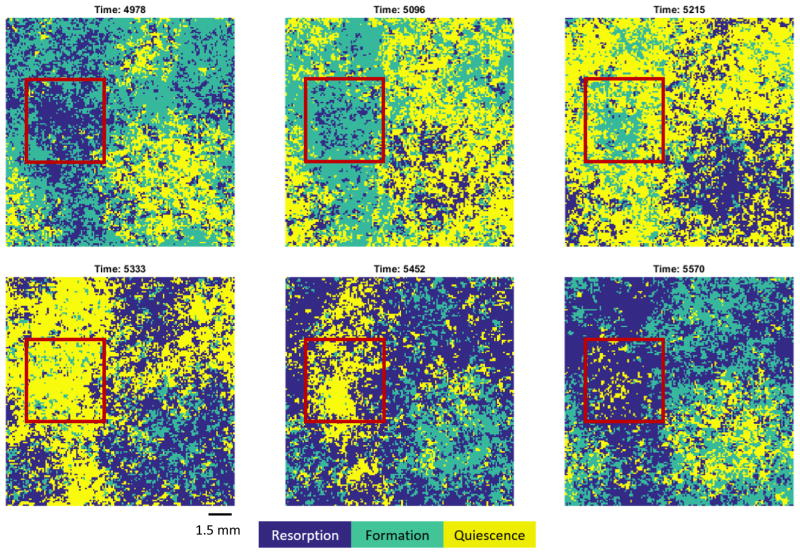
In Section 3.1 we saw that Case 1A reaches a global equilibrium state, whereas Cases 4A and 4B exhibit long-time oscillatory behavior, see also Figure 3. Case 4B is particularly interesting with respect to emerging spatial structure. In fact, following a fixed volume within the same bone section over time, see the red frame in Figure 5, we found that the patch was cyclicly dominated by formation, quiescence and resorption. As we will see in Section 3.3, these local dynamics are consistent with the outward spiraling trajectories of the associated replicator dynamics. However, because the total volume consists of many such asynchronously cycling patches, the global dynamics become stabilized and exhibit the bounded behavior shown in Figure 3. Overall, this example illustrates how spatial structure can fundamentally alter the dynamics, and we turn our attention now to a systematic exploration of the role of spatial structure in bone remodeling.

Figure 5. The Local Dynamics of Case 4B.

Successive 2D sections of the unstable rock-paper-scissors game (Case 4B, see Figure 2A) are shown. A realization of the stochastic process was simulated on a cubic lattice of side length L = 150, with initial field seeded using a product measure with probabilities 0.2 (R), 0.3 (F) and 0.5 (Q). Identical 2D sections (size: 150 × 150 elements) of the 3D domain are shown at times 4978, 5096, 5215, 5333, 5452, and 5570, respectively. The size of individual lattice elements is not directly specified (see text), but expected to be of the order of 100 microns, as indicated by the bar in the figure. Locally, see red frame, the system is cyclicly dominated as it transitions from primarily resorptive (time 4978) to primarily bone forming (time 5096), to primarily quiescent (time 5333) and back to primarily resorptive (time 5570). Because the total volume consists of asynchronously cycling patches, the global dynamics remain bounded, see also Figures 2B and 3. Remaining parameter values: θ = 0.485, ω = 0.1, α₁ = −0.6, α₂ = −0.6, α₃ = −0.4, β₁ = 0.6, β₂ = 0.2, β₃ = 0.4.

3.3 The Role of Space in Bone Remodeling

To enable a direct comparison between the spatial game and the replicator dynamics of the non-spatial version, we first need to analyze the replicator dynamics.

Replicator Dynamics

Similarly to the spatial case, analysis of the replicator dynamics of the non-spatial game revealed seven dynamic regimes, see Appendix A for details. Figure 6A illustrates the coexistence regions in a phase diagram projected onto the (α₃, β₃)-plane, and Figure 6B provides a concrete example for each case. As seen in Figure 6A, a necessary condition for coexistence is β₃ = g₂₁ − g₁₁ > 0, which means osteoclast-derived paracrine stimulation of osteoblasts (g₂₁) dominates osteoclast-derived autocrine stimulation (g₁₁). If this condition is not satisfied, i.e. β₃ < 0, resorption outperforms formation and the global bone density continues to decrease until it vanishes, see Cases 2A, 2B and 3 in Figure 6B. On the other hand, if β₃ > 0, then coexistence is possible for specific parameter combinations, namely Cases 1A and 4A. The boundaries between physiological and pathological regimes (dashed lines between Cases 1A/1B and 4A/4B, respectively) depend on the values of the remaining model parameters in a nonlinear fashion. These boundaries specify upper and lower bounds for α₃ that allow for physiological remodeling, and coexistence is possible for a range of both negative and positive values. In case 4B, the system cycles through resorption-, formation- and quiescence-dominated regimes and spirals towards the boundary of the simplex, see Figure 6B.

Figure 6. Coexistence in the Non-Spatial Model.

(A) Phase diagram showing regions of coexistence (green) and lack of coexistence (red) in the (α₃, β₃)-plane. The (×) mark the parameter choices for the examples in panel B; the remaining parameters were fixed at α₁ = −0.1, α₂ = −0.5, β₁ = 0.6, β₂ = 0.2. (B) For each case in panel A, the replicator dynamics are solved up to t = 2000, with initial conditions (x₁(0), x₂(0), x₃(0)) = (0.3, 0.2, 0.5). The values of α₃ and β₃ are indicated by (×) in panel A, and all remaining parameters as specified above.

Comparison to Spatial Dynamics

Comparing the phase diagram of the spatial game in Figure 2A to its non-spatial counterpart in Figure 6A, we make several observations. First, the four uniform quadrants corresponding to Cases 1, 2, 3 and 4 of the non-spatial game are transformed into two larger (Cases 3 and 4) and two smaller (Cases 1 and 2) sections in the spatial game. It follows that for a given parameter set, the dynamics of the non-spatial version can be fundamentally different from the dynamics of the spatial version. This is particularly striking in Case 4B, which is unstable in the non-spatial setting, but becomes stabilized in the spatial setting: instead of spiraling outward towards the boundary of the simplex in absence of spatial structure (see Case 4B in Figure 6B), the system remains confined to the interior of the simplex in the spatial model (see Case 4B in Figures 2B and 3). Due to this stabilizing effect of space, the entire Case 4 allows for coexistence in the spatial setting. In other words, spatial structure stabilizes the dynamics.

4 Discussion

The remodeling of trabecular bone is an intrinsically spatial process regulated by complex cellular and biochemical processes. To date, most mathematical models of the biological and biochemical mechanisms of remodeling have been formulated in non-spatial settings. Existing spatial generalizations of these models suffer from two shortcomings: they are high-dimensional and not amenable to systematic analyses and they do not account for the the role played by bone-embedded osteocytes. In this work, we sought to overcome these limitations by developing a three-dimensional evolutionary game theory model of bone remodeling that explicitly accounts for bone-embedded osteocytes.

The proposed model describes the nonlinear interactions between zones of resorption, formation and quiescence in a reductionist framework and is amenable to analysis in both the spatial and non-spatial settings. Direct comparison between spatial (Figure 2A) and non-spatial (Figure 6A) models revealed the existence of parameter space regions that lead to coexistence of resorption, formation and quiescence in the spatial setting, but not in the well-mixed setting (see Case 4B). This emphasizes the critical role of spatial structure in enabling physiological remodeling regimes, and highlights the necessity to use fully spatial models when seeking to elucidate the biological mechanisms of the process.

Case 4B, also known as the unstable rock-paper-scissors game [27], is a particularly interesting scenario. In the non-spatial scenario it was found to be unstable with alternating periods of resorption-, formation- and quiescence-dominated states, reminiscent of the uncontrolled episodes of resorption and formation in Paget’s disease [3, 46]. In the spatial setting on the other hand, cyclic turnover of the three types remained present within spatially separated patches, but due to asynchronous cycling of the patches, the overall dynamics became stabilized. Based on the reasoning by Durrett and Levin [47] and simulations (Figure 3B), we conjecture that the cyclic behavior may be a finite size effect and would eventually disappear for sufficiently large domain sizes. Such properties of non-hierarchical competition models in spatial settings, and the role of space in dynamic multi-species models in general, have long been acknowledged in the mathematical ecology literature [47, 48]. To our knowledge, we are the first to directly address this issue in the context of bone remodeling.

By performing systematic model analyses we identified parameters critical for maintaining physiological remodeling in the sense of three species coexistence. As shown in the phase diagram in Figure 2A, two parameters are particularly important for coexistence: β₃ (= g₂₁ − g₁₁), which is the balance between osteoclast-derived stimulation of osteoblasts and osteoclast-derived autocrine stimulation, and α₃ (= g₁₂), which represents osteoblast-derived regulation of osteoclasts. In the spatial game, coexistence is ensured whenever β₃ > 0 and α₃ < 0, as well as a small extension of this quadrant, see Cases 4A and 4B in Figure 2A. The first constraint, β₃ > 0, emphasizes the importance for osteoclasts to effectively recruit osteoblasts after resorption has been completed; deficiencies in this mechanism lead to loss of coexistence due to unbalanced bone resorption. The second constraint, α₃ < 0, requires there to be a negative feedback from osteoblasts to osteoclasts in order to avoid immediate resorption of newly formed tissue. If this constraint is violated, osteoclasts invade zones of formation and trigger onset of pathological remodeling. This is in alignment with our previous findings regarding the critical role of the spatial expression profiles of RANKL and its inhibitor OPG, by which osteoblasts control resorptive activity [14–16]. Finally, a note about the role of the remaining model parameters. As long as α₃ and β₃ satisfy the Case 4 constraints, coexistence is guaranteed independent of the values of α₁, α₂, β₁, and β₂. However, for α₃ and β₃ satisfying the Case 1 constraints, these four parameters determine the shape of the boundary between coexistence (1A) and lack thereof (1B), see dotted line in Figure 2A. Most importantly, all six model parameters play a role in determining the quantitative outcome of the spatial game, and hence the bone density in the stationary state of the system.

Previously, Dingli and colleagues [49] used a non-spatial EGT model to study the interactions between multiple myeloma cells, osteoclasts and osteoblasts. Their underlying model of bone remodeling (in absence of multiple myeloma cells) leads to different conclusions, even if analyzed in the spatial context. In fact, it is easy to show that the Dingli model allows for physiological remodeling only in Cases 1A and 1B of Figure 6A (see Section 6 of [33]). In particular, it exhibits pathological remodeling in the entire lower right quadrant, which was found to exhibit stable coexistence in the three-player game thanks to the presence of osteocyte regulation. While there is insufficient experimental evidence to test these differential predictions, recent experimental [25,26] and theoretical work [50–52] has emphasized the importance of osteocyte-derived regulation of remodeling.

The model developed in this study captures the dynamics of the cellular interactions between osteoclasts, osteoblasts, and bone-embedded osteocytes in a reductionist, low-dimensional framework. Importantly, in order to enable systematic analyses of the models, we made a number of simplifying assumptions about the model structure. In future work, it will be important to address the sensitivity of the model to different functional forms of the interaction terms. Furthermore, we only considered nearest neighbor interactions between lattice elements, and an investigation of the impact of long-range interactions that account for diffusive cytokines poses an interesting research question. Another important aspect for future efforts is a full mechano-biological extension of the model. In fact, we did not account for mechanical loading, which plays an important role in guiding the overall bone remodeling process [1]. However, thanks to the lattice-based formulation of the evolutionary game model, it can easily be coupled to a mechanical loading model, especially within the continuum mechanics framework developed by Hellmich and colleagues [53, 54] and Scheiner and colleagues [55], or the lattice-based approach by Weinkamer and colleagues [56]. In this context, it would be interesting to further investigate the observed clustering dynamics of bone tissue under different regimes of loading, and to characterize the clustering length scales. Finally, the current model constitutes a stepping stone to the study of stromal cells in physiological and pathological remodeling, and the interactions between bone and cancer cells in metastatic bone cancer and multiple myeloma.

A Analysis of the Non-Spatial Game

To analyze the replicator equation (3) on the simplex defined by x(t) ≥ 0 and x₁(t)+x₂(t)+x₃(t) = 1, we first analyze the three subgames that take place on the edges of the simplex: resorption-formation, resorption-quiescence, and formation-quiescence. Denoting by G = (g_ij), i, j ∈ {a, b} the pay-off matrix of a generic two-player game with players a and b of densities x_a and x_b, respectively, the interior fixed point, if it exists, is located at

$${\overline{x}}_a=\frac{g_{12}-g_{22}}{g_{12}-g_{22}+g_{21}-g_{11}},{\overline{x}}_b=1-{\overline{x}}_a.$$

Subgame 1: Resorption (r) vs Formation (f). From (2), the subgame pay-off matrix between resorption and formation is

$$\left(\begin{array}{cc}0& {\alpha }_3\\ {\beta }_3& 0\end{array}\right),$$ (7)

with potential interior fixed point ${\overline{x}}_r=\frac{{\alpha }_3}{{\alpha }_3+{\beta }_3}$. Since there are no a priori restrictions on α₃ and β₃ (see Table 1), we distinguish between four different cases. (i) α₃ > 0 and β₃ > 0: in this case, there is an interior fixed point, and by noticing that x_r evolves according to (3),

$$\frac{{dx}_r}{dt}=x_r(1-x_r)({\alpha }_3-({\alpha }_3+{\beta }_3)x_r),$$ (8)

we find that x̄_r is attracting. (ii) α₃ < 0 and β₃ < 0; in this case there is an interior fixed point, and by (8) it is repulsive. (iii) α₃ > 0 and β₃ < 0: in this case there is no interior fixed point, and resorption will take over. (iv) α₃ < 0 and β₃ > 0: in this case there is no interior fixed point, and formation will take over.

Subgame 2: Resorption (r) vs Quiescence (q). The pay-off matrix of this subgame is

$$\left(\begin{array}{cc}0& {\beta }_2\\ {\alpha }_2& 0\end{array}\right).$$ (9)

Recalling that α₂ < 0, β₂ > 0 (Table 1), we find ${\overline{x}}_r=\frac{{\beta }_2}{{\beta }_2+{\alpha }_2}\notin (0,1)$, which means there is no interior fixed point. In addition, the evolution equation for resorption is

$$\frac{{dx}_r}{dt}=x_r(1-x_r)({\beta }_2-({\beta }_2+{\alpha }_2)x_r),$$ (10)

which means x̄_r = 1 is globally attracting. This is consistent with the biology because as long as there are active osteoclasts attached to the bone matrix, the latter should be completely resorbed.

Subgame 3: Formation (f) vs Quiescence (q). The pay-off matrix is

$$\left(\begin{array}{cc}0& {\alpha }_1\\ {\beta }_1& 0\end{array}\right),$$ (11)

and the evolution equation for formation is

$$\frac{{dx}_f}{st}=x_f(1-x_f)({\alpha }_1-({\alpha }_1+{\beta }_1)x_f).$$ (12)

Due to the parameter restrictions α₁ < 0 and β₂ > 0 from (2), there is no interior fixed point: ${\overline{x}}_f=\frac{{\alpha }_1}{{\alpha }_1+{\beta }_2}\notin (0,1)$. We note that the resulting attractive fixed point at x̄_f = 0 is consistent with the biology which requires zones of formation to produce new bone.

Now that we have a complete understanding of the subgame dynamics, we can investigate the three-player game. An important concept in this analysis is the notion of invadability of edge fixed points [57], which ascertains whether a small addition of player 3 can invade the edge equilibrium between players 1 and 2 or not. Because Durrett [33] previously characterized the dynamic regimes relevant to this analysis, we follow his notation and refer to his proofs where possible. On occasion, we will also refer to the work of Bomze [58,59] who has provided a complete characterization of the the replicator dynamics on the simplex.

Due to the parameter restrictions listed in Table 1, there are a total of seven different dynamic regimes to be discussed below. The corresponding partition of parameter space in the plane spanned by α₃ and β₃, together with examples of trajectories for all seven cases, are shown in Figure 2.

Case 1

α₃ > 0 and β₃ > 0. On the resorption-formation edge of the simplex, there is an attracting edge equilibrium at $({\overline{x}}_1,{\overline{x}}_2,{\overline{x}}_3)=\left(\frac{{\alpha }_3}{{\alpha }_3+{\beta }_3},\frac{{\beta }_3}{{\alpha }_r+{\beta }_3}\right)$ and $\langle F\rangle =F_1=F_2=\frac{{\alpha }_3{\beta }_3}{{\alpha }_3+{\beta }_3}$. We distinguish two subcases depending on whether quiescence can invade this equilibrium or not. According to (3), invadability is possible if the expansion rate of quiescence exceeds the average expansion rate in the system, F₃ > 〈F〉, which is equivalent to

$${\alpha }_2{\alpha }_3+{\beta }_1{\beta }_3-{\alpha }_3{\beta }_1>0.$$ (13)

• Case 1A. If condition (13) is satisfied, quiescence can invade the resorption-formation equilibrium, and there is an attracting interior fixed point, see Example 7.3 in [33].

• Case 1B. If condition (13) is not satisfied, quiescence cannot invade the resorption-formation equilibrium, and there is no interior fixed point; all trajectories converge onto the resorption-formation equilibrium, see example 7.3.D in [33].

Case 2

α₃ < 0 and β₃ < 0. There is a repelling equilibrium on the resorption-formation edge. First, we note that the numerator of ρ₁ in (4) is positive. The numerator of ρ₃ is positive if and only if condition (13) is satisfied, which is equivalent to

$$\frac{{\alpha }_2}{{\beta }_3}>1-\frac{{\beta }_1}{{\alpha }_3}.$$ (14)

Similarly, the numerator of ρ₂ is positive if and only if β₂β₃ + α₁α₂ − α₂β₂ > 0, which is equivalent to

$$\frac{{\beta }_3}{{\alpha }_2}<1-\frac{{\alpha }_1}{{\beta }_2}.$$ (15)

• Case 2A. If condition (14) is satisfied, α₂/β₃ > 1. This implies that (15) is satisfied, too, and hence there is an interior fixed point. This is the time-reversed case 15 in [58], which means the interior fixed point is unstable and the vertex (1, 0, 0) is globally attracting.

• Case 2B. If condition (14) is not satisfied, the numerator of ρ₃ is negative, whereas the one of ρ₁ remains positive. In consequence, there is no interior fixed point. This corresponds to the time-reversal of case 41 in [58], and (1, 0, 0) is again the global sink.

Case 3

α₃ > 0 and β₃ < 0. In this case, there are no edge fixed points, and resorption will take over, see Example 7.4.A in [33].

Case 4

α₃ < 0 and β₃ > 0. In this case, the game matrix is a generalized Rock-Paper-Scissors game. There is an interior fixed point, and its stability is determined by the sign of Δ = β₁β₂β₃ + α₁α₂α₃, see example 7.4 in [33].

• Case 4A. If Δ > 0, then there is an interior fixed point, and the solutions spiral inwards toward the fixed point.

• Case 4B. If Δ < 0, then the system is unstable and the boundary of the simplex is a limit cycle.

Note that if Δ = 0, there is a 1-parameter family of periodic orbits, but this is on a set of measure zero in parameter space, so we are not concerned with this case.

B Analysis of the Spatial Game

To characterize the dynamics of the spatial game, we need to analyze the limiting behavior of the system in the weak selection limit, characterized by the PDE (5). Since the behavior of this equation is determined by the structure of the modified pay-off matrix H, we first analyze the local dynamics specified by the nonlinear reaction term ϕ_H in (5). In other words, we study the behavior of equation (3) where we replace G by H. Based on these local analyses, and where possible, we then refer to the general theory for proofs about coexistence in the fully spatial equation (5). For cases where we cannot rigorously prove coexistence (or lack thereof), we will rely on the local analyses to make conjectures. The latter are then corroborated by means of extensive computer simulations, see Figure 2. Analyzing first the embedded two-player games as in the non-spatial scenario (see Appendix A), it is straightforward to establish that quiescence dominates formation, and resorption dominates quiescence. The outcome of the resorption-formation game depends on the respective signs of h₁₂ and h₂₁, which are determined by

$$h_{12}>0\iff {\alpha }_3>{\beta }_3\frac{\theta }{1+\theta }$$

and

$$h_{21}>0\iff {\alpha }_3<{\beta }_3\frac{1+\theta }{\theta }.$$

Case 1

If h₁₂, h₂₁ > 0, then as in Case 1 of the non-spatial game, there is an attracting fixed point on the resorption-formation edge, and we are interested in the invadability of this edge equilibrium. The latter is determined by the invadability condition

$$h_{12}{h}_{31}+h_{21}{h}_{32}>h_{12}{h}_{21}.$$ (16)

• Case 1A. If condition (16) is satisfied, the resorption-formation equilibrium of the H-matrix replicator dynamics is invadable. It follows from the theory developed in [33] that there is an interior attracting fixed point for the spatial game, see Example 7.3 in Section 8.3 of [33].

• Case 1B. If condition (16) is not satisfied, the resorption-formation equilibrium is not invadable, and the H-matrix replicator dynamics do not admit coexistence of all three species. We conjecture that the same conclusion holds for the spatial game, but we are not able to explicitly prove this assertion. Nevertheless, simulations corroborate the conjecture, see Figure 2B.

Case 2

If h₁₂, h₂₁ < 0, then the resorption-formation subgame has a repelling fixed point, with two possible cases:

• Case 2A. If (16) is satisfied, the boundary equilibrium is invadable, and there is no interior fixed point for the H-matrix replicator dynamics. In the spatial game, we conjecture takeover off resorption, and simulations support this hypothesis, see Figure 2B.

• Case 2B. If (16) is not satisfied, the boundary equilibrium is not invadable, and there is an unstable interior fixed point. Again, we conjecture takeover by resorption in the spatial game, and corroborate the conjecture by simulation, see Figure 2B.

Case 3

If h₁₂ > 0 and h₂₁ < 0, then the resorption-formation subgame is dominated by resorption. We conjecture take-over by resorption in the spatial game and corroborate this by simulation, see Figure 2B.

Case 4

If h₁₂ < 0 and h₂₁ > 0 then the H-matrix dynamics constitute a generalized Rock-Paper-Scissor game, and the outcome of the temporal dynamics is determined by the sign of Δ:= h₁₃h₂₁h₃₂ + h₁₂h₂₃h₃₁.

• Case 4A. If Δ > 0, there is an attracting interior fixed point for the H-matrix replicator dynamics. While it seems intuitive that this leads to coexistence in the spatial case a proof is out of reach. We corroborated our hypothesis by simulation, see Figures 2B and 3.

• Case 4B. If Δ < 0, then the interior fixed point is unstable, and the solutions to the H-matrix replicator dynamics spiral outwards (with the boundary of the simplex as a limit-cycle). Following the discussion of non-hierarchical competition models by Durrett and Levin [47], we conjecture long-time coexistence in the spatial game. Simulations corroborated this hypothesis, see Figures 2B and 3.