Discharge decision-making after complex surgery: surgeon behaviors compared to predictive modeling to reduce surgical readmissions

Structured Abstract

BACKGROUND

Little is known about how information available at discharge affects decision-making and its effect on readmission. We sought to define the association between information used for discharge and patients’ subsequent risk of readmission.

METHODS

2009–2014 patients from a tertiary academic medical center’s surgical services were analyzed using a time-to-event model to identify criteria that statistically explained the timing of discharges. The data were subsequently used to develop a time-varying prediction model of unplanned hospital readmissions. These models were validated and statistically compared.

RESULTS

The predictive discharge and readmission regression models were generated from a database of 20,970 patients totaling 115,976 patient-days with 1,565 readmissions (7.5%). 22 daily clinical measures were significant in both regression models. Both models demonstrated good discrimination (C statistic = 0.8 for all models). Comparison of discharge behaviors versus the predictive readmission model suggested important discordance with certain clinical measures (e.g., demographics, laboratory values) not being accounted for to optimize discharges.

CONCLUSIONS

Decision-support tools for discharge may utilize variables that are not routinely considered by healthcare providers. How providers will then respond to these atypical findings may affect implementation.

INTRODUCTION

The Centers for Medicare and Medicaid Services (CMS) have placed increased scrutiny on hospital readmissions.(1–3) As mandated by the Patient Protection and Affordable Care Act, CMS has begun adjusting hospital payments through the Hospital Readmissions Reduction Program according to hospitals’ rate of “excess” vs. “expected” Medicare readmissions for pneumonia, acute myocardial infarction and heart failure with a future planned expansion into surgical patients.(2, 4–7) Previous estimates suggest that even a small reduction of 5% in readmission rates could prevent over 2,000 inpatient hospitalizations with Medicare cost savings of $31 million.(8)

One of the surgeon’s most challenging clinical decisions is balancing the need to promptly discharge patients versus a clinical and financially incentivized goal of reducing readmissions.(8–10)

Balancing countervailing needs has often been addressed through the use of risk-based modeling and decision-support tools. The financial implications of readmissions have also led to many scientific inquiries into risk-adjusted predictions for readmission. A recent systematic review found 26 unique models of readmission employing a variety of data sources and types of inpatient populations.(11) An ongoing limitation of these prediction tools has been the decreasing statistical discrimination of models when broadening patient populations to include surgical patients, especially those undergoing a wide variety of procedures.(11–15)

We believe that improving discharge decision-making via evidence-based decision-support tools will lower readmissions while maintaining or decreasing LOS. This approach requires two central elements: (a) statistical identification of variables that discriminate between likelihood of discharge and likelihood of subsequent readmission; and (b) development of decision-support software that can aid discharge decision-making by effectively operationalizing this risk-adjusted understanding of readmission into the clinical provider’s daily work.

We sought to develop a data-driven predictive model for surgical readmission to identify the association between clinical information used for discharge decision-making and patients’ subsequent risk of readmission. Retrospective, large-data analysis of a prospectively collected clinical data warehouse was used in a time-to-event model aiming at identifying criteria that (statistically) explain timing of inpatient postoperative discharge. Subsequent development of a prediction model of readmission with validation helps identifying dissonant criteria across postoperative discharges and readmissions. Specifically, we researched possible discordance between intrinsic human behavior and optimized modeling with the assumption that such discordance could interfere with future uptake of decision-support tools. In particular, we wanted to identify differences in how surgeons behave in practice and how a predictive model of readmission might improve discharge decision-making.

MATERIALS AND METHODS

Patient Population

De-identified patient data from all patients undergoing inpatient general (including gastrointestinal, endocrine, skin and soft tissue) and vascular surgical procedures between 2009 and 2014 were obtained from the academic medical center’s clinical data warehouse. Both elective and emergency cases were included and controlled for in the models described below. Patients who were dead at discharge were excluded. This dataset included all electronically collected information during the patient’s admission including demographic information, procedures performed, medications administered, laboratory test results, diagnostic imaging, and nursing documentation. Readmissions were captured by repeat encounters within 30 days of index admission. Outside hospital encounters that did not result in a transfer back to the index hospital could not be obtained.

Designing Discharge and Readmission Models with Validation

Time-varying and fixed data for all patients were analyzed using a time-to-event regression model to identify significant time-point predictors of discharge on a given hospital day and a logit regression model to identify significant predictors of readmission. With the exception of the dummy variables, standardized values of all independent variables were used in both models. Both models included 23 procedural grouping variables (e.g., colectomy, hepatectomy, ventral hernia repair) to control for the type of procedure performed. In addition, we created a dummy variable (“PreOptimize”) to control for patients who were admitted for a surgical procedure with the procedure delayed beyond the initial day of admission.

A Cox survival model was used for time-point (i.e., daily) discharge predictions allowing for different baseline hazards across procedures. Time-varying variables were grouped for analysis by hospital day. Variables reported more than once daily (up to 3) were averaged. Patients with a missing variable on the hospital day examined had the last known observed value of that variable carried over (i.e., step imputation). If a variable was never recorded for the entire hospital stay, the normalized value (i.e., mean of the upper and lower limit) of that variable within the population was used for all hospital days. Using other methods of imputation did not meaningfully change the predictive factors of the model. A logit model with procedure-fixed effects was used to model readmissions using data from the day prior to discharge; a time-to-event specification for readmissions was not possible without time-point data following discharge. All explanatory variables were selected for using stepwise Akaike information criterion thresholds, which also accounted for Type I multiple testing error.(16)

Both models were validated via a series of in-sample and out-of-sample tests using bootstrapped, partitioned patient data and C statistic test for discrimination. Iterations were conducted with a 90% in-sample and 10% out-of-sample partition, 70% in-sample and 30% out-of-sample partition, and a 50% in-sample and 50% out-of-sample partition. The normalized regression estimated coefficients of the empirical discharge model and the readmission predictive model were directly compared. All statistical analyses and modeling were performed using Stata® version 14.0 (StataCorp, College Station, TX).

Both methodologies were reviewed and approved by the Emory University and Georgia State University Institutional Review Boards.

RESULTS

A total of 20,970 patients were identified from the institution’s clinical data warehouse representing a wide range of surgical procedures. The median age of the patient population was 54 (range 13–96); 38.8% were male; 57.7% were white and 33.0% were black. Patients had a median length of stay after surgery of 2 days, and the distribution was skewed toward patients with prolonged lengths of stay (mean = 5.5 days, IQR = 1–6 days). Common comorbidities such as cancer (11.2%), hypertension (39.5%), and diabetes (16.1%) were frequently observed. The majority of operations (69.5%; 14,570) were gastrointestinal in nature. The 30-day readmission rate was 7.5% (1,565 patients), which is comparable to previously reported rates in general surgery patients.(2, 8, 14, 17) Demographics, comorbidities, and surgical procedures of the patient population are fully described in Table 1.

Table 1.

Study population summary statistics. 20,970 patients’ daily clinical observations were extracted from an institutional data warehouse for all inpatient general and vascular surgery procedures from 2009 to 2014.

Age, median	54
Age, range	13–96
LOS, median (days)	2
LOS, mean (days)	5.53
	n (%)
Sex
Male	8,143 (38.8%)
Female	12,827 (61.2%)
Race
White	12,101 (57.7%)
Black	6,913 (33.0%)
Other	1,956 (9.3%)
Comorbidities
Diabetes	3,376 (16.1%)
Cancer	2,354 (11.2%)
Heart disease	1,203 (5.74%)
Hypertension	8,270 (39.5%)
Procedure Category
Gastrointestinal	14,570 (69.5%)
Endocrine	3,097 (16.8%)
Skin and Soft Tissue	2,668 (12.7%)
Ortho	426 (2.03%)
Thoracic	87 (0.4%)
Vascular	122 (0.6%)
30-day readmission	1,565 (7.47%)
TOTAL PATIENTS	20,970
TOTAL PATIENT-DAYS OF OBSERVATIONS	115,976

Predictive Modeling

For each of the 23 procedure groups, 41 observed measures were routinely collected and stored in the clinical data warehouse (64 total collected variables). All of these were obtained for each of the 20,970 patients described above totaling 115,976 patient-days, including 1,565 readmitted patients with 20,560 patient-days. These datasets were then used for discharge and readmission regression analyses. All 41 observed variables were included as regressors in both models after demonstrating the lack of multicollinearity (mean variance inflation factor = 1.51; range 1.01–3.52) and survival via stepwise selection. 34 variables were found to be predictive (at conventional level of significance) of the discharge decision-making. Post hoc analysis suggested that difficult post-operative, in-hospital recoveries were indicative of increased readmission risk, so length of stay was added to the readmission model. 30 of the 42 variables were found to be significantly predictive of readmissions. The complete regression results for both models are reported in Table 2 and eTable 1.

Table 2.

Normalized effect of 42^† observed clinical variables on discharge and readmission (n = 20,970 patients with 115,976 daily observed clinical measures; 1,565 readmitted patients with 20,560 daily observed clinical measures). Column A reports the normalized regression coefficient for each clinical variable for a time-to-event model analysis predicting daily likelihood of discharge based on actual discharges of the patient population. A positive value indicates the presence or increased magnitude of the variable increases the likelihood of discharge, and vice versa. Column B reports the normalized coefficient for each clinical variable for a logit regression model predicting likelihood of 30-day readmission as predicted on the day of discharge. A positive value indicates the presence or increased magnitude of the variables increases the likelihood of readmission. Confidence intervals of the coefficient estimates are reported to aid in the interpretation of conventional p-values for large sample sizes.(23) Each patient was also controlled for the procedure performed (eTable 1).

	(A)					(B)
Clinical Variable†	Discharge Regression Estimated Coefficient¶	95% CI		p		Readmission Regression Estimated Coefficient¶	95% CI		p
Ascites	−0.452	−0.546	−0.358	0.000	***	0.193	−0.019	0.404	0.074	*
CHF	−0.193	−0.258	−0.128	0.000	***	0.275	0.123	0.427	0.000	***
DM	−0.038	−0.071	−0.004	0.026	**	0.254	0.149	0.358	0.000	***
CANCER	−0.167	−0.366	0.031	0.099	*	0.13	−0.015	0.276	0.080	*
HTN	−0.052	−0.086	−0.019	0.002	***	0.144	0.027	0.261	0.016	**
Emer Admit	−0.075	−0.220	0.070	0.311		0.08	−0.175	0.336	0.538
Reg Admit	−0.098	−0.182	−0.013	0.023	**	0.074	−0.204	0.353	0.602
Male Gender	−0.045	−0.096	0.005	0.080	*	0.061	−0.004	0.125	0.066	*
PtAge	−0.043	−0.072	−0.013	0.005	***	0.004	−0.080	0.089	0.921
WhiteRace	−0.046	−0.069	−0.022	0.000	***	0.279	0.087	0.472	0.005	***
BlackRace	−0.114	−0.164	−0.064	0.000	***	0.366	0.133	0.599	0.002	***
IVDU	−0.481	−0.689	−0.273	0.000	***	0.251	0.158	0.343	0.000	***
NPO	−2.069	−2.908	−1.229	0.000	***	−0.331	−0.875	0.213	0.233
Albumin	−0.021	−0.031	−0.012	0.000	***	−0.04	−0.062	−0.018	0.000	***
AlkPhos	0.017	−0.023	0.056	0.403		0.075	0.029	0.121	0.001	***
AST/ALT	−0.039	−0.063	−0.016	0.001	***	−0.186	−0.337	−0.035	0.016	**
BUN	−0.170	−0.228	−0.113	0.000	***	0.086	−0.012	0.184	0.084	*
Calcium	0.182	0.108	0.256	0.000	***	−0.178	−0.236	−0.120	0.000	***
Bicarb	−0.002	−0.028	0.024	0.865		−0.01	−0.056	0.036	0.665
Cr	0.014	−0.033	0.062	0.552		−0.036	−0.105	0.034	0.313
HCT	0.070	0.018	0.121	0.008	***	−0.138	−0.179	−0.097	0.000	***
INR	0.008	−0.010	0.026	0.387		−0.015	−0.049	0.020	0.408
K+	−0.035	−0.072	0.003	0.072	*	0.13	0.068	0.191	0.000	***
Sodium	−0.061	−0.121	−0.002	0.043	**	−0.08	−0.130	−0.031	0.002	***
PLT	0.075	0.050	0.100	0.000	***	−0.042	−0.084	0.000	0.048	**
PTT	−0.016	−0.029	−0.004	0.009	***	0.056	0.028	0.084	0.000	***
TBili	−0.109	−0.151	−0.067	0.000	***	0.065	−0.006	0.137	0.073	*
WBC	−0.190	−0.233	−0.147	0.000	***	0.112	0.020	0.203	0.017	**
Katz Score	0.314	0.271	0.356	0.000	***	−0.062	−0.098	−0.026	0.001	***
Stool+	0.008	0.005	0.011	0.000	***	−0.153	−0.292	−0.013	0.032	**
BMI	0.035	0.020	0.051	0.000	***	−0.01	−0.086	0.066	0.792
HR	−0.166	−0.203	−0.130	0.000	***	0.108	0.030	0.187	0.007	***
O2Sat	−0.026	−0.039	−0.013	0.000	***	−0.026	−0.060	0.007	0.127
RR	−0.003	−0.031	0.025	0.819		0.11	0.028	0.192	0.009	***
DBP	0.017	−0.008	0.042	0.179		0.065	0.026	0.104	0.001	***
SBP	−0.024	−0.040	−0.008	0.003	***	−0.084	−0.133	−0.035	0.001	***
TEMP	0.003	−0.030	0.036	0.847		0.048	0.005	0.092	0.031	**
PainScore	−0.068	−0.089	−0.047	0.000	***	0.158	0.130	0.185	0.000	***
DxImg	−0.650	−1.282	−0.018	0.044	**	0.175	−0.020	0.369	0.078	*
Complexity (RVUs)	−0.198	−0.364	−0.032	0.020	**	0.069	−0.027	0.165	0.161
UnivHosp vs Other	−0.469	−0.567	−0.370	0.000	***	0.372	0.145	0.598	0.001	***
HighRisk	−0.856	−0.986	−0.726	0.000	***	−0.175	−0.311	−0.039	0.011	**
LOS						−0.015	−0.023	−0.006	0.001	***
LnLOS						0.659	0.504	0.814	0.000	***

Abbreviations: Ascites – history of ascites, CHF – history of congestive heart failure, DM – history of diabetes, CANCER – history of cancer, HTN – history of hypertension, Emer Admit – unplanned emergency admission, Reg Admit – elective admission, PtAge – patient’s age, IVDU - intravenous drug use, NPO – oral diet prohibited, Alk Phos – serum alkaline phosphatase, AST/ALT – serum liver transaminases (averaged), BUN – serum blood urea nitrogen, Calcium – serum calcium, Bicarb – serum bicarbonate, Cr – serum creatinine, HCT – hematocrit, INR – international normalized ratio, K + - serum potassium, PLT – platelet count, PTT – partial thromboplastin time, TBili – total serum bilirubin, WBC – white blood cell count, Stool+ - post operative bowel movement, BMI – body mass index, HR – heart rate, O2 Sat – pulse oximetry oxygen saturation, RR – respiratory rate, DBP – diastolic blood pressure, SBP – systolic blood pressure, TEMP – body temperature, DxImg – diagnostic imaging in last 24 hours, UnivHosp – modifier for geographic site of operation, PreOptimize – dummy variable for hospital stay prior to surgery, LnLOS – natural logarithm of length of stay, LOS – length of stay

^***p<0.01,

^**p<0.05,

^*p<0.1

^†Variables found to be statistically insignificant with both models are not shown.

^¶Estimated coefficients instead of estimated hazard ratios were reported because of ease of signage interpretation.

^§Katz scores are calculated from the Katz Index of Independence in Activities of Daily Living (Gerontological Society of America). 1 point in each of six domains: bathing, dressing, toileting, transferring, continence, and feeding. A total of 6 points ndicates complete functional independence, and a total of 0 points indicates no independence.

Model Validation

Both models were tested with serial in-sample and out-of-sample bootstrapped, partitioned iterations. The discharge model employed 200 total iterations and the readmission model performed 300 total iterations with equal number of iterations conducted with 90% in-sample and 10% out-of-sample partitions, 70%/30%, and 50%/50%, respectively (50/50 for readmission model only due to regression methodology). The mean in-sample and out-of-sample C statistics were found to be 0. 82 and 0. 80 for the readmission model whereas for the discharge model the in-sample as well as out-of-sample mean C-statistic was 0.79.

Comparative Analysis of Discharge and Readmission Models

The discharge and readmission models were directly compared to identify possible discharge behaviors that were discordant with the goal of reducing surgical readmissions. All of the estimated coefficients used for this analysis - as well as their interpretation – are described in Table 2 and eTable 1. Table 3 and Figure 1 show comparisons of estimated coefficients for standardized variables from the two regression models. Table 3 demonstrates the relationship between a clinical variable’s normalized discharge regression coefficient and its normalized readmission regression coefficient. Using the patient’s reported pain score as an example, the marginal effect on the odds of readmission by a one unit increase in the standardized pain score is estimated to be 17% (the exponential function of 0.158 minus 1) and the estimated marginal effect on the rate of discharge is −6.6% (the exponentional function of −0.068 minus 1). This constellation of coefficients imply that higher pain scores are associated with a greater likelihood of readmission, and that physicians heeded pain concerns by holding discharges on those with higher pain scores.

Table 3.

Comparison of the effect of observed clinical variables on predictive models of discharge and readmission. The sign of the readmission regression coefficient has been reversed for easier direct comparison of the variable’s effect on discharging the patient (larger regression coefficient is a higher likelihood of discharge) versus the variable’s effect on preventing readmission (larger regression coefficient is a lower likelihood of readmission). Confidence intervals of the coefficeints estimates are reported to aid in the interpretation of conventional p-values for large sample sizes.(23)

		(A)				(B)
Qualitative Assessment of Discharge Decision	Clinical Variable†	Discharge Regression				Readmission Regression
		Est.¶	95% C.I.			Est.¶	95% C.I.
Non-Optimal Discharge (Insufficient Attention)	TEMP	0.003	−0.030	0.036		−0.048	−0.005	−0.092	**
	RR	−0.003	−0.031	0.025		−0.110	−0.028	−0.192	***
	AlkPhos	0.017	−0.023	0.056		−0.075	−0.029	−0.121	***
	DBP	0.017	−0.008	0.042		−0.065	−0.026	−0.104	***
Non-Optimal Discharge (Inappropriate effect)	AST/ALT	−0.039	−0.063	−0.016	***	0.186	0.337	0.035	**
	HighRisk	−0.856	−0.986	−0.726	***	0.175	0.311	0.039	**
	SBP	−0.024	−0.040	−0.008	***	0.084	0.133	0.035	***
	Sodium	−0.061	−0.121	−0.002	**	0.080	0.130	0.031	***
	Albumin	−0.021	−0.031	−0.012	***	0.040	0.062	0.018	***
Optimal Discharge (Appropriate effect)	UnivHosp vs Other	−0.469	−0.567	−0.370	***	−0.372	−0.145	−0.598	***
	BlackRace	−0.114	−0.164	−0.064	***	−0.366	−0.133	−0.599	***
	WhiteRace	−0.046	−0.069	−0.022	***	−0.279	−0.087	−0.472	***
	CHF	−0.193	−0.258	−0.128	***	−0.275	−0.123	−0.427	***
	DM	−0.038	−0.071	−0.004	**	−0.254	−0.149	−0.358	***
	IVDU	−0.481	−0.689	−0.273	***	−0.251	−0.158	−0.343	***
	Ascites	−0.452	−0.546	−0.358	***	−0.193	0.019	−0.404	*
	Calcium	0.182	0.108	0.256	***	0.178	0.236	0.120	***
	DxImg	−0.650	−1.282	−0.018	**	−0.175	0.020	−0.369	*
	PainScore	−0.068	−0.089	−0.047	***	−0.158	−0.130	−0.185	***
	Stool+	0.008	0.005	0.011	***	0.153	0.292	0.013	**
	HTN	−0.052	−0.086	−0.019	***	−0.144	−0.027	−0.261	**
	HCT	0.070	0.018	0.121	***	0.138	0.179	0.097	***
	CANCER	−0.167	−0.366	0.031	*	−0.130	0.015	−0.276	*
	K+	−0.035	−0.072	0.003	*	−0.130	−0.068	−0.191	***
	WBC	−0.190	−0.233	−0.147	***	−0.112	−0.020	−0.203	**
	HR	−0.166	−0.203	−0.130	***	−0.108	−0.030	−0.187	***
	BUN	−0.170	−0.228	−0.113	***	−0.086	0.012	−0.184	*
	TBili	−0.109	−0.151	−0.067	***	−0.065	0.006	−0.137	*
	Katz Score	0.314	0.271	0.356	***	0.062	0.098	0.026	***
	Male Gender	−0.045	−0.096	0.005	*	−0.061	0.004	−0.125	*
	PTT	−0.016	−0.029	−0.004	***	−0.056	−0.028	−0.084	***
	PLT	0.075	0.050	0.100	***	0.042	0.084	0.000	**
Optimal Discharge (Unknown effect)	NPO	−2.069	−2.908	−1.229	***	0.331	0.875	−0.213
	Complexity (RVUs)	−0.198	−0.364	−0.032	**	−0.069	0.027	−0.165
	Reg Admit	−0.098	−0.182	−0.013	**	−0.074	0.204	−0.353
	PtAge	−0.043	−0.072	−0.013	***	−0.004	0.080	−0.089
	BMI	0.035	0.020	0.051	***	0.010	0.086	−0.066
	O2Sat	−0.026	−0.039	−0.013	***	0.026	0.060	−0.007

^***p<0.01,

^**p<0.05,

^*p<0.1

^¶Estimated coefficients instead of estimated hazard ratios were reported because of ease of signage interpretation.

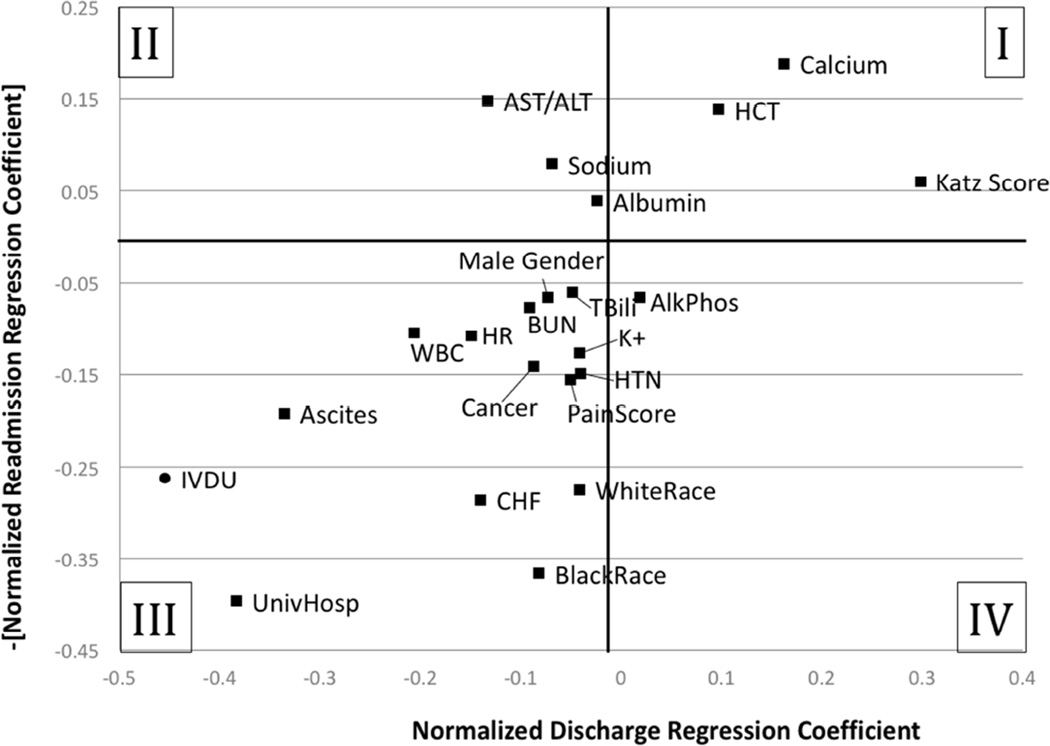
Figure 1. Comparison of the effect of observed clinical variables on predictive models of discharge and readmission.

The x-axis plots the normalized regression coefficient of a time-to-event model of the likelihood of discharge for a given day’s observed clinical variables. The y-axis plots the normalized coefficient of a logit regression model of the likelihood of 30-day readmission. The sign of the readmission regression coefficient has been reversed for easier direct comparison of the variable’s effect on discharging the patient (larger regression coefficient is a higher likelihood of discharge) versus the variable’s effect on preventing readmission (larger regression coefficient is a lower likelihood of readmission). In its current projection, Quadrant I demonstrates variables that both increase the likelihood of discharge and reduce the risk of readmission; Quadrant III demonstrates variables that decrease the likelihood of discharge and increase the risk of readmission. Quadrants II and IV represent discordance between behavior and readmission with the former indicating variables that increase length of stay but reduce the risk of readmission and the latter indicating variables that decrease length of stay but increase risk of readmission. Variables found to be statistically insignificant with either model are not shown.

All clinical variables were divided into important qualitative categories based on signage of the estimated coefficients. “Non-optimal discharges” were those in which a variable did not appear to be used effectively in the discharge process. This category of variables was further subdivided into "insufficient attention” (those variables not significantly predictive of discharge but demonstrating an increased risk of readmission) and “inappropriate effect” (those variables that decrease the probability of discharge but were ultimately protective against readmission. The majority of variables fall into the “Optimal Discharge – Appropriate effect” subcategory suggesting that in most cases surgeons were responding to variables predictive of readmission by prolonging their initial hospital stays. There is a final category, “Optimal Discharge – Unknown effect” which highlights the variables that were predictive of discharge but were not found to be significant predictors of readmission. Based on this study’s methodology, it is impossible to interpret whether these variables were being appropriately selected for by surgeons or if these clinical delays were unnecessary for reducing readmissions.

For variables statistically significant in both models, Figure 1 graphically demonstrates the degree of alignment between factors that are predictive of discharge and those that are predictive of readmission. Quadrants I and III of the figure show concordance between current discharge behaviors and reducing surgical admissions. For example, a patient carrying a diagnosis of congestive heart failure (CHF) is both less likely to be discharged and more likely to be readmitted. In contrast, Quadrants II and IV represent discordant results between the models. Using liver function as an example, elevated liver transaminases lead to less likely discharge even though that patient is less likely to be readmitted. On the other hand, patients with an isolated elevated alkaline phosphatase are more likely to be discharged and more likely to be readmitted. In addition, there are several effect size discrepancies noted. Patient race appears to have an important impact on readmission with white patients substantially more likely to be readmitted than non-white patients, but discharge decision-making does not appear to be significantly affected by it. Conversely, a history of intravenous drug use (IVDU) decreases likelihood of discharge but this effect may be disproportionate to the effect of IVDU on readmission risk.

DISCUSSION

This study illustrates the feasibility of using large patient data sets to construct predictive models for readmission that highlight clinical data that is not conventionally used by surgeons when making the decision to discharge a patient from the hospital after an inpatient surgical procedure.

Tables 2 and 3 with Figure 1 highlight the variables found to be significant in a logit regression model for readmission, demonstrating that variation in a number of variables may be drivers of – or at least likely indicators of – a higher risk of readmission. This predictive model of readmissions was also validated with standard statistical techniques demonstrating good discrimination (C statistics of 0.82 and 0.80) that is better than many discrimination measures reported in prior readmission modeling studies.(11) When this predictive model was compared with the clinical predictors of discharge, the observed differences in the two models highlighted opportunities for improving discharge decision-making.

Currently observed discharge behaviors might not be fully aligned with current readmission reduction goals. Table 3 highlights variation in predictors of discharge versus their effect on readmission. What surgeons practice does not appear to always align with reducing readmissions (Table 2, eTable 1, Table 3, and Figure 1). For example, variables that were not significantly associated with surgeons’ discharge decisions but positively associated with the likelihood of being readmitted suggest that surgeon behavior may be missing important readmission-reducing data trends. It is possible that some of these less carefully considered variables (e.g., diastolic blood pressure, respiratory rate, liver function tests) are picking up subtle variations – so-called “microtrends” – in clinical trajectories that are not traditionally considered to be relevant to overall discharge decision-making. Perhaps readmissions could be reduced by using a data-driven predictive model that incorporates these less commonly considered clinical data points. This discordance also highlights the potential for poor acceptance of discharge decision-support tools that utilize statistical predictors of readmission that diverge from factors that surgeons believe to be important predictors of a successful discharge. For example, a decision-support tool may highlight a patient’s race as an indication that the patient may require more intensive discharge planning with the potential for prolonged index admission. If the surgeon does not intrinsically believe that patient characteristic is relevant for discharge decision-making, he or she may discount the tool’s recommendations. Creative strategies to incorporate the best data analysis with display modes that overcome reluctance to use less intuitive but data-driven predictive models are a necessary step for the promotion of such decision-support technologies (Figure 2).

Figure 2. Human-machine interface of decision-support tools.

This schematic illustrates that the ways in which patient data are presented to clinical decision-makers may be as important to the successful implementation of a decision-support tool as the underlying analytical methodology.

Previous efforts to reduce readmission have started by identifying processes and bundling strategies in the pre- and postoperative period.(12, 18) An alternative but not yet proven strategy suggested for reducing surgical readmissions is the risk stratification of postoperative patients and enhanced discharge decision-making.(19, 20) Each patient is a unique individual, and the patient’s physician must retain responsibility for the decision to discharge the patient from the hospital. But these central features of the physician-patient relationship are not at direct odds with the need for further decision-support in the discharge process.

An innovation with promise for promoting evidence-based discharge decision-making involves the development of decision-support software. Expanding on the predictive readmission modeling discussed above, the authors believe that alternative, support-vector regression models that can predict the probability of patient readmission continuously over a patient’s hospital stay would be useful to optimize clinicians’ discharge decisions. Ultimately, this more comprehensive model could provide dynamically updated marginal probabilities of patient readmission within 30 days of discharge for a specific patient using real-time clinical, demographic, and census data.

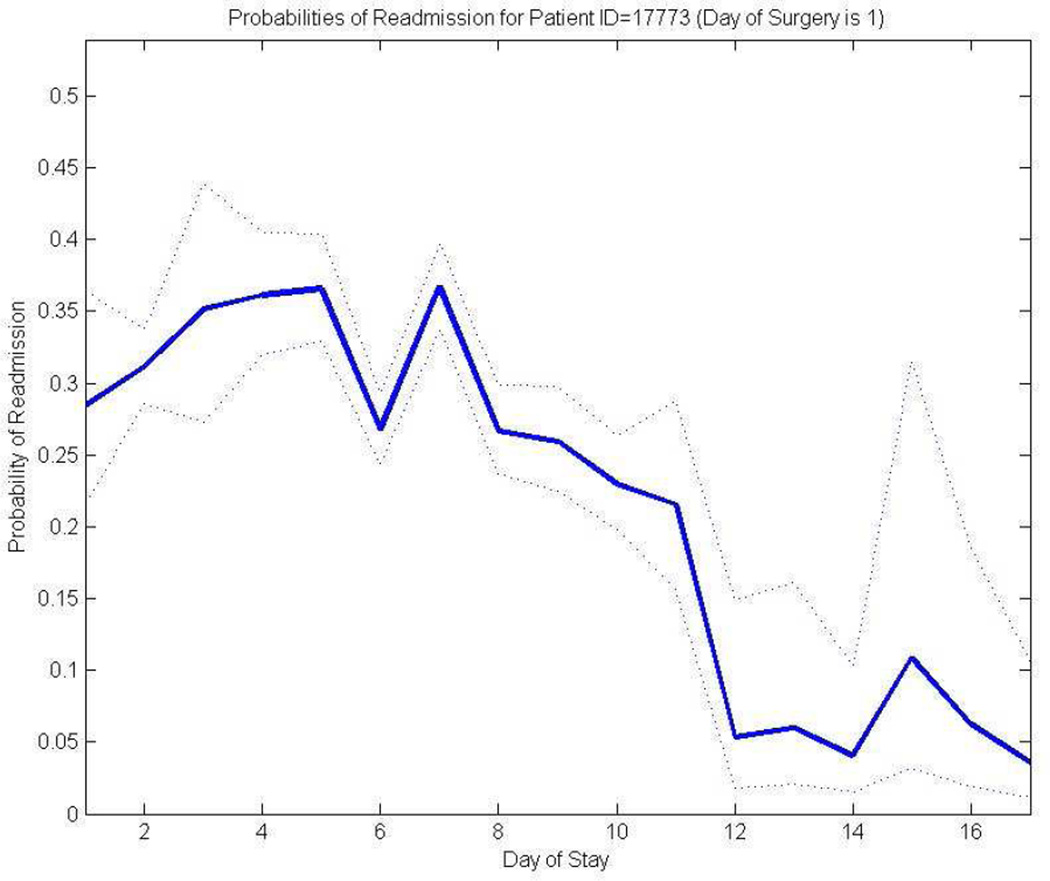
Figure 3 provides an example of a comprehensive predictive model illustrating how a patient’s LOS may have been unnecessarily prolonged. Although this patient stayed in the hospital for 17 days, the model predicts that the likelihood of readmission is not statistically different from day 12 onward. This example illustrates how a discharge decision might have been improved by the use of a decision-support algorithm.

Figure 3. A regression-based algorithm predicting daily risk of readmission for a sample inpatient.

The x-axis indicates elapsed days since surgery (i.e., length of stay) and the y-axis shows predicted risk of readmission if discharged on that day. The solid line represents the point estimates of readmission probabilities generated by the regression model. The dotted lines represent the 80% confidence intervals. For this specific graph, estimates were run from virtual Day 2 of admission because of the extreme unlikelihood of next day discharge for a complex surgical patient.

The algorithm also provides the foundation for a decision-support tool by treating the patient’s measured characteristics as one “patient observation” within a large sample of archived patients with similar measured characteristics but known outcomes. In this way, a current discharge decision can be informed by the aggregated experience with thousands of similar patients with known histories. Such a decision-support tool provides a statistically informed answer to the central question: “If this patient is discharged today, what is the likelihood of readmission within 30 days?”

Limitations

The findings reported here are not without interpretative limitations. First, this study was performed with surgeons and patient data from a single institution limiting the generalizability of the variables identified. Importantly, this institution was a relative under-performer compared to its peers with a length of stay index of 1.12 versus a teaching hospital baseline of 1.06 and a readmission rate of 5.26% versus 5.24% (unpublished data, University HealthSystem Data, accessed 2015). Therefore, this institution may have specific processes and patient factors that lead it to benefit more than average from clinical decision support tells that help optimize patient care. It is likely that institutions already out-performing their peers on quality metrics may demonstrate a different set of predictors than under-performers. It is also possible that outperformers may benfit less from such decision support optimization with limited ability to incrementally improve quality performance further. Moreover, the group of procedures included in this analysis was predominantly gastrointestinal surgery cases limiting generalizability to other surgical procedures. However, we argue that the analytical exercise described in this study is not meant to be directly portable to other clinical sites but instead demonstrates an approach to optimizing decision support tools for the specific patients and surgeon preferences of each healthcare environment. It is very likely that the predictors of readmission will vary with different populations of surgeons and patients. We believe site-specific customization of decision-support tools will be increasingly important with increasing use of these technologies, and methodologies – rather than ready-made decision tools – will be the currency of future large-scale quality improvement interventions.

Another limitation of this study is the imperfect comparison between what was observed at discharge and these variables’ subsequent impact on readmission. A variable that the regression model found to be relatively unimportant is not necessarily unimportant for discharge but simply may indicate observations of a variable that fall within such a narrow range for all discharges as to appear insignificant.

Arguing that all of the discordance between surgeon’s preferences and the predictive model is the result of human decision-making errors would be an over-interpretation of this analysis. Instead, what the authors choose to highlight is that the discordance between surgeon behaviors and readmission-optimized behaviors based on a predictive model highlight variables for closer examination to determine marginal improvements in discharge decision-making. For example, the discharge regression model suggests that a number of clinical variables have an overemphasized effect on discharge when compared to their effect on readmission (Table 3). Perhaps the proper decision-support tool could better align these effects by reducing selected variables’ impact on discharge decision-making.

CONCLUSIONS

Predictive models suggest considerable discordance exists between how surgeons behave in practice and what may optimize discharge decision-making and limit subsequent hospital readmission. The real-world application of such a predictive model is a question in itself. Behavioral experiments are necessary to ascertain how and whether medical decision makers will use decision support software.(21, 22) If so, is the decision support tool effective in reducing readmissions? These further issues will need to be addressed through ongoing research.