Intraindividual Variability in Cortisol: Approaches, Illustrations, and Recommendations

Abstract

Most of the variance in diurnal cortisol is attributable to intraindividual variability (IIV), defined as relatively short-term, reversible changes. Multiple methods for measuring IIV have been proposed, and some have already been applied to cortisol IIV. In the present review, measurement methods are described and applied to simulated cortisol data with known underlying differences in IIV and to real cortisol data from first-year law students. More slope variance and more residual or net variance were well captured by their individual standard deviations. Explorations of reliability suggested that 10 slopes and 50 residuals result in reliable and stable estimates of the individual standard deviations. A data-analytic plan for cortisol IIV is provided.

1. Introduction

Intraindividual variability (IIV) is “relatively short-term changes that are construed as more or less reversible and that occur more rapidly [than developmental change]” (Nesselroade, 1991). Many psychological processes have substantial IIV, including cognitive function, affect, appraisals, and even personality (e.g., Eid & Diener, 1999; Fleeson, 2001; Sliwinski, Almeida, Smyth, & Stawski, 2009; Vasquez, Binns, & Anderson, 2016; Whitehead & Bergeman, 2014). Furthermore, IIV is associated with psychological and physical health. Higher reaction time IIV predicted greater likelihood of progression from mild cognitive impairment to dementia, and short-term IIV in cognitive tasks may be associated with loss of gray and white matter integrity, particularly in the frontal lobes (McDonald, Nyberg, & Bäckman, 2006; Tales et al., 2012). Higher affective IIV characterizes people high in neuroticism (Eid & Diener, 1999; Kuppens et al., 2007; Timmermans, van Mechelen, & Kuppens, 2010) and predicted worsening psychological and physical health (Hardy & Segerstrom, 2016). Higher IIV in life satisfaction and in perceived control predicted earlier mortality (Boehm, Winning, Segerstrom, & Kubzansky, 2015; Eizenman, Nesselroade, Featherman, & Rowe, 1992). These findings reflect “the new person-specific paradigm in psychology” that emphasizes people as dynamic systems (Molenaar & Campbell, 2009, p. 112).

IIV also characterizes physiological processes. Stressful life events were associated with higher IIV in sleep duration and fragmentation but not with averages (Mezick et al., 2009). Whereas IIV in psychological domains has been associated with worse psychological and physical health, respiratory sinus arrhythmia contributes to IIV in the cardiac interbeat interval and is associated with better health (Appelhans & Luecken, 2006; Stein & Kleiger, 1999; Thayer & Sternberg, 2006).

With regard to cortisol, pulsatile secretion follows both circadian and ultradian patterns. A predictable diurnal pattern is characterized by peak levels just after awakening and decreasing levels during the daytime hours that reach a nadir in the late evening and early morning hours (Dickmeis, Weger, & Weger, 2013). Superimposed on the diurnal rhythm, cortisol reacts to stressors that are novel, unpredictable, uncontrollable, or involve a social-evaluative threat (Dickerson & Kemeny, 2002). Cortisol IIV (cIIV), however, overwhelms stable individual differences. Variance in cortisol levels at specific times of day (morning and evening) over short periods of time (3 consecutive days) was attributable about equally to stable individual differences and to cIIV (Kertes & van Dulmen, 2012). Over longer periods of time (weeks to years), stable individual differences in diurnal cortisol parameters such as the diurnal slope and area under the curve account for a minority of the variance (10–25%; Hruschka, Kohrt, & Worthman, 2005; Ross et al., 2014; Segerstrom, Boggero, Smith, & Sephton, 2014; Shirtcliff et al., 2012). The largest amount of variance in diurnal cortisol parameters over days or months is not systematically related to the passage of time but rather is attributable to idiosyncratic fluctuations, that is, cIIV (Miller et al., 2014; Ram & Gerstorf, 2009; Segerstrom et al., 2014).

Although high cIIV is the rule, not the exception, there has been little examination of individual differences in cIIV and their relationship to psychological and physical health. In the existing research, cIIV seems to follow the same pattern as psychological IIV: Higher IIV is associated with poorer health. Outpatients with major depressive disorder had a lower autocorrelation between cortisol observations (indicating higher cIIV) than did healthy controls (Peeters, Nicholson, & Berkhof, 2004). After fitting models predicting cortisol from time of day, the standard deviation of the residuals was higher (indicating higher cIIV) among caregivers who had poorer psychological health and among adopted children whose adoptive mothers engaged in more overreactive parenting (Marceau et al., 2013; Sannes, Mikulich-Gilbertson, Natvig, & Laudenslager, 2016). Similarly, depressed patients had higher residual error around the circadian rhythm, compared with controls and PTSD patients (Yehuda et al., 1996). cIIV may reflect person influences (e.g., reactivity or neuroticism), situation influences (e.g., unstable or intermittently stressful environments), or dysregulation of the HPA axis (e.g., insensitivity to negative feedback inhibition; Yehuda et al., 1996).

Further research is needed to establish the causes and correlates of cIIV. The present review is intended to facilitate such research by providing methodological demonstrations and recommendations. It compares statistical approaches for quantifying IIV, considers their implications for measuring cIIV, and applies them to both simulated and real diurnal cortisol data. The measurement of IIV is not always straightforward, and multiple methods have been proposed that capture different properties of variability. Furthermore, cIIV differs from many other IIV domains in that people have IIV at multiple levels. The diurnal cortisol slope can and does vary from day to day, and individual values can deviate more or less from this slope. Therefore, cIIV has at least two levels: IIV in the slope from day to day (slope cIIV), and IIV net of this slope (net cIIV), that is, the degree to which individual cortisol values deviate from the line of the slope (see Table 1).

Table 1.

Constructs in cortisol IIV: Acronyms and definitions

cIIV	Cortisol intraindividual variability	Short-term, reversible changes in levels or derived measures of cortisol. Can be, for example, raw cIIV (variability in observations), slope cIIV (variability in diurnal slopes), or net cIIV (variability in residuals of diurnal slopes)
iSD	Intraindividual standard deviation	The standard deviation of all of an individual’s observations, slopes, residuals, or other derived measure (e.g., area under the curve)
iM	Intraindividual mean	The mean of all of an individual’s observations; not a measure of IIV, but it is good practice to control for the iM when testing effects of IIV
rMSSD	Root mean squared successive difference	The differences between successive observations (i.e., between the first and second, second and third, and so on) are squared and summed, and the square root of this value is taken
AR(1)	Autocorrelation or autoregression	The correlation between successive observations (modeled across all observations)
RMSE	Root mean squared error	The residuals from a regression model for each individual are squared, and the square root of the mean squared residual is taken. When there are multiple regression models (e.g., a diurnal slope fit for each day), the iRMSE is the mean of all of an individual’s RMSEs
MLM	Multilevel modeling	A modeling technique used to analyze clustered data (e.g., observations within people; Snijders & Bosker, 1999). Can be used to derive individual slopes and residuals of those slopes or, in more complex models, to test effects of a predictor on IIV.

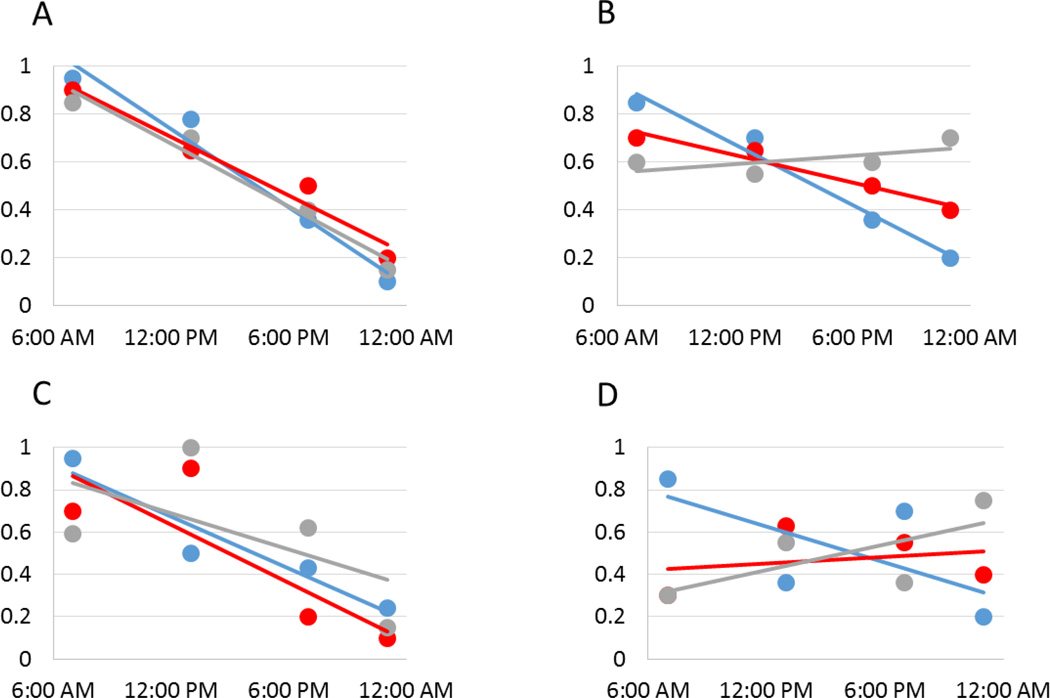
Figure 1 shows 4 hypothetical individuals with 12 cortisol observations each. Points represent cortisol observations (4 per day over 3 days), and lines represent the slopes on each day. Individual A has low cIIV at both levels; slopes across days are similar and the individual cortisol values lie close to the slopes. B has high slope cIIV, but low net cIIV; slopes differ across days, but the cortisol values on each day lie close to that slope. C is just the reverse; slopes are similar across days, but the cortisol values vary markedly from those slopes. D has high cIIV at both levels because slopes across days are different, and the cortisol values also vary markedly from those slopes.

Figure 1.

Hypothetical patterns of intraindividual variability in diurnal cortisol.

These two sources of variance may have different underlying correlates. As an example of how two different levels of cIIV might arise, it is possible that B is reactive to the environment but well-regulated with regard to the daily slope: the diurnal slope reacts to environmental variation across days, but individual cortisol values conform to that day’s slope. By contrast, C is not reactive but also not well-regulated: the diurnal slope is the same across days, but the cortisol values vary markedly around that slope. One possibility is that one of these types of cIIV predicts health outcomes to a greater degree than the other. Therefore, appropriate selection of a measurement strategy for cIIV and understanding what level of IIV is captured by that strategy is important for the development of research on cIIV.

2. Measurement of IIV

The following section reviews a number of measurement strategies that can be used to quantify IIV, focusing on their practical implications for cIIV. For the mathematical bases of these strategies, see Wang et al. (2012). The strategies are considered in order of their computational complexity, from least complex to most complex. See Table 1 for a summary.

2.1 Intraindividual standard deviation (iSD)

The iSD is the simplest method for quantifying IIV, and perhaps for that reason is the most commonly used measure. Its simplicity is also its strength: It is easy to calculate and to understand. The iSD is merely each individual’s standard deviation over all of his or her observations. A higher iSD reflects more IIV.

However, some properties of the iSD require consideration. First, the iSD is agnostic with regard to the order of observations. As a simple example, the data sequence 4-3-2-1 and the sequence 1-4-2-3 have the same iSD, but reflect entirely structured IIV in the first case (variability is perfectly correlated with order) and entirely unstructured IIV in the second case (variability is uncorrelated with order). Cortisol has both levels of IIV – structured, slope cIIV and unstructured, net cIIV – and the iSD of all measurements does not discriminate between these two levels. One way to isolate net cIIV is to remove variance due to the diurnal slope (i.e., detrend within day) by regressing cortisol levels on time of day and taking the iSD of the residuals (Marceau et al., 2013; Sannes et al., 2016; Wang, Hamaker, & Bergeman, 2012). When applied within each day (i.e., detrending by clock time), the iSD of the residuals reflects net cIIV and excludes slope cIIV. Conversely, slope cIIV can be isolated by taking the iSD of the diurnal slope (or other derived measure such as area under the curve). The iSD of the diurnal slopes excludes net cIIV. Finally, combining days (i.e., fitting one slope to all available observations over multiple days), the iSD of the residuals yields a combination of net cIIV and slope cIIV, because variability in slopes across days contributes to the residuals of the single diurnal slope.

A second property of the iSD that requires consideration is that it can be correlated with the corresponding intraindividual mean (iM), particularly when there are floor and ceiling effects and when the distribution of the outcome is skewed (Baird, Le, & Lucas, 2006). As Baird and colleagues (2006) illustrate, an intraindividual mean of 0 on a 0–5 scale is only possible if all of that individual’s observations are 0, in which case the iSD is also 0. In the presence of floor and ceiling effects, the iSD is largest in the middle of the distribution and smallest at the extremes. In that case, the iSD is partially a quadratic function of the intraindividual mean. In addition, the iSD can be linearly correlated with the intraindividual mean if the distribution is skewed. In the presence of a floor effect and if the distribution of means is positively skewed, the mean and the iSD will be positively correlated. Before computing the iSD, the distribution of the outcomes should be carefully examined and transformed to achieve a normal distribution if possible, and the possibility of ceiling and floor effects should be carefully considered. Regardless, it is standard practice to control for the corresponding iM when testing effects of the iSD.

In the case of cortisol, the limits of assays may create floor and (less likely) ceiling effects. In addition, the distribution of cortisol values is positively skewed and is typically log-transformed before analysis. Where the iSD is being used to quantify cIIV, the success of this transformation should be critically examined. In addition, the iM should always be included with the iSD in predictive models, whether the focus is cIIV of derived variables such as slope or AUC (in which case, iMs of the slope or AUC should be included) or net cIIV.

Finally, when taking the iSD of derived cortisol parameters such as the slope, there may be relatively few days of data available. For example, many investigators have followed a longstanding recommendation from the MacArthur Network that assessment of cortisol levels should be based on 3–4 days of sample collection, and often assessment of cortisol slopes is based on the same protocol (http://www.macses.ucsf.edu/research/allostatic/salivarycort.php). Three observations is the minimum number to calculate the iSD, but this minimum has undesirable properties. Although the value of the iSD does not change based on the number of contributing observations, it is less reliable than the iM taken from the same number of observations. In a simulation study, the iSD based on fewer than 20 observations achieved minimally acceptable reliability (.60) only when measurement accuracy was high (.80), IIV was high, and there were large individual differences in IIV (Estabrook et al., 2012). Likewise, Wang and Grimm (2012) showed that the reliabilities of the iSD and intraindividual variance (iSD²) were lower than that for the intraindividual mean and, depending on the magnitude of individual differences in IIV and measurement error, can be unacceptably low.

2.2 Root mean squared successive difference (rMSSD)

The strength of the rMSSD, compared with the iSD, is that it takes the ordering of observations into account. The difference between successive observations is squared, and the square root of the mean of these squared differences comprises rMSSD. Therefore, in the examples from above, the sequence 4-3-2-1 has an rMSSD of 1, but the sequence 1-4-2-3 has an rMSSD of 3.74. The rMSSD is well known to psychophysiology, as it is often applied to the interbeat interval and used as a measure of heart rate variability (Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology, 1996). A higher rMSSD reflects more IIV.

Use of the rMSSD with cortisol observations (as typically measured) is complicated by the large interval between evening and next-morning observations, which would strongly influence a series that used all observations across multiple days. However, applied within a day, it may provide a reasonable measure of cIIV. Using this approach with the data shown in Figure 1, A and B have the lowest mean rMSSD across the three days (0.26 and 0.14, respectively), and C and D have the highest (0.38 and 0.32, respectively). Note, however, that A and D, who are ostensibly the least and most variable people, have similar mean rMSSD. This can occur because larger deviations (e.g., zig-zag patterns) and steeper slopes both increase the rMSSD. For example, although 4-3-2-1 has a smaller rMSSD than 1-4-2-3, 3-3-2-2 has an even smaller rMSSD. Therefore, A has a larger rMSSD than B as a function of having steeper slopes. The rMSSD can be applied to residuals to isolate net from time-structured differences.

Like the iSD, rMSSD could also be applied to a series of derived variables over days to yield, for example, slope cIIV. This application of the rMSSD to cIIV is more straightforward to interpret, because in the absence of longer-range trends (e.g., a trend for diurnal slopes to become flatter over a matter of weeks, months, or years), a larger rMSSD reflects larger fluctuations between adjacent observations.

Part of the difficulty in interpreting the rMSSD lies in the fact that it is a combination of the iSD and the autocorrelation (AR(1); the correlation between the current observation and the immediately previous one; see next section.) Mathematically, MSSD = 2*iSD²*(1-AR(1)) (Jahng et al., 2008). Therefore, larger rMSSD can occur because either the iSD is larger or the autocorrelation is smaller. If IIV due to all causes is of interest, then the rMSSD may be appropriate (Jahng et al., 2008). However, if they are thought to represent different processes with potentially different effects, then each should be estimated separately (Wang et al., 2012). For example, both high iSD (more IIV) and high autocorrelation (less IIV) in affect are associated with poorer psychological health (Hardy & Segerstrom, 2016; Kuppens et al., 2010). If these two measures of IIV were combined in the rMSSD, they would offset each other, and their individual relationships would be obscured. Finally, because the rMSSD is related to the iSD, the cautions that apply to the iSD (e.g., control for the iM) also apply to the rMSSD.

2.3 Autocorrelation

The autocorrelation is the correlation between the current observation and the immediately previous one. A higher autocorrelation reflects more resistance to dramatic change, or “inertia” (Kuppens, Allen, & Sheeber, 2010, p. 984). High autocorrelation means that a variable at time t can be predicted well from itself at t-1. Therefore, a higher autocorrelation reflects less IIV. Time-structured IIV can have quite high autocorrelation: A linear slope by definition implies that adjacent observations are more alike than observations more distant in time (e.g., as in the series 4-3-2-1 as compared with the series 1-4-2-3).

The autocorrelation can be estimated using multilevel modeling with an AR(1) random coefficient (Wang et al., 2012). Peeters and colleagues (2004) employed a multilevel model with 3 levels (people, days, and observations) and modeled the cortisol autocorrelation only at the observation level. A two-level model could similarly be used to model the autocorrelation at the day level for derived variables. However, because the autocorrelation is a function of the MSSD and the iSD², it is simple to calculate these two parameters and solve for the autocorrelation ρ: ρ = 1 – (MSSD/(2*iSD²)).

2.4 Derivation

The previous strategies to quantify cIIV (iSD, rMSSD, and autocorrelation) can be applied to either the observations net of the daily slope (e.g., residuals) or the daily slopes themselves. It is possible to estimate parameters for slope and net cIIV using ordinary least-squares regression to derive both. For each person and day, cortisol observations (log transformed to simplify the relationship between cortisol and time of day) are regressed on clock time, and the individual slopes and root mean squared errors (RMSE) are output. Each person therefore has d days’ worth of slopes and d values of RMSE. Slope cIIV can then be characterized using any of the above strategies, and net cIIV can be characterized by taking the mean of the RMSE across days (iRMSE). The advantage of this strategy is that the same model generates both the slope and the net cIIV. It is also accessible in that it does not require complex statistical modeling. However, multiple observations per day are required for the residuals to have any meaning, and missing data could provide a further challenge.

Derivation can also be accomplished using multilevel models. For each person and day (Level 2), cortisol observations are regressed on clock time (Level 1), including a random slope of time. These models calculate a fixed effect of time across all people and days and a random effect of time for each person and day, which is the difference between the fixed slope and slope on a particular day for a particular person. Variability in these random effects reflects slope cIIV. Variability in the residuals from the model reflects net cIIV.

2.5 Multilevel prediction

The most complex approach to assessing IIV is to integrate measures of IIV and their correlates in a single multilevel model. The advantage of this approach is that a single model is used across all people and observations; however, these complex models may not be accessible to the average data analyst. Hoffman (2007) provides a description of these models when the predictor of IIV is continuous and syntax on the internet (http://www.lesahoffman.com/Research/MLM.html). Kuppens and Yzerbt (2014) provide a description when the predictor is categorical, including syntax for running the model. Another disadvantage is that although the relationship between the predictor and IIV can be tested in an integrated model, these models do not routinely output descriptive information about the IIV per se.

3. Reliability and validity of cIIV measurement approaches: Simulated data

3.1 Data simulation and analysis

By constructing datasets with known properties, it is possible to observe which analytic strategies are best able to detect those properties: “Applying statistical methods to simulated data … helps us better to understand those methods” (Gentle, 2009, pp. xi-xii). The purpose of these simulated data is to investigate the relationships among different ways of operationalizing cIIV and their validity with regard to known differences in slope cIIV and net cIIV.

To simulate slopes, a normal distribution (M = −1) having either a large or small SD was specified, and 14 slopes (representing “days”, a number selected as large but not unobtainable for a study of cIIV) were drawn at random from this distribution for each “person”. These slopes were then used to generate cortisol values at 7 equally spaced observations in each “day” (again, selected as a large but not unobtainable number) by predicting the observation value from time of day and the slope for that “person” and “day”. Therefore, each “person” had 98 values (14 “days” with 7 observations/”day”). To simulate random residuals, a normal distribution (M = 0) with either a large or small SD was specified, and an error was drawn at random from this distribution and added to each observation.

Two sets of 1000 datasets each were created. For each of the slope datasets, 50 “people” came from a distribution with high slope variance and 50, low (SDs = 0.5 vs. 0.3), but both groups came from a distribution with the same, low error variance (SD = 0.2). Therefore, in each slope dataset, one group (high variance) had slopes and residuals that resembled Figure 1 (B), and one group (low variance) resembled Figure 1 (A). For each of the net datasets, 50 “people” came from a distribution with high error variance and 50, low (SDs = 0.5 vs. 0.3), but both groups came from a distribution with the same, low slope variance (SD = 0.2). Therefore, in each net dataset, one group (high variance) had slopes and residuals that resembled Figure 1 (C), and one group (low variance), Figure 1 (A).

cIIV parameters were calculated for three types of IIV in “cortisol”. The first was the raw cIIV, which was calculated over all observations for each person. Although these data, which do not differentiate between slope cIIV and net cIIV, were not expected to best reflect cIIV at either level, this relatively naïve approach was included for comparison. The iSD was calculated across all values, the rMSSD was taken based on all differences within the same day (i.e., excluding the interval between the last value on day d and the first on day d+1), and the autocorrelation was calculated from the iSD² and the MSSD from all observations, as shown above under “Autocorrelation”. SAS syntax for all computations is included in the Supplemental Online Material A.

The second type was the slope cIIV. Time slopes were calculated from MLMs with time at Level 1 and people*days at Level 2. Random effects of time (i.e., the individual differences in slopes for each person and day) were output and are referred to as MLM slopes. The iSD, rMSSD, and autocorrelation were calculated for the MLM slopes. Slopes were also calculated by regressing time on “cortisol” values for each person and day and are referred to as regression slopes. The iSD of the regression slopes was included to assess its similarity to that obtained from the MLM slopes.

The third type was the net cIIV. Residuals were output from the MLMs that generated the MLM slopes, and the RMSE was output for the regression models that generated the regression slopes. The iSD, rMSSD, and autocorrelation were calculated for the MLM residuals.

Correlations among the cIIV parameters and between them and high vs. low variance group were computed individually in each of the 1000 datasets. From the resulting distributions of 1000 correlations, the mean correlations and bootstrapped 95% confidence intervals (CI) were calculated and are shown in Table 2 by cIIV type (raw, slope, net; the full correlation table is available in the Supplemental Online Material B). To minimize bias in these estimates, correlations were converted from r to Z, the mean and CI were calculated, and the estimates were converted back to r (Corey, Dunlap, & Burke, 1998).

Table 2.

Correlations among measures of cIIV within type (raw, slope, net) and correlations between measures of cIIV and variance group (high or low).

(A) Slope cIIV datasets
	1. r [95% CI]		2. r [95% CI]		3. r [95% CI]		Variance: high (1) vs. low (0) r [95% CI]		iM r [95% CI]
Raw values
1. iSD	-	-					.29	[.21–.37]	.24	[.04–.42]
2. rMSSD	.99	[.99–.99]	-	-			.28	[.20–.36]	.24	[.04–.41]
3. AC	.18	[−.05–.41]	.16	[−.07–.38]	-	-	.55	[.46–.63]	.18	[−.03–.37]
Slopes
1. iSD (MLM)	-	-					.78	[.71–.83]	.08	[−.11–.26]
2. rMSSD	.29	[.10–.47]	-	-			.13	[−.07–.32]	.01	[−.17–.21]
3. AC	.05	[−.14–.22]	–.23	[−.40 – −.04]	-	-	.00	[−.04–.04]	.00	[−.27–.28]
4. iSD (regression)	1.0	[1.0–1.0]	.29	[.10–.47]	.05	[−.14–.22]	.78	[.71–.83]	.08	[−.10–.26]
Net
1. iSD (MLM)	-	-					.32	[.15–.45]	-	-
2. rMSSD	.47	[.33–.58]	-	-			.94	[.91–.95]	-	-
3. AC	.09	[−.10–.28]	−.12	[−.32–.06]	-	-	.03	[−.16–.22]	-	-
4. iRMSE (regression)	.90	[.84–.93]	.48	[.33–.60]	−.12	[−.31–.09]	.26	[.08–.41]	-	-

(B) Net cIIV datasets
	1. r [95% CI]		2. r [95% CI]		3. r [95% CI]		Variance: high (1) vs. low (0) r [95% CI]		iM r [95% CI]
Raw values
1. iSD	-	-					.16	[−.04–.34]	.01	[−.20–.18]
2. rMSSD	.68	[.55–.77]	-	-			.76	[.67–.82]	.01	[−.20–.20]
3. AC	.08	[−.13–.28]	−.23	[−.41– −.05]	-	-	−.18	[−.34– −.01]	−.02	[−.25–.20]
Slopes
1. iSD (MLM)	-	-					.15	[−.04–.32]	.01	[−.19–.23]
2. rMSSD	.83	[.75–.88]	-	-			.13	[−.07–.32]	.01	[−.18–.21]
3. AC	.08	[−.13–.26]	−.48	[−.63– −.31]	-	-	.00	[−.20–.18]	.00	[−.20–.21]
4. iSD (regression)	1.0	[.99–1.0]	.83	[.75–.88]	.08	[−.13–.26]	.15	[−.04–.32]	.01	[−.19–.23]
Net
1. iSD (MLM)	-	-					.95	[.93–.96]	-	-
2. rMSSD	.98	[.97–.98]	-	-			.93	[.91–.95]	-	-
3. AC	−.08	[−.28–.12]	−.25	[−.44– −.07]	-	-	–.08	[−.28–.12]	-	-
4. iRMSE (regression)	.99	[.98–.99]	.99	[.98–.99]	−.16	[−.35–.04]	.94	[.92–.95]	-	-

Note: CI = confidence interval; iM = intraindividual mean; iSD = individual standard deviation; rMSSD = root mean squared successive difference; MLM = multilevel model; iRMSE = individual root mean squared error. Mean for raw values is the mean of raw values for each individual; mean for slopes is the mean of the random slopes for each individual.

3.2 Results and conclusions

Table 2(A) contains the correlations for the slope datasets, which had differences in the slope variance but not the residual variance. The correlation matrices (on the left half of the table) show that for all types of cIIV (raw, slope, net), the iSD and rMSSD were moderately to highly correlated with each other (r = .29 – .99) and less strongly correlated with the autocorrelation (r = −.23 – .18). In addition, the slope iSDs from MLM and regression were indistinguishable from each other (r = 1.00), suggesting that the procedures used to derive slopes (MLM or regression) were equivalent for the purposes of calculating the slope iSD.

The correlations between cIIV measures and slope variance group (high = 1, low = 0) are presented on the right half of the table. These correlations reflect the validity of cIIV measures insofar as there are known differences in cIIV that a valid method should capture at the correct level. Both the iSD of the MLM slopes and of the regression slopes captured group differences in slope cIIV (r = 0.78 for both). There were also, however, correlations between slope variance group and most measures of raw cIIV and net cIIV. To test whether these correlations were artifacts of the relationship with slope cIIV, they were repeated partialling the iSD of the MLM slopes. All of these partial correlations were close to 0 (r = −.02 – .03). The only substantial correlation remaining was between slope variance group and the rMSSD of the MLM residuals (r = .86, 95% CI = .81 – .91).

Finally, the corresponding intraindividual mean, which can be confounded with measures of IIV (see Section 2.1), correlated modestly with measures of raw cIIV but not measures of slope cIIV. The correlation of the mean with variance group was .21 (95% CI = .02 – .37) for the raw data and .03 (95% CI = −.04 – .10) for the slope. Correlations between net cIIV and means are not shown because the means of residuals are by definition 0.

Table 2(B) contains the correlations for the net datasets, which had differences in the residual variance but not the slope variance. The iSD and rMSSD were moderately to highly correlated with each other (r = .68 – .98 across data types) and less strongly correlated with the autocorrelation (r= −.48 – .08 across data types), similar to results from the slope datasets. The iSD of the MLM residuals and the iRMSE were nearly indistinguishable from each other (r = .99), suggesting that the procedure (MLM or regression) used to derive residuals or error was not important.

Both the iSD of the MLM residuals and the iRMSE from regression models captured group differences in net cIIV (r = .95 for the iSD and r = .94 for the iRMSE). The relationships between net variance group and the measures of slope cIIV were not large or statistically significant.

Finally, the corresponding intraindividual mean was essentially uncorrelated with the measures of cIIV for raw values (r = −.02 – .01) and for slopes (r = .00 – .01) in these datasets. The correlation of the iM with variance group was .01 (95% CI = −.19 – .20) for the raw data and .00 (95% CI = −.19 – .20) for the slope.

There are some conclusions to be drawn from this simulation study: first, the iSD of the raw data did not effectively capture group differences in cIIV at either level (r = .24 with slope cIIV; r = .16 with net cIIV). Therefore, regardless of the true underlying level of cIIV, taking the iSD of the raw data will not effectively capture this cIIV. In contrast, both the iSD of the slopes and of the residuals captured the corresponding group differences in cIIV well. cIIV of both estimates (slope and net) should be routinely investigated, because a relationship with net cIIV can emerge as an artifact of an underlying, larger relationship with slope cIIV. Second, the relationships with the rMSSD, as in the simple examples from Figure 1, were unpredictable from the underlying qualities of the data. For example, the correlations between slope variance group and the rMSSD of the raw data (r = 0.28) and of the residuals (r = 0.94) were both higher than that between variance group and the rMSSD of the slopes (where the true group differences in cIIV were; r = 0.13). The contribution of both the iSD and the autocorrelation to rMSSD may further contribute to these unpredictable results.

3.3 Effects of sampling design

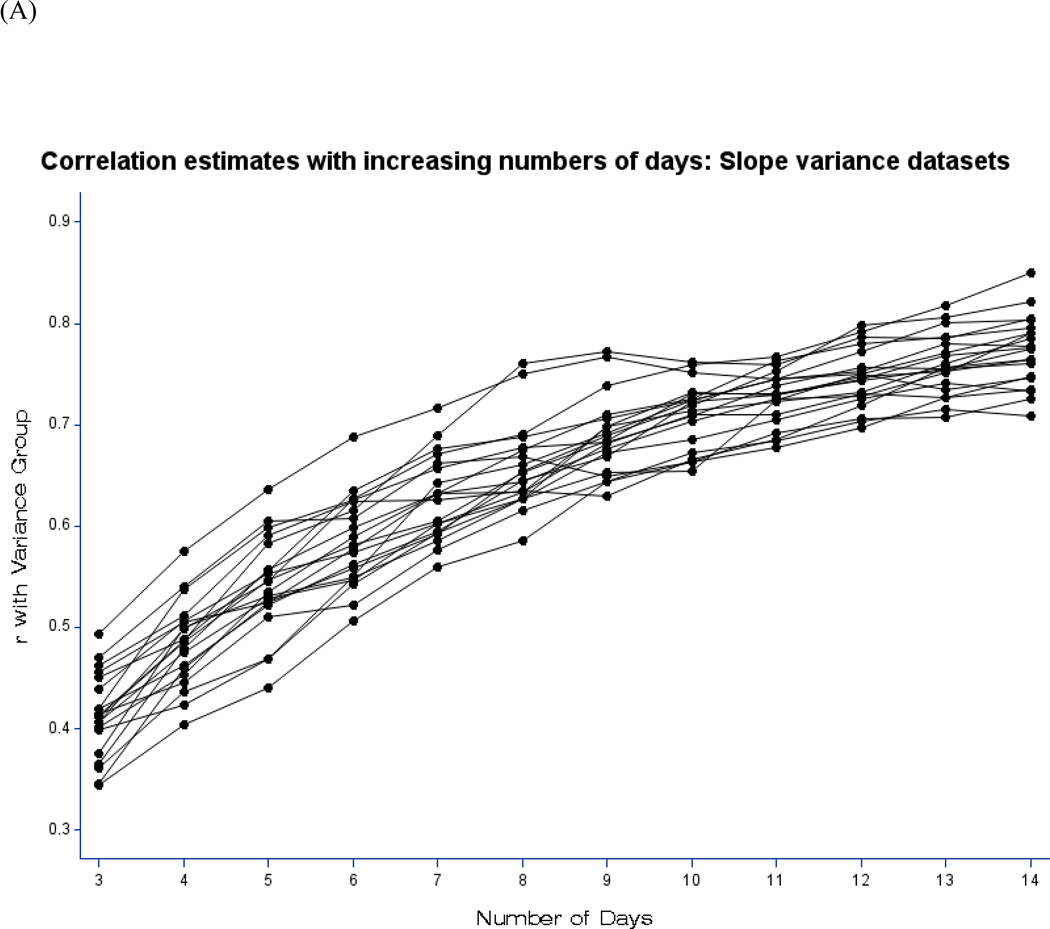
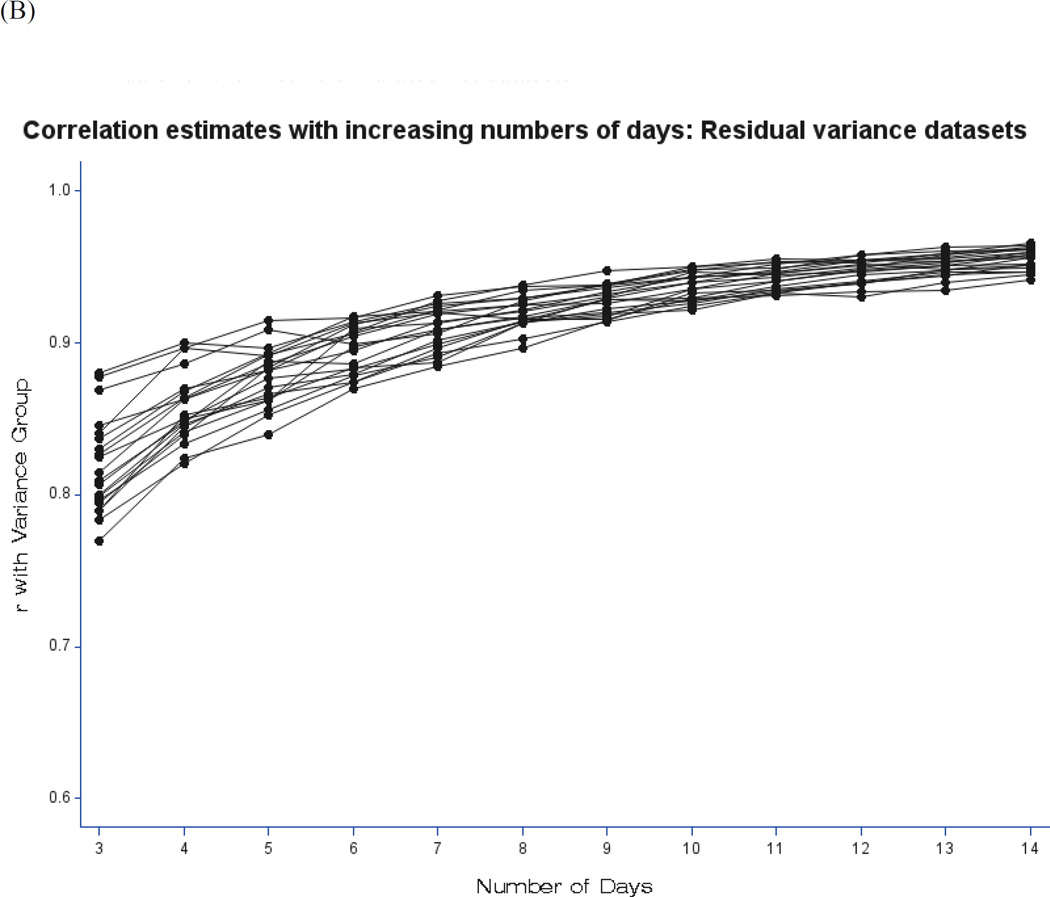
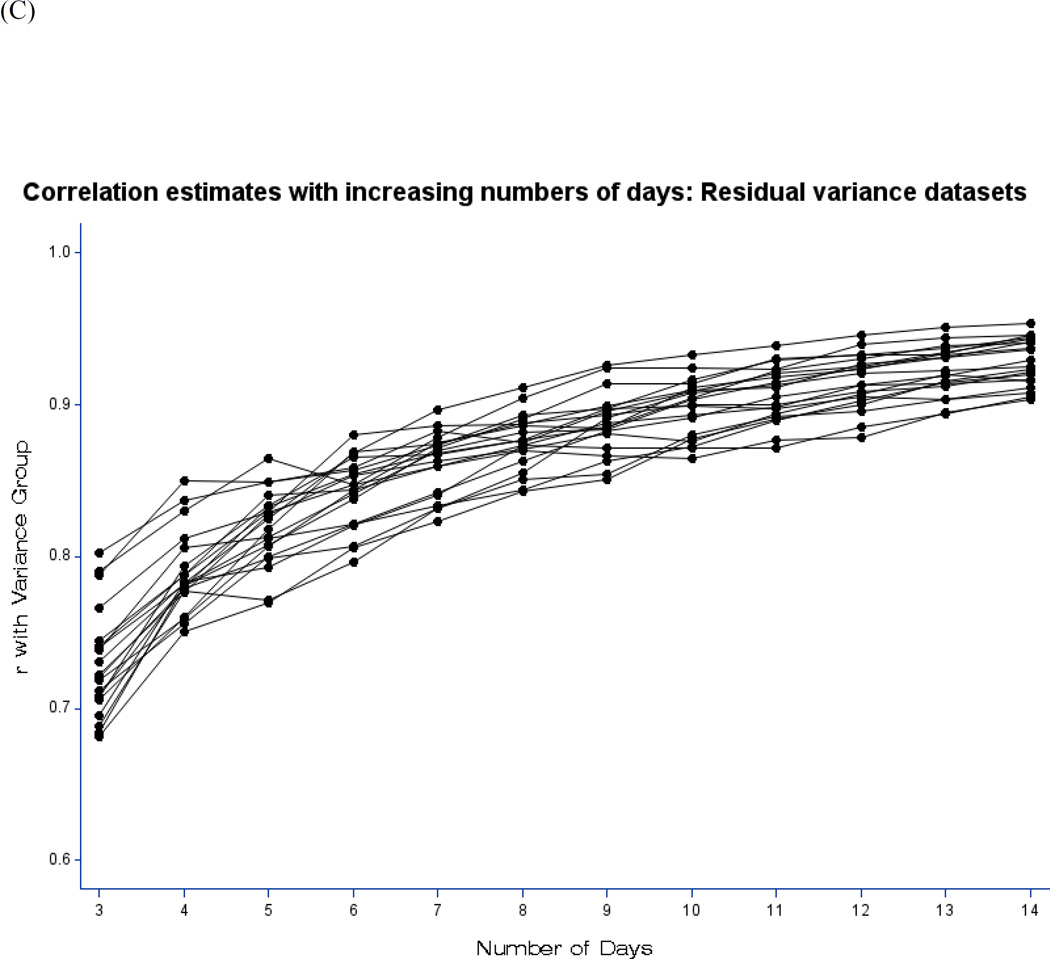
To show the effects of changing the numbers of days contributing to measures of slope and net cIIV, iSDs and their correlations with variance group were recalculated, using incremental numbers of days from 3 to 14. These correlations show what might have resulted had the “investigator” decided to stop data collection after each number of days. Figure 2 illustrates the results for the first 20 datasets. Panel A shows the correlations between high (1) or low (0) variance group and the iSD of the MLM slope in the slope datasets. For slope cIIV, there was an advantage to having more days’ data. Correlations with the iSD based on fewer than about 10 days’ data were clearly attenuated, and the spread of correlation estimates was also larger. The estimates begin to converge and asymptote at about 10 days. Panel B shows the correlations between high (1) or low (0) variance group and the iSD of the MLM residuals in the net datasets. For net cIIV, there was less attenuation (with 7 samples/day, the number of residuals contributing to the iSD increased from 21 at 3 days to 98 at 14 days), but the estimates still began to converge and asymptote at about 7 days.

Figure 2. Effects of number of days of data on the estimation of correlations between measures of cIIV and corresponding criterion group (high or low variance).

(A) Effects of adding days of data on the correlation between variance group and the iSD of the MLM slope for the first 20 simulated slope datasets.

(B) Effects of adding days of data on the correlation between variance group and the iSD of the MLM residuals for the first 20 simulated net datasets

(C) Effects of adding days of data on the correlation between variance group and the iSD of the MLM residuals for the first 20 simulated net datasets, using 4 observations per day.

For comparison, the correlations were recalculated using only the first, third, fifth, and seventh observations on each day (i.e., with 4 samples/day, the number of residuals contributing to the iSD increased from 12 at 3 days to 56 at 14 days). Attenuation was more obvious, and convergence was later. Together, these two graphs suggest that about 50 residuals result in a reasonably accurate and stable estimate of net cIIV.

4. cIIV approaches applied to actual cortisol data

4.1 Data and analysis

To complement the results of the simulations, the same analyses were applied to actual cortisol data. The simulated data had properties (i.e., a diurnal slope and deviations from that slope) that resembled cortisol data, but actual data may have other properties not captured by the simulation (e.g., asynchrony between observations and pulsative secretion). Furthermore, actual data often pose analytic challenges (e.g., missing data) that simulated data do not. Data came from first-year law students who collected saliva four times daily on 15 days (3 consecutive days at 5 waves; for details of the sample, saliva collection, and assays, see Segerstrom et al., 2014). As in the simulated data, the different measures of cIIV were correlated with each other to examine their similarities and differences. Because cIIV is an emerging area of research, there is no clear criterion to correlate with the cIIV measures. However, neuroticism has been associated with higher IIV in multiple psychological domains (Eid & Diener, 1999; Kuppens et al., 2007; Moskowitz & Zuroff, 2004; Robinson & Tamir, 2005; Timmermans et al., 2010). Because some of these domains, such as affect, also correlate with cortisol (e.g., Adam, 2006), neuroticism might also correlate with cIIV.

Neuroticism was measured once for each person at the first wave. There were 5 cohorts of students (i.e., from 5 consecutive incoming classes); the first two completed the Trait Anxiety Inventory (Spielberger, 1985), and the last 3 completed the Neuroticism scale from the NEO-FFI (Costa & McCrae, 1992). Watson and Clark (1984) provide an extensive analysis of the degree to which different measures of negative affectivity (including trait anxiety and neuroticism) correlate with each other, concluding that they are “in fact measures of the same stable and pervasive trait” (p. 465). Under the assumption that both scales capture neuroticism/negative affectivity, we standardized the scores to Z scores within scale, and the standardized scores were used as the measure of neuroticism.

For the purposes of this demonstration and to maximize the number of days available for analysis, waves were ignored (i.e., days were numbered consecutively from 1 to 15). We gauged the appropriateness of this approach by comparing AR(1) coefficients from models (1) with days nested within waves and (2) with days consecutively numbered across waves. These models suggested that there was not serious violation of the structure of the data. For example, the AR(1) of the slopes (from Segerstrom et al., 2014) estimated across 3 days within waves was .15, and estimated across all 15 days was .11. These estimates were small, suggesting that cortisol slope on day d did not strongly predict cortisol slope on day d+1, and there was little change in the AR(1) estimate when it was compared within waves and then ignoring waves. Therefore, we concluded that our approach to maximizing the number of days that contributed to cIIV estimates, although not reflecting an ideal design, was acceptable for these data.

One important difference between the simulated data and the law student data is that in the simulation, we stipulated that all “samples” were taken at exactly the same times. However, in the law student data (and probably all real cortisol data), actual collection times differed. For most models, this was easily accounted for by using actual clock time rather than target time of collection as a predictor (e.g., in MLMs and regressions). However, the rMSSD could be affected by variability in collection time, as longer intervals would be expected to result in more change than shorter intervals. Therefore, the cortisol difference was divided by the time difference to yield cortisol difference/hour before calculating the rMSSD. We encountered another anomaly when calculating the rMSSD of the raw scores: There were a few cases with extremely high rMSSD. Further examination suggested that these were cases with few days’ data (6 or fewer). This finding should reinforce the recommendation that a large number of days be available for calculation of cIIV measures.

4.2 Results and conclusions

Table 3 contains the descriptive statistics for and correlations among the cIIV measures. The estimates below are from only the cases with data from 6 or more days’ data (N = 119). The correlation matrices (on the left half of the table) show that for raw cIIV, the iSD and rMSSD were moderately correlated (r = .39), but for the slope and net cIIV, the iSD and rMSSD were highly correlated (r = .84 – .93). The iSD and rMSSD were less strongly correlated with the autocorrelation (r = −.39 – .33). Most of the correlations between the autocorrelation and other measures of cIIV were positive. In the simulations, autocorrelations correlated positively with other measures of cIIV in the slope datasets, but negatively in the net datasets. Therefore, these correlations in the real data suggest individual differenes in slope cIIV. In addition, the slope iSDs from MLM and regression were highly similar to each other (r = .86 – .88), suggesting that the procedures used to derive slopes (MLM or regression) were similar for the purposes of calculating the slope iSD. Finally, the mean autocorrelation in the sample was only substantial (and negative) for the MLM residuals (r = −.33, t(119) = 15.14, p < .0001) and not for the raw data (t(115) = 1.65, p = .10) or the slopes (t(119) = .38, p = .70). The lack of a significant autocorrelation suggests why the rMSSD and iSD were highly correlated in these data: The equation showing that the MSSD is a function of the iSD² and the autocorrelation also implies that as the autocorrelation approaches 0, the correlation between the MSSD and the iSD² will approach 1.0.

Table 3.

Correlations among measures of cIIV within type (raw, slope, net) and correlations between measures of cIIV and neuroticism and intraindividual means

	1. r	2. r	3. r	Neuroticism r	iM r
Raw values
1. iSD	-			−.15†	−.06
2. rMSSD	.39***	-		.00	−.03
3. Autocorrelation	.18*	−.25*	-	.06	.06
Slopes
1. iSD (MLM)	-			−.21*	.28*
2. rMSSD	.84***	-		−.20*	.26*
3. Autocorrelation	.33**	−.13	-	−.09	.08
4. iSD (regression)	.86***	.70***	.31**	−.21*	.23*
Net
1. iSD (MLM)	-			−.13	-
2. rMSSD	.93***	-		−.13	-
3. Autocorrelation	−.02	−.39***	-	.03	-
4. iRMSE (regression)	.88***	.93***	−.32**	−.05	-

^†p < .10;

^*p < .05;

^**p < .001;

^***p < .0001

Note: iM = intraindividual mean; iSD = individual standard deviation; rMSSD = root mean squared successive difference; MLM = multilevel model; iRMSE = individual root mean squared error. Mean for raw values is the mean of raw values for each individual; mean for slopes is the mean of the random slopes for each individual. Correlations between net cIIV and means are not shown because the means of residuals are by definition 0.

The rightmost columns of Table 3 show the correlations with neuroticism and the cortisol iMs. The raw cIIV measures were not strongly related to individuals’ raw cortisol iMs; however, there were statistically significant correlations between individuals’ slope iM and their measures of slope cIIV. Recall that such correlations are why analyses of cIIV should control for the iM. Neuroticism was essentially unrelated to raw cortisol iMs (r = .06, p = .51) and cortisol slope iMs (r = .08, p = .41). However, neuroticism was negatively correlated with measures of cIIV, particularly slope cIIV. These correlations were slightly larger after controlling for slope iMs (iSD of MLM slopes: pr = −.24, p = .008; rMSSD: pr = −.23, p = .012; iSD of regression slopes: pr = −.24, p = .010). The smaller correlations between neuroticism and raw and net cIIV were, as in the simulation study, artifacts of the larger correlations with slope cIIV. After partialling the iSD of the MLM slopes, these correlations were close to 0 (iSD of raw values: pr = −.07, p = .46; iSD of MLM residuals: pr = .03, p = .78; rMSSD of MLM residuals: pr = −.01, p = .94).

4.3 Reliability

To explore reliability, a split-half reliability analysis in which iM and iSD of raw scores, MLM slopes, and MLM residuals were calculated separately for the odd- and even-numbered days (i.e., basing reliabilities on 7–8 days’ data) and correlated with each other. The reliability of the mean was very high (r = .88, p < .0001). As expected, however, the reliability of the iSD of the raw data was lower (r = .60, p < .0001), and the reliability of the iSD of the derived measures was lower still (slopes, r = .31, p = .0006; residuals, r = .38, p < .0001). Therefore, consistent with the simulated data, fewer than 10 days’ data may not yield reliable estimates of cIIV.

4.4 Multilevel prediction models

For comparison with the correlational results, Table 4 shows the results of using MLM prediction models to assess the relationship between neuroticism and the slopes and residuals (Hoffman, 2007). Preliminary analyses recommended by Hoffman (2007) indicated that slopes could be detrended across days individually for each person by including a random effect of day (i.e., allowing each person to increase or decrease systematically over the 15 days), but no such detrending was necessary for residuals. For slopes, there was no statistically significant fixed effect of neuroticism (p = .25), indicating that people who differed in neuroticism did not have different average slopes. However, there was a statistically significant negative relationship between neuroticism and slope cIIV (the random neuroticism estimate, p = .0009), indicating that people higher in neuroticism had more variability in their slopes. This finding was consistent with the correlations in Table 3 and accounted for 1.5% of the unexplained variance compared with a model without neuroticism. For residuals, one would not expect a statistically significant fixed effect (as each person’s mean residuals should be close to 0), which was the case. As with the correlations, there was a smaller negative relationship between neuroticism and net cIIV, accounting for 0.5% of the unexplained variance. However, this relationship was statistically significant (p = .005), unlike the correlations.

Table 4.

Results of MLM models incorporating neuroticism as a predictor of cIIV (MLM slopes and residuals).

	Slopes as Outcome		Residuals as Outcome
	Estimate	SE	Estimate	SE
Fixed effects
Intercept	.00045	.00016	.0014	.0093
Day	.00034	.00028	-	-
Neuroticism	.00019	.00016	.0098	.0096
Random effects
Intercept variance	.00023*	.00004	.0055*	.0014
Day variance	.0000052*	.0000012
Neuroticism	.−13*	.04	.−052*	.019
Unexplained variance	.00102*	.00004	.26*	.005

^*p < .05

5. Conclusions and Recommendations

Based on this review, we offer the following recommendations for quantifying cIIV. First, measures of cIIV that confound levels of measurement should not be used. Instead, where there is the potential for variability between and within days, cIIV at each of those levels should be calculated separately. Estimates from MLM (slopes and residuals for each person) and regression (slopes and RMSE for each person) are similar and equally valid. Both the simulation and law student data suggest that correlations with net cIIV should be interpreted with caution, as they may be an artifact of a larger, true underlying relationship with slope cIIV. Second, the rMSSD should be avoided, as it confounds the iSD and the autocorrelation.

Third, recommended sampling frames are similar to those suggested for estimation of the slope (Segerstrom et al., 2014): at least 10 days’ data for estimation of slope cIIV. The recommended number of samples/day, however, differs. For estimation of the slope, morning and evening samples are sufficient (Kraemer et al., 2006; Segerstrom et al., 2014). However, for estimation of net cIIV, this approach is not appropriate because it does not yield any residuals. Because 50 residuals appears to be reasonable in terms of providing a reasonably reliable and accurate measurement, sampling that yields 50 residuals (e.g., 5 samples/day over 10 days) is recommended.

We suggest the following analytic plan:

1. Check cortisol data for floor and ceiling effects. Check to ensure that a log transformation of cortisol values yields a linear relationship with time. Check for missing data, particularly waking or evening samples, which disproportionately affect slopes (Segerstrom et al., 2014).

2. Obtain estimates for slopes and RMSE or residuals, using regression or MLM.

3. If data are clustered (e.g., days within waves), examine whether an autocorrelation exists across within waves, and whether it changes when waves are ignored. If there is an autocorrelation within waves that is noticeably decreased when ignoring waves, it may not be a valid approach to ignore clustering.

4. Check for systematic time trends over days by regressing slopes and residuals on day using an MLM with people at Level 2 and fixed and random effects of day at Level 1. The question of whether a trend is a real or spurious source of cIIV is a substantive one that can only be answered by a particular scientific goal. For example, in affective IIV, if negative affect declines over a diary period, one might be concerned about reactivity to the diary questions rather than real change and detrend the data on that basis. On the other hand, if negative affect declines following a stressful event, one might conclude that this change is of interest as a contributor to IIV and not detrend the data.

5. Obtain the iSD of the slopes and residuals. The autocorrelation may also be obtained if it is of interest.

6. Any iSD should be accompanied in predictive models by the iM of that parameter.

cIIV is a promising direction for research; indeed, that research has already yielded interesting results (Marceau et al., 2013; Peeters et al., 2004; Sannes et al., 2016). In the present paper, the substantive result for the law students suggests that people higher in neuroticism had less variable slopes. This finding is contrary to much of the psychological literature, in which higher neuroticism has been associated with more variability in affect, for example (Eid & Diener, 1999; Kuppens et al., 2007; Timmermans et al., 2010). However, there is an important distinction between raw iSD (e.g., as used to operationalize affect IIV) and slope iSD (e.g., as used to operationalize slope cIIV): A high slope iSD does not imply disruption of the diurnal rhythm of cortisol across the day, although the slope may vary across days. One way of interpreting the present finding is that people higher in neuroticism had less flexibility in cortisol regulation (cf., Hardy & Segerstrom, 2016), which could be maladaptive in a system that is designed to be sensitive to environmental demands. These findings can be contrasted with the higher net cIIV observed in depressed (but not PTSD) patients compared with controls (Yehuda et al., 1996). These findings reinforce the fact that there are many ways in which cortisol can be sampled and cIIV measured, with implications for the conclusions that will be drawn. The present review was designed to illustrate which of these are likely to yield reliable, reproducible, and valid results.

Highlights.

• There are multiple ways to measure intraindividual variability in cortisol, including the individual standard deviation, root mean squared successive difference, and autocorrelation

• Individual standard deviations in simulated cortisol slopes and residuals best captured known underlying differences in variance

• In simulated cortisol data, 10 slopes and 50 residuals resulted in reliable and stable estimates of the individual standard deviations