Understanding metabolism with flux analysis: from theory to application

Abstract

Quantitative and qualitative knowledge of metabolic rates (i.e. fluxes) over a metabolic network and in specific cellular compartments gives insights into the regulation of metabolism and helps to understand the contribution of metabolic alterations to pathology. In this review we introduce methodology to resolve metabolic fluxes from stable isotope labeling and relevant techniques in model development, model simplification, flux uncertainty analysis and experimental design that together is termed metabolic flux analysis. Finally we discuss applications using metabolic flux analysis to elucidate mechanisms pertinent to tumor cell metabolism. We hope that this review gives the readers a brief introduction of how flux analysis is conducted, how technical issues related to it are addressed, and how its application has contributed to our knowledge of tumor cell metabolism.

1. Introduction

Metabolism is essential to cell physiology by providing energy, building blocks, signaling molecules and redox reagents that together are indispensable for cell survival and growth. Metabolic networks for multiple organisms, including human tissues, have been annotated (Thiele et al., 2013; Thiele and Palsson, 2010) and other ‘omics’ datasets, including genomics, transcriptomics, proteomics and metabolomics, have expanded rapidly in the last decade (Yizhak et al., 2015). However, the most biologically and physically relevant aspects of metabolism, metabolic fluxes, cannot be completely determined directly from other omics data. In analogy to the traffic condition in a city (Hiller and Metallo, 2013; Sauer and Zamboni, 2008), the city is in a traffic jam if its streets are filled with slowly moving cars. Knowing how many cars are on the road (concentration of metabolites), how many people are driving on each road (abundance of transcripts or proteins), the reasons for why people would be driving at a certain time (genetic events and environmental factors) are insufficient to know exactly whether the cars are stalled or are able to move freely (flux configuration in the metabolic network).

Due to the inability of molecular measurements to completely determine metabolic fluxes, technical approaches towards resolving metabolic fluxes are indispensable. Here we refer to metabolic flux analysis as the collective set of techniques and information related to rates of metabolic reactions taking place inside a cell and exchange of metabolites between the cell and the extracellular environment or between intercellular compartments. For exchange fluxes through which metabolites are absorbed or released by the cells, the fluxes can be determined by time-dependent profiles of metabolites in the media since the exchange flux is the only factor contributing to the dynamics of metabolites in media (Jain et al., 2012). However, in the case of intracellular fluxes, metabolite kinetics are determined by multiple chemical reactions producing or consuming the metabolite or by its exchange into and out of numerous cellular compartments, which hinders direct evaluation of fluxes from isolated metabolite dynamics alone. On the other hand, most metabolic network models contain more fluxes than metabolites, resulting in an underdetermined system if only information on the level of metabolites is considered.

Stable isotope labeling experiments, or often referred to as tracing experiments, in which incorporation of labeled substrates into intermediates of the metabolic network is utilized to resolve the fluxes, afford a solution. Most frequently used tracers in tracing experiments are ¹³C-labeled substrates, but other tracers including ²H, ¹⁵N and ¹⁸O are also used (Klein and Heinzle, 2012). Besides its application in quantitatively determining the flux configuration in a metabolic network, tracing experiments are also applicable in qualitative evaluation of metabolic fluxes such as the dependence of metabolic pathways on certain carbon sources and the partitioning of fluxes into diverging pathways at a branch point (Buescher et al., 2015). At the most descriptive level, a pathway's activity that originates from a substrate is implied if intermediates in this pathway become significantly enriched with when that labeled substrate is supplemented. This strategy is widely applied in identifying nutrient dependencies of metabolic pathways in cancer, which will be discussed further in Section 4. Partitioning of metabolic flux into multiple pathways at a branch point could also be qualitatively evaluated if the products of the alternative pathways have different labeling patterns. Examples include the glycolysis versus oxidative branch of pentose phosphate pathway traced by [1-¹³C]-glucose (Zhao et al., 2016), oxidative versus reductive metabolism of glutamine through the TCA cycle traced by [U-¹³C]-glutamine (Mullen et al., 2012), and pyruvate entering TCA cycle through pyruvate dehydrogenase (PDH) versus through pyruvate carboxylase (PC) traced by [U-¹³C]-glucose (Sellers et al., 2015) or [1-¹³C]-pyruvate (Cheng et al., 2011). In order to achieve a quantitative evaluation of fluxes, labeling patterns obtained from tracing experiments must be combined with detailed information of the metabolic network including both stoichiometry and atom-transition matrices. There are several techniques that vary in model, algorithm and experimental data used, which have been introduced by previous reviews and protocols (Buescher et al., 2015; Niedenführ et al., 2015; Shestov et al., 2013; Yuan et al., 2008; Zamboni, 2011; Zamboni et al., 2009) and will be discussed in detail in the next section.

2. Overview of methods

2.1 Isotopic steady-state methods

Among the myriad of techniques for flux analysis, isotopic stationary metabolic flux analysis, or ¹³C metabolic flux analysis (¹³C MFA), is the most commonly used method (Buescher et al., 2015; Wiechert et al., 1999, 1997; Wiechert and de Graaf, 1997; Zamboni et al., 2009). By feeding cells with ¹³C labeled substrates, different distributions of carbon fluxes into branched and convergent metabolic pathways result in different steady state distribution of isotopomers for intermediate metabolites, which can be determined by techniques like mass spectrometry (MS), or nuclear magnetic resonance (NMR) spectroscopy and utilized in inferring the flux ratio at branching points or absolute fluxes, with the supplementary knowledge of absolute exchange fluxes with the extracellular environment. Here we refer to isotopomers as metabolites that only differ in isotope distribution. For a molecule with N carbon atoms, there are 2^N isotopomers in total. Two points regarding the metabolic network are essential considerations: the stoichiometry and atom mapping information for each reaction. With this knowledge and under the assumption of metabolic steady state (metabolite concentrations do not change with time) and isotopic steady state (isotopomer distributions do not change with time), algebraic equations connecting metabolic fluxes and steady state isotopomer distributions can be derived by balancing the rate of production and consumption of each isotopomer:

$$\frac{{\mathrm{dM}}_{\mathrm{ij}}}{\mathrm{dt}}={\sum }_{\mathrm{k}\in \ln \left(\mathrm{i}\right)}{V}_{\mathrm{k}}{\sum }_{\Theta \in \mathrm{Gen}(\mathrm{k},\mathrm{i},\mathrm{j})}{\prod }_{(\mathrm{l},\mathrm{m})ϵ\Theta }{\mathrm{r}}_{\mathrm{lm}}-\left({\sum }_{\mathrm{k}ϵ\mathrm{Out}\left(\mathrm{i}\right)}{\mathrm{V}}_{\mathrm{k}}\right){\mathrm{r}}_{\mathrm{ij}}=0$$ (1).

In this equation, M_ij is the abundance of the jth isotopomer of metabolite M_i, In(i) and Out(i) are the sets containing all indexes of fluxes producing and consuming M_ij, respectively. Gen(k,i,j) is the set containing all substrate isotopomer combinations that produce M_ij via the flux v_k, r_ij is the fraction of isotopomer M_ij, v is the flux vector which is also constrained by the metabolic steady state assumption and nonnegative constraints:

$$\mathbf{S}\ast \mathbf{v}=0,\mathbf{v}\ge 0$$ (2).

Here, S is the stoichiometric matrix describing a metabolic network.

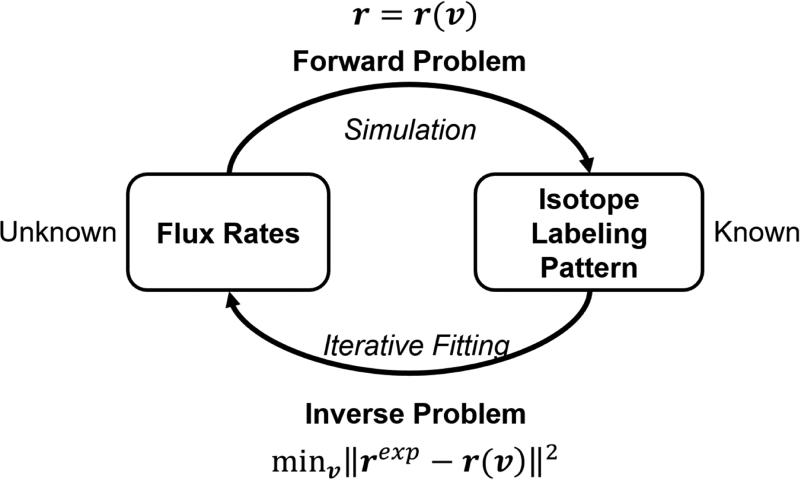
By solving the algebraic equations, the flux vector v can be calculated from the isotopomer distribution r = {r_ij}. With efficient algorithms for simulating profiles of steady state isotopomer distributions available, the unknown flux variables can be evaluated by solving a large-scale constrained non-linear least squares problem, in which the difference between isotopomer distribution profiles simulated from assumed flux configurations and measured by experiments is minimized (Fig 1):

$${\min }_{\mathbf{v}}{\Vert {\mathbf{r}}^{\exp }-\mathbf{r}\left(\mathbf{v}\right)\Vert }^2$$ (3).

The non-linear least squares problem could be solved using optimization algorithms such as sequential quadratic programming, the Levenberg-Marquardt algorithm and so on (Boggs and Tolle, 1995; Marquardt, 1963; Wiechert et al., 1997). Note that since the algebraic equations (1) and the metabolic steady state constraints (2) are both linear to the flux variables, solutions of the equations (1) and (2) form a convex cone, that is, all linear combinations of some feasible flux configurations with nonnegative coefficients will still be feasible solutions. Thus, absolute flux rates cannot be determined solely by solving (1) and (2). In order to infer absolute fluxes, tracing experiments must be combined with metabolite exchange rates measured by other techniques or assumptions on metabolic objective functions, which are commonly used in flux balance analysis.

Fig 1. Metabolic flux analysis as an inverse problem.

Inferring metabolic fluxes from isotope labeling profiles is typically done by minimizing the difference between isotope labeling patterns simulated from fluxes and measured by experiments.

A simpler alternative of ¹³C-MFA, flux ratio (FR) analysis, has some practical advantages over ¹³C-MFA when the goal is to determine relative forward fluxes of converging pathways. Mass isotopomer balance equations that have very simple forms are easily written at branch points of the metabolic network, which enables direct calculation of the relative fluxes from mass isotopomer distribution vectors (MDVs) of the product and the alternative substrates (Fischer and Sauer, 2003; Zamboni et al., 2009). Besides its simplicity in computation, FR doesn't require the complete topology of metabolic network to be constructed, thus facilitating application where there is incomplete knowledge of the metabolic reaction network.

2.2 Isotopic non-steady state methods

A limitation of ¹³C-MFA is that it is based on the assumption of isotopic steady state, which is hard to determine and can take several hours upon addition of the labeled substrate in a mammalian system. This analysis is also difficult to interpret when cells are undergoing a response to a perturbation such as a drug treatment or growth factor withdrawal. By relaxing the assumption of isotopic steady state while keeping the assumption of metabolic steady state, we have isotopically non-stationary metabolic flux analysis (INST-MFA), which essentially treats the metabolic network as a dynamical system. Instead of isotopomer balance equations at the steady state which are solved in ¹³C-MFA, ordinary differential equations (ODEs) describing how the isotopomer distributions change with time are solved to simulate the dynamical isotopic profile, which is fit to corresponding experimental data (Wiechert and Nöh, 2013). In INST-MFA, since isotopomer distribution is measured on multiple time points and isotopomer dynamics is simulated by solving ODEs instead of making measurements on only one time point and solving linear equations, it is apparently more demanding in computational time than ¹³C-MFA.

A special case of INST-MFA, termed kinetic flux profiling (KFP), is also applied in resolving metabolic fluxes due to its simplicity in data analysis (Munger et al., 2008; Yuan et al., 2008, 2006). In KFP time-dependent profile of unlabeled fraction of a metabolite is measured after switching to labeled substrate, which leads to exponential decay of the unlabeled form, in which the rate is determined by flux through the metabolite. This explicit form enables direct parameter estimation instead of fitting a complex ODE-based model, which is the case of general INST-MFA. For mammalian cells, KFP has been applied in quantifying flux through oxidative pentose phosphate pathway (oxPPP), in which [U-¹³C]glucose was used as the tracer and the exponential decay of unlabeled 6-phosphogluconate was analyzed to infer the oxPPP flux (Fan et al., 2014). Another study applying KFP to mammalian cells profiled the flux configuration in central carbon metabolism to characterize metabolic reprogramming caused by virus infection, thus identifying upregulated fatty acid synthesis in the infected cells as potential antiviral target (Munger et al., 2008). Furthermore, flux ratio analysis could also be extended to flux analysis in isotopic non-steady state (Hörl et al., 2013), but the relative fluxes are evaluated by iterative fitting instead of direct calculation, which is the case of isotopically stationary flux ratio analysis. Also these methods can be extended to evaluate fold changes in metabolic fluxes that occur in the more common setting of comparing two conditions such as wild type and knockout or vehicle vs. drug treated (Huang et al., 2014). Other strategies for improving efficiency of isotopically non-stationary flux analysis include parallel measurements of intracellular and extracellular metabolite pools (Shlomi et al., 2014), using hybrid model containing both isotopically stationary and non-stationary dynamics of metabolites (Tedeschi et al., 2015).

It is worth noting that the assumption of metabolic steady state is still necessary in INST-MFA, or the fluxes, which then vary with time, could not be treated as model parameters. In the case of a non-stationary metabolic system, other techniques are needed to resolve the metabolic fluxes. One approach is to introduce kinetic parameters (e.g. V_max and K_m of enzymes) and functional forms (e.g. Michaelis-Menten mechanism) of the reactions to the metabolic model and solving the corresponding parameter estimation problem instead of inferring the fluxes. Fluxes can be calculated from kinetic parameters and metabolite concentrations based on the function form of the kinetics (Wahl et al., 2008). An alternative is a discretization-based approach, in which the time-dependent fluxes are approximated by a step function and solved from the change in isotopomer profile in a time interval using linear regression (Baxter et al., 2007). A similar discretization-based approach is also applied in dynamic metabolic flux analysis, in which fluxes are inferred from the kinetic profile of metabolites instead of the isotopomer distribution (Leighty and Antoniewicz, 2011).

3. Advanced issues for ¹³C-MFA

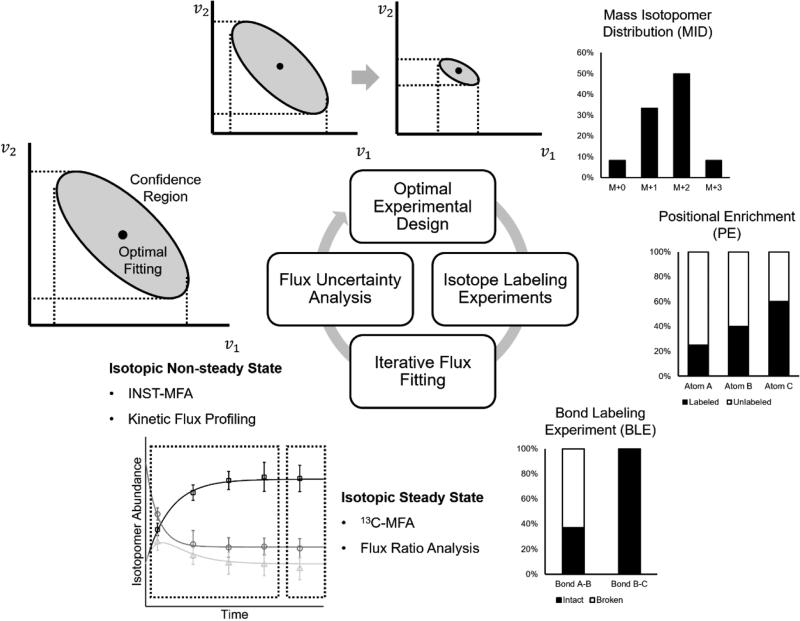
Although the framework of ¹³C-MFA has been well defined in the last section, several factors may affect the reliability of the calculated flux configuration, including the experimental scheme, the metabolic model and the biological system of interest. Identifiability of fluxes may be impaired due to noisiness in measurements, redundancy of the metabolic network, and compartmentalization of the intracellular space that are unaccounted for, hence calling for techniques addressing these problems. Difficulties in computation arise from both non-linear terms in the equations caused by bi- or tri- molecular reactions and the extremely larger number of isotopomers resulting in high-dimensional non-linear equations. The choice of advanced representation of the isotopomer balancing system provides can simplify some of these issues (Wiechert et al., 1999). Techniques to evaluate flux uncertainty (Wiechert et al., 1997), to optimize the experimental scheme (Möllney et al., 1999) and to resolve metabolic fluxes of compartmentalized systems (Wahrheit et al., 2011) have been developed to improve accuracy of metabolic flux analysis. These techniques are implemented as modules in several software packages for metabolic flux analysis of both isotopic stationary and non-stationary systems (Table 1) and applied in an integrated workflow of metabolic flux analysis (Fig 2). Here these topics will be discussed in detail.

Table 1.

Summary of software for metabolic flux analysis

Software	Isotopomer Balancing Model	Statistical Analysis	Optimal Experimental Design	Discription
13CFLUX(Wiechert et al., 2001)	Isotopomer	Linear	Supported	C++ software for 13C-MFA
13CFLUX2(Weitzel et al., 2013)	Cumomer/EMU	Linear/Monte Carlo	Supported	C++ software for 13C-MFA
FiatFlux(Zamboni et al., 2005)	Flux ratio analysis	Linear	Not supported	Matlab software for flux ratio analysis
OpenFlux(Quek et al., 2009)	EMU	Non-linear search/Monte Carlo	Supported	Matlab software for 13C-MFA
OpenFlux2(Shupletsov et al., 2014)	EMU	Non-linear search/Monte Carlo	Supported	Matlab software for 13C-MFA
influx_s(Sokol et al., 2012)	Cumomer/EMU	Linear/Monte Carlo	Not supported	Software package for 13C-MFA implementing an efficient algorithm for iterative fitting, programmed in R and Python
INCA(Young, 2014)	EMU	Linear/Non-linear search/Monte Carlo	Supported	Matlab software for 13C-MFA and INST-MFA
OpenMebius(Kajihata et al., 2014)	EMU	Non-linear search		Matlab software for 13C-MFA and INST-MFA
C13(Cvijovic et al., 2010; Garcia-Albornoz et al., 2014)	Isotopomer	Not Supported	Not Supported	A module for 13C-MFA in the software packages BioMet Toolbox and BioMet Toolbox 2.0

Fig 2. An integrated workflow of metabolic flux analysis.

Isotope labeling data obtained from isotope labeling or bond labeling experiments and detected by mass spectrometry or nuclear magnetic resonance are used to determine the fluxes by iterative fitting and confidence region of the flux configuration, which provides a metric of flux uncertainty. The flux uncertainty is minimized in the optimal experimental design procedure to achieve a more accurate evaluation of the fluxes.

3.1. Simplifying the isotopomer equations

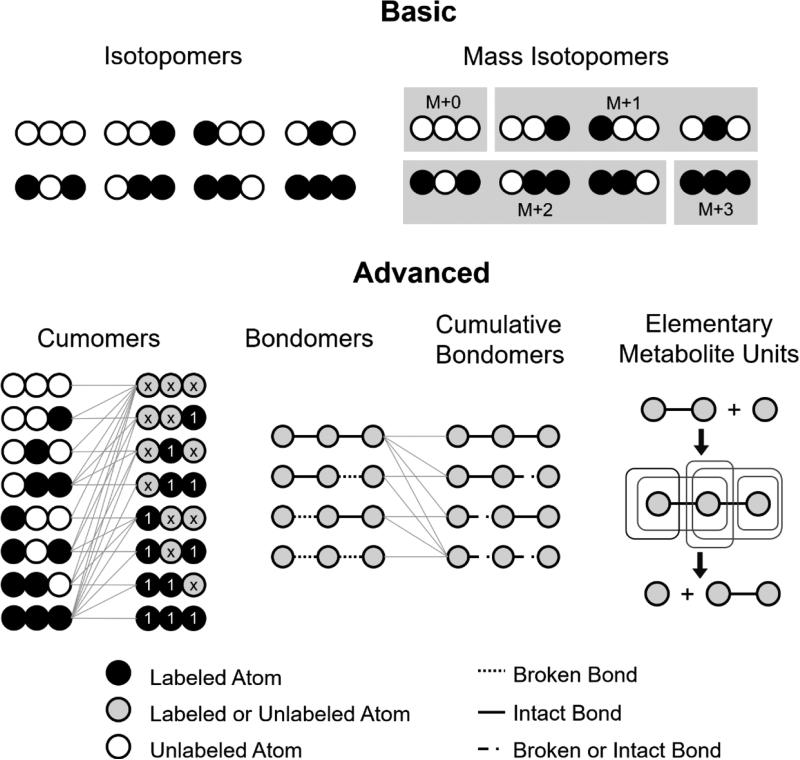
Two major difficulties in solving the isotopomer balance equations arise from the nonlinearity caused by bi- or tri-molecular reactions and the extremely large number of isotopomers. To overcome the difficulties, several techniques have been developed to simplify the equations by both reducing the number of variables needed in simulating the isotopomer distribution and eliminating the nonlinearity, including cumomers (Wiechert et al., 1999), bondomers (Sriram and Shanks, 2004), cumulative bondomers (Van Winden et al., 2002) and elementary metabolite units (EMUs) (Antoniewicz et al., 2007). Among the variety of equation-simplifying techniques, the EMU approach can for example reduce the number of equations by 95% in a tricarboxylic acid (TCA) cycle model, as well as eliminate the bilinear terms (Antoniewicz et al., 2007). Using advanced representations of the flux-isotopomer system, all of these methods are able to transform the coupled non-linear equations in equation (1) to several subsets containing only linear equations, which can be solved successively in a much more efficient way than directly solving the nonlinear equations (Fig 3). The bondomers and cumulative bondomer approaches are specially designed to resolve metabolic fluxes from 2D [¹³C, ¹H] COSY NMR spectroscopy obtained from bond labeling experiments (Szyperski, 1995), in which the cells are cultured on a mixture of uniformly labeled and naturally labeled substrate to track the breaking and re-forming of carbon-carbon bonds, while the cumomers and EMU approaches are suitable for both mass isotopomer distributions (MIDs) detected by MS and positional enrichment detected by NMR (Fig 1C). There are also techniques specifically designed for tandem mass spectrometry measurements to extract more precise information of isotopomer distribution and reduce computational cost, including the tandemer approach (Tepper and Shlomi, 2015) and mass isotopomer multi-ordinate spectral analysis (MIMOSA) (Alves et al., 2015). The Jacobian matrix of the isotopomer fractions with respect to the flux variables are also analytically determined, which is further applicable in the following flux uncertainty analysis and experimental design.

Fig 3. Different representations of the isotopomer system.

By transforming the basic isotopomers and mass isotopomers to cumomers, bondomers, cumulative or mass isotopomers of EMUs, the high dimensional non-linear equations connecting isotopomer distribution and fluxes could be transformed to a simpler form containing several subsets consisting of linear equations only, which could be solved easily. The number of equations to be solved could also be reduced by the bondomers, cumulative bondomers and EMUs approaches.

3.2. Flux uncertainty analysis

Non-linear least squares problems have been shown to be ‘sloppy’; that is, the cost function is very insensitive to variation along certain directions in parameter space (Gutenkunst et al., 2007; Transtrum et al., 2010). In other words, the flux configurations resulting in similar isotopic profiles are not unique. Moreover, noise in isotopomer distributions measured from experiments propagate to the inferred flux configuration, which further impairs the identifiability of fluxes. Thus, proper tools to identify confidence or credibility intervals for each flux variable is indispensable for a reliable estimation of the fluxes. The simplest method to evaluate the confidence region of flux configurations is based on linear statistics, in which the covariance matrix of flux variables, Cov(v), which could be directly calculated from the covariance matrix of measurements, Cov(M) and the Jacobian matrix, $\frac{\partial \mathbf{M}}{\partial \mathbf{v}}$ (Wiechert et al., 1997), is used. This approach has the lowest computational complexity since it only needs a finite number of matrix calculations, but the confidence region of fluxes estimated in this way are limited due to the non-linear relationship between flux variables and steady state isotopomer distributions (Antoniewicz et al., 2006). One solution to achieve a more accurate estimation of the confidence region is based on a Monte Carlo method, in which the experimental measurements are perturbed many times to simulate the distribution of noise, thus enabling evaluation of the confidence region by inferring flux configurations from the perturbed measurements. A Markov Chain Monte Carlo (MCMC) approach can also be applied in sampling the joint probability distribution of fluxes and isotopomer measurements under the assumption of Gaussian noise (Kadirkamanathan et al., 2006; Yang et al., 2005). For determination of confidence intervals of a single flux, an iterative one-dimensional search strategy was shown to achieve accuracy close to that of a Monte Carlo strategy and a brute-force search (Antoniewicz et al., 2006). All strategies, except for MCMC, are implemented in several software packages for ¹³C-MFA to facilitate application by non-expert users (Table 1).

3.3. Experimental design

As we mentioned, since fluxes cannot be uniquely determined, assessment of flux identifiability is indispensable for metabolic flux analysis. Uncertainty in calculated fluxes is also affected by the experimental procedures, including selection of tracers and measurements. A good choice of experimental scheme will dramatically improve the quality of flux evaluation, as studies on experimental design have shown (Antoniewicz, 2013). One purpose of experimental design is to determine what choice of labeled substrate and measurements is able to achieve lowest flux uncertainty; that is, to narrow the confidence region as much as possible. Hence, a metric to quantify the size of the confidence region is necessary. A commonly used metric is the D-value, which approximates the volume of the confidence region by an ellipsoid according to the covariance of flux variables (Möllney et al., 1999):

$$\mathrm{D}(\mathbf{v},\mathrm{T},\mathrm{M})=\det \left[\mathrm{Cov}(\mathbf{v},\mathrm{T},\mathrm{M})\right]$$ (4)

In which T and M denote the labeled tracer used and the measurements chosen. An optimal experimental scheme can be determined by searching for T and M that minimize the D-value. Note that the D-value depends on the true flux vector, hence an initial guess of it is necessary for the experimental design. As an alternative of the D-value, a precision metric based on confidence intervals of individual fluxes is also used to assess different ¹³C tracers’ ability to provide information in flux analysis (Metallo et al., 2009). One strategy to improve the tracer selection is to consider a mixture of several tracers and then search for the optimal fraction of each tracer which minimizes the flux uncertainty metric (Bouvin et al., 2015; Crown and Antoniewicz, 2012; Möllney et al., 1999; Nöh and Wiechert, 2006; Walther et al., 2012). Other factors including the cost of the tracer (U-13C glucose is relatively cheap) and number of experiments possible are also taken into consideration. An example software package, IsoDesign, is available for selecting the input tracers for ¹³C-MFA (Millard et al., 2014). Another task in experimental design is to choose the smallest set of metabolites to be measured which affords the same amount of information as the full set of metabolites. A mixed integer linear programming strategy has been applied to identify such minimal measurement sets (Chang et al., 2008; Rantanen et al., 2006).

3.4. Extending the scope of ¹³C metabolic flux analysis

¹³C metabolic flux analysis techniques have been widely applied in resolving central carbon metabolism in unicellular organisms like Escherichia coli, Corynebacterium glutamicum, Saccharomyces cerevisiae and Bacillus subtilis, which are species with richest resource of flux analysis data according to a recently published database (Zhang et al., 2015). However, application of ¹³C metabolic flux analysis in mammalian cells is complicated due to existence of different subcellular compartments in eukaryotic cells, while in most cases only the average ¹³C labeling pattern could be measured. In some cases compartmentalized metabolism could be resolved by using labeling patterns of metabolites whose synthesis takes place in different compartments (Allen et al., 2007) or experimental techniques allowing separation of subcellular compartments (Wahrheit et al., 2011), but it is unlikely to be practical for resolving compartmentalized fluxes under all conditions. In the computational analysis, there are three ways to address this problem: (i) using a simplified model which only contains metabolic reactions in a single compartment or ignores the compartmentalization (Fan et al., 2014); (ii) treating metabolite pool sizes in different compartments as additional parameters which are evaluated simultaneously with the fluxes (Davidson et al., 2016; Ma et al., 2014; Murphy et al., 2013); (iii) generating multi-compartment models with parameters that estimate exchange fluxes across intercellular compartments (Jiang et al., 2016; Mehrmohamadi et al., 2014). Also in qualitative flux analysis, specially designed tracers yielding labeled products only in one compartment could be used to probe compartmentalized metabolism. An interesting application of this strategy is enabling propagation of deuterium from NADPH to 2-HG only in cytoplasm or mitochondria by expressing compartment-specific mutant isocitrate dehydrogenase (Lewis et al., 2014).

Besides applications in more complicated mammalian cells, ¹³C metabolic flux analysis can be extended to cover larger metabolic networks. One strategy combining ¹³C-MFA and GSMM is using isotope labeling in fitting flux configurations on a smaller metabolic network, then utilizing the inferred flux rates in constraining flux configuration in the whole GSMM (García Martín et al., 2015). The first study directly applying ¹³C-MFA in a genome-scale metabolic model (GSMM) of E. coli was published in 2015, showing high consistency between MFA using the GSMM and a small core model as well as increased flux uncertainty associated with the GSMM (Gopalakrishnan and Maranas, 2015). In spite of the extremely large size of metabolic model used, this study utilized labeling patterns of 10 intracellular amino acids to resolve metabolic fluxes, which is likely to be further improved by additional measurements.

4. Applications in cancer cell metabolism

Cancer cells alter their metabolism in order to survive in the microenvironment in which nutrients and oxygen supplies are limited (Gatenby and Gillies, 2004) and to satisfy the demands of cell proliferation (Pavlova and Thompson, 2016). Reprogramming of cancer metabolism is an essential component of basic cancer biology and a therapeutic target (Galluzzi et al., 2013). With ¹³C metabolic flux analysis techniques, multiple mechanisms of metabolic abnormality in cancer cells have been identified (Hiller and Metallo, 2013)), including altered dependence on nutrients, metabolic reprogramming in response to oncogenic mutations, enhanced glycolysis and biosynthetic pathways.

It is known as the ‘Warburg Effect’ that cancer cells increase glucose uptake and ferment the glucose to make lactate even in presence of oxygen. This phenomenon was discovered based on the enhanced glucose uptake and lactate production of tumors compared to normal tissues, which was the earliest, to our knowledge, contribution of flux measurements to our understanding of cancer metabolism (Koppenol et al., 2011; Liberti and Locasale, 2016; Warburg, 1956; Warburg et al., 1924). Studies applying metabolic flux analysis techniques to construct flux configurations in central carbon metabolism for cells under different genetic contexts showed that activation of oncogenes is able to drive the enhancement of glycolysis as well as active oxidative metabolism in mitochondria, which is dependent on glutamine and other nutrients (Fan et al., 2014; Murphy et al., 2013). Similar up-regulation of glycolysis (Ying et al., 2012) and glutamine-dependent TCA cycle (DeBerardinis et al., 2007) in cancer cell lines was supported by numerous studies utilizing qualitative isotope labeling techniques or ¹³C-MFA, providing evidence for pathways of glutamine metabolism including glutaminolysis (DeBerardinis et al., 2007; Le et al., 2012) and reductive carboxylation (Jiang et al., 2016; Metallo et al., 2011; Mullen et al., 2012; Zhao et al., 2016), which is associated with malignancy-related factors including hypoxia, oncogenic mutations, detachment from the extracellular matrix. However, the importance of glutamine in supplying cancer cell growth was questioned by two recent studies applying in vivo ¹³C-MFA to evaluate nutrient dependence of tumors. Despite the evidence suggesting a major contribution of glutamine to active TCA cycle in cultured cancer cells, certain tumor models were shown to rely less on glutamine for anaplerosis (i.e. replenishing of intermediates of TCA cycle) and be insensitive to GLS inhibition (Davidson et al., 2016). Moreover, the nutrient dependence was shown to be affected by tissue perfusion in human lung tumors, thus highlighting the profound impact of microenvironment on cancer metabolism (Hensley et al., 2016). In addition, application of isotope labeling based metabolic flux analysis in these two studies identified pyruvate dehydrogenase as the enzyme carrying the majority of pyruvate entering the TCA cycle (Davidson et al., 2016; Hensley et al., 2016). Besides glucose and glutamine, other amino acids also play important roles in proliferation in cancer cells. Tracing experiments showed significant contribution to biomass of amino acids other than glutamine, as well as considerable contribution of other carbon sources including lipids and acetate (Hosios et al., 2016; Kamphorst et al., 2014; Yao et al., 2016).

Among the non-essential amino acids consumed by cancer cells, serine is one of particular interest. In addition to uptake of exogenous serine, some cancer cells exhibit upregulated de novo synthesis of serine from glucose, especially in serine deprivation conditions (Maddocks et al., 2013; Possemato et al., 2011). Stable isotope labeling experiments have shown that in mammalian cells the carbon flux from glucose diverted by serine synthesis pathway is comparable to that of lactate production (Locasale et al., 2011). However, the estimated fraction of glucose utilized in serine synthesis varies, thus indicating a context-dependent manner of glucose contribution in de novo serine synthesis (DeNicola et al., 2015). Serving as a building block of protein is not the only function of serine in cell physiology (Locasale, 2013). Using [²H]-labeled tracers to probe NADPH production, serine-fueled folate metabolism was shown to have substantial contribution to NADPH production which is comparable to that of oxidative phosphate pathway, indicating potential role of serine metabolism in keeping redox balancing (Fan et al., 2014; Liu et al., 2016). Notably a similar conclusion was found in a study using ¹³C serine as a tracer. This study also revealed a coordinate portioning of serine derived flux into nucleotides and glutathione synthesis (Mehrmohamadi et al., 2014). To summarize, stable isotope labeling experiments affords a powerful tool to identify crucial factors for functioning of metabolic pathways and to quantitatively characterize metabolic alterations in cancer cells.

Concluding Remarks

Metabolic flux analysis of stable isotope labeling data, in combination with advanced analytical approaches to measure the isotope labeling pattern, is a powerful tool to evaluate rates of metabolic reactions. Application of such techniques, although still in its nascent stage, is beginning to advance our knowledge of cancer metabolism. However, there is still a significant gap between the theory and application. Although computational frameworks of metabolic flux analysis for both stationary and dynamic systems have been well-established and multiple software packages implementing the algorithms have been developed, most studies are still restricted to the simpler qualitative flux analysis strategy or central carbon metabolism to study cancer cells whose metabolic network is more complicated than that of unicellular organisms. Furthermore, large-scale fluxomics datasets for human cells are still unavailable, thus hindering more accurate integrated computational modeling of context-dependent cancer metabolism, for which the most frequently used strategy currently is integrating metabolic network model with tissue-specific transcriptomics or proteomics datasets (Agren et al., 2014; Folger et al., 2011; Yizhak et al., 2014). We expect more attempts of applying quantitative metabolic flux analysis to human cells in greater detail and with larger networks to emerge in the future, which will surely result in a better understanding of complexity associated with cancer metabolism.

Highlights.

• Metabolic reaction rates can be resolved by flux analysis techniques that use data from stable isotope labeling experiments

• Accuracy and efficiency of flux analysis are improved by advanced mathematical techniques for equation simplification, statistical analysis and experimental design

• Several software packages implementing these methods are available

• Application of flux analysis techniques is starting to bring new insights to our understanding of cancer metabolism