Hierarchical group testing for multiple infections

Summary

Group testing, where individuals are tested initially in pools, is widely used to screen a large number of individuals for rare diseases. Triggered by the recent development of assays that detect multiple infections at once, screening programs now involve testing individuals in pools for multiple infections simultaneously. Tebbs, McMahan, and Bilder (2013, Biometrics) recently evaluated the performance of a two-stage hierarchical algorithm used to screen for chlamydia and gonorrhea as part of the Infertility Prevention Project in the United States. In this article, we generalize this work to accommodate a larger number of stages. To derive the operating characteristics of higher-stage hierarchical algorithms with more than one infection, we view the pool decoding process as a time-inhomogeneous, finite-state Markov chain. Taking this conceptualization enables us to derive closed-form expressions for the expected number of tests and classification accuracy rates in terms of transition probability matrices. When applied to chlamydia and gonorrhea testing data from four states (Region X of the United States Department of Health and Human Services), higher-stage hierarchical algorithms provide, on average, an estimated 11 percent reduction in the number of tests when compared to two-stage algorithms. For applications with rarer infections, we show theoretically that this percentage reduction can be much larger.

1. Introduction

Group testing, also known as pooled testing, was proposed by Dorfman (1943) as a strategy to screen military recruits for syphilis during World War II. Dorfman envisioned that instead of testing each recruit’s blood specimen separately, multiple specimens could be pooled together and tested at once. Individuals from negative pools would be declared negative, and specimens from positive pools would be retested individually to identify which recruits had contracted syphilis. Over 70 years later, pooling biospecimens through group testing is commonplace in a variety of infectious disease settings. This is especially true in large-scale screening programs where, because of cost constraints or other physical limitations, there are restrictions on the number of tests that can be performed.

Dorfman’s motivation for using group testing was to reduce testing costs while still identifying all syphilitic-positive recruits. Today, this would be described as the “case identification problem,” because the goal is to identify all positive individuals among all individuals tested. Dorfman’s approach to case identification can be viewed as a two-stage hierarchical algorithm; i.e., non-overlapping pools are tested in the first stage and individuals from positive pools are tested in the second. When the disease prevalence is small, higher-stage algorithms have proven to be useful at further reducing the number of tests needed. For example, motivated by HIV testing in North Carolina, Pilcher et al. (2005) use a three-stage algorithm where individuals are first tested in a master pool of size 90. If positive, 9 non-overlapping subpools of size 10 are tested in the second stage, and individual testing is used to resolve all positive subpools in the third stage. Sherlock, Zelota, and Klausner (2007), in their survey of HIV screening practices in the United States, describe how variations of this three-stage algorithm are used in Atlanta, Los Angeles, San Francisco, and Seattle. In other applications, Kleinman et al. (2005) propose a three-stage algorithm to screen blood donors for HBV in the United States and Quinn et al. (2000) implement a four-stage algorithm for HIV testing in India.

Group testing research for case identification has been largely motivated by applications involving a single infection, such as HIV. However, large-scale sexually transmitted disease screening practices are rapidly moving towards the use of “multiplex assays,” that is, assays that detect multiple infections at once. For example, as part of national screening programs in the United States, several federally funded testing centers use the Aptima Combo 2 Assay (Hologic/Gen-Probe, Inc.), a nucleic acid amplification test that simultaneously detects the presence of chlamydia and gonorrhea in pooled and individual specimens (Jirsa, 2008; Lewis, Lockary, and Kobic, 2012). For screening blood banks, the United States Food and Drug Administration (FDA) and the more recent infectious disease testing literature points to the development of multiplex assays that detect HIV, HBV, and HCV in pools while being able to discriminate against each one (Xiao et al., 2013; FDA, 2013). With the ongoing development of new assays and testing platforms that accommodate multiple disease screening, generalizing group testing algorithms for use with multiple infections is an important next step.

In this article, we develop S-stage hierarchical algorithms for multiple infections, where S ≥ 2. Our goal is to generalize Tebbs, McMahan, and Bilder (2013), who characterized the performance of Dorfman’s two-stage (S = 2) algorithm for two infections. In Section 2, we introduce notation and state assumptions. In Section 3, we derive expressions for the expected number of tests and classification accuracy probabilities in a general S-stage hierarchical algorithm. This is accomplished by viewing the testing process from within a Markov chain framework, allowing us to characterize performance succinctly using transition probability matrices. In Section 4, we discuss different pool splitting strategies and show that higher-stage algorithms can be far more cost efficient than two-stage algorithms. In Section 5, we use chlamydia and gonorrhea testing data collected in Alaska, Idaho, Oregon, and Washington to illustrate the benefits of implementing higher-stage algorithms with multiple diseases. In Section 6, we provide a summary discussion.

To mitigate the complexity of the notation used in this article, we restrict attention herein to two infections (e.g., chlamydia and gonorrhea, etc.). We use the Web Appendix to show how one can quickly generalize our derivations to handle three or more infections as needed.

2. Notation and Assumptions

Our work is motivated by the recent development of multiplex assays that test for multiple infections. Some multiplex assays are non-discriminating; i.e., a positive result means only that at least one infection is detected. For example, the cobas TaqScreen MPX Test (Roche, Inc.) screens plasma specimens for HIV, HBV, and HCV in pools of size up to 96, but it does not determine which virus(es) is(are) detected (Ohhashi et al., 2010). On the other hand, assays are described as discriminating when upon application a diagnosis for each infection is provided separately. Most multiplex assays based on nucleic acid amplification technology used for chlamydia/gonorrhea detection discriminate between the two infections in swab and urine specimens (Gaydos et al., 2010; CDC, 2014); as noted earlier, the Aptima Combo 2 Assay is an example. For three infections, the Procleix Ultrio Assay (Hologic/Gen-Probe, Inc.) discriminates among HIV, HBV, and HCV in plasma/serum pools of size up to 16. In this article, we assume that a discriminating assay is used each time a specimen is tested (pool or individual) and that one such assay is used throughout the testing process.

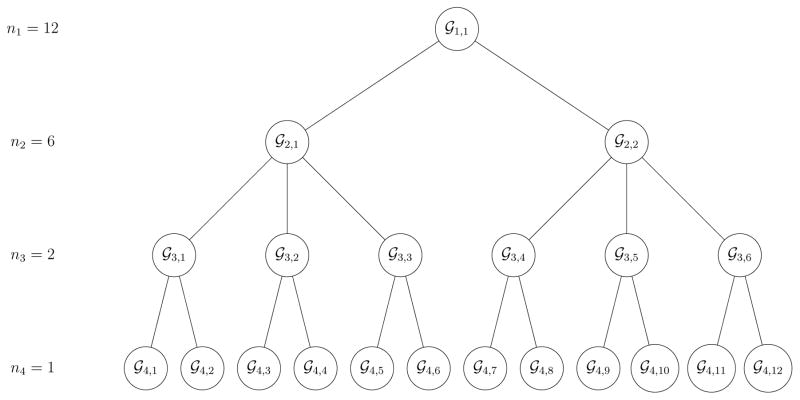
An S-stage hierarchical algorithm begins with testing n₁ individuals in a master pool at stage 1. Let n_s denote the pool size at the sth stage, where s = 1, 2, ..., S – 1 and n_S = 1. If a pool at the sth stage tests positively for at least one infection (excluding at stage S), it is split into n_s/n_s+1 subpools and each subpool is tested. Any pool or subpool that tests negatively for both infections is not split further, and its members are declared negative for both infections. Individual testing is used in stage S where final diagnoses are made. Figure 1 depicts the complete version of an S = 4 stage algorithm with master pool size n₁ = 12 and subpool sizes n₂ = 6, n₃ = 2, and n₄ = 1 at stages 2, 3, and 4, respectively.

Figure 1.

Hierarchical algorithm with S = 4 stages and master pool size n₁ = 12. Pools that test positively for at least one infection are split into subpools. Pools that test negatively for both infections are not split further. The last stage is individual testing where final diagnoses are made. The maximum number of pools tested in stage s is n₁/n_s.

We assume n_s/n_s+1 is a positive integer for s = 1, 2, ..., S – 1; i.e., pool sizes are equal within a given stage. Denote the lth individual by ℐ_l, for l = 1, 2, ..., n₁. Let Ỹ_lj = 1 if individual ℐ_l is truly positive for the jth infection, Ỹ_lj = 0 otherwise, for j = 1, 2. We assume Ỹ_l = (Ỹ_l1, Ỹ_l2)′ are independent and identically distributed with probability mass function $\text{pr}({\stackrel{\sim }{Y}}_{l1}={\stackrel{\sim }{y}}_1,{\stackrel{\sim }{Y}}_{l2}={\stackrel{\sim }{y}}_2)=p_{00}^{(1-{\stackrel{\sim }{y}}_1)(1-{\stackrel{\sim }{y}}_2)}{p}_{10}^{{\stackrel{\sim }{y}}_1(1-{\stackrel{\sim }{y}}_2)}{p}_{01}^{(1-{\stackrel{\sim }{y}}_1){\stackrel{\sim }{y}}_2}{p}_{11}^{{\stackrel{\sim }{y}}_1{\stackrel{\sim }{y}}_2}$, for ỹ₁, ỹ₂ ∈ {0, 1}, where p₀₀ + p₁₀ + p₀₁ + p₁₁ = 1. Because of potential misclassification arising from assay error, the Ỹ_l’s are best regarded as latent. Let 𝒢_s,i denote the ith pool at the sth stage whose true status is denoted by Z̃_s,i = (Z̃_s,i1, Z̃_s,i2)′, for s = 1, 2, ..., S and i = 1, 2, ..., n₁/n_s. At the sth stage, the true pool statuses Z̃_s,ij are determined by the true statuses of those individuals within 𝒢_s,i; i.e., Z̃_s,ij = 1 if pool 𝒢_s,i contains at least one positive individual for the jth infection, Z̃_s,ij = 0 otherwise. Note that “pools” 𝒢_S,i tested at stage S contain only one individual. Finally, let θ_nsz̃1z̃2denote the probability a pool of size n_s has true statuses z̃₁ ∈ {0, 1} and z̃₂ ∈ {0, 1} for the first and second infection, respectively. In Web Appendix A, we show that ${\theta }_{n_s,00}=p_{00}^{n_s},{\theta }_{n_s,10}={(p_{10}+p_{00})}^{n_s}-p_{00}^{n_s}$, and ${\theta }_{n_s,01}={(p_{01}+p_{00})}^{n_s}-p_{00}^{n_s}$.

Let $S_{e:j}^{(s)}$ and $S_{p:j}^{(s)}$ denote the assay sensitivity and specificity, respectively, for the jth infection at the sth stage of testing, for j = 1,2 and s = 1, 2, ..., S, and let Z_s,i = (Z_s,i1, Z_s,i2)′ denote the vector of (potentially incorrect) testing outcomes for pool 𝒢_s,i. We assume all testing outcomes are mutually independent, conditional on the true statuses of the specimens being tested. This type of assumption is pervasive in the group testing literature for single infections in the presence of testing error (Litvak, Tu, and Pagano, 1994; Kim et al., 2007; Kim and Hudgens, 2009) and is used to derive relevant quantities in closed form. For further discussion on our assumptions with multiple infections, see Section 6. To characterize the decoding process as a Markov chain, we utilize the notion of an “ancestor pool.” For pool 𝒢_s,i at stage s, denote its ancestor pool at stage s′ < s by ${\mathcal{G}}_{s,i}^{(s^{\prime })}$, for s′ = 1, 2, ..., s – 1. We also use the term “parent pool” when referring to the ancestor pool at the previous stage. For example, consider pool 𝒢_3,2 in Figure 1, which is the second pool tested in the third stage. Both 𝒢_1,1 and 𝒢_2,1 are ancestor pools of 𝒢_3,2 and can be labeled as ${\mathcal{G}}_{3,2}^{(1)}$ and ${\mathcal{G}}_{3,2}^{(2)}$, respectively. Also, the master pool 𝒢_1,1 is the parent pool of 𝒢_2,1, which is the parent pool of 𝒢_3,2.

3. Operating Characteristics

3.1. Expected Number of Tests

In an S-stage algorithm, a pool at stage s+1, s = 1, 2, ..., S–1, is tested only when its parent pool in stage s tests positively for at least one infection. Let T_s+1 denote the number of tests expended at stage s+1 so that E(T_s+1) = (n₁/n_s+1)pr(Z_s,i1+Z_s,i2 > 0), for s = 1, 2, ..., S–1, a result established in Web Appendix A. Let T^(S) denote the number of tests needed to classify all individuals in a master pool when using S stages. Including the master pool test and then summing over the stages, the expected value of T^(S) is given by

$$E(T^{(S)})=1+\sum _{s=1}^{S-1}\left(\frac{n_1}{n_{s+1}}\right)\text{pr}(Z_{s,i1}+Z_{s,i2}>0).$$ (1)

The challenging part of Equation (1) is calculating pr(Z_s,i1 + Z_s,i2 > 0), the probability that pool 𝒢_s,i in stage s tests positively. We use a Markov chain conceptualization of the decoding process to calculate this probability, as we now describe.

If pool 𝒢_s,i tests positively for at least one infection, then each of its ancestor pools ${\mathcal{G}}_{s,i}^{(s^{\prime })}$, s′ = 1, 2, ..., s–1, must have as well. Therefore, calculating pr(Z_s,i1+Z_s,i2 > 0) for 𝒢_s,i requires information on all of its ancestor pools’ true statuses. At any stage, each pool has four possible true statuses, denoted by “00,” “10,” “01,” and “11.” Traversing from the master pool ${\mathcal{G}}_{s,i}^{(1)}$ to pool 𝒢_s,i in stage s admits a potentially large number of paths, and it is not practical to keep track of the probability of each one on a case-by-case basis. To simplify the problem, we conceptualize the true status path of ${\mathcal{G}}_{s,i}^{(1)},{\mathcal{G}}_{s,i}^{(2)}$, ..., 𝒢_s,i as a Markov chain with possible states in Ω = {00, 10, 01, 11}. The Markov property is satisfied because transition probabilities involving true statuses depend only on those at the previous state.

To illustrate this last point, refer again to Figure 1. Suppose the true status of the master pool 𝒢_1,1 is “11,” the true status of the stage 2 pool 𝒢_2,1 is “10,” and the true status of the stage 3 pool 𝒢_3,2 is “00.” In other words, the true status process starts in state 11, transitions to state 10 in stage 2, and then transitions to state 00 in stage 3. Given the true status of 𝒢_2,1, the true status of 𝒢_1,1 does not provide additional information about the true status of 𝒢_3,2. For this specific path realization, the joint probability can be calculated as

$$\begin{array}{l}\text{pr}({\stackrel{\sim }{\mathbf{Z}}}_{3,2}^{\prime }=(0,0),{\stackrel{\sim }{\mathbf{Z}}}_{2,1}^{\prime }=(1,0),{\stackrel{\sim }{\mathbf{Z}}}_{1,1}^{\prime }=(1,1))\\ =\text{pr}({\stackrel{\sim }{\mathbf{Z}}}_{3,2}^{\prime }=(0,0)\mid {\stackrel{\sim }{\mathbf{Z}}}_{2,1}^{\prime }=(1,0))\text{pr}({\stackrel{\sim }{\mathbf{Z}}}_{2,1}^{\prime }=(1,0)\mid {\stackrel{\sim }{\mathbf{Z}}}_{1,1}^{\prime }=(1,1))\text{pr}({\stackrel{\sim }{\mathbf{Z}}}_{1,1}^{\prime }=(1,1)).\end{array}$$ (2)

Note that $\text{pr}({\stackrel{\sim }{\mathbf{Z}}}_{3,2}^{\prime }=(0,0)\mid {\stackrel{\sim }{\mathbf{Z}}}_{2,1}^{\prime }=(1,0))$ and $\text{pr}({\stackrel{\sim }{\mathbf{Z}}}_{2,1}^{\prime }=(1,0)\mid {\stackrel{\sim }{\mathbf{Z}}}_{1,1}^{\prime }=(1,1))$ in Equation (2) can be viewed as “one-step” transition probabilities associated with the true status process. The probability $\text{pr}({\stackrel{\sim }{\mathbf{Z}}}_{1,1}^{\prime }=(1,1))={\theta }_{n_1,11}$ describes the initial state of the process.

To generalize this discussion; i.e., so that we can account for all possible paths, define M = diag(θ_n1,00, θ_n1,10, θ_n1,01, θ_n1,11) and

$${\mathit{\pi }}^{(t)}=\left(\begin{array}{llll}{\pi }_{00\to 00}^{(t)}\hfill & {\pi }_{00\to 10}^{(t)}\hfill & {\pi }_{00\to 01}^{(t)}\hfill & {\pi }_{00\to 11}^{(t)}\hfill \\ {\pi }_{10\to 00}^{(t)}\hfill & {\pi }_{10\to 10}^{(t)}\hfill & {\pi }_{10\to 01}^{(t)}\hfill & {\pi }_{10\to 11}^{(t)}\hfill \\ {\pi }_{01\to 00}^{(t)}\hfill & {\pi }_{01\to 10}^{(t)}\hfill & {\pi }_{01\to 01}^{(t)}\hfill & {\pi }_{01\to 11}^{(t)}\hfill \\ {\pi }_{11\to 00}^{(t)}\hfill & {\pi }_{11\to 10}^{(t)}\hfill & {\pi }_{11\to 01}^{(t)}\hfill & {\pi }_{11\to 11}^{(t)}\hfill \end{array}\right).$$

The matrix M contains probabilities corresponding to the initial state of the true status process (i.e., for the master pool in stage 1). The entries in π^(t) are of the form ${\pi }_{\mathrm{A}\to \mathrm{B}}^{(t)}$ and give the probability that the parent pool ${\mathcal{G}}_{t+1,i}^{(t)}$ in stage t transitions from state A to state B with its subpool 𝒢_t+1,i in stage t + 1. For example,

$${\pi }_{10\to 00}^{(t)}=\text{pr}({\stackrel{\sim }{\mathbf{Z}}}_{t+1,i}={(0,0)}^{\prime }\mid {\stackrel{\sim }{\mathbf{Z}}}_{t+1,i}^{(t)}={(1,0)}^{\prime })={\theta }_{n_t,10}^{-1}{\theta }_{n_{t+1},00}{\theta }_{n_t-n_{t+1},10},$$

where ${\stackrel{\sim }{\mathbf{Z}}}_{t+1,i}^{(t)}={({\stackrel{\sim }{Z}}_{t+1,i1}^{(t)},{\stackrel{\sim }{Z}}_{t+1,i2}^{(t)})}^{\prime }$ denotes the true status of ${\mathcal{G}}_{t+1,i}^{(t)}$. In Web Appendix A, we derive expressions for each transition probability in π^(t). Because the transition matrix π^(t) characterizes the true status process, it is lower triangular. Note also that π^(t) changes from stage to stage because different stages use different pool sizes. In the language of Markov processes, the chain identified by the true status paths of ${\mathcal{G}}_{s,i}^{(1)},{\mathcal{G}}_{s,i}^{(2)}$, ..., 𝒢_s,i is therefore best described as time-inhomogeneous.

Joint probabilities for all possible true status paths are collected in the entries of C = Mπ⁽¹⁾π⁽²⁾ · · ·π^(s–1). However, this matrix does not account for misclassification (which can occur at any stage), so we must augment the matrix to incorporate it. Recall that if the sth stage pool 𝒢_s,i tests positively for at least one infection, then each of ${\mathcal{G}}_{s,i}^{(1)},{\mathcal{G}}_{s,i}^{(2)},\dots ,{\mathcal{G}}_{s,i}^{(s-1)}$ must have too, even if one or more of these pools is truly negative. Therefore, we need a matrix “operator” that, at any stage, allows us to diagnose both truly positive and truly negative pools as positive for at least one infection. Under our assumptions,

$${\mathbf{P}}^{(s)}=\text{diag}(1-S_{p:1}^{(s)}{S}_{p:2}^{(s)},1-{\overline{S}}_{e:1}^{(s)}{S}_{p:2}^{(s)},1-S_{p:1}^{(s)}{\overline{S}}_{e:2}^{(s)},1-{\overline{S}}_{e:1}^{(s)}{\overline{S}}_{e:2}^{(s)}),$$

where ${\overline{S}}_{e:j}^{(s)}=1-S_{e:j}^{(s)}$ and ${\overline{S}}_{p:j}^{(s)}=1-S_{p:j}^{(s)}$ for j = 1, 2, is the matrix that does this at stage s, s = 1, 2, ..., S – 1. To understand what role P^(s) plays, take, for example, the initial state matrix M and post-multiply it by P⁽¹⁾ to form MP⁽¹⁾. The (1,1) entry in MP⁽¹⁾, which is ${\theta }_{n_1,00}(1-S_{p:1}^{(1)}{S}_{p:2}^{(1)})$, gives the probability a truly negative master pool (in stage 1) is incorrectly diagnosed as positive for at least one infection. Other diagonal entries inMP⁽¹⁾ have analogous interpretations, and the matrix π^(t)P^(t+1) summarizes similar diagnosis calculations at stage t + 1, for t = 1, 2, ..., s – 1. Because pools can be diagnosed correctly or incorrectly at any stage, joint probabilities for all paths where 𝒢_s,i tests positively for at least one infection are collected in the entries of D = MP⁽¹⁾π⁽¹⁾P⁽²⁾π⁽²⁾P⁽³⁾ · · ·π^(s–1)P^(s). The quadratic form ${\mathbf{1}}_4^{\prime }\mathbf{D}{\mathbf{1}}_4$, where ${\mathbf{1}}_4^{\prime }=(1,1,1,1)$, then adds these probabilities to obtain pr(Z_s,i1 + Z_s,i2 > 0).

Updating our expression in Equation (1), we can write the expected number of tests as

$$E(T^{(S)})=1+\sum _{s=1}^{S-1}\left(\frac{n_1}{n_{s+1}}\right){\mathbf{1}}_4^{\prime }\mathbf{M}{\mathbf{P}}^{(1)}\prod _{t=0}^{s-1}({\mathit{\pi }}^{(t)}{\mathbf{P}}^{(t+1)}){\mathbf{1}}_4,$$ (3)

where π⁽⁰⁾ = (P⁽¹⁾)⁻¹. We include the t = 0 term in Equation (3) only so that our expression for E(T^(S)) remains correct when S = 2. In this case, $E(T^{(2)})=1+n_1{\mathbf{1}}_4^{\prime }\mathbf{M}{\mathbf{P}}^{(1)}{\mathbf{1}}_4$ reduces to Equation (1) in Tebbs et al. (2013) for two-stage Dorfman algorithms. We call $n_1^{-1}E(T^{(S)})$ the expected number of tests per individual; this measure allows us to compare the efficiency of hierarchical algorithms using different values of n₁ and S. It is straightforward to extend Equation (3) to J > 2 infections. This is done by making obvious modifications to ω, π^(t), M, and P^(s), and then changing 1₄ to 1_2^J. Details are provided in Web Appendix B.

3.2. Classification Accuracy

To complete our characterization of hierarchical algorithms for multiple infections, we derive accuracy measures commonly cited in the case identification literature. For the jth infection, define the pooling sensitivity as PS_e:j = pr(Z_S,ij = 1|Z̃_S,ij = 1), that is, the probability an individual is classified as positive for the jth infection given that the individual is truly positive for the jth infection. The pooling specificity PS_p:j is defined analogously for truly negative individuals being classified negatively. An individual is classified negatively if and only if it is not classified positively in stage S; therefore, PS_p:j = 1 − pr(Z_S,ij = 1/Z̃_S,ij = 0). Deriving expressions for PS_e:j and PS_p:j is possible by again viewing the decoding process from within our Markov chain framework. We now illustrate this with PS_e:1 when S > 2.

Consider the true status path of ${\mathcal{G}}_{S,i}^{(1)},{\mathcal{G}}_{S,i}^{(2)}$, ..., 𝒢_S,i, but now, conditional on the event that each pool in this sequence contains a common individual (𝒢_S,i) that is truly positive for the first infection. For t = 1, 2, ..., S − 1, let ${\stackrel{\sim }{\mathbf{Z}}}_{-S,i}^{(t)}$ denote the true status of pool ${\mathcal{G}}_{S,i}^{(t)}$ after individual G_S,i is removed. The joint probability of the true status path of ${\mathcal{G}}_{S,i}^{(1)},{\mathcal{G}}_{S,i}^{(2)}$, ..., 𝒢_S,i, conditional on the event {Z̃_S,i1 = 1}, can be found by calculating

$$\begin{array}{l}\text{pr}({\stackrel{\sim }{\mathbf{Z}}}_{-S,i}^{(1)}={\stackrel{\sim }{\mathbf{z}}}_1,{\stackrel{\sim }{\mathbf{Z}}}_{-S,i}^{(2)}={\stackrel{\sim }{\mathbf{z}}}_2,\dots ,{\stackrel{\sim }{\mathbf{Z}}}_{-S,i}^{(S-1)}={\stackrel{\sim }{\mathbf{z}}}_{S-1},{\stackrel{\sim }{\mathbf{Z}}}_{S,i}={(1,{\stackrel{\sim }{z}}_2)}^{\prime }\mid {\stackrel{\sim }{Z}}_{S,i1}=1)\\ =\text{pr}({\stackrel{\sim }{\mathbf{Z}}}_{S,i}={(1,{\stackrel{\sim }{z}}_2)}^{\prime }\mid {\stackrel{\sim }{Z}}_{S,i1}=1)\text{pr}({\stackrel{\sim }{\mathbf{Z}}}_{-S,i}^{(1)}={\stackrel{\sim }{\mathbf{z}}}_1,{\stackrel{\sim }{\mathbf{Z}}}_{-S,i}^{(2)}={\stackrel{\sim }{\mathbf{z}}}_2,\dots ,{\stackrel{\sim }{\mathbf{Z}}}_{-S,i}^{(S-1)}={\stackrel{\sim }{\mathbf{z}}}_{S-1}),\end{array}$$ (4)

where ${\stackrel{\sim }{\mathbf{z}}}_1^{\prime },{\stackrel{\sim }{\mathbf{z}}}_2^{\prime },\dots ,{\stackrel{\sim }{\mathbf{z}}}_{S-1}^{\prime }\in \{(0,0),(1,0),(0,1),(1,1)\}$ and z̃₂ ∈ {0, 1}. The first probability on the right-hand side of Equation (4) is p_1z̃2/(p₁₀ + p₁₁). The second probability is calculated by recognizing the Markov structure of ${\mathcal{G}}_{S,i}^{(1)},{\mathcal{G}}_{S,i}^{(2)},\dots ,{\mathcal{G}}_{S,i}^{(S-1)}$ that emerges after removing G_S,i. That is, the same conceptualization we exploited in calculating E(T^(S)) applies and probabilities of the form $\text{pr}({\stackrel{\sim }{\mathbf{Z}}}_{-S,i}^{(1)}={\stackrel{\sim }{\mathbf{z}}}_1,{\stackrel{\sim }{\mathbf{Z}}}_{-S,i}^{(2)}={\stackrel{\sim }{\mathbf{z}}}_2,\dots ,{\stackrel{\sim }{\mathbf{Z}}}_{-S,i}^{(S-1)}={\stackrel{\sim }{\mathbf{z}}}_{S-1})$ are collected in the entries of ${\mathbf{C}}_{-1}={\mathbf{M}}_{-1}{\mathit{\pi }}_{-1}^{(1)}{\mathit{\pi }}_{-1}^{(2)}\cdots {\mathit{\pi }}_{-1}^{(S-2)}$. The matrices M₋₁ and ${\mathit{\pi }}_{-1}^{(t)}$ are the same as M and π^(t) in Section 3.1, respectively, except that all pool sizes are reduced by one.

To complete our derivation, all that remains is to incorporate the effect of misclassification that can occur at any stage. Misclassification can arise due to either infection, so the two values of z̃₂ ∈ {0, 1} in Equation (4) must be treated separately. If z̃₂ = 0, then ${\mathcal{G}}_{S,i}^{(t)}$ must be truly positive for the first infection, because Z̃_S,i1 = 1 by assumption, and the second infection's true status is determined by ${\stackrel{\sim }{\mathbf{Z}}}_{-S,i}^{(t)}$. If z̃₂ = 1, then each pool in the sequence ${\mathcal{G}}_{S,i}^{(1)},{\mathcal{G}}_{S,i}^{(2)}$, ..., 𝒢_S,i, must be truly positive for both infections. To cover both cases, respectively, we define the two matrix operators ${\mathbf{P}}_{+-}^{(s)}=\text{diag}(1-{\overline{S}}_{e:1}^{(s)}{S}_{p:2}^{(s)},1-{\overline{S}}_{e:1}^{(s)}{S}_{p:2}^{(s)},1-{\overline{S}}_{e:1}^{(s)}{\overline{S}}_{e:2}^{(s)},1-{\overline{S}}_{e:1}^{(s)}{\overline{S}}_{e:2}^{(s)})$ and ${\mathbf{P}}_{++}^{(s)}=(1-{\overline{S}}_{e:1}^{(s)}{\overline{S}}_{e:2}^{(s)}){\mathbf{I}}_4$, where I₄ is the 4 × 4 identity matrix. The matrices ${\mathbf{P}}_{+-}^{(s)}$ and ${\mathbf{P}}_{++}^{(s)}$ then augment C₋₁ accordingly for the two values of z̃₂ ∈ {0, 1} in the same way P^(s) augmented C in Section 3.1. Adding up the probabilities for all transition paths, we obtain

$${\text{PS}}_{e:1}=\left(\frac{p_{10}}{p_{10}+p_{11}}\right){\mathbf{1}}_4^{\prime }{\mathbf{M}}_{-1}{\mathbf{P}}_{+-}^{(1)}\prod _{t=1}^{S-2}({\mathit{\pi }}_{-1}^{(t)}{\mathbf{P}}_{+-}^{(t+1)}){\mathbf{1}}_4{S}_{e:1}^{(S)}+\left(\frac{p_{11}}{p_{10}+p_{11}}\right){\mathbf{1}}_4^{\prime }{\mathbf{M}}_{-1}{\mathbf{P}}_{++}^{(1)}\prod _{t=1}^{S-2}({\mathit{\pi }}_{-1}^{(t)}{\mathbf{P}}_{++}^{(t+1)}){\mathbf{1}}_4{S}_{e:1}^{(S)}.$$ (5)

The additional “ $S_{e:1}^{(S)}$” in the expression for PS_e:1 accounts for the final diagnosis at stage S where individual testing occurs.

The preceding derivation also applies when S = 2; i.e., for the Dorfman-type algorithm in Tebbs et al. (2013). The only difference is that ${\prod }_{t=1}^{S-2}({\mathit{\pi }}_{-1}^{(t)}{\mathbf{P}}_{+-}^{(t+1)})$ and ${\prod }_{t=1}^{S-2}({\mathit{\pi }}_{-1}^{(t)}{\mathbf{P}}_{++}^{(t+1)})$ in Equation (5) are replaced by identity matrices. Furthermore, as shown in Web Appendix C, general expressions for PS_e:2, 1 − PS_p:1, and 1 − PS_p:2 all possess the same form as PS_e:1; i.e., each one can be written as a convex combination of two quadratic forms. Each quantity is derived by exploiting the Markov structure of ${\mathcal{G}}_{S,i}^{(1)},{\mathcal{G}}_{S,i}^{(2)},\dots ,{\mathcal{G}}_{S,i}^{(S-1)}$ that arises after removing one individual. This structure remains regardless of the number of infections considered, so generalizing these expressions when J > 2 is also straightforward.

Two additional measures of classification accuracy are the pooling positive predictive value and the pooling negative predictive value. For the jth infection, these are given by

$${\text{PPV}}_j=\frac{{\eta }_j{\text{PS}}_{e:j}}{{\eta }_j{\text{PS}}_{e:j}+(1-{\eta }_j)(1-{\text{PS}}_{p:j})}\text{and}{\text{NPV}}_j=\frac{(1-{\eta }_j){\text{PS}}_{p:j}}{(1-{\eta }_j){\text{PS}}_{p:j}+{\eta }_j(1-{\text{PS}}_{e:j})},$$

respectively, where η₁ = p₁₀ +p₁₁ and η₂ = p₀₁ +p₁₁ are the marginal probabilities. In words, PPV_j (NPV_j) gives the probability that an individual is truly positive (negative) for the jth infection given that the individual has been classified positively (negatively) for the jth infection. Expressions for PPV_j and NPV_j are found by using Bayes’ Rule.

4. Comparisons

We now compare hierarchical algorithms that use a different number of stages. For an S-stage algorithm, we first identify the optimal configuration of n₁, n₂, …, n_S for given values of p₀₀, p₁₀, p₀₁, and p₁₁. In this article, we define the “optimal” configuration as the one that minimizes $n_1^{-1}E(T^{(S)})$, the expected number of tests per individual, subject to the constraint that (n₁, n₂, …, n_S)′ resides in

$$\mathbb{O}=\{{(n_1,n_2,\dots ,n_S)}^{\prime }:n_s/n_{s+1}\in {\mathbb{N}}_{>1},s=1,2,\dots ,S-1;n_S=1\},$$

where ℕ_>1 = {2, 3, …,}. The condition n_s/n_s+1 ∈ ℕ_>1 simply ensures that pool sizes will be common within a given stage. Because extremely large pool sizes are rarely seen in the infectious disease testing literature, we assume the master pool size n₁ is no larger than 100. This restriction was also used by Kim and Hudgens (2009) who evaluated the utility of higher-stage array group testing algorithms for single infections. For us, this restriction puts a constraint on the space of possible configurations and allows us to identify the optimal one using a direct search. Hierarchical algorithms which implement halving; i.e., n_s/n_s+1 = 2, for s = 1, 2, …, S − 2 and n_S = 1, arise as a special case. Halving algorithms for single infections were highlighted by Litvak et al. (1994) and Black, Bilder, and Tebbs (2012).

In Table 1, we calculate the expected number of tests per individual for different values of S under different configurations of p₀₀, p₁₀, p₀₁, and p₁₁ with $S_{e:j}^{(s)}=0.95$ and $S_{p:j}^{(s)}=0.99$, for j = 1, 2 and s = 1, 2, …, S. To evaluate the performance of algorithms with different levels of disease prevalence, we let p₀₀ ∈ {0.90, 0.95, 0.97, 0.99, 0.999} and vary the other probabilities accordingly. Values of p₀₀ = 0.90, 0.95 were chosen to be consistent with our chlamydia and gonorrhea application in Section 5. Values of p₀₀ = 0.99, 0.999 were chosen to emulate what would occur when the two infections are very rare (e.g., HIV-1 and HIV-2, etc.). For each setting, we calculate the overall optimal testing configuration by minimizing $n_1^{-1}E(T^{(S)})$ and, separately, the master pool size that corresponds to the most efficient use of halving. We kept $S_{e:j}^{(s)}=0.95$ and $S_{p:j}^{(s)}=0.99$ constant across the stages in Table 1 for simplicity. Proper assay calibration and/or the adjustment of dilution ratios would be needed to make this assumption reasonable; see McMahan, Tebbs, and Bilder (2013) and the references therein. Web Appendix D contains additional results where $S_{e:j}^{(s)}$ varies across stages.

Table 1.

Expected number of tests per individual $n_1^{-1}E(T^{(S)})$ when $S_{e:j}^{(s)}=0.95,S_{p:j}^{(s)}=0.99$, and number of stages S ∈ {2, 3, 4, 5, 6}. The column labeled “Optimal” gives the configuration of n₁, n₂ … , n_s that minimizes $n_1^{-1}E(T^{(S)})$. The column labeled “Halving” gives the master pool size for the optimal halving algorithm. The percent reduction in $n_1^{-1}E(T^{(S)})$ when compared to $n_1^{-1}E(T^{(2)})$ is provided. The expected proportion of correct classifications $n_1^{-1}E(C^{(S)})$ is also shown; see the discussion at the end of Section 4. The maximum allowable master pool size is 100.

	S	Optimal	$n_1^{-1}E(T^{(S)})$	% Reduction	$n_1^{-1}E(C^{(S)})$	Halving	$n_1^{-1}E(T^{(S)})$	% Reduction	$n_1^{-1}E(C^{(S)})$
	2	4 : 1	0.593	– –	0.985	n1 = 4	0.593	– –	0.985
p00 = 0.90	3	9 : 3 : 1	0.569	4.0	0.984	n1 = 6	0.574	3.2	0.984
p10 = 0.05	4	99 : 9 : 3 : 1	0.577	2.7	0.984	n1 = 12	0.595	−0.3	0.982
p01 = 0.04	5	90 : 45 : 9 : 3 : 1	0.595	−0.3	0.983	n1 = 24	0.620	−4.6	0.980
p11 = 0.01	6	96 : 48 : 24 : 6 : 3 : 1	0.619	−4.4	0.982	n1 = 48	0.637	−7.4	0.980
	2	5 : 1	0.433	– –	0.991	n1 = 5	0.433	– –	0.991
p00 = 0.95	3	9 : 3 : 1	0.371	14.3	0.992	n1 = 8	0.385	11.1	0.991
p10 = 0.03	4	18 : 6 : 3 : 1	0.370	14.5	0.990	n1 = 12	0.373	13.9	0.990
p01 = 0.01	5	90 : 18 : 6 : 3 : 1	0.377	12.9	0.990	n1 = 24	0.381	12.0	0.989
p11 = 0.01	6	96 : 48 : 12 : 6 : 3 : 1	0.388	10.4	0.989	n1 = 48	0.392	9.5	0.989
	2	7 : 1	0.345	– –	0.994	n1 = 7	0.345	– –	0.994
p00 = 0.97	3	16 : 4 : 1	0.273	20.9	0.995	n1 = 10	0.289	16.2	0.994
p10 = 0.01	4	27 : 9 : 3 : 1	0.260	24.6	0.994	n1 = 16	0.269	22.0	0.994
p01 = 0.01	5	36 : 12 : 6 : 3 : 1	0.264	23.5	0.994	n1 = 24	0.265	23.2	0.994
p11 = 0.01	6	96 : 24 : 12 : 6 : 3 : 1	0.271	21.4	0.994	n1 = 32	0.272	21.2	0.994
	2	11 : 1	0.209	– –	0.997	n1 = 11	0.209	– –	0.997
p00 = 0.990	3	25 : 5 : 1	0.135	35.4	0.998	n1 = 16	0.156	25.4	0.997
p10 = 0.004	4	48 : 12 : 4 : 1	0.117	44.0	0.998	n1 = 24	0.131	37.3	0.997
p01 = 0.004	5	81 : 27 : 9 : 3 : 1	0.112	46.4	0.998	n1 = 32	0.118	43.5	0.998
p11 = 0.002	6	72 : 24 : 12 : 6 : 3 : 1	0.112	46.4	0.997	n1 = 48	0.113	45.9	0.997
	2	33 : 1	0.081	– –	0.999	n1 = 33	0.081	– –	0.999
p00 = 0.9990	3	99 : 11 : 1	0.032	60.5	1.000	n1 = 48	0.046	43.2	0.999
p10 = 0.0004	4	96 : 24 : 6 : 1	0.024	70.4	1.000	n1 = 68	0.034	58.0	1.000
p01 = 0.0004	5	96 : 48 : 16 : 4 : 1	0.023	71.6	1.000	n1 = 96	0.027	66.7	1.000
p11 = 0.0002	6	96 : 48 : 24 : 12 : 4 : 1	0.022	72.8	1.000	n1 = 96	0.023	71.6	1.000

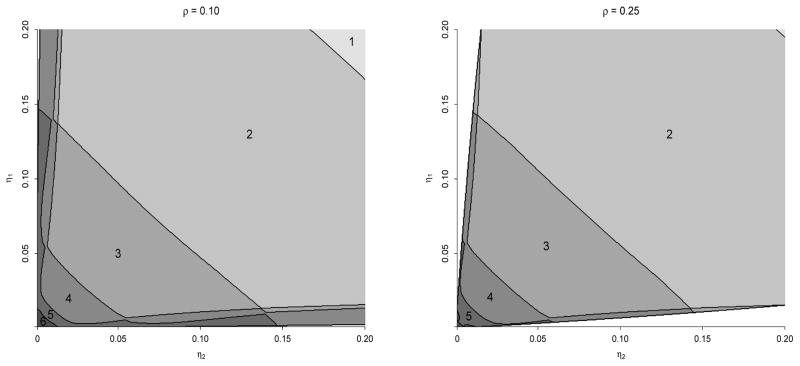
Our calculations in Table 1 show that as the combined disease prevalence decreases (p₀₀ increases), higher-stage algorithms for multiple infections can markedly reduce the value of $n_1^{-1}E(T^{(S)})$. For example, when p₀₀ = 0.97 and the marginal disease probabilities η₁ = p₁₀+p₁₁ and η₂ = p₀₁+p₁₁ are each 0.02 (the third case in Table 1), the optimal hierarchical algorithm uses S = 4 stages (with pool sizes n₁ = 27, n₂ = 9, n₃ = 3, and n₄ = 1) and confers a 24.6% reduction in the expected number of tests per individual when compared to the optimally sized Dorfman algorithm from Tebbs et al. (2013). The optimal halving algorithm in this same setting uses S = 5 stages (with master pool size n₁ = 24) and confers a 23.2% reduction when compared to the best Dorfman algorithm. Those cases in Table 1 involving rarer infections (i.e., p₀₀ = 0.99, 0.999) provide even larger reductions. To provide a panoptic examination, we display in Figure 2 the best number of stages S to use when the marginal disease probabilities η₁ and η₂ range from 0.001 to 0.20, $S_{e:j}^{(s)}=0.95$ and $S_{p:j}^{(s)}=0.99$, and the correlation between the true disease statuses ρ = corr(Ỹ_l1, Ỹ_l2) is fixed at ρ = 0.10 and ρ = 0.25. At each configuration of η₁ and η₂, the optimal hierarchical algorithm is determined for each S ≥ 2, and the regions in Figure 2 identify the number of stages S that minimizes $n_1^{-1}E(T^{(S)})$. Clearly, there is a sizeable subset of the parameter space for which higher-stage designs are more efficient than those that use only two stages.

Figure 2.

Optimal number of stages S when $S_{e:j}^{(s)}=0.95$ and $S_{p:j}^{(s)}=0.99$. The maximum allowable master pool size is 100. In the lower left corner of each subfigure, we did not show values of S larger than 6 to avoid crowding. Values of η₁ and η₂ in the white regions (barely detectable in the ρ = 0.10 subfigure) are not possible because correlations for binary random variables are restricted. Note that “S = 1” corresponds to individual testing.

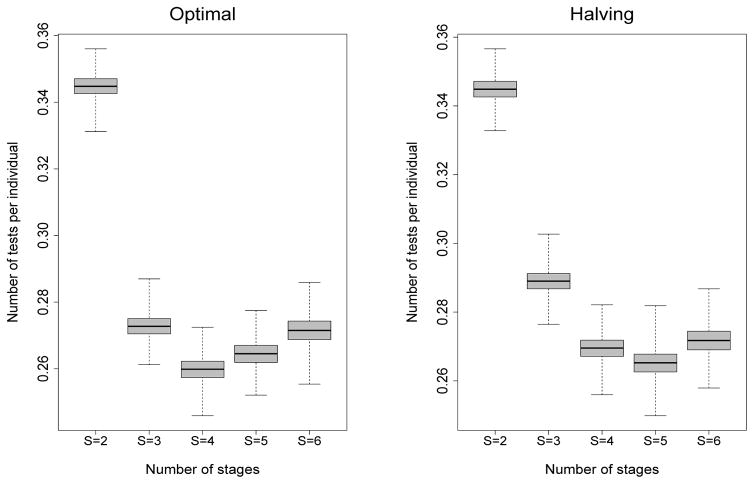
To better understand how hierarchical algorithms will perform in practice, we conducted a simulation study to assess the variability in the number of tests expended on a per-individual basis. For each parameter configuration in Table 1, we first generated the true infection statuses of 100,000 individuals according to the specified cell probabilities. This sample size was chosen to be comparable to our data application in Section 5. Under each optimal and halving configuration in Table 1, we assigned our 100,000 individuals to pools, performed our hierarchical algorithms using $S_{e:j}^{(s)}=0.95$ and $S_{p:j}^{(s)}=0.99$, and recorded the number of tests per individual. This process was repeated B = 5000 times for each design listed in Table 1. For the third case in Table 1 where p₀₀ = 0.97, Figure 3 displays boxplots of 5000 values of the number of tests per individual for each number of stages S. One notes that the variation in the number of tests per individual for this case is fairly constant across the values of S and that higher-stage algorithms are always preferred. Similarly constructed figures for the other four parameter configurations in Table 1 are provided in Web Appendix D.

Figure 3.

Simulation study for the third case in Table 1 with p₀₀ = 0.97, $S_{e:j}^{(s)}=0.95$, and $S_{p:j}^{(s)}=0.99$. Boxplots of the number of tests per individual are constructed from B = 5000 replications under the optimal and halving group configurations shown in Table 1.

Finally, a comparison of the classification accuracy measures derived in Section 3.2 is given in Web Appendix D under the same settings as in Table 1. This comparison shows that pooling sensitivity PS_e:j decreases as the number of stages S increases, as expected, but not as rapidly as it would in S-stage hierarchical algorithms for single infections where the pooling sensitivity equals ${\prod }_{s=1}^S{S}_{e:j}^{(s)}$. In fact, provided that $S_{e:j}^{(s)}<1$ for s = 1, 2, …, S, one can show algebraically that ${\text{PS}}_{e:j}>{\prod }_{s=1}^S{S}_{e:j}^{(s)}$ for all S ≥ 2, an important additional benefit of using hierarchical algorithms with multiplex assays. Also, the pooling positive predictive value PPV_j increases in higher-stage algorithms for multiple infections, substantially so when both infections are rare. Values of PS_p:j and NPV_j remain fairly constant across values of S.

We conclude this section with a remark. While we have used the expected number of tests per individual $n_1^{-1}E(T^{(S)})$ to determine optimal group configurations in this section, other objective functions which incorporate classification accuracy could be used. Based on the recommendations of anonymous referees, we have also determined optimal configurations in this section by maximizing E(C^(S))/E(T^(S)), where C^(S) denotes the number of individuals correctly classified in a master pool tested in S stages. This type of objective function was recommended by Malinovsky, Albert, and Roy (2016) for single infections and two-stage testing. In Web Appendix D, we use our Markov chain framework to derive E(C^(S)) for multiple infections with any number of stages, and we reproduce Table 1 and Figure 2 using the configurations obtained from maximizing E(C^(S))/E(T^(S)). For the cases we considered in this section, there is nearly perfect agreement between the configurations found from minimizing $n_1^{-1}E(T^{(S)})$ and from maximizing E(C^(S))/E(T^(S)).

5. Region X Infertility Prevention Project Data

The Infertility Prevention Project (IPP) was a national program that started in 1988 and was implemented in all 50 states. The purpose of the program was to screen individuals for chlamydia and gonorrhea in high-risk populations and to offer treatment services for those who were infected. Chlamydia and gonorrhea are two of the most common sexually transmitted diseases in the United States with approximately 1.6 million new infections reported each year (CDC, 2014). The IPP, which was funded by the Department of Health and Human

Services (HHS) and overseen by the Centers for Disease Control and Prevention (CDC), was discontinued in 2013 after the Affordable Care Act was passed. This has since forced STD clinics and public health laboratories nationwide to rely on other sources of external funding (e.g., private health insurance, Medicaid, etc.) for the purpose of screening these same high-risk populations. As a result, public-health officials have experienced increased pressure to be mindful of testing costs (JSI Research & Training Institute, Inc., 2013).

Because chlamydia and gonorrhea remain moderately rare even in higher-risk populations, our higher-stage hierarchical algorithms emerge as excellent candidates to further reduce the number of tests. Public health laboratories in multiple states have used two-stage Dorfman algorithms with multiplex assays to screen for chlamydia and gonorrhea (Jirsa, 2008; Lewis et al., 2012), and Tebbs et al. (2013) show this provides a sizeable reduction in the number of tests when compared to individual testing. Our goal is to determine if higher-stage algorithms (i.e., S > 2) can provide additional savings. To accomplish this, we use chlamydia and gonorrhea data collected from HHS Region X during 2010–2011. Region X consists of four states, Alaska, Idaho, Oregon, and Washington, and our data set contains about 260,000 individual testing results for both chlamydia and gonorrhea among these states (roughly 130,000 individuals each year). Because approximately 99% of the testing results were obtained from using the Aptima Combo 2 Assay, we focus on these individuals in our analysis.

To illustrate the potential use of higher-stage algorithms, we use female specimens only. Male subjects are more likely to be tested only when they exhibit symptoms of infection (e.g., painful urination, etc.), resulting in much higher positivity rates and therefore making higher-stage testing less attractive. On the other hand, females are routinely screened as part of annual health examinations and visits to family-planning health centers. In Web Appendix E, we provide the observed prevalences for the 107,463 females tested in 2010, cross-classiffied by specimen type (swab/urine) and state within Region X. We also provide values of the Aptima Combo 2 Assay sensitivity and specificity for each infection; these values were taken from the most recent product literature available at the manufacturer's website.

Using the 103,690 females tested in 2011, we investigate the performance of hierarchical algorithms with S = 2, 3, and 4 stages. For each state and within specimen type, we randomly assign the 2011 individuals to master pools under the optimal testing configuration which we determine using the 2010 prevalences. In doing so, we set the maximum allowable master pool size at 20, because documented applications of group testing for chlamydia and gonorrhea do not use pool sizes larger than this. In order to measure classification accuracy, we treat the 2011 individuals' responses as the \true" statuses; we then test and decode pools ourselves by simulating test outcomes using the assay accuracies reported for the Aptima Combo 2 Assay at each stage. This entire procedure was repeated B = 5000 times to include multiple sets of possible pools and to average over the effects of simulation.

For each state in Region X, Table 2 displays the number of tests expended for female subjects during 2011 (averaged over the 5000 implementations) and, for higher-stage algorithms, the percent reduction in the average number of tests when compared to S = 2. Boxplots of the 5000 simulated values of T^(S), shown cross-classified by specimen type (swab/urine) and state (AK, ID, OR, WA), are given in Web Appendix E. Our results suggest that using higher-stage hierarchical algorithms in all four states would be highly beneficial. For example, for females tested using swabs in Alaska, a three-stage algorithm (with pool sizes n₁ = 9, n₂ = 3, and n₃ = 1) confers an 11.0% reduction in the average number of tests when compared to the best two-stage algorithm from Tebbs et al. (2013). This same reduction for swabs is 10.8%, 11.8%, and 12.4% for Idaho, Oregon, and Washington, respectively. Note that higher-stage gains are smaller when testing urine specimens because the 2011 marginal infection rates are slightly larger (see Web Appendix E); however, the corresponding three-stage gains still do range from 5.9–10.5%. There are even a few instances in Table 2 where an optimal four-stage algorithm is the most efficient (i.e., swab testing in Oregon and Washington). However, four-stage gains for these data are small when compared to the best three-stage algorithms.

Table 2.

Region X 2011 chlamydia and gonorrhea data. Average number of tests (sample standard deviation, SD) from B = 5000 sets of pools for 2-, 3-, and 4-stage hierarchical algorithms. The optimal configuration is determined by minimizing $n_1^{-1}E(T^{(S)})$ using the 2010 prevalences; see Web Appendix E. The percent reduction in the average number of tests is also shown. The maximum allowable master pool size is 20.

State	# Stages	Swab			Urine
		Configuration	# Tests (SD)	% Reduction	Configuration	# Tests (SD)	% Reduction
Alaska	S = 2	5 : 1	1509.9 (30.7)	– –	4 : 1	2615.6 (31.5)	– –
	S = 3	9 : 3 : 1	1343.7 (31.2)	11.0	9 : 3 : 1	2460.4 (42.1)	5.9
	S = 4	18 : 6 : 3 : 1	1352.4 (38.5)	10.4	18 : 6 : 3 : 1	2512.0 (54.1)	4.0
Idaho	S = 2	5 : 1	3938.0 (49.9)	– –	5 : 1	2253.4 (34.8)	– –
	S = 3	9 : 3 : 1	3511.3 (51.1)	10.8	9 : 3 : 1	2047.1 (37.4)	9.2
	S = 4	18 : 6 : 3 : 1	3516.0 (66.0)	10.7	18 : 6 : 3 : 1	2082.2 (48.5)	7.6
Oregon	S = 2	5 : 1	19633.1 (108.9)	– –	4 : 1	4459.0 (39.2)	– –
	S = 3	9 : 3 : 1	17322.5 (112.1)	11.8	9 : 3 : 1	4073.1 (52.7)	8.7
	S = 4	18 : 6 : 3 : 1	17272.5 (140.2)	12.0	18 : 6 : 3 : 1	4134.2 (68.3)	7.3
Washington	S = 2	5 : 1	10497.1 (80.4)	– –	5 : 1	8324.5 (66.2)	– –
	S = 3	9 : 3 : 1	9199.5 (81.0)	12.4	9 : 3 : 1	7454.5 (70.2)	10.5
	S = 4	18 : 6 : 3 : 1	9162.6 (103.8)	12.7	18 : 6 : 3 : 1	7521.1 (90.1)	9.7

Overall, our analysis demonstrates that moving from two-stage to three-stage hierarchical algorithms would be preferred for Region X and in other regions where the marginal infection rates of chlamydia and gonorrhea are similar. Among the 103,690 Region X females tested in 2011, implementing the optimal two-stage algorithm from Tebbs et al. (2013) requires 53,231 tests on average, calculated by summing across the states and specimen types in Table 2. Optimal three-stage hierarchical algorithms require 47,412 tests on average, an overall 11% reduction and a savings of over 5,800 tests. Finally, we use Web Appendix E to display the classification accuracy results from our investigation. There is a loss in pooling sensitivity for both infections as the number of stages increases, which is expected for any hierarchical procedure; however, this loss is often minor for gonorrhea. On the other hand, higher-stage algorithms provide larger positive predictive values for both infections.

6. Discussion

We have introduced S-stage hierarchical group testing algorithms for multiple infections, simultaneously generalizing Tebbs et al. (2013) and the extensive literature on hierarchical algorithms for single infections. Our operating characteristic derivations exploit a novel conceptualization of the decoding process by viewing testing results as error-laden realizations of a Markov chain. Our analysis of the IPP data from Region X illustrates the benefit of using higher-stage algorithms for chlamydia and gonorrhea detection.

The assumptions we have made in this article regarding the testing outcomes do not affect our Markov chain calculations because these calculations refer to the underlying true status process. Therefore, relaxing any of these assumptions should be possible by modifying the misclassification operators P^(s) (Section 3.1), ${\mathbf{P}}_{++}^{(s)}$ and ${\mathbf{P}}_{+-}^{(s)}$ (Section 3.2), and those in Web Appendix C. For example, one assumption we made was that testing responses are conditionally independent given the true statuses of all pools tested. This is certainly reasonable when misclassification is driven primarily by factors related to test implementation; however, it may not be reasonable otherwise. We also implicitly assumed that $S_{e:j}^{(s)}$ and $S_{p:j}^{(s)}$ for one infection in stage s do not depend on the true status of the other infection, an assumption that requires the multiplex assay used to possess adequate discriminating power. Future research in group testing could investigate ways to avoid making either or both assumptions. McMahan et al. (2013) provide one way to relax the conditional independence assumption when additional biomarker information is available for each group testing response. Albert and Dodd (2004) provide an excellent summary of this issue when individual testing is used.

The merger of group testing for multiple infections and Markov processes brings with it exciting opportunities to investigate other case identification algorithms. For example, it should be possible to extend the S-stage array procedures in Berger, Mandell, and Subrahmanya (2000) and Kim and Hudgens (2009) to allow for multiple infections using the framework outlined in this article. This extension would be more difficult because individuals are placed in overlapping pools; however, the underlying Markov chain structure for the true status decoding process still remains. We also believe that multiple-disease algorithms could be developed to incorporate risk factor information (e.g., age, race, number of sexual partners, etc.) on each individual. Bilder and Tebbs (2012) provide a review of recently proposed \informative" algorithms involving single infections. The approach outlined in Section 3 of this article could serve as a starting point towards generalizing their work.