Abstract
Reactive mineral–water interfaces exert control on the bioavailability of contaminant arsenic species in natural aqueous systems. However, the ability to accurately predict As surface complexation is limited by the lack of molecular-level understanding of As–water–mineral interactions. In the present study, we report the structures and properties of the adsorption complexes of arsenous acid (As(OH)3) on hydrated mackinawite (FeS) surfaces, obtained from density functional theory (DFT) calculations. The fundamental aspects of the adsorption, including the registries of the adsorption complexes, adsorption energies, and structural parameters are presented. The FeS surfaces are shown to be stabilized by hydration, as is perhaps to be expected because the adsorbed water molecules stabilize the low-coordinated surface atoms. As(OH)3 adsorbs weakly at the water–FeS(001) interface through a network of hydrogen-bonded interactions with water molecules on the surface, with the lowest-energy structure calculated to be an As–up outer-sphere complex. Compared to the water–FeS(001) interface, stronger adsorption was calculated for As(OH)3 on the water–FeS(011) and water–FeS(111) interfaces, characterized by strong hybridization between the S-p and O-p states of As(OH)3 and the surface Fe-d states. The As(OH)3 molecule displayed a variety of chemisorption geometries on the water–FeS(011) and water–FeS(111) interfaces, where the most stable configuration at the water–FeS(011) interface is a bidentate Fe–AsO–Fe complex, but on the water–FeS(111) interface, a monodentate Fe–O–Fe complex was found. Detailed information regarding the adsorption mechanisms has been obtained via projected density of states (PDOS) and electron density difference iso-surface analyses and vibrational frequency assignments of the adsorbed As(OH)3 molecule.
1. Introduction
Arsenic is recognized as one of the most serious inorganic contaminants in soil and groundwater worldwide, with significant public health implications. Arsenic often makes its way into soil and water courses by the natural processes of weathering and dissolution of minerals such as arsenian pyrite, Fe(As,S)2, and arsenopyrite, FeAsS.1 Anthropogenic activities, particularly mineral extraction and processing can also introduce arsenic-rich effluents into the environment if not carefully monitored and controlled.2 The effects of arsenic on human health are highly detrimental, with arsenic poisoning being linked to neurological disorders, dermatological and gastrointestinal problems, and it is also a known carcinogen.3,4
Arsenic can exist in a range of oxidation states from −3 to +5, although in aqueous solutions it is most commonly found as As(III) or As(V) oxyacids. As(III) is both more toxic (20–65 times) and more mobile (being able to travel five to six times faster) than As(V) and is one of the main toxic species in natural waters.5−7 Analyses of hydrothermal fluids show that As is transported mainly as As(III),8 and the uptake of As(III) from aqueous solutions is reported to occur via neutral molecules, which suggest that arsenous acid (As(OH)3) or related species could be the common form of arsenic in contaminated waters.9,10 An understanding of the geochemistry of As(OH)3 in low temperature anoxic sedimentary environments is therefore crucial to the development of safe drinking water and food supplies in many countries.11,12 Of the processes influencing arsenite mobility, reactive mineral–water interfaces exert control on the bioavailability of contaminant arsenic species in natural aqueous systems. The adsorption of arsenic species onto mineral surfaces strongly affects their concentrations in aqueous environments.13
In recent years, iron sulfide mackinawite (FeS), has attracted significant interests for environmental remediation due to its natural abundance and high treatment efficiency in anoxic environments.14−26 FeS is a layered iron sulfide mineral that crystallizes in the tetragonal structure shown in Figure 1,27,28 and it is known to be the first crystalline ferrous sulfide phase to form under sulfate reducing conditions.29,30 FeS is a nontoxic mineral and a precursor to other stable iron sulfide minerals, such as greigite and pyrite.29,30 Like other 2D layered materials, for example, MoS2, FeS possesses a high specific surface area and reactive surfaces that are ideal for the uptake of aqueous contaminants. Furthermore, FeS nanoparticles can be synthesized easily,31−35 which makes it a promising candidate for the treatment of groundwater and soil contaminated with arsenic,14−18 selenium,19,20 and heavy metals, including mercury,21−23 and chromium.24−26
Figure 1.
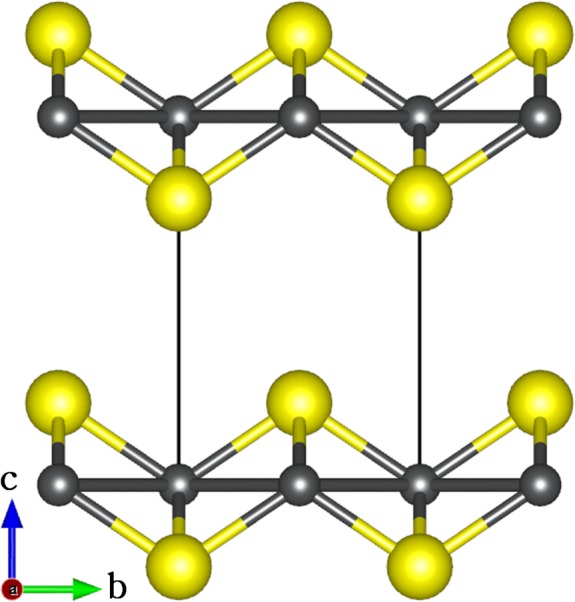
Layered structure of mackinawite, with the tetragonal unit cell highlighted by dash lines. (Color scheme: Fe = gray, S = yellow).
Owing to its unique structure and surface chemical properties, mackinawite has been reported to be very effective in immobilizing divalent metals such as Mg2+, Ca2+, Mn2+, Ni2+, Cd2+, and Hg2+ from aqueous solutions.36−39 FeS has also been shown to have a high removal capacity for inorganic oxyanions, including As under anoxic conditions.14−20 It has been reported that mackinawite suspensions and synthetic nanoparticulate mackinawite can effectively remove As(III) at a pH range of 5–10.14,40 A comparative study of the removal capacity of As(III) and As(V) in aqueous solutions by goethite, lepidocrocite, mackinawite, and pyrite, by Farquhar et al.17 has shown that mackinawite was more efficient than iron-oxide phases or pyrite. Their results suggested that the arsenic uptake by freshly prepared mackinawite was due to outer-sphere complexation,17 but fundamental aspects of this process, including the registries of the adsorption complexes, adsorption energies, and structural parameters remain unclear. Such information cannot be obtained directly from experimental work and the underlying physical driving forces that control the reactivity of arsenic species with the FeS surfaces remain poorly understood. The diverse interactions and reactions occurring at the mineral–water interfaces often create complex situations that are difficult to interpret. However, molecular simulations provide an alternative way to gain fundamental insight into these processes.41−44 Calculations based on the density functional theory (DFT) have become indispensable in unravelling the interactions of organic and inorganic molecules with solid surfaces as they are capable of accurately predicting lowest-energy adsorption geometries and identifying charge transfer and other electronic effects.45−47 For example, DFT-based studies have been instrumental in elucidating the complex adsorption processes of arsenic and arsenate on iron oxide mineral surfaces.42,43 Goffinet and Mason employed spin-polarized DFT calculations to study the inner-sphere As(III) complexes on hydrated α-Fe2O3(0001) surface models.42 Blanchard and co-workers have modeled arsenate adsorption on the hydrated (10–12) hematite surface, investigating charged inner- and outer-sphere complexes using DFT calculations.43 To date, no systematic theoretical study has been conducted to investigate the detailed adsorption mechanism of arsenous acid at the water–FeS interface, which makes this investigation timely.
In this study, the structures and properties of the adsorption complexes of As(OH)3 on hydrated mackinawite (FeS) surfaces were studied using dispersion-corrected density functional theory calculations (DFT-D2). The energetically preferred As(OH)3 surface complexes on the hydrated (001), (011), and (111) surfaces of mackinawite have been identified. Detailed structural analysis of the adsorption complexes and insight into the nature of adsorption on the different surfaces was determined via analysis of projected density of states and differential charge density iso-surfaces. Vibrational frequency assignment of the different identified adsorption complexes of As(OH)3 was carried out, which will be useful for comparison with any future experimental studies.
2. Computational Details
The calculations were carried out using the VASP code,48,49 which employs a basis set of plane-waves to solve the Kohn–Sham (KS) equations of the density functional theory (DFT) in a periodic system. Long-range dispersion forces were accounted for in our calculations using the Grimme DFT-D2 method,50 which is essential for the accurate description of the FeS interlayer interactions,51−54 as well as the interactions between the As(OH)3 molecule and the water–FeS surfaces. The D2 method was used in this study to remain consistent with previous work and to ensure that direct comparison could be made with our earlier studies. However, we have carried out a number of test calculations using the DFT-D3 method, as mentioned in the text where relevant, but no significant differences between the two methods were observed.
The generalized gradient approximation (GGA), with the PW91 functional55 was used to calculate the total free energies. The interactions between the valence electrons and the cores were described with the projected augmented wave (PAW) method56 in the implementation of Kresse and Joubert.57 The on-site potential, GGA+U, was not employed for these calculations as previous studies on FeS using VASP have shown that the extra localization of the d-electrons through the inclusion of a +U correction term provides inadequate structural optimizations.54 An energy cutoff of 400 eV for the plane-wave basis set was tested to be sufficient to converge the total energy of mackinawite to within 0.0001 eV and the Brillouin zone was sampled using 11 × 11 × 7 and 5 × 5 × 1 Monkhorst–Pack58 K-points mesh for bulk and surface calculations, respectively, which ensures electronic and ionic convergence. Geometry optimizations were performed using the conjugate gradient minimization algorithm until the magnitude of the residual Hellman–Feynman force on each relaxed atom reached 0.001 eV/Å.
The bulk FeS was modeled in the tetragonal structure (Figure 1). From a full geometry optimization, the equilibrium lattice parameters were predicted to be a = 3.587 Å, c = 4.908 Å, and c/a = 1.368,44,51−54 which agree well with those measured experimentally (a = 3.674 Å, c = 5.033 Å, and c/a = 1.370).27,28 Similar results were obtained within the DFT-D3 scheme, which predicted the lattice parameters to be a = 3.590 Å, c = 4.992 Å, and c/a = 1.390. From the fully relaxed bulk structure, we created the (001), (011), and (111) surfaces of FeS, which are the commonly observed facets in mackinawite nanoparticles.44,59 The surfaces were created using the METADISE code,60 which generates nonpolar supercells, avoiding dipole moments perpendicular to the surface plane, as is required for reliable and realistic surface calculations.61
For each surface, a minimum slab thicknesses of 10 Å was used in each simulation cell, and a vacuum region of 15 Å was tested to be sufficient to avoid interactions between periodic slabs. The converged slab thickness used to model the (001), (011), and (111) surfaces were constructed of 6, 9, and 12 atomic layers, respectively. Because the processes take place in an aqueous environment, the FeS surfaces were hydrated through associative adsorption of a monolayer of water, to provide a realistic picture of the As(OH)3 complexation in natural aqueous systems at the mackinawite–water interface. In an earlier study, we showed that dissociative water adsorption did not occur spontaneously at FeS surfaces.62 We considered that a monolayer of water was obtained when all surface cations/anions had been terminated by water. The hydrated (001), (011), and (111) surfaces are modeled by large slabs constructed as (3 × 3)–9water, (4 × 2)–8water, and (3 × 2)–6water supercells, respectively. These simulation supercells are large enough to minimize lateral interaction between the As(OH)3 molecules in neighboring image cells.
Different binding modes of the As(OH)3 molecule were considered, for example, monodentate or bidentate adsorption configurations, in order to obtain the lowest-energy adsorption complexes. The adsorption energy (Eads) of the As(OH)3 on the hydrated FeS surfaces was calculated as follows:
| 1 |
where Ewater–surf+As(OH)3 represents the total energy of the adsorbate–substrate system, Ewater–surf represents the total energy of the relevant hydrated FeS substrate, and EAs(OH)3 is the energy of the free As(OH)3 molecule. Differences in the adsorption energies reflect trends in surface reactivity, thus Eads is useful for characterizing activity trends and relative energetics. A Bader population analysis was carried out for all the As(OH)3–water–FeS complexes, using the code developed by Henkelman and co-workers63 in order to quantify any charge transfer between the substrate surfaces and the adsorbate molecule. Vibrational frequency assignment of the As–O and O–H bond stretching modes was performed within the framework of the self-consistent density functional perturbation theory.64
3. Results and Discussion
3.1. Hydrated FeS (001), (011), and (111) Surface Models
Prior to studying the adsorption and surface reactions of As(OH)3, we have characterized the interaction of water with the (001), (011), and (111) surfaces of FeS and how hydration affects their relative stabilities. Shown in Figure 2 are the optimized structures of the hydrated (001), (011), and (111) surfaces. The relaxed surface energies (γr) of the pure symmetric stoichiometric slabs were calculated using the equation:
| 2 |
where Eslabrelaxed and Eslab are the energies of the relaxed and unrelaxed slabs, respectively, nEbulk is the energy of an equal number (n) of bulk FeS units, and A is the area of one side of the slab. Considering that the adsorption of water on the FeS surfaces may affect their stability, we have also calculated the surface energies of the surfaces after water adsorption using eqs 3.
| 3 |
where Eslab + waterrelaxed is the energy of the surface with adsorbed water molecules and nEwater is the energy of an equivalent number of free water molecules.
Figure 2.
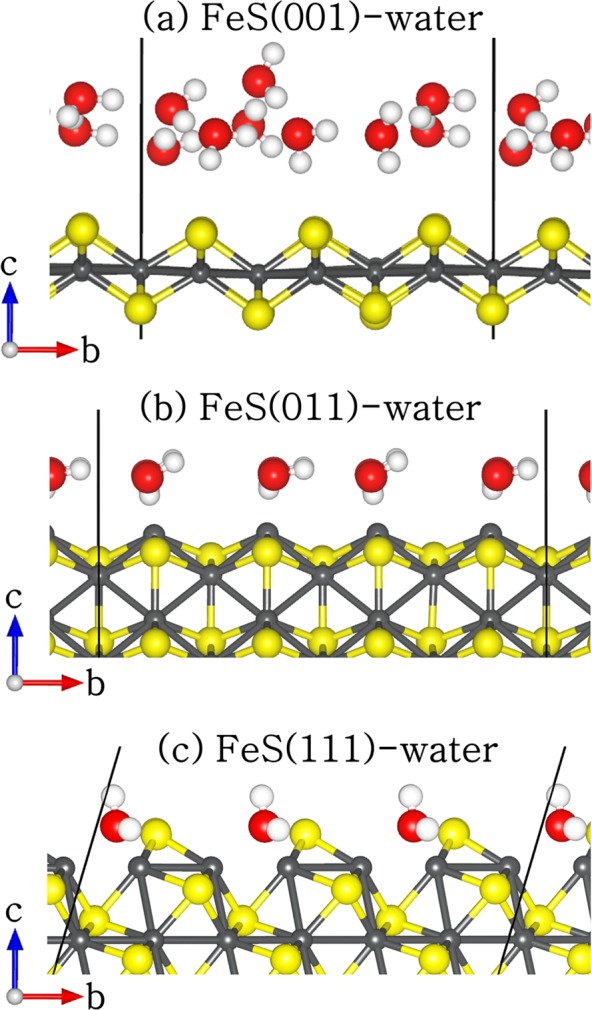
Side view of the geometry-optimized structures of hydrated FeS (a) (001), (b) (011), and (111) surfaces. (Color scheme: Fe = gray, S = yellow, O = red, and H = white).
The calculated surface energies of different surfaces (pristine and hydrated) as listed in Table 1, show that the order of increasing surface energies, and therefore decreasing stability, before and after hydration is (001) < (011) < (111). All the FeS surfaces were stabilized through hydration, as is perhaps to be expected because the adsorbed water molecules stabilize the low-coordinated surface atoms. At the FeS(001) surface, we found that the water molecules were only physisorbed with the hydrogen atoms pointing toward the terminating surface sulfur ions (Figure 2a), similar to results obtained from previous DFT,53,62 and molecular dynamics (MD) simulations65 of the structure and dynamics of water at the FeS(001) surface. The shortest H–S distance is calculated at 2.319 Å, which is larger than the typical hydrogen-bond length in water of 1.97 Å,66 and therefore suggests that dispersion forces may play an important role in stabilizing the water molecule on the FeS(001) surface. In a previous study, we showed that the dispersion interactions contribute approximately 87% of the total adsorption energy of water on the FeS(001).62 The average hydrogen to oxygen (H---O) interatomic distance between the water molecules on the (001) surface is calculated at 1.824 Å.
Table 1. Calculated Surface Energies of Pristine (γr) and Hydrated (γhydrated) FeSa.
| surface | γr (J m–2) | γhydrated (J m–2) | % relaxation |
|---|---|---|---|
| (001) | 0.19 | 0.14 | 26.31 |
| (011) | 0.95 | 0.71 | 25.26 |
| (111) | 1.51 | 1.21 | 19.87 |
The corresponding percentage relaxation after hydration is denoted as % relaxation.
Compared to the (001) surface, the water molecules on the (011) surface are oriented in such a way that now the O atoms are closest to the surface Fe sites (average Fe–O = 2.253 Å) as shown in Figure 2b. The hydrogen atoms are oriented toward the sulfur ions in the next FeS layer at an average distance of 2.703 Å, which is larger than the average Fe–O bond length of 2.253 Å and therefore suggests that the major interactions between the adsorbing water molecules and the (011) surface is through the interaction of their oxygen ions with surface Fe ions. In the case of the water–FeS(111) complex (Figure 2c), the water molecules are located above the bridge sites between adjacent Fe ions (average Fe–O = 2.205 Å). The hydrogen atoms are oriented toward the sulfur ions in the next FeS layer at an average distance of 2.043 Å, compared to 2.703 Å at the FeS(011) surface, which indicates stronger hydrogen-bonding at the FeS(111) surface than at the FeS(011). Generally, the FeS surfaces were found to undergo modest relaxations relative to the bulk interlayer spacings upon hydration, where the topmost three percentage relaxations of the interlayer spacings are calculated to be +6.5%, + 3.3%, and −3.4% for the (001), – 24.1%, + 10.9%, and −2.3% for the (011), and +29.3%, + 12.1%, and −6.6% for the (111). The multilayer relaxations for the hydrated surfaces were calculated as the percentage difference in the surface interlayer spacing, dij-hydrated, from the layer spacing of the same orientation in the geometry of the unrelaxed surface structure, dij-unrelaxed, created from the equilibrium bulk material. In these simulations, since the models are constructed from the optimized bulk structure, the required surface layer spacing is given by the spacing of the unrelaxed bulk-terminated slab structure.
| 4 |
Within this definition, negative values correspond to inward relaxation (contraction) and positive values denote outward relaxation (dilation) of the interlayer spacings.
3.2. As(OH)3 Structural Conformations
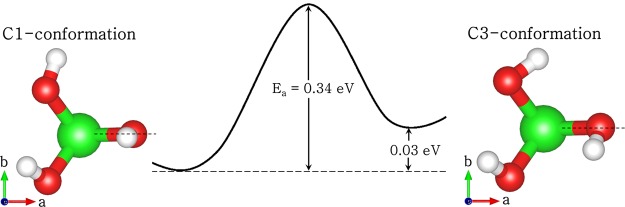
Arsenous acid (As(OH)3) exists in two conformations in the gas phase with either C1 or C3 symmetry. The optimized geometries of the C1 and C3 conformations are shown in Figure 3 and the calculated interatomic bond distances and bond angles along with earlier theoretical results41,67 are listed in Table 2. From our geometry optimization calculations, we found that the C1 symmetry is 0.03 eV more stable than the C3 symmetry, in agreement with earlier theoretical results of Ramírez-Solís et al.67 and Tossell et al.68 We show from climbing-image nudged elastic band (cNEB) calculations that the C1 conformation has to overcome an activation barrier of 0.34 eV to transform to the higher-energy C3 conformation. The three As–O bond distances of the C1 and the C3 conformers do not differ significantly, calculated to be 1.798, 1.801, and 1.811 Å for the C1 symmetry and 1.810, 1.811, and 1.813 Å for the C3 symmetry. Our calculated bond distances (As–O and O–H) and angles (O–As–O and As–O–H) show good agreement with earlier theoretical results41,67,68 and with those obtained from X-ray absorption and EXAFS analysis.69,70 In our study, we have explored several possible adsorption structures including monodentate or bidentate binding geometries on the different hydrated FeS surfaces.
Figure 3.
Optimized structures and energetics of C1 and C3 conformations of As(OH)3. (Color scheme: As = green, O = red and H = white).
Table 2. Structural Data (Interatomic Bond Distance and Angles) of As(OH)3, the experimental As–O bond length is 1.77–1.82 Å69,70.
| C1 symmetry |
C3 symmetry |
|||||
|---|---|---|---|---|---|---|
| parameter | this work | PBE41 | B3LYP67 | this work | PBE41 | B3LYP67 |
| d(As–O) /Å | 1.798 | 1.811 | 1.796 | 1.810 | 1.829 | 1.813 |
| 1.801 | 1.818 | 1.800 | 1.811 | 1.829 | 1.813 | |
| 1.811 | 1.841 | 1.826 | 1.813 | 1.829 | 1.813 | |
| d(O–H) /Å | 0.975 | 0.977 | 0.967 | 0.975 | 0.982 | 0.970 |
| 0.978 | 0.980 | 0.969 | 0.978 | 0.982 | 0.970 | |
| 0.978 | 0.983 | 0.970 | 0.978 | 0.982 | 0.970 | |
| α(O–As–O) /° | 90.17 | 88.79 | 90.86 | 97.25 | 96.92 | 97.34 |
| 99.84 | 99.75 | 99.61 | 97.48 | 96.94 | 97.36 | |
| 100.94 | 103.22 | 100.89 | 97.57 | 96.99 | 97.37 | |
| α(As–O–H) /° | 108.6 | 105.33 | 110.16 | 108.6 | 104.87 | 109.93 |
| 110.9 | 109.83 | 112.68 | 110.8 | 104.98 | 109.94 | |
| 111.2 | 111.77 | 112.78 | 111.0 | 105.02 | 109.93 | |
3.3. As(OH)3 Adsorption Complexes at Water–FeS(001) Interface
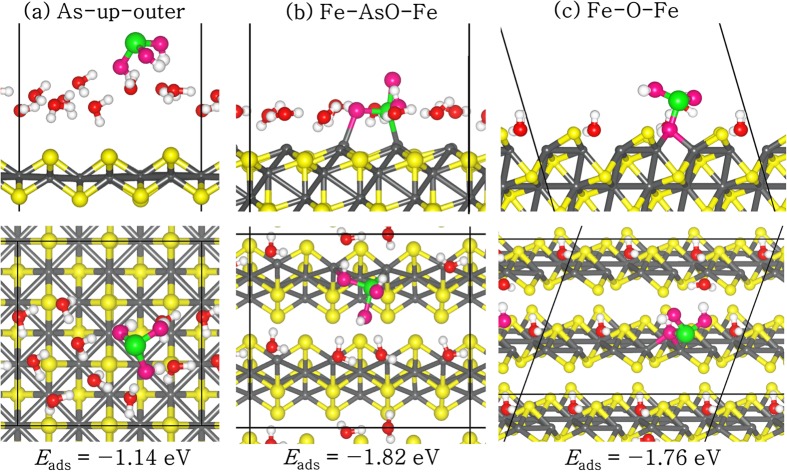
Several possible modes of adsorption sites and configurations were studied for As(OH)3 adsorption at the water-FeS(001) interfaces but only the lowest-energy structure (denoted As–up–outer) is shown in Figure 4a (the remaining conformations and calculated binding energies are given in the Supporting Information (SI) Figure S1 and Table S1, respectively). In the lowest-energy As–up–outer complex, the As(OH)3 is adsorbed outside the water layer with the As atom pointing upward, while the hydroxyl groups form hydrogen-bonded interactions with the surface-bound water molecules. The adsorption energy of this structure is −1.14 eV, which is 0.2 eV more favorable than the As–up inner-sphere complex (SI Figure S1b), in which the As(OH)3 molecule is adsorbed within the water layer by displacing some of the water molecules during the adsorption process. In the case of As–down configurations, the inner-sphere complex (SI Figure S1c) is found to be energetically more favorable than the outer-sphere complex (SI Figure S1d) by 0.23 eV. In all adsorption geometries, we observe only small elongations in the As–O and O–H bonds (Table 3 and SI Table S1) compared to the structural data of the free As(OH)3 molecule (Table 2), which may be attributed to the hydrogen-bonded interactions with the surface water molecules. In the lowest-energy outer-sphere As–up complex, the three hydrogen atoms of the As(OH)3 molecule interact with three different surface water molecules at Hmol–Owat distances of 1.702, 1.747, and 1.960 Å. We also observe hydrogen-bonded interactions between hydrogen atoms of two water molecules and O atoms of As(OH)3 at Hwat–Omol distances of 1.639 and 1.783 Å. The Hmol–Owat and Hwat–Omol bond lengths calculated in the present study compare closely with the typical hydrogen-bond length in water of 1.97 Å,66 which therefore suggests that hydrogen-bonded interactions contribute significantly to the stabilization of As(OH)3 at the water–FeS(001) interface.
Figure 4.
Lowest-energy adsorption complexes of As(OH)3 at the (a) (001), (b) (011), and (c) (111) water–FeS interfaces, in side (top) and top (bottom) views. (Color scheme: Fe = grey, S = yellow, As = green, Owater = red, OAs(III) = pink, and H = white).
Table 3. Adsorption Energies, Variation of the Total Bader Charge, Representative Geometrical Parameters, And Interatomic Distances of the Lowest-Energy As(OH)3 Adsorption Complexes at Water–FeS (001), (011), and (111) Interfaces (the DFT-D3 Eads are shown in parentheses).
| surface | FeS(001) | FeS(011) | FeS(111) |
|---|---|---|---|
| configuration | As–up–outer | Fe–AsO–Fe | Fe–O–Fe |
| Eads /eV | –1.14 (−1.06) | –1.82 (−1.73) | –1.76 (−1.68) |
| ∑q/e– | 0.04 | 0.30 | 0.28 |
| d(As–O) /Å | 1.834 | 1.889 | 1.946 |
| 1.835 | 1.838 | 1.810 | |
| 1.781 | 1.877 | 1.765 | |
| d(O–H) /Å | 0.988 | 1.024 | 1.018 |
| 1.003 | 0.977 | 1.004 | |
| 1.005 | 0.980 | 0.977 | |
| d(Hmol–Owat) /Å | 1.702, 1.747, 1.960 | 1.645 | 1.817 |
| d(Hwat–Omol) /Å | 1.639, 1.783 | 1.803 | 3.240 |
| d(Hwat–S) /Å | 2.301 | 2.034 | |
| d(As–S) /Å | 3.382 | 3.675 | |
| d(As–Fe) /Å | 2.269 | 3.365 | |
| d(O–Fe) /Å | 2.133 | 2.149 |
3.4. As(OH)3 Adsorption Complexes at Water-FeS(011) Interface
As with the water–FeS(001) surface, we have considered different possible adsorption structures for As(OH)3 on the water–FeS(011) surface. During the adsorption, some of the water molecules were displaced from the surface by the As(OH)3, enabling direct stronger interactions with the surface cations sites. Shown in Figure 4b is the lowest-energy adsorption configuration identified (the remaining conformations are given in the SI Figure S2, whereas the calculated adsorption energies and optimized structural parameters are reported in Table 3 and SI Table S2. The lowest-energy adsorption structure of As(OH)3 at the water–FeS(011) interface is calculated to be a bidentate Fe–AsO–Fe complex (Figure 4b), wherein the As(OH)3 molecule interacts with the surface Fe atoms via the As and one O atom. The adsorption energy of this structure is calculated at −1.82 eV, compared to the adsorption energy of −1.43 eV for the monodentate Fe–O complex (SI Figure S2b), wherein the As(OH)3 molecule interacts with the surface Fe atoms via only one O atom, – 1.06 eV for the monodentate Fe–As complex (SI Figure S2c), wherein the As(OH)3 molecule interacts with the surface Fe atoms via the As atom, and −0.89 eV for the As–bridge complex (SI Figure S2d), wherein the As(OH)3 is adsorbed in a bridging position between the FeS layers and stabilized through hydrogen-bonded interactions with the surface water molecules. The As–S interatomic distances are calculated in the range of 2.960–4.147 Å, whereas the As–Fe are calculated in the range of 2.269–3.787 Å (Table 3 and SI Table S2). Similar interatomic distances were reported from spectroscopic and extended X-ray absorption fine structure (EXAFS) data fitting of As(III) sorbed on mackinawite (As–S = 3.1 Å and As–Fe = 3.4–3.5 Å) in aqueous solution.17
3.5. As(OH)3 Adsorption Complexes at Water-FeS(111) Interface
Again, we have explored several possible sites and modes of adsorption of As(OH)3 on the water–FeS(111) surface. Similar to the water–FeS(011) surface, some of the water molecules were displaced by As(OH)3 during the adsorption process, which allows for the formation of direct interactions with the surface cation sites. Displayed in Figure 4c is the lowest-energy adsorption complex identified (the remaining conformations are given in the SI Figure S3).The lowest-energy As(OH)3 adsorption configuration at the water–FeS(111) interface was calculated to be the Fe–O–Fe complex (Figure 4c), wherein the As(OH)3 molecule adsorbs at the bridge site between adjacent surface Fe atoms via one O atom. The adsorption energy of this structure (Fe–O–Fe complex) is calculated at −1.76 eV, whereas the energies of the other stable adsorption configurations are calculated at −1.57 eV for the Fe–AsO–Fe complex (SI Figure S3b), – 1.17 eV for the Fe–As complex (SI Figure S3c), and −0.86 eV for the Hwat–OH–Ssurf complex (SI Figure S3d). In the lowest-energy Fe–O–Fe complex, the bridging O–Fe distances were calculated at 2.159 and 2.138 Å, and the average values are reported in Table 3. The As–S and As–Fe interatomic distances are converged at 3.675 and 3.365 Å, respectively. Similar interatomic distances were calculated for the As atom interacting with the surface S and Fe ions in the other adsorption configurations (SI Table S3). At all three water–FeS interfaces, we have observed elongations in the As–O bonds in all adsorption complexes (1.765–1.946 Å), especially in the complexes in which the O atom interacts directly with the surface Fe ions. O–H bond elongations were also observed (0.976–1.046 Å), which can be attributed to the presence of hydrogen-bonded interactions between the hydrogen atom of As(OH)3 and the O atom of the surface water molecules as reported in Table 3 and SI Tables S1–S3.
3.6. Electronic Structures
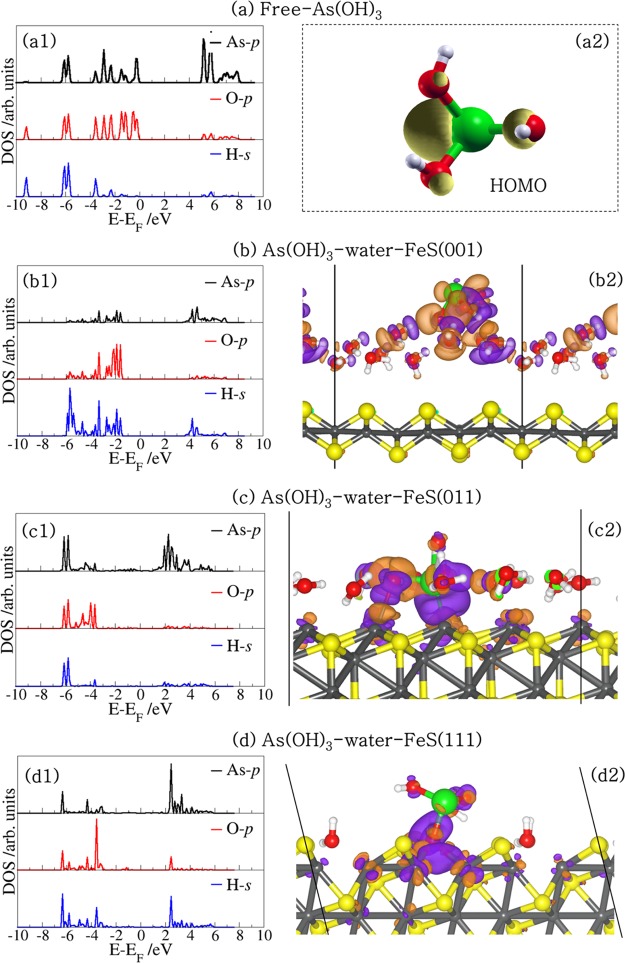
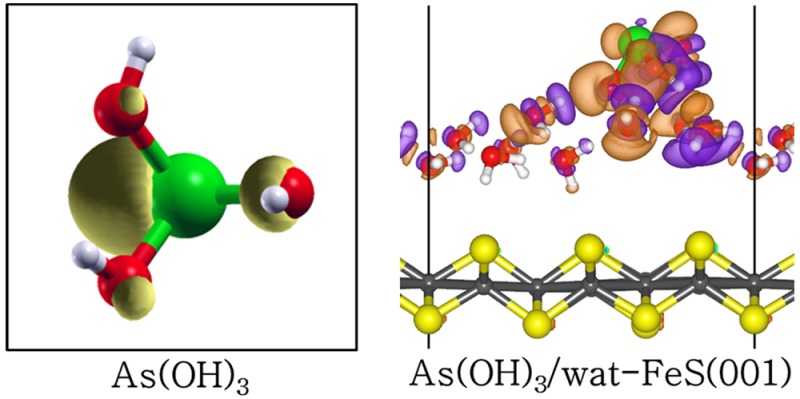
To gain insight into the nature of the interactions between the As(OH)3 molecule and the different hydrated FeS surfaces, we have carried out an atom-by-atom projected density of states (PDOS) analysis of the free molecule and compared it to those of the adsorbed states. The PDOS for the free As(OH)3 molecule is shown in Figure 5a1, whereas those for the lowest-energy adsorption configurations at the water–FeS (001), (011), and (111) interfaces are shown in Figures 5b1, c1, and d1, respectively. In the free As(OH)3 PDOS, we note that the states around the Fermi level are dominated by p-states of As and O, which are associated with the lone pair electron density of the As and O atoms as shown in the highest occupied molecular orbital (HOMO) in Figure 5a2. These orbitals are therefore expected to interact strongly with the orbitals of the surface species during sorption processes at the mineral surfaces. Indeed, we found that at the water–FeS (011) and (111) interfaces where the As(OH)3 interacts directly with the surface Fe ions, we observe disappearance or reduction of the As-p and O-p states of As(OH)3 around the Fermi level, due to their strong hybridization with the interacting surface Fe-d states (Figures 5c1 and d1). At the water–FeS(001) interface, however, we only observe a shift toward lower energy levels (Figure 5b1), which signifies stabilization of the As(OH)3 via physisorption. The PDOS for the interacting surface Fe-d-states before and after the adsorption of As(OH)3 at the water–FeS(111) and water–FeS(011) interface, and for the interacting surface S-p-states at the water–FeS(001) interface are shown in Figure 6. We found that the electronic properties of the surfaces were essentially preserved after the adsorption of As(OH)3, with only small shifts in the peak positions and heights, which indicates adsorption induced changes due to the interactions between the As(OH)3 species and the water–FeS interfaces. The electron density redistributions within the adsorbate–substrate systems were determined through analyses of the iso-surface plots of the differential charge density, which is obtained by subtracting from the charge density of the total adsorbate–substrate complex, the sum of the charge densities of the As(OH)3 molecule and the hydrated FeS surface. The atomic positions of the water–FeS surface and of the As(OH)3 molecule are kept the same as those of the total adsorbate–substrate system. In this way, the presentation highlights local electron density rearrangement and bond formation in the As(OH)3–water–FeS complexes. Shown in Figures 5b2, c2, and d2 are the isosurfaces of the electron density differences due to As(OH)3 adsorption at the water–FeS (001), (011), and (111) interfaces, respectively. An inspection of the iso-surfaces reveals electron density accumulation within the bonding regions between As(OH)3 and the water–FeS (011) and (111) interacting surface Fe ions, which is consistent with the formation of new bonds. In the case of the As(OH)3–water–FeS (001) complex, we see electron density accumulation between the hydrogen and O atoms indicative of hydrogen-bonded interactions. Despite the strong electron density redistribution within the As(OH)3–water–FeS complexes, only little charge transfer occurs from the interacting surface species to the adsorbed As(OH)3 molecule, as revealed from our Bader charge population analyses (Tables 3 and SI Tables S1–S3). The charge gained by the As(OH)3 in the different adsorption complexes is calculated to be in the range of 0.01–0.04 e– at the water–FeS(001) surface, 0.08–0.30 e– at the water–FeS(011) surface, and 0.01–0.28 e– at the water–FeS(111) surface (Tables 3 and SI Tables S1–S3).
Figure 5.
(Right) PDOS for As(OH)3 in the (a) free state and adsorbed in the lowest-energy geometry at the water–FeS interfaces (b–d). (Left) the corresponding isosurfaces of the differential charge density, where the purple and orange contours indicate electron density increase and decrease by 0.02 e/Å3, respectively.
Figure 6.
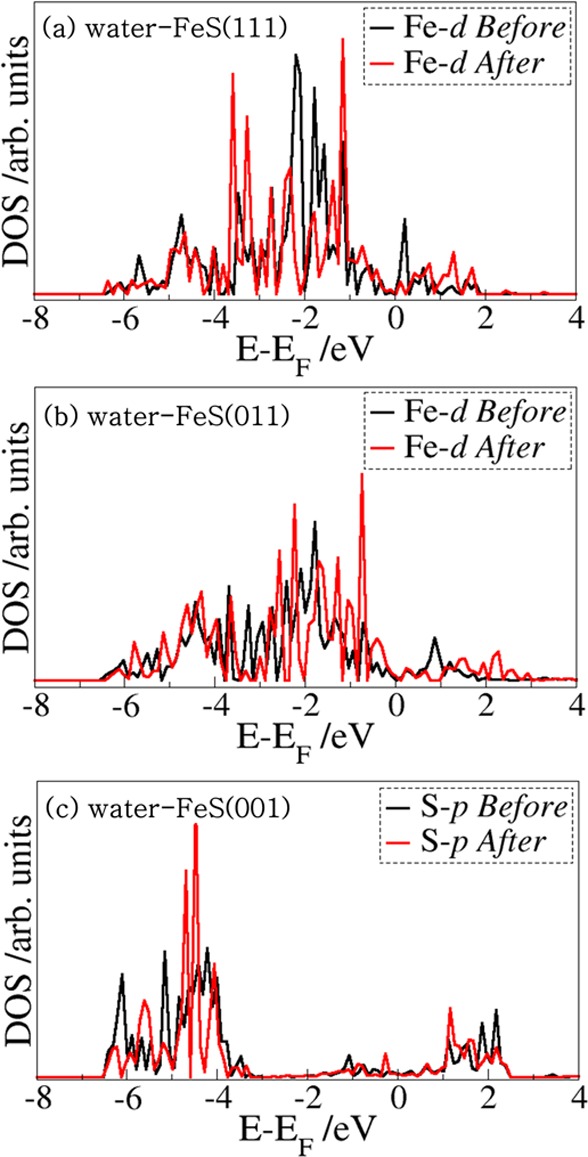
PDOS for the interacting surface Fe d-states before and after the adsorption of As(OH)3 at the (a) water–FeS(111) and (b) water–FeS(011) interface, and (c) for the interacting surface S-p-states at the water–FeS(001) interface.
3.7. Vibrational Properties
In order to propose an assignment for the As–O and O–H stretching vibrational modes of the adsorbed As(OH)3, which can serve as a guide for future experimental identification of the different adsorption complexes of As(OH)3 at the water–FeS interfaces, we have computed the wavenumbers of the normal modes of all the stable adsorption complexes at the different water–FeS interfaces (Table 4 and SI Table S4). Our calculated As–O and O–H stretching vibrational modes for the free As(OH)3 molecule compare closely with experimental data,71 as shown in Table 4, which ensures the reliability and accuracy of our approximate assignments. The three As–O stretching vibrational modes for the free As(OH)3 molecule were calculated at 700.8, 639.1, and 638.3, which compares with the experimental values of 710.0, 655.0, and 655.0 cm–1.71 The O–H stretching vibrational modes are calculated at 3743.5, 3715.3, and 3674.6 cm–1 which are similar to the O–H stretching modes of water.72 Compared to the free As(OH)3 molecule, we observe a reduction in the stretching vibrational modes of the As–O bonds upon As(OH)3 adsorption, indicative of weakening of these bonds, in agreement with the elongated As–O bonds calculated for the As(OH)3 adsorption complexes at the different water–FeS surfaces (Table 4). For example, the three stretching As–O bands of As(OH)3 adsorbed in the lowest-energy configuration at the water–FeS(011) and water–FeS(111) surfaces can be assigned at 580.2, 501.5, 488.9 cm–1 and 673.5, 616.5, 456.1 cm–1, respectively, which are lower than the gas phase stretching As–O band assigned at 700.8, 639.1, and 632.3 cm–1. We have also observed reductions in the stretching O–H bands of the adsorbed As(OH)3 compared to the free unbound state (Table 4), which can be attributed to the formations of hydrogen-bonded interactions with the oxygen ions of the surface water molecules.
Table 4. Molecular Vibrational Frequencies (in cm–1) of Adsorbed As(OH)3 at Water–FeS Interfaces.
| ν(As–O) |
ν(O–H) |
||||||
|---|---|---|---|---|---|---|---|
| surface | configuration | As–O1 | As–O2 | As–O3 | O1–H | O2–H | O2–H |
| free As(OH)3 | 700.8 (710)71 | 639.1 (655)71 | 638.3 (655)71 | 3738.1 | 3711.5 | 3674.7 | |
| FeS(001) | As–up–outer | 695.1 | 620.7 | 585.8 | 3465.9 | 3182.9 | 3140.5 |
| FeS(011) | Fe–AsO–Fe | 580.2 | 501.5 | 488.9 | 3715.1 | 3670.9 | 2829.1 |
| FeS(111) | Fe–O–Fe | 673.5 | 616.5 | 456.1 | 3731.2 | 3204.2 | 2884.3 |
The unique information provided by our atomic-level investigations provide fundamental insights into the structure–property relationships of FeS–water–As(OH)3 interfaces. Our simulations show that As(OH)3 adsorbs weakly onto the water–FeS(001) interface through a network of hydrogen-bond interactions with water molecules at the surface. Stronger interaction is, however, calculated for As(OH)3 adsorption on the water–FeS(011) and water–FeS (111) interfaces, which is characterized by hybridization between the S-p and O-p states of As(OH)3 and the surface Fe-d states. Our calculated As–Fe and As–S interatomic distances in the lowest-energy adsorption complexes at the various water-mackinawite interfaces (As–Fe = 2.269–3.369 Å and As–S = 3.382–3.675 Å) show good agreement with those obtained from K-edge EXAFS and XANES spectroscopic data (As–Fe = 3.4–3.5 Å and As–S = 3.1 Å).17 The long distances obtained from experiment clearly suggest As interactions via outer sphere complexes at the FeS surface. However, from our simulation results, the short As–Fe distances (2.217–2.530 Å) calculated for the Fe–AsO–Fe and Fe–As adsorption complexes at the water-FeS (011) and (111) interfaces indicate that, depending on the surface structure and composition, inner-sphere complexation with respect to the As atom is also possible at the water-mackinawite interface. Future investigations will expand the work presented here to include classical MD simulations which will provide a complete description of the dynamic processes occurring at the As(OH)3–water–FeS interfaces. The calculated interatomic distances and adsorption energies from this work will be useful in the derivation of force fields to be employed in the classical MD simulations to simulate more complex systems, including single and multiple As(OH)3 species adsorption from an explicit 3-dimensional aqueous environment.
Acknowledgments
We acknowledge The Netherlands Foundation for Fundamental Research on Matter (FOM) for funding (Grant No. 13CO26-2). This work made use of the facilities of ARCHER (http://www.archer.ac.uk), the UK’s national supercomputing service via our membership of the UK’s HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.est.7b00107.
Figures of all other As(OH)3 adsorption conformations, and tables of adsorption energies, structural parameters and vibrational frequencies of As(OH)3 adsorbed on water-FeS (001), (011), and (111) interfaces. It contains three figures and four tables (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Welch A. H.; Westjohn D. B.; Helsel D. R.; Wanty R. B. Arsenic in ground water of the United States: Occurrence and geochemistry. Groundwater 2000, 38, 589–604. 10.1111/j.1745-6584.2000.tb00251.x. [DOI] [Google Scholar]
- Nordstrom D. K. Worldwide occurrences of arsenic in ground water. Science 2000, 296, 2143–2144. 10.1126/science.1072375. [DOI] [PubMed] [Google Scholar]
- Hughes M. F. Arsenic toxicity and potential mechanism of action. Toxicol. Lett. 2002, 133, 1–16. 10.1016/S0378-4274(02)00084-X. [DOI] [PubMed] [Google Scholar]
- U. S. Environmental Protection Agency. Special Reports on Ingested Inorganic Arsenic Skin Cancer: Nutritional Essentiality, Report EPA/625 3-87-13, 1999.
- Ferguson J. F.; Gavis J. A review of the arsenic cycle in natural waters. Water Res. 1972, 6, 1259–1274. 10.1016/0043-1354(72)90052-8. [DOI] [Google Scholar]
- Amin N.; Kaneco S.; Kitagawa T.; Begum A.; Katsumata H.; Suzuki T.; Ohta K. Removal of arsenic from aqueous solutions by adsorption onto water rice husk. Ind. Eng. Chem. Res. 2006, 45, 8105–8110. 10.1021/ie060344j. [DOI] [Google Scholar]
- Gulens J.; Champs D. R.; Jackson R. E.. Influence of redox environments on the mobility of arsenic in groundwater. In Chemical Modelling of Aqueous systems. ACS Symposium Series, Jenne E.A., Ed.; 1979; Vol. 93, pp 81–95. [Google Scholar]
- Ballantine J. M.; Moore J. N. Arsenic geochemistry in geothermal systems. Geochim. Cosmochim. Acta 1988, 52, 475–483. 10.1016/0016-7037(88)90102-0. [DOI] [Google Scholar]
- Liu Z.; Shen J.; Carbrey J. M.; Mukhopadhyay R.; Agre P.; Rosen B. P. Arsenite transport by mammalian aquaglyceroporins AQP7 and AQP9. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 6053–6058. 10.1073/pnas.092131899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders O. I.; Rensing C.; Kuroda M.; Mitra B.; Rosen B. P. Antimonite Is Accumulated by the Glycerol Facilitator GlpF in Escherichia coli. J. Bacteriol. 1997, 179, 3365–3367. 10.1128/jb.179.10.3365-3367.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smedley P. L.; Kinniburgh D. G. A review of the source, behaviour and distribution of arsenic in natural waters. Appl. Geochem. 2002, 17, 517–568. 10.1016/S0883-2927(02)00018-5. [DOI] [Google Scholar]
- Williams P. M.; Price A. H.; Raab A.; Hossain S. A.; Feldmann J.; Meharg A. A. Variation in arsenic speciation and concentration in paddy rice related to dietary exposure. Environ. Sci. Technol. 2005, 39, 5531–5540. 10.1021/es0502324. [DOI] [PubMed] [Google Scholar]
- Gallegos-Garcia M.; Ramírez-Muñiz K.; Song S. Arsenic Removal from Water by Adsorption Using Iron Oxide Minerals as Adsorbents: A Review. Miner. Process. Extr. Metall. Rev. 2012, 33, 301–315. 10.1080/08827508.2011.584219. [DOI] [Google Scholar]
- Han Y.; Jeong H. Y.; Demond A. H.; Hayes K. F. X-ray absorption and photoelectron spectroscopic study of the association of As(III) with nanoparticulate FeS and FeS-coated sand. Water Res. 2011, 45, 5727–5735. 10.1016/j.watres.2011.08.026. [DOI] [PubMed] [Google Scholar]
- Han Y.; Gallegos T. J.; Demond A. H.; Hayes K. F. FeS-coated sand for removal of arsenic (III) under anaerobic conditions in permeable reactive barriers. Water Res. 2011, 45, 593–604. 10.1016/j.watres.2010.09.033. [DOI] [PubMed] [Google Scholar]
- Wolthers M.; Charlet L.; van Der Weijden C. H.; van der Linde P. R.; Rickard D. Arsenic mobility in the ambient sulfidic environment: sorption of arsenic (V) and arsenic (III) onto disordered mackinawite. Geochim. Cosmochim. Acta 2005, 69, 3483–3492. 10.1016/j.gca.2005.03.003. [DOI] [Google Scholar]
- Farquhar M. L.; Charnock J. M.; Livens F. R.; Vaughan D. J. Mechanisms of arsenic uptake from aqueous solution by interaction with goethite, lepidocrocite, mackinawite, and pyrite: an X-ray absorption spectroscopy study. Environ. Sci. Technol. 2002, 36, 1757–1762. 10.1021/es010216g. [DOI] [PubMed] [Google Scholar]
- Jeong H. Y.; Han Y. S.; Hayes K. F. X-ray absorption and X-ray photoelectron spectroscopic study of arsenic mobilization during mackinawite (FeS) oxidation. Environ. Sci. Technol. 2010, 44, 955–961. 10.1021/es902577y. [DOI] [PubMed] [Google Scholar]
- Han D. S.; Batchelor B.; Abdel-Wahab A. Sorption of selenium (IV) and selenium(VI) to mackinawite (FeS): effect of contact time, extent of removal, sorption envelopes. J. Hazard. Mater. 2011, 186, 451–457. 10.1016/j.jhazmat.2010.11.017. [DOI] [PubMed] [Google Scholar]
- Breynaert E.; Bruggeman C.; Maes A. XANES-EXAFS analysis of Se solid phase reaction products formed upon contacting Se(IV) with FeS2 and FeS. Environ. Sci. Technol. 2008, 42, 3595–3601. 10.1021/es071370r. [DOI] [PubMed] [Google Scholar]
- Jeong H. Y.; Klaue B.; Blum J. D.; Hayes K. F. Sorption of mercuric ion by synthetic nanocrystalline mackinawite (FeS). Environ. Sci. Technol. 2007, 41, 7699–7705. 10.1021/es070289l. [DOI] [PubMed] [Google Scholar]
- Skyllberg U.; Drott A. Competition between disordered iron sulfide and natural organic matter associated thiols for mercury (II)-An EXAFS Study. Environ. Sci. Technol. 2010, 44, 1254–1259. 10.1021/es902091w. [DOI] [PubMed] [Google Scholar]
- Liu J.; Valsaraj K. T.; Devai I.; DeLaune R. D. Immobilization of aqueous Hg(II)by mackinawite (FeS). J. Hazard. Mater. 2008, 157, 432–440. 10.1016/j.jhazmat.2008.01.006. [DOI] [PubMed] [Google Scholar]
- Mullet M.; Boursiquot S.; Ehrhardt J. J. Removal of hexavalent chromium from solutions by mackinawite, tetragonal FeS. Colloids Surf., A 2004, 244, 77–85. 10.1016/j.colsurfa.2004.06.013. [DOI] [Google Scholar]
- Patterson R. R.; Fendorf S.; Fendorf M. Reduction of hexavalent chromium by amorphous iron sulfide. Environ. Sci. Technol. 1997, 31, 2039–2044. 10.1021/es960836v. [DOI] [Google Scholar]
- Boursiquot S.; Mullet M.; Ehrhardt J. J. XPS study of the reaction of chromium (VI) with mackinawite (FeS). Surf. Interface Anal. 2002, 34, 293–297. 10.1002/sia.1303. [DOI] [Google Scholar]
- Lennie A. R.; Redfern S. A. T.; Schofield P. F.; Vaughan D. J. Synthesis and Rietveld crystal structure refinement of mackinawite, tetragonal FeS. Mineral. Mag. 1995, 59, 677–683. 10.1180/minmag.1995.059.397.10. [DOI] [Google Scholar]
- Berner R. A. Tetragonal Ion sulfide. Science 1962, 137, 669. 10.1126/science.137.3531.669-a.13872168 [DOI] [Google Scholar]
- Rickard D.; Luther G. W. Chemistry of Iron Sulfides. Chem. Rev. 2007, 107, 514–562. 10.1021/cr0503658. [DOI] [PubMed] [Google Scholar]
- Lennie A. R.; Redfern S. A. T.; Champness P. E.; Stoddart C. P.; Schofield P. F.; Vaughan D. J. Transformation of mackinawite to greigite: An in situ X-ray powder diffraction and transmission electron microscope study. Am. Mineral. 1997, 82, 302–309. 10.2138/am-1997-3-408. [DOI] [Google Scholar]
- Jeong H. Y.; Lee J. H.; Hayes K. F. Characterization of synthetic nanocrystalline mackinawite: crystal structure, particle size, and specific surface area. Geochim. Cosmochim. Acta 2008, 72, 493–505. 10.1016/j.gca.2007.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolthers M.; van der Gaast S. J.; Rickard D. The structure of disordered mackinawite. Am. Mineral. 2003, 88, 2007–2015. 10.2138/am-2003-11-1245. [DOI] [Google Scholar]
- Liu Y.; Xiao W.; Wang J.; Mirza Z. A.; Wang T. Optimized Synthesis of FeS Nanoparticles with a High Cr(VI) Removal Capability. J. Nanomater. 2016, 2016, 1–9. 10.1155/2016/7817296. [DOI] [Google Scholar]
- Kim E. J.; Kim J. H.; Azad A. M.; Chang Y. S. Facile synthesis and characterization of Fe/FeS nanoparticles for environmental applications. ACS Appl. Mater. Interfaces 2011, 3, 1457–1462. 10.1021/am200016v. [DOI] [PubMed] [Google Scholar]
- Feng H.; SiEmail P.-Z.; Xiao X.-F.; Jin C.-H.; Yu S.-J.; Li Z.-F.; Ge H.-L. Large scale synthesis of FeS coated Fe nanoparticles as reusable magnetic photocatalysts. Front. Mater. Sci. 2013, 7, 308–311. 10.1007/s11706-013-0213-9. [DOI] [Google Scholar]
- Morse J. W.; Arakaki T. Adsorption and coprecipitation of divalent metals with mackinawite (FeS). Geochim. Cosmochim. Acta 1993, 57, 3635–3640. 10.1016/0016-7037(93)90145-M. [DOI] [Google Scholar]
- Arakaki T.; Morse J. W. Coprecipitation and adsorption of Mn(II) with mackinawite (FeS) under conditions similar to those found in anoxic sediments. Geochim. Cosmochim. Acta 1993, 57, 9–14. 10.1016/0016-7037(93)90463-7. [DOI] [Google Scholar]
- Kornicker W. A.Interactions of Divalent Cations with Pyrite and Mackinawite in Seawater and Sodium–Chloride Solutions. Ph.D. Thesis, Texas A&M University, 1988. [Google Scholar]
- Wharton M. J.; Atkins B.; Charnock J. M.; Livens F. R.; Pattrick R. A. D.; Collison D. An X-ray absorption spectroscopy study of the coprecipitation of Tc and Re with mackinawite (FeS). Appl. Geochem. 2000, 15, 347–354. 10.1016/S0883-2927(99)00045-1. [DOI] [Google Scholar]
- Gallegos T. J.; Han Y. S.; Hayes K. F. Model predictions of realgar precipitation by reaction of As(III) with synthetic mackinawite under anoxic conditions. Environ. Sci. Technol. 2008, 42, 9338–9343. 10.1021/es801669g. [DOI] [PubMed] [Google Scholar]
- Blanchard M.; Wright K.; Gale J. D.; Catlow C. R. A. Adsorption of As(OH)3 on the (001) Surface of FeS2 Pyrite: A Quantum-mechanical DFT Study. J. Phys. Chem. C 2007, 111, 11390–11396. 10.1021/jp072468v. [DOI] [Google Scholar]
- Goffinet C. J.; Mason S. E. Comparative DFT study of inner-sphere As(III) complexes on hydrated α-Fe2O3(0001) surface models. J. Environ. Monit. 2012, 14, 1860–1871. 10.1039/c2em30355h. [DOI] [PubMed] [Google Scholar]
- Blanchard M.; Morin M.; Lazzeri M.; Balan E.; Dabo I. First-principles simulation of arsenate adsorption on the (1–12) surface of hematite. Geochim. Cosmochim. Acta 2012, 86, 182–195. 10.1016/j.gca.2012.03.013. [DOI] [Google Scholar]
- Dzade N. Y.; Roldan A.; de Leeuw N. H. Surface and shape modification of mackinawite (FeS) nanocrystals by cysteine adsorption: a first-principles DFT-D2 study. Phys. Chem. Chem. Phys. 2016, 18, 32007–32020. 10.1039/C6CP05913A. [DOI] [PubMed] [Google Scholar]
- Groß A.Theoretical Surface Science; Springer: Berlin, Germany, 2003. [Google Scholar]
- Nilsson A.; Pettersson L. G. M. Chemical bonding on surfaces probed by X-ray emission spectroscopy and density functional theory. Surf. Sci. Rep. 2004, 55, 49–167. 10.1016/j.surfrep.2004.06.002. [DOI] [Google Scholar]
- Bligaard T.; Nørskov J. K.. Chemical Bonding at Surfaces and Interfaces, 1st ed.; Nilsson A., Petterson L. G. M., Nørskov J. K., Eds. Elsevier: Amsterdam, 2008. [Google Scholar]
- Kresse G.; Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 558. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
- Grimme S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
- Dzade N. Y.; Roldan A.; de Leeuw N. H. The surface chemistry of NOx on mackinawite (FeS) surfaces: A DFT-D2 study. Phys. Chem. Chem. Phys. 2014, 16, 15444–15456. 10.1039/c4cp01138d. [DOI] [PubMed] [Google Scholar]
- Dzade N. Y.; Roldan A.; de Leeuw N. H. Adsorption of methylamine on mackinawite (FeS) surfaces: A density functional theory study. J. Chem. Phys. 2013, 139, 124708. 10.1063/1.4822040. [DOI] [PubMed] [Google Scholar]
- Dzade N. Y.; Roldan A.; de Leeuw N. H. DFT-D2 study of the adsorption and dissociation of water on clean and oxygen-covered {001} and {011} surfaces of mackinawite (FeS). J. Phys. Chem. C 2016, 120, 21441–21450. 10.1021/acs.jpcc.6b06122. [DOI] [Google Scholar]
- Devey A. J.; Grau-Crespo R.; de Leeuw N. H. Combined density functional theory and interatomic potential study of the bulk and surface structures and properties of the iron sulfide mackinawite (FeS). J. Phys. Chem. C 2008, 112, 10960–10967. 10.1021/jp8001959. [DOI] [Google Scholar]
- Perdew J. P.; Chvary J. A.; Vosko S. H.; Jackson K. A.; Pederson M. R.; Singh D. J.; Fiolhais C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 46, 6671–6687. 10.1103/PhysRevB.46.6671. [DOI] [PubMed] [Google Scholar]
- Blöchl P. E. Projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
- Monkhorst H. J.; Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
- Ohfuji H.; Rickard D. High resolution transmission electron microscopic study of synthetic nanocrystalline mackinawite. Earth Planet. Sci. Lett. 2006, 241, 227–233. 10.1016/j.epsl.2005.10.006. [DOI] [Google Scholar]
- Watson G. W.; Kelsey E. T.; de Leeuw N. H.; Harris D. J.; Parker S. C. Atomistic simulation of dislocations, surfaces and interfaces in MgO. J. Chem. Soc., Faraday Trans. 1996, 92, 433–438. 10.1039/ft9969200433. [DOI] [Google Scholar]
- Tasker P. W. The stability of ionic crystal surfaces. J. Phys. C: Solid State Phys. 1979, 12, 4977–4984. 10.1088/0022-3719/12/22/036. [DOI] [Google Scholar]
- Dzade N. Y.; Roldan A. DFT-D2 simulations of water adsorption and dissociation on the low-index surfaces of mackinawite (FeS). J. Chem. Phys. 2016, 144, 174704. 10.1063/1.4947588. [DOI] [PubMed] [Google Scholar]
- Henkelman G.; Arnaldsson A.; Jónsson H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. 10.1016/j.commatsci.2005.04.010. [DOI] [Google Scholar]
- Baroni S.; de Gironcoli S.; Dal Corso A.; Giannozzi P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. 10.1103/RevModPhys.73.515. [DOI] [Google Scholar]
- Terranova U.; de Leeuw N. H. Structure and dynamics of water at the mackinawite (001) surface. J. Chem. Phys. 2016, 144, 094706. 10.1063/1.4942755. [DOI] [PubMed] [Google Scholar]
- Yang M.; Stipp S. L. S.; Harding J. Biological Control on Calcite Crystallization by Polysaccharides. Cryst. Growth Des. 2008, 8, 4066–4074. 10.1021/cg800508t. [DOI] [Google Scholar]
- Ramírez-Solís A.; Hernandez-Cobos J.; Vargas C. A New Nonsymmetric As(OH)3 Species. Comparison with the Known C3 Species and Themochemistry at the HF, DFT(B3LYP), MP2, MP4, and CCSD(T) Levels of Theory. J. Phys. Chem. A 2006, 110, 7637–7641. 10.1021/jp0601365. [DOI] [PubMed] [Google Scholar]
- Tossell J. A. Theoretical studies on arsenic oxide and hydroxide species in minerals and in aqueous solution. Geochim. Cosmochim. Acta 1997, 61, 1613–1623. 10.1016/S0016-7037(97)00030-6. [DOI] [Google Scholar]
- Ramírez-Solís A.; Mukopadhyay R.; Rosen B. P.; Stemmler T. L. Experimental and theoretical characterization of arsenite in water: insights into the coordination environment of As-O. Inorg. Chem. 2004, 43, 2954–2959. 10.1021/ic0351592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Testemale D.; Hazemann J. L.; Pokrovski G. S.; Joly Y.; Roux J.; Argoud R.; Geaymond O. Structural and electronic evolution of the As(OH) 3 molecule in high temperature aqueous solutions: An x-ray absorption investigation. J. Chem. Phys. 2004, 121, 8973. 10.1063/1.1785150. [DOI] [PubMed] [Google Scholar]
- Loehr T. M.; Plane R. A. Raman spectra and structures of arsenious acid and arsenites in aqueous solution. Inorg. Chem. 1968, 7, 1708–1714. 10.1021/ic50067a004. [DOI] [Google Scholar]
- Shimanouchi T. Tables of Molecular Vibrational Frequencies, Consolidated Volume II, NSRDS NBS-39. J. Phys. Chem. 1977, 6, 3. 10.6028/NBS.NSRDS.39. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.