Segmentation Based Sparse Reconstruction of Optical Coherence Tomography Images

Abstract

We demonstrate the usefulness of utilizing a segmentation step for improving the performance of sparsity based image reconstruction algorithms. In specific, we will focus on retinal optical coherence tomography (OCT) reconstruction and propose a novel segmentation based reconstruction framework with sparse representation, termed segmentation based sparse reconstruction (SSR). The SSR method uses automatically segmented retinal layer information to construct layer-specific structural dictionaries. In addition, the SSR method efficiently exploits patch similarities within each segmented layer to enhance the reconstruction performance. Our experimental results on clinical-grade retinal OCT images demonstrate the effectiveness and efficiency of the proposed SSR method for both denoising and interpolation of OCT images.

I. Introduction

Optical coherence tomography (OCT) is a non-invasive imaging modality which is employed in diverse medical applications [1, 2], especially for diagnostic ophthalmology. Automated remote analysis of ophthalmologic OCT images is becoming more prevalent for the diagnosis and study of ocular diseases [3]. However, sample-based speckle and detector noise corrupts OCT images. On another front, to accelerate the acquisition process, relatively low spatial sampling rate is often used in capturing clinical OCT images [3–6]. Both the heavy noise and low spatial sampling rate negatively affect automated and even manual OCT image analysis performance, necessitating utilization of effective denoising and interpolation techniques, respectively.

Denoising and interpolation are two well-known reconstruction problems in the image processing [7]. In the past decade, various models have been proposed to reconstruct high quality OCT images for various applications [8–17]. Classical reconstruction approaches often construct a smoothness priori based model (e.g., anisotropic filtering, Tikhonov filtering, and total variation [9]), and reconstruct the image in spatial domain. Some recent approaches transform the input degraded image into another domain (e.g., using the wavelet transformation [18], dual tree complex wavelet transformation [19], and curvelets transformation [20]). While the transform based methods (e.g. wavelet) usually achieve a better reconstruction performance than the spatial domain methods, they are built on a fixed mathematical model and may have limited adaptability [21] for representing structures inocular OCT volumes.

Inspired by the sparse coding mechanism of human vision system [22], the sparse representation is demonstrated to be a powerful tool for many image processing applications [4, 23–30]. The sparse representation decomposes an input image into a linear combination of an over-complete dictionary of basis functions. Basis functions can be chosen from a set of training images similar to the input image [31] and thus can be more adaptive for the representation of specific features. Several recent works have also applied the sparse representation to OCT image reconstruction problems [4, 6,12, 14–16, 24, 32–34]. While different retinal layers have varied pathologic structures [35–37] and even speckle patterns, most of the sparse reconstruction methods only train one general dictionary to represent complex structures and textures in the ocular OCT images.

The above traditional sparse model directly decomposes each local image patch. Both heavy noise in the test patch and high correlations in the dictionary atoms [23] may mislead the sparse decomposition process, thus negatively affecting the final reconstruction. More recently, a nonlocal sparse reconstruction model [38–40] has been introduced, which exploits the nonlocal patch self-similarities to improve the reconstruction. Specifically, for each processed patch, the nonlocal based sparse model searches similar patches from the whole image (or a large searching window) and then jointly decomposes the similar patches on the dictionary [40] to find a more accurate sparse solution. Nonetheless, the nonlocal based sparse representation requires searching the whole image to find the similar patches, which creates very high computational burdens and also will be interfered by the heavy noise in the OCT image. Therefore, how to construct effective spare dictionaries for representing complex structures and efficiently exploiting patch self-similarities for accurate sparse decomposition are the two key issues in the sparse reconstruction model.

In this paper, we utilize the segmentation algorithm for OCT image reconstruction. We particularly focus on the retina, a layered structure where each layer has its own specific features. Noting that since structural elements of each layer, resulting in speckle, have different size, shape, and distribution, the signal and noise model of each layer is expected to be different [3, 35, 36, 41]. Moreover, pathologic structures with distinct features appear in specific layers. For example, drusenoid structures appears immediately below or above the retinal pigment epithelium (RPE) layer [42], while hyper-reflective foci associated with age-related macular degeneration are not expected to appear in the nerve fiber layer (NFL) [43]. Utilizing the structural information in the layers, we propose a segmentation based sparse reconstruction (SSR) model to develop a fast and accurate reconstruction algorithm. Our general approach first utilizes a graph based algorithm [35] to automatically segment the retinal OCT images into multiple layers. Then, for each layer, SSR constructs a dedicated structural dictionary to better represent the anatomic and pathologic structures within this layer. Finally, instead of searching the whole image, SSR efficiently searches for the similar patches within each layer and exploits the patches’ similarities within each layer to improve the sparse decomposition.

Note that, the strategy of segmentation-based denoising has been previously applied to several other image denoising problems [44–46]. In contrast, this paper proposes a segmentation based sparse representation (SSR) model for retinal OCT image reconstruction, which utilizes the segmented layer information to enhance the effectiveness and efficiency of the sparse reconstruction model. Specifically, the main contributions of our paper are detailed as follows.

1. The SSR method introduces a layer segmentation based structural dictionary construction strategy, which effectively preserves the anatomic and pathologic structures in the OCT image.

2. The SSR method proposes a layer segmentation based sparse reconstruction strategy, which utilizes the segmented layer information to significantly accelerate the similar patch searching process and exploits the correlations among similar patches to enhance the reconstruction performance.

The remainder of this paper is organized as follows. Section II briefly reviews the sparse reconstruction model and nonlocal means reconstruction model. We introduce the proposed SSR method for the denoising and interpolation of OCT images in Section III. Experimental results on clinical OCT data are presented in Section IV. Section V concludes this paper and suggests for future works.

II. Background: Sparse Reconstruction Model and Nonlocal Means Based Reconstruction Model

A. Sparse Reconstruction Model

Given a degraded image, most sparse reconstruction models first divide the input image into ϒ overlapping patches X_i ∈ ℝ^n×m, i = 1, 2,…, ϒ. The vector form for each patch X_i is denoted as x_i ∈ ℝ^q×1 (q = n × m), obtained by lexicographic ordering. For a denoising problem, the sparse reconstruction model assumes that the clean retinal OCT signal can be well represented by a weighted linear combination of a few atoms selected from the dictionary D ∈ ℝ^q×z, q < z), whereas the noise cannot be decomposed on the dictionary. Therefore, the sparse reconstruction model for the denoising problem can be formulated as follows [47]:

$${\widehat{\mathbf{\alpha }}}_i=arg\underset{{\mathbf{\alpha }}_i}{min}\left\{{\Vert {\mathbf{x}}_i-\mathbf{D}{\mathbf{\alpha }}_i\Vert }_2^2+\lambda {\Vert {\mathbf{\alpha }}_i\Vert }_0\right\},$$ (1)

where α_i ∈ ℝ^z×1 represents the sparse coefficients vector for the x_i and ||α_i||₀ is the ℓ₀ -norm, counting the number of non-zero coefficients in α_i. To solve (1), there are two main considerations: 1) dictionary D construction, and 2) sparse coefficients vector α_i estimation. To address the first problem, popular algorithms [31, 48] train one dictionary D from a number of relevant sampled patches H = {x_1, …, x_Z}, where Z is the number of training patches. Concretely, the dictionary D can be trained by the following optimization problem:

$$\widehat{\mathbf{D}}=arg\underset{\widehat{\mathbf{D}}}{min}\left\{{\Vert \mathbf{H}-\mathbf{DA}\Vert }_2^2+\lambda {\Vert \mathbf{A}\Vert }_0\right\},$$ (2)

where A = {α_i, …, α_Z} is the sparse coefficient matrix for the H. This equation can be solved by the K-SVD algorithm [31]. To address the second problem, which is known to be a nondeterministic polynomial-time hard (NP-hard) [49], the orthogonal matching pursuit (OMP) [50] algorithms can be utilized to obtain an approximate solution for the sparse coefficient vector α̂_i. Then, we can use Dα̂_i to reconstruct the related patch and all the reconstructed patches are returned to their original positions to create the final denoised image.

For the image interpolation problem, we first denote an original high resolution image as Y_H ∈ ℝ^N×M, the decimation operator as S, and the corresponding low resolution image as Y_L = SY_H ∈ ℝ^(N/S)×(M/S). Given the observation degraded image Y_L, the objective of the image interpolation is to obtain the Ŷ_H such that Ŷ_H ≈ Y_H. To solve the interpolation problem, recent sparse reconstruction models [51] attempt to infer the relationship of the sparse coefficients and dictionaries between the high resolution space χ_H and low resolution space χ_L. In [51], Yang et. al. jointly trained both the low resolution dictionary D_L and the high resolution dictionary D_H, which ensures that the sparse coefficient ${\mathbf{\alpha }}_i^L$ in the space χ_L is the same as the sparse coefficient ${\mathbf{\alpha }}_i^H$ in the space χ_H. Inspired by the work of Yang et. al., we utilized a semi-coupled learning algorithm to construct the matched dictionaries D_L and D_H, and then trained a mapping function M to link the sparse coefficients ${\mathbf{\alpha }}_i^L$ and ${\mathbf{\alpha }}_i^H$ [4]. After obtaining the relationship between the spaces χ_L and χ_H, the sparse reconstruction model can first find the sparse coefficient ${\mathbf{\alpha }}_i^L$ of each observation patch ${\mathbf{x}}_i^L$, and then restore the latent image patches ${\mathbf{x}}_i^H$ as well as the corresponding high resolution image Ŷ_H by utilizing the high resolution dictionary D_H and mapping function M.

B. Nonlocal Means Reconstruction Model

For the image denoising and interpolation problems, another very effective reconstruction model is the nonlocal means, which exploits the self-similarities inherent to images [52]. Specifically, for each patch x_i extracted from the degraded image, the nonlocal means method first searches the W patches with the highest similarity to x_i from the whole image (or a large searching window). The similarity can be measured by the squared ℓ₂ -norm of the intensity differences between two patches:

$$d\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }_2^2,j\subset \mathrm{\Lambda }$$ (3)

where Λ is a set containing the indexes of all patches in the whole image. Then, the patches that are found to be similar are processed by a weighted average filtering or patch similarity penalty to achieve denoising [52] or interpolation [53], respectively.

In the sparse reconstruction model, the sparse coefficient estimations are affected by the noise in observation image, thus leading to suboptimal reconstruction. To suppress noise interference, recent works including [23, 24, 40] incorporate the nonlocal means into the sparse reconstruction model. Specifically, the nonlocal sparse model first conducts the similar patch search [using (3)] in the whole image and then jointly exploits correlations among similar patches by decomposing them on the same atoms of the dictionary to improve the sparse coefficient solution. The performance improvement is due to, in the sparse solution process, jointly considering the decisions of multiple similar patches is usually more robust to external disturbances [54], similar to the principles of majority voting. However, the nonlocal sparse model requires searching for similar patches across the whole image, which is computational costly. In addition, the heavy noise in the OCT image might still interfere with the similar patch searching process.

III. Proposed SSR Method For OCT Reconstruction

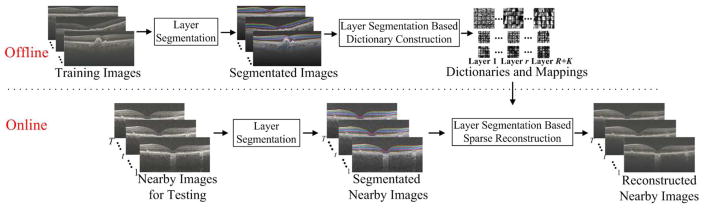
We propose the SSR method, which utilizes the layer specific structural information to enhance the effectiveness and cost efficiency of our previous sparse reconstruction techniques. The SSR method is composed of three main parts: a) layer segmentation; b) layer segmentation based dictionary construction; and c) layer segmentation based sparse reconstruction. The outline of the proposed SSR method is illustrated in Fig. 1.

Fig. 1.

Outline of the proposed SSR algorithm.

A. Layer Segmentation

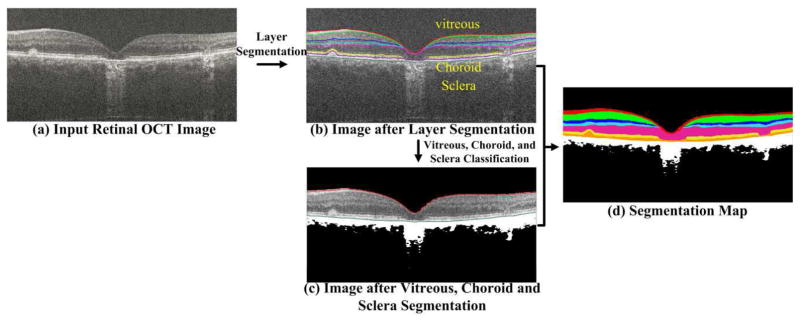
For all the testing and training retinal images, we utilize the popular graph theory and dynamic programming (GTDP) method [35] to automatically segment these images into R layers, as illustrated in Fig. 2(b). The region between two color lines in Fig. 2(b) represents one layer. Note that the intensity of the vitreous and choroid/sclera regions (above and below the segmented layers, respectively) are not uniformly distributed (due to pathology or limited penetration of the 800 nm OCT beam in the choroid layer). Therefore, we further utilize a k-means algorithm to classify the vitreous and choroid/sclera regions into K parts (e.g., see the white and black regions in Fig. 2(c)). To exploit the spatial information for the classification, we extract a patch (of size n×m) for each pixel in the vitreous and choroid/sclera regions, and use its vectorization form for the k-means clustering. We then fuse the results from both the layer segmentation and classification to create a segmentation map, which includes R+K layers (see the Fig. 2(d), each color represents one layer). The whole segmentation process is illustrated in Fig. 2.

Fig. 2.

Outline for the OCT segmentation. In (b), the retinal OCT image is segmented into seven layers using eight color lines, and the region between two color lines represents one layer. Three distinct regions, above and below the retina include vitreous, visible choroid, and sclera. In (c), the vitreous and choroid/sclera regions are further classified into two clusters (one is the black area and one is the white area). In (d), different color regions represent varied segmented layers or classified regions. The dimly visible regions of choroid can be regarded as the background area (delineated in black) with less structural information. The visible regions of choroid can be considered as the foreground area with comparatively rich structural information, delineated in white. Therefore, we set the clustering number K of the X-means algorithm to 2, which further clusters the vitreous, choroid, and sclera regions into two groups, i.e. the black and white areas in (c) and (d).

B. Layer Segmentation Based Dictionary Construction

In the retinal OCT image, different layers contain various types of anatomic and pathologic structures (e.g., vessels, drusen, edema, and fovea), and different thicknesses and speckle structures [3, 35, 36, 41]. Therefore, to well represent complex structures in varied layers, we utilize the segmented layer information to train multiple structural dictionaries (each corresponding to one layer), rather than one general dictionary [40,47].

Specifically, for denoising, we first employ segmentation maps of training images to extract patches for each specific layer and construct the related R+K training sets ${\left\{{\mathbf{H}}_r\right\}}_{r=1}^{R+K}$. As in [24], the training images can be considered noiseless, which are obtained by registration and averaging of a number of repeated B-scans acquired from spatially very close positions. Then, we train one structural dictionary D_r (of size q×s) on one training set H_r [see Fig. 3(a)], by modifying (2) as the following optimization problem,

Fig. 3.

Layer segmentation based dictionary construction for (a) denoising problem; (b) interpolation problem.

$${\left\{{\mathbf{D}}_r\right\}}_{r=1}^{R+K}=arg\underset{{\widehat{\mathbf{D}}}_r}{min}{\Vert {\mathbf{H}}_r-{\mathbf{D}}_r{\mathbf{A}}_r\Vert }_2^2+\lambda {\Vert {\mathbf{A}}_r\Vert }_0,r=1,\dots ,R+K,$$ (4)

where A_r is the sparse coefficient matrix for the training set H_r. The optimization problem in (4) is solved by separately performing the K-SVD algorithm [31] on each set H_r. Note that, to construct the structural dictionary for the layer in the black regions (e.g., vitreous and sclera), we randomly select a small number of training patches from that layer as the dictionary atoms. This is because these regions have less structural information and are easy to be represented.

For the image interpolation problem, following [4], we use a set of high SNR and high resolution images, each acquired by averaging a set of repeated densely sampled B-scans, as our high-resolution framing image set ${\left\{{\mathbf{Y}}_{H,v}^{\mathit{Train}}\right\}}_{v=1}^V$. We subsample one frame from each set of the repeated B-Scans, to attain the corresponding low-resolution training image set ${\left\{{\mathbf{Y}}_{L,v}^{\mathit{Train}}\right\}}_{v=1}^V$. Utilizing the segmentation maps of the ${\left\{{\mathbf{Y}}_{L,v}^{\mathit{Train}}\right\}}_{v=1}^V$ and ${\left\{{\mathbf{Y}}_{H,v}^{\mathit{Train}}\right\}}_{v=1}^V$, we can extract spatially matched low resolution and high resolution patches for each layer as the matching training sets ${\left\{{\mathbf{H}}_r^L\right\}}_{r=1}^{R+K}$ and ${\left\{{\mathbf{H}}_r^H\right\}}_{r=1}^{R+K}$. Then, we separately adopt the semi-coupled dictionary learning algorithm [4] on each training set pair ${\mathbf{H}}_r^L$ and ${\mathbf{H}}_r^H$, and obtain R + K matched dictionary pairs ${\left\{{\mathbf{D}}_r^L\right\}}_{r=1}^{R+K}$ and ${\left\{{\mathbf{D}}_r^H\right\}}_{r=1}^{R+K}$ [see Fig. 3(b)]. In addition, as described in Section II. A, we further train R + K mapping functions ${\left\{{\mathbf{M}}_r\right\}}_{r=1}^{R+K}$ [see Fig. 3(b)] to relate the sparse coefficients ${\left\{{\mathbf{\alpha }}_r^L\right\}}_{r=1}^{R+K}$ and ${\left\{{\mathbf{\alpha }}_r^H\right\}}_{r=1}^{R+K}$ for each layer,

$${\mathbf{\alpha }}_r^H={\mathbf{M}}_r\times {\mathbf{\alpha }}_r^L,r=1,\dots ,R+K.$$ (5)

Following [4], we train these mapping functions using the low resolution sparse matrices ${\left\{{\mathbf{A}}_r^{L,\mathit{Train}}\right\}}_{r=1}^{R+K}$ and high resolution sparse matrices ${\left\{{\mathbf{A}}_r^{H,\mathit{Train}}\right\}}_{r=1}^{R+K}$ created from the dictionary learning stage,

$${\widehat{\mathbf{M}}}_r=arg\underset{{\widehat{\mathbf{M}}}_r}{min}{\Vert {\mathbf{A}}_r^{H,\mathit{Train}}-{\mathbf{M}}_r{\mathbf{A}}_r^{L,\mathit{Train}}\Vert }_F^2+\beta {\Vert {\mathbf{M}}_r\Vert }_F^2,r=1,\dots ,R+K.$$ (6)

where β is the regularization parameter for balancing the objective terms. This optimization problem has a closed form solution [55],

$${\widehat{\mathbf{M}}}_r=({\mathbf{A}}_r^{H,\mathit{Train}}){({\mathbf{A}}_r^{L,\mathit{Train}})}^T\times {\left(({\mathbf{A}}_r^{L,\mathit{Train}}){({\mathbf{A}}_r^{L,\mathit{Train}})}^T+\beta ·\mathbf{I}\right)}^{-1},r=1,\dots ,R+K.$$ (7)

where I is an identity matrix.

Note that, since each layer based structural dictionary is designed for one specific layer, it has a significantly smaller number of atoms compared to the universal dictionary in [31, 47], and thus can achieve a more efficient representation. In addition, the dictionary construction step is an off-line process and in practice does not add to the computational cost of denoising or interpolation.

C. Layer Segmentation Based Sparse Reconstruction

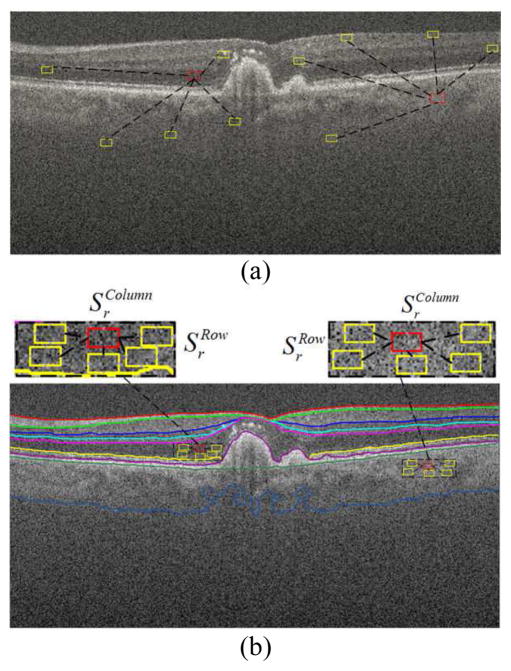
As noted, the anatomic and pathologic structures, intensities, and speckle patterns within each layer are expected to have strong similarities. Therefore, instead of searching the whole image [52], we propose to seek the similar patches in a searching window within each segmented layer, which can greatly reduce the search space [see Fig. 4(b)]. Specifically, for each patch ${\mathbf{x}}_i^r$ in the r-th layer of the test image, we first define a search window (of size $S_r^{\mathit{Row}}\times S_r^{\mathit{Column}}$) within the r-th layer, and then find J patches $\left\{{\mathbf{x}}_i^{r,1},\dots ,{\mathbf{x}}_i^{r,J}\right\}$ with the highest similarity to ${\mathbf{x}}_i^r$ using the similarity measure in (3). Note that if the rectangular search window goes beyond the boundaries of r-th layer, only the window part within the layer is considered as part of the search region. After finding these similar patches, instead of directly conducting the sparse decomposition (as in [23, 24, 40]), we apply a weighted average on these similar patches to obtain an average patch ${\mathbf{x}}_i^{\mathit{Ave},r}$,

Fig. 4.

Similar patch searching by (a) nonlocal searching; (b) layer segmentation based searching.

$${\mathbf{x}}_i^{\mathit{Ave},r}=\sum _{j=1}^J{\omega }_l^{r,j}{\mathbf{x}}_i^{r,j}$$ (8)

where ${\omega }_i^{r,j}$ is the weight for the patch ${\mathbf{x}}_i^{r,j}$, computed as

$${\omega }_i^{r,j}=\frac{exp\left(-{\Vert {\mathbf{x}}_i^{r,j}-{\mathbf{x}}_i^r\Vert }_2^2/w\right)}{{\displaystyle \sum _{j=1}^J}exp\left(-{\Vert {\mathbf{x}}_i^{r,j}-{\mathbf{x}}_i^r\Vert }_2^2/w\right)}$$ (9)

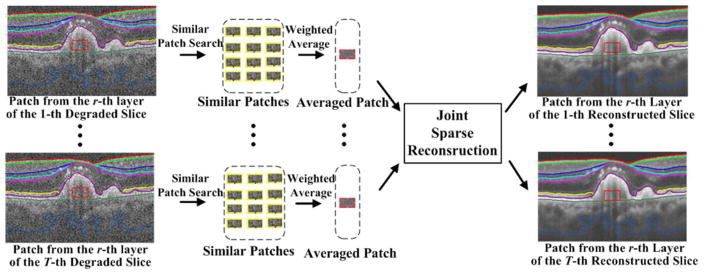
where W is a predetermined scalar. This weighted averaging scheme is an effective way to reduce noise, which affects direct sparse decomposition of the similar patches. Next, we use the average patches for the sparse reconstruction. Since the 3-D OCT image also has strong correlations among nearby slices [4, 32], we simultaneously process the averaged patches from the same position of nearby slices (called as the nearby patches ${\left\{{\mathbf{x}}_{i,t}^{\mathit{Ave},r}\right\}}_{t=1}^T$, where T is number of nearby patches) with a joint sparse decomposition technique. This technique decomposes the nearby patches on the same dictionary atom with different coefficient values, which can enhance the decomposition efficiency. The joint sparse reconstruction for the denoising and interpolation are separately described, as follows (see the Fig. 5).

Fig. 5.

Illustration of nearby patch estimation process in the proposed layer segmentation based sparse reconstruction.

1) Joint Sparse Reconstruction for Denoising

In denoising, simultaneous decomposition of the nearby averaged patches ${\left\{{\mathbf{x}}_{i,t}^{\mathit{Ave},r}\right\}}_{t=1}^T$ in the r-th layer of nearby images with the joint sparse technique amounts to the following problem,

$$\begin{array}{l}{\left\{{\widehat{\mathbf{\alpha }}}_{i,t}^{\mathit{Ave},r}\right\}}_{t=1}^T=\underset{{\left\{{\widehat{\mathbf{\alpha }}}_{i,t}^{\mathit{Ave},r}\right\}}_{t=1}^T}{min}\sum _{t=1}^T{\Vert {\mathbf{x}}_{i,t}^{\mathit{Ave},r}-{\mathbf{D}}_r{\mathbf{\alpha }}_{i,t}^{\mathit{Ave},r}\Vert }_2^2\\ \text{subject}\text{to}{\Vert {\mathbf{\alpha }}_{i,t}^{\mathit{Ave},r}\Vert }_0\le Ft=1,\dots ,T,\end{array}$$ (10)

where F is the maximum number of nonzero coefficients in ${\mathbf{\alpha }}_{i,t}^{\mathit{Ave},r}$. This optimization problem is efficiently solved by a simultaneous orthogonal matching pursuit (SOMP) algorithm [56]. Then, we estimate the reconstructed nearby patches as

$${\widehat{\mathbf{x}}}_{i,t}^r={\mathbf{D}}_r{\widehat{\mathbf{\alpha }}}_{i,t}^{\mathit{Ave},r},t=1,\dots ,T.$$ (11)

Note that, for the patches in the layer of the black region (e.g., vitreous and sclera), rather using the SOMP, we use the Euclidean distance to search the most representative atom for each patch. Finally, as in [32], a weighted average operation is conducted on the nearby patches and then these recovered nearby patches are returned to the original positions to reconstruct the denoised nearby images.

2) Joint Sparse Reconstruction for Interpolation

For the interpolation problem, given the averaged patches ${\left\{{\mathbf{x}}_{L,i,t}^{\mathit{Ave},r}\right\}}_{t=1}^T$ from nearby low resolution images, we obtain the low resolution sparse matrix ${\left\{{\mathbf{\alpha }}_{L,i,t}^{\mathit{Ave},r}\right\}}_{t=1}^T$ by utilizing the SOMP to solve (10) with the dictionary ${\mathbf{D}}_r^L$. Then, we estimate the corresponding high resolution sparse matrix as

$${\mathbf{\alpha }}_{H,i,t}^{\mathit{Ave},r}={\mathbf{M}}_r\times {\mathbf{\alpha }}_{L,i,t}^{\mathit{Ave},r},t=1,\dots ,T,$$ (12)

and the nearby high resolution patch set as

$${\widehat{\mathbf{x}}}_{H,i,t}^r={\mathbf{D}}_r^H{\mathbf{\alpha }}_{H,i,t}^{\mathit{Ave},r},t=1,\dots ,T.$$ (13)

As in [32], we also conduct a weighted average operation on the nearby patches, and return the set of nearby patches ${\left\{{\widehat{\mathbf{x}}}_{H,i,t}^r\right\}}_{t=1}^T$ to the original positions to reconstruct the high resolution nearby images.

IV. Experimental Results

A. Data Sets

Our experiments used a dataset of retinal OCT volumes from 41 different human subjects with and without nonneovascular age-related macular degeneration (AMD). The images in this dataset were imaged by a Bioptigen SDOCT system (Durham, NC, USA) with an axial resolution of ~4.5 μm per pixel in tissue. This dataset was originally introduced in our previous works [4, 24], and can be freely downloaded online¹. This dataset is attained with adherence to the tenets of the Declaration of Helsinki and is a subset of the image captured in the A2A SD-OCT Study, which was registered at ClinicalTrials.gov (Identifier: NCT00734487) and approved by the institutional review boards of the 4 A2A SD-OCT clinics (Devers Eye Institute, Duke Eye Center, Emory Eye Center, and National Eye Institute) [57].

For the denoising problem, images from 28 different human subjects are utilized. Two sets of scans were acquired from each subject. The first scan was focused at the fovea with 40 repeatedly sampled B-scans, each with 900 A-scans. The second scan was a 3D volume, with 900 A-scans and 100 B-scans including the fovea. We registered the first set of repeatedly sampled scans using the StackReg image registration plug-in in ImageJ [58] and then averaged them to obtain an averaged image of the fovea. The averaged image can be regarded as the “noiseless” reference image to train the dictionaries or compute the quantitative metrics. We selected datasets of 18 subjects to test the denoising performance of the proposed SSR method, while the datasets of the other 10 subjects were utilized for training the dictionaries and setting the parameters. Note that, the datasets of subjects used in the dictionary training stage were different from those used in the testing stage and the segmentation labels in the training stage have been manually corrected.

The dataset for interpolation problem included the images used for the denoising experiment. We used the averaged image created from the first scan as the high resolution image and subsampled the central foveal B-scan within the second scan as the corresponding low resolution image. Similar to the denoising problem, the high resolution and low resolution image pairs of 10 different subjects are used for training the dictionaries and mappings, while the remaining image pairs from 18 subjects are used for the testing. In addition, densely sampled and real subsampled datasets from another 13 human subjects are also used for the testing. For each subject, the real subsampled dataset has 450 A-scans per B-scan and 100 B-scans per volume, containing the fovea area.

B. Compared Methods

For the OCT image denoising problem, the proposed SSR method is compared with other five well known denoising approaches: BRFOE [59], K-SVD [47], PGPD [60], BM3D [39], and MSBTD [24]. The BRFOE is a modification of the field-of-experts model, which constructs filters by modeling the noisy image statistics. The K-SVD is a popular sparsity based denoising method, which trains one universal dictionary on the input noisy image. The BM3D is a widely popular benchmark denoising method, which exploits patch self-similarities of the input image by nonlocal searching and 3-D collaborative filtering. The MSBTD is a nonlocal based structural sparse denoising method, which utilizes nonlocal searching to exploit patch self-similarities and uses structural clustering to construct multiple structural dictionaries.

For the OCT image interpolation problem, we compared the proposed SSR method with five well-known interpolation approaches: Bicubic, Tikhonov [61], BM3D [39]+Bicubic, ScSR [51], and SBSDI [4]. The BM3D+Bicubic method is a combination of the BM3D denoising approach and the Bicubic interpolation approach. The ScSR is a popular sparsity based interpolation method, which utilizes the joint dictionary learning strategy to train a pair of low resolution and high resolution dictionaries. The SBSDI uses structural clustering to train multiple low resolution and high resolution dictionary pairs and employs a joint sparse operation to exploit the correlations among nearby slices for interpolation.

C. Algorithm Parameters

The parameters of the proposed SSR algorithm were empirically selected based on our experiments on the training data, and kept unchanged for all the test images. As in [35], the number of segmented layers R was set to seven. Since the vitreous, choroid, and sclera regions can be generally classified into background areas with less structural information and foreground areas with comparatively rich structural information, the cluster number K was selected to two. We chose the number of nearby slices T to be 5, based on the azimuthal resolution of the OCT volume, as slices from farther distances might have large differences, decreasing the effectiveness of the joint sparse reconstruction. The parameter W in (9) was set to 80. Using larger W values increases the averaging property in (8) and thus will create a stronger smoothing effect. The size of the search window $S_r^{\mathit{Row}}\times S_r^{\mathit{Column}}$ was set to 6×40. Increasing the size of the search window might further enhance the reconstruction performance, but create more computational cost. In each search window, the target number of similar patches J was set to 60. Further increasing in the number of similar patches number might result in over-smoothing. The sparsity level F for both the dictionary construction and the sparse reconstruction stages was set to 3. The above parameters were similarly set for both denoising and interpolation problems. For the denoising problem, the number of dictionary atoms is separately set to 30 and 80 for the layer of black region (e.g., vitreous and sclera) and other layers, respectively. For the interpolation problem, the number of dictionary atoms is set to 80 for all the layers. Increasing the number of dictionary atoms will improve the performances, but results in higher computational burden. Since most of the structures in the OCT image lay in the horizontal direction, the patch size n×m was set to 5×10 for the denoising problem. For the interpolation problem, the low resolution image patch size was set to 4×4, while the high resolution image patch sizes were chosen to be 4×8 and 4×16, when 50% and 75% data are missing, respectively. In the Section IV. G, we will further discuss the effect of the patch size on the performance of the proposed SSR method. The parameters of the compared methods: BRFOE [59], K-SVD [47], PGPD [60], BM3D [39], and MSBTD [24], BM3D [39]+Bicubic, ScSR [51], and SBSDI [4] are set to the default values as in their references [4, 24, 39, 47, 51, 59, 60]. The parameters for the Tikhonov method were tuned to reach the best results.

D. Quantitative Metrics

We adopted the peak signal-to-noise-ratio (PSNR), mean-to-standard-deviation ratio (MSR) [62], contrast-to-noise ratio (CNR) [63] and Wilcoxon signed-rank test [64] to quantitatively evaluate the results of the reconstruction methods. PSNR is a global quality metric and its calculation needs a high-quality reference image. Since all the datasets used in our experiments are acquired in clinic (not simulated) with heavy noise, we utilized the registered and averaged images created from the repeatedly sampled scans as the “noiseless” reference image. We used StackReg in [58] to register the reference image and reconstructed images in order to reduce the motion between them. After the registration, both the reference and recovered images might be slightly resized to compute the PSNR. MSR and CNR are two non-reference quality metrics and their calculations focus on some selected local regions. That is, MSR and CNR compute the means and standard deviations of background regions (e.g., red box #1 in Fig. 6) and foreground regions (e.g., red box #2–#6 in Fig. 6) in the reconstructed images. The Wilcoxon signed-rank test was used to test for statistical significance between the SSR method and each compared method on the evaluated PSNR, MSR and CNR.

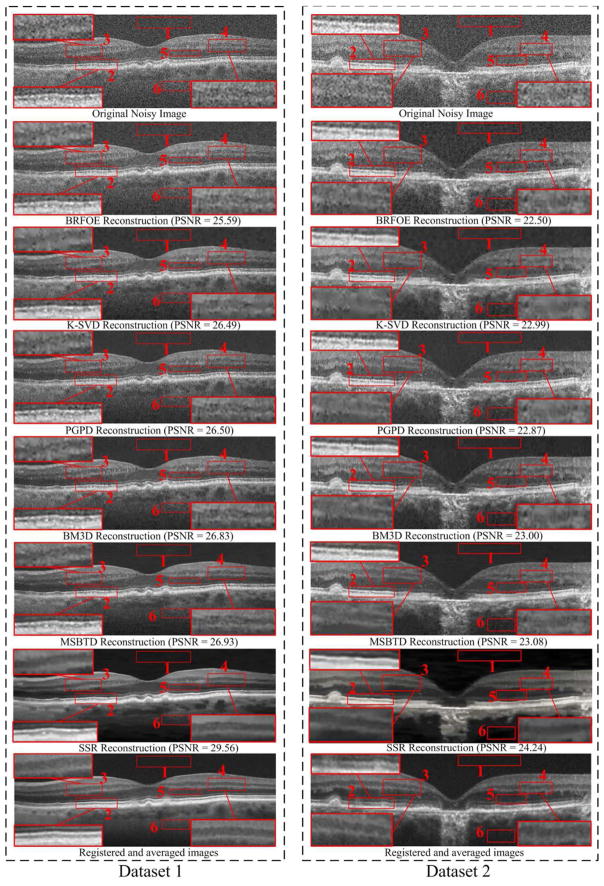
Fig. 6.

Two retinal OCT datasets and their Denoising results using the BRFOE [59], K-SVD [47], PGPD [60], BM3D [39], MSBTD [24] and SSR methods.

E. Results for OCT Image Denoising

Fig. 6 provides visual comparison of denoising results obtained from the BRFOE [59], K-SVD [47], PGPD [60], BM3D [39], MSBTD [24], and SSR methods on two real retinal OCT images. As can be observed, results from the BPFOE exhibit rather noisy appearance. The K-SVD, PGPD, and BM3D methods significantly remove noise, but appear over-smoothed with visible artifacts (see the zoomed layer areas in red boxes #2, #3, and #4 in Fig. 6). Though the MSBTD method can further reduce the artifacts, it still has indistinct layer boundaries (see the zoomed layer areas in red boxes #2, #3, and #4 in Fig. 6). By contrast, utilization of the proposed SSR method can achieve noticeably improved noise suppression while preserving the layer structural details as compared to other methods. This demonstrates that the proposed layer-segmentation based dictionary construction and sparse reconstruction strategies can significantly suppress the noise while still achieving better layer structure representation.

Average quantitative results (over 18 foveal images) of all the test methods are tabulated m the Table I. The proposed SSR method consistently outperforms the compared methods in terms of the three quantitative metrics (i.e., PSNR, MSR, and CNR). The average running time (over 18 foveal images) of all the test methods are reported in Table I. All the compared methods as well as the segmentation and sparse reconstruction parts of the proposed SSR method (in both the denoising and interpolation applications) are executed on a desktop PC with an 17-5930 CPU at 3.5 GHz and 64 GB of RAM. As can be seen, the reconstruction part of the SSR method needs much less running time than the non-local based denoising approaches: PGPD, BM3D, and MSBTD. This shows that searching for similar patches within each specific layer can greatly reduce the computational cost in comparison with the non-local similar patch searching strategy. Furthermore, we observe that the reconstruction part of the SSR method is faster than that of the original sparse denoising method (K-SVD). This is because the proposed SSR utilizes much smaller size layer based dictionaries and can reduce the computational cost for the sparse solution. Note that, the main part of the proposed SSR algorithm (except the SOMP code²) is coded with MATLAB, and can be further greatly accelerated with more efficient coding and a general purposed graphics processing unit (GPU).

TABLE I.

Mean and Standard Deviation of the PSNR, MSR, CNR Together With Running Time (in Seconds) for 18 Foveal Images From 18 Different Subjects Reconstructed by BRFOE [59], K-SVD [47], PGPD [60], BM3D [39], MSBTD [24], And SSR Methods. “Seg” and “Rec” Denotes the Required Running Time For the Layer Segmentation Part (R Layers Segmentation) And Sparse Reconstruction Part (Including vitreous and choroid/sclera regions Classification), Respectively. When p<0.05, The Metrics (I.E. PSNR, MSR, CNR) For Each Test Method are Considered Statistically Significant and were Marked By “*”. Best Results in the Mean Values are Labeled in Bold.

Metric\Method		BRFOE	K-SVD	PGPD	BM3D	MSBTD	SSR
PSNR	Mean	25.32	27.03	27.01	27.04	27.08	28.10
	Stand deviation	1.72	2.47	2.51	2.49	2.47	2.63
	p value	1.96E-04*	1.96E-04*	1.96E-04*	1.96E-04*	1.96E-04*
MSR	Mean	7.05	9.79	9.57	9.27	10.96	13.04
	Stand deviation	0.84	2.34	2.29	2.19	3.37	3.51
	p value	1.96E-04*	1.96E-04*	1.96E-04*	1.96E-04*	2.33E-04*
CNR	Mean	3.32	4.41	4.12	4.06	4.58	5.34
	Stand deviation	1.05	1.34	1.19	1.17	1.32	1.31
	p value	1.96E-04*	1.96E-04*	1.96E-04*	1.96E-04*	1.96E-04*
Running Time		63.53	2.90	69.35	4.45	1646.35	Seg	Rec
							0.49	1.01

F. Results for OCT Image Interpolation

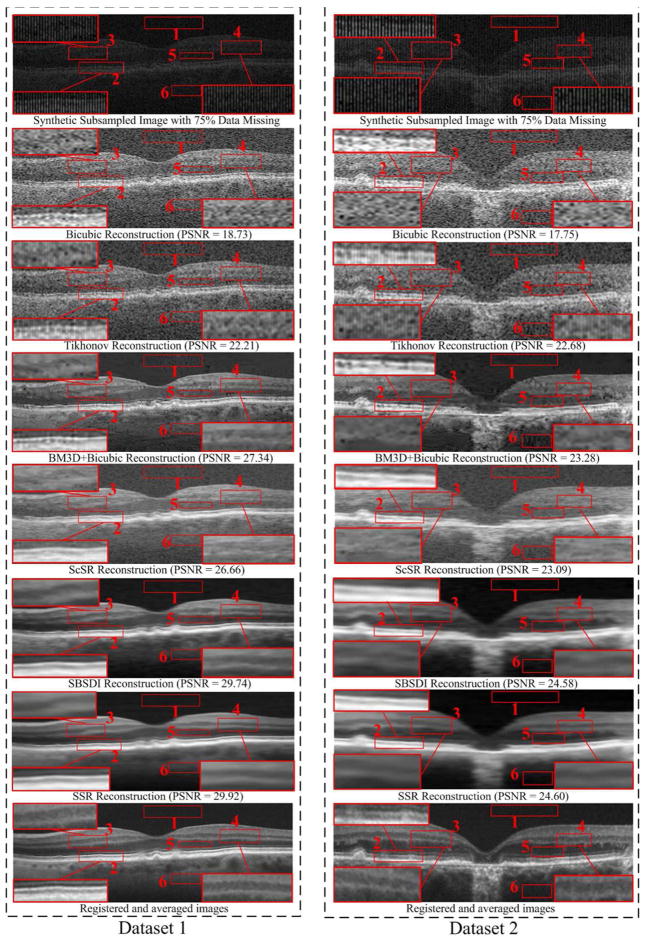
For interpolation, we conducted the experiments on two sampling conditions (with 50% data missing and with 75% data missing). For the condition with 50% missing, we first tested the Bicubic, Tikhonov [61], BM3D [39]+Bicubic, ScSR [51], SBSDI [4], and SSR methods on the real subsampled datasets from 13 different subjects. For each dataset, we adopted the central foveal B-scan and another two B-scans located approximately 1.5 mm below and above the fovea. Therefore, there are totally 3 × 13=39 images for this real subsampled experiment. Fig. 7 shows two real subsampled images and their visually reconstructed results obtained from all the test methods. As can be observed, the Bicubic, Tikhonov, and ScSR methods result in noisy reconstructions. The BM3D+Bicubic can greatly reduce the noise, but blurs the layer boundaries (see the zoomed layer areas in red boxes #2, #3, and #4 in Fig. 7). Although the layer boundaries can be preserved in the SBSDI method, it still introduces some artifacts. In contrast, the proposed SSR method can well preserve the structural details while significantly suppressing noise. In addition, we also adopted a regular sampling pattern to remove the 50% data information of the 18 foveal images used in the above denoising problem and used them for the interpolation testing. Table II reports the average quantitative results (over 39 real subsampled + 18 synthetic subsampled images) of all the test methods. As can be observed, the proposed SSR method delivers the best quantitative results. Furthermore, the reconstruction part of the SSR method requires less running time than the Tikhonov, BM3D+Bicubic, ScSR, and SBSDI methods, but has a higher computational cost than the simple Bicubic method. Note that, for the interpolation problem, the SBSDI and SSR methods adopts similar reconstruction framework, except for the proposed layer segmentation based dictionary construction and similar patch searching strategies.

Fig. 7.

Two real subsampled retinal OCT datasets (with 50% data missing) and their reconstruction results by using the Bicubic, Tikhonov [61], BM3D [39]+Bicubic, ScSR [51], SBSDI [4], and proposed SSR methods.

TABLE II.

Mean and Standard Deviation of the PSNR, MSR, CNR Together With Running Time (in Seconds) for 18 Foveal Images (With 50% Data Missing) From 18 Different Subjects and 39 Real Subsampled Images (Including Foveal and Nonfoveal Images With 50% Data Missing) From 13 Different Subjects Reconstructed by Bicubic, Ttkhonov [61], BM3D [39]+Bicubic, ScSR [51], SBSDI [4], and SSR Methods. “Seg” and “Rec” Denotes the Required Running Time For the Layer Segmentation Part (R Layers Segmentation) And Sparse Reconstruction Part (Including vitreous and choroid/sclera regions Classification), Respectively. When p<0.05, The Metrics (I.E. PSNR, MSR, CNR) For Each Test Method are Considered Statistically Significant and were Marked By “*”. Best Results in the Mean Values are Labeled in Bold.

Metric\Method		Bicubic	Tikhonov	BM3D+Bicubic	ScSR	SBSDI	SSR
PSNR	Mean	18.24	22.47	25.55	22.74	26.07	26.20
	Stand deviation	0.77	1.58	2.44	3.09	2.73	2.70
	p value	5.14E-11*	5.14E-11*	5.14E-11*	5.14E-11*	2.08E-08*
MSR	Mean	3.53	5.87	9.39	6.76	13.04	14.12
	Stand deviation	0.37	0.70	1.83	0.92	3.18	3.73
	p value	5.14E-11*	5.14E-11*	5.14E-11*	5.14E-11*	1.99E-07*
CNR	Mean	1.62	3.49	4.58	3.21	5.44	5.83
	Stand deviation	0.45	0.89	1.06	1.02	1.51	1.62
	p value	5.14E-11*	6.71E-11*	5.14E-11*	5.14E-11*	1.44E-06*
Running Time		0.01	2.24	2.34	96.29	4.61	Seg	Rec
							0.43	0.53

For the condition with 75% data missing, we also used the regular sampling pattern to remove the 75% data information of the 18 foveal images in the denoismg problem. Fig. 8 and Table III show the qualitative and quantitative reconstruction results from all the test methods on datasets with 75% data missing. As can be observed, the proposed SSR method provides the best performance.

Fig. 8.

Two synthetic Subsampled Retinal OCT datasets (with 75% data missing) and their reconstruction results by using the Bicubic, Tikhonov [61], BM3D [39]+Bicubic, ScSR [51], SBSDI [4], and proposed SSR methods.

TABLE III.

Mean and Standard Deviation of the PSNR, MSR, CNR Together With Running Time (in Seconds) for 18 Foveal Images (With 75% Data Missing) From 18 Different Subjects by Bicubic, Ttkhonov [61], BM3D [39]+Bicubic, ScSR [51], SBSDI [4], and SSR Methods. “Seg” and “Rec” Denotes the Required Running Time For Layer Segmentation Part (R Layers Segmentation) And Sparse Reconstruction Part (Including vitreous and choroid/sclera regions Classification), Respectively. When p<0.05, The Metrics (I.E. PSNR, MSR, CNR) For Each Test Method are Considered Statistically Significant and were Marked By “*”. Best Results in the Mean Values are Labeled in Bold.

Metric\Method		Bicubic	Tikhonov	BM3D+Bicubic	ScSR	SBSDI	SSR
PSNR	Mean	18.52	22.52	27.26	25.76	28.30	28.31
	Stand deviation	0.49	0.95	2.50	1.63	2.54	2.50
	p value	1.96E-04*	1.96E-04*	1.96E-04*	1.96E-04*	0.31
MSR	Mean	3.63	5.35	10.72	9.00	14.53	15.26
	Stand deviation	0.47	0.55	0.27	1.05	4.57	4.48
	p value	1.96E-04*	1.96E-04*	1.96E-04*	1.96E-04*	0.01*
CNR	Mean	1.68	2.53	4.62	3.82	5.89	6.25
	Stand deviation	0.56	0.80	1.31	1.26	1.43	1.64
	p value	1.96E-04*	1.96E-04*	1.96E-04*	1.96E-04*	1.96E-04*
Running Time		0.01	1.48	1.14	48.88	2.32	Seg	Rec
							0.51	0.31

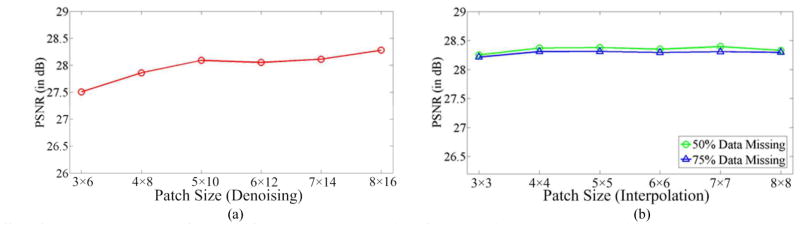
G. Effects of Patch Size

In this section, we analyze the effect of the patch size on the performance (in the PSNR sense) of the proposed SSR method. In the analysis of each specific parameter, we vary this parameter in a certain range and set the other parameters to the fixed values described in Section IV. C. Note that, the reported values are the averaged results over all 18 synthetic test images described in Section IV. E and F. For the denoismg problem, the patch size was varied from 3 × 6 to 8 × 16. The performance of the proposed SSR algorithm under varied patch sizes is shown in Fig. 9(a). For the interpolation problem, we changed the low resolution patch size from 3×3 to 8×8. The corresponding high resolution patch was enlarged in the horizontal direction according to the interpolation scale number (e.g., two times for 50% data missing and four times for 75% data missing). The performance of the proposed SSR algorithm under different patch sizes for two interpolation cases (e.g., 50% and 75% data missing) is illustrated in Fig. 9(b). As can be observed in Fig. 9, small patch sizes negatively affect the performance of our SSR algorithm. This is due to the fact that small patch size contains very limited spatial information for the reconstruction. The SSR algorithm generally performs the best when the patch size is increased to 5 × 10 and 4 × 4 for the denoising and interpolation problems, respectively. The performance of the proposed SSR algorithm, when using larger patch sizes, might become stable or even slightly worse based on qualitative evaluation. This is because using too large patches might create an over-smoothing effect, which blurs the final reconstruction results. In addition, using larger patches has higher computational costs.

Fig. 9.

Effect of the patch size on the performance of the proposed SSR algorithm for (a) Denoising and (b) Interpolation.

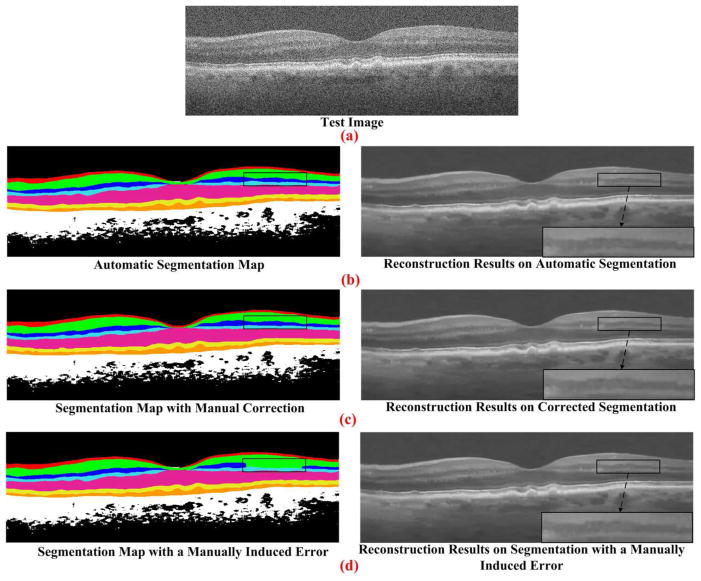
H. Effect of Segmentation Errors

Our next experiment assessed the sensitivity of our denoising algorithm to small errors in segmentation. We segmented a B-Scan using the automatic GTDP technique [35]. Next, we modified this B-Scan to correct segmentation errors (corrected segmentation). Since automatic and corrected segmentation results were very close, we manually modified the automatic segmentation, intentionally introducing errors in segmentation (manually induced error). As shown in Fig. 10, the corrected segmentation case might slightly perform better than the automatic and manually induced error segmentation cases. However, these differences are negligible.

Fig. 10.

SSR reconstruction results using three different layer segmentations. The image in (a) is a raw OCT B-Scan. Automatic segmentation of retinal layers using GTDP algorithm (delineated in different colors in the left column) is used to produce the denoised image of the right column in (b). We carefully manually corrected the automatic segmentation of layer boundaries, resulting in the slightly modified layer boundaries shown in the left column of the (c). Corresponding denoised image is shown in the right column of the (c). To artificially create more severe segmentation errors, we intentionally introduced errors in segmentation of the inner nuclear layer in the black box region (manually induced error), resulting in the images of the (d).

In general, the segmentation information has been utilized in three stages of the proposed SSR algorithm: dictionary construction, similar patch searching, and sparse representation. Errors in segmentation can potentially affect each of these stages. Since manual corrections can be applied to the automatically segmented images in the offline dictionary construction stage, the segmentation accuracy in this stage can be as high as needed. In the similar patch searching stage, since the similarity metrics are tested for each patch, the search process significantly reduces the effects of segmentation errors on reconstruction. The sparse representation stage is relatively more sensitive to segmentation accuracy, as segmentation error can result in the selection of a dictionary from an incorrect layer to represent the patch being processed. However, even with a suboptimally selected dictionary, the sparse solution process (e.g. the orthogonal matching pursuit algorithm [50]) can find well-suited atoms to represent the processed patch and the final reconstruction result is expected to be stable, as shown in Fig. 10. As indicated in Section IV E and F, only with the classic GTDP automatic segmentation algorithm [35], the proposed SSR algorithm’s performance is superior to several state-of-the-art non-segmentation based reconstruction methods.

I. Effect of Image Reconstruction to the Layer Segmentation

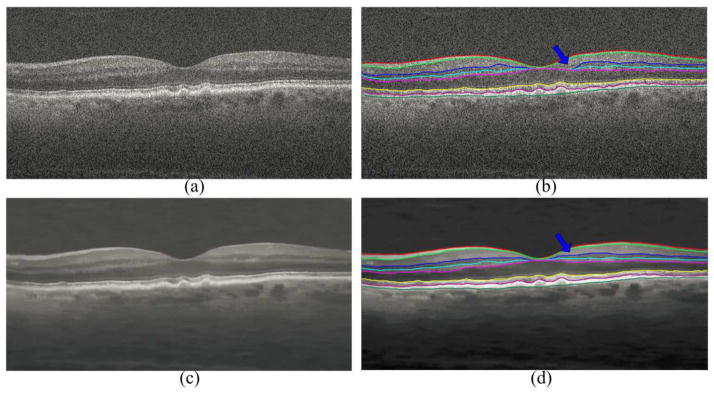
The experiment in Fig. 10 showed that our denoising algorithm is not sensitive to small errors in automated segmentation. In a recursive process, once the SSR denoised images are in hand, they can be segmented again using the GTDP method, which is expected to result in equal or better segmentation. The experiment in Fig. 11 shows such a case. In this example, there is a small error in the segmentation of the inner nuclear layer boundaries delineated by blue and cyan colors near the fovea, when the GTDP technique is applied on the noisy images. When GTDP is applied on the SSR denoised image, these small segmentation errors are mostly eliminated.

Fig. 11.

Impact of SSR reconstruction on automatic GTDP layer segmentation performance. The raw B-Scan in (a) is segmented using automated GTDP technique in (b). The blue arrow points to a small region with errors in automatic segmentation of the inner nuclear layer boundaries (delineated in blue and cyan colors). SSR denoised image using the segmentation results in (b) is shown in (c). Automatic segmentation of the image in (c) using GTDP technique is shown in (d), where the accuracy of segmentation is improved for the previous erroneously segmented region.

V. CONCLUSIONS

In this paper, we presented a novel layer-segmentation based sparse reconstruction method named SSR for efficient denoising and interpolation of 3D SDOCT images. Unlike our previous sparse denoising [24] and interpolation [4] methods, the proposed SSR method utilizes segmented layer information to construct the structural dictionaries and conduct similar-patch searching. Both the layer-segmentation based dictionaries and similar-patches searching can aid sparse reconstruction in order to achieve better representation, while greatly reducing the computational cost. Our experiments demonstrated the high efficiency and effectiveness of the proposed SSR method over several current state-of-the-art denoising and interpolation approaches.

Following our previous work, the denoising and interpolation software developed for this project publically will be available at https://sites.google.com/site/levuanfang/home.

There is space for improving the performance_of our SSR algorithm. One limiting factor in our proposed technique is the utilization of fixed-size rectangular patches. Today, OCT technology is used for imaging a variety of pathologic structures in eyes and other human and animal organs, the shape of which might not be optimally represented by the fixed-size rectangular patches. Therefore, in our future work, we will incorporate shape adaptive patches (e.g. utilizing superpixel [65] or adaptive kernels [66]) into the proposed sparse model, which we expect to improve the reconstruction performance. In addition to the fixed-size patch, several parameters need to be tuned for the proposed method. So, a future line of work will also be on designing efficient automatic parameter selection algorithms.

There are two potential utilities for our segmentation-based reconstruction technique. The first application is the OCT image quality improvement for visual inspection of complex anatomic and pathologic structures (e.g., vessels, drusen, hyperreflective foci, edema, etc.). The second important utility of our reconstruction approach is improving the performance of automated segmentation algorithms. Note that, our algorithm utilizes automated layer segmentation (a problem for which several solutions are available in the literature) and results in denoised images from which other features (e.g. hyperreflective foci, edema, vessel, etc.) can be automatically segmented. The proposed SSR method based on the layer segmentation can even recursively improve the accuracy of segmentation. While our automatic GTDP retinal layer segmentation algorithm is accurate, it is not perfect and occasionally results in erroneous segmentation, especially for noisy images. Utilizing our SSR reconstruction algorithm can improve the GTDP segmentation accuracy as shown in the experiment of Fig. 12. A complete quantitative assessment of the proposed method impact for enhancing the performance of various automated segmentation methods is a part of our ongoing works.

In this paper, we utilized the segmented retinal layer information for enhancing volumetric OCT images. However, the proposed mathematical framework is general and applicable to virtually any other tissue. Also, for segmentation, we utilized the GTDP method of [35], which can be replaced by any other layer or feature segmentation technique [24, 67–69]. Therefore, in our future publications, we will investigate the applicability of the proposed segmentation based reconstruction model for enhancing the quality of a wide variety of images from different tissues (e.g. dermatology, Gastroenterology, and cardiology) captured via OCT or other imaging modalities such as MRI or ultrasound.

Finally, despite the fact that our algorithm utilized the classic GTDP automatic segmentation algorithm [35], the final reconstructed results demonstrated the superiority of the proposed SSR algorithm over several state-of-the-art non-segmentations based reconstruction methods. More recent and advanced 3-D segmentation methods such as [3, 70, 71], which are more robust to imaging and pathologic artifacts, can also be utilized to improve segmentation accuracy, if needed. However, more complex 3-D segmentation algorithms often increase the computational load of the overall algorithm.