Anisotropic cerebral vascular architecture causes orientation dependency in cerebral blood flow and volume measured with dynamic susceptibility contrast magnetic resonance imaging

Abstract

Measurements of cerebral perfusion using dynamic susceptibility contrast magnetic resonance imaging rely on the assumption of isotropic vascular architecture. However, a considerable fraction of vessels runs in parallel with white matter tracts. Here, we investigate the effects of tissue orientation on dynamic susceptibility contrast magnetic resonance imaging. Tissue orientation was measured using diffusion tensor imaging and dynamic susceptibility contrast was performed with gradient echo planar imaging. Perfusion parameters and the raw dynamic susceptibility contrast signals were correlated with tissue orientation. Additionally, numerical simulations were performed for a range of vascular volumes of both the isotropic vascular bed and anisotropic vessel components, as well as for a range of contrast agent concentrations. The effect of the contrast agent was much larger in white matter tissue perpendicular to the main magnetic field compared to white matter parallel to the main magnetic field. In addition, cerebral blood flow and cerebral blood volume were affected in the same way with angle-dependent variations of up to 130%. Mean transit time and time to maximum of the residual curve exhibited weak orientation dependency of 10%. Numerical simulations agreed with the measured data, showing that one-third of the white matter vascular volume is comprised of vessels running in parallel with the fibre tracts.

Introduction

Perfusion measurements of the brain are widely used in research and clinical imaging.¹ With widespread availability, magnetic resonance imaging (MRI) has become a frequently used method for assessing cerebral blood perfusion. Perfusion measurements with MRI offer good spatial and temporal resolution while ionizing radiation is not required. An important MRI technique for the assessment of cerebral tissue perfusion is dynamic susceptibility contrast (DSC) imaging, which uses the administration of a paramagnetic contrast agent (CA) during the repeated acquisition of a rapid imaging technique that is sensitive to the CA.^2,3 The MRI DSC scan is usually a series of gradient echo planar scans with a repetition time between 1 and 2 s, which is shorter than the time needed for a CA to transit through the brain so that the CA dynamics can be visualized. The CA's paramagnetic properties lead to a reduction of the gradient echo signal due to the generation of magnetic field inhomogeneities around blood vessels containing the CA. The signal reduction is thought to be proportional to the CA concentration within the tissue of interest. Using pharmacokinetic models,³ important hemodynamic parameters can be computed from the measured signal time series in cerebral tissue: cerebral blood flow (CBF), cerebral blood volume (CBV), mean transit time (MTT), and time to peak, or the time to maximum of the residue function (Tmax). These parameters depend on physiological parameters, such as haematocrit, cardiac output, and regional blood volume and flow. In addition, the measured values also depend on technical parameters, such as type of CA, the way it is administered, and the type of MRI sequence, magnetic field strength, as well as other data acquisition parameters. The calculation of absolute perfusion parameter values, especially of CBF and CBV requires knowledge of the CA concentration over time in the arteries feeding into the tissue of interest, the so-called arterial input function (AIF). The AIF represents the deviation of the bolus from the ideal delta-function-shaped bolus. Deconvolution of the concentration time curve with the AIF results in the residue function, which is corrected for the AIF contribution and describes the fraction of tracer present in the capillaries at each time point. The residue function is typically used for the calculation of quantitative perfusion parameters, such as CBF and CBV.

The pharmacokinetic models used for calculation of perfusion parameters maps from DSC MRI assume a spatially isotropic vascular architecture, so that the orientation of the vascular bed relative to the main magnetic field can be neglected. However, if the vascular network is not isotropic, the orientation of the anisotropic component, e.g. a large vessel traversing the imaging voxel starts to play a role in the signal reduction. Orientation effects of single blood vessels have been investigated extensively in the context of venography based on susceptibility-weighted imaging (SWI).^4–6 In SWI, the paramagnetic venous blood is used as an intrinsic CA to map venous vasculature in high detail. Due to the field inhomogeneities created by a vein,⁷ the magnetization of a voxel containing a vein loses coherence more rapidly than a voxel without a vein. With increasing angle between the vein and the main magnetic field, the field inhomogeneities around the vessel become more pronounced and the signal decreases more rapidly. Due to this effect, vessels with diameters less than 100 µm can be imaged at 3T using an SWI scan with a spatial resolution of 0.25 mm³.⁸ In DSC, which uses much larger voxel sizes in the range of 20 mm³, the vasculature within a voxel has been assumed to be isotropic and potential orientation effects have not been investigated so far. However, there is evidence that white matter (WM) blood vessels do not form a perfectly isotropic vascular tree, but rather have a tendency to run in parallel with the WM tracts. Nonaka et al. presented postmortem images of WM vessels with considerable anisotropy.^9,10 Detailed images of vessels in a rodent model of ischaemia also provide evidence of vessels running in parallel with WM fibres.¹¹ It was also shown that the blood oxygenation level dependency (BOLD) of the T2*-weighted MR signal depends strongly on the orientation of the cortical tissue.¹² Finally, maps of perivascular spaces exhibit anisotropic vascular trees that resemble fibre tracts mapped with diffusion tensor imaging (DTI).¹³

It is impossible to directly map the orientation of very small vessels and difficult to map medium-sized (30–200 µm) vessels in the human brain in vivo. If, however, vessels are assumed to run in parallel with WM tracts, their orientation can be assessed indirectly at high angular precision using DTI. The purpose of this study was, therefore, to combine gradient echo DSC and DTI to investigate tissue orientation effects on DSC measurements.

Methods

Standard protocol approval, registrations and patient consents

This study was approved by the Clinical Research Ethics Board of the University of British Columbia (H12-01153, 20 June 2012) and is in accord with the Declaration of Helsinki. All subjects gave written informed consent.

Subjects

Thirteen patients with multiple sclerosis (eight relapsing remitting; three secondary progressive; two primary progressive; nine female; EDSS = 2.5–5, median = 4; age = 44–61 years, median = 53 years; disease duration = 4–42 years, median = 20 years) were included in this study.

Data acquisition

All data were acquired on a 3 Tesla system (Philips Achieva) equipped with an eight-channel SENSE head coil. The protocol included a 3D T1-weighted scan (T1w), a 3D turbo spin echo scan (TSE), DTI (b=1000, 32 directions), gadolinium (Gd) injection (Magnevist, 0.2 ml/kg body weight at 5 ml/s followed by 20 ml saline flush at 5 ml/s) at the second time point of the perfusion scan (gradient echo planar imaging; 40 dynamic scans), followed by a 3D Fluid Attenuated Inversion Recovery scan. All 3D anatomical scans were acquired in sagittal orientation. The perfusion and the DTI scans were acquired with the imaging plane parallel to the subcallosal line. Other relevant imaging parameters are listed in Table 1.

Table 1.

MRI scans and their parameters.

Sequence	TR/TE/TEequiv	Matrix	Acq. voxel size (mm3)	Recon. voxel size (mm3)	SENSE acceleration	Acquisition time (min)
3D T1w	6/3/-	256 × 255 × 200	1 × 1 × 1.6	0.8 × 0.8 × 0.8	1 (AP) 1 (RL)	6:22
3D TSE	2500/363/133	256 × 256 × 200	1 × 1 × 1.6	0.8 × 0.8 × 0.8	2 (AP) 1.5 (RL)	4:42
3D FLAIR	8000/337/156/ TI = 2400	256 × 256 × 200	1 × 1 × 1.6	0.8 × 0.8 × 0.8	2.5 (AP) 2 (RL)	5:04
DTI	5640/75	96 × 95 135 slices	2.5 × 2.5 × 2.5	1.88 × 1.88 × 2.5	2.4 (AP)	4:42
Perfusion	2417/40/-	96 × 95 144 slices	2.33 × 2.33 × 4	1.75 × 1.75 × 4	2.3 (AP)	1:46

DTI: diffusion tensor imaging; FLAIR: fluid attenuated inversion recovery; TSE: turbo spin echo scan.

Data processing

DTI data were processed using FMRIB Software Library (FSL).^14,15 Eddy current and head motion correction of DTI data were performed via a linear registration (FLIRT) and non-brain voxels were removed using FSL's brain extraction tool. Eigenvalues and their corresponding eigenvectors were calculated using FSL's DTIFIT. T1w and TSE were linearly registered to the DTI space using FLIRT. The combination T1wTSE = (T1w - TSE) / (T1w + TSE) enhances contrast between WM, grey matter (GM) and subcortical structures¹⁶ and was used for tissue segmentation with FSL's FAST, using the non-binary partial volume maps with a threshold of 0.95 for WM. Maps of the angle between the main magnetic field and the principal diffusion direction of every voxel as a measure of local fibre orientation were computed spanning angles between 0 ° and 90 °.¹⁷

For quantitative evaluation of the angle dependency of perfusion parameters, the DSC datasets were processed using the software tool AnToNIa.¹⁸ Briefly, an in-slice rigid registration was used for motion correction. After this, each DSC signal intensity curve S(t) was converted to a relative transverse relaxivity curve $\Delta {\text{R}}_2^{*}$ using the following equation

$$\Delta R_2^{*}=-\frac{1}{\mathrm{TE}}\text{ln}(\frac{S(t)}{S_0})$$ (1)

where TE denotes the echo time, and S₀ the baseline MRI signal, which was determined based on the first five time points of the acquisition individually for each voxel. A B-spline approximation was used to correct for slice time differences due to the interleaved DSC perfusion-weighted imaging (PWI) acquisition but also for noise reduction and temporal resampling to a temporal resolution of 1 s. After this, the AIF was identified using an atlas-based approach. All tissue relative transverse relaxivity curves were converted to concentration time curves C(t) using the correction formulas described in Kjølby et al.¹⁹ The block-circulant singular value decomposition²⁰ together with a truncation threshold of 0.2 was used to solve the fundamental perfusion equation

$$C(t)=\mathrm{CBF}·R(t)\otimes C_a(t)$$ (2)

where CBF is the cerebral blood flow, C_a(t) the AIF and R(t) the residue function. Aside from the CBF parameter, which is equal to the maximum value of the residual function defined by the time point Tmax, the CBV parameter was calculated by determining the area under the curve of the residue function. The MTT parameter can be calculated from the CBV and CBF parameter using the central volume theorem.²¹

Perfusion maps were registered to DTI using FLIRT. Voxels with orientations within 5 ° intervals were pooled and averaged and then used to calculate $\Delta {\text{R}}_2^{*}$, CBF, CBV, MTT and Tmax as functions of the fibre orientation. See Figure 1 in Hernández-Torres et al.²² for further details on the use of DTI to measure tissue orientation.

Figure 1.

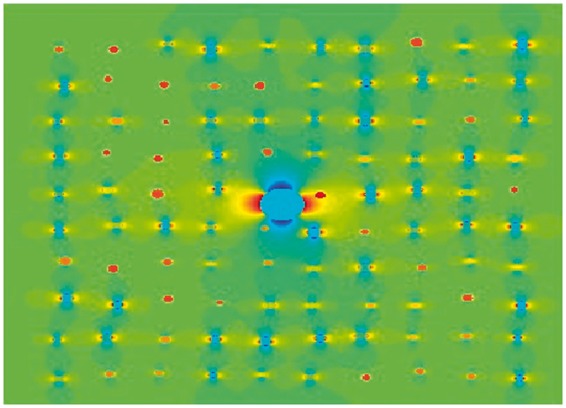
Numerical simulation of an isotropic vascular network and one large vessel. Vessels with a normal distribution of radii (mean = 13.4 µm, standard deviation of 2.1 µm) were simulated. The orientations ranged from 0 ° to 90 °. The large vessel has a radius of 68 µm and an orientation of 90 ° to the external magnetic field. For blood volumes encountered in the human brain, the distance between vessels can be regarded large in comparison to the vessel diameter. Therefore, small changes in individual vessels' positions had no influence on the result of the simulation.

Numerical simulations

Numerical simulations of the change in DSC signal due to the presence of a CA were performed using Matlab (R2012b). In order to understand the effects of vascular architecture on the DSC signal, simulations were performed for anisotropic vessels embedded in an isotropic vascular bed and for different CA concentrations. All parameters are given in SI units. Simulations were conducted for a DSC gradient echo time of 40 ms and a field strength of 3 T. Separate simulations were performed for single blood vessels, for isotropic vascular networks and finally for combinations of single vessels and networks. For each orientation of the large vessels with respect to the main magnetic field, $\Delta {\text{R}}_2^{*}$ was computed for a range of volume fractions occupied by the vessels and the vessel network and a range of CA concentrations.

The field inside and outside blood vessels was computed according to

$$\Delta B_{\mathrm{inside}}=\frac{\Delta x}{6}(3\cos 2(\alpha )-1)·B\Delta B_{\mathrm{outside}}=\frac{\Delta x}{2}(\sin 2(\alpha )·\frac{a2}{|r|2}·\cos (2\phi ))·B$$ (3)

where ΔB is the change in magnetic field strength, Δχ is the difference in magnetic susceptibility between the vessel and the surrounding tissue, and α is the angle between the vessel and the main magnetic field. The position of the observation point is given in polar coordinates r and φ, where r describes the distance from the cylinder axis and φ the polar angle in the plane defined by B₀ and the cylinder axis. The susceptibility difference Δχ is computed as

$$\Delta x=\text{Hct}·(1-Y)·2.26+x_{\mathrm{CA}}·C$$ (4)

where Hct is the haematocrit describing the volume percentage of red blood cells, which was set to 0.4.²³ Y is the oxygen saturation of the blood, which was set to 0.6 and C is the CA concentration.²⁴ For χ_CA a value of 0.34 ppm (1/mM) was used.²⁴ As the susceptibility difference between fully oxygenated and deoxygenated blood is small compared to the effects of the CA and the total vascular cross section is larger for veins than for arteries, magnetic differences between venous and arterial vessels were neglected and all vessels were treated as veins.

The vascular network was simulated in two dimensions on a quadratic grid as a large number of non-intersecting vessels with orientations distributed uniformly between 0 ° and 90 ° and diameters distributed normally around 13.7 µm with a standard deviation of 2.1 µm, according to Jochimsen et al.²⁵ The magnetization at a certain echo time t and at a location r within the voxel is the determined by R₂ relaxation (vessel, WM) and the local magnetic field

$$M_{\mathrm{xy}}=M_0·e-i\Upsilon \Delta B(r)t·e-R_{2}t,$$ (5)

where γ denotes the gyromagnetic ratio of the proton. The phase in this equation and R₂ both depend on the CA concentration. The R₂ tissue relaxation rates at 3 T are 31.1 s⁻¹ for blood, 14.5 s⁻¹ for WM (5) and for the CA 5.2 s/mM.²⁶ The field inhomogeneities created by the vessels create intravoxel dephasing which results in a signal reduction. The signal from a voxel is then given by the integral over all magnetizations within the voxel

$$S(t)={\int }_r{M}_{\mathrm{xy}}(r,t)\text{dr}$$ (6)

The baseline signal S₀ was computed for vessels with venous blood only, i.e. no added CA. The changes in ${\text{R}}_2^{*}$ due to CA were computed relative to S(0) according to equation (1). The simulation was conducted for one vessel in the centre, as well as for 4, 9 and 16 vessels, keeping the total blood volume fraction (BVF) constant, to test whether the number of anisotropic vessels influences the signal. The total volume fractions of the vascular configuration were varied in steps of 0.2% up to 5%. The volume fractions of the isotropic background and the anisotropic vessels were varied independently. The CA concentration was varied between 0 and 8% in steps of 0.2%.²⁷ Figure 1 displays the general configuration of the isotropic background and an anisotropic component represented by a single vessel in the voxel's centre. Least square fits to the measured data were performed for each simulated combination of volumes of the isotropic background and anisotropic vessels, and CA concentration, and for each orientation of the anisotropic vessel.

Results

Measurements

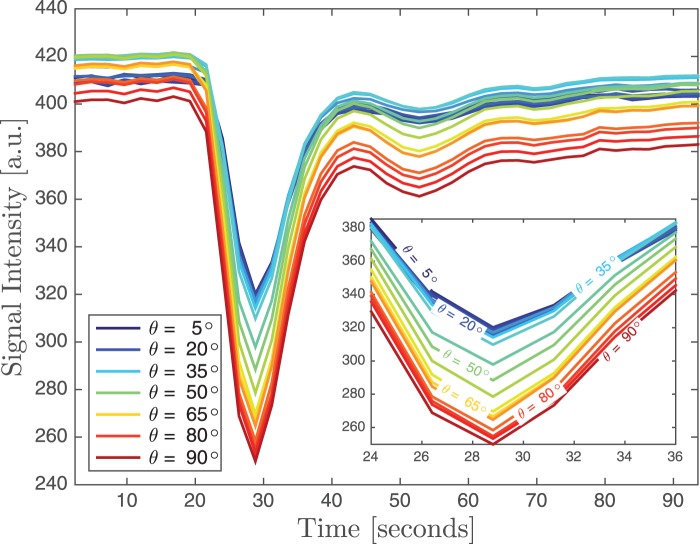
The concentration time curve of the brain's WM showed a dependency on fibre orientation with increasing signal reduction for increasing angles between WM and the main magnetic field (Figure 2). There was also a variation of about 5% in the baseline signal depending on fibre orientation. For WM fibre orientations between 0 ° and 5 ° (i.e. parallel to B₀) the reduction at peak CA concentration was about 22%, whereas for fibres perpendicular to B₀ the reduction was almost 80% larger with 38% signal loss compared to baseline.

Figure 2.

Signal reduction for one subject as a function of CA concentration for voxels with different WM tissue orientation. With increasing angle between the tissue and the main magnetic field, the reduction becomes larger. Note also that there are small angle-dependent variations of up to 5% in the baseline signal. The inset shows a zoomed view of the concentration time curves around the maximum CA concentration.

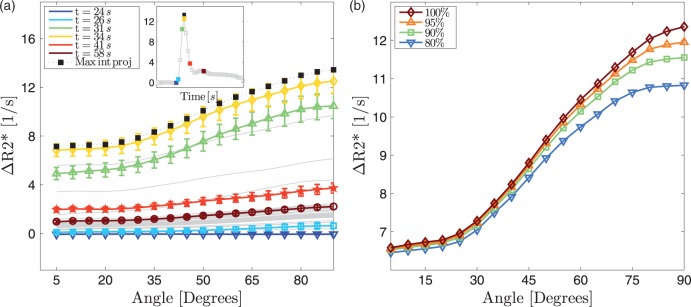
The change in ${\text{R}}_2^{*}$ due to the presence of CA within the vascular system ($\Delta {\text{R}}_2^{*}$) showed a strong angle dependency (Figure 3(a)). At the peak CA concentration, the change in ${\text{R}}_2^{*}$ was 80% larger for perpendicular fibres compared to parallel fibres. The $\Delta {\text{R}}_2^{*}$ plots exhibit an offset and an angle dependency, which both become more pronounced with increasing CA concentration. When a temporal maximum intensity projection through the DSC time series is computed to capture the moment of maximum CA concentration for each voxel and to remove individual differences in regional CA arrival time, the resulting curve resides slightly above the curve associated with the peak CA. By excluding voxels with the highest blood volume in the CBV map, most likely corresponding to large vessels, the orientation dependency is only slightly reduced, which indicates that smaller vessels also contribute to the orientation dependency and that the results are not driven by a few large vessels (Figure 3(b)). If more voxels with high blood volume are excluded, the orientation dependency is further reduced, suggesting that the orientation dependency is due to mid-size vessels.

Figure 3.

(a) Changes in ${\text{R}}_2^{*}$ as a function of time (average of 13 subjects) relative to the average signal of the first five scans of the time series. Before averaging, the time courses of individual subjects were shifted so that the maxima coincide for all subjects. The inset shows the change in ${\text{R}}_2^{*}$ averaged over all voxels between 85 ° and 90 °. When the CA reaches its maximum (yellow square in the inset and yellow line in the main plot), the angle dependency also reaches its maximum. There are both an angle independent offset and an angle-dependent component to these plots. The black squares represent $\Delta {\text{R}}_2^{*}$ of a maximum intensity projection along the time axis. This means that for each voxel the maximum CA concentration is captured, which removes regional differences in CA arrival time. Therefore, the black line is located slightly above the yellow line. The bars represent standard errors. The colours in the inset correspond to the colours of the main plot. (b) The angle dependency in $\Delta {\text{R}}_2^{*}$ changes when voxels with high CBV values are removed. However, even when the top 20% voxels are removed the angle dependency remains high.

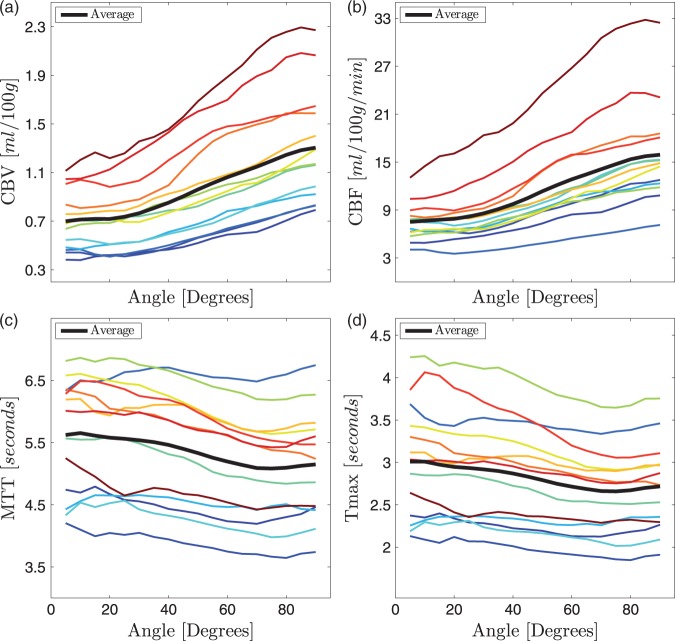
The orientation dependency in $\Delta {\text{R}}_2^{*}$ leads to corresponding dependencies in CBV (Figure 4(a)) and CBF (Figure 4(b)). There are considerable individual differences in absolute CBF and CBV values as well as in the angular dependency. Both CBF and CBV differed by up to 130% between parallel and perpendicular fibres. On the other hand, MTT (Figure 4(c)) and Tmax (Figure 4(d)) showed a considerable smaller angle dependency in the range of only 10%.

Figure 4.

Orientation dependency in CBV (a), CBF (b), MTT (c) and Tmax (d) in the same subjects shown in Figure 3. Again, there is a large orientation dependency and considerable inter-subject variability in CBV and CBF. The orientation dependency in MTT and Tmax is small at around 10%. The thick black lines are the averages across the 13 subjects.

Numerical simulations

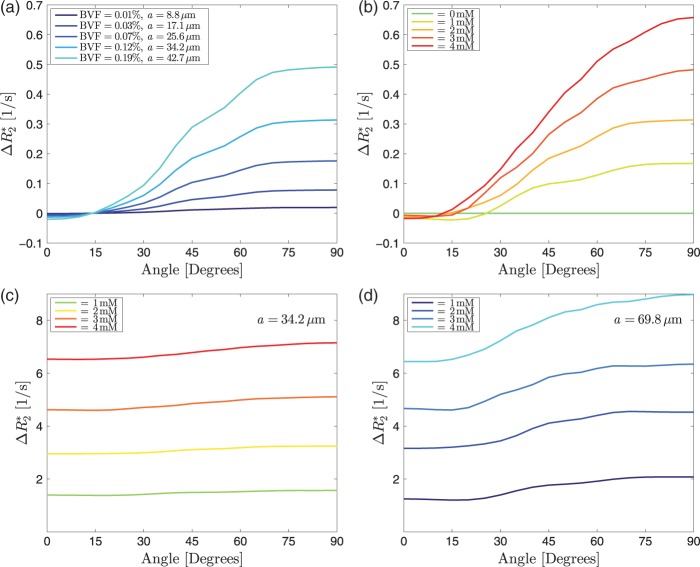
Simulations for one very small vessel in the centre of the voxel, with no isotropic vascular background, show how $\Delta {\text{R}}_2^{*}$ increases with increasing angles. The angle dependency increased with increasing vessel size. For very small angles (below 20 °), there is a small negative ${\text{R}}_2^{*}$ effect (Figure 5(a)). With increasing CA concentration for a fixed vessel radius, the angle dependency also becomes more prominent (Figure 5(b)). Adding the isotropic background to the small vessel results in the observed CA-dependent offset and an angle dependency (Figure 5(c)), which increases with increasing vessel radius (Figure 5(d)). Finally, when fitting for both BVF of the background and the anisotropic component, the fit for a volume fraction of 1.0% for the isotropic background and 1.0% of the anisotropic vascular component matches the measured data (Figure 6). Fits were computed for one, four, nine and 16 vessels of equal total volume fraction and results were very similar. All other fits were therefore performed for four vessels running in parallel. The total range of CA concentration according to the fit ranged from 0 to a peak concentration of 7.6 mM. Fits to data acquired at different CA concentrations resulted in the same vessel volume fractions and only the CA concentration changed. As an additional consistency test, vascular volumes and CA concentration were determined by fitting to the curve measured at the peak CA concentration. Then, the vascular parameters were kept constant and the CA concentration was reduced by 50%. The resulting numerical simulation coincides with the measured curve at half the CA peak height.

Figure 5.

(a) Simulations of $\Delta {\text{R}}_2^{*}$ for single vessels with varying radii and a constant CA concentration of 2 mM. With increasing volume fraction (i.e. increasing vessel radius), the angle dependency increases. However, there is no noticeable angle independent offset. Small negative values for $\Delta {\text{R}}_2^{*}$ at low angles are due to the fact that for the echo time used in this simulation (40 ms) the intravascular signal has decayed due to the CA. (b) Vessels with a radius of 34.2 µm at different CA concentrations. The angle dependency increases with increasing CA concentration. For very small angles there is a small negative effect. For this vessel size, the change in ${\text{R}}_2^{*}$ is about one order of magnitude smaller than in the measured data. (c) $\Delta {\text{R}}_2^{*}$ for a 1.75 × 1.75 mm² voxel with 100 isotropic background vessels as in Figure 1 and one major vessel with a radius of 34.2 µm. (d) $\Delta {\text{R}}_2^{*}$ for a background with 100 isotropic background vessels as in Figure 2 and one major vessel with a radius of 69.8 µm. While the offset is similar in both scenarios, the orientation dependency is more pronounced for the larger anisotropic vessel.

Figure 6.

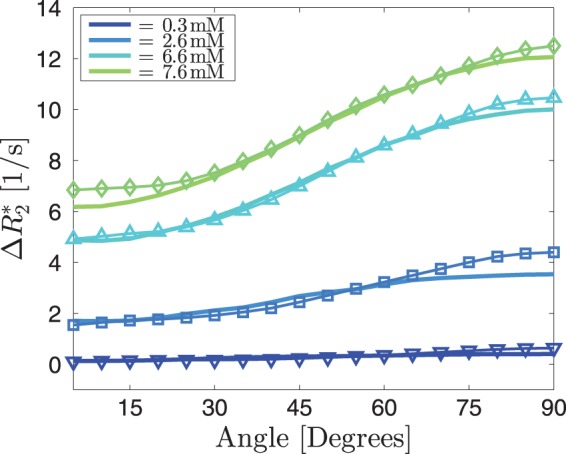
The thin lines represent the average angle dependencies across 13 subjects for four different CA concentrations. The thick lines are the best fits, resulting in a background blood vessel volume fraction of 1.0% and an anisotropic blood vessel volume fraction of 1.0%. The resulting CA concentrations are 0.3, 2.6, 6.6 and 7.6 mM. The anisotropic part was simulated assuming four parallel vessels of equal radius.

Discussion

We found a strong relationship between WM fibre orientation measured with DTI and perfusion parameters measured with gradient echo DSC imaging while the temporal perfusion parameters MTT and Tmax showed only slight orientation dependency. The most likely explanation for this phenomenon consistent with current scientific knowledge and with our numerical simulations is that a considerable proportion of the vascular network in WM runs in parallel with the fibre tracts that are mapped with the DTI scan. The measured data are in good agreement with our numerical simulations of an isotropic vascular network combined with blood vessels that run in parallel with the WM fibres. Simulations for the isotropic background alone were not able to explain the angle dependency. Simulations for a single vessel or a few vessels running in parallel, on the other hand, were not able to explain the CA-dependent offset in ${\text{R}}_2^{*}$ encountered in the measured data. The measurements and the simulations suggest that a considerable fraction of blood is contained within vessels that have a net orientation parallel to the WM bundles.

For small angles and for single vessels parallel to the WM, the changes in ${\text{R}}_2^{*}$ are marginal, which can be explained by the very small volume fraction occupied by the vessel. Since the extravascular field inhomogeneities are very weak at small angles, there is no magnifying glass effect that accelerates the signal decay. Moreover, due to the short T2 relaxation inside the vessel in the presence of a CA, there is not much signal left at 40 ms to annihilate extravascular signal. This signal cancellation means that the venous vessels without CA may result in a lower signal at 40 ms than the vessels with CA (and the arterial vessels). For larger angles, the extravascular inhomogeneities occupy large volume fractions of a voxel, even if the vessel is small, leading to an increase in ${\text{R}}_2^{*}$ irregardless whether the intravascular signal has undergone significant decay or not. Similar effects have been described for single vessels in the SWI literature.^4,5

WM vasculature has been described histologically, with positron emission tomography (PET) and with MRI. Histologically, vascular density in WM was shown to be reduced compared to GM.²⁸ Studies using PET, the gold standard, report CBV of 2.6 ml/100 g in WM and 4.6 ml/100 g in GM.²⁹ Using MRI, Jochimsen et al. showed that vessel density in WM is about half of the density in GM and that the average vessel radius is about 13.5 µm in both GM and WM.²⁵ Using spin echo DSC, Helenius et al.³⁰ reported a CBV of 1.3 ml/100 g tissue for WM and 4.6 ml/100 g tissue for GM, while Arakawa et al. reported a CBV of 1.44 ml/100 g tissue for normal WM and 1.86 ml/100 g tissue for normal GM.³¹ However, both studies did not report on potential anisotropy of WM vasculature. The work by Nonaka and colleagues presents some spectacular images on the vascular anatomy of the subcortical and deep WM.^9,10 These authors report large blood vessels passing through the cortex and continuing through the WM towards the ventricular angle. Figure 1 in Nonaka et al.⁹ shows considerable anisotropy for larger vessels in the WM, whereas the GM exhibits a more isotropic vascular tree. Blood vessel anisotropy in WM was also reported in a rodent model of ischaemia.¹¹

The numerical simulation of susceptibility and relaxation effects of the CA on the MRI signal for different geometries was able to explain the effects of tissue (i.e. vessel) orientation on the DSC signal. Only a combination of an isotropic background and anisotropic vessels was able to explain the observed changes in signal with changing tissue orientation. The simulation was kept simple in the sense that it was performed for two-dimensional voxels and that it did not take the effects of diffusion or extravasation of CA into account. Semmineh et al. also showed that $\Delta {\text{R}}_2^{*}$ is affected by vascular tree heterogeneity, but the extent of this effect and the details of it haven't been studied so far.³² Already a simple geometry of one vessel inside a voxel, surrounded by WM is able to describe the effect of the vessel orientation quite well. After including more parameters, the simulation is close to what we observe in vivo. The interactions of numerous arrangements of vessels and the interactions of their magnetic field inhomogeneities lead to a wide range of $\Delta {\text{R}}_2^{*}$ curves. Three main parameters have a major influence on the $\Delta {\text{R}}_2^{*}$ curve: the CA concentration, and the BVFs of the oriented vessels and of the isotropic background. The total BVF obtained by fitting the numerical simulations to the data was 2% and the CA concentration range was between 0 and 7.6 mM^27,33 which is in good agreement with the values reported in the literature.²⁹

In addition to the considerable angle dependency in $\Delta {\text{R}}_2^{*}$, we also demonstrated that CBF and CBV depend strongly on WM fibre orientation. There may be two reasons that this orientation dependency of CBF and CBV has remained unnoticed. First, upon visual inspection, the contrast on these maps is dominated by the differences between grey and WM. Second, the orientation dependency becomes apparent when voxels with the same angle are pooled together from the entire brain.

Our findings have far-reaching consequences for gradient echo-based perfusion mapping of WM. The results of previous studies may have to be interpreted with caution. For instance, comparisons to contralateral WM would have to be controlled for the presence and orientation of venous vessels.³⁴

In contrast to the CBV and CBF parameters, only minimal influence of the tissue orientation was found for the temporal parameters Tmax and MTT. This finding can be explained by the fact that tissue orientation has an effect on the magnitude of the measured signal but doesn't lead to a dispersion or delay of the CA bolus. This conclusion is especially relevant for the image-based analysis of patients with an acute ischaemic stroke where DSC PWI is typically used to determine the tissue at risk of infarction using the Tmax parameter.³⁵ Thus, it can be argued that no correction for tissue orientation is necessary for Tmax and MTT and the established procedure as well as findings of previous studies using the Tmax or MTT parameter are not affected by differences in tissue orientation.

In the present study, there were large differences in CBV and CBF between subjects. These may be due to imperfect measurements of AIF, due to actual physiological differences, or due to orientation dependency of the AIF itself.^36–38 The cohort consisted of patients with multiple sclerosis of various disease duration and severity as well as different WM lesion load. These factors likely play a role in the observed differences. Nevertheless, the relative changes associated with tissue orientation are still comparable between the subjects (see Figure 4) so that it can be argued that the absolute differences between subjects have no influence on the general findings of this study. It should be noted that we did not normalize the perfusion measurements on a patient per patient basis. Our cohort was too small to perform a systematic analysis and comparison with clinical presentation. However, the orientation-dependent analysis of DSC data in MS presented here may become an interesting avenue of future research into the vascular aspects of the disease.³⁹ Changes in blood flow are a major consequence of inflammation.^40,41 The analysis presented herein may reveal differences in perfusion in patients with MS that are masked by the orientation dependency of CBF and CBV.

Our findings also have implications for functional MRI (fMRI) of WM, an emerging field of research.⁴² WM fMRI is known to suffer from very low signal to noise due to the much smaller vascular volume in WM compared to GM. Our finding that CA-related changes are twice as large for WM perpendicular to B₀ compared to WM parallel to B₀ can be translated directly to the BOLD of the MRI signal. The BOLD sensitivity in tracts parallel to the main magnetic field may be much smaller than the sensitivity in tracts that run perpendicular to B₀, for instance in the corpus callosum. Since the sensitivity is already very low in WM in general, it is likely that WM fMRI suffers from false negatives in WM bundles parallel to B₀. A solution for this problem may be to use spin echo fMRI at very high field strengths of 7T and above in order to mitigate orientation effects and while having sufficient SNR.

Wong et al. observed that the whole brain histograms of CBF were much broader for gradient echo DSC than for spin echo DSC and 3D pseudo-continuous arterial spin labelling.⁴³ The orientation dependency observed in the present study may be an explanation for this observation.

The data were acquired in patients with multiple sclerosis. There may be subtle quantitative differences in the observed effect between patients and healthy subjects. However, if MS was the cause of this strong orientation effect, it would have to cause a dramatic reorganization of the vascular architecture throughout the brain's WM. There are no reports of such reorganization in the MS literature. Moreover, it has been shown previously that both people with MS and healthy controls exhibit a considerable orientation-dependent behaviour in ${\text{R}}_2^{*}$.²² Furthermore, the MS group in that study showed the same behaviour independently whether lesion tissue was included in the analysis or not. Moreover, DSC studies in MS showed that both CBF and CBV differ by about 10–20% between the WM of patients and controls,⁴⁴ which is much smaller than the orientation-dependent effect observed in the present study. Finally, considerable vascular anisotropy has been reported in healthy WM tissue.¹⁰ In summary, while there may be quantitative differences between patient groups and healthy subjects, there is no evidence that suggests that this effect may be absent in healthy people.

There are also several simplifications for the numerical simulation. We did not model for potential CA leakage or for changes in T1 due to the CA. Leakage is present in enhancing lesions (none of the subjects in this study had an enhancing lesion) but it may also be present below the detection threshold of the MRI scan used to identify enhancing lesions. However, the total volume of enhancing MS lesions is small compared to the total WM volume. Only 2D voxels were simulated although in real experiments 3D voxels with higher in-plane resolution and thick slices are usually used. For an axial acquisition this means that vessels parallel to B₀ occupy a larger volume fraction than vessels at larger angles to B₀. Only a limited number of background vessels at different orientations and with different angles were simulated. With a range of numbers of vessels in a 3D voxel, the simulations become computationally very expensive. Finally, the simulations assumed the same vascular architecture across the entire brain. In real life both the background and the volume fraction of the anisotropic component should vary across the large number of voxels. In some voxels there may not be any anisotropic vessels, whereas in other voxels a larger number of small parallel vessels may be present. In the experiment a large number of these scenarios get averaged into a final result. Moreover, blood oxygenation effects were ignored in the current simulation. While arterial vessels carry almost fully oxygenated blood, oxygenation in venous vessels is around 60%, resulting in paramagnetic properties already at baseline. However, the angle dependency is very small at baseline compared to the situation when CA is present (Figure 2). Since the total venous cross section is larger than the total arterial cross section, all vessels were assumed to be veins with a blood oxygenation of 0.6. It should be noted, however, that even without CA, there is a small angle dependency.^17,22,45 This angle dependency in the absence of a CA has been ascribed to the properties of the myelin sheath. However, the data presented here suggest, that components of venous vasculature that run in parallel with the WM bundles also play a role. Another limitation is that we only investigated WM. It has been shown previously that the BOLD effect also depends on the orientation of the cortex,¹² suggesting that DSC in the cortical grey matter also exhibits considerable orientation dependency. At 2.4 s, the repetition time of the DSC scan was rather long, which may have an effect on the measurement of the perfusion parameters. The main finding presented here, however, is based on the raw $\Delta {\text{R}}_2^{*}$ curves and low temporal resolution does not limit the finding of an angle dependency in the gradient echo DSC signal. A potential source of error is change in head orientation between the DTI and the DSC scan, which cannot be corrected for by image registration. However, the error due to typical head rotation is still small compared to the large differences in $\Delta {\text{R}}_2^{*}$ between parallel and perpendicular fibres.

In conclusion, there is a strong angle dependency of the apparent change in ${\text{R}}_2^{*}$, CBF and CBV measured with gradient echo DSC, while temporal perfusion parameters are not significantly affected. The effect is likely due to a disruption of the symmetry of the vascular bed by blood vessels with a preferred direction. The angle dependency may have important implications for the interpretation of gradient echo-based DSC and fMRI of WM.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: EHT and VW are supported by the Milan and Maureen Ilich Foundation and NSERC. AR is supported by Canada Research Chairs. VW is supported by the Multiple Sclerosis Society of Canada. NK was supported by the DAAD RISE program. Data acquisition was funded by CIHR.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Authors' contributions

EH-T: data analysis, interpretation of results, manuscript editing NK: data analysis, interpretation of results, manuscript editing N-DF: data analysis, interpretation of results, manuscript editing LW: data analysis, interpretation of results VW: interpretation of results, manuscript editing MD: data analysis DL: study design, interpretation of results, manuscript editing LM: study design AT: study design AR: idea, study design, study supervision, interpretation of results, manuscript writing