Bridging computational approaches to speech production: The semantic–lexical–auditory–motor model (SLAM)

Abstract

Speech production is studied from both psycholinguistic and motor-control perspectives, with little interaction between the approaches. We assessed the explanatory value of integrating psycholinguistic and motor-control concepts for theories of speech production. By augmenting a popular psycholinguistic model of lexical retrieval with a motor-control-inspired architecture, we created a new computational model to explain speech errors in the context of aphasia. Comparing the model fits to picture-naming data from 255 aphasic patients, we found that our new model improves fits for a theoretically predictable subtype of aphasia: conduction. We discovered that the improved fits for this group were a result of strong auditory-lexical feedback activation, combined with weaker auditory-motor feedforward activation, leading to increased competition from phonologically related neighbors during lexical selection. We discuss the implications of our findings with respect to other extant models of lexical retrieval.

Speech production has been studied from several theoretical perspectives, including psycholinguistic, motor control, and neuroscience, often with little interaction between the approaches. Recent work, however, has suggested that integration may be productive, particularly with respect to applying computational principles from motor control, such as the combined use of forward and inverse models, to higher-level linguistic processes (Hickok, 2012, 2014a, 2014b). Here we explore this possibility in more detail by modifying Foygel and Dell’s (2000) highly successful psycholinguistic, computational model of speech production, using a motor-control-inspired architecture, and assess whether the new model provides a better fit to data and in a theoretically interpretable way.

We first present the theoretical foundations for this work by (1) describing the motivations behind Foygel and Dell’s (2000) semantic–phonological model (SP), (2) briefly summarizing the motor-control approach, (3) highlighting some principles from our recent conceptual attempt to integrate the approaches, and (4) describing our modification of SP using a fundamental principle from motor-control theory to create our new semantic–lexical–auditory–motor model (SLAM). We then present the computational details of both the SP and SLAM models, along with simulations comparing SP with SLAM. To preview the outcome of these simulations, we found that SLAM outperforms SP, particularly with respect to a theoretically predictable subcategory of aphasic patients. We conclude with a discussion of how the new model relates to some other extant models of word production.

The SP model

SP has its roots in Dell’s (1986) theory of retrieval in sentence production, which was developed to account for the speech errors, or slips of the tongue, found in large collections of natural speech. To this end, the theory integrated psychological and linguistic concepts: From psychology it adopted the notion of computational simultaneity, in which multiple internal representations compete for selection prior to production, and from linguistics it incorporated hierarchical levels of representation, as well as the separation at each level between stored lexical knowledge and the applied generative rules.

Dell, Schwartz, Martin, Saffian, and Gagnon (1997) proposed a computational model that limited the focus to single-word production, but extended the theoretical scope to include explanations of speech errors in the context of aphasia. The basic idea was that the pattern of aphasic speech errors reflects the output of a damaged speech production system, which could be modeled by adjusting parameters in the normal model to fit aphasia data. The model’s architecture consisted of a three-layer network with semantic, lexical, and phonological units, and the connections among the units were selected by the experimenters to approximate the structure of a typical lexical neighborhood (Fig. 1). Word production was modeled as a spreading-activation process, with noise and decay of activation over time. Damage was implemented by altering the parameters that control the flow of activation between representational levels. Simulations were then used to identify parameter values that generated frequencies of error types that were similar to those made by aphasic patients.

Fig. 1.

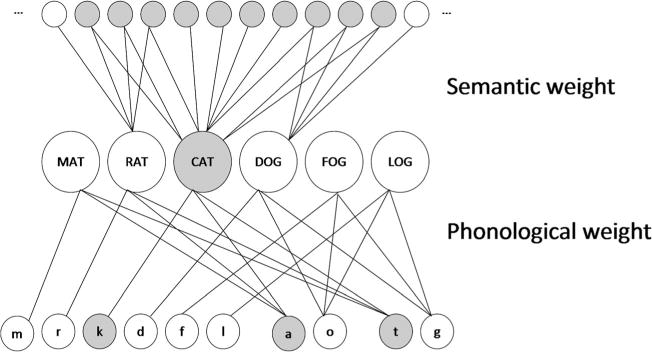
The semantic-phonological (SP) model architecture

Due to the computationally intensive nature of the simulation method, however, comprehensive explorations were effectively limited to only two parameters at a time. Nevertheless, in a series of articles beginning with Foygel and Dell (2000), two free parameters in the model were identified that account for an impressive variety of the data derived from a picture-naming task, including clinical diagnostic information (Abel, Huber, & Dell, 2009), lexical frequency effects (Kittredge, Dell, Verkuilen, & Schwartz, 2008), characteristic error patterns associated with different types of aphasia (Schwartz, Dell, Martin, Gahl, & Sobel, 2006), characteristic patterns of recovery (Schwartz & Brecher, 2000), and interactive error effects (Foygel & Dell, 2000). These two free parameters were the connection strengths between semantic and lexical representations (the s-weight) and between lexical and phonological representations (the p-weight), an architecture known as SP. SP has been used to explain performance on other tasks, as well, such as word repetition (Dell, Martin, & Schwartz, 2007), and to predict the location of neurological damage seen in clinical imaging (Dell, Schwartz, Nozari, Faseyitan, & Branch Coslett, 2013), although here we will focus primarily on its relevance to picture-naming errors.

SP pertains specifically to computations that occur between the semantic and phonological levels. It is assumed that the output of the model is a sequence of abstract phonemes that must then be converted into motor plans for controlling the vocal tract. We next turn to some fundamental constructs that have come out of research on how motor effectors are, in fact, controlled.

Motor-control theory

At the broadest level, motor control requires sensory input to motor systems for initial planning and feedback control. It requires input for planning to define the targets of motor acts (e.g., a cup of a particular size and orientation and in a particular location relative to the body) and to provide information regarding the current state of the effectors (e.g., the position and velocity of the hand relative to the cup). Without sensory information, action is impossible, as natural (Cole & Sedgwick, 1992; Sanes, Mauritz, Evarts, Dalakas, & Chu, 1984) and experimental (Bossom, 1974) examples of sensory deafferentation have demonstrated. Sensory information has also been shown to provide critical feedback information during movement (Wolpert, 1997; Wolpert, Ghahramani, & Jordan, 1995), which provides a mechanism for error detection and correction (Kawato, 1999; Shadmehr, Smith, & Krakauer, 2010). When precise movements are performed rapidly, however, as in speech production, feedback mechanisms may be unreliable, due to feedback delay or a noisy environment. In this case, a state feedback control system can be supplemented with forward and inverse models (Jacobs, 1993), enabling the use of previously learned associations between motor commands and sensory consequences to guide the effectors toward sensory goals. This arrangement implies that the motor and sensory systems are tightly connected, even prior to online production or perception.

In the case of speech, the most critical sensory targets are auditory (Guenther, Hampson, & Johnson, 1998; Perkell, 2012), although somatosensory information also plays an important role (Tremblay, Shiller, & Ostry, 2003). Altered auditory feedback has been shown to dramatically affect speech production (Houde & Jordan, 1998; Larson, Burnett, Bauer, Kiran, & Hain, 2001; Yates, 1963), and changes in a talker’s speech environment can lead to “gestural drift”—that is, changes in his or her articulatory patterns (i.e., accent; Sancier & Fowler, 1997). Additionally, neuroimaging experiments investigating covert speech production have consistently reported increased activation in auditory-related cortices in the temporal lobe (Callan et al., 2006; Hickok & Buchsbaum, 2003; Okada & Hickok, 2006).

Some particularly relevant evidence for the role of the auditory system in speech production has come from neuropsychological investigations of language. Striking patterns of impaired and intact language-processing abilities resulting from neurological injury have led theorists to propose separate auditory and motor speech representations in the brain (Caramazza, 1991; Jacquemot, Dupoux, & Bachoud-Lévi, 2007; Pulvermüller, 1996; Wernicke, 1874/1969). Patients with conduction aphasia (Goodglass, 1992), for example, have fluent speech production, suggesting preserved motor representations. These patients also have good auditory comprehension and can recognize their own errors, suggesting spared auditory representations. Despite these abilities, they make many phonemic errors in production and have trouble with nonword repetition. This pattern is typically explained as resulting from damage to the interface between the separate auditory and motor systems (Anderson et al., 1999; Geschwind, 1965; Hickok, 2012; Hickok et al., 2000). This point regarding conduction aphasia has important theoretical implications, as we discuss below.

Conceptual integration

The hierarchical state feedback control (HSFC; Hickok, 2012) model provides a theoretical framework for the integration of psycholinguistic notions with concepts from biological motorcontrol theory. This conceptual framework is organized around three central principles. The first is that speech representations have complementary encodings in sensory and motor cortices that are activated in parallel during speech production, all the way up to the level of (at least) syllables. The second principle is that a particular pattern of excitatory and inhibitory connections between the sensory and motor cortices, mediated by a sensorimotor translation area, implements a type of forward/inverse model that can robustly guide motor representations toward sensory targets, despite the potential for errors in motor program selection during early stages of motor planning/activation. The third principle is that the sensorimotor networks supporting speech production are hierarchically organized, with somatosensory cortex processing smaller units on the order of phonemes (or more accurately, phonetic-level targets such as bilabial closure, which can be coded as somatosensory states), and auditory cortex processing larger units on the order of syllables (i.e., acoustic targets). A schematic of the HSFC framework is presented in Fig. 2; it is clear that the top portion (darker colors) embodies the two steps of SP but breaks down the phonological component into two subcomponents, an auditory–phonological network and a motor–phonological network. This conceptual overlap has inspired our creation of a new computational model that is directly related to the first principle and is partially related to the other two principles. We reasoned that the architectural assumptions of the HSFC model can be evaluated, in part, by integrating them with an established and successful computational model of naming, SP; if the architectural changes led to improved modeling performance, this would provide support for the new framework.

Fig. 2.

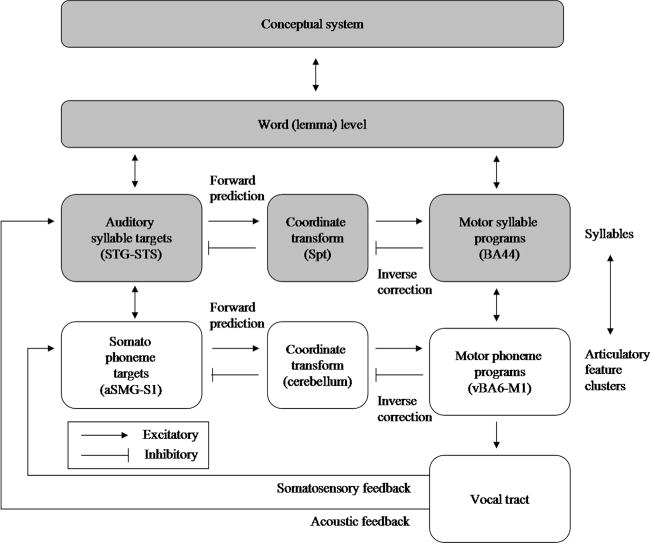
A schematic diagram of the hierarchical state feedback control (HSFC) framework (Hickok, 2012)

The SLAM model

SLAM is a computational model of lexical retrieval that divides phonological representations into auditory and motor components (Fig. 3). The dual representation of phonemes directly follows from the first HSFC principle. The choice to label the sensory units as auditory representations is motivated by the third principle—specifically, that this level of coding is larger than the phonetic feature. Neither SP nor SLAM includes inhibitory connections, and thus the second HSFC principle is not directly implemented; however, the pattern of connections in the SLAM model does implement a type of forward/inverse model that can reinforce potentially noisy motor commands. Our goal here was to modify the computational assumptions of SP as little as possible in order to assess the effects of the architectural assumption of separate motor and sensory phonological representations.

Fig. 3.

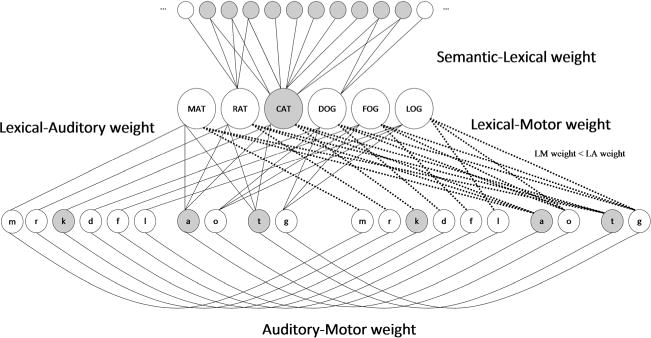
The semantic–lexical–auditory–motor (SLAM) model architecture

During picture-naming simulations, activation primarily flows from semantic to lexical to auditory to motor units— hence the model’s acronym, SLAM. There is also a weaker, direct connection between lexical and motor units. The existence of this lexical–motor connection acknowledges that speech production may occur via direct information flow from lexical to motor units, an assumption dating back to Wernicke (1874/1969), which is needed to explain preserved fluency and spurts of error-free speech in conduction aphasia. However, the connection is always weaker than the lexical–auditory route (again, Wernicke’s original idea), motivated by several points. First, the auditory–lexical route is presumed to develop earlier and to be used more frequently than the lexical–motor route. Longitudinal studies have shown that children begin to comprehend single words several months before they produce them, and they acquire newly comprehended words at nearly twice the rate of newly produced words (Benedict, 1979). Second, motor-control theory dictates that motor plans are driven by their sensory targets. During development, the learner must make reference to auditory targets, in order to learn the mapping between speech sounds and the motor gestures that reproduce those sounds (Hickok, 2012; Hickok, Houde, & Rong, 2011). Third, in the context of aphasia, comprehension deficits tend to recover more than production deficits (Lomas & Kertesz, 1978), suggesting a stronger association between lexical and auditory–phonological representations.

The assumption that the lexical-auditory mapping is always stronger than the lexical–motor mapping has an important consequence: It means that the SLAM model is not merely the SP model with an extra part; in fact, there is effectively zero overlap in the parameter spaces covered by SP and SLAM. The reason for this is as follows. Given the SLAM architecture shown in Fig. 3, it is clear that one could implement SP simply by setting the connection weights in the lexical–auditory and auditory–motor mappings to zero and letting the lexical–motor weights vary freely. This would make SP a proper subset of SLAM, allowing SLAM to cover a parameter space (and therefore fits to data) identical to that of SP. However, this architectural possibility was explicitly excluded by implementing our assumption that lexical–auditory weights are always stronger than lexical–motor weights: If the lexical–auditory weights are zero, then the lexical–motor weights must also be zero and cannot vary freely—thus effectively excluding the parameter subspace used by SP. This further allows us to test SLAM’s assumption that the lexical-auditory route is the primary one used in naming. We can also examine model performance with the opposite constraint—namely, when the lexical-auditory weights are always less than the lexical–motor weights—a variant we might call “SLMA” to reflect the lexical–motor dominance and that would include SP parameter space as a subset. SLAM and SLMA have the same numbers of free parameters, both of which are more than that of SP, but with different assumptions regarding the connection strength patterns. If SLAM were to do better than SLMA, even though SLMA implements SP as a proper subset of its parameter space, it would demonstrate that the primacy of the lexical–auditory route is not only theoretically motivated, but also necessary for the observed improvements.

To summarize, we hypothesized that SLAM would characterize deficits in the general aphasia population at least as well as SP, and would primarily benefit the modeling of conduction aphasia. Recall that conduction aphasia is best explained as a dysfunction at the interface between auditory and motor speech representations that affects the phonological level, in particular (Hickok, 2012; Hickok et al., 2011). Thus, a naming model that incorporates a mapping between auditory–phonological and motor–phonological representations should provide a better fit for speech errors resulting from dysfunction in this mapping. To test this hypothesis, we compared the SP and SLAM model fits to a large set of aphasic picture-naming data.

Computational implementation

Patient data

All data were collected from the Moss Aphasia Psycholinguistic Project Database (Mirman et al., 2010; www.mappd.org). The database contains deidentified data from a large, representative group of aphasic patients, including responses on the Philadelphia Naming Test (PNT; Roach, Schwartz, Martin, Grewal, & Brecher, 1996), a set of 175 line drawings of common nouns. All patients in the database had postacute aphasia subsequent to a left-hemisphere stroke, without any other diagnosed neurological comorbidities, and they were able to name at least one PNT item correctly. We analyzed the first PNT administration for all patients in the database with the demographic information available, including aphasia type and months postonset (N=255). The cohort consisted of 103 anomic, 60 Broca’s, 46 conduction, 35 Wernicke’s, and 11 other aphasics with transcortical sensory, transcortical motor, postcerebral artery, or global etiologies. The median months poststroke was 28 [1, 381], and the median PNT percent correct was 76.4 [1, 99].

Computational models

As we mentioned above, SP was first presented by Foygel and Dell (2000). The model’s approach to simulating picture naming instantiates an interactive, two-step, spreading-activation theory of lexical retrieval and consists of a three-layer network, with individual units representing semantic, lexical, and phonological symbols (Fig. 1). The number of units and the pattern of connections are intended to approximate the statistical probabilities of speech error types in English, by implementing the structure of a very small lexical neighborhood consisting of only six words, one of which is the target. The model includes six lexical units, with each connected to ten semantic units representing semantic features. Semantically related words share three semantic units, meaning that on a typical trial, with only one word that is semantically related to the target, the network has a total of 57 semantic units. Each lexical unit is also connected to three phonological units, corresponding to an onset, vowel, and coda. There are ten phonological units total: six onsets, two vowels, and two codas. Words that are phonologically related to the target differ only by their onset unit, and the network always consists of two such words. Finally, the remaining two words in the network are unrelated to the target, with no shared semantic or phonological units. On 20 % of the trials, one phonologically related word is also semantically related, creating a neighbor that has a “mixed” relation to the target.

Simulations of picture naming begin with a boost of activation delivered to the semantic units. Two parameters, S and P, specify the bidirectional weights of lexical-semantic and lexical–phonological connections, respectively. Activation spreads simultaneously between all layers, in both directions, for eight time steps according to a linear activation rule with noise and decay. Then, a second boost of activation is delivered to the most active lexical unit, and activation continues to spread for a further eight time steps. Finally, the most active phonological onset, vowel, and coda units are selected as output to be compared with the target. Production errors occur due to the influence of noise as activation levels decay, which can be mitigated by strong connections. Responses are classified as correct, semantic, formal, mixed, unrelated, or neologism. For a given parameter setting, a multinomial distribution over these six response types is estimated by generating many naming attempts with the model. These distributions may then be compared with those that result from the naming responses produced by aphasic patients.

SLAM retains many of the details of SP, consistent with our aim to primarily assess the effects of the architectural modification. The semantic and lexical units remain unchanged, but there is an additional copy of the phonological units, with one group designated as auditory and the other as motor (Fig. 3). Four parameters specify the bidirectional weights of semantic–lexical (SL), lexical–auditory (LA), lexical–motor (LM), and auditory–motor (AM) connections. The LA and LM connections are identical to the P connections in the SP model, with each lexical unit connecting to three auditory and three motor units, whereas the AM connections are simply one-to-one. Simulations of picture naming are carried out in the same two-step fashion as with SP, with boosts delivered to the semantic and then the lexical units, and phonological selection occurring within motor units.

Fitting data

In order to fit data, the model is evaluated with different sets of parameters that yield sufficiently different output distributions, creating a finite-element map from parameter space to data space, and vice versa. This process involves, first, selecting a set of parameter values (e.g., S and P weights), then generating many naming attempts with the model using that parameter set, in order to estimate the frequency of each of the six types of responses that occur with that particular model setup. Once those frequencies have been determined, that weight configuration becomes associated with the output distribution in a paired list called a map. Each point in the map represents a prediction about the type of error patterns that are possible when observing aphasic picture naming. One way to evaluate a model, then, is to measure how close its predictions come to observed aphasic error patterns. The distance between an observed distribution and the model’s nearest simulated distribution is referred to as the model’s fit for that data point. The root mean squared deviation (RMSD) is an arbitrary but commonly used measure of fit, which can be interpreted as the average deviation for each response type. For example, an RMSD of .02 indicates that the observed proportions deviate from the predicted proportions by .02, on average (e.g., predicted=[.50, .50]; observed=[.48, .52]). Thus, a lower RMSD value indicates a better model fit. Immediately, the question arises of how many points one should generate, and how to select the parameters to avoid generating redundant predictions.

In their Appendix, Foygel and Dell (2000) provided guiding principles for generating a variable-resolution map of parameter space, along with an example algorithm. They noted that the particular choice of mapping algorithm likely would have little impact on the fit results, as long as it yielded a comprehensive search; however, given the inherently high computational cost of mapping, a particular algorithm may affect the map’s maximum resolution in practice. A second algorithm for parameter space mapping was given by Dell, Lawler, Harris, and Gordon (2004), and these maps are considered to be the standard for SP, since they are available online and have been used in subsequent publications. This SP map has 3, 782 points with 10,000 samples at each point and required several days of serial computation to generate. Clearly, the computational cost associated with the mapping procedure represents a considerable bottleneck for developing and testing models. Adding new points to the map improves the chances of a prediction lying closer to an observation, with diminishing returns as the model’s set of novel predictions winnows. As Dell has suggested, because the goal is to find the best fit, adding more points to improve model performance is probably a worthy pursuit (G. Dell, personal communication, July 12, 2013). Moreover, because SLAM has two additional parameters, we needed to modify the mapping procedure to generate maps more efficiently.

We greatly improved efficiency by redesigning the mapping algorithm to take advantage of its inherent parallelism. There are two main iterative steps in the mapping algorithm: point selection and point evaluation. The coordinates of a point in parameter space are defined by a possible parameter setting for the model (point selection), and a corresponding point in data space is defined by the proportions of response types generated with that parameter setting (point evaluation). The point evaluation step is extremely amenable to parallelization, because the simulations involve computations across independent units, independent samples, and independent parameter sets. Point selection, however, required a new approach to foster parallelism: Delaunay mesh refinement.

The Delaunay triangulation is a graph connecting a set of points, such that the circumcircle of any simplex does not include any other points in the set. This graph has many favorable geometric properties, including the fact that edges provide adjacency relationships among the points. The new point selection algorithm takes advantage of these adjacency relationships. Beginning with the points lying at the parameter search range boundaries and their centroid, if the separation between any two adjacent points in parameter space exceeds a threshold distance (RMSD) in data space, their parameter space midpoint is selected for evaluation and is added to the map. These new points are then added to the Delaunay mesh, and the process reiterates until all edges are under threshold. Thus, on each iteration, the point selection algorithm yields multiple points to be evaluated in parallel across the entire parameter search range. Parallel processing was executed on a graphics processing unit (GPU) to further improve efficiency.¹

Before statistically comparing SP’s and SLAM’s performances, we studied the effects of map resolution on the model fits. First, we generated a very high-resolution map for each model using a low RMSD threshold of .01 to encourage continued exploration of the parameter space. Each map included 10,000 samples at each point, and the parameters varied independently in the range [.0001, .04]. The maximum parameter values were selected to be near the lowest values that yielded the highest frequency of correct responses, so that reduced values would lead to more errors. Due to the use of a low mapping threshold, the algorithm was halted before completion, after generating an arbitrarily large number of points. Early termination is not a great concern, because the algorithm efficiently selects points over the full search range. This fact also makes it a trivial matter to reduce the map resolution while still covering the full space.

The mapping procedure generated an initial 31,593 points for the SLAM model, with parameters freely varying; then, in accordance with the SLAM architecture, all points with LM ≥ LA were removed, yielding a SLAM map with 17,786 points. The full SP map had 57,011 points. Next, we created 50 lower-resolution maps for each model by selecting subsets from the larger maps, with logarithmically spaced numbers of points from 5 to 17,000. For each map, we calculated the mean fit for the aphasic patients as a whole and for each of the diagnosis groups, excluding the heterogeneous diagnosis group. Figure 4 plots the fit curves. As we expected for both models, adding points improved the fits with diminishing returns. The relative fit patterns appeared to stabilize around 2,321 points, marked by vertical lines in the figure. We therefore chose to compare SP and SLAM at this map resolution; our findings should apply to any higher-resolution map comparisons, with trends favoring SLAM as resolution increases.

Fig. 4.

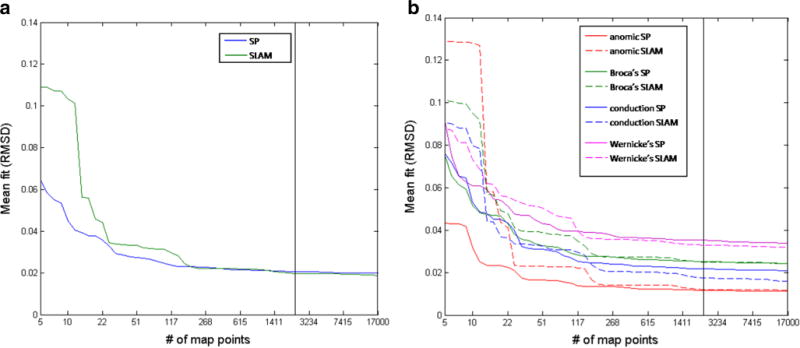
Mean fit curves for (A) all patients and (B) diagnosis groups. The black vertical lines in the panels indicate the maps that were used for statistical comparisons

To compare the new parallel-generated maps with the standard serially generated maps, we also identified a parallel SP map resolution that yielded similar performance in terms of mean and maximum fit to the values reported in Schwartz et al. (2006). For this set of 94 patients, a parallel SP map with 189 points resulted in a mean and a maximum RMSD of .0238 and .0785, as compared with the reported values of .024 and .084, respectively. As expected, the parallel algorithm selected points much more efficiently than the serial algorithm, requiring many fewer predictions to achieve similar performance. We used this lower map resolution as a baseline, to compare the effects of adding points to the standard SP map with the effects of augmenting SP’s structure. Because our fitting routine yielded better fits than the standard SP maps that have been available to researchers online (Dell et al., 2004), we have provided our fitting routine, with adjustable map resolutions, along with our new model, at the following Web address: http://cogsci.uci.edu/~alns/webfit.html

Results

First, we examined our hypothesis that SLAM would fit the data at least as well as SP for the general aphasia population. All analyses were performed using the MATLAB software package. As we mentioned above, we chose to use RMSD as our measure of fit (where a lower value means a better fit). Table 1 provides descriptive statistics of the model fits for the entire sample of patients, as well as for the five subtypes of aphasia. Figure 5 shows a scatterplot comparing the SP and SLAM fits. The solid diagonal line represents the hypothesis that the models are equivalent, and the dotted lines indicate one standard deviation of fit difference in the sample. It is clear that both models do quite well overall, with the majority of patients clustering below .02 RMSD. Although the models tend to produce similar fits in general, it is also clear that a subgroup of patients falls well outside the 1-SD boundaries. The inset in Fig. 5 shows a bar graph comparing the numbers of patients who were better fit (>1 SD) by SP or SLAM, demonstrating that SLAM provides better fits for a subgroup of patients without sacrificing fits in the general population.

Table 1.

Descriptive statistics for SLAM and SP model fits

		SP			SLAM
		S	P	RMSD	RMSD	SL	LM	LA	AM
All N =255	Mean	.0241	.0232	.0194	.0187	.0242	.0152	.0300	.0254
	St. Dev.	.0118	.0075	.0189	.0189	.0121	.0059	.0085	.0135
	Median	.0256	.0224	.0127	.0111	.0250	.0151	.0300	.0300
	IQR	[.0170, .0341]	[.0179, .0281]	[.0071, .0264]	[.0067, .0246]	[.0176, .0347]	[.0113, .0200]	[.0225, .0388]	[.0151, .0388]
	Range	[.0001, .0400]	[.0062, .0400]	[.0010, .1273]	[.0019, .1977]	[.0001, .0400]	[.0026, .0300]	[.0010, .0400]	[.0001, .0400]
Anomic N = 103	Mean	.0299	.0274	.0110	.0115	.0299	.0181	.0308	.0296
	St. Dev.	.0081	.0070	.0095	.0095	.0085	.0054	.0080	.0113
	Median	.0296	.0266	.0082	.0085	.0300	.0176	.0325	.0350
	IQR	[.0241, .0376]	[.0219, .0318]	[.0049, .0137]	[.0056, .0141]	[.0250, .0400]	[.0151, .0200]	[.0250, .0400]	[.0204, .0400]
	Range	[.0054, .0400]	[.0106, .0400]	[.0010, .0654]	[.0019, .0685]	[.0063, .0400]	[.0038, .0300]	[.0101, .0400]	[.0001, .0400]
Broca’s N =60	Mean	.0215	.0218	.0238	.0240	.0217	.0143	.0267	.0266
	St. Dev.	.0125	.0071	.0243	.0250	.0128	.0053	.0088	.0144
	Median	.0205	.0202	.0145	.0149	.0200	.0126	.0250	.0325
	IQR	[.0139, .0334]	[.0174, .0262]	[.0076, .0312]	[.0075, .0300]	[.0144, .0313]	[.0101, .0176]	[.0200, .0350]	[.0188, .0400]
	Range	[.0001, .0400]	[.0075, .0400]	[.0012, .1273]	[.0019, .1292]	[.0001, .0400]	[.0026, .0275]	[.0101, .0400]	[.0001, .0400]
Conduction N =46	Mean	.0245	.0182	.0203	.0157	.0250	.0120	.0323	.0163
	St. Dev.	.0110	.0053	.0153	.0137	.0110	.0048	.0089	.0134
	Median	.0259	.0177	.0175	.0110	.0275	.0126	.0375	.0144
	IQR	[.0020, .0331]	[.0145, .0219]	[.0078, .0282]	[.0063, .0217]	[.0188, .0338]	[.0088, .0138]	[.0250, .0400]	[.0038, .0238]
	Range	[.0001, .0400]	[.0062, .0300]	[.0019, .0720]	[.0028, .0727]	[.0001, .0400]	[.0038, .0275]	[.0101, .0400]	[.0001, .0400]
Wernicke’s N =35	Mean	.0126	.0195	.0332	.0318	.0123	.0115	.0305	.0233
	St. Dev.	.0095	.0059	.0209	.0225	.0096	.0051	.0080	.0130
	Median	.0133	.0193	.0294	.0275	.0126	.0101	.0325	.0250
	IQR	[.0039, .0187]	[.0152, .0248]	[.0155, .0448]	[.0139, .0472]	[.0032, .0185]	[.0076, .0151]	[.0232, .0388]	[.0123, .0350]
	Range	[.0002, .0400]	[.0070, .0327]	[.0042, .0979]	[.0038, .0989]	[.0001, .0400]	[.0038, .0225]	[.0163, .0400]	[.0001, .0400]
Other N = 11	Mean	.0180	.0255	.0275	.0283	.0178	.0173	.0293	.0246
	St. Dev.	.0148	.0073	.0222	.0221	.0148	.0057	.0080	.0123
	Median	.0173	.0257	.0143	.0125	.0176	.0176	.0275	.0275
	IQR	[.0019, .0265]	[.0220, .0301]	[.0087, .0488]	[.0106, .0488]	[.0023, .0250]	[.0151, .0200]	[.0250, .0372]	[.0200, .0319]
	Range	[.0003, .0400]	[.0133, .0400]	[.0049, .0617]	[.0057, .0628]	[.0001, .0400]	[.0076, .0288]	[.0151, .0400]	[.0001, .0400]

Fig. 5.

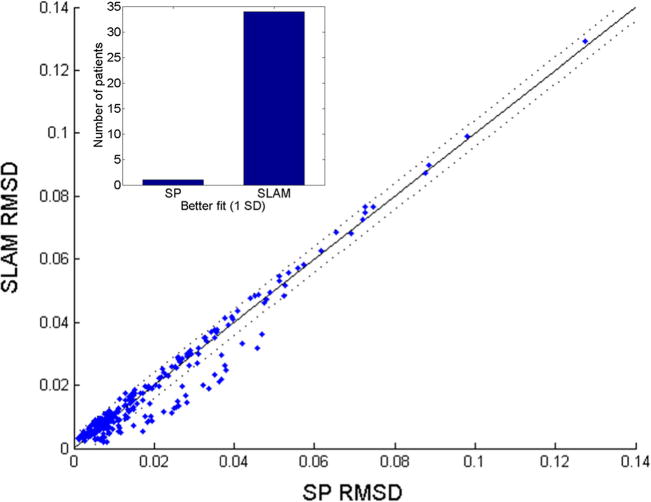
Scatterplot comparing model fits between SP and SLAM. The solid diagonal line represents equivalent fits; the dotted lines represent 1 SD of fit difference in the sample. The majority of patients are fit well by both models, and a subgroup of patients are fit notably better by SLAM (inset)

Next, we examined our hypothesis that SLAM would improve the model fits specifically for conduction aphasia. Figure 6 displays the RMSD differences between the models for individual patients, grouped by aphasia type; positive difference values indicate improved fits for SLAM over SP. It is clear that the SLAM model provides the largest and most consistent fit improvements for the conduction group, and a majority of the fits for Wernicke’s patients also benefit from the new model. The fact that Wernicke’s aphasia was also better fit by SLAM is consistent with the HSFC theory. Wernicke’s aphasia is associated with neuroanatomical damage very similar to that of conduction aphasia, and acute Wernicke’s aphasia often recovers to be more like a conduction profile, suggesting a partially shared locus of impairment. For a statistical comparison of the fit improvements between the five aphasia subtypes, we performed a one-way analysis of variance (ANOVA) on the RMSD changes, which indicated at least one significant difference between the group means (p < .001). A follow-up multiple comparison test indicated that the conduction group benefited more from SLAM than any other group, since the 95 % confidence interval for the mean fit improvement did not overlap with that of any other group, including Wernicke’s.

Fig. 6.

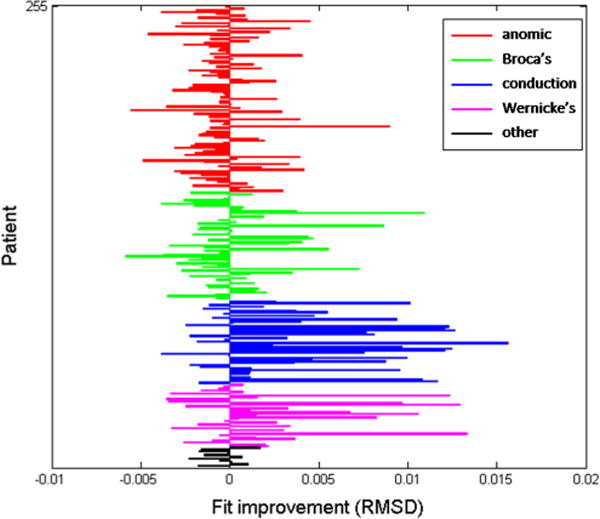
Individual fit changes between the SP and SLAM models. Positive values indicate better SLAM fits

To further validate these results, we tested whether fit improvements due to increasing the SP map resolution specifically favored any of the diagnosis groups. Unlike our theoretically motivated structural changes, this method of improving model fits was not expected to favor any particular group. We compared the model fits for an SP map with 189 points, which on average is equivalent to the standard SP map in the literature, to the higherresolution SP map with 2,321 points. For the group of 255 patients, increasing the number of SP map points significantly improved the average fit from .0230 RMSD to .0206 RMSD (p < .001). The improvement in fit was significant for all diagnosis groups (all ps < .001); however, a one-way ANOVA with follow-up multiple comparison tests showed that no group had significantly greater improvement than every other group (no disjoint confidence intervals), unlike the result produced by our structural changes, which specifically favored the conduction group. Instead, the Wernicke’s group improved most, whereas the anomic group improved least, consistent with the observation that these groups are already the worst and best fits for SP, respectively. The implication is that the improvements in fit caused by our theoretically motivated manipulation of the SP model’s architecture are qualitatively different from the improvements gained by other methods.

We also hypothesized that the conduction naming pattern should be fit by a particular SLAM configuration: strong LA and weak AM weights. For the patients who exhibited the greatest improvements in fit, this was indeed the case. Figure 7 uses boxplots to display the SLAM weight configurations for the 20 patients (13 conduction, five Wernicke’s, one anomic, one Broca’s) who exhibited the greatest fit improvements (>2 SDs). Figure 8 shows data from an example patient with conduction aphasia, along with the corresponding SP and SLAM model fits. The best-fitting weights in the SP model were .022 and .017, for S and P, respectively. The SLAM model for this patient yielded .023 and .013 for SL and LM, respectively, whereas the LA weight was maximized at .04, and the AM weight was minimized at .0001. For this patient, SLAM reduced the SP fit error by .0135 RMSD. This example also illustrates that SLAM’s largest fit improvements over SP are accompanied by a consistent increase in the predicted frequency of formal errors, along with a consistent decrease in semantic (and in unrelated) errors. This trade-off in formal errors for semantic errors is most likely to occur at the first, lexical-selection step. The dual nature of formal errors, that they can occur during either lexical or phonological selection, is one of the hallmarks of the SP model. Foygel and Dell (2000) showed that formal errors during lexical selection increase when phonological feedback to lexical units outweighs the semantic feedforward activation. In conduction aphasia, large LA weights provide strong phonological feedback to lexical units, whereas small AM and LM weights provide weak phonological feedforward to the motor units. With LM greater than AM, more activation flows from the incorrect, phonologically related lexical items, thereby increasing formal errors at the expense of semantic errors. The implication, that strong auditory–phonological feedback influences lexical selection in conduction aphasia, represents a novel prediction of our model that is supported by the data.

Fig. 7.

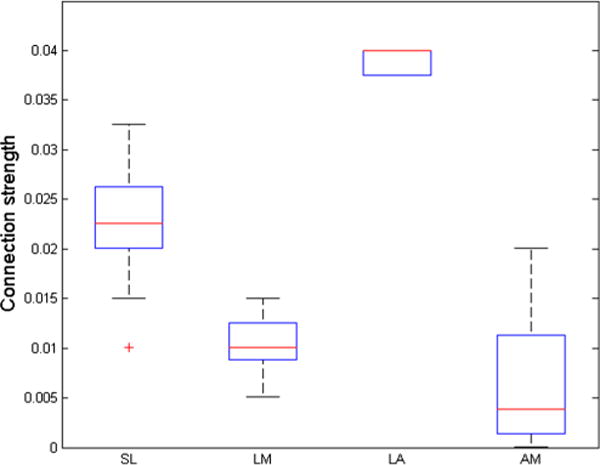
Boxplots showing the SLAM weights for the group of 20 patients with the greatest fit improvements. As expected, a model profile with high lexical–auditory and low auditory–motor weights leads to the greatest improvements over the SP model

Fig. 8.

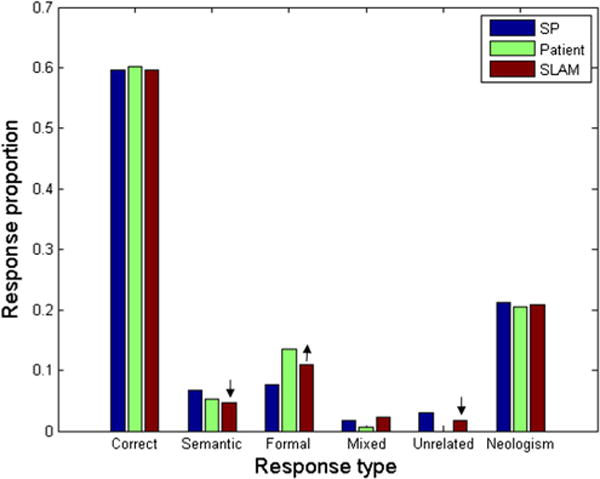
Naming response distribution from an example patient with conduction aphasia, along with the corresponding SP and SLAM model fits. Arrows indicate how SLAM improves the fit to data, by increasing formal at the expense of semantic and unrelated errors. The SLAM model reduced the fit error for this patient by .0135 RMSD

Finally, we tested the criticality of our assumption that LA weights must be greater than LM weights. We repeated our original analysis, this time comparing SP to SLMA, an alternative version of SLAM that has lexical–motor dominance instead of lexical–auditory dominance. SLMA was fit with a four-parameter map with 2,321 points, the same size as the SLAM map, culled from the 13,807 discarded SLAM points, ensuring that LM weights were always greater than or equal to the LA weights. Figure 9 is a scatterplot comparing the SP and SLMA model fits; the diagonal lines are the same as those in Fig. 5. When this alternative model architecture was used, there were no noticeable improvements over SP; the maximum change in fit was only .0038 RMSD. Thus, the mere presence of additional parameters in SLAM was not what caused the observed fit improvements; their theoretically motivated arrangement was necessary, as well.

Fig. 9.

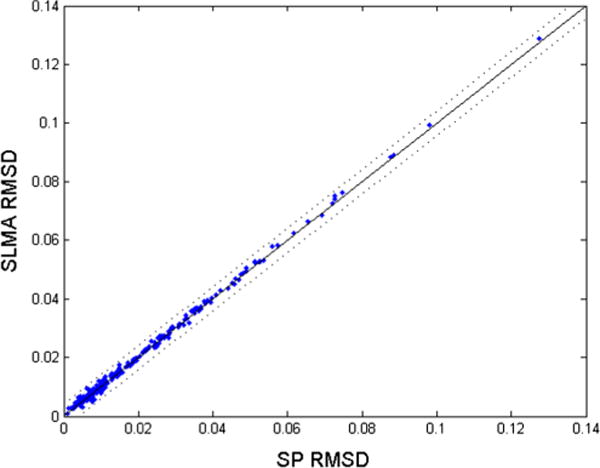
Scatterplot comparing model fits between SP and the semantic–lexical–motor–auditory (SLMA) model, an alternative architecture with the same number of parameters as SLAM, but with lexical–motor dominance instead. The lines are the same as in Fig. 5. Unlike SLAM, SLMA provides no obvious fit improvements over SP

We also explored the necessity of the LM weights, testing the importance of our two routes. We fixed the LM weights at .0001 (effectively zero) by using 323 points from the full SLAM map to fit the data, thus yielding a three-parameter model, and we compared these fits with the fits from an SP map that had the same number of points. This three-parameter model that lacked direct LM connections did much worse than the two-parameter SP model, yielding an average fit of .10 RMSD. This catastrophic failure was due to the fact that not enough activation reached the motor units via the lexical–auditory–motor route. Recall that activation is multiplied by a fraction at each level, yielding lower activation after two steps through the lexical–auditory–motor route than after the one-step lexical–motor route. Without the combined inputs to motor units from the two routes, the model could only produce a maximum estimate of 65 % correct responses. Although HSFC theory does predict that direct lexical–motor connections are required for normal levels of correctness, the weaker input to motor units from the auditory–motor route raises the concern that our initial choice of SLAM parameter constraints gave more prominence to the lexical–motor route than the HSFC theory warrants. We therefore explored the SLAM parameter space further, and we discovered alternative parameter constraints that yielded qualitatively similar results: In the “healthy model,” the SL and LA weights have the usual maximum value of .04, whereas the LM weights have a maximum of .02, and AM weights have a maximum of .5; in aphasia, the parameters are free to vary below those values. This parameter arrangement ensures that the primary source of phonological feedback to the lexical layer is usually from auditory units, enables the auditory–motor route to provide strong activation to motor units during naming, and removes the previous constraint that in damaged states, the LM weights must always be lower than the LA weights. As with the original choice of SLAM parameter constraints, we observed fits similar to that of SP in the general population (Fig. S1), with noticeable improvements for the conduction naming pattern (Fig. S2), accompanied by high LA and low AM weights. With this alternative arrangement, a three-parameter model with LM weights fixed at .0001 still does not perform as well as the two-parameter SP model (Fig. S3), although the failure is no longer catastrophic, due to compensation by strong AM weights. To summarize, these investigations confirm our main finding that a second source of phonological feedback, predicted by HSFC theory to come from the auditory system, is the critical component for improving model fits.

Discussion

We put forward a new computational model of naming, SLAM, inspired by a recent conceptual model, HSFC, aimed at integrating psycholinguistic and motor-control models of speech production. SLAM implemented the HSFC claims that sublexical linguistic units have dual representations within auditory and motor cortices, and that the conversion of auditory targets to motor commands is a crucial computation for lexical retrieval, even prior to overt production.

We showed that augmenting the well-established SP model to incorporate auditory-to-motor conversion into the lexical-retrieval process allowed the model to explain general aphasic naming errors at least as well as the original SP model, while improving the model’s ability to account for conduction naming patterns in particular. The improvements in model fits were predicted to result from parameter settings with strong LA and weak AM weights. Examining the naming responses of 255 aphasic patients—the largest analysis of PNT responses to date—we confirmed our predictions, and additionally demonstrated that, unlike our theoretically motivated structural changes, improvements due to added map resolution were not specific to any aphasia type. We also discovered that the predicted weight configuration, which yielded the greatest fit improvements, did so by increasing formal errors at the expense of semantic errors. It is worth noting in this context that Schwartz et al. (2006) identified three anomalous subgroups whose naming patterns significantly deviated from SP’s predictions, one of which exhibited too many formal errors. Two of the patients in this subgroup had conduction aphasia, and the other had Wernicke’s aphasia. SLAM provides a plausible explanation for this subgroup. The increase of formal errors at the expense of semantic errors in conduction aphasia suggests that a significant proportion of their phonologically related errors were generated at the lexical-selection stage, rather than the phonological-selection stage, a novel prediction of our model. We also found that two separate phonological routes were required to produce the effect. Although the auditory–motor integration loop described by HSFC theory currently is not modeled in detail within SLAM, parallel inputs and feedback to separate auditory and motor systems are a prerequisite for state feedback control. The results of our modeling experiments thereby support the assumptions of the HSFC framework.

Although we pitted SP and SLAM against one another, they share many of their essential features. Thus, much of SLAM’s success can be attributed to the original SP model’s assumptions. The notions of computational simultaneity, hierarchical representation, interactivity among hierarchical layers, localized damage, and continuity between random and well-formed outputs are what enabled good predictions. The fact that we were able to successfully extend the model reinforces the utility of these ideas. Similarly, much of the criticism of SP applies equally to SLAM. For instance, the very small lexicon can only approximate the structure of a real lexicon, and the semantic representations are arbitrarily defined. Although the model is interactive, it does not include lateral or inhibitory connections, which are essential features of real neurological systems. Also, the model does not deal directly with temporal information, which constitutes a large body of the psycholinguistic evidence regarding speech processing. Nevertheless, for examining the architectural assumptions of the HSFC, SP provided a useful test bed, in that it has been the best computational model available.

One further advantage of SLAM over SP (and over similar models that assume a unified phonological network) is that SLAM provides a built-in mechanism for repetition. Repetition is often used in addition to naming as a test of lexical-retrieval models, because repetition involves the same demands on the motor production system as naming, but lacks the semantic search component. In order to simulate repetition, however, some form of auditory representation is necessary, even if it is implicit. In Foygel and Dell (2000), the single-route SP model was used to simulate repetition, without explicitly modeling the auditory input, by assuming that perfect auditory recognition delivers a boost directly to lexical units, essentially just the second step of naming. Later, to account for patients with poor naming but spared repetition abilities, a direct input-to-output phonology route was added to the model (Hanley, Dell, Kay, & Baron, 2004). This dual-route model grafts the “nonlexical” route on to SP, leaving the architecture and simulations of naming unchanged; the two routes are used only during repetition. Although several studies have generated empirical support for the idea that the two routes are indeed used in repetition (Nozari, Kittredge, Dell, & Schwartz, 2010), our study suggests that both routes are used in naming as well, potentially providing a more cohesive account of the computations underlying these tasks. Given that SLAM already requires the auditory component for naming, we intend to develop it to simulate repetition as well, allowing for more direct comparisons to this alternative dual-route model in the future.

Although SLAM does not employ learning or time-varying representations, another lexical retrieval model that does implement these features has also adopted a similar separation of auditory and motor speech representations. Ueno, Saito, Rogers, and Ralph (2011) presented Lichtheim 2, a “neurocomputational” model, which simulates naming, repetition, and comprehension for healthy and aphasic speech processing, using a network architecture in which each layer of units corresponds to a brain region. Lichtheim 2 does not categorize speech error types according to SP’s more detailed taxonomy, however, making it hard to compare directly with SLAM. Furthermore, since our goal with SLAM was to investigate the effects of the separate phonological representations, and Lichtheim 2 shares this architectural assumption, we did not compare the models directly. In Lichtheim 2, the phonology of the input and the output is represented by a pattern of phonemic features presented one cluster at a time, and semantic representations are temporally static and statistically independent of their corresponding phonological representations. The model is simultaneously trained on all three tasks, and hidden representations are allowed to form in a largely unconstrained manner. The trained network can then be “lesioned” in specific regions to simulate aphasic performance. We see much in common between our approaches in terms of their theoretical motivations, proposing psycholinguistic representations grounded in neuroanatomical evidence. Furthermore, the use of a single network to perform multiple tasks is very much in line with our plans to develop the SLAM model. One major difference between SLAM and Lichtheim 2 is that SLAM maintains an explicit hierarchical separation between lexical units and phonological units, allowing for selection errors at either stage. This hierarchical separation was essential for making our successful predictions regarding conduction naming patterns. It remains to be seen how our proposed architecture will cope with multiple tasks simultaneously.

Another model of lexical production, WEAVER++/ARC (Roelofs, 2014), has been proposed as an alternative to Lichtheim 2. Although this model uses spreading activation through small, fixed networks, as SP does, it also employs condition-action rules to mediate task-relevant selection of the network’s representations, thereby implementing a separation of declarative and procedural knowledge. Like Lichtheim 2, this model does not apply the detailed error taxonomy examined by SLAM, and so we did not compare them directly. Importantly, though, WEAVER++/ARC and Lichtheim 2 largely agree on most cognitive and computational issues, especially the primary one investigated by SLAM: the participation of separate auditory and motor–phonological networks in speech production. Additionally, like SLAM and Lichtheim 2, WEAVER++/ARC simulates the conduction aphasia pattern by reducing weights between the input and output phonemes. The primary disagreement between WEAVER++/ARC and Lichtheim 2 is an anatomical one: Should the lexical-motor connections for speech production be associated with the (dorsal) arcuate fasciculus or the (ventral) uncinate fasciculus? At present, the SLAM model is compatible with either position.² WEAVER++/ARC does differ from SLAM with respect to one important theoretical point, however. In WEAVER++/ARC, the input and output lexical units are separated, and in naming, activation primarily flows from lexical output units to motor units. Auditory units then provide stabilizing activation to motor units through an auditory feedback loop (i.e., motor to auditory to motor), rather than being activated by a single lexical layer in parallel with motor units to serve as sensory targets. This runs contrary to our finding that strong lexical–auditory feedback influenced lexical selection for conduction aphasia. Again, it remains to be seen whether our assumption of a single lexical layer can account for multiple tasks as Lichtheim 2 and WEAVER++/ARC do, which we intend to explore in future work.

The SLAM model falls into a broad class of models that can be described as “dual-route” models—that is, models that posit separate but interacting processing streams controlling behavior. Much of this work relates directly to Hickok and Poeppel’s (2000, 2004, 2007) neuroanatomical dual-stream framework for speech processing, in that the mapping between auditory and motor speech systems corresponds to the dorsal stream, whereas the mapping between auditory and lexical-semantic levels corresponds to the ventral stream. Although Hickok and Poeppel discussed this cortical network from the perspective of the auditory speech system, which diverges into the two streams, picture naming traverses both streams, going from conceptual to lexical to auditory (ventral stream) and from auditory to motor (dorsal stream). One difference between the SLAM model and the Hickok and Poeppel framework is that explicit connectivity is assumed between the lexical and motor–phonological networks. Hick-ok and Poeppel assumed (but didn’t discuss) connectivity between conceptual and motor systems, but did not specifically entertain the possibility of lexical-to-motor speech networks. The present model, along with the HSFC, thus refines the Hickok and Poeppel dual-stream framework.