Abstract
Many households display inertia in investment management over their life cycles. Our calibrated dynamic life cycle portfolio choice model can account for such an apparently ‘irrational’ outcome, by incorporating the fact that investors must forgo acquiring job-specific skills when they spend time managing their money, and their efficiency in financial decision making varies with age. Resulting inertia patterns mesh well with findings from prior studies and our own empirical results from Panel Study of Income Dynamics (PSID) data. We also analyze how people optimally choose between actively managing their assets versus delegating the task to financial advisors. Delegation proves valuable to both the young and the old. Our calibrated model quantifies welfare gains from including investment time and money costs as well as delegation in a life cycle setting.
Keywords: Portfolio inertia, Life cycle saving, Household finance, Human capital, Financial advice
1. Introduction
Investor inertia, or the tendency to maintain one’s investment portfolio for long periods of time without changing it, has sometimes been interpreted as evidence of irrationality or financial illiteracy.3 By contrast, here we incorporate the opportunity cost of time associated with investment management and show that such inertia can be consistent with optimal behavior. To this end, we develop a rational agent life cycle model that generates household portfolio inertia patterns consistent with much empirical evidence. In a dynamic consumption and portfolio framework with endogenous labor supply, we account for time costs devoted to portfolio management. This time becomes particularly valuable when the individual has the opportunity to accumulate job-specific human capital via learning by doing. Our structure for financial decision making costs posits an age-related time efficiency pattern for financial decision making. We also evaluate the role of financial advisors who, for a fee, help investors manage their financial portfolios. This possibility enables individuals to invest in their job-related human capital and thus to enhance lifetime earnings.
Several prior studies on portfolio choice have shown that people rarely alter their financial portfolios. For instance, Bilias, Georgarakos, and Haliassos (2010) analyzed investor trading behavior in the Panel Study of Income Dynamics (PSID) and found that most stock account owners (up to 70%) exhibited portfolio inertia. They also showed that portfolio inertia followed a U-shaped profile over the life cycle because younger workers owned almost no stock, while older persons who did have assets traded them infrequently. Ameriks and Zeldes (2004) studied TIAA-CREF account holders over a dozen years, during which 73% of investors never changed their asset allocation at all, while another 14% rebalanced only once. Agnew, Balduzzi, and Sunden (2003) also reported substantial inertia among investors, particularly in their retirement accounts, with close to 90% never altering their portfolios. Similarly, a 2008 survey commissioned by the Securities and Exchange Commission (SEC) asked investors how often they traded stocks, bonds, or mutual funds (outside employer-sponsored retirement accounts), and found that over 70% of investors changed their investment allocations at most once a year (SEC, 2008). In other words, inertia is the norm for a wide range of investors.4
Notwithstanding this evidence, a large body of research on household finance has focused on optimal dynamic portfolio allocation patterns selected by rational forward-looking consumers who decide on their own how to allocate their wealth between stocks and bonds.5 This approach has been extended to include flexible labor supply decisions.6 Building on these prior studies, we focus on how the opportunity cost of time devoted to investment management influences portfolio choice, in the context of endogenous human capital accumulation. This allows us to diagnose reasons for portfolio inertia and the demand for financial advisors over the life cycle.
We show that when investors cannot delegate, young and old investors optimally exhibit inertia, while middle-aged investors are more active. This is because the young have little job-specific human capital and have the longest time horizon, so they prefer to invest in job-related skills. In turn, they also optimally stay out of the stock market and exhibit inertia in non-participation. Middle-aged investors with more job-specific human capital have lower opportunity costs of financial investment and engage more actively in portfolio management. Newly retired individuals become quite active in managing their portfolios because they no longer forgo learning on the job but must optimally withdraw from their financial accounts before inefficiency in portfolio management and increasing mortality risk become important. Later in retirement, older persons are less involved in trading their financial assets, because growing mortality risk and falling decision making efficiency render active management costly. Accordingly, different portfolio management approaches are optimally chosen over the life cycle depending on the investor’s financial and labor market status. Using PSID data, we confirm this pattern in longitudinal micro data. We also show that the average equity share of liquid assets is hump-shaped with age, consistent with empirical evidence (see, for example, Ameriks and Zeldes, 2004 and US Census Bureau, 2012).
When households have the opportunity to delegate money management to a financial advisor, we observe that this reduces both inertia and active self-management. The delegation option proves attractive to both younger and older investors: around one-quarter (25%) of investors younger than age 65, and around 30% of retirees now optimally delegate to financial advisors. Interestingly, access to delegation also reduces active management among the youngest and oldest investors: having an advisor available at typical fees implies low active management among the young (~8%) and the oldest investors (less than 1%), with more among the middle-aged (~20%) and early retirees (~25%). Early retirees are again the most active investor group because they have no opportunity cost of forgone labor supply and must optimally withdraw from their financial accounts to cover consumption. Rather than paying a delegation fee, they instead actively manage their finances by withdrawing on their own. Later in life, retirees are more likely to delegate and become less active due to rising mortality risk and decision making inefficiency. We also evaluate how having access to a financial advisor might compare to investing in a conventional Target Date suite of mutual funds (hereafter TDFs). Interestingly, we find that investors having TDFs still manage their own investments actively, since the simple age-based rule for equity investing in TDFs is not personalized for peoples’ preferences and specific circumstances in the financial and labor markets.
To compare the welfare gains of having access to a financial advisor or TDFs, we compute the changes in the certainty-equivalent (CE) consumption streams when investors do versus do not have access to these alternatives. Given average fees charged, households having access to financial advisors enjoy a 1.1% improvement in their consumption streams, whereas access to the TDF option enhances welfare by about half that level. Sensitivity analysis for different financial advice costs shows that eliminating the minimum advisory fee can enhance welfare by 1.3%, compared to the no delegation case. Overall, lowering the entry barriers to access financial advisors can help people of all ages to better manage their finances and save their scarcest resource, the time for accumulating more job-specific skills or enjoying leisure. The young and the old benefit most.
Our work differs from other studies on equity market participation in that we model portfolio inertia among individuals having free access to the stock market, in contrast to Gomes and Michaelides (2005), for instance. For example, we show that, while most individuals (59% in our model) rationally choose inertia unconditional on stock ownership, almost half (49%) of stock investors also elect portfolio inertia. In comparative statics analysis, we also evaluate how initial market participation costs influence portfolio inertia patterns, and we show such an initial cost is not required to produce portfolio inertia among equity owners.
In what follows, Section 2 describes our specification of the investor’s portfolio problem when the primary opportunity cost of financial management is the time that could otherwise be used for job-related human capital accumulation. Section 3 describes the dynamic portfolio choice problem when investors have an option to hire financial advisors. Section 4 presents our calibration of parameters and approach to numerical solution of the model. Section 5 illustrates results of investors’ portfolio choice problems without delegation, and it also offers sensitivity analysis as well a comparison of model predictions with PSID evidence. Section 6 provides results on portfolio choice with the option of advice from a financial professional, and it evaluates the welfare impact of delegation and TDFs. We conclude with a discussion of implications of our findings for investors, the financial advisory industry, retirement plan sponsors, and policymakers.
2. Dynamic portfolio choice with inertia
In this section, we specify the investor’s problem when allocating his portfolio, on the assumption that active management of financial assets requires individuals to devote time to the process.
2.1. Financial decision making efficiency and time budgets over the life cycle
We posit a consumer dynamically determining his optimal equity share and labor supply over his life cycle, both of which influence his current and future labor income as well as his financial wealth. The individual is endowed with a per-period time available (normalized to one). Before retirement, he can allocate his time to work in the paid labor market (lt) to generate income, or to leisure (Lt). His decision period (t = 0, 1, …, T) is measured in years; at t = 0 he begins his work life at age 20. He also faces mortality risk over the course of his (uncertain) lifetime (the maximum age here is set to 100, so T = 80).
An individual who is not a financial expert will need to devote both time and mental resources to the task of financial management (Abel, Eberly, and Panageas, 2013; Campbell, Jackson, Madrian, and Tufano, 2011). This can be costly, inasmuch as managing financial assets requires collecting and processing information about market conditions (Christelis, Jappelli, and Padula, 2010), analyzing financial product risk/return characteristics, and evaluating product fee structures. And while there may be a one-time initial entry cost of equity participation (Gomes and Michaelides, 2005), it will still be necessary each period for investors to expend resources to evaluate changing financial market conditions and understand new products (Carlin, 2009). This imposes on individuals an opportunity cost every period, inasmuch as labor earnings depend on job-specific skills derived from work each period.7
We capture the explicit opportunity cost of adjusting one’s portfolio by the fraction of time (ϕt) that is devoted to financial decision making. Someone who is not well-informed about financial markets will need to allocate more time to acquire and process information about his portfolio. Accordingly, the investor faces the following time budget constraint:
| (1) |
where at is a variable taking the value of one if he actively manages, and zero otherwise. This time constraint implies that the investor can make use of his time to either work or enjoy leisure, if he elects not to actively manage his financial portfolio.
We also posit that the time cost of making an efficient financial decision ϕt can vary with age (see Gamble, Boyle, Yu, and Bennett, 2015). Consistent with the economics and neuroscience literatures on decision making over the life span (Horn and Cattell, 1967; Agarwal, Driscoll, Gabaix, and Laibson, 2009), we suppose that middle-aged investors are more efficient in managing their wealth than are younger or older individuals. Accordingly, we model the age-dependent time cost of financial management as a U-shaped function over the life cycle with the highest efficiency (i.e., lowest ϕt) in middle age. This reflects the fact that the young are cognitively able but inexperienced in the labor force; also older workers have job experience but may have diminished cognitive ability (Korniotis and Kumar, 2011). Middle-aged investors tend to be at their best, having gained job experience but not yet experienced cognitive decline. Since investors incur time costs per period when they manage their financial portfolios actively,8 there is no assumed value of experience in financial management (Chiang, Hirshleifer, Qian, and Sherman, 2011).
2.2. The human capital accumulation process
We posit that job-specific human capital is accumulated through learning by doing. In keeping with Arrow (1962) and Becker (1964), we denote with Ht and lt, respectively, as the time devoted to developing job-specific human capital and work time each period. The law of motion for job-specific human capital is:
| (2) |
where Ft(Ht, lt) is an experience formulation function and δt is a depreciation rate9 for job-specific human capital. An idiosyncratic temporary shock (λt) also affects the accumulation level of human capital in the next period.
This formulation makes clear that work in the current period (lt) not only generates current labor income, but it also raises the stock of human capital resulting in higher future labor income. Previous research on endogenous labor supply in a dynamic portfolio choice model has incorporated uncertain wage rates as an important source of risk, but there the decision to work was assumed to affect only current income (Bodie, Merton, and Samuelson, 1992; Gomes, Kotlikoff, and Viceira, 2008; Chai, Horneff, Maurer, and Mitchell, 2011). Since life cycle wage profiles in prior models were assumed to be determined only by age and exogenous labor market shocks, those studies implicitly assumed that work time substituted for current leisure time, so the price of leisure was simply the current wage. By contrast, in our approach, we model investors who know that taking time away from work today influences their human capital accumulation and hence future labor earnings.
Specifically, we specify the experience acquisition function as follows, following Ben-Porath (1967):
| (3) |
where a is a parameter that represents an individual’s efficiency for accumulating human capital. The elasticity of human capital accumulation θ is assumed to display decreasing returns to scale (θ ∈ (0, 1)).
2.3. Labor income and asset returns
Disposable yearly labor income (Et) is determined by the individual’s job-specific human capital level (Ht), wage shock (Yt), and labor supply (lt):
| (4) |
where ht and τt represent housing expenditures and labor income tax, respectively. Ut is a temporary idiosyncratic shock in the labor market. The level of human capital or job-specific skill Ht plays a role similar to the age-specific deterministic wage trend in the life cycle literature (Cocco, Gomes, and Maenhout, 2005; Gomes, Kotlikoff, and Viceira, 2008; Hubener, Maurer, and Mitchell, 2013).10 In the present case, however, Ht is endogenously accumulated over time when the individual works (i.e., learning by doing), as per Eq. (2). The permanent wage shock (yt ≡ log Yt) follows a random walk process and is influenced by an idiosyncratic shock where , following Carroll (1997) and Cocco, Gomes, and Maenhout (2005). The transitory wage shock (Ut) is independent and identically log normally distributed . After the (exogenous) age-65 retirement age (t = 45), the individual stops working (lt = 0) and receives a lifelong pension benefit equal to a fraction of his final labor earnings.
Two asset classes are available for the consumer’s investment portfolio: riskless bonds and risky stocks. Bonds have a constant annual real gross return of Rf in all periods. The real stock gross return is assumed to be serially independent and identically log normally distributed with parameters μS and σS, implying that .11 The correlation between the stock log return and the innovation to the permanent wage shock is denoted by σεS. We denote as the stock gross return from time t to t + 1, so that the fraction of the individual’s wealth invested in stocks is determined in period t, and returns are realized in t + 1. Following Gomes, Kotlikoff, and Viceira (2008), we consider a proportional tax rate τC applied to all asset returns the household receives. Therefore, the after-tax bond return is given by R̄ = 1 + (Rf − 1)(1 − τC) and the after-tax stock return is given by .
2.4. Preferences
We suppose the investor has a standard time-separable power utility function defined over a composite good consisting of current consumption (Ct) and time devoted to leisure (Lt), which is given by , as in Gomes, Kotlikoff, and Viceira (2008). As is conventional, here α > 0 captures the investor’s preference for leisure relative to consumption and the parameter γ measures relative risk aversion.
2.5. Wealth dynamics and portfolio inertia versus active management
The investor is assumed to have a stock market account and a bond market account.12 Each period t, the investor must decide how much to consume (Ct) from his available total wealth (or cash on hand, Wt), and how much to invest in the stock market for the next period (St ≥ 0). His remaining wealth is invested in bonds (Bt = Wt − Ct − St). Let Zt be the balance of his stock market account at time t. The dynamic budget constraint and evolution of wealth can then be formulated as follows:
| (5) |
| (6) |
| (7) |
The stock balance (Zt+1) in period t + 1 is determined by his previous period’s stock investment choice (St) and stock market return (Rt+1). The next period’s total wealth (Wt+1) is the sum of realized financial investment (stock account plus bond account balances) and labor earnings (Et+1). Depending on how the investor elects next period’s stock investment, we have two cases.
Inertia (St = Zt)
The investor exhibits portfolio inertia in period t when he retains his current stock balance for the next period. This is equivalent to passively electing the current stock balance as his new investment choice (St = Zt): i.e., there are no withdrawals from or new investments into the stock account. In so doing, he incurs no time cost for financial decision making (ϕt = 0) that he would otherwise devote to collecting and analyzing new financial information to implement a change. Accordingly, someone electing portfolio inertia has the following budget and time constraints:
| (8) |
| (9) |
| (10) |
Also, when electing inertia, the investor does not finance his current consumption by liquidating part of his stock account, which makes the consumption constraint more binding (Ct ≤ Wt − Zt). Of course his next-period balance in the stock account (Zt+1) may differ from that of the prior period (Zt) because of uncertain investment returns (Rt+1).
Active management (St ≠ Zt)
The investor exhibits active portfolio management in period t when he explicitly chooses an investment amount in stocks: that is, he makes additional investments into or takes withdrawals from his stock account based on his investment decisions. Accordingly, the amount invested in stocks for the next period can differ from the current stock balance (St ≠ Zt). In return, the investor must incur (age-dependent) time costs (ϕt > 0) this period.13 The wealth and time budget constraints evolve as follows:
| (11) |
| (12) |
| (13) |
Optimization
By defining inertia as a situation where the investor does not alter his stockholdings, we treat the stock account balance (Zt) as a state variable within a dynamic optimization framework. This is because it is necessary for the investor to know his current stock balance before deciding whether to leave it as is (i.e., St = Zt), or to actively evaluate some different allocation. Other state variables include total wealth (Wt), accumulated human capital (Ht), and the wage shock (yt). There are also four choice variables: the portfolio management method (i.e., portfolio inertia or active management), labor supply (lt), stock holdings going into the next period (St), and consumption (Ct).
Because the portfolio management method is a discrete choice variable, we formulate the investors’ problem using a dynamic discrete choice model (Adda and Cooper, 2000). We define as the investor’s discounted lifetime utility when he actively manages his portfolio; conversely, denotes his discounted lifetime utility when he elects portfolio inertia. Then the value function at time t is specified as:
| (14) |
Let β < 1 be the investor’s time preference and pt the probability that he survives to the next period. Then the value function for active management is as follows:14
| (15) |
The value function for portfolio inertia is as follows:
| (16) |
When an investor elects portfolio inertia, he does not need to remaximize the value function with respect to stock holdings; instead, he takes his current stock balance (Zt) as his next period’s stock investment (St). If , the investor opts for active management (at=1), otherwise, he opts for portfolio inertia.
These two value functions differ due to their different time constraints and next period’s portfolio choice. The appeal of portfolio inertia is that the time saved can then either be used to work and accumulate more human capital, thereby raising future earnings, or to enjoy more leisure. During retirement, the investor does not work, so if he decides to actively manage his portfolio, he sacrifices only his leisure time. Later in retirement, decreasing financial decision making efficiency and rising mortality risk make inertia more appealing.
3. The role of financial advisors and dynamic portfolio choice with delegation
Next we extend the model to examine how introducing financial advisors can add value to life cycle decision makers. Reasons for delegating portfolio management can include time costs, efficiency gains due to lower transaction costs, and beliefs regarding professional managers’ skills. In what follows, we focus mainly on the investor’s forgone opportunity to accumulate more human capital associated with active management during the work life.
When an investor elects to delegate his portfolio management to an advisor, he must pay a management fee from his wealth (Wt). In the financial advisory service industry, the charges generally consist of a minimum fixed fee (φmin) plus a percentage fee (φptg) levied on total assets under management.15 Formally, this structure may be expressed as follows:
| (17) |
The financial advisor not only selects the individual’s investment portfolio, but he also proposes optimal levels of consumption and labor supply that are in the client’s best interest.16 The value function for the delegated portfolio management method is then:
| (18) |
Note that the investor pays the management fee φt out of his total wealth, but he does not incur any time cost ϕt. The advantage of hiring the financial advisor is either more leisure or the time savings which can then be used to work and accumulate more job-specific knowledge.
Accordingly, the investor’s optimization problem of finding the best portfolio management method can be summarized as:
| (19) |
where at = 0 denotes portfolio inertia, at = 1 active management, and at = 2 hiring a financial advisor. where is the value function for the portfolio inertia case, is the value function for active management, and is the value function for delegating portfolio management.
4. Model calibration and solution
4.1. Numerical procedure for model solution
There is no simple Euler equation linking the marginal benefit of today’s portfolio adjustment with future marginal benefits in our model, inasmuch as the investor is unsure about which portfolio management method he will select at each point in the future. For this reason, it is intractable to solve the model in a closed form. We therefore solve the model numerically via backward induction, multi linear interpolation, and Monte-Carlo integration (see online Appendix B for details).
4.2. Parameter calibration
We calibrate the model using a reasonable set of base case parameters, setting the discount factor β to 0.96, the coefficient of relative risk aversion to γ = 3, and the leisure preference parameter to α = 1.0, as is conventional in other life cycle studies (see Gomes, Kotlikoff, and Viceira, 2008; Chai, Horneff, Maurer, and Mitchell, 2011; and Cocco and Gomes, 2012). One-period survival rates pt in the utility function are calculated from the 2009 US Social Security Administration Trustees Report cohort mortality table for male high school graduates born in 1990 (Bell and Miller, 2012).
An important element of the model is the human capital accumulation process (Ht), which generates the opportunity cost of time when an investor elects to actively manage his financial assets. As noted above, accumulated human capital serves a similar role as the age-dependent wage profile in prior studies. To this end, we calibrate the human capital accumulation process by matching the model-generated moments with those of an age-dependent wage rate profile for male high school graduates derived from PSID data (as in Hubener, Maurer, and Mitchell, 2013).17 Based on this moment-matching process, we find that human capital Ht depreciates at an annual rate of δt = 0.16% + 0.023595 × year; the elasticity parameter in the experience accumulation function is set to θ = 0.0462; and the accumulation rate to a = 0.7596. The idiosyncratic shocks to human capital follow an independent and identically distributed (i.i.d.) lognormal distribution ln (λt) ~ N(−0.5 · 0.04342, 0.0434). The standard deviation of the permanent wage shock is 0.0710 and the pre-retirement transitory wage shock standard deviation is 0.1726; in retirement it is 0.28 (as in Love, 2010). The post-retirement shocks may be interpreted as income or consumption surprises due to unexpected out-of-pocket medical expenses or long-term care expenses.
Retirement benefits are assumed to replace 50% of the individual’s last labor income Et = 0.2H45Y45 (t = 45, 46, …, T). This formulation generates higher (lower) replacement rates for workers with lower (higher) average career earnings, consistent with the progressive benefit rules of the US Social Security system (Chai, Horneff, Maurer, and Mitchell, 2011). The riskless asset return is set to 1% and the risk premium for stocks is 4% with a standard deviation of 20.5% (Cocco, Gomes, and Maenhout, 2005). Labor income is taxed at 30% during working period and 15% after retirement. Capital gains are taxed at 20%. These rates reflect effective tax rates facing the typical household in the US (Gomes, Kotlikoff, and Viceira, 2008).
So that the calibration embodies relatively realistic delegation fees, we collect and analyze advisory charges of Registered Investment Advisors (RIAs) reporting to the US Securities and Exchange Commission.18 We focus on retail-oriented advisors charging a percent of total assets under management (AUM), as this is the most common form of fee (see online Appendix A). Since these fees average 1.41% per year, our baseline calibration uses this level (φptg = 1.41%). To cover fixed costs of advisory service, financial advisors often stipulate a minimum balance they require if they are to take on the client for a percentage fee. Below that level, they charge a fixed fee calculated as a set percentage times the minimum required account balance. For retail-oriented advisors, the minimum required account balances average about $240,000, which translates into a fixed fee level of $3,400. Such a high threshold for delegation will discourage most consumers from delegation in the real world and in our model.19 Accordingly, for the baseline case below, we explore investors’ choice of a delegation option by setting the minimum fee at φmin = $2, 115 (commensurate with a minimum required account balance of $150,000 × 1.41%). In sensitivity analysis, we also analyze how different fixed fees affect investor behavior and welfare.
The age-dependent efficiency function ϕt for financial decision making is postulated to be U-shaped, as discussed above. Middle-aged investors are assumed to be more efficient than inexperienced young investors and older investors with declining cognitive abilities. A parsimonious and also general functional form to produce such a U-shaped pattern is given by . Here, represents the year (after age 20) of highest efficiency, where investors have the lowest time costs for financial decision making given by the parameter ϕ1. The parameter ϕ2 ≥ ϕ1 specifies the time cost for the youngest workers and n > 0 allows us to model the level and the speed of efficiency change for younger and older investors. To calibrate this functional form, we assume n = 4, where the 4th power generates modest efficiency pattern changes around middle age, in keeping with evidence provided by Agarwal, Driscoll, Gabaix, and Laibson (2009), Gamble, Boyle, Yu, and Bennett (2015), and Horn and Cattell (1967). The parameters (ϕ1, ϕ2, Θ) are calibrated using a formal matching procedure that provides the closest fit between the simulated inertia patterns from the model and the values observed in PSID data (see Section 5). To do so, we run the model for various sets of (ϕ1, ϕ2, Θ) such that for various age brackets i = 1, …, m the sum of the quadratic deviations of the average fraction of inertia-investors generated by the model and the values observed in PSID data is minimized, i.e., . In implementation, we use 5-year non-overlapping age brackets starting from ages 20 to 95 and search for various integer values of Θ and a discrete set of (ϕ1, ϕ2) spaced by 0.01 apart. This procedure generates the estimated values ϕ1 = 0.04, ϕ2 = 0.06, and Θ= 23 (i.e., age 43). The estimated value of ϕ1 = 0. 04 (that is, investors sacrifice 4% of their normalized time to manage their own portfolios) is comparable to the value reported by the American Time Use Survey (Bureau of Labor Statistics, 2012). Here, people spend an average of 0.35 hours a day on financial management, or around 3% of daily discretionary time (of 13 hours, calculated by deducting time spent on necessary activity such as sleeping, eating/drinking, essential household activities, and caring for household members). Baseline parameters of the life cycle model are summarized in Table 1.
Table 1. Summary of parameter values for base case model.
This table summarizes parameter values for the base case model.
| Parameter | Baseline value |
|---|---|
| Working periods | 45 |
| Retirement periods | 35 |
| Time discounting β | 0.96 |
| Risk aversion γ | 3 |
| Leisure preference α | 1.0 |
| Experience formulation a | 0.0462 |
| Elasticity of Ht accumulation θ | 0.7596 |
| Depreciation of human capital δt | 0.16% + 0.023595 × year |
| Inefficiency of financial decision making ϕt | (t − 23)4 + 0.04 |
| Std. dev. of permanent wage shock | 0.0710 |
| Std. dev. of human capital shock | 0.0434 |
| Std. dev. of transitory wage shock (pre-retirement) | 0.1726 |
| Std. dev. of transitory earnings shock (post-retirement) | 0.28 |
| Replacement rate | 20% of maximum earnings at age 65 |
| Risk premium | 0.04 |
| Std. dev. of stock return σstock | 0.205 |
| Risk free rate Rf | 1.01 |
| Delegation annual fee: variable rate φptg | 1. 41% per annum |
| Delegation annual fee: fixed fee φmin (1.41% of min. required balance of $150,000) |
$2,115 |
| Correlation between wage and stock return σεS | 0.0 |
| Initial wealth for simulation W0 | 0 |
| Initial human capital for simulation H0 | 10 |
| Initial stock balance for simulation Z0 | 0 |
| Initial wage shock for simulation y0 | 0.1 |
5. Results and discussion for the baseline case
Next we describe investor behavior in our baseline case when no delegation option is available;20 in Section 6, we report results when individuals can elect to delegate their money matters to a financial advisor. To this end, we first discuss life cycle profiles for the key choice variables with special attention to the portfolio management method (i.e., inertia versus active management). Next we compare predictions from our model with empirical evidence on portfolio inertia patterns estimated using PSID data, as well as other findings in the literature. A final subsection provides sensitivity analysis for key parameters.
5.1. Profiles for consumption, wealth, earnings, stock holdings, and labor supply
We use the optimal controls of the baseline parameterization to generate 2,000 simulated lifetimes reflecting realizations of stock returns and labor income shocks. All investors begin with a zero stock account balance (i.e., no inheritance Zi, 1 = 0). Fig. 1 summarizes our baseline results for the key choice variables (consumption, wealth, labor supply, and earnings) when delegation is not an option. Panel A shows that the model generates hump-shaped wealth, earnings, and consumption profiles over the life cycle, consistent with those reported in other studies (e.g., Gomes, Kotlikoff, and Viceira, 2008). Consumption drops sharply at age 66 when households retire and begin to consume more leisure. Such a profile is in line with other life cycle models with endogenous work hours (Chai, Horneff, Maurer, and Mitchell, 2011); it is also in line with empirical studies documenting a substantial decline in spending around the retirement date (Battistin, Brugiavini, Rettore, and Weber, 2009). Panel B illustrates the average stock balance which also traces out a hump-shaped pattern over the life cycle. Starting with no stock holdings, individuals then invest more in the stock market until they retire, after which they gradually decrease their exposure to stocks. This result is consistent with empirical findings of a hump-shaped equity share profile along with a hump-shaped wealth profile over the life cycle (Ameriks and Zeldes, 2004).21 Panel C traces out the labor supply pattern which is slightly hump-shaped over time. Average lifetime labor supply equals 0.35, which corresponds to about 1,820 work hours per year (assuming a time endowment of 100 waking hours per week). This is similar to prior work (e.g., Gomes, Kotlikoff, and Viceira, 2008; Chai, Horneff, Maurer, and Mitchell, 2011) and it is also in line with empirical evidence for US workers.22 On average, the stock of human capital rises with age, but at a decreasing rate. Overall, the baseline model generates patterns of key variables consistent with other studies in the life cycle model literature.
Fig. 1.
Life cycle profiles of consumption, earnings, equity share, labor supply, and human capital with no delegation option. This figure shows average life cycle profiles when only active management or inertia are feasible, generated from 2,000 independent simulations based on optimal feedback controls from the baseline specification of the life cycle model (see Table 1). Panel A displays average consumption, labor income, and total wealth paths ($1,000s); Panel B shows the average amount of stock account balance ($1,000s); and Panel C depicts average work and human capital profiles. Human capital is normalized by its initial level.
5.2. Portfolio inertia and equity choice
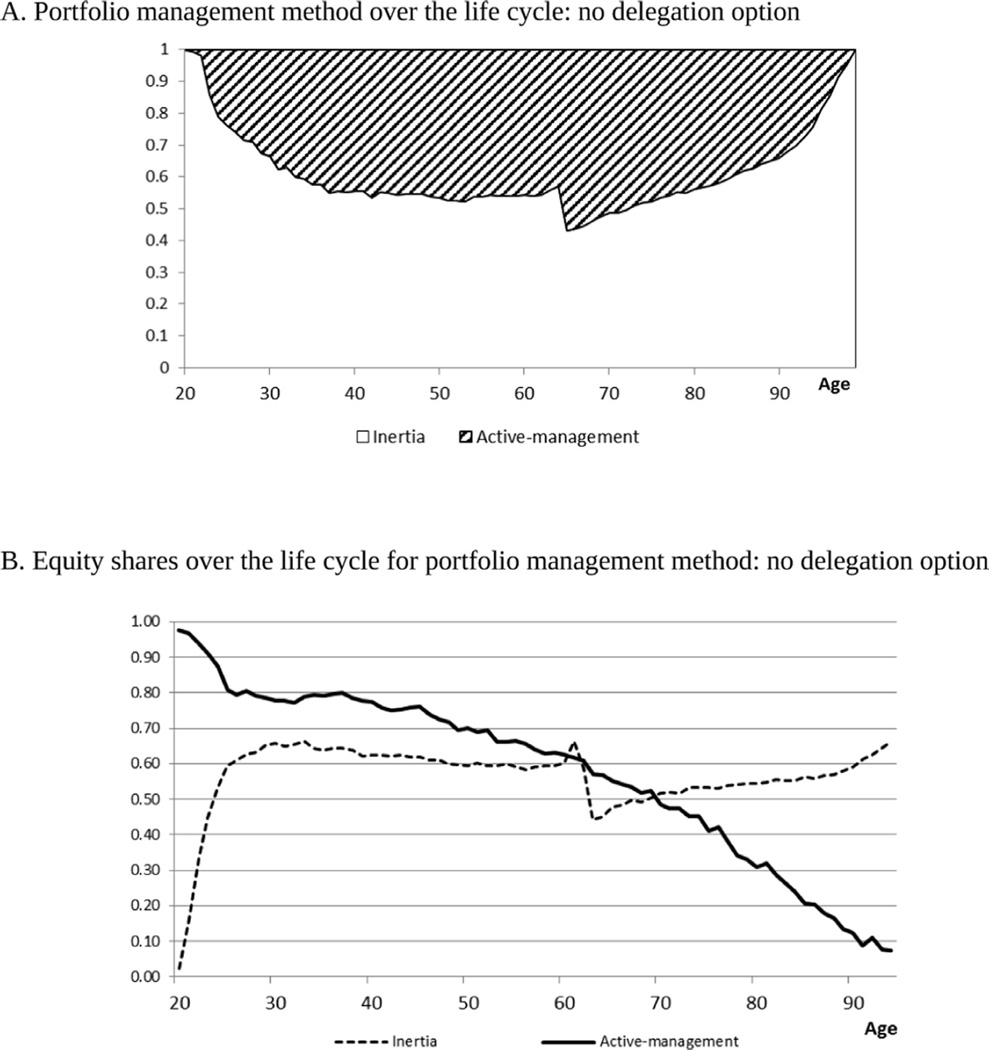
Fig. 2 shows optimal choice patterns of portfolio management method and equity holdings over the life cycle when delegation is unavailable. Panel A illustrates how people optimally manage their portfolios depending on whether inertia or active management dominates. As is evident, inertia is the dominant strategy for young investors to about age 30; thereafter, active management becomes more prevalent until retirement, whereupon even more switch to active management early in retirement (the fraction of active managing investors rises from around half at age 64 to about 60% at age 65). Later in life, people again revert to inertia.
Fig. 2.
Choice of portfolio management method and equity share over the life cycle: no delegation option. This figure shows life cycle patterns of portfolio management method and equity shares selected with no delegation option. Panel A shows the fraction of investors selecting inertia versus active management by age. Panel B shows the life cycle pattern of equity shares depending on whether the investor elects inertia or active management. Equity share is defined as stock holdings as a share of savings (St / (St + Bt)) in period t conditional on each portfolio management approach. Averages are generated from 2,000 independent simulations for individuals based on optimal feedback controls in the baseline specification of the life cycle model.
The reason for this pattern is that the young have little financial wealth, yet they would still need to forgo substantial human capital investment if they devoted time to manage their meager financial assets. They also have a longer horizon over which they can use their human capital to generate labor earnings. Later in life, people have more wealth and a smaller opportunity cost of time. This is because they have shorter work lives remaining and have already accumulated substantial human capital. Accordingly, sacrificing a small amount of time to manage their finances has only a modest impact on their wages. Still, however, almost half of the middle-aged group does not change portfolio allocations. Among the older group with lower wealth, their reduced decision making efficiency and increased mortality risk somewhat depresses their interest in active management. Early in retirement, older people are more likely to switch to active management to rebalance their portfolios, now that they have more free time and need to liquidate stock holdings to finance their consumption during retirement. The fraction of actively managing investors thus jumps from 50% at age 64 to about 60% at age 65. As time goes by, however, reduced wealth and income shrink the budget constraint for consumption, which in turn reduces utility from actively managing financial assets. Additionally, rising mortality risk boosts their preference for current consumption and leisure. These factors all lead to more inertia later in life.
Panel B of Fig. 2 illustrates the fraction of financial wealth invested in equity changes over the life cycle when no delegation option is available.23 The dotted line reflects the average fraction in equities for the subgroup of inertia investors. The solid line refers to the corresponding equity share for active investors. Conditional on becoming active, they follow the traditional investment strategy recommended by previous life cycle studies (as in Cocco, Gomes, and Maenhout, 2005). Consistent with most prior life cycle models with uncertain labor income, active investors hold almost 100% of their savings in equity early in life, and glide down to lower shares as they age. The explanation is that future labor income can be thought of as an implicit bond position, so workers will seek to diversify their overall wealth position consisting of human capital and financial wealth. By contrast, inertia investors allocate less to equity when young and invest more when old. This is because young investors start with a zero stock balance and little wealth, so they are more likely to choose inertia and hence invest nothing in equity. As they accumulate wealth, they begin to manage more actively and accumulate equity. Between ages 30–60, the equity fraction of the inertia investor is rather flat, at around 60%. Interestingly, at retirement there is a sharp drop in the equity fraction for inertia investors. The reason is that early retirees reallocate substantial amounts of equities toward bonds, just before they start to draw down during retirement. This, in turn, can be explained by the fact that older investors facing rising mortality risk and inefficiency in financial decision making understand that active financial management implies rising opportunity costs.24 Because inertia investors gradually deplete their wealth from their bond accounts and defer selling off their equity accounts, their equity share increases in later years.
Overall, combining the cases of inertia and active management investors, we observe the average equity shares rise for younger individuals and steadily decline afterward. The average equity shares for all investors is hump-shaped: 47% (age group 20–35), 70% (age group 36–50), 63%, (age group 51–65), 51% (age group 66–80), and 46% (age group 80+), respectively. Although those electing active management at older ages optimally choose lower equity shares, the fact that older inertia investors retain a high equity share implies that stock holdings do not decline sharply with age. In sum, in our model, people optimally do not invest in stocks early in life, but in middle age they gradually move into stock, and then they curtail stockholdings later in life while still retaining a reasonable share.
Fig. 3 displays scatter plots of stock account balances for active and inertia investors; the solid line indicates average stock balances in each case. It is clear that those active managers hold more in equities than do inertia investors. Individuals having greater equity exposure find it optimal to allocate more time to portfolio management and become active investors. Nevertheless, the average does not imply that all inertia investors eschew equities. In fact, as the left panel in Fig. 3 illustrates, a large group of those who are inactive still hold substantial stock positions. If an investor expects he will end up choosing a similar consumption/labor supply pair next period, a small change in his portfolio will be costly without enhancing his discounted lifetime utility. In such a case, it will then be optimal for him not to alter his portfolio.25
Fig. 3.
Scatter plot of stock balances conditional on portfolio management method: no delegation option. This figure shows a scatterplot of stock balances depending on whether the investor elects inertia or active management in the current period. The solid line indicates average stock balances for each portfolio management method. Averages generated from 2,000 independent simulations for individuals based on optimal feedback controls from the baseline specification. Account balance in 2012 US$ (000).
Table 2 presents summary statistics concerning the dynamics of portfolio management methods when no delegation option is feasible. On average, the first time that people elect active management is about 9 years after entering the labor force. They then elect inertia for 49 years and manage their own portfolios for 31 years, altering their management strategies 11 times over their lifetimes. Some 12% of people (= 1 – [1,760/2,000]) never elect active management and remain inactive throughout their entire life-times.
Table 2. Dynamics of portfolio management over the life cycle with no delegation option.
This table tabulates results from 2,000 simulation runs of base case model (see Table 1). No. of switches refers to the number of times someone changed portfolio management method (from actively managed to inertia or vice versa) between ages 20 and 100, conditional on survival. Years of inertia refers to the total length of the inertia period, and Years of active mgmt refers to the total length of the active management period, over simulated life cycle paths. First year of active mgmt refers to the first year an individual changes from inertia to active management. Some people never elect active management and remain inactive throughout their entire lifetimes, which is why the total number of observations for First year of active mgmt is less than the total number of simulations.
| Mean | StDev | Median | 5%-Q | 95%-Q | N | |
|---|---|---|---|---|---|---|
| No. of switches | 11.44 | 7.08 | 12.00 | 0.00 | 22.00 | 2,000 |
| Years of inertia | 49.21 | 23.78 | 47.00 | 15.00 | 80.00 | 2,000 |
| Years of active mgmt | 30.79 | 23.78 | 33.00 | 0.00 | 65.00 | 2,000 |
| First year of active mgmt | 8.02 | 7.23 | 6.00 | 4.00 | 17.00 | 1,760 |
5.3. Comparing model predictions on inertia with empirical evidence
Next we compare our model’s predictions with new empirical evidence as well as with prior studies on portfolio inertia. Our analysis draws on the Panel Study of Income Dynamics, a longitudinal microeconomic survey which follows family units and their financial status over time. We use the Main Interview (Family) File where households were asked every 2 years whether they had purchased or sold stocks since the last survey wave, and, if so, the amounts transacted. We focus on the survey waves (2001–2007) which asked this question every 2 years.26 If a household had not any purchases or sales of stocks, we denote this as exhibiting inertia.
Our sample selection process follows prior studies in excluding families belonging to the special low-income Survey of Economic Opportunities subsample in the PSID (Brunnermeier and Nagel, 2008; Bilias, Georgarakos, and Haliassos, 2010).27 We exclude survey years when families had headship changes, as wealth can fluctuate substantially due to marriage, divorce, or widowhood. We also focus on those with non-negative liquid and financial wealth, and we exclude those with less than $1 in cash and those having more than $50 million in net liquid wealth or net real wealth, to ensure investors do not have options to delegate their financial management as in the benchmark case.28
5.3.1. Portfolio inertia patterns by age and wealth
We first compare portfolio inertia patterns nonparametrically over the life cycle, in the PSID data and in our model. Fig. 4 illustrates that the empirical inertia pattern (dots) is U-shaped with age, consistent with our model’s prediction (solid line): both younger and older investors are more prone to inertia than are the middle-aged. Our predicted level of inertia also lines up well with the PSID data with 95% significance level. In our model, retirement happens at age 65, so there is a downward bump in inertia as peoples’ time becomes more flexible. By contrast in the PSID, not everyone retires at once, which mitigates the decline in inertia. After that, our model produces inertia comparable to the PSID. Overall, the PSID evidence is supportive of our model predictions that younger and older investors are least likely to trade in their stock accounts. This U-shaped pattern of portfolio inertia is also consistent with that reported in several prior empirical studies (Ameriks and Zeldes, 2004; Bilias, Georgarakos, and Haliassos, 2010; Calvet, Campbell, and Sodini, 2009).
Fig. 4.
Portfolio inertia over the life cycle: empirical evidence from the PSID data. This figure shows our non-parametric estimation of the portfolio inertia pattern in the PSID (waves 2001, 2003, 2005, and 2007). The solid line represents the baseline model’s prediction of the fraction of investors selecting inertia (as in Fig. 2A). Each dot represents weighted average of inertia investors for each age group in PSID data, where the sampling weight comes from the 2001 survey. The shaded region represents the 95% confidence interval of PSID data using Epanechnikov kernel density functions for non-parametric estimation of inertia pattern by age.
It is also of interest to note that our inertia levels are comparable to findings reported by Bilias, Georgarakos, and Haliassos (2010) who also used the PSID but included earlier years when survey waves were spaced further apart. Across all ages, they reported 40–70% inertia among stock owners (depending on the survey year). By comparison, our model generates 49% inertia among those who own stocks (and 59% unconditional on stock ownership). If we more narrowly define inertia as no trading over a 5-year time span, as did they, our model generates 34% inertia conditional on stock holding, close to their 39–56% ratio.
Table 3 illustrates how portfolio inertia and equity trading patterns vary over the life cycle, in our model as well as the PSID sample. We also show how results differ by wealth level (above/below $150,000), to illustrate how wealth is related to portfolio management choice and subsequent trading patterns. Here, Panel A reports findings for simulated results from the life cycle model, while Panel B provides evidence for the PSID sample.
Table 3. Portfolio inertia and stock trading behavior over the life cycle with no delegation option.
This table shows the proportion of investors by total wealth and age who exhibited inertia (i.e., no stock purchase), purchased additional stock, or sold stock. Panel A tabulates results from 2,000 independent simulation runs of base case model without a delegation option. The cut-off point for total wealth (see Eq. (8)) is based on the medium level of wealth for middle-aged investors. Panel B shows the corresponding results based on PSID data of waves 2001, 2003, 2005, and 2007. Numbers are weighted averages for each age group using the 2001 survey weights. The cut-off point for liquid wealth is based on the medium level of wealth for middle-aged investors in the model.
| Panel A: Simulated data results | ||||||
| Total wealth < $150,000 | Total wealth ≥ $150,000 | |||||
| Inertia | Active management | Inertia | Active management | |||
| Age | No trade | Bought | Sold | No trade | Bought | Sold |
| 20–35 | 0.784 | 0.161 | 0.055 | 0.132 | 0.622 | 0.246 |
| 36–50 | 0.691 | 0.133 | 0.175 | 0.228 | 0.418 | 0.354 |
| 51–65 | 0.770 | 0.093 | 0.136 | 0.202 | 0.361 | 0.437 |
| 66–80 | 0.736 | 0.105 | 0.159 | 0.039 | 0.381 | 0.580 |
| 80+ | 0.838 | 0.069 | 0.093 | 0.079 | 0.348 | 0.573 |
| Panel B: PSID data results | ||||||
| Liquid wealth < $150,000 | Liquid wealth ≥ $150,000 | |||||
| Inertia | Active management | Inertia | Active management | |||
| Age | No trade | Bought | Sold | No trade | Bought | Sold |
| 20–35 | 0.682 | 0.194 | 0.124 | 0.313 | 0.531 | 0.156 |
| 36–50 | 0.624 | 0.197 | 0.179 | 0.247 | 0.503 | 0.249 |
| 51–65 | 0.621 | 0.181 | 0.199 | 0.253 | 0.460 | 0.287 |
| 66–80 | 0.679 | 0.145 | 0.175 | 0.312 | 0.390 | 0.297 |
| 80+ | 0.731 | 0.150 | 0.119 | 0.316 | 0.336 | 0.349 |
Panel A shows that two-thirds (69%) of the lower wealth middle-aged investors (age 36–50) elect inertia, while only one-fifth (23%) of the same age group with more than $150,000 elect inertia. This pattern results from the opportunity costs of active financial management: low-wealth investors avoid sacrificing time to manage their accounts, while wealthier individuals can afford to do so. Panel A also shows that the factors driving active management vary over the work life. Active investors buy stocks while young, and they sell stocks later in life. In the 20–35 age range, more than 60% of wealthy investors buy equities seeking to capture the equity premium; in their 60s and 70s, almost 60% actively sell stocks to finance consumption.
Panel B tabulates the fraction of inertia versus active stock traders by age in the PSID sample. Most of the patterns are in line with our model’s predictions: for instance, both wealth groups show an inertia pattern that traces a U-shaped pattern with age. The less-wealthy PSID respondents track our model predictions quite well, trading a bit more at all ages. Wealthier PSID respondents exhibit more inertia than predicted in the older age group (66+), perhaps because of factors not modeled here (e.g., a bequest motive). The trading motivation for active management is also consistent with the model; active investors are buying stocks when young to capture the equity premium and selling them when old. Overall, the model generates similar trading patterns with the PSID except for the wealthy older investors, which calls for further research.
5.3.2. Determinants of portfolio inertia
To succinctly summarize the factors associated with investors’ portfolio management methods, we turn to descriptive multinomial logit regressions with results appearing in Table 4. In particular, we show how the probability of choosing inertia over active management is associated with (log) wealth, lagged stock market shocks, and lagged wage shocks in our simulated data (column 1) and the full PSID sample (column 2). We also provide results for the subset of PSID respondents with no business wealth (column 3), a group less likely to have rather uncertain income streams. This latter group was also the focus of Agnew, Balduzzi, and Sunden (2003), Bilias, Georgarakos, and Haliassos (2010), and Calvet, Campbell, and Sodini (2009).
Table 4. Factors associated with portfolio inertia (versus active management): key marginal effects from a descriptive logit analysis of simulated and PSID data.
Each column of this table reports the estimated impact of key variables from separate logit regressions, where the dependent variable equals one if the individual elected inertia in that period, or zero if active management. The first column reports results from simulated data from our life cycle model. The second and third columns report results from the full PSID sample and the subsample of non-business owners. Standard errors in parentheses.
| Inertia chosen (versus active management) | |||
|---|---|---|---|
| Simulated data | PSID data | PSID (non-business) | |
| Log wealth | −1.868*** (0.01) |
−0.084*** (0.01) |
−0.083*** (0.01) |
| Stock market shock | −0.139*** (0.04) |
−0.267 (0.18) |
−0.339* (0.19) |
| Wage shock | 1.304*** (0.10) |
0.056*** (0.02) |
0.055** (0.02) |
*, **, and *** indicate statistical significance at the 10%, 5%, and 1% levels, respectively. See online Appendix E for more on variable construction and controls.
Wealthier investors in our model are less likely to engage in inertia, all else equal, as indicated by the positive coefficient on log wealth of Table 4, column 1. This confirms our earlier results and those from prior work (see, e.g., Agnew, Balduzzi, and Sunden, 2003; Calvet, Campbell, and Sodini, 2009; Bilias, Georgarakos, and Haliassos, 2010). A similar result obtains in the next two columns for the full PSID sample and the subset of non-business owners. This is because sticking to a non-optimal level of equity exposure is more prejudicial for the wealthy, compared to their poorer counterparts. The negative coefficient on the lagged stock market return indicates that investors who experience a lagged positive stock market shock are less likely to elect portfolio inertia, both in our model and also in the PSID data. This is because a positive stock market shock boosts investors’ wealth, subsequently enhancing their interest in actively managing their portfolios. We also report comparable results from a lagged positive wage shock, which has a positive impact on the prevalence of inertia in both the model-generated data, and the two PSID samples. When wages are higher, investors will devote more time to acquiring training on the job, and less to managing their portfolios.
5.4. Sensitivity analysis
5.4.1. Examining the impact of learning-by-doing
To more clearly illustrate the importance of learning by doing in our model, we next conduct a sensitivity analysis by building and solving a model without the learning-by-doing mechanism used in our base case above. To do so, we restate the human capital function as follows:
| (20) |
The experience accumulation portion of our original human capital process Ft (lt, Ht) is now replaced by a deterministic function of age with parameters (a0, a1, a2). We then re-estimate parameters of this new human capital process (δ0, δ1, a0, a1, a2, λ) along with parameters of wage rate shocks (both transitory and permanent) by matching the model’s moment conditions with the moments of empirically observed wage profiles of male high school graduates derived using the PSID (Hubener, Maurer, and Mitchell, 2013; see also online Appendix C).29
Having turned off learning by doing, we next re-solve the model and compare results with our benchmark case. Before discussing findings, it is useful to note that there are two competing forces driving inertia when there is no learning by doing. The first is the reduced opportunity cost of active management which boosts active management (i.e., decreases inertia): an investor who manages his own assets must sacrifice only current leisure time or earnings, but not future human capital. The second results from the reduced attractiveness of work, given that employment no longer enhances future wages. This reduces labor supply and earnings as well as wealth, which in turn makes active management less profitable; the result is to discourage active management and increase inertia.
Table 5 replicates our baseline results in column 1, and the new findings appear in column 2. Clearly, the latter effect dominates, with an overall increase in inertia. Compared to our baseline findings, the inertia fraction rises by 10.5%, 13.09%, 9.2%, 10.89%, and 6.16% for ages 20–35, 36–50, 51–65, 66–80, and 80+, respectively, on average. Additionally, labor supply falls by about 44.41%, 29.19%, and 21.64% for those age 20–35, 36–50, and 51–65 respectively. When there is a learning-by-doing mechanism, the marginal benefit from additional work includes not only higher current income but also higher future earnings. Because young investors have a longer working horizon, their marginal benefit of working exceeds that of other age groups. For this reason, they seek to increase their working time by more (i.e., decrease their leisure time under the time budget constraint) compared to a model lacking a learning-by-doing mechanism.
Table 5. Sensitivity analysis: changes in portfolio management method with no delegation option.
This table shows the life cycle patterns of key variables for alternative model specifications. Column 1 uses baseline parameters as in Table 1. Column 2 shows results when human capital is deterministic over the life cycle, with no learning by doing. Column 3 shows results when the investor must pay a fixed initial stock market participation cost in addition to a recurring time cost. Column 4 provides results when the time cost of active management is set at a fixed 4% for all ages. Column 5 shows results when the endogenous human capital process is matched with the wage trends of college graduates in the PSID.
| Ages | (1) Baseline |
(2) No learning by doing |
(3) Initial participation cost |
(4) Flat time cost |
(5) College graduates |
|
|---|---|---|---|---|---|---|
| Inertia fraction | 20–35 | 0.755 | 0.860 | 0.770 | 0.742 | 0.729 |
| 36–50 | 0.552 | 0.682 | 0.556 | 0.547 | 0.502 | |
| 51–65 | 0.540 | 0.632 | 0.536 | 0.534 | 0.499 | |
| 66–80 | 0.496 | 0.605 | 0.498 | 0.439 | 0.460 | |
| 80+ | 0.703 | 0.765 | 0.701 | 0.573 | 0.694 | |
| Wealth | 20–35 | 0.432 | 0.240 | 0.422 | 0.435 | 0.455 |
| 36–50 | 0.982 | 0.675 | 0.970 | 0.986 | 1.039 | |
| 51–65 | 1.262 | 1.006 | 1.261 | 1.274 | 1.317 | |
| 66–80 | 1.163 | 0.963 | 1.151 | 1.190 | 1.201 | |
| 80+ | 0.685 | 0.572 | 0.680 | 0.825 | 0.697 | |
| Consumption | 20–35 | 0.224 | 0.131 | 0.225 | 0.223 | 0.231 |
| 36–50 | 0.267 | 0.188 | 0.265 | 0.266 | 0.279 | |
| 51–65 | 0.290 | 0.235 | 0.289 | 0.291 | 0.305 | |
| 66–80 | 0.216 | 0.196 | 0.215 | 0.214 | 0.224 | |
| 80+ | 0.229 | 0.209 | 0.228 | 0.233 | 0.234 | |
| Labor supply | 20–35 | 0.441 | 0.242 | 0.443 | 0.439 | 0.457 |
| 36–50 | 0.372 | 0.263 | 0.370 | 0.372 | 0.393 | |
| 51–65 | 0.323 | 0.254 | 0.323 | 0.325 | 0.347 | |
| Equity shares | 20–35 | 0.467 | 0.219 | 0.435 | 0.486 | 0.472 |
| 36–50 | 0.696 | 0.413 | 0.691 | 0.713 | 0.721 | |
| 51–65 | 0.632 | 0.431 | 0.627 | 0.646 | 0.683 | |
| 66–80 | 0.510 | 0.365 | 0.495 | 0.532 | 0.565 | |
| 80+ | 0.458 | 0.357 | 0.444 | 0.439 | 0.492 | |
| Earnings | 20–35 | 0.261 | 0.151 | 0.262 | 0.260 | 0.271 |
| 36–50 | 0.267 | 0.199 | 0.266 | 0.267 | 0.279 | |
| 51–65 | 0.267 | 0.224 | 0.267 | 0.268 | 0.278 | |
| 66–80 | 0.174 | 0.166 | 0.174 | 0.174 | 0.176 | |
| 80+ | 0.175 | 0.167 | 0.175 | 0.175 | 0.178 | |
| Human capital | 20–35 | 1.080 | 1.066 | 1.080 | 1.079 | 1.091 |
| 36–50 | 1.209 | 1.154 | 1.209 | 1.208 | 1.229 | |
| 51–65 | 1.271 | 1.218 | 1.270 | 1.270 | 1.294 | |
5.4.2. The impact of an initial stock market participation cost
We can also extend our model to include a fixed initial cost of stock market participation as in Cocco, Gomes, and Maenhout (2005) and Gomes and Michaelides (2005) to determine whether this could be driving inertia patterns. Because our model already has a stock account balance (Zt) as a state variable, we can define initial stock market participation as the case when the investor’s current period’s stock balance (Zt) is zero, but his chosen stock investment (St) out of savings is positive. This allows us to avoid creating an additional state variable.30
We model the fixed market participation cost as a fraction of the permanent wage shock as in Gomes and Michaelides (2005). Given an initial fixed cost of stock market participation, wealth evolves as follows:
| (21) |
where Yi, t is a permanent wage shock and Ii, t is an indicator variable for initial stock market participation that equals one when Zt = 0 and St > 0. As in Gomes and Michaelides (2005), the fixed cost F is set at 2.5% of the permanent wage shock. Column 3 of Table 5 presents the result of portfolio management methods with an initial participation cost. The new solution produces an overall pattern of inertia over the life cycle similar to what we have seen previously. The proportion of inertia managers increases only marginally early in life: during the first 15 years, initial participation costs increase inertia only by 1.5%. After that, the impact becomes minimal. In other words, an initial participation cost cannot fully explain observed inertia patterns in the data.
We also examine whether the U-shaped time cost is solely responsible for the U-shaped pattern of inertia our model generates over the life cycle. Our analysis shows that this is not the case. For instance, when we set the time cost at a flat 4% for all ages, column 4 of Table 5 shows that 74% of young investors (age 20–35) choose inertia, as do 53% of middle-aged investors (ages 51–65), 44% of early retirees (age 66–80), and 57% of older investors (age 80+). The ratio of inertia investors is slightly lower for the youngest and oldest investors, compared to the baseline case, but the U-shaped pattern is still clearly evident.
Column 5 of Table 5 presents a sensitivity analysis for college graduates, to evaluate how wage/age profiles influence results. We re-estimate parameters of the human capital process with the observed wage trend for college graduates in the PSID and re-solve the model. Compared to the baseline case of high school graduates, college graduates earn higher labor income, have higher wealth, work more, and invest more in equity. Compared to the baseline case, the inertia level for college grads is modestly less than for the high school educated: 73% versus 76% for ages 20–35, 50% versus 54% for ages 51–65, and 69% versus 70% for ages 80+). The U-shaped pattern of inertia again persists.
6. Results and discussion with a delegation option
6.1. Portfolio management patterns
Next we turn to an evaluation of how portfolio management methods change when a financial advisor is available. Table 6 summarizes results from our model simulations.31 On average, investors now change their portfolio management approach much more often, almost 18 times over their lives (17.91 versus 11.44 in Table 2), and they elect inertia for a shorter period (46.76 years versus 49.21 in Table 2). Of most interest is the fact that people devote about one-third as many years to active management (10.87 versus 30.79 previously), and they engage advisors for about one-quarter of their adult lives (= 22.37 years/80). Investors begin to delegate relatively soon, only 10.03 years from beginning to work, and about 80% of people elect to delegate at some point (80% = 1,570/2,000). Additionally, when delegation is an option, fewer choose active management; among those who do, they begin later, 13.47 years after starting work (versus 8.02 in Table 2).
Table 6. Dynamics of portfolio management over the life cycle with a delegation option.
This table tabulates results from 2,000 simulation runs of base case model. For definitions, see Table 2. Years of delegation refers to the length of the delegated management period for specific simulated life cycle paths. First year delegation refers to the first year when people change to delegation from inertia or from active management. Some people never elect active management or delegation which is why the total number of observations of First year of active mgmt and First year delegation is less than the total number of simulations.
| Mean | StDev | Median | 5%-Q | 95%-Q | N | |
|---|---|---|---|---|---|---|
| No of switches | 17.91 | 10.71 | 20.00 | 0.00 | 33.00 | 2,000 |
| Years of inertia | 46.76 | 25.38 | 43.50 | 12.00 | 80.00 | 2,000 |
| Years of active mgmt | 10.87 | 7.52 | 11.00 | 0.00 | 23.00 | 2,000 |
| Years of delegation | 22.37 | 20.12 | 22.00 | 0.00 | 52.05 | 2,000 |
| First year change | 7.75 | 6.87 | 6.00 | 4.00 | 16.00 | 1,770 |
| First year active mgmt | 13.47 | 8.94 | 12.00 | 5.00 | 29.00 | 1,765 |
| First year delegation | 10.03 | 9.86 | 6.00 | 4.00 | 29.00 | 1,570 |
Table 7 shows what happens when investors can delegate their investment management to a financial advisor. Panel A illustrates patterns of portfolio management methods by age, where we see that access to delegation reduces inertia and active management compared to results in Fig. 2. Delegation is attractive for investors of all ages: approximately 20% of young investors (under age 35), 27% of middle-aged investors (age 36–65), and around 37% of older retirees (age 80+) now optimally delegate to a financial advisor. Access to delegation substantially reduces active management, especially among the youngest and oldest investors. Active management is adopted by only a small fraction of the youngest (8%) and oldest investors (less than 1%), but by many more (around 20%) middle-aged and early retirees (about 25%). Early retirees become the most active investor group because they have no opportunity cost of forgone labor supply and must optimally withdraw from their stock accounts to meet retirement consumption needs. Rather than paying a delegation fee, they instead actively manage their stock accounts by withdrawing before mortality risk raises, and prior to a decline in decision making efficiency.
Table 7. Portfolio management transitions and equity choice over the life cycle with a delegation option.
This table illustrates investors’ life cycle patterns of portfolio management methods and equity shares when delegation is feasible. Panel A shows the fraction of investors selecting inertia, active management, or delegation, by age. Panel B traces transitions across portfolio management methods, given a delegation option. Panel C depicts the average fraction of savings invested in equities depending on whether the investor elects inertia, active management, or delegation. Savings refer to total wealth minus consumption. Averages are generated from 2,000 independent simulations for individuals based on optimal feedback controls from the baseline specification of the life cycle model.
| Panel A: Choice of portfolio management method, by age (%) | ||||||
| Age | 20–35 | 36–50 | 51–65 | 66–80 | 80+ | Total |
| Inertia | 73.44 | 53.1 | 51.98 | 48.87 | 63.25 | 58.45 |
| Active mgmt | 7.93 | 19.54 | 19.1 | 25.67 | 0.16 | 13.58 |
| Delegation | 18.63 | 27.35 | 28.92 | 25.46 | 36.59 | 27.97 |
| Panel B: Portfolio management transitions, by age (%) | ||||||
| Age | 20–35 | 36–50 | 51–65 | 66–80 | 80+ | Total |
| Inertia to: | ||||||
| Inertia | 94.45 | 84.21 | 85.24 | 93.80 | 87.45 | 89.12 |
| Active mgmt | 1.46 | 7.09 | 6.21 | 2.90 | 0.04 | 2.99 |
| Delegation | 4.09 | 8.70 | 8.56 | 3.30 | 12.51 | 7.88 |
| Active management to: | ||||||
| Inertia | 8.66 | 14.85 | 12.97 | 4.57 | 5.83 | 9.43 |
| Active mgmt | 27.93 | 34.86 | 34.22 | 48.11 | 0.44 | 30.51 |
| Delegation | 63.41 | 50.29 | 52.80 | 47.32 | 93.73 | 60.06 |
| Panel C: Equity fraction out of savings, by age (%) | ||||||
| Age | 20–35 | 36–50 | 51–65 | 66–80 | 80+ | Total |
| Inertia | 34.9 | 64.3 | 61.3 | 50.8 | 46.8 | 50.0 |
| Active mgmt | 92.3 | 85.2 | 73.6 | 56.1 | 26.5 | 72.4 |
| Delegation | 74.4 | 74.3 | 67.9 | 49.2 | 38.6 | 57.1 |
| Total | 46.8 | 71.1 | 65.5 | 51.8 | 43.8 | 55.0 |
Panel B of Table 7 decomposes portfolio management methods when the delegation option is available. Among those initially electing inertia or active management when a delegation option is not available, younger and older investors are more likely to switch to delegation. Among middle-aged individuals (36–65), active investors are also likely to continue with active management. This pattern is related to the opportunity cost of time. Young investors, who have the longest horizon to earn human capital returns, find it optimal to elect the delegation option. Older investors facing high mortality risk and inefficiency of financial management also favor financial advisors, to save them leisure time. By contrast, middle-aged investors with high wealth and human capital face a lower opportunity cost of time, and hence they will manage their portfolios themselves and avoid paying the delegation fee. Early retirees are more likely to engage in active management as they need not worry about accumulating job-specific skills any more. It should be noted that the decision to delegate among the young and old investors is affected by the assumption regarding a required minimum fixed fee: some inertia investors cannot gain access to financial advisors, as they have insufficient wealth. Below, we discuss how lowering the minimum fixed fee shapes investors’ decisions to hire an advisor.
Panel C of Table 7 represents the average fraction of savings invested in equities, depending on whether the investor elects inertia, active management, or delegation. For investors choosing active management, the fraction of savings invested in equity follows a glide path consistent with the traditional portfolio choice literature. Inertia investors hold little equity when young and more equity when old, similar to the no-delegation case. Interestingly, the delegated portfolio also follows a downward-sloping glide path, but the slope is flatter.
Table 8 summarizes how behavior changes for profiles of wealth, equity share, labor income, labor supply, human capital, and consumption by age, when a delegation option is available. All results are expressed as a percent of the no-delegation base case. We see that having access to an advisor increases wealth by 1.1–2.7% across age groups before retirement and up to 13% in the 80+ age group. This is due to the higher equity share noted above in the early career stages, and also to spending more time on the job which builds human capital. Having access to an advisor also increases leisure around 2–4% before age 80 and up to 20% in the very older ages (80+) when the time cost of active management is high, and it also raises consumption considerably across all age groups.
Table 8. Change in key variables with versus without a delegation option (%).
The numbers in this table represent the percentage increase in key variables summed over individuals in the relevant age group having access to a delegation option, versus not having access to a delegation option. Equity share refers to the fraction of savings invested in equities (St / (St + Bt)). Averages for total wealth are value-weighted. See text.
| Age | Total wealth | Equity share | Labor income | Consumption | Labor supply | Human capital | Leisure |
|---|---|---|---|---|---|---|---|
| 20–35 | 1.08 | 0.09 | 4.50 | 2.99 | 4.22 | 0.06 | 1.62 |
| 36–50 | 2.35 | 1.63 | 9.43 | 7.72 | 8.16 | 0.18 | 4.01 |
| 51–65 | 2.66 | 2.25 | 12.09 | 13.09 | 10.65 | 0.27 | 3.94 |
| 66–80 | 0.96 | 0.87 | – | 0.22 | – | – | 4.23 |
| 80+ | 13.44 | −2.24 | – | 6.35 | – | – | 19.68 |
6.2. Welfare gains from access to financial advice
To assess how consumers value access to a delegation option, we next compare consumer welfare in a delegation regime versus that in a no-delegation world. We measure this in terms of a certainty equivalent (CE) consumption stream change, or the stream of consumption that would afford the investor the same level of expected lifetime utility if he lacked access to the delegation option, versus having it.32 Table 9, Panel A, shows for our baseline specification (column 1) that providing investors with access to a financial advisor increases lifetime welfare by the equivalent of a 1.1% enhancement in their lifetime consumption. This is similar in magnitude to the improvement reported by Cocco, Gomes, and Maenhout (2005) who compared welfare levels in two worlds, one with a fixed and the other with a flexible equity share.
Table 9. Sensitivity analysis: welfare gains and change in portfolio management method with a delegation option.
Panel A presents welfare gains or losses from having a delegation option versus the no-delegation (baseline) case for alternative specifications of minimum fixed delegation fees. Welfare gain is the percentage increase in the household’s certainty-equivalent consumption stream compared to the no-delegation case. Panel B describes the proportion of investors electing each portfolio management method under different specifications of fees. Delegation, Inertia, and Active mgmt refer to the proportions of investors across all ages choosing delegation, inertia, and active management, respectively. Column 1 shows baseline results with a minimum fee of $2,115 (commensurate with a minimum balance of $150,000). Column 2 provides results when there is no minimum fee for delegation. Column 3 reports results from imposing a minimum fee commensurate with a higher required minimum balance ($243,360), consistent with the industry average. Panel C presents the welfare gain/loss of having access to a Target Date Fund (TDF) but not the delegation option. Column 1 reports the welfare gain with a target date fund fee equal to the current industry level (0.084%). Columns 2 and 3 provide results using a zero and 0.5% TDF fee, respectively. Panel D describes the proportion of investors electing each portfolio management method including target date funds. TDF refers to the proportion of investors choosing target date funds.
| Panel A: Welfare gain from a delegation option (%) | |||
| (1) Baseline |
(2) No minimum fee |
(3) Current industry fees |
|
| Welfare gain | 1.066 | 1.2973 | 0.9044 |
| Panel B: Fraction by portfolio management method with delegation (%) | |||
| (1) Baseline |
(2) No minimum fee |
(3) Current industry fees |
|
| Delegation | 27.97 | 36.20 | 13.59 |
| Inertia | 58.45 | 54.70 | 60.04 |
| Active | 13.59 | 9.10 | 26.37 |
| Panel C: Welfare gain from a target date fund instead of a delegation option (%) | |||
| (1) Baseline |
(2) TDF fee = 0.5% |
(3) TDF fee = 0% |
|
| Welfare gain | 0.382 | 0.5655 | 1.0102 |
| Panel D: Life cycle fraction by portfolio management method with target date fund (%) | |||
| (1) Baseline |
(2) TDF fee = 0.5% |
(3) TDF fee = 0% |
|
| TDF | 21.38 | 23.18 | 42.23 |
| Inertia | 45.27 | 44.00 | 21.04 |
| Active | 33.35 | 32.81 | 36.73 |
In a sensitivity analysis for different costs of financial advice, we evaluate investors’ potential welfare gains from lowering entry barriers to financial advisory services. As noted above, current industry practice is to set a minimum fixed fee commensurate with a required minimum asset balance of about $240,000, which is high, compared to average investors’ asset levels. Column 2 of Panel A shows that eliminating the minimum fee for advisory services would raise welfare by 1.3%, compared to the case where no delegation is available. This welfare improvement results from the fact that less-wealthy investors gain access to cheaper financial advice, allowing them to use their time for leisure or work leading to higher labor income. Conversely, as seen in column 3, Panel A, a higher minimum fee commensurate with the industry’s average required minimum balance of around $240,000 cuts the welfare gains by about 30%, compared to the case of no minimum fee (column 2).
Column 2 of Panel B shows that, compared to the baseline case, eliminating the minimum fee increases investors’ usage of a financial advisor by 9 percentage points. At the same time, both inertia and active management decline. In column 3 of Panel B where financial advisors impose high minimum fees, we see that very few people, mainly those at the top of the wealth distribution, access the service at this higher cost. Only about 13.6% of investors select the delegation option. Compared to the no minimum fee case (column 2), a higher minimum fee induces most people to find it optimal to manage their money themselves (i.e., actively manage), rather than to pay the high advisory fee (i.e., delegation). In other words, lowering the entry barrier to financial advisory services can help people of all ages manage their financial assets optimally, especially the young and the old. This saves their scarcest resource, which is time for accumulating more job-specific skills or enjoying leisure.
It is also of interest to consider how target date funds (TDFs) might compare as a low-cost alternative to the delegation option. With TDFs, investors need not actively manage their portfolios, but their equity investments still follow a glide path without having to hire a financial advisor. We incorporate TDFs in our model along with inertia and active management in the following way:
| (22) |
where is a percentage fee of total wealth (Wt) and πt is an age-based rule for equity investment defined as (Cocco, Gomes, and Maenhout, 2005; Malkiel, 1996).33 With this option, investors need not decide on equity investments, but instead they can concentrate on choosing consumption and leisure paths to maximize utility. Accordingly, they need not incur the time costs associated with investing in stock.34
Results appear in Table 9 in Panel C. To compute welfare changes, we adopt the average TDF fee of 0.84% per year reported by Yang and Lutton (2014). Compared to the baseline model with only inertia and active management options, the target date fund does enhance welfare by about 0.38%. Nevertheless, this is lower than having a delegation option by about half a percentage point. This lower gain results from the fact that target date portfolios follow an age-based glide path, without taking into account investors’ particulars with regard to financial and labor market shocks. Only if the target date fund were available at no charge would it generate welfare on par with that from the delegation option (compare column 3 of Panel C and column 1 of Panel A). Panel D reports the proportion of investors choosing TDFs along with inertia and active management. Interestingly, in the baseline case of TDFs (column 1 of Panel D), we observe investors choose more active management with TDFs than with a delegation option (column 1 of Panel B). This is consistent with investors’ needs to customize their portfolios from time to time if they have only a choice between inertia or an age-based equity rule under the TDF.35
7. Conclusions and discussion
Workers and retirees are increasingly expected to manage their own finances with ever-more complex financial products. Nevertheless, most people exhibit investor inertia, devoting only sparse attention to their financial portfolios and fail to actively manage their finances. To understand what might seem to be puzzling behavior, we build and solve a realistically calibrated life cycle model where the time cost required to manage one’s portfolio is traded off with the opportunity to accumulate job-specific knowledge.
Our resulting inertia patterns mesh well with findings from prior studies and our own empirical analysis with PSID data. Investors who can accumulate job-specific knowledge by working tend to devote less time to managing their money when young. Middle-aged individuals have more assets to invest and suffer less from the opportunity costs of active portfolio management, though many still elect inertia. Declining decision making efficiency and rising mortality risk later in life prompts many older investors to elect portfolio inertia. When investors can optimally delegate portfolio management to a financial advisor, this enables many to avoid portfolio inertia. In general, our model predicts that younger and older investors will find financial advisors most attractive. Charging industry-average fees, we find that having access to a delegation option raises lifetime welfare by a reasonable 1.1%. By contrast, an investor only having access to standard target date funds instead of a financial advisor would enjoy half the welfare gain, because the simple age-based glide path offered by TDFs does not take into account the financial and labor market shocks affecting investors.
This research contributes to a growing body of research on financial decision making over the life cycle using insights from cognitive science (Agarwal, Driscoll, Gabaix, and Laibson, 2009; Korniotis and Kumar, 2011; Samanez-Larkin and Knutson, 2014). This is an area of substantial policy interest in the wake of the global financial crisis and the continued trend toward global aging. In the US for instance, the White House recently convened a multi-agency meeting of behavioral economists and psychologists to better understand how decision making changes for older persons (National Institute on Aging, 2013). Our work adds to the discussion by illustrating optimal portfolio management methods selected by finitely lived investors who face portfolio management costs and an age-dependent inefficiency pattern for financial decision making. We also show the impact of different management fees.
One topic we do not take up here is the possibility of a conflict of interest between an investor seeking to maximize his utility, and his financial advisor seeking to maximize his own income. For example, if an advisor’s compensation is commission-based, he might be likely to encourage “return-chasing” or high-fee actively managed mutual funds (Mullainathan, Noeth, and Schoar, 2012). The present paper considers only fee-based advice, which is less susceptible to such conflicts, but future work could consider the potential for moral hazard if investors are uninformed. Additional extensions might also extend our model with parameter uncertainty and learning (Xia, 2001). Nevertheless, our key insight linking job-specific human capital and portfolio inertia will be relevant as long as a time cost of financial management has negative consequences for labor market earnings.
Our findings should be of interest to a variety of stake-holders including individual investors, financial advisors, retirement plan sponsors, and policymakers. In particular, we show that those who most value financial advisory services are the younger and the older age groups, so targeting these groups could enhance their well-being. Also of interest is the prediction that some middle-aged clients will wish to continue actively managing their own financial assets even when a delegation option (or a less-costly target date suite of mutual funds) is available. Policymakers could do more to enhance welfare gains by improving investor access to financial advisory services. When financial advisors with fiduciary responsibility can help investors manage their financial wealth optimally, this will enable more people to accrue job-specific skills, thus contributing to the economy as a whole.
Supplementary Material
Acknowledgments
The authors are grateful for research support provided by NIH/NIA grant no. P30 AG12836 and NIH/NICHD Population Research Infrastructure Program R24 HD-044964, and the Pension Research Council/Boettner Center for Pensions and Retirement Security at the University of Pennsylvania. The authors also received research funding from the Special Research Fund at the SKK GSB, SKK University, the Metzler Exchange Professor program at the Goethe University of Frankfurt, and the German Investment and Asset Management Association (BVI). They are grateful for comments from Santosh Anagol, Alex Gelber, Itay Goldstein, Andreas Hubener, Dana Kiku, Jialun Li, David Love, David Musto, Stijn Van Nieuwerburgh, Greg Nini, Nick Roussanov, Kent Smetters, Robert Stambaugh, Jeremy Tobacman, Steve Utkus, Jessica Wachter, and Jacqueline Wise. The authors also thank conference and seminar participants at European Conference on Household Finance 2014, American Risk and Insurance Association Meeting 2011, Goethe University, KAIST Business School, Korea University, SKK GSB, Seoul National University, University of Cincinnati and Wharton School. The Wharton High Performance Computing Platform provided an excellent setting for the numerical analysis. All opinions, findings, interpretations, and conclusions represent the views of the authors and not those of the affiliated institutions.
Footnotes
For additional evidence on this point, see Calvet, Campbell, and Sodini (2009), Choi, Laibson, Madrian, and Metrick (2002), Dellavigna and Pollet (2009), Madrian and Shea (2001), and Tang, Mitchell, Mottola, and Utkus (2010). Barber and Odean (2000) did find evidence of churning among some account holders at a large discount brokerage company in 1996, yet their unusual sample is not characteristic of typical investors.
Among these are Bodie, Merton, and Samuelson (1992), Gomes, Kotlikoff, and Viceira (2008), and Chai, Horneff, Maurer, and Mitchel (2011).
There is a vast literature on on-the-job skill acquisition; see, for in-stance, Arrow (1962), Becker (1964), Lucas (1988), and Levitt, List, and Syverson (2013), among others. Some people may enjoy self-management or believe they can outperform the market as well as professional investors, though few actually do so in practice: their performance is often worse than average (Barber and Odean, 2000; Lusardi and Mitchell, 2007). Additionally, peoples’ portfolio allocations across mutual funds often yield low returns due to infrequent rebalancing (Frazzini and Lamont, 2008).
In our model, the agent must re-solve his life cycle model and implement new choices each period, so he incurs new time costs every time he engages in active management.
This can also be interpreted as a rate of skill obsolescence; that is, some knowledge becomes outdated by the advent of new technology.
Below we estimate the parameters of a human capital accumulation process by matching the model-generated moments with those of the age-specific deterministic wage profile taken from the PSID data as in Hubener, Maurer, and Mitchell (2013).
Tang, Mitchell, Mottola, and Utkus (2010) report that people receive lower returns when they manage their own portfolios, compared to having professionals manage them. For simplicity, we assume that equity returns are the same for all portfolio management methods (inertia, active management, and delegation).
We could have considered three accounts, namely, a brokerage account for stock investment, a savings account for bond investments, and a checking account for consumption as in Abel, Eberly, and Panageas (2013). In our study, however, the focus is not on the transaction costs of transferring between checking and investment accounts (i.e., stock and bond investment accounts). Moreover, evidence on investor inertia also suggests that investors are not greatly affected by transaction costs (Brunnermeier and Nagel, 2008). Additionally, most banks provide free transfers between savings and checking accounts, and US money market funds provide bond returns while allowing frequent withdrawals. For these reasons, we focus here on a case where investors can consume from their total liquid assets (stock plus bonds plus labor earnings) and incur time costs when collecting or processing information to manage their stock/bond portfolios.
The recurring time cost (or cognitive attention/resources) for gathering and processing information for financial management is also consistent with a recent literature on optimal inattention and economic decision making (e.g., Abel, Eberly, and Panageas, 2013; Sims, 2003).
We could introduce a direct transaction cost TC(St, Zt) for portfolio adjustment, in which case the equation for total wealth would be Wt+1 = StRt+1 + BtR̄ + Et+1 − TC(St, Zt) 1{adjustment}. Nevertheless, we do not focus here on direct monetary costs; see Bonaparte and Cooper (2009) and Campanale, Fugazza, and Gomes (2014) for more on that approach.
See online Appendix A for a discussion of the fee structures used by US Registered Investment Advisors (RIA) under SEC regulations.
We do not model a possible conflict of interest between clients and financial advisors; these have been analyzed by Ou-Yang (2003), Bergstresser, Chalmers, and Tufano (2009), Stoughton, Wu, and Zechner (2011), Hackethal, Haliassos, and Jappelli (2012), and Mullainathan, Noeth, and Schoar (2012), among others.
Technically, we implement a simulated method of moment procedure (SMM) by numerically minimizing the distance of various moments (i.e., mean, standard deviation, median, skewness, kurtosis, max, min, and the age of maximum wage) of the simulated human capital accumulation process given in Eqs. (2) and (3) relative to the (deterministic) age-dependent wage profile used in the literature (Gomes, Kotlikoff, and Viceira, 2008; Hubener, Maurer, and Mitchell, 2013). A more detailed explanation of this procedure appears in online Appendix C.
Registered Investment Advisors (RIAs) in the US must file with the SEC before they can provide advice on financial investments including stocks, bonds, and mutual funds. They can also help implement clients’ optimal portfolio choices; see Mitchell and Smetters (2013).
This is one reason that our baseline model without a delegation option appears realistic for the majority of real-world investors.
As discussed in online Appendix A, the current minimum advisory fee commensurate with a $250,000 balance makes the no delegation case a realistic environment for most individual investors.
More specifically, Ameriks and Zeldes (2004, Fig. 7) provide empirical evidence of a hump-shaped equity investment pattern unconditional on stock market participation and controlling on cohort effects. This is consistent with our model setting where we do not have cohort effects and consider an average equity investment pattern unconditional on stock market participation.
The Bureau of Labor Statistics (BLS Economic releases, Table B-2) reports average weekly working hours of 34.6 hours. The Organization for Economic Cooperation and Development (OECD) documents about 1,800 annual working hours for US workers (http://stats.oecd.org/index.aspx?DataSetCode=ANHRS), a similar value to that reported in Low (2005) using data from the Consumer Expenditure Survey.
In our notation, the equity share of each investor is defined as St / (St + Bt).
The gradual drawdown of assets from the bond account does not impose time costs, in contrast to transactions in the stock account.
Online Appendix D discusses a sufficient condition for inertia choice.
Earlier PSID survey waves (prior to 1999) collected transaction data only every five years, which makes those data highly subject to recall error. We also exclude two later waves (from 2009 and 2011) to avoid the confounding effects of the financial crisis. Nevertheless, when we include 2009 and 2011, our results (available on request) are similar to those reported here.
See online Appendix E for further details on the definition of variables and the sample selection process.
Raising the wealth cutoff to $100 million or higher produces results both qualitatively and quantitatively similar; results available on request.
The estimated values are −0.0125 (δ0), −0.00012542 (δ1), 0.0011 (a0), −0.0080 (a1), 0.000081419 (a2), 6.49% (λ), 30.78% (transitory wage shock), 6.87% (permanent wage shock).
This specification cannot rule out the possibility that an investor would need to incur participation costs again when he returns to the stock market after liquidating his entire equity position. However, our simulation results show that the fraction of returning stock investors is minimal to none (zero in 2,000 simulations).
We are unaware of any micro longitudinal data reporting portfolio management methods including a delegation option comparable to the PSID, which we might use to compare with our model results in this section.
While there are some variations in age-based glide paths across different fund family target date mutual fund offerings, the average TDF profile has about 80–90% equities at age 20 and about 40% at age 65 (Yang and Lutton, 2014).
With the TDF as an alternative option to the delegation, the value function is defined as .
When we compare the (inertia + TDF) case with the (inertia + active) case, the former produces a 6.88% welfare decline compared to the latter. In the context of our model of portfolio inertia, this implies that people having access to TDFs would not completely eschew active management. When we compare the (inertia + TDF) case with the (inertia + active + TDF) case, the former produces a 7.25% welfare decline compared to the latter; this implies that investors still value a flexible portfolio choice option even when they have a low-cost portfolio rebalancing vehicle available.
Appendix
Please check internet appendix.
References
- Abel A, Eberly JC, Panageas S. Optimal inattention to the stock market with information costs and transaction costs. Econometrica. 2013;81:1455–1481. [Google Scholar]
- Adda J, Cooper RW. Balladurette and Juppette: a discrete analysis of scrapping subsidies. Journal of Political Economy. 2000;108:778–806. [Google Scholar]
- Agarwal S, Driscoll JC, Gabaix X, Laibson D. The age of reason: financial decisions over the life-cycle with implications for regulation. Brookings Papers on Economic Activity. 2009;40:51–117. [Google Scholar]
- Agnew J, Balduzzi P, Sunden A. Portfolio choice and trading in a large 401(k) plan. American Economic Review. 2003;93:193–215. [Google Scholar]
- Ameriks J, Zeldes SP. Working paper. Columbia University; 2004. How do household portfolio shares vary with age? [Google Scholar]
- Arrow KJ. The economic implications of learning by doing. Review of Economic Studies. 1962;29:155–173. [Google Scholar]
- Barber BM, Odean T. Trading is hazardous to your wealth: the common stock investment performance of individual investors. Journal of Finance. 2000;55:773–806. [Google Scholar]
- Battistin E, Brugiavini A, Rettore E, Weber G. The retirement consumption puzzle: evidence from a regression discontinuity approach. American Economic Review. 2009;99:2209–2226. [Google Scholar]
- Becker G. Human Capital. Chicago, IL: The University of Chicago Press; 1964. [Google Scholar]
- Bell FC, Miller ML. Life tables for the US Social Security Area 1900–2010. OACT Actuarial Study No. 120. 2012 http://www.ssa.gov/oact/NOTES/as120/LifeTables_Body.html.
- Ben-Porath Y. The production of human capital and the life cycle of earnings. Journal of Political Economy. 1967;75:352–365. [Google Scholar]
- Bergstresser D, Chalmers JMR, Tufano P. Assessing the costs and benefits of brokers in the mutual fund industry. Review of Financial Studies. 2009;22:4129–4156. [Google Scholar]
- Bilias Y, Georgarakos D, Haliassos M. Portfolio inertia and stock market fluctuations. Journal of Money, Credit and Banking. 2010;42:715–742. [Google Scholar]
- Bodie Z, Merton RC, Samuelson WF. Labor supply flexibility and portfolio choice in a life cycle model. Journal of Economic Dynamics and Control. 1992;16:427–449. [Google Scholar]
- Bonaparte Y, Cooper R. Costly portfolio adjustment. NBER working paper no. 15227. 2009 [Google Scholar]
- Brunnermeier MK, Nagel S. Do wealth fluctuations generate time-varying risk aversion? Micro-evidence on individuals’ asset allocation. American Economic Review. 2008;98:713–736. [Google Scholar]
- Bureau of Labor Statistics (BLS) American Time Use Survey. US Department of Labor; 2012. http://www.bls.gov/tus/ [Google Scholar]
- Calvet LE, Campbell JY, Sodini P. Fight or flight? Portfolio rebalancing by individual investors. Quarterly Journal of Economics. 2009;124:301–348. [Google Scholar]
- Campanale C, Fugazza C, Gomes F. Life cycle portfolio choice with liquid and illiquid financial assets. Journal of Monetary Economics. 2014;71:67–83. [Google Scholar]
- Campbell JY, Jackson HE, Madrian BC, Tufano P. Consumer financial protection. Journal of Economic Perspectives. 2011;25:91–114. doi: 10.1257/jep.25.1.91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlin BI. Strategic price complexity in retail financial markets. Journal of Financial Economics. 2009;91:278–287. [Google Scholar]
- Carroll CD. Buffer-stock saving and the life-cycle/permanent income hypothesis. Quarterly Journal of Economics. 1997;112:1–55. [Google Scholar]
- Chai J, Horneff W, Maurer R, Mitchell OS. Optimal portfolio choice over the lifecycle with flexible work, endogenous retirement, and lifetime payouts. Review of Finance. 2011;15:875–907. [Google Scholar]
- Chiang Y, Hirshleifer D, Qian Y, Sherman AE. Do investors learn from experience? Evidence from frequent IPO investors. Review of Financial Studies. 2011;24:1560–1589. [Google Scholar]
- Choi J, Laibson D, Madrian B, Metrick A. Defined contribution pension: plan rules, participant choices, and the path of least resistance. In: Poterba JM, editor. Tax Policy and the Economy. Vol. 16. Cambridge, MA: MIT Press; 2002. [Google Scholar]
- Christelis D, Jappelli T, Padula M. Cognitive abilities and portfolio choice. European Economic Review. 2010;54:18–38. [Google Scholar]
- Cocco JF, Gomes FJ. Longevity risk, retirement savings, and financial innovation. Journal of Financial Economics. 2012;103:507–529. [Google Scholar]
- Cocco JF, Gomes FJ, Maenhout PJ. Consumption and portfolio choice over the life cycle. Review of Financial Studies. 2005;18:491–533. [Google Scholar]
- Dellavigna S, Pollet J. Investor inattention and Friday earnings announcements. Journal of Finance. 2009;64:709–749. [Google Scholar]
- Frazzini A, Lamont OA. Dumb money: mutual fund flows and the cross-section of stock returns. Journal of Financial Economics. 2008;88:299–322. [Google Scholar]
- Gamble KJ, Boyle PA, Yu L, Bennett DA. Aging and financial decision making. Management Science. 2015;61(11):2603–2610. doi: 10.1287/mnsc.2014.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gomes FJ, Kotlikoff LJ, Viceira LM. Optimal life cycle investing with flexible labor supply: a welfare analysis of life cycle funds. American Economic Review Papers and Proceedings. 2008;98:297–303. [Google Scholar]
- Gomes FJ, Michaelides A. Optimal life cycle asset allocation: understanding the empirical evidence. Journal of Finance. 2005;60:869–904. [Google Scholar]
- Hackethal A, Haliassos M, Jappelli T. Financial advisors: a case of babysitters? Journal of Banking and Finance. 2012;36:509–524. [Google Scholar]
- Horn RB, Cattell RB. Age differences in fluid and crystalized intelligence. Acta Psychologica. 1967;26:107–129. doi: 10.1016/0001-6918(67)90011-x. [DOI] [PubMed] [Google Scholar]
- Hubener A, Maurer R, Mitchell OS. How family status and social security claiming options shape optimal life cycle portfolios. NBER working paper 19583. 2013 doi: 10.1093/rfs/hhv070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korniotis GM, Kumar A. Do older investors make better investment decisions? Review of Economics and Statistics. 2011;93:244–265. [Google Scholar]
- Levitt DS, List JA, Syverson C. Toward an understanding of learning by doing: evidence from an automobile assembly plant. Journal of Political Economy. 2013;121:643–681. [Google Scholar]
- Love AD. The effects of marital status and children on savings and portfolio choice. Review of Financial Studies. 2010;23:385–432. [Google Scholar]
- Low H. Self-insurance in a life cycle model of labor supply and savings. Review of Economic Dynamics. 2005;8:945–975. [Google Scholar]
- Lucas RE., Jr On the mechanics of economic development. Journal of Monetary Economics. 1988;22:3–42. [Google Scholar]
- Lusardi A, Mitchell OS. Baby boomer retirement security: the roles of planning, financial literacy, and housing wealth. Journal of Monetary Economics. 2007;54:205–224. [Google Scholar]
- Lusardi A, Mitchell OS. The economic importance of financial literacy: theory and evidence. Journal of Economic Literature. 2014;52:5–44. doi: 10.1257/jel.52.1.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madrian B, Shea D. The power of suggestion: inertia in 401(k) participation and savings behavior. Quarterly Journal of Economics. 2001;116:1149–1188. [Google Scholar]
- Malkiel BG. A Random Walk Down Wall Street: Including a Life–Cycle Guide to Personal Investing. sixth. New York: Norton; 1996. [Google Scholar]
- Mitchell OS, Smetters K, editors. The Market for Financial Advice. Oxford, Oxford: Oxford University Press; 2013. [Google Scholar]
- Mullainathan S, Noeth M, Schoar A. The market for financial advice: an audit study. NBER working paper no. 17929. 2012 [Google Scholar]
- National Institute on Aging (NIA) Meeting Summary: Psychological Science and Behavioral Economics in the Service of Public Policy. 2013 http://www.nia.nih.gov/sites/default/files/psychological_science_and_behavioral_economics.pdf.
- Ou-Yang H. Optimal contracts in a continuous-time delegated portfolio management problem. Review of Financial Studies. 2003;16:173–208. [Google Scholar]
- Samanez-Larkin GR, Knutson B. Reward processing and risky decision making in the aging brain. In: Reyna VF, Zayas V, editors. The Neuroscience of Risky Decision Making. Washington, DC: American Psychological Association; 2014. [Google Scholar]
- Sims CA. Implications of rational inattention. Journal of Monetary Economics. 2003;50:665–690. [Google Scholar]
- Stoughton N, Wu Y, Zechner J. Intermediated investment management. Journal of Finance. 2011;66:947–980. [Google Scholar]
- Tang N, Mitchell OS, Mottola GR, Utkus SP. The efficiency of sponsor and participant portfolio choices in 401(k) plans. Journal of Public Economics. 2010;94:1073–1085. [Google Scholar]
- US Census Bureau. The 2012 Statistical Abstract. Table 1211 Stock ownership by age of head of family and family income: 2001 to 2007. 2012 http://www.census.gov/compendia/statab/cats/banking_finance_insurance/stocks_and_bonds_equity_ownership.html.
- US Security and Exchange Commission (SEC) Mandatory disclosure documents telephone survey. 2008 http://www.sec.gov/pdf/disclosuredocs.pdf.
- van Rooij M, Lusardi A, Alessie R. Financial literacy and stock market participation. Journal of Financial Economics. 2011;101:449–472. [Google Scholar]
- Xia Y. Learning about predictability: the effects of parameter uncertainty on dynamic asset allocation. Journal of Finance. 2001;56:205–246. [Google Scholar]
- Yang J, Lutton LP. Target-Date Series Industry Survey. 2014. Morningstar Research Report. 2014 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.