Abstract
We describe a new residual for general regression models, defined as pr(Y* < y) − pr(Y* > y), where y is the observed outcome and Y* is a random variable from the fitted distribution. This probability-scale residual can be written as E {sign(y, Y*)} whereas the popular observed-minus-expected residual can be thought of as E(y − Y*). Therefore, the probability-scale residual is useful in settings where differences are not meaningful or where the expectation of the fitted distribution cannot be calculated. We present several desirable properties of the probability-scale residual that make it useful for diagnostics and measuring residual correlation, especially across different outcome types. We demonstrate its utility for continuous, ordered discrete, and censored outcomes, including current status data, and with various models including Cox regression, quantile regression, and ordinal cumulative probability models, for which fully specified distributions are not desirable or needed, and in some cases suitable residuals are not available. The residual is illustrated with simulated data and real datasets from HIV-infected patients on therapy in the southeastern United States and Latin America.
Keywords and phrases: Diagnostics, generalized linear model, HIV, quantile regression, rank statistics, survival analysis
1. INTRODUCTION
For model diagnostics and analyses of residual correlation, it is desirable to have a residual that is well defined, easily computable, and robust across many outcome types with a common scale. A well known residual in linear regression is y − ŷ, where y is an observed value and ŷ is a fitted value, typically an estimated conditional expectation. This observed-minus-expected residual (OMER) is simple and has many desirable properties, but is not easily extendable to outcomes where a conditional expectation is not meaningful or readily calculated. For example, for ordinal outcomes there is no natural definition of difference or conditional expectation unless scores are assigned to the ordered categories; for right censored outcomes with partially defined fitted distributions one may not be able to calculate the conditional expectation. Furthermore, the OMER may be misleading with models where one is fitting a non-symmetric distribution to data. This has led to context-specific residuals, e.g., martingale residuals for censored outcomes (Therneau et al., 1990); a general scheme for defining residuals in specific contexts (Cox and Snell, 1968); and residuals defined for generalized linear models, e.g., deviance and Pearson residuals (McCullagh and Nelder, 1989); to mention just a few. Deviance residuals have many nice properties and are quite popular across a wide variety of models (Pierce and Schafer, 1986), but they involve disjoint components (the deviance and the sign) and they are not naturally constructed for some models including ordinal models and quantile regression.
One could define a residual as some measure of discrepancy between an observed value and a fitted distribution; for example, a contrast of the observed value with a random variable Y* from the fitted distribution. One such contrast is the difference, y − Y*, and its mean, E(y − Y*) = y − ŷ, is the OMER. A different contrast function that is useful more generally is sign(y, Y*). We refer to the mean of this contrast, E {sign(y, Y*)} = pr(Y* < y) − pr(Y* > y), as the probability-scale residual (PSR).
Li and Shepherd (2010, 2012) introduced the PSR for ordered categorical outcomes, and in that context, showed that it has several desirable properties including that it results in only one value per subject irrespective of the number of categories of the ordinal outcome, it does not require assigning arbitrary numbers to the categories, and it has expectation zero. These, and other properties, make the PSR useful for model diagnostics or tests of residual correlation with ordinal data. The residual has been used as a statistic for other purposes with ordinal data: it is closely related to a ridit (Bross, 1958), and it has been proposed as part of a test statistic in genetic analysis of ordinal traits (Zhang et al., 2006).
The PSR is actually remarkably useful across a wide variety of other outcome types and models because it does not require calculation of E(Y*). Although the PSR measures discrepancy using a probability scale, it does not require full specification of a fitted distribution, which makes it useful for models that are not fully parametric – e.g., Cox regression, quantile regression, or cumulative probability models; the latter two of which do not have a particularly suitable residual. It also has a nice connection with ranks. There are benefits to having a residual that has a common scale, is easy to compute, and is applicable across many outcome types. In this paper we study properties of the PSR, compare it with other residuals, and demonstrate its application to continuous, discrete, and censored data.
2. DEFINITION, NOTATION, AND GENERAL PROPERTIES
Let Y be an orderable random variable from a distribution F; Y can be continuous or discrete. An observed value of this random variable is designated as y. Let F* be an assumed or fitted distribution of Y. The PSR is defined as
where Y* is a random variable with distribution F*, F* (y−) = limt↑y F* (t), and sign(a, b) is −1, 0, and 1 for a < b, a = b, and a > b, respectively. The expectation is with respect to F*, which may be different from the true distribution of Y. The distribution F* may be conditional on covariates Z and parameters θ, and we will sometimes denote it as . We will also sometimes denote random variables or observations from subject i using subscripts. For subject i, let Yi be the outcome and the assumed distribution of Yi given Zi. Given data (yi, zi) and a fitted model with parameter estimates θ̂, the PSR for subject i is .
The residual has several important and desirable properties. It is monotonic in y and monotonic in F* (with respect to stochastic ordering), and its range of possible values is symmetric about zero in [−1, 1]. By definition, full specification of the fitted distribution is not needed to compute the PSR; only the fitted cumulative probabilities at observed y and y− are needed. In particular,
Property 1. E {r(Y, F*)} = 0 if F* = F, which is proved in the Appendix.
3. CONTINUOUS OUTCOMES
3.1. Properties
If F* is continuous, then r(y, F*) = 2F* (y) − 1 and has the following additional properties:
Property 2. If F* (y1) + F* (y2) = 1, then r(y1, F*) = −r(y2, F*).
Property 3. If , then .
Property 4. r {median(F*), F*} = 0.
Property 5. If a function r0(y, F*) is monotonic in y and satisfies Properties 2 and 3, then r0(y, F*) = g{r(y, F*)}, where g(t) is a strictly increasing odd function (i.e., g(t) = −g(t) for all t). The reverse is also true.
Property 6. The random variable r(Y, F*) ~ Unif(−1, 1) if F* = F.
Properties 2–4 are expected and are desirable for a residual based on a probability scale. In fact, as described in property 5, a residual satisfying properties 2–3 and monotonicity will be unique with respect to an odd function transformation; the proof is in the Appendix. An example odd function is g(t) = Φ−1{(t + 1)/2}, where Φ(·) is the standard normal cumulative distribution function. This leads to g{r(y, F*)} = Φ−1{F* (y)}, a ‘quantile residual’ defined by Dunn and Smyth (1996), and mentioned earlier by Davison and Tsai (1992). Property 6 arises from the fact that the PSR is a re-scaling of the probability integral transformation, which can be used to assess goodness of fit (Pearson, 1938; David and Johnson, 1948; Cox and Snell, 1968).
In a model fitting scenario, if the estimated parameters θ̂ converge in probability to θ and F* is continuous at θ, then and . Therefore, converges in distribution to Unif(−1, 1) if is correctly specified. That is, if the sample size is sufficiently large, the PSR from the true model will be approximately uniformly distributed, with expectation 0 and constant variance (1/3) at all values of Z. Therefore, a residual-by-predictor plot that shows a trend in its expectation as a function of Z would suggest poor model fit. In addition, a quantile-quantile (QQ) plot of the empirical quantiles of the PSR versus the theoretical quantiles of Unif(−1, 1) can be used to detect lack of fit.
3.2. Examples
3.2.1. Exponential Model
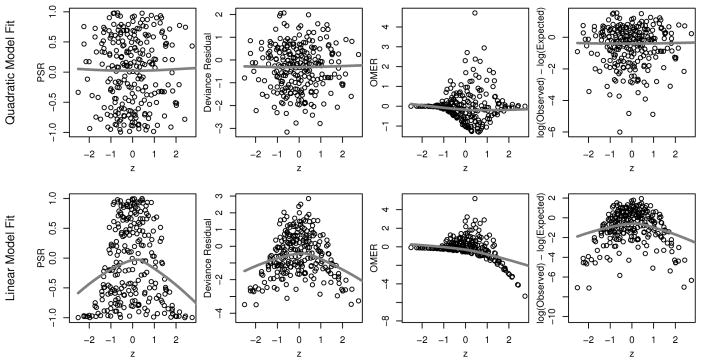
Suppose that conditional on Z = z, Y is exponentially distributed with rate e−z+z2. When an exponential model is properly fit, there is no relationship between z and the PSR, and the residuals are uniformly distributed (Figure 1, column 1). In contrast, the need for a quadratic term can be spotted in residual-by-predictor plots using the PSR when only a linear relationship is assumed. Similar information can be obtained using deviance residuals (Figure 1, column 2), but not the OMER (Figure 1, column 3) unless the observed and fitted values are first transformed (Figure 1, column 4).
Figure 1.
Left column: Residual-by-predictor plots from a properly fitted model of exponentially distributed data including a quadratic term (top row) and not including the quadratic term (bottom row). The first column is the probability-scale residual (PSR), the second column is the deviance residual, the third column is the observed-minus-expected residual (OMER), and the fourth column is the log(observed) minus log(expected). 250 observations were generated with rate exp(−z + z2) and Z generated from a standard normal distribution. Smoothed curves using lowess are added.
3.2.2. Cumulative Probability Regression Models
Consider a semi-parametric transformation model for continuous outcomes, Y = H(βZ + ε), where H(·) is an unspecified monotonic function and ε follows a specified distribution (Zeng and Lin, 2007). Harrell (2015) proposed fitting these models using ordinal cumulative probability regression models. Specifically, this approach models the distribution of Y with , where G is a link function (the inverse cdf of ε), θ = (α(y), β), and α(y) = H−1(y) are intercepts; when fit to observed data with n observations, this model results in n − 1 intercepts and is therefore quite flexible. The PSR is a natural residual for these models, with , whereas other common residuals may be less useful and/or more difficult to compute.
We illustrate using biomarker data from 70 pre- or non-diabetic HIV-infected persons on stable antiretroviral therapy. HIV-infected persons have an increased risk of developing diabetes, so there is interest in modeling metabolic biomarkers. Here we focus on alpha-ketoglutarate, which is a key intermediate in the Krebs cycle, through which aerobic organisms generate energy. Measurements of alpha-ketoglutarate were quite skewed in our dataset, ranging from 2.4 to 20.4 μM, with a median and mean of 4.6 and 5.2, μM, respectively. We considered three models for this biomarker: a linear model, a linear model after log-transforming the outcome, and an ordinal cumulative probability model with a probit link. Predictor variables were age, sex, race, body mass index, CD4 cell count, and duration of antiretroviral therapy.
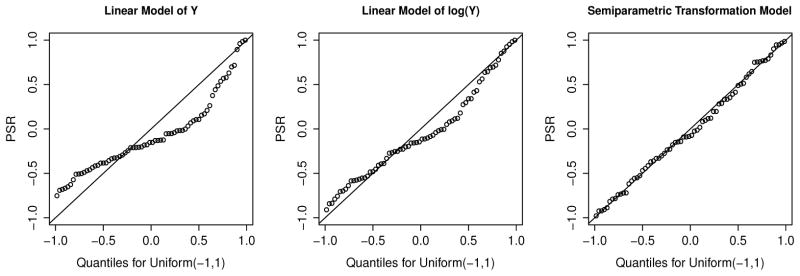
Figure 2 shows QQ plots of PSRs from the 3 models versus the uniform(−1, 1) distribution. From these figures it is clear that the linear model is a poor fit, the linear model after log-transformation is a better fit, and that the semi-parametric transformation model is the best fit. PSRs for the two linear models were computed as 2Φ {(yi − ŷi)/σ̂} − 1. Note that under the assumptions of normality, the PSR is simply a transformation of standardized OMERs. An alternative, empirical approach to computing the PSR from the linear models that does not assume normality is described in the Discussion; results using this empirical approach were similar (data not shown).
Figure 2.
QQ plots of PSRs from linear (left), linear after log-transformation (center), and semiparametric transformation models (right) of alpha-ketoglutarate compared to a Uniform(−1,1) distribution.
Although one could have detected the poor fit of the linear model and the better fit of the log-transformed linear model using OMERs, the use of the OMER for the semi-parametric transformation model is less straightforward (see Supplemental Material). In contrast, computation of the PSR from the linear models was appropriate and simple. By investigating the distribution of the PSR for all three models, we were able to compare apples to apples, so to speak, illustrating the benefits of having a residual that is well-defined across a wide variety of statistical models.
3.2.3. Quantile Regression
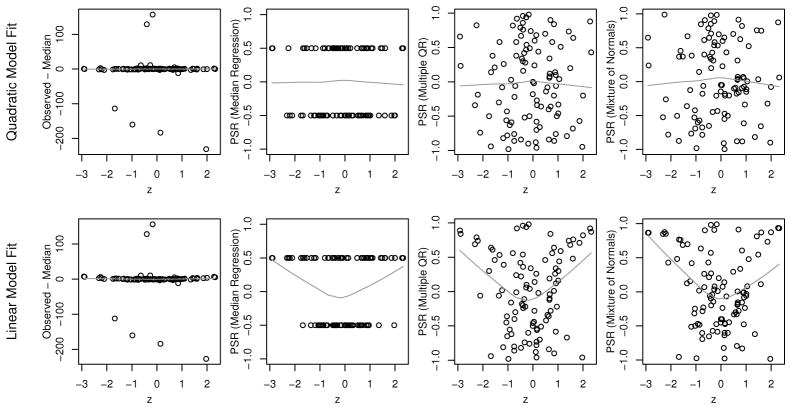
The PSR is also useful with quantile regression (Koenker, 2005). Suppose that conditional on Z = z, Y is a mixture of two normal distributions, πN(−z + z2, 12) + (1 − π)N(0, 1002), with mixing probability π = 0.9 and Z following a standard normal distribution; this set-up is meant to create a setting with a substantial number of outliers. Median regression with a properly specified model results in consistent estimates of the conditional expectation of Y given Z. However, one might be unaware of the quadratic relationship between Y and Z and incorrectly fit a model assuming a linear relationship. Ideally, a residual-by-predictor plot would detect this lack of fit, but we are not aware of a residual specifically designed for median regression. Figure 3 (left column) shows the OMER from median regression, replacing the estimated conditional expectation with the conditional median, as a function of z for 100 simulated observations both with a model including the quadratic term (top row) and a model missing the quadratic term (bottom). Neither plot is very helpful for detecting the missing quadratic term because the figure is dominated by outliers. One could remove outliers or zoom in to observe the quadratic shape of the OMERs as a function of z. However, in some cases it may be difficult to decide which data points to remove. More importantly, outlier removal is contrary to the nature of median regression. In general, residuals are used to detect model misspecification, and if a model is properly specified then it is undesirable for a residual plot to detect misspecification to a model different from that used. Given that median regression is quite robust to outliers in the outcome, residual plots from a median regression model should ideally not be dominated by outliers in the outcome.
Figure 3.
Residual-by-predictor plots from a properly specified median regression model including a quadratic term (top row) and from a model ignoring the quadratic term (bottom row). From left to right, the residuals are OMER, PSR using only information obtained from median regression, PSR with fitted distribution estimated using quantile regression (QR), and PSR with fitted distribution properly specified as a mixture of normals. Smoothed curves using lowess are added.
From median regression, we are unable to estimate F* (y), but we know whether it is in (0,0.5) or (0.5,1). Using this information, we can construct the PSR as either −0.5 or 0.5 depending on whether y is less than or greater than its predicted median. Even in this case, the PSR can be informative with the help of smoothing (Figure 3, second column). Estimation of the PSR could be more refined by estimating additional quantiles of the outcome conditional on covariates, and then calculating the PSR as , where is the estimated fitted distribution. For example, the third column of Figure 3 shows a plot of the PSR as a function of Z when the fitted distribution was estimated using quantile regression for the 0.01, 0.02, …, 0.99 quantiles; the linear (quadratic) models were fit assuming a linear (quadratic) relationship between Z and each quantile of Y. This is a stronger assumption than that made in the original median regression models (which only assumed these relationships for the 0.5 quantile), but similar in spirit. The missing quadratic term is easy to spot (bottom row) and the PSR behave well when the quadratic term is included (top row). For comparison, the fourth column of Figure 3 shows the PSR with the fitted distribution correctly specified as a mixture of normals and parameters estimated using the EM algorithm (Benaglia et al., 2009). The residuals based on quantile regression are very similar to the residuals where the mixture distribution was properly specified.
4. DISCRETE OUTCOMES
4.1. Properties
The PSR was originally proposed for ordered categorical outcomes and is directly applicable to other types of orderable discrete outcomes including count and binary data. The residual is 2F* (y) f* (y) − 1, where f* is the probability mass function of the fitted distribution F*. Although the range of the PSR for discrete outcomes is symmetric, the residual itself, typically, is not symmetric, its distribution is not uniform, and r(median(F*), F*) does not necessarily equal zero. When Y contains only 2 categories (0 or 1), the PSR reduces to y − pr(Y* = 1), which is the unscaled Pearson residual for binary outcomes (Hosmer and Lemeshow, 2000). The variance of the residual for discrete outcomes is {1 − Σ f* (y)3}/3 if F* = F, where the summation is over the support of Y*. As the number of outcome categories increases with the maximum probability mass decreasing to zero, the residual’s variance converges from below to 1/3 and the residual becomes uniformly distributed over (−1, 1). On the other hand, the PSR for discrete outcomes can be viewed as an integrated version (i.e., the expectation) of the PSR for some underlying latent continuous variable. Details and a proof are in the Appendix.
4.2. Example
The use of the PSR with ordered categorical outcomes was illustrated in Li and Shepherd (2012). Here we illustrate the PSR with count data.
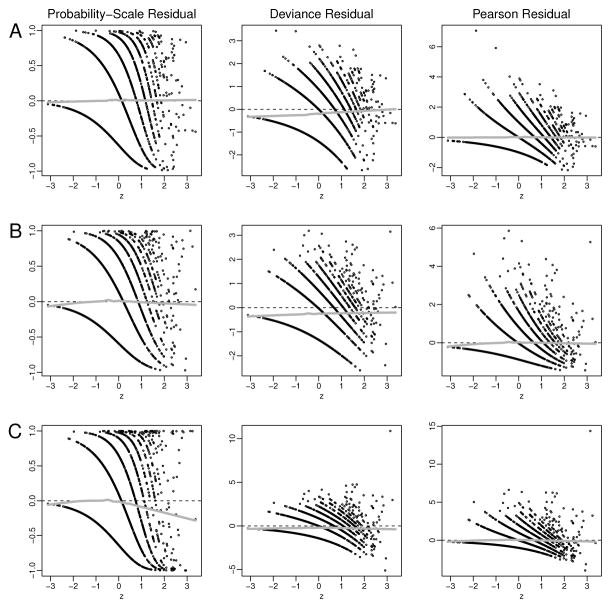
Figure 4 shows residual-by-predictor plots under properly and improperly fit models. Count data were generated with mean eβ0+β1Z and with Z drawn from a standard normal distribution; β0 = 0 and β1 = 1. Data were first generated from a Poisson model and then fit with a Poisson model. Row A of Figure 4 shows probability-scale, deviance, and Pearson residuals from the properly specified model. Realized values of Y can be seen as bands in all plots. Row B shows the residuals when data were generated under a negative binomial model with dispersion parameter ϕ=3, corresponding to variance of eβ0+β1Z + e2(β0+β1Z)/ϕ, and analyzed with a properly specified negative binomial model. As stated in Property 1 and seen in rows A–B, the PSR have expectation 0; Pearson residuals behave similarly, although there is no such guarantee for deviance residuals. Row C shows data generated under the negative binomial model but incorrectly fitted using a Poisson model, thereby ignoring over-dispersion. The PSR no longer has expectation 0; for larger values of Z the residual tends to be negative. Intuitively, with over-dispersion, as Z increases, the variance increases faster than that of a Poisson model; therefore the predicted distribution for larger values of Z is biased upward compared to what is actually observed, leading to residuals that tend to be negative. Over-dispersion cannot be detected using the expectation for the deviance or Pearson residuals (row C, columns 2–3).
Figure 4.
Plots of the PSR (first column), deviance (middle column), and Pearson (last column) residuals versus Z for 2000 data points generated under A) a Poisson model and analyzed with a Poisson model, B) a negative binomial model and analyzed with a negative binomial model, and C) a negative binomial model and analyzed with a Poisson model. Smoothed curves using Friedman’s ‘super smoother’ are added.
5. CENSORED OUTCOMES
5.1. Properties
We now consider the PSR with censored data. We focus on the classic right-censored time-to-event setting, where T is the time to the event of interest, C is the time to censoring, T > 0, C ≥ 0, Y = min{T, C}, and Δ = I{T≤C}. Rather than observing (T, C), we observe realizations of the random variables (Y, Δ).
If we could always observe the failure time, t, then the PSR would be its usual form, r(t, F*) = F* (t−) − {1 − F* (t)}, where F* is the assumed distribution of T. However, since we do not always observe t, the PSR, r(y, F*, δ), must be defined in terms of y and δ, the observed values of random variables Y and Δ. If δ = 1, then t = y and r(y, F*, 1) = F* (y−) − {1 − F* (y)}. If δ = 0, the failure time is unknown, except that it occurs some time after the censoring time y. In this case, the residual is computed as its conditional expectation given that t > y,
The proof is in the Appendix. Therefore,
The properties listed in Section 2 continue to hold for the PSR for censored outcomes, except that the expectation of the residual is 0 if the fitted distribution is correct and T is independent of C (denoted T ⊥ C). The proof is in the Appendix. Note that for censored observations the residual will always be non-negative; this is consistent with other popular residuals for time-to-event outcomes which also always have the same sign for censored observations (e.g., martingale residuals (Therneau et al., 1990), discussed in more detail below).
If T ⊥ C and F* = F, the distribution of T, then the variance of the PSR is
This implies that the variance of the residual depends on the distributions of both T and C. The quantity EC [{1 − F(C)}3] is the fraction of reduction in variance induced by censoring. Of note with continuous F, if Δ = 1 with probability 1, then F(C) = 1 and the variance equals its maximum, 1/3, the variance of Unif(−1, 1). As the probability of censoring increases, the residual becomes less uniformly distributed. We are unable to derive the distribution of the PSR in general for censored outcomes. In the special case where T and C are independent and exponentially distributed with means θ and β, respectively, the probability density function of the residual can be written as a mixture distribution π [2Beta(1,1/π) − 1] + (1 − π)Beta(1,1/π), where π = β/(θ + β) = pr(Δ = 1); details are in Supplementary Material.
When a fully parametric model is fit to survival data (e.g., Weibull regression), computation of the PSR is straightforward. The PSR can also be easily computed after fitting a semiparametric model such as the Cox proportional hazards model, because the residual only requires estimates of the cumulative distribution at the event and censoring times in the data. For example, with a Cox model, one can estimate F* (y) for all observed y using an empirical estimator of the cumulative baseline hazard together with the estimated relative hazard conditional on subject covariates (Cox, 1972; Breslow, 1972).
The PSR offers a new suite of residuals parallel to the trio of martingale, Cox-Snell, and deviance residuals, each of which can be written as a one-to-one function of the PSR given δ. The Cox-Snell residual for subject i is the estimated cumulative hazard, , the martingale residual is mi = δi − ci, and the deviance residual is a transformed martingale residual to make it more symmetric and normally shaped, (Therneau et al., 1990). The PSR with continuous failure time can be written as a transformation of the martingale residual: . The direction of the PSR is opposite to that of the martingale residual, but it is consistent with that of most residuals for continuous/discrete data: For example, a positive PSR indicates that the time-to-event was longer than expected whereas a positive martingale residual indicates that an event was observed sooner than expected. Like the martingale residual, the PSR can be used to examine the adequacy of the functional form of the model, although unlike the martingale residual, which ranges from −∞ to 1 and can therefore be quite skewed (Baltazar-Aban and Pena, 1995), the PSR has a symmetric range. A Cox-Snell-like PSR can be constructed as , which is simply the PSR evaluated at the observed time (ignoring censoring). With continuous data, , and similar to the Cox-Snell residual which corresponds to a censored exponential(1) distribution if the model is correct and the outcome continuous, this Cox-Snell-like PSR corresponds to a censored uniform(−1,1) distribution with which its Kaplan-Meier estimate can be compared to assess goodness of fit. Finally, analogous to the deviance residual, the PSR can be normalized, to make the residual more normally shaped and more capable of detecting outliers. This normalized PSR extends the ‘quantile residual’ proposed by Dunn and Smyth (1996) to time-to-event data.
5.2. Example
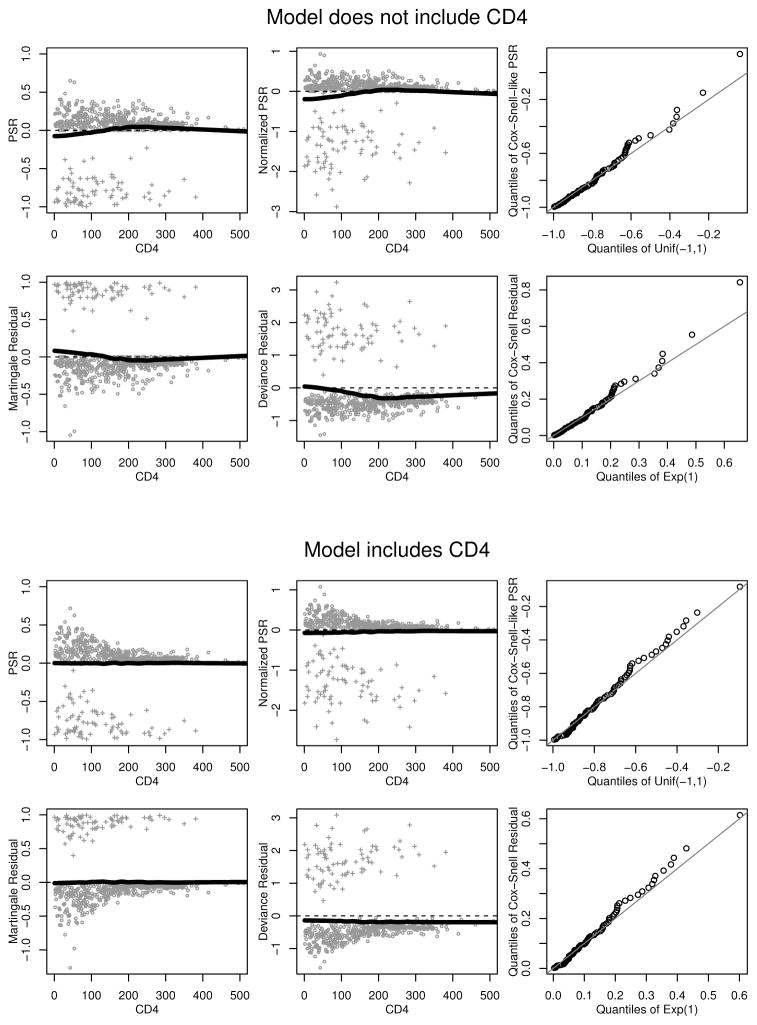
Figure 5 demonstrates the use of the PSR with time-to-event data from 589 HIV-infected women ≥ 50 years of age initiating antiretroviral therapy at one of seven sites in Latin America and the Caribbean (McGowan et al., 2007). Researchers were interested in predicting survival probabilities based on patient characteristics and determining factors associated with an elevated risk of mortality. To this end, a Cox model was fit with the outcome of time from therapy initiation until death. Patients were followed for a median of 3.7 years. A total of 80 (13.6%) patients died during follow-up; the remaining patients were censored at the time of study close or loss to follow-up. The time to death was assumed independent of the time to censoring, conditional on model covariates. An initial model included age, prior AIDS-defining event, calendar year, and regimen class as predictors with a separate baseline hazard estimated per site.
Figure 5.
Residual plots for models of the time to death. Rows 1–2 are for a model that does not include CD4, rows 3–4 are for a model that includes CD4. Rows 2 and 4 correspond to traditional residual plots using martingale, deviance, and Cox-Snell residuals, respectively. Rows 1 and 3 correspond to analogous plots using the PSR. The plots in columns 1 and 2 are limited to CD4<500 as this includes >98% of all measurements. Smoothed curves using Friedman’s ‘super smoother’ are added. Observed events are denoted with crosses, censored are denoted with circles.
The upper left panel of Figure 5 shows PSRs from this model plotted against CD4 count at therapy initiation, which was not included in the model. The PSRs for censored patients are ≥ 0, whereas the PSRs for those who died are < 0 (although this need not always be the case). The figure includes a smoothed curve showing the relationship between the PSR and CD4. At low CD4 (e.g., < 150) the mean of the PSRs tends to be negative, suggesting that the fitted model is under-estimating the probability of death. The normalized PSRs (upper middle panel) lead to a similar conclusion. From the QQ-plot (upper right panel) we can see the fit is not bad, but the residual-by-predictor plots suggest that CD4 should be included in the model. The lower panels in Figure 5 show residuals from the model with CD4 included after square-root transformation and using natural splines to account for potential non-linearity; the relationship between CD4 and the PSRs disappear. Figure 5 also shows similar residual plots using martingale, deviance, and Cox-Snell residuals; conclusions are similar.
5.3. Current Status Data
Current status data can be thought of as an extreme form of censoring (Jewell and van der Laan, 2004), and the PSR remains well defined in this setting. Let T be the time-to-event of interest. Rather than observing T, we observe C, the observation time, and Δ, whether the event has occurred by the observation time (i.e., Δ = I{T≤C}). The PSR for current status data with observed c and δ, r(c, F*, δ), can be defined as the expectation of r(T*, F*) given the constraints imposed by the observed values. Specifically, if δ = 0 then r(c, F*, 0) = E{r(T*, F*)|T* > c} = F* (c), as shown for time-to-event outcomes. If δ = 1 then r(c, F*, 1) = E{r(T*, F*)|T* ≤ c} = F* (c) − 1 (proof in Appendix). Therefore,
As in the other settings considered, the PSR with current status data has expectation 0 when F* is properly specified and T ⊥ C (proof in the Appendix).
6. DISCUSSION
We have described a probability-scale residual that can be applied across a wide range of outcomes and models. Originally developed to fill a gap in the analysis of ordinal data, the residual has several nice properties with continuous, other types of discrete, and censored data. The residual is easy to understand and interpret, it has expectation zero with properly fitted models, and it does not require a fully specified distribution. Some of these properties make it better for diagnostics than traditional residuals in certain situations. The utility of the PSR across a wide variety of models can be leveraged to compare fit between diverse models, some of which may not have a good alternative residual.
Because it is well defined with the same scale for a wide variety of outcomes, the PSR is also useful for tests of residual correlation between variables of possibly different types (Li and Shepherd, 2010). Tests of residual correlation using the PSR were not highlighted in this manuscript, but are being investigated. The PSR is closely related to ranks, as ranks are effectively on a probability scale (e.g., the empirical CDF is ranks divided by the sample size). In Section 3.2.2, we mentioned that an empirical PSR (ePSR) could be constructed from a linear model that assumes homoscedasticity but not necessarily normality. Specifically, one could obtain estimates of ε̂i = yi − ŷi and their empirical distribution , and estimate the fitted distribution for observation i as a location shift by ŷi of , denoted as . The corresponding empirical PSR would be , which is simply a linear transformation of the rank of the OMER; specifically, ePSRi = {2rank(ε̂i) − 1 − n}/n. Thus the residual’s efficiency and robustness are analogous to that of rank-based statistics (Lehmann and D’Abrera, 2006) and classical rank-based statistics and tests (e.g., Spearman’s rank correlation) can be constructed using the PSR.
We have focused our comparisons of the PSR with some of the most popular residuals, but there are certainly many others we could have investigated including generalized residuals (Gourieroux et al., 1987a), rank residuals (McKean et al., 1990), and others (Espinheira et al., 2008; Cysneiros and Vanegas, 2008). The banded nature of residuals from discrete data (e.g., Figure 4) may be undesirable to some, and jittering has been used to make them look more like residuals for continuous data (Dunn and Smyth, 1996; Gourieroux et al., 1987b); similar approaches could be applied to the PSR. As with most residuals, PSRs across observations are correlated, albeit weakly, because they are computed using parameter estimates derived from all observations; recursive residual techniques (Kianifard and Swallow, 1996) could be applied to produce uncorrelated PSRs.
The PSR has some limitations. Since it is bounded between −1 and 1, it is not good for outlier detection; for this purpose we recommend the transformation Φ−1{(PSR + 1)/2}. The PSR may provide little or no information on the adequacy of some model assumptions such as the proportional odds assumption in ordered logistic regression (Li and Shepherd, 2012). Adjusting the PSR for the effects of leverage (Cook and Weisberg, 1982; Davison and Tsai, 1992) is not straightforward because its finite sample variance is not easily written or approximated as a function of the hat matrix; the Supplementary Material contains a brief discussion and approximation of a leverage-adjusted PSR in a special case. Although the PSR is well defined and easily computed with least squares regression, the traditional observed-minus-expected residual would typically be preferable for these models as they minimize the sum of the squared OMERs. With continuous data, the PSR is often a 1-to-1 transformation of the OMER, thereby capturing the same information but delivering it on a different, probability scale. There are other settings where the PSR may not offer much more than existing residuals, for example, with binary data where the PSR is the unscaled Pearson residual. Similarly, although the PSR has some advantages over traditional residuals for time-to-event data, we admit that these advantages may not be strong enough to get an analyst to switch to the PSR for their model diagnostics. It would be great to have a single residual definition that is uniformly superior in all cases, but this is unrealistic. That the PSR is useful across such a wide range of models is actually quite remarkable.
We have uploaded to CRAN an R package, PResiduals, that computes the PSR for a wide variety of fitted models. Code for all analyses are posted at http://biostat.mc.vanderbilt.edu/ArchivedAnalyses.
Supplementary Material
Acknowledgments
This work was supported in part by the United States National Institutes of Health. The authors thank John Koethe and the Caribbean, Central, and South American Network for HIV Epidemiology for the use of their data.
APPENDIX
Proof of Property 1: E{r(Y,F*)} = 0 when F* = F
Since F(y−) = ∫ I{x<y}dF(x), we have
Similarly, since 1 − F(y) = ∫ I{x>y}dF(x), we have
These two are equal due to the symmetry between x and y. Therefore, E{r(Y,F)} = ∫ r(y,F)dF = ∫ F(y−)dF − ∫ {1 − F(y)}dF = 0.
Proof of Property 5
It is easy to show that if g(t) is a strictly increasing odd function, then g{r(y,F*)} is monotone in y and satisfies Properties 2 and 3. We now show the reverse. Let r0 = r0(y,F*) be a residual that is monotone in y and satisfies Properties 2 and 3, and r = r(y,F*) = 2F*(y) − 1 be the PSR. Let h(t) = 2t − 1 be a function over t ∈ (0, 1). Then r(y,F*) = h {F*(y)}.
Since F* is continuous, for every t ∈ (0, 1), there is a yt such that t = F*(yt). We define h0(t) = r0(yt, F*); Property 3 ensures that h0(t) is well defined, i.e., that for every t there is a unique h0(t). Monotonicity ensures that h0(t) is strictly increasing as t increases. Then there is a one-to-one mapping between the residuals r and r0: r0 = G(r), where G(r) = h0 {h−1(r)}. It is obvious that G is strictly increasing. We now show that it is an odd function.
Property 2 ensures that for any t1, t2 ∈ (0, 1) satisfying t1 + t2 = 1, h0(t1) = −h0(t2). Let r1 and r2 be their PSR. Then r1 = h(t1) = −h(t2) = −r2, and
That is, G(−r) = −G(r) for any r.
For discrete random variables, if max(f*) → 0 and F* = F, then R = r(Y,F*) = r(Y,F) → Unif(−1, 1) in distribution
Let ε = max(f) > 0, then 0 ≤ f(y) ≤ ε for all y. Since
We will show below that c − ε < pr {F(Y ) ≤ c} ≤ c + ε. Therefore,
Then when ε → 0, pr(R ≤ t) → (t + 1)/2 for −1 ≤ t ≤ 1, and R → Unif(−1, 1) in distribution.
We now show that
| (1) |
for any 0 ≤ c ≤ 1. This is obvious when c = 1 because pr {F(Y ) ≤ 1} = 1. We note that F is a right-continuous step function and F(y) → 1 as y → +∞. When c < 1, there exists a y such that c < F(y). If y is the lowest outcome category and 0 ≤ c < F(y), then pr {F(Y) ≤ c} = 0 < c + ε and c − ε ≤ c − F(y) < 0; thus (1) holds. If F(y1) ≤ c < F(y2), where y1 and y2 are two outcome categories, we can always find y1 and y2 such that F(y1) ≤ c < F(y2) and F(y2) − F(y1) ≤ ε. Then pr {F(Y) ≤ c} ≤ pr(Y <y2 ) ≤ F(y2) ≤ F(y1) + ε ≤ c + ε, and c − ε < F(y2) − ε ≤ F(y1) = pr(Y ≤ y1) ≤ pr {F(Y ) ≤ c}.
The discrete outcome PSR can be viewed as an integrated version of the continuous outcome PSR
Specifically, let R be the real set, and S ⊂ R be the set of categories of a discrete outcome with CDF F. Suppose there is a latent continuous variable with CDF F0 such that F(k) = F0(k) for all k ∈ S. We show that r(k,F) = E {r(T,F0) | j < T ≤ k} for all k ∈ S, where j is the category immediately before k (or j = −∞ if k is the lowest category):
Proof that r(y,F*, 0) = F*(y) for time-to-event outcomes
Since r(y,F*, 0) = ET*{r(T*, F*) | T* > y} = ∫t>y r(t, F*)dF*(t)/{1 − F*(y)}, it suffices to show that F*(y){1 − F*(y)} = ∫t>y r(t, F*)dF*(t) = ∫t>y F*(t−)dF*(t) − ∫t>y{1 − F*(t)}dF*(t). The last two items are
and
Due to the symmetry between s and t, ∫∫y<s<t 1dF*(s)dF*(t) = ∫∫y<t<s 1dF*(s)dF*(t), and thus ∫t>y F*(t−)dF*(t) − ∫t>y{1 − F*(t)}dF*(t) = ∫∫s≤y<t 1dF*(s)dF*(t) = ∫s≤y 1dF*(s) ∫y<t 1dF*(t) = F*(y){1 − F*(y)}.
Proof that E{r(Y,F*, Δ)} = 0 when F* = F and T ⊥ C
For brevity, let
| (A1) |
| (A2) |
Since E(R) = EC{ET|C(R | C)} = EC{ET (R | C)}, where the inner expectation is over T because T ⊥ C, it suffices to show that ET (R | C) = 0, or that both ET (A1 | C) = 0 and ET (A2 | C) = 0.
Given a fixed c, since
and similarly,
we have ET (A1 | C) = 0 due to the symmetry between s and t. In addition, since ET [I{T≤C} {1 − F(C)} | C] = F(C) {1 − F(C)}, and ET {I{T>C}F(C) | C} = {1 − F(C)} F(C), we have ET (A2 | C) = 0.
Derivation of the Variance with Censored Outcomes
Again, let R = r(Y,F, Δ). When T ⊥ C, since E(R) = 0, var(R) = E(R2) = EC {ET|C(R2 | C)} = EC {ET (R2 | C)}, where the inner expectation is over T because T ⊥ C. We decompose R2 as follows:
| (B1) |
| (B2) |
| (B3) |
We will calculate ET (· | C) for B1, B2, and B3, separately.
First, consider the conditional distribution of T given T ≤ c, denoted G(t) = F(t)/F(c), where c is a fixed value. The mean of a properly specified PSR for this distribution is 0 = ∫[G(t−) − {1 − G(t)}]dG(t) = F(c)−2 ∫t≤c[F(t−) − {F(c) − F(t)}]dF(t), and its variance, v(c) = ∫ [G(t−) − {1 − G(t)}]2dG(t) = F(c)−3 ∫t≤c[F(t−) − {F(c) − F(t)}]2dF(t).
Then ET (B1 | C) = ∫t≤C[F(t−) − {F(C) − F(t)}]2dF(t) = F(C)3v(C), ET (B2 | C) = −2{1 − F(C)} ∫t≤C[F(t−) − {F(C) − F(t)}]dF(t) = 0, and ET (B3 | C) = F(C){1 − F(C)}2 + {1 − F(C)}F(C)2 = F(C){1 − F(C)}. Therefore, ET (R2 | C) = F(C)3v(C) + F(C){1 − F(C)}.
For continuous outcomes, v(c) = 1/3. Thus,
and E(R2) = 1/3 − EC[{1 − F(C)}3]/3.
For discrete outcomes, v(c) = 1/3 −Σt≤c{f(t)/F(c)}3/3 (Li and Shepherd 2012). Thus,
and E(R2) = 1/3 − EC[{1 − F(C)}3 +Σt≤C f(t)3]/3.
Proof that r(c, F*, 1) = F*(c) − 1 with current status data
Since r(c, F*, 1) = E{r(T*, F*)|T* ≤ c} = ∫t≤c r(t, F*)dF*(t)/F*(c), it suffices to show that ∫t≤c r(t, F*)dF*(t) = F*(c){F*(c) − 1}.
Proof that E(r(C, F*, Δ)=0 with current status data if F = F* and T ⊥ C
BIBLIOGRAPHY
- Baltazar-Aban I, Pena EA. Properties of hazard-based residuals and implications in model diagnostics. Journal of the American Statistical Association. 1995;90(429):185–197. [Google Scholar]
- Benaglia T, Chauveau D, Hunter DR, Young D. mixtools: An R package for analyzing finite mixture models. Journal of Statistical Software. 2009;32(6):1–29. [Google Scholar]
- Breslow N. Discussion of ‘Regression models and life-tables’ by D.R. Cox. Journal of the Royal Statistical Society Series B. 1972;34:216–217. [Google Scholar]
- Bross IDJ. How to use ridit analysis. Biometrics. 1958;14:18–38. [Google Scholar]
- Cook RD, Weisberg S. Residuals and Influence in Regression. Chapman and Hall; New York: 1982. [Google Scholar]
- Cox DR. Regression models and life tables, with Discussion. Journal of the Royal Statistical Society Series B. 1972;34:187–220. [Google Scholar]
- Cox DR, Snell EJ. A general definition of residuals. Journal of the Royal Statistical Society Series B. 1968;30:248–275. [Google Scholar]
- Cysneiros FJA, Vanegas LH. Residuals and their statistical properties in symmetrical nonlinear models. Statistics and Probability Letters. 2008;78(18):3269–3273. [Google Scholar]
- David FN, Johnson NL. The probability integral transformation when parameters are estimated from the sample. Biometrika. 1948;35:182–190. [PubMed] [Google Scholar]
- Davison AC, Tsai CL. Regression model diagnostics. International Statistical Review. 1992;60:337–353. [Google Scholar]
- Dunn PK, Smyth GK. Randomized quantile residuals. Journal of Computational and Graphical Statistics. 1996;5(3):236–244. [Google Scholar]
- Espinheira PL, Ferrari SL, Cribari-Neto F. On beta regression residuals. Journal of Applied Statistics. 2008;35(4):407–419. [Google Scholar]
- Gourieroux C, Monfort A, Renault E, Trognon A. Generalised residuals. Journal of Econometrics. 1987a;34(1):5–32. [Google Scholar]
- Gourieroux C, Monfort A, Renault E, Trognon A. Simulated residuals. Journal of Econometrics. 1987b;34(1):201–252. [Google Scholar]
- Harrell F. Regression Modeling Strategies with Applications to Linear Models, Logistic Regression, and Survival Analysis. 2. Springer; 2015. [Google Scholar]
- Hosmer DW, Lemeshow S. Applied Logistic Regression. 2 Wiley; New York: 2000. [Google Scholar]
- Jewell N, van der Laan M. Current status data: Review, recent developments and open problems. Advances in Survival Analysis. Handbook of Statistics. 2004;23:625–642. [Google Scholar]
- Kianifard F, Swallow WH. A review of the development and application of recursive residuals in linear models. Journal of the American Statistical Association. 1996;91(433):391–400. [Google Scholar]
- Koenker R. Quantile Regression. Cambridge University Press; Cambridge: 2005. [Google Scholar]
- Lehmann EL, D’Abrera HJM. Nonparametrics: Statistical Methods Based On Ranks. Springer; New York: 2006. [Google Scholar]
- Li C, Shepherd BE. Test of association between two ordinal variables while adjusting for covariates. Journal of the American Statistical Association. 2010;105(490):612–620. doi: 10.1198/jasa.2010.tm09386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C, Shepherd BE. A new residual for ordinal outcomes. Biometrika. 2012;99:473–480. doi: 10.1093/biomet/asr073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCullagh P, Nelder JA. Generalized Linear Models. 2 Chapman & Hall; London: 1989. [Google Scholar]
- McGowan CC, Cahn P, Gotuzzo E, Padgett D, Pape JW, Wolff M, Schechter M, Masys DR. Cohort Profile: Caribbean, Central and South American Network for HIV research (CCASAnet) collaboration within the International Epidemiologic Databases to Evaluate AIDS (IeDEA) programme. International Journal of Epidemiology. 2007;36(5):969–976. doi: 10.1093/ije/dym073. [DOI] [PubMed] [Google Scholar]
- McKean J, Sheather S, Hettmansperger T. Regression diagnostics for rank-based methods. Journal of the American Statistical Association. 1990;85(412):1018–1028. [Google Scholar]
- Pearson ES. The probability integral transformation for testing goodness of fit and combining independent tests of significance. Biometrika. 1938;30:134–148. [Google Scholar]
- Pierce DA, Schafer DW. Residuals in generalized linear models. Journal of the American Statistical Association. 1986;81(396):977–986. [Google Scholar]
- Therneau TM, Grambsch PM, Fleming TR. Martingale-based residuals for survival models. Biometrika. 1990;77(1):147–160. [Google Scholar]
- Zeng D, Lin D. Maximum likelihood estimation in semiparametric regression models with censored data. Journal of the Royal Statistical Society Series B. 2007;69:507–564. [Google Scholar]
- Zhang H, Wang X, Ye Y. Detection of genes for ordinal traits in nuclear families and a unified approach for association studies. Genetics. 2006;172(1):693–699. doi: 10.1534/genetics.105.049122. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.