Band structure evolution during the ultrafast ferromagnetic-paramagnetic phase transition in cobalt

Using spin- and time-resolved XUV photoemission, researchers monitor the band structure evolution of Co during its phase transition.

Abstract

The evolution of the electronic band structure of the simple ferromagnets Fe, Co, and Ni during their well-known ferromagnetic-paramagnetic phase transition has been under debate for decades, with no clear and even contradicting experimental observations so far. Using time- and spin-resolved photoelectron spectroscopy, we can make a movie on how the electronic properties change in real time after excitation with an ultrashort laser pulse. This allows us to monitor large transient changes in the spin-resolved electronic band structure of cobalt for the first time. We show that the loss of magnetization is not only found around the Fermi level, where the states are affected by the laser excitation, but also reaches much deeper into the electronic bands. We find that the ferromagnetic-paramagnetic phase transition cannot be explained by a loss of the exchange splitting of the spin-polarized bands but instead shows rapid band mirroring after the excitation, which is a clear signature of extremely efficient ultrafast magnon generation. Our result helps to understand band structure formation in these seemingly simple ferromagnetic systems and gives first clear evidence of the transient processes relevant to femtosecond demagnetization.

INTRODUCTION

For the simple ferromagnets Fe, Co, and Ni, two fundamentally different limiting models of itinerant and localized electrons are used to describe the band structure evolution during the ferromagnetic-paramagnetic phase transition. Despite this very simple and very old description, however, little is known about the real effects on band structure in these ferromagnetic materials during this phase transition. Even in thermal equilibrium, band magnetism in these 3d ferromagnetic systems at finite temperatures has been a topic of discussion for decades (1–11), with different theoretical models considering, for instance, spin fluctuations and 3d electron correlations.

From an experimental point of view, one problem of the experiments carried out in the early 1980s was that the phase transition had to be thermally induced (1–11), which intrinsically caused problems considering the very high Curie temperatures of these elemental materials, reaching from about 630 K for Ni up to 1400 K for Co. Nowadays, however, a way to bypass this issue is to selectively excite the electronic system with an ultrashort laser pulse, which heats the electronic system easily far above 1000 K, before the energy is transferred to the lattice. Even though the material is not in thermal equilibrium, this procedure represents a valuable approach for studying the electronic band structure evolution in a ferromagnetic-paramagnetic phase transition, if the necessary tools are available.

Fortunately, in recent years, groundwork has been done so that experiments studying the ultrafast ferromagnetic-paramagnetic phase transition become more and more feasible. For example, Weinelt et al. have carried out benchmark experiments using time-resolved photoemission, which have had a considerable impact on our understanding of the demagnetization process in 4f ferromagnetic systems (12–15). In a more recent work, they have shown that the spin polarization in the ultrafast demagnetization of Gd decreases exponentially within about 15 ps, whereas the corresponding d-band component shows a Stoner-like shift on a subpicosecond time scale (15). However, no clear experiment has been carried out for the 3d systems so far.

Here, we use time-, spin-, and angle-resolved photoelectron spectroscopy (16, 17), in combination with a high harmonic light source in the extreme ultraviolet (XUV) region (Fig. 1A) (18). The XUV photon energy allows us to access the transient behavior of a 3d ferromagnetic material over the full energy range of the valence bands for the first time. Moreover, our experimental technique also provides direct information about the origin of the detected photoelectrons within the electronic band structure. This enables us to follow the energy-resolved electron and spin dynamics in the valence bands of a Co-on-metal film during the ferromagnetic-paramagnetic phase transition (that is, “demagnetization”) in detail. A critical issue that we seek to clarify is the role of band energy shifts versus band mirroring of the spin-polarized bands. We find that, at energies near the Fermi level, the spin dynamics is predominantly driven by a redistribution of spin-polarized carriers. However, at higher binding energies >1 eV, quenching of the spin polarization exhibits transient band dynamics that can unambiguously be traced back to rapid band mirroring of the electronic states. Our results indicate that collective excitations play a dominant role in the demagnetization process in this sample, and elucidate why previous work that probed different parts of the electronic band structure seemingly yielded contradictory results.

Fig. 1. Schematic of the time- and spin-resolved XUV photoemission spectroscopy experiment and the potential response of the electronic and spin systems to laser-induced demagnetization.

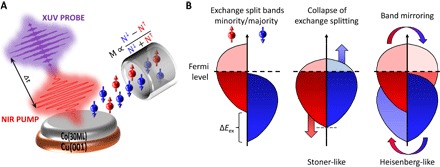
(A) The thin, in-plane-magnetized Co film (30 ML) is excited with near-infrared (NIR) laser pulses (74 ± 1 fs, 1.6 eV) that induce demagnetization. The evolution of the band structure is measured via spin- and time-resolved photoemission using XUV pulses (33 ± 7 fs, 22 eV) from high-harmonic generation (HHG). (B) Exchange split density of states for a 3d ferromagnet (left). Reduced magnetization in the Stoner-like picture via a potential collapse of the exchange splitting (middle) and in the localized spin picture via band mirroring (right).

Figure 1B illustrates how the electronic and spin systems might respond during the ferromagnetic-paramagnetic phase transition. These processes are commonly discussed in the limiting pictures of an itinerant electron Stoner-like approach versus a localized electron Heisenberg spin picture. In the case of a Stoner-like behavior of itinerant electrons, the magnetic moments are quenched via single-particle excitations that induce a collapse of the exchange splitting and therefore a shift of the spin-polarized bands. In the case of a localized spin or Heisenberg picture, magnetic moments change their orientation via collective excitations, that is, due to spin fluctuations and/or magnon generation (15, 19–21). This spatially and time-dependent modification of the orientation of the magnetic moments leads to rapidly fluctuating spin-split electronic states in space and time. Because the experiment probes only the macroscopic average of these fluctuations/magnons, one observes the so-called band mirroring effect in the spin-dependent density of states (22). Thus, a clear observation of energetic shifts or band mirroring during ultrafast laser-driven demagnetization would help to understand the nature of the spin interactions and their dynamics in 3d ferromagnets.

Early and pioneering time-resolved photoelectron spectroscopy studies of the evolution of the band structure during ultrafast demagnetization of 3d ferromagnetic materials were carried out by Rhie et al. (20). In their time- and energy-resolved, but spin-integrated, photoemission studies of Ni/W(110), they found that the collapse of the exchange splitting is the driving force of the demagnetization process, which evolves on a time scale of 300 ± 70 fs. However, in this first result, the spin-integrated shift of the bands above the Fermi level is intermixed with the excitation of hot electrons by the pump pulse. Moreover, the use of 6-eV probe pulses restricts these studies to the evolution of the electron and spin dynamics at the very center of the Brillouin zone, which might contain only partial information about the relevant dynamics. In other work using time-resolved magneto-optical Kerr spectroscopy, Carpene et al. (19) recently concluded that ultrafast demagnetization in Fe is most dominantly driven by magnon generation. Although Rhie et al. carried out their measurements on Ni on W, whereas Carpene et al. use an Fe on MgO sample, these contradictory conclusions are surprising. They suggest that, already within 3d ferromagnetic materials, different microscopic processes are likely to be responsible for the evolution of the band structure during the phase transition. Moreover, the interpretation of results is made even more complicated by the importance of the sample structure for ultrafast demagnetization because ferromagnetic films on metals demagnetize at a faster rate in comparison to ferromagnets deposited on insulators, due to a large contribution of fast superdiffusive spin currents (23–26). In addition, it was shown that different techniques for the measurement of the ultrafast demagnetization process interact with different parts of the band structure and therefore may also produce seemingly contradicting results (13, 27–30). In summary, all these works illustrate the need for more complete measurement techniques that can measure the full spin-resolved band structure evolution of materials, as we use here (see Fig. 2A and Materials and Methods).

Fig. 2. Investigated region of the band structure.

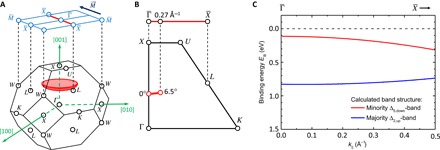
(A) Bulk (bottom) and surface Brillouin zones (BZ; top) of the Co fct lattice. The red shaded spherical section illustrates the observed region in the Brillouin zone. Note that the central point of the sphere is the Γ point in the Brillouin zone above (not shown) because the value of k_⊥ = 2.9 Å⁻¹ for our experimental conditions exceeds the size of the first Brillouin zone with k_⊥ = 1.8 Å⁻¹. (B) Cut through the ΓKUX plane of one side of the bulk Brillouin zone and the projection to the surface. The red line represents the region in reciprocal space over which we integrate with our spin detector. (C) Calculated band dispersion for the majority Δ_2,up band and minority Δ_5,down band by a tight-binding method based on the work of Miyamoto et al. (32).

RESULTS

Figure 2A shows the bulk (bottom) and surface Brillouin zones of the Co face-centered tetragonal (fct) lattice. Using a value of 15 eV for the inner potential (31), we determine k_⊥ = 2.9 Å⁻¹ for our measurement conditions (hν = 22 eV, E_B = 1 eV, normal emission, work function φ = 4.8 eV) and are therefore in the middle of the Brillouin zone, as indicated by the red shaded spherical section. Our spin detector integrates over k_ll = ±0.27 Å⁻¹ (emission angle, ±6.5°), which is shown in Fig. 2B for the ΓKUX plane in one direction of the bulk Brillouin zone. The valence band structure in this direction is dominated by a majority Δ_2,up band and a minority Δ_5,down band. Figure 2C shows the calculated band dispersion of both bands along the $\overline{\mathrm{\Gamma }}$ - $\overline{\mathit{X}}$ direction of the surface Brillouin zone (32). In this region, the corresponding bands exhibit relatively low dispersion, and we observed homogeneous electron excitation and electron dynamics using time- and angle-resolved photoelectron spectroscopy (see the Supplementary Materials). More information about the slice of the Brillouin zone that we access under our measurement conditions, as well as a detailed analysis of the static band structure of Co/Cu(001), can be found in the study of Miyamoto et al. (31).

Figure 3A shows spin-integrated photoemission spectra of Co/Cu(001) (30 ML) before and after optical excitation at pump-probe delays of −100 fs and 100 fs, respectively. The spin-integrated spectrum exhibits a distinct peak below the Fermi level, which is composed of photoemission intensity contributions from both a majority Δ_2,up band and a minority Δ_5,down band (see Fig. 2C) (31). The spectrum measured at 100 fs after optical excitation shows a redistribution of electrons in an energy range of about 0.5 eV around the Fermi level in comparison to the unpumped spectrum at −100 fs. Electrons are excited by the pump pulse from the 3d bands, where the intensity decreases, to unoccupied states above E_F, where an increase of intensity is observed.

Fig. 3. Spin-resolved photoemission spectra.

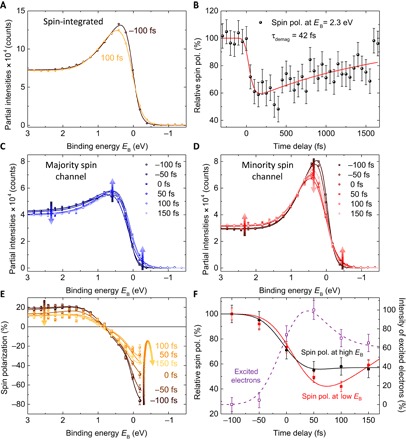
(A) Spin-integrated photoemission spectra of Co/Cu(001) (30 ML) before (−100 fs) and after (100 fs) optical excitation. (B) Spin dynamics extracted from the measured spin polarization at E_B = 2.3 eV. (C and D) Partial intensities of majority- and minority-spin photoemission spectra as a function of time. Lines correspond to the fits, as described in the text, whereas the arrows indicate a decrease/increase in spectral weight. (E) Transient quenching of the spin polarization. (F) Transient spin polarization extracted from energies around the Fermi level (red squares) and at higher binding energies (black circles), together with the appearance of hot electrons (violet open squares). All lines in (F) are guides to the eye.

Next, we use the spin-resolved capability of our spectrometer to observe both the majority and minority bands separately. Using the additional information of the individual number of spin-down majority (N^↓) and spin-up minority electrons (N^↑), we can calculate the spin polarization P = (N^↓ − N^↑)/(N^↓ + N^↑), which is proportional to the magnetization (see Fig. 1A). Figure 3B plots the transient spin polarization using the spin detector at a binding energy of about 2.3 eV after laser excitation with a pump fluence of 12 mJ/cm². We want to emphasize that this binding energy is well away from the energetic region ≈±0.5 eV around the Fermi energy that is directly affected by the laser pump pulse (see also the Supplementary Materials). The data in Fig. 3B nevertheless exhibit spin dynamics resembling a typical demagnetization curve and provide a clear indication of an ultrafast ferromagnetic-paramagnetic phase transition. Moreover, the fitted decay time constant of surprisingly fast τ = 42 ± 44 fs is indicative of superdiffusive spin currents driving the demagnetization process (33, 34). However, as explained above, this response at a single energy is insufficient to unambiguously deduce the different microscopic mechanisms at work.

In the next step, we therefore extract the partial intensities of the majority- and minority-spin channels as a function of time in 50-fs steps (Fig. 3, C and D). We observe that both spin channels show a clear, but different reaction to ultrafast laser excitation. As expected from the spin-integrated results, both spin channels show an increase of intensity above the Fermi energy. In contrast, however, we observe that, below the Fermi level in the energetic region of the peaks (at around E_B = 0.5 eV), only the minority channel exhibits the expected decrease of photoemission intensity, whereas the intensity in the majority channel increases. In addition, we observe further distinct dynamics at high binding energies (E_B > 1 eV), where no redistribution of electrons is observed in the spin-integrated spectra and, moreover, in the region that is not at all accessed by the pump pulse via linear photoexcitation (E_B > 1.6 eV). Here, an opposite behavior, in comparison to the intensity changes in the regions of the peaks, is observed: The majority-spin intensity decreases, whereas the minority-spin intensity increases, as indicated by the arrows in Fig. 3 (C and D). These observations cannot be understood in a simple picture considering only the excitations of hot electrons. In particular, the increase of spectral weight in the occupied region of the band structure already evidences some type of transient band dynamics upon demagnetization.

The measured spectral spin polarization from which the partial intensities in Fig. 3 (C and D) were extracted is shown in Fig. 3E. Here, we observe an overall reduction of the spin polarization on ultrafast time scales. In addition, a closer look at the transient quenching of the spin polarization also reveals spectrally different responses. When we analyze the spin polarization around the Fermi level (red filled squares in Fig. 3F), which is strongly modified by the partially thermalized laser-excited hot electrons (violet open squares in Fig. 3F), the dynamics is distinct from the dynamics seen at higher binding energies (black circles in Fig. 3F). At 150 fs, the spin polarization at higher binding energies still shows a maximum quenching, whereas around the Fermi level, a partial relaxation process of the quenched magnetization already has begun. This observation illustrates why measurements over a limited energy range in the band structure are insufficient to understand what is occurring during the demagnetization process. Moreover, as a consequence, techniques that probe different parts of the band structure might be expected to yield different results (13, 27–30). However, in contrast to traditional approaches for probing femtomagnetism, spin-, energy-, and angle-resolved photoemission can disentangle different contributions by directly accessing information about the origin of the probed electrons in the band structure.

DISCUSSION

We now analyze in more detail the energy-resolved transient dynamics of the partial majority- and minority-spin polarized band intensities to quantify the roles of collapsed exchange versus band mirroring processes. We find simple fit functions for the static (that is, unpumped) peaks and background of the partial intensities so that subsequent fits to elucidate how the dynamics changes with time will have less parameters and be consequently more reliable. For the majority spins, we need a constant background plus a Gaussian peak function to account for the nonuniform background intensity, together with a second Gaussian for the peak in this energy range (according fits can be found in Fig. 3C as lines). For the minority channel, a constant background with a single Gaussian peak is sufficient to fit the data (compare lines in Fig. 3D). To account for the increased electronic temperature of the thermalized laser-excited electrons that we detect around the Fermi level, we include a Fermi function with the electronic temperature as a fitting parameter. At the same time, we leave the energetic position of Fermi level fixed, and we therefore do not account for minor shifts of the chemical potential during the demagnetization process (35).

We start with an analysis of whether energetic shifts of the majority and minority photoemission peaks occur as a function of time. A reduction of the exchange splitting would involve a shift of the majority Δ_2,up band toward lower binding energies because the corresponding minority band is located in the unoccupied regime (36). The observed minority Δ_5,down band would shift to higher binding energies because the corresponding majority band is located at E_B = 2 eV (36). Note that the latter band cannot be observed as a peak in our recorded spectra due to correlation effects (6). Figure 4A shows the extracted shifts of the majority and minority peaks as a function of time. As expected from a Stoner-like approach, the majority bands seemingly shift about 200 meV toward lower binding energies; however, the minority bands stay rigid within our energy resolution. Nevertheless, we would like to point out explicitly that the energy shifts extracted here have to be treated with caution because the laser-excited hot electrons cannot be assumed to be fully thermalized within 150 fs (36).

Fig. 4. Analysis of possible exchange collapse versus band mirroring.

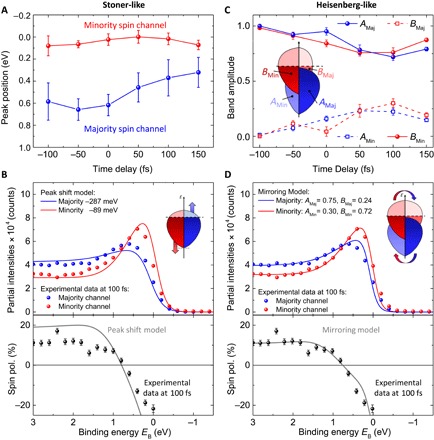
(A) Extracted energetic shifts of the majority and minority bands as a function of time. (B) Modeled majority and minority spectra (top) and spin polarization (bottom), if only energetic shifts are considered, in comparison to the measured experimental data at t = 100 fs. (C) Extracted amount of band mirroring. The scaling prefactors A_Maj and B_Maj (blue solid and red dashed lines) that were multiplied with the unpumped (“initial”) majority and minority spectra, respectively, to fit the data of the majority channel after excitation are shown. One sees that the majority channel loses spectral weight from its initial majority spectrum and gains spectral weight from the initial minority spectrum accordingly. The same was carried out for A_Min and B_Min in the minority channel (blue dashed and red solid lines). (D) Same as (B), if only band mirroring is considered.

In our next step, we therefore cross-check this result. Figure 4B (top) displays our fitted spectral line shapes that are shifted by the extracted values at 100 fs from Fig. 4A and plotted together with our experimental data at 100 fs (red and blue data points). A pure shift of the majority and minority spectra shows a rather weak agreement with the observed experimental data. In particular, a pure shift does not reproduce a collapse of the spin polarization at high binding energies E_B > 1.5 eV (Fig. 4B, bottom). Because both the majority and minority bands show a rather flat spectral shape in the energy range E_B > 1.5 eV, shifts in the range of several electron volts would be required to induce a change in the minority/majority photoemission intensity ratio at these binding energies. We therefore draw three conclusions. First, an analysis of energy shifts has to be taken with caution because of the influence of nonthermalized hot electrons in the fitting routine. Second, for changes in the partial intensities and the accompanied considerable reduction of the spin polarization as observed experimentally at high E_B, shifts on the order of several electron volts would be needed, which are not present in our data. Last, another process must be responsible for the observed 50% quenching of the spin polarization at high binding energies.

We now focus on the second potential process that can cause demagnetization, that is, band mirroring. Here, we want to further clarify the origin of band mirroring and also discuss the expected impact on our measured spin-resolved data. In the Heisenberg picture, magnetic moments deviate from perfect ferromagnetic alignment due to spin fluctuations and/or magnons (15, 19–21). Therefore, with respect to the spin detection axis of the spin analyzer, photoemission intensity that is lost in one spin channel will appear in the opposite channel, whereas the total spectral weight remains constant. In the case of the 3d ferromagnets, because of spin-orbit coupling, we always measure electronic states with a certain spin mixing, of which we detect the partial majority and minority intensities. If we now assume that spin fluctuations or magnons are present in our sample, the induced deviation of magnetic alignment would induce a change of this ratio of majority versus minority spectral weight with respect to the used spin detection axis. Therefore, if a specific band in our measurement would exhibit an increase in minority character upon laser excitation (or vice versa), these electrons would show up in our spin-resolved measurement in the minority channel, with a partial spectral weight according to the initial majority band, because the total spectral weight should remain constant.

In our analysis, we define that, before the Co is excited by the pump pulse, the initial condition (no dynamical band mirroring) is that the majority channel of our detector measures the full spectral weight “A_Maj = 1” of the majority spectrum “Spectrum_Maj” and zero spectral weight “B_Maj = 0” of the minority spectrum “Spectrum_Min,” that is

$${\text{Channel}}_{\text{Maj}}={\mathit{A}}_{\text{Maj}}\cdot {\text{Spectrum}}_{\text{Maj}}+{\mathit{B}}_{\text{Maj}}\cdot {\text{Spectrum}}_{\text{Min}}$$ (1)

and vice versa

$${\text{Channel}}_{\text{Min}}={\mathit{A}}_{\text{Min}}\cdot {\text{Spectrum}}_{\text{Maj}}+{\mathit{B}}_{\text{Min}}\cdot {\text{Spectrum}}_{\text{Min}}$$ (2)

with now “A_Min = 0” and accordingly “B_Min = 1.” This initial condition is plotted in Fig. 4C at a time delay of −100 fs. We now carry out fits of all transient partial intensities in the valence band structure with only the prefactors “A_Maj/Min” and “B_Maj/Min” as fit parameters. In this fitting routine, where we test the dynamics for the effect of band mirroring only, we need to exclude the effect of the redistribution of excited carriers (compare angle-resolved excited carrier dynamics in the Supplementary Materials). Hence, only the valence band structure at E_B > 0.5 eV is taken into account in the fitting routine. Note that this was not possible for the fitting routine of energetic shifts because the 3d peak positions are too close to E_F. The fitted evolution of the prefactors, which are indicative of the band mirroring process, is shown in Fig. 4C. Upon demagnetization, the majority channel of the spin detector measures less and less spectral weight from the initial majority spectrum as a function of time (blue circles), whereas the amount of majority electrons in the detector originating from the initial minority spectrum increases by the identical rate (red open squares). The same behavior is seen for the minority channel of the spin detector, where the measured minority electrons of the initial minority band decrease (red circles) at the same rate as the amount of measured minority electrons from the initial majority band increases (blue open squares). Hence, this analysis procedure strongly supports the idea that band mirroring is a relevant process at play for the quenching of the spin polarization at high binding energies. From our analysis, we extract a maximum band mirroring of

$$\begin{array}{c}{\text{Channel}}_{\text{Maj}}=0.75\pm 0.03\ast {\text{Spectrum}}_{\text{Maj}}+0.24\pm 0.02\ast {\text{Spectrum}}_{\text{Min}}\\ {\text{Channel}}_{\text{Min}}=0.30\pm 0.04\ast {\text{Spectrum}}_{\text{Maj}}+0.72\pm 0.03\ast {\text{Spectrum}}_{\text{Min}}\end{array}$$

That is, the initially spin-polarized band structure as measured with our detector is mixed by 43 ± 10% in the majority-spin channel and by 50 ± 3% in the minority-spin channel during the demagnetization process. These values are also consistent with the reduction of spin polarization measured at high binding energies of 45 ± 7%, as shown in Fig. 3F. Once again, as a cross-check, we plot the fitted spectral line shapes mirrored with the extracted values of A_Maj/Min and B_Maj/Min from Fig. 4C together with the experimental data at 100 fs in Fig. 4D. We note a very good agreement between the modeled spectra and the experimental data throughout the entire spectral range for minority channel, majority channel, and the measured spin polarization. In consequence, we conclude that band mirroring, and not the collapse of exchange splitting, must be the dominant process that drives the observed reduction of the spin polarization at high binding energies.

A static investigation of band magnetism at finite temperatures of ultrathin fct Co films via static heating supports a band mirroring model (22). Here, the authors find that the magnetization, when approaching the Curie temperature, is completely quenched without an energetic shift of the 3d bands, which disagrees with a Stoner-like picture. Their result was explained by a quenching of the long-range magnetic order, whereas short-range order, and therefore an exchange split band structure, remains. The long-range noncollinear magnetic moments thus introduce band mirroring in the photoemission spectrum.

Moreover, our observation of strong band mirroring and no large exchange reduction in combination with a very fast decay constant of the spin polarization at high binding energies provides a new perspective to an ongoing discussion on the understanding of ultrafast demagnetization. Regarding Elliot-Yafet–type spin-flip scattering as the microscopic model, it is known that a rigid band structure model would not be consistent with experimental results for 3d ferromagnets (33, 37–39). Moreover, it was even concluded that demagnetization rates and quenching, as observed in experiments, cannot be reproduced without a collapse of the exchange splitting, independent of the particular scattering process under investigation (33). A very recent work that studied Co on an insulating substrate shows both a band mirroring and a collapse of exchange splitting (21). Here, the insulating substrate and the long demagnetization times again indicate a significant contribution of spin-flip scattering processes (τ > 150 fs). Over the last years, however, an emerging picture did arise, in which other microscopic processes, besides spin-flip scattering, are at play, depending on the specific structure of the magnetic layers (23–26). In our case, in contrast to the abovementioned works, the Co film is grown on the spin-conducting substrate Cu(001). It was shown by Wieczorek et al. that, for this particular system, spin currents can be the dominant process within the first 100 fs (34, 40), whereas Elliott-Yafet scattering was predicted to be less important (41). This agrees with our observation of very fast spin dynamics of τ = 42 ± 44 fs at high binding energies, which is considerably faster than the expected overall Elliot-Yafet–induced demagnetization time for a Co film (42). Therefore, we conclude that the observed demagnetization process in Co/Cu(001) is driven by superdiffusive spin currents and that these superdiffusive spin currents induce band mirroring in the electronic structure, with little effect on the exchange splitting of the states. However, from a theoretical point of view, the impact of spin currents on the band structure is as yet unknown, and we hope that our findings will trigger further theoretical treatment in this field.

We moreover like to add that, despite great progress in recent years (43), a quantitative theoretical description of correlation effects in 3d ferromagnets appears to be still out of reach. Therefore, it is as yet completely unknown how an ultrafast rearrangement of charge carriers might affect and renormalize the band structure of the Co 3d ferromagnet. Aspects of these dynamics might be included in our experimental findings, and we hope that our work will serve as a benchmark experiment to test the role of many-body Coulomb interactions in these materials in the future.

Our time- and spin-resolved photoelectron spectroscopy study with pulsed XUV light from HHG is the first of its kind and represents a “complete” photoemission experiment, with time, energy, momentum, and spin resolution. Hence, it opens new avenues for our understanding of band magnetism at finite temperatures and of the ferromagnetic-paramagnetic phase transition that is driven with ultrashort laser pulses, as shown here. Accordingly, a direct observation of transient energetic shifts and/or band mirroring allows a much deeper microscopic interpretation of the nature of the spin interactions and their dynamics in 3d ferromagnets. In addition, our experiment exemplifies the tremendous possibilities that will become available at future free-electron laser and HHG photoemission beamlines for the study of complex materials.

MATERIALS AND METHODS

Experimental setup

Our setup (see Fig. 1A) used a high-order harmonic generation light source with a repetition rate of 10 kHz optimized for photoemission studies (16, 44). The photon energies of the s-polarized pulses used were 1.6 eV (near-infrared pump) and 22 eV (XUV probe), with pulse lengths of 74 ± 1 and 33 ± 7 fs [measured with autocorrelation and the laser-assisted photoelectric effect (45)], respectively. The system was equipped with a cylindrical sector analyzer with an iron-based spin detector using exchange scattering (46) to enable spin-resolved photoelectron spectroscopy. In our studies, we focused on fct Co films (≈30 ML) grown on a Cu(001) crystal as a well-characterized sample system (31) to distinguish the role of collapsed exchange versus band mirroring in the ultrafast demagnetization process.

Sample preparation

The Cu(001) single crystal was cleaned by repetitive sputtering (1 kV for 30 min and 0.5 kV for another 30 min) and annealing cycles (20 min, 800 K). Co (30 ML) was deposited at room temperature (RT) on the Cu(001) substrate with electron beam epitaxy. The deposition rate was determined by the intensity signal of the Cu d bands in the photoemission spectra. The films show, at RT, a perfect Stranski-Krastanov (layer by layer) epitaxy on Cu(001).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/3/e1602094/DC1

section S1. Time- and angle-resolved photoemission spectroscopy.

section S2. Time- and angle-resolved photoemission spectroscopy: Difference spectra.

fig. S1. Time- and angle-resolved photoemission spectroscopy.

fig. S2. Time- and angle-resolved photoemission spectroscopy: Difference spectra.