Microscopic assessment of bone toughness using scratch tests

Abstract

Bone is a composite material with five distinct structural levels: collagen molecules, mineralized collagen fibrils, lamellae, osteon and whole bone. However, most fracture testing methods have been limited to the macroscopic scale and there is a need for advanced characterization methods to assess toughness at the osteon level and below. The goal of this investigation is to present a novel framework to measure the fracture properties of bone at the microscopic scale using scratch testing. A rigorous experimental protocol is articulated and applied to examine cortical bone specimens from porcine femurs. The observed fracture behavior is very complex: we observe a strong anisotropy of the response with toughening mechanisms and a competition between plastic flow and brittle fracture. The challenge consists then in applying nonlinear fracture mechanics methods such as the J-integral or the energetic Size Effect Law to quantify the fracture toughness in a rigorous fashion. Our result suggests that mixed-mode fracture is instrumental in determining the fracture resistance. There is also a pronounced coupling between fracture and elasticity. Our methodology opens the door to fracture assessment at multiple structural levels, microscopic and potentially nanometer length scale, due to the scalability of scratch tests.

Graphical Abstract

Highlights

• •We measure bone toughness at the osteon level using microscopic scratch tests.
• •Scratch tests induce a ductile-to-brittle transition in cortical bone.
• •Toughening mechanisms are observed at the microscopic scale.
• •The J-integral and the size effect law are employed to predict the fracture energy.

1. Introduction

Bone has evolved to a fascinating structure, being lightweight and yet tough. Nonetheless, accidents, injuries or diseases make bone fracture a common phenomenon with an estimated average of 2 fracture events per individual during their lifetime. Unfortunately, bone fracture is also among the 20 most expensive medical conditions, leading to a heavy socio-economical burden(Office of the Surgeon General (US), 2004). Like most biological tissues, bone has a complex hierarchical design. It is mostly made up of collagen, hydroxyapatite and water molecules arranged precisely into 5 distinct length scales - nanoscale (mineralized collagen fibril), sub microscale (single lamella), microscale (lamellar structure), mesoscale (osteons) and macroscale (whole bone). Fracture occurrences in bone are related to the quality of bone, which in turn is influenced by several biological factors, the mechanical behavior and the micro-structure. Hence, understanding the toughness and fracture properties of bone will help in developing better orthopedic treatments.

Despite many investigations, the fracture response of bone is not fully understood. On the one hand, previous approaches have been limited by the use of single-size specimens in single mode (mode I or mode II) fracture. The challenge here consists in capturing the inelastic behavior that manifests at several length scales under complex loadings. To-date most fracture assessment methods for compact bone rely on pure mode I testing and very few mixed-mode investigations (Norman et al., 1996, Zimmermann et al., 2009, Zimmermann et al., 2010) have been reported. Early studies focused on linear elastic fracture mechanics (Norman et al., 1995, Phelps et al., 2000), based on traditional fracture tests such as the compact tension test (Behiri and Bonfield, 1984, Behiri and Bonfield, (1989), Bonfield and Datta, 1976, Norman et al., 1995, Wright and Hayes, 1977) or the three point bending test on single-edge notched specimens (Lucksanasombool et al., 2001, Robertson et al., 1978, Yan et al., 2006). However, bone exhibits a rising R-curve behavior (Malik et al., 2003, Nalla et al., 2004a, Nalla et al., 2005a, Vashishth, 2004) due to multiple toughening mechanisms (Yeni et al., 1997) such as microcracking (Vashishth et al., 2000), diffuse damage (Diab and Vashishth, 2007, Parsamian and Norman, 2001), fiber bridging (Nalla et al., 2004b), crack deflection (Koester et al., 2008) or osteon pull-out (Cooke et al., 1973). As a result, the fracture energy or critical energy release rate is a better metric than the critical stress intensity factor because it also accounts for the non-linearity of the behavior or the presence of plastic flow during the fracture of bone (Yan et al., 2007). Moreover, recent works (Yang et al., 2006a, Yang et al., 2006b) have recommended the use of a multi-parameter fracture criteria such as cohesive fracture to fully capture the complex behavior. Yet the coehsive fracture model was calibrated by testing specimens of the same size. In contrast, a recent study (Kim et al., 2013) showed that due to significant size effects, the fracture parameters must be assessed by testing specimens of different sizes. The reason is the non-uniqueness of the work-of-fracture method or cohesive fracture method for tests on same-size specimens. Thus, new methods are needed that can incorporate nonlinear fracture mechanics, size effects and mixed-mode fracture.

On the other hand, previous studies have evaluated the fracture parameters of the macrostructure instead of probing the behavior at the level of the microstructure (haversian system, osteon or single trabeculae), sub-microstructure (single lamella) or the nanostructure (fibrillar collagen). Because bone is a multi-scale material, it is important to capture the local behavior at smaller length scales to gain a better understanding of crack initiation, propagation as well as toughening mechanisms. A couple of methods have been proposed—indentation fracture and nanoscratch tests–yet a rigorous framework is still lacking. Although indentation fracture was introduced (Mullins et al., 2007) to access the fracture toughness of bone as a function of crack length, those tests tend to be unreliable and highly subjective due to the need to measure the crack length, which highly depends on the observer's skill (Quinn and Bradt, 2007). In another study, nanoscratch tests were employed in an attempt to assess fracture toughness at the ultra-structural level (Islam et al., 2012). However, owing to the use of a plastic limit model, the resulting metric, scratch work consumed per unit volume of the scratch groove, is very akin to a strength measurement. Thus, new methods must be developed to evaluate the fracture characteristics at the microscopic level.

Herein, we implement a novel approach, micro-scratch testing, to quantify the fracture toughness of bone at the mesoscale (osteon level) and micro-scale (concentric lamella). We use a recently introduced experimental and analytical framework (Akono et al., 2012, Akono et al., 2011, Akono and Ulm, 2011, Akono and Ulm, 2012) based on non-linear fracture mechanics. The technique used here allows for fracture characterization in both the longitudinal and transverse directions at the micro scale. In what follows, we first present the experimental procedure followed by a brief review of the scratch test model and a detailed discussion of results.

2. Materials and methods

2.1. Specimen preparation procedure

Fresh bones from 22–26 weeks old porcine animals were harvested 24 h after slaughter from the Department of Animal Sciences at the University of Illinois, Urbana-Champaign. The donor pigs had an average diet of corn and weighed about 275 lbs. To keep the bone fresh, femurs were stored at −20 °C before use. Cortical bone specimens were thawed and then sampled using first a table-top band saw and then a diamond precision saw (Isomet 5000^®, Buehler, LakeBluff, IL). Two set of specimens were prepared to observe the fracture behavior in two different orientations. On the one hand, longitudinal-transverse (LT) specimens were used to study fracture perpendicular to the long axis of bone and they were cut into about 5-mm thick sections as shown in Fig. 1. On the other hand, short longitudinal (SL) specimens, approximately 15-mm long and 10-mm wide, were used to study fracture parallel to the long axis of bone. After sectioning, these smaller pieces were defattened, defleshed and then cleansed in a solution of 1.5% Alconox + 5% bleach. For further ease of handling during polishing and testing, each individual section was embedded in polymethylmethacrylate, allowed to cure for 8–9 hours, cut into 5-mm thick discs using the linear precision diamond saw and mounted onto aluminum discs using cyanoacrylate adhesive. To assure a smooth and flat surface finish, a rigorous grinding and polishing operation was carried out. Samples were ground using consecutively a 400, 600, 800 and 1200 grit size of alumina oxide abrasive pads. Wet coarse and fine polishing was ensued using consecutively 3, 1 and 0.25 μm diamond suspension solutions along with TexMet P^® (Buehler, LakeBluff, IL) polishing cloths. Finally, a 0.05 μm Microcloth (Buehler, LakeBluff, IL) pad was used for ultra fine polishing. The specimens were wrapped in a gauge soaked in Hank's Balanced Salt Solution to keep them wet and then stored at 4 °C until tested.

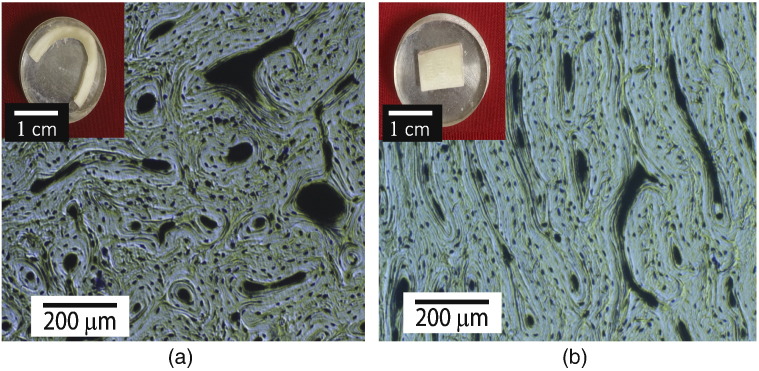
Fig. 1.

Optical microscopy and surface features: (a) digital photo of a Longitudinal-Transverse (LT) specimen and a representative optical microscopy image of the specimen surface; visible surface features are circular osteons with central Haversian canal and evenly distributed lacunae. (b) Digital photo of a Short-Longitudinal (SL) specimen and a representative optical microscopy image of the specimen surface; surface features are relatively elongated since the Haversian canals run parallel to this orientation. The final polished surface is clean, smooth and free of abrasion marks.

Credits: Amrita Kataruka, UIUC, 2016.

2.2. Scratch testing

A scratch test is performed by pulling a hard stylus across the surface of a softer material, under a linearly increasing vertical force. The method can be traced back to the mineralogist Friedrich Mohs in 1820 and is currently extensively used in many materials science applications, including strength assessment of rocks (Bard and Ulm, 2010), damage of polymers (Wredenberg and Larsson, 2009), and adhesion and cohesion properties of thin films and coatings (C1624-05, 2015, Randall et al., 2001). We employed an Anton Paar Micro Scratch Tester (MST) (Anton Paar, Switzerland), with a maximum loading capacity of 30 N, and used a Rockwell C diamond scratch probe. The Rockwell C is a conical probe with a half-apex angle of θ = 60° and a spherical tip of radius R = 200μm: in particular, the transition from hemisphere to cone happens for d/R = 0.13, d being the penetration depth. During the test, the scratch forces (both vertical and horizontal) and the penetration depth are continuously measured using high-accuracy linear variable differential transformer sensors. In addition, fracture-induced acoustic waves are recorded by the embedded acoustic sensors.

3. Microscopic scratch testing of cortical bone

Fig. 2 illustrates the micro-scratch test procedure on cortical bone for both the longitudinal-transverse and short-longitudinal directions. LT and SL specimens characterize the fracture toughness perpendicular and parallel to the long axis of bone respectively. Due to the small scale of our experiments and the natural variability of bone, numerous complications needed to be addressed. First, bone exhibits a high local variability in osteon density, shape and size. Since, the toughening mechanisms and hence the fracture toughness of bone are greatly influenced by surface features, this variability demands meticulous efforts in finding appropriate spots to create scratches. Second, the specimens must always be kept wet in order to mimic in-situ conditions, requiring a constant relative humidity during experimentation. Last but not least, a major problem, especially for LT specimens, is the surface area available to create scratches of a desired length. Porcine femur bones are thin-walled allowing only 2-mm long scratches in LT specimens. For the same reason, in SL orientation, samples are thin and need careful polishing to ensure a reasonable specimen thickness.

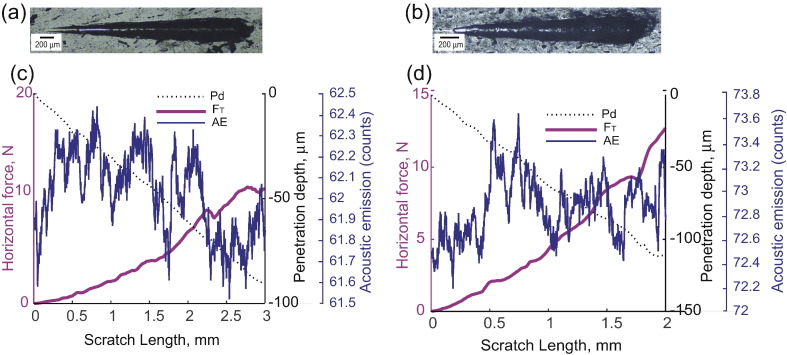
Fig. 2.

Scratch test experiments on cortical bone: (a) digital photo of a scratch test being conducted on cortical bone. Credits - Amrita Kataruka, Kavya Mendu and Ange-Therese Akono, UIUC, 2016. (b) Schematic of scratch test on LT specimen; probing in this orientation generates fracture surfaces in the transverse direction. (c) Schematic of scratch test on SL specimen; probing in this orientation creates fracture surfaces parallel to the long axis of bone.

3.1. Experimental protocol

In order to obtain accurate measurements, it is important to use a scratch probe that is clean and damage-free. Before conducting scratch tests, the tip of the stylus is observed under an optical microscope to make sure it is pristine. The sample is then mounted on the testing platform and a desired area to create scratches is found by monitoring the surface through optical microscope. Scratches are carried out at a loading rate of 60 N/min on both LT and SL specimens as per the parameters shown in Table 1.

Table 1.

Experimental parameters used for scratch testing of swine cortical bone.

Orientation	Scratch length (mm)	Maximum vertical force (N)	Scratch speed (mm/min)
Longitudinal transverse	2	30	4
Short longitudinal	3	30	6

Fig. 3 shows representative load vs displacement curves for tests in both orientations. The penetration depth ranges from 0.022 μm to about 100 μm, spanning 5 orders of magnitudes. Given this broad range of depths, the test is truly multi-scale. In return, the horizontal force increases from 0.6 N to 10–15 N. The acoustic emissions released during the process of scratching are also plotted against the scratch length. These emissions support the existence of fracture processes during scratch test. The optical microscopy panoramic pictures of the top surface after testing in both LT and SL directions are shown in Fig. 3: a residual groove is clearly visible, pointing toward material removal processes such as cracking and chipping.

Fig. 3.

Load-displacement curves for scratch test on cortical bone. (a) Panorama of a scratch in LT direction. (b) Panorama of a scratch in SL direction. (c) Variation of the horizontal force, penetration depth and acoustic emission along the crack length for LT specimen. (d) Variation of the horizontal force, penetration depth and acoustic emission along the crack length for SL specimen. The magnitudes of both the horizontal force and penetration depth increase as the test progresses. In addition, acoustic emissions are observed.

3.2. Micro-mechanisms of fracture

Although the scratch panoramas show a residual groove, optical microscope is unable to capture detailed surface phenomena. As such, Scanning Electron Microscopy (SEM) was employed to observe the top surface after testing. A JEOL 6060 V ESEM (Frederick Seitz Material Research Laboratory, UIUC) was used. Copper strips were attached from the bone surface onto the metal surface in order to enhance conduction during the imaging process for the otherwise non-conductive and un-coated specimens. Back-scattering electron detectors were used in a low vacuum mode. The accelerating voltage was 15 kV with a working distance in the range of 10–14 mm and a spot size in the range of 45–50 for LT Specimens and 60–62 for SL Specimens.

Given that cement lines are weaker than the lamellae, cracks in bone tend to grow along the cement lines. This phenomenon is visible in the SEM images (Fig. 4) for fracture processes around the Haversion canal. Since cement lines binding the concentric lamellae together are circular within the osteons, the cracks too have a circular path (Fig. 4). Additionally, in both the LT and SL orientations, newly generated fracture surfaces can be seen on the surface of the residual groove. Several toughening mechanisms (Peterlik et al., 2006) are distinctly visible in the scratch groove and there is a strong anisotropy of the fracture behavior. For instance, for transverse fracture, crack deflection has been reported to be a significant toughening mechanism (Koester et al., 2008, Nalla et al., 2005b). This is because in this orientation, the prescribed direction is perpendicular to the preferred direction where cracks tend to grow along the weak cement lines. In Fig. 5 almost perpendicular crack deflections are observed along with microcracks, crack bridging and flaking. For longitudinal fracture, crack bridging, which is thought to be an important toughness contributor (Koester et al., 2008, Nalla et al., 2005b), is visible in Fig. 5 in addition to micro-cracking and some crack deflections.

Fig. 4.

Failure micro-mechanisms around Haversian canal: scanning electron microscopy image of a scratch that shows fracture mechanisms around a Haversian canal. Cracks grow in circular paths around the cavity. These circular paths are cement lines that bind the concentric lamellae together.

Fig. 5.

Observed fracture mechanisms: (a) Scanning Electron Microscopy image of a scratch groove in LT specimen. The black arrow points in the direction of scratch. (b) A magnified SEM image of the scratch groove; mechanisms like (1) crack deflection with almost perpendicular deviations, (2) crack bridging and (3) flaking or chipping are observed along with microcracks.

Therefore, scratch testing of cortical bone generates acoustic emissions and leads to a residual groove. When observed under a scanning electron microscope, fracture surfaces are clearly visible along with well-known fracture toughening mechanisms. All these observations serve as physical evidence supporting the hypothesis of scratch-induced fracture processes in cortical bone. Consequently, our findings suggest that scratch tests can be employed to assess the fracture properties of cortical bone. In the next section, we provide a brief overview of the theoretical models implemented in this study.

4. Nonlinear fracture mechanics theory

4.1. General theory

In order to rationalize the observed fracture behavior, we carry out a nonlinear fracture mechanics analysis based on two approaches: the J-integral and the energetic size effect law. Consider a straight horizontal crack emerging from the tip of the scratch tool as schematically shown in Fig. 7. The crack propagates when the energy release rate $\mathcal{G}$ reaches a threshold value equal to the fracture energy G_f or critical energy release rate. We employ a path-independent contour integral to evaluate $\mathcal{G}$ via the J-integral:

$$\mathcal{G}=\frac{1}{p}{\oint }_S\left[\psi n_x-\underset{\_}{T}\cdot \frac{\partial \underset{\_}{\xi }}{\partial x}\right]dS$$ (1)

Where p is probe perimeter. We select the closed contour S so that the only non-zero contribution comes from the blade-material interface (Akono and Ulm, 2011, Akono and Ulm, 2012). We allow for inelastic plastic dissipation; yet, we assume that plastic yield is confined to the crack tip, below the scratch probe. As a consequence, the behavior is elastic at the probe-tool interface and the J-integral can be evaluated considering the linear elastic solution. In a first step, we apply an isotropic model to correlate the scratch force F_T and penetration depth d to the fracture toughness K_c. Assuming the top portion of material above the crack surface to behave like a beam, the stress tensor ahead of the probe is given by $\underset{\_}{\underset{\_}{\sigma }}=-\frac{F_T}{A}{\underset{\_}{e}}_x\otimes {\underset{\_}{e}}_x+{\sigma }_{yy}{\underset{\_}{e}}_y\otimes {\underset{\_}{e}}_y$, where A is the horizontally projected load area that depends on the shape of the scratch probe as well as the depth of penetration d. In plane strain, the linear elastic strain tensor is given by $\underset{\_}{\underset{\_}{\epsilon }}=(1-{\nu }^2)\frac{{\sigma }_{xx}}{E}{\underset{\_}{e}}_x\otimes {\underset{\_}{e}}_x+\nu (1+\nu )\frac{{\sigma }_{xx}}{E}{\underset{\_}{e}}_z\otimes {\underset{\_}{e}}_z$. Herein, x indicates the horizontal direction whereas z is the vertical direction. The elastic free energy density is $\psi =\frac{1}{2}\underset{\_}{\underset{\_}{\sigma }}:\underset{\_}{\underset{\_}{\epsilon }}=\frac{1}{2}(1-{\nu }^2)\frac{{\sigma }_{xx}^2}{E}$ and the stress vector at the blade-material interface is equal to $\underset{\_}{T}=-{\sigma }_{xx}{n}_x{\underset{\_}{e}}_x$. Therefore, the quantity under the integrand in Eq. (1) is equal to $\psi n_x-\underset{\_}{T}\cdot \frac{\partial \underset{\_}{\xi }}{\partial x}=\frac{1}{2}\frac{1-{\nu }^2}{E}{\sigma }_{xx}^2{n}_x-{\sigma }_{xx}{n}_x{\epsilon }_{xx}=-\frac{1}{2}\frac{1-{\nu }^2}{E}{\sigma }_{xx}^2{n}_x$. By using the definition of the horizontally projected area $A={\int }_S-n_{x}dS$ along with the fracture criterion at the onset of cracking — $\mathcal{G}=G_f$—, we derive the following relation:

$$\frac{F_T}{\sqrt{2pA}}=K_c$$ (2)

where $K_c=\sqrt{G_{f}E/(1-{\nu }^2)}$ is the plane strain fracture toughness and G_f is the fracture energy. The quantity 2pA is called the shape function of the probe. For a spherical probe, we have 2pA ∝ d² whereas for a conical probe 2pA ∝ d³. In practice, the probe shape function is calibrated prior to testing using a reference material (Akono et al., 2012, Akono and Ulm, 2014).

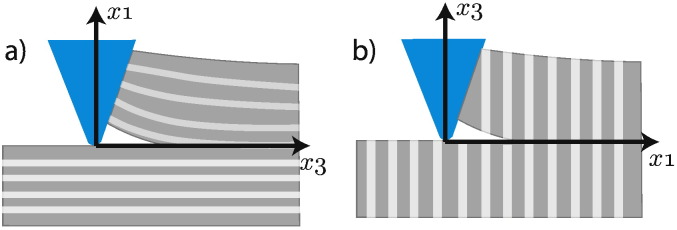
Fig. 7.

Schematic representation of scratch testing of anisotropic materials. a) Short longitudinal orientation. b) Longitudinal transverse orientation.

Eq. (2) assumes small-scale yielding and is valid as long as brittle fracture is the dominant failure mechanism. This leads to two major questions: (1) is there brittle fracture and (2) when does the shift from ductile behavior to brittle cracking occur? One may try to answer these questions by pointing to the acoustic emissions peaks (cf. Fig. 3) as well as the crack surfaces observed on the residual groove post-testing as displayed in Figs. 4–6. However, the pictures only provide a qualitative answer. To reply assertively and in a quantitative fashion, we resort to the famous energetic Size Effect Law (Bažant, 2002, Bažant and Planas, 1997):

$${\sigma }_N=\frac{B{f}_t^{\prime }}{\sqrt{1+D/D_0}}$$ (3)

σ_N is the ultimate nominal strength, D is the structure nominal size, $f_t^{\prime }$ is the tensile strength and B and D₀ are the size effect law parameters. The energetic size effect law describes the release of stored energy to generate new fracture surfaces. Size effect law has been extensively applied for the last 30 years to describe the failure behavior at the macroscopic length-scale of various quasi-brittle materials including but not limited to concrete, cement, rock, ice and bone. We recently extended the size effect law to scratch tests (Akono, 2016, Akono et al., 2014, Bouche and Akono, 2016). For progressively loaded scratch tests with a conical probe of half-apex angle θ, the ultimate nominal strength is given by ${\sigma }_N=\frac{F_T}{d^2\tan \theta }$ and the structure nominal size is defined by $D=\frac{d\sin \theta }{4}$ (Akono, 2016). As a consequence, if failure occurs via plastic flow, the horizontal force should scale as F_T ∝ d². Instead, if fracture processes are dominant, we expect to have F_T ∝ d^3/2. Thus, by monitoring the force scaling with respect to the penetration d, we can verify the existence of a fracture-driven regime, in which Eq. (2) would be suitable to yield the fracture properties. Another route toward the fracture properties is through the size effect law itself; in fact, the fracture toughness K_c is a function of the size effect law coefficients, B and D₀ according to:

$$K_c=B{f}_t^{\prime }\sqrt{D_0}$$ (4)

Thus, both the J-integral and the size effect law provide two rigorous methods to extract the fracture characteristics from scratch tests.

Fig. 6.

Observed fracture mechanisms: (a) Scanning Electron Microscopy image of a scratch groove in SL specimen. The black arrow points in the direction of scratch. Fracture processes are evident on the surface (b) A magnified SEM image of the scratch groove; apart from micro-cracking, other fracture mechanisms like (1) crack bridging and (2) crack deflection are observed.

4.2. Application to anisotropic materials

The last step consists in connecting the scratch fracture toughness K_c to the fracture energy G_f while taking into account the anisotropic behavior of the material. The problem of scratch testing in a transversely isotropic medium was solved by Laubie and Ulm (2014) and Laubie (2013) using the method of complex potentials as well as finite element simulations. Herein, we recall their final analytical expressions. Let ${\underset{\_}{e}}_3$ be the axis of symmetry and $({\underset{\_}{e}}_1,{\underset{\_}{e}}_2)$ be the plane of symmetry. In the case of cortical bone, ${\underset{\_}{e}}_3$ corresponds to the longitudinal direction or long axis of the bone, meanwhile ${\underset{\_}{e}}_1$ and ${\underset{\_}{e}}_2$ represent respectively the circumferential and radial directions as shown in Fig. 7. Rigorously speaking, bone is an orthotropic material; nevertheless, in many instances (Kim et al., 2013, Reilly and Burstein, 1975, Yang et al., 2006a, Yang et al., 2006b) the behavior is approximated by transverse isotropy and we will work under this hypothesis. Assuming then a transversely isotropic response, the fracture toughness in the longitudinal transverse, K_c(LT), and the short longitudinal, K_c(SL) directions depends on the fracture energy values measured in those directions, G_f(LT) and G_f(SL), and on four—out of five— transverse isotropy elastic constants, (E₁,E₃,ν₁₂,ν₃₁), according to:

$$K_c(LT)=\sqrt{\frac{E_1}{1-{\nu }_{12}^2}{G}_f(LT)};K_c(SL)=\sqrt{\frac{E_3}{1-{\nu }_{31}^2\frac{E_1}{E_3}}{G}_f(SL)}$$ (5)

Both K_c(LT) and K_c(SL) are determined using Eqs. (2) and (4) for tests on respectively longitudinal transverse and short longitudinal specimens. In the next section, we apply this nonlinear and anisotropic theoretical framework to cortical bone.

5. Results & discussion

5.1. Ductile-to-brittle transition

Plastic dissipation is known to precede bone fracture (Yan et al., 2007). However, as the prescribed vertical force and hence the penetration depth is increased, fracture processes develop. The reason is the ongoing competition between plasticity and fracture. Fig. 8 displays the force scaling during scratch testing. In Fig. 8 (a), a clear ductile-to-brittle transition is observed as the curve $F_T/\sqrt{2pA}$ converges toward a straight and horizontal line for d/R ≥ 0.26. For lower penetration depths, the fracture toughness is much higher due to plastic flow. In particular, Fig. 8 (b) shows that below a depth of 20 μm, there is a strong deviation from the straight line predicted by the LEFM model. In other words, plasticity is predominant at depths of 20 μm and below. This result confirms previous investigations that concluded to the intrinsic plastic nature of bone at scales of 10 μm (Luczynski et al., 2015) and below (Ritchie et al., 2009, Zimmermann et al., 2010). Plasticity in bone is the result of the sliding of hydroxyapatite crystals in the extrafibrillar space (Eberhardsteiner et al., 2014, Fritsch et al., 2009), along with sliding at the hydroxyapatite/collagen interface, or molecular uncoiling (Zimmermann et al., 2010, Zimmermann et al., 2011).

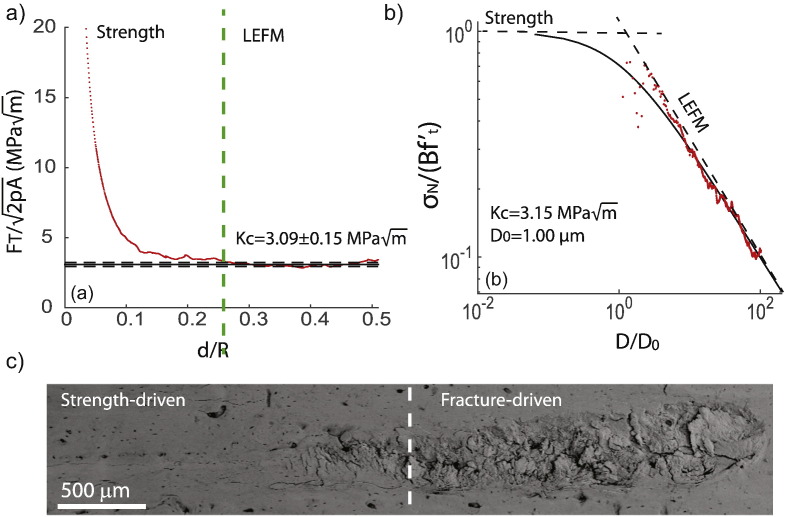
Fig. 8.

Nonlinear fracture analysis of scratch test data on cortical bone. (a) Representative J-integral fracture scaling. d is the penetration depth and R = 200μm is the probe tip radius. F_T is the horizontal force and 2pA is the scratch probe shape function. (b) Energetic size effect law: the solid black line is the nonlinear fracture mechanics estimate and the red line represents the experimental data. σ_N is the nominal strength and $(B{f}_t^{\prime },D_0)$ are the size effect law parameters. (c) SEM panorama of residual groove after scratch testing.

The convergence of $F_T/\sqrt{2pA}$ toward a straight line is characteristic of brittle fracture where energy is dissipated via brittle crack propagation. Fig. 8 (c) shows an SEM panorama of the residual groove: in the strength-driven region, the surface is smooth. In contrast, in the fracture-driven region, micro-cracking and chipping processes can be observed. Finally, the ductile-to-brittle transition can also observed by application of the size effect law (cf. Eq. (3)) as shown on Fig. 8 (b). In the brittle fracture regime, the curve (σ_N vs. D) coincides with the Linear Elastic Fracture Mechanics asymptote (σ_N ∝ D ^−1/2).

5.2. Fracture characteristics

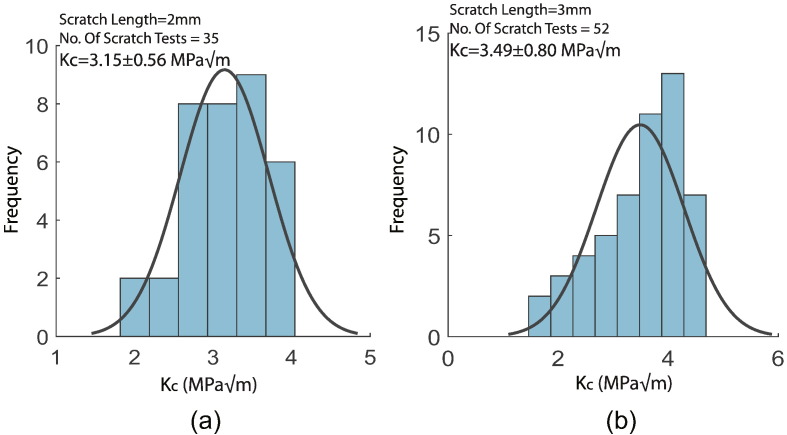
We applied the J-integral model (Eq. (2)) and the energetic size effect law (Eq. (4)) in order to assess the fracture toughness in both the transverse and longitudinal directions. The mean toughness obtained in the LT direction was 3.15 ± 0.56 MPa$\sqrt{\mathtt{m}}$ and that in SL direction was 3.49 ± 0.80 MPa$\sqrt{\mathtt{m}}$. Our test results fall within the range of toughness values reported in the scientific literature for macroscopic fracture tests: 2.2 − −4.6 MPa$\sqrt{\mathtt{m}}$ (Bonfield and Datta, 1976, Bonfield et al., 1978, Norman et al., 1995, Wright and Hayes, 1977). At the microscopic level, very few studies have attempted to measure the fracture resistance. Mullins et al. (Mullins et al., 2007) carried out indentation fracture tests on bovine cortical bone and reported a fracture toughness K_c in the range 0.5–2.3 MPa$\sqrt{\mathtt{m}}$. They attributed the lower values they measured to short crack lengths, 5–65 μm. However, indentation fracture methods are notorious for their subjectivity and inaccuracy due to the need to visualize and measure the crack length (Quinn and Bradt, 2007). In contrast, our scratch tests rely on objective force and depth measurements — recorded using high-accuracy sensors. In our tests, the fracture toughness values were higher, in the ranges given above.

5.3. Variability

Bone possesses a high local variability in structural features at the microscopic scale. This is the reason why we conducted multiple scratches in both directions. Based on the quality of our specimens and the availability of cortical bone area for each specimen, we conducted 35 scratches on LT specimens and 52 scratches on SL specimens. Each test data was analyzed in MATLAB to yield a single fracture toughness and the combined histogram of the result was created as shown in Fig. 9. For both orientations, there is a wide spread in the individual results. This high variability is due to local structural heterogeneity and variability in osteon density. An important factor that might be contributing to this variation is the presence of minerals in bone microstructure (Alexander et al., (2012), Alexander et al., (2012), Lees et al., 1984, Lees et al., 1994). Since, the volume fraction of minerals in the interstitial part of cortical bone plays a significant role in the elastic properties of bone (Crolet et al., 1993, Eberhardsteiner et al., 2014, Hellmich and Ulm, 2002, Morin and Hellmich, 2014), any localized variation in mineral content would ultimately affect the fracture toughness. We also expect some environmental factors to have contributed to this large dispersion of the results. Particularly, the temperature in the testing environment varied from 15–20 °C and the relative humidity varied from 20% to 60%. Because bone is sensitive to degree of hydration and temperature, these factors could have added to the variability of toughness for different tests.

Fig. 9.

Fracture toughness of swine cortical bone: (a) Histogram of fracture toughness of bone in LT direction. In total, 35 2-mm long scratches were carried out. (b) Histogram of fracture toughness of bone in SL direction. A total of 52 3-mm long scratches were carried out for this orientation. The value of fracture toughness is within the range reported in the scientific literature.

5.4. Anisotropy

As seen in Fig. 1, Table 2, bone is highly anisotropic and we expect this trait to be reflected in the fracture response. Fig. 9 shows that in the case of scratch testing, the fracture toughness is higher for short longitudinal specimens compared to transverse longitudinal specimens. This behavior seems contrary to the trend most commonly reported in the literature: the fracture toughness was higher for transverse specimens than longitudinal specimens (Behiri and Bonfield, (1989), Behiri and Bonfield, (1989), Koester et al., 2008, Lucksanasombool et al., 2001, Yan et al., 2006). This apparent discrepancy is connected to the mode of fracture induced during the test. Most experimental studies in the past have heavily focused on single-mode fracture, either mode I—via compact tension tests on single-edge notched bend specimens— or mode II. Indeed, if only a single mode of fracture is present, pure tension or in-plane shear, then fracture propagates along the path of least resistance and as a result, longitudinal specimens exhibit a lower fracture toughness compared to transverse specimens. However, in mixed-mode fracture as is the case for scratch testing, the behavior becomes much more complex and there is no clear-cut trend. Zimmerman et al. (Zimmermann et al., 2009, Zimmermann et al., 2010) carried out asymmetric bend tests on cortical bone specimens and they reported opposing trends: in the longitudinal orientation, the critical energy release rate increases as the phase angle, ψ = tan ⁻¹(K_II/K_I), increases. In contrast, in the transverse orientation, the critical energy release decreases as the phase angle increases. Due to these two competing tendencies, they concluded that transverse fracture yield higher values of the fracture energy compared to longitudinal fracture for ratios K_II/K_I less than 1/21. On the other hand, Akono and Ulm (2014) carried out finite element simulations of scratch testing and they showed that the scratch test induces a mixed-mode fracture, and the mixity angle, ψ, is a function of the probe back-rake angle as well as the friction coefficient at the blade-material interface. Nevertheless for all 120 configurations simulated, the ratio K_II/K_I, was much greater than 2. Thus the high value of the phase angle for scratch testing may explain why for cortical bone the critical stress intensity factor, K_c, is higher for short longitudinal specimens than for longitudinal transverse specimens.

Table 2.

Measured fracture energy, G_f of cortical bone for both the longitudinal transverse (LT) and the short longitudinal (SL) orientations. (E₁,E₃,ν₁₂,ν₁₃) are four of the five transversely isotropic elastic constants. The subscripts 1, 2 and 3 correspond to the circumferential, radial and longitudinal directions.

Source	E1 (GPa)	E3 (GPa)	ν12	ν31	Gf(LT), J/m2	Gf(SL), J/m2
Fritsch and Hellmich (2007)	12.3	20.8	0.38	0.37	690	538
Franzoso and Zysset (2009)	9.2	24.7	0.25	0.56	1011	445

In Table 2, we apply the anisotropic fracture model, cf. Eq. (5), to calculate the fracture energy, G_f, from the average values of the critical stress intensity factor for both the longitudinal transverse and the short longitudinal orientations. The values of the anisotropic elastic constants for bones are drawn from micro-scale studies in the scientific literature based on ultrasonic velocity measurement tests (Fritsch and Hellmich, (2007), Fritsch and Hellmich, (2007)), and nano-indentation tests (Fan et al., 2002, Feng et al., 2012, Franzoso and Zysset, 2009). There is a clear coupling between fracture and elastic characteristics. In particular, the ratio E₃/E₁ of the longitudinal Young's modulus to the transverse modulus plays a significant role. As a consequence of values E₃/E₁ > 1.5, the fracture energy is greater for longitudinal transverse specimens than for short longitudinal ones. Thus, it is only when we factor in the stiffness tensor that our results agree with the trend reported in the scientific literature.

6. Conclusion

In this study, we investigated the fracture response of cortical bone at the osteon level using microscopic scratch tests along with advanced imaging. The resulting behavior is complex and calls for a nonlinear fracture analysis. On the one hand, there is a competition between brittle fracture and ductile fracture, which is evidenced in a ductile-to-brittle transition. On the other hand, the presence of both mode I, tensile opening, and mode II, in-plane shear, combined with microstructural features results in a marked anisotropy of the fracture response. Finally, there is a strong coupling between fracture and elastic characteristics. The methodology and findings presented are unique as they make it possible to measure the fracture toughness and fracture energy directly at the microscopic length-scale. Given the scalability of scratch tests, this study represents an important step to gain a fundamental understanding of fracture in hard biological tissues.