Bone fracture healing in mechanobiological modeling: A review of principles and methods

Abstract

Bone fracture is a very common body injury. The healing process is physiologically complex, involving both biological and mechanical aspects. Following a fracture, cell migration, cell/tissue differentiation, tissue synthesis, and cytokine and growth factor release occur, regulated by the mechanical environment. Over the past decade, bone healing simulation and modeling has been employed to understand its details and mechanisms, to investigate specific clinical questions, and to design healing strategies. The goal of this effort is to review the history and the most recent work in bone healing simulations with an emphasis on both biological and mechanical properties. Therefore, we provide a brief review of the biology of bone fracture repair, followed by an outline of the key growth factors and mechanical factors influencing it. We then compare different methodologies of bone healing simulation, including conceptual modeling (qualitative modeling of bone healing to understand the general mechanisms), biological modeling (considering only the biological factors and processes), and mechanobiological modeling (considering both biological aspects and mechanical environment). Finally we evaluate different components and clinical applications of bone healing simulation such as mechanical stimuli, phases of bone healing, and angiogenesis.

Highlights

• •Bone fracture healing is a series of biological processes, regulated by the mechanical environment and biological factors.
• •Conceptual models of bone fracture healing aim to understand the qualitative process and to formulate its general mechanism.
• •Mechanobiological models consider the effects of both mechanical environment and biological factors.
• •Mechanobiological regulations and mechanical stimuli effects on growth factors can potentially have clinical applications.
• •While important, the inflammatory phase in the bone healing process is not included in mechanobiological simulations.

1. Introduction

Bone fracture is one of the more common injuries, and is associated with treatment costs exceeding billions of dollars, societal productivity loss, and individual disability (Pivonka and Dunstan, 2012, Bonafede et al., 2013). As access to motorized transportation has increased throughout the developing world, there has been a dramatic increase in trauma and life-threatening long bone fractures (Web-based Injury Statistics Query and Reporting System (WISQARS); Cottrell and O'Connor, 2010). Fracture healing is an intricate coordination of various cellular and mechanosensitive processes. Approximately five to 10% of fractured bones end in nonunion and/or incomplete healing (Einhorn, 1995, Praemer et al., 1992). Understanding the biomechanical aspects of the healing process in detail is a crucial for orthopedic surgeons to properly create the optimal healing environment for an injured bone (Pivonka and Dunstan, 2012, Einhorn and Gerstenfeld, 2015).

There are two general approaches to studying the bone healing process: 1) experimental methods and 2) computational modeling. Both of these methods have benefits and limitations. Experimental methods work with real scenarios and generally provide results attributable to clinical applications. However, experimental methods require state of the art equipment, high accuracy, controlled conditions, high cost, and are often confounded by other factors such as unknown subject backgrounds, comorbidities, and genetic variation (Lacroix et al., 2002, Moran et al., 2016). On the other hand, computational modeling and simulation of the bone healing process have been utilized to overcome the limitations associated with experimental methods (Lacroix and Prendergast, 2002). Nevertheless, computational modeling approaches have their own limitations in clinical applications. Thus, these models need to be further developed and validated in order to achieve clinically relevant results (Pivonka and Dunstan, 2012, Carlier et al., 2015a). These models help us better understand the mechanism of bone healing by emphasizing the known correlation between the mechanical environment and the bone healing process (Claes and Heigele, 1999, Prendergast et al., 1997). They can even help us predict how mechanical environments and drug treatment strategies affect the biological processes and cellular activities of bone healing (Geris et al., 2010a, Carlier et al., 2014). Modeling can also provide valuable insight for the design, optimization, and final outcome predictions in future treatment strategies. Nevertheless, computational modeling approaches have their own limitations in clinical applications. Thus, these models need to be further developed and validated in order to achieve clinically relevant results (Pivonka and Dunstan, 2012, Isaksson, 2012).

This review aims to summarize the present understanding of the biomechanical processes affecting healing and nonunion. We first review the bone healing biology, factors, and processes previously addressed in modeling approaches. Some of the well-known mechanobiological regulation theories are then reviewed, and specific mechanical factors which influence biological processes and cellular activities of bone healing are outlined. Finally, we focus on the mechanobiological model's potential contributions to different real-world clinical and research applications, followed by prospective research directions.

2. Biology of Bone Healing

Fracture healing starts with an initial anabolic phase, where local tissue volume increases through inflammation. Following bone fracture, a hematoma is formed at the fracture site, which acts as a temporary scaffold for stem cell differentiation into fibrous tissue, cartilage, and bone. In the inflammatory phase, several biological factors including TNF-Alpha, transforming growth factor-beta (TFG-β) superfamily, bone morphogenetic proteins (BMP), IL-1β, IL-6, IL-17F, and IL-23 are released. In addition to these cytokinetic factors, mechanical loads such as strain or hydrostatic pressure also play a vital role in bone fracture healing (Pivonka and Dunstan, 2012, Einhorn and Gerstenfeld, 2015, Claes et al., 2012, McKibbin, 1978).

The aforementioned biological factors and the mechanical environment regulate the activities of mesenchymal stem cells (MSC), which are some of the most important contributors to the bone formation (Nagel and Kelly, 2010), in addition to the activities of chondrocytes, osteoblasts, fibroblasts, and endothelial cells (Prendergast et al., 1997, McKibbin, 1978, Pauwels, 1959). However, the interaction between cellular activities and the mechanical environment remains undefined (Pivonka and Dunstan, 2012, Einhorn and Gerstenfeld, 2015).

With progressive healing, cartilaginous callus (soft callus) is formed through the activities of skeletal and endothelial cells, which bridge the gap between the bone fragments (Pivonka and Dunstan, 2012, Einhorn and Gerstenfeld, 2015, Claes et al., 2012). Soft callus then progresses to hard callus. There are two typical mechanisms of bone formation: intramembranous ossification and endochondral ossification. In intramembranous ossification, MSCs differentiate to osteoblasts, creating bone tissue directly in an anabolic process (typical of flat bones such as skull and clavicle). In endochondral ossification, MSCs differentiate into chondrocytes, which create cartilage tissue. The synthesized cartilage extracellular matrix (ECM) mineralizes through chondrocyte apoptosis. Subsequently, the osteoblast cells penetrate this dead structure and lay down the bone tissue (Einhorn and Gerstenfeld, 2015, McKibbin, 1978, Oryan et al., 2015). Long bones typically grow and heal by this process.

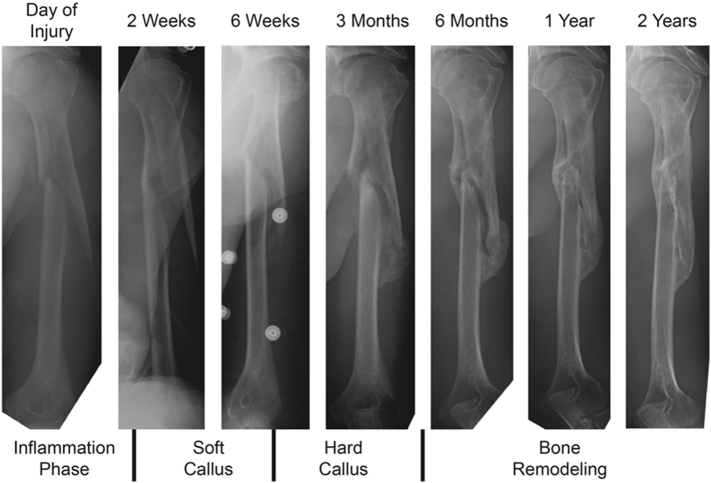
There are two forms of bone healing: primary and secondary. Primary bone healing occurs when the bony fragments are tightly fixed together under compression from implantation. There is no callus formation, and two bone fragments are connected together and healed directly by osteoclasts and osteoblasts activities (Claes et al., 2012, Marsell and Einhorn, 2011). Secondary bone healing, the most common form of bone healing, occurs when there is a small amount of motion in the fracture site. The interfragmentary motion causes soft callus formation, and leads to secondary bone formation through both intramembranous and endochondral ossifications (Claes et al., 2012, Gerstenfeld et al., 2006). This form of bone healing begins with the anabolic phase, and overlaps with the catabolic phase when callus volume is reduced. Following these processes, the bone remodeling phase begins by coordinated osteoblast and osteoclast activities over a span of several months. Callus tissues are reabsorbed and lamellar bone is formed (Schindeler et al., 2008, Little et al., 2007). Fig. 1 illustrates a clinical example of this healing and remodeling process in a comminuted spiral humerus shaft fracture over a two-year time period.

Fig. 1.

Clinical example of humerus fracture healing.

Fig. 1 illustrates a typical humeral shaft fracture that is clinically recognized as not requiring surgery for its successful healing. Humeral extra-articular fractures, even very distal ones, can be treated successfully without surgical fixation simply with a brace and the bone's ability to self-heal through callus formation when mechanically stable. The array of instrumentation and techniques at an orthopedic surgeon's disposal provides the means to create the most ideal and stable healing environment. Fractures along the diaphysis, like the one illustrated in Fig. 1, can heal through callus formation via endochondral ossification, as the callus is unlikely to interfere with mechanical function. On the other hand, an intra-articular fracture is more likely to require open reduction and internal fixation in order to promote primary bone healing or Haversian remodeling. A callus does not form because it would interfere with joint function. Primary healing can be achieved surgically by creating an environment of absolute stability with compression screw and plate fixation, in the humerus, this can easily be achieved with an external brace as Fig. 1 illustrates. In a weight bearing bone such as the femur, a relatively stable condition can usually be achieved with an intramedullary nail. This allows not only callus formation, but also weight bearing during the healing process.

3. Hematoma phase

Immediately after bone fracture, a hematoma is formed from the bleeding at the fracture site, and the healing process is initiated. The hematoma fills the fracture gap in the initial step of bone healing, acts as temporary scaffolding for cellular activity, and provides an appropriate environment for the subsequent biologic cascade of events ultimately resulting in healing (Chung et al., 2006, Axelrad and Einhorn, 2009, Echeverri et al., 2015). The hematoma first transitions to granulation tissue (Kolar et al., 2011). A majority of mechanobiological models considered this phase as the starting point of healing, while mostly neglecting the hematoma phase and its effects on bone healing (Pivonka and Dunstan, 2012, Isaksson, 2012, Pivonka and Komarova, 2010). While the biological aspects and cellular effects of the hematoma phase in bone healing remain unclear, the hematoma phase is critical in initiating the healing process. Its removal leads to delayed healing or nonunion (Kolar et al., 2010). Many primary cellular activities and biological processes, which include migration and differentiation of MSC, angiogenesis, and inflammatory and immune system activities, start at the hematoma phase (Ozaki et al., 2000). The immune cell spectrum of the hematoma component also changes quickly in a matter of few days (Kolar et al., 2010). Consequently, hematomas and successfully healed fractures provide the appropriate environment for launching several cellular and biological activities critical to successfully healed fractures (Claes et al., 2012, Kolar et al., 2010, Schmidt-Bleek et al., 2014).

4. Angiogenesis and vascularity network

Angiogenesis and redevelopment of the vascular network supplies cells, nutrition, oxygen, growth factors and other components required for fracture healing. Angiogenesis precedes osteogenesis and plays a vital role in both intramembranous and endochondral ossification (Einhorn, 1998, Geris et al., 2008). During endochondral ossification in particular, the cartilaginous matrix is penetrated by a vascular network before transforming into osseous tissue (Einhorn, 1998). Several studies have demonstrated that deficient angiogenesis leads to healing impairment (Carlier et al., 2015b, Kanczler and Oreffo, 2008, Saran et al., 2014, Tomlinson and Silva, 2013). Moreover, angiogenesis is a key factor for bone remodeling, because it provides the appropriate conditions for osteoblastic and osteoclastic activities (Kanczler and Oreffo, 2008, Saran et al., 2014, Claes et al., 2002). The endothelial cell plays a critical role in cell migration and transformation, secretion of growth factors, cell signaling, and other biological processes (Carlier et al., 2015b, Hankenson et al., 2015, Mayr-wohlfart et al., 2002).

5. Growth factors

Several biological growth factors influence the process of bone healing by regulating cellular proliferation, migration, differentiation and other cellular processes. Table 1, presented by Saran et al. (with permission of reuse from the publisher), indicates the osteogenic or angiogenic function of the aforementioned growth factors in the bone healing process (Saran et al., 2014).

Table 1.

Growth Factors involved in osteogenesis and angiogenesis by Saran et al. (2014) (with permission of reuse from the publisher).

Growth Factors	Osteogenic or angiogenic effect	Function	Influence of/over other growth factor
VEGF	Both	Chemoattractant for osteoblasts, MSC and Endothelial Cells	Central mediator for other growth factors
TGF-β	Both	Chemoattractant for MSC, differentiation of osteoblasts	FGF, VEGF
PDGF	Both	Chemoattractant and mitogenic stimulation for osteoblasts	VEGF
FGF	Angiogenic	Stimulated osteoblast migration, mitogenic factor for Endothelial Cells, MSC and osteoblasts	VEGF
BMP-2, 4, 7	Osteogenic, indirectly angiogenic	Differentiation of osteoblast-like cells; Chemoattractant for neighboring EC	VEGF-A

5.1. TGF-β

Transforming Growth Factor Beta (TFG-β) is a protein superfamily of growth factors regulating cellular activities including proliferation, differentiation, and tissue migration (Einhorn and Gerstenfeld, 2015). After bone fracture and formation of hematoma, the expression of TFG-β increases at the fracture site and continues to be expressed throughout the remodeling phase (Patil et al., 2011, Poniatowski et al., 2015). TFG-β plays a key role in the differentiation and formation of both cartilage and bone tissue by enabling the cellular activities of MSCs, fibroblasts, chondrocytes, osteoblasts and also inhibiting osteoclastic activity (Patil et al., 2011, Narine et al., 2006). Furthermore, TFG-β has a function in maintaining homeostasis of cartilage and bone, ECM synthesis, angiogenesis, intracellular signaling, and interactions with other growth factors (Patil et al., 2011, Davidson et al., 2007).

5.2. BMP

Bone Morphogenetic Proteins (BMPs), act as signals for cellular migration, differentiation, division, and matrix synthesis, (Einhorn and Gerstenfeld, 2015, Garrison et al., 2010). Their presence is vital for bone healing, and have been used clinically since the commercial introduction of BMP-2 and BMP-7 to enhance the timing and quality of bone fracture healing (Einhorn and Gerstenfeld, 2015). The combination of BMP treatments with other procedures such as bone grafts and surgery are commonly used to improve the outcome of bony fusions (Garrison et al., 2010, Nauth et al., 2010), and have been used off label for the management of recalcitrant nonunions (Axelrad and Einhorn, 2009, Garrison et al., 2010). However, complications such as hematomas, enhanced inflammatory responses, swelling, and longer periods of hospitalization have been reported with their use (Garrison et al., 2010, Nauth et al., 2010, Shields et al., 2006).

5.3. PDGF

Platelet-Derived Growth Factor (PDGF) functions in bone formation by regulating cell migration, growth, and division in order to promote angiogenesis (Nauth et al., 2010, Hollinger et al., 2008). A combined PDGF and β-tricalcium phosphate scaffold has been analyzed as a potential treatment for bone fracture healing in preclinical and clinical stages (Nauth et al., 2010, DiGiovanni et al., 2013). PDGF treatments are also an area of interest for periodontal defect repairs, especially in the context of diabetes and smoking (Nauth et al., 2010, DiGiovanni et al., 2013).

5.4. PTH

Parathyroid hormone (PTH) is an 84 amino acid peptide naturally produced and secreted by parathyroid glands, which adjusts the systemic metabolism of calcium, phosphate, and vitamin D. Although continuous exposure of this hormone is associated with osteoclastic activities, periodic exposure stimulates osteoblastic function and improves bone density. The increase in bone density can help enhance bone fracture healing in osteoporosis treatments (Einhorn and Gerstenfeld, 2015, Little et al., 2007, Nauth et al., 2010, Bukata et al., 2009, Alkhiary et al., 2005). PTH analogs are commercially available (Forteo uses the noncommercial name teriparatide) and have been used to manage severe osteoporosis (Brixen et al., 2004, Daddona et al., 2011, Hodsman et al., 2005) and are now progressively used off-label to manage recalcitrant nonunion as well (Cipriano et al., 2009).

5.5. FGF

Fibroblast Growth Factors (FGF) play a vital role in angiogenesis, MSC mitosis, chondrogenesis, and osteoblast activity during fracture healing (Nauth et al., 2010, Nakajima et al., 2001). There are several FGFs, including FGF1 to FGF22 and FGFR1 to FGFR4, involved in bone healing (Kawaguchi et al., 2010, Riazuddin et al., 2011, Du et al., 2012, Toydemir et al., 2006). Experimental studies have shown that the appropriate dosage of FGF can enhance bone healing and serve as a potential clinical application (Einhorn and Gerstenfeld, 2015, Kawaguchi et al., 2010, Du et al., 2012).

5.6. VEGF

Vascular Endothelial Growth Factor (VEGF) is a signaling protein that stimulates angiogenesis (Nauth et al., 2010). VEGF also directly influences bone formation and stimulates osteoblast differentiation and proliferation (Keramaris et al., 2008). Moreover, combinations of VEGF with BMP growth factors and gene therapy techniques have been suggested to enhance bone fracture healing (Peng et al., 2002, Senel et al., 2013).

6. Mechanical strain and pressure

Mechanical factors such as strain, pressure, stability, and fluid velocity are important parameters that act as stimuli for tissue formation during bone healing. However, the transduction from mechanical factors to cellular stimuli has not yet been fully understood (Isaksson, 2012, Epari et al., 2010, Isaksson et al., 2006a).

Prendergast et al. investigated the correlation between strain and relative fluid/solid velocity as mechanical stimuli for the survival and differentiation of cells. They developed a biphasic finite element (FE) model and simulated a bone healing experiment previously conducted by Saballe (1993), which aimed to deduce the required mechanical environment for musculoskeletal tissue regeneration. They presented a hypothesis in which three types of mechanical stimuli (strain and relative fluid/solid velocity) drive the formation of fibrous tissue (high strain and velocity), cartilage tissue (moderate strain and velocity), and bone tissue (low strain and velocity) (Prendergast et al., 1997).

Carter et al. studied MSC differentiation as a function of mechanical stimulus. They utilized FE modeling to calculate mechanical stimulus during bone healing and its association with the formation of different tissue types. They found that hydrostatic stress and tensile strain were the mechanical stimuli for tissue regeneration, and assigned different ranges of stress and strain for formation of bone, cartilage, fibrocartilage and fibrous tissue (Carter et al., 1998).

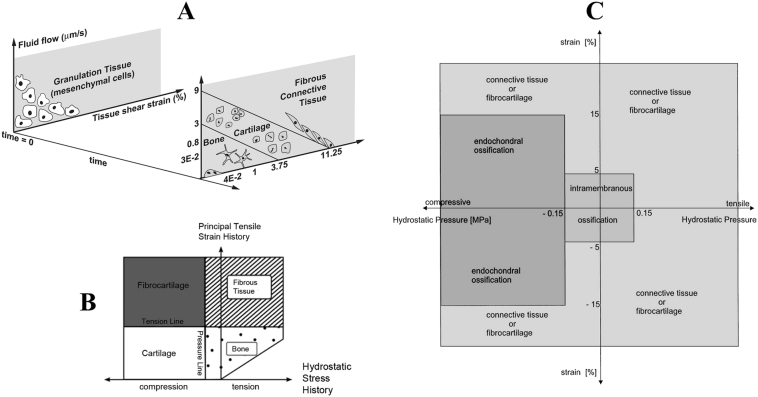
Claes et al. presented a hypothesis on the relationship between mechanical strain, hydrostatic pressure, and cell differentiation in bone healing. They utilized FE modeling and histological data to outline different regions of mechanical stimuli corresponding to different types of differentiation and tissue formation. Intramembranous ossification (for strains less than ± 5% and hydrostatic pressures less than ± 0.15 MPa) and endochondral bone formation (for strains less than ± 15% and compressive pressure larger than − 0.15 MPa) were predicted by their hypothesis. With larger mechanical stimuli, connective and fibrous tissues formed (Claes and Heigele, 1999). Fig. 2 illustrates the mechanobiological regulations presented by Prendergast et al. (1997), Carter et al. (1998) and Claes and Heigele (1999).

Fig. 2.

Different mechanobiological regulations presented: A) Prendergast et al. (1997) B) Carter et al. (1998) C) Claes and Heigele (1999) (with permission of reuse from the publisher).

In the mechanobiological regulations presented by Carter et al. and Cleas et al., bone forms in a relatively low strain - low stress environments, in which bone typically functions. Cartilage, which is known for tolerating compression and absorbing shock, forms in a low strain - high compression zone. Connective tissues and fibrocartilage, that are able to sustain large deformations, form in high strain regions. Therefore, in these mechanobiological regulations, the mechanical zone that is consistent with the type of tissue formation is analogous to the same mechanical environment where the tissue performs its normal activities.

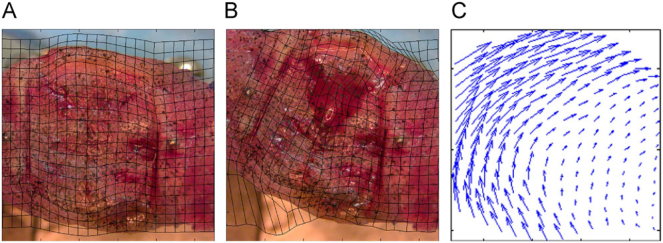
On the other hand, the mechanobiological regulations presented in Prendergast et al. are based on shear deformation of MSCs. Both fluid velocity and shear strain lead to shear deformation of MSCs, which is a well-known stimulus for MSC activities. Using Digital Image Correlation (DIC) (Fig. 3), Morgan et al. reported a significant correlation between octahedral shear strain and tissue type differentiation, especially in the early steps of bone healing; however, the lowest correlation was between volumetric strain and tissue differentiation (Morgan et al., 2010). In contrast from Claes et al. and Carter et al., Prendergast et al. considered the shear components of strain to be more compatible with the experimental data.

Fig. 3.

Strain measurement by DIC method: A) before loading, B) after loading, and C) displacement vector. Morgan et al. (2010) (with permission of reuse from the publisher).

Based on Prendergast et al.’s regulations, bone formation occurs when both mechanical stimuli are minimal. Therefore, the appropriate mechanical environment for bone formation in the healing process differs from that of normal bone formation. In the first few weeks of healing, the fracture site is usually fixed completely, while in the non-injured state, bone that is inactive for a long duration will be resorbed by osteoclast activities (Pivonka and Dunstan, 2012, Prendergast et al., 1997, McKibbin, 1978, Banijamali et al., 2015). In spite of mechanobiological regulations, Comiskey et al. found a positive correlation between callus stiffening rate and strain, based on their meta-analysis data from multiple studies. They also reported that healing rate is linear at low strain and nonlinear (exponential) at high strain (Comiskey et al., 2010). One possible reason for this inconsistency is that Comiskey et al. only considered the initial interfragmentary gap for strain, while mechanobiological regulations involve temporal and spatial strain. Thus, these inconsistencies emphasize the importance of studying initial bone fracture healing mechanisms.

Distraction osteogenesis is the controlled, gradual increase of distance between bone fragments in order to form new bone. It is used to treat some clinical diseases and orthopedic disorders. Unlike typical bone healing, the fracture site is under dilatation rather than compression, and stress relaxation is involved in tissues growth (Brunner et al., 1994, Morgan et al., 2006). Therefore, distraction osteogenesis requires mechanobiological regulations for healing, tissue growth and stress relaxation (Morgan et al., 2006, Isaksson et al., 2007, Reina-Romo et al., 2010, Rodriguez et al., 1994). Moreover, residual stress has been reported as an important factor involved in soft and hard tissue growths (Cowin, 2004, Yamada and Tadano, 2013). Both mathematical formulation and experimental studies have indicated that there is a positive correlation between tissue growth and residual stress. Hence, tissue growth can produce residual stress and vice versa (Rodriguez et al., 1994, Yamada and Tadano, 2013, Holzapfel, 2000).

Bone healing is not only dependent on the magnitude and type of loading, but also the rate and frequency of cyclic loading. These parameters can influence the quality of healing because of the viscoelastic properties of connective tissue (Epari et al., 2010, Goodship et al., 1998, Kenwright and Goodship, 1989, Augat et al., 2001, Wolf et al., 1981). Experimental studies have shown there is a relatively positive correlation between compression rate and bone healing (Goodship et al., 1998, Hente et al., 2004). However, the reports on distraction and tension rate have been inconsistent. While some studies have shown that healing quality does not depend on distraction rate (Augat et al., 2001, Hente et al., 2004), others have data which indicate the opposite (Isaksson et al., 2007, Aarnes et al., 2002, Ilizarov, 1989). One possible explanation for this inconsistency, might be that the tissues and cells involved in bone healing are more sensitive to compression rather than tension. Also, endochondral ossification and chondrogenesis occur only in compression, based on mechanobiological regulation (Claes and Heigele, 1999, Carter et al., 1998). Therefore, the rate of compressive loading might be more important for the bone healing process.

7. Conceptual models

Conceptual models are qualitative tools that help us better understand the concept of bone fracture healing. Therefore, they are very useful for hypothesis formulation, experimental design, and detailed mathematical modeling development. Conceptual modeling simplifies the complex process of bone fracture healing into a simple and understandable theory (Pivonka and Dunstan, 2012, Pivonka and Komarova, 2010).

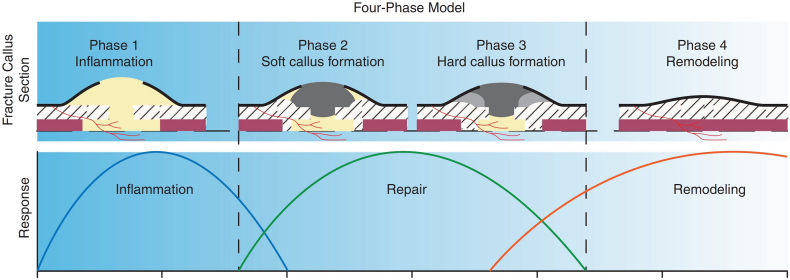
Fracture healing is commonly described as a 4-phase concept: 1) inflammation phase, 2) soft callus formation (cartilage form), 3) hard callus formation (woven bone), and 4) bone remodeling (Fig. 4). The first step is the inflammatory phase where several cells and materials prepare the fracture area for healing. The second step is the formation of soft callus (cartilage) around the fracture area. The third step is the conversion of soft callus to hard callus (cartilage to woven bone), and the final phase 4) is the remodeling of bone, where woven bone changes to lamellar bone (Pivonka and Dunstan, 2012, Einhorn and Gerstenfeld, 2015, Claes et al., 2012, Pivonka and Komarova, 2010).

Fig. 4.

Schematic of the 4-phase conceptual model for bone fracture healing by Pivonka and Dunstan (2012) (with permission of reuse from the publisher).

Little and his colleagues described the healing process as a set of anabolic (bone forming) and catabolic (bone resorbing) responses. They outlined the two responses as a net response leading to either bone healing, incomplete healing, or nonunion. All mechanical, biological, and pharmacological stimuli activate cellular responses for either anabolic or catabolic functions. Their model investigated the effects of changes in the magnitude or time of anabolic and catabolic responses on bone healing, and also included factors such as BMP, PTH, and Nitrogen-containing bisphosphonates (N-BPs) (Schindeler et al., 2008, Little et al., 2007).

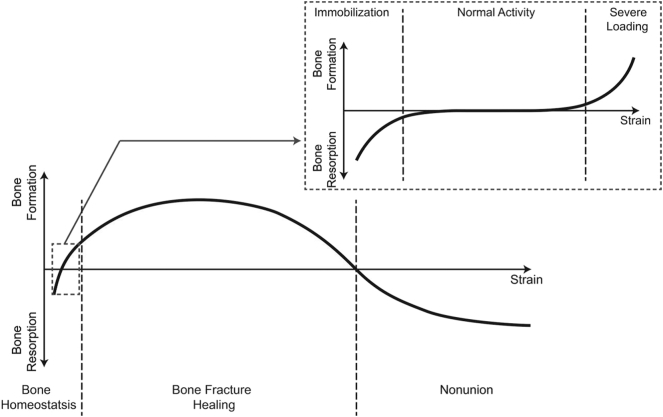
Elliott et al. considered the whole fracture to be a “bone-healing organ,” which works as a functional unit and responds to biological and mechanical stimuli. They combined Wolff's law (i.e. normal bone response to mechanical environment) (Wolff, 1892), Perren's strain theory (i.e. broken bone response to mechanical environment) (Perren, 1978), and Frost's “mechanostat” model (i.e. bone homeostasis response to mechanical environment) (Frost, 1987) to create their own model of bone homeostasis, healing, and nonunion (BHN conceptual model). Using BHN, the behavior of “bone healing organ” was determined with respect to the mechanical strain applied to the organ (Fig. 5). In BHN, the bone is in homeostatsis when under tolerable strain (much less than 2%). For strains greater than 2% and less than 100%, a fracture occurs and is considered to be the beginning of the “bone-healing organ.” Finally, for strains above 100%, the “bone-healing organ” stops and fails to heal, leading to nonunion (Elliott et al., 2016).

Fig. 5.

Schematic of BHN conceptual model by Elliott et al. (2016).

The conceptual models do not look at the bone healing process through the conventional four-phase process perspective. For instance, the model proposed by Little et al. divided the whole process in catabolic and anabolic phases. The conceptual model in Elliot et al. presented the whole process only based on strain. Although these models are simple, they are straightforward and can be employed as a guide to formulate the healing process. For instance, the different parameters could be formulated into the mathematical model depending on their temporal catabolic and anabolic roles. In addition, interfragmentary strain can be utilized to account for healing rate in mathematical formulation. Therefore, conceptual models are useful in formulating the temporal aspect of healing, but are unable to incorporate spatial evolution. However, the approximations for the temporal aspect of healing are sometimes not accurate. This occurs because some biological parameters can possess both anabolic and catabolic roles which depend on spatial conditions. In addition, strain is not the only mechanical stimulus that affects the healing process. Furthermore, in the conceptual model of Elliott et al., strain in the normal activity zone is less than the strain in the healing zone. Based on experimental data, in order to have a successful healing, the fracture site must be well-fixed. Consequently, interfragmentary strain in healing might be less than that of regular activities (Pivonka and Dunstan, 2012, Prendergast et al., 1997, McKibbin, 1978).

8. Mathematical models

Conceptual models give a general qualitative understanding of the bone fracture healing process. However, to quantitatively describe the bone healing process, design of growth factor delivery, optimization of bone healing, and investigate different kinds of treatments or causes of nonunion, sophisticated mathematical modeling is required (Pivonka and Dunstan, 2012, Claes et al., 2012, Pivonka and Komarova, 2010, Geris et al., 2008). Biological approaches in mathematical models consider only the effects of growth factors, cell density, chemotaxis, haptotaxis, or other factors affecting cellular activities and matrix synthesis in bone healing (Geris et al., 2008, BailÓN-Plaza and Van Der Meulen, 2001). In contrast, mechanobiological approaches consider the effects of mechanical loading on the cellular activities and biology of healing bone (Lacroix and Prendergast, 2002, Isaksson et al., 2006a). Some mechanobiological approaches aim to combine both models together and consider the effects resulting from biological factors and mechanical loading on healing (Bailón-Plaza and van der Meulen, 2003, Geris et al., 2010b).

9. Biological modeling

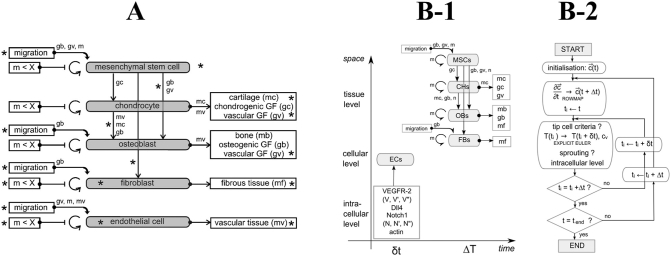
In biological modeling, cellular activity, and matrix synthesis are regulated by biological and biochemistry factors such as growth factors, chemotaxis, or haptotaxis. Temporal and spatial systems of nonlinear partial differential equations (PDE) describe the change in concentration and density of cells, ECMs, and growth factors (Geris et al., 2008, BailÓN-Plaza and Van Der Meulen, 2001). For instance, in a study by BailÓN-Plaza and Van Der Meulen (2001), cell density was determined using the haptotactic and haptokinetic migration speed, cell proliferation rate, and cell differentiation rate as a function of growth factor concentration. In this study, Bailon-Plaza et al. considered only the haptotaxis effects on cell migration. Geris et al. (2008) extended this formulation by adding the chemotactic effects on cellular activities and migration (Fig. 6-A). The chemotaxis effects, in addition to the haptotaxis effects, enhanced bone healing in simulation as well as the distribution of bone density during bone healing.

Fig. 6.

Schematic of mathematical modeling: A) developed by Geris et al. (2008) and B) developed by Carlier et al. (2012) (B-1: scale map and B-2: model) (with permission of reuse from the publishers).

The abovementioned models simulated bone healing at the tissue level; however, Carlier et al., 2014, Carlier et al., 2012 simulated bone healing in tissue at the cellular and intra-cellular levels (Fig. 6-B) (Peiffer et al., 2011). Incorporating cellular and intra-cellular level simulation provided the opportunity to investigate cell movement and vascular sprouting direction in a discrete space (i.e. lattice-based space). In an agent-based model, Buenzli et al. (2012) tracked osteoclast activities such as migration, proliferation, bone resorption, and apoptosis in a lattice-based discrete space. Simulation at the cellular level could individually track and control each cell or capillary. Therefore, this methodology will be suitable if the pattern of cellular activities or an angiogenesis map is the goal (Carlier et al., 2012, Buenzli et al., 2012).

Although biological models simulate a spatial and temporal evolution in bone healing biology, they neglect the mechanical parameters which undeniably affect the bone healing process. Thus, they are not able to explain mechanical bone healing issues including fixation, interfragmentary stability or rate of loading effects on union or nonunion. Nonetheless, biological models provide detailed mathematical equations for biological processes and factors, which can be combined with mechanical parameters to be employed in mechanobiological modeling. Also, these models might better formulate some healing processes such as cell migration or growth factor effects, since they depend more on biological parameters rather than the mechanical environment (Pivonka and Dunstan, 2012).

10. Mechanobiological modeling

Due to the computational complexity of modeling mechanical and biological components simultaneously in fracture healing, progress in its implementation has been successful only in recent years. A primary limitation, when considering both the mechanical and biological aspects, is that is it necessary to solve a series of PDEs and formulate a FE implementation within an iterative procedure (Isaksson, 2012, Anderson et al., 2014, Betts and Müller, 2014).

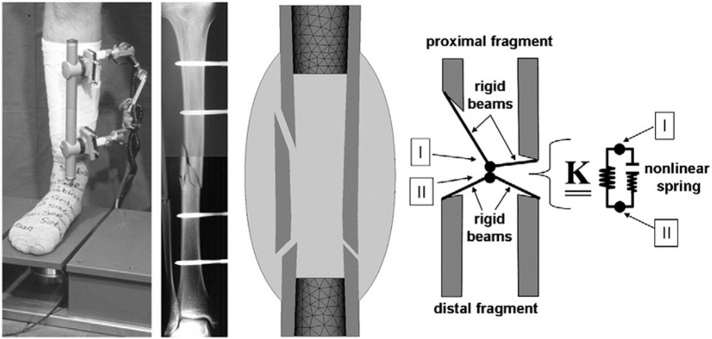
To the best of our knowledge, Lacroix et al., 2002, Lacroix and Prendergast, 2002 were the first group to develop a mechanobiological model of bone healing. Typically, the process of mechanobiological modeling starts from the initial phase (granulation tissue) at the fracture site. Mechanical parameters such as stress, strain, pressure, and fluid velocity are then calculated utilizing a FE analysis. Subsequently, the calculated mechanical parameters regulate the biological processes, which include cellular activity and tissue formation, by solving the PDEs corresponding to the biological processes of interest. As a general expression, higher values of mechanical loading and deformation lead to the formation of fibrous tissue, and lower values lead to bone formation. By allowing new tissue formation and updating the tissue type, material properties and geometry are revised in each iteration and are used for calculations of the mechanical parameters in the next iteration (Fig. 7) (Pivonka and Dunstan, 2012, Isaksson, 2012, Irandoust and Muftu, 2015, Irandoust and Muftu, 2014).

Fig. 7.

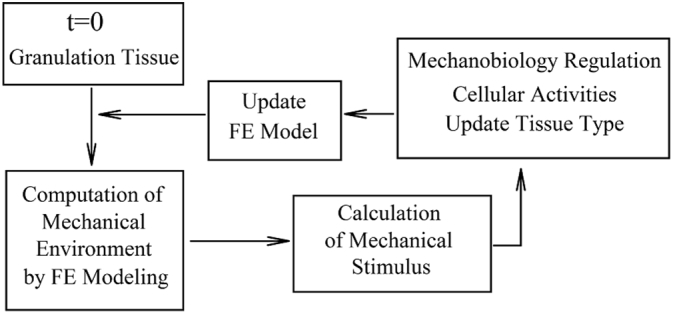
Schematic of a general mechano-bioregulatory model.

Similar to biological modeling, bone healing has been investigated through discrete lattice-based mechanobiological modeling (Byrne et al., 2011, Checa and Prendergast, 2009, Khayyeri et al., 2009). Instead of solving PDEs, mechanobiological modeling simulates cell migration, vascular network redevelopment, and other cellular activities. These are tracked in a lattice based model, and regulated by mechanical and biological factors. As an additional benefit, stochastic movement of cells can be inserted in the model, and activities of each cell can be tracked (Checa and Prendergast, 2009).

Fuzzy logic mechanobiological modeling is another methodology to simulate bone healing. Fuzzy logic methodology is a set of if-then rules (i.e. if a premise is true, then there is a consequent) to formulate conditional statements based on “degrees of truth” instead of usual “true or false”. In fuzzy logic modeling of bone healing, the mechanobiological regulations are simulated by fuzzy rules and the mechanical stimulus calculations can be performed by FE analysis (Shefelbine et al., 2005, Simon et al., 2003, Ament and Hofer, 2000). Fuzzy rules provide a rather qualitative expression of mechanobiological regulation and preclude the need to solve sets of several nonlinear PDEs Wehner et al., 2012, Wehner et al., 2010.

11. Mechanical stimulus

There are some well-known mechanobiological formulations, such as those introduced by Prendergast et al. (1997), 3 et al. (Carter et al., 1998), and Claes and Heigele (1999), which employ different mechanical stimuli such as shear strain (or other strain), hydrostatic pressure, and fluid velocity. In stress-strain tensor algebra, there are two deviatoric and volumetric components. Octahedral shear strain, derived from the deviatoric part, contributes to shape distortion and hydrostatic pressure, derived from the volumetric part, contributes to the volume change (Shames, 1997). Because bone and other tissues involved in bone healing are biphasic, some studies introduced fluid velocity instead of hydrostatic pressure as the mechanical stimulus (Prendergast et al., 1997). Based on the mechanics of biphasic materials, fluid velocity is proportional to the hydrostatic pressure gradient (Dorfmann and Ogden, 2015). Fluid velocity is also a time dependent parameter. Thus, the effects of time dependent factors such as loading rate on bone healing can be investigated using fluid velocity instead of hydrostatic pressure (Lacroix and Prendergast, 2002, Prendergast et al., 1997, Epari et al., 2010).

Implementation of different mechanical stimuli in bone healing simulations can lead to different results. Isaksson et al., 2006a, Isaksson et al., 2006b reported that simultaneously utilizing both deviatoric strain and fluid velocity led to a better and more compatible result with experimental data. Ribeiro et al. (2014) also found that combining interfragmentary strain and the second invariant of deviatoric gap strain tensor as mechanical stimuli with inflammatory factors as chemical stimuli, achieved the callus shape most compatible with histological data. In addition, when axial, shear, or torsion loading are applied to the bone during healing, a different set of mechanical stimuli should be utilized to predict bone healing that is consistent with experimental data. Hence, the selected mechanical stimuli in mechanobiological modeling depend on the mechanical environment during the bone healing process (Isaksson et al., 2006b, Epari et al., 2006).

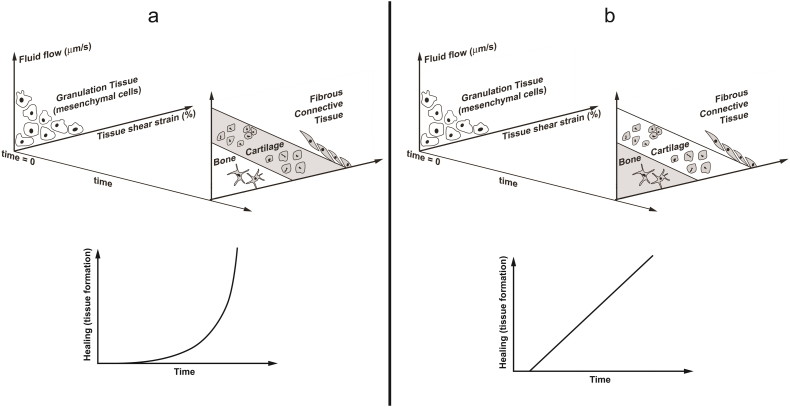
Experimental studies have shown that healing rate is not always linear during the whole process (Comiskey et al., 2010). Therefore, the consideration of different patterns for tissue formation, MSCs differentiation or growth factor secretion rates can improve bone healing simulation. For instance, Alierta et al. investigated the different patterns of tissue formation in each healing zone as a result of mechanobiological regulations. In the zone corresponding to chondrogenesis, healing (i.e. tissue formation) has an exponential relationship with the time, and in the zone corresponding to bone formation, healing has a linear relationship with the time (Fig. 8) (Alierta et al., 2014, Alierta et al., 2015.

Fig. 8.

exponential and linear patterns of healing in chondrogenesis and bone formation zones of mechanobiological regulations, respectively, presented by Alierta et al. (2014).

Moreover, some threshold should be assigned to the mechanical stimulus to determine the type of differentiated tissue. For instance, when shear strains are lower than a determined threshold, bone tissue will be formed; otherwise, cartilage tissue will be formed instead. The threshold magnitudes of mechanical stimulus could be determined through experimental data or based on an optimization process in which some aspects of bone healing such as healing rate would designated as the optimized variable (Lacroix et al., 2002, Isaksson et al., 2006a). Mechanical stimulus thresholds can also depend on the animal or bone size. In a comparison of mechanobiological models in sheep versus rat, Checa et al. (2011) suggested higher thresholds for larger animals, while Wehner et al. (2014) implemented higher thresholds for smaller animals. Since Wehner et al. (2014) and Checa et al. (2011) employed different mechanobiological regulations, material models, and experimental data to set their selected thresholds, this reveals significant inconsistencies in the modeling process.

Ribeiro et al. (2014) utilized optimization algorithms to investigate the effects of different mechanical and chemical stimulus on callus shape and stability. After studying different regions of the callus under each stimulus, they concluded that callus growth can be an optimal response to the local mechanical instability and inflammatory reaction. Wilson et al. (2015) showed that mechanical stimuli such as deviatoric and dilatational strain could also affect the pattern of bone formation (i.e. start point and direction of bone formation) in initial callus and subsequent hard callus development. Repp et al. (Vetter et al., 2012, Vetter et al., 2010, Repp et al., 2015) investigated three scenarios of mechanical stimulus regulations including: 1) A time delay between the mechanical stimulation of cells and tissue formation, 2) variable and bell shaped thresholds instead of step function for mechanical stimulus, and 3) an alteration of mechanical stimulus during bone healing. All three of these had the largest effect on cartilage formation, as opposed to other tissues.

12. Steps of healing included in simulation

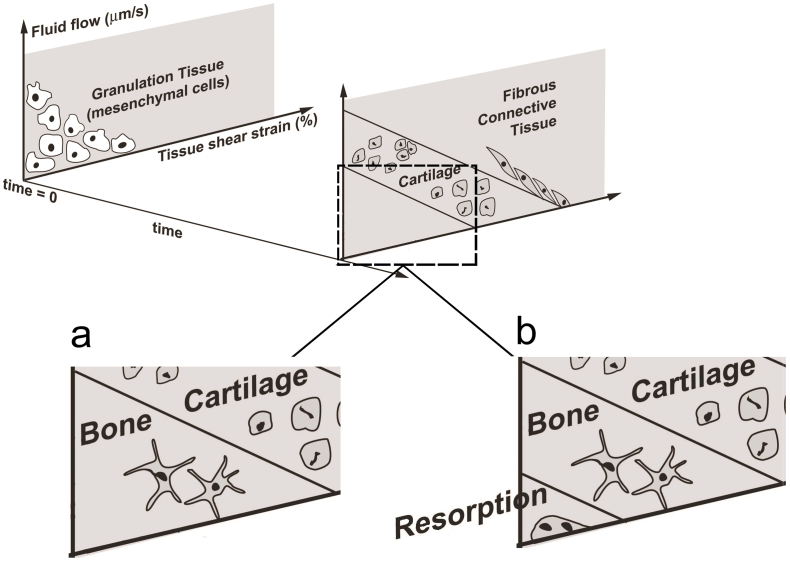
In bone healing simulations, either all or a subgroup of the four bone healing processes (i.e. inflammation phase, soft callus, hard callus and remodeling) can be considered. Some studies have focused only on soft callus or hard callus by utilizing a predefined, fixed callus geometry in their simulation (Carlier et al., 2014, Bailón-Plaza and van der Meulen, 2003, Geris et al., 2010b, Checa and Prendergast, 2009). However, a number of researchers have included callus resorption in the remodeling phase of their bone healing simulation (Lacroix and Prendergast, 2002, Isaksson et al., 2006a, Irandoust and Muftu, 2015, Shefelbine et al., 2005). Hence, if the level of loading falls under a certain threshold, there will be bone resorption and eventual callus resorption at the end of the bone healing simulation (Fig. 9). However, this remodeling simulation algorithm covers only geometry and does not include structure remodeling or directional mechanical properties in bone.

Fig. 9.

Mechanobiological regulations by Prendergast et al. (1997) without bone resorption (a) and with bone resorption (b).

On the other hand, simulations of the initial bone healing phases, such as inflammation, granulation tissue formation, and callus development have not been frequently modeled (Isaksson et al., 2007, Gómez-Benito et al., 2005a, Ribeiro et al., 2015). This may be partly due to mechanical factors playing a lessor role in this phase, while biological and chemical factors are much more significant (Pivonka and Dunstan, 2012, Claes et al., 2012). Furthermore, the material properties of the hematoma and granulation tissues have also not been completely established (Isaksson et al., 2006b). Callus development, as a transient state from the inflammatory phase to the soft callus formation phase, has been simulated through a pseudo volume expansion, made possible by thermal expansion (Gómez-Benito et al., 2005a, Gómez-Benito et al., 2005b) or application of a swelling pressure (Isaksson et al., 2007).

13. Angiogenesis

Proper vascular regeneration is a key factor in bone healing (Martin et al., 1998). Shefelbine et al. (2005) considered angiogenesis for the first time in healing bone healing simulation by developed with a fuzzy logic controller. Geris et al., 2008, Geris et al., 2010b, Geris et al., 2010c proposed PDEs for endothelial cellular activities, vascular matrix synthesis, and angiogenesis growth factor such as VEGF. Carlier et al. (2015b) improved the angiogenesis effects by introducing oxygen to bone healing simulations. Oxygen dependent cellular activities include cell differentiation, endochondral ossification, cell proliferation, oxygen consumption, production of growth factors, and cell death.

Checa and Prendergast (2009) utilized a lattice-based model to develop two sets of mechanobiological regulations for bone healing and angiogenesis, which involved sprout branching and sprout growth. In their angiogenesis algorithm (Fig. 10), sprout growth and branching were regulated by mechanical stimuli and biochemical parameters such as a growth factor gradient and sprout length. Having separate mechanobiological regulations for angiogenesis offered the possibility of studying factors, diseases, and treatments for bone that were influenced by angiogenesis (Checa and Prendergast, 2009, Checa et al., 2011, Checa and Prendergast, 2010). Although consideration of another mechanobiological regulation for angiogenesis complicates the simulation, it could provide a map of vascular network evolution during the healing process. The effects from the mechanical environment on different aspects of angiogenesis could then also be involved in the simulation.

Fig. 10.

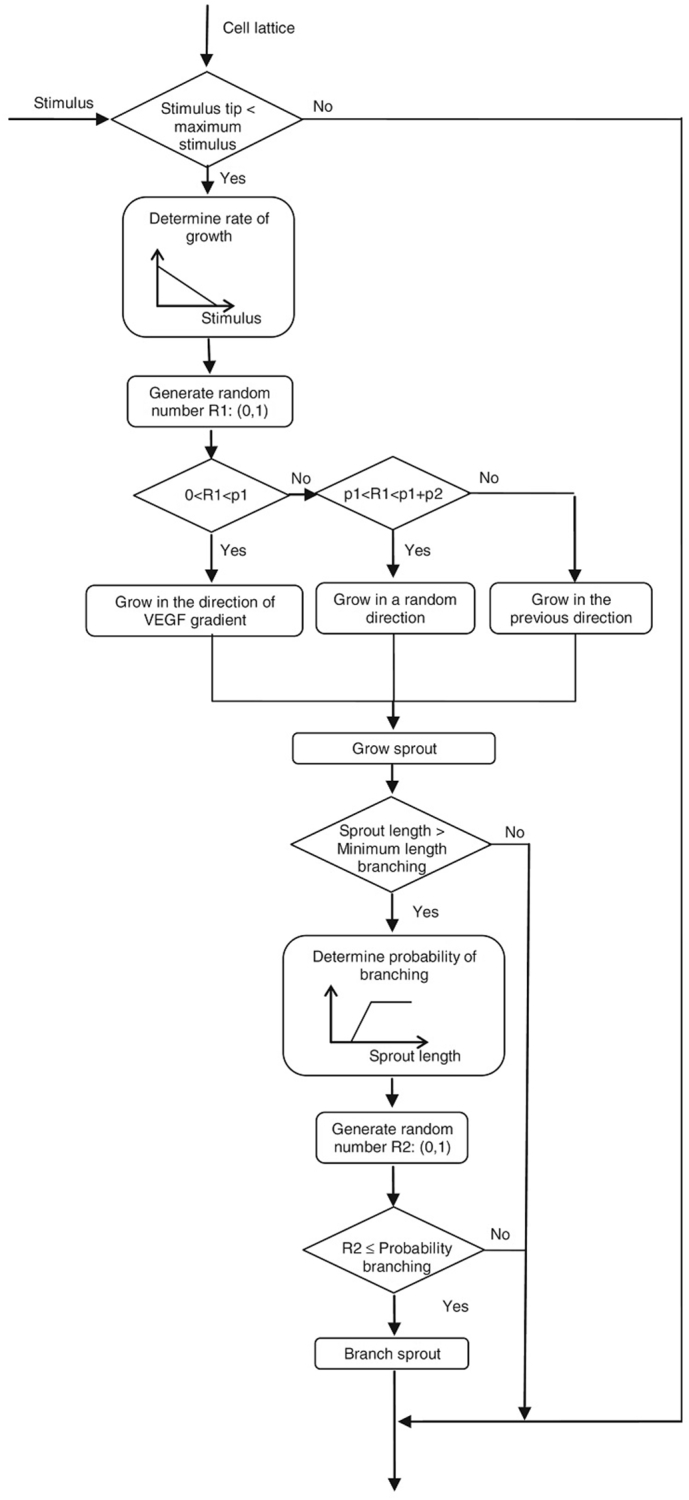
Algorithm of model for angiogenesis of bone fracture healing by Checa et al. (Checa and Prendergast, 2009) (with permission of reuse from the publisher).

14. Clinical application

The final goal of bone healing simulation and modeling is to be employed for clinical applications such as assessing diagnosis and treatment strategies. The limitations involve a scope mismatch between existing models and clinical requirements, limited quantitative experimental data, and lack of human case studies for clinical applications (Carlier et al., 2015a). A model should be predictive, case sensitive, and adjustable for different individuals (Khayyeri et al., 2011, Khayyeri et al., 2015).

Interfragmentary fixation has been investigated by different simulation research efforts. Gomez-Benito et al. (Gómez-Benito et al., 2005b) studied the effects of external fixation stiffness on the shape and tissue distribution of calluses. In a human case study, Wehner et al. (Wehner et al., 2010) studied the effects of fixation stability and interfragmentary movement through both simulation and experimentation on a fractured tibia. In their experimental study, fixation stability could be adjusted by altering the length of the fixator. An asymmetric fracture geometry was considered to be compatible with the patients' fracture geometry (Fig. 11). In agreement with clinical observations, they reported that lower fixation stiffness led to larger callus and longer healing time (Wehner et al., 2010, Gómez-Benito et al., 2005b). Modeling can be employed for implant modifications to achieve optimal design. For instance, Wehner et al. (Wehner et al., 2012, Wehner et al., 2014, Wehner et al., 2011) suggested that a stiffer and thicker nailing implant could lead to quicker healing.

Fig. 11.

Study of fixation stability via modeling and experimental study by Wehner et al. (Wehner et al., 2010) (with permission of reuse from the publisher).

Determining appropriate interfragmentary gap size is another challenging clinical issue for optimal bone healing. Interfragmentary gap size can affect the mechanism of bone healing (i.e. intramembranous bone formation versus endochondral bone formation) and healing time (Lacroix and Prendergast, 2002, Claes et al., 2012). In line with clinical and experimental data, simulations have shown that larger gap size leads to greater instability of the fracture site, a delay in healing, and possible nonunion (Lacroix and Prendergast, 2002, Carlier et al., 2014). Isakson et al. (Isaksson et al., 2007) simulated distraction osteogenesis as a means to create controlled increases of gap size, which consequently increased bone length. They reported that a decrease in distraction rate led to longer healing time. Ultimately all simulation results need to be verified by experiments and clinical observations (Carlier et al., 2015a).

Computational modeling of bone healing can be useful in investigating the effects of growth factors or cell treatments. First, a computational model (i.e. biological or mechanobiological models) is developed and validated. Different scenarios of injection, seeding, and production of growth factors or cells are simulated through the validated model (Carlier et al., 2015a, Geris et al., 2010a), which allow the study of different aspects such as dosage and density effects (Geris et al., 2008, Checa and Prendergast, 2010, Geris et al., 2006), injection location, mode of seeding (i.e. uniform or peripheral seeding) (Checa and Prendergast, 2010), type of growth factors (i.e. chondrogenic growth factors such as BMP-2/4 or osteogenic growth factor such as TGF-β1) (Geris et al., 2008, BailÓN-Plaza and Van Der Meulen, 2001, Bailón-Plaza and van der Meulen, 2003, Ribeiro et al., 2015, Geris et al., 2006), release duration (BailÓN-Plaza and Van Der Meulen, 2001, Bailón-Plaza and van der Meulen, 2003), scaffold implantation (Ribeiro et al., 2015, Checa and Prendergast, 2010), or mechanical loading effects (Geris et al., 2010a, Checa and Prendergast, 2010).

Parametric studies have been employed to determine the sensitivity and importance of different parameters such as cellular characteristics, angiogenesis factors, or material properties in the many aspects of bone healing, which include sequential healing events, bone formation quantity, mechanical stability, and healing time (Checa and Prendergast, 2009, Geris et al., 2006, Isaksson et al., 2008a, Isaksson et al., 2008b, Isaksson et al., 2008c, Isaksson et al., 2009). Parametric studies improve simulation quality and experiments by testing which parameters are important and which can be neglected in the simulation (Isaksson, 2012).

15. Summary and future directions

In this article, we focused on the bone fracture healing process and the biological and mechanical factors involved in it. In the past decade, several well-known investigations have considered both mechanical and biological perspectives to analyze and simulate the bone healing process. Mechanobiological modeling helps us understand how mechanical factors interact with biological processes, and considers both of these aspects simultaneously. This has improved the accuracy of modeling predictions. Recently, due to advances in computational modeling, the effects of different drugs, implants, healing strategies, and injection of growth factors in fracture sites have been studied. However, there are a number of unknown parameters and mechanisms like the role of growth factors in healing, the mechanism of cellular activities, and angiogenesis in bone healing that have yet to be incorporated into modeling efforts.

To the best of our knowledge, there is no comprehensive simulation and model for bone fracture healing that encompasses all the phases of healing, from inflammation to remodeling. Due to its nonlinearity and complexity, the initial phase of bone healing has been mostly excluded from past simulations or has been only considered linearly. In addition, the bone remodeling phase has its own special theories with different simulation methodologies and different external loading regimens. By considering bone fracture healing as a whole package and simulating it from beginning to the end, it can help provide us a better understanding of the process and contribute to our understanding of each phase. Furthermore, the introduction of optimization and artificial intelligence algorithms may help improve the accuracy of models and outline novel and optimal treatment strategies.