Abstract
Tendons transmit load from muscle to bone by utilizing their unique static and viscoelastic tensile properties. These properties are highly dependent on the composition and structure of the tissue matrix, including the collagen I hierarchy, proteoglycans, and water. While the role of matrix constituents in the tensile response has been studied, their role in compression, particularly in matrix pressurization via regulation of fluid flow, is not well understood. Injured or diseased tendons and tendon regions that naturally experience compression are known to have alterations in glycosaminoglycan content, which could modulate fluid flow and ultimately mechanical function. While recent theoretical studies have predicted tendon mechanics using poroelastic theory, no experimental data have directly demonstrated such behavior. In this study, we use high-bandwidth AFM-based rheology to determine the dynamic response of tendons to compressive loading at the nanoscale and to determine the presence of poroelastic behavior. Tendons are found to have significant characteristic dynamic relaxation behavior occurring at both low and high frequencies. Classic poroelastic behavior is observed, although we hypothesize that the full dynamic response is caused by a combination of flow-dependent poroelasticity as well as flow-independent viscoelasticity. Tendons also demonstrate regional dependence in their dynamic response, particularly near the junction of tendon and bone, suggesting that the structural and compositional heterogeneity in tendon may be responsible for regional poroelastic behavior. Overall, these experiments provide the foundation for understanding fluid-flow-dependent poroelastic mechanics of tendon, and the methodology is valuable for assessing changes in tendon matrix compressive behavior at the nanoscale.
Keywords: poroelasticity, viscoelasticity, tendon, AFM, nanomechanics
Introduction
Tendons function to facilitate precise skeletal movement by connecting and transmitting force from muscle to bone. They are able to do this through a unique set of mechanical properties at multiple hierarchical scales. These properties are dynamic, depending highly on loading rate, duration, and magnitude (Mow and Huiskes, 2005). Additionally, tendons are both inhomogeneous and anisotropic. The mechanical properties of the tissue are strongest in the direction of fiber orientation, typically along the longitudinal axis of the tendon, but many tendons, such as the rotator cuff and Achilles tendons, experience multiaxial loading in vivo and, therefore, have more complex properties in certain regions of the tendon (Lake et al., 2010, 2009; Miller et al., 2012b). This is particularly important at the insertion site, where two very different materials (tendon, bone) attach via a four-zone transitional tissue with gradients of fiber organization, extracellular matrix composition, and cell type (Saadat et al., 2016; Thomopoulos et al., 2003, 2002). In addition, some tendon regions which are subjected to compressive loading, such as the sub-acromial portion of the human supraspinatus tendon or tendons that wrap around bones like flexor tendons, may have varying mechanical properties at different regions within the tendon midsubstance (Longo et al., 2011; Ralphs et al., 1991; Vogel et al., 1993).
The mechanical response of tendon is thought to be highly controlled by the innate structure and composition of the tissue. The majority of tendon’s dry weight consists of a hierarchically arranged collagen I network (Birk et al., 1997, 1995). Collagen molecules arrange in a staggered packing arrangement to form individual fibrils, which then bundle to form fibers, fascicles and eventually tendon proper. This collagen network is able to respond dynamically to load through a series of structural arrangements known as collagen re-alignment, uncrimping, sliding, and deformation (Connizzo et al., 2016, 2014b; Miller et al., 2012a; Szczesny and Elliott, 2014a). In addition, a number of other extracellular matrix components may be responsible for the mechanical response. In addition to recent interest in the contribution of elastin and fibrillins (Fang and Lake, 2016), the role of proteoglycans in contributing to the elastic response has long been investigated and debated (Fessel and Snedeker, 2011, 2009; Legerlotz et al., 2013; Lujan et al., 2009, 2007; Screen et al., 2005). However, several studies suggest a role for these important macromolecules primarily in dynamic and viscoelastic properties (Connizzo et al., 2013; Dourte et al., 2012; Dunkman et al., 2013; Rigozzi et al., 2013, 2009), alluding to their interaction with intra-tissue fluid.
Proteoglycans regulate fluid flow in tissues via their glycosaminoglycan chains (GAGs), which have a negative charge (Hascall, 1986; Mow and Huiskes, 2005) and, when densely packed, provide the highest nanoscale resistance to interstitial fluid flow (Maroudas, A, 1979; Nia et al., 2015b). As tendons are primarily composed of water, about 75% of the wet weight, regulation of fluid flow is crucial to dynamic mechanical behavior. In articular cartilage, for example, the abundance of the large proteoglycan aggrecan is responsible for the tissue’s complex poroelastic properties (Azadi et al., 2016; Nia et al., 2015b, 2013, 2011). It has recently been shown that proteoglycan concentration and type can vary dramatically along and between tendons, and specifically that rotator cuff tendons contain aggrecan in addition to decorin and biglycan (Berenson et al., 1996; Matuszewski et al., 2012). Furthermore, regions that experience some compressive loading normally, as well as regions of injured or diseased tendon, have also been shown to express aggrecan mRNA and protein, which likely contributes to altered fluid control and therefore altered function (Archambault et al., 2007; Buckley et al., 2013a; Corps et al., 2006; Longo et al., 2011; Matuszewski et al., 2012; Vogel et al., 1993).
Recent studies have investigated the effect of altered fluid exudation on tissue mechanics using both experimental and theoretical methods (Ahmadzadeh et al., 2015; Buckley et al., 2013b; Butler et al., 1997; Chen et al., 1998; Lavagnino et al., 2008). Furthermore, several studies exploring shear-lag models seem to predict ranges of tissue mechanics well assuming poroelastic behavior (Ahmadzadeh et al., 2015, 2013; Atkinson et al., 1997; Szczesny and Elliott, 2014b). Poroelastic behavior is associated with fluid-solid interactions and fluid pressurization, which underlie important mechanical functions such as frequency-dependent self-stiffening, energy dissipation, and hydraulic permeation. However, due to the difficulty of measuring fluid exudation in tensile mechanics, there have been limited experimental studies to either confirm present models or inform future models. Therefore, the objective of this study was to determine if tendon exhibits poroelastic behavior, to characterize the response, and to determine if there is regional heterogeneity in the poroelastic response based on tissue structure. Our approach focuses on the nanoscale compressive response of tendons, which is motivated both by the recently determined presence of aggrecan in regions of some normal tendons, as well as clinical cases of rotator cuff and Achilles tendinopathies. We hypothesized that tendons would exhibit a poroelastic response similar to that of articular cartilage (Nia et al., 2011), with a dominant peak in the phase angle response occurring at a peak frequency that scales with the square of the characteristic length associated with deformation-induced fluid flow, a hallmark of poroelastic behavior. However, we also hypothesize that this response would be regionally-specific, as both structure and mechanical function have been shown to vary along the length of the tendon, with a decreased hydraulic permeability closer to the junction of tendon and bone.
Methods
Sample Preparation
Achilles and supraspinatus tendons, along with muscle and bone attached, were harvested from the limbs of 2–3 month old male C57BL/6 mice sacrificed for an unrelated study, as described (Connizzo et al., 2014a). Excess soft tissue was gently removed from the tendons, but the bony insertion and myotendinous junction were kept intact for all experiments. Tendon fascicles were gently harvested with tweezers from the tails of 2–3 month old Sprague-Dawley rats sacrificed for an unrelated study. Rat tail tendon fascicles contain the essential collagenous components of tendon in the most simplified and aligned structure, while the Achilles and supraspinatus tendons are more complex in structure and are more clinically relevant for tendon disease and injury (Fallon et al., 2002; Herod et al., 2016; Pang et al., 2016; Rowe, 1985; Screen et al., 2015). In this study, we used the rat tail tendon fascicles to study the behavior of the most simplified tendon structure and composition (highly aligned collagen fibrils and organized distribution of extracellular matrix proteins), and the mouse supraspinatus and Achilles tendons to investigate the role of the tendon-to-bone junction, as well as the more complicated composition and structure (inhomogeneous fibril packing and fibril size/shape, increased inhomogeneity in type and distribution of proteoglycans, and decreased collagen organization), in the poroelastic response. In addition, we tested samples of bovine calf cartilage as previously described (Nia et al., 2011) in order to compare the compression-induced phase angle response, and therefore the hydraulic permeability, between tendon and cartilage. All samples were maintained at physiological ionic strength in phosphate buffered saline (PBS) with protease inhibitors and mechanical tests were performed within 6 hours of harvesting the samples.
All samples were affixed to a custom stage for testing using a very thin layer of cyanoacrylate glue and kept hydrated with PBS for the duration of the experiments (Fig 1A–B). For Achilles and supraspinatus tendons, regional evaluation was performed by indenting samples in regions as close as possible to the bony insertion on the calcaneus or humerus (less than 100μm), respectively, as well as several regions least 200μm away from bone which were defined as midsubstance. It’s important to note that for both Achilles and supraspinatus tendons, samples were tested only on the joint side of the tendon for simplicity (Fig 1A, right), although future experiments will investigate varying nanomechanical function between the joint and bursal sides. For all tendons, indentations were performed near the center of the tissue to avoid unwanted boundary effects from glue or tendon edge. In addition, indentations at each region were performed on multiple tendons, in 3–5 locations within a 50μm radius, with at least 10–15 indentations per location. Locations were visualized with the built-in top-view optics of the AFM, which has a 10x objective (Fig. 1B), and their positions were controlled with the built-in x-y translational stage, which has an accuracy of ~5μm.
Figure 1.
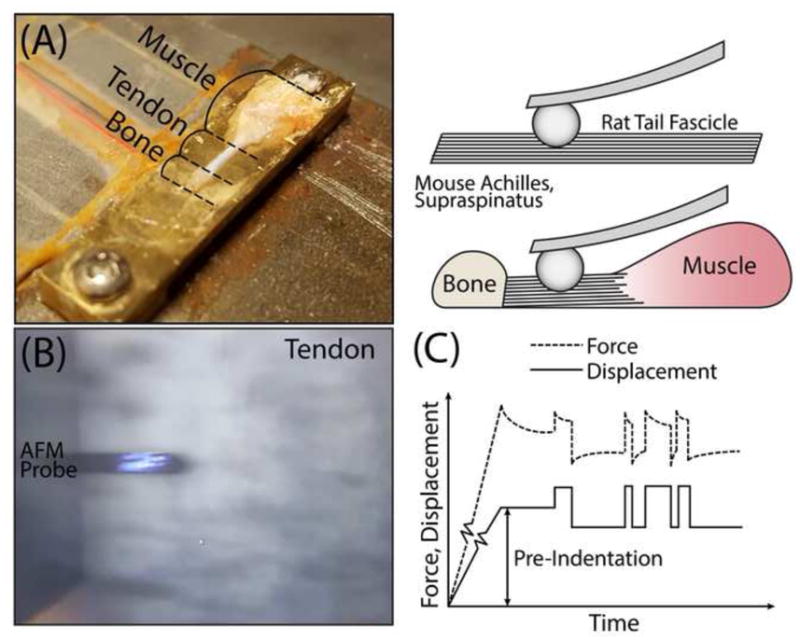
(A) Photograph and schematic of experimental setup highlighting orientation of tendon as well as muscle and bone where appropriate. (B) Image of AFM probe with laser contacting crimped tendon surface. (C) Force and displacement over time profile consisting of pre-indentation followed by dynamic frequency response.
High-frequency AFM-based Rheology System
To measure the complex modulus of samples over a wide frequency range (1 Hz to 10 kHz), we used our custom high-frequency rheology system coupled to a commercial atomic force microscope (AFM) (MFP-3D, Asylum Research, Santa Barbara, CA) (Azadi et al., 2016; Nia et al., 2013). We used polystyrene colloidal probe tips with varying diameters of ~4.5–50 μm (Polysciences, Warrington, PA) attached to tipless cantilevers with nominal spring constant k ~ 7.4 N/m (Budget Sensors, Sofia, Bulgaria). Spring constants were directly measured for all tips using the thermal calibration method (Hutter and Bechhoefer, 1993). The colloidal probes were attached to the cantilever by the lift-off process: a dot of UV-curable glue (Loctite 3211) was placed on a tipless cantilever by making quick contact between the cantilever and a thin layer of glue spread over one half of a glass slide. We then made immediate contact between the tip of the cantilever and a colloid probe resting on the other side of the glass slide and waited for ~5 min with the cantilever pushing against the colloid. This process was followed by UV curing for at least 12 h in a standard biosafety hood.
Based on previous studies, we chose the indentation loading profile consisting of an initial ramp-and-hold pre-indentation of approximately ~0.5–4 μm followed by force relaxation to equilibrium (Fig. 1C). This corresponds to less than 5% initial offset compressive strain for all of the tendons studied here. Random binary sequence (RBS) displacements of amplitude in the range 8–12 nm (Fig. 1C) were then applied after the specimen had reached equilibrium (Nia et al., 2015a). To generate the RBS signal, we applied a low-pass filter and then a sign operator (sign(x) = 1 for x ≥ 0 and sign(x) = −1 for x < 0) to simulated white Gaussian noise. The amplitude of the resulting dataset was then scaled to the maximum allowable excitation given to the secondary piezo actuator. In this study, the sampling rate of the measurement was set to fs=100 kHz, the length of the time series was set to T=30 s, and the cut-off frequency of the low pass filter was set at fc=1 Hz.
The z-piezo voltage from the secondary piezo and the deflection voltage from the MFP-3D were measured and data processing was then performed in MATLAB (The MathWorks, Natick, MA). A discrete Fourier transform was used to obtain the fundamental frequency component of the dynamic force Fosc and displacement δ signals (Nia et al., 2013). The magnitude and phase of the dynamic complex indentation modulus at each frequency was obtained from the measured force and applied displacement amplitudes as previously described (Mahaffy et al., 2004; Nia et al., 2015a). The magnitude is:
where R is the probe radius and δ0 is the initial static offset indentation depth. The phase angle Φ of the dynamic modulus represents the phase of the measured Fosc with respect to the applied dynamic displacement amplitude δ.
Results and Discussion
The high-bandwidth dynamic complex modulus of tendon in compression was measured in this study for the first time, revealing self-stiffening and energy dissipation. Similar to tendon dynamic tensile behavior and to the poroelastic behavior of cartilage, the magnitude of the tendon compressive modulus increased with increasing frequency. However, tendon exhibited a more complicated dynamic response than cartilage (Fig. 2A). Mouse Achilles and supraspinatus, as well as rat tail fascicles, exhibited a two-peak response in the phase angle, with an initial peak at lower frequencies (~10 Hz in Fig. 2 for mouse Achilles tendon) and a second peak at higher frequencies (~1 kHz in Fig. 2), typically with a plateau region between the peaks. In contrast to biopsy-punched cartilage samples previously studied (Nia et al., 2013, 2011), the murine tendons are whole specimens dissected from the joint including all associated tissues. Due to the native structural hierarchy of tendon collagen (Birk et al., 1997, 1995), it is possible that fluid forced to pass through the non-collagenous layers encounters multiple hydraulic permeabilities (associated with local matrix heterogeneities), resulting in complicated magnitude and phase curves having multiple inflections and peaks, respectively. While much is known about the collagenous organization of tendon, the roles of the interfibrillar (collagen fibril size, packing density, shape, crosslinks) and interfascicular matrix (glycosaminoglycans, elastin, etc.) in mechanics, fluid flow, and injury are only just beginning to be investigated. Recent studies have shown that these matrices may play a distinct functional role in tensile mechanics which varies with tendon type (Thorpe et al., 2015) and altered proteomic composition (Thorpe et al., 2016) compared to the collagenous compartments of the tendon. Thus, there may be interplay with fluid flow between compartments elicited by compression that has not previously been observed or hypothesized.
Figure 2.
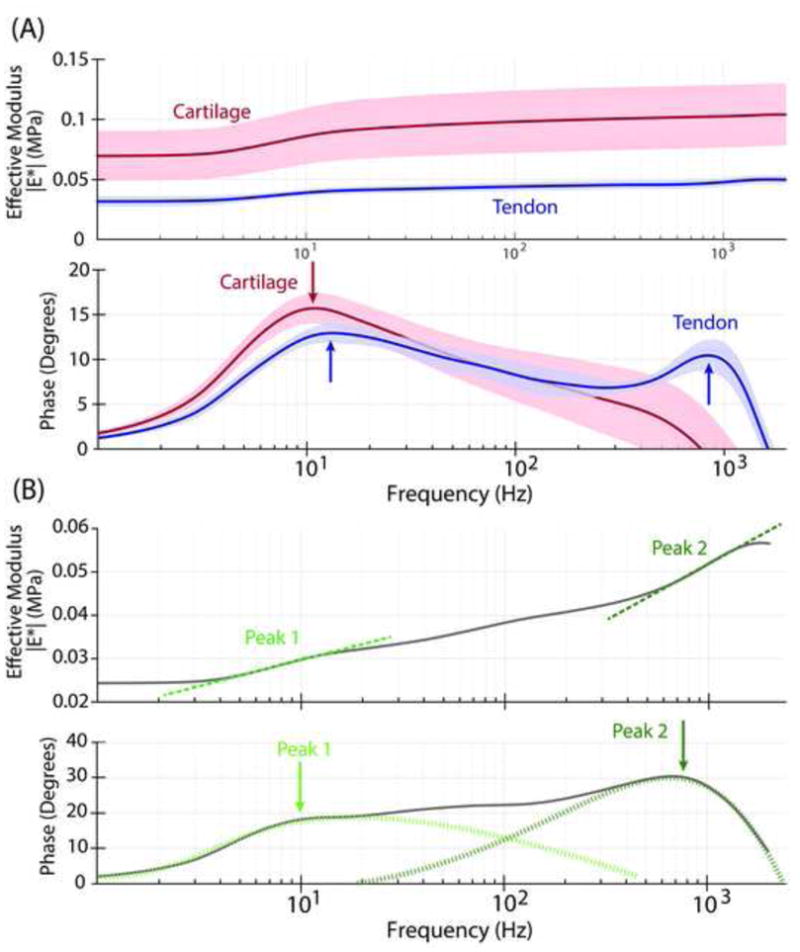
(A) Typical full bandwidth frequency response of mouse Achilles tendon (blue; top: effective modulus magnitude, bottom: phase angle of force with respect to the applied displacement) consists of two peaks with one peak occurring at low frequencies (~10 Hz) and one peak occurring at higher frequencies (~ 1kHz). In contrast, the frequency response of articular cartilage (red) exhibits a phase angle having a single peak. Lines and shading indicate the median and 95% confidence interval, respectively, of 10–15 indentations on a single region. (B) Example curve of the magnitude and phase of single mouse Achilles tendon indentation showing two inflections in the magnitude accompanied by peaks in the phase angle at these same inflection frequencies. Solid line indicates experimental data while dotted lines indicate hypothetical deconvolution of peaks.
However, tendons did exhibit classic poroelastic behavior as revealed by length-scaling of the peak frequency of the phase angle. Linear poroelastic theory states that, fpeak ∝ [(EL • k)/d2], where fpeak is the peak frequency of the phase angle, EL is the equilibrium compressive modulus, k is the hydraulic permeability, and d2 is the probe-tissue contact area (Fig. 3), i.e., the square of the characteristic length over which fluid flows in response to compression by an AFM probe tip of radius R (Nia et al., 2011). This length scaling was investigated in our experiments by varying both the probe tip diameter (Fig 3A) and the initial offset indentation depth δo (prior to dynamic compression) (Fig 3B). This classic behavior was observed in the high frequency peak (peak 2), but not in the low frequency peak (peak 1) of the phase angle response. Specifically, the low frequency peak did not shift with either increased offset indentation depth or increased probe tip diameter (and therefore contact area), while the higher frequency peak was especially sensitive to changes in contact area (Fig 3). A purely viscoelastic response of the tissue would typically result in a single peak in the phase angle response. This peak is flow-independent, and would not be shifted if the contact area was altered, whether due to increased indentation depth or probe tip diameter. In contrast, a purely poroelastic response is directly dependent on fluid flow through the matrix, and therefore altering contact area would shift the frequency of the peak. Furthermore, linear poroelastic theory states that the peak of the phase angle is inversely proportional to the probe-tissue contact area, which was observed in the data of both Fig. 3A and the complementary measurements of Fig. 3B.
Figure 3.
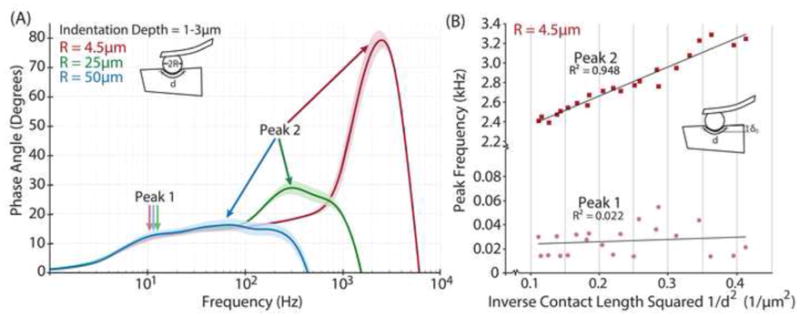
(A) Effect of altered AFM probe tip particle size (using 4.5μm, 25μm, and 50μm particles), which alters probe-tissue contact area (proportional to d2), on full frequency phase angle response of rat tail tendon fascicle, with initial indentation depths approximately 1–3μm. (B) Effect of altered initial indentation depth, δo, which also alters contact area (proportional to d2) on the peak frequencies of the phase angle response of rat tail tendon fascicles indented with 4.5μm particles from (A). Both (A) and (B) indicate a characteristic poroelastic response whereby peak frequency decreases with increasing contact area in the second, or high frequency, peak. The first, or low frequency, peak does not change with particle size or δ o, which indicates that this first peak is not associated with a poroelastic response.
Therefore, we hypothesize that the low frequency peak (peak 1) is dominated by the inherent flow-independent viscoelastic response of the collagenous matrix, while the high frequency peak (peak 2) is dominated by solid-fluid flow-dependent poroelasticity. This would explain well why the hydraulic permeability k (associated with the frequency of the peak in phase angle of peak 2) shifts clearly with alterations in contact area, similar to that reported for poroelastic cartilage (Nia et al., 2011), whereas peak 1 shows no such change with contact area. Furthermore, when the poroelastic phase peak shifts to lower frequency with increased contact area (Fig. 3A), the hypothesized viscoelastic and poroelastic peaks begin to overlap, thus resulting in no clear separation of two peaks (Fig. 3A). Given this hypothesis, our results suggest that the hydraulic permeability of tendon would be higher than that of cartilage, agreeing with observations in the literature. The very dense network of aggrecan and associated GAGs within the collagen network in cartilage hinders fluid movement and traps fluid inside, resulting in a pressurized tissue with rate-dependent compressive mechanics. In contrast, tendon primarily contains smaller proteoglycans that have less ability to trap fluid inside the tissue, and thus the tendon is able to imbibe and exude fluid more freely, resulting in large Poisson ratios (Ahmadzadeh et al., 2015; Chen et al., 1998; Reese et al., 2010) and highly viscoelastic behavior in tension.
Interestingly, Achilles and supraspinatus tendons also exhibit regional heterogeneity in the tissue response (Fig 4). In these tendons, the phase angle response appeared to be broadened, with peak 2 of the phase angle shifted towards higher frequencies at the insertion site. Since the probe radius is much larger than the average diameter of a collagen fibril, it is not likely that this heterogeneity is due to contact with interfibrillar matrix. However, probe radius is similar to the dimensions of individual collagen fibers and therefore, we probed multiple regions and performed multiple indentations per region to measure the overall response of the tissue. With this in mind, the regional heterogeneity in the tissue response found here is likely due to alterations in structure or composition in the tissue. Specifically, the insertion site of the tendon had an increased and broadened response in peak 2 of the phase angle, suggesting a higher permeability in this region of the tendon. We originally hypothesized that due to the increased GAGs near the bony insertion site of the tendon, the permeability in this region would be lower. However, these areas are marked by an abundance of decorin and biglycan, as opposed to previous studies in cartilage which studied the removal of aggrecan (Nia et al., 2013). Therefore, it is likely that fluid flow-dependent interactions regulated by these smaller and less abundant proteoglycans in tendon may be much less impactful in the tendon dynamic response, but future studies could differentially remove these elements to understand their direct role.
Figure 4.
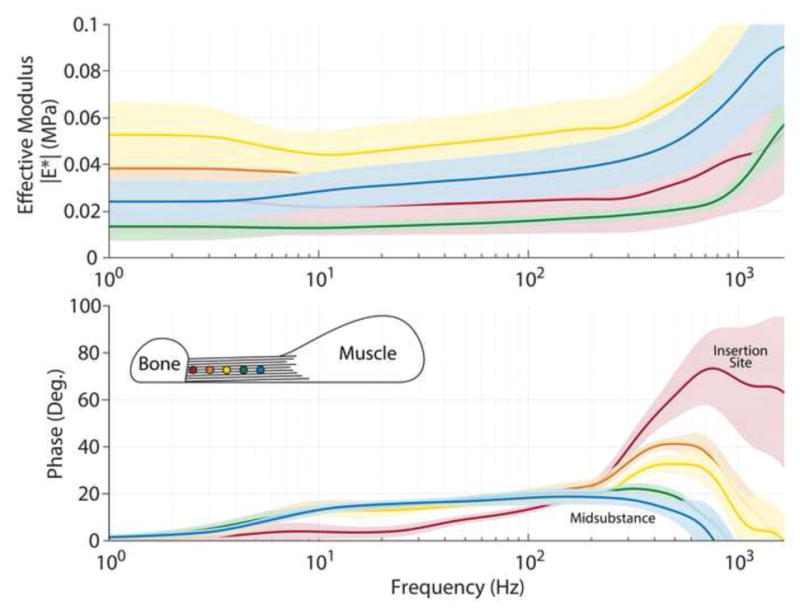
Representative frequency response curves of mouse supraspinatus tendons along the length of the tendon demonstrating the shift in peak from the tendon-bone insertion site to the midsubstance. The first point (insertion site) was defined as within 100μm of the tendon-bone junction (red, dot closest to bone) and the points that followed were approximately every 100μm with the lines indicated by the colors shown in the schematic. Lines and shading represent the median and 95% confidence intervals, respectively, of 10–15 indentations on a single region.
Furthermore, an increased permeability is counterintuitive at the junction of a highly compliant tendon with a stiff and less permeable bone. Previous studies have not investigated tissues with interfacial boundaries linking muscle and bone, as studied here, so it is unclear what role these other tissues may play in the dynamic response. Other changes present in this region that could contribute to the dynamic response include the introduction of mineralization, the decreased collagen organization as the fibers insert into bone, and the inherent boundary conditions caused by the introduction of a material with varying composition, structure and material properties, such as bone. Regardless, the studies here posit that keeping native tendon-bone structure intact, as opposed to dissection techniques where the tendon is cut from the bone, is crucial for understanding the in vivo dynamic response using our approach. It is possible that this higher hydraulic permeability near the tendon-to-bone insertion site may be responsible for joint damage to other structures, which is well established in the biceps tendon and articular cartilage as a result of cuff tears (Peltz et al., 2009; Reuther et al., 2012). Signals released from the injured tendon into the synovial fluid are able to permeate easily into the adjacent tendons, thus leading to matrix degradation and/or remodeling. In addition, this region of the tendon is limited by unidirectional fluid flow due to the boundary of stiff bone and the anisotropy of the tissue, and therefore the increased permeability in this region may allow for fluid to exude more easily to reduce tissue pressurization. This would be particularly important for regions that are experiencing high compressive and shear stresses, such as the insertion site of the supraspinatus tendon which passes under the acromial arch during movement (Gohlke et al., 1993; Zuckerman et al., 1992).
While the present study provides important insights into the fluid-flow-dependent poroelastic properties of tendon, there are some important issues that should be considered. These studies are done in compression, as opposed to typical experimental and modeling studies of tendon which are performed in tension. Thus, these experiments are better suited to understanding mechanical changes in tendon regions that are subjected to compression (such as in the rotator cuff) and are also relevant for understanding the functional consequences of biological changes, such as accumulation or loss of GAGs, that may occur with aging and tendinopathy. Furthermore, compression at the nanoscale may be a good model for fluid exudation in tension due to Poisson effects, particularly in a highly anisotropic tissue such as tendon. Additionally, although all samples reached a relaxed equilibrium state prior to the application of dynamic loading, preconditioning was not performed in these samples prior to indentation and loading history prior to sample preparation was not considered. While we did not notice any significant effects qualitatively over multiple indentations within the same region, differences in the relaxation response were prevalent across different samples and in different regions. More generally, the initial offset indentation-stress relaxation (prior to dynamic compression) was performed in load control (while subsequent dynamic loading was performed in displacement control). With this method, an initial marked impaction of softer tissues can occur without a significant amount of deflection in the cantilever during the pre-indentation. Therefore, it is not uncommon for softer tissue to appear to be stiffer during the dynamic response due to this initial increase in compaction of the tissue. The role of tenocytes and their contribution to active fluid transport are also not considered here. While we don’t expect active fluid transport to play a role on the time scale or frequency range used in this study, changes in permeability could affect cell metabolism and subsequent gene expression that could lead to maladaptation (Archambault et al., 2002; Wall and Banes, 2005). Finally, flow-dependent poroelastic properties measured in this study were not direction-dependent, and it is still unclear what role direction of flow may play in the dynamic response measured here given that tendon is highly anisotropic.
Taken together, to our knowledge, this study is the first to investigate and provide experimental evidence for the poroelastic behavior of tendon. Interestingly, we found that tendons exhibit a complex dynamic response, with multiple peaks in the dynamic phase angle, which we hypothesize are a result of the interaction between viscoelastic and poroelastic mechanical function. Future studies will investigate this hypothesis with finite element modeling similar to our previous studies in cartilage. Furthermore, complex multi-axially loaded tendons, such as the rotator cuff and Achilles tendons, exhibit regional heterogeneity in their dynamic response. Overall, these experiments provide the crucial foundation for understanding fluid-flow-dependent mechanics in tendon and are a valuable tool to assess change in mechanical function at the nanoscale.
Acknowledgments
This study was supported by an NIH/NIA NRSA Postdoctoral Fellowship (F32-AG052284) and NSF Grant CMMI-1536233. The authors thank Drs. Ramin Oftadeh and Hadi Nia for their assistance and technical expertise.
Footnotes
Author Contributions Statement: BK Connizzo has contributed to all aspects of this study, including research design, data acquisition, interpretation/analysis of data, and drafting/revision of the manuscript. AJ Grodzinsky has contributed significantly in research design, interpretation/analysis of data and drafting/revision of the manuscript. All authors have read and approved the final submitted manuscript.
Conflict of Interest Statement
There are no known conflicts of interest associated with this publication or any of its authors and there has been no significant financial support for this work that could have influenced its outcome.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ahmadzadeh H, Connizzo BK, Freedman BR, Soslowsky LJ, Shenoy VB. Determining the contribution of glycosaminoglycans to tendon mechanical properties with a modified shear-lag model. J Biomech. 2013;46:2497–2503. doi: 10.1016/j.jbiomech.2013.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahmadzadeh H, Freedman BR, Connizzo BK, Soslowsky LJ, Shenoy VB. Micromechanical poroelastic finite element and shear-lag models of tendon predict large strain dependent Poisson’s ratios and fluid expulsion under tensile loading. Acta Biomater. 2015;22:83–91. doi: 10.1016/j.actbio.2015.04.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Archambault JM, Elfervig-Wall MK, Tsuzaki M, Herzog W, Banes AJ. Rabbit tendon cells produce MMP-3 in response to fluid flow without significant calcium transients. J Biomech. 2002;35:303–309. doi: 10.1016/s0021-9290(01)00217-2. [DOI] [PubMed] [Google Scholar]
- Archambault JM, Jelinsky SA, Lake SP, Hill AA, Glaser DL, Soslowsky LJ. Rat supraspinatus tendon expresses cartilage markers with overuse. J Orthop Res Off Publ Orthop Res Soc. 2007;25:617–624. doi: 10.1002/jor.20347. [DOI] [PubMed] [Google Scholar]
- Atkinson TS, Haut RC, Altiero NJ. A poroelastic model that predicts some phenomenological responses of ligaments and tendons. J Biomech Eng. 1997;119:400–405. doi: 10.1115/1.2798285. [DOI] [PubMed] [Google Scholar]
- Azadi M, Nia HT, Gauci SJ, Ortiz C, Fosang AJ, Grodzinsky AJ. Wide bandwidth nanomechanical assessment of murine cartilage reveals protection of aggrecan knock-in mice from joint-overuse. J Biomech. 2016;49:1634–1640. doi: 10.1016/j.jbiomech.2016.03.055. [DOI] [PubMed] [Google Scholar]
- Berenson MC, Blevins FT, Plaas AH, Vogel KG. Proteoglycans of human rotator cuff tendons. J Orthop Res Off Publ Orthop Res Soc. 1996;14:518–525. doi: 10.1002/jor.1100140404. [DOI] [PubMed] [Google Scholar]
- Birk DE, Nurminskaya MV, Zycband EI. Collagen fibrillogenesis in situ: fibril segments undergo post-depositional modifications resulting in linear and lateral growth during matrix development. Dev Dyn Off Publ Am Assoc Anat. 1995;202:229–243. doi: 10.1002/aja.1002020303. [DOI] [PubMed] [Google Scholar]
- Birk DE, Zycband EI, Woodruff S, Winkelmann DA, Trelstad RL. Collagen fibrillogenesis in situ: fibril segments become long fibrils as the developing tendon matures. Dev Dyn Off Publ Am Assoc Anat. 1997;208:291–298. doi: 10.1002/(SICI)1097-0177(199703)208:3<291::AID-AJA1>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- Buckley MR, Huffman GR, Iozzo RV, Birk DE, Soslowsky LJ. The location-specific role of proteoglycans in the flexor carpi ulnaris tendon. Connect Tissue Res. 2013a;54:367–373. doi: 10.3109/03008207.2013.832232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckley MR, Sarver JJ, Freedman BR, Soslowsky LJ. The dynamics of collagen uncrimping and lateral contraction in tendon and the effect of ionic concentration. J Biomech. 2013b;46:2242–2249. doi: 10.1016/j.jbiomech.2013.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butler SL, Kohles SS, Thielke RJ, Chen C, Vanderby R. Interstitial fluid flow in tendons or ligaments: a porous medium finite element simulation. Med Biol Eng Comput. 1997;35:742–746. doi: 10.1007/BF02510987. [DOI] [PubMed] [Google Scholar]
- Chen CT, Malkus DS, Vanderby R. A fiber matrix model for interstitial fluid flow and permeability in ligaments and tendons. Biorheology. 1998;35:103–118. doi: 10.1016/S0006-355X(99)80001-8. [DOI] [PubMed] [Google Scholar]
- Connizzo BK, Adams SM, Adams TH, Jawad AF, Birk DE, Soslowsky LJ. Multiscale regression modeling in mouse supraspinatus tendons reveals that dynamic processes act as mediators in structure-function relationships. J Biomech. 2016;49:1649–1657. doi: 10.1016/j.jbiomech.2016.03.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connizzo BK, Bhatt PR, Liechty KW, Soslowsky LJ. Diabetes alters mechanical properties and collagen fiber re-alignment in multiple mouse tendons. Ann Biomed Eng. 2014a;42:1880–1888. doi: 10.1007/s10439-014-1031-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connizzo BK, Sarver JJ, Birk DE, Soslowsky LJ, Iozzo RV. Effect of age and proteoglycan deficiency on collagen fiber re-alignment and mechanical properties in mouse supraspinatus tendon. J Biomech Eng. 2013;135:21019. doi: 10.1115/1.4023234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connizzo BK, Sarver JJ, Han L, Soslowsky LJ. In situ fibril stretch and sliding is location-dependent in mouse supraspinatus tendons. J Biomech. 2014b;47:3794–3798. doi: 10.1016/j.jbiomech.2014.10.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corps AN, Robinson AHN, Movin T, Costa ML, Hazleman BL, Riley GP. Increased expression of aggrecan and biglycan mRNA in Achilles tendinopathy. Rheumatol Oxf Engl. 2006;45:291–294. doi: 10.1093/rheumatology/kei152. [DOI] [PubMed] [Google Scholar]
- Dourte LM, Pathmanathan L, Jawad AF, Iozzo RV, Mienaltowski MJ, Birk DE, Soslowsky LJ. Influence of decorin on the mechanical, compositional, and structural properties of the mouse patellar tendon. J Biomech Eng. 2012;134:31005. doi: 10.1115/1.4006200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunkman AA, Buckley MR, Mienaltowski MJ, Adams SM, Thomas SJ, Satchell L, Kumar A, Pathmanathan L, Beason DP, Iozzo RV, Birk DE, Soslowsky LJ. Decorin expression is important for age-related changes in tendon structure and mechanical properties. Matrix Biol J Int Soc Matrix Biol. 2013;32:3–13. doi: 10.1016/j.matbio.2012.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fallon J, Blevins FT, Vogel K, Trotter J. Functional morphology of the supraspinatus tendon. J Orthop Res Off Publ Orthop Res Soc. 2002;20:920–926. doi: 10.1016/S0736-0266(02)00023-2. [DOI] [PubMed] [Google Scholar]
- Fang F, Lake SP. Multiscale mechanical integrity of human supraspinatus tendon in shear after elastin depletion. J Mech Behav Biomed Mater. 2016;63:443–455. doi: 10.1016/j.jmbbm.2016.06.032. [DOI] [PubMed] [Google Scholar]
- Fessel G, Snedeker JG. Equivalent stiffness after glycosaminoglycan depletion in tendon--an ultra-structural finite element model and corresponding experiments. J Theor Biol. 2011;268:77–83. doi: 10.1016/j.jtbi.2010.10.007. [DOI] [PubMed] [Google Scholar]
- Fessel G, Snedeker JG. Evidence against proteoglycan mediated collagen fibril load transmission and dynamic viscoelasticity in tendon. Matrix Biol J Int Soc Matrix Biol. 2009;28:503–510. doi: 10.1016/j.matbio.2009.08.002. [DOI] [PubMed] [Google Scholar]
- Gohlke F, Barthel T, Gandorfer A. The influence of variations of the coracoacromial arch on the development of rotator cuff tears. Arch Orthop Trauma Surg. 1993;113:28–32. doi: 10.1007/BF00440591. [DOI] [PubMed] [Google Scholar]
- Hascall VC. Functions of the proteoglycans. Introduction Ciba Found Symp. 1986;124:1–8. [PubMed] [Google Scholar]
- Herod TW, Chambers NC, Veres SP. Collagen fibrils in functionally distinct tendons have differing structural responses to tendon rupture and fatigue loading. Acta Biomater. 2016;42:296–307. doi: 10.1016/j.actbio.2016.06.017. [DOI] [PubMed] [Google Scholar]
- Hutter JL, Bechhoefer J. Calibration of atomic-force microscope tips. Rev Sci Instrum. 1993;64:1868–1873. doi: 10.1063/1.1143970. [DOI] [Google Scholar]
- Lake SP, Miller KS, Elliott DM, Soslowsky LJ. Tensile properties and fiber alignment of human supraspinatus tendon in the transverse direction demonstrate inhomogeneity, nonlinearity, and regional isotropy. J Biomech. 2010;43:727–732. doi: 10.1016/j.jbiomech.2009.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lake SP, Miller KS, Elliott DM, Soslowsky LJ. Effect of fiber distribution and realignment on the nonlinear and inhomogeneous mechanical properties of human supraspinatus tendon under longitudinal tensile loading. J Orthop Res Off Publ Orthop Res Soc. 2009;27:1596–1602. doi: 10.1002/jor.20938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavagnino M, Arnoczky SP, Kepich E, Caballero O, Haut RC. A finite element model predicts the mechanotransduction response of tendon cells to cyclic tensile loading. Biomech Model Mechanobiol. 2008;7:405–416. doi: 10.1007/s10237-007-0104-z. [DOI] [PubMed] [Google Scholar]
- Legerlotz K, Riley GP, Screen HRC. GAG depletion increases the stress-relaxation response of tendon fascicles, but does not influence recovery. Acta Biomater. 2013;9:6860–6866. doi: 10.1016/j.actbio.2013.02.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longo UG, Berton A, Khan WS, Maffulli N, Denaro V. Histopathology of rotator cuff tears. Sports Med Arthrosc Rev. 2011;19:227–236. doi: 10.1097/JSA.0b013e318213bccb. [DOI] [PubMed] [Google Scholar]
- Lujan TJ, Underwood CJ, Henninger HB, Thompson BM, Weiss JA. Effect of dermatan sulfate glycosaminoglycans on the quasi-static material properties of the human medial collateral ligament. J Orthop Res Off Publ Orthop Res Soc. 2007;25:894–903. doi: 10.1002/jor.20351. [DOI] [PubMed] [Google Scholar]
- Lujan TJ, Underwood CJ, Jacobs NT, Weiss JA. Contribution of glycosaminoglycans to viscoelastic tensile behavior of human ligament. J Appl Physiol Bethesda Md 1985. 2009;106:423–431. doi: 10.1152/japplphysiol.90748.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahaffy RE, Park S, Gerde E, Käs J, Shih CK. Quantitative Analysis of the Viscoelastic Properties of Thin Regions of Fibroblasts Using Atomic Force Microscopy. Biophys J. 2004;86:1777–1793. doi: 10.1016/S0006-3495(04)74245-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maroudas A. Physicochemical properties of articular cartilage. In: Freeman MAR, editor. Adult Articular Cartilage. J.P. Lippincott Co; Philadelphia, PA: 1979. [Google Scholar]
- Matuszewski PE, Chen YL, Szczesny SE, Lake SP, Elliott DM, Soslowsky LJ, Dodge GR. Regional variation in human supraspinatus tendon proteoglycans: decorin, biglycan, and aggrecan. Connect Tissue Res. 2012;53:343–348. doi: 10.3109/03008207.2012.654866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KS, Connizzo BK, Feeney E, Soslowsky LJ. Characterizing local collagen fiber realignment and crimp behavior throughout mechanical testing in a mature mouse supraspinatus tendon model. J Biomech. 2012a;45:2061–2065. doi: 10.1016/j.jbiomech.2012.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KS, Edelstein L, Connizzo BK, Soslowsky LJ. Effect of preconditioning and stress relaxation on local collagen fiber re-alignment: inhomogeneous properties of rat supraspinatus tendon. J Biomech Eng. 2012b;134:31007. doi: 10.1115/1.4006340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mow VC, Huiskes R. Basic Orthopaedic Biomechanics & Mechano-biology. Lippincott Williams & Wilkins; 2005. [Google Scholar]
- Nia HT, Bozchalooi IS, Li Y, Han L, Hung HH, Frank E, Youcef-Toumi K, Ortiz C, Grodzinsky A. High-bandwidth AFM-based rheology reveals that cartilage is most sensitive to high loading rates at early stages of impairment. Biophys J. 2013;104:1529–1537. doi: 10.1016/j.bpj.2013.02.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nia HT, Gauci SJ, Azadi M, Hung HH, Frank E, Fosang AJ, Ortiz C, Grodzinsky AJ. High-bandwidth AFM-based rheology is a sensitive indicator of early cartilage aggrecan degradation relevant to mouse models of osteoarthritis. J Biomech. 2015a;48:162–165. doi: 10.1016/j.jbiomech.2014.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nia HT, Han L, Bozchalooi IS, Roughley P, Youcef-Toumi K, Grodzinsky AJ, Ortiz C. Aggrecan nanoscale solid-fluid interactions are a primary determinant of cartilage dynamic mechanical properties. ACS Nano. 2015b;9:2614–2625. doi: 10.1021/nn5062707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nia HT, Han L, Li Y, Ortiz C, Grodzinsky A. Poroelasticity of cartilage at the nanoscale. Biophys J. 2011;101:2304–2313. doi: 10.1016/j.bpj.2011.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pang X, Wu JP, Allison GT, Xu J, Rubenson J, Zheng M-H, Lloyd DG, Gardiner B, Wang A, Kirk TB. The three dimensional microstructural network of elastin, collagen and cells in Achilles tendons. J Orthop Res Off Publ Orthop Res Soc. 2016 doi: 10.1002/jor.23240. [DOI] [PubMed] [Google Scholar]
- Peltz CD, Perry SM, Getz CL, Soslowsky LJ. Mechanical properties of the long-head of the biceps tendon are altered in the presence of rotator cuff tears in a rat model. J Orthop Res Off Publ Orthop Res Soc. 2009;27:416–420. doi: 10.1002/jor.20770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ralphs JR, Benjamin M, Thornett A. Cell and matrix biology of the suprapatella in the rat: a structural and immunocytochemical study of fibrocartilage in a tendon subject to compression. Anat Rec. 1991;231:167–177. doi: 10.1002/ar.1092310204. [DOI] [PubMed] [Google Scholar]
- Reese SP, Maas SA, Weiss JA. Micromechanical models of helical superstructures in ligament and tendon fibers predict large Poisson’s ratios. J Biomech. 2010;43:1394–1400. doi: 10.1016/j.jbiomech.2010.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reuther KE, Sarver JJ, Schultz SM, Lee CS, Sehgal CM, Glaser DL, Soslowsky LJ. Glenoid cartilage mechanical properties decrease after rotator cuff tears in a rat model. J Orthop Res Off Publ Orthop Res Soc. 2012;30:1435–1439. doi: 10.1002/jor.22100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rigozzi S, Müller R, Snedeker JG. Local strain measurement reveals a varied regional dependence of tensile tendon mechanics on glycosaminoglycan content. J Biomech. 2009;42:1547–1552. doi: 10.1016/j.jbiomech.2009.03.031. [DOI] [PubMed] [Google Scholar]
- Rigozzi S, Müller R, Stemmer A, Snedeker JG. Tendon glycosaminoglycan proteoglycan sidechains promote collagen fibril sliding-AFM observations at the nanoscale. J Biomech. 2013;46:813–818. doi: 10.1016/j.jbiomech.2012.11.017. [DOI] [PubMed] [Google Scholar]
- Rowe RW. The structure of rat tail tendon fascicles. Connect Tissue Res. 1985;14:21–30. doi: 10.3109/03008208509089840. [DOI] [PubMed] [Google Scholar]
- Saadat F, Deymier AC, Birman V, Thomopoulos S, Genin GM. The concentration of stress at the rotator cuff tendon-to-bone attachment site is conserved across species. J Mech Behav Biomed Mater. 2016;62:24–32. doi: 10.1016/j.jmbbm.2016.04.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Screen HRC, Berk DE, Kadler KE, Ramirez F, Young MF. Tendon functional extracellular matrix. J Orthop Res Off Publ Orthop Res Soc. 2015;33:793–799. doi: 10.1002/jor.22818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Screen HRC, Shelton JC, Chhaya VH, Kayser MV, Bader DL, Lee DA. The influence of noncollagenous matrix components on the micromechanical environment of tendon fascicles. Ann Biomed Eng. 2005;33:1090–1099. doi: 10.1007/s10439-005-5777-9. [DOI] [PubMed] [Google Scholar]
- Szczesny SE, Elliott DM. Interfibrillar shear stress is the loading mechanism of collagen fibrils in tendon. Acta Biomater. 2014a;10:2582–2590. doi: 10.1016/j.actbio.2014.01.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczesny SE, Elliott DM. Incorporating plasticity of the interfibrillar matrix in shear lag models is necessary to replicate the multiscale mechanics of tendon fascicles. J Mech Behav Biomed Mater. 2014b;40:325–338. doi: 10.1016/j.jmbbm.2014.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomopoulos S, Hattersley G, Rosen V, Mertens M, Galatz L, Williams GR, Soslowsky LJ. The localized expression of extracellular matrix components in healing tendon insertion sites: an in situ hybridization study. J Orthop Res Off Publ Orthop Res Soc. 2002;20:454–463. doi: 10.1016/S0736-0266(01)00144-9. [DOI] [PubMed] [Google Scholar]
- Thomopoulos S, Williams GR, Gimbel JA, Favata M, Soslowsky LJ. Variation of biomechanical, structural, and compositional properties along the tendon to bone insertion site. J Orthop Res Off Publ Orthop Res Soc. 2003;21:413–419. doi: 10.1016/S0736-0266(03)00057-3. [DOI] [PubMed] [Google Scholar]
- Thorpe CT, Godinho MSC, Riley GP, Birch HL, Clegg PD, Screen HRC. The interfascicular matrix enables fascicle sliding and recovery in tendon, and behaves more elastically in energy storing tendons. J Mech Behav Biomed Mater. 2015;52:85–94. doi: 10.1016/j.jmbbm.2015.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorpe CT, Peffers MJ, Simpson D, Halliwell E, Screen HRC, Clegg PD. Anatomical heterogeneity of tendon: Fascicular and interfascicular tendon compartments have distinct proteomic composition. Sci Rep. 2016;6:20455. doi: 10.1038/srep20455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogel KG, Ordög A, Pogány G, Oláh J. Proteoglycans in the compressed region of human tibialis posterior tendon and in ligaments. J Orthop Res Off Publ Orthop Res Soc. 1993;11:68–77. doi: 10.1002/jor.1100110109. [DOI] [PubMed] [Google Scholar]
- Wall ME, Banes AJ. Early responses to mechanical load in tendon: role for calcium signaling, gap junctions and intercellular communication. J Musculoskelet Neuronal Interact. 2005;5:70–84. [PubMed] [Google Scholar]
- Zuckerman JD, Kummer FJ, Cuomo F, Simon J, Rosenblum S, Katz N. The influence of coracoacromial arch anatomy on rotator cuff tears. J Shoulder Elb Surg Am Shoulder Elb Surg Al. 1992;1:4–14. doi: 10.1016/S1058-2746(09)80010-4. [DOI] [PubMed] [Google Scholar]


