Impulsivity in Rodents with a Genetic Predisposition for Excessive Alcohol Consumption is Associated with a Lack of a Prospective Strategy

Abstract

Increasing evidence supports the hypothesis that impulsive decision-making is a heritable risk factor for an alcohol use disorder (AUD). Clearly identifying a link between impulsivity and AUD risk, however, is complicated by the fact that both AUDs and impulsivity are heterogeneous constructs. Understanding the link between the two requires identifying the underlying cognitive factors that lead to impulsive choices. Rodent models have established that a family history of excessive drinking can lead to the expression of a transgenerational impulsive phenotype, suggesting heritable alterations in the decision-making process. The current study explored the cognitive processes underlying impulsive choice in a validated selectively bred rodent model of excessive drinking – the alcohol preferring (‘P’) rat. Impulsivity was measured via delay discounting (DD) and P rats exhibited an impulsive phenotype compared to their outbred foundation strain - Wistar rats. Steeper discounting in P rats was associated with a lack of a prospective behavioral strategy, which was observed in Wistar rats and was directly related to DD. To further explore the underlying cognitive factors mediating these observations, a drift diffusion model of DD was constructed. These simulations supported the hypothesis that prospective memory of the delayed reward guided choice decisions, slowed discounting, and optimized the fit of the model to the experimental data. Collectively, these data suggest that a deficit in forming or maintaining a prospective behavioral plan is a critical intermediary to delay reward, and by extension, may underlie the inability to delay reward in those with increased AUD risk.

Introduction

Impulsivity is broadly defined as the predisposition to act prematurely without foresight (Dalley et al., 2011). The propensity to make impulsive choices is a risk factor for substance abuse disorders including alcoholism; however, the strength of this relationship is unknown (Verdejo-Garcia et al., 2008, de Wit, 2009, Dick et al., 2010, Lejuez et al., 2010, MacKillop, 2013, Dougherty et al., 2014, Jentsch et al., 2014, Jentsch and Pennington, 2014). One challenge in accurately quantifying this relationship is that both impulsivity and alcohol use disorders (AUDs) are heterogeneous constructs, influenced by a number of factors like sensation seeking, positive/negative urgency, or a lack of planning (de Wit, 2009, Lejuez et al., 2010, Rogers et al., 2010, Dalley et al., 2011, Coskunpinar et al., 2013, Jentsch et al., 2014). The broad goal of the present study was to explore the underlying factors contributing to the relationship between impulsivity and risk for excessive drinking.

Delay discounting (DD) is a behavioral measure of cognitive impulsivity and a relationship between DD and AUD has been reported (Kollins, 2003, MacKillop et al., 2011, Mitchell, 2011, MacKillop, 2013, Bickel et al., 2014a, Bickel et al., 2014b, Jentsch et al., 2014). Both alcoholism risk (Johnson et al., 1998, Enoch and Goldman, 2001, Dick and Bierut, 2006) and DD (Anokhin et al., 2014) are heritable, and there is increasing evidence that these traits are also genetically correlated (Wilhelm and Mitchell, 2008, Oberlin and Grahame, 2009, Acheson et al., 2011, Dougherty et al., 2014, Perkel et al., 2015). It is still unclear, however, to what extent excessive DD increases risk of developing an AUD, and which underlying cognitive processes might mediate this risk.

Alcohol Preferring “P” rats have been selectively bred for excessive alcohol consumption and have proven extremely useful for exploring the heritable factors and neural systems leading to this phenotype (McBride et al., 2014). Evidence is emerging that, like humans with a family history of alcoholism, rodents selectively bred for excessive drinking also exhibit impaired measures of cognition - including impulsivity (Oberlin and Grahame, 2009, Wenger and Hall, 2010, Walker et al., 2011, Beckwith and Czachowski, 2016). Moreover, alcohol naïve P rats discount delayed rewards more robustly than rodent populations that lack increased genetic risk (Beckwith and Czachowski, 2014, Perkel et al., 2015). These data suggest that the impulsive phenotype is not a consequence of excessive drinking, but rather that these two traits are regulated by similar genes and neural systems. The specific goal of the current study was to further characterize how altered cognitive processing in P rats predisposes them towards impulsive decision-making.

Drift diffusion models provide a powerful tool to explore the cognitive processes guiding fast, two-choice decisions (Ratcliff and McKoon, 2008). These models have been used extensively to examine cognitive processes required to withhold a prepotent response (Verbruggen and Logan, 2009), in addition to how environmental stimuli guide perceptual-based decisions (Shadlen et al., 1996, Romo and Salinas, 2001). Two-choice perceptual decision-making modeled as a diffusion process assumes that noisy sensory information is integrated to guide decision-making, and can account for the shape of response time distributions, the speed-accuracy tradeoff, and changes in neural firing during intertemporal choices (Ratcliff and McKoon, 2008, Kim and Lee, 2011). A recent study using a drift diffusion model supported the hypothesis that assigning value to a delayed reward requires that it be mapped to the context in which it will be received (Kurth-Nelson et al., 2012). These simulations concluded that the mapping process requires prospective memory and is critical for delaying reward (Kurth-Nelson et al., 2012). The drift diffusion model presented herein also explores how future, delayed rewards, are mapped and maintained during cognitive search, and was used to further test the hypothesis that steep delay discounting in P rats is due in part to alterations in the use of a prospective strategy. This was motivated by the fact that of the candidate cognitive processes that might mediate DD to increase AUD risk, the ability to, or use of, envisioning the future (i.e. prospection) has been shown recently to be negatively related to the severity of an individuals drinking problems (Griffiths 2012) or alcohol dependence (Heffernan, 2008). Using a modified DD task in rodent populations with varying risk of excessive alcohol consumption, and a drift diffusion model of these data, these studies tested the hypothesis that the ability to plan goal-directed behaviors involves a cognitive search process which is influenced by genetic risk and mediates impulsivity.

Materials and Methods

Animals

Sixteen male Indiana University Alcohol Preferring (P) rats and 16 non-genetically predisposed (heterogeneous) Wistar rats were provided by the Indiana University Alcohol Research Center animal production core or purchased from Harlan (Indianapolis, IN), respectively. Upon arrival animals were acclimated to single housing and a 12 hour reverse light/dark cycle with lights off at 7:00 AM for at least a week prior to testing. All animals were at least 70 days of age prior to testing and had ad lib access to food and water prior to food restriction/habituation. Over the course of approximately 2 weeks, animals were food restricted to 85% of their starting free-feeding weight and maintained under this condition throughout all experiments. All procedures were approved by the Purdue School of Science Animal Care and Use Committee and conformed to the Guidelines for the Care and Use of Mammals in Neuroscience and Behavioral Research (National Academic Press, 2003).

Operant Apparatus

Standard one compartment operant boxes (20.3 cm × 15.9 cm × 21.3 cm; Med Associates, St Albans, VT) were used for all DD procedures. Each box contained left and right retractable levers on one wall, left and right stimulus lights positioned immediately above each lever, and an easily accessible pellet hopper positioned between these left and right positioned devices. The opposite wall contained a house light and a tone generator (2,900 Hz) on the top most position.

Habituation/Shaping

Ten sucrose pellets were placed in the animals’ home cage on the final day of the 2 week induction/maintenance of food deprivation. Animals were then habituated to the operant apparatus and trained to press levers for the delivery of sucrose pellets. The first day served to habituate the animals to the operant box and familiarize them with the location of the pellet hopper where sucrose pellets were delivered. Animals were placed in the operant box for 30 minutes where 10 sucrose pellets were already available in the hopper. Animals were then progressively shaped to press the levers for delivery of sucrose pellets and habituated to the stimuli and stimuli contingencies over approximately 8 consecutive days. On day 1 of shaping, single sucrose pellets were delivered into the food hopper with increasing time intervals over a 20 minute period (30 total trials/pellets); no stimuli were used other than the sucrose pellet dispenser. On day 2 of shaping, illumination of the house light signaled the start of a trial. After 10 seconds, it was extinguished and a single sucrose pellet was dispensed. The inter trial interval (ITI) on these sessions were 15, 25, or 35 seconds, chosen at random (30 trials/pellets total). The levers and the stimulus lights above the levers were introduced on days 3 and 4, and animals were trained (i.e. ‘hand-shaped’) to press the left and the right bars for sucrose pellet delivery using successive approximation. Animals were randomly assigned to one of two levers on the first day and the opposite lever was used the following day. Some animals required one additional day of training/shaping before moving on to the next training/shaping phase. A minimum of 30 lever presses was required before moving on. On days 5 and 6, illumination of the house light signaled the start of a trial. After 10 seconds, it was extinguished and a single lever and corresponding stimulus light were extended and illuminated respectively. A response on the lever resulted in the simultaneous sounding of a 100 millisecond tone (marking the reinforced response) and delivery of a single sucrose pellet. One lever/light side was used per day, and side assignments matched those on days 3 and 4. Each session terminated following 30 minutes or 30 sucrose pellets earned, whichever came first. Days 7 and 8 included all of the stimuli. Illumination of the house light signaled the start of a trial. After 10 seconds, the house light was extinguished and both levers were extended into the chamber. The animals were required to initiate the start of the trial by pressing any one of the two levers. If a lever was not pressed after 10 seconds, the levers were retracted and the house light was presented again. If a trial was initiated, the levers retracted for 1 second, and then were extended back into the chamber as choice levers with their corresponding stimulus lights illuminated. A response on either lever resulted in the simultaneous sounding of a 100 millisecond tone (marking the reinforced response) and delivery of a single sucrose pellet. Additionally, the stimulus light above the non-chosen bar was turned off while the light above the chosen lever remained on until the end of the trial. Trials were always 35 seconds in total duration. These sessions lasted 35 minutes or were terminated following 30 sucrose pellets earned. The preferred choice lever was determined for each animal from these final 2 sessions.

Delay Discounting (DD)

Within-session adjusting amount DD procedures were adapted from Oberlin et al., (2009), and are illustrated in Table 1. The presentation of stimuli was identical to the last 2 days of shaping, except that lever pressing now resulted in the outcomes detailed here. A ‘delay lever’ was assigned for each animal to be the lever corresponding to the animal’s non-preferred side. Pressing the delay lever always resulted in the delivery of 6 sucrose pellets following a delay. The ‘immediate lever’ was the opposite lever. Pressing the immediate lever resulted in the delivery of 0–6 pellets immediately. The number of pellets delivered following a response on the immediate lever (i.e. the ‘value’ of the immediate lever) always started at 3 on a given day. On ‘choice trials’, the value of the immediate lever was increased by 1 pellet after each delay lever press, and decreased by 1 pellet after each immediate lever press. ‘Forced trials’ were incorporated to expose the animals to both the delayed and immediate reinforcers. Forced trials resulted from a response on the same choice lever for 2 consecutive choice trials, and were presented on the following trial. Failure to respond on a forced trial resulted in the repetition of an identical trial. Forced trial responses did not affect the immediate lever value. Each session terminated following 35 minutes or 30 choice trials completed. Four to 6 sessions were given for each delay in ascending, fixed delay intervals (0, 1, 2, 4, 8, and 16 seconds). Animals were given 6 daily sessions at the 0 second delay, and four daily sessions at every other delay. However, only animals who met our inclusion criteria of 70% of the maximum reward value of 6 (4.2 pellets) at the 0 second delay were moved on to the other delays. The average value of the immediate lever over the last 10 choice trials was determined for the last 3 days of each delay and used to determine the indifference point of each animal. Mean indifference points for each delay were determined for all animals and evaluated as detailed below.

Table 1.

Inter-lever Response Interval (IRI) Manipulation

To better characterize choice lever consistency (see results), a subset of the original Wistar rats were used for an additional follow-up experiment (n=8). These studies were identical to the DD procedures detailed above, except that the latency with which the levers were re-extended following trial initiation presses was manipulated (i.e. the Inter-lever Response Interval or IRI). Animals were run for 6 consecutive days at each of three delays (0, 4 and 16 seconds). However, the IRI was increased over daily sessions (within each reward delay condition) from 1 second to 16 seconds. Animals first had 2 days at the 1 second (normal) IRI delay for each of the 3 reward delay conditions; one day to re-acclimate them to the delay and the other for evaluating baseline behavior. For each subsequent day within a reward delay, IRI increased daily with delays of 2, 4, 8, and 16 seconds. In total, animals had 6 consecutive days within 3 reward delays (18 days). Our hypothesis was that by increasing IRI, Wistar rats would shift away from using a consistent lever press strategy.

Behavioral Statistics

Delay discounting data was evaluated using methods adapted from Oberlin and Grahame (2009). We opted to use this model vs. a generalized hyperbola model (Green and Myerson, 2004) since it is simpler and reduces the number of variables necessary for the model. Mean indifference point across the final 3 days of each delay were evaluated using mixed factor ANOVAs, with rat population as the between-groups factor and delay as the within-groups factor. The rate of discounting was determined using the hyperbolic fitting function: v=a/(1+kd) (Mazur, 1987). v Is the subjective value of the reward, a is the fixed value of the delay reward (6 pellets), d is the length of the delay (0–16 seconds), and k is the value fitted by the hyperbolic function. With this formula, impulsivity (k) is measured by the steepness of the rate of discounting. Thus, the larger the k value, the more impulsive the individual. Correlation and regression analyses were conducted to determine the strength and significance of particular variables of interest. Bonferroni corrected post-hoc tests were performed based on the number of comparisons when appropriate. Data were considered significant at p<0.05.

Model of Delay Discounting

To assess the possible cognitive processes that guide decision making in the within-session adjusting amount discounting task, a one dimensional drift diffusion model was used to simulate this task. The model was constructed such that a random walk accumulated towards two possible “decision-boundaries” (Figure 5A+B). The model was parameterized so one of the decision boundaries was found on each walk (i.e. similar to the behavioral data, there were very few model omissions (<1%); average experimental daily omissions P=0.5177±0.04; Wistar=0.42±0.08). A trial was defined as a series of walks with the location of the lower boundary corresponding to delay choices and the location of the upper boundary corresponding to immediate choices. The distance of the delay boundary from the origin was fixed at a distance that was proportional to the duration of the delay. The upper/immediate boundary was adjusted on each walk (moved closer to or farther from the origin), with distance from the origin inversely proportional to the subjective value (v) of the reward. The immediate boundary was adjusted depending on which boundary was found on the previous walk (i.e. the preceding “decision”), such that if a delay boundary was found on the previous walk, the immediate boundary moved closer to the origin, and vice versa. Thus, conceptually, the immediate boundary distance represented the value of the immediate lever from behavioral experiments. One trial in the model consisted of 500 walks, which was meant to simulate one day of discounting at a fixed delay as in the behavioral experiments. One-hundred trials (i.e. bootstraps) were run at each delay, which can be thought of as multiple observations (i.e. animals) over the delays. The step size and direction of the random walk y was determined by

Figure 5. Description and performance of drift diffusion model of delayed discounting.

A figure describing how each decision boundary is altered by changing the delay (d) and value of the reinforcer (a), red lines denote delay (lower) boundaries and blue lines denote the immediate (upper) boundaries (A). Representative random walks are shown that find the delay (red) and immediate (blue) boundaries (dashed lines) (B). The response time distribution for all trials acquired in the experimental data are shown in (C1) and the response time distribution for all walks in the model data are shown in (C2). Notice the similarity in the shape of each distribution. The value (mean±SEM) of the immediate lever at each trial in the experimental data is shown in (D1; trial*delay interaction F(115, 3450)=6.84, p<0.0001). The mean value of the immediate boundary is shown for the model data in (D2). The color of each line in both D1 and D2 corresponds to the same delay. Notice that each line eventually reaches a unique asymptote (i.e. indifference point) depending on the delay. Simulations were run using the k values from experiments in each rat population in (E). The discounting function (mean±SD) is plotted for simulated Wistars (blue), P rats (red), and the mean k value from P’s and Wistars (black). The inset in E shows the distribution of k values generated by the model for 500 bootstraps (blue bars=simulated Wistars, red bars=simulated P’s). The arrows denote the experimental k values for each rat population; notice they are much lower than simulated values.

$$y=\sum _{i=2}^n(d{x}_i)$$

where n was the duration of the random walk (5000 steps for all simulations), d was a diffusion coefficient which adjusted the size of each step on the walk and was 0.04 for all simulations. x_i was randomly selected for each step i from N(0,1), unless noted otherwise. The trajectory of the walk accumulated from the origin (x₁=0), (unless otherwise noted) towards a decision boundary located at either 1/v or −1/v, where v is the subjective value of the reward defined by the discounting function described in the behavioral experiments:

$$v=\frac{a}{1+k_{\langle e\rangle }d}$$

where a = actual value of the reward (in food pellets, [1…6]), and d = temporal delay (in seconds, [0, 1, 2, 4, 8, 16]). The DD parameter was defined as k_〈e〉 (‘e’ denoting the mean from the experimental data; see results). In this way, the decision boundaries (±1/v) representing higher value “rewards” were closer to the origin. Our rationale for this was based on the observation that high value rewards have a higher probability of being chosen, and thus they should be easier to locate in “cognitive search-space” (Howard et al., 2005, Ratcliff and McKoon, 2008, Kurth-Nelson et al., 2012)

The lower decision boundary was constructed as a proxy for a delayed choice, a = 6 and was fixed so that −1/v was a fixed distance from the origin on each trial for a delay (d). The upper decision boundary was designed as a proxy for the immediate choice (Figure 5A+B), if the random walk crossed the upper decision boundary first (i.e. immediate choice, Figure 5B, blue line), the boundary was moved away from the origin on the next walk:

$$ify=1/v,\{\begin{array}{c}a\to a-1\\ a<1,a\to 1\end{array}$$

However, if the trajectory crossed the lower decision boundary first (i.e. delay choice, Figure 5B, red line) it was moved towards the origin:

$$ify=-1/v,\{\begin{array}{c}a\to a+1\\ a>6,a\to 6\end{array}$$

To extract k_m from each simulation (‘m’ denoting modeled data) the mean of the immediate decision boundary was computed from each trial and for each bootstrap, which resulted in a bootstrap x delay matrix of values and k_m was then computed for each row resulting in 100 values per simulation (see Figure 5E, inset). The mean of these values is denoted as k_〈m〉.

The origin of the random walk was adjusted in a subset of experiments to include a “memory” of which decision boundary was found by the walk on the previous trial (Figure 6A1). The rationale for this feature was arrived at following initial simulations and was based on the premise that the accumulation of information about past choices, and how they might relate to the current choice, is a necessary process in DD by which indifference points develop and differ as a function of delay length. If one boundary was found repeatedly, this would bias the walk towards this boundary. The origin bias function adjusted the origin of the walk along a sigmoidal function (Leibowitz et al., 2010) towards the previously found decision boundary via:

$$\begin{array}{c}if{v}_w=v_{w-1},\{\begin{array}{c}o\to o+1\\ o>40,o\to 40\end{array}\\ if{v}_w\ne v_{w-1},\{\begin{array}{c}o\to o-1\\ o<0,o\to 0\end{array}\end{array}$$

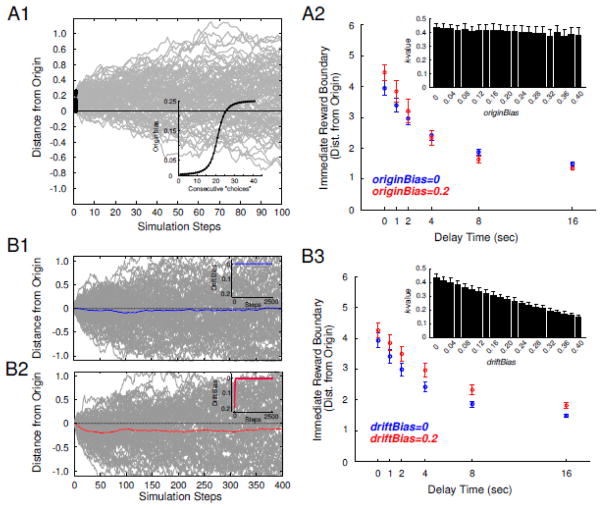
Figure 6. The performance of the origin and drift bias on simulations of delay discounting.

The performance of the origin bias is presented in (A). Representative walks are shown in A1 for a 16 second delay, where origin bias=0.2. Notice how the origin of the random walk moves closer to the immediate boundary (top). The inset in A1 shows the origin bias function, where the origin is incrementally moved towards a decision boundary based on how often it was found on previous choices. The resulting discounting function is shown in A2 for an origin bias=0 or 0.2 (blue and red symbols respectively). The inset in A2 shows how k values are altered by increasing the origin bias. The performance of the drift bias is shown in (B). Random walks are shown where the driftBias=0 or 0.2 in B1 and B2, respectively. In B1–2 the blue and red lines are the mean of all random walks and the inset shows the driftBias at each step of the walk. In B3 the discounting functions are shown for driftBias=0 or 0.2 (blue and red symbols respectively). The inset in B3 shows how k values are altered by increasing the drift bias. All data in panels A2 and B2, including insets, are presented as mean±SD.

Where v_w is the decision boundary found on walk w and o is a value that accumulates each consecutive time the boundary is found (o =[0…40]) and used to update the origin of the random walk via:

$$\mathit{originBias}=\mathit{originScale}\left(\frac{1}{1+e^{(-0.5(o)-11)}}\right)$$

where originScale sets the maximum the origin could be moved towards the decision boundary. The origin of the walk (x₁) on the next walk (w+1) was then set to the product of originBias(1/v) if the upper decision boundary was found or originBias(−1/v) for the lower. For example, if originScale = 0.25 then the random walk could be maximally initiated 25% closer to the decision boundary.

An additional term in the random walk was developed following initial simulations and also introduced in a subset of experiments in order to model how the prospective representation of the delayed choice, and its decay over time, might influence which decision boundary was found by the random walk (see Figure 6B1+2). The ‘drift bias’ decayed exponentially via modifying the distribution of the random walk N(d_i,1) where

$$d_i=\mathit{scaleDriftBias}(-1/v)\ast {0.95}^i,\text{where}i=[\mathit{0}\dots n]$$

and n, as previously, was the duration of the walk (5000 steps for all simulations). The assumption of exponential memory decay is common in a number of models (Murdock, 1997, Mensink and Raaijmakers, 1998).

To quantify the fit of the model to the experimental data prediction error was calculated as:

$$PE=\sqrt{\mathrm{\sum }{\left(Y_d-{\widehat{Y}}_d\right)}^2}$$

Where Y = the mean value of the immediate lever from the experimental data at delay d, and Ŷ is the mean value of the immediate reward boundary recovered from the model at delay d.

Results

Delay Discounting

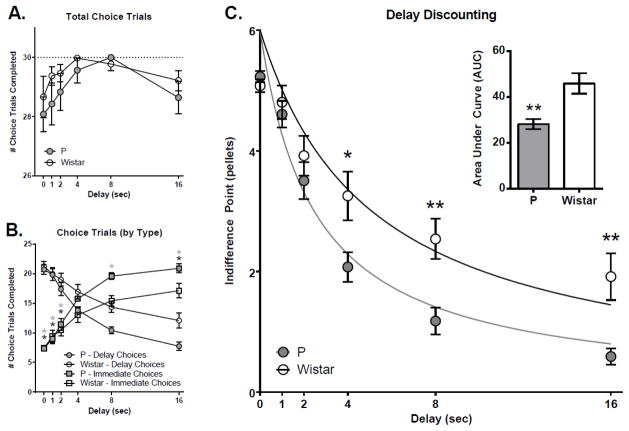
One Wistar rat did not learn to lever press, and 1 Wistar and 1 P rat did not meet our inclusion criterion for magnitude discrimination (70% of the maximum reward value of 6 = 4.2 pellets) and were therefore excluded. No rat population differences were observed in the number of completed trials at any delay (main effect rat pop [F (1, 27) = 1.145, p = 0.2940]; delay*rat pop. interaction [F (5, 135) = 0.5886, p = 0.7087; Figure 1A). A clear preference for the larger-magnitude delay lever was observed at the zero second delay in both rat populations thus indicating that each rat population discriminated the magnitude of the reward (Figure 1B). Additionally, no rat population differences in indifference point were observed at the zero second delay indicating that the larger, delayed reward was valued similarly (Figure 1C). A clear shift in the preference for the delayed lever was observed across delays (choice type*delay interactions [P rats: F (5, 130) = 151.2, p<.0001]; [Wistar rats: F (5, 140) = 72.97, p<0.0001]) indicating that the animals understood the relationship between reinforcer size and the delay (Figure 1B). The pattern of forced choice trials inversely mirrored that of choice trials in the expected direction - there were a greater number of forced choices to the delay lever across delay in both groups (due to discounting/choosing more consecutive immediate rewards), with P rats displaying more forced choices to the delay lever than Wistar over delays (data not shown). Choice responding reached a stable asymptote by the final choice trial indicating that animals titred their choices based on the delay within a trial (Figure 5D1).

Figure 1. Slower delay discounting in Wistar rats versus P rats.

P and Wistar rats completed the same number of choice trials across delays (A). However, a greater number of immediate vs. delay choices were made in P rats over ascending delays (B), resulting in steeper discounting in P rats compared to Wistar rats (C). *’s in panel B indicate within-rat population differences in mean number of immediate vs delay choices (grey *’s=P rat differences; black *’s=Wistar rat differences). *’s in panel C indicate differences between rat populations. *p<0.05; **p<0.01 ****.

The results of analysis of DD across delays can be seen in Figure 1C. There were significant main effects of delay [F(5, 135)=97.60, p<0.0001], rat population [F(1, 27)=4.284, p<0.05], and a delay*rat population interaction [F(5, 135)=4.21 p<0.01]. Post-hoc testing indicated that P and Wistar rats differed significantly at the 4 (p<0.05), 8 (p<0.01), and 16 (p<0.01) second delays, with P rats displaying lower indifference points. Analysis of area under the curve (AUC) derived from 1) indifference points at each delay [t(27) = 3.46, p<0.01; see Figure 1C inset] and 2) the best-fit lines from nonlinear hyperbolic fitting [t(27) = 2.91, p<0.01] both also indicated significant group differences, with lower values in P rats. To evaluate differences in the rate of discounting (i.e. the steepness of the best-fit hyperbolic curve), k values were evaluated. Data was not normally distributed (Shapiro-Wilk; W=0.83, p<0.01), thus non-parametric Mann-Whitney tests were performed and indicated significant differences between P and Wistar rats [U(27) = 50, p<0.05]. K values were then natural-log transformed to allow for analysis with parametric statistics (and comparison with other normally distributed variables). The results of this analysis supported the results of non-parametric rat population differences in k [t(27) = 2.76, p=0.01], with steeper slopes in P rats. Thus, rat populations differed in DD with P rats displaying increased impulsivity compared to Wistar.

Lever Consistency

To further explore the cognitive processes that underlie DD, the extent to which the same lever was pressed to initiate a trial and subsequently make a choice response was quantified (i.e. initiation/choice ‘consistency’). This was based on the premise for which our study was designed; that consistent trials would reflect choice decision intent (i.e. a prospective decision strategy). The probability that trials were consistent depended on the frequency of delay vs. immediate lever initiations as well as the frequency of delay vs. immediate lever choices. The chance probability of a consistent trial for each animal/subject (s) at each delay (d) was calculated as:

$$p\left(\mathit{consistent}{\mathit{choice}}_{n,d}\right)=\left(\frac{D_{i,s,d}}{T_{i,s,d}}\ast \frac{D_{c,s,d}}{T_{c,s,d}}\right)+\left(\frac{I_{i,s,d}}{T_{i,s,d}}\ast \frac{I_{c,s,d}}{T_{c,s,d}}\right)$$

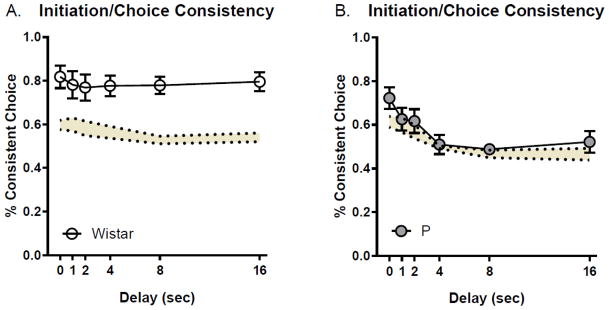
Where D and I represent responding on the delayed or immediate lever, respectively and T is the total number of choices. The subscripts i and c represent choices during the initiation or choice phase, respectively. Thus, each animal had its own chance level probability of making consistent responses, which was derived from the observed pattern of initiations and choices. An analysis of chance probabilities (shaded lines in Figure 2A+B) indicated that there were no differences between rat populations. However, there was a significant main effect of delay [F(5, 135)=6.57, p<0.0001], with the chance probability of consistent choices decreasing with increasing delay length. Analysis of observed consistency revealed a significant main effect of delay [F(5, 135)=4.10, p<0.01] driven almost entirely by P rats, a main effect of rat population [F(1, 27)=15.26, p<0.001], and a significant delay*rat population interaction [F(5, 135)=2.64, p<0.05]. Bonferroni-corrected post-hoc testing detected differences between the observed consistency between rat populations at the 4 (p<0.01), 8 (p<0.001), and 16 second (p<0.001) delays, with Wistar rats displaying higher consistency than P rats at each of these delays. An analysis of the chance versus the observed consistency found a main effect in Wistar rats [F(1, 28)=21.04, p<0.0001] driven by higher consistency than chance at all delays (p’s<0.05; Figure 2A). In P rats there were no differences in chance probability versus the observed consistency (p’s>0.30; Figure 2B). Thus, Wistar rats displayed levels of consistency greater than expected by chance, whereas P’s did not. This indicates that a behavior plan guiding the choice at the initiation phase of the task was maintained through the choice phase in Wistars.

Figure 2. Slower delay discounting in Wistar rats is paralleled by consistent responding across initiation and choice epochs.

Wistar rats (A) displayed greater than chance initiation/choice consistency across delays whereas P rats (B) did not. The yellow shaded region denotes the ± SEM of the expected probability of a consistent choice at each delay.

Response latencies

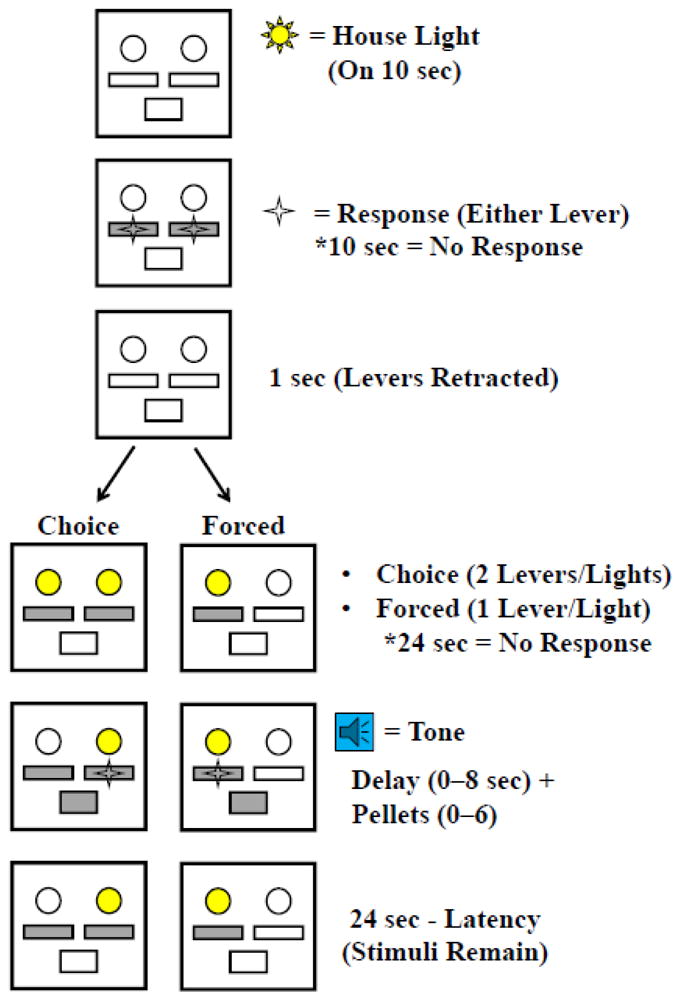
Separate analyses were conducted on latency to make choices on each of the two possible levers. In these analyses the median response time latency was taken for each animal over the last three days at each delay and the mean of this value was used for statistics. For immediate choice latency, there was a significant main effect of delay only [F(5, 135)=10.37, p<0.0001; Figure 3B], with generally longer latencies at the 1 and 2 second delays than other delays. However, it is important to note that latencies at the 1 and 2 second delays were not significantly greater than at other delays. For delay choice latency, there was a significant delay*rat population interaction [F(5, 135)=5.43, p=0.0001; Figure 3C], which post hoc testing indicated was driven by significantly slower responding in P rats at the 8 and 16 second delays (p’s<.05).

Figure 3. Increased decision times are observed in P rats at long delays.

There was no difference in choice latency across delays in either Wistar or P rats (A). When stratified by choice type no differences were observed between Wistar and P rats in latency to make immediate choices (B). However delay choice latencies in P’s at the 8 and 16 second delays were longer relative to earlier delays and to Wistars at the same delay (C). *p<0.05; **p<0.01 ****.

Relationships between behavioral measures

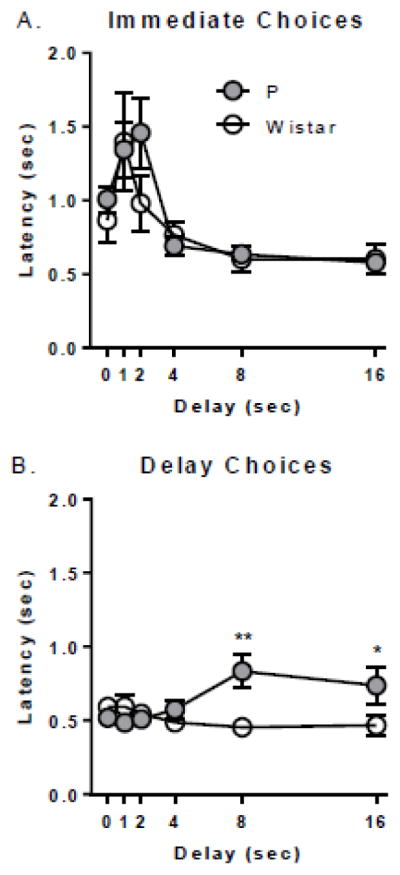
To evaluate the relationship between measures of impulsivity, lever consistency, and latency to make choices, correlation and a linear regression analyses were conducted. Initiation/choice consistency was significantly negatively associated with natural log transformed k values (i.e. impulsivity) in Wistar rats (r=−0.57, p<.05) but not in P rats (p=.24; Figure 4A). Initiation/choice consistency was also significantly negatively associated with choice latency in Wistar rats (r=−0.54, p<.05), but not in P rats (p=.70; Figure 4B). However, k values were significantly positively associated with choice latency in P rats (r=0.66, p<.05) but not Wistar rats (p=.17; Figure 4C). Thus, for Wistar rats, the more consistent the less impulsive, and the faster the choice decision, and for P rats, the slower the choice the more impulsive.

Figure 4. Impulsivity is correlated with choice consistency and latency.

(A) Choice consistency was significantly negatively associated with k in Wistar rats only; the more consistent the less impulsive. (B) Choice consistency was significantly negatively associated with choice latency in Wistar rats only; the more consistent the faster the choice responses. (C) Choice latency was significantly positively associated with k in P rats only; the more impulsive the slower the choice responses.

Drift Diffusion Model

The model was parameterized (see below) so that values could be interpreted similarly as the experimental data. For example, the decision boundaries were set as 1/v so that the immediate decision boundary could be roughly interpreted as number of pellets. In addition, the diffusion constant was fit so that 1 step corresponded to ~10 milliseconds in the experimental data (the sampling rate of behavioral hardware), resulting in similar response time distributions [two-sample KS test: D(100)=0.0875, p>0.05] between the experimental data (Figure 5C1) and the model (Figure 5C2).

The experimental data were acquired via within session adjusting amount DD procedure. This DD procedure is attractive due to the fact that an indifference point can be calculated which provides an accurate within-session measurement of the subjective value of the delayed reward. In both the experimental data and the model the value of the immediate lever was dynamic on early walks/trials and eventually reached asymptote based upon the distance of the delayed boundary from the origin (Figure 5D2) or the duration of the delay (Figure 5D1), thus the model (even prior to addition of bias features) recreated this important feature of the DD procedure.

The value of the actual reward v could be manipulated by changing the discounting function k. Manipulating v to reflect changes in the value of the reinforcer created a hyperbolic discounting function, where the probability of finding the delayed boundary decreased as a function of delay. To explore if simply modifying k was sufficient to recreate the observed discounting functions from the experimental data, the experimentally derived k values (k_e) were initially used in the simulations. Upon providing the model with the values observed in the experimental data (k_〈e,w〉 = 0.1963 to simulate Wistars and k_〈e,p〉 = 0.4054 to simulate P rats) clear discounting was observed in each condition and discounting was slowed in simulated Wistars relative to simulated P’s (Figure 5E). However, the k values recovered from these simulations (k_m) were much higher than those observed in experimental data. In the case of the Wistars, the experimental k_〈e,w〉 = 0.1963, which was −5.1 standard deviations lower than those observed in the simulations((k_m,w) = 0.3327 ± 0.027, one sample z-test, p<0.0001). In simulated P rats the experimental k_〈e,p〉 = 0.4054, which was −3.08 standard deviations lower than those observed in the simulations ((k_m,w) = 0.5219 ± 0.038, one sample z-test, p=0.0021) (Figure 5E, inset). Thus, by only changing k, the discounting functions created by the model did not adequately recreate discounting observed in either population suggesting that additional parameters should be considered to better describe discounting in each rat population. Furthermore, the discounting parameter, k, in its pure form, provides only a mathematical description of how the perception of time interval influences perceived reward magnitude, which could each be influenced by a number of cognitive processes.

A number of observations in the behavioral data shed light on the differences in decision making that lead to altered DD between rat populations. First, Wistars discount slower (Figure 1C) and slower discounting is correlated with a propensity to respond on to-be-selected choice lever at initiation (Figure 4A). These data suggest that, in Wistars, a relationship exists in the lever selected to initiate a trial and the lever selected at the choice. There were no differences between P and Wistar in the number of initiation decisions on either the delay or immediate lever [main effect of rat population: F(1, 27)=0.13, p>0.7; rat population*delay interaction: F(5, 135)=0.92, p>0.4], but there was a slight bias in favor of initiating trials on the delay lever in both groups (≈66% delay initiations in P, and ≈64% delay initiations in Wistar). Since P and Wistar rats tend to initiate a trial on the delay lever with equal probability, this rules out an initiation bias as the cause for population differences in discounting. Rather, this suggests that, in Wistars, the initiation choice reflects a prospective strategy that may guide the decision about which lever is chosen during the choice phase. This is supported by the observation that the Wistars that were the most consistent also exhibited faster response latencies (Figure 4B). In addition, at the 8 and 16 second delay Wistars were faster to choose the delayed lever compared with P rats whereas there were no differences between populations for immediate choices (Figure 3C). Consistency between the initiation and the delay lever may reflect a process where a bias for the preferred lever accumulates over trials, reducing the need for deliberation as the preferred choice is clear. Alternatively, the consistent choices may reflect prospective process whereby the animal forms and maintains a trace of the to-be-selected lever, which then guides their decision (i.e. facilitates the mapping of the delayed reward to context). These possibilities were each modeled separately as additional parameters to explore potential differences in discounting in P and Wistar rats. For all subsequent simulations the k_〈e〉 value used in the model was 0.3009 (the mean of Wistar and P rats, Figure 5E, black symbols).

To explore how an accumulating bias based on past choices might affect decision making, the origin of the random walk was updated based on which boundary was found on the previous trial. This could reflect a number of cognitive constructs such as value judgments about past choices (was it worth waiting for the delayed reward), integrating the temporal information about the delay (how long was the delay), building an association between the temporal delay and the number of pellets available immediately, or the decision process becoming increasingly easier. As such, the accumulation of information about past choices, and how they might relate to the current choice, was modeled as a sigmoidal function - the origin bias (see OriginBias equation). Modifying scaleOriginBias alone had a modest effect on the k values recovered from the simulations (Figure 6A). While it was possible to recover k values from the model similar to those observed in the P rats by modifying scaleOriginBias alone, modifying this variable did not yield k values similar to those observed in the Wistar rats. Modifying scaleOriginBias, resulted in discounting functions with an increased probability the random walk found the delay boundary at short delays (0, 1 second) and the immediate boundary at long delays (8,16 second; Figure 6A2).

Prospective memories are conceptualized as transient representations of future actions (Crystal and Wilson, 2015). To explore if a prospective process could account for alterations in discounting, random walks were transiently biased towards the delay boundary using the scaleDriftBias term. The walk was biased towards the delay boundary, and not the immediate, for the following reasons: First, there is evidence that the ability to withhold an impulsive response requires that a representation of the delayed reward must be formed and maintained (Buckner and Carroll, 2007, Kurth-Nelson et al., 2012). Second, each rodent population exhibited an initiation bias for the delay lever indicating the higher incentive motivational value of this lever. Additionally, an immediate decision does not likely require the level of planning and maintenance of information about the to-be-made-choice compared with a delay choice. This is supported by the observation that the Wistars that choose the delay lever most often (e.g. slowest discounters) are the ones that are the most consistent (Figure 4A). Further support for this idea is observed as an increase in latency to choose on immediate choices versus delay choices [main effect of choice type, F (1, 28) = 8.57, p = 0.0067] and a strong relationship between choice latency and consistency in Wistars (Figure 4B).

We hypothesized that if a memory of the incentive motivational value of this lever can be maintained up to the choice, then this can bias the choice process. Indeed the inclusion of the scaleDriftBias term dramatically slowed discounting and was capable of yielding k_〈m〉 values in the range observed in the experimental data for both Wistar and P rats (Figure 6B1). An example where scaleDriftBias = 0.20, and scaleOriginBias = 0 is shown in Figure 6B3. After including this variable, the k_〈m〉 values recovered from the simulations were 0.27335 ± 0.024 (μ ± σ), which slowed discounting relative to when scaleDriftBias = 0 (k_〈m〉 = 0.4294 ± 0.035).

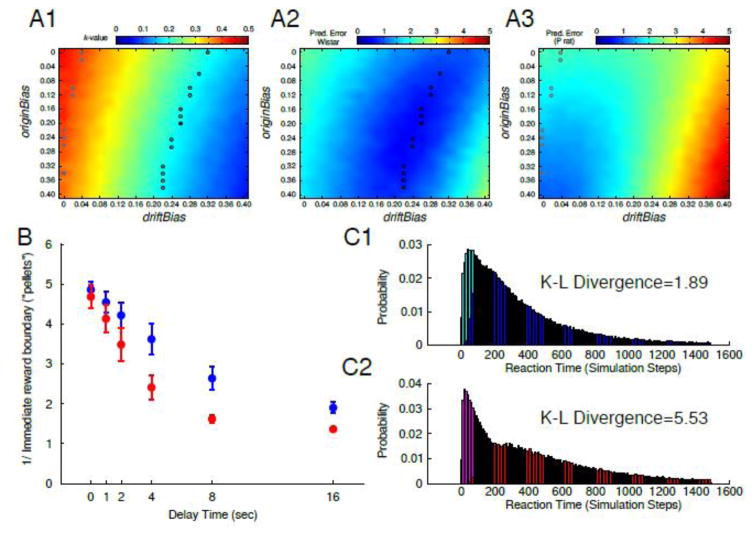
While k_〈e,p〉 values of the P rat experimental data could be recreated by changing the scaleOriginBias or scaleDriftBias (grey circles, Figure 7A1), the fit of the model to the P rat experimental data was best (e.g. prediction error was minimized) when the scaleOriginBias=0.36 and scaleDriftBias=0 (Figure 7A3), indicating that changing the origin bias more adequately models the P rat experimental data.

Figure 7. The optimal model parameters to fit Wistar and P rat experimental data.

The mean k values recovered from simulations (100 bootstraps) of delay discounting after altering the origin and drift bias is shown in (A1). The open circles on the heat plots indicate where the mean k value of the simulations were within ±0.01 of the experimental data and the two closed circles denote the origin and drift bias combination that yielded the k value that was closest for each rat population (grey=P rats, black=Wistars). Model fits were further evaluated by measuring the prediction error of mean i-values at each delay in the model and the experimental data for both Wistars (A2) and P rats (A3). The overlaid circles in A2–3 are identical to those in A1. The resulting discounting functions for the origin and drift bias parameters that optimally fit the Wistar (blue) and P rat (red) experimental data are shown in (B). Average Kullback-Leibler (K–L) divergence in Wistar (C1) and P (C2) rats between simulated reaction time distributions of immediate (cyan/magenta) vs delay (blue/red) choices. There was a greater difference in reaction times between immediate vs. delay choices in P rats (C1), with longer latencies on delay choices (red) vs. immediate choices (magenta). All data are presented as mean±SD.

A number of combinations of the origin and drift bias existed that yielded values close to those observed in the Wistar experimental data (i.e. several parameter combinations generated low prediction error; see black circles in Figure 7A1–2). However, the parameters that best minimized the prediction error (Figure 7) were scaleOriginBias=0.2 and scaleDriftBias=0.26. The improvement in the fit of the model to the Wistar data was small when the scaleOriginBias=0, indicating that while this parameter made improvements in the fit, the drift bias was far more important in creating an optimal fit to the experimental data in Wistar rats.

If Wistar rats formed a plan of their choice at the initiation of the task and maintained this in memory, one would expect a faster response time at the choice. In the experimental data, faster response latencies for delayed rewards were observed in Wistar rats at 8 and 16 second delays (Figure 3C). To explore this finding in the model we used the parameters for the origin and drift bias that optimally recreated the k_〈m〉 values and minimized prediction error for each rat population (see above). Similar to the experimental data, a rat population*choice (immediate vs. delay) interaction [F(1,499987)=76614.43, p<0.0001] was observed for the natural log transformed response times recovered from the model. In addition, the distributions for the response times for an immediate versus a delay response were more similar in modeled Wistars (Kullback-Leibler Divergence=1.89) than the P’s (Kullback-Leibler divergence=5.53; Figure 7C1+2). Collectively, these data indicate that, similar to the experimental data, optimizing the model parameters based on the Wistar data decreased the latency of the random walk to find the delay boundary. Thus the inclusion of the origin bias optimized the fit of the model to the P rat experimental data and the Wistar experimental data was optimally fit by including the drift bias. Taken together, these data highlight potential differences in strategy employed by each rat population used to guide decision-making and further suggest that the ability to effectively plan a decision is key to mitigating an impulsive choice.

Inter-lever Response Interval (IRI)

We next designed a set of experiments to evaluate the influence of inserting a delay between the initiation lever and access to the choice lever in the subset of Wistar rats. The primary goal of these experiments was to determine if increasing the temporal delay between trial initiation and choice availability would interfere with lever consistency. We hypothesized that increasing IRI delay would interfere with consistency and increase choice latency.

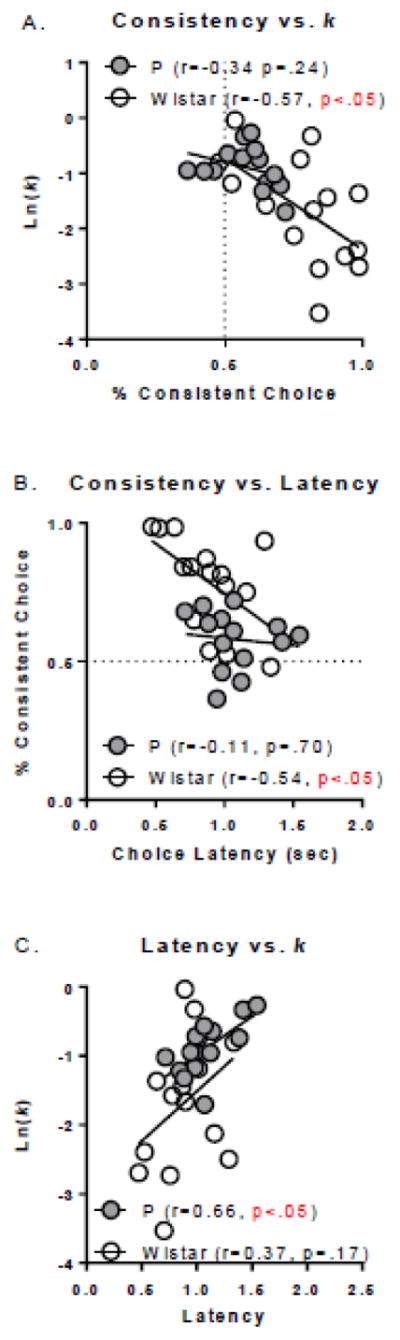
At all 3 reward delays there were significant IRI*consistency interactions [0sec: [F(4, 64)=7.02, p<0.0001; 4sec: F(4, 64)=3.95, p<0.01; 16sec: F(4, 64)=3.95, p<0.01]. Post-hoc testing indicated above chance differences in consistency at the 1 (p’s<.001) and 2 (p’s<.001) second IRIs at all 3 reward delays, and above chance differences at the 4 (p’s<.01) and 8 (p’s<.05) second IRIs at the 4 and 16 second reward delays (Figure 8). At all 3 reward delays the 16 second IRI decreased consistency to chance levels. Thus, longer IRI intervals decreased consistent lever responding.

Figure 8. Influence of IRI on consistency and choice latency in Wistar rats.

As consistency decreased to chance levels across IRI’s, choice latency increased; an effect which was observed at all 3 reward delays tested. The 0 second reward delay is shown in (A), the 4 second reward delay is shown in (B), and the 16 second reward delay is shown in (C). †’s indicate differences in consistency from chance (p’s<.05). *’s indicate differences from 1 second IRI with a given reward delay (*p<.05; **p<.01; ***p<.001).

IRI length increased choice latency at all reward delays (main effects of IRI). Interestingly, significant increases in choice latency were only observed at IRI lengths where consistency was no greater than chance. These results support the observation that the consistent lever press strategy in Wistar rats leads to decreases in latency to choose a reward. IRI had no impact on indifference points as a function of IRI delay (no main effects or interactions of IRI).

Discussion

These results support recent work demonstrating that alcohol preferring “P” rats display increased impulsivity relative to other alcohol-preferring, non-alcohol-preferring, and heterogeneous rat strains (Beckwith and Czachowski, 2014, Perkel et al., 2015), as well as reports of greater impulsivity in other populations of selectively bred alcohol preferring rodents (Wilhelm and Mitchell, 2008, Oberlin and Grahame, 2009, Mitchell, 2011). These data are also consistent with human studies that find a relationship between impulsivity, measured via DD, and those FH+ for an AUD (Mitchell, 2011). While these data clearly indicate a relationship between impulsivity and FH of excessive drinking, the relationship between impulsivity and FH does not appear to extend to all FH+ subjects or rodents selectively bred for excessive drinking (Wilhelm et al., 2007, Wilhelm and Mitchell, 2012, Beckwith and Czachowski, 2014). These studies highlight the need to further refine our understanding of the various cognitive functions that influence impulsivity and the specific modalities of alcohol drinking each is related to.

In the experimental data used to fit the model a clear preference for the delay lever was observed at the zero second delay (Figure 1B), increasing delays also reduced the probability of choosing the delay lever (Figure 1B), and a stable choice responding was observed at the end of the trial (Figure 5D1). Collectively these data indicate that both P and Wistar rats demonstrated mastery of the behavioral task. A previous study, also employing a computational model, found no evidence that adjusting the delay influenced decision-making in a within-session adjusting delay task (Cardinal et al., 2002). However, a number of experimental and procedural differences prevent the comparison of these data to the model presented herein.

It is possible that the light cue remaining on following choice decisions exacerbated the difference in DD between the 2 different rat populations given that cues marking delay choices have been shown to increase DD in groups of highly impulsive animals and decrease DD in groups of animals with low impulsivity (Zeeb et al., 2010). That this cue was present regardless of which reward lever was chosen in our studies vs. only the delay choice in the study referenced above, and given the fact that it remained on up to many seconds after reward delivery until trial end (24 seconds – choice latency) makes this less likely in our view, but still a possibility.

In the current study a clear relationship was observed in the behavioral strategy used (e.g. consistency) and DD - but only in Wistar rats (Figures 1+2+4). No detectable strategy was observed in P rats (Figure 2B+4A), who discounted steeply (Figure 1). The effect of an animals ‘family history’ on consistency was robust and reproducible across all reward delay conditions tested (Figure 2A+B). This observation was key to better understand why P rats discounted more steeply than Wistar rats, and to further explore this a drift diffusion model of DD was employed.

Drift diffusion models are attractive because by modifying a few, well-defined parameters a number of phenomena related to decision-making can be modeled. As in previous studies, a random walk was used to model the cognitive search process (Kurth-Nelson et al., 2012), whereby information about the reward and delay are integrated to guide decision-making. The origin of the walk and the mean of the distribution from which the random walk was constructed, were each initially set to zero, which lead to a search process that was only influenced by reward magnitude and delay (i.e. the location of the decision boundaries). The decision boundaries, however, reflect an environmental variable that is external to the cognitive search process. In this regard, the cognitive search process was initiated de novo on each walk. However, as the animal progressed through the task, it was likely that information acquired from previous trials influenced the search process. In line with this view, it has been shown that information gleaned from previous trials, such as value judgments, can shape future decisions (Steiner and Redish, 2014).

Sequential sampling algorithms are attractive given their ability to accurately model response time distributions (Brown and Heathcote, 2008, Ratcliff and McKoon, 2008, Rodriguez et al., 2014). Response time distributions in two choice decision making procedures are typically positively skewed and in the current study, this phenomena was also observed in both the experimental and modeled data (Figure 3A+5C). As choices become more difficult or in situations where accuracy is stressed over speed, response times increase (Bogacz et al., 2010). Temporally discounted rewards have also been shown to result in longer response times for choice selection (Roesch et al., 2006, Oberlin and Grahame, 2009, Beckwith and Czachowski, 2014, Rodriguez et al., 2014). The geometry of the model presented herein lead to an increase in response time with increasing delays, which is consistent with previous experimental and modeling data.

Increases in reaction times with increasing delays may be related to the fact that as a reward becomes more temporally distant, it takes longer for the cognitive search process to map the reward to context (Kurth-Nelson et al., 2012). However, a linear increase in response times across delays was not observed in our experimental data, suggesting the search process was altered in our task compared with those previously reported (Figure 3). For delayed choices, response times tended to decrease in Wistar rats across delays, whereas they increased in P rats at the 8 and 16 second delays (Figure 3). The observed delay choice response times suggest the search process was facilitated somehow in Wistar rats and, at short delays, in P rats. For immediate choices, response times across delays were complex. In both rat populations, reaction times increased up to the 2 second delay and then dropped dramatically at the 4–16 second delays. This observation suggests that decision-making is a dynamic process that is influenced by genetic background, evolves across delays, and possibly influenced by cognitive strategy.

When the experimentally derived k_〈e〉 values were used in the model, the resulting fit of the discounting functions was poor in terms of recovered k_〈m〉 values and the mean immediate boundary values observed at each delay. The recovered k_〈m〉 values from the model were considerably higher than those observed experimentally (Figure 5E) and the function was “compressed” compared to the experimental data (i.e. immediate lever values tended to be too small at short delays and too large at long delays). This suggested that parameters other than k value should be considered, and motivated the decision to explore how biasing the random walk changed the fit of the model to the experimental data.

The origin bias was introduced to model a decision-making strategy where the current choice was biased by information gleaned from previous choices. In other words, finding one boundary on previous walks increased the probability of finding it in the future, which could reflect the decision process becoming easier (i.e. little deliberation is required). The inclusion of this parameter improved the fit of the k_〈m〉 values and minimized prediction error of the model to the experimental data from Wistar or P rats. In addition, this parameter increased the mean immediate boundary value at the 0 second delay indicating that the walk was increasingly biased towards the delayed boundary. Thus the model data suggest that, when no delay is present, making the decision-making process easier was necessary to optimally model the experimental data. However, while the inclusion of the origin bias optimized the fit of the model to the P rat data, this was not sufficient to model the Wistar data.

Wistar, but not P rats, consistently initiated a trial on the lever that was ultimately chosen in the choice epoch. This suggested that a behavioral plan was formed at, or close to, the initiation of the trial and was used to guide responding in the choice epoch. This was interpreted as Wistar rats forming a prospective memory of their choice thus reflecting a ‘proactive’ mechanism of behavioral control (Braver, 2012). This bias in the behavioral plan for the delayed lever was conceptualized in the model as a transient prospective memory of the delayed reward that decayed over time and modeled as the drift bias. The inclusion of this factor, slowed discounting, and provided an optimal fit to the Wistar experimental data. In addition, the inclusion of the drift bias reduced the number of steps required by the walk to find the delayed boundary, bringing it closer to the number of steps required to find the immediate boundary (Figure 6). This better modeled the experimental data as the choice latencies in Wistar rats were similar for immediate and delay choices at the 8 and 16 second delay, whereas delay choices were longer in P rats. The ability of the drift bias to slow discounting and optimize the fit of the model to Wistar data suggests that a prospective memory, or behavioral plan, will facilitate the decision-making process. These data were further supported by follow-up experiments in which increasing IRI length simultaneously decreased consistency and increased choice latency in Wistar rats (Figure 8). Collectively these data underscore the importance of the ability to create a behavioral plan and hold this in prospective memory to delay reward and mitigate impulsive choices.

Addiction is characterized by an inability to delay immediate reward in light of future outcomes (de Wit, 2009). In this way, the alcoholic is constantly faced with a choice; do I drink excessively to feel good now, or shall I abstain to feel good in the future? This choice requires that future consequences be conceptualized and integrated into a decision to drink or abstain. As discussed, conceptualizing future rewards requires their value be mapped to context in order to form a prospective memory, which may be a critical intermediary to delay reward. Lack of planning, which involves prospective memory, has been described as one of five types of impulsivity (Whiteside and Lynam, 2003) and a recent meta-analysis found that lack of planning was one of the strongest predictors of alcohol dependence (Coskunpinar et al., 2013). In line with this view, non-planning impulsiveness in recovering alcoholics has been shown to be associated with alterations in the activation and functional connectivity of brain regions thought to be critical for cognitive control such as the dorsal anterior cingulate cortex (Jung et al., 2014).

The coordinated activity of multiple brain regions is necessary for tasks involving inter-temporal decision-making such as those described here. Among these regions, alterations in neural processing in the hippocampus and frontal cortex are prime candidates for the differences observed between P and Wistar in the current studies (Peters and Buchel, 2010, 2011). The hippocampus participates in the regulation of retrospective and prospective forms of episodic memory (Ferbinteanu and Shapiro, 2003), with the former necessary for taking into account the consequences of previous reward choices, and the later necessary for forming plans based on the consequences of these previous choices. Given that lesions of the hippocampus in rats have been shown to increase impulsive choices (Rawlins et al., 1985, Cheung and Cardinal, 2005, Mariano et al., 2009), and alterations have been reported in mRNA, protein, monoamines, etc., in this brain region in P rats (McBride et al., 1990, Stewart and Li, 1997, McBride and Li, 1998, Witzmann et al., 2003, Edenberg et al., 2005), functional differences between P and Wistar in the hippocampus may account in part for differences behavioral strategy and DD we observed in these studies. Regions of the frontal cortex are also known to be involved in the discounting of rewards (Cardinal, 2006) as well as regulating other cognitive and executive functions (Dalley et al., 2004). Interestingly, P rats display lower basal dopamine (DA) concentrations in the Prefrontal Cortex (PFC) compared to Wistar rats (Engleman et al., 2006). PFC dopamine has been found to facilitate the modification of choice biases during cost/benefit decision-making (St Onge et al., 2012) suggesting that hypodompaminergia of the PFC in P rats may also be an important neurobiological mediator of DD in this rat population.

Collectively these data identify heritable alterations in the decision-making process that lead to an impulsive phenotype and a heightened risk for excessive drinking. Moreover, these data highlight the need for further study on the neural processes that mediate impulsivity, and on the cognitive control mechanisms by which these processes are altered in individuals FH+ for an AUD.