The Pursuit of Word Meanings

Abstract

We evaluate here the performance of four models of cross-situational word learning; two global models, which extract and retain multiple referential alternatives from each word occurrence; and two local models, which extract just a single referent from each occurrence. One of these local models, dubbed Pursuit, uses an associative learning mechanism to estimate word-referent probability but pursues and tests the best referent-meaning at any given time. Pursuit is found to perform as well as global models under many conditions extracted from naturalistic corpora of parent child-interactions, even though the model maintains far less information than global models. Moreover, Pursuit is found to best capture human experimental findings from several relevant cross-situational word-learning experiments, including those of Yu and Smith (2007), the paradigm example of a finding believed to support fully global cross-situational models. Implications and limitations of these results are discussed, most notably that the model characterizes only the earliest stages of word learning, when reliance on the co-occurring referent world is at its greatest.

1. Introduction

This paper presents a computational investigation of “early word learning” – the process by which a human when exposed to a community of speakers, comes to understand some initial set of vocabulary items that belong to the language used by the group. In this case, the human learner can be an infant acquiring their first language or an adult acquiring an additional language. For all these individuals, a primary source of information is likely to be what they perceive happening in the world as the community goes about talking to the learner. And perhaps not surprisingly, the early vocabulary is made up of words that, for the most part, have concrete meanings – meanings that most straightforwardly refer to the “here and now” of the speaker and learner. Despite the “simplicity” of these meanings, theorists and researchers have long noted the complexity that belies the problem of early word learning. We investigate here proposed computational solutions to this problem, focusing on perhaps the central challenge to successful early word learning: the challenge of referential uncertainty.

1.1. Early word learning and referential uncertainty

When hearing a word that initially has no meaning for the learner, the set of possible meanings that exists in the moment is enormous and technically infinite. Without any constraints or prior knowledge, an utterance like “…the dog” could be referring to a dog, but also any of the co-present objects in the scene, parts or properties of these objects, or even any combination of these alternatives within and across the objects (Quine, 1960). Even with some reasonable “human-like” constraints on how the world is to be interpreted, mapping a word like “dog” onto a person’s current perceptual experience is obviously daunting, since humans, be they infants or adults, are perceptually and conceptually sophisticated, representing their environment as an array of objects, events, properties, spatial relations, and causes (e.g., Carey, 2009; Csibra & Shamsudheen, 2015; Gleitman, 1990; Spelke & Kinzler, 2007).

The current computational-psycholinguistic literature is populated with a large number of proposals for how humans learn words under conditions of referential uncertainty. We can think of these accounts as, broadly speaking, falling into two computational approaches. “Global” approaches (e.g., Fazly, Alishahi, & Stevenson, 2010; Siskind, 1996; Yu, 2008) resolve ambiguity gradually by aggregating situational data from a large number of word occurrences within a particular lexical item (“dog”) and across the emerging lexicon as a whole. In this way, the learning of all early words is accomplished through a global intersective process, an assumption that is commonly understood to underlie the idea of cross-situational word learning (e.g., Quine 1960; Osgood, Succi, & Tanenbaum, 1956; Yu & Smith, 2007). These approaches tend to allow the learner to use the whole range of prior experience to revise their interpretation of a word. In contrast, “local” approaches (e.g., Medina, Snedeker, Trueswell & Gleitman, 2011; Speigel & Halberda, 2011; Trueswell, Medina, Hafri & Gleitman, 2013) attempt to resolve ambiguity in the moment, during each word’s occurrence. Specifically, the learner attempts to identify the speaker’s intended message for the utterance and stores only that information. These approaches limit the amount of prior experience that can be brought to bear on the current learning situation, e.g. by ignoring all potential word meanings that do not serve to confirm or disconfirm a word’s favored interpretation. At the extreme, local approaches completely abandon any attempt at global cross-instance comparison and become “one trial” learners, learning only from “clear cases” of referential success and ignoring cases for which no unique referent is identifiable.

The experimental literature offers findings that can be interpreted as consistent with local approaches to early word learning. Novice language learners, when faced with referential ambiguity, have been found to radically limit alternatives in the moment based on: immediate evidence regarding a speaker’s intent, local situational information, and assumptions or ‘priors’ about word meaning. For example, children as young as 18 months of age use the attentional stance of a speaker (as gleaned from body posture, head orientation and gaze) to reduce referential alternatives (e.g., Baldwin, 1991, 1993). Likewise, objects that naturally attract a learner’s attention (due to size, movement, etc.) have been found to filter referent alternatives (e.g., Yu & Smith, 2012). These social and physical constraints on reference occur on rare special occasions in naturalistic settings, but when they do occur are precisely timed and highly informative toward accurate referent identification (Trueswell, Lin, Armstrong, Cartmill, Goldin-Meadow & Gleitman, 2016). Finally, children prefer word meanings that fall at some “basic level” (e.g., dog, rather than mammal) (Markman, 1990; Mervis, 1987) and prefer to distinguish object meanings for words by shape, rather than color or substance (e.g., Landau, Smith, & Jones, 1988). These data suggest novices adopt an approach to learning in which ambiguity is to be resolved or reduced locally. And consistent with local learning, others have shown that use of these local cues can result in so-called “one-trial” learning; i.e., evidence that the child can successfully learn a word’s meaning from just one occurrence (e.g., Bartlett & Carey, 1977; Carey, 1978; Speigel & Halberda, 2011).

Despite the evidence supporting local approaches, the findings do not rule out a need for global learning – i.e., learning that occurs gradually over “big data” – nor are the findings incompatible with such an approach. In particular, it is important to keep in mind that successful, unique referent identification in the moment from extra-linguistic information alone should in practice be quite rare because of the complexity of the typical word-learning environments, thus raising concerns about the influence that local learning could have on vocabulary growth as a whole. In fact, it has been found that most caregiver’s word utterances in the home occur in situations in which it is either impossible to determine what the speaker was referring to, or in contexts in which the social-situational cues only meagerly limit referential alternatives (Gillette, H. Gleitman, L. Gleitman & Lederer, 1999); highly informative, referentially transparent acts are quite rare (see also Cartmill, Medina, Armstrong, Goldin-Meadow, Gleitman & Trueswell, 2013; Medina et al., 2011). And importantly, none of the laboratory work mentioned above as support for local learning approaches addresses what a learner might do with these more ambiguous, less informative, word occurrences. It is possible then that, as global approaches would predict, ambiguous situational information is aggregated across these instances to identify likely word meanings.

Indeed, Yu, Smith and colleagues offer experimental evidence showing that adults (Yu & Smith, 2007) and 1-year-olds (Smith & Yu, 2008) can in the lab learn word meanings from a series of referentially ambiguous word occurrences, i.e., seemingly global learning in the absence of any local evidence that would permit unique referent identification. In these studies, learners were exposed to a set of novel spoken words (“dax”, “mipen”, etc.) each in the presence of a set of equally salient nonsense objects (for infants, set size of 2; for adults, set sizes of 2, 3 or 4). Local, in the moment, information did not support any particular pairing of word and object, making each occurrence ambiguous. But, across multiple word occurrences, each object perfectly co-occurred with a particular nonsense word. Thus a global learning mechanism that tracked all word-to-object pairings would be able to identify the correct pairings by the end of the experiment. And indeed, post-experiment tests revealed learners identified these pairings significantly better than chance, with accuracy for adults being negatively related to set size (see Section 4.1, Table 6, below).

Table 6.

Proportion correct guesses in model simulations of Yu/Smith experiments vs. actual reported values. Fazly et al. and modified Fazly et al. models guessed via sampling with meaning probabilities; variants which guess via choosing the maximally probable candidate perform at ceiling on all conditions. Significant differences determined via pairwise comparison of predictor p-values under a binomial mixed effects regression model with condition (4×4, etc.) as a predictor of correctness with random subject and item effects.

	4×4	3×3	2×2	significant differences	CI overlaps w/ observed
Propose/Verify	0.54 (95% CI = 0.43–0.63)	0.63 (95% CI = 0.54–0.72)	0.76 (95% CI = 0.68–0.84)	4×4 / 2×2 3×3 / 2×2 4×4 / 3×3	yes / yes / yes
Fazly et al. 2010	0.98 (95% CI = 0.94–1.00)	0.98 (95% CI = 0.94–1.00)	0.99 (95% CI = 0.98–1.00)	4×4 / 2×2 3×3 / 2×2	no / no / yes
Modified Fazly	0.96 (95% CI = 0.95–0.97)	0.97 (95% CI = 0.96–0.98)	0.99 (95% CI = 0.99–1.00)	4×4 / 2×2 3×3 / 2×2	no / no / yes
Pursuit	0.71 (95% CI = 0.62–0.80)	0.84 (95% CI = 0.76–0.91)	0.96 (95% CI = 0.92–0.99)	4×4 / 2×2 3×3 / 2×2 4×4 / 3×3	yes / yes / yes
Reported	0.53 (95% CI = 0.37–0.69)	0.76 (95% CI = 0.62–0.90)	0.89 (95% CI = 0.79–0.99)

Yet, like the evidence for local learning, this particular evidence in favor of global learning is largely equivocal, in that it does not actually distinguish between global and local learning theories. As noted by Gleitman, Trueswell and colleagues (Medina et al., 2011; Trueswell et al., 2013), successful learning across referentially ambiguous trials (like those used in the studies of Yu & Smith, 2007, and Smith & Yu, 2008) can be accomplished by a local learning process. If learners in the moment guess a particular word-object pairing (despite the ambiguity) and store just that pairing for later test on the next occurrence of the word (abandoning it if isn’t supported), a learner across trials could in principle identify some or all of the correct word-object pairings over the course of word exposures.¹ This win-stay, lose-shift learning procedure was dubbed “Propose-but-Verify” (henceforth, PbV), and was supported in a series of word-learning studies on adults (Medina et al., 2011; Trueswell et al., 2013; and below) and 2- and 3-year old children (Woodard, Gleitman & Trueswell, in press). The findings from these studies were also inconsistent with global learning models.

Despite these findings, Trueswell et al. (2013) noted that a local learning procedure such as PbV would be too fragile to support early vocabulary acquisition more generally. For example, homophones could not be learned by a win-stay-lose-shift procedure: the baseball meaning of “bat” would be abandoned the moment the learner went to the zoo, and heard discussion of the flying mammal in the absence of baseball bats. He/she would then proceed to re-learn the baseball meaning (and unlearn the mammal meaning) when going to the ballpark. Moreover, word occurrences in the absence of the target referent (consider: “where is the bat?” when no bats are in sight) would also trigger a shift away from a correctly learned meaning to some other meaning. Thus the local learning procedure, if it were to be successful outside simple experimental settings, would need to be robust to homophonic meaning alternations and robust to noise generally. In what follows, we develop here a robust variant of PbV, which we will call Pursuit.

1.2. A simple example

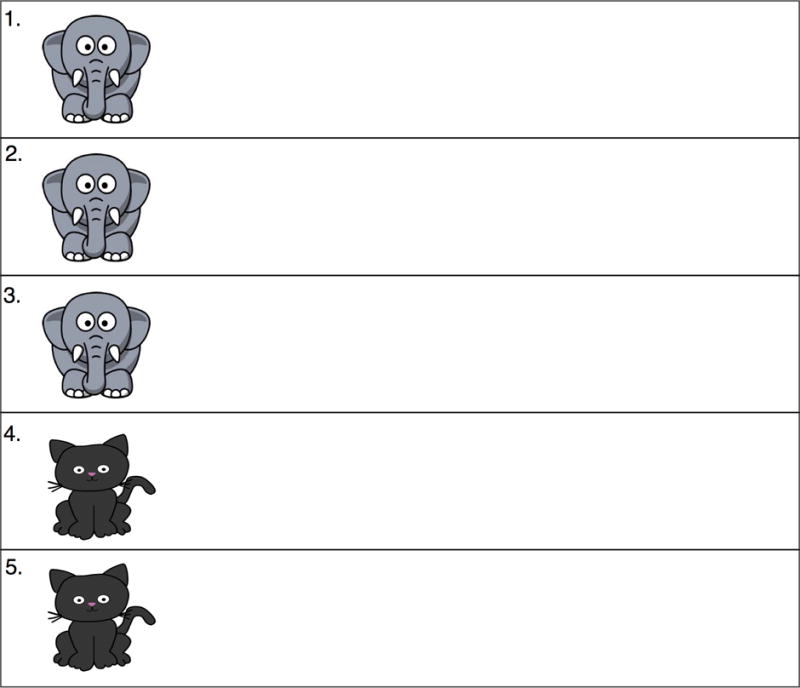
We begin with an artificial example designed to illustrate how an idealized global learning device would operate over a series of referentially ambiguous word occurrences. We then illustrate the operation of PbV over the same sequence. The resulting behaviors of these two accounts will then be used to motivate and illustrate Pursuit. In this simple example, five occurrences of the nonsense word “mipen” are each time accompanied by three potential referents (Fig. 1). For illustrative purposes, assume that no other words are encountered or learned and assume that each referent corresponds to a single basic-level semantic category (such as elephant, cat, etc.). Obviously these assumptions will be too much for a broader account of early word learning to bear, but our focus here is primarily to highlight the different computational mechanisms by which the mapping between words and semantic categories is established.

Figure 1.

Simple example of “mipen” across five referentially ambiguous word occurrences.

Consider first the operation of perhaps the simplest global learning device: one that counts all word-object pairings, with referent selection on each learning instance taking place by selecting the object that at that moment has the highest co-occurrence count. Fig. 2A illustrates the internal state of the model during each learning instance. On learning instance one, counts for each referential alternative are increased by one, and the model, if forced to choose, would select at random among these three. On learning instance 2, counts are increased based on the new referent set; and selection of the elephant would occur because it has the highest co-occurrence count. Counts would increase again on instance 3, and elephant is again the winner. On instance 4 however, the elephant is not present in Fig. 1 (perhaps if indeed “mipen” means elephant, this is an occurrence of the word in the absence of its referent in the visual world, or perhaps “mipen” is a homophone). Counts here (Fig. 2A) would increase, and if forced to choose, the model would pick the dog because it is the co-present referent that enjoys the highest count (albeit slightly lower than the currently absent elephant). Instance five would result in selection of the elephant again because it has the highest count among present referents. The final state of this model after five learning instances is one with a broad set of alternatives for “mipen”.

Figure 2.

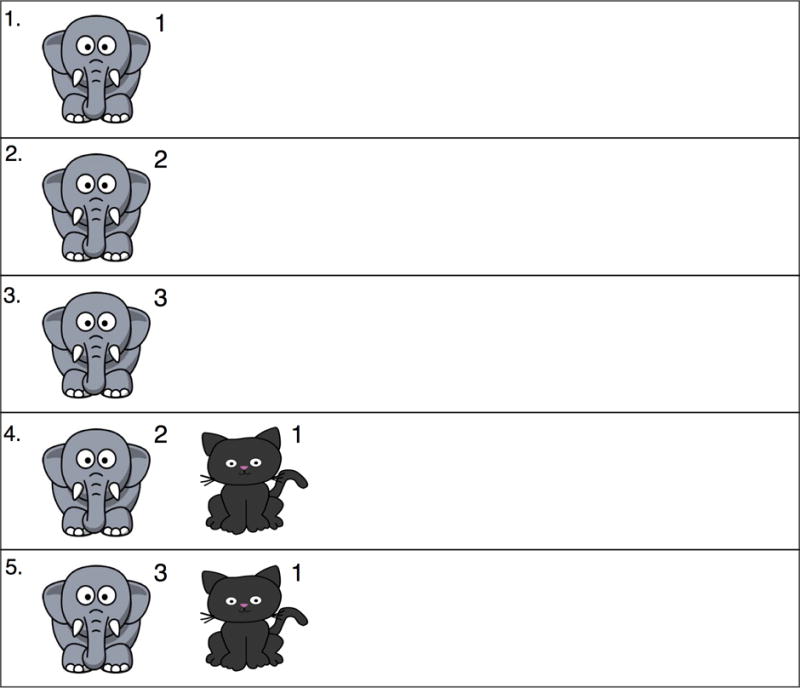
Internal state of three different word learning models, as each encounters the six occurrences of “mipen” from Figure 1. (A) Idealized global model; (B) Propose-but-verify local model; (C) Idealized Pursuit local model.

There are of course advantages and disadvantages to such a broad distribution of alternatives from a global learning device. On the one hand, if “mipen” in fact has more than one meaning, the second meaning could very well be among the lower ranked alternatives. However, without further refinements to this global model, it is clearly suffering from a “dilution” effect: despite the high regularity of elephant in the input, the model possesses only a small preference for this alternative over the many other alternatives that it has been keeping track of. Additional word encounters would likely further dilute this preference.

Consider now the internal state of PbV (Fig. 2B) as it passes through the same sequence depicted in Fig. 1. On the first occurrence, PbV, like a global learner, is expected to choose at random among the referents. However, unlike the global learner, learning here stems from the referential act itself, thus the only thing stored in memory is the selected referent. Assume here the model randomly selects the elephant, making elephant the current hypothesized meaning of “mipen”; no other information (about cats or crabs) is stored. On the second instance, “mipen” is heard and the hypothesis ‘elephant’ is retrieved from memory and tested against the referent world; because an elephant is present in this second instance, it is selected again.² On instance 3, PbV would again retrieve elephant from memory and again it is confirmed and selected. On instance 4, “mipen” is heard, elephant is retrieved but it is not confirmed here: no elephant is present. In its simplest form PbV would be expected to “shift” here, randomly selecting a new referent (and hence a new meaning); let’s say it picks the cat –it has no preference for dog because it has no memory that dog has now occurred three times and cat only twice. Now on instance 5, cat is retrieved from memory and confirmed, resulting in a final state of “mipen” meaning cat.

The advantage of this final state is that the memory is not diluted with alternatives (many of which are likely noise). But it has the disadvantage of not having any ‘stickiness’ to its hypothesis memory. Without any constraint on shifting, the memory state of ‘mipen’ is too fragile, switching toward and away from a likely referent based on potentially noisy input. Moreover it has no “counting” mechanism by which it could encode strength of a hypothesis (though the implemented version had a mechanism for boosting the probability of successful hypothesis retrieval after further confirmation of a hypothesis, see Trueswell et al., 2013). Perhaps there are ways of combining properties of global and local learning to accomplish an optimal outcome.

To this end, consider our proposal for Pursuit. Like PbV, hearing a word results in the retrieval of a single word-meaning hypothesis, which can be tested against the current referent set. Also like PbV, Pursuit learns from selected referents only (not the entire referent set). But unlike PbV, Pursuit retains disconfirmed meanings, which may be tested later. Finally, like the simple global model, Pursuit retains “counts” of referential success. As discussed below, the “counting” in the actual Pursuit model is more complex: it is in fact an associative learning mechanism at its core (see Section 2), but for simplifying purposes, we assume counting here for the example. Remember though, this model restricts its counting to just one class of information: how often a particular referent was selected – i.e., the output of a local selection process.

Consider now the internal state of Pursuit as it passes through the same sequence (Fig. 2C). On the first occurrence, like all other models, Pursuit is expected to choose at random from among the referents. Like PbV but not the global learner, learning here stems from the referential act itself, thus the only thing stored in memory is the selected referent. Assume here the model randomly selects the elephant; thus elephant is the current hypothesized meaning of “mipen”, no other information (about cats or crabs is stored). The count for ‘elephant’ is 1. On instance 2, hearing “mipen” triggers retrieval of the hypothesis ‘elephant’, which is confirmed, increasing the count to 2. (Like PbV, selection of any other referent on instance 1 would have resulted in chance performance on instance 2 since these other referents are not present on instance 2.) On instance 3, elephant is again confirmed, increasing the count to 3. On instance 4 however, the hypothesis that “mipen” means ‘elephant’ is not confirmed. Now, rather than completely shifting away from this hypothesis, confidence in the elephant hypothesis is simply reduced (let’s say that the count of 3 is reduced by 1, to 2) and a new referent is randomly selected: let’s say ‘cat’. This new hypothesis is entered alongside ‘elephant’, and currently has a count of 1. On learning instance 5, the final instance, “mipen” causes the retrieval of ‘elephant’ (and ‘elephant’ only) since it is the highest ranked hypothesis – hence the notion of Pursuit, as the model always goes after the highest ranked hypothesis. This hypothesis is confirmed because an elephant is present. Thus the final state of Pursuit after these five instances is a set of weighted hypotheses about the meaning of mipen (‘elephant’ = 3; ‘cat’ = 1).

At least in this example, Pursuit appears to have captured the best of both a local and a global model. It has a strong single hypothesis, and a back-up hypothesis that could in principle get further support. It was not misled by a single instance (instance 4), i.e., it was “sticky” and thus at least somewhat robust to noise. Note however that if ‘cat’ rather than ‘elephant’ eventually turned out to be the true meaning of “mipen” as the learner saw additional instances, the score of ‘elephant’ would become sufficiently reduced for cat to be leading the way. This is another way in which Pursuit can make cumulative use of evidence.

Relatively little can be concluded from this simple example, which is meant to illustrate the computational mechanisms under different conceptions of word learning. So, what follows are answers to two broad empirical questions. (1) Which of these three models – a global cross-situational model, PbV, or Pursuit – performs best on “naturalistic” corpora of English spoken by caregivers to their children? And, (2) which of these models best accounts for the patterns observed in laboratory experiments – key laboratory experiments that have been claimed as decisive tests of global and local learning accounts? We address these two broad classes of questions in Section 3 and 4 respectively but first, we provide a detailed specification of the Pursuit model of word learning.

2. The Pursuit model of word learning

2.1. Description of model

An essential component of word learning is to establish a reliable connection between a word form and meaning; Pursuit is a computational model of how such connections are established. The link varies in strength as a function of the evidence supporting reference and as a function of frequency with which reference has been established. In this sense, it is an associative link. Note also that the link is between two abstract representations: the word form category (“dog”) and the semantic category used to characterize the referent (the meaning ‘dog’); it is not a link between a particular auditory stimulus (e.g. the sensory stimulation of Margaret saying “dog”) and a particular perceptual stimulus (e.g., the sensory stimulation under certain lighting conditions when her pet poodle comes into view). Thus it is fundamentally a cognitive learning model.

Pursuit uses a variant of reinforcement learning that is frequently used to model associative learning processes (Bush & Mosteller, 1951; Rescorla & Wagner, 1972). The details of the model will be given in Section 2.2; here we present the reader with a brief description of its key properties. The links between a word form and its candidate meanings are represented as probabilities, and learning consists of updating these probabilities as learning instances are presented. Crucially, Pursuit is a “greedy” form of probabilistic learning (Sutton & Barto, 1998): when a word form is presented, the learner only assesses—or pursues—the best, i.e., most probable, among the set of candidates. If the best candidate meaning is confirmed, its probability increases: the rich get richer. If it fails to be confirmed, its probability is decreased: the learner will add a new candidate from the learning instance, but the just defeated candidate may still remain the best if its probability was sufficiently high to begin with.

The privileged status of a single best meaning in the Pursuit model embodies two features, one conceptual and the other empirical, which we believe to be essential to word learning. Conceptually, we hold that word learning is not simply a matter of incidental co-occurrence but only happens when a referential link has been made. In this sense, learning is guided by the learner’s model of how communication works. That is, for a given linguistic act, the mere presence of objects is not sufficient for a link to be made, nor even is the mere act of attending to objects while hearing an utterance. Rather, the learner-listener is attempting to select a unique referent and selection leads to learning. Empirically, as we will review in later sections, a series of experimental results from our group and elsewhere suggest that human subjects appear to have limited access to all the co-occurring meanings (Medina et al., 2011; Trueswell et al., 2013).

2.2. The algorithm

We begin with an explanation of the notations. The input data is a sequence of utterances U = (W_U, M_U), where W_U and M_U are the sets of words and available meanings in that utterance U. The learner has access to the sets of words, meanings and their associations (W, M, A), and adjusts their values after each utterance. For notational convenience, let A_w for a given word w be the set of associations {A(w, x)} for all meanings x that have been hypothesized for w. Similarly, let A_m be {A(x, m)} for all words x for which meaning m has been hypothesized. We can speak of the conditional probability of a word meaning, P(m|w), by normalizing A(w, m) with respect to A_w with smoothing to prevent zero probabilities. This is shown in Equation 1, where N is the number of observed meaning types, and λ is a small smoothing factor.

$$P(m|w)=\frac{A(w,m)+\lambda }{{\displaystyle \sum }{\mathbf{A}}_{\mathbf{w}}+N\times \lambda }$$ (1)

The term P(m|w) can be viewed as the learner’s belief in the word-meaning (w, m) pairing. The smoothing factor λ reserves a small amount of probability mass to unseen mappings, a standard practice in computational linguistics that is also used in virtually all statistical learning models including Fazly, Alishahi & Stevenson (2010), which explicitly uses smoothing, and Frank, Goodman & Tenenbaum (2009), which reserves probability mass for “non-referential” use of words (i.e., when the speaker does not refer to an observable object in the scene). If P(m|w) exceeds a certain threshold value, then the learner concludes m to be the meaning of the word w.

Consider now the learning algorithm in Box 1. Let’s first consider the Pursuit step, which is the core of our model; we will return to the Initialization step, which chooses a meaning candidate for a novel word that the learner encounters for the first time. Our approach could be described as “pursuit with abandon”: the privileged status of a single meaning hypothesis comes at the expense of other meanings. This is the fundamental difference between our model and global learning models, which track co-occurrence statistics over all available word and meaning pairs.

Box 1.

INPUT: The learner’s words (W), meanings (M), their associations A, and the new utterance U = (W_U,M_U).

For every w∈W_U:

1. Initialization

   If w is a novel word, initiate A_w = {A(w,h₀) = γ }, where h₀ = arg min _m∈MU max(A_m)

2. Pursuit

   Select the most probable meaning h for w (i.e., arg max _h A(w,h)):

   1. If h is confirmed (h∈M_U), reward A(w,h), go to (c)
   2. If h is disconfirmed (h∉M_U), penalize A(w,h) and reward A(w,h’) for a randomly selected h’∈M_U

3. Lexicon

   If any conditional probability P(ĥ|w) exceeds a certain threshold value (θ), then file (w,ĥ) into the lexicon.

In Pursuit, the learner selects the most favored meaning hypothesis (h) for the word w, i.e., the one with the highest association score. It then adjusts the association score A(w,h) according to its presence or absence in the current utterance context. If h is confirmed (i.e., found in M_U, the current set of meanings), then A(w, h) increases, and if h fails to be confirmed, it decreases. In the case of confirmation, the learner ignores all other meanings present in the current utterance context and moves on. In the case of disconfirmation, its association score decreases, and the learner randomly chooses a single new meaning from the current set M_U to reward (using the same reward rule which is given in Box 2 below), again ignoring all other available meanings.

Box 2.

Adjust association A(w,h) against an utterance U = (W_U,M_U) where w∈W_U:

If h is confirmed (h∈MU):	$A(w,h)\text{'}=A(w,h)+\mathrm{\gamma }(1-A(w,h\left)\right)$
If h is disconfirmed (h∉MU):	$A(w,h)\text{'}=A(w,h)\times (1-\mathrm{\gamma })$

Lest there be any confusion about the minimalist nature of Pursuit: if the most probable hypothesis fails to be confirmed, the model does not test out the second most probable hypothesis, but rather chooses a meaning from the current context instead. Furthermore, the selection of the new meaning also follows a minimalist strategy: if there are multiple meanings available, the model does not favor meanings it has seen before, but chooses completely randomly. These properties of Pursuit keep the computational cost at an absolute minimum, which we believe is an important feature of a realistic model of word learning given the volume of linguistic data the child is bombarded with during language acquisition.

Under Pursuit, the currently favored hypothesis h may retain its privileged status if confirmed, but may lose it to the hypothesis immediately below it. Step 3 (Lexicon) describes the criterion for success: a meaning ĥ may emerge as the winner if its conditional probability P(ĥ|w), a normalization of A(ĥ, m) as described in Equation 1, exceeds a certain threshold.

Again, it is instructive to compare Pursuit with global cross-situational learning models as well as the PbV approach (Medina et al., 2011; Trueswell et al., 2013). Like global cross-situational learning, the association between words and meanings is probabilistic and dynamically updated in response to the learning data. Like PbV but unlike global cross-situational learning, the Pursuit model considers only one hypothesis at a time and ignores all other meanings upon confirmation. Unlike PbV, however, a disconfirmed meaning is not discarded but only has its association value lowered. Given the Pursuit scheme, a disconfirmed meaning may still remain the most probable hypothesis and will be selected for verification next time the word is presented in the learning data. This crucial feature adds considerable robustness to learning behavior (as compared to PbV) as we shall see.

The function that specifies the magnitude of a reward/penalty is found in Box 2. We use a simple reinforcement learning model to adjust the association scores for words and their meanings (Bush & Mosteller, 1951; Sutton & Barto, 1998), which has been successfully applied to other cases of language acquisition (Yang, 2002, 2004). The amount of adjustment is determined by the learning rate γ, usually a small value between 0 and 1. The Pursuit model falls in the subclass of greedy algorithms: instead of sampling over hypotheses thereby giving every hypothesis a chance to be selected, the learner simply chooses the most favored hypothesis. As long as the most favored meaning continues to be confirmed, the learner ignores all other competing meanings. This is a familiar idea sometimes known as error-driven learning in the formal studies of language acquisition (Berwick, 1985), and is the basis of Pursuit’s congruence with the experimental findings (Medina et al., 2011; Trueswell et al., 2013).

Let’s now consider the Initialization process, which deals with novel words that the learner has not seen before. This step encodes a probabilistic form of the “mutual exclusivity” constraint (Markman & Wachtel, 1988; equivalently for our purposes the “no synonym” linguistic constraint offered by Clark, 1987), which has been implemented in various ways by many computational models of word learning (Fazly et al., 2010; Frank et al., 2009; Yu & Ballard, 2007): when encountering novel words, children favor mappings to novel rather than familiar meanings. For instance, Fazly et al. (2010) build in the mutual exclusivity constraint in that the learner gives larger association boosts to newer meanings and smaller association boosts to meanings that are already associated with other words in the utterance. The Bayesian model of Frank et al. (2009) penalizes many-to-one mappings and places a higher prior probability on smaller lexicons, which is also a probabilistic encoding of mutual exclusivity. In our model, the learner chooses an initial hypothesis for a brand-new word that is least likely to be referred to by another word in the learner’s hypothesis space. For example, say the new word is “cat”, and both ‘cat’ and ‘dog’ are available candidate meanings in the scene. Now imagine that the meaning ‘dog’ is already paired with the word “dog” with an association score of 0.8, and that the meaning ‘cat’ is paired with the word “whisker” with association score 0.6 and with the words “dog” and “ball” each with association score 0.1. In this case, the learner’s best guess for the word that means ‘cat’ has association score max(A_CAT)=0.6, and the learner’s best guess for ‘dog’ has association score max(A_DOG)=0.8. Thus, it is less likely that she knows the word for ‘cat’ than for ‘dog’, making ‘cat’ a better guess for the new word “cat”; ‘dog’ is ignored completely.

In summary, Pursuit maintains the essential statistical machinery of a cross-situational learning model, i.e. a mechanism for representing association strengths and meaning probabilities, but shares a core component of hypothesis-testing models like Trueswell et al.’s (2013) PbV model. Namely, our model places a strong limit on how much information can be maintained across learning trials. Where a full probabilistic model increases associations between the words of an utterance and all visible candidate meanings, the Pursuit model picks winners. As we discuss in Section 4, Pursuit appears to provide the best account for a range of experimental results. But perhaps more surprisingly, Pursuit competes with, and can in some cases outperform, global cross-situational learning models (in terms of numerical measures of accuracy and completeness) when tested on annotated corpora of child-caregiver linguistic interactions. We report these simulation results first as they generate a useful discussion of the design features of the Pursuit model and address the somewhat paradoxical question: how (and under what conditions) could a limited resource learner that ignores much of the available data remain competitive against a learner that tracks cross-situational statistics in their entirety? The reason, as we shall see, also provides the background for the explanation of the experimental results.

3. Pursuit of word meanings in child-directed corpus data

In this section we present the results from a computational comparison of several word-learning models, each operating over the same codings of naturally occurring parent-child interactions. We will provide as input to the model child-directed speech and our codings of the co-present referent world; We will use two data sets: (1) selected video samples of the Rollins corpus within CHILDES database (the Rollins Corpus); and (2) video samples of parent-child interactions that were used in the Human Simulation Paradigm (HSP) experiments of Cartmill, et al. (2013).

3.1. Rollins corpus simulations

3.1.1. Data

We chose to use the Rollins Corpus to maintain continuity with previous modeling research (Yu & Ballard, 2007; Frank et al., 2009). In line with these two previous computational simulations of word learning, we manually coded data from four videos of mother-child interaction from the Rollins corpus, where two videos were used for training and two for evaluation. The data consists of mothers talking to their infant children while playing with toys from a box. We coded only these verbal interactions, skipping songs, periods of fussiness, etc. Following the past work (Yu & Ballard, 2007; Frank et al., 2009), the annotator coded which concrete noun meanings were available to the learner (e.g., visible on the video, judged not to be outside the baby’s visual field, and judged to be in the attentional focus of an observer of this scene). Again following the past work, the coding was only of basic-level categories of discrete and whole objects. Thus, for example, if we included the meaning ‘bird’ in the interpretation of a scene, we did not also include ‘beak’ or ‘animal’. this coding scheme assumes (within very broad limits) that learners were also capable of making assumptions about the likely gist of the scenario, i.e., that they can exclude from their list of hypotheses visible items that none of the interlocutors are attending to, or that are just about always there and therefore not “newsworthy” except under special circumstances, e.g., one of the shoes that the speaker or listener is wearing. Thus the coding scheme used in this and other computational modeling efforts was treated (rightly or wrongly) as an approximation of the linguistic and contextual information available to the human subject, especially a language-learning child. Its purpose is to provide a common dataset on which alternative conceptions of word learning can be tested and compared. There were 496 distinct utterances in the training set and 184 in the evaluation set, 680 total.

The performance of all models was evaluated based on comparison to a single gold standard lexicon consisting of the set of word-meaning pairs that, in the judgment of the experimenters, could have reasonably been learned. The two criteria for inclusion in the gold standard were: (1) the word must refer to a concrete object (since only concrete object meanings were coded as “present” in the scenes), and (2) the word must appear more than once in the data, and must refer to a meaning that is at some point visible to the child as judged from the video.

3.1.2. Simulations

We tested four models on the derived data sets from CHILDES: two global cross-situational learning models, plus the two local models, PbV and Pursuit.³ First, we ran an implementation of the Fazly et al. (2010) cross-situational learning model exactly following the description in their paper. The Fazly et al. model is a cross-situational model par excellence as it tabulates word-meaning co-occurrences throughout the learning process. It is also explicit in its use of mutual exclusivity effects. It avoids the mapping of multiple words within an utterance to the same meaning by calculating “alignments” between words and meanings, where for each meaning in the scene, a fixed amount of alignment mass is distributed among the words in the utterance proportionally to the value of P(m|w) for each word. The alignments determine the amount by which association strength is boosted. The effect of this is that if the learner is already certain that a word w has meaning m, then other words that co-occur in the same utterance as w do not get mapped to m with the same strength. The Pursuit model makes use of a similar strategy (see Initialization), which allows for direct comparison between the models. Second, we implemented an additional global learning model, with a modification of the model presented in Alishahi, Fazly, Koehne, & Crocker (2012). Where Fazly et al.’s model distributes a fixed alignment mass among words, this modified model distributes a fixed alignment mass among meanings. This is implemented by having alignments proportional to P(w|m) for each visible meaning, rather than P(m|w) for each uttered word.⁴ This model is more similar to Pursuit in that it favors strong initial candidates, and “late-comers” are penalized. We also implemented PbV with perfect memory (Trueswell et al., 2013): that is, the learner’s retrieval of the current hypothesis is unfailing and not subject to other memory constraints. Finally, we implemented the Pursuit model as it is described in Box 1.

As is standard in computational linguistics and previous word-learning research, all four models were independently optimized for maximum performance on the training data. These include, for all models, the smoothing parameter λ (e.g., Equation 1) and threshold value above which a word-meaning pair is considered to be learned.⁵ For the Pursuit model, the learning rate parameter (γ in Box 2)is set to a small value (0.02) following earlier applications to language learning (Yang, 2002, 2004). All models are tuned to maximize the F-score on the training data (see technical supplement for more details).

Models were evaluated based on precision, recall and the combined F-score (the harmonic mean of precision and recall) of the learned lexicon against the gold standard. Precision refers to the percentage of accurate word-meaning pairs, compared to the gold standard lexicon, that the model has learned, and recall refers to the percentage of all word-meaning pairs in the gold standard that have been learned by the model. Due to the probabilistic nature of the algorithm (e.g., the hypothesis is randomly selected from the set of possible meanings in the context), Pursuit yields slightly different lexicons each time the model is run. PbV is similarly stochastic. Therefore, the results reported for the Pursuit and PbV models were obtained by averaging precision and recall over 1000 simulations and using those averages to calculate an F-score. By contrast, the two global cross-situational learners, which track the co-occurring statistics over the entire dataset, produce deterministic results.

3.1.3. Results and analysis

Performance of the four models on the training data is shown in Table 1. This represents the optimized, best-case performance for these models on this set of learning instances. We see that PbV achieves the highest recall (i.e. learns the most correct words), and yet cannot compete on overall performance due to its low precision (it must make some mapping for every word, even function words which of course are co-present with many target meanings). Pursuit performs comparably though slightly worse in terms of recall but drastically boosts average precision (i.e. proportion of learned mappings which are correct) from 4 to 45 percent. Both precision and recall for both global cross-situational models are lower than that of Pursuit.

Table 1.

496 utterances from hand-coded videos from the Rollins corpus, with best-case parameter values. CIs for non-deterministic models calculated by bootstrapping from 1000 resamples of the F-scores.

	Precision	Recall	F1
Propose/Verify	0.04	0.45	0.07 (95% CI = 0.071–0.075)
Fazly et al. 2010	0.39	0.21	0.27
Modified Fazly	0.42	0.24	0.30
Pursuit	0.45	0.37	0.41 (95% CI = 0.402–0.410)

To combat over-fitting, we ran all trained models on a smaller set of evaluation data, which is also part of the Rollins corpus. The results are given in Table 2. We see that, although Pursuit loses its precision advantage to the original Fazly et al. (2010) model, which does somewhat better on this data set, overall performance as represented by the F-score is still highest for the Pursuit model. Confidence intervals obtained by resampling Pursuit’s output 1000 times indicate that the advantage is reliable.

Table 2.

184 utterances from hand-coded videos from the Rollins corpus, with parameters fine-tuned on training data. CIs for non-deterministic models calculated by bootstrapping from 1000 resamples of the F-scores.

	Precision	Recall	F1
Propose/Verify	0.03	0.50	0.06 (95% CI = 0.053–0.057)
Fazly et al. 2010	0.75	0.21	0.33
Modified Fazly	0.25	0.43	0.32
Pursuit	0.60	0.25	0.35 (95% CI = 0.343–0.360)

3.2. Cartmill et al. (2013)

3.2.1. Data from the Human Simulation Paradigm

It must be said that the Rollins Corpus, which was collected in a controlled laboratory setting, does not fully reflect the complexity of real-world language learning situations. At the same time, one needn’t make the task of computational learning unnecessarily hard—by tracking all and every aspect of the learning situation, for instance—as it is widely recognized that children bring cognitive and perceptual biases to language learning which narrow down the range of referential choices. The effects of these biases can be approximated by the scene coding scheme called the Human Simulation Paradigm (henceforth, HSP), which was developed precisely for the purpose of quantifying the referential complexity of word learning in realistic situations (Gillette et al., 1999; Snedeker & Gleitman, 2004; Medina et al., 2011). In HSP, mother-child interactions during varied everyday circumstances were videotaped. Naïve human subjects (usually adults, but sometimes children as in Piccin & Waxman, 2007; Medina et al., 2011) are asked to “guess what the mother said” when they are shown the videotaped segments, but with the audio turned off: the only audible aspect is a beep or nonsense syllable occurring exactly when the mother said the word of interest. HSP provides us with a “crowd-based” estimate of the set of plausible referents for a given word utterance with several obvious advantages: the HSP crowd is blind to the actual word uttered by the mother, and can only use the extra-linguistic context and not the linguistic content of the rest of the utterance to make their guess. This “simulates” the early word learner, who similarly does not have linguistic knowledge and can only use the unfolding extra-linguistic social interaction to form one or many referential hypotheses.

We use the Cartmill et al. (2013) HSP corpus, which consists of 560 forty-second videos (“vignettes”), ten each from each of the 56 families – 6.2 hours in total. All vignettes are examples of parents talking to their 14- and 18-month-old children. Each vignette was an example of the parent uttering one of the 41 most common concrete nouns from the entire transcript sample, uttered usually within a sentence context (e.g., Can you give me the book?). Vignettes were aligned so that 30sec into the video, the parent uttered the target word (at which point a beep was inserted). To select vignettes, Cartmill et al. (2013) ranked concrete nouns uttered to children at 14–26 months by frequency, and randomly chose a single example of each of the 10 highest-ranked words parents produced at 14–18 months. Because highest-ranked nouns varied across parents, the final test corpus contained 41 different nouns. Further details about this corpus can be found in Cartmill et al. (2013).

Cartmill et al. (2013) asked naïve subjects (200+ in total) to view subsets of these videos (approximately 15 subjects per video) and to guess what word the mother had said at the beep. We took these ~15 responses as an estimate of plausible referential candidates of the word, and used this as our “coding” of the referent scene. Each scene was then paired with the transcript of the utterance containing the target word, as in the following example.

Utterance	“are you offering your book”
Meanings	{‘stop’, ‘done’, ‘give’, ‘read’, ‘read’, ‘book’, ‘book’, ‘book’}

As one might expect, the words guessed by HSP participants were almost unexceptionally ones that parents say to their children (e.g., bear, hello, teddy, hair, handsome, head, mess, silly, sit, book, done, going, read, toy, where, yellow). Although Cartmill et al. (2013) selected concrete nouns as their target words of study, HSP subject responses were not limited to them – nor should they be, because Cartmill et al. did not tell subjects anything about the lexical class of the “mystery words” they were to identify. This more open-ended nature of word reference (as, potentially, in the real life of child learners) yields a much higher degree of ambiguity: rather than an average of 3.1 possible referent-meanings per scene in the Rollins Corpus, the Cartmill et al. video corpus averages 7.4 unique meanings supported by the observational context.

3.2.2. Simulation results on HSP data and the Role of referential ambiguity

How well did our word-learning models perform on this new, considerably more complex referent set? Results are given in Table 3 where the models are individually optimized for the Cartmill et al. corpus. We see for these data Pursuit is still competitive, and still outperforms one of the cross-situational comparison models. The other comparison model, our implementation of the original Fazly et al. (2010) algorithm, performs especially strong here. We now ask why this is.

Table 3.

Results from simulations on the corpus of video vignettes used by Cartmill et al. (2013).

	Precision	Recall	F1
Propose/Verify	0.03	0.42	0.06 (95% CI = 0.057–0.061)
Fazly et al. 2010	0.47	0.37	0.41
Modified Fazly	0.17	0.71	0.27
Pursuit	0.59	0.29	0.39 (95% CI = 0.378–0.394)

One of the most striking differences between the Rollins and Cartmill corpora is not only that there are more (and more varied types of) meanings in the scenes, but also that the Cartmill corpus exhibits only about a 60% rate of co-occurrence between target word and its intended meaning. Contrast this with Rollins, where a learnable word co-occurs with its referent on more than 90% of the instances. So a reasonable initial hypothesis would be that Pursuit is more hindered than the other models by increased referential uncertainty and comparatively low co-occurrence rates. But, as we explore here in an additional set of simulations, this explanation is not supported.

To understand the conditions that favor different learning models, we created a series of artificial HSP corpora based off of the Cartmill data, which vary along two dimensions: (1) the degree of referential uncertainty, i.e. the average number possible meanings per learning instance, and (2) the consistency with which a target word occurs with its target referent. The utterances used were the same as above, but the scenes were generated randomly according to the relevant constraints. For example, the “60% – 4” corpus has the referent present on 60% of the word instances and has on average 4 referents present per instance. We generated this corpus by starting with the target meaning for the target word in each utterance, then adding between 0 and 6 random distractor meanings (taken from a set of 500 possible distractor types), such that the average number of overall meanings is close to 4, and then replacing 40% of the target meanings with distractors. The purpose of these manipulations is to enumerate/simulate a wide range of conditions, which are likely to arise in real-world learning situations, and explore the robustness of the word-learning models. For instance, previous research has demonstrated that the referential ambiguity of words are quite uneven, and some words are much easier to identify than others (see Gleitman, Cassidy, Nappa, Papafragou & Trueswell, 2005 for review); these distributional aspects of referential ambiguity are effectively simulated in our manipulation of the Cartmill et al. corpus. Since children need to learn easy and hard words alike, a desirable word-learning model should show “graceful degradation” as the complexity of the task increases, rather than suffer from catastrophic failure.

Tables 4 and 5 show the resulting F-scores (with values for Pursuit obtained by averaging over 50 simulations per condition). Pursuit is quite robust to increases in average number of competing meanings, especially in the 80% and 100% conditions. While both models suffer as the uncertainty increases and consistency decreases, Pursuit is robust enough to surpass the comparison model on the more “difficult” conditions in the lower right area of the tables.

Table 4.

Performance of Pursuit on simulated Cartmill-style corpora. Bold face indicates better performance than the Fazly et al. model on that condition.

PURSUIT	3	4	6	7	8	10	15
100%	.45	.47	.47	.47	.47	.44	.37
80%	.45	.47	.44	.44	.44	.42	.31
60%	.41	.40	.37	.33	.35	.32	.19
40%	.38	.38	.26	.26	.18	.15	.08
20%	.05	.09	.04	.00	.02	.00	.00

Table 5.

Performance of Fazly et al. (2010) on simulated Cartmill-style corpora. Bold face indicates better performance than Pursuit on that condition.

FAZLY	3	4	6	7	8	10	15
100%	.71	.66	.66	.55	.54	.51	.33
80%	.65	.63	.63	.53	.42	.36	.09
60%	.55	.51	.45	.36	.33	.22	.00
40%	.44	.39	.29	.18	.14	.00	.00
20%	.13	.00	.00	.00	.00	.00	.00

One difference between the Cartmill and Rollins corpora which may favor full cross-situational models for the former and Pursuit for the latter is the degree of meaning-meaning co-occurrence. The Rollins corpus has a high degree of meaning-meaning co-occurrence, such that more than half of the observed meaning tokens co-occur with at least one other meaning on most of the scenes containing that token. Intuitively, this reflects an aspect of real-life learning, e.g., that the family dog and the family cat will often be seen together. The Cartmill corpus and the artificially constructed corpora used for the experiments taken up in the next section do not have this property; meaning-meaning co-occurrence is very low for those data sets. It is not hard to see why this might favor Pursuit: if the learner has the opportunity to guess correctly from an early, highly informative exposure, then those consistent competitors will be ignored altogether, whereas they will dilute the probability space of the full cross-situational learner, making the learner less confident in her mappings, and increasing the likelihood of either omissions from or erroneous additions to her lexicon. In other words, the Rollins corpus, like some real-life learning contexts, and unlike the Cartmill data set, is akin to Figs. 1 and 2 from Section 1 above, in that there are rather consistent distractors to deal with.

Taken together, the results from both the Rollins Corpus and the Cartmill et al. corpus (including the manipulations to simulate the real world) suggest that Pursuit, a local model that keeps track of a smaller number of meaning candidates, is competitive across a wide range of conditions against global models that retain the cross-situational statistics of all word-meaning associations. A systematic investigation of the formal properties of global vs. local models will have to await future research, but a plausible explanation of this apparently paradoxical finding is that Pursuit is better equipped at capitalizing the few but highly informative learning instances, which tend to get diluted by global learners in the averaging process across all instances. In any word-learning model, the successful acquisition of a word requires the learner having considerably higher confidence in a meaning over its competitors. This notion corresponds to the threshold value above which the word learning is considered to have been learned, which, in the computational models implemented here, is a threshold for the normalized probabilistic associations between a word and all of its possible meanings. Thus, the more competitor meanings a word has, the less will the target meaning stands out in the end. Pursuit, being a strictly local model, keeps track of many fewer candidates than global models which keep track of all available candidates: thus, it degrades much more gracefully as the ambiguity of learning instances increases, as we have seen in the simulation of the Cartmill et al. corpus. Interestingly, in experimental studies of cross-situational learning, which employ idealized, “easier” learning tasks on which global models are expected to learn quite accurately, the global models are in fact “too good” to model human subjects: subjects’ behavior is more in line with a probabilistic local model as we will see. We now turn to this point as we explore the suitability of these computational models as models of psychological mechanisms of early word learning.

4. Testing learning models on experimental conditions

In this section we show that the Pursuit algorithm captures key behaviors found in several experimental studies of word learning (in particular, Yu & Smith, 2007; Trueswell et al., 2013; Koehne, Trueswell & Gleitman, 2013). We show that the results of Yu and Smith (2007), which are often cited as evidence for a global learning mechanism, are better modeled by the PbV and Pursuit models than they are by the comparison models which tabulate full cross-instance statistics. Our simulations of the first experiment of Trueswell et al. (2013) show that Pursuit and PbV – and not the other two models – accurately capture the qualitative behavior of experimental subjects. Finally, we show that only Pursuit – and not PbV – can capture the additional results of Koehne et al. (2013), whose findings suggest that word learners do maintain multiple possible meanings for a word, while still only one such meaning is tested by the learner during any given learning instance.

4.1. Yu and Smith (2007)

The word-learning experiments of Yu and Smith (2007) and similar studies have provided the key evidence that individuals can learn word meanings from a series of referentially underdetermined learning instances. Adult subjects were exposed to pictures on a computer screen, with either two, three or four objects depicted on the screen at a time. During each exposure, each of the visible objects was named aloud with a nonsense word, but subjects were not told which word went with which object. After six exposures to each nonsense word, subjects were asked to pick the correct intended meaning of each word from a set of four possible referents. The correct referent was always visible during the utterance of each word. The principal finding of these experiments is that when subjects learned from instances with lower referential ambiguity, i.e. fewer objects on screen at a time, subjects’ guesses at the end were more accurate overall (see Table 6 for their results). That lower ambiguity across learning instances has a positive effect on learning has been interpreted as support for global models that track all possible word-referent pairings (e.g., Yu & Smith, 2007; Yu, 2008).

As we noted above in Section 1.1, the Yu and Smith finding (2007) is also consistent with a simple local learning device. Namely, the effect of lower ambiguity in learning is expected from a learner who makes guesses and tests their guesses against later instances. When only two possible referents for a word are visible, the learner has a 50/50 chance of guessing the correct meaning on any given instance, and if the correct guess continues to be tested and confirmed, the word is very likely to be learned after just a few instances. If, on the other hand, there are four possible referents, it is more likely for the learner to get through six instances of a word without ever happening upon the right meaning, thus reducing final average accuracy after this more ambiguous condition. While the learner must remember previous guesses in order to confirm their hypothesis, it is not necessary for the learner to attend to more than one possible meaning per instance. In fact, the learner need not store any information about statistical distribution in order to produce this effect.

We sought here to verify that the PbV model can in fact capture the Yu and Smith (2007) findings; we also sought to compare PbV to the performance of the Pursuit model and the two global models (Fazly et al., and Modified Fazly et al.). Table 6 presents the results of these four simulations for Yu and Smith’s first experiment. This table gives average accuracy of responses from 300 total simulated subjects as produced from each model, with variance across subjects indicated by 95% CI. Experiments were simulated by first constructing artificial stimuli according to the specifications given in Yu & Smith (2007), processing those stimuli using the various models, and then forcing the system to guess between the correct meaning and three other randomly chosen distractor meanings for final testing. For the Pursuit learner, guessing means choosing the most probable candidate meaning, if it is present (in accordance with step (b-i.) in Box 1 in Section 2), and otherwise randomly selecting a visible meaning if the preferred hypothesis is absent (step (b-ii.)). For the PbV learner, hypotheses are categorical, and thus to guess a word’s meaning is simply to select the single hypothesis associated with that word. In contrast, model behavior for the two global learning models is completely deterministic and will always generate the same network of word-meaning probabilities whenever passed through the training set. Applying a winner-take-all guessing mechanism to the probabilities that were generated by the global models yields a completely undesirable result: 100% correct responses regardless of the degree of ambiguity. So instead we sampled the resulting probability space proportionally, with each sample representing the response of a different simulated subject; this is equivalent to the normalization of word-meaning associations.

As anticipated, PbV captures the Yu and Smith findings very well. In particular, PbV predicts statistically significant differences between each pair of conditions, and the 95% confidence intervals around the average simulated performance overlap with the 95% confidence intervals around average human performance in all three conditions (4×4, 3×3 and 2×2). Given that PbV provides a good fit for these experiment results, it is perhaps no surprise that the Pursuit model, which is similar to PbV, also provides a good fit: again, performance on each condition is significantly different from the others, again with overlap in 95% CI in all three conditions. What is perhaps more surprising though is that the two global models do not do particularly well in fitting the effect in question. We see in Table 6 that both of the global models predict less of an effect of referent set size, with near-ceiling performance across the board, contrary to what is actually observed. This is because the target meaning, which is always present, thoroughly overwhelms the competitor meanings, which are available only about 20% of the time, so sampling from their probabilistic associations overwhelmingly favors the target meaning. Nonetheless, it should be noted that all models replicate the observed qualitative pattern to some extent, perhaps with the exception of the unmodified Fazly et al. (2010) model. We do not claim that the inability to exactly match quantitative data precludes, in and of itself, the usefulness of the global models. After all, post hoc memory constraints could be imposed on a global learner to make the numbers match better. But importantly, our results show that findings like this do not at all support a global approach at the expense of a local one.

In addition to the role of within-trial ambiguity, Yu and Smith (2007) report a second experiment that manipulated the number of exposures to target words vs. number of misleading distractor referents. The most striking result is that, using only the four-referent scenario, giving learners 12 exposures to 9 words does not improve performance over the case where subjects are given 6 exposures to 18 words. The reason is that in the 9-word condition there is a significantly higher probability of repeated, misleading distractor meanings, making co-occurrences less informative on average than in the 18-word condition. The authors take this as further evidence of pure global learning: one might expect a local hypothesis-testing model to benefit from having 12 exposures rather than 6, because this presents double the opportunities to guess the correct meaning. However, it turns out that the increased number of “pretender” meanings similarly affects both PbV and Pursuit models, and again, the global models outperform human subjects. In particular, where the observed proportion of correct guesses in the 9-word condition is about 60%, Pursuit yields 64% and PbV yields 58% on simulations of this condition, and the global cross-situational models yield around 95%. Taken together, the simulation results on Yu and Smith’s (2007) experiments suggest that the paradigm study in support of cross-situational learning is well accounted for by local models such as PbV and Pursuit.

4.2. Trueswell, Medina, Hafri and Gleitman (2013)

In Trueswell et al. (2013), adult subjects were presented with repeated sequences of nonsense words accompanied by visual stimuli, and asked to learn meanings for those words from the visual scenes. Each target word was associated with a unique target meaning. The possible meanings were presented using a constructed layout of static images on a computer screen. Subjects were asked to indicate their guesses by clicking on an image with a mouse. The target meaning was always present. For example, a subject might have been presented with five instances of the word “mipen” throughout the experiment (intermixed with other word trials), and although each of the five instances was accompanied by a different visual scene, an exemplar of the meaning ‘ball’ was always visible. Subjects were asked to guess the intended meaning of each nonsense word after each instance, and the experimenters tracked the rate at which subjects guessed “correctly” (e.g., guessed ‘ball’ for “mipen”).

The authors found that subjects were more likely to guess correctly when they had guessed correctly on the previous instance of a word. When the subject had guessed incorrectly on the previous instance, performance was at chance (20%), indicating they had not retained any alternative meaning hypotheses from the previous learning instance (though see Dautriche & Chemla, 2014 and Yurovsky & Frank, 2015, and our discussion of this work below). Trueswell et al. (2013) used this data to motivate the “Propose-but-Verify” (PbV) model of word learning.

We simulated Trueswell et al.’s first experiment, in which every instance presented the learner with exactly five possible meanings. Fig. 3A reproduces these experimental findings from Trueswell et al. (2013). Fig. 3B presents the results of the memory-restricted PbV model and Fig. 3C the idealized PbV without memory restrictions. Fig. 3D presents the results from the Pursuit model. All three models capture the behavior accordingly, with perfect memory models (Figs. 3C and 3D) remembering their previous guess better than human subjects. But all models, as expected, are at chance (20% correct) after guessing incorrectly.

Figure 3. Simulations of Trueswell et al (2013), Experiment 1.

(A) Performance of human subjects, from Trueswell et al (2013); (B) Propose/Verify model; (C) Propose/Verify with no memory constraints; (D) Pursuit; (E) Modified Fazly et al. (2010) model with guesses made via weighted sampling; (F) Original Fazly et al. model.

Contrast this behavior with the global cross-situational models (Figs. 3E and 3F). The modified Fazly et al. model (3E), which is similar to Pursuit in that it is sensitive to the order of learning instances, does show some effect of having guessed correctly on the previous instance, but crucially, accuracy after a previous incorrect guess is much higher than predicted, and—at about 65%—much higher than chance level, which represents a qualitative difference between this model, on the one hand, and Pursuit and PbV, on the other. The original Fazly et al. model (3F) is equally above chance regardless of whether or not the model had been correct on the previous learning instance, contra the human results (Fig. 3A). Under both global cross-situational comparison models, the probability of the correct meaning is increased slightly with each instance, and thus having guessed incorrectly has either a much smaller effect than predicted (3E) or no effect at all (3F). See Table 7 for a full quantitative comparison. Note that Figs. 3E and 3F both assume a model where guesses are made probabilistically, unlike Pursuit which always chooses the best candidate. As mentioned in 4.1, to incorporate a winner-takes-all guessing mechanism into the global models would yield an even worse prediction: for both models in both conditions, performance is at ceiling. This is again due to the global models’ incrementally increasing the association between target word and target meaning on each instance.

Table 7.

Trueswell (2013), Experiment 1, proportion of correct guesses on instances > 1 by whether the subject guessed correctly on the previous instance. Significance determined by a mixed effects regression model.

	Previously incorrect	Previously correct	significant difference?	greater than chance	CI overlaps w/ observed
Propose/Verify	0.19 (95% CI = 0.183–0.207)	0.46 (95% CI = 0.431–0.491)	yes	no / yes	yes / yes
Propose/Verify (perfect memory)	0.18 (95% CI = 0.171–0.195)	1.00 (95% CI = 1.000–1.000)	yes	no / yes	yes / no
Fazly et al. 2010	0.35 (95% CI = 0.341–0.369)	0.35 (95% CI = 0.325–0.371)	no	yes / yes	no / yes
Modified Fazly	0.65 (95% CI = 0.640–0.669)	0.87 (95% CI = 0.857–0.877)	yes	yes / yes	no / no
Pursuit	0.21 (95% CI = 0.197–0.224)	0.80 (95% CI = 0.781–0.825)	yes	no / yes	yes / no
Human subjects	0.21 (95% CI = 0.171–0.249)	0.47 (95% CI = 0.332–0.700)	yes	no / yes

Finally, Trueswell et al. (2013) reported (in Exp. 3) that a correct guess on trial N-2 did not correlate with a correct guess on trial N if trial N-1 was guessed incorrectly. Fig. 4 presents this result for Pursuit, by showing performance on the fourth instance of each word as a function of whether the second and third guesses were correct. In the case where the third guess was incorrect, whether the second guess was correct has no bearing on whether the fourth guess is correct. This is straightforward under PbV, because once the learner has chosen a wrong hypothesis, their previous hypothesis is not stored in memory at all. Pursuit exhibits this same behavior, though for a somewhat more complex reason. Under part ii. of the Pursuit step of the algorithm (Box 1), if the most probable hypothesis is disconfirmed, the learner chooses a random object from the set of visible objects, and this random choice could happen to be correct. However, this is no guarantee that the learner will choose the correct hypothesis next time, because the disconfirmed hypothesis, despite being penalized once in the immediate past, may still remain most probable. Thus, under Pursuit the learner may happen to guess correctly on the second instance even if a different hypothesis remains the most probable. In that case, the subject is likely to choose a false hypothesis for the third instance, and the correct hypothesis maintains a low probability. This places the rate of correct guessing for the fourth instance around chance level. Choosing the maximally probable candidate under the global cross-situational comparison models does not yield valid behavioral predictions in that by the third instance, all guesses are correct, due to the fact that in this experiment the correct referent is always present. Moreover, choosing the instance based on probabilities does not yield expected results either, as is evident from the previous data on the influence of N-1 (Figs. 3E and 3F).

Figure 4.

Average performance of Pursuit model on the fourth learning instance in Trueswell et al (2011) simulations, by whether second and third guesses had been correct.

Although we do not include the results here, we were also able to produce similar results for Medina et al.’s (2011) first experiment, which uses video vignettes in the human simulation paradigm, similarly to the Cartmill et al. (2013) study. Medina et al. show that those subjects who guessed the correct target on the first instance were more likely to have learned the word by the end of the experiment, and this was independent of how easy it was to guess the correct meaning in isolation (as determined in a separate experiment). Pursuit behaves on these simulations exactly like a memory-unrestricted version of PbV,⁶ and exhibits a similar contrast to the comparison models as is shown here.

4.3. Koehne, Trueswell and Gleitman (2013)

Thus far, our simulations have shown that both Pursuit and PbV, but not a cross-situational model, capture the patterns observed in experimental data. We now turn to our simulations of the first experiment in Koehne et al. (2013), which differentiate Pursuit from PbV on a behavioral level, in that only the former captures the observed behaviors. Koehne et al. tested whether subjects would maintain prior knowledge about chosen hypotheses when making guesses about word meaning. The study uses a similar paradigm to the experiments of Trueswell et al. (2013), but there are two target referents for each target word: a “fifty percent referent” (FPR) which is present for exactly half of the instances of a given word, and a “hundred percent referent” (HPR) which is present for every instance. At the end of the learning trials, the subjects were asked to guess each word’s meaning from a set of eight candidate meanings. Crucially, the HPR was absent during these testing trials. Thus, the subject was forced to choose between the FPR and a number of distractor referents.

The experimenters manipulated the order in which instances were presented. Each learning instance was classified as a “Present” (P) instance if the FPR was present, or an “Absent” (A) instance if the FPR was absent. Each word occurred six times during the learning phase of the experiment, with the same number of possible referents for each instance. Four orders were tested: AAAPPP, APAPAP, PAPAPA, and PPPAAA.

The PbV model of Trueswell et al. (2013) predicts that subjects will only choose the FPR above chance level during the final test for a word if the last instance of that word was a P-instance, i.e., conditions AAAPPP and APAPAP. This is because in conditions PPPAAA and PAPAPA, there is no possibility that the subject chose the FPR as her most recent hypothesis for that word. Therefore, the subject will not have any reason to choose it above chance level during testing. Contrary to this prediction, the experimenters find that subjects do in fact choose the FPR above chance level in all conditions (Fig. 5A), with an elevated probability of picking the FPR in the absent-final conditions (PAPAPA and PPPAAA)–precisely the conditions in which PbV predicts chance-level selection of the FPR.

Figure 5. Simulations of Koehne et al., Experiment 1, rate of choosing Fifty Percent referent.

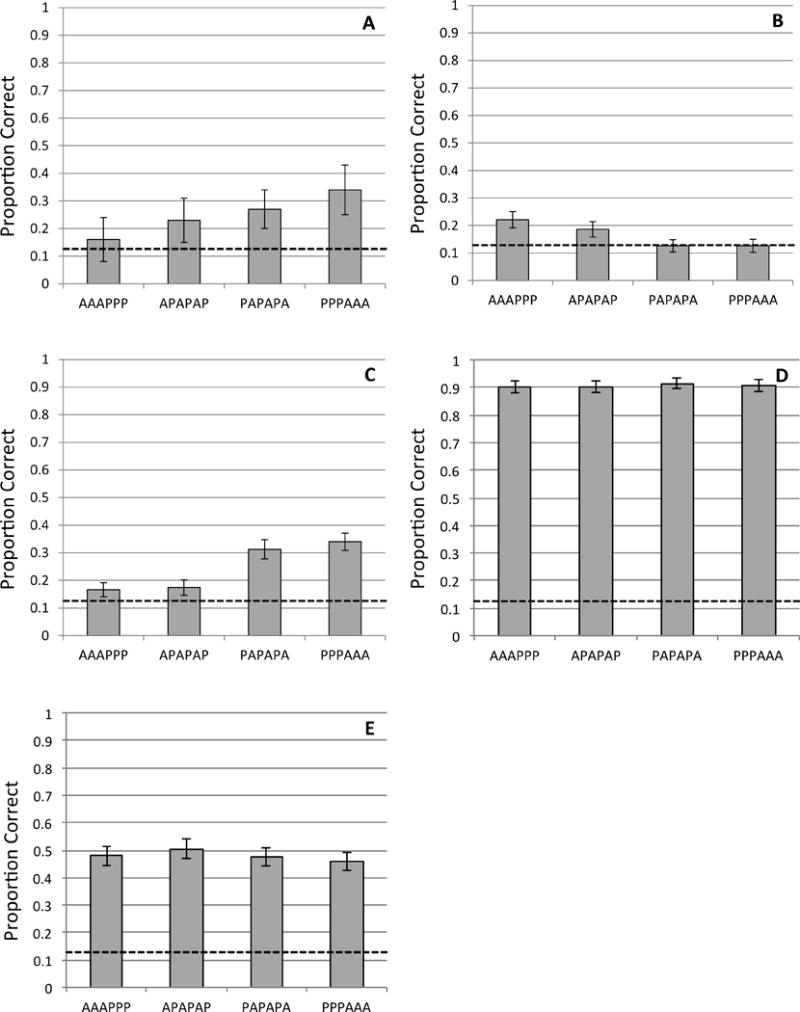
(A) Performance of human subjects, from Koehne et al (2013); (B) Propose/Verify; (C) Pursuit; (D) Modified Fazly et al. (2010) model with guesses made via weighted sampling; (E) Original Fazly et al. model.

PbV does not correctly predict Koehne et al.’s (2013) results because once a hypothesis has been rejected and a new one chosen, there is no record of the rejected hypothesis having previously succeeded. Pursuit, by contrast, does not completely reject a hypothesis in the face of disconfirming evidence. Rather, it only lowers the association score of that word-meaning pair. If a particular hypothesis succeeds multiple times and then fails, it is still possible for that hypothesis to maintain its position as the most probable candidate. We see this in Fig. 5C: Pursuit yields a higher advantage for the FPR in the PPPAAA condition, because the likelihood of giving the FPR a very high probability score based on consistent initial evidence from the first three trials is higher in this condition. This is exactly the trend found by Koehne et al. (see Graph 1 in that paper). And, as expected, PbV does not replicate this trend, as we see in Fig. 5B. Moreover, the global comparison models do not replicate the qualitative pattern either, as seen in Figs. 5D and 5E.

Interestingly, Koehne et al. find that participants are only above chance at selecting the FPR at final test if and only if they had selected an FPR at least once during the learning trials (Fig. 6A). This would be expected by Pursuit because consideration as a referent is the only way an item can enter the word meaning set. And indeed, Fig. 6C below replicates Koehne et al.’s result using Pursuit simulations, whereas PbV fails to capture this result (see Fig. 6B). See Table 8 for a quantitative comparison of Pursuit, PbV and human performance.

Figure 6. Koehne et al. (2013), Experiment 1, average rate of choosing Fifty Percent Referent, by whether Fifty Percent Referent had been chosen after a previous instance.

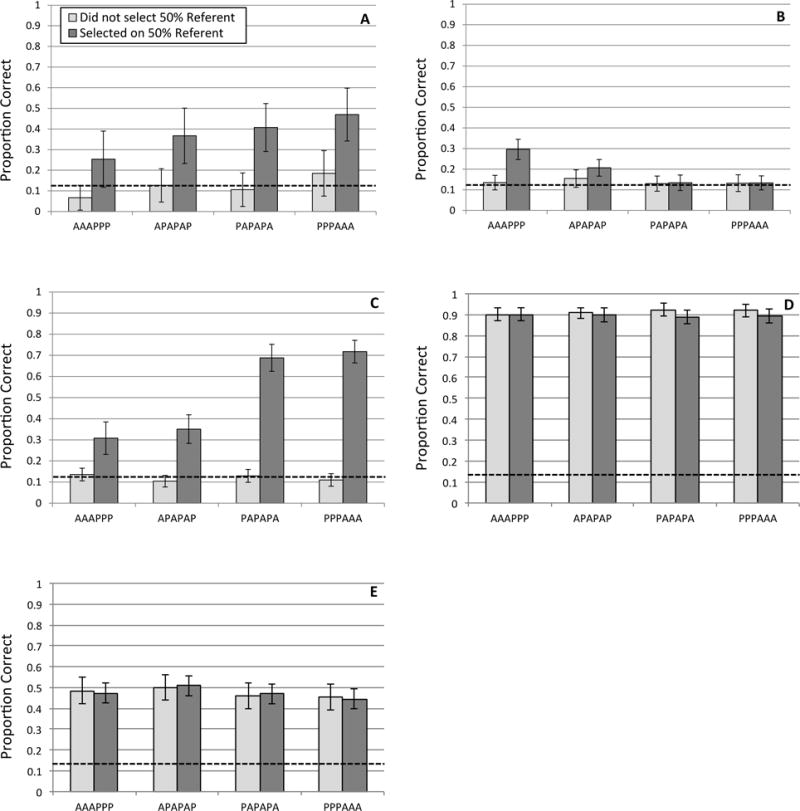
(A) Performance of human subjects; (B) Propose/Verify; (C) Pursuit; (D) Modified Fazly et al. (2010) model with guesses made via weighted sampling; (E) Original Fazly et al. model.

Table 8.

Koehne et al. (2013), overall proportion of guesses of the fifty percent referent (FPR) during testing by (1) whether the FPR was guessed at least once during training, and (2) whether the FPR was present on the first instance. Significance determined by pairwise comparison of predictors under a binomial mixed effects regression model.

	FPR not guessed, A<P	FPR not guessed, P<A	FPR guessed, A<P	FPR guessed, P<A	significant differences	greater than chance?
Propose/Verify	0.14 (95% CI = 0.113–0.165)	0.12 (95% CI = 0.100–0.147)	0.26 (95% CI = 0.235–0.295)	0.13 (95% CI = 0.108–0.151)	3rd / 1st 3rd / 2nd 3rd / 4th	no / no / yes / no
Pursuit	0.12 (95% CI = 0.100–0.134)	0.12 (95% CI = 0.101–0.140)	0.34 (95% CI = 0.294–0.387)	0.71 (95% CI = 0.670–0.745)	3rd / 1st 3rd / 2nd 3rd / 4th 1st / 4th 2nd / 4th	no / no / yes / yes
Human subjects	0.09 (95% CI = 0.029–0.159)	0.14 (95% CI = 0.046–0.225)	0.41 (95% CI = 0.233–0.584)	0.47 (95% CI = 0.343–0.606)	3rd / 1st 3rd / 2nd 1st / 4th 2nd / 4th	no / no / yes / yes

5. General discussion

5.1. Learning by Pursuit: Summary and evaluation

In this paper, we proposed the Pursuit model of word learning, which combines insights from general considerations of probabilistic learning as well as experimental demonstrations of the word-learning process. Our model pursues the highest-valued word meaning at the expense of other meaning candidates. By contrast, fully global cross-situational models do not favor any one particular meaning, but rather tabulate statistics across all learning instances to look for consistent co-occurrences.

Our main results are twofold. On the one hand, the Pursuit model provides a mechanistic account of human learning behavior as revealed in a series of word-learning experiments (Trueswell et al., 2013; Medina et al., 2011) and improves upon the PbV model, as shown in the behavioral study of Koehne et al. (2013) and the simulation results based on that study. By contrast, the global learning models we tested (Fazly et al., 2010, and a more apples-to-apples modified version of that model) do not capture the experimental results. Moreover, the Pursuit model also accounts for the results from Yu and Smith (2007), the paradigm study for cross-situational learning of word meanings, and in fact provides a closer match with subject responses than the global models tested here. On the other hand, we have seen simulation results on two distinct types of child-directed corpus that Pursuit is competitive against cross-situational models. We have argued that the apparent limitation of Pursuit is in fact the key ingredient for its success in realistic word-learning situations: a local model that keeps track of few options is better equipped to capitalize on the rare but highly informative learning instances, which are diluted under models that keep track of all options.

Future work will explore the predictions of the Pursuit model in an experimental setting, which may further refine the details of the model. Additionally, more effort should be devoted to expand the empirical ground of model testing, by both increasing the amount of data as well as using more realistic learning situations: our use of the Cartmill et al. (2013) corpus takes an initial step in this direction, moving beyond the limitations of the Rollins Corpus used in previous computational studies of word learning. That investigation suggests that perhaps a Pursuit learner has an advantage over a global cross-situational learner in cases where there are frequently co-occurring competing referents. For example, a Pursuit learner might decide early on that “dog” means ‘dog’, and then ignore the fact that the family cat is also present for a large number of utterances of “dog”. A global learner, by contrast, will dilute her probability space with ‘cat’. More sophisticated global learning algorithms (like our modified global model) seem to dampen this effect down, but not get rid of it entirely. This would explain why Pursuit outperforms all other models on the Rollins corpus, where meaning-meaning co-occurrence is very high, but not on other corpora for which meaning tokens are more evenly distributed. Finally, a virtue of computational models lies in their explicitness; as such, both local and global models may be evaluated as general frameworks in which other cues for word meaning can be incorporated.

5.2. Results unaccounted for by Pursuit

It is important to note that some recent findings are not so straightforwardly accounted for by Pursuit (Dautriche & Chemla, 2014; Yurovsky & Frank, 2015). Most notably, Yurovsky and Frank find that at least under some specific situations, adult word learners can extract and retain more than one referential alternative from a given occurrence of a word. In a paradigm similar to Trueswell et al. (2013), each experimental trial consisted of subjects hearing a nonsense word and selecting among several visually depicted referents. In the Yurovsky and Frank study, the scene that accompanied the second occurrence of a nonsense word always contained objects that were not present during the word’s first occurrence plus exactly one object from the first occurrence; this object was either the one selected by the subject or an object that had not been selected. Like Trueswell et al. (2013), they find an effect of prior selection, with participants being much better at selecting the prior object if they had selected it on the first word occurrence. However, unlike Trueswell et al. and inconsistent with the expectations of Pursuit and PbV, participants were found to be reliably above chance at selecting the previously unselected referent, suggesting they retained more than one referential alternative from the word’s first occurrence.

Yurovsky and Frank suggest that their results differ from Trueswell et al. (2013) because Trueswell et al. used a greater trial interval between word occurrences (11 intervening trials) than they did in their studies (7 or fewer trials). And indeed, manipulations of interval length and referent set size by Yurovsky and Frank suggest that as interval and referent set size increase, learners behave in the limit like a purely local learner, in line with Pursuit and PbV. For greater distances between words with highly ambiguous contexts, learners are at chance when considering a previously unselected referent. The results for smaller set sizes are however important and warrant further investigation; for instance, it is notable that the conditions used by Yurovsky and Frank are optimal for recalling the prior context, in that the co-occurring object of interest only occurred once before in one context; yet typically in studies of word learning, an object will also appear in other contexts in the study, as a low probability co-occurring object with other words and other objects (as would be the case in real-life). And indeed, memory research suggests that memory for the context of an item becomes much poorer the more other contexts in which that item also occurred (c.f., Anderson et al., 1974). (We thank Judith Koehne for this observation.) In general, we point out that the Pursuit model is meant to be a model of an idealized core learning mechanism: we should expect that, under certain favorable conditions (like when word instances are close together), a Pursuit learner will be able to retain some additional contextual information in virtue of being able to remember recent experiences. The important prediction of our model is that contextual information that is not actively used for hypothesizing about meanings will decay rather quickly, as it is not represented within the learning mechanism itself. As a whole though, the findings of Yurovsky and Frank suggest that the word-learning strategies of adults are more complex than the global and local models we have presented here.

Notably though, young children behave like local rather than global word learners, as observed in other work by Trueswell and colleagues (Woodard, Gleitman & Trueswell, in press) and by Yurovsky and Frank (Yurovsky and Frank, in prep.). For instance, Woodard et al. find that 2- and 3-year olds show no sign of recalling an unselected referential alternative in a child-friendly version of this experimental paradigm, even when the referent set size was small (2 referents) and the interval was short (2 intervening trials). Yurovsky and Frank (as reported in Yurovsky and Frank, 2015) similarly find that children who are 4 years old and younger do not consider previously unselected referents. Taken together, these findings suggest that children’s memory and attentional limitations drive them toward single referent consideration during word learning. Our simulation work above suggests that in doing so, there may be little cost for accurate word learning, and may in many circumstances be beneficial.

There are other challenging cases that involve learning under conditions of close word instance proximity. Kachergis, Yu & Shiffrin (2012) provide evidence that adult subjects retain multiple hypotheses during word learning, but the effect they report only arises when a particular meaning occurs six or nine times in a row along with the intended target meaning. Along the same lines, the massed learning trials of Smith, Smith & Blythe (2011)—those where one instance of a word is immediately followed by another instance of the same word—show better performance than the non-massed trials. In general, there seems to be support for the retention of multiple hypothesis when learning instances are massed, just as there is support for such retention when word instances occur closer together more generally. As discussed above, this is likely due to the recruitment of additional short-term memory resources that are not available to the learner in most realistic learning contexts (where instances of a given word can be quite far apart). We take non-massed learning to be more indicative of the word-learning task in the real world, and thus take the Pursuit model to be a good candidate for modeling a “core” learning mechanism. Further exploration of how such a mechanism can be made to recruit additional memory resources in certain situations must be left to future work.

5.3. Do the models model human children?

Before ending this paper, we feel it necessary to consider how the formal models considered here might link to the questions of how young children acquire the lexicons of their native tongue. Though we cannot attack such questions in all their full (and partly unknown) glory, we here point to some of our own underlying assumptions about what would properly constitute evidence linking the modeling findings to the population whose behavior they purport to describe.

We start by reiterating that our proposal here, in the form of the Pursuit model, is only a very small part of the very complex character and process of word learning. The linguistic, cognitive and perceptual constraints on words and their acquisition, amply documented in previous research, are in a sense “built in” in our model as well as in other computational models compared here. Nevertheless we have assumed throughout that word-to-world pairing constitutes a proper part of the word-learning task, and that it is in play early, serving as a scaffold for further learning steps (Gleitman et al., 2005). And for this constrained mapping problem, simulation results suggest advantages of the Pursuit model over a range of alternative solutions, both in terms of its congruence with observed behavior and its relative effectiveness as a learning algorithm.

Second, we would like to address the tension that naturally arises when one conducts computational modeling research, which sits at the intersection of linguistics, psychology, and computer science. For instance, in computational linguistics, progress and success are in general measured by performance results (e.g., F-score). Models are not bound by psychological concerns and computational complexity is of secondary concern as long as it does not affect practicality. In light of the discussion above, we may ask the question: is it reasonable at all to say that the more accurately (the faster and least errorfully) the model learns from some approximation of realistic data (e.g., the corpora as used herein), the more that model resembles The Human Child? This is unclear. Children’s early vocabulary initially grows quite sluggishly (e.g., approximately 1 word at 8 months to just 20–25 words six months later, Bates, Dale, & Thal, 1995) although recent evidence suggests that, at least for discrimination in two-alternative-choice tasks, even very young children may grasp some aspects of the meanings of everyday words (Bergelson & Swingley, 2012). Thus, it may be a virtue – in terms of realism – for a proposed formal model that it be quite poor at acquiring the Gold Standard Lexicon. Maybe the real infant is a simpler machine than even the Pursuit model suggests and so learns slowly and errorfully until overtaken by sophisticated multiple-cue machinery that can redress its inherent inadequacies in terms of character and rate of learnable items. In this sense, global cross-situational learning models are problematic when tested on the experimental stimuli from Smith and Yu (2007): they outperform the human subjects considerably and hence better numerical performance is a defect rather than a virtue. Thus we acknowledge that it is simplistic to identify the best formal model with its presumed target, the human infant performing word-to-world pairing over a restricted semantic space.

Nevertheless, researchers learn a great deal by going back and forth between idealized models of learning and experimental exploration of the behaviors observed in the child (and adult) language learner. Computational models of the sort explored here provide a way of specifying the range of logical solutions to a problem, in ways typically not possible from experimentation alone. Moreover, a computational model that is motivated by an existing body of behavioral results can produce imminently testable predictions upon the manipulation of the learning data it receives. Experimentation, in turn, allows researchers to understand which of these possible logical solutions is practical ‘on the ground’ in the everyday life of a learner, who is faced with the non-ideal situation of exploring the real, sometimes confusing and unhelpful, world. Our work suggests that those logical solutions that simplify the input and simplify the learning procedure may solve the problem of early word learning better than those that maintain the complexity of the world within the learning model itself.