Inter-site and inter-scanner diffusion MRI data harmonization

Abstract

We propose a novel method to harmonize diffusion MRI data acquired from multiple sites and scanners, which is imperative for joint analysis of the data to significantly increase sample size and statistical power of neuroimaging studies. Our method incorporates the following main novelties: i) we take into account the scanner-dependent spatial variability of the diffusion signal in different parts of the brain; ii) our method is independent of compartmental modeling of diffusion (e.g., tensor, and intra/extra cellular compartments) and the acquired signal itself is corrected for scanner related differences; and iii) inter-subject variability as measured by the coefficient of variation is maintained at each site. We represent the signal in a basis of spherical harmonics and compute several rotation invariant spherical harmonic features to estimate a region and tissue specific linear mapping between the signal from different sites (and scanners). We validate our method on diffusion data acquired from seven different sites (including two GE, three Philips, and two Siemens scanners) on a group of age-matched healthy subjects. Since the extracted rotation invariant spherical harmonic features depend on the accuracy of the brain parcellation provided by Freesurfer, we propose a feature based refinement of the original parcellation such that it better characterizes the anatomy and provides robust linear mappings to harmonize the dMRI data. We demonstrate the efficacy of our method by statistically comparing diffusion measures such as fractional anisotropy, mean diffusivity and generalized fractional anisotropy across multiple sites before and after data harmonization. We also show results using tract-based spatial statistics before and after harmonization for independent validation of the proposed methodology. Our experimental results demonstrate that, for nearly identical acquisition protocol across sites, scanner-specific differences can be accurately removed using the proposed method.

Introduction

Multi-site diffusion imaging studies are increasingly being used to study brain disorders, such as Alzheimer’s disease, Huntington’s disease, and schizophrenia (Mueller et al., 2005; Magnotta et al., 2012). However, inter-site and inter-scanner variability in the acquired data sets poses a potential problem for joint analysis of diffusion MRI (dMRI) data (Vollmar et al., 2010; Matsui, 2014). This inter-site (or inter-scanner) variability in the measurements can come from several sources including number of head coils used (16 or 32 channel head coil), sensitivity of the coils, the imaging gradient non-linearity, the magnetic field homogeneity, the differences in the algorithms used to reconstruct the data, as well as changes made during software upgrades and other scanner related factors (Zhu et al., 2011; Jovicich et al., 2014; Teipel et al., 2011). These can cause non-linear changes in the images acquired as well as the estimated diffusion measures such as fractional anisotropy (FA) and mean diffusivity (MD). Thus, aggregating data sets from different sites are challenging due to the inherent differences in the acquired images from different scanners (Veenith et al., 2013; Giannelli et al., 2014). Although the inter-site variability of neuroanatomical measurements can be minimized by acquiring images using similar type of scanners (same vendor and version) with similar pulse sequence parameters and same field strength (Cannon et al., in press; Lemkaddem et al., 2012; Shokouhi et al., 2011), many recent studies as well as our own, have shown that there still exist large differences between diffusion measurements from different sites (Foxa et al., 2012; Nyholm et al., 2013; Han et al., 2006). Specifically, the inter-site variability in FA and MD is not uniform over the entire brain, but is tissue specific as well as region specific. Inter-site variability in FA can be up to 5% in major white matter tracts and between 10 and 15% in gray matter areas (Vollmar et al., 2010). On the other hand, FA differences in diseases such as schizophrenia are often of the order of 5%. Thus, harmonizing data across sites is imperative for joint analysis of the data.

Broadly, there are two approaches used to combine data sets from multiple sites. One approach is to perform the analysis at each site separately, followed by a meta-analysis as in (Salimi-Khorshidi et al., 2009). In this case, a z-score is computed for each subject (for a given diffusion measure) for the two groups under investigation for each of the sites separately; a z-score is a statistical measurement of a score’s (say, FA) relationship to the mean in a group of scores; the z-score of a raw score x is z=(x−μ)/σ, where μ and σ are the mean and the standard deviation of the population, respectively. A z-score of 0 means the score is the same as the mean. A z-score can also be positive or negative, indicating whether it is above or below the mean and by how many standard deviations. By combining the z-scores from all the sites, we can determine statistical differences. However, this method has several limitations. For example, the subject population at each site may not be sufficient to capture the variance of the entire population, a critical requirement to ensure proper computation of the z-score (which depends on the variance and not just the mean). Note that, the z-score is a non-linear function of the variance and small changes in variance can result in large changes in the estimated z-score. For example, the inter-subject variance of a diffusion measure (say, FA) at site #1 may be very different than the variance at site #2. This can result in vastly different estimates of the z-score, leading to erroneous results. Another limitation is that such an analysis has to be repeated for each measure of interest and each region or fiber tract of interest.

As one of the well-known software based on meta and mega analysis, we can point to ENIGMA-DTI (Jahanshad and et al., 2013; Kochunov and et al., 2014). This method is very similar to the methods using meta-analysis. ENIGMA-DTI allows using site-specific meta-analysis to compute z-scores to obtain statistical group differences. Alternatively, the software also allows to regress-out (using statistical covariates) site-specific variables from the data to compute z-scores which are then analyzed in an integrated manner (mega-analysis). Thus, the ENIGMA-DTI methodology involves several steps, where analysis is done several steps downstream from the original data, i.e.: dMRI signal ↦ preprocessing ↦ model specific analysis (e.g. single tensor) ↦ tensor derived measures (e.g. FA) ↦ regression to remove site differences ↦ z-score analysis. While this is a perfectly acceptable method to analyze multi-site DTI data, it does not harmonize the data, but rather transforms the derived variables of interest (FA) using a series of steps into a common coordinate system (z-scores) to finally analyze the data. While this methodology has been shown to be quite successful (Jahanshad and et al., 2013; Kochunov and et al., 2014), it does have a few limitations: First, the pre-processing steps could be very different (eddy current correction, motion correction, tensor estimation, interpolation kernel used, etc.) for each site (if each site computes FA independently), which could potentially bias the subsequent analysis. Second, such analysis has to be done separately for each variable (such as FA, MD, radial diffusivity, kurtosis, etc.). Third, since the acquisition parameters could be different, the accuracy of estimating the correct parameters for the dMRI model used (e.g., using multi-tensor or multi-compartment models) could affect the final result.

Most importantly, as it relates to the current work, the ENIGMA-DTI method is a nice way to compare two groups of populations. However, it cannot be used to purely harmonize the data as is the focus of our current work. As explained in Our contributions section, our proposed work directly harmonizes the dMRI signal, allowing any type of subsequent analysis to be done in a consistent manner with any type of model used. Consequently, all the variability and bias due to the preprocessing and post-processing algorithms used is removed (since the same algorithms are used for processing all of the data sets).

Statistical covariate is another standard practice to account for signal changes that are scanner-specific (Forsyth and Cannon, 2014; Venkatraman et al., 2015). The first approach (meta-analysis) does not allow for a “true” joint analysis of the data, while the second method requires the use of a separate statistical covariate for each diffusion measure analyzed. Further, the latter method is inadequate to analyze results from tractography where tracts travel between distant regions. For example, in the cortico-spinal tract, scanner related differences in the brain stem might be quite different from those in the cortical motor region. Thus, using a single statistical covariate for the entire tract may produce false positive or false negative results. Consequently, region-specific scanner differences should be taken into account for such type of analyses. Another alternative is to add a statistical covariate at each voxel in a voxel based analysis method. However, such methods are susceptible to registration errors and a linear covariate is typically estimated for each voxel in the brain, requiring myriad of additional parameters to be estimated, which could potentially reduce sensitivity of the diffusion measures. Additionally, it is not clear if a linear covariate is adequate for modeling scanner specific differences, which potentially could have a non-linear component.

Our contributions

In this work, we propose a novel scheme to harmonize diffusion MRI data from multiple scanners, taking into account the brain region-specific and tissue specific (e.g., white, gray, CSF) differences in the acquired signal from different scanners. Our method harmonizes the acquired signal at each site to a reference site using several rotation invariant spherical harmonic (RISH) features. A region specific linear mapping is proposed between the rotation invariant features to remove scanner specific differences between a group of healthy age-matched subjects at each site. The method directly harmonizes the raw signal obtained from the scanner, allowing for any type of downstream analysis. Thus, once the data is harmonized, any derived quantity from the diffusion data is also automatically harmonized and can be pooled from different sites for further analysis. Thus, our approach is substantially different than existing methods which correct for scanner-related differences directly on the diffusion measures of interest. Further, spherical harmonics form a non-parametric basis without any particular assumption about the model of diffusion (e.g., single tensor, multi-tensor, or multi-compartment models); i.e., there is no a priori assumption made with respect to the diffusion process in terms of the compartments or the number of fiber bundles. To the best of our knowledge, this is a first work that has explicitly addressed the issue of dMRI data harmonization without the use of statistical covariates.

The current study is an extension of our recently published work (Mirzaalian et al., 2015). Compared to Mirzaalian et al. (2015), in this study: i) we perform a more extensive validation of our method over 7 different sites rather than 4 sites, using more subjects in each group; ii) we harmonize gray-matter and sub-cortical structures in addition to the white-matter areas; iii) we propose a novel way to correct the Freesurfer parcellated label maps based on the RISH features, which are often inaccurate when mapped to the subject specific dMRI space; iv) to remove local scanner-specific differences in large Freesurfer regions, we propose a way to sub-divide them into smaller regions, for better tissue characterization and robustness in removing scanner differences; and v) using synthetic experiments, we show that the signal differences between the disease and control population at the target site are preserved after harmonization into the reference site.

Method

Fig. 1 shows an outline of the proposed dMRI data harmonization method, where we describe the entire methodology succinctly with details about each step in the subsequent sections. Our goal is to map the dMRI data from a target site to an arbitrarily chosen reference site. We start by computing a set of RISH features from the estimated SH coefficients (Diffusion MRI and RISH features section). Then, using the RISH features, we refine the Freesufer label maps (Optimizing Freesurfer label map and Refining large regions into smaller regions sections), followed by computing a region-specific linear mapping between the RISH features of the two sites (Mapping RISH features between sites section), i.e., a separate mapping is computed for each Freesurfer defined region. Next, a secondary mapping is computed that appropriately updates each of the SH coefficients at each voxel in the Freesurfer parcellated region-of-interest (ROI) (Mapping RISH features between sites section). From the mapped SH coefficients, the mapped diffusion signal is computed at a canonical set of gradient directions for each subject in the target site (Mapping RISH features between sites section).

Fig. 1.

Outline of the proposed method for inter-site dMRI data harmonization and the section numbers where we discuss the related sub-problems. In our pipeline, the reference and the target sites are shown in green and red, respectively. Given the input images represented by their corresponding SH coefficients, we start by extracting a set of RISH features followed by updating the Freesurfer label map and finding a proper region-wise mapping for the RISH features as well as a voxel-wise mapping for the SH coefficients. The mapped coefficients are then used to estimate the harmonized dMRI signal of the target site making it statistically similar to the reference site.

Diffusion MRI and RISH features

Let S=[s₁ … s_G]^T represent the dMRI signal along G unique gradient directions at a single b-value. In the spherical harmonic (SH) basis, the signal S can be written as (Descoteaux et al., 2007):

$$S\approx \sum _i\sum _{j=1}^{i+1}{C}_{ij}{Y}_{ij},$$ (1)

where Y_ij is a SH basis function of order i and phase j and C_ij are the corresponding SH coefficients. Since the signal S is symmetric, the SH basis used in this study has only real part.

It is well-known that the “energy” or l₂ norm of the SH coefficients for each order forms a set of rotation invariant (RISH) features (Kazhdan et al., 2003):

$${\Vert C_i\Vert }^2=\sum _{j=1}^{2i+1}{(C_{ij})}^2,$$ (2)

One can think of the RISH features ||C_i||² as the total energy in a particular frequency band (order) in the SH space. We compute region-wise RISH features denoted by ${\Vert {\overline{C}}_i^n\Vert }^2$ for each subject n as the average of the voxel-wise RISH features over all the voxels of each region of the brain, where brain regions are obtained using Freesurfer (Fischl et al., 2001). Given the RISH features for N_t subjects for the tth site, we approximate the expected value of the region-wise RISH features as the sample mean:

$${\mathbb{E}}_t\left(\left[\Vert {\overline{C}}_i{\Vert }^2\right]\right)\approx \sum _{n=1}^{N_t}[\Vert {\overline{C}}_i^n{\Vert }^2]/N_t,$$ (3)

where n is an index for the subject number, i.e. ${\Vert {\overline{C}}_i^n\Vert }^2$ represents averaged RISH features computed at order i for the nth subject.

In this work, we computed the RISH features for i∈{0,2,4,6,8} orders¹ and ignored the higher order terms as they are the high frequency terms primarily capturing noise in the data. However, if required, the proposed methodology is quite general and can be extended to SH of any order. Note that to include SHs up to the 8th order, we need to have at least 45 measurements.

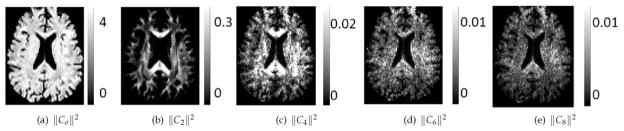
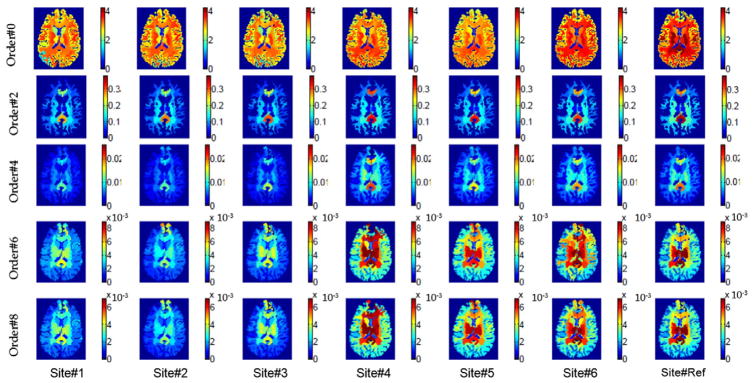
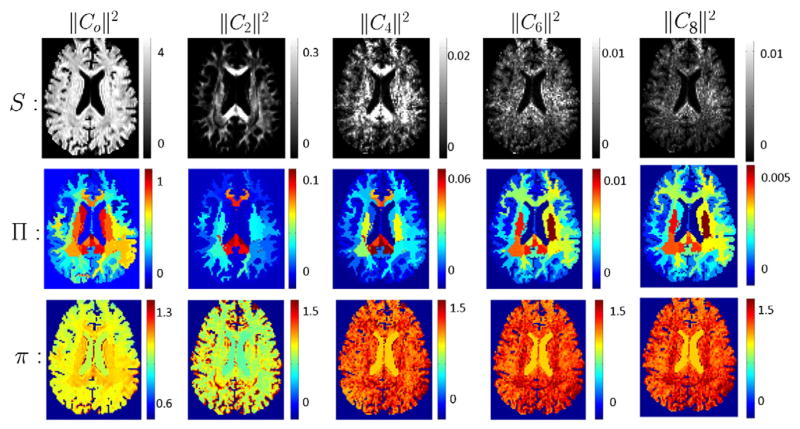
Figs. 2 and 3 show maps of the computed voxel-wise and region-wise RISH features, respectively. From Fig. 2 it is clear that a large portion of the signal energy is contained in the lower-order RISH features. In Fig. 3, it can be seen that the region-wise RISH features vary significantly between sites as well as for different regions, showing that a regionally specific mapping is required to ensure proper harmonization of the diffusion data.

Fig. 2.

Visualization of the voxel-wise RISH features for spherical harmonics of different orders.

Fig. 3.

Freesurfer region based RISH features for different SH orders and sites.

As we will see in Mapping RISH features between sites section, the extracted means (𝔼) are used to compute a set of mappings between the RISH features of the target and reference sites. These maps depend on the brain label map provided by any brain parcellation algorithm, which may not be accurate at the boundary between gray-white or white-CSF areas. In general, the label maps are transported from the T₁-space in which the parcellation is done to dMRI space using a non-rigid registration algorithm. However, due to geometric distortions common in dMRI acquisitions as well low contrast in the b = 0 images, registration errors can occur while obtaining an appropriate map in the dMRI space. One of the most popular method to obtain brain parcellation is Freesurfer, which we use in this work. However, some of the Freesurfer ROI’s obtained using the standard Desikan atlas are too large, consisting of several different types of tissue, which makes them heterogeneous in composition. Additionally, such large regions (e.g., centrum-semiovale white matter) are non-linearly affected by scanner specific inhomogeneities, which cannot be modeled using a single linear mapping. To ensure proper mapping and removal of tissue-specific differences, we consequently refine the brain label maps and sub-segment the large ROI’s into smaller regions. This procedure results in the computation of a better and more accurate harmonization of the data. In the next section, we explain our optimization approach, which aims to maximize the homogeneity of brain features within each region.

Updating Freesurfer label map

At this step in our pipeline, we first sub-segment large regions into smaller regions (Refining large regions into smaller regions section). Then, based on a set of RISH features computed at each voxel, we apply a simple region-based clustering algorithm to sub-divide large regions of the Freesurfer label map (Optimizing Freesurfer label map section).

Refining large regions into smaller regions

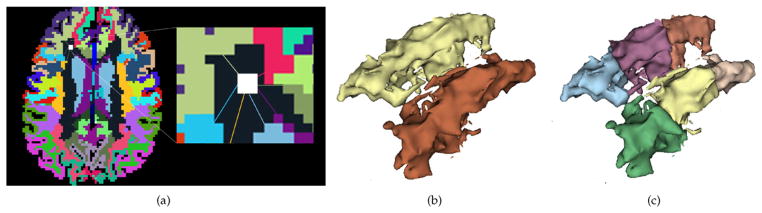
To break down a large region, e.g. centrum-semiovale, into smaller regions, we first start by finding the regions that form neighbors of the given region of interest (ROI). Then, each voxel within the ROI is assigned a feature vector, whose entries are the minimum Euclidean distance of the current voxel to the neighboring regions of the ROI. In fact, these features encode spatial location of each voxel with respect to the nearby regions. In Fig. 4, a voxel within centrum-semiovale region (our ROI) is shown in white, which is connected to the nearby regions of the centrum-semiovale by a number of edges.

Fig. 4.

Representation of the distance based features used to segment large regions into smaller regions. (a) A voxel within centrum-semiovale (large dark region), is connected to the nearby regions by a number of edges. The entries of the feature vector assigned to this voxel represent the minimum distance of the edges connecting the white voxel to the nearby regions. (b) 3D surface representation of the left and right centrum-semiovale regions, (c) segmented smaller regions by performing k-mean clustering (k = 3).

After computing these features for all the voxels within the ROI, we perform k-means clustering over the voxels with the assigned features to segment the voxels into k different groups. Note that we expect to extract continuous blocks of regions since the features used are based on physical distances. An example output of the k-mean clustering applied over the centrum-semiovale region is shown in Fig. 4(c). The number of clusters k was chosen for each ROI separately in a heuristic fashion depending on the size of the original ROI. For example, k worked well for the centrum-semiovale region, where the size of the subdivided regions is smaller than 400 voxels.

Optimizing Freesurfer label map

Registering the Freesurfer label map into the dMRI subject space can lead to mislabeling due to registration errors. This is specifically the case due to the lower resolution and geometric distortions of the dMRI data set. As such, several tissue types are labeled incorrectly leading to large variations in the estimated RISH features for each ROI. Thus, it is imperative to correct for these errors before proceeding with the harmonization step.

Given the dMRI data and its corresponding Freesurfer label map L, we start by updating the labels of the voxels on the boundary of each region. To do so, at each voxel on the boundary of our ROI, we extract a set of RISH feature vector as:

$$\varphi (v)=\left[{\Vert C_o(v)\Vert }^2,{\Vert C_2(v)\Vert }^2,\dots ,{\Vert C_8(v)\Vert }^2\right].$$ (4)

Using the current label map L, we compute the average RISH features of all the nearby regions of the voxel v belonging to the boundary of the ROI. Let {R₁ … R_K} and {ϕ̄(R₁) … ϕ̄(R_K)} represent the nearby regions of voxel v and their corresponding region-wise RISH features, respectively. Then, we relabel v to the region whose feature vector is the closest to ϕ(v), i.e.:

$$L(v)=\underset{R_k}{argmin}\Vert \varphi (v)-\overline{\varphi }(R_k)\Vert ,R_k\in \{R_1\dots R_K\}.$$ (5)

This procedure is repeated until the variance of the parameters at the current ROI does not change much compared to the previous iteration.

As shown in the Results section, this refining of the label map leads to better tissue characterization and lower variance in the RISH features for each ROI. Given the refined label map, we compute the expected value 𝔼 of the RISH features per region of the brain using Eq. (3). Then, the next step in our pipeline is mapping these RISH features between the target and reference sites, which is explained in the following section.

Mapping RISH features between sites

Given two groups of subjects who are matched for age, gender, handedness and socio-economic status, we expect that at a group level, they should have similar diffusion profiles and hence none of the RISH features should be statistically different between the two groups, barring differences due to scanner. In other words, the diffusion measures such as FA, between the two groups of matched healthy subjects are statistically different only due to scanner related differences. Thus, our aim is to find a proper mapping Π(·) between the RISH features such that all scanner related group differences between two sites are removed, i.e.,

$${\mathbb{E}}_t\left({\prod }_i\left({\Vert {\overline{C}}_i\Vert }^2\right)\right)={\mathbb{E}}_r\left({\Vert {\overline{C}}_i\Vert }^2\right),i=\{0,2,4,6,8\},$$ (6)

where r is the reference site and t is the target site. Any difference in the sample mean for the two sites (or scanners) t and r can be computed as the difference Δ𝔼 = 𝔼_r−𝔼_t. By linearity of the expectation operator, the mapping for each subject n and RISH feature i is given by:

$$\begin{array}{l}{\prod }_i\left({\Vert {\overline{C}}_i\Vert }^2\right)={\Vert {\overline{C}}_i\Vert }^2+{\mathbb{E}}_r\left({\Vert {\overline{C}}_i\Vert }^2\right)-{\mathbb{E}}_t\left({\Vert {\overline{C}}_i\Vert }^2\right)\\ ={\Vert {\overline{C}}_i\Vert }^2+\mathrm{\Delta }\mathbb{E}.\end{array}$$ (7)

Note that, this mapping for feature i, Π_i(·), only gives the amount of shift required to remove any scanner specific group differences for a given ROI. Thus, this mapping is only at the region level and a separate mapping is required that will change the individual SH coefficient at each voxel such that Eq. (7) is satisfied. For a subject n in a given ROI (to keep the notation simple, we disregard the indexing for each subject), we have the following map for each voxel in that ROI:

$$\begin{array}{l}{\prod }_i\left({\Vert C_i(v)\Vert }^2\right)={\Vert C_i(v)\Vert }^2+\mathrm{\Delta }\mathbb{E}\\ ={\sum _{j=1}^{2i+1}[{\pi }_i(C_{ij}(v))]}^2.\end{array}$$ (8)

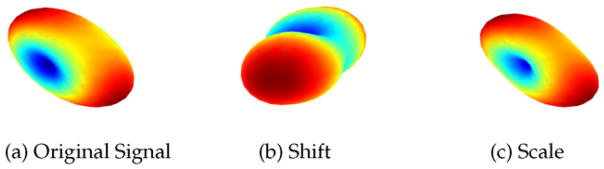
Thus, our aim is to determine an appropriate mapping function π_i which satisfies equation Eq. (8), allowing to update each SH coefficient individually. We extend this mapping to each voxel in an ROI, by uniformly changing the SH coefficients at each voxel v. There are two possible ways to obtain a mapping π_i(·) for each SH coefficient C_ij. One possibility is to use π_i(C_ij)= C_ij + δ (for all j) such that Eq. (8) is satisfied. However, this would entail adding a positive or negative constant δ to all coefficients (i.e. shifting the coefficients), which could potentially lead to a change in sign for coefficients that are smaller than δ. The effect of such a “shifting” operation is shown in Fig. 5(b), where the sign of some of the coefficients was changed by adding a small constant δ. This leads to a change in orientation and shape of the signal, which is erroneous and undesirable.

Fig. 5.

Effect of using different mapping functions π — shift vs scale. (a) Original dMRI signal. (b) π used as a shift map, (c) Estimated signal with π as a scaling map Eq. (9).

A more appropriate mapping π_i(·) is to uniformly scale the SH coefficients belonging to a given SH order so that Eq. (8) is satisfied. Such a mapping is given by:

$${\pi }_i(C_{ij}(v))=\sqrt{\frac{{\prod }_i\left({\Vert C_i(v)\Vert }^2\right)}{{\Vert C_i(v)\Vert }^2}}{C}_{ij}(v).$$ (9)

Such scaling only changes the “size” and “shape” of the signal and not its orientation (or equivalently, the orientation of ODF), as seen in Fig. 5 and as shown via experiments in the Results section. Note that, shape changes are indeed desirable and required as this is what is different between the data acquired on the scanners. This is amply evident from the fact that FA (shape change in tensor) is statistically different between two matched groups (see Fig. 7) from different scanners. Thus, the proposed methodology changes the “shape” of the signal in such a way that scanner related changes are removed (see Fig. 7), but the orientation of the fiber bundle is kept intact. Consequently, this will necessarily change any measure derived from the diffusion signal. For example, if a single tensor model is used, then, FA, linear and planar diffusion measures will necessarily change so that group differences are removed, which is the goal and desirable feature of the algorithm. However, the proposed method does not lead to any change in orientation (as we show in the Experiments section).

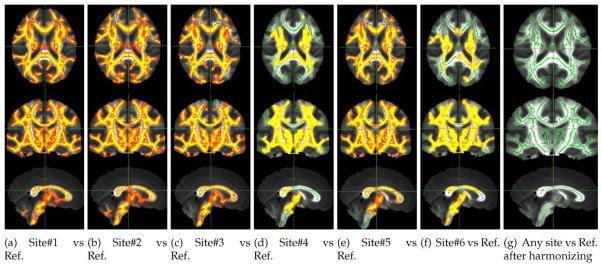
Fig. 7.

TBSS results for the target sites before (a–f) and after (g) applying our method. The yellow-red colormap displays p-values less than 0.05.

An important point to note is that the scaling above via the π_i function is at a voxel level, while the amount of shift introduced by Π_i function is at a region level, which is shown in Fig. 6.

Fig. 6.

First row (left to right): RISH features of order {0, 2, 4, 6, 8}. Second row: amount of shift for each region introduced by Π_i (𝔼_r −𝔼_k); different columns correspond to different order of spherical harmonics {0, 2, 4, 6, 8}. Third row: Scale computed at each voxel by π_i; different columns correspond to SH of order {0, 2, 4, 6, 8} respectively.

Thus, for a given site t, and subject n, the harmonized diffusion signal at a voxel v of a given ROI can be computed using:

$$\widehat{S}{(v)}^{t,n}=\sum _i\sum _j{\pi }_i^{t,n}(C_{ij}(v)){\mathit{\Upsilon }}_{ij}.$$ (10)

Using the above equation, the harmonized signal at each voxel is recomputed for each subject in the target site.

Experiments

We used our method on a data set acquired from 7 different sites and scanners, acquired as part of the InTRUsT mild TBI consortium; see Table 1 for details about each of the scanners as well as the number of subjects from each site. A nearly identical dMRI scan protocol was used at each site with the following acquisition parameters: spatial resolution of 2 × 2 ×2 mm³, maximum b-value of b = 900 s/mm² and TE/TE = 87/10000 ms. For the GE sites, the data was acquired with a 5/8 partial Fourier encoding, while the Siemens and Philips used 6/8 partial Fourier acquisition. Subjects from each site were age-matched to the group at the reference site. In all our experiments, we chose the Siemens site at the Brigham and Women’s hospital as the reference site since it had the most number of subjects.

Table 1.

Scanner details and subject numbers for each site (M — Male, F — Female, R — right handed, L — left handed).

Site#	Manufacturer	Field strength	Model	Software version	# of channels	# of subjects	# of directions	Age	Handedness	Gender
1	Philips	3 T	Achieva	2.6.3	8	20	64	35 ± 11	20R 0L	10F 10M
2	Philips	3 T	Achieva	2.6.3	8	20	64	35 ± 12	17R3L	14F 6M
3	Philips	3 T	Achieva	2.6.3	8	7	64	36 ± 12	7R0L	4F 3M
4	GE	3 T	MR750	20xM4	8	6	86	37 ± 10	6R0L	1F5M
5	GE	3 T	MR750	M4	8	16	86	37 ± 9	14R 2L	12F 4M
6	Siemens	3 T	Tim Trio (102 × 32)	vb17	12	24	87	35 ± 12	23R 1L	6F 18M
Ref.	Siemens	3 T	Tim Trio (102 × 18)	VB15	12	23	87	36 ± 11	20R 3L	13F 10M

We performed eddy current and motion correction prior to our harmonization procedure for each subject, by registering each individual diffusion weighted volume to the corresponding non-diffusion weighted volume using FSL FLIRT software (Jenkinson and Smith, 2001). Thus, most physiological noise was removed retrospectively, as is routinely done as a standard procedure in all dMRI data processing pipelines (Van Essena et al., 2012).

As mentioned in Mapping RISH features between sites section, we consider SH decomposition up to order 8 although the b-values of our dataset are rather low. It is known from several earlier works (Tuch, 2004; Tuch et al., 2002, 2003; Descoteaux et al., 2006) that multiple fiber crossings can be detected even at low b-values of 900 to 1000. Thus, the information content in the signal is more than just that of a single tensor (since SH of order 2 is essentially equivalent to a tensor). Further, our method does not depend on the b-value used. If not much energy is seen in higher order RISH features, those could be easily discarded (as we did by discarding RISH features higher than order 8).

Results

Statistical group differences before and after harmonization

Since the subjects were age-matched healthy controls across all the sites/scanners, at a statistical group level, we do not expect to see biological differences. Therefore, it is reasonable to hypothesize that the differences in the RISH features and standard diffusion measures are only due to scanner related inconsistencies.

To validate our hypothesis, we used a paired t-test to compute p-values of RISH features and standard diffusion measures (such as, FA, MD, and generalized fractional anisotropy (GFA)) between the reference site and all of the target sites. These tests were performed both before and after harmonizing the data using the proposed method. An appropriate mapping was computed for each of the ROIs, after correcting the Freesurfer regions for mislabeling, as well as after dividing the larger ROIs into smaller regions (as described earlier). Overall a total of 211 ROIs were used. For each ROI, we first determined if RISH features were statistically different between the reference site and the target sites (sites: #1, #2, #3, #4, #5, #6) and then used the algorithm described above to harmonize the signal if statistical differences were seen (p < 0.05; not corrected for multiple comparison).

Table 2 gives the p-values for each of the ROIs (nomenclature is —lFrontal is left-frontal and rFrontal is right-frontal lobe) before and after the harmonization of the data. Notice that MD was statistically different for almost all regions and sites as compared to the reference site, but these differences were completely removed. The p-value after mapping is almost 1 in this case following Eq. (9) and the fact that MD is directly proportional to the l₂ norm of the SH coefficients. All statistical group differences between FA and GFA were also removed for each of the sites after harmonization. We should note that, the group differences were removed for each of the 211 ROIs, but for brevity, we have only reported results in this table for a selected set of anatomical regions (by combining several ROIs) of the brain.

Table 2.

P-values before and after harmonization for MD, FA, GFA for different sites and ROIs.

	Site#1		Site#2		Site#3		Site#4		Site#5		Site#6
	Before	After	Before	After	Before	After	Before	After	Before	After	Before	After
MD
lFrontal	7.7e-02	1	9.9e-02	1	8.0e-03	1	2.9e-02	1	8.5e-05	1	1.7e-01	1
lParietal	2.6e-11	1	2.7e-10	1	8.4e-07	1	1.2e-03	1	1.1e-09	1	2.2e-02	1
lTemporal	6.8e-04	1	1.2e-01	1	2.6e-03	1	7.1e-04	1	7.8e-05	1	1.3e-02	1
lOccipital	2.6e-07	1	1.9e-09	1	7.2e-03	1	1.0e-01	1	6.5e-04	1	2.2e-01	1
lCentrumSemiovale	5.9e-16	1	4.2e-14	1	1.9e-09	1	9.2e-06	1	4.2e-13	1	6.0e-06	1
lCerebellum	2.3e-09	1	3.9e-15	1	2.6e-05	1	9.5e-05	1	2.2e-05	1	3.4e-03	1
rFrontal	1.8e-05	1	1.3e-03	1	5.8e-03	1	1.6e-02	1	3.9e-05	1	1.7e-01	1
rParietal	3.8e-10	1	2.9e-09	1	4.7e-06	1	6.1e-02	1	2.3e-06	1	2.1e-01	1
rTemporal	6.4e-04	1	8.5e-03	1	4.4e-02	1	3.4e-02	1	4.4e-05	1	8.9e-02	1
rOccipital	1.5e-03	1	3.2e-02	1	6.6e-02	1	2.6e-01	1	6.2e-01	1	6.4e-01	1
rCentrumSemiovale	5.6e-15	1	9.9e-14	1	1.3e-08	1	1.5e-05	1	9.4e-15	1	1.3e-07	1
rCerebellum	1.4e-04	1	5.7e-10	1	8.4e-04	1	4.9e-02	1	8.8e-01	1	2.1e-03	1
Corpus callosum	9.0e-14	1	1.3e-09	1	4.7e-07	1	3.8e-02	1	4.1e-09	1	1.7e-01	1
FA
lFrontal	2.9e-02	4.2e-01	5.0e-02	4.3e-01	1.1e-02	6.3e-01	5.8e-01	6.7e-01	7.8e-02	5.2e-01	2.3e-01	6.1e-01
lParietal	4.3e-10	2.5e-01	7.5e-10	2.1e-01	2.6e-05	4.7e-01	8.0e-02	6.8e-01	9.5e-06	2.3e-01	2.9e-02	5.4e-01
lTemporal	2.5e-05	3.5e-01	5.1e-05	3.7e-01	2.8e-02	5.8e-01	3.8e-01	7.4e-01	7.0e-02	4.6e-01	4.8e-01	6.1e-01
lOccipital	1.5e-02	2.9e-01	3.3e-02	3.7e-01	6.3e-02	6.1e-01	2.0e-01	7.1e-01	5.7e-01	2.8e-01	5.9e-01	5.7e-01
lCentrumSemiovale	1.1e-12	1.3e-01	8.9e-11	2.3e-01	1.0e-08	3.9e-01	2.9e-03	5.1e-01	1.6e-07	2.8e-01	7.1e-03	3.4e-01
lCerebellum	9.6e-06	9.5e-02	7.6e-07	6.3e-02	2.0e-07	7.8e-02	2.4e-01	4.2e-01	8.2e-01	4.1e-01	6.2e-01	2.3e-01
rFrontal	5.3e-04	3.9e-01	3.8e-03	5.0e-01	1.3e-02	5.8e-01	3.5e-01	6.5e-01	6.1e-02	4.8e-01	1.7e-01	6.5e-01
rParietal	1.6e-08	2.5e-01	6.4e-08	3.3e-01	3.3e-05	5.2e-01	2.4e-01	7.7e-01	2.7e-04	3.4e-01	2.5e-01	5.8e-01
rTemporal	2.5e-05	3.4e-01	3.3e-05	4.0e-01	9.5e-03	5.7e-01	5.2e-01	7.0e-01	1.3e-01	5.1e-01	4.2e-01	6.3e-01
rOccipital	3.1e-04	4.0e-01	1.1e-05	3.0e-01	1.5e-04	3.6e-01	5.8e-01	7.9e-01	3.9e-01	3.9e-01	9.2e-01	8.2e-01
rCentrumSemiovale	1.1e-11	1.0e-01	7.3e-10	1.1e-01	2.3e-07	4.0e-01	3.9e-02	5.8e-01	9.0e-07	2.4e-01	1.7e-02	2.9e-01
rCerebellum	1.8e-06	1.1e-01	3.4e-10	2.5e-01	4.2e-06	1.1e-01	1.7e-01	4.2e-01	4.5e-02	9.4e-01	8.8e-01	3.7e-01
Corpus callosum	7.4e-13	1.0e-01	4.5e-10	2.0e-01	4.2e-05	5.6e-01	2.5e-01	5.1e-01	8.5e-04	8.6e-01	1.3e-01	8.1e-01
GFA
lFrontal	5.8e-02	5.6e-01	5.0e-02	5.3e-01	1.0e-01	7.2e-01	9.1e-02	6.4e-01	2.1e-01	5.9e-01	4.0e-01	6.8e-01
lParietal	6.3e-03	3.9e-01	3.3e-03	3.7e-01	8.0e-02	5.1e-01	2.6e-01	6.1e-01	4.4e-01	2.2e-01	3.2e-01	4.3e-01
lTemporal	1.6e-02	3.5e-01	1.1e-01	3.8e-01	3.4e-01	5.8e-01	1.9e-01	7.8e-01	5.0e-01	5.4e-01	1.5e-01	6.7e-01
lOccipital	3.1e-01	5.4e-01	6.4e-01	4.2e-01	3.2e-01	7.4e-01	1.2e-01	7.4e-01	2.1e-01	4.5e-01	4.9e-01	6.7e-01
lCentrumSemiovale	1.2e-05	1.7e-01	7.9e-06	2.2e-01	2.1e-04	3.3e-01	2.8e-01	6.4e-01	6.3e-01	5.1e-01	2.7e-01	4.6e-01
lCerebellum	6.7e-03	1.9e-01	1.7e-03	1.3e-01	2.9e-06	1.9e-01	4.4e-01	6.3e-01	2.8e-02	5.6e-01	4.9e-02	4.8e-01
rFrontal	1.9e-03	5.5e-01	2.7e-04	6.2e-01	8.4e-02	6.4e-01	8.5e-02	6.7e-01	1.1e-01	5.7e-01	2.9e-01	7.6e-01
rParietal	1.1e-03	4.3e-01	6.8e-04	4.9e-01	8.0e-02	5.3e-01	4.2e-01	7.1e-01	2.1e-01	3.3e-01	3.7e-01	6.5e-01
rTemporal	8.1e-04	3.0e-01	1.1e-05	3.8e-01	3.3e-02	4.7e-01	1.6e-01	6.7e-01	9.3e-02	3.8e-01	2.1e-01	7.1e-01
rOccipital	2.7e-04	4.6e-01	9.2e-06	4.0e-01	8.4e-04	4.5e-01	5.7e-01	7.6e-01	3.5e-01	4.2e-01	8.2e-01	8.6e-01
rCentrumSemiovale	5.2e-06	1.7e-01	3.6e-05	1.6e-01	6.6e-04	3.6e-01	1.1e-01	7.1e-01	5.2e-02	4.5e-01	3.1e-02	4.9e-01
rCerebellum	3.2e-07	1.6e-01	7.4e-09	4.6e-02	1.3e-05	2.2e-01	6.3e-01	5.7e-01	1.4e-01	8.0e-01	1.8e-02	6.3e-01
Corpus callosum	2.7e-05	8.1e-01	5.8e-04	8.2e-01	1.8e-01	6.6e-01	2.0e-01	2.5e-01	5.4e-01	5.3e-01	4.3e-01	7.0e-01

To test the efficiency of our method, we created two distinct data sets, one for training and one for test. Although our dataset in this study is not large enough to run such leave-many-out experiments for all the sites, we set up an experiment using the data from Site#1 and the reference site (where we could afford to remove some subjects for testing purposes). We used 70% of the subjects in the reference and the target sites (Site#1) to learn the parameters and computed the p-values before and after harmonization for rest of the 30% of the subjects, which were excluded from the training stage. Note that, in this experiment, the images in the training/testing groups of the two sites were age-matched. Computed p-values are reported in Table 3, which are very similar to results shown in Table 2. Thus, the proposed method could be used in a true data harmonization scenario, at least when the acquisition protocol is the same across sites.

Table 3.

P-values before and after harmonization for MD, FA, GFA for different sites and ROIs using test data excluded from training.

	MD		FA		GFA
	Before	After	Before	After	Before	After
lFrontal	8.3e-03	0.84	3.4e-05	0.35	3.4e-07	0.20
lParietal	1.2e-06	0.77	6.4e-07	0.22	3.6e-05	0.12
lTemporal	9.3e-08	0.97	1.8e-06	0.53	4.3e-04	0.48
lOccipital	2.4e-03	0.67	6.3e-05	0.20	4.9e-05	0.31
lCentrumSemiovale	1.0e-10	0.48	7.5e-09	0.73	6.6e-03	0.30
lCerebellum	1.0e-04	0.45	5.5e-08	0.69	3.7e-06	0.96
rFrontal	3.3e-03	0.73	1.5e-05	0.18	4.3e-07	0.14
rParietal	1.1e-03	0.73	3.3e-07	0.21	1.2e-08	0.20
rTemporal	3.9e-04	0.73	1.5e-06	0.25	2.9e-08	0.57
rOccipital	9.5e-02	0.69	8.0e-04	0.45	3.5e-08	0.55
rCentrumSemiovale	1.9e-08	0.68	1.5e-07	0.25	8.5e-05	0.53
rCerebellum	0.26	0.87	7.5e-05	0.31	2.3e-10	0.69
Brain Stem	2.7e-13	0.08	2.5e-09	0.17	9.7e-01	0.53
Corpus	1.6e-06	0.49	9.9e-05	0.83	2.1e-03	0.39

In Fig. 6, we show scalar maps of the various RISH features. Also shown is the estimated shift function Π_i for different Freesurfer regions of the brain. The figure also shows the scaling function π_i that scales each SH coefficient at each voxel. An important point to note is that, the scaling function π_i is spatially quite consistent despite the region-based shift function Π_i showing discontinuities between the different ROIs. Note that, the signal change is caused by a change in the SH coefficients, driven by the scaling function π_i, which, as mentioned, is spatially smooth. Thus, the harmonization process does not introduce sharp spatial discontinuity in the signal between neighboring regions.

Another observation from Fig. 6 is that the scanner related differences are substantially different for sub-cortical gray, versus the neighboring white matter region or the distant cortical gray matter region. Further, these differences vary substantially in the different frequency bands of the SH basis (i.e., in different RISH features). Consequently, it is clear that several non-linear effects due to magnetic field inhomogeneities, coil sensitivity, and other scanner related effects can cause non-linear changes in the signal in different tissue types.

TBSS results before and after harmonization

To validate our results using an independent approach, and also to ensure that small statistical differences are also removed, we computed the statistical group difference in FA between each of the target and the reference site using the standard Tract-based-spatial-statistical (TBSS) algorithm (Smitha et al., 2006). Fig. 7 shows widespread group differences between the subjects from the reference site (Siemens scanner) and the target sites. After data harmonization, all white matter group differences were removed confirming the results seen in Table 2.

Evaluation of the refined brain label map

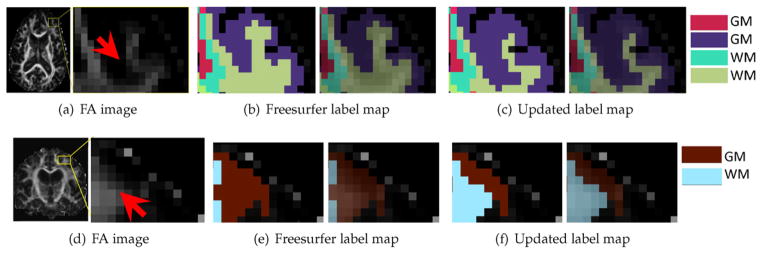
In Fig. 8, we show some qualitative results for the updated Freesurfer label map after applying our algorithm (Optimizing Freesurfer label map section) where the number of iterations is limited to 5. It can be seen that several voxels near the gray-white tissue boundary in the cortical region are labeled incorrectly; see Fig. 8(b) and (e). After applying our correction algorithm to relabel the voxels based on the RISH features (note — we did not use FA to relabel the voxels), a more accurate labeling of the Freesurfer ROIs is obtained, see Fig. 8(c) and (f).

Fig. 8.

Comparison between the Freesurfer parcellated label map and the updated one after applying our algorithm (Optimizing Freesurfer label map section). A part of the brain with low FA labeled as WM (b) is relabeled to GM (c). A part of the brain with high FA originally labeled as GM (e), but is relabeled to WM (f) using our method. Note that in subfigures (b, c, e, f) the images on the left side visualize crisp labels, which are transparent on top of FA on the right side.

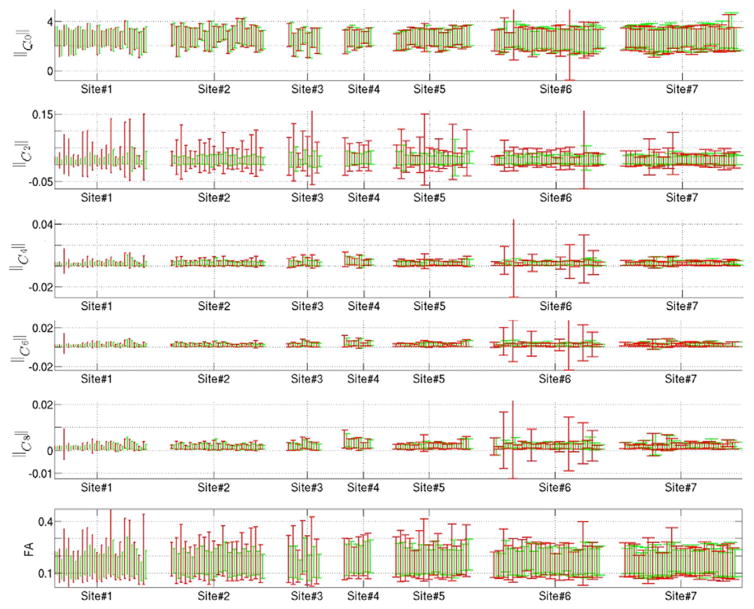
To provide some quantitative results, we computed the mean and standard deviation of FA and the RISH features in different brain regions of the Freesurfer label map, before and after updating the label map. As can be seen in Fig. 9, the variance of these features in each ROI is significantly reduced after update (green) compared to the original label-map (red).

Fig. 9.

The bars in red and green represent the mean and variance of the parameters (||C₀||², ||C₂||², etc.) before and after modifying the Freesurfer label map. Note that Site#7 is our reference site.

Fiber orientation changes and intra-site variability before and after harmonization

In order to ensure that our harmonization process does not in any way change the fiber orientation, we also compared the average error in degrees in the orientation of the fibers. Change in angle was computed using the standard DTI model and SH-based orientation distribution function (ODF) at each voxel, before and after data harmonization. For the tensor and ODF based models, the average change in orientation at each voxel was always less than 1°; changes in the orientations averaged over the entire brain are reported in Table 4. We also computed the coefficient of variation (CoV) in FA (Vollmar et al., 2010) for each site before and after the harmonization procedure. The CoV per site is computed as the ratio between the standard deviation and mean of FAs over the whole brain as summarized in Table 5. It can be seen that, the within site CoV did not change much after the mapping. Thus, within-site or intra-site variability in diffusion measures is preserved while inter-site scanner-related variability is removed. Consequently, we believe that this methodology can be quite useful for pooling large data sets for joint analysis.

Table 4.

Changes in the orientation of the fibers (estimated using the single tensor model and ODF) before and after applying our harmonization method.

	Site#1	Site#2	Site#3	Site#4	Site#5	Site#6
Single tensor	0.76 ± 0.12°	0.14 ± 0.08°	0.72 ± 0.21°	0.79 ± 0.03°	0.10 ± 0.00°	0.95 ± 0.05°
ODF	0.24e–5 ± 0.03e–5°	0.17e–5 ± 0.02e–5°	0.26e–5 ± 0.07e–5°	0.79 ± 0.03°	0.10 ± 0.00°	0.95 ± 0.05°

Table 5.

Changes in the coefficient of variation (CoV) in FA for each site before and after the harmonization procedure.

	Site#1	Site#2	Site#3	Site#4	Site#5	Site#6
CoV (before)	0.5673	0.6119	0.6231	0.4939	0.5406	0.5835
CoV (after)	0.5652	0.5956	0.6038	0.5026	0.5787	0.5906

Synthetic experiments to demonstrate the effect of signal abnormalities due to disease on the harmonization procedure

Since we only “shift” the energy in the RISH features, the changes done to the signal are relative, i.e., the signal at each voxel is changed relative to the original signal at that location. Thus, if the FA at a particular location is lower due to disease, it will only be shifted (or changed) by an amount as determined from a set of healthy subjects and not to an absolute value. Thus, lower FA will still stay lower after harmonization. We demonstrate this synthetically using the following experiment.

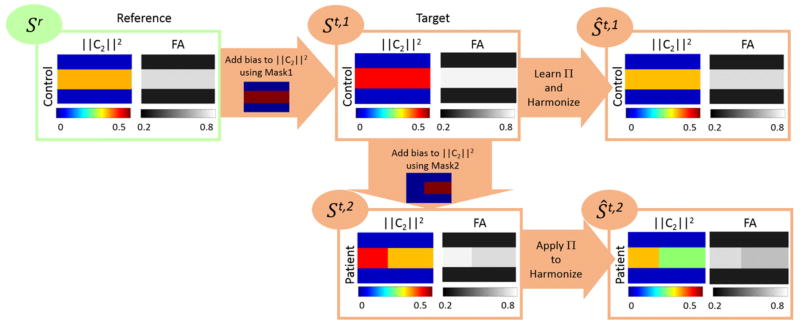
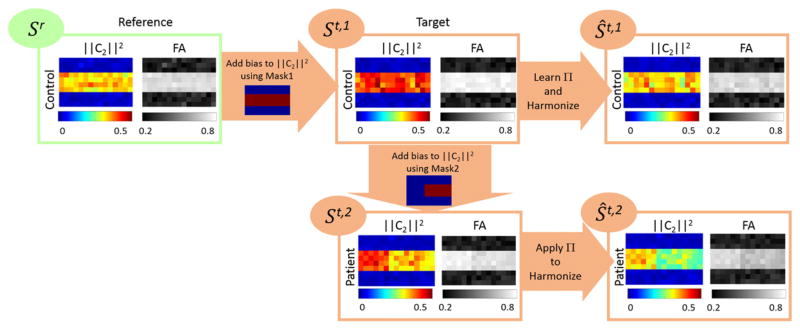
We generate three synthetic images called {S^r,S^t,1,S^t,2}, where i) S^r is the control image at the reference site; ii) S^t,1 is the control image at the target site; and iii) S^t,2 is a synthetically generated diseased image at the target site. We generate S^t,1 by adding some bias to the second order RISH features of S^r; the bias is added to the voxels within a mask denoted by Mask1 (Fig. 10). This will generate a data set where the data acquired at the target and reference site is different, as is typically the case in in-vivo data. In particular, the FA in the simulated white matter region for S^r is 0.79, for S^t,1 is 0.82, while for the S^t,2 is 0.79.

Fig. 10.

Visualization of the generated synthetic images {S^r,S^t,1,S^t,2} to study the effect of applying our method on diseased based biological effects (Synthetic experiments to demonstrate the effect of signal abnormalities due to disease on the harmonization procedure section). The feature differences of the diseased and control subjects at the target site before (i.e. S^t,1 vs S^t,2) and after harmonization (i.e. Ŝ^t,1 vs Ŝ^t,2) are reported in Fig. 12, which indicate that our method would preserve the differences.

The data, S^t,2 is generated by adding some bias to the second order RISH features of S^t,1 using another mask denoted by Mask2; in fact, we assume that the voxels within Mask2 are affected due to the disease. The second order RISH features of {S^r,S^t,1,S^t,2} and the masks are shown in Fig. 10. We use {S^r,S^t,1} to learn Π parameters in our pipeline, which are used to harmonize the images in the target site {S^t,1,S^t,2}. Let’s denote the harmonized images by {Ŝ^t,1,Ŝ^t,2}, respectively. Examples of the generated noisy images after adding rician noise are shown in Fig. 11. The noise-level is the standard deviation of noise ranging from 0 to 0.2.

Fig. 11.

Representation of the images in Fig. 10 with added rician noise.

In Fig. 12, for the voxels within Mask2 with different levels of rician noise, we report the difference of ||C₂||², FA, and GFA between: i) S^r and Ŝ^t,1; ii) iii) S^t,1 and S^t,2; and iii) Ŝ^t,1 and Ŝ^t,2. Each of these are respectively the differences between i) the reference image and the harmonized image obtained at the reference site, ii) difference between the original control and disease images at target site, and iii) difference between the harmonized control and disease image at the reference site. Our ideal outcome is to see similar differences between the control and disease at the target and reference site. It can be seen that within Mask2 (the part of the brain affected by disease), our method preserves the changes due to the disease; i.e. the difference between the features of the normal and the disease case at the target site are preserved in the harmonized images as well. In this experiment, we modified the signal so that it represents typical variations in signal (and in FA and GFA) that are expected in diseases such as schizophrenia or mild traumatic brain injury. While a controlled study where data are truly acquired and validated at two different site would be ideal, yet due to lack of any such existing data set, we believe that the synthetic experiment above is a good initial evaluation of our method.

Fig. 12.

Difference of ||C₂||², FA, and GFA between: i) S^r and Ŝ^t,1; ii) S^t,2 and S^t,2; and iii) Ŝ^t,2 and Ŝ^t,2 for different levels of rician noise added to the images. It can be seen that the differences computed between the normal and patient cases at the target site are preserved after applying our harmonization method.

Validation on a traveling subject

To further validate our method, we used data from a traveling human subject. The dMRI data was acquired on six different sites {Site#1, Site#2, Site#4, Site#5, Site#6, Ref.site} in quick succession (within 1 month). Using the learnt parameters in our pipeline, we harmonized the images of the traveling subject from all of the target sites. To see if scanner related statistical differences were removed, we computed the p-values for {MD, FA, GFA} between voxels from each Freesurfer ROI before and after data harmonization. The p-values are reported in Tables 6–9, with all statistical differences removed after harmonization. These results indicate that the harmonization parameters can safely remove scanner related differences even in a single traveling subject, for each of the brain regions defined by the Freesurfer ROIs.

Table 6.

P-values computed for the traveling subject (Site#1).

	MD		FA		GFA
	Before	After	Before	After	Before	After
lFrontal	1.1e-01	9.1e-01	2.1e-01	7.0e-01	1.8e-01	5.6e-01
lParietal	4.0e-04	1.8e-01	2.7e-01	8.6e-01	4.8e-01	7.3e-01
lTemporal	7.1e-02	5.5e-01	3.7e-02	3.0e-01	6.7e-02	2.7e-01
lOccipital	3.1e-01	8.3e-01	1.1e-01	4.2e-01	1.9e-01	7.8e-01
lCentrumSemiovale	4.6e-02	7.2e-01	2.8e-02	4.8e-01	4.3e-01	3.7e-01
lCerebellum	8.6e-02	9.5e-02	2.5e-02	8.6e-02	9.4e-01	2.4e-01
rFrontal	2.2e-01	5.6e-01	1.4e-01	5.4e-01	9.2e-02	3.4e-01
rParietal	3.4e-01	1.2e-01	2.5e-01	8.5e-01	1.9e-01	4.7e-01
rTemporal	3.3e-01	4.8e-01	4.7e-03	6.2e-02	6.3e-03	7.3e-02
rOccipital	5.1e-01	6.8e-01	2.6e-01	7.4e-01	2.4e-01	9.2e-01
rCentrumSemiovale	7.7e-01	3.3e-01	6.3e-01	9.3e-01	6.5e-01	8.6e-01
rCerebellum	2.3e-01	2.7e-01	1.3e-01	1.1e-01	8.3e-01	2.8e-01
Brain Stem	8.1e-01	6.8e-01	7.9e-01	8.3e-01	2.2e-02	8.3e-02
Corpus	1.7e-01	7.4e-01	9.9e-02	5.8e-01	8.3e-02	2.8e-01

Table 9.

P-values computed for the traveling subject (site#6).

	MD		FA		GFA
	Before	After	Before	After	Before	After
lFrontal	2.6e-04	5.2e-01	3.9e-01	8.5e-01	8.7e-01	8.4e-01
lParietal	1.0e-02	7.8e-01	2.0e-01	6.4e-01	5.5e-01	5.7e-01
lTemporal	2.6e-02	1.5e-01	7.6e-02	1.8e-01	4.4e-01	7.3e-01
lOccipital	1.3e-01	9.1e-01	4.2e-01	7.1e-01	6.9e-01	6.8e-01
lCentrumSemiovale	2.4e-04	5.1e-02	3.8e-03	8.3e-02	6.3e-01	8.9e-01
lCerebellum	4.0e-02	1.2e-01	1.2e-01	9.8e-01	9.9e-01	2.4e-01
rFrontal	4.3e-04	3.0e-01	6.7e-01	9.9e-01	6.2e-01	8.0e-01
rParietal	6.4e-02	1.1e-01	5.6e-01	7.8e-01	7.1e-01	6.8e-01
rTemporal	7.1e-03	1.0e-01	8.8e-01	3.2e-01	6.9e-01	6.4e-01
rOccipital	7.7e-01	1.3e-01	9.9e-01	6.2e-01	8.0e-01	9.4e-01
rCentrumSemiovale	9.5e-01	7.7e-01	7.8e-01	9.9e-01	9.5e-01	7.3e-01
rCerebellum	4.6e-01	7.8e-01	8.7e-01	8.8e-01	4.8e-01	5.9e-02
Brain Stem	9.8e-02	1.7e-01	2.6e-01	2.1e-01	9.8e-01	5.3e-01
Corpus	1.3e-01	8.9e-01	4.5e-01	7.4e-01	9.6e-01	5.8e-01

Conclusion and limitations

In this work, we proposed a novel method that allows to harmonize the dMRI signal acquired at different sites in a region-specific, subject-dependent manner, while maintaining the intra-subject variability at each site, but removing scanner specific differences in the signal across sites. Once such a mapping is computed for healthy subjects, it can then be potentially used to map another cohort of diseased subjects allowing for a joint analysis of the data using any type of diffusion derived measure. The proposed method is model independent and directly maps the signal to the reference site. The method can be of great use to aggregate data from multiple sites making it feasible to do joint analysis of a large sample of data sets. We should note that, to the best of our knowledge, this is the first work that has explicitly addressed the issue of dMRI data harmonization by modifying the acquired signal directly, as opposed to adding linear statistical covariates to detect group differences in diffusion derived measures. This methodology ensures that once the data is harmonized, any type of subsequent analysis can be done by pooling the data, regardless of the analysis technique or model used. This is one of the key advantages of our method. Using several experiments, we demonstrated the efficacy of our method in removing scanner related differences from each of the 7 sites analyzed in this study. Further, the proposed method can be used to separately harmonize each b-value shell for multi-shell diffusion data.

Note that in our pipeline, RISH features are used as the basis although there are other tensor-based RI features (Kindlmann, 2003; Ennis and Kindlmann, 2006) such as the eigenvalues, MD, FA, and other fourth-order tensor invariants (Fuster et al., 2011). While one can use the fourth-order tensor invariants (Fuster et al., 2011) instead of the RISH features, yet using the eigenvalues, FA and other measures from the single tensor model would only be acceptable in case the original raw data has very few gradient directions (e.g. less than 15 gradient directions).

Nevertheless, our methodology has a few limitations, which we will address in our future work. First, an ideal scenario for our method to work optimally would be the availability of a few traveling subjects who are scanned at each site (in quick succession), ensuring that little anatomical differences in dMRI data exist between the scans acquired at each site. The harmonization parameters obtained from such a set of subjects could then be used to harmonize data across all sites. Thus, this is the optimal experimental design to use this method, for prospective harmonization of the data, with similar acquisition parameters used at all sites. However, in many scenarios such a cohort of data does not exist. In such cases, we have to provide a cautionary note that the number of healthy subjects (used for the harmonization data) should be sufficient enough (at each site) to capture most of the anatomical variability. We should however note that, our method relies on computing the average difference in RISH features and does not depend on the variance of a particular diffusion measure as is the case when using meta-analysis. Thus, our method is less sensitive to the number of subjects used to harmonize the data at each site. Another limitation of our method, is that it can be used in its current form, only for similar acquisition parameters across all sites (scanners). For example, a data set with 60 gradient directions cannot be exactly harmonized with the one having only 10 gradient directions as the higher order RISH features cannot be computed from the latter one. Consequently, harmonization can only be done for RISH features up to order 2. Thus, while some differences in the number of gradient directions can be tolerated, the same is not true about the b-value or the spatial resolution. In our future work, we will address these challenges.

Our work is still a first step towards a full-fledged methodology for comparing two groups of subjects acquired from different scanners. While we have shown the robustness of our method on synthetic data in preserving the group effect after harmonization, yet, a comprehensive validation needs to be done involving several acquisitions and scans on multiple sites. This will form part of our future work. However, the work done in this paper is a necessary first step to take the field forward so that a comprehensive method is available that can harmonize the dMRI signal directly, allowing for any type of model based analysis at a later stage.

Scanner related artifacts, such as table vibration can influence statistical results in our pipeline. If such artifacts consistently exist in the data acquired at the target site (not the reference site), these might be partially removed. However, we do not have access to such data and hence can’t demonstrate this using experiments. Nevertheless, if such artifacts exist in the “reference” site, then this could potentially “add” artifacts to the data, which is certainly undesirable. This limitation can be mitigated by careful inspection and choice of the reference site data.

To summarize, we propose a model-independent method for harmonizing diffusion MRI data acquired at multiple sites with almost similar acquisition parameters. This will allow for pooling data acquired from multiple sites by removing scanner specific differences. In particular, we recommend that a set of traveling heads be used to acquire data from all sites in quick succession, which can then be used to harmonize data across these sites. Such a data set will be the most ideal data for application of the proposed algorithm.

Table 7.

P-values computed for the traveling subject (site#2).

	MD		FA		GFA
	Before	After	Before	After	Before	After
lFrontal	3.4e-02	1.4e-01	2.3e-01	6.3e-01	2.9e-01	9.6e-01
lTemporal	1.2e-02	7.5e-01	3.3e-02	4.1e-01	2.3e-01	6.7e-01
lOccipital	2.1e-02	4.7e-01	4.6e-02	1.8e-01	2.8e-01	5.5e-01
lCentrumSemiovale	3.2e-05	8.6e-02	1.2e-02	4.3e-01	6.0e-01	1.6e-01
lCerebellum	6.9e-03	6.5e-02	2.3e-02	9.4e-02	3.2e-01	1.6e-01
rFrontal	1.1e-02	1.7e-01	1.8e-01	5.4e-01	2.5e-01	8.1e-01
rParietal	8.7e-05	1.1e-01	5.7e-02	3.3e-01	1.1e-01	3.7e-01
rTemporal	1.3e-01	5.6e-01	1.7e-03	5.1e-02	4.4e-03	8.7e-02
rOccipital	1.6e-02	6.7e-02	3.9e-02	1.7e-01	5.9e-02	5.3e-01
rCentrumSemiovale	1.8e-01	3.1e-01	7.1e-01	9.4e-01	7.8e-01	9.6e-01
rCerebellum	2.0e-01	2.7e-01	5.9e-01	8.9e-01	4.9e-01	1.6e-01
Brain Stem	9.4e-01	7.0e-01	4.4e-02	8.5e-02	9.9e-01	9.3e-01
Corpus	5.6e-03	8.9e-02	1.5e-02	9.8e-02	2.5e-02	1.9e-01

Table 8.

P-values computed for the traveling subject (site#5).

	MD		FA		GFA
	Before	After	Before	After	Before	After
lFrontal	9.6e-04	5.0e-01	5.8e-01	8.9e-01	7.2e-01	7.2e-01
lParietal	1.8e-03	3.9e-01	3.9e-01	6.7e-01	7.2e-01	5.9e-01
lTemporal	1.8e-02	8.2e-01	1.9e-01	8.8e-01	8.9e-01	3.1e-01
lOccipital	3.5e-01	5.3e-01	7.7e-01	6.4e-01	8.6e-01	5.9e-01
lCentrumSemiovale	4.4e-01	3.9e-01	3.7e-01	9.5e-01	3.3e-01	7.9e-01
rFrontal	2.6e-03	4.3e-01	7.7e-01	9.1e-01	6.3e-01	8.6e-01
rParietal	1.6e-01	1.3e-01	6.9e-01	9.6e-01	7.3e-01	3.7e-01
rTemporal	2.5e-01	7.3e-02	9.1e-01	2.7e-02	7.5e-01	7.3e-01
rOccipital	8.8e-01	2.4e-01	8.9e-01	9.2e-01	9.0e-01	3.9e-01
rCentrumSemiovale	8.1e-01	9.6e-01	7.5e-01	8.1e-01	9.7e-01	4.2e-01
rCerebellum	7.3e-03	5.0e-02	1.7e-01	7.2e-02	8.1e-01	1.8e-01
Brain Stem	2.3e-01	5.3e-01	7.3e-02	5.9e-02	7.8e-01	9.4e-01
Corpus	2.8e-01	7.6e-01	9.7e-01	6.8e-01	5.2e-01	9.9e-01