Abstract
Dielectrophoretic (DEP) phenomena have been explored to great success for various applications like particle sorting and separation. To elucidate the underlying mechanism and quantify the DEP force experienced by particles, the point-dipole and Maxwell Stress Tensor (MST) methods are commonly used. However, both methods exhibit their own limitations. For example, the point-dipole method is unable to fully capture the essence of particle-particle interactions and the MST method is not suitable for particles of non-homogeneous property. Moreover, both methods fare poorly when it comes to explaining DEP phenomena such as the dependence of crossover frequency on medium conductivity. To address these limitations, the authors have developed a new method, termed volumetric-integration method, with the aid of computational implementation, to reexamine the DEP phenomena, elucidate the governing mechanism, and quantify the DEP force. The effect of an electric double layer (EDL) on particles' crossover behavior is dealt with through consideration of the EDL structure along with surface ionic/molecular adsorption, unlike in other methods, where the EDL is accounted for through simply assigning a surface conductance value to the particles. For validation, by comparing with literature experimental data, the authors show that the new method can quantify the DEP force on not only homogeneous particles but also non-homogeneous ones, and predict particle-particle interactions fairly accurately. Moreover, the authors also show that the predicted dependence of crossover frequency on medium conductivity and particle size agrees very well with experimental measurements.
I. INTRODUCTION
Dielectrophoresis (DEP) has been a subject of active research in the past few decades and has shown promising applications in Lab-on-Chip devices. One of the active applications of DEP is to manipulate small particles (usually in the range of several microns to tens of microns) like cells for their sorting and separation (Church et al., 2011; Huang et al., 1992; and Li et al., 2013). Particles can be separated by being pushed towards either the strong field region or the weak field region through excitation via an alternating current (AC) signal at an appropriate frequency determined by the dielectric properties of particles and surrounding medium. They can also be guided into different channels depending on their physical properties (e.g., particle size). Lately, efforts have been made to explore the application of DEP in the biomanufacturing field. For example, cells of different types have been aligned to form 2D tissue-like patterns (Ho et al., 2006; 2013). Attempts have also been made to construct 3D tissue structures (Ramón-Azcón et al., 2012). Encouraged by this success, several technological improvements for DEP applications have also been developed. For example, insulator-based DEP (iDEP) creates large scale arrays and makes use of the strong local electric field generated by insulating materials to capture cells so that the configuration of electrodes can be largely simplified (Zellner et al., 2013). Optically induced DEP (oDEP) takes advantage of the property of photosensitive materials so that the control of particles is not limited by fixed geometry of electrodes (Huang et al., 2013).
A. Elucidating the DEP phenomena based on the dipole and multipole concepts
While new techniques of DEP applications are emerging constantly, not much progress has been made on elucidating the mechanism governing the DEP phenomena (Pethig, 2010). The prevailing DEP theory, which treats particles as point dipoles, predicts the DEP force () exerted on a spherical particle as , in which a is the radius of the particle, is the absolute permittivity of the medium, Re(f_cm) is the real part of the Clausius-Mossotti factor, and E is the electrical field (Wang et al., 1994). This method has its unique advantage as it provides a closed-form expression to quantify the DEP force on individual spherical particles. With this expression, the direction and magnitude of the DEP force on a single spherical particle can be estimated. To date, almost all DEP applications have relied on this expression as the guiding principle, although its limitations are quite obvious. First, due to its point-dipole nature, this method does not consider volumetric polarization of particles, which in turn will distort electric field by the presence of particles. When the influence of surrounding particles is considered, the particle-particle interaction force is often assumed to vary inversely to the fourth order with the distance (L) between particles, or ∼1/L4 (Aubry and Singh, 2006). Second, although the force expression is often applied to non-uniform electric field, in its derivation E is actually regarded as a vector independent of any spatial variations (namely, a uniform field). In reality, the electric field can be highly non-uniform.
To address these issues, a multipole method containing higher-order terms is developed (Jones and Washizu, 1996 and Washizu and Jones, 1996a). The contribution of higher-order terms has been found not negligible under certain conditions (Liang et al., 2004). This multipole method has further been expanded from dealing with individual spherical particles to considering non-spherical particles (Green and Jones, 2006) as well as particle-particle interactions (Washizu and Jones, 1996b). Although the multipole method provides an improved estimate for DEP force, it is rarely used in experimental design or numerical analysis because it is not intuitive how many high-order terms are needed.
B. Elucidating the DEP phenomenon based on the Maxwell stress tensor (MST)
While the dipole and multipole methods are useful in estimating the magnitude of DEP force, numerical integration often provides more accurate quantitative solutions. The Maxwell stress tensor (MST) method is one such method currently regarded as providing the most robust and accurate solution to DEP force quantification. In the MST method, the DEP force is calculated by integrating a stress tensor over the surface of a particle as , in which is the Maxwell stress tensor, is the norm vector along the surface, is the electric field at the surface, is the conjugate of , and is the unit tensor (Wang et al., 1997). This method can be applied to particles of various shapes. Moreover, because the electric-field-distortion effect from neighboring particles has already been considered in the determination of the electric field of a given particle, the obtained DEP force inherently includes the effect of particle-particle interactions.
While the MST method has shed valuable insight into the alignment of particles due to particle-particle interactions (Ai and Qian, 2010; Hossan et al., 2013; and Xie et al., 2015), its application has been limited to studying relative movements of a small number of particles, and in most cases in simplified 2D situations. In applying the MST method, the stress tensor is integrated over the particle surface (Kumar and Hesketh, 2012 and Song et al., 2015), which often leads to a misconception that the resulting force is a physical surface force. This in turn could result in incorrect predictions of DEP force and physical movement of particles (Rinaldi and Brenner, 2002). Moreover, because of the surface integration nature, the MST method is not suited for dealing with particles of non-homogeneous dielectric properties like cells.
C. Dealing with particles' non-homogeneity and the influence of surface conductivity
To account for the various components of cells, a shell-model approach based on the dipole method is often used by considering the average dielectric property of all components as effective permittivity (Gascoyne et al., 1997). While this modified dipole method is useful in predicting the crossover frequency of cells, which is recognized as one crucial metric for cell separation, it does not capture other DEP behavior such as self-rotation of cells in non-rotating electric field (Chau et al., 2013 and Zhao et al., 2013).
Predicting the crossover frequency of particles possessing different surface properties from bulk is often challenging. For example, experimental observations show that small polystyrene particles experience positive DEP (pDEP) at a lower frequency and transition from pDEP to negative DEP (nDEP) as frequency increases (Green and Morgan, 1999). This crossover behavior is attributed to the high surface conductivity of the particles caused by the presence of an electric double layer (EDL) at the particle surface (Arnold et al., 1987 and O'Konski, 1960). Because polystyrene particles carry net negative surface charge, they will attract positive counter-ions to the surface and form a thin EDL with high conductivity.
Although both the point-dipole method and MST method have been used to study the crossover frequency of polystyrene particles, the influence of the EDL is often considered by assigning a surface conductance value without dealing with the actual structure and ion distribution inside the EDL. For example, a typical way to deal with this issue is to express surface conductivity as by assuming that the overall surface charge is balanced with counter ions, where is the surface charge density and is the mobility of counter-ions (O'Konski, 1960). With this surface conductivity expression, one can write the total conductivity of the particle as , where is the bulk conductivity and a is the radius of the particle (Arnold et al., 1987). This relationship, however, does not capture the dependence of crossover frequency on medium conductivity (Green and Morgan, 1999). One reason, as argued by Green and Morgan, is that the balance between counter-ion density and surface charge density does not hold when the thickness of the double layer is not negligible in relation to the size of particles. To reflect this, an additional term accounting for the effect of thickness change in the Debye length is included: , where is the inverse of Debye length, and A1 and A2 are constants determined through curve fitting. A similar approach by Hughes and Morgan (1999) sought empirical fit to the data by adding a term of medium conductivity, , as .
While in both cases the fitting curves match experimental data well, the physical meaning of the relevant terms is not clear. To provide physical relevance, the surface conductivity was divided into two parts: conductance due to charge movement in the Stern layer and conductance due to charge movement in the diffuse layer governed by zeta potential, with both the Stern layer conductance and zeta potential obtained through statistical fit to experimental data (Hughes et al., 1999). Two main limitations remain with this approach. First, applying an analytical expression derived for a flat surface to the ionic distribution in the EDL of a spherical surface could lead to inaccurate results (Yang and Zhang, 2007). Second, the Stern layer conductance and zeta potential are interrelated. With an increase in electrolyte concentration, zeta potential will decrease given that the surface charge is fixed (Elimelech and O'Melia, 1990). However, the zeta potential and Stern layer conductance are treated as constants for the full range of medium conductivity (Hughes et al., 1999), which could lead to errors in solutions.
D. Purpose of this study
Based on the aforementioned limitations, it is apparent that the true mechanism governing the DEP phenomena appears to be more complicated than we have recognized. In this work, we have developed a volumetric-integration method, with the assistance of finite element software COMSOL Multiphysics, to reexamine some of the DEP phenomena and quantify the force by considering particle-particle interactions and investigate the effect of the EDL on the crossover frequency of particles in detail. For outcome assessment, we compare our results with those obtained by the point-dipole method and the MST method, as well as reported observations on DEP phenomena of particles.
II. DEVELOPMENT OF A NEW METHOD TO REEXAMINE DEP PHENOMENA
A. Considering the volumetric polarization of particles
We consider a spherical infinitesimal unit of a particle which is placed in an electric field, either uniform or non-uniform. As the size of the particle unit becomes negligible in relation to the scale of the electric field, the electric field passing through the particle unit can be treated as approximately constant. Thus, we can express the force acting on the particle unit as
| (1) |
where is the dipole moment of the particle unit and denotes the original electric field (as if the particle possesses the same property as the surrounding medium or is not there) at the location of the particle unit. The induced electric field, namely, the difference between the electric field inside the particle unit and the original electric field, is generated by the dipole. The dipole is considered to have a structure of two charges with opposite polarity ( and ) separated by a distance of ( is the diameter of the spherical particle unit). The induced electric field can be represented by the electric field at the center of line connecting the two charges
| (2) |
where is the permittivity of medium and is the unit vector pointing from the negative charge to positive charge.
According to the definition of polarization density , we have
| (3) |
With Eq. (3), the relationship between the electric fields and polarization of the particle unit can be established as
| (4) |
Clearly, polarization of the particle unit is proportional to the difference between the original electric field and the electric field inside the particle unit. By replacing with , the force acting on the particle unit becomes
| (5) |
The net force on the target particle can then be expressed in a summation as follows:
| (6) |
With this expression, the influence of the dielectric property of the particle and medium and the possible impact of neighboring particles are all inherently considered. As the derivation process does not rely on assumptions such as homogeneous particles and spherical shape, the formula can be applied to calculate DEP force on non-homogeneous particles and irregular shaped particles as well. This new approach is also different from both the point-dipole and MST methods. In the point-dipole method, the electric field is taken at the center of the particle (which seems problematic when the field is location dependent), whereas in the MST method the force density is calculated as the product of charge and electric field.
B. Considering the effects of the EDL structure and ionic adsorption
As discussed in the Introduction section, the crossover frequency of a particle is affected by its EDL. Therefore, to be able to correctly predict the crossover frequency it is necessary to consider the effect of the EDL structure influenced by ion distributions.
By assuming that the electrolyte is composed of monovalent ions, the concentration of cations and anions in the EDL is expressed as and , respectively, according to Boltzmann distribution, where c is the concentration of the electrolyte, q is the elementary charge unit, k is the Boltzmann constant, T is the temperature, and is the potential distribution generated by surface charge. Then by Gauss's law through Poisson equation, is determined as
| (7) |
where F is the Faraday constant. The boundary condition at the particle surface can be expressed in terms of surface charge density () as
| (8) |
With the potential distribution () solved from Eqs. (7) and (8), the conductivity of any given point inside the EDL, , can be determined
| (9) |
where and are the limiting molar conductivities of the cation and anion, respectively. is the viscosity of medium and is zeta potential. The first two terms represent the conductivity due to conductive transfer of ions in the diffuse layer and the third term represents the electro-osmotic conductivity (Lyklema, 1995).
Note that the boundary condition given in Eq. (8) is valid only when the surface charge density is constant. However, experimental measurements of electrophoretic mobility of polystyrene particles in potassium chloride (KCl) solutions of different medium conductivities show that specific adsorption of co-ions will take place on the surface of particles (Elimelech and O'Melia, 1990). To consider this effect, Langmuir adsorption is used to describe the adsorption process. According to Langmuir adsorption, the surface charge from adsorption can be expressed as (Lyklema, 1995)
| (10) |
where represents the maximum amount of charge that can be adsorbed on the surface, is the dimensionless concentration (c* = c/(1 mol/m3)), and is the intrinsic binding constant, which is determined by the non-electrostatic adsorption Gibbs energy. is the potential at the inner Helmholtz plane (iHp). The difference between and , which is the potential at the outer Helmholtz plane (oHp), can be determined as (Lyklema, 1995)
| (11) |
where d is the distance between iHp and oHp and is the permittivity of the region in between. Then, Eq. (10) can be modified to
| (12) |
Considering that is small, the exponential term can be replaced by through Taylor series expansion. In this way, the surface charge from adsorption can be analytically expressed as
| (13) |
where and .
By replacing with in the boundary condition, Eq. (8), the potential distribution and surface ionic adsorption can be recalculated. To determine the crossover frequency, the contribution of adsorbed ions to Stern layer conductance is also included
| (14) |
where is the mobility of co-ions in the Stern layer. Based on the common understanding that the mobility in the Stern layer is smaller than that in the diffuse layer, we assign in the models, where is the mobility of co-ions in the diffuse layer. Through coupling our volumetric-integration method with our new EDL model, the effect of the EDL structure on the electric field distribution is inherently included by accounting for the continuously varying dielectric property within the EDL, unlike in other methods, where the influence of the EDL is simplified by assigning a surface conductance.
III. NUMERICAL IMPLEMENTATION
To solve the original and distorted electric field simultaneously, we use a computational approach by developing 2D and 3D models using COMSOL Multiphysics with the Electric Current Module and Frequency Domain Study. In these models, the differential electric field is determined by considering cases with and without particle presence. Note that in the case with particle presence, different intrinsic dielectric properties for the particle and the medium are assigned, and in the case without particle presence, the dielectric property of the medium is assigned to the particle as well. With the electric field expressed in a complex form along with a possible phase lag between polarization and electric field, the expression for the DEP force in the models is expressed as
| (15) |
For situations with multiple particles, the effect of electrical field distortion caused by the volumetric polarization of surrounding particles is considered when solving the electric fields. The geometry and setup of models are discussed in each individual study in Sections III A and III B. It is worth noting that in computational modeling, 2D situations are regarded as simplified 3D situations with the third dimension assigned a unity in size (1 m in SI units). This means that for all 2D studies, volumetric integration is performed over 2D domains of particles.
A. Validation through comparisons
1. Quantification of DEP force
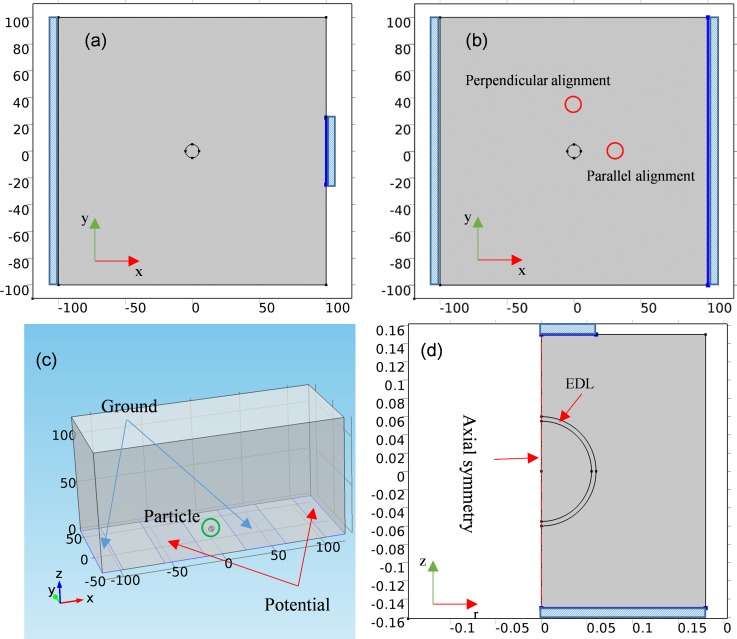
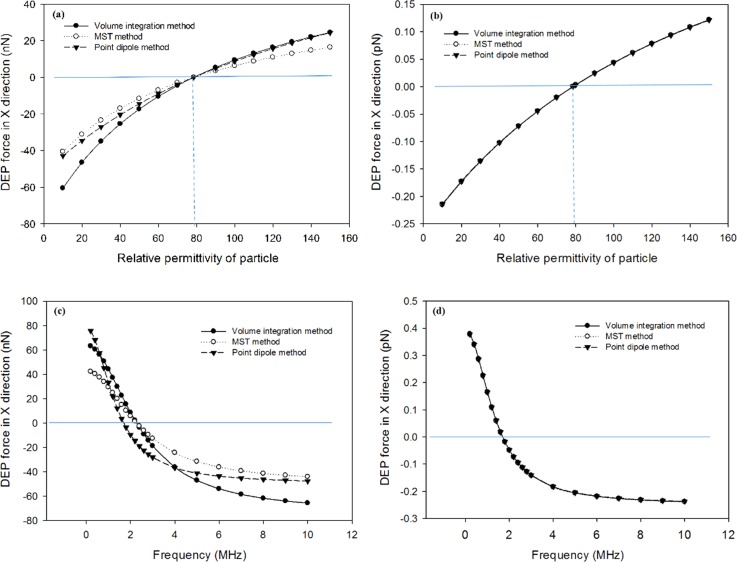
Both 2D and 3D COMSOL models are built to quantify the DEP force on a single homogeneous particle. The 2D model geometry shown in Fig. 1(a) represents a square domain with a spherical particle located in the center. The side length of the square domain is 40a and the diameter of the particle is 2a (a = 5 μm in this case). The entire left edge of the square domain is grounded and the middle segment of the right edge with length of 10 a is biased by an AC signal of 5 V (equivalent to a 10 Vpp biasing in experiments). In this setting, the electric field on the right side will be stronger than on the left side, causing the DEP force exerted on particle to point to the right under pDEP and to the left under nDEP. By considering a third dimension with depth of 40a and placing the spherical particle in the center of the cubic domain, we can obtain the geometry of the 3D model. To compare our modeling results with those from other methods such as the point-dipole and the MST methods, we quantify the DEP force in x direction. We consider two situations. In the first, both the particle and surrounding medium are treated as a pure dielectric material (conductivity equals zero), with the relative permittivity of medium set at 78.5 and the relative permittivity of particles varied from 10 to 150. In the second situation, the influence of frequency on the DEP force is studied. The relative permittivity and conductivity are set at 78.5 and 10−3 S/m for the medium and 2.5 and 10−2 S/m for the particle, while the frequency is varied from 200 kHz to 10 MHz.
FIG. 1.
(a) Geometry of a 2D model for quantifying the DEP force on a single particle located at center of a square domain medium. (b) Geometry of a 2D model for quantifying the particle-particle interaction, with one particle fixed at the center and the other particle (red) placed along either the x or y direction. (c) Geometry of a 3D model showing a particle in the center region of the gap. The bottom electrodes are marked by blue color. (d) Geometry of a 2D axisymmetric model for determining the crossover frequency of polystyrene particles (the outer layer is where the EDL resides).
2. Examination of particle-particle interaction
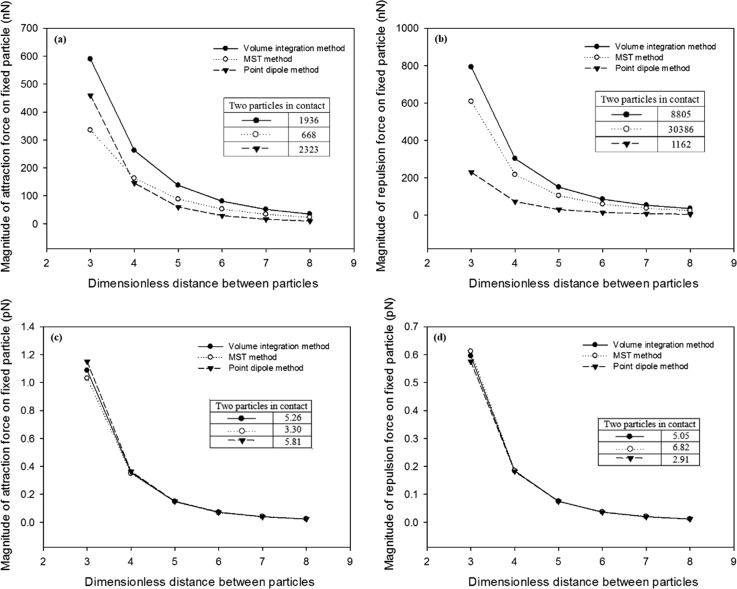
To study the interaction between two particles, a second 2D model as shown in Fig. 1(b) is built. To minimize the effect of non-uniform electric field, the entire right edge of the square domain is biased to create a uniform electric field. For the two particles, we consider two alignment configurations: (1) parallel to the electric field and (2) perpendicular to the electric field. In both cases, one particle is fixed at the center and the other is placed along either a parallel or perpendicular direction (shown by the red circles). In the model, the distance between the centers of the two particles is varied from 2a to 8a. Additionally, we constructed a 3D model by considering a third dimension with depth of 40a and fixing one spherical particle at the center. Parallel and perpendicular alignment of a second particle is considered. For convenience sake, both the particle and medium are treated as a pure dielectric material with the relative permittivity for the particle and medium set at 2.5 and 78.5, respectively. The DEP force on the fixed particle in-line with the particles is determined using our volumetric-integration method, the MST method, and point-dipole method.
3. A close look of the crossover behavior of nonhomogenous particles
Aside from investigating the DEP behavior of homogeneous particles, we also investigated the crossover phenomena of nonhomogeneous particles with the same model shown in Fig. 1(a) except that the homogeneous particle is replaced by a particle with multiple layers. For non-homogeneous particles, the computational demand will become overwhelming if we mesh the thin layers in the 3D model. Thus, we only compared the volumetric-integration method and MST method in 2D situations. Polystyrene particles with the entire surface coated with gold or with one half of the surface coated with gold (commonly known as the Janus particle) are considered. For comparison with experimental results, the particles are assigned with the same properties as provided in the literature (Table I) (García-Sánchez et al., 2012 and Zhang and Zhu, 2010). The frequency is varied from 104 to 105 Hz for the particle with the entire surface coated by gold and from 25 kHz to 20 MHz for the Janus particle. For the latter, an additional alkanethiol coating atop of the gold part is also considered. Although it might be a debatable issue whether the listed dielectric property of gold is valid for predicting the DEP behavior of particles within the range of frequency examined here (e.g., García-Sánchez stated that the frequency-dependent DEP behavior of gold coated particles is attributed to the EDL charging around the gold layer, but in Zhang and Zhu's work Maxwell-Wagner relaxation is applied in the shell model without considering the EDL to explain the crossover behavior of Janus particles), we utilize it in this study for quantitative evaluation purpose.
TABLE I.
Parameters for particles with entire and half surface coated by gold (García-Sánchez et al., 2012 and Zhang and Zhu, 2010).
| Particle with entire surface coated by gold | Particle with half surface coated by gold | |
|---|---|---|
| Diameter of particle | 10 μm | 3.8 μm |
| Thickness of gold layer | 50 nm | 30 nm |
| Medium conductivity | 0.7 mS/m | 2 mS/m |
| Thickness of alkanethiol layer | NA | 2 nm |
| Relative permittivity of alkanethiol | NA | 2.0 |
| Relative permittivity of gold | 6.9 | |
| Conductivity of gold | 4.5 × 107 S/m | |
4. A close look of the particle levitation behavior
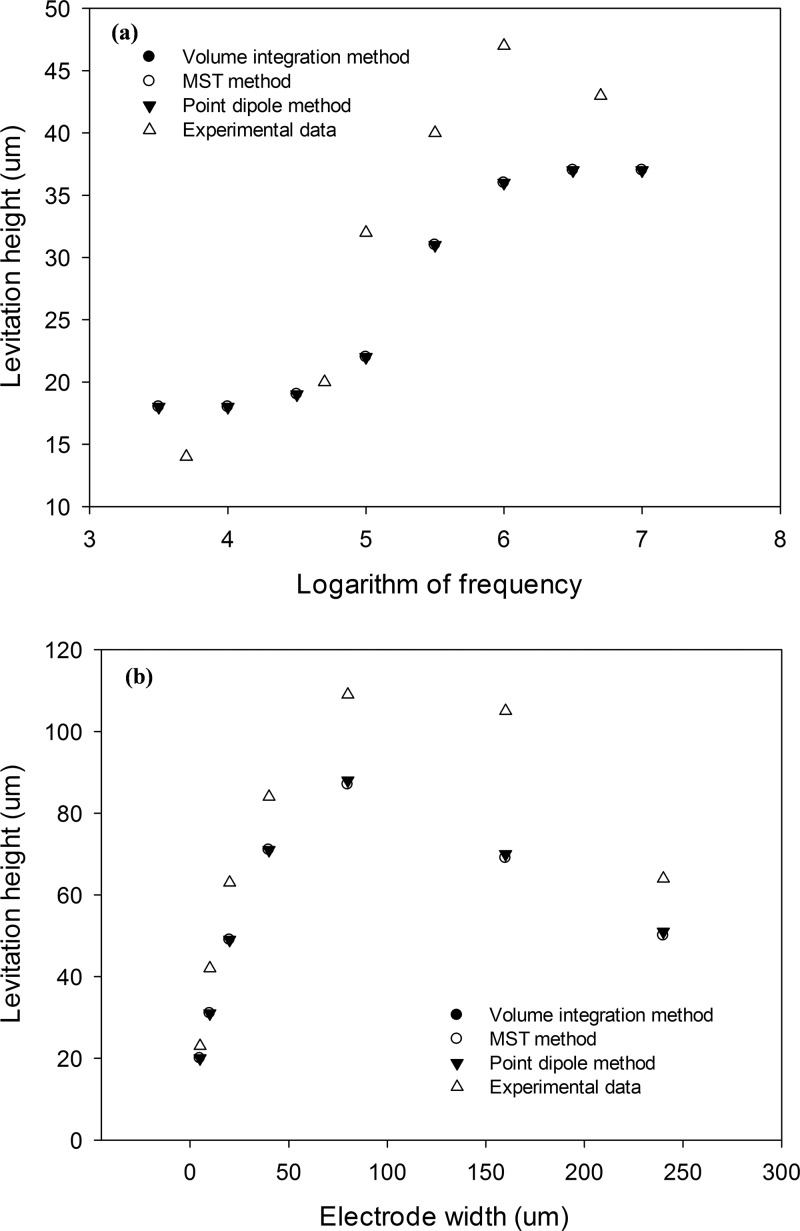
To examine particles' levitation behavior, a 3D model is developed to evaluate the vertical levitation height of the particle (6 μm in diameter). Fig. 1(c) shows the 3D model with the same setup and dimensions as in Markx's experiment (1997). For comparison, the vertical lifting DEP force is calculated using the volumetric-integration method, the MST method, and the point-dipole method. The levitation height is determined in three steps: First, with a fixed horizontal position, the vertical position of particles is parametrically varied until a height position is reached, where the DEP force is in equilibrium with the net of gravitation and buoyance forces. Second, a series of new horizontal positions for the particle are assigned and the vertical equilibrium positions are found by repeating the previous step. Third, we assess the horizontal stability of these vertical equilibrium positions, and the point at which equilibrium is reached in both the vertical and horizontal directions is considered as the stable levitation point for the particle with the vertical position regarded as the levitation height.
B. The influence of the EDL on the dependence of crossover frequency on medium conductivity and particle size
To examine the influence of the EDL on crossover frequency, a 2D axisymmetric model considering the EDL structure is constructed as shown in Fig. 1(d), in which a represents the radius of particle. A thin layer with thickness of t is included for refining the meshes for the space near the surface, where the EDL resides. For easy size scaling, the height of the rectangular domain is set at 5(a + t) and the width of the rectangular domain at 3(a + t). The entire bottom edge of the rectangular domain is grounded and a segment of the top edge with width of (a + t) is biased by 5 V. The crossover frequency is determined as the frequency point at which DEP force in z direction changes sign.
To study the medium conductivity effect, KCl is used as the medium electrolyte so the simulation result can be compared with experimental measurements. The limiting molar conductivities of potassium ions and chloride ions are assigned with values of 7.36 mS m2/mol and 7.62 mS m2/mol, respectively (Vanysek, 2000). Particles of three different sizes (93 nm, 216 nm, and 557 nm in diameter) are considered.
To highlight the differences in considering the influence of EDL, in our model we first assign the particle of a given size a fixed surface charge density at all medium conductivities. In this case, we determine the surface charge density through an iterative procedure as described below. With an initially estimated value for the charge density, we first solve Eq. (7) through (9) to find electric field distribution. Then with Eq. (6), we determine the crossover frequency. The obtained crossover frequency is compared with the crossover frequency data shown in Fig. 5(a) in a lower conductivity range (<10−3 S/m). If the two values differ, we adjust the initial estimate for the charge density (e.g., if the obtained frequency is higher, we will reduce the initial value, or vice versa, and repeat process). With the resolved surface charge density, we determine the change of crossover frequency as a function of medium conductivity.
FIG. 5.
Variation of crossover frequency with medium conductivity obtained from our volumetric-integration method and experimental measurements for particles of three different sizes when the effect of the EDL (a) is considered with fixed surface charge density and (b) is considered with ionic adsorption fully accounted for.
By contrast, we also consider the effect of the EDL influenced by surface adsorption of co-ions. In this case, the above resolved charge-density value is used as the initial surface charge density and the surface adsorption effect (discussed in Section II B) is considered to determine the overall surface charge density for the evaluation of crossover frequency at each medium conductivity. For easy comparison, the particle sizes and medium conductivity are all taken as the same as in experiments (Ermolina and Morgan, 2005; Green and Morgan, 1999; and Wei et al., 2009).
IV. RESULTS AND DISCUSSION
A. Validation through comparisons
1. Quantification of DEP force
Fig. 2(a) shows the variation of the x component of DEP force with the dielectric property of the particle for our volumetric-integration method, the MST method, and the point-dipole method, respectively, in 2D models. For all cases, the particle undergoes a transition from nDEP to pDEP when the relative permittivity is 78.5. The force magnitude for the MST method is slightly smaller compared with that for the two other cases. Fig. 2(b) shows the corresponding results in 3D models. All three methods produce identical DEP force magnitude. Fig. 2(c) shows the variation of the DEP force with frequency, in which the force magnitude of the MST method is again smaller than that for the two other cases. The MST method and the volumetric-integration method predict a similar crossover frequency (2.2 MHz), while the point-dipole method yields a slightly lower crossover frequency (1.6 MHz). Similarly, in 3D models, all three methods yield almost identical DEP force magnitude (Fig. 2(d)). These results suggest that when particles are homogenous, these three methods predict comparable outcomes. The observed difference in the force magnitude is attributed to the 2D simplification of the actual 3D situations. The DEP force is essentially a volume force and the Maxwell stress tensor is the result of mathematical operation based on Gauss's theorem. In a 2D model, the circular particle is actually a cylinder structure when we consider the third dimension extrusion. Because of this, only the circumferential edges are exposed to medium. This is different from a 3D model in which the entire outer surface is exposed to medium. Therefore, it is not expected to yield the same results when the volume integration is converted to surface integration by Gauss's theorem, leading to the disagreement in results of the two methods. While the 2D model provides less accurate estimation of force magnitude, it is often used to simplify the modeling process.
FIG. 2.
Results of DEP force determined from three different methods for a single particle: (a) and (b) Variation of DEP force on the single particle with relative permittivity. (c) and (d) Variation of DEP force on the single particle with frequency. (a) and (c) are results from 2D models. (b) and (d) are results from 3D models.
2. Examination of particle-particle interactions
To quantify particle-particle interactions, we examined the results from our volumetric-integration method, the MST method, and point-dipole method. In plotting the results, the distance between two particles is non-dimensionalized through division by the radius of particles. The results for particles aligning parallel to electric field in 2D models are shown in Fig. 3(a). The volumetric-integration method and point-dipole method predict a higher force magnitude than the MST method when the two particles are close to each other. The magnitude of attraction force for the point-dipole method decays faster than that for the two other methods. When particles align perpendicular to the electric field (see Fig. 3(b)), the repulsion force for both the volumetric-integration method and MST method is much higher than that for the point-dipole method. Since the electric field is highly non-uniform when two particles are close in distance due to the field distortion effect, the point-dipole method appears to generate a much smaller force (4 to 8 times lower) than our volumetric-integration method. On the other hand, the MST method predicts a much higher repulsion force (see data given in the inset table in the figure) when two particles are in contact. But this force decays to below that for the volumetric-integration method when the particles are more than half-particle distance apart. This is caused by the same reason previously discussed for the single particle case, where disagreement in results of the volume-integration method and MST method occurs. The difference becomes larger when the particle-particle interaction is involved. The 3D model results are shown in Fig. 3(c) (parallel alignment) and Fig. 3(d) (perpendicular alignment). All three methods predict close interaction force magnitude when particles are more than half-particle distance apart. The difference appears when particles get into contact. It is obvious that the MST method tends to underestimate the interaction force in parallel alignment and the point-dipole method tends to underestimate the interaction force in perpendicular alignment. We also compare the consistency between 2D and 3D models by referring to the force magnitude ratio between the case when particles are in contact and the case when particles are half-particle distance apart. In the perpendicular alignment case, the volumetric-integration method predicts a ratio around 10 in both 2D and 3D models. The MST method predicts a ratio of 50 in the 2D model and 10 in the 3D model. These results suggest that the volumetric-integration method can appropriately characterize particle-particle interaction in different particle orientations in both 2D and 3D models.
FIG. 3.
Results of DEP force determined from three different methods between two particles: (a) and (c) Variation of DEP force between two particles with the particle distance when particles are aligned parallel to the electric field. (b) and (d) Variation of DEP force between two particles with the particle distance when particles are aligned perpendicular to the electric field. (a) and (b) are results from 2D models. (c) and (d) are results from 3D models.
3. A close look of the crossover behavior of nonhomogenous particles
Table II lists the x component DEP force obtained for our volumetric-integration method and the MST method. In comparison, experimental measurement shows that gold coated polystyrene particles experience almost constant pDEP in the frequency range from 104 to 105 Hz under the given condition listed in Table I (García-Sánchez et al., 2012). Clearly, the volumetric-integration method predicts a constant DEP force (∼80 nN) close to the value obtained for a homogeneous particle (see Fig. 2(c)), suggesting that the results are reasonable. In comparison, the MST method predicts opposite DEP behavior with a force of ∼42 μN, which is about 500 times higher in magnitude.
TABLE II.
DEP force on gold coated particles.
| 104 Hz | 104.5 Hz | 105 Hz | |
|---|---|---|---|
| Volumetric-integration method (nN) | 80.04 | 80.04 | 80.04 |
| MST method (nN) | −4.24 × 104 | −4.24 × 104 | −4.23 × 104 |
Experimentally, Janus particles are observed (Zhang and Zhu, 2010) to exhibit pDEP behavior in the frequency range from 25 kHz to 20 MHz. When a layer of alkanethiol is added atop of the gold part, a crossover frequency is observed around 100 kHz when the medium conductivity is 2 mS/m. The results from our volumetric-integration method show that the Janus particle is always under pDEP in the given frequency range, but with an additional alkanethiol coating layer it exhibits transitional behavior at around 75 kHz, which is close to experimental data (Table III). The MST method, however, predicts that both types of particles experience nDEP, contradicting the experimental observation, thus suggesting that it may not be valid for predicting the DEP behavior of non-homogeneous particles. The failure of the MST method is attributed to the inappropriate use of Gauss's theorem. In Gauss's theorem, is only valid when has continuous first order partial derivatives. Due to the non-homogeneous dielectric property inside the particle, the electric field is discontinuous so that the Gauss's theorem is not valid, meaning the MST method is not applicable to non-homogeneous particles.
TABLE III.
DEP force on Janus particles
| Volumetric-integration method | |||||||
|---|---|---|---|---|---|---|---|
| 25 kHz | 50 kHz | 75 kHz | 100 kHz | 1 MHz | 5 MHz | 20 MHz | |
| Janus particle (nN) | 27.4 | 27.4 | 27.6 | 27.8 | 51.7 | 105 | 114 |
| Janus particle with alkanethiol layer (nN) | −77.2 | −17.3 | 2.1 | 10.2 | 32.1 | 77.0 | 97.4 |
| MST method | |||||||
|---|---|---|---|---|---|---|---|
| 25 kHz | 50 kHz | 75 kHz | 100 kHz | 1 MHz | 5 MHz | 20 MHz | |
| Janus particle (nN) | −1.23 × 104 | −3.40 × 104 | −5.08 × 104 | −6.04 × 104 | −8.02 × 104 | −2.76 × 104 | −2.95 × 103 |
| Janus particle with alkanethiol layer (nN) | −9.63 × 104 | −9.63 × 104 | −9.62 × 104 | −9.61 × 104 | −7.32 × 104 | −1.06 × 104 | −667 |
4. A close look of the particle levitation behavior
To assess the accuracy of the DEP force predicted by the volumetric-integration method in a real case, a 3D model with the same conditions as in the levitation experiment (Markx et al., 1997) is analyzed with a surface conductance of 1.2 nS assigned to the particle. For a homogeneous particle placed in an electric field with a dimensional scale much larger than the particle size, the results for the three methods show almost the same levitation height under different conditions (Figs. 4(a) and 4(b)), confirming again that all these methods can be used to quantify the magnitude of DEP force when particles are homogenous. The difference between the simulation and experimental results is possibly attributed to the negligence of the Stokes drag force (Cao et al., 2008).
FIG. 4.
Variation of the particle levitation height with (a) frequency and (b) electrode width obtained from three different methods along with experimental measurements.
In the above discussion, we only examined the situations of homogeneous spherical particles. However, this volumetric integration method is also applicable to non-spherical particles (e.g., ellipsoid particles) and non-homogeneous particles (e.g., cells). Due to the space limitation, we would discuss these situations in separate papers.
B. The influence of the EDL on the dependence of crossover frequency on medium conductivity and particle size
1. Effect of medium conductivity
First, we examine the situation with the assumption of constant surface charge density. With a resolved surface charge density value of −13 mC/m2, we found that the crossover frequency predicted by our model agrees well with the measurement data for all three sizes of particles only when medium conductivity is low, as shown in Fig. 5(a). As the medium conductivity increases, experimental measurements (Green and Morgan, 1999) start to deviate drastically from the modeling results in all cases, suggesting that the assumption of constant surface charge density is questionable when the medium conductivity varies.
Second, we look at the situation in which the EDL structure affected by ionic adsorption is considered with the parameters listed in Table IV, where the values of and are taken from the literature (He et al., 2006 and Yang and Zhang, 2007). Since the value of is unknown and the initial surface charge normally only occupies a small portion of surface area, we assume = 10 . Then with = e2 (for is an exponential function of the adsorption Gibbs energy), we found that our results capture almost perfectly the measured data as shown in Fig. 5(b).
TABLE IV.
Parameters for dealing with the EDL and surface ionic adsorption (He et al., 2006 and Yang and Zhang, 2007)
| Parameter | Value | Physical meaning |
|---|---|---|
| −13 mC/m2 | Initial surface charge | |
| −130 mC/m2 | Maximum amount of charge adsorption | |
| 0.3 nm | Thickness between iHp and oHp | |
| 40 | Permittivity of the region between iHp and oHp | |
| e2 | intrinsic binding constant |
Here, we compare our approach of modeling EDL with the methods discussed in the three papers by Basuray and Chang (2007), Basuray et al. (2010), and Basuray and Chang (2010). In the 2007 paper (Basuray and Chang, 2007), the authors used an analytical approach to determine the impact of the EDL on dipole moment by treating the particle as a point dipole. It also argued that the conductance of the Stern layer and diffuse layer cannot be directly added to obtain the total surface conductance when the thickness of the diffuse layer is comparable to the size of particles. In this paper, we used integration of polarization density to account for the dipole moment, which allowed us to fully determine the EDL effect by quantifying the distorted electric field distribution inside the particle due to the EDL. For the Stern and diffuse layers, we used surface conductance to capture the Stern layer effect because its thickness is always negligible compared with the particle size, but considered the diffuse layer as a separate band region outside the Stern layer having varying conductivity due to charge accumulation. However, regarding ionic adsorption in the Stern layer, while Basuray et al. related the amount of charge adsorption to the space charge in diffuse layer in a linear manner, their curve fitting did not seem to consider the effect of the adsorbed charges on the Stern layer conductance. Instead, the conductance of the Stern layer was empirically estimated. In our work, we considered surface adsorption as a function of medium conductivity, as observed experimentally (Elimelech and O'Melia, 1990). While both results captured the experimental observations very closely, the benefits of our using a numerical approach based on Finite Element Analysis (FEA) include: (1) consideration of the EDL effect can be implemented much easily and with great quantitative accuracy, and (2) the impact of the EDL can be related to the underlying physics including the amount of charge adsorbed and Stern layer conductance.
In the two other papers (Basuray et al., 2010 and Basuray and Chang, 2010), the authors improved the analytical approach from two aspects. First, the full nonlinear Poisson-Boltzmann equation was solved to replace the Debye-Hückel linearization assumption used in the 2007 paper. Second, different structures of the EDL under different conditions were considered. Below a critical bulk electrolyte concentration, a collapsed layer was used to represent the EDL. The thickness and conductivity were independent of the medium conductivity. Beyond this critical bulk electrolyte concentration, the collapsed layer was replaced by an ionic-strength dependent Debye diffuse layer with varying thicknesses. This treatment inherently introduced unrealistic discontinuity in the EDL behavior. In our method, the issue of a fully nonlinear limit does not exist as we do not need to use linearization to analytically solve the potential distribution. The Poisson-Boltzmann equation was always expressed in an exponential form. Linearization was only used when we considered the contribution of adsorbed co-ions in the Stern layer because the amount of adsorption is very low. Due to this advantage, we do not need to estimate the thickness of the diffuse layer and compare it to the Debye length, which is not a precise representation of the EDL structure sometimes. Our modeling approach provided a continuous means to capture the actual EDL behavior. This was made possible by building upon our previous works, where we distinctively defined the interface between the Stern layer and diffuse layer through consideration of the interior structure of the Stern layer along with the inner and outer Helmholtz plane (Yang and Zhang, 2007; 2008).
In summary, the above results and discussions suggest that the consideration of the effect of the EDL influenced by ionic adsorption in our model allows a much coherent elucidation of the dependence of the crossover frequency on medium conductivity when incorporated with our volumetric polarization approach.
2. Effect of particle size
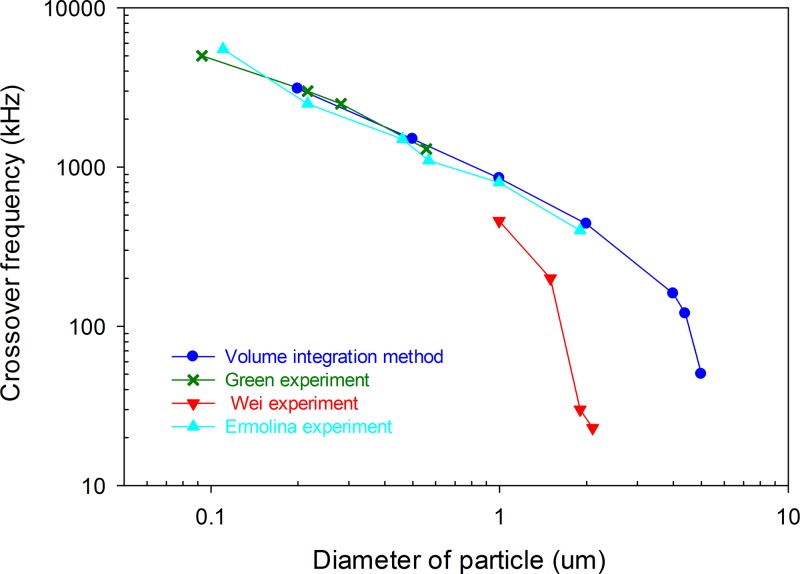
Fig. 6 shows the variation of crossover frequency as a function of particle size obtained from our volumetric-integration method, along with measurements from Green and Morgan (1999), Wei et al. (2009), and Ermolina and Morgan (2005), all obtained at the same medium conductivity of 10−3 S/m. Overall, our modeling results almost overlap with data from Green and Ermolina's work. In comparison with Wei's measurements, however, our predictions captured the same sudden dropping trend but with a slight offset in values. The observed differences between these experiments may be attributed to the differences in the particle surface property and in the measurement methods. Nevertheless, these results clearly show that our volumetric-integration method is able to predict the crossover frequency of different sized polystyrene particles with very good agreement with experimental measurements.
FIG. 6.
Variation of crossover frequency with particle size obtained from our volumetric integration method and several experimental measurements.
V. CONCLUSIONS
We have developed a volumetric integration method assisted by computational modeling to reexamine some of the DEP phenomena and quantify the DEP force such that the effects of particle size, shape, location, particle volumetric polarization, and the influence of the EDL structure along with surface adsorption of co-ions are all inherently considered. In comparison with the other methods such as the point-dipole method and the MST method, our results show that our method can predict very well the DEP force and particle-particle interactions of homogenous particles. Moreover, our method is proven relevant to explaining the crossover behavior of dielectric particles of homogenous and non-homogenous properties, which appears to be a major challenge for other methods including the point-dipole method and the MST method. This work has shed significant new insight into the DEP behavior of particles and provided the basis for elucidating the underlying mechanisms for more complicated DEP phenomena.
ACKNOWLEDGMENTS
We appreciate the use of Clemson's Palmetto Cluster computing resources and the support from the Department of Bioengineering and the Institute for Biological Interfaces of Engineering at Clemson University. The funding supported for this work is provided by Tokyo Electron through a research agreement with Clemson University and by the Institute for Biological Interfaces of Engineering at Clemson University.
References
- 1. Ai, Y. and Qian, S. , “ DC dielectrophoretic particle–particle interactions and their relative motions,” J. Colloid Interface Sci. , 448–454 (2010). 10.1016/j.jcis.2010.03.003 [DOI] [PubMed] [Google Scholar]
- 2. Arnold, W. M. , Schwan, H. P. , and Zimmermann, U. , “ Surface conductance and other properties of latex particles measured by electrorotation,” J. Phys. Chem. , 5093–5098 (1987). 10.1021/j100303a043 [DOI] [Google Scholar]
- 3. Aubry, N. and Singh, P. , “ Control of electrostatic particle-particle interactions in dielectrophoresis,” Europhys. Lett. , 623–629 (2006). 10.1209/epl/i2005-10569-0 [DOI] [Google Scholar]
- 4. Basuray, S. and Chang, H. C. , “ Induced dipoles and dielectrophoresis of nanocolloids in electrolytes,” Phys. Rev. E , 060501 (2007). 10.1103/PhysRevE.75.060501 [DOI] [PubMed] [Google Scholar]
- 5. Basuray, S. , Wei, H. H. , and Chang, H. C. , “Dynamic double layer effects on ac-induced dipoles of dielectric nanocolloids,” Biomicrofluidics , 022801 (2010). 10.1063/1.3455720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Basuray, S. and Chang, H. C. , “ Designing a sensitive and quantifiable nanocolloid assay with dielectrophoretic crossover frequencies,” Biomicrofluidics , 013205 (2010). 10.1063/1.3294575 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Cao, J. , Cheng, P. , and Hong, F. , “ A numerical analysis of force imposed on particles in conventional dielectrophoresis in microchannels with interdigitated electrodes,” J. Electrost. , 620–626 (2008). 10.1016/j.elstat.2008.09.003 [DOI] [Google Scholar]
- 8. Chau, L. H. , Liang, W. , Cheung, F. W. , Liu, W. K. , Li, W. J. , Chen, S. C. , and Lee, G. B. , “ Self-rotation of cells in an irrotational AC E-field in an opto-electrokinetics chip,” PloS One , e51577 (2013). 10.1371/journal.pone.0051577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Church, C. , Zhu, J. , and Xuan, X. , “ Negative dielectrophoresis‐based particle separation by size in a serpentine microchannel,” Electrophoresis , 527–531 (2011). 10.1002/elps.201000396 [DOI] [PubMed] [Google Scholar]
- 10. Elimelech, M. and O'Melia, C. R. , “Effect of electrolyte type on the electrophoretic mobility of polystyrene latex colloids,” Colloids Surf. , 165–178 (1990). 10.1016/0166-6622(90)80194-9 [DOI] [Google Scholar]
- 11. Ermolina, I. and Morgan, H. , “ The electrokinetic properties of latex particles: comparison of electrophoresis and dielectrophoresis,” J. Colloid Interface Sci. , 419–428 (2005). 10.1016/j.jcis.2004.11.003 [DOI] [PubMed] [Google Scholar]
- 12. García-Sánchez, P. , Ren, Y. , Arcenegui, J. J. , Morgan, H. , and Ramos, A. , “ Alternating current electrokinetic properties of gold-coated microspheres,” Langmuir , 13861–13870 (2012). 10.1021/la302402v [DOI] [PubMed] [Google Scholar]
- 13. Gascoyne, P. R. , Wang, X. B. , Huang, Y. , and Becker, F. F. , “ Dielectrophoretic separation of cancer cells from blood,” IEEE Trans. Ind. Appl. , 670–678 (1997). 10.1109/28.585856 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Green, N. G. and Jones, T. B. , “ Numerical determination of the effective moments of non-spherical particles,” J. Phys. D: Appl. Phys. , 78–85 (2007). 10.1088/0022-3727/40/1/S12 [DOI] [Google Scholar]
- 15. Green, N. G. and Morgan, H. , “ Dielectrophoresis of submicrometer latex spheres. 1. Experimental results,” J. Phys. Chem. B , 41–50 (1999). 10.1021/jp9829849 [DOI] [Google Scholar]
- 16. He, R. , Chen, S. , Yang, F. , and Wu, B. , “ Dynamic diffuse double-layer model for the electrochemistry of nanometer-sized electrodes,” J. Phys. Chem. B , 3262–3270 (2006). 10.1021/jp060084j [DOI] [PubMed] [Google Scholar]
- 17. Ho, C. T. , Lin, R. Z. , Chang, W. Y. , Chang, H. Y. , and Liu, C. H. , “ Rapid heterogeneous liver-cell on-chip patterning via the enhanced field-induced dielectrophoresis trap,” Lab Chip , 724–734 (2006). 10.1039/b602036d [DOI] [PubMed] [Google Scholar]
- 18. Ho, C. T. , Lin, R. Z. , Chen, R. J. , Chin, C. K. , Gong, S. E. , Chang, H. Y. , Peng, H. L. , Hsu, L. , Yew, T. R. , Chang, S. F. , and Liu, C. H. , “ Liver-cell patterning lab chip: Mimicking the morphology of liver lobule tissue,” Lab Chip , 3578–3587 (2013). 10.1039/c3lc50402f [DOI] [PubMed] [Google Scholar]
- 19. Hossan, M. R. , Dillon, R. , Roy, A. K. , and Dutta, P. , “Modeling and simulation of dielectrophoretic particle–particle interactions and assembly,” J. Colloid Interface Sci. , 619–627 (2013). 10.1016/j.jcis.2012.12.039 [DOI] [PubMed] [Google Scholar]
- 20. Huang, Y. , Holzel, R. , Pethig, R. , and Wang, X. B. , “ Differences in the AC electrodynamics of viable and non-viable yeast cells determined through combined dielectrophoresis and electrorotation studies,” Phys. Med. Biol. , 1499–1517 (1992). 10.1088/0031-9155/37/7/003 [DOI] [PubMed] [Google Scholar]
- 21. Huang, S. B. , Wu, M. H. , Lin, Y. H. , Hsieh, C. H. , Yang, C. L. , Lin, H. C. , Tseng, C. P. , and Lee, G. B. , “ High-purity and label-free isolation of circulating tumor cells (CTCs) in a microfluidic platform by using optically-induced-dielectrophoretic (ODEP) force,” Lab Chip , 1371–1383 (2013). 10.1039/c3lc41256c [DOI] [PubMed] [Google Scholar]
- 22. Hughes, M. P. and Morgan, H. , “ Dielectrophoretic characterization and separation of antibody-coated submicrometer latex spheres,” Anal. Chem. , 3441–3445 (1999). 10.1021/ac990172i [DOI] [Google Scholar]
- 23. Hughes, M. P. , Morgan, H. , and Flynn, M. F. , “The dielectrophoretic behavior of submicron latex spheres: Influence of surface conductance,” J. Colloid Interface Sci. , 454–457 (1999). 10.1006/jcis.1999.6542 [DOI] [PubMed] [Google Scholar]
- 24. Jones, T. B. and Washizu, M. , “ Multipolar dielectrophoretic and electrorotation theory,” J. Electrost. , 121–134 (1996). 10.1016/0304-3886(96)00006-X [DOI] [Google Scholar]
- 25. Kumar, S. and Hesketh, P. J. , “ Interpretation of ac dielectrophoretic behavior of tin oxide nanobelts using Maxwell stress tensor approach modeling,” Sens. Actuators, B , 1198–1208 (2012). 10.1016/j.snb.2011.12.010 [DOI] [Google Scholar]
- 26. Li, M. , Li, S. , Li, W. , Wen, W. , and Alici, G. , “ Continuous manipulation and separation of particles using combined obstacle‐and curvature‐induced direct current dielectrophoresis,” Electrophoresis , 952–960 (2013). 10.1002/elps.201200546 [DOI] [PubMed] [Google Scholar]
- 27. Liang, E. , Smith, R. L. , and Clague, D. S. , “ Dielectrophoretic manipulation of finite sized species and the importance of the quadrupolar contribution,” Phys. Rev. E , 066617 (2004). 10.1103/PhysRevE.70.066617 [DOI] [PubMed] [Google Scholar]
- 28. Lyklema, J. , Fundamentals of Interface and Colloid Science: Vol. II: Solid-Liquid Interfaces ( Academic Press, London, 1995). [Google Scholar]
- 29. Markx, G. H. , Pethig, R. , and Rousselet, J. , “The dielectrophoretic levitation of latex beads, with reference to field-flow fractionation,” J. Phys. D: Appl. Phys. , 2470–2477 (1997). 10.1088/0022-3727/30/17/013 [DOI] [Google Scholar]
- 30. O'Konski, C. T. , “ Electric properties of macromolecules. V. Theory of ionic polarization in polyelectrolytes,” J. Phys. Chem. , 605–619 (1960). 10.1021/j100834a023 [DOI] [Google Scholar]
- 31. Pethig, R. , “ Review article—dielectrophoresis: Status of the theory, technology, and applications,” Biomicrofluidics , 022811 (2010). 10.1063/1.3456626 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Ramón-Azcón, J. , Ahadian, S. , Obregón, R. , Camci-Unal, G. , Ostrovidov, S. , Hosseini, V. , Kaji, H. , Ino, K. , Shiku, H. , Khademhosseini, A. , and Matsue, T. , “ Gelatin methacrylate as a promising hydrogel for 3D microscale organization and proliferation of dielectrophoretically patterned cells,” Lab Chip , 2959–2969 (2012). 10.1039/c2lc40213k [DOI] [PubMed] [Google Scholar]
- 33. Rinaldi, C. and Brenner, H. , “ Body versus surface force in continuum mechanics: Is the Maxwell stress tensor a physically objective Cauchy stress?,” Phys. Rev. E , 036615 (2002). 10.1103/PhysRevE.65.036615 [DOI] [PubMed] [Google Scholar]
- 34. Song, M. , Lei, Y. , and Sun, H. , “Comparison of spherical and non-spherical particles in microchannels under dielectrophoretic force,” Microsyst. Technol. , 381–391 (2015). 10.1007/s00542-013-2024-4 [DOI] [Google Scholar]
- 35. Vanysek, P. , “Ionic conductivity and diffusion at infinite dilution,” in Handbook of Chemistry and Physics ( CRC Press, Boca Raton, FL, 2000), p. 83. [Google Scholar]
- 36. Wang, X. B. , Huang, Y. , Becker, F. F. , and Gascoyne, P. R. , “A unified theory of dielectrophoresis and travelling wave dielectrophoresis,” J. Phys. D: Appl. Phys. , 1571–1574 (1994). 10.1088/0022-3727/27/7/036 [DOI] [Google Scholar]
- 37. Wang, X. , Wang, X. B. , and Gascoyne, P. R. , “ General expressions for dielectrophoretic force and electrorotational torque derived using the Maxwell stress tensor method,” J. Electrost. , 277–295 (1997). 10.1016/S0304-3886(97)00126-5 [DOI] [Google Scholar]
- 38. Washizu, M. and Jones, T. B. , “ Generalized multipolar dielectrophoretic force and electrorotational torque calculation,” J. Electrost. , 199–211 (1996a). 10.1016/S0304-3886(96)00025-3 [DOI] [Google Scholar]
- 39. Washizu, M. and Jones, T. B. , “ Dielectrophoretic interaction of two spherical particles calculated by equivalent multipole-moment method,” IEEE Trans. Ind. Appl. , 233–242 (1996b). 10.1109/28.491470 [DOI] [Google Scholar]
- 40. Wei, M. T. , Junio, J. , and Ou-Yang, H. D. , “ Direct measurements of the frequency-dependent dielectrophoresis force,” Biomicrofluidics , 012003 (2009). 10.1063/1.3058569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Xie, C. , Chen, B. , Ng, C. O. , Zhou, X. , and Wu, J. , “ Numerical study of interactive motion of dielectrophoretic particles,” Eur. J. Mech.-B/Fluids , 208–216 (2015). 10.1016/j.euromechflu.2014.08.007 [DOI] [Google Scholar]
- 42. Yang, X. and Zhang, G. , “ Simulating the structure and effect of the electrical double layer at nanometre electrodes,” Nanotechnology , 335201 (2007). 10.1088/0957-4484/18/33/335201 [DOI] [Google Scholar]
- 43. Yang, X. and Zhang, G. , “ The effect of an electrical double layer on the voltammetric performance of nanoscale interdigitated electrodes: A simulation study,” Nanotechnology , 465504 (2008). 10.1088/0957-4484/19/46/465504 [DOI] [PubMed] [Google Scholar]
- 44. Zellner, P. , Shake, T. , Sahari, A. , Behkam, B. , and Agah, M. , “ Off-chip passivated-electrode, insulator-based dielectrophoresis (OπDEP),” Anal. Bioanal. Chem. , 6657–6666 (2013). 10.1007/s00216-013-7123-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Zhang, L. and Zhu, Y. , “ Dielectrophoresis of Janus particles under high frequency ac-electric fields,” Appl. Phys. Lett. , 141902 (2010). 10.1063/1.3378687 [DOI] [Google Scholar]
- 46. Zhao, Y. , Hodge, J. , Brcka, J. , Faguet, J. , Lee, E. , and Zhang, G. , “ Elucidating the mechanism governing the cell rotation behavior under DEP,” in Proceedings of the 2013 COMSOL Conference in Boston (2013). [Google Scholar]