Skip to main content
NCBI home page
Howard Hughes Medical Institute Author Manuscripts logoLink to Howard Hughes Medical Institute Author Manuscripts
. Author manuscript; available in PMC: 2017 Jun 5.
Published in final edited form as: Nat Chem. 2016 Dec 5;9(4):353–360. doi: 10.1038/nchem.2673

Computational Design of Self-Assembling Cyclic Protein Homo-oligomers

Jorge A Fallas 1,2,*, George Ueda 1,2,*, William Sheffler 1,2,*, Vanessa Nguyen 2, Dan E McNamara 4,7, Banumathi Sankaran 5, Jose Henrique Pereira 5,6, Fabio Parmeggiani 1,2, TJ Brunette 1,2, Duilio Cascio 4, Todd R Yeates 4, Peter Zwart 5, David Baker 1,2,3,#
PMCID: PMC5367466  NIHMSID: NIHMS823204  PMID: 28338692

Abstract

Self-assembling cyclic protein homo-oligomers play important roles in biology and the ability to generate custom homo-oligomeric structures could enable new approaches to probe biological function. Here we report a general approach to design cyclic homo-oligomers that employs a new residue pair transform method for assessing the design ability of a protein-protein interface. This method is sufficiently rapid to enable systematic enumeration of cyclically docked arrangements of a monomer followed by sequence design of the newly formed interfaces. We use this method to design interfaces onto idealized repeat proteins that direct their assembly into complexes that possess cyclic symmetry. Of 96 designs that were experimentally characterized, 21 were found to form stable monodisperse homo-oligomers in solution, and 15 (4 homodimers, 6 homotrimers, 6 homotetramers and 1 homopentamer) had solution small angle X-ray scattering data consistent with the design models. X-ray crystal structures were obtained for five of the designs and each of these were shown to be very close to their design model.

Cyclic homo-oligomers assembled from multiple identical protein subunits symmetrically arranged around a central axis play key roles in many biological processes including catalysis, signaling and allostery1-3. Despite their prevalence in natural systems, currently there is no systematic approach to design cyclic homo-oligomers starting from a monomeric protein structure. A number of prior design studies have relied on canonical structural motifs such as α-helical coiled coils4, β-propeller motifs5,6, unpaired β-strands7 or metal binding sites8. Recently a C2 dimer mediated by an α-helical interface was reported but the design protocol required extensive iteration between computation and experiment9. In contrast, there has been considerable progress in designing proteins that fold into predetermined target structures ranging from idealized versions of natural folds10-13 to topologies that appear not to have been explored during evolution14,15. Particularly interesting from an engineering perspective are de novo designed α-helical repeat proteins with a wide range of shapes which can be readily shortened or lengthened simply by changing the number of repeats in their sequence15.

Here we present a general method for designing cyclic homo-oligomers in silico and use it to design interfaces onto recently developed repeat proteins13,15,16 that direct their assembly into dimeric, trimeric, tetrameric and pentameric complexes. Structural characterization shows that many of the designs adopt the target oligomerization state and structure, demonstrating that we have a basic understanding of the determinants of oligomerization state. The capability of designing proteins with tunable shape, size, and symmetry enables rigid display of binding domains at arbitrary orientations and distances for a range of biological applications.

Results

The self-assembly of naturally occurring complexes is driven by chemical and shape complementarity. Protein-protein interfaces are generally comprised of a hydrophobic core that is buried upon binding and surrounded by a rim of polar residues that prevent non-specific aggregation17-21. We developed a design strategy to generate such interfaces between protein monomers docked in a range of cyclic geometries. The strategy has two steps (Figure 1): first, low resolution docking to sample and rank symmetric arrangements of a given scaffold protein based on their design ability (the likelihood of finding an amino acid sequence that can stabilize a given rigid body conformation), and second, full atom RosettaDesign22 calculations to optimize the sequence at the protein-protein interfaces for high affinity binding. To explore the generality of the method, symmetries ranging from C2 through C6 were designed. 96 designs were selected for experimental characterized, and 4 homodimers, 6 homotrimers, 6 homotetramers and 1 homopentamer were found to form stable monodisperse homooligomers in solution.

Figure 1.

Figure 1

Open in a new tab

Computational design protocol. Left, starting with a monomeric protein we exhaustively sample cyclic docked configurations, score them using the RPX model and generate sequences to drive the complex formation using a full atom RosettaDesign21 calculation. Right, schematic representation of the RPX model scoring procedure.

Computational Design

Existing methods for protein-protein docking fall into three general categories: (1) voxelized rigid representations with Fast Fourier Transform (FFT)-based docking23,24, (2) docking based on patches of high-resolution local shape complementarity25, and (3) Monte Carlo sampling with soft centroid models26,27. The first two categories are not ideal for the protein design problem because the precise shape and chemical detail of the docked surfaces are unavailable, as the interface residues are not known in advance. The approach we take is most similar to (3), in which docked backbones are generated and then scored using a low-resolution representation of the proteins (requiring only the backbone coordinates and secondary structure assignments) but with two notable improvements. First, we employ a six-dimensional implicit side chain scoring methodology, which better predicts the result of subsequent full atom design calculation than a traditional coarse-grained model, and second, we use an enumerative strategy to generate docked backbones, which samples more robustly the low-dimensional docking space than a Monte Carlo search.

In past efforts, scoring at the docking stage has been accomplished using coarse-grained models in which the absent side chains are represented by one or two points in space, and the interaction potential between two amino acids is evaluated as a function of the distance or distances between these points, and in some cases an associated angle27-31. These representations are incomplete since they do not capture the full six-dimensional rigid body relationship between pairs of side chains. To avoid loss of information, we have developed a Residue Pair Transform (RPX) model that represents the interaction between two residues by the full six dimensional rigid body transformation between their respective backbone N, Cα and C atoms. We employ a precompiled database of all favorable residue pair interactions found in structures from the Protein Data Bank involving alanine, isoleucine, leucine, valine, and methionine, binning these data based on the rigid body transform between amino acids. The score of a given docked configuration is the sum, over each pair of residues across the interface, of the lowest Rosetta full atom energy found in the associated spatial transformation bin of the database. This approach predicts the interface energy resulting from full atom sequence design calculation better than the Rosetta centroid energy function (Supplementary Figure 1). As the residue-pair-transform database is compiled offline, arbitrary data selection (different subsets of amino acid identities) and processing (alternative smoothing and scoring schemes) can be employed with no impact on runtime of the docking calculations. Details on the database utilized for this study are available in the Methods and Supplementary Methods online.

To best leverage the RPX scoring methodology described above, we employ deterministic sampling of the complete docking space. The configurational space for cyclic docking is four dimensional: the usual six degrees of freedom required for orienting a rigid body, minus translations along and rotations around the symmetry axis of the oligomer (to which the structure is invariant). These four degrees of freedom can be reduced effectively to three by the requirement that the subunits must be roughly in contact. We realize this dimensionality reduction using a fast slide-into-contact algorithm. To rapidly compute the translational distance along a slide vector, which will bring two rigid clouds of atoms into contact, we create a pair of two-dimensional arrays containing the leading face of each cloud along the slide vector. Corresponding cells of each array are checked, and the pair of atoms with least separation along the slide vectors defines an upper bound on the slide distance. The final slide distance is calculated using a local octree-like data structure (Methods). This results in a significant savings in the total number of samples that must be evaluated compared to a simpler brute force search.

For the ten best RPX scoring docked arrangements of each monomer, low energy and shape complementary interfaces between protomers were generated using Rosetta sequence design calculations employing a Monte-Carlo simulated annealing protocol (details on the RosettaScript32 encoding the protocol are provided in the methods section and supplementary methods online).Designs were filtered on number of mutations, buried surface area, shape complementarity and computed interaction energy (Supplementary Figure 2), and 96 were selected for experimental characterization. The 11 dimers, 34 trimers, 19 tetramers, 17 pentamers and 15 hexamers are named according to the following nomenclature: the first 4 letters refer to the scaffold protein (as described in the supplementary information), the symmetry is denoted as Cn, and finally an integer is added to differentiate oligomers of identical symmetry and scaffold identity.

Protein Expression and Oligomerization State Screening

Synthetic genes encoding each of the 96 designs were synthesized and cloned into a vector with a T7 promoter system and either an N- or C-terminal (His)6tag, and the corresponding proteins expressed in E. coli. The proteins were purified by immobilized nickel-affinity chromatography (Ni2+ IMAC) and size-exclusion chromatography (SEC). 64 designs were soluble and amenable to purification (Supplementary Figure 3 and 4). The oligomerization states for 44 designs that eluted from SEC with a single predominant species were determined by size-exclusion chromatography in tandem with multi-angle light scattering (SEC-MALS). For 21 of the designs, the molecular weights determined by light scattering agreed with the designed oligomerization state.

Structural Characterization

To further assess the configuration of the designed proteins in solution, small-angle X-ray scattering (SAXS) measurements were performed on designs that had predominantly monodisperse traces in the SEC screen. A total of 26 designs (the 21 with consistent SEC-MALS data and 5 additional designs that had monodisperse SEC profiles) were characterized with this technique and the measured scattering profile was compared to that expected from the computational model. Designs with a deviation of less than or equal to 3.1 a.u. using the χ measure33 and a deviation of less than 11% between the computed and experimental radius of gyration were considered to be in the designed supramolecular arrangement (these thresholds were chosen based on the deviations between computed and measured values for designs with crystal structures consistent with the corresponding models; see below).

Of the 26 designs, 15 fulfill these criteria; 5 dimers, 6 trimers, 3 tetramers, and 1 pentamer. The docked configurations and designed interfaces of 13 of these are unique (three of the trimers have similar geometries with pairwise r.m.s.d. values between 1.9-2.5Å; the lowest pairwise r.ms.d. among the remaining designs is 5.3Å with no similarity in designed interface). Computational models, in silico symmetric docking energy landscapes, SEC-MALS chromatograms and SAXS experimental and computed profiles for the 15 designs are summarized in Figure 2 and Supplementary Figure 5; data on the full set of designs is provided in Supplementary Tables 1-4.

Figure 2.

Figure 2

Open in a new tab

Assessment of the solution conformation of selected cyclic oligomers. From left to right: computational model, symmetric docking energy landscape, SEC chromatogram used for molecular weight determination, and SAXS scattering profiles experimentally measured (black dots) and computed from the model (red line). “MW (design)” refers to the molecular weight of the oligomer design and “MW (MALS)” refers to the experimentally determined molecular weight. a, ank3C2_1. b, HR79C2. c, HR08C3 d, HR00C3_2. e, HR04C4_1. f, HR10C5_2. Analogous data for the nine other successful designs are provided in Sup Fig 5.

Crystal structures that contain the designed interface were obtained for five of the designed proteins: two dimers, two trimers and one tetramer, and are compared to the design models in Figure 3. For each of the five cases the side chain rotamers of the hydrophobic residues are similar to those in the design model. The two dimers, ank3C2_1 and ank1C2_1, are both built from idealized ankyrin repeat proteins and are shown in Figure 3a and 3b. The ank3C2_1 design has a large hydrophobic patch (1100 Å2 ) that is buried upon binding; all interface hydrophobic side chains are in the same rotameric state in the design model and the crystal structure with the exception of methionine 90 (Figure 3a, right panel). The backbone r.m.s.d. between the design model and the crystal structure is 1.0 Å. The agreement between the model and the structure of ank1C2_1 (Figure 3b) is even closer: both polar and hydrophobic side chain rotamers were correct and the r.m.s.d. to the model is only 0.9 Å.

Figure 3.

Figure 3

Open in a new tab

Comparison between the experimentally determined crystal structures and corresponding design models. Crystal structures are shown in cyan and models in gray. Left column, full model and crystal structure superposition; Right column, superposition showing hydrophobic side chains at the designed interface. a, ank3C2_1 (r.ms.d. to model 1 Å) b, ank1C2_1 (r.ms.d. to model 0.9 Å) c, 1na0C3_3 (r.ms.d. to model 1 Å) d, HR00C3_2 (r.ms.d. to model 0.9 Å) e, ank1C4_2 pair of chains (r.ms.d. to model 1.1 Å)

The two trimeric designs with solved structures are 1na0C3_3 (Figure 3c) built from a consensus designed tpr protein16, and HR00C3_2 (Figure 3d) built from a de novo designed repeat protein. 1na0C3_3 has a hydrophobic core that lies on the 3-fold axis formed by residues in all subunits. The r.m.s.d. between the crystal structure and design model is 1.0 Å. HR00C3_2 contains a pore on the symmetry axis and is stabilized by three separate heterologous interfaces. This trimer was designed using the computational model of a designed repeat protein whose structure had not previously been confirmed by X-ray crystallography. Thus the crystal structure, which has a backbone r.m.s.d. to the model of 0.9 Å, validates the design of both the monomer and oligomer simultaneously. This ability to accurately design higher order structures based on design models of monomers will considerably streamline future computational design of nanomaterials using monomers with custom designed properties.

For the two dimers and the two trimers, the χ values between the measured SAXS scattering profiles and the profiles computed from either the corresponding design models or crystal structures are less than 3.1. In contrast, the experimental SAXS data for the designed tetramer, ank1C4_2 (Figure 3e), deviates considerably from that computed using the crystal structure (Supplementary Figure 6). The ank1C4_2 crystal structure adopts a C2 symmetric tetrameric structure in which 2 pairs of chains accurately match the design model (r.m.s.d. of 1.1 Å), but exhibit clear overall distortion relative to the C4 symmetric design model (r.m.s.d. of 4.5 Å). There are two distinct interfaces present in the structure, one of which corresponds to the designed interface. The experimental SAXS profile is closer to the design model of the tetramer than the crystal structure, and hence it seems likely that the symmetry breaking in the crystal is due to lattice contacts.

A sixth structure was solved for design ank4C4, which shows a single symmetric peak by SEC and forms a tetrameric complex in solution as determined by MALS. The SAXS profile of this design does not match that computed from the design model (χ = 3.8), and the crystal structure exhibits D2 symmetry rather than the target C4 symmetry. The SAXS profile computed from the D2 oligomer matches the measured scattering curve better than the target C4 model (χ = 1.2) indicating that the D2 state corresponds to the conformation of the design in solution (Supplementary Figure 8).

Subunit extensions

To explore the modularity of the designs and the robustness of the designed interfaces, we extended two of the designed oligomers by appending two additional repeats to the original constructs. Extended versions of ank1C2_1 and HR04C4_1 were expressed and characterized as described above. SEC-MALS traces of the long constructs show the expected shifts to larger apparent sizes compared to the original constructs (Figure 4, third column), and the calculated molecular weights are close to those expected. Experimental SAXS profiles of the extended designs are in good agreement with the extended computational models (χ values are given in Supplementary Table 3) suggesting that the supramolecular arrangement of the subunits is maintained upon extending the scaffold protein. This ability to maintain oligomer geometry while extending the length of the monomers will be very useful for systematically varying the distance between binding moieties and for nanomaterial design.

Figure 4.

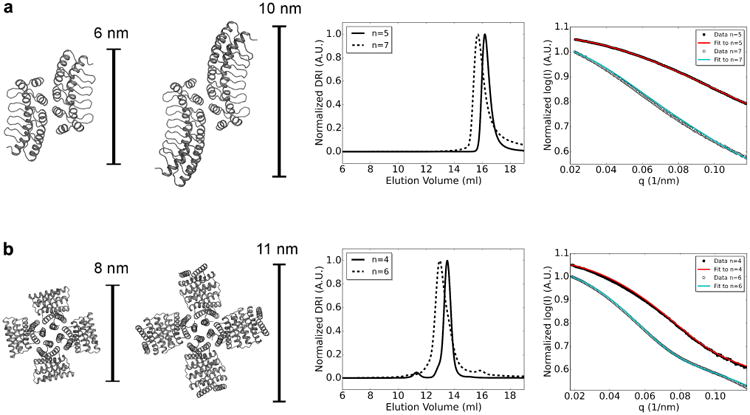
Figure 4

Open in a new tab

Robustness of designs to subunit extension by repeat addition. From left to right: computational model of the original design, computational model of the extended design, SEC-MALS chromatogram used for molecular weight determination (n represents number of repeat modules in each monomer; original design: solid line; extended design: dotted line), SAXS scattering profiles (original design: experimental data in black circles, computed profile in red; extended design: experimental data open circles, computed profile in cyan). a, ank1C2_1. B, HR04C4_1.

Resilience to guanidine denaturation

The repeat protein scaffolds used to construct the designed oligomers are very stable proteins, and thus guanidine denaturation can be used to probe the stability of the designed interfaces independent of effects on the monomers. Four designed oligomers (one selected from each symmetry C2-C5) were purified in an initial round of IMAC and SEC, and subsequently run through SEC-MALS in TBS supplemented with 1M or 2M GuHCl. In both conditions, all four designs remained in their designed oligomeric state (as determined by MALS) without indications of smaller assembly formation (Supplementary Figure 7).

Discussion

Our results show that homo-oligomeric protein complexes with cyclic symmetry can be generated from repeat protein building blocks by computationally designing geometrically complementary, low-energy interfaces. A key advance is the new fast method for assessing design ability that provides a reasonable estimate of the energy obtained after a full atom combinatorial sequence design calculation with roughly six orders of magnitude less computational cost. This allows exhaustive evaluation of the possible cyclically docked configurations of a monomer, which would not be possible with a combinatorial, all-atom sequence design calculation. The broad applicability of the computational pipeline developed here is highlighted by the number of successful designs (15) and symmetries (C2-C5). Supplementary Figure 9 provides an overview of all of the experimentally validated dimers, trimers, tetramers and pentamer--the broad range of structures and the variety of interface geometries and architectures far exceeds that reported in any previous study (the elegant beta propeller designs described in ref 6 are shown for comparison). The combination of RPX search for designable interfaces followed by Rosetta all atom design calculations can clearly generate a wide range of new interfaces involving three to five alpha helices; the ability of the approach to design new beta sheet and loop containing interfaces is an area for future investigation.

Progress in protein design will require study not only of the successes but also the failures. The results reported in this paper provide a valuable resource for understanding failure modes as the input scaffolds are all very stable designed proteins (in previous design studies, the often unknown stability of the starting native scaffolds and the robustness to amino acid substitutions were potentially confounding factors). We are able to distinguish distinct failure modes for the designs reported: 32 were not expressed solubly in E. Coli, 24 adopt multiple oligomerization states, 4 were monomeric, 15weremonodisperse but had an oligomerization state different from that designed, and 6 occupied the designed oligomerization state but had unanticipated configurations based on SAXS data. Analysis of the properties of the design models revealed that designs with (1) a high total charge (greater than -50), (2) small (under 750 Å2) interfaces, (3) poor shape complementarity (sc< 0.625), or (4) for which asymmetric pairwise docking calculations found much lower energy alternative arrangements than the two body interactions in the design model were generally unsuccessful. Furthermore, despite the success with HR00C3_2, designs based on monomers with crystal structures had higher success rates (19%) than those based on monomers validated only by SAXS (4%). The fraction of designs experimentally confirmed to be in the designed state increases from 15/96 in the overall population to 14/45 restricting to models that satisfy the above criteria (low electrostatic repulsion, larger shape complementary interfaces, absence of much lower energy competing dimeric states, and crystallographically validated monomer structures). Evidently, we currently understand some but not all the factors determining the accuracy of the design calculations--as this is clearly an important area for future investigation, we provide all of the experimental data for both unsuccessful and successful designs, the design models and sequences, and a variety of metrics computed from the models in the supplementary material.

The design success rate also clearly decreases with increasing oligomerization state -- indeed there were no successes with hexamers. Higher oligomerization states present several challenges: an increase in translational entropy loss (formation of 3 dimers from 6 subunits results in 3 independently translating bodies, whereas formation of a single hexamer results only in one), an increase in electrostatic repulsion, and a decrease in the difference in interface geometry between competing alternative oligomerization states (smaller reorientations are required to convert a pentamer to a hexamer than a dimer to a trimer). There are clear ways forward to address the second and third challenges: the total charge of the designs can be adjusted to be close to zero at pH 7.0 by suitable redesign of the surface (although some experimentation may be required to maintain solubility), and employing hydrogen bond networks34 could provide the conformational specificity required to distinguish between higher order oligomerization states.

Our robust design pipeline can be combined with the modularity of computationally designed repeat proteins to control the three-dimensional arrangement of the protomers at multiple length scales. While the designed interfaces control the nanoscale three-dimensional arrangement, extensions of the repeat proteins allow for the placement of functional motifs with sub-nanometer resolution in each of the interacting proteins. Designed proteins can remain folded under strongly denaturing conditions14, and the design process provides unparalleled control over their geometry15,35 and amino acid composition allowing for reactive chemical moieties, such as thiols or aromatic rings, to be reserved to engineer function in downstream applications. An immediate use for these designed oligomers is to probe how the geometry and valency of tethered signaling molecules affects the clustering of receptors and the cellular response. The relationship between ligand valency, spatial orientation, and signaling outcome is not well understood, and designed homoligomerization with systematically tunable lengths should be very well suited for investigating this and other basic biochemical questions.

Methods

Scaffold Set

A set of 17 monomeric designed repeat proteins with high-resolution crystal structures as well as 6 computational models that were validated by SAXS were used as a scaffold set for our design protocol. PDB IDs of the scaffolds used are available in supplementary methods online.

Motif Database and Scoring

We construct Cartesian frames given two N-Cα -C backbone segments across the symmetric interface. The relative position and orientation of the two N-Cα-C segments form a six dimensional space that can be divided into bins, assigning to any possible position/orientation a bin index. The best-scoring, superimposable residue-pair available in a large database of candidates can then be found with a single memory lookup keyed on the bin index. The residue pair-motif database was constructed from residue pairs observed in a set of high quality structures from the Protein Data Bank (PDB), filtered for energetic favorability, separation by at least 10 residues in sequence, and residue composition of only alanine, isoleucine, leucine, valine, and methionine. To compute an aggregate score for each conformation, we consider all pairs of N-Cα-C backbone segments across the newly formed symmetric interface within 9Å of one another. For each such pair, the score of the best superimposable residue pair motif is looked up, and the results are summed.

Cyclic Docking

To generate cyclic homooligomeric arrangements of n copies of a protein monomer, we center it at the origin, finely sample the 3 rotational degrees of freedom, generate a symmetric copy by (360/n)° rotation around the Z-axis, and slide the two bodies into contact along the X-axis allowing a small range of X offsets close to the contact value. For each of these, the axis of symmetry is determined from the relative orientation of the two subunits, and the full oligomer is generated and evaluated using the residue pair motif database. A rapid slide into contact operation is required for this sampling strategy. Computing the slide distance along a given slide vector is accomplished using two two-dimensional arrays perpendicular to the slide direction into which the atoms along the leading face of each body are placed. Corresponding cells are checked, and the pair with the least separation provides an estimate of the slide distance. The bodies are placed according to this estimate, but may still have clashes. All contacting pairs of atoms across the bodies are checked using an octree-like data structure, and the bodies are backed off so as to relieve the largest clash found. This process is repeated until no clashes are found. In practice, only one or two iterations through the fast clash check are required in most cases, making the slide move rapid. The source code and pre-compiled executable along with the scoring tables and motif database are available upon request.

Interface Design

An interface design protocol was implemented in RosettaScripts and is described briefly here and extensively in the supplementary methods available online. In each design trajectory, the protomer was initially perturbed by a small translation perpendicular to the axis of symmetry, as well as a random rotation around its center of mass. An oligomer with the specified cyclic symmetry was then generated using the information stored in the symmetry definition file (described in the supplementary methods). Amino acids at the interface were optimized using theMonte-Carlo simulated annealing protocol available in the Rosetta Macromolecular Modeling suite. An initial optimization step was executed with a modified score function with a soft repulsive term. Once a sequence was converged upon, designable positions were allowed to minimize side chain torsion angles using the same reduced repulsive term weight. A subsequent round of design and minimization was conducted, but with the standard score function in order to obtain a sequence that corresponds to a local minimum of the energy function. Initially, the extended rotamer library available in Rosetta was utilized but in later design rounds it was augmented with the rotamers available in the residue pair motif database. Individual design trajectories were filtered by the following criteria: difference between Rosetta energy of bound (oligomeric) and unbound (monomeric) states less than -20.0 Rosetta energy units, interface surface area greater than 700 Å2, Rosetta shape complementarity greater than 0.65, and less than 45 mutations made from the respective native scaffold. Designs that passed these criteria were manually inspected and refined by single point reversions for mutations that were deemed as not contributing to stabilizing the bound state of the interface. The design with the best overall scores for each docked configuration was then added to a set of finalized proteins to be experimentally validated.

Details on protein expression, purification, size exclusion chromatography, molecular weight determination and structural characterization of the proteins characterized in this study are available in the supplementary methods online.

Supplementary Material

1

Table 1.

Summary of the experimental results for the designed cyclic homooligomeric proteins.

Symmetry Designs Soluble Expression Target Molecular Weight Structural Validation
C2 11 11/11 7/11 5/11
C3 34 20/34 6/34 6/34
C4 19 13/19 6/19 3/19
C5 17 9/17 1/17 1/17
C6 15 11/15 1/15 0/15
total 96 (100 %) 64 (67 %) 21 (22 %) 15 (16 %)
Open in a new tab

Acknowledgments

This work was supported by the Howard Hughes Medical Institute, Air Force Office for Scientific Research AFOSR FA950-12-10112), the National Science Foundation (NSF MCB-1445201 and CHE-1332907), the Bill and Melinda Gates Foundation (OPP1120319) and the Defense Threat Reduction Agency (HDTRA1-11-C-0026 AM06). We thank Rie Koga and Lauren Carter for assistance with SEC-MALS. We thank Michael Collazo and Michael Sawaya supported by DOE Grant DE-FC02-02ER63421. We thank M. Capel, K.Rajashankar, N.Sukumar, J.Schuermann, I. Kourinov and F. Murphy at NECAT supported by grants from the National Center for Research Resources (5P41RR015301-10) and the National Institute of General Medical Sciences (P41 GM103403-10)from the National Institutes of Health. Use of the APS is supported by the DOE under Contract DE-AC02-06CH11357. X-ray crystallography and SAXS data were collected at the Advanced Light Source (ALS, Lawrence Berkeley National Laboratory, Berkeley, CA Department of Energy, contract no. DE-AC02-05CH11231); SAXS data was collected through the SIBYLS mail-in SAXS program under the aforementioned contract no. and is funded by DOE BER IDAT, NIH MINOS (RO1GM105404), and the Advanced Light Source, and we thank Kathryn Burnett and Greg Hura. The Berkeley Center for Structural Biology is supported in part by the National Institutes of Health, National Institute of General Medical Sciences, and the Howard Hughes Medical Institute. The Advanced Light Source is supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.

Footnotes

Author Information: Crystal structures have been deposited in the RCSB protein data bank with the accession numbers 5HRY (ank3C2_1), 5HRZ (1na0C3_3), 5HS0 (ank1C4_2), 5KBA (ank1C2_1), 5K7B (HR00C3_2) and 5KWD (ank4C4).

Author contributions: J.A.F., G.U., W.S. and D.B. designed the research. W.S. developed the RPX method and wrote the program code. J.A.F., G.U. and V.N. carried out design calculations, purified and biophysically characterized the designed proteins. F.P. and T.B. designed and characterized monomeric repeat proteins used as scaffolds. D.E.M., D.C., T.R.Y., J.H.P., G.U. and J.A.F crystallized the designed proteins. D.E.M, D.C., B.S. and P.Z. collected and analyzed crystallographic data. J.A.F., D.E.M., D.C., B.S. and P.Z. solved the structures. All authors discussed results and commented on the manuscript.

References

  • 1.Ali MH, Imperiali B. Protein oligomerization: How and why. Bioorganic & Medicinal Chemistry. 2005;13:5013–5020. doi: 10.1016/j.bmc.2005.05.037. [DOI] [PubMed] [Google Scholar]
  • 2.Goodsell DS, Olson AJ. Structural symmetry and protein function. Annual Review of Biophysics and Biomolecular Structure. 2000;29:105–153. doi: 10.1146/annurev.biophys.29.1.105. [DOI] [PubMed] [Google Scholar]
  • 3.Nishi H, Hashimoto K, Madej T, Panchenko AR. Evolutionary, Physicochemical, and Functional Mechanisms of Protein Homooligomerization. Oligomerization in Health and Disease. 2013;117:3–24. doi: 10.1016/b978-0-12-386931-9.00001-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Fletcher JM, et al. A Basis Set of de Novo Coiled-Coil Peptide Oligomers for Rational Protein Design and Synthetic Biology. Acs Synthetic Biology. 2012;1:240–250. doi: 10.1021/sb300028q. [DOI] [PubMed] [Google Scholar]
  • 5.Smock RG, Yadid I, Dym O, Clarke J, Tawfik DS. De Novo Evolutionary Emergence of a Symmetrical Protein Is Shaped by Folding Constraints. Cell. 2016;164:476–486. doi: 10.1016/j.cell.2015.12.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Voet ARD, Nogushi H, Addy C, Simoncini D, Terada D, Unzai S, Park SY, Zhang KYJ, Tame JRH. Computational Design of a Self-assembling Symmetrical β-propeller protein. PNAS. 2014;111:15102–15107. doi: 10.1073/pnas.1412768111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Stranges PB, Machius M, Miley MJ, Tripathy A, Kuhlman B. Computational design of a Symmetric Homodimer Using Beta-strand Assembly. Proceedings of the National Academy of Sciences of the United States of America. 2011;108:20562–20567. doi: 10.1073/pnas.1115124108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Der BS, et al. Metal-Mediated Affinity and Orientation Specificity in a Computationally Designed Protein Homodimer. Journal of the American Chemical Society. 2012;134:375–385. doi: 10.1021/ja208015j. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Mou Y, Huang PS, Hsu FC, Huang SJ, Mayo SL. Computational Design and Experimental Verification of a Symmetric Protein Homodimer. Proceedings of the National Academy of Sciences of the United States of America. 2015;112:10714–10719. doi: 10.1073/pnas.1505072112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Huang PS, et al. De novo Design of an Ideal TIM-barrel Scaffold. Protein Science. 2015;24:186–186. [Google Scholar]
  • 11.Lin YR, et al. Control Over Overall Shape and Size in de novo Designed Proteins. Proceedings of the National Academy of Sciences of the United States of America. 2015;112:E5478–E5485. doi: 10.1073/pnas.1509508112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Koga N, et al. Principles for Designing Ideal Protein Structures. Nature. 2012;491:222–227. doi: 10.1038/nature11600. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Parmeggiani F, et al. A General Computational Approach for Repeat Protein Design. Journal of Molecular Biology. 2015;427:563–575. doi: 10.1016/j.jmb.2014.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Huang PS, et al. High Thermodynamic Stability of Parametrically Designed Helical Bundles. Science. 2014;346:481–485. doi: 10.1126/science.1257481. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Brunette TJ, et al. Exploring the Repeat Protein Universe through Computational Protein Design. Nature. 2015 doi: 10.1038/nature16162. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Main ERG, Xiong Y, Cocco MJ, D'Andrea L, Regan L. Design of Stable Alpha-helical arrays from an Idealized TPR Motif. Structure. 2003;11:497–508. doi: 10.1016/s0969-2126(03)00076-5. [DOI] [PubMed] [Google Scholar]
  • 17.Pechmann S, Levy ED, Tartaglia GG, Vendruscolo M. Physicochemical Principles that Regulate the Competition between Functional and Dysfunctional Association of Proteins. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:10159–10164. doi: 10.1073/pnas.0812414106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Levy ED, Teichmann S. Structural, Evolutionary, and Assembly Principles of Protein Oligomerization. Oligomerization in Health and Disease. 2013;117:25–51. doi: 10.1016/b978-0-12-386931-9.00002-7. [DOI] [PubMed] [Google Scholar]
  • 19.Bahadur RP, Chakrabarti P, Rodier F, Janin J. Dissecting Subunit Interfaces in Homodimeric Proteins. Proteins-Structure Function and Bioinformatics. 2003;53:708–719. doi: 10.1002/prot.10461. [DOI] [PubMed] [Google Scholar]
  • 20.Bahadur RP, Chakrabarti P, Rodier F, Janin JA. Dissection of Specific and Non-specific Protein - Protein Interfaces. Journal of Molecular Biology. 2004;336:943–955. doi: 10.1016/j.jmb.2003.12.073. [DOI] [PubMed] [Google Scholar]
  • 21.Janin J, Bahadur RP, Chakrabarti P. Protein-protein Interaction and Quaternary Structure. Quarterly Reviews of Biophysics. 2008;41:133–180. doi: 10.1017/s0033583508004708. [DOI] [PubMed] [Google Scholar]
  • 22.Leaver-Fay A, et al. Methods in Enzymology, Vol 487: Computer Methods, Pt CMethods in Enzymology. Elsevier Academic Press Inc; 2011. pp. 545–574. [Google Scholar]
  • 23.Chen R, Weng ZP. Docking Unbound Proteins Using Shape Complementarity, Desolvation, and Electrostatics. Proteins-Structure Function and Genetics. 2002;47:281–294. doi: 10.1002/prot.10092. [DOI] [PubMed] [Google Scholar]
  • 24.Pierce B, Tong WW, Weng ZP. M-ZDOCK: a Grid-based Approach for C-n Symmetric Multimer Docking. Bioinformatics. 2005;21:1472–1478. doi: 10.1093/bioinformatics/bti229. [DOI] [PubMed] [Google Scholar]
  • 25.Schneidman-Duhovny D, Inbar Y, Nussinov R, Wolfson HJ. PatchDock and SymmDock: Servers for Rigid and Symmetric docking. Nucleic Acids Research. 2005;33:W363–W367. doi: 10.1093/nar/gki481. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Gray JJ, Baker D. Protein-protein Docking Predictions with RosettaDock. Biophysical Journal. 2004;86:306A–306A. [Google Scholar]
  • 27.Gray JJ, et al. Protein-protein Docking with Simultaneous Optimization of Rigid-body Displacement and Side-chain Conformations. Journal of Molecular Biology. 2003;331:281–299. doi: 10.1016/s0022-2836(03)00670-3. [DOI] [PubMed] [Google Scholar]
  • 28.Wei H, et al. Lysozyme-stabilized gold fluorescent cluster: Synthesis and Application as Hg2+ Sensor. Analyst. 2010;135:1406–1410. doi: 10.1039/c0an00046a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Lu M, Dousis AD, Ma J. OPUS-PSP: An Orientation-dependent Statistical All-atom Potential Derived from Side-chain Packing. Journal of Molecular Biology. 2008;376:288–301. doi: 10.1016/j.jmb.2007.11.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Zheng WH, Schafer NP, Davtyan A, Papoian GA, Wolynes PG. Predictive Energy Landscapes for Protein-protein Association. Proceedings of the National Academy of Sciences of the United States of America. 2012;109:19244–19249. doi: 10.1073/pnas.1216215109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.DeBartolo J, Dutta S, Reich L, Keating AE. Predictive Bcl-2 Family Binding Models Rooted in Experiment or Structure. Journal of Molecular Biology. 2012;422:124–144. doi: 10.1016/j.jmb.2012.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Fleishman SJ, et al. RosettaScripts: A Scripting Language Interface to the Rosetta Macromolecular Modeling Suite. Plos One. 2011;6 doi: 10.1371/journal.pone.0020161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Schneidman-Duhovny D, Hammel M, Sali A. FoXS: a Web server for Rapid Computation and Fitting of SAXS Profiles. Nucleic Acids Research. 2010;38:W540–W544. doi: 10.1093/nar/gkq461. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Boyken SE, et al. De novo Design of Protein Homo-oligomers with Modular Hydrogen-Bond Network-mediated Specificity. Science. 2016;352:680–687. doi: 10.1126/science.aad8865. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Park K, et al. Control of Repeat-protein Curvature by Computational Protein Design. Nature Structural & Molecular Biology. 2015;22:167–174. doi: 10.1038/nsmb.2938. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1
NIHMS823204-supplement-1.pdf (6.7MB, pdf)

RESOURCES