The First Letter Position Effect in Visual Word Recognition: The Role of Spatial Attention

Abstract

A prominent question in visual word recognition is whether letters within a word are processed in parallel or in a left to right sequence. Although most contemporary models posit parallel processing, this notion seems at odds with well-established serial position effects in word identification that indicate preferential processing for the initial letter. The present study reports 4 experiments designed to further probe the locus of the first position processing advantage. The paradigm involved masked target words presented for short durations and required participants to subsequently select from two alternatives, one which was identical to the target and one that differed by a single letter. Experiment 1 manipulated the case between the target and the alternatives to ensure that previous evidence for a first position effect was not due to simple perceptual matching. The results continued to yield a robust first position advantage. Experiment 2 attempted to eliminate post-perceptual decision processes as the explanatory mechanism by presenting single letters as targets and requiring participants to select an entire word that contained the target letter at different positions. Here the first position advantage was eliminated, suggesting post-perceptual decision processes do not underlie the effect. The final two experiments presented masked stimuli either all vertically (Experiment 3) or randomly intermixed vertical and horizontal orientation (Experiment 4). In both cases, a robust first position advantage was still obtained. We consider alternative interpretations of this effect and suggest that these results are consistent with a rapid deployment of spatial attention to the beginning of a target string which occurs post-stimulus onset.

The computation of letter identity and position within a word is a critical component of visual word recognition. This computation must occur rapidly and accurately within a very crowded perceptual space. Questions regarding how such computations are performed have been the subject of much debate in the scientific literature. In particular, research has addressed whether letters are activated simultaneously or are processed in a left to right sequence across the word. Most contemporary models of visual word recognition posit that all letters within a word are processed in parallel (Coltheart, Rastle, Perry, Langdon, & Ziegler, 2001; Perry, Ziegler, & Zorzi, 2010; Plaut, McClelland, Seidenberg, & Patterson, 1996; Rumelhart & McClelland, 1982; Seidenberg & McClelland, 1989) although some models do argue for a serial process (Davis, 2010; Whitney, 2001).

A particularly compelling demonstration of parallel letter processing comes from a study by Adelman, Marquis, and Sabatos-DeVito (2010). These authors created a series of 4-letter word pairs that differed by a single letter (e.g., lung vs. sung). Critically, the position of the mismatching letter varied across items. Specifically, the differing letter could occur at the first, second, third or fourth position within the word. In this paradigm, participants were shown one word of the pair between a forward and backward mask of hashmarks (######). The duration of the target ranged from 12 to 54 milliseconds (ms). After the display of the target, participants were shown both words of the pair and were asked to identify which of the two words was just presented. Adelman et al. were interested in determining the target duration at which correct identification would rise above chance and whether that duration would vary by position of the letter mismatch. Their results showed that accuracy was at chance at 18 ms but rose to significantly higher than chance performance after 24 ms. Although performance was greater than chance at all letter positions, there was a significant linear decrease in accuracy indicating variability in the efficiency of processing across letter positions. These data suggest that information about all letters becomes available simultaneously at some point between 18 and 24 milliseconds post stimulus onset. Indeed, if letters were processed in a strictly serial fashion, one would expect accuracy to rise above chance earlier for the initial letters of a word compared to later letters.

The mechanisms underlying letter perception have also been studied using single letter identification paradigms. For example, when presented with briefly displayed 5-character strings of letters or numbers (e.g., XHJML) and then cued to identify a random item within the array, participants typically exhibit a “W” shaped function in accuracy such that performance is highest for the central letter as well as the end letters (typically more so for the initial letter than for the final letter), and an “M” shaped function for reaction times such that the center and exterior letters are responded to more quickly (Hammond & Green, 1982; Mason, 1982; Merikle, Coltheart & Lowe, 1971; Tydgat & Grainger, 2009). Interestingly, these patterns only hold for letter strings (i.e., both words and nonwords) and do not hold for strings of symbols ($%^&). Symbol stimuli instead typically show an inverted “U” function where performance is highest for the center letter and drops with increasing eccentricity and the opposite pattern emerges in reaction times (Hammond & Green, 1982; Mason, 1982).

The processing advantage for the central target (both letters and symbols) can easily be accounted for by increased visual acuity at fixation. However, the additional advantage for the first letter position (known hereafter as the first position advantage) cannot be attributed to an overall advantage for exterior letters, because the efficiency of processing letters at the final position is less robust compared to the initial position. This pattern of results requires the assumption of additional processes and the primary goal of this research is to further elucidate those mechanisms.

Typically, parallel processing models accommodate the first position advantage by assuming that certain letter positions have differential rates of accumulation (Adelman,2011; Rumelhart & McClelland, 1982) or smaller standard deviations when positional uncertainty is normally distributed over letter position (Gomez, Ratcliff, & Perea, 2008). However, such accounts leave unanswered the question of why the first position is subject to such preferential processing. To address this issue, Tydgat and Grainger (2009, see also Chanceaux & Grainger, 2012; Chanceaux, Mathot & Grainger, 2013; Grainger, Tydgat, & Issele 2010) proposed the modified receptive fields hypothesis (MRFH), which suggests that during the acquisition of skilled reading, aspects related to low-level visual perception undergo an adaptive modification to improve processing of the initial letters of words and the constraining information they provide (e.g., Chanceaux et al., 2013; Grainger, Bertrand, Lété, Beyersman, & Ziegler, 2016; Tydgat & Grainger, 2009). Specifically, visual receptive fields of location-specific letter detectors selectively reduce in size. Furthermore, those receiving information from the left visual field elongate to the left, at least for languages read from left to right, in order to optimize processing of the first letter. This leftward elongation reduces interference for the initial letter relative to other letters within the word and as such produces the first position advantage. To support this notion, Tydgat and Grainger (2009) conducted a series of experiments in which they presented highly masked strings of random letters, digits or symbols (e.g., “XYCGR”) and then cued participants to identify the item at a given location. Interestingly, a processing advantage emerged for the middle item regardless of the type of stimulus, however the first position advantage occurred only for letter and number stimuli but not for symbols. This supports the account that the mechanism underlying the first position advantage is tied to processes engaged during processing of word-like materials.

Importantly, as noted, the studies by Tydgat and Grainger (2009) utilized a single letter identification design. This contrasts with the Adelman et al. (2010) paradigm in which participants discriminated between whole words. Arguably, the latter, “whole word” paradigm, where emphasis is placed on entire word forms as opposed to single letters, is more consistent with the processes that are engaged during reading and indeed one may not expect the same results to emerge across the two paradigms. Importantly, in the whole word design, a numerical advantage for the initial letter was still obtained in the Adelman et al. results. This work was recently extended by Scaltritti and Balota (2013) who showed a consistent and robust first position advantage in both accuracy and reaction times using words that both varied in length (3 to 6 letters) and were randomly intermixed. Thus, from trial to trial, participants could not accurately predict where the start of the target string would appear. Consistent with the Tydgat and Granger (2009) results, the first position advantage was not found for non-alphanumeric stimuli. Taken as a whole, the first position advantage in this paradigm, selective for letter strings, is consistent with the predictions of the modified receptive fields hypothesis.

However, despite the robustness of the first position advantage across the two paradigms (i.e., single letter vs. whole word) there are important differences in the overall pattern of effects. Most prominently, the letter identification studies show an advantage for the central (and to a lesser extent, final letters) in addition to the initial letter, but only the first position shows a consistent advantage in the whole word paradigms (Scaltritti & Balota, 2013). These differing patterns raise the possibility that the two paradigms are measuring distinct processes.

With this in mind, the goals of the current study were twofold. We first assessed whether the first position effect in the whole word paradigm is simply a byproduct of the task constraints imposed by the design. In Experiment 1, we assessed whether the first position advantage truly arises from increased activation of an abstract letter code. It is possible that participants engaged in a form of perceptual comparison between the briefly presented target item and the response alternatives. Such an effect would limit inferences to low level feature processors and provide little insight into the mechanisms engaged during reading. For example, consider a model of orthographic processing proposed by Grainger and Van Heuven (2003). Briefly, this model suggests that there is an array of letter detectors that are activated by feature information to form an orthographic code that then activates whole word representations. Critically, the letter detectors should be insensitive to overall size and shape of the letters, an assumption that is supported by, among other things, case invariance in masked form priming effects (e.g., Chauncey, Holcomb, & Grainger, 2008), and in parafoveal preview effects (e.g., Rayner, McKonkie & Zola, 1980). Thus, in Experiment 1, we greatly reduced the possibility of perceptual matching processes by changing the case of the target (lower-case) and alternatives (upper-case). If a first position advantage is still obtained, the effect can be more readily attributed to abstract letter codes as opposed to low-level feature information.

In our second experiment, we addressed whether the first position advantage is the result of processes engaged during the decision process in the two alternative forced choice paradigm, and hence may have limited relevance to processes involved in reading. Specifically, once the target has been processed and the alternatives displayed, it is possible that participants engage in a serial, left-to-right scan of the responses looking for a mismatch between the stored memory trace and the two choices. Assuming that the memory trace decays rapidly, such a scanning process could produce a strong first position advantage because that letter will likely be scanned first, a process that again would afford little insight into processes related to reading, but is more task dependent. We address this possibility by presenting participants with single letter stimuli and then whole word response alternatives with the instructions of choosing the word that contained the target letter. We hypothesized that because the response alternatives are identical to Experiment 1, this procedure would also induce the hypothesized scanning process at test. Hence, if this mechanism is responsible for producing the first position advantage, we should again see a strong first position advantage. If it is not, the first position advantage should be eliminated.

The second overarching goal of this study was to further examine the cognitive mechanisms that underlie the first position advantage. To this end, our third experiment was designed as a test of the modified receptive fields hypothesis (MRFH). This was done by presenting the target item and the response alternatives vertically, from top to bottom, rather than in the traditional left to right orientation. If the first position effect is due to the leftward elongation of receptive fields as proposed by the MRFH, such a benefit should not be observed in the vertical orientation. In contrast, if the initial letter still exhibits evidence for preferential processing then additional or alternative mechanisms must be explored. Here we argue for the role of spatial attention in producing the first position advantage. Specifically, we hypothesize that participants may be able to quickly direct attention to the start of a letter string post-stimulus onset.

In our final experiment, we specifically address the contribution of attentional processes in the whole word design by randomly intermixing vertically and horizontally presented items. If participants can quickly focus spatial attention to the beginning of the letter array, we should observe a robust first position effect regardless of target orientation.

Experiment 1

Method

Participants

Thirty-two participants were initially recruited from the undergraduate psychology research pool at Washington University in St. Louis and participated for course credit. All had self-reported normal or corrected to normal vision and were native speakers of English. One individual performed at chance level accuracy across all letter positions in this task and was replaced with a new participant from the same participant pool.

Materials

The stimuli were identical to those used by Scaltritti and Balota (2013). Briefly, word pairs were constructed that were either 3, 4, 5 or 6 letters in length. Each word pair differed by a single letter at different positions within the word (e.g. zero vs. hero, chair vs. chain), with 20 items selected for each letter position at each length. Examples of each type of stimulus are shown in Table 1. Items across the different lengths were matched for word frequency and number of orthographic and phonological neighbors. Within each pair, one word was designated the target and the other the foil. Items were counterbalanced across subjects so that each word served as both the target and the foil across lists. In order to ensure there were equal numbers of items for each word length, filler items were selected for 3, 4 and 5 letter words. These filler items were never analyzed and served only to balance the lists.

Table 1.

Examples of stimuli used in each experiment.

Position	Three-Letter Words	Four-Letter Words	Five-Letter Words	Six-Letter Words
1	jug-tug	bomb-tomb	brush-crush	herbal-verbal
2	shy-sly	golf-gulf	ample-apple	grants-giants
3	odd-ode	crab-crib	draft-drift	insect-infect
4		goal-goat	chart-chant	denial-dental
5			spoon-spool	accept-accent
6				threat-thread

Procedure

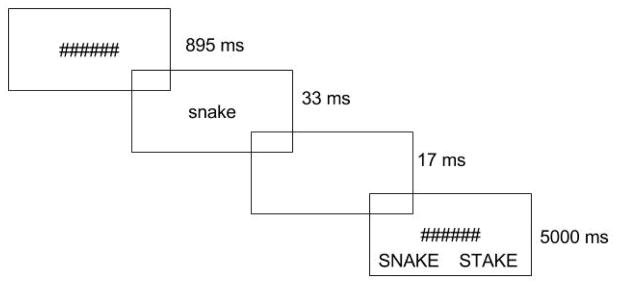
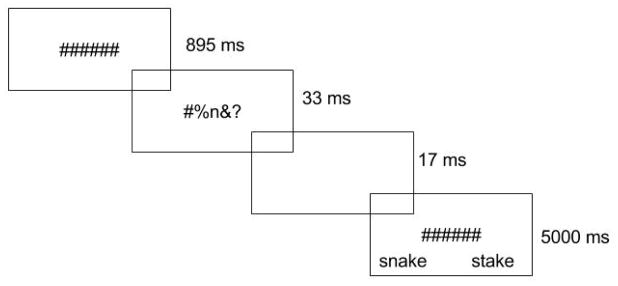
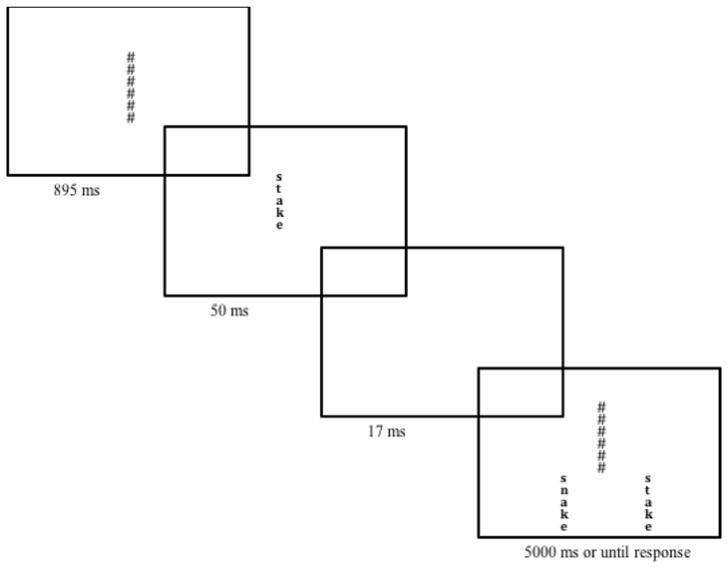
The procedure closely replicated that used by Scaltritti and Balota (2013), which was modeled after the original Adelman et al. (2010) paradigm. The experiment was conducted in individual testing rooms on PCs running E-prime 2.0 software. Computer monitors were placed approximately 40 cm from the participant. This, and all experiments, were run on monitors that measured 44 by 25.5 centimeters with a 1600 × 900 resolution with a 60 Hz refresh rate. On each trial, the following events occurred: a) a string of 6 hashmarks was displayed in the center of the screen for 895 ms, b) the target array (displayed in lower case letters) replaced the mask, centered at fixation, for 32 ms, c) a blank screen was shown for 17 ms, d) the hashmarks returned along with the response alternatives (presented below the target in all capital letters) for 5000 ms or until a response was made. Prior to beginning the experiment, participants were told to fix their gaze at the center of the mask and further instructed to select the word they had seen in the brief display by pressing the “A” key for the word on the left and the “L” key for the word on the right. The side of the screen on which the correct response appeared was counterbalanced across subjects¹. Participants were told that it might be difficult to precisely recognize the word and that they may have to guess if necessary. Selection of a response initiated a 1590 ms inter-trial interval. The full procedure is illustrated in Figure 1.

Figure 1.

Schematic representation of the experimental procedure in Experiment 1.

The task began with 16 practice trials to allow participants to acclimate to the short presentation duration of the target item. These practice trials were followed by 360 experimental trials and 120 filler trials randomly divided between four blocks. Within each block, the length and letter position (i.e., the position of the letter that differentiated the two alternatives) used for a given trial were randomly intermixed. Participants were given feedback on their average accuracy and reaction time after each block of trials.

Results

Accuracy data were analyzed with generalized linear mixed effects models in R using the lme4 package (Bates, Maechler, Bolker & Walker, 2014), and reaction times (RT) with linear mixed effects (LME) models using the same package. Words of each length were analyzed separately with letter position as a fixed effect and random intercepts of subjects and items. Models with additional random effects (e.g., random slopes across letter position) were tested but ultimately were not included due to an inability for many of the models to converge². The “significance” of letter position was established by using a chi-square deviance test between a model that included the fixed effect of letter and one that did not³. If model comparisons indicated the more complex model was preferred (i.e., the effect of letter position was significant), follow-up comparisons of each letter position were performed. Tukey adjustments were employed as a correction for multiple comparisons and we provide odds ratios as a measure of effect size for the accuracy analysis and mean RT difference and percentage RT change are provided as effect sizes for the reaction time analysis.

Accuracy

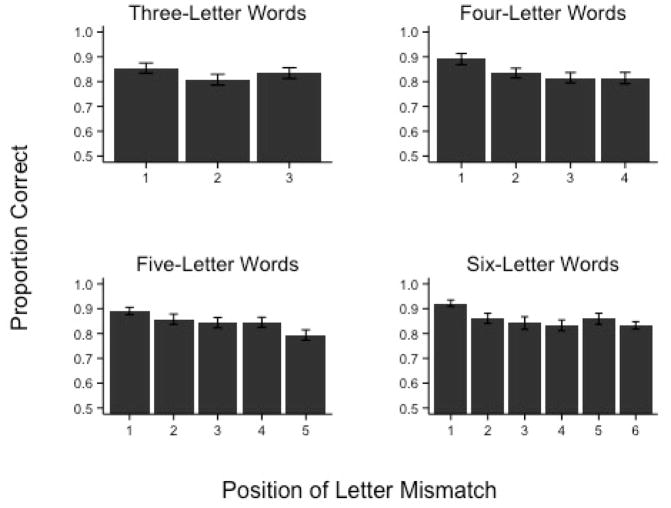
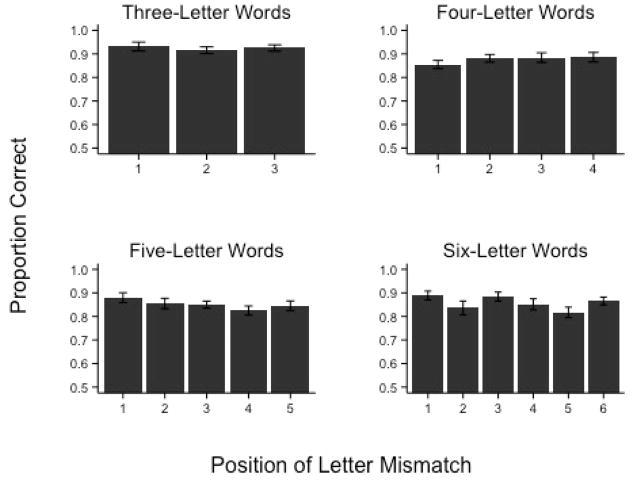
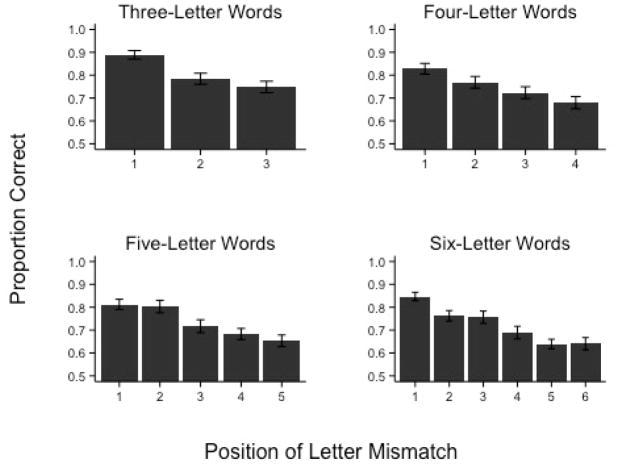
The proportion of correct responses at each length and letter position are shown in Figure 2. The main effect of letter position was not significant for three-letter words χ²(2) = 3.23, p = .199, but was reliable for four-letter words, χ² (3) = 14.13, p = .003, five-letter words, χ² (4) = 14.07, p = .007, and six-letter words, χ² (5) = 24.08, p < .001. Follow-up comparisons are provided in Table 2. As shown, there was a strong first position advantage for four and six letter words but the effect did not consistently appear for three- or five-letter words. However, it should be noted that the linear trend across letter positions for five-letter words was reliable, β = −.168, SE = .048, z = −3.52, p < .001, indicating a linear decrease in accuracy across positions.

Figure 2.

Mean proportion of correct responses as a function of word length and letter position in Experiment 1. Errors bars represent the standard error of the mean.

Table 2.

Planned comparisons for accuracy and reaction time for each length and letter position in Experiment 1.

Word length and position of mismatch	Accuracy		Reaction Time
	z-value	Odds Ratio	t-value	Mean Difference	Percent Change
Three-letter words
1 vs. 2	1.79	1.44	−5.52***	−98.75	12%
1 vs. 3	0.78	1.17	−4.78***	−85.27	10%
2 vs. 3	−1.02	0.81	0.75	13.48	2%
Four-letter words
1 vs. 2	2.59*	1.68	−5.13***	−83.25	10%
1 vs. 3	3.30**	1.93	−5.57***	−90.83	11%
1 vs. 4	3.34**	1.94	−5.58***	−91.03	11%
2 vs. 3	0.73	1.15	−0.46	−7.59	1%
2 vs. 4	0.77	1.15	−0.47	−7.78	1%
3 vs. 4	0.04	1.01	−0.01	−0.20	0%
Five-letter words
1 vs. 2	1.53	1.40	−4.74***	−82.53	10%
1 vs. 3	2.05	1.57	−4.55***	−79.45	9%
1 vs. 4	2.02	1.56	−4.77***	−83.51	10%
1 vs. 5	3.70**	2.21	−3.59**	−63.61	7%
2 vs. 3	0.52	1.12	0.18	3.08	0%
2 vs. 4	0.49	1.11	−0.06	−0.99	0%
2 vs. 5	2.20	1.58	1.06	18.91	2%
3 vs. 4	−0.03	0.99	−0.23	−4.07	0%
3 vs. 5	1.68	1.41	0.89	15.83	2%
4 vs. 5	1.71	1.42	1.11	19.90	2%
Six-letter words
1 vs. 2	3.21*	2.06	−6.50***	−96.93	11%
1 vs. 3	3.99***	2.43	−8.15***	−122.56	14%
1 vs. 4	4.24***	2.55	−9.40***	−141.77	16%
1 vs. 5	3.26*	2.08	−8.79***	−131.37	15%
1 vs. 6	4.34***	2.61	−7.21***	−108.47	12%
2 vs. 3	0.82	1.18	−1.69	−25.62	3%
2 vs. 4	1.07	1.24	−2.94*	−44.84	5%
2 vs. 5	0.05	1.01	−2.28	−34.44	4%
2 vs. 6	1.18	1.27	−0.76	−11.53	1%
3 vs. 4	0.25	1.05	−1.25	−19.21	2%
3 vs. 5	−0.77	0.86	−0.58	−8.81	1%
3 vs.6	0.36	1.07	0.92	14.09	2%
4 vs. 5	−1.02	0.81	0.68	10.40	1%
4 vs. 6	0.11	1.02	2.17	33.30	4%
5 vs. 6	1.14	1.26	1.50	22.90	3%

^*p < .05

^**p < .01

^***p < .001

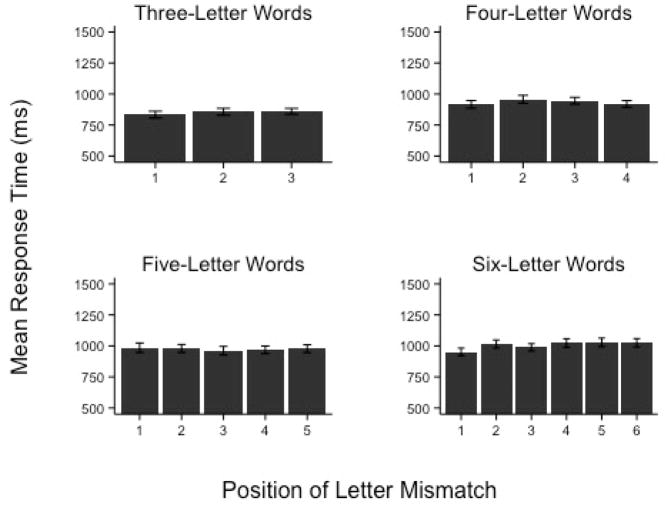
Reaction Time

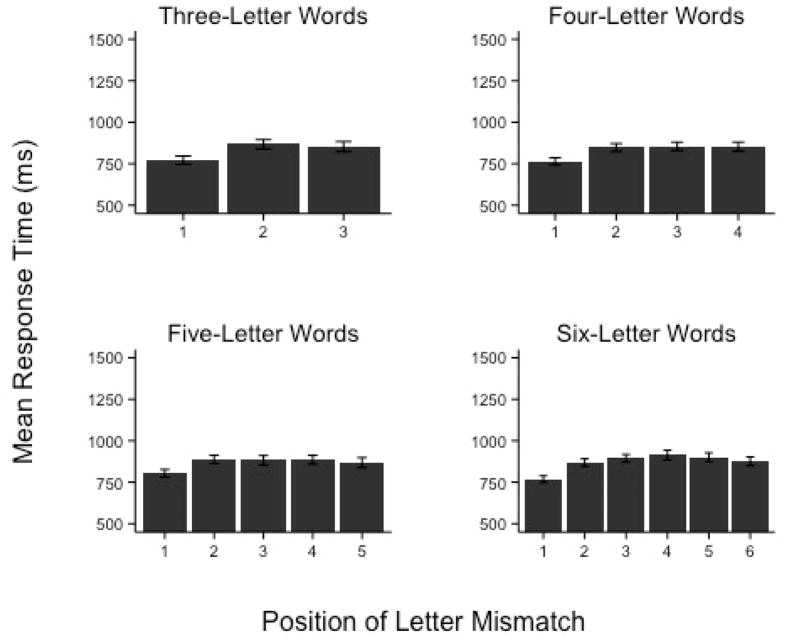
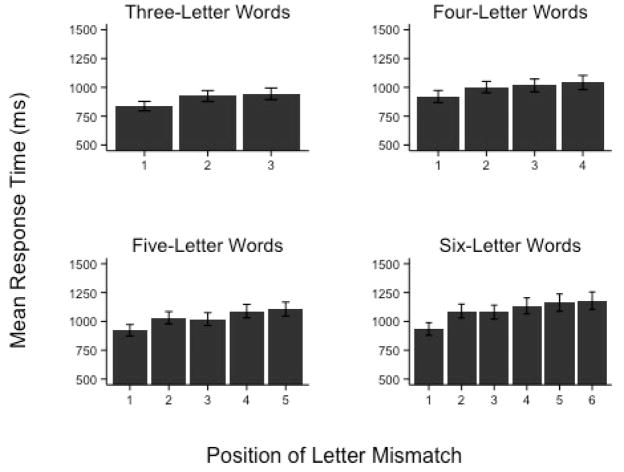
Reaction time data are displayed in Figure 3 as a function of word length and letter position. The main effect of letter position was reliable for three-letter words χ² (2) = 36.14, p < .001, four-letter words, χ² (3) = 45.13, p < .001, five-letter words, χ² (4) = 33.29, p < .001, and six-letter words, χ² (5) = 120.26, p < .001. Follow-up comparisons are provided in Table 2. As shown, there was a clear first position advantage for all word lengths, and with few exceptions, words that differed at later positions were not reliably different from one another.

Figure 3.

Mean reaction times as a function of word length and letter position in Experiment 1. Error bars represent the standard error of the mean.

Discussion

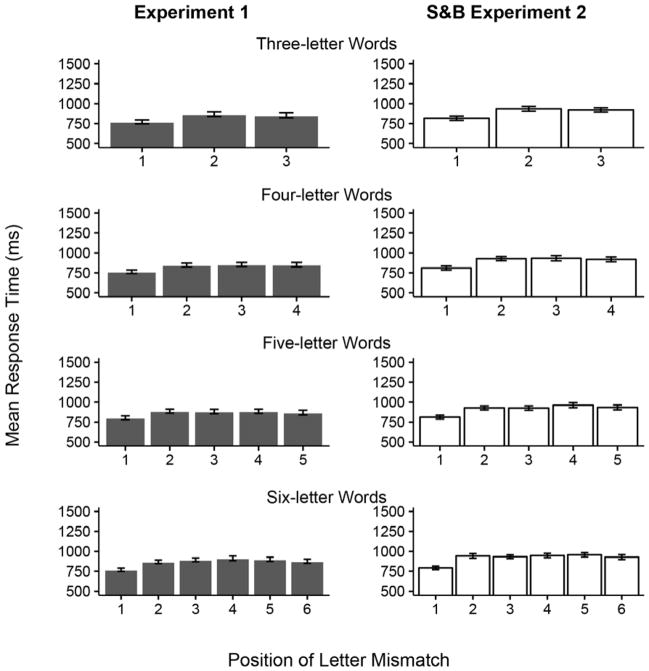
These results are consistent with those reported by Scaltritti and Balota (2013) despite the fact that the present experiment included a change in case between target and alternatives whereas Scaltritti and Balota did not. Specifically, there was a clear first position advantage in RTs for initial letters and, although less consistent, similar patterns emerged from the accuracy data. There was no evidence for a specific advantage for letters at fixation, either in reaction times or in accuracy. Importantly, these results indicate that the first position advantage in this paradigm cannot be fully attributed to low-level feature matching processes. If participants were engaging in such a matching process, we would expect an elimination of the first position effect in this paradigm due to the case change manipulation.

Of course, certain letters have some degree of overlap between the lower and upper case variants (e.g., o and O, v and V etc.). It is possible, therefore, that the first position advantage revealed here is being driven by the subset of letters that have overlapping features. To address this question, we coded for whether or not the lower and upper case letters had similar features and included “overlap” as an additional factor in the analyses. A letter was deemed overlapping if the uppercase variant was simply an enlarged version of the lowercase letter (c, f, i, k, l, m, o, p, s, t, u, v, w, x, y, z). Overlap did not interact with the letter position effect at any position in accuracy (ps > .38) nor in RTs (ps > .05) with the exception of length 5 words (p = .011). This interaction indicated a larger first position effect for words that had feature overlap but importantly even when analyses were restricted to the non-overlapping characters, the first position advantage was still reliable (p = .022).

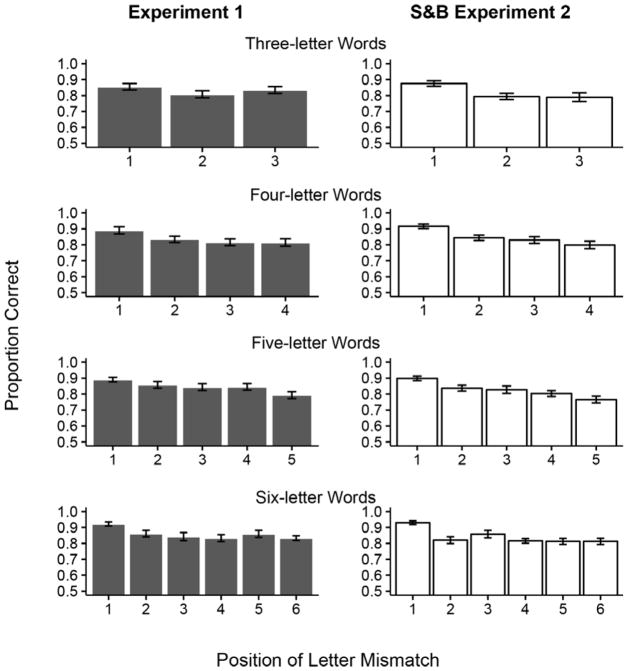
In order to further support this post-hoc analysis, we conducted additional analyses in which accuracy and RTs of the present experiment were compared with Experiment 2 in Scaltritti and Balota (2013). The only difference between the two experiments, in terms of experimental procedure, was that the case changed between the targets and alternatives in the current experiment and did not in Scaltritti and Balota. The comparison was separately conducted within each word length. The experiment by letter position interaction was never significant (all ps > .15), except for RTs in five-letter words (χ² [4] = 13.62, p = .009) and for accuracy in three-letter words, where the interaction approached conventional significance (χ² [2] = 5.23, p = .07). Notwithstanding the single significant interaction and the marginal interaction, the first-position advantage in RTs appears equally robust across the two experiments. Figures 4 and 5 reports the results from both experiments in terms of accuracy and RTs, respectively for a direct comparison. Importantly, if feature overlap were driving performance, one would expect larger effects in the experiments that do not manipulate case in any fashion.

Figure 4.

Mean proportion of correct responses for Experiment 1 (first column) and for Experiment 2 from Scaltritti and Balota, 2013 (second column) as a function of word length and letter position. Errors bars represent the standard error of the mean.

Figure 5.

Mean RTs for Experiment 1 (first column) and for Experiment 2 from Scaltritti and Balota, 2013 (second column) as a function of word length and letter position. Errors bars represent the standard error of the mean.

Experiment 2

In Experiment 2, we address the possibility that the first position effect is due to operations invoked during the decision process required by this task. Specifically, it is possible that participants engage in a serial left to right scan of the alternatives looking for the mismatching letter. Again, such a mechanism is a simple consequence of the task design and may have limited relevance to processes engaged in the initial processing of the masked stimulus. Thus, we tested this decision account by presenting a single letter at fixation surrounded by flanking symbol stimuli as a mask. Participants were then presented with the two word alternatives at test (precisely as in the previous experiments) and were instructed to choose the word that contained the target letter. We assumed that this design would engage the same serial scanning process during the forced choice task as in the previous experiments, and hence, if that scanning process accounts for the first letter advantage, then we should again observe a first position effect under these conditions.

Method

Participants

Thirty-two participants were initially recruited from the same source as in Experiment 1. All were native speakers of English and reported normal or corrected to normal vision. Two participants were at chance performance at all word lengths and were replaced with two new individuals from the same research participant pool.

Materials and Procedure

The materials were identical to those used in Experiment 1. In this experiment, for each target pair (e.g., lung vs. sung), the mismatching letter was presented at fixation surrounded by symbols drawn from a pool of 8 possible stimuli (%, /, ?, @, }, <, £, §). The number of flanking symbols was selected to approximately match the length of the target words and the symbols were randomly chosen anew for each item. Continuing the above example, “l” would be presented at fixation and flanked by four symbols (two on each side). The items “lung” and “sung” would then be presented as alternatives. Otherwise the procedure was identical to the first experiment. It should be noted that the target duration was increased to 67 ms based on pilot testing that indicated chance level performance for all items at shorter display durations. This procedure is illustrated in Figure 6.

Figure 6.

Schematic representation of the experimental procedure in Experiment 2.

Results

Accuracy

Accuracy data are displayed in Figure 7 as a function of word length and letter position. In contrast to the previous experiments, the main effect of letter position was not significant for three-letter words χ² (2) = 0.76, p = .683, four-letter words, χ² (3) = 1.99, p = .574, or five-letter words, χ² (4) = 4.51, p = .341, but was reliable for six-letter words, χ² (5) = 13.05, p = .023. Follow-up comparisons are provided in Table 3. As shown, the significant main effect for the six letter words was not found in the individual pair-wise tests after correcting for multiple comparisons via the Tukey adjustment. Furthermore, the linear trend was not reliable at any word length (ps > .1). Thus, it appears that accuracy is not robustly affected by letter position in this paradigm.

Figure 7.

Mean proportion of correct responses as a function of word length and letter position in Experiment 2. Error bars represent the standard error of the mean.

Table 3.

Planned comparisons for accuracy and reaction time for each word length and letter position in Experiment 2.

Word length and position of mismatch	Accuracy		Reaction Time
	z-value	Odds Ratio	t-value	Mean Difference	Percent Change
Three-letter words
1 vs. 2	0.87	1.27	−1.58	−24.12	3%
1 vs. 3	0.38	1.11	−2.02	−30.83	4%
2 vs. 3	−0.49	0.88	−0.44	−6.71	1%
Four-letter words
1 vs. 2	−1.03	0.78	−2.30	−42.82	5%
1 vs. 3	−1.14	0.76	−1.66	−30.71	3%
1 vs. 4	−1.22	0.75	−0.44	−8.20	1%
2 vs. 3	−0.11	0.97	0.66	12.11	1%
2 vs. 4	−0.19	0.96	1.88	34.62	4%
3 vs. 4	−0.08	0.98	1.22	22.52	2%
Five-letter words
1 vs. 2	1.04	1.29	0.24	4.14	0%
1 vs. 3	1.15	1.33	1.12	19.42	2%
1 vs. 4	2.10	1.68	0.68	11.93	1%
1 vs. 5	1.31	1.38	0.12	2.08	0%
2 vs. 3	0.12	1.03	0.88	15.28	2%
2 vs. 4	1.08	1.30	0.44	7.78	1%
2 vs. 5	0.28	1.07	−0.12	−2.06	0%
3 vs. 4	0.96	1.26	−0.43	−7.49	1%
3 vs. 5	0.16	1.04	−0.99	−17.34	2%
4 vs. 5	−0.80	0.83	−0.56	−9.84	1%
Six-letter words
1 vs. 2	2.21	1.69	−3.12*	−61.88	6%
1 vs. 3	0.02	1.00	−1.89	−36.99	4%
1 vs. 4	1.44	1.42	−3.64**	−72.03	7%
1 vs. 5	2.78	1.93	−3.86**	−75.88	8%
1 vs. 6	0.91	1.25	−3.60**	−71.21	7%
2 vs. 3	−2.19	0.59	1.25	24.89	2%
2 vs. 4	−0.77	0.84	−0.51	−10.16	1%
2 vs. 5	0.58	1.14	−0.70	−14.00	1%
2 vs. 6	−1.31	0.74	−0.47	−9.34	1%
3 vs. 4	1.42	1.41	−1.77	−35.04	3%
3 vs. 5	2.76	1.92	−1.96	−38.89	4%
3 vs.6	0.89	1.24	−1.73	−34.22	3%
4 vs. 5	1.35	1.36	−0.19	−3.85	0%
4 vs. 6	−0.54	0.88	0.04	0.82	0%
5 vs. 6	−1.89	0.65	0.23	4.67	0%

^*p < .05

^**p < .01

^***p < .001

Reaction Time

Reaction time data are displayed in Figure 8 as a function of word length and letter position. Once again, the main effect of letter position was not significant for three-letter words, χ² (2) = 4.53, p = .104, four-letter words, χ² (3) = 6.83, p = .078, or for five-letter words, χ² (4) = 1.71, p = .789, but was reliable for six-letter words, χ² (5) = 22.43, p < .001. Follow-up comparisons are displayed in Table 3 and as shown, for six-letter words, the first position was reliably faster than all other positions except for position 3. This effect did not hold for the other word lengths.

Figure 8.

Mean reaction times as a function of word length and letter position in Experiment 2. Error bars represent the standard error of the mean.

Discussion

The goal of this experiment was to examine the possibility that the first position advantage in the Scaltritti and Balota (2013) study, along with the current Experiment 1, was produced by participants engaging in a serial, left-to-right scan of the response alternatives. These data make it clear that such a mechanism is not operating in the whole word design, otherwise we would have found a robust first-position effect in the present experiment. Although there was a first-position advantage for six letter words in the reaction time data, this effect was marginal in accuracy and not reliable at any other word length in either accuracy or RT. It is possible that the increased demands of a 6-letter string increased the reliance on such a scan process. Clearly, by comparison with the previous experiments, there is not the clear first position advantage that is independent of word length in Experiment 2, as has been found in the Scaltritti and Balota experiments.

Given that we have now provided evidence that the first position advantage (a) is not due to a perceptual overlap, but does appear to be due to an abstract letter code, and (b) the effect is not due to post perceptual decision processes, we can now turn to the question of why the first letter is granted such preferential processing. At present, the most well-articulated explanation is that of modified receptive fields hypothesis (MRFH: Tydgat & Grainger, 2009). As noted, however, this explanation was developed within a single letter identification task, and so may not extend to the whole word paradigm, which is the target of the current experiments. Therefore, in the following experiments we examine the first position effect under conditions which are unfavorable to the receptive fields hypothesis, specifically by changing the orientation of the target item from horizontal (i.e., left to right) to vertical (top to bottom). Arguably, if receptive fields are leftward elongated due to constraints imposed by reading, which in English occurs from left to right, such a mechanism should not provide any advantage when the target items are presented vertically. If the first position advantage persists, then additional mechanisms need to be considered.

Experiment 3

Method

Participants

Thirty-two participants were initially recruited from the undergraduate psychology research pool at Washington University in St. Louis who participated for course credit. All had self-reported normal or corrected to normal vision and were native speakers of English. Two chance level performers were replaced with new participants from the same participant pool.

Materials and Procedure

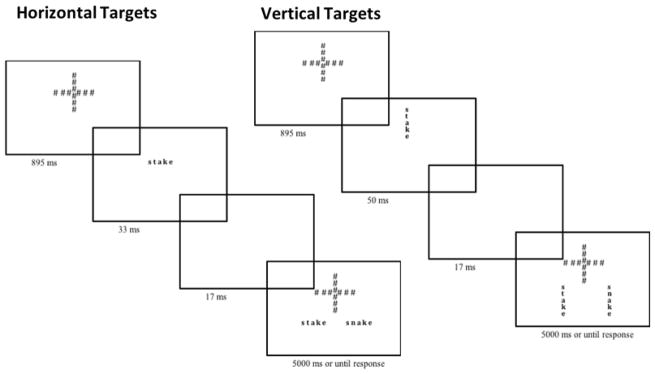
The materials and procedure were similar to Experiment 1. The exceptions were that now the target item and the response alternatives were constructed to appear in a vertical orientation rather than horizontal. The display was constructed by creating a series of 6 boxes (24 × 24 pixels) that were separated by 18 pixels. For the mask, each text box was filled with a hashmark, as in the previous experiments. When the target was displayed, each letter of the word filled one box, centered at fixation. For example, the word lung would fill the four boxes nearest the center. In contrast to the previous experiment, the target was displayed for 50 ms (compared to the 32 ms in Experiment 1 and in the Scaltritti and Balota experiments) to ensure comparable performance to the horizontal presentations. This was followed by the hashmarks in their original locations with two vertically oriented response alternatives. The alternatives also filled a 6 box display; however, the first letter filled the top box and then moved down. For example, the “l” in lung and the “l” in lunch both started at the top most box. The top of the alternatives began in line horizontally with the bottom character of the mask and shifted 51 pixels to the left or the right. The entire procedure is depicted graphically in Figure 9.

Figure 9.

Schematic illustration of the experimental procedure in Experiment 3.

Results

Accuracy

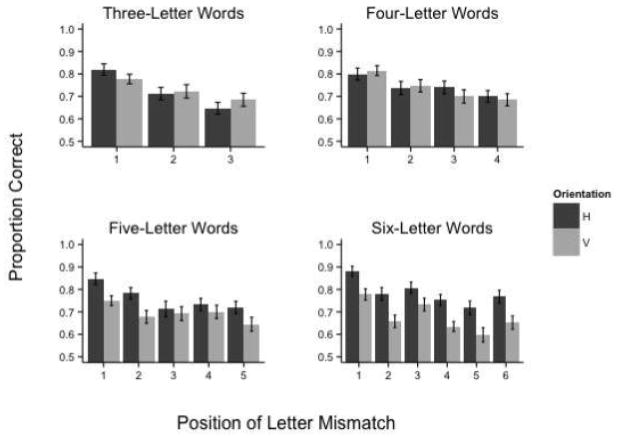
Accuracy data are displayed in Figure 10 as a function of word length and letter position. The LME analysis revealed a significant effect of letter position for three-letter words, χ² (2) =29.71, p < .001, for four-letter words, χ² (3) = 31.22, p < .001, for five-letter words, χ² (4) = 59.04, p < .001, and for six-letter words, χ² (5) = 81.79, p < .001. Follow-up contrasts are listed in Table 4. As shown, the first position was significantly more accurate than any other position for any word length with two exceptions. Specifically, the first and second positions were statistically equivalent for 5-letter words and was marginal for 4-letter words (p = .07).

Figure 10.

Proportion of correct responses as a function of word length and letter position in Experiment 3. Error bars represent the standard error of the mean.

Table 4.

Planned comparisons for accuracy and reaction time for each word length and letter position in Experiment 3.

Word length and position of mismatch	Accuracy		Reaction Time
	z-value	Odds Ratio	t-value	Mean Difference	Percent Change
Three-letter words
1 vs. 2	4.18***	2.39	−4.72***	−95.93	11%
1 vs. 3	5.28***	2.98	−5.52***	−113.24	13%
2 vs. 3	1.17	1.25	−0.83	−17.31	2%
Four-letter words
1 vs. 2	2.39	1.51	−3.70**	−82.69	8%
1 vs. 3	3.96***	1.95	−4.46***	−101.47	10%
1 vs. 4	5.35***	2.45	−5.15***	−118.50	12%
2 vs. 3	1.60	1.30	−0.82	−18.77	2%
2 vs. 4	3.03*	1.62	−1.54	−35.81	4%
3 vs. 4	1.44	1.25	−0.72	−17.04	2%
Five-letter words
1 vs. 2	0.41	1.07	−4.88***	−111.11	11%
1 vs. 3	3.81**	1.76	−4.57***	−106.58	10%
1 vs. 4	5.04***	2.10	−7.32***	−172.78	17%
1 vs. 5	6.05***	2.42	−7.88***	−188.31	18%
2 vs. 3	3.41**	1.65	0.19	4.53	0%
2 vs. 4	4.65***	1.97	−2.60	−61.67	6%
2 vs. 5	5.67***	2.27	−3.21*	−77.19	7%
3 vs. 4	1.27	1.19	−2.74	−66.20	6%
3 vs. 5	2.32	1.37	−3.34**	−81.73	8%
4 vs. 5	1.06	1.15	−0.63	−15.53	2%
Six-letter words
1 vs. 2	3.43**	1.77	−7.27***	−161.41	15%
1 vs. 3	3.63**	1.82	−7.01***	−155.43	14%
1 vs. 4	5.94***	2.62	−9.36***	−213.41	19%
1 vs. 5	7.48***	3.33	−9.77***	−231.38	21%
1 vs. 6	7.43***	3.30	−10.68***	−251.86	23%
2 vs. 3	0.20	1.03	0.26	5.98	1%
2 vs. 4	2.60	1.48	−2.22	−51.99	5%
2 vs. 5	4.23***	1.88	−2.88*	−69.97	6%
2 vs. 6	4.18***	1.87	−3.73**	−90.45	8%
3 vs. 4	2.40	1.44	−2.48	−57.97	5%
3 vs. 5	4.03***	1.82	−3.13*	−75.95	7%
3 vs.6	3.98**	1.81	−3.99**	−96.43	9%
4 vs. 5	1.66	1.27	−0.72	−17.98	2%
4 vs. 6	1.60	1.26	−1.56	−38.46	4%
5 vs. 6	−0.06	0.99	−0.80	−20.48	2%

^*p < .05

^**p < .01

^***p < .001

Reaction Time

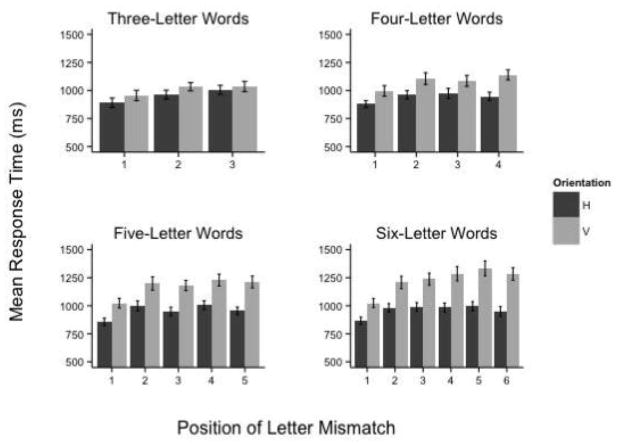
Reaction time data are displayed in Figure 11 as a function of word length and letter position. The analysis revealed a significant effect of letter position for three-letter words, χ² (2) =36.16, p < .001, four-letter words, χ² (3) = 32.43, p < .001, five-letter words, χ² (4) = 79.79, p < .001, and six-letter words, χ² (5) = 161.90, p < .001. The follow-up tests are listed in Table 4. As before, there was a robust and consistent first position advantage, relative to all other letter positions, for all word lengths.

Figure 11.

Mean reaction times as a function of word length and letter position in Experiment 3. Error bars represent the standard error of the mean.

Discussion

The results were clear. Even when the target item was presented vertically, a robust first position advantage was still obtained. This finding is inconsistent with the MRFH which suggests the first position advantage is due to selective and horizontal elongation of the visual receptive fields for location-specific letter detectors. Furthermore, this elongation is specific to the left visual field with respect to fixation (Chanceaux et al. 2013). Therefore, an unmodified version of this account could not produce a first position effect with vertically presented items.

Thus, we propose a new hypothesis. Specifically, we argue that the first position advantage, at least with vertically presented items, is most consistent with a rapid reallocation of attention to the beginning of the word. However, before entertaining this possibility further, one alternative explanation needs to be addressed. Specifically, in Experiment 3, all items were presented vertically and it is possible that participants developed an expectancy to maintain attention towards the top half of the screen before the stimulus was ever presented. It should be noted of course, that items of different lengths were randomly intermixed in that experiment and therefore participants would have been unable to predict precisely where the initial letter would appear prior to stimulus onset. Nevertheless, we designed a final experiment to provide converging evidence for the ability to rapidly direct attention towards the start of a stimulus after stimulus onset. To this end, we presented items with horizontal and vertical orientations randomly intermixed across trials, making it impossible to predict the orientation of the stimulus (and thus the general location of the initial letter) prior to stimulus onset. If the first position advantage is dependent upon a general location where the beginning of the stimuli will appear in a given orientation, then the first position advantage should be eliminated (or greatly reduced) when horizontal and vertical orientations are randomly intermixed.

Experiment 4

Method

Participants

Forty undergraduate students participated in this experiment in exchange for course credit. They were required to be native speakers of English and have normal or corrected to normal vision. Four chance level performers were replaced with new participants from the same participant pool.

Materials and Procedure

The materials were identical to the previous experiments. We split the original 20 critical items per letter position into two lists. Items in one list were displayed in the typical, horizontal orientation and the other list in a vertical orientation. These lists were randomly intermixed for each participant and the items that were displayed in a vertical vs. horizontal fashion were counterbalanced across participants. The forward and backward mask now consisted of 6 vertical hashmarks and 6 horizontal hashmarks organized in a cross pattern. Participants were instructed to fix their gaze at the center of the cross. In order to maintain consistency with our past experiments, horizontal items were displayed for 33 ms and vertical items for 50 ms, and the orientation of the response alternatives always matched that of the target. The procedure is depicted graphically in Figure 12. The current list structure afforded 10 observations per letter position and orientation for each participant.

Figure 12.

Schematic representation of the experimental procedure in Experiment 4.

Results

Accuracy

Accuracy data are displayed in Figure 13 as a function of word length, target orientation and letter position. The data were analyzed using LME with letter position, target orientation and the letter by orientation interaction specified as fixed effects. For three-letter words, there was a significant effect only of letter position, χ² (2) =26.04, p < .001, and neither the main effect of orientation, χ² (1) =2.46, p = .117, nor the letter by orientation interaction, χ² (2) = 3.99, p = .136 were reliable. For four-letter words, the main effect of letter position was again reliable, χ² (3) =9.34, p =.025, but there was no main effect of target orientation, χ² (1) = 0.34, p = .562, nor was there an orientation by letter position interaction, χ² (3) = 2.25, p = .522. For five-letter words, there was a main effect of letter position, χ² (4) = 25.97, p < .001, and of target orientation, χ² (1) = 12.53, p < .001 but the interaction was not reliable, χ² (4) = 8.15, p = .086. Finally, for six-letter words, the main effect of letter position was significant, χ² (5) = 31.80, p < .001, as was the main effect of target orientation, χ² (1) = 15.60, p < .001, but again there was no interaction, χ² (5) = 1.64, p = .896. As shown in Table 5, there was a consistent first position effect in the planned comparisons in the accuracy data for both vertical and horizontal orientations.

Figure 13.

Mean proportion of correct responses as a function of word length, letter position and target orientation in Experiment 4. Error bars represent the standard error of the mean.

Table 5.

Planned comparisons for accuracy and reaction time for each word length and letter position in Experiment 4.

Word length and position of mismatch	Accuracy		Reaction Time
	z-value	Odds Ratio	t-value	Mean Difference	Percent Change
Three-letter words
1 vs. 2	3.27**	1.62	−3.79***	−79.81	8%
1 vs. 3	5.01***	2.07	−5.35***	−114.94	12%
2 vs. 3	1.79	1.28	−1.60	−35.13	4%
Four-letter words
1 vs. 2	2.64*	1.52	−4.81***	−98.61	10%
1 vs. 3	3.40**	1.71	−4.74***	−97.77	10%
1 vs. 4	4.38***	1.98	−5.43***	−113.29	11%
2 vs. 3	0.77	1.12	0.04	0.84	0%
2 vs. 4	1.77	1.31	−0.69	−14.68	1%
3 vs. 4	1.00	1.16	−0.73	−15.52	2%
Five-letter words
1 vs. 2	3.00*	1.52	−6.61***	−145.25	14%
1 vs. 3	4.17***	1.78	−5.60***	−124.27	12%
1 vs. 4	3.65**	1.66	−7.33***	−162.53	15%
1 vs. 5	4.88***	1.96	−6.65***	−148.34	14%
2 vs. 3	1.17	1.17	0.93	20.97	2%
2 vs. 4	0.65	1.09	−0.77	−17.28	2%
2 vs. 5	1.91	1.29	−0.14	−3.10	0%
3 vs. 4	−0.53	0.93	−1.68	−38.25	4%
3 vs. 5	0.74	1.10	−1.05	−24.07	2%
4 vs. 5	1.27	1.18	0.62	14.18	1%
Six-letter words
1 vs. 2	4.52***	2.01	−6.11***	−141.23	13%
1 vs. 3	2.64	1.51	−6.73***	−153.99	14%
1 vs. 4	5.39***	2.29	−7.51***	−175.65	16%
1 vs. 5	6.65***	2.76	−9.35***	−223.65	20%
1 vs. 6	4.84***	2.11	−7.49***	−174.88	16%
2 vs. 3	−1.93	0.75	−0.54	−12.76	1%
2 vs. 4	0.90	1.14	−1.42	−34.41	3%
2 vs. 5	2.22	1.37	−3.34*	−82.42	8%
2 vs. 6	0.33	1.05	−1.39	−33.65	3%
3 vs. 4	2.83	1.51	−0.91	−21.65	2%
3 vs. 5	4.13***	1.82	−2.85	−69.66	6%
3 vs.6	2.26	1.39	−0.88	−20.89	2%
4 vs. 5	1.31	1.20	−1.93	−48.01	4%
4 vs. 6	−0.58	0.92	0.03	0.77	0%
5 vs. 6	−1.89	0.77	1.96	48.77	4%

^*p < .05

^**p < .01

^***p < .001

Reaction Time

Reaction time data are displayed in Figure 14 as a function of word length, target orientation, and letter position. For three-letter words, there was a significant main effect of letter position, χ² (2) =19.43, p < .001, and of target orientation, χ² (1) = 9.52, p = .002, but the letter by orientation interaction was not reliable, χ² (2) = .58, p = .748. For four-letter words, the main effect of letter position was again reliable, χ² (3) = 15.85, p < .001, as was the main effect of target orientation, χ² (1) = 22.19, p < .001, but there was no interaction, χ² (3) = 6.28, p = .10. For five-letter words, there was a main effect of letter position, χ² (4) = 31.95, p < .001, and of target orientation, χ² (1) = 44.03, p < .001 but the interaction was not reliable, χ² (4) = 7.46, p = .113. Finally, for six-letter words, the main effect of letter position was significant, χ² (5) = 35.67, p < .001, as was the main effect of target orientation, χ² (1) = 42.52, p < .001, and now there was a reliable interaction, χ² (5) = 30.40, p < .001, such that the first position advantage was significantly larger for the vertically oriented words. As shown in Figure 14, there was a consistent first position effect in the planned comparisons for both vertical and horizontal orientations.

Figure 14.

Mean reaction times as a function of word length, letter position and target orientation in Experiment 4. Error bars represent the standard error of the mean.

Discussion

The results from Experiment 4 clearly indicate the presence of a robust first position advantage regardless of the display orientation of the target. Indeed, overall, the magnitude of the first position advantage was statistically equivalent across both orientations suggesting a similar mechanism underlies both. There was an interaction in the reaction time data for six-letter words but the nature of this interaction indicated a larger influence of the first position for vertical targets relative to horizontal, which clearly is not predicted by the MRFH. Again, we argue that these patterns of data are best accommodated by a rapid re-direction of attention to the initial letter of a target string. This can occur quickly and is engaged regardless of the display orientation of the target item⁴.

General Discussion

In a series of four experiments, we explored the locus of the first letter advantage in a masked, two-alternative forced choice, whole word paradigm. Based on the arguments developed by Tydgat and Grainger (2009) to accommodate the first position advantage in single letter identification performance, Scaltritti and Balota (2013) suggested that the consistent first position advantage in the whole word paradigm may be best accomodated by the MRFH which states that during the acquisition of skilled reading, receptive fields for location-specific letter detectors become reduced in size and elongated to the left which reduces interference from nearby letters (also see Chanceaux & Grainger, 2012; Grainger, Tydgat, & Isselé, 2010). This reduced interference leads to the first position advantage specifically for letter strings and not symbols or other non-alphanumeric stimuli.

However, as noted earlier, the whole word design used by Scaltritti and Balota produces a different pattern of results compared to single letter identification studies indicating that different processes are likely engaged across these paradigms. For example, in the single letter identification paradigm, one typically finds an advantage for the center position and both of the exterior positions, with the first position producing the most robust advantage (e.g., Tydgat & Grainger, 2009). The whole word forced choice paradigm primarily yields a first position advantage. Thus, a first step in this research program was to ensure there are no idiosyncratic aspects of the current paradigm that minimize its relevance to the extant letter and word identification literature.

In pursuit of this goal, we first addressed the access code in the whole word paradigm. For example, it is quite possible that the observed effects are due to low-level overlap in features, as opposed to abstract letter level information. This would minimize contact with other research indicating the importance of letter level access codes. For example, Rayner, McConkie and Zola (1980) have demonstrated, via parafoveal preview studies, that case changes do not influence the benefits of parafoveal previews, suggesting the importance of an abstract letter code en route to early visual processing. In addition, Evett and Humphreys (1981) demonstrated that masked repetition priming is independent of case change. Hence, we first attempted to examine if the first position advantage observed in the Scaltritti and Balota study was also due to increased activation of letter codes rather than lower level perceptual features. If abstract letter codes are being preferentially activated, the first position advantage should persist under conditions in which features change from the target to the alternatives. Thus, in Experiment 1, we changed the case (lower to upper) between the target and the forced-choice alternatives. The results continued to yield a robust first position advantage. Moreover, the size of the first position advantage in this experiment appeared to be comparable to the size of the effect obtained in the Scaltritti and Balota study. Therefore, consistent with the literature on the importance of abstract letter codes, it appears that results seen with the whole word paradigm is not due a feature level match.

We also considered the possibility that the first letter advantage is due to unique constraints imposed by the whole word design, which may minimize its importance for models of letter processing in the context of word recognition. Specifically, it is possible that after the target offset, participants serially scan each of the alternatives looking for a mismatch with the target and that this left-to-right scan leads to the advantage for initial letters since they will be scanned first. Therefore, in Experiment 2, we only presented a single letter that was masked before the forced choice alternatives. If left to right scanning during the forced choice was the critical mechanism, then one should continue to see a first position advantage. However, the results indicated that the first position advantage was greatly reduced in this procedure and indeed there was no evidence in the 3, 4, or 5 letter strings for a first letter advantage. Interestingly, there was some evidence of a first letter advantage for the response time data for the 6 letter strings, and hence, it is possible that such a process does come into play for longer more complex stimuli, but even here the effect was much smaller than that found in Experiment 1 for the same 6 letter strings (β = −56, t = −3.74, p < .001). Therefore, we conclude that post perceptual decision processes during the two alternative forced choice test play, at best, a minimal role in producing the robust first position advantage.

The results from these findings suggest that the first position advantage in the forced choice whole word paradigm is not simply feature based nor is it due to decision processes engaged post target offset. Of course, both of these findings are still consistent with the predictions of the MRFH. Thus, Experiment 3 provided a more direct test of this theory by presenting targets in a vertical orientation. If the first position advantage is due to the leftward elongation of receptive fields for letter detectors, no such advantage should be found for vertical targets. Contrary to this prediction, the results from Experiment 3 yielded a first position advantage for vertically presented stimuli.

It is possible that within the experimental context of Experiment 3, participants developed an expectation to direct attention to the top half of the visual field, since the words were oriented from top to bottom, and hence, this was producing the first position advantage. Although this expectation directed attention mechanism would not be localized to the first position, since length was randomly varied across trials, we decided to test if such an expectancy could nevertheless be playing a role. Hence, Experiment 4 randomly varied the orientation of the strings, such that half were presented top to bottom and half were presented left to right. Remarkably, a robust first position advantage was still observed. Indeed, the first position advantage was of comparable magnitude in both horizontally and vertically oriented words, a finding which cannot be accommodated by the MRFH. Of course, one might still argue that participants may learn to focus attention to the upper left quartile of the display. However, because attention should become less focused in Experiment 4 compared to Experiment 3 (i.e., attention to both top half and left half vs. just left half), one would expect a reduction in the first position advantage across experiments, which was not observed.

We propose that these data are most consistent with a rapid redirection of spatial attention to the beginning of a target string, at least when that string contains letters. The first position advantage, in fact, was found to be reliable even when the first letter was displayed across a notable variety of spatial locations, such as in Experiment 4 where word length and orientation were randomly intermixed. The consistency of the phenomenon points toward a flexible mechanism that operates on-line after stimulus presentation, rather than towards low level structural properties of location specific letter detectors. One might argue that this attentional bias is the consequence of adapting to the particular constraints imposed by reading, namely interference from nearby letters. For example, Risko, Stolz, and Besner (2010) used a spatial cueing paradigm to show that deployment of attention can serve to reduce “cross-talk” among features within the word leading to faster and more accurate identification. Similarly, spatially pre-cueing a single letter can eliminate the word superiority effect (Johnston & McClelland, 1974) and the semantic Stroop effect (Labuschange & Besner, 2015). The fact that spatial cueing is additive with respect to other variables, such as lexicality in the context of lexical decision, suggests this phenomenon is pre-lexical in nature (McCann, Folk, & Johnston, 1992). Furthermore, single cell recording studies have demonstrated that spatial attention can effectively increase the signal strength of a particular stimulus (Reynolds, Pasternak & Desimone, 2000) and thus if attention is directed to the initial character, response gain should be increased for the attended positions relative to others. Spatial attention might thus serve a critical role in modulating the efficiency of letter-level processing. Of course, the critical question is why would attention be driven to the first position. One possibility is the argument that first letters are more discriminative for word identification (Clark & O’Regan, 1999; see also Stevens & Grainger, 2003). In addition, readers tend to fixate slightly to the left of the middle of the words (e.g., Nazir, Jacobs, & O’Regan, 1998; Rayner, 1979) possibly to optimize processing for leftmost letters. Also, reading is more strongly and more consistently disrupted by transpositions involving initial letters than other letters (e.g., Johnson & Eisler, 2012). Given these findings, the simplest account is that the reading systems is particularly sensitive to the initial position and capitalizes on its importance by enhancing processing via visuo-spatial attention.

At least two modern computational models of letter coding are able to account for the first position advantage by varying certain parameters to account for location specific performance. For example, in the Overlap Model (Gomez et al. 2008), each letter within a word is associated both with its position within the word along with adjacent positions, which is reflected by a standard deviation which captures the letter’s spatial uncertainty. In order to accommodate the first position advantage, the first position has a smaller standard deviation which produces less overlap with other positions, and hence, increased efficiency. In the Letters in Time and Retinotopic Space model (LTRS, Adelman, 2011), all letters begin processing at the same time, but the strength of each letter varies as a function of input position. The LTRS model captures the advantage for the first position by assigning higher values of processing strength for the first position. Although both models have implemented procedures to accommodate the first letter advantage, it is unclear whether these models can also accommodate the strong effects observed for vertical presentations. Moreover, we believe that a fast acting allocation of spatial attention to the beginning of the word is a likely candidate that may underlie either of these modeling attempts at accounting for the robust first position advantage.

Another computational implementation of orthographic processing, the SERIOL model (Whitney, 2001), appears to be consistent with first position advantage at least for horizontally presented words. In this model, beginning-to-end lateral inhibition operating on retinotopic letter detectors paired with cross-hemispheric inhibition transform activation levels into a left-to-right decreasing activation gradient with stronger activation for the beginning of words. However, this account of the present results would appear to be challenged by the finding of a first-position advantage for vertically presented words.

It is finally worth noting that models of visual word recognition have considered the differential processing occurring for letters as a function of their position in the array. The classic Interactive Activation Model (Rumelhart & McClelland, 1982) implements differential input rates for different positions with highest rates for the first one. A more recent development of this class of models, the Spatial Coding Model (Davis, 2010), assigns greater weights to the letter-to-word connections for exterior letters, deemed as perceptually more salient. Importantly, all these implementations do not assume the operation of specific attentional mechanisms. In contrast, if our proposal is correct, this would represent additional weight to the claim that attentional dynamics need to be considered in models of visual word recognition (e.g., Balota, Paul, & Spieler, 1999; Besner, Risko, & Sklair, 2005; Lachter, Forster, & Ruthruff, 2004; McCann et al., 1992; Risko et al., 2010). It is also noteworthy that recent evidence suggests that visual spatial attention is an important predictor for the acquisition of reading skills (e.g., Franceschini, Gori, Ruffino, Pedrolli, & Facoetti, 2012).

The power of the first position in lexical processing likely reflects a more general cognitive phenomenon. For example, Tversky and Kahneman (1973) correctly argued that to accommodate the influence of accessibility bias in decision making individuals more easily generate candidates from the first letter position in a word than in the third letter position in a word, i.e., reflecting the power of the first position in searching the lexicon. Also, the first letter of a word can often be produced when one is in a tip-of-the-tongue state (Brown, 1991; Lovelace, 1987), even though the full form cannot be retrieved. Moreover, providing the first syllable of the word resolves more such states, at least for younger adults (White & Abrams, 2002). Similarly, performance on tests of phonological awareness in kindergarten age children is higher when the critical phoneme occurs in the initial position (Stanovich, Cunningham, & Cramer, 1984). Thus, the first position advantage in the present paradigm may be the consequence of a more general attentional bias towards initial perceptual units (e.g., letters, phonemes, syllables, etc.) that is developed over the lifespan.

Although the data in the current report are consistent with the proposed attentional account, there are a number of questions that remain to be addressed in future research. For example, it is unclear precisely when attention is moved to the initial character. The results of the second experiment suggest this process occurs prior to the decision stage (i.e., prior to the presentation of the alternatives), however there is no direct evidence as to whether attention is shifted immediately upon presentation of the target stimulus or at some point thereafter. Furthermore, it is possible that attention also operates post stimulus offset. That is, it is possible that there is parallel activation of the stimulus upon presentation, but attention acts to selectively preserve the initial letter of that representation. Additionally, although there was little evidence of a word orientation by letter position interaction in Experiment 4, there was a main effect of orientation such that vertical words were responded to more slowly. It is possible that attention is first drawn along the horizontal plane and then switches to the vertical dimension. Future research could address these questions about time course by examining response latencies to detect probes after stimulus onset to examine where attention had been drawn by the letter string.

One potential limitation to the present work is although participants were instructed to fix their gaze at the center of the mask, eye fixations were not monitored and one might be concerned that the initial letter advantage we report here is due to participants prospectively adjusting fixation to the first letter position string prior to the presentation of the target. However, we feel this will have minimal influence on the results for several reasons. First, words of different lengths (from 3–6 letters) were randomly intermixed. Thus, the participant could not predict with any reasonable degree of accuracy the location of the initial letter prior to stimulus onset. Indeed, Scaltritti and Balota (2013) directly compared randomly mixed lengths with blocked lengths and found no evidence for a difference in the pattern of results. Second, in Experiment 4, orientations were randomly intermixed with no way to predict whether the word will be vertical or horizontal and thus again there is no way to adjust fixation prior to stimulus onset to the first letter position. Third, of course, if fixation was being adjusted prior to stimulus presentation to the early positions, because these positions were unpredictable, it is unclear how this would produce the selective advantage for the first position as opposed to a more general leftward increase in performance. Finally, even when additional steps are taken, such as including vertical bars above and below the location at which the participant should be fixating, the first position advantage is still obtained (for example, in Tydgat & Grainger, 2009).

Another issue to be addressed in future work is whether the first letter effect is really letter level or possibly phonological in nature. Given that a clear first letter position also occurs for unpronounceable letter strings (see Scaltritti & Balota, 2013), we believe that the current results are most consistent with an orthographic level.

Finally, we have contrasted the attention account with the modified receptive fields hypothesis that has been proposed to account for serial position effects in single letter identification. We argued that the MRFH cannot account for the serial position effect in vertically presented strings (which it was never designed to do). However, this fact in and of itself does not imply that the MRFH is not operating for the horizontally presented strings. Indeed, both the attention mechanism and the MRFH could be operating jointly, however the strong prediction from this explanation would be an interaction of the letter position effect with word orientation such that the first position effect would be stronger for horizontal words (where both attention and MRFH are operating) compared to vertical words (where presumably only attention can be playing a role). This pattern was not observed in the present experiment.

In sum, there is clear utility of the first letter position to be particularly informative as an access code. The consistent advantage of the initial letter contradicts the strong claim of parallel models that all letters are processed equally, unless other mechanisms are assumed. We argue that the increased utility of the initial letter drives attention in an adaptive fashion to this particularly useful unit. At present, we believe these results are most consistent with a rapid deployment of spatial attention during the stimulus presentation that, remarkably can be flexibly directed to the unpredictable orientations of letters strings (as seen in Experiment 4). Although this bias in the first position may be quite independent of the rich literature on single letter identification where attention is specifically directed to letter-level processing (Chanceaux & Grainger, 2012; Grainger, Tydgat, & Isselé, 2010; Hammond & Green, 1982; Mason, 1982; Tydgat & Grainger, 2009), it is important to note that most models of visual word recognition are silent on the role of spatial attention and the present results reinforce the necessity of incorporating attentional processes into these computational accounts (Balota et al., 1999; Besner, Risko, Stolz, White & Reynolds, 2016; Grainger, Dufau, & Ziegler, 2016; Lachter et al. 2004; McCann et al. 1992).