Magnetic resonance fingerprinting based on realistic vasculature in mice

Abstract

Magnetic resonance fingerprinting (MRF) was recently proposed as a novel strategy for MR data acquisition and analysis. A variant of MRF called vascular MRF (vMRF) followed, that extracted maps of three parameters of physiological importance: cerebral oxygen saturation (SatO₂), mean vessel radius and cerebral blood volume (CBV). However, this estimation was based on idealized 2-dimensional simulations of vascular networks using random cylinders and the empirical Bloch equations convolved with a diffusion kernel. Here we focus on studying the vascular MR fingerprint using real mouse angiograms and physiological values as the substrate for the MR simulations. The MR signal is calculated ab initio with a Monte Carlo approximation, by tracking the accumulated phase from a large number of protons diffusing within the angiogram. We first study the identifiability of parameters in simulations, showing that parameters are fully estimable at realistically high signal-to-noise ratios (SNR) when the same angiogram is used for dictionary generation and parameter estimation, but that large biases in the estimates persist when the angiograms are different. Despite these biases, simulations show that differences in parameters remain estimable. We then applied this methodology to data acquired using the GESFIDE sequence with SPIONs injected into 9 young wild type and 9 old atherosclerotic mice. Both the pre injection signal and the ratio of post-to-pre injection signals were modeled, using 5-dimensional dictionaries. The vMRF methodology extracted significant differences in SatO₂, mean vessel radius and CBV between the two groups, consistent across brain regions and dictionaries. Further validation work is essential before vMRF can gain wider application.

1. INTRODUCTION

Magnetic resonance fingerprinting (MRF) has been developed as a novel strategy for MR data acquisition and analysis [1]. It has similarities to compressed sensing and to quantitative MR imaging (qMRI), and it has been used to quantify multiple magnetic relaxation properties simultaneously, or even derived physiological quantities. Instead of acquiring qualitative images, or fitting data acquired from several scans to a biophysical model, which are two typical uses of MRI data, MRF differs in that it compares data to a “dictionary” of possible signals using a biophysical model and then models the MRI data by selecting the best matching entry in the dictionary. In turn, this selection yields the whole set of biophysical model parameters that were used to generate the specific dictionary entry. Vascular MRF (vMRF, [2], see Fig. 1 for a schematic description) differs from MRF and is more ambitious, in that the parameters to be extracted (cerebral oxygenation (SatO₂), mean vessel radius and cerebral blood volume (CBV) in the voxel) are of greater physiological interest but are less immediately related to the magnetic properties directly reported with MRF, namely longitudinal (T₁) and transverse (T₂, T₂*) relaxation.

Fig. 1.

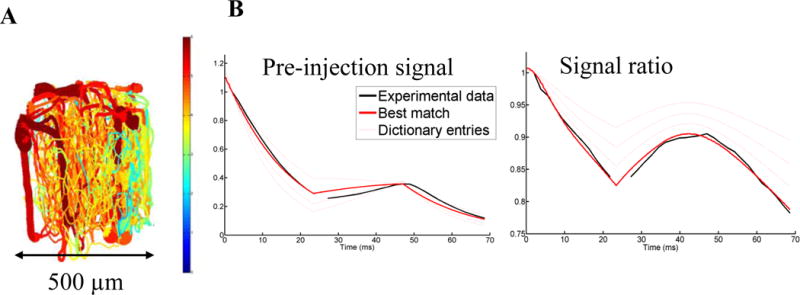
Illustration of vMRF methodology. A. Representation of a realistic angiogram, used to generate by deformations a dictionary of MR signals. B. Sample modeling of cortical mouse vMRF data (black line) to the best matching entry in the dictionary (thick red line), with the thin red lines representing 3 out of the 175 thousand other dictionary entries. From this model, simulated parameters which generated that entry are extracted, e.g. for this match: SatO₂ = 52.7%, mean vessel radius = 7.4 μm, CBV = 8.0%, SPION concentration = 3.0 and ΔB₀ = 0.0015.

These MRF efforts at extracting physiological information from MRI scans belong to a much broader enterprise geared at understanding the microscopic origins of the MRI signal [3]–[5]. While generating high initial excitement, the MRF and vMRF novelty demands precise validation work. In particular, vMRF requires extensive biophysical modelling for fingerprinting dictionary generation. In principle, different modelling assumptions could lead to different end results, a potentially serious problem for vMRF. Yet, initial published results showed promise. For example, Christen et al. obtained stable and reasonable but not validated high resolution brain SatO₂, mean radius and CBV maps in humans [2]. Among the assumptions that can be questioned, their results were based on a simple model of the cerebral vasculature, which was 2-dimensional and used vessels of constant radius. The dependence of the results on this simplistic modeling remains to be established.

To address these issues, a more detailed model of the vasculature can be used: with two-photon optical microscopy, detailed vascular information with an isotropic resolution of about 1 μm can be obtained, including oxygenation information [6]. However, this latter information is typically acquired invasively in mice and efforts to apply MRF to animals are required [7].

We sought to answer two questions: can a vMRF approach using realistic angiograms produce reasonable results? Will the vMRF results depend on the underlying angiograms? Thus herein, we propose using a more precise calculation of the MR signal following our recent work [8], [9], by using Monte Carlo simulations of a large number of water protons diffusing in time in the imaging voxel. Another improvement is to base the calculations on realistic models of the vasculature obtained from three-dimensional high-resolution angiograms of the mouse cortex, instead of the simpler but far-from-realistic two-dimensional model of cylinders used in [2]. We make a detailed analysis of the estimability of parameters using simulations to conclude that, when using single angiograms, only differences in parameters are estimable in this realistic framework. Finally, we applied the methodology in animal experiments where large differences in the vMRF parameters between two groups are anticipated a priori: young wild type (WT) mice and aged atherosclerotic (ATX) mice. Large, statistically significant differences in parameters were seen between the two groups, consistent across brain regions and across angiograms underlying the vMRF dictionaries, especially in cerebral white matter [10], [11]. Although these results are promising, resolving the bias issue in the extracted parameters would be essential for vMRF to gain acceptance.

2. METHODS

Animal model and preparation

We followed recommendations of the Canadian Council on Animal Care, and all procedures, were approved by the Animal Research Ethics Committee of the Montreal Heart Institute. The protocol described below was carried out on 10 Wild Type (WT) young mice (8–9 weeks old) and 10 Atherosclerotic (ATX, [12]–[15]) aged mice (11.1 ± 2.0 months) with LDLr−/−, hApoB+/+ genotype. Both WT and ATX mice are from the C57/B6 lineage. The choice of the atherosclerotic (ATX) mice for the animal model was based on its well-documented characteristics as a model of cerebro-vascular dysfunction. Genetically altered LDLR−/−, hApoB+/+ ATX mice have a mean life-span of 14 months, spontaneously develop atherosclerotic plaques and were used by our team and others as a model of cerebro-microvasculature dysfunction [12]–[15]. Previous studies showed that in 6-m/o ATX mice, carotid arteries stiffen (reduced compliance) [13]. As a parallel to observations in humans, a lower resting cerebral blood flow (CBF) in ATX mice was associated with reduced CBF increase during neuronal activity (hyperemia). In measures of cognition, ATX mice have a weak but significant learning deficit at 6 months of age that is associated with a reduced basal CBF and a reduced CBF response to neuronal stimulation [27]. Altogether, this model recapitulates features of premature arterial aging and offers the possibility of studying the consequences of vascular diseases. The two age groups were chosen so as to maximize the expected physiological differences (young healthy vs old diseased) in this proof-of-concept study. One mouse in each group was lost due to heater malfunction. A total of N=9+9 mice were used in the experiments and analyses below without any exclusion. See Suppl. Methods for information on the MRI experiments.

MRI acquisitions

A multi-slice 2D gradient-echo sampling of free induction decay and echo (GESFIDE) [16] sequence (Fig. 2A) was implemented on a 7 Tesla 30 cm bore horizontal scanner (Agilent, CA) and tested on phantoms. The scanner was equipped with a 12 cm inner diameter gradient coil insert (gradient strength 600 mT/m, rise-time 130 μs).

Fig. 2.

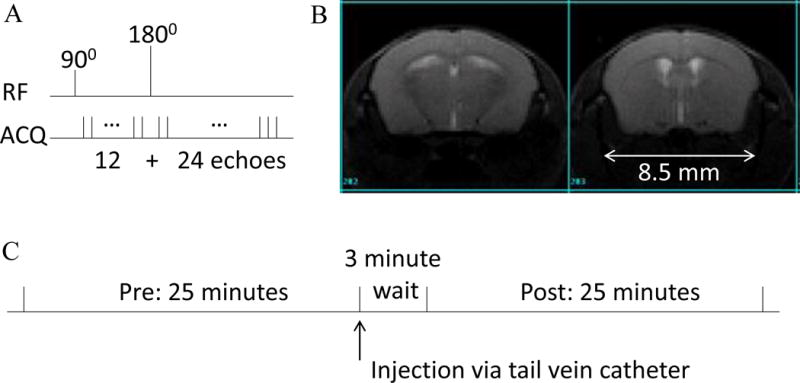
A. Schematic of the GESFIDE sequence. B. Sample mouse GESFIDE data, at the spin echo (echo #24) with SNR ~ 50. C. Imaging protocol.

After scouting, shimming was performed to reach a linewidth of 50 Hz or less over the whole brain. A baseline GESFIDE scan was run first (Fig. 2B), then the SPIONs syringe in the middle of the MRI was manually agitated gently and the SPION solution was slowly injected over a period of 15–20 seconds (see Fig. 2C for a depiction of our imaging protocol). After waiting 3 minutes, a second GESFIDE scan was acquired, followed with an anatomical TFISP scan [17]. GESFIDE sequence parameters were TR/TE₁/TE₂=3 s/2 ms/1.8 ms, 36 echoes, 180° pulse after 12^th echo, 12 axial slices covering the whole brain, acquisition bandwidth=208 kHz (corresponding to a line acquisition time of 614 μs), 128 × 128 matrix, 20 × 20 mm FOV, 1 mm thickness, 4 repetitions, adding up to 25 min per scan. The 3-dimensional TFISP sequence parameters were TR/TE=4.8/2.4 ms, 180 × 180 × 90 matrix, with a longitudinal readout direction, for a 100 μm isotropic resolution, with FA=35° and 20 min scan duration.

MRI signal simulations

All MRI signal simulations were performed in Matlab (Natick, USA). A modified version of the MR simulation code in [8] was used, itself based on principles detailed in [18], [19], [20], as summarized below. This code was optimized for speed and modified to explore the parameter space of angiogram deformations and other parameters affecting the MR signal as explained in the next section.

The 6 angiogram constructs built in Gagnon et al. [8], [21] were used as the substrates for the simulations. These constructs, referred here as Ai, i=1,…,6, were derived from measurements in the mouse somatosensory cortex using two-photon microscopy (2PH) and optical coherence tomography (OCT). They consisted of connected segments of blood vessels each with a specified radius. They were stored as volumes (3-dimensional arrays) with 1 μm isotropic resolution. Their total volumes were 0.27 ± 0.05 mm³ (see [8], [21] for details). The vessel type (artery, vein, capillary) as well as oxygen saturation were provided by experimental measurements with a PO₂ sensitive molecular probe for these angiograms [6], [22].

It was assumed that the MRI signal in the mouse brain could be sufficiently accurately modeled by a large number of hydrogen water protons diffusing in a background with spatially constant T₁ relaxation, fixed values of T₂ in tissue and spatially varying T₂* relaxation due to the combination of deoxyhemoglobin and SPION concentration within the vasculature in the imaging voxel and macroscopic magnetic field variations, e.g. due to imperfect shimming. As with previous vascular fingerprinting efforts, the following effects were assumed to be small enough to be negligible: contributions from other hydrogen atoms not bound to water (e.g. fat), additional iron presence in some structures like basal ganglia [23], additional sources of B₀ inhomogeneities, B₁ field inhomogeneity, gradient nonlinearity, hematocrit variability [24], and finally all differences between gray and white matter that are not captured by the blood vessels [25], such as T₁ and T₂ relaxation differences [26], chemical exchange effects between gray and white matter (only affecting the signal phase) [27], proton density differences [28], geometrical orientation differences of constituents such as myelin [29], and partial volume effects with cerebrospinal fluid and skull. Note that some of these effects (e.g. B₀ inhomogeneities) cancel out in the ratio of post-to-pre injection scans.

Thus conceptually, the MRI signal simulation problem was reduced to the diffusion of protons in the magnetic field produced by a static angiogram. Diffusion was assumed isotropic. The magnetic field perturbation was calculated using a linear approximation for the magnetic fields and susceptibilities, and a dipole approximation, see [4], [8], [30], [31]: in brief, the magnetic field perturbation experienced by the diffusing proton was proportional to the 3D convolution of the SPION + deoxyhemoglobin concentrations with an ellipsoidal kernel oriented with B₀ (see [2] for all the details). For speed, this was implemented with Fourier transforms.

An idealized GESFIDE sequence with the same parameters as that used in the MRI acquisitions was simulated on these angiograms by positioning N water ¹H protons randomly throughout the volumes, and calculating the time evolution of their spins, following the application of magnetic field gradients (namely, the butterfly for the 180° pulse) and radiofrequency pulses (90° and 180° pulses) in a B₀ field of 7 Tesla. The protons were let to diffuse isotropically with a diffusivity constant of 0.8 μm²/ms [32] and the MR signal was finally computed by summing the accumulated complex phase from each proton, adding the contributions from the different magnetic field perturbations. The pulses were assumed to act instantaneously and the B₁ field was assumed ideal. T₁ relaxation effects were included as an exponential decay assuming T₁ in tissue of 1590 ms [33]. Hematocrit values assumed were 0.44 in arterioles and venules, 0.33 in capillaries [34] [35]. These values were kept constant even as the angiograms were deformed.

For time evolution, a time step of Δt = 0.2 ms was used, which was commensurate by design with the MRI sequence parameters. The time between the 90° pulse and the 1^st gradient echo readout was TE₁=10Δt. 12 echoes were then generated, separated by TE₂ = 9Δt. A gap of 2*TE₂ was provided for the 180° pulse generation, during which no gradient echoes were simulated. Finally, 24 additional gradient echoes were generated, again separated by TE₂ each. To correct for imperfect refocusing pulses, crusher gradients are typically included in spin echo sequences. Therefore, crushers of 13 mT/m were applied during 2Δt before and after the 180° pulse, with gap of 7Δt between the two crushers.

The descending pial arteries of the mouse somatosensory cortex 2PH scans were oriented orthogonally to the B₀ field, for a horizontal scanner. The readout direction was also in the vertical direction. The effect of B₀ inhomogeneity was simulated by applying a constant magnetic field gradient in a direction orthogonal to the readout direction (actually the B₀ direction), across the imaging voxel. The crushers were simulated by another gradient in the remaining direction. The readout gradients were not simulated.

Preprocessing of MRI data

For each mouse, specific brain masks were made using dsiStudio [36] and ITK-Snap [37] for the GESFIDE and the anatomical TFISP scans. N4 intensity correction of the GESFIDE and TFISP scans was performed using ANTS [38], [39]. Coregistration of the Allen Mouse Atlas [40] was performed onto the TFISP scan of each mouse brain using ANTS [41] to define regions of interest (ROIs). The Allen Atlas was agglomerated so that 10 relatively large and familiar brain regions remained, with 1300 ± 1000 voxels (Suppl. Table 1). Coregistration of the 2D GESFIDE to the 3D TFISP scans for each mouse was also performed (Suppl. Fig. 1). Voxel-wise GESFIDE time series were then obtained. Average GESFIDE time series were computed for 10 brain regions from the Allen Atlas, by averaging the signal over each region, for the 9 WT mice and 9 ATX mice, for each time point of the pre and post injection scans. The GESFIDE time series were all normalized to unity at the first gradient echo. Thus, after processing, experimental data consisted of 36 data time points for the echo times of the GESFIDE sequence from 2.0 ms to nearly 68 ms with a 3.6 ms gap during the emission of the 180° spin echo pulse, for each of 9 mice in each group (WT, ATX), for each of 10 regions, for the pre-injection and post-injection scans. The ratio of post to pre-injection scans was calculated for these region-averaged signals.

Dictionary generation: experimental data

Five parameters were varied to generate vMRF dictionaries. An essential point to reflect upon is that, in deformations of realistic angiograms, naïvely varying the radius by a constant will also affect the CBV. With the simplified model of cylinders in [2], it was straightforward to find a parameter basis where radius and CBV could be varied independently. This independence is important to avoid cross-talk between the parameters, which in turn has a confusing effect on parameter estimability. This issue was addressed in the 3-dimensional dictionaries generated for simulations, see further below, but not for the larger dictionaries used on experimental data.

In addition to the 3 physiological parameters of interest (SatO₂, vessel radius, CBV), two parameters were essential to match the experimental data: the SPION concentration for matching the signal ratio (required due to the experimental variability in the small injection volume) and the magnetic field inhomogeneity ΔB₀ for matching the pre-injection signal. Thus, to generate the dictionaries, the MR signal simulations outlined in the previous section were performed to explore the parameter space along 5 dimensions for dictionaries D_i, with i=1,…,6, labeling the underlying angiogram A_i:

1. CBV was reduced by deleting a fraction of the blood vessels, sorted by size, starting with the large vessels. Note that deleting blood vessels had the effect of changing the effective mean vessel radius at the same time.

2. The mean vessel radius was varied by multiplying all vessel radii values by a constant, and truncating the results between 1.75 (a physical lower cut-off dictated by the size of a red blood cell) and a sufficiently large value of 90 μm. Of course, CBV was also modified by this operation.

3. SatO₂ was varied by multiplying uniformly all oxygen saturation values in the angiogram by a constant, truncating the results between 0 and 100% and then taking the average SatO₂ value across the angiogram.

4. The SPION concentration was varied around the injected value, quoted in arbitrary units (due to an undetermined factor between the SPION T₂* relaxivity and the implied susceptibility).

5. The magnetic field inhomogeneity ΔB₀ was varied between 0 and a value high enough such that the MR signal was strongly suppressed everywhere else than at the spin echo.

For these dictionaries D_i, the MR signals were Monte Carlo generated for N=8*10⁵ protons, for a subset of the desired deformation parameters, and interpolated to fill the desired parameter space. See Suppl. Table 2 for details on the simulated parameter values. The generation of the pre-interpolated dictionary Di for each mouse angiogram took 70 hours on a computer cluster (Guillimin, McGill University and Calcul Québec), with 15 processes running in parallel. The interpolation took about 2 days for each angiogram and was not parallelized. It was done using the Matlab interpn function in 5 dimensions for linear interpolation, without extrapolation.

In summary, the simulated dictionaries D_i consisted of 404K entries and occupied 1.1GB in storage, for each of the 6 angiograms A_i, exploring a 5-dimensional parameter space. Each entry consisted of two curves, one for the pre-injection scan and one for the ratio of the post to pre-injection scans, each with 343 points (68.6 ms) and normalized to 1 at time t = 1.4 ms, corresponding to the first measured gradient echo (at 2 ms) in the experimental data less a 0.6 ms adjustment for the finite duration of the excitation pulse. Thus to each dictionary entry was associated a set of 5 labels for the simulated parameters and 5 labels for their corresponding physical values.

Fingerprinting match of experimental data to the dictionaries

The best match between the experimental data and a dictionary was obtained by minimizing the square root of the sum of squares (Euclidean norm) of the difference between the experimental signal and the dictionary entries, weighing equally each data time point of the pre-injection curve and of the ratio of post to pre-injection curve. The dictionary curves were naturally restricted to the 36 measured time points (the GESFIDE echoes).

Experimental MR signals from each mouse and region were plotted against the dictionary matches to visually check the match quality. A statistical 2-sample paired t-test was performed for each region and each angiogram. A Bonferroni correction was applied, correcting for 10 brain regions and the 5 parameters. In each case, an average Avg was obtained by averaging the parameter values over the 6 dictionaries, for each mouse, parameter and region. This should be understood as a mathematical operation to summarize the results, without implying any biophysical interpretation.

From the MR phase data of the first 4 echoes of the pre-injection GESFIDE scans, a value for ΔB₀ was calculated by least-square linear match voxel-by-voxel. These ΔB₀ values were averaged over the ROIs and compared to the extracted ΔB₀ parameters and to the measured shimming linewidths.

Dictionary generation: Simulations

A detailed study of parameter estimability was carried out in simulations exploring the 3 dimensions associated with physiology (i.e. neglecting parameters ΔB₀ and SPIONS concentrations). For the built dictionaries, D0_i, with i=1,…,6, labeling the underlying angiogram Ai, an effort was made so that deformations of mean radius and CBV would approximately fit on a grid in the (vessel radius, CBV) space and that this grid of deformations would contain a substantial overlap common to all angiograms (Suppl. Fig. 2). This was done to enable a better comparison with the work of Christen et al. [2]. To achieve that, the deformations of types 1 and 2 for radius and CBV described above were not sufficient, and another deformation was introduced, consisting of varying radii in proportion to their radius value (e.g. large radii get larger while small radii get smaller, with respect to a radius pivot chosen at an intermediate radius value of 7.5 μm). Along these 3 types of deformations, 11 × 45 × 35 = 17325 deformations of each of the 6 angiograms were generated. A grid of points (21 × 26) was chosen in the (vessel radius, CBV) space, with relative spacing of 10% in a central region covering 6 to 21 μm for radius and 2% to 9% for CBV, except on the edges of that space where spacing was increased to 25%. The deformed angiograms amongst the 17325 × 6 deformations that were closest to points on the grid, and no further than 5% away in both dimensions, were selected (Suppl. Fig. 2). For each A_i, about 250 deformed angiograms (255 ± 35) survived this projection on the grid in (radius, CBV) space. The MR signals were then generated for the points on the grid only, at 10 SatO₂ values (5% spacing), and for N=10⁷ protons. Thus, dictionaries D0_i consisted of approximately 2500 entries (of which 1030 entries were on the overlap) identified by 3 labels (SatO₂, Radius, CBV).

Dictionary properties

Estimability of parameters in simulations

For a more direct assessment of parameter estimability, detailed simulations were carried out, where noise was added to the MR signal originating from selected entries of one dictionary D0_i and then this noisy signal was modeled by fingerprinting with another dictionary D0_j, possibly the same. The admissible entries for the simulated noisy MR signals were all those on the overlap of the dictionaries (Suppl. Fig. 3, 103 points) for SatO₂ values within 25% of baseline (6 SatO₂ values). The admissible entries were all included and with equal weighting. 100 sets of noisy series were generated, using the corresponding same random numbers on the different admitted entries and also when varying the SNR as below.

As mentioned earlier, the mean number of voxels in the 10 brain ROIs for the mouse data was 1300 ± 1000 while the typical SNR of a voxel at the spin echo was 50. Thus an SNR gain of sqrt(1300) ~ 36 could optimistically be expected in our upcoming ROI analysis of the mouse data. To reflect this range of SNR values in the experimental data, three SNR values were chosen for the simulations: 50, 50*6=300 and 50*36=1800. Gaussian uncorrelated white noise was added to the pre and post injection MR signals, and the ratio was then calculated.

Thus a total 100 random series × 103 (radius, CBV) pairs × 3 SNR values × (6 for SatO₂) × (6 for underlying angiogram) MR signals were generated. They were then matched to either the 6 dictionaries for D0_i.

Additional methods are available in the suppl. materials.

3. RESULTS

Simulations

Properties of dictionaries D0_i

Suppl. Fig. 2 shows the constructed parameter space in the (mean vessel radius, CBV) plane. As mentioned previously, the overlapping grid common to all 6 angiograms contained 103 points. It was thus feasible to build deformations of all the angiograms that were sufficiently large to allow for a non-trivial overlap. However, the overlap contained the baseline parameter values of only angiograms 3 and 6, and even for those, the baseline values were very near the edges of the overlap region. On the other hand, deformations of angiograms 3 and 5 included the baseline values of all the other angiograms. Suppl. Fig. 3 shows the differences between the constructed and targeted parameter space, with constructed values of mean radius and CBV falling within 5% of targeted values. Thus there is a large variability between real angiograms and they do not individually support all of the parameter space.

Suppl. Table 3 shows the results of the eigenvalues analysis of dictionaries D0_i. In all cases considered, none of the eigenvalues were zero, implying that all parameters are theoretically identifiable in the linear approximation of the dictionaries. However, the first eigenvalue is much larger than the next one, by a factor of ~290. This suggests that estimability of more than one combination of parameters requires high SNR. An increase in the ratio of the first to the next eigenvalue was noted in two cases: when only the post-to-pre injection ratio is used for the match (a 60% increase in the eigenvalue ratio), and when one uses the average dictionary (a 23% increase).

Suppl. Fig. 4 illustrates the sensitivity of the dictionaries based on the 6 angiograms, around the baseline point described above. The MR pre-injection signal changes and changes in the ratio of post-to-pre injection signals were calculated under 10% changes in SatO₂, mean vessel radius and CBV. We observed that the signal change curves were quite different for different angiograms. This observation might cast doubt on parameter identifiability. The average signal changes averaged over the 6 dictionaries are also drawn. For 10% changes in SatO₂ and in CBV, the similarity of the average curves to the curves from each angiogram suggests that averaging over dictionaries might be a successful technique to identify these 2 parameters, since averaging over angiograms might be a sensible thing to do. On the other hand, the average curves for changes in the vessel radius are approximately null, with changes from some angiograms completely offsetting the changes from other angiograms.

Estimability of parameters and of parameter differences in simulations

Suppl. Fig. 5 shows the estimability of parameters when the same underlying angiogram is used for dictionary generation and for generation of the MR signals to be matched with the dictionary. Histograms of relative differences between the estimated and simulated parameter values are shown, and either only the ratio of the post to the pre-injection signals was modeled as in [2] or both the ratio and the pre-injection signal were matched. There is a substantial improvement in estimability by matching both signals, such that all parameters are nearly perfectly estimable at an SNR = 1800, while some uncertainty (3.2% for the radius) remain when matching only the ratio. For this figure, dictionary D0₅ was used, and an equal weight was given to estimations based on MR signals generated on all 103 points on the overlap in the (radius, CBV) space and with SatO₂ values within 25% of the baseline value.

This same simulation space was used for Figs. 3 and 4. Fig. 3 shows typical parameter estimation results in simulations, with a different angiogram used for dictionary generation and for the simulated noisy signal to be matched to the dictionary. A bias in the estimated parameters is observed in that case even at high SNR, especially for the radius.

Fig. 3.

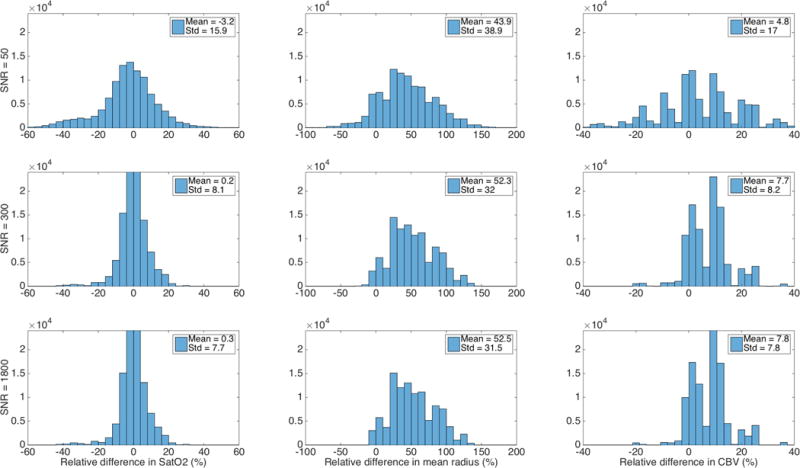
Non-estimability of parameters with a different angiogram (angiogram 4) used for dictionary generation (D0₄) and for the simulated noisy signal (angiogram 5) to be matched to the dictionary (D0₄). A bias in the estimated parameters remains even at high SNR, especially for the radius.

Fig. 4.

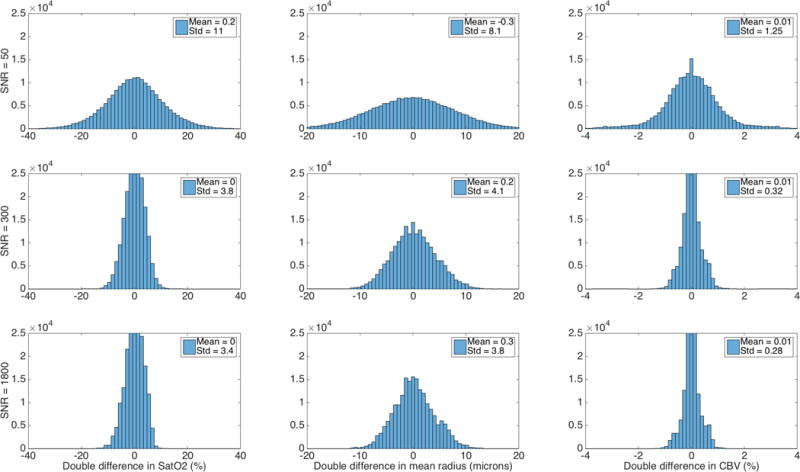
Estimability of differences in parameters. As with Fig. 3, angiogram 4 was used for the dictionary D0₄ while the simulated noisy signal S_a was based on a different angiogram (#5). The set of all pairs (S_a,S_b) of simulated signals with different underlying parameters a and b was considered. For each pair, the double difference was calculated by subtracting the difference between the extracted and simulated parameters for parameters a from the same quantity calculated for parameters b.

Fig. 4 shows a better estimability for the differences in parameters, using the same set up as in Fig. 3. Pairs (S_a,S_b) of simulated signals from one angiogram with different underlying parameters a and b were considered. For each pair, the double difference was calculated by subtracting the difference between the extracted and simulated parameters for parameters (a) from the same quantity calculated for parameters (b). Histograms produced from a large number of such pairs have nearly zero mean and a relatively small standard deviation that however remains non-zero even at high SNR. This could be due in part to the relative spacing between entries in the dictionaries of 10% for Radius and CBV (and 5% for SatO₂). Estimability results were similar for all the other angiograms and angiogram pairs.

Experimental data

Properties of dictionaries and estimability of parameters

Using realistic angiograms, our simulations indicated that when estimating parameters across different angiograms (i.e. estimating physiological parameters simulated with one angiogram from another), or with the mean value over all angiograms, vMRF parameters were biased and generally not estimable. However, differences of vMRF parameters were seen to be estimable in simulations. We thus focussed on estimating differences with the experimental data below.

Graphs of RMSD to baseline for the dictionaries

Suppl. Fig. 6 shows the RMSD graphs for all 10 pairs of parameters. While the ΔB₀ parameter is well constrained, valleys are present for the other parameter pairs. The crosstalk between radius and CBV is also apparent.

Spatial maps of the vMRF parameters

Suppl. Fig. 7 shows all the vMRF extracted parameters for 1 representative mouse, for all the dictionaries, as well as the average Avg and standard deviation maps of the parameters, and the extracted parameters labeled “best”.

Suppl. Fig. 8 shows the SatO₂ vMRF extracted parameters for slice #7 for the 18 mice, for the “best” match over dictionaries. Anatomical features such as the cerebrospinal fluid compartments and the corpus callosum can be readily noticed, reflecting the quality of match.

Correlations between vMRF extracted radius and CBV and steady-state radius and CBV

As a validation step, steady-state radius (ss_R) and CBV (ss_CBV) measures were derived from the experimental data (please see [2] for defining formulas). Suppl. Fig. 9 shows correlation maps between vMRF extracted R and CBV values and steady-state estimates ss_R and ss_CBV, for the 6 dictionaries, for the mid coronal slice (#7). It also shows correlations of paired differences: for this, each of the 9 ATX mice was paired to a different WT mouse; for each ATX-WT pair, the difference in vMRF R and the difference in ss_R were calculated. The correlations shown are between these vMRF R differences and ss_R differences and the same was repeated for CBV vs ss_CBV. These showed strong correlations between extracted vMRF measures and steady-state measures. However, the possibility of biases in these relationships was not investigated here.

Statistical Parameter Maps (SPM) of the vMRF parameters

Fig. 5 shows the SPMs of 2-sample t-tests for the hypothesis WT > ATX for the 5 parameters, for the “best” match, for the average Avg and for one dictionary. We note that while the absolute values of the parameters are subject to bias, the spatial distribution of their relative values were quite stable and reasonable. A paired t-test for WT > ATX for the ss_radius and ss_CBV measures was also done, which showed similar spatial distributions of t-statistics as the vMRF maps.

Fig. 5.

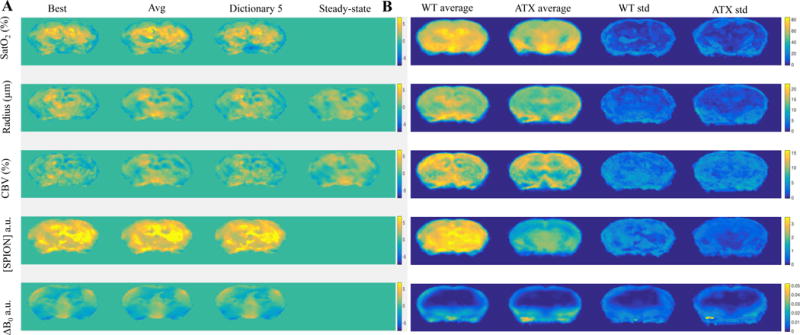
A. 2-sample t-tests SPMs for WT > ATX for the 5 parameters, on the vMRF maps obtained either using the “best” matching entries, the average “Avg” of the vMRF extracted values, or one of the dictionaries (#5), for the same slice as Suppl. Figs. 11 and 12. B. For the “best” matching entries, the vMRF parameter averages for WT and ATX mice, and their standard deviations. 2-sample t-tests SPMs for WT > ATX are also shown for the steady state values ss_R and ss_CBV.

Analysis of extracted parameters by region-of-interest (ROI)

While the parameter maps shown were limited to 1 of the 12 slices (#7) for practical purposes, it is of interest to summarize the results on the whole brain by ROIs. The SPM results above were qualitatively consistent with the results obtained on ROIs.

In Fig. 6, we show boxplots of 2-sample t-tests comparing WT to ATX physiological parameters on 4 regions, for each of the 6 dictionaries while the results for all parameters and all regions are in Suppl. Figs. 10A and B. Results show a trend for smaller SatO₂, Radius and CBV for all dictionaries and nearly all regions (9/10, except for the cerebellar cortex). For the Avg results, this trend was significant after Bonferroni correction in white matter (corpus callosum and thalamus), for SatO₂ and Radius. It was also significant for CBV in the cortex and thalamus.

Fig. 6.

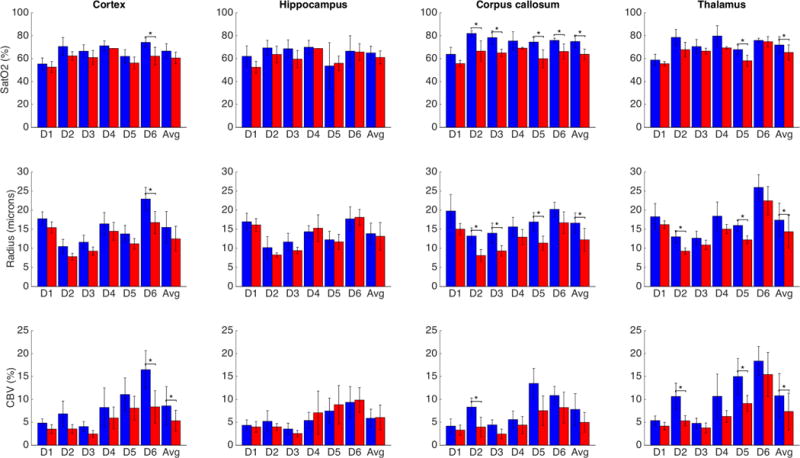
Results of paired t-tests for 4 regions of interest for the 3 physiological parameters. SatO₂ and Radius were significantly higher in white matter (corpus callosum and thalamus) for the mean of the extracted parameters. Blue bars (darker when printed in grayscale): WT mice; red bars: ATX mice.

*: p < 0.05 Bonferroni corrected.

Match of SatO₂, radius and CBV

Fig. 6 shows significantly reduced SatO₂ in ATX mice compared to WT in white matter: in corpus callosum for dictionaries built on angiograms 2, 3, 5, 6 and the average of extracted values, and in thalamus for angiogram 5 and the average. For gray matter structures, there was typically a trend for reduced SatO₂ in ATX mice, but it was not significant with the exception of dictionary #6 in cortex.

Similarly, a reduced mean vessel radius was extracted by vMRF in ATX mice in white matter: in corpus callosum for dictionaries 2, 3, 5 and the average (Avg), and in thalamus for dictionaries 2, 5 and Avg. A significantly reduced radius was also seen in cortex for dictionary 6 and in the hypothalamus for dictionaries 1, 2, 4, 5, 6 and Avg, but not in other regions.

Finally, a reduced CBV was found in ATX mice in 4 regions: in cortex for dictionary 6 and Avg, in corpus callosum for dictionary 2, in thalamus for dictionaries 2, 5 and Avg, and in hypothalamus for dictionaries 1, 4 and Avg.

In summary, a trend for reduced SatO₂, mean vessel radius and CBV was found in ATX mice compared to WT, becoming significant mainly in some white matter structures.

4. DISCUSSION

Comparison to literature values in mice

Our simulation results indicated that vMRF parameters are potentially biased. It is still of interest to compare vMRF parameters with available data. Experimentally determined average values for the six 2-photon angiograms in 8-week old Wild Type mouse somatosensory cortex [8] were 60.1 ± 5.6% for SatO₂, 10.2 ± 4.3 μm for mean radius and 3.5 ± 1.4% for CBV, while they are at present unknown for ATX mice. These values are similar within experimental errors to the average values we obtained from fingerprinting in mouse cortex, of 66.6 ± 8.3% for SatO₂, 15.5 ± 4.8 μm for mean radius and 8.6 ± 5.2% for CBV. An explanation for the higher value of our average vMRF SatO₂ is isoflurane anesthesia which is known to be vasodilatory (see Limitations). Higher values of vMRF mean radius and CBV can also be explained by experimental bias in microscopy experiments: when the 2-photon angiograms were obtained, larger arteries were methodologically avoided, thus biasing these measures to lower values.

For CBV, micro-CT was used [42] to obtain whole brain average CBV in WT mouse of 5.8%, reduced to 4.4% for small vessels along with detailed information on similar sub-regions to the ones chosen in this work. Although our vMRF extracted values have higher uncertainties (Suppl. Table 4), they are fully consistent with previously reported values [42].

Comparison between vMRF on realistic angiograms vs. models of cylinders

The motivation and focus of this work was to investigate the implications of applying vMRF to realistic angiograms. It showed in simulations that different physiological parameters were extracted from the same MRF signals depending on the underlying baseline angiogram. On the other hand, there is much interest in the literature in models of 2D and 3D cylinders (see references in [2]). While studying this is left for future work, one can assert that it follows a priori that, without further controlling for this effect, a naïve model of the vasculature such as with 2D or 3D cylinders of constant radius will produce biased estimates for physiological parameters. This follows because, explicitly, (1) different dictionaries were generated for equal physiological parameters based on different underlying baseline angiograms and (2) within the dictionary constructed on one underlying angiogram, different deformations could lead to the same physiological parameters but produce different MRF signals. Thus, at least for the GESFIDE sequence, the natural diversity in angiogram structure does not lead to believe that a vascular model can be used to predict the MRF signal. It is possible that at a larger scale, such as the voxel size used in human imaging, some of this variability disappears, or that the above problems could be reduced with other imaging sequences. This could be explored in future work.

Simulating additional parameters

Beyond the 5 dimensions of vMRF parameter space studied in this work, several other dimensions were explored but not reported in detail. Tissue T₁ seemed to have negligible effects but this was not demonstrated here; in particular, exploiting the known difference in gray vs. white matter T₁ would be of interest. A 6^th dimension was simulated for the dictionaries, by varying tissue T₂ by ±20% from a baseline value of 50 ms [43], generating the MR signals, and then interpolating the signals to 4% spacing. However, parameter identifiability was poor when including this dimension, and it was ignored (projected out) for all the remaining analysis. Also, these dictionaries, exceeding 2GB each in size, were impractically large to carry out all the later required vMRF parameter extractions. Proton density and proton diffusion directionality are other effects of interest that were not considered.

Hematocrit values were assumed constant, and during dictionary generation, the blood vessel types were kept constant as their radii were modified. Any systematic differences in hematocrit values would directly affect SatO₂ estimates.

It is possible that the vMRF approach on realistic angiograms could benefit from adding other geometric parameters (such as vessel density, distribution of vessel diameters, orientations, etc.) However, the practical difficulties with dictionary size growing exponentially with the number of parameters, and their identifiability will become more severe.

Constraining the dictionaries to fewer parameters

Two of the parameters presented little intrinsic interest but were essential to matching the data to the dictionaries: the SPION concentration and ΔB₀. It would be of interest to fix these parameters in order to better constrain the physiological parameters which are of greater interest. This is an interesting future direction that was not much explored, mainly due to imperfections in the dictionaries and to experimental limitations. Initial attempts did not show improvements at reducing uncertainties in the physiological parameters and were not pursued.

Regarding SPION concentrations, the experimental difficulty was uncertainties on the injected SPION concentrations, due to working with very small sample amounts, and on the injected volume, due to the requirement of a saline buffer for installation and operation of the catheter. Despite this, the average of vMRF extracted SPION concentrations appeared consistent with the theoretically injected values, as explained in the Results.

Regarding ΔB₀ values, one could use the ΔB₀ values calculated from the first few echoes (here the first 4 were used) of the GESFIDE signal to correct for the signal decay of the MR pre-injection signal, and thus remove the need for the ΔB₀ dimension in the dictionaries. However, in our data, this also reduced the vMRF matching quality.

Including priors

In some instances, the extracted vMRF parameters were on the edge of the generated dictionary, i.e. stuck on the boundary of parameter space. While this could indicate that an extended dictionary was required for a better parameter estimation, we covered known expected physiological range in all dictionaries. Including priors to constrain matches to be within the bulk of the dictionaries would be an alternative to better parameter estimations.

LIMITATIONS

Defects of constructed dictionaries

An important limitation is that the dictionaries Di used to match the experimental data were not optimal: there was nearly no overlap along the mean radius and CBV directions common to all dictionaries, the interpolation step introduced noise in the MR signals and the map between angiogram deformations and realized physiological parameters was indirect. One message of this study is that it is not straightforward to construct vMRF dictionaries satisfying all desirable properties. In [2], the simple vessel geometry led to a direct, one-to-one, relationship between model parameters and realized physiological parameters. This simplicity is lost with real angiograms. The relationship between deformations of the angiograms and the realized physiological parameters is non-trivial, nonlinear and not even one-to-one, since of course many different deformations can lead to the same values of mean radius and CBV.

Anesthesia and SatO₂

One limitation of the study is that isoflurane was the anesthetics used for convenience for all the experiments, but it is a known vasodilatator with the effect of increasing SatO₂ in the brain. This is consistent with our vMRF extracted SatO₂ values which are high. Other anesthetics would have been preferable, but more difficult to use, such as ketamine with xylazine requiring a mechanism for continuous injection during the long scans.

Modeling white matter

Our 2PM angiogram data were only obtained in the gray matter of mouse somatosensory cortex. As the tissue T₂ and the vasculature of white matter areas are known to be qualitatively different from gray matter T₂ and vasculature, our model may not have modeled white matter accurately. However, our white matter (corpus callosum) data were among the best matched data on the RMS measure, giving confidence that the current approach was reasonable.

Comparison of vMRF to other quantitative MR approaches

There is a vast quantitative MR literature which we could not review due to space constraints. While quantitative sequences as described in [44] and in Troprès et al. [45] allow estimation of vessel caliber and perfusion using a single gradient-echo spin-echo DSC MRI sequence, estimation of SatO2 in all vessels including small vessels is more difficult and usually requires more than one scan and some modeling. While vMRF is unique in obtaining SatO₂, vessel size and CBV from one type of scan, various MRI methods can measure each of these parameters separately. By combining several types of scans and contrast agent injections, as well as Monte-Carlo simulations of the MR signal similar to ours albeit based on a 3D-model of cylinders, these parameters were obtained in humans in [44]. The question of whether their results could be potentially biased, as well as any comparison of vMRF to other quantitative MR approaches, e.g. in mice, is interesting but beyond the scope of this article.

5. CONCLUSION

In summary, 5-dimensional dictionaries for fingerprinting were generated from 6 real angiograms of mouse somatosensory cortex. Within the scope of the stated modeling limitations, these dictionaries adequately represented the universes of observable MR signals produced by the GESFIDE sequence. Matching the dictionaries on real mouse data produced arguably realistic, interesting and consistent results on brain oxygen saturation, mean vessel radius and CBV in different regions of mouse brains.

While simulation results on the estimability of differences in parameters and the extracted differences in groups of ATX and WT mice are encouraging, much further work to rigorously validate the vMRF approach is necessary. In particular, optical microscopy experiments would be of interest, along with comparing the vMRF approach to other emerging quantitative MR methods. This work showed that it will be essential to correctly account for the variability observed in realistic angiograms in order for vascular fingerprinting to produce unbiased results for physiological parameters.

Highlights.

• Modeling GESFIDE fingerprinting from realistic angiograms of microvasculature

• Validation with in vivo acquisition in wild-type and atherosclerotic mice

• Evidence of bias in the vMRF extracted parameters, using simulations

• However, differences in vMRF extracted parameters are more robust to bias

• Group differences observed in cerebral oxygen saturation, mean vessel radius and CBV