Exploring the origins of TE-dependent QSM measurements in healthy tissue and cerebral microbleeds

Abstract

Quantitative susceptibility mapping (QSM) is increasingly used to measure variation in tissue composition both in the brain and in other areas of the body in a range of disease pathologies. Although QSM measurements were originally believed to be independent of the echo time (TE) used in the gradient-recalled echo (GRE) acquisition from which they are derived; recent literature (Sood et al., 2016) has shown that these measurements can be highly TE-dependent in a number of brain regions.

In this work we systematically investigate possible causes of this effect through analysis of apparent frequency and QSM measurements derived from data acquired at multiple TEs in vivo in healthy brain regions and in cerebral microbleeds (CMBs); QSM data acquired in a gadolinium-doped phantom; and in QSM data derived from idealized simulated phase data. Apparent frequency measurements in the optic radiations (OR) and central corpus callosum (CC) were compared to those predicted by a 3-pool white matter model, however the model failed to fully explain contrasting frequency profiles measured in the OR and CC.

Our results show that TE-dependent QSM measurements can be caused by a failure of phase unwrapping algorithms in and around strong susceptibility sources such as CMBs; however, in healthy brain regions this behavior appears to result from intrinsic non-linear phase evolution in the MR signal. From these results we conclude that care must be taken when deriving frequency and QSM measurements in strong susceptibility sources due to the inherent limitations in phase unwrapping; and that while signal compartmentalization due to tissue microstructure and content is a plausible cause of TE-dependent frequency and QSM measurements in healthy brain regions, better sampling of the MR signal and more complex models of tissue are needed to fully exploit this relationship.

1 Introduction

Quantitative susceptibility mapping (QSM) provides image contrast by using measured B₀ field perturbations derived from gradient recalled echo (GRE) MRI phase data to calculate local variations of magnetic susceptibility in tissue [1–6]. This contrast can reveal features that are poorly depicted or entirely absent in conventional MRI images; and susceptibility heterogeneity within a region of interest (ROI) may be used to draw inferences about variations in tissue content including iron and myelin levels [7–16]. These qualitative and quantitative observations are increasingly used as an adjunct to conventional MRI in the study of aging and a range of disease pathologies [11, 14–38]. It has recently been reported that frequency shift [39, 40] and QSM [41] values calculated in various brain regions vary with echo time when calculated from individual echoes from a multi-echo GRE acquisition. These observations are inconsistent with the assumption inherent in QSM that frequency shift is a time-independent function of the local magnetic field; and proper analysis and understanding of this effect is essential both for the interpretation of susceptibility measurements made using QSM and potential exploitation of new information that may be derived from multi-echo GRE data.

All QSM algorithms are fundamentally based on the inversion of the known relationship between an arbitrary magnetic susceptibility distribution and the perturbation of an applied magnetic field [42]. These algorithms contain two assumptions: that each voxel may be approximated as a point-like source whose susceptibility is an isotropic (orientation-independent) scalar quantity; and that the measured phase in a voxel is a linear product of the local magnetic field perturbation and echo time. The assumed linearity of accumulated phase with time should make the calculated magnetic field perturbation, and therefore calculated magnetic susceptibility, TE-independent. These assumptions, however, are flawed. Some biological materials such as lipids have been shown to have an anisotropic magnetic susceptibility that must be characterized as a second order tensor, causing them to generate orientation-dependent field perturbations [8, 39, 40, 43–45]. Orientation-dependent susceptibility effects have been demonstrated in vivo, particularly in tissues with highly ordered microstructure [43, 45–47]. Non-linear phase evolution has also been demonstrated in vivo in some white matter fiber tracts [39, 40] and, as expected, has been shown to cause TE-dependent QSM measurements in healthy brain tissue [41]. These observations have been attributed to sub-voxel level compartmentalization of the MRI signal [39–41]. In the white matter, two and three compartment hollow cylinder models have been used to simulate microstructural compartmentalization [39, 40, 46–48]; and multi-component fitting has been used to test for compartmentalization of real data acquired in vivo [40, 49–57].

In this work we explore the phenomenon of TE-dependent frequency and QSM measurements through analysis of in vivo and simulated data; a gadolinium-doped phantom; and a simple three-compartment hollow cylinder model of white matter.

2 Materials and Methods

2.1 MRI acquisition

2.1.1 Human data

Six patients (2 male and 4 female, 57–71 y.o.) with previously diagnosed cerebral microbleeds (CMBs) were scanned using a GE Signa HDxt 3.0 T scanner (GE Healthcare, Waukesha, WI) equipped with a 32-channel head coil. Magnitude and phase images with whole-brain coverage were acquired using a standard there-dimensional (3D) spoiled gradient-recalled echo (SPGR) sequence with the following parameters: TE1/ΔTE/TE16=3.0/3.1/49.5 ms; TR =54.4 ms; FA = 12°; FOV = 220×220×124 mm³; matrix size = 0.86 × 0.86 × 1 mm³; readout bandwidth (BW) = 62.5 kHz. The total acquisition time was about 15 mins. Coil combination was achieved with SENSE reconstruction (ASSET on GE scanners). Prior to the gradient echo acquisition, coil sensitivity was calibrated with a low resolution scan. Given correct sensitivity maps, the SENSE algorithm results in accurate image reconstruction including both magnitude and phase.

In vivo brain image data from five adult (25 – 33 y.o.) healthy volunteers were acquired on a GE MR 750 3.0T (GE Healthcare, Waukesha, WI) scanner using an 8-channel head coil and a 3D SPGR sequence with the following parameters: TE1/ΔTE/TE16=4.0/2.3/38.5 ms; TR= 50 ms; FA=12°; FOV=192 × 192 × 124 mm³; matrix size= 192×192×124; spatial resolution = 1×1×1 mm³; readout bandwidth (BW) = 62.5 kHz. The total acquisition time was about 12 mins. Coil combination was achieved by separately unwrapping and removing background fields from the phase data for each coil individually (see Section 2.2 for algorithm details) and combining the filtered data using a complex summation. The same experiments were repeated 5 times over 16 days. All the experiments were approved by the local institutional review boards.

2.1.2 Gadolinium phantom

To further evaluate TE-dependent QSM measurements in strong susceptibility sources, a cylindrical phantom with a known susceptibility distribution was constructed. Five straws, each in 5.5 mm in diameter and 50 mm in length, containing varying concentrations of gadolinium (0, 0.125, 0.25, 0.5, and 1 mM) were made with gadoteridol (ProHance^®), and placed in a larger container filled with saline solution. A 5-ml volume of each solution was poured into separate straws. The cylindrical shape and low wall thickness of the straws (about 100 μm), as well as their orientation parallel to the field ensured that the susceptibility effects created by the straws were negligible. The five straws were separated by a plastic disk with five holes designed to keep the straws aligned in the container.

Imaging was conducted using a single-channel birdcage coil on a 20-cm bore 7 T scanner (Bruker BioSpec 70/20 USR, Billerica, MA) interfaced to an Avance III system. The phantom was positioned in the coil so that the long axes of the straws were parallel to the B₀ field. A multi-echo, 3D gradient echo (MGE) sequence was performed with the following parameters: flip angle (FA) =20°; TE1/ΔTE/TE20=2.3/2.2/44.1 ms; TR = 200 ms; field of view (FOV) = 128*128*128 mm³, spatial resolution = 400×400×400 μm³ isotropic; readout bandwidth (BW) = 62.5 kHz.

2.2 Quantitative Susceptibility Mapping and ROI Analysis

For QSM processing, the phase data were unwrapped at each TE using Laplacian-based, path-based, and voxelwise temporal unwrapping algorithms in the CMB patients and Gd phantom [8, 57, 58], while phase data for the healthy volunteers were unwrapped using the Laplacian-based and voxelwise algorithms.

Voxelwise temporal unwrapping was carried out in MATLAB (Mathworks, Natick, MA, USA). The magnitude image was used to generate a binary mask of the brain tissue using the brain extraction tool (BET) in FSL [59] for the human data and a cylindrical ROI defined manually in MATLAB for the Gd phantom. For each voxel in the mask, the 1D phase evolution across the range of echo times was extracted and unwrapped using the ‘unwrap’ function in MATLAB, and the resulting unwrapped phase values assigned to the unwrapped phase volumes at each TE. The first echo was then subtracted from echoes 2:16 (human data) or 2:20 (Gd phantom data) to remove remaining wraps and B₁ phase.

The background phase was removed using V-SHARP [8, 9].

Frequency maps were generated by scaling the processed phase by TE:

$$f(\mathbf{r})=-\varphi (\mathbf{r})/(2\pi \times TE),$$ (1)

where f is the frequency offset relative to the Larmor frequency, ϕ is the phase, TE is the echo time of the image, and r is the spatial coordinate of the voxel.

Quantitative susceptibility maps were then calculated using iLSQR [60, 61]. Additional QSM data were generated for the purpose of comparison for the healthy volunteers using streaking artifact reduction for QSM (STAR-QSM) [62], and a threshold-based k-space division method using the modified dipole kernel inversion described in [2, 63]. All algorithms were implemented in MATLAB. QSM data were not normalized relative to a control ROI (e.g. relative to values in the CSF) in order to avoid combination of TE dependence of QSM values in the control ROI with TE dependence in the structures under consideration.

ROIs of CMBs, grey, and white matter regions including the corpus callosum (CC); genu of the corpus callosum (GCC); splenium of corpus callosum (SCC); caudate nucleus (CN); putamen (PU); globus pallidus (GP); thalamus (TH); pulvinar (PUL); posterior limb of the internal capsule (IC); optical radiations (OR); red nucleus (RN); and susbstantia nigra (SN), were drawn manually (without software assistance) on QSM images based on their anatomical features using ITK-SNAP (www.itksnap.org) [54][64]. Identification of sub-cortical nuclei was carried out with some reference to labelled anatomical MRI images published online (www.w-radiology.com last accessed 01/03/17).

2.3 Testing the effect of phase unwrapping on TE-dependence using simulated data

In order to separate artificial TE-dependence introduced by QSM processing from intrinsic tissue effects in the real in vivo data, simulated data was used to generate additional susceptibility maps. In the simulated data, the phase in each voxel accumulates linearly through time based upon the local field perturbation; and so any variation in time of the QSM values calculated from this data must be introduced during unwrapping, filtering, or QSM inversion. In order to achieve a close approximation of the real data, the real QSM data was used in these simulations as the ‘true’ susceptibility distribution, and field maps were generated using the forward Fourier calculation [42]. QSM from the first echo of the path-unwrapped CMB patient data was used to simulate the CMBs due to their extremely high apparent susceptibility (~400–1500 ppb) and the rapid decay with TE observed in the real data. QSM from the 16^th echo of Laplacian-unwrapped data from a single healthy volunteer was used to simulate the healthy tissue as the structures were better defined in the later echoes. Path-unwrapped data was chosen as a basis for the CMB simulations as it generated higher QSM values at early echoes in some CMBs than Laplacian- or voxelwise-unwrapped data.

These field maps were then used to generate idealized phase data using

$$\varphi =-\gamma \mathrm{\Delta }{B}_{z}TE,$$ (2)

where ϕ is the phase, γ is the proton gyromagnetic ratio (= 267.514 rad s⁻¹ T⁻¹), ΔB_z is the z-component of the magnetic field perturbation, and TE is the echo time. Simulated phase data were generated for echo times of TE1/ΔTE/TE16=3.0/3.1/49.5 ms for the CMB data and TE1/ΔTE/TE16=4.0/2.3/38.5 ms for the healthy brain data, reflecting those used to acquire data in vivo. Wrapped phase data were then generated using

$${\varphi }_w=\arctan \left(\frac{Im(\mathit{exp}(i\varphi ))}{Re(\mathit{exp}(i\varphi ))}\right),$$ (3)

where ϕ_w is the wrapped phase, and Im and Re denote the imaginary and real components of a complex number.

QSM data were then generated from the simulated phase data using the same algorithms applied to the experimental data. Additionally, VSHARP and iLSQR processing were applied to the simulated phase data that had not been wrapped to test the effect of phase unwrapping.

2.4 Fiber Bundle Simulation

In an attempt to explain the variation of frequency and QSM profiles observed in white matter regions, a three-compartment hollow cylinder model was used to simulate the evolution of the frequency from a voxel containing a bundle of white matter fibers. Myelinated axons were modeled as infinitely long, parallel cylinders, with a solid cylindrical axon of radius r_i surrounded by a cylindrical myelin sheath with internal radius r_i and outer radius r_o. These radii are related by the G-ratio where G=r_i/r_o. The magnetic susceptibility in the axon and extracellular space was set to 0 ppm, and the magnetic susceptibility in the myelin sheath was represented as a radially oriented susceptibility tensor with isotropic susceptibility χ_I and anisotropic susceptibility χ_A such that

$$\underset{\_}{\chi }=\underset{\_}{\mathrm{I}}{\chi }_I+\left[\begin{array}{ccc}{\chi }_A& 0& 0\\ 0& -\frac{{\chi }_A}{2}& 0\\ 0& 0& -\frac{{\chi }_A}{2}\end{array}\right],$$ (4)

where $\underset{\_}{\mathrm{I}}$ is a 3×3 identity matrix. The field perturbation ΔB_z (r) due to an individual axon centered on a 1024×1024 point grid was then calculated analytically for the axonal (r < r_i), myelin (r_i < r < r_o), and external (r > r_o) compartments using the expressions previously published by Wharton and Bowtell [39]. The 1024×1024 grid was chosen so that the field due to an axon centered at any point on a 512×512 grid could be extracted by choosing an appropriate region of the calculated field.

A simulated voxel was then generated by populating a 512×512 point grid with randomly distributed axons until the desired fiber volume fraction was achieved. The field perturbation due to each axon was linearly summed over the grid. Each point in the grid was treated as an individual source of signal, with a magnitude weighting of 1 for each point in the axon and extracellular space, and 0.6 in the myelin, reflecting their relative water content [40]. The signal was then calculated pointwise such that

$$S(t)=M{e}^{-i\gamma \mathrm{\Delta }{B}_z(\mathbf{r})t}{e}^{-t/T_2}$$ (5)

where S(t) is the complex signal from the point, M is the magnitude weighting of the compartment in which the point resides, ΔB_z (r) is the z-component of the field perturbation at coordinate r of the voxel within the compartment, and T₂ is the transverse relaxation time in the compartment. The complex sum of the signal from the points in each compartment was calculated to yield complex signals from the myelin, axon, and extracellular space, and these were then combined to yield a complex signal from the whole voxel. The apparent frequency was then calculated by dividing the phase at each time point by the echo time following Eq. (1).

As the most striking difference observed in the in vivo WM frequency and QSM profiles was between those measured in the corpus callosum and optic radiations (see Results), G-ratios and FVFs were chosen based on the values estimated for these regions by Mohammadi et al [65], whose in vivo measurements gave G=~0.65 and FVF=~0.4 in the central CC, and G=~0.57 and FVF=~0.27 in the OR. The outer radius r_o was fixed at 20 points. If the axonal diameter is taken to be 3 microns (a typical axonal diameter in the body of the corpus callosum [66]), the simulation is representative of a voxel with a 76.8×76.8 micron² cross section and arbitrary length. Voxels were simulated at 0, 30, 60 and 90 degrees to B₀ in order to investigate the full range of possible frequency profiles. The values for χ_I and χ_A were set to −0.06 and −0.14 ppm respectively, reflecting the values found in [39]. The axonal, myelin water, and extracellular T₂ values were set to 34, 9.5, and 37 ms respectively, using the values found by Sati et al [40].

3 Results

3.1 Phase, Frequency, and QSM measurements in cerebral microbleeds

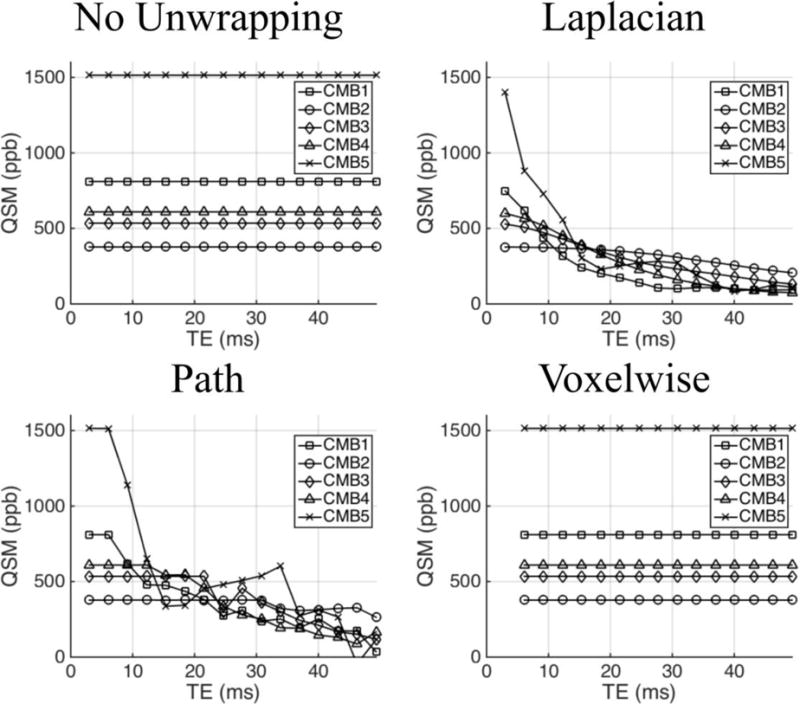
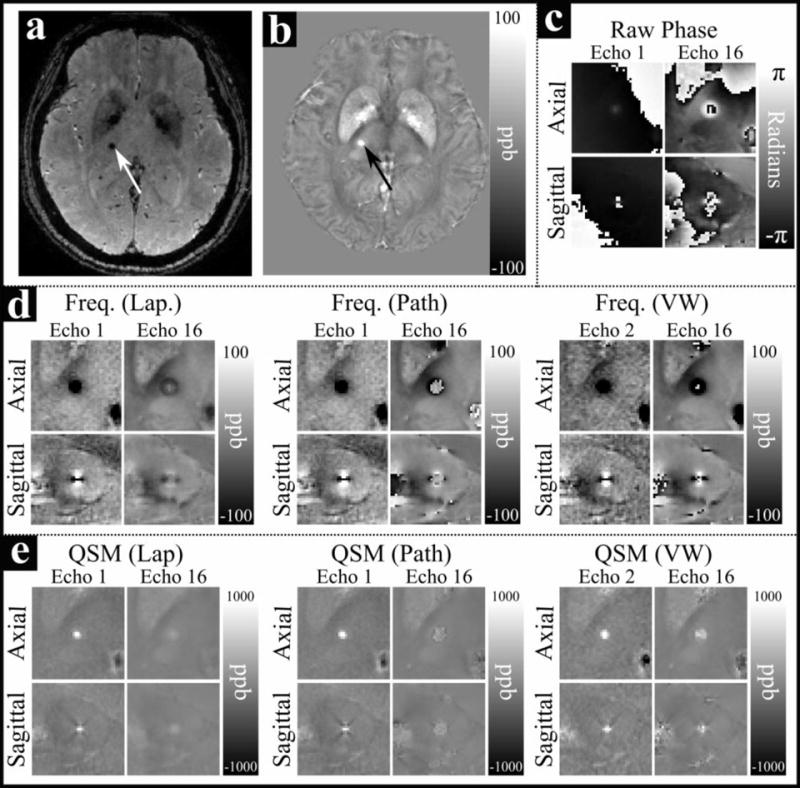
Figure 1a–b shows whole head axial GRE magnitude and QSM images of an example CMB. Figure 1c–e shows axial and sagittal images centered on the CMB in the raw phase images as well as frequency maps and QSM images derived from Laplacian-, path-, and voxelwise-unwrapped phase data. Figure 2 shows mean values of the raw phase and Laplacian-, path-, and voxelwise-unwrapped frequency and QSM data in ROIs drawn in 5 CMBs from two patients (CMB 5 is shown in Figure 1). Figure 3 shows simulated QSM profiles calculated in the same 5 CMBs from idealized linear phase data based on field maps calculated from echo 1 of the real path-unwrapped QSM data. QSM profiles are shown for simulated data which has undergone no unwrapping, and for data which has been wrapped before unwrapping with Laplacian-, path-, and voxelwise-unwrapping algorithms.

Figure 1.

An example of a cerebral micbrobleed in vivo in a) a GRE magnitude image; b) a QSM image; c) raw phase data; d) Laplacian-, path-, and voxelwise-unwrappped frequency maps; and e) QSM images derived from Laplacian-, path-, and voxelwise-unwrappped frequency maps. The microbleed is indicated by an arrow in a) and b). All images in c–e) are centered on the microbleed. A wrap can be seen surrounding the CMB the sagittal image from echo 1 in c), and multiple wraps can be seen in echo 16. Dipolar frequency patterns are clear in the frequency images in d)

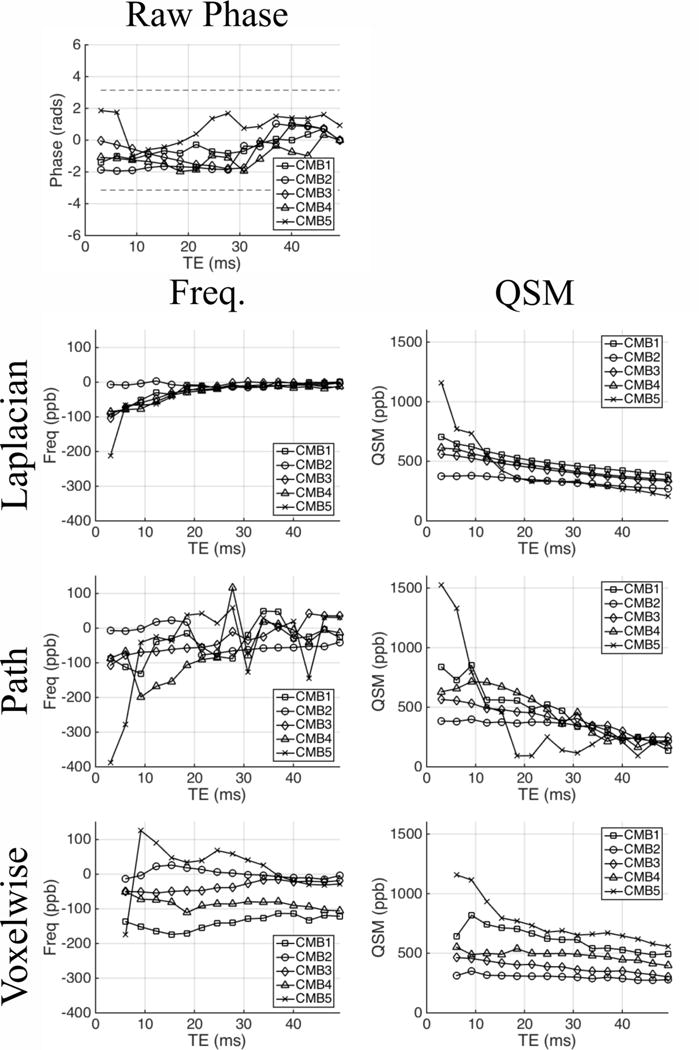
Figure 2.

Mean values in raw phase, and frequency and QSM images derived from Laplacian-, path-, and voxelwise- unwrapped phase data; in ROIs drawn in 5 cerebral microbleeds from 2 patients. CMB 5 is the example shown in Figure 1.

Figure 3.

Mean QSM values derived from simulated idealized phase data which has undergone no phase unwrapping (data was not wrapped in this case) and data which has undergone Laplacian-, path-, and voxelwise-unwrapping algorithms. No TE-dependence is seen in the data which underwent no unwrapping. Both Laplacian- and path-unwrapped data show varying degrees of TE-dependence, with path-unwrapped date remaining consistent in early echoes before falling in magnitude as TE increases. Voxelwise-unwrapped data gives TE-independent QSM values which are consistent with the wrap-free data.

The raw phase in and surrounding the example CMB (Figure 1c) shows a clear dipolar field centered on the CMB which already contains wraps in echo 1 (TE = 3.0 ms), and contains multiple wraps in echo 16 (TE = 49.5 ms). However, the raw phase profiles in the ROI analysis of 5 CMBs, shown in Figure 2, show no clear trend or obvious wraps. This result may be explained by partial volume effects where ROIs (defined on QSM images) cover both positive and negative lobes of the dipole field in the phase such that the mean phase accumulated in the ROI remains relatively low.

The Laplacian- and path-unwrapped frequency maps (Figure 1d) show a clear dipolar field centered on the CMB in both echo 1 and echo 16 suggesting strong, non-local field effects due to a source with high magnetic susceptibility. However, in echo 16 the magnitude of the frequency offset in the dipole lobes has notably diminished, and the center of the CMB appears to have a frequency of ~0 ppb; this suggests either a systematic underestimation of accumulated phase at later echoes or intrinsic nonlinear phase accumulation of the MR signal in this region of the CMB. While both algorithms yield very similar field maps in echo 1, in echo 16 the central region of the dipole field in the path-unwrapped data is more clearly delineated from the surrounding field by a wrap-like discontinuity, compared to the smooth transition seen in the Laplacian-unwrapped data. The Laplacian- and path-unwrapped QSM images (Figure 1e) show contrast consistent with their respective frequency maps, with a strong focal region of paramagnetic material in the CMB whose magnitude is diminished in echo 16 relative to echo 1. In echo 16 of the path-unwrapped data the QSM contrast covers a region slightly larger than the CMB appears in echo 1, with a boundary corresponding to the discontinuity surrounding the central region in the frequency map.

The voxelwise-unwrapped data behaves somewhat differently to the Laplacian- and path-unwrapped data. In Figure 1d, the frequency map from echo 2 closely resembles those seen in the Laplacian- and path-unwrapped data, however the dipolar field in the frequency map from echo 16 has declined in magnitude less than in the other data. A small central region in the CMB (that is uniformly negative in the axial image from echo 2) contains a mix of strongly positive and strongly negative voxels, and the lobes of the dipole field are still somewhat reduced in magnitude, but the apparent frequency pattern is mostly preserved. This is again reflected in the QSM images shown in Figure 1e, where the QSM image in echo 2 shows a focal region of strongly paramagnetic region in the CMB; while echo 16 shows a slightly larger and more diffuse region of less paramagnetic material that is brighter than the Laplacian- and path-unwrapped data.

The ROI analysis of the 5 CMBs in the Laplacian- and path-unwrapped frequency ranges from 0 to −400 ppb in echo 1. The Laplacian-unwrapped frequency then converges on ~0 ppb at later echoes in a manner consistent with the negative frequency offset in the center of the axial image of the example CMB in Figure 1d in echo 1 changing to a central region of ~ 0 ppb frequency offset at echo 16. In contrast, the path-unwrapped frequency varies erratically. As with the raw phase, partial volume effects likely play some role in the apparent phase in the ROI due to the strong dipolar field. The corresponding mean QSM values are all strongly paramagnetic (~300–1500 ppb) in echo 1, decreasing relatively smoothly through echo times, with the greatest change occurring in the most paramagnetic CMB (CMB5) and the smallest change in the least paramagnetic CMB (CMB2). The echo 1 QSM values in CMB1 and CMB 5 are higher path-unwrapped data than the Laplacian-unwrapped data. These observations suggest either nonlinear frequency accumulation causing a change in the apparent frequency calculated at TE increases; a systematic and TE-dependent underestimation of the true phase in and around the microbleed by the Laplacian unwrapping algorithm; or some combination of such effects. The simulated QSM data shown in Figure 3 behaves similarly to the real QSM, returning values that fall as TE increases at a rate which increases with the QSM value of the CMB in echo 1. The simulated path-unwrapped data appears to be TE-independent in early echoes, for a number of echoes that increases as the initial QSM value decreases. This may suggest that the path-based algorithm is slightly more robust than the Laplacian-based algorithm around strong sources such as CMBs; but ultimately both algorithms fail as TE increases. By comparison, the simulated QSM data which have undergone no unwrapping show no TE-dependence. This suggests that the dominant cause of TE-dependent QSM measurements in CMBs is systematic failure of the algorithm to recover the true phase from wrapped phase data. The simulated data suggest that the path-based algorithm is slightly more robust than the Laplacian-based algorithm around strong sources such as CMBs; but ultimately both algorithms fail as TE increases.

The ROI analysis of the voxelwise-unwrapped data shows different behavior. The mean frequency offsets range from ~0 to ~−200 ppb in echo 2, and with the exception of CMB5 show significantly less variation with TE than the frequencies derived from the path-unwrapped data, and do not all tend towards 0 ppb as seen in the Laplacian-unwrapped data. The mean QSM values are lower in echo 2 than in echo 1 of either the Laplacian- or path-unwrapped data; however the most paramagnetic CMBs (CMB 1 and CMB5) appear more paramagnetic in echo 16 than either of the other datasets. The voxelwise-unwrapped simulated QSM (Figure 3) is strikingly different in all CMBs than that derived from Laplacian- or path-based algorithms, showing no significant difference from the QSM derived from wrap-free data that had not undergone any phase unwrapping. This result suggests that while systemic phase unwrapping errors must contribute to the TE-dependence seen in data processed with Laplacian- or path-based unwrapping algorithms; there is also some non-linear behavior intrinsic to the MRI signal. The lower QSM values in echo 2 of the voxelwise-unwrapped data compared to echo 1 of the Laplacian- and path-unwrapped data may be evidence of a relatively high frequency, short T₂* signal component whose contribution is negligible after ~ 3 ms, and whose contribution is therefore lost through the subtraction of echo 1 during the voxelwise unwrapping process.

Laplacian-unwrapped real data from one healthy volunteer was compared to Laplacian-unwrapped, path-unwrapped, and wrap-free simulated data in the CC, OR, PU, SN, and RN, shown in Supplementary Figure 1. No TE-dependence was found in the simulated data, suggesting that both Laplacian- and path-based unwrapping algorithms are robust in and around the susceptibilities found in healthy brain structures.

Evaluation of different QSM inversion algorithms, shown in Supplementary Figure 2, shows that the TE variation is not an artifact of the iterative algorithms used in iLSQR or STAR-QSM.

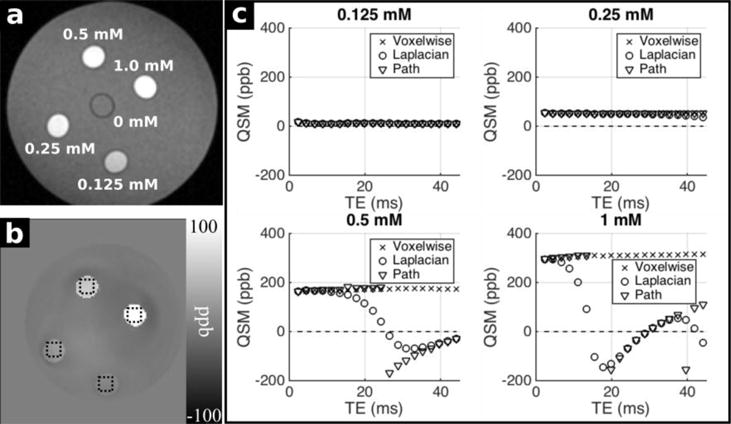
3.2 QSM variation in a gadolinium-doped phantom

Results of the phantom experiments are shown in Figure 4. In the magnitude image (a), 5 tubes with different Gd concentration can be distinguished clearly. In the QSM image (b) the un-doped tube is not visible, while the Gd-doped tubes show hyperintense contrast proportional to their Gd concentration. In (c), plots show the variation of QSM values with TE in data unwrapped using Laplacian-, path-, and voxelwise- unwrapping algorithms.

Figure 4.

a) Magnitude image of the gadolinium phantom. Five straws can be clearly distinguished, with Gd-containing tubes increasing in brightness with increasing Gd concentration. b) QSM image of the gadolinium phantom derived from voxelwise-unwrapped data. ROIs used for analysis are outlined with dotted lines. c) ROI analysis of QSM in the Gd-doped tubes derived from Laplacian-, path-, and voxelwise-unwrapped data. QSM values remain relatively stable in 0.125 and 0.25 mM straws. In 0.5 and 1 mM straws the Laplacian-and path-unwrapped data shows strong TE-dependence, while the voxelwise-unwrapped data remains stable throughout.

When Gd concentration is low (0.125 mM and 0.25 mM), QSM derived from phase processed with Laplacian-, path-, and voxelwise- unwrapping algorithms give similar susceptibility values with little TE-dependence. At higher Gd concentrations (0.5 and 1 mM), the Laplacian-unwrapped data gives QSM values that change significantly through echoes, initially decaying towards 0 before apparently flipping in polarity once in the 0.5 mM tube at TE=~25 ms and three times in the 1 mM tube at TE= ~15, 30 and 40 ms. The path-unwrapped data shows similar behavior to that seen in the simulated CMB data (Figure 3). The mean QSM values remain constant through early echoes in the 0.5 and 1 mM tubes, for a number of echoes that reduces as the Gd concentration increases, before flipping in polarity (indicating a clear breakdown of the algorithm) and decaying towards 0 ppb (0.5 mM) or even back past 0 ppb before varying erratically (1 mM). The voxelwise-unwrapped data gives QSM values that show no TE-dependence at any Gd concentration. As we know that there is no microstructure or compartmentalization within the straws, these results clearly demonstrate that Laplacian- and path-based spatial unwrapping algorithms fail in the presence of strong susceptibility sources as TE increases, systematically causing TE-dependent QSM measurements. Voxelwise unwrapping, however, appears to be robust at the susceptibilities and echo times tested here. The consistent QSM results in the tubes doped with lower concentrations of Gd (resulting in QSM values of < ~55 ppb) suggest that Laplacian- and path-based phase unwrapping is robust in the range of susceptibilities typically found in healthy brain structures, particularly at shorter echo times (or equivalently lower B₀ field strengths).

3.3 Frequency and QSM variation in healthy brain ROIs

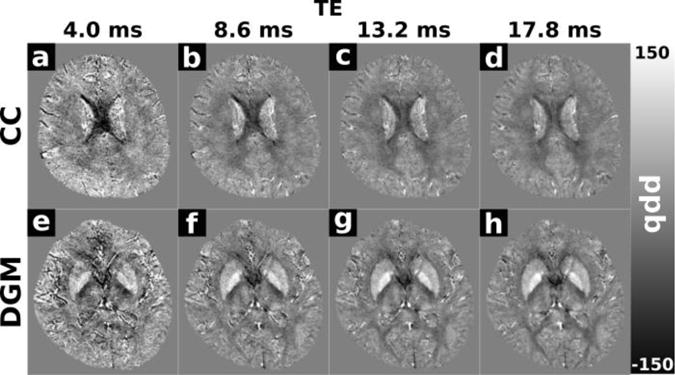
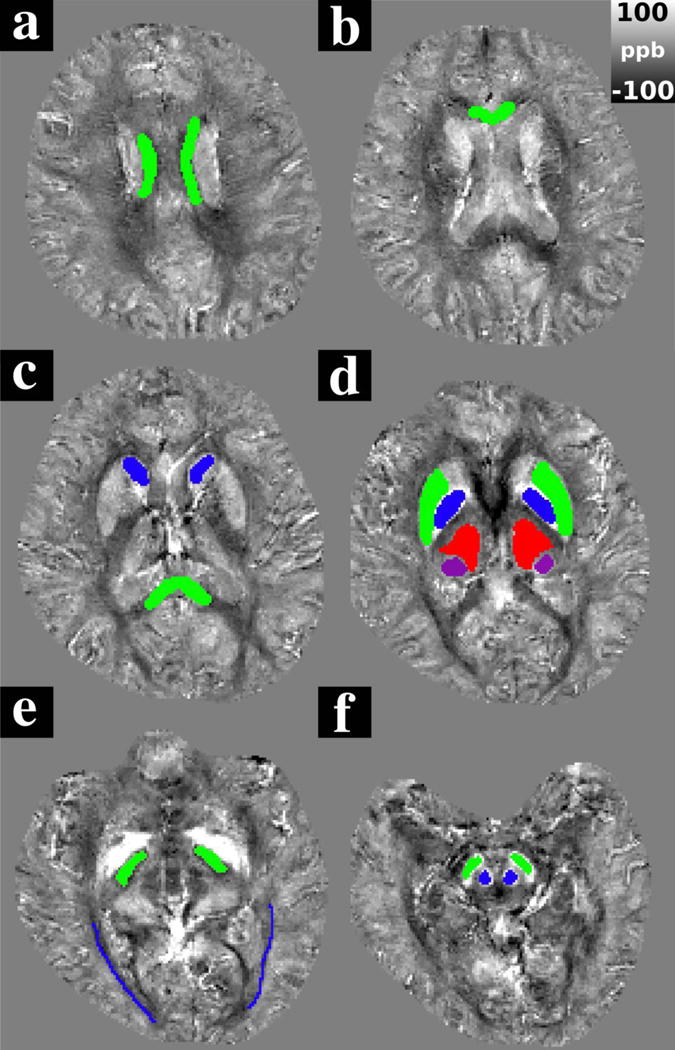
Figure 5 a–f shows representative slices from echo 16 of the Laplacian-unwrapped QSM data containing ROIs drawn on the QSM image from one healthy volunteer in the central body of the corpus callosum (CC); genu of the corpus callosum (GCC); splenium of the corpus callosum (SCC); head of the caudate nucleus (CN); putamen (PU); globus pallidus (GP); thalamus (TH); pulvinar (PUL), internal capsule (IC); optic radiations (OR); red nucleus (RN); and substantia nigra (SN). Figure 6 shows representative slices from the Laplacian-unwrapped QSM including the CC and deep grey matter (DGM) structures in echo 1 (4.0 ms), echo 3 (8.6 ms), echo 5 (13.2 ms), and echo 7 (17.8 ms). Anatomical contrast is present in all echoes; with a particularly noticeable change in calculated susceptibility in the CC which appears less diamagnetic as TE increases.

Figure 5.

Representative images transecting ROIs drawn in one healthy subject. ROIs were drawn in a) The central corpus callosum (green), b) the genu of the corpus callosum (green), c) the splenium of the corpus callosum (green) and the caudate nucleus (blue), d) the putamen (green), globus pallidus (blue), the thalamus (red) and the pulvinar (purple) e) the posterior limb of the internal capsule (green) and the optic radiations (blue), and f) The red nucleus (blue) and the substantia nigra (green). QSM images are taken from echo 16 of the Laplacian-unwrapped QSM data from a healthy subject.

Figure 6.

Representative Laplacian-unwrapped QSM images from a healthy volunteer showing the corpus callosum (a–d) and deep grey matter structures (e–h) in echo 1 (4.0 ms), echo 3 (8.6 ms), echo 5 (13.2 ms) and echo 7 (17.8 ms). Anatomical contrast is apparent in all echoes. The corpus callosum has a pronounced negative (diamagnetic) contrast relative to surrounding white matter in early echoes, that reduces as TE increases.

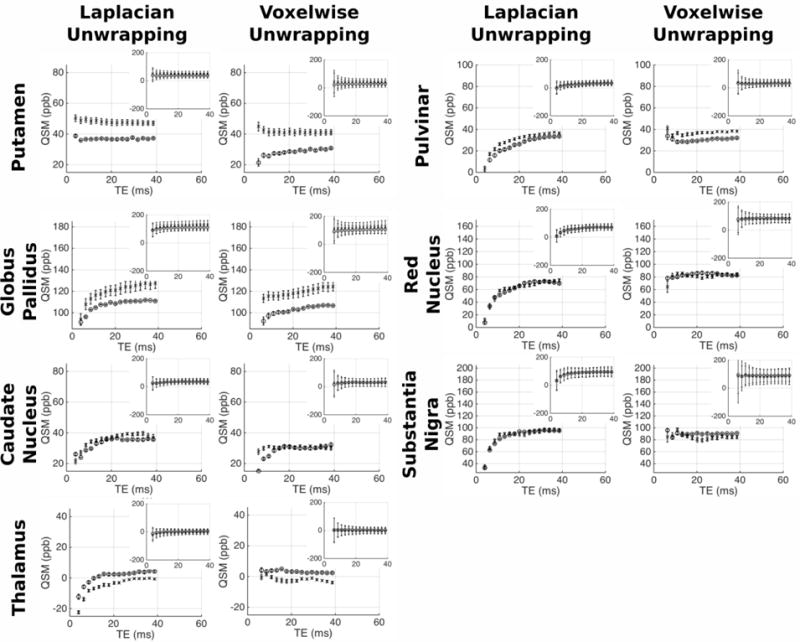
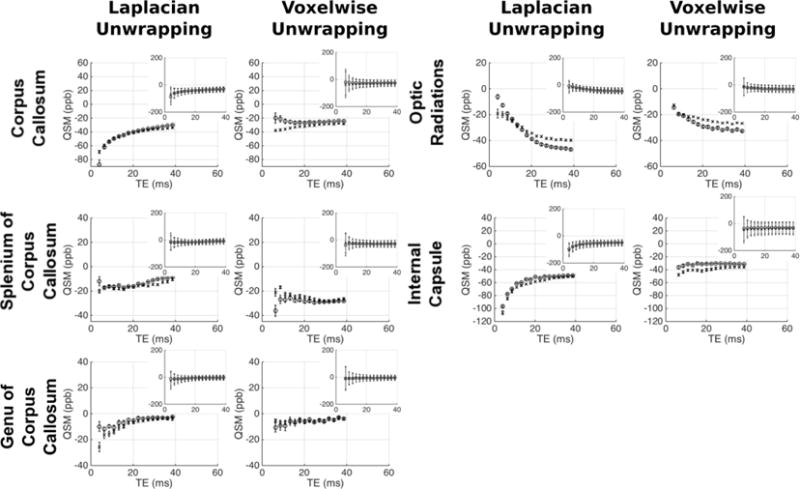
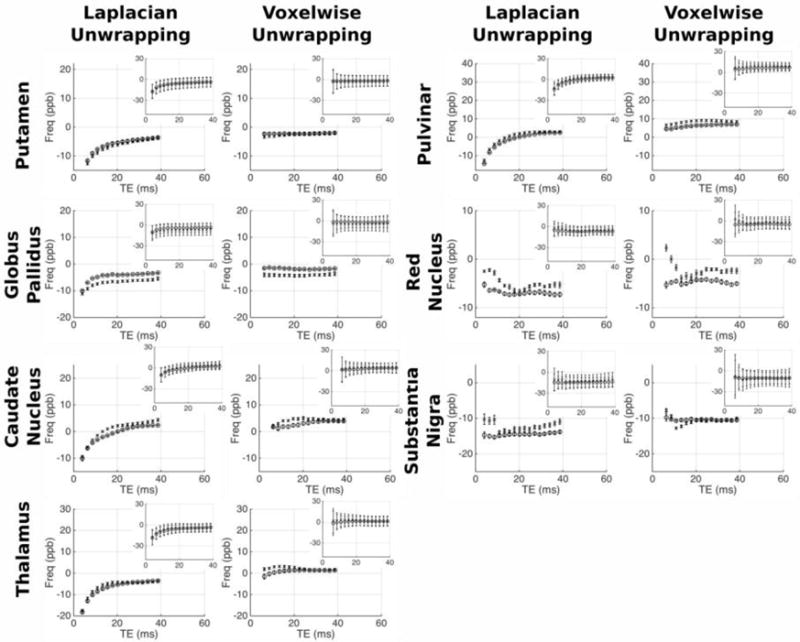
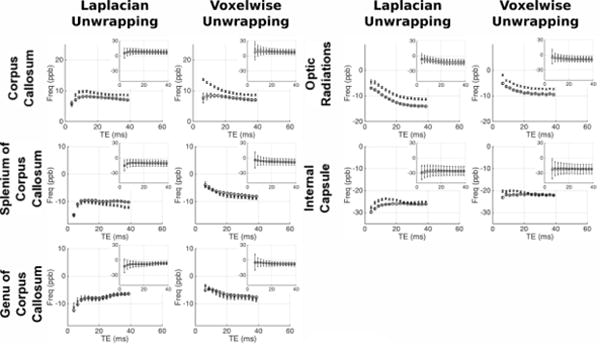
Figures 7/8 and figures 9/10 respectively show the variation of frequency and QSM values with TE in the grey/white matter ROIs; with values derived from both Laplacian-and voxelwise-unwrapped phase data. Each figure shows mean values at each TE in 5 scans acquired over 5 visits in one healthy subject (circles), and the mean values at each TE in 5 individual scans acquired from 5 healthy subjects (crosses). Inset plots show the data plotted on identical axes for each ROI. Error bars in the main plot show the standard error of the mean, indicating the variability in the absolute frequency/QSM measurements between subjects/visits. Error bars in the subplots indicate the mean of the standard deviation calculated in each ROI in each subject/visit, indicating the relative homogeneity of frequency/QSM values in each structure.

Figure 7.

Mean frequency vs TE in the healthy WM regions. For each ROI separate plots show frequency averaged over 5 datasets from the same subject (circles), and 1 dataset from 5 subjects (crosses). Inset plots show data on fixed axes in all ROIs. Errorbars in main plots show the standard error on the mean of the 5 datasets; errorbars on the subplots indicate the mean standard deviation in each ROI across the 5 datasets averaged.

Figure 8.

Mean frequency vs TE in the healthy GM regions. For each ROI separate plots show frequency averaged over 5 datasets from the same subject (circles), and 1 dataset from 5 subjects (crosses). Inset plots show data on fixed axes in all ROIs, with errorbars indicating the mean standard deviation in the ROI across the 5 datasets averaged. Errorbars in main plots show the standard error on the mean of the 5 datasets; errorbars on the subplots indicate the mean standard deviation in each ROI across the 5 datasets averaged.

Figure 9.

Mean QSM vs TE in the healthy WM regions. For each ROI separate plots show QSM averaged over 5 datasets from the same subject (circles), and 1 dataset from 5 subjects (crosses). Inset plots show data on fixed axes in all ROIs, with errorbars indicating the mean standard deviation in the ROI across the 5 datasets averaged. Errorbars in main plots show the standard error on the mean of the 5 datasets; errorbars on the subplots indicate the mean standard deviation in each ROI across the 5 datasets averaged.

Figure 10.

Mean QSM vs TE in the healthy GM regions. For each ROI separate plots show QSM averaged over 5 datasets from the same subject (circles), and 1 dataset from 5 subjects (crosses). Inset plots show data on fixed axes in all ROIs, with errorbars indicating the mean standard deviation in the ROI across the 5 datasets averaged. Errorbars in main plots show the standard error on the mean of the 5 datasets; errorbars on the subplots indicate the mean standard deviation in each ROI across the 5 datasets averaged.

The analysis reveals varying magnitudes of TE-dependence in frequency and QSM measurements; with contrasting profiles found in different ROIs and between data processed with unwrapping algorithms. The profiles show consistent trends across scanning sessions and between subjects. This repeatability through time and across individuals suggests that TE-dependent frequency and QSM profiles are linked to tissue characteristic tissue microstructure or content in different brain structures. In some ROIs there is a clear difference between results derived from Laplacian- and voxelwise-unwrapped phase data (beyond the missing 1^st echo in the voxelwise-unwrapped data). The voxelwise-unwrapped data returns comparatively stable frequency measurements relative to the Laplacian-unwrapped data in the IC, PU, GP, CN, TH, and PUL; and relatively stable QSM measurements in the CC, IC, TH, PUL, RN, and SN. There is also a notable difference in the frequency profiles derived from Laplacian- and voxelwise-unwrapped data in the SCC, GCC, and CC in data averaged over 5 subjects. One explanation for this discrepancy may be a significant contribution from a signal component with a very short T₂* causing rapid phase accumulation between the signal excitation and measurement of echo 1; but whose contribution is small or negligible in the phase accumulated beyond this time.

There is an interesting contrast between the frequency and QSM profiles in the CC and OR ROIs (considering that both are myelinated fiber bundles running at oblique angles to B₀). In the OR, both frequency and QSM values becomes increasingly negative as TE increases. In contrast, the Laplacian-unwrapped frequency and QSM values in the CC increase (become less negative in the QSM) through early echoes, with the frequency gradually decreasing after TE = ~10 ms and the QSM values continuing to gradually increase. In the voxelwise-unwrapped data, the frequency profile in the CC averaged over 5 visits from 1 subject appears to change little besides losing the first echo. This repeatable discrepancy between profiles measured in structures which are nominally similar in microstructure and content suggests that these profiles are sensitive to subtle differences between similar tissues; which in the case of the CC and OR may include fiber volume fraction, G-ratio, or spatial distribution/packing of myelinated nerve fibers. The mean standard deviation of frequency and QSM values in each ROI is greater at early echoes relative to later echoes.

3.4 Fiber bundle simulation using hollow cylinder model

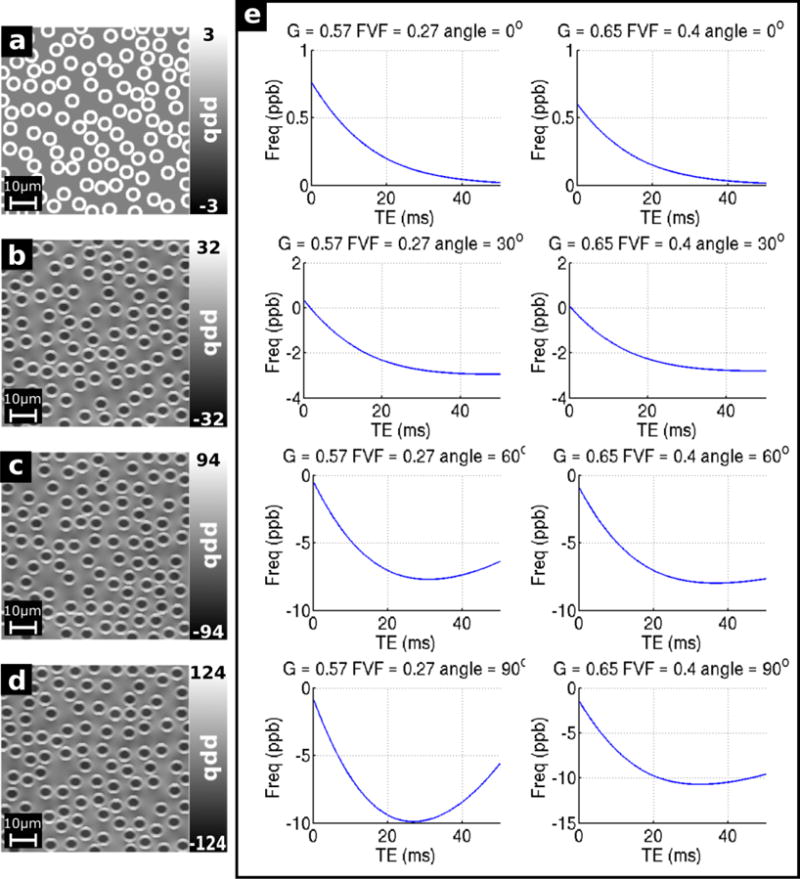
Figure 11 a–d shows the local frequency distribution in the simulated OR fiber bundles oriented at 0, 30, 60, and 90 degrees relative to B₀. Table 1 shows the mean frequency offset in each compartment in both the OR and CC models at 0, 30, 60 and 90 degrees relative to B₀; as well as the orientations drawn from the DTI atlas for each structure (62 degrees in the CC and 78 degrees in the OR). When the fibers run parallel to B₀ the perturbation is entirely confined to a uniform, slightly positive (~3 ppb) frequency shift in the myelin sheath, with no perturbation in the axon or extracellular space. When the angle of the fibers to B₀ becomes non-zero, a uniform, negative frequency perturbation is generated in the axon, and the non-uniform perturbations are observed in the myelin sheath and extracellular space. The distribution of these field perturbations remains consistent with increasing angle, however the magnitude of the perturbation at each point increases. In the myelin sheath the mean frequency becomes increasingly positive, while in the extracellular space the mean frequency remains ~ 0 ppb (magnitude no greater than 0.2 ppb). The same pattern was observed in the simulated CC fiber bundles (images not shown, see Table 1).

Figure 11.

Field maps for the simulated OR fiber bundles (G = 0.57, FVF = 0.27) oriented at a) 0 degrees, b) 30 degrees, c) 60 degrees, and d) 90 degrees with respect to B0; and e) Simulated frequency profiles from the OR (G = 0.57, FVF = 0.27) and CC (G = 0.65, FVF = 0.4) fiber bundles oriented at 0, 30, 60 and 90 degrees with respect to B0.

Table 1.

Frequency and T2* values in the axonal, myelin, and external pools of the simulated fiber bundles.

	Angle (degrees)	Freq – ax (ppb)	T2* ax (ms)	Freq – my (ppb)	T2* my (ms)	Freq ext (ppb)	T2* ext (ms)
G=0.65 FVF=0.4	90	−45.21	33.72	48.84	8.82	0.06	34.49
	60	−34.22	33.82	37.12	9.12	0.42	35.45
	30	−11.27	33.98	14.76	9.45	−0.01	36.82
	0	0	34	3.33	9.5	0	37
	62	−35.344	33.85	38.686	9.07	−0.839	35.44
G=0.57 FVF=0.27	90	−62.24	33.6	43.21	8.88	−0.18	33.12
	60	−47.2	33.82	32.73	9.12	0.07	34.89
	30	−15.57	33.98	13.42	9.46	−0.14	36.71
	0	0	34	3.33	9.5	0	37
	78	−60.146	33.69	43.028	8.92	−0.191	33.62

Figure 11 e shows the frequency the of combined signal from the voxels over time. When the fibers run parallel to the field, the signal has a small positive frequency offset at low TE, decaying towards 0 as TE increases. This is consistent with the positive frequency contribution from the myelin water decaying over time with a relatively short T₂ and the signal becoming dominated by the signal from the axonal and extracellular compartments where there is no frequency offset. As the angle of the fibers with respect to B₀ increases, the initial frequency decreases slightly, from ~0.6–0.75 ppb to ~−2 ppb. The magnitude of the subsequent drop in frequency increases as the angle increases, and when theta = 60 and 90 degrees, the frequency falls to a minimum at TE = ~25–35 ms, before increasing. This increase is slight in the CC model and more pronounced in the OR model, rebounding by ~5 ppb in the OR model when theta = 90 degrees. The increasing rate and magnitude of the drop in frequency when TE=~0–30 ms corresponds to the increasingly negative frequency offset in the axon (see Table 1). The longer T₂ of the axonal pool means that the relative contribution of the signal from this pool will increase due to the faster decay of the signal from the myelin pool.

Comparing these results to the 5-subject average in vivo frequency measurements presented Figure 7, we see that the frequency profile measured in the OR corresponds to the profile generated by the hollow cylinder model when G = 0.65, FVF = 0.4, and the angle of the fibers with respect to B₀ is 30° or 60°. Although the G ratio and FVF of this profile were not those chosen to represent the OR, it should be noted that these values were estimated from in vivo MRI measurements rather than measured directly from histology, and cross-validation of such methods is difficult due to the limited amount of literature on the subject [56]. The behavior in the CC is less consistent. The initial rise in frequency in the CC in the Laplacian-unwrapped data is not reproduced by any of the simulated frequency profiles. However, in the voxelwise-unwrapped data the frequency in the CC shows a smooth decline of ~7–8 ppb, which like the OR reflects the profile generated by the hollow cylinder model when G = 0.65, FVF = 0.4, and the angle of the fibers with respect to B₀ is 60°.

4 Discussion

Multi-exponential signal decay and non-linear frequency and phase evolution in the MRI signal from biological tissues has been noted in numerous studies [39–41, 49, 53–56, 67], with such effects generally being attributed to the compartmentalization of the signal due to microstructure within imaging voxels. In the white matter, these effects are increasingly explained using multi-compartment tissue models, with the magnetic susceptibility anisotropy in the myelin sheath playing a key role [39–41]. Recently published work by Sood et al has reported that susceptibility values calculated using QSM are also TE-dependent and the profile of this variation varies by brain region as expected based on the TE-dependence of the apparent frequency shift [41].

In this work we systematically probed the potential causes of TE-dependent frequency and QSM measurements. We tested the robustness of QSM processing in strong susceptibility sources through analysis of highly paramagnetic cerebral microbleeds in vivo; and using a gadolinium-doped phantom known to be free of microstructure. We then examined the TE-dependent frequency and QSM measurements in healthy brain structures of 5 healthy subjects, establishing consistent profiles by comparing averages calculated across multiple visits and across multiple subjects. Finally, potential microstructural bases for these observations in the white matter were considered through comparison of a 3-pool hollow cylinder model of myelinated fiber bundles to in vivo frequency measurements in the optic radiations and central corpus callosum.

4.1 Evaluating the causes of TE-dependent QSM measurements

In general, quantitative susceptibility mapping (QSM) consists of three steps after the generation of raw magnitude and phase images: 1) Phase unwrapping; 2) Background field removal; 3) QSM reconstruction from the resulting field map. Each step may introduce errors in the calculated susceptibility values. In this study, the V-SHARP method was used for background field removal, and the iLSQR algorithm was used for QSM inversion, with STAR-QSM and a threshold-based k-space division algorithm with a modified dipole kernel applied to data from a healthy subject for comparison. Three phase unwrapping methods were used: Laplacian based phase unwrapping, path-based unwrapping, and voxelwise phase unwrapping. QSM were calculated from healthy subjects and CMB patients, as well as a Gd phantom. In addition, idealized simulated phase data were generated to evaluate the effect of the various algorithms used in QSM on data free from any intrinsic frequency variation.

Our results suggest that, at the spatial and temporal resolution of our data, TE-dependence of frequency and QSM measurements in strong sources is caused in part by the failure of Laplacian- and path-based spatial unwrapping algorithms to recover the true phase from wrapped phase; and suggest that in this case voxelwise unwrapping is a more robust method of removing phase wraps in and around strong susceptibility sources. Furthermore, we find that care must be taken when interpreting ROI analysis in phase and frequency data in strong, focal sources of susceptibility such as CMBs.

4.1.1 Effects of background field removal and QSM inversion

The simulated QSM results plotted in Figure 3 and supplementary Figure 1 show that QSM data derived from wrap-free V-SHARP filtered phase data, which has not been processed with any unwrapping algorithm, does not vary with TE; even in strong sources such as CMBs where χ can be as high as ~1500 ppb. This suggests that the results of V-SHARP background field removal and iLSQR QSM inversions are TE-independent. The similar TE-dependent susceptibility variations calculated from different QSM reconstruction algorithms (Supplementary Figure 2) also suggest that this behavior not a result of QSM reconstruction algorithms. The observed TE-dependence in the in vivo and simulated data must therefore be explained as an artifact of phase unwrapping process; a result of real phase behavior that is not accounted for by the QSM simulation process; or a combination of these factors.

4.1.2 Effect of phase unwrapping on QSM

There are several algorithms to remove phase wraps by imposing continuity or smoothness in phase data, which is an essential step in QSM reconstruction. Failure of phase unwrapping to reveal the true phase will result in errors in the calculation of susceptibility regardless of the QSM algorithm used. The dipolar magnetic field perturbations generated by susceptibility variations within a volume are assumed to cause phase accumulation in each voxel at a rate proportional to the strength of the local field perturbation. Where the true phase exceeds ± π, a phase wrap will occur in the phase image recorded by the scanner. However, a strong susceptibility source, such as a highly paramagnetic CMB, may cause phase differences significantly more than ± π between neighboring voxels, resulting in phase wraps that exist below the resolution of the image and remain uncorrected in the unwrapped data. Failure of an unwrapping algorithm to recognize and correct such wraps may cause a systematic and increasing underestimation of the strength of the dipole field at locations close to strong susceptibility sources as TE increases. This underestimation of the dipole field would then lead to a systematic underestimation of the magnetic susceptibility of the source during QSM inversion. As the wraps in this case are closed around the strong source, QSM values in the rest of the brain would remain unaffected. Analogously, if the phase accumulated between echoes exceeds ± π in a voxel then simple voxelwise phase unwrapping will also fail (although advanced algorithms have been developed to temporally unwrap multi-echo phase data containing inter-echo wraps [68]). As such, the accurate recovery of phase information from GRE scans requires either sufficient spatial or temporal resolution in the data.

Insufficient spatial resolution may explain the decay through time of the susceptibility values derived from Laplacian- and path- unwrapped phase in the CMBs measured in vivo and in the simulated data. The consistency between the path-based and wrap-free simulated data at early echoes suggests that path-based unwrapping is less sensitive to these effects than the Laplacian-based unwrapping at low echo times, since the Laplacian unwrapping method may underestimate the regions with strong susceptibility variations due to the second order derivatives and the spatially discrete sampling of the MRI signal [69, 70]. The increasing echo times during which the path-unwrapped and wrap-free QSM are consistent as the susceptibility of the source decreases is also consistent with this explanation, as seen in Figures 3 and 4. The lack of TE-dependence in the voxelwise-unwrapped simulated QSM data indicates that this method is significantly more robust in and around strong susceptibility sources at this spatial resolution and echo spacing. The consistent TE-dependence of the QSM values measured in vivo in CMBs is notable in itself, as QSM values in CMBs were previously considered to be TE-independent [17]; and the persistence of some TE-dependence in the voxelwise-unwrapped data suggests that these profiles may be indicative of content or compartmentalization within them. If useful information can be extracted from such data, analysis of QSM profiles may provide unique insight into the pathology of CMBs in vivo.

The simulated susceptibility profiles in supplementary figure 1 show little or no TE-dependence in the healthy brain ROIs, regardless of the choice of (or lack of) unwrapping algorithm used. This indicates that at the spatial resolution used in this data (1mm isotropic), both spatial unwrapping methods can give TE-independent QSM measurements in healthy brain tissue (which has low susceptibility values relative to CMBs). This interpretation is supported by the phantom results with lower Gd concentration (0.125 mM and 0.25 mM) (Figure 4)). While no significant TE-dependence was observed in the simulated healthy tissue ROIs, there was a TE-independent offset of ~ ±5–10 ppb observed between the data which underwent no unwrapping and that which was subject to unwrapping algorithms. This offset caused both increased (in the CC, RN and SN) and decreased (in the OR and PT) QSM values in the unwrapped data relative to the wrap-free data. This result suggests that even in the absence of signal compartmentalization/nonlinear phase accumulation there is a fundamental limit to the precision of QSM in measuring bulk susceptibility when using these algorithms.

4.2 TE-dependence of QSM measurements due to intrinsic tissue properties

The real QSM values in the healthy brain ROIs show significant variation with TE; and this variation appears to be consistent between subjects and across multiple scans. This variation is most pronounced in the Laplacian-unwrapped data, while the profiles tend to show substantially reduced TE-dependence in the voxelwise-unwrapped data; a discrepancy which may be linked to the loss of phase contributions from short T₂* components when echo 1 is subtracted.

Although the results presented here in addition to previously published findings [30] raise concerns about the accuracy and interpretation of QSM measurements, they also suggest that useful information about sub-voxel level microstructure may be contained in multi-echo GRE MRI data.

In healthy brain regions where the local signal phase can be correctly recovered via unwrapping and background field removal, TE-dependence in QSM measurements appears to be strongly linked to the TE-dependence of local frequency measurements; as can be seen through comparison of the frequency and phase profiles shown in Figures 7–10. Previous studies have analyzed these effects via two main approaches: multi-exponential fitting to MR signal decay [39–41, 49, 52–54, 56, 67] to identify contributions from multiple compartments; and simulation of white matter microstructure using 2 and 3 compartment hollow cylinder models [39, 40, 49, 51] in an attempt to recreate measurements made in vivo. Multi-exponential fitting can be applied to the signal from any region in the brain; however, in order to interpret the results a plausible model of the tissue or structure under consideration is needed in which the extracted components can be assigned to physically realistic compartments. This presents a challenging problem, particularly in areas where the exact content and microstructure of the tissue is not well known. In white matter fiber tracts, however, 2 and 3 compartment hollow cylinder models have been used with some success in explaining orientation-dependent frequency difference measurements [39] and in signal magnitude and frequency measurements in the marmoset brain [40].

Here, we attempted to use a 3-compartment hollow cylinder model to explain the contrasting TE-dependent frequency (and therefore QSM) measurements observed in the central corpus callosum and optic radiations.

The success of previous studies and partial success of this study in recreating in vivo results using a hollow cylinder model of white matter suggests is a useful tool in the study and interpretation of TE-dependent frequency measurements [39, 40]. However, the results presented here also show that this relatively simple model alone cannot provide a complete representation of microstructural effects in tissue.

While the hollow cylinder model produced frequency profiles resembling those measured in the OR and in the voxelwise-unwrapped data in the CC; it does not explain the initial rise in the Laplacian-unwrapped frequency in the CC. This initial rise may be suggestive of a high-frequency short T₂* signal component not represented in our model, whose relative contribution to the apparent frequency diminishes as TE increases; and which is not accounted for by the simple hollow cylinder model. In order to fully characterize the compartmentalized MR signal must therefore be sampled with TE1 as short as possible.

However, this necessity must be balanced against the need for adequate phase SNR in the structures of interest, the absence of which may compromise the reliability of ROI-based measurements particularly in finer structures such as the optic radiations.

As seen in Figure 4a and 4e, there is limited SNR and limited contrast and outside of the larger ROIs such as the CC and DGM structures in our data at 4 ms. This is also reflected in the increased error bars in the subplots of Figures 7 and 8 reflecting the increased mean standard deviation of points in each ROI. While the phase SNR at a given TE can be increased by scanning at higher field strengths, this benefit may be offset by a corresponding decrease in T₂* in signal compartments already subject to rapid decay at 3T. Furthermore, the contrasting profiles in different ROIs make accurate definition of the ROIs essential for the avoidance of partial-volume errors.

Another important factor not represented by our model is the potential influence of nonrandom distribution of WM fibers. The fiber volume fractions found in white matter are such that the external fields produced by myelinated axons interact; and significant differences in phase accumulation have been demonstrated between volumes containing randomly vs hexagonally packed fibers in similar models [71]. Our model was further limited by the qualitative nature of the analysis of the in vivo data and of the comparison with the hollow cylinder simulation.

Even where the in vivo results correspond to the frequency profiles generated by the hollow cylinder simulation, we find that both the CC and OR correspond most closely to the model when G = 0.65, FVF = 0.4, and the angle of the fibers with respect to B₀ is 60°. At face value, this suggests that the nerve fibers in the CC and OR are more similar in FVF and G-ratio than previously predicted [65]. However, representation of nerve fibers as parallel cylinders is a convenient approximation as the field perturbations due to cylindrical shells with radial anisotropic susceptibility can be calculated analytically, and a voxel of arbitrary length need only be represented using a single 2D array. In reality, nerves are neither perfectly parallel, perfectly straight, nor do they have a consistent cross section throughout their length, and each of these differences represents a limitation to the hollow cylinder model.

Firstly, the field perturbations caused by structures of different shapes will clearly be different. Additional inaccuracies may be introduced by failure to correctly account for transverse relaxation in the different compartments within the voxel. The model used here accounts for T₂ relaxation through by modulating the complex signal in each compartment by an exponential decay term based on previously published T₂ values. T₂′, however, is incorporated by loss of phase coherence between the signals calculated from each grid point within each compartment. When the nerves are modelled as perfect cylinders, the field perturbation within each axon due to the magnetization of its myelin sheath is uniform across the axon, leading to no T₂′ effects due to inhomogeneity in this field. In reality, the non-circular cross section and intra-axonal organelles of the fibers would lead to significant inhomogeneity in the axonal pool and increased T₂′ relative to this model. Secondly, in assuming that the nerve fibers are straight, parallel, and uniform in size, the model does not account for the range of sizes and orientations of fibers with respect to B₀ that would be found within a voxel of tissue.

While the simulations presented here focus exclusively on white matter fiber tracts, the Laplacian-unwrapped human data also shows TE-dependent frequency and QSM measurements in the deep grey matter, including the globus pallidus, head of the caudate nucleus, thalamus, pulvinar, red nucleus, and substantia nigra. The voxelwise-unwrapped data mostly shows lesser or no variation in the grey matter regions, indicating that a short T₂* component may be an explanation of the TE-dependence seen in the Laplacian-unwrapped data; however, modelling of the grey matter to identify the potential source of such a component presents a significant challenge. These brain regions have a more complex microstructure than white matter tracts, containing both axons (typically smaller and more thinly myelinated than those found in the white matter) and a variety of other inclusions such as disc-shaped neurons and iron stored in Ferritin, which itself has a complex structure [72–76]. Although previous studies have found multiple components in the MR signal from grey matter regions by multi-component fitting, the literature lacks any detailed physical model linking compartmentalization of the signal with compartmentalization of the microstructure. Further development of accurate tissue models and associated non-linear mixed models of the MR signal evolution would be an informative avenue of future research.

5 Conclusions

In this study, TE-dependent frequency and QSM measurements derived from gradient-recalled echo MRI data were demonstrated in vivo in various grey and white matter regions of healthy human brains and also in cerebral microbleeds. Potential causes of this TE-dependence were systematically investigated through physical modeling using a gadolinium-doped phantom; computer modeling using simulated phase data; and comparison of in vivo data with a simple hollow cylinder model of white matter.

The results showed that TE-dependence can arise both from failure of spatial phase unwrapping algorithms to recover the true phase near strong susceptibility sources such as CMBs, and from non-linear phase accumulation by the MR signal that may be linked to intrinsic tissue properties. Voxelwise temporal unwrapping may be more robust in some cases (depending on the balance of spatial and temporal resolution of the data), however the loss of phase information from the first echo acquired may cause short T₂* signal components to be lost, and significantly affect the measured frequency profiles. Careful planning of acquisition sequences and processing algorithms is therefore essential recover the maximum amount of useful information. The simple hollow cylinder model of white matter produced frequency profiles reflecting some of those observed in vivo in the optic radiations and central body of the corpus callosum; however, it failed to reproduce effects seen in early echoes of the Laplacian-unwrapped data in the CC. Overall, these results suggest that careful choice of unwrapping algorithm, better sampling of the MR signal at extremely short echo times, and more complex physical models are needed to understand TE-dependent frequency and QSM measurements and potentially exploit them to probe tissue at the sub-voxel level.

Supplementary Material

1

Supplementary Figure 1 shows simulated and real QSM profiles from one healthy subject in the corpus callosum; optic radiations; putamen; red nucleus; and substantia nigra. Like the wrap-free data, the simulated QSM values for both Laplacian- and path- based unwrapping do not show any notable TE dependence. A constant susceptibility offset of ~ ±5–10 ppb can be seen in the unwrapped simulated data relative to the wrap-free simulated data. In the real QSM data, however, the profiles show a clear TE-dependence. This difference suggests that effects unique to the real data must be influencing the susceptibility values resulting in a TE-dependence.

2

Supplementary figure 2 shows the variation of QSM values in the CC, OR, PT, RN, and SN in one healthy subject in one visit when data is processed using the iLSQR, STAR-QSM, and TKD algorithms. The variation with TE is consistent between inversion algorithms. In the CC, OR, PT, and RN, the QSM values calculated using the TKD algorithm are notably greater in magnitude than those calculated using iLSQR and STAR. As the TKD algorithm included a correction factor to compensate for underestimation of susceptibility values due to the modified dipole kernel, the magnitude increase in these ROIs suggests that the underestimation is not uniform across the brain. A single, global correction factor does not appear to adequately correct the data. Nonetheless, the profile of the variation of QSM values with TE in this simple thresholded k-space division is consistent with the more complex iLSQR and STAR algorithms, showing that the variation is not an artefact of the iterative fitting algorithms used.

Highlights.

• Potential causes of TE-dependent QSM measurements are investigated.

• Causes identified include unwrapping errors and intrinsic signal behavior.

• Where TE-dependence is intrinsic it is likely linked to tissue microstructure.

Abbreviations

QSM

Quantitative Susceptibility Mapping

GRE

Gradient Recalled Echo

CMB(s)

cerebral microbleed(s)

CSF

Cerebrospinal fluid

CC

Corpus Callosum

CN

Caudate Nucleus

GCC

Genu of the Corpus Callosum

GP

Globus Pallidus

OR

Optic Radiations

IC

Internal Capsule

PU

Putamen

PUL

Pulvinar

RN

Red Nucleus

SCC

Splenium of the Corpus Callosum

SN

Substantia Nigra

TH

Thalamus