Abstract
Osteocytes interconnect with each other forming an intricate cell network within the mineralized bone matrix. One important function of the osteocyte network is the mechano-regulation of bone remodeling, where a possible mechanism includes the fluid flow through the porosity housing the cell network - the osteocyte lacuno-canalicular network (OLCN). In our study the OLCN in human osteons was three-dimensionally imaged with the aim to obtain a quantitative description of the canalicular density and spatial variations of this quantity within osteons. The topology of the OLCN was determined by first staining the bone samples with rhodamine, then imaging the OLCN with confocal laser scanning microscopy and finally using image analysis to obtain a skeletonized version of the network for further analysis. In total 49 osteons were studied from the femoral cortical bone of four different middle-aged healthy women. The mean canalicular density given as length of the canaliculi in a unit volume was 0.074 ± 0.015 μm/μm3 (corresponding to 74 km/cm3). No correlation was found between the canalicular density and neither the size of the osteon nor the volume fraction occupied by osteocyte lacunae. Within osteons the canalicular density varied substantially with larger regions without any network. On average the canalicular density decreases when moving from the Haversian canal outwards towards the cement line. We hypothesize that a decrease in accessible canaliculi with tissue age as a result of micropetrosis can reduce the local mechanosensitivity of the bone. Systematic future studies on age- and disease-related changes on the topology of the OLCN have to demonstrate the diagnostic potential of the presented characterization method.
Keywords: Osteocyte network, Canalicular density, Network analysis, Confocal microscopy, Micropetrosis, Mechano-regulation
Highlights
-
•
accurate three-dimensional representation of the canalicular network topology using confocal microscopy and image analysis
-
•
quantitative network description with an average canalicular density of 74 km per cubic centimeter in healthy human osteons
-
•
substantial variability of the canalicular density within osteons with 10% of the bone having a density twice the average
-
•
in osteons large regions lacking an accessible network were found
-
•
radial decrease of the canalicular density from the Haversian canal towards the cement line
1. Introduction
Although osteocytes are by far the most abundant bone cells, they attracted only recently the specific attention of bone researchers (Bonewald, 2011). One crucial reason for this late popularity is that osteocytes live buried in the mineralized matrix and, therefore, their activity is more difficult to observe than the activity of osteoblasts and osteoclasts. In living bone, osteocytes occupy lacunae of about 15 μm in their largest dimension and use a network of canaliculi of about 300 nm in diameter (Varga et al., 2015) to connect with each other via gap junctions. The high density of this network entails that the osteocyte lacuno-canalicular network (OLCN) contributes with > 1% to the overall porosity of cortical bone (Cardoso et al., 2013), and its total surface in the human skeleton was estimated to be as large as 215 m2 (Buenzli & Sims, 2015). Different functions have been attributed to the network of osteocytes. The osteocytes are known to be strongly mechano-sensitive cells (Kleinnulend et al., 1995, Klein-Nulend et al., 2013) with their cell processes more sensitive than the cell bodies (Adachi et al., 2009). The network of osteocytes is thought to control the structural adaptation of bone to mechanical needs (Schaffler et al., 2014, Lanyon et al., 1993). Different mechanisms have been proposed of how the mechanical stimulation is sensed by the network. The fluid flow hypothesis states that the mechanical loading squeezes bone fluid through the canaliculi creating shear forces on the cell processes of osteocytes (Han et al., 2004, Burger and Klein-Nulend, 1999). An alternative hypothesis proposes that microdamage results in the interruption of cell processes resulting in the death of the osteocyte (Verborgt et al., 2000). Besides mechanosensing, recently the role of the osteocyte network in mineral homeostasis has been extensively revisited (Qing & Bonewald, 2009). In a process called osteocytic osteolysis (Belanger, 1969, Teti and Zallone, 2009), osteocytes dissolve mineral from the surrounding matrix, thereby enlarging the lacunae (Qing & Bonewald, 2009) and influencing the mineral characteristics of the surrounding bone (Kerschnitzki et al., 2013).
This work focuses on the osteocyte lacuno-canalicular network in human osteons. Osteons are the result of cortical bone remodeling and constitute the basic building block of cortical bone (Parfitt, 1994). Most of the research on the OCLN in osteons concentrated on the osteocyte lacunae due to their larger spatial dimensions compared to the canaliculi. In particular, using synchrotron radiation tomography, the size and arrangement of osteocyte lacunae in osteons was measured in great detail (Hannah et al., 2010, Dong et al., 2014). It was reported that in human osteons the osteocyte density on average increased from 4 ∗ 104/mm3 close to the Haversian canal to 9 ∗ 104/mm3 at 80% of osteon radius. The nearest-neighbor distance between lacunae peaked at 23 μm (Hannah et al., 2010). Moreover, a framework has been established to quantify the osteocyte lacunae, in particular their shape and orientation (Mader et al., 2013).
However, for a proper assessment of the proposed functions of the osteocyte network mentioned above, the properties of the canalicular network seem even more essential. Different methods are nowadays available for a quantitative three-dimensional imaging of the OLCN (Schneider et al., 2010). The strength of synchrotron radiation based methods like phase nanotomography (Varga et al., 2015, Langer et al., 2012) and the combination of scanning electron microscopy (SEM) and focused ion beam (FIB) (Schneider et al., 2011) are a high spatial resolution. The method to combine staining and confocal laser scanning microscopy (Kerschnitzki et al., 2013, Tate et al., 2004, Ciani et al., 2009, Sugawara et al., 2005, Kerschnitzki et al., 2011) has the advantage to provide an image of the OCLN of large bone volumes. With this method, which is used in our study, the network can be analyzed over distances as large as a diameter of an osteon. Applied to the OCLN in sheep it was demonstrated that 80% of the bone matrix is within a distance of only 1.4 μm to the closest canaliculus (Kerschnitzki et al., 2013). Based on histological observations it was suggested that the integrity and three-dimensional organization of the osteocyte network change in disease states such as osteoporosis, osteoarthritis, and osteomalacia (Tate et al., 2004). Alterations in the osteocyte lacunar–canalicular microenvironment were reported with an increase of the effective canalicular size as a result of estrogen deficiency (Sharma et al., 2012).
For future investigations of changes in the OLCN linked to bone diseases, a first essential step constitutes in a quantitative description of the healthy state, which then can serve as a reference. Therefore, the aim of the current study is to quantify the architecture of the osteocyte canalicular network within osteons of healthy individuals. The main descriptor of the network is the canalicular length density of the network, i.e. the length of canaliculi present per bone volume measured in μm/μm3. As a more concise term in the following only canalicular density is used, since length is the natural physical quantity of the network to be quantified per bone volume. For the functionality of the network, in particular the bone tissue permeability, the canalicular density is an essential parameter (Cardoso et al., 2013, Steck and Knothe-Tate, 2003, Verbruggen et al., 2012).
In this study special attention is dedicated on local variations of the network density within an osteon. Marotti and co-workers were first in addressing the question whether the density of the network changes in radial direction, i.e. the direction of bone apposition during remodeling, and found no statistical significant variation (Marotti et al., 1995). With the novel possibility to evaluate now the three-dimensional topology of the network we revisited this question. As the OLCN is imaged via a stain penetrating the network, only the accessible part of the network is imaged. Consequently, when canaliculae and/or lacunae get blocked by mineralized tissue – a process termed micropetrosis (Frost, 1960) – then this part of the network remains unstained. It has been reported that the amount of highly mineralized lacunar occlusions increases with age (Busse et al., 2010) and that osteoporosis and osteoarthritis can be responsible for a higher fraction of hypermineralized osteocyte lacunae (Carpentier et al., 2012). Since micropetrosis most likely has a strong impact on the mechanosensitivity of the bone tissue, a focus of our network evaluation was the detection of regions in the osteon which do not contain an accessible canalicular network.
2. Materials and methods
2.1. Samples
Osteons for the investigation of the OLCN were selected from transversal cross sections of the femoral midshaft from four different human cadavers. Directly after the necropsy bone samples were frozen and stored at − 20 °C and transferred into 70% ethanol prior to further preparation. The sample preparation preserved a large part of the lateral region of the cortex covering the whole cortical thickness. Form such a sample transversal cuts of 0.5 mm thickness were then used for rhodamine staining. By polishing one of the surfaces using abrasive paper with grit designation P 1200 under wet conditions, the image quality could be improved due to removal of the rhodamine stained surface layer.
All individuals were female and middle-aged (age of death between 48 and 56 years) without any known bone-related metabolic disease. The cause of death was in all individuals related to cardiovascular diseases. Samples were provided by the Department of Forensic Medicine of the Medical University of Vienna in accordance with the ethic commission board of the institution (EK #: 1757/2013).
2.2. Staining and confocal imaging
Samples were placed in a phosphate buffered saline (PBS) solution with dissolved rhodamine-6G powder (0.02 %wt) for two days under constant movement. With the small size of the rhodamine molecule (roughly 1 nm ∗ 1 nm ∗ 0.4 nm (Lu & Penzkofer, 1986)) this time is sufficient that rhodamine can penetrate into all the accessible parts of the OLCN as tested by time dependent staining analyses and to attach to its mineralized surface. Using confocal laser scanning microscopy (CLSM) (Leica TCS SP5) the rhodamine fluorescence allows to image the canalicular network (Kerschnitzki et al., 2011), where the unembedded samples are not kept in the rhodamine solution during imaging. Rhodamine was excited with combined laser light of 488 nm and 514 nm and the fluorescence signal was then detected in the wavelength range of 550–650 nm (Fig. 1a). The microscope setting with a 100 × oil-immersion objective (HCX PL APO CS 100.0 × 1.40 OIL) and a numerical aperture of 1.4 would result in a theoretical lateral resolution of about 280 nm. For the imaging the used voxel size was (300 nm)3. Imaged volumes were 155 μm ∗ 155 μm ∗ 40 μm, where the smallest value in axial direction is due to the limited transparency of the mineralized bone. During the measurement the decay of intensity of the fluorescence signal with increasing imaging depth was compensated by adapting the laser intensity and the voltage of the detecting photo multiplier tubes. For the imaging, in each of the four samples multiple osteons were selected over the whole width of the lateral femoral cortex. The selected osteons were middle-sized, had a roughly circular cross-section and were all alternating following standard terminology (Ascenzi & Bonucci, 1968). In total 49 osteons were investigated with at least 11 osteons in each sample (see Table 1 for number of investigated osteons in each sample).
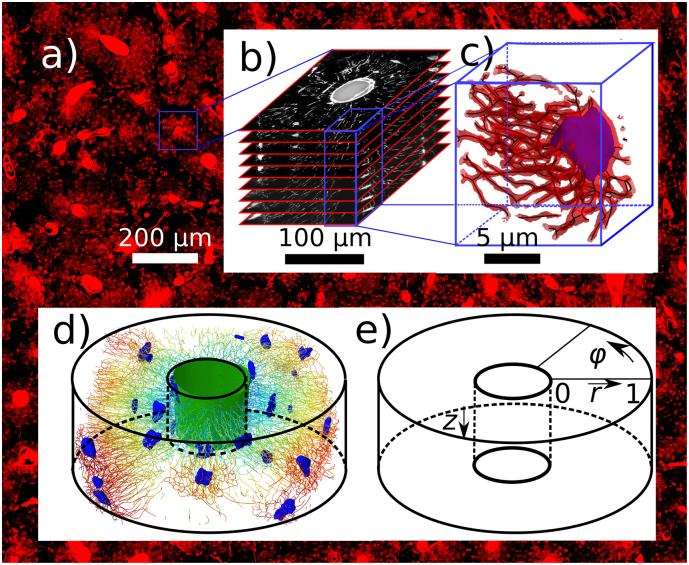
Fig. 1.
a) In the background: overview image of part of the femoral cross-section. Stained in red by rhodamine are the Haversian canals, the osteocyte lacunae and the canaliculi. b) Stack of images obtained by confocal laser scanning microscopy (CLSM) used to render the three-dimensional topology of the OLCN. c) Visualization of a small subvolume to demonstrate the steps in the image analysis: the three-dimensional CLSM image is thresholded to obtain the red contour surface. Subsequent skeletonization and fitting with smoothing splines (dark lines) provides a mathematical rendering of the network topology. A segmented lacuna is visualized in purple. In d) the network of a representative dataset is visualized: osteocyte lacunae (blue), Haversian canal in the center of the osteon (green) and skeletonized canaliculi, which are color coded to indicate their distance from the Haversian canal (from blue to red). The subvolumes of 400 μm3 used to assess the heterogeneity of the canalicular density are of equal size than medium osteocyte lacunae. The cylindrical coordinate system used in the evaluation of the canalicular density is sketched in e).
Table 1.
Parameters characterizing the studied osteons and the osteocyte lacuno-canalicular network within the osteons. Values are given for all the four samples together (all) and for each sample separately (femur1 to 4) as medians and lowest/largest quartile (in square brackets). Reported parameters are: canalicular density Ca.Dn, the standard deviation of the canalicular density distribution Ca.Dn.stddev, the first bin in the canalicular density distribution, Ca.Dn.firstbin, which provides the percentage of the bone volume without accessible canalicular network (Fig. 4), the volume fraction occupied by osteocyte lacunae Lc.V.Dn, the radius of the osteon On.Rd, the radius of the Haversian canal HCa.Rd, the osteon wall thickness On.W.Th and the bone volume that was included in the evaluation of the OLCN, evaluated.BV.
| All n = 49 | Femur1 n = 12 | Femur2 n = 13 | Femur3 n = 11 | Femur4 n = 13 | |
|---|---|---|---|---|---|
| Ca.Dn [μm/μm3] | 0.076 [0.066, 0.083] | 0.086 [0.072, 0.092] | 0.067 [0.065, 0.078] | 0.082 [0.076, 0.089] | 0.064 [0.057, 0.076] |
| Ca.Dn.stddev [μm/μm3] | 0.046 [0.04, 0.05] | 0.087 [0.04, 0.055] | 0.046 [0.043, 0.048] | 0.049 [0.047, 0.051] | 0.041 [0.039, 0.044] |
| Ca.Dn.firstbin [μm/μm3] | 0.075 [0.067, 0.086] | 0.086 [0.074, 0.094] | 0.07 [0.067, 0.078] | 0.083 [0.077, 0.091] | 0.062 [0.056, 0.075] |
| Lc.V.Dn [μm3/μm3] | 0.0068 [0.0054, 0.0089] | 0.0058 [0.0054, 0.0081] | 0.0071 [0.0058, 0.01] | 0.0071 [0.0055, 0.0081] | 0.007 [0.0063, 0.0079] |
| On.Rd [μm] | 107 [96.4, 136] | 119 [102, 137] | 89.6 [83.9, 113] | 100 [95.3, 116] | 120 [99.7, 154] |
| HCa.Rd [μm] | 31.8 [26.2, 42.2] | 37.2 [27, 45.5] | 27.6 [23.6, 38.2] | 31.6 [26.3, 36.5] | 35.9 [31.8, 60.3] |
| On.W.Th [μm] | 72.5 [63.5, 92.9] | 80.1 [64.7, 95.3] | 65.9 [60.3, 86] | 72.9 [64.3, 79.6] | 69.3 [67.5, 94.1] |
| evaluated.BV [105 ∗ μm3] | 7.3 [6.4, 7.8] | 6.6 [5.9, 6.9] | 7.5 [6.8, 7.8] | 7.7 [6.5, 7.8] | 7.7 [6.8, 8.2] |
2.3. Image analysis
As a first step in the analysis the stack of images from confocal microscopy (Fig. 1b) was binarized employing a customized adaptive thresholding algorithm. The used algorithm is based on difference of Gaussians (DoG) (Marr & Hildreth, 1980), a classical feature enhancement algorithm in image science, and was repetitively applied to properly threshold both, the canaliculi and the much larger lacunae (supplementary material, Fig. S1). The difference in spatial extensions between canaliculi and lacunae allowed the segmentation of these structures: “bulky” clusters of voxels belonging to the network were tested to be part of a lacuna by further extending these clusters using a morphological dilation algorithm (Fig. S1). With the diameter of a canaliculus of about 300 nm (Varga et al., 2015) (reported values between 100 and 500 nm (Cardoso et al., 2013)) being smaller than the image resolution, it was obvious that the obtained binarized and segmented image cannot provide an accurate representation of the canalicular porosity. The aim of the imaging, however, was not a 3D representation of the network but of the network topology. For this reason the next step in the image analysis was a skeletonization of the image data. By removing voxels from the surface the result of the skeletonization was a thinned version of the original image that is roughly equidistant to its original boundaries and conserves the topological features of the network like connectivity, edge length and orientation. To this end the removal of surface voxels had to stop when only a network of chains of voxels remained and any further voxel removal would have caused a change in network topology. The discrete nature of the network as collection of voxels was then mitigated by fitting the skeletonized image data by third order smoothing splines (Dierckx, 1982) (Fig. 1c). The outcome of the image analysis of the OLCN is a separation between lacunae and canaliculi, where the topology of the canalicular network (as a graph) is defined by nodes (i.e. meeting points of canaliculi) and connecting edges (i.e. canaliculi). The canaliculi themselves are represented by a number of spline segments each with a length comparable to the voxel size (Fig. 1d).
2.4. Network evaluation
The basic quantity analyzed in this study is the canalicular density Ca.Dn which characterizes the length of all the canaliculi in a given volume and is therefore measured in μm/μm3. This quantity is related to the number density of canaliculi defined as number of canaliculi intersecting a given area as reported in earlier studies (Marotti et al., 1995). However, our definition of canalicular density being defined per unit volume has the advantage to be less sensitive to orientational effects in the evaluation. For a better illustration of the canalicular density, also a length in units of μm is reported, which corresponds to a characteristic distance dc between two canaliculi. For the conversion of Ca.Dn into a length the simplest geometry of the canalicular network is assumed, i.e. a two-dimensional dense packing of straight and parallel canaliculi. In such a hexagonal arrangement of canaliculi, the half distance between neighboring canaliculi dc is given by .
The canalicular density is analyzed on two length scales: firstly, on the length scale of the whole osteon. The length of the canaliculi is evaluated within the volume of the osteon, i.e. regions outside the cement line and the Haversian canal were excluded. In addition, also the volume of the osteocyte lacunae was excluded, which comprises about 0.6 ± 0.3% of the volume of the osteon (see Table 1). Parameters employed to characterize the investigated osteons are the mean radius of the osteon, On.Rd, the mean radius of the Haversian canal, HCa.Rd, the mean osteon wall thickness, On.W.Th, and the bone volume within the osteon that was included in the evaluation of the OLCN, evaluated.BV. The OLCN in the osteons was described by the canalicular density, Ca.Dn, the standard deviation of the canalicular density distribution Ca.Dn.stddev, the first bin in the canalicular density distribution Ca.Dn.firstbin, which provides the percentage of bone volume in the osteon without canalicular network (Fig. 4) and the volume fraction occupied by osteocyte lacunae, Lc.V.Dn.
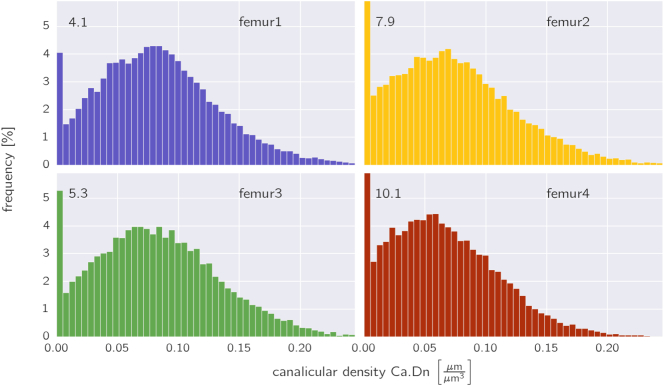
Fig. 4.
Frequency distribution of the canalicular density evaluated using subvolumes of 400 μm3 averaged over all osteons within a sample. The numbers in the upper left corner refers to the height of the first bins, which extend beyond the plots for femurs 2 and 4.
Secondly, to characterize the observed spatial heterogeneity of the canalicular network, the volume of the osteon was partitioned into smaller subvolumes and the canalicular density evaluated in each subvolume. The inhomogeneity, characterized by the width of the distribution of the canalicular density within subvolumes, clearly depends on the size of the subvolumes. In the extreme case that the subvolumes have dimensions smaller than the mean distance between canaliculi, the result would be a large percentage of empty subvolumes and a smaller part of the subvolumes with high canalicular density. Our choice of the size of the subvolume as a representative volume was 400 μm3, which is large enough to include several canaliculi in most of the subvolumes and has a size comparable to the osteocyte lacunae. The cylindrical shape of the osteon suggests performing the partition into subvolumes in a cylindrical coordinate system (Fig. 1e) with rings in radial directions r, circular sectors in azimuthal direction φ and slices in depth direction z. The azimuthal angle φ and the depth coordinate z were subdivided equidistantly with ∆ φ = π/36 and ∆ z = 8 μm. To fulfill the constraint of equal volume of all subvolumes, the radial coordinate was then subdivided in a non-equidistant manner. The outcome of the analysis is a frequency distribution describing how likely it is to find a subvolume with a given canalicular density in the osteon. The partitioning into subvolumes is further used to study changes of the canalicular density in different directions, e.g. whether the network density decreases with distance from the Haversian canal. To account for the different sizes of the osteons, the radial distance from the osteonal center is normalized to be 0 at the border between Haversian canal and bone and 1 at the cement line.
The source code used for both the image analysis and network evaluation will be available for download (Repp, n.d.).
2.5. Value reporting and statistics
In the text the results of the quantification of the osteocyte network are reported as mean value ± standard deviation when averaged over all 49 osteons. Values obtained as means over the 4 investigated samples are reported as the range between the minimum and maximum value. The values summarized in Table 1 are given as medians and the boundary values of the lowest and largest quartile.
To test differences of the canalicular density between the four different samples for their statistical significance, a one way ANOVA was performed with appropriate Bonferroni correction. The correlation between the canalicular density and the osteon geometry and lacunar volume fraction (Fig. 3), respectively, was determined by linear regression t-tests. To test the hypothesis that the canalicular density decreases with distance from the Haversian canal, t-tests were performed using the slope of the radial canalicular density dependence for each of the samples independently. The significance level was p < 0.05.
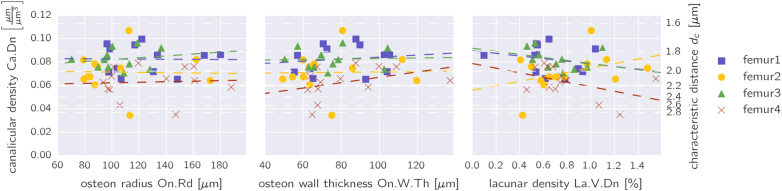
Fig. 3.
a) Canalicular density as a function of the osteon radius (left), osteon wall thickness (middle) and the lacunar volume fraction (right), for all osteons in the 4 samples. The straight lines denote linear regressions performed for each sample separately. The y-axis on the right side is a linear measure for the density of the canalicular network and is calculated as (see Methods section).
3. Results
Table 1 summarizes basic information about the 49 osteons investigated. Their sizes were in the medium range with a mean radius of 116 μm ± 36 μm. The sizes of the Haversian canals showed larger relative variations – 40 μm ± 22 μm. The field of view of the microscope did not allow imaging the whole osteons if they were larger than 155 μm in diameter. Consequently, the mean bone volume that was used for the evaluation of the OLCN in a single osteon was (7.1 ± 1.1) ∗ 105 μm3.
A first quantification of the density of the canalicular network is obtained by calculating the shortest Euclidian distance of all the bone voxels in the image to its closest canaliculus or lacuna (Kerschnitzki et al., 2013). In Fig. 2 the obtained frequency distributions for all four samples and the corresponding cumulative distribution (dashed curves) are shown. The typical distance of bone to the next canaliculus or lacuna denoted by the peak of the distribution is only slightly above 1 μm. The cumulative distributions show that 80% of the bone in human osteons has a canaliculus not farther away than 2.47–3.08 μm. The values of the canalicular density for the four samples showed a significant difference (ANOVA, p = 0.0008). Pairwise testing showed that only the differences between femur1 and femur4, and femur 3 and femur 4 are significant (Bonferroni corrected p = 0.005 and p = 0.002, respectively).
Fig. 2.
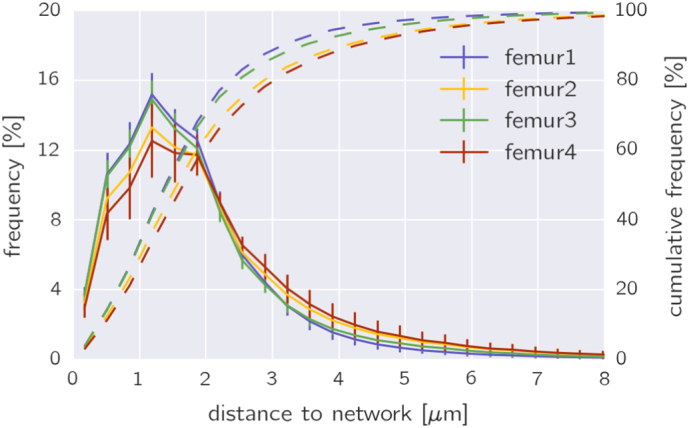
Frequency distribution of the shortest Euclidian distance of every bone voxel to its nearest canaliculus or lacunae for all the osteons in the four femoral bone samples (solid line). The four dashed lines (together with the y-axis on the right) show the corresponding cumulative distributions obtained by integration of the distributions. From these cumulative distributions it can be inferred that approximately 80% of the bone is closer than 2.77 μm to the next canaliculus or lacuna.
To test the hypothesis whether larger osteons have a less dense network, Fig. 3a and b show the canalicular density, defined as the length of the network within a unit volume, plotted versus the osteon radius and the osteon wall thickness, respectively, for all the 49 osteons measured in the four samples of femoral cortical bone. Performing a linear regression for all samples (dashed lines in Fig. 3), the obtained low values of the slope suggest an independence of network density from osteon radius (p-values in the range of 0.61–0.97 for a significant difference of the slope from zero; Fig. 3, left) and osteon wall thickness (p-values in the range of 0.91–0.92; Fig. 3, middle). Also no correlation was found when testing the canalicular density against the lacunar volume fraction (p-values in the range of 0.11–0.46; Fig. 3, right).
When probing the heterogeneity of the network within the osteon by subdividing its volume into smaller subvolumes of 400 μm3 (see Methods section) and making a frequency histogram of the canalicular density with these subvolumes, the following features are observed (Fig. 4, histogram averaged over all osteons in one sample): except for the first sample the highest bar is found on the very left corresponding to subvolumes virtually free of any network (7.5 ± 1.6% of the osteon volume). The distributions have a mean value between 0.063 and 0.084 μm/μm3 with a standard deviation of 0.045–0.051 μm/μm3. The value of the 90th percentile is 0.125–0.152 μm/μm3, i.e. 10% of the osteon volume is penetrated by a canalicular network that is roughly twice as dense as the mean canalicular network.
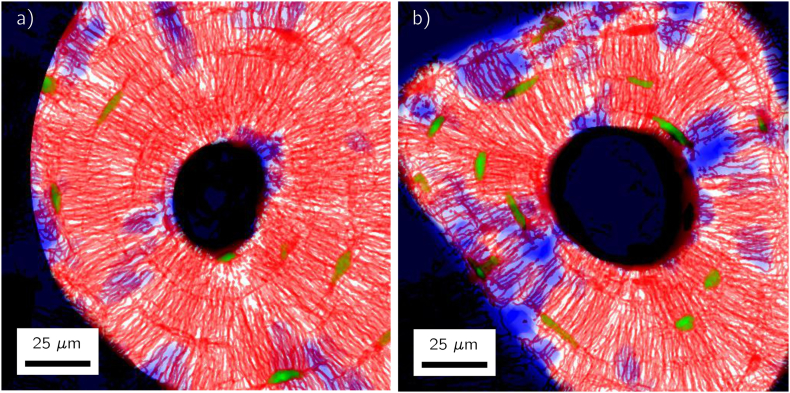
Fig. 5 shows two representative osteons in which regions with no network are located (highlighted in blue). The plots demonstrate that these regions without network are not equally distributed over the whole osteon, but are concentrated only in a few locations. They display some preferred orientation in radial direction towards the center of the osteon as can be seen in the osteon on the right in Fig. 5.
Fig. 5.
Projections along the depth axis of two typical datasets of osteons with regions outside of the osteon (including the Haversian canal) in black. The canalicular network stained by rhodamine is visualized in red, detected lacunae in green and regions without canalicular network on a length scale larger than 5 μm are highlighted in blue. Note that both the blue color for the regions free of network and the green color of the lacunae are the result of an image analysis and do not correspond to a staining of the sample.
The partition in subvolumes allows analyzing how the canalicular density varies along the radial, the azimuthal and the depth direction (see Fig. 1e for the definition of the directions). The evaluation for the two osteons shown in Fig. 5 confirms the impression that the network of the osteon on the left in Fig. 5 is azimuthally almost homogeneous, whereas the network in the osteon on the right is more organized like spokes in a wheel resulting in strong variations of the canalicular density as a function of the azimuthal angle φ (Fig. 6, middle). The canalicular density is relatively constant with the imaging depth (Fig. 6, bottom). Most interesting is the question whether the network density changes in radial direction, i.e. the direction in which the bone is deposited during osteon formation. For both osteons the canalicular density decreased in a roughly linear manner with distance from the Haversian canal (Fig. 6, top). The result of a linear regression for the radial dependence of the canalicular density for all the osteons is shown in Fig. 7. The value of the fitted slope is negative for most of the osteons. For the 49 osteons we obtained a negative slope of − 0.038 ± 0.04. A statistical analysis showed that the slope is significantly smaller than zero when considering all the osteons (p = 6.4 ∗ 10− 8) and the same was true for three of the four individual bone samples (p-values ranging from 0.0004 to 0.02).
Fig. 6.
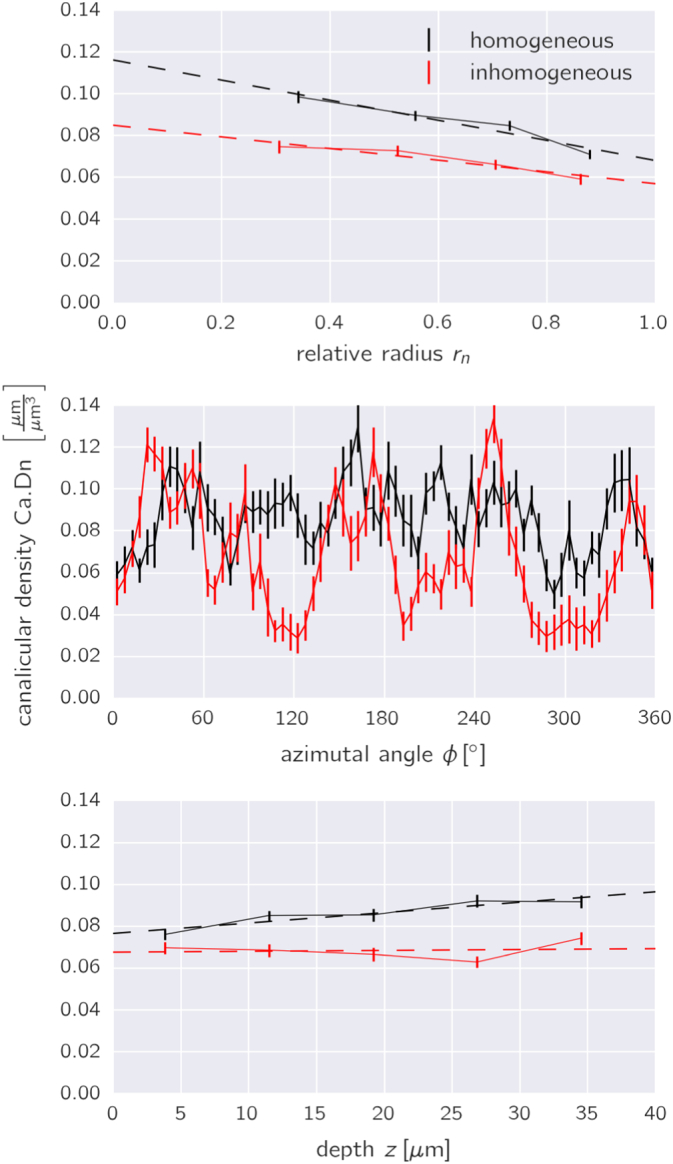
Spatial variation of the canalicular densities along the three directions of the cylindrical coordinate system as defined in Fig. 1e. The relative radius rn is defined to be 0.0 at the outer rim of the Haversian canal and 1.0 at the cement line. The black (red) data corresponds to the osteon of Fig. 5 on the left (right); error bars denote the standard error. The dashed lines in the plots on the top and bottom are the result of a linear regression. The obtained slopes for all the osteons were further analyzed (see Fig. 7).
Fig. 7.
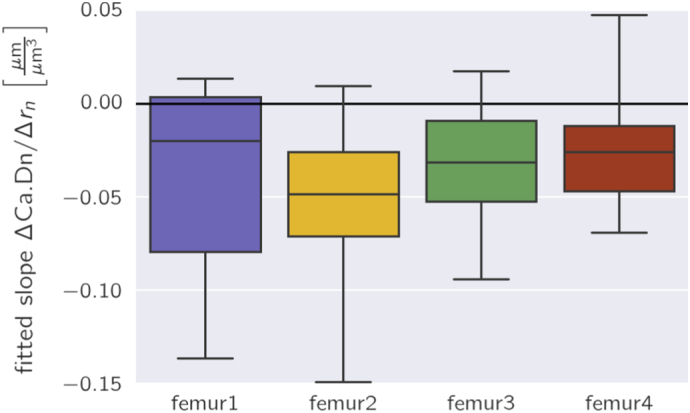
Box plots of the slopes of the canalicular density as a function of the radius as obtained by linear regression (see Fig. 6, top, for the example of two osteons). For the plots all 49 osteons were analyzed in the four samples separately.
4. Discussion
Bone health is crucially linked to properly functioning osteocytes, and their function is in turn intimately related to their mutual connection via the canalicular network. With the vision in mind to obtain a more functional assessment of the canalicular network, we performed in this study a quantitative analysis of the network structure. A combination of confocal laser scanning microscopy and 3D image analysis was used to image and analyze the osteocyte lacuno-canalicular network (OLCN) in osteons of healthy human individuals. The main quantity of analysis was the canalicular density defined as the length of the canaliculi per unit volume. As average over all 49 investigated osteons in healthy individuals, we obtained a canalicular density of 0.074 ± 0.015 μm/μm3. This value means that a cube of bone with a side length of 1 cm contains a canalicular network of a length of 74 km. In comparison Marotti et al. counted 5.5 ± 1.9 canaliculi per 100 μm2 penetrating the surface of Haversian canals in a human tibia (Marotti et al., 1995). Assuming that these canaliculi are continuing parallel into the bone matrix, this value fits well to our slightly higher density taking into account that Marotti's method could not account for canaliculi running parallel to the bone surface. Our reported value of the canalicular density is in agreement with the value of 0.1 μm/μm3 from the estimation in the Appendix of (Buenzli & Sims, 2015) based on OLCN data from sheep (Kerschnitzki et al., 2013). However, our value is almost four-times smaller than the value measured in embryonic chick calvaria (Sugawara et al., 2005). Artefacts in both the experimental staining method and in the image analysis tend rather “to lose” functional canaliculi than “to create” non-existing canaliculi. For this reason, the obtained value is in our interpretation probably an underestimation of the canalicular density in healthy humans. The density of the network in human osteons is markedly lower than in the fibrolamellar bone of sheep. In ovine samples 80% of the bone was found within only a distance of 1.4 μm to the closest canalicular network structure (Kerschnitzki et al., 2013). In human osteonal bone the corresponding value is with 2.8 μm twice as large.
Our analysis did not show any correlation of the canalicular density with the geometry of the osteon, i.e. the size of the osteon described by its radius or the osteonal wall thickness. Additionally, no correlation was found between the canalicular density and the volume occupied by the osteocyte lacunae. This universality of canalicular density between osteons suggests that the distance between canaliculi is under control of a local mechanism that is independent of global osteon geometry or lacunar density during formation of the canalicular network.
The partition of the osteons into smaller subvolumes and analysis of the network in these subvolumes revealed a substantial variability of the canalicular density. Remarkable are the large regions in osteons without network – on average in > 7% of the subvolumes no network was found. As the network is imaged via a stain entering into the canalicular porosity, it has to be emphasized that our statement is not that in these regions no network was formed during osteon formation or that no canalicular structures can be found there. Our statement is rather that these regions do not contain any network accessible to the stain. Due to the small size of the rhodamine molecule, we conclude that these regions do not contain any functional network. A simple mathematical model how to interpret the observed variability in the canalicular density is to construct an abstract network model based on the following assumptions: (i) the evaluation volume of 400 μm3 is assumed to be a cube with a side length of 7.37 μm; the network is evaluated in a large two-dimensional array of such cubes; (ii) the network consists only of straight and parallel aligned canaliculi which traverse the cube perpendicular to the extension of the two-dimensional array; (iii) the intersection points of the canaliculi with one of these cubic faces are chosen randomly and (iv) the mean canalicular density of the abstract network equals the measured canalicular density. In such a cube on average four parallel canaliculi would cross the cube from side to side. The resulting frequency distribution of the canalicular density of this abstract network model of randomly placed canaliculi would result in a Poisson-like distribution with a standard deviation σ = 0.037 μm/μm3. This distribution is quite similar to the experimental distributions shown in Fig. 4. For the relation between the network density and the variance σ2, the model predicts a linear relation. Fig. 8 shows that the experimental data from all the osteons follow reasonably such a linear relation (linear regression with R2 = 0.54). We want to state clearly that this comparison is not thought to explain in any way the formation of the network, but may provide a better intuitive understanding of the measured variability. From the comparison with the abstract model of randomly placed canaliculi, we can naturally understand that networks with higher density are also more heterogeneous. However, a feature that is not reproduced by this abstract network model is the presence of large volumes without network at all.
Fig. 8.
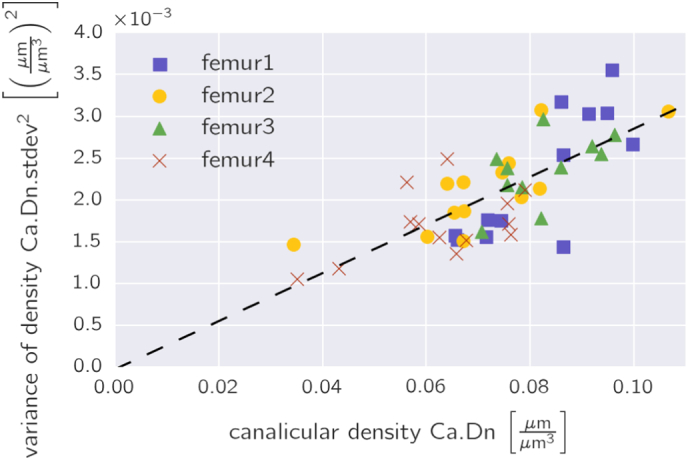
The inhomogeneity of the network density as quantified by its variance as a function of the network density plotted for all evaluated osteons.
The variability of the canalicular density was specifically analyzed along the natural coordinate system of an osteon, i.e. in the radial direction parallel to the direction of bone formation, in the azimuthal direction with the angle φ denoting angles around the osteon, and the depth direction along the axis of osteoclast tunneling during remodeling.
Highlighted has to be the radial dependence of the canalicular density, where we found a decrease with increasing distance from the Haversian canal. This result is consistent with the outcome by Marotti et al. (Marotti et al., 1995), who found also a decreasing canalicular number density in a radial direction moving outwards for all three investigated individuals of very different age. However, their presented data were not statistically significant. Our evaluation of the canalicular density from 3D image data demonstrates a decrease in canalicular density as a function of the distance from the Haversian canal with statistical significance for each sample. Two additional analyses of our data corroborate the negative correlation between canalicular density and radial distance. We excluded from the analysis all the subvolumes without network to test the hypothesis whether the decrease is only due to a higher probability of network-free regions close to the cement line. The outcome was that the average negative slope became smaller (− 0.032 ± 0.04 compared to − 0.038 ± 0.04 including all subvolumes), but remained highly statistically significant (p = 1.3 ∗ 10− 6) and 3 out of 4 samples showed a significant negative slope (p-values ranged from 0.00068 to 0.092) (supplementary material, Fig. S2). The second observation is obtained when plotting the canalicular density of an osteon versus the slope of the decrease in canalicular density with radial distance. The plot shows a negative correlation (linear regression with R2 = 0.29) with the densest networks displaying the strongest decrease of canalicular density with radial distance (supplementary material, Fig. S3). Following the line of interpretation that the density of accessible canaliculi in an osteon decreases with time (e.g., due to closing of canaliculi by micropetrosis (Frost, 1960)), so that osteons with the highest density are the “best conserved ones” and tend to be younger, we conclude that the canalicular network in osteons is formed with a clear increase in canalicular density from the cement line towards the Haversian canal. It is interesting to confront this result with observations on the number density of osteocyte lacunae within osteons and the bone apposition rate during osteon formation. When filling of the osteon starts, the apposition rate is high and - compared to average values in the osteon - the number density of osteocyte lacunae is increased (Hannah et al., 2010). The density of the canalicular network has initially values lower than average. At the end of filling of the osteon the apposition rate is low after a roughly exponential decrease as a function of the deposited wall thickness (Lee, 1964, Polig and Jee, 1990). At this final stage of osteon formation the lacuna number density is low and the density of the canalicular network is high. Since osteocytes make use of the canalicular network to interact with the surrounding bone material via osteocytic osteolysis (Belanger, 1969, Teti and Zallone, 2009), these topological characteristics of the network should also leave their traces in the bone material. Using different synchrotron radiation techniques it could be demonstrated that both the mineral content (Hesse et al., 2015) and the nanoscopic mineral particle size (Kerschnitzki et al., 2013) is altered in close vicinity of the canaliculi.
The present study should be considered as a start of systematic studies of the topology of the OLCN in bones of humans and animals. It provides a reference value of the canalicular density in human osteons in a load bearing long bone and how this quantity varies within osteons. The observation of larger regions without accessible network suggests that with time the network structure can deteriorate, most likely due to osteocyte death and the closing of canaliculi by micropetrosis. A less dense and a less connected network could carry important implications having in mind the important role of the osteocyte network in the mechano-control of bone remodeling. If it is possible to read out from the network topology a quantity related to the local mechanosensitivity of the bone, an important step in the diagnosis of bone diseases with dysfunctional mechano-regulation would be achieved. On the path towards developing canalicular density as a potential diagnostic tool, the time evolution of the OLCN with age has to be quantified. It was shown that the number of canaliculi per osteocyte lacuna decreases with the age of the individual (Milovanovic et al., 2013). Because of bone remodeling topological changes of the canalicular network with age have to be analyzed with a careful distinction between the tissue age under investigation and the age of the individual.
Acknowledgement
The authors want to thank Peter Fratzl for his significant input in the planning of the project and during discussions of the results.
Footnotes
Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.bonr.2017.03.001.
Appendix A. Supplementary data
Fig. S1 Example showing the advantages of the adaptive thresholding algorithm in the segmentation of lacunae and canaliculi: top, raw data image showing part of the Haversian canal at the bottom of the image and three lacunae with high fluorescence intensity. The two plots below compare the outcome of the applied adaptive thresholding algorithm with the result of applying a global threshold with a low value (middle) and a high value (bottom). In these plots of comparison yellow voxels denote image voxels which are attributed to the osteocyte lacuna-canalicular network for both adaptive and global thresholding; cyan denotes voxels where this attribution occurs only for the global threshold, and red only for the adaptive threshold. A high global threshold value (bottom) would result in the loss of large parts of the canalicular network. A low global threshold leads to a significant overestimation of the volume of the lacunae (large cyan seams around the lacunae). Note that the higher intensity of lacunae is considered in the adaptive threshold algorithm with the consequence that even in the comparison with the high global threshold the lacunae still have a cyan seam.
Fig. S2: Box plots of the slopes of the canalicular density as a function of the radius as obtained by linear regression (see Fig. 6, top, for the example of two osteons). For the plots all 49 osteons were analyzed in the four samples separately. In contrast to the corresponding Fig. 7, in the analysis all the regions in the osteons without canalicular network were excluded corresponding to the first bin in Fig. 4.
Fig. S3: The slope of the canalicular density as a function of the radius as obtained by linear regression plotted versus the canalicular density Ca.Dn for all 49 osteons of the study. The slope is stronger negative, i.e. the canalicular density decreases faster when moving from the Haversian canal to the cement line, for osteons with a dense network. Assuming that the network density decreases with the time passed after its formation this indicates that osteons are formed with a pronounced gradient of the network density when moving from their inside to their outside border.
References
- Adachi T., Aonuma Y., Tanaka M., Hojo M., Takano-Yamamoto T., Kamioka H. Calcium response in single osteocytes to locally applied mechanical stimulus: differences in cell process and cell body. J. Biomech. 2009;42:1989–1995. doi: 10.1016/j.jbiomech.2009.04.034. [DOI] [PubMed] [Google Scholar]
- Ascenzi A., Bonucci E. Compressive properties of single osteons. Anat. Rec. 1968;161 doi: 10.1002/ar.1091610309. (377-&) [DOI] [PubMed] [Google Scholar]
- Belanger L.F. Osteocytic osteolysis. Calcif. Tissue Res. 1969;4 doi: 10.1007/BF02279101. (1-&) [DOI] [PubMed] [Google Scholar]
- Bonewald L.F. The amazing osteocyte. J. Bone Miner. Res. 2011;26:229–238. doi: 10.1002/jbmr.320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buenzli P.R., Sims N.A. Quantifying the osteocyte network in the human skeleton. Bone. 2015;75:144–150. doi: 10.1016/j.bone.2015.02.016. [DOI] [PubMed] [Google Scholar]
- Burger E.H., Klein-Nulend J. Mechanotransduction in bone - role of the lacuno-canalicular network. FASEB J. 1999;13:S101–S112. [PubMed] [Google Scholar]
- Busse B., Djonic D., Milovanovic P., Hahn M., Puschel K., Ritchie R.O., Djuric M., Amling M. Decrease in the osteocyte lacunar density accompanied by hypermineralized lacunar occlusion reveals failure and delay of remodeling in aged human bone. Aging Cell. 2010;9:1065–1075. doi: 10.1111/j.1474-9726.2010.00633.x. [DOI] [PubMed] [Google Scholar]
- Cardoso L., Fritton S.P., Gailani G., Benalla M., Cowin S.C. Advances in assessment of bone porosity, permeability and interstitial fluid flow. J. Biomech. 2013;46:253–265. doi: 10.1016/j.jbiomech.2012.10.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpentier V.T., Wong J.Q., Yeap Y., Gan C., Sutton-Smith P., Badiei A., Fazzalari N.L., Kuliwaba J.S. Increased proportion of hypermineralized osteocyte lacunae in osteoporotic and osteoarthritic human trabecular bone: Implications for bone remodeling. Bone. 2012;50:688–694. doi: 10.1016/j.bone.2011.11.021. [DOI] [PubMed] [Google Scholar]
- Ciani C., Doty S.B., Fritton S.R. An effective histological staining process to visualize bone interstitial fluid space using confocal microscopy. Bone. 2009;44:1015–1017. doi: 10.1016/j.bone.2009.01.376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dierckx P. Algorithms for smoothing data with periodic and parametric splines. Comput. Vis. Graph. 1982;20:171–184. [Google Scholar]
- Dong P., Haupert S., Hesse B., Langer M., Gouttenoire P.J., Bousson V., Peyrin F. 3D osteocyte lacunar morphometric properties and distributions in human femoral cortical bone using synchrotron radiation micro-CT images. Bone. 2014;60:172–185. doi: 10.1016/j.bone.2013.12.008. [DOI] [PubMed] [Google Scholar]
- Frost H.M. Micropetrosis. J. Bone Joint Surg. Am. 1960;42:144–150. [PubMed] [Google Scholar]
- Han Y.F., Cowin S.C., Schaffler M.B., Weinbaum S. Mechanotransduction and strain amplification in osteocyte cell processes. Proc. Natl. Acad. Sci. U. S. A. 2004;101:16689–16694. doi: 10.1073/pnas.0407429101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hannah K.M., Thomas C.D.L., Clement J.G., De Carlo F., Peele A.G. Bimodal distribution of osteocyte lacunar size in the human femoral cortex as revealed by micro-CT. Bone. 2010;47:866–871. doi: 10.1016/j.bone.2010.07.025. [DOI] [PubMed] [Google Scholar]
- Hesse B., Varga P., Langer M., Pacureanu A., Schrof S., Mannicke N., Suhonen H., Maurer P., Cloetens P., Peyrin F., Raum K. Canalicular network morphology is the major determinant of the spatial distribution of mass density in human bone tissue: evidence by means of synchrotron radiation phase-contrast nano-CT. J. Bone Miner. Res. 2015;30:346–356. doi: 10.1002/jbmr.2324. [DOI] [PubMed] [Google Scholar]
- Kerschnitzki M., Wagermaier W., Roschger P., Seto J., Shahar R., Duda G.N., Mundlos S., Fratzl P. The organization of the osteocyte network mirrors the extracellular matrix orientation in bone. J. Struct. Biol. 2011;173:303–311. doi: 10.1016/j.jsb.2010.11.014. [DOI] [PubMed] [Google Scholar]
- Kerschnitzki M., Kollmannsberger P., Burghammer M., Duda G.N., Weinkamer R., Wagermaier W., Fratzl P. Architecture of the osteocyte network correlates with bone material quality. J. Bone Miner. Res. 2013;28:1837–1845. doi: 10.1002/jbmr.1927. [DOI] [PubMed] [Google Scholar]
- Kleinnulend J., Vanderplas A., Semeins C.M., Ajubi N.E., Frangos J.A., Nijweide P.J., Burger E.H. Sensitivity of osteocytes to biomechanical stress in-vitro. FASEB J. 1995;9:441–445. doi: 10.1096/fasebj.9.5.7896017. [DOI] [PubMed] [Google Scholar]
- Klein-Nulend J., Bakker A.D., Bacabac R.G., Vatsa A., Weinbaum S. Mechanosensation and transduction in osteocytes. Bone. 2013;54:182–190. doi: 10.1016/j.bone.2012.10.013. [DOI] [PubMed] [Google Scholar]
- Langer M., Pacureanu A., Suhonen H., Grimal Q., Cloetens P., Peyrin F. X-ray phase nanotomography resolves the 3D human bone ultrastructure. PLoS One. 2012;7 doi: 10.1371/journal.pone.0035691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lanyon L.E., Rubin Raisz, Marotti Lees. Osteocytes, strain detection, bone modeling and remodeling. Calcif. Tissue Int. 1993;53:S102–S107. doi: 10.1007/BF01673415. [DOI] [PubMed] [Google Scholar]
- Lee W.R. Appositional bone formation in canine bone - quantitative microscopic study using tetracycline markers. J. Anat. 1964;98 (665-&) [PMC free article] [PubMed] [Google Scholar]
- Lu Y., Penzkofer A. Absorption behavior of methanolic rhodamine 6g solutions at high-concentration. Chem. Phys. 1986;107:175–184. [Google Scholar]
- Mader K.S., Schneider P., Muller R., Stampanoni M. A quantitative framework for the 3D characterization of the osteocyte lacunar system. Bone. 2013;57:142–154. doi: 10.1016/j.bone.2013.06.026. [DOI] [PubMed] [Google Scholar]
- Marotti G., Ferretti M., Remaggi F., Palumbo C. Quantitative-evaluation on osteocyte canalicular density in human secondary osteons. Bone. 1995;16:125–128. doi: 10.1016/s8756-3282(94)00019-0. [DOI] [PubMed] [Google Scholar]
- Marr D., Hildreth E. Theory of edge-detection. Proc. R. Soc. Ser. B. 1980;207:187–217. doi: 10.1098/rspb.1980.0020. [DOI] [PubMed] [Google Scholar]
- Milovanovic P., Zimmermann E.A., Hahn M., Djonic D., Puschel K., Djuric M., Amling M., Busse B. Osteocytic canalicular networks: morphological implications for altered mechanosensitivity. ACS Nano. 2013;7:7542–7551. doi: 10.1021/nn401360u. [DOI] [PubMed] [Google Scholar]
- Parfitt A.M. Osteonal and hemi-osteonal remodeling - the spatial and temporal framework for signal traffic in adult human bone. J. Cell. Biochem. 1994;55:273–286. doi: 10.1002/jcb.240550303. [DOI] [PubMed] [Google Scholar]
- Polig E., Jee W.S.S. A model of osteon closure in cortical bone. Calcif. Tissue Int. 1990;47:261–269. doi: 10.1007/BF02555907. [DOI] [PubMed] [Google Scholar]
- Qing H., Bonewald L.F. Osteocyte remodeling of the perilacunar and pericanalicular matrix. Int. J. Oral Sci. 2009;1:59–65. doi: 10.4248/ijos.09019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Repp F. https://www.bitbucket.com/refelix
- Schaffler M.B., Cheung W.Y., Majeska R., Kennedy O. Osteocytes: master orchestrators of bone. Calcif. Tissue Int. 2014;94:5–24. doi: 10.1007/s00223-013-9790-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider P., Meier M., Wepf R., Muller R. Towards quantitative 3D imaging of the osteocyte lacuno-canalicular network. Bone. 2010;47:848–858. doi: 10.1016/j.bone.2010.07.026. [DOI] [PubMed] [Google Scholar]
- Schneider P., Meier M., Wepf R., Muller R. Serial FIB/SEM imaging for quantitative 3D assessment of the osteocyte lacuno-canalicular network. Bone. 2011;49:304–311. doi: 10.1016/j.bone.2011.04.005. [DOI] [PubMed] [Google Scholar]
- Sharma D., Ciani C., Marin P.A.R., Levy J.D., Doty S.B., Fritton S.P. Alterations in the osteocyte lacunar-canalicular microenvironment due to estrogen deficiency. Bone. 2012;51:488–497. doi: 10.1016/j.bone.2012.05.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steck R., Knothe-Tate M.L. Summer Bioengineering Conference; Sonesta Beach Resort in Key Biscayne: 2003. Influence of Osteocyte Density on Bone Tissue Permeability: Insights from a Stochastic Network Model. [Google Scholar]
- Sugawara Y., Kamioka H., Honjo T., Tezuka K., Takano-Yamamoto T. Three-dimensional reconstruction of chick calvarial osteocytes and their cell processes using confocal microscopy. Bone. 2005;36:877–883. doi: 10.1016/j.bone.2004.10.008. [DOI] [PubMed] [Google Scholar]
- Tate M.L.K., Adamson J.R., Tami A.E., Bauer T.W. The osteocyte. Int. J. Biochem. Cell Biol. 2004;36:1–8. doi: 10.1016/s1357-2725(03)00241-3. [DOI] [PubMed] [Google Scholar]
- Teti A., Zallone A. Do osteocytes contribute to bone mineral homeostasis? Osteocytic osteolysis revisited. Bone. 2009;44:11–16. doi: 10.1016/j.bone.2008.09.017. [DOI] [PubMed] [Google Scholar]
- Varga P., Hesse B., Langer M., Schrof S., Mannicke N., Suhonen H., Pacureanu A., Pahr D., Peyrin F., Raum K. Synchrotron X-ray phase nano-tomography-based analysis of the lacunar-canalicular network morphology and its relation to the strains experienced by osteocytes in situ as predicted by case-specific finite element analysis. Biomech. Model. Mechanobiol. 2015;14:267–282. doi: 10.1007/s10237-014-0601-9. [DOI] [PubMed] [Google Scholar]
- Verborgt O., Gibson G.J., Schaffler M.B. Loss of osteocyte integrity in association with microdamage and bone remodeling after fatigue in vivo. J. Bone Miner. Res. 2000;15:60–67. doi: 10.1359/jbmr.2000.15.1.60. [DOI] [PubMed] [Google Scholar]
- Verbruggen S.W., Vaughan T.J., McNamara L.M. Strain amplification in bone mechanobiology: a computational investigation of the in vivo mechanics of osteocytes. J. R. Soc. Interface. 2012;9:2735–2744. doi: 10.1098/rsif.2012.0286. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig. S1 Example showing the advantages of the adaptive thresholding algorithm in the segmentation of lacunae and canaliculi: top, raw data image showing part of the Haversian canal at the bottom of the image and three lacunae with high fluorescence intensity. The two plots below compare the outcome of the applied adaptive thresholding algorithm with the result of applying a global threshold with a low value (middle) and a high value (bottom). In these plots of comparison yellow voxels denote image voxels which are attributed to the osteocyte lacuna-canalicular network for both adaptive and global thresholding; cyan denotes voxels where this attribution occurs only for the global threshold, and red only for the adaptive threshold. A high global threshold value (bottom) would result in the loss of large parts of the canalicular network. A low global threshold leads to a significant overestimation of the volume of the lacunae (large cyan seams around the lacunae). Note that the higher intensity of lacunae is considered in the adaptive threshold algorithm with the consequence that even in the comparison with the high global threshold the lacunae still have a cyan seam.
Fig. S2: Box plots of the slopes of the canalicular density as a function of the radius as obtained by linear regression (see Fig. 6, top, for the example of two osteons). For the plots all 49 osteons were analyzed in the four samples separately. In contrast to the corresponding Fig. 7, in the analysis all the regions in the osteons without canalicular network were excluded corresponding to the first bin in Fig. 4.
Fig. S3: The slope of the canalicular density as a function of the radius as obtained by linear regression plotted versus the canalicular density Ca.Dn for all 49 osteons of the study. The slope is stronger negative, i.e. the canalicular density decreases faster when moving from the Haversian canal to the cement line, for osteons with a dense network. Assuming that the network density decreases with the time passed after its formation this indicates that osteons are formed with a pronounced gradient of the network density when moving from their inside to their outside border.