Reconciling the understanding of ‘hydrophobicity’ with physics-based models of proteins

Abstract

The idea that a ‘hydrophobic energy’ drives protein folding, aggregation, and binding by favoring the sequestration of bulky residues from water into the protein interior is widespread. The solvation free energies (∆G_solv) of small nonpolar solutes increase with surface area (A), and the free energies of creating macroscopic cavities in water increase linearly with A. These observations seem to imply that there is a hydrophobic component (∆G_hyd) of ∆G_solv that increases linearly with A, and this assumption is widely used in implicit solvent models. However, some explicit-solvent molecular dynamics studies appear to contradict these ideas. For example, one definition (ΔG_LJ) of ΔG_hyd is that it is the free energy of turning on the Lennard–Jones (LJ) interactions between the solute and solvent. However, ΔG_LJ decreases with A for alanine and glycine peptides. Here we argue that these apparent contradictions can be reconciled by defining ΔG_hyd to be a near hard core insertion energy (ΔG_rep), as in the partitioning proposed by Weeks, Chandler, and Andersen. However, recent results have shown that ΔG_rep is not a simple function of geometric properties of the molecule, such as A and the molecular volume, and that the free energy of turning on the attractive part of the LJ potential cannot be computed from first-order perturbation theory for proteins. The theories that have been developed from these assumptions to predict ΔG_hyd are therefore inadequate for proteins.

1. The empirical understanding of hydrophobicity

Oil separates from water, and the free energy cost (ΔG_cav) of creating a macroscopic cavity in water is often computed from simple geometric properties of the cavity [1–20]. This free energetic penalty generally increases with both the surface area (A) and volume (V) of the cavity. The proportionality constant between ΔG_cav and A defines the surface tension of the water, and the linearity of ΔG_cav in V reflects the pressure-volume work of forming the cavity. Because an energy that increases with cavity size would favor aggregation and collapse of molecules as large as proteins in solution, the idea that a hydrophobic cavity-formation energy (ΔG_hyd) that increases with A drives these processes is widely discussed [6, 8–13, 15, 19, 21–52]. As we discuss in the following sections, this idea is also supported by the observations of the solvation free energies (ΔG_solv) of small nonpolar solutes. In the Kauzmann–Tanford picture such small, organic compounds are used as molecular analogs of the side chains of the equivalent amino acids [6, 7, 15, 22, 30, 35, 39, 43, 45, 46, 53–57]. Since for these compounds ΔG_solv generally increases with A [7, 10, 11, 13–15, 26, 27, 30, 32, 33, 35, 37, 39, 40, 43, 46, 51, 53, 54, 56–81] we are led to the idea that proteins tend to bury bulkier, nonpolar residues removing them from solvent exposure during folding and binding [6, 11, 15, 22, 30–32, 34–36, 39, 40, 43–46, 50, 54, 56, 82–85]. The ΔG_solv of small nonpolar solutes is dominated by an entropic contribution (ΔS_solv) at room temperature. Both TΔS_solv and the enthalpy (ΔH_solv) of hydration tend to both increase linearly with T, whereas ΔG_solv = ΔH_solv − TΔS_solv tends to be relatively independent of T over the range of biological interest. Additionally, the heat capacity (ΔC_p = ∂ΔH_solv/∂T) of non-polar solutes tends to be large [9, 12, 15, 16, 19, 21, 27, 34, 37, 39, 40, 43, 45, 48, 51, 59, 61, 64, 66, 71, 74–76, 78, 86–94]. Similarly, the ΔC_p of protein folding and binding free energies are often large [15, 19, 21, 22, 32, 34, 39, 43, 44, 47, 48, 51, 94, 95], suggesting a thermodynamic parallel between these processes and the solvation of small nonpolar solutes.

In this contribution, we consider the theoretical models used in interpreting these fundamental observations. We do not cover all the uses of such implicit solvent effect models but note their common uses in particular areas. Many excellent recent reviews of hydrophobicity exist.(see for instance [96]) Here, we seek to show where theoretical commonalities exist and fundamental problems remain.

1.1. The solvation free energies of small nonpolar solutes

Protein folding and binding in solution are many-body problems. Several common notions are used to simplify the fundamental complexity of the problem. One assumption often made in trying to understand protein folding and binding is that the contributions of each amino acid to ΔG_solv can be divided into a contribution from the protein backbone, which does not vary among most of the amino acids, and a contribution from its side chain [6, 8, 11, 22, 30–32, 35, 39, 43, 45, 46, 51, 53–57, 85]. If this assumption holds, then the relative solubilities of different amino acids can be determined by measuring the solubilities of small-molecule side-chain analogs. For the nonpolar, or, in other words, the least polar residues, the natural side-chain analogs are small alkanes and aromatics.

1.1.1. Solvation versus transfer free energies of side-chain analogs

Several investigators have therefore attempted to measure or compute the relative solubilities of small alkanes [7, 10, 11, 13, 26, 27, 29, 30, 33, 35, 37, 39, 43, 45, 46, 51, 53, 55–67, 69, 73, 74, 77, 78, 80, 88, 97]. Transfer free energies of alkanes from nonpolar solvents into water typically appear to increase linearly with A [7, 12, 13, 15, 26, 27, 30, 32, 35, 37, 39, 43, 45, 46, 51, 53, 54, 57, 61, 64–74, 79, 81, 88], but the slopes of plots of these transfer free energies versus A depend critically on what environment the alkanes were in prior to being transfered into water [6, 7, 10, 15, 30, 35, 39, 43, 45, 46, 51, 57, 71, 79, 88]. Much of this research has been conducted with an eye to a specific definition of ΔG_hyd, that it is the free energy of transferring an amino acid from the protein ‘interior’ to its ‘surface.’ [6, 7, 15, 21, 23, 30–32, 34, 35, 39, 40, 43, 46, 51, 53, 54, 71, 79] Such an interpretation requires the reference state to be analogous to the protein ‘interior.’ Typically, some liquid hydrocarbon has been taken as the reference state, and several studies have advocated for several different choices of reference state, each yielding slightly different slopes of plots of ΔG_hyd versus A [6, 7, 15, 26, 30, 32, 35, 39, 40, 43, 45, 51, 79].

The approach of using a transfer free energy of peptides and proteins among multicomponent aqueous solutions has been used to complement the studies where transfer was between very different solvents as mentioned above [98–101]. In these studies a component which either stabilizes the solution, such as trimethylamine N-oxide, or destabilizes, such as urea, are used to measure a difference in free energies between solutions which have a direct measurable effect on protein thermodynamics. The change in transfer free energies versus A for each of the amino acids in a variety of proteins show similar trends as the older measurements, until corrected for the solution activities [100]. The effect of solubility changes of the sidechains on folding is nearly indiscernible in the data, however the effect on the back bone becomes strikingly clear. Some issues remain such as a concentration or reference state dependence and even how one models the exposed area changes between the solutions [102, 103]. These effect change the weighting of backbone versus sidechain influences for different applications [104] but the lack of activity corrections in the older literature of compound transfers remains an issue for interpreting the size of the hydrophobic effect on sidechains versus backbones.

This definition of ΔG_hyd, although common, is not ideal for comparison to molecular dynamics simulations, partly because the protein’s ‘interior’ and its ‘surface’ do not have single, accepted definitions [6, 15, 32, 34, 39, 40, 43, 45, 71, 88]. These regions are not well defined because they do not trivially follow directly from the system’s Hamiltonian. For simulations and many-body theories, the free energy of turning on the Lennard–Jones interactions between the solute and solvent (ΔG_LJ, defined in section 2.1) and its near-hard-core component (ΔG_rep, defined in section 2.3) may be more useful definitions of ΔG_hyd. If we define ΔG_hyd to be ΔG_LJ, then the natural reference state is vapor (or near vacuum), and several experimental and computational studies have indeed used this reference state, even though the slopes (γ_LJ) of plots of ΔG_LJ versus A for alkanes (~1 cal⁻¹ mol Å⁻²) are orders of magnitude smaller than the surface tension of water (~100 cal⁻¹ mol Å⁻²). This observation can be partly ascribed to the creation of attractive dispersive interactions between the solute and solvent, as discussed in section 2.3 [10, 15, 40, 51, 80, 105–107]. Because in experiment one cannot turn off the dispersive interactions between the solute and solvent, we have no experimentally accessible reference state from which we can obtain ΔG_rep. Interestingly, however, because the depth of the Lennard–Jones potentials between a solute and a hydrocarbon liquid is similar to that between the solute and water and because both states are densely packed liquids, the attractive dispersive interactions that the solute loses when being transferred from a liquid hydrocarbon to water may partially cancel against those it gains upon transfer to water. This cancellation may explain why the slopes of plots of the transfer free energies of alkanes from liquid hydrocarbons to water versus A tend to be larger than γ_LJ [6, 30].

1.1.2. The anomalous entropy of solvation of nonpolar solutes

The original understanding of hydrophobic solvation included the observation that the ΔG_solv of hydrophobic solutes was dominated by a large negative TΔS_solv. This finding was originally interpreted to imply that the water molecules reorganized themselves to make room for the hydrophobic solute in an ice-like or clathrate-like cage, maximizing their enthalpy at the expense of entropy. Many studies have since provided computational and experimental evidence that the water around nonpolar solutes is not as rigid as originally suggested, but the idea that the water undergoes some sort of entropically unfavorable rearrangement around nonpolar solutes is widespread [7, 9, 12, 13, 15–17, 19, 21, 27, 34, 39, 40, 45, 48, 51, 58, 59, 61, 66, 69, 71, 74–76, 80, 81, 86–92, 94, 108–114].

However, some researchers [15, 39, 43, 48, 74, 88, 91–94] pointed out that TΔS_solv is essentially linear for hydrophobic solutes and that ΔG_solv is nearly independent of temperature. Therefore, although ΔG_solv is dominated by a negative TΔS_solv at room temperature, at some higher temperature TΔS_solv is 0 and ΔG_solv is dominated by the enthalpic (ΔH_solv) contribution. These researchers concluded that hydrophobic solvation is defined by two characteristic features: first that the heat capacity (ΔC_p) of solvation is large and second that ΔG_solv is nearly independent of T and the sum of two nearly compensating terms, ΔH_solv and −TΔS_solv. As has been pointed out, these two conditions in this case are equivalent [48].

An alternative explanation for the large ΔS_solv of the solvation of nonpolar solutes has been advanced by a number of researchers [8, 9, 12, 15, 19, 40, 71, 74, 80, 81, 87, 89, 91, 111]. These works point out that the energy of inserting a hard cavity into solution can be related directly to the probability of finding an appropriately sized cavity in pure water. Because the probability distribution of cavities in water is roughly Gaussian for small cavities, the energy of inserting a cavity into solution should increase with the size of the cavity. This free energy should also be entropic and arises principally because of the small size of the water molecules, as creating a larger cavity requires the displacement of more water molecules.

These two ideas of the origin of ΔS_solv should be understood as complementary rather than contradictory [9, 12, 19, 40, 41, 51, 76, 87, 89, 111, 115]. Placing a solute into a solvent, such as liquid argon, that interacts with itself only through excluded volume interactions will require an entropy cost to be paid to displace the atoms. This contribution to ΔS_solv does not require the solvent to form strong hydrogen bonds and is analogous to the entropic term discussed by Hummer et al [12, 41, 115]. However, water does form strong hydrogen-bonding networks, and this implicit symmetry breaking will inevitably lead to a loss of solvent entropy, partly compensated for by a gain in solvent enthalpy, upon the solvation of nonpolar solutes, leading to an entropic change analogous to that discussed by Frank and Evans [58]. Determining which of these components of ΔS_solv should be larger for realistic molecules theoretically would be difficult because for cavities larger than the smallest alkanes neither the introduction of an excluded volume or hard core nor the introduction of hydrogen-bonding interactions between the water molecules can be treated as a small perturbation of the system.

1.2. The empirical understanding of the importance of hydrophobicity in protein folding and binding and hydrophobicity scales

Many studying the processes of protein folding and binding have found several apparent parallels between them and the the solvation of nonpolar solutes. Because ΔG_solv increases with solute size for small nonpolar solutes [4, 7, 10, 11, 13–15, 19, 26, 30, 32, 35, 37, 39, 42, 43, 51, 56, 57, 59, 68, 70–72, 74, 77, 79, 80], residues with large nonpolar side chains should be preferentially buried in the protein interior. This expectation has indeed been validated in that amino acids with bulkier side chains do appear to preferentially reside in the protein interior [6, 15, 22, 30–32, 34–36, 39, 40, 43, 45, 46, 56, 82–85]. In addition, many proteins can be denatured either by heating or cooling [11, 16, 19, 34, 40, 42, 45, 116, 117]. That proteins denature upon heating is not surprising, as the chain entropy of the denatured protein is higher than that of the folded state. That proteins denature upon cooling is more interesting, as decreasing the temperature would be expected to decrease entropy, yet by denaturing the protein’s chain, entropy increases. This entropy increase must be more than compensated for by some other decrease in entropy. If the solvating water has to become more ordered upon denaturation at low temperatures to accommodate the exposed nonpolar residues, as would be expected when water becomes more ordered around hydrophobic solutes, then this decrease in entropy could compensate for the increase in entropy from the denaturing of the protein. Finally, the binding free energies (ΔG_bind) of many protein-protein complexes are primarily entropic, and the interfaces between the binding partners can contain a number of nonpolar residues.

The idea that the mechanisms driving protein folding and binding are similar to those that govern the solvation of small nonpolar solutes has inspired efforts to rank amino acids quantitatively by their hydrophobicity, either by ranking them by experimental or computational transfer free energies of side-chain analogs from some reference environment into water [7, 30–32, 35, 40, 46, 53–56] or by statistical analyses of the probability that a given residue will be found in the protein interior. Although these different hydrophobicity scales differ on the ranking of a handful of amino acids, they essentially agree that proteins preferentially bury those residues that rank as more hydrophobic during folding [30–32, 34, 35, 39, 40, 45, 46, 54, 56, 82–85] and the interfaces of proteins that form protein-protein complexes tend to be enriched by these more hydrophobic residues [15, 42]. The lack of a single definition for this concept limits its quantitative utility.

From these observations an empirical picture of the importance of hydrophobicity in protein folding and binding has, none the less, been created [21–28, 30–32, 34–36, 38–52, 82–84, 117]: proteins fold in part, because removing the hydrophobic residues from solution into the protein interior is favorable. Proteins bind, in part, because burying hydrophobic residues at the protein interface is favorable. Both of these processes contain large entropic components because of the large water reorganization required to solvate the nonpolar residues when they are on the protein surface.

2. Free energy definitions

Before we can test this empirical understanding of the importance of hydrophobicity in protein folding and binding with explicit-solvent models and explore the consequences of these findings for implicit-solvent models, we have to define the folding free energy (ΔG_fold), the binding free energy (ΔG_bind), and the hydrophobic component (ΔG_hyd) of the solvation free energy in these models. As discussed below, different definitions of ΔG_hyd lead to different conclusions about its significance in protein folding and binding. Different partitions of free energy changes into terms that are not state functions, while often convenient, can lead to process-dependent conclusions.

2.1. Decomposing the solvation energy in explicit- and implicit-solvent models

In most classical nonpolarizable force fields, the interaction energy between the solute and solvent is modeled by

$$U={\displaystyle \sum _{ij}{U}^{ij}},$$ (1)

where

$$U^{ij}=(U_{\text{LJ}}^{ij}+U_{\text{Coul}}^{ij}),$$ (2)

$$U_{\text{LJ}}^{ij}={\epsilon }_{ij}\left[{(r_{\min }^{ij}/r_{ij})}^{12}-2{(r_{\min }^{ij}/r_{ij})}^6\right],$$ (3)

$$U_{\text{Coul}}^{ij}=q_i{q}_j/4\pi {\epsilon }_0{r}_{ij},$$ (4)

$U_{\text{LJ}}^{ij}$ and $U_{\text{Coul}}^{ij}$ are the Lennard–Jones and Coulombic interaction energies between atoms i and j, ε_ij is the depth of the Lennard–Jones potential between atoms i and j, $r_{\min }^{ij}$ is the distance to this minimum, r_ij is the distance between atoms i and j, q_i and q_j are the charges on atoms i and j, ε₀ is the vacuum permittivity, and these summations are taken over all atom pairs that contain one solute and one solvent atom.

In such a model ΔG_solv can be defined as the free energy required to go from a state where the solute and solvent do not interact to one where their interaction energy is U^ij. Additionally, ΔG_solv can be naturally broken into two components, a nonelectrostatic (ΔG_LJ) component that is the free energy required to go from a system where the solute and solvent do not interact to one where their interaction energy is $U_{\text{LJ}}^{ij}$ and an electrostatic (ΔG_el) component that is the free energy required to go from a system where the solute-solvent interaction energy is $U_{\text{LJ}}^{ij}$ to one where it is U^ij. From this definition, ΔG_solv = ΔG_LJ + ΔG_el [6, 44, 79, 107]. This decomposition, it should be noted, depends on defining a process whereby the LJ cavity is created before the charge is introduced. With such a process the decomposition naturally follows terms in the Hamiltonian.

Several implicit-solvent models, such as the Poisson-Boltzmann equation [44, 57, 79, 107, 118–120], the generalized Born model [79], integral equation theories [79], and structured continuum models, have been developed to compute ΔG_el.

2.2. The electrostatic component of the solvation free energy, but not the nonpolar component, is amenable to perturbation theory

The success of implicit-solvent models at predicting ΔG_el can be partly attributed to the feasibility of computing ΔG_el with low-level perturbation theory. If a λ-dependent energy $(U_{\text{el}}^{ij}(\lambda )=U_{\text{LJ}}^{ij}+\lambda U_{\text{el}}^{ij})$ is constructed to link a system where the solute-solvent interaction energy is $U_{\text{LJ}}^{ij}$ to one where it is U^ij, then ΔG_el can be computed from thermodynamic integration (TI),

$$\mathrm{\Delta }{G}_{\text{el}}={\displaystyle {\int }_0^1{\langle \partial U_{\text{el}}(\lambda )/\partial \lambda \rangle }_{\lambda }\mathrm{d}\lambda },$$ (5)

where 〈…〉_λ indicates an averaging over a system where the solvent-solute interaction energy is $U_{\text{el}}^{ij}(\lambda )$ and $U_{\text{el}}(\lambda )={\sum }_{ij}{U}_{\text{el}}^{ij}(\lambda )$ where this summation is taken over all solvent-solute atom pairs. In biomolecular systems 〈∂U_el(λ)/∂λ〉_λ tends to be linear in λ, and ${\langle \partial U_{\text{el}}^{ij}(0)/\partial \lambda \rangle }_0\approx 0$ (figure 1). Following (5) ΔG_el is the area under this curve, so

$$\mathrm{\Delta }{G}_{\text{el}}\approx 1/2{\langle \partial U_{\text{el}}(1)/\partial \lambda \rangle }_1.$$ (6)

Figure 1.

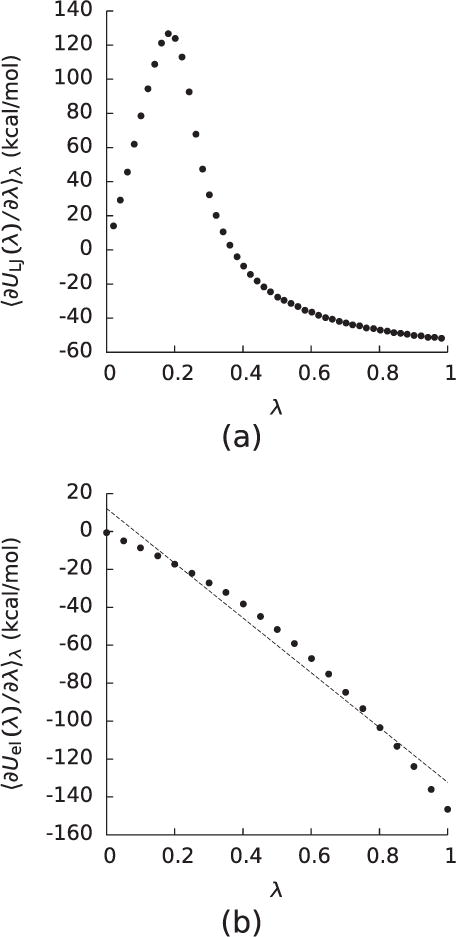
(a)The integrand (〈∂U_LJ(λ)/∂λ〉_λ) of the integral used to compute the free energy (ΔG_LJ) of turning on the Lennard–Jones interactions between the solute and solvent for a decaalanine peptide as a function of λ. (b) The integrand (〈∂U_el(λ)/∂λ〉_λ) of the integral used to compute the free energy (ΔG_el) of turning on the electrostatic interactions between the solute and solvent once the Lennard–Jones interactions had been turned on for the decaalanine in (a).

Therefore, ΔG_el can be accurately estimated solely from information obtained from an ensemble defined by a system where the solute-solvent interaction energy is U^ij.

In contrast, computing ΔG_LJ is more difficult. In principle a λ-dependent potential $(U_{\text{LJ}}^{ij}(\lambda ))$ can be defined that links a system where the solute and solvent do not interact to one where the solute-solvent interaction energy is $U_{\text{LJ}}^{ij}$, and ΔG_LJ can then be computed from TI,

$$\mathrm{\Delta }{G}_{\text{LJ}}={\displaystyle {\int }_0^1{\langle \partial U_{\text{LJ}}(\lambda )/\partial \lambda \rangle }_{\lambda }\mathrm{d}\lambda },$$ (7)

where 〈…〉_λ indicates an averaging over a system where the solute-solvent interaction energy is $U_{\text{LJ}}^{ij}(\lambda )$ and $U_{\text{LJ}}(\lambda )={\sum }_{ij}{U}_{\text{LJ}}^{ij}(\lambda )$, where this summation is taken over all solute-solvent atom pairs. However, the obvious choice of a λ-dependent potential $(U_{\text{LJ}}^{ij}(\lambda )=\lambda U_{\text{LJ}}^{ij})$ that varies linearly with λ leads to a 〈∂U_LJ(λ)/∂λ〉_λ that diverges at λ = 0. Although this pole is in principle integrable, the computational expense of doing so has led to the development of a number of ‘softcore’ $U_{\text{LJ}}^{ij}(\lambda )$ for which 〈∂U_LJ(λ)/∂λ〉_λ does not diverge at λ = 0. However, although softcore $U_{\text{LJ}}^{ij}$ do not generate poles in 〈∂U_LJ(λ)/∂λ〉_λ, their 〈∂U_LJ(λ)/∂λ〉_λ still display large peaks associated with the drying of the cavity interior due to excluded volume (figure 1). This observation implies that ΔG_LJ cannot be computed from simple perturbative expansions around λ = 0 and λ = 1.

2.3. Empirical models of the nonpolar component of the solvation free energy

Partly because ΔG_LJ is not amenable to perturbation theory, many implicit-solvent models have instead assumed that ΔG_LJ is linear in A and possibly V [11, 13, 15, 18, 19, 44, 57, 79, 105, 107, 118–121]. For instance

$$\mathrm{\Delta }{G}_{\text{LJ}}={\gamma }_{\text{LJ}}A+{\rho }_{\text{LJ}}V+b$$ (8)

in analogy with the free energy of creating a macroscopic cavity in solution, which increases linearly with A and V. Many other forms of ΔG_LJ exist in the literature.

Alternatively, some researchers have argued that the process of going from a system where the solute and solvent do not interact to one where their interaction energy is U_LJ is not directly analogous with the creation of a macroscopic cavity because of the attractive 1/r⁶ tail in $U_{\text{LJ}}^{ij}$ used to represent the dispersive interactions between the solute and solvent [10, 13, 15, 17, 19, 71, 74, 80, 105–107, 122]. Instead, they propose to divide $U_{\text{LJ}}^{ij}$ into purely repulsive $(U_{\text{rep}}^{ij})$ and attractive $(U_{\text{att}}^{ij})$ components. In this study, we will further discuss the decomposition proposed first by Weeks, Chandler, and Andersen (WCA) [14, 26, 27, 80, 105, 107, 123–125],

$$U_{\text{rep}}^{ij}={\epsilon }_{ij}\{\begin{array}{l}{\left(\frac{r_{ij}^{\min }}{r_{ij}}\right)}^{12}-2{\left(\frac{r_{ij}^{\min }}{r_{ij}}\right)}^6+\text{lif}{r}_{ij}<r_{ij}^{\min }\\ 0\text{otherwise}\end{array}$$ (9)

and

$$U_{\text{att}}^{ij}=U_{\text{LJ}}^{ij}-U_{\text{rep}}^{ij}.$$ (10)

Following the WCA decomposition, we can break ΔG_LJ into two components: that (ΔG_rep) of going from a system where the solute and solvent do not interact to one where their interaction energy is $U_{\text{rep}}^{ij}$ and that (ΔG_att) of going from a system where the solute-solvent interaction energy is $U_{\text{rep}}^{ij}$ rep to one where it is $U_{\text{LJ}}^{ij}$. Following this definition, ΔG_LJ = ΔG_rep + ΔG_att. Note that in this definition the repulsive cavity is formed before the attractive interactions are added.

Several researchers have attempted to go further and quantitatively predict ΔG_rep and ΔG_att with simple models. Typically, these theories assume that ΔG_rep should be linear in A and V, i.e.

$$\mathrm{\Delta }{G}_{\text{rep}}={\gamma }_{\text{rep}}A+{\rho }_{\text{rep}}V+b,$$ (11)

where γ_rep, ρ_rep, and b are constants to be fit to various small molecules, in analogy with the energy required to create macroscopic cavities in water, and that ΔG_att can be computed from a single-step perturbation expression [17, 71, 74, 105, 107, 125],

$$\mathrm{\Delta }{G}_{\text{att}}={\displaystyle \sum _i\int U_{\text{att}}^{ij}}(|\mathbf{r}-{\mathbf{r}}_i|)\widehat{\rho }(\mathbf{r})\mathrm{d}\mathbf{r}$$ (12)

around an approximate water distribution $(\widehat{\rho }(\mathbf{r}))$, where $U_{\text{att}}^{ij}(|\mathbf{r}-{\mathbf{r}}_i|)$ is the attractive component of the Lennard–Jones interaction energy between solute atom i and a water molecule placed at r.

Alternatively, some researchers, following Tolman, have proposed that either ΔG_LJ or ΔG_rep should depend not just on A but on the curvature of the molecular surface [3, 6, 7, 13, 14, 18–20, 57, 73, 105, 118, 126]:

$$\mathrm{\Delta }{G}_{\text{LJ}}={\gamma }_{\text{mac}}(1-2\delta /R+\dots )A,$$ (13)

or

$$\mathrm{\Delta }{G}_{\text{rep}}={\gamma }_{\text{mac}}(1-2\delta /R+\dots )A,$$ (14)

where γ_mac is the surface tension of making a macroscopic cavity in solution, where the interface can be considered planar on a molecular scale, R is the radius of curvature of the surface, and δ is here defined as the Tolman length. The quanti ty in parentheses is an expansion in powers of 1/R, which in principle could be extended but in practice is typically truncated at this order [19, 79, 126].

For small cavities scaled particle theory predicts that ΔG_rep should increase linearly with V, and so some have supposed that for small molecules [11, 14, 15, 17, 18, 105, 107],

$$\mathrm{\Delta }{G}_{\text{rep}}={\rho }_{\text{rep}}V,$$ (15)

because creating a larger cavity requires the exclusion of more waters and the number of excluded waters should scale roughly as V. Additionally, they claim that for larger cavities ΔG_rep should increase linearly with A,

$$\mathrm{\Delta }{G}_{\text{rep}}={\gamma }_{\text{rep}}A,$$ (16)

because that is the behavior observed for macroscopic cavities. In between, in a proposed transition region, they then assume that ΔG_rep should be a function of both A and V. Some of them have further assumed that ΔG_rep should follow (11) in this crossover region.

2.4. Defining the protein binding and folding free energies

In classical force fields we can approximate the free energy (ΔG) required to create a protein in a particular ‘state,’ such as the unfolded state, as

$$\mathrm{\Delta }G\approx \int \rho (\mathbf{r})\left[\mathrm{\Delta }{G}_{\text{solv}}(\mathbf{r})+1/2{\displaystyle \sum _{ij}{U}^{ij}}\right]\mathrm{d}\mathbf{r},$$ (17)

where ΔG_solv(r) is the is the solvation energy of a single configuration taken from that state, the integral is taken over all configurations (r) in the state, ρ(r) is the probability of configuration r, and these summations are taken over all atom pairs in the protein in configuration r. Equation (17) neglects the formation of the internal bonded interactions, but these interactions tend not to change much upon folding and binding.

We can then write an expression for the ΔΔG_fold of a protein:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{fold}}={\langle \mathrm{\Delta }{G}_{\mathrm{f}}\rangle }_{\mathrm{f}}-{\langle \mathrm{\Delta }{G}_{\mathrm{u}}\rangle }_{\mathrm{u}},$$ (18)

where

$${\langle \mathrm{\Delta }{G}_{\mathrm{f}}\rangle }_{\mathrm{f}}={\langle \mathrm{\Delta }{G}_{\text{solv}}(\mathbf{r})\rangle }_{\mathrm{f}}+{\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{f}}+{\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{f}},$$ (19)

$${\langle \mathrm{\Delta }{G}_{\mathrm{u}}\rangle }_{\mathrm{u}}={\langle \mathrm{\Delta }{G}_{\text{solv}}(\mathbf{r})\rangle }_{\mathrm{u}}+{\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{u}}+{\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{u}},$$ (20)

$$U_{\text{Coul}}^{\text{vac}}=1/2{\displaystyle \sum _{ij}{U}_{\text{Coul}}^{ij},}$$ (21)

$$U_{\text{LJ}}^{\text{vac}}=1/2{\displaystyle \sum _{ij}{U}_{\text{LJ}}^{ij},}$$ (22)

〈…〉_f and 〈…〉_u represent averaging over configurations taken from the folded and unfolded ensembles, and the summations are taken over all atom pairs in the protein in each configuration.

Similarly, for an equilibrium binding event

$$a+b\rightleftharpoons c$$

we can write

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{bind}}={\langle \mathrm{\Delta }{G}_{\mathrm{c}}\rangle }_{\mathrm{c}}-({\langle \mathrm{\Delta }{G}_{\mathrm{a}}\rangle }_{\mathrm{a}}+{\langle \mathrm{\Delta }{G}_{\mathrm{b}}\rangle }_{\mathrm{b}}),$$ (23)

where

$${\langle \mathrm{\Delta }{G}_{\mathrm{c}}\rangle }_{\mathrm{c}}={\langle \mathrm{\Delta }{G}_{\text{solv}}(\mathbf{r})\rangle }_{\mathrm{c}}+{\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{c}}+{\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{c}},$$ (24)

$${\langle \mathrm{\Delta }{G}_{\mathrm{a}}\rangle }_{\mathrm{a}}={\langle \mathrm{\Delta }{G}_{\text{solv}}(\mathbf{r})\rangle }_{\mathrm{a}}+{\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{a}}+{\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{a}},$$ (25)

$${\langle \mathrm{\Delta }{G}_{\mathrm{b}}\rangle }_{\mathrm{b}}={\langle \mathrm{\Delta }{G}_{\text{solv}}(\mathbf{r})\rangle }_{\mathrm{b}}+{\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{b}}+{\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{b}},$$ (26)

$$U_{\text{Coul}}^{\text{vac}}=1/2{\displaystyle \sum _{ij}{U}_{\text{Coul}}^{ij},}$$ (27)

$$U_{\text{LJ}}^{\text{vac}}=1/2{\displaystyle \sum _{ij}{U}_{\text{LJ}}^{ij},}$$ (28)

〈…〉_c, 〈…〉_a, and 〈…〉_b represent averaging over configurations, for instance, taken from molecular dynamics simulations of the complex and its two separated components, and the summations are taken over all atom pairs in the protein in each configuration.

Using the breakdowns of ΔG_solv defined above,

$$\mathrm{\Delta }{G}_{\text{solv}}=\mathrm{\Delta }{G}_{\text{LJ}}+\mathrm{\Delta }{G}_{\text{el}},$$ (29)

or

$$\mathrm{\Delta }{G}_{\text{solv}}=\mathrm{\Delta }{G}_{\text{rep}}+\mathrm{\Delta }{G}_{\text{att}}+\mathrm{\Delta }{G}_{\text{el}},$$ (30)

we can rewrite (18) as

$$\begin{array}{l}\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{fold}}=({\langle \mathrm{\Delta }{G}_{\text{LJ}}(\mathbf{r})\rangle }_{\mathrm{f}}-{\langle \mathrm{\Delta }{G}_{\text{LJ}}(\mathbf{r})\rangle }_{\mathrm{u}})\\ +[({\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{f}}+{\langle \mathrm{\Delta }{G}_{\text{el}}(\mathbf{r})\rangle }_{\mathrm{f}})\\ -[({\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{u}}+{\langle \mathrm{\Delta }{G}_{\text{el}}(\mathbf{r})\rangle }_{\mathrm{u}})]\\ +({\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{f}}-{\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{u}})\end{array}$$ (31)

or

$$\begin{array}{l}\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{fold}}=({\langle \mathrm{\Delta }{G}_{\text{rep}}(\mathbf{r})\rangle }_{\mathrm{f}}-{\langle \mathrm{\Delta }{G}_{\text{rep}}(\mathbf{r})\rangle }_{\mathrm{u}})\\ +[({\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{f}}+{\langle \mathrm{\Delta }{G}_{\text{el}}(\mathbf{r})\rangle }_{\mathrm{f}})\\ -[({\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{u}}+{\langle \mathrm{\Delta }{G}_{\text{el}}(\mathbf{r})\rangle }_{\mathrm{u}})]\\ +[({\langle \mathrm{\Delta }{G}_{\text{att}}(\mathbf{r})\rangle }_{\mathrm{f}}+{\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{f}})\\ -({\langle \mathrm{\Delta }{G}_{\text{att}}(\mathbf{r})\rangle }_{\mathrm{u}}+{\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{u}})]\end{array}$$ (32)

Similarly, we can rewrite (23) as

$$\begin{array}{l}\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{bind}}=[{\langle \mathrm{\Delta }{G}_{\text{LJ}}(\mathbf{r})\rangle }_{\mathrm{c}}-({\langle \mathrm{\Delta }{G}_{\text{LJ}}(\mathbf{r})\rangle }_{\mathrm{a}}+{\langle \mathrm{\Delta }{G}_{\text{LJ}}(\mathbf{r})\rangle }_{\mathrm{b}})]\\ +\{[{\langle \mathrm{\Delta }{G}_{\text{el}}(\mathbf{r})\rangle }_{\mathrm{c}}-({\langle \mathrm{\Delta }{G}_{\text{el}}(\mathbf{r})\rangle }_{\mathrm{a}}+{\langle \mathrm{\Delta }{G}_{\text{el}}(\mathbf{r})\rangle }_{\mathrm{b}})]\\ +[{\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{c}}-({\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{a}}+{\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{b}})]\}\\ +[{\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{c}}-({\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{a}}+{\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{b}})]\end{array}$$ (33)

or

$$\begin{array}{l}\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{bind}}=[{\langle \mathrm{\Delta }{G}_{\text{rep}}(\mathbf{r})\rangle }_{\mathrm{c}}-({\langle \mathrm{\Delta }{G}_{\text{rep}}(\mathbf{r})\rangle }_{\mathrm{a}}+{\langle \mathrm{\Delta }{G}_{\text{rep}}(\mathbf{r})\rangle }_{\mathrm{b}})]\\ +\{[{\langle \mathrm{\Delta }{G}_{\text{el}}(\mathbf{r})\rangle }_{\mathrm{c}}-({\langle \mathrm{\Delta }{G}_{\text{el}}(\mathbf{r})\rangle }_{\mathrm{a}}+{\langle \mathrm{\Delta }{G}_{\text{el}}(\mathbf{r})\rangle }_{\mathrm{b}})]\\ +[{\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{c}}-({\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{a}}+{\langle U_{\text{Coul}}^{\text{vac}}\rangle }_{\mathrm{b}})]\}\\ +\{[{\langle \mathrm{\Delta }{G}_{\text{att}}(\mathbf{r})\rangle }_{\mathrm{c}}-({\langle \mathrm{\Delta }{G}_{\text{att}}(\mathbf{r})\rangle }_{\mathrm{a}}+{\langle \mathrm{\Delta }{G}_{\text{att}}(\mathbf{r})\rangle }_{\mathrm{b}})]\\ +[{\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{c}}-({\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{a}}+{\langle U_{\text{LJ}}^{\text{vac}}\rangle }_{\mathrm{b}})]\}\end{array}$$ (34)

3. The value of a near-hard-core definition of the hydrophobic solvation free energy

The most convenient definition of ΔG_hyd in implicit-solvent models would be that ΔG_hyd was the free energy, ΔG_LJ, required to transfer a solute that interacts with the solvent through a Lennard–Jones interaction from vacuum into solvent. If ΔG_LJ could be computed from a simple model, such as (8), then ΔG_solv could be computed by combining the resulting estimates of ΔG_LJ with estimates of ΔG_el from implicit-solvent models. From these ΔG_solv estimates of more interesting free energies, such as ΔG_fold and ΔG_bind, could then be computed as outlined above.

However, many studies have measured or computed with simulation the ΔG_solv for alkanes [7, 10, 11, 15, 32, 39, 45, 51, 57, 74, 77, 78, 80], and although ΔG_solv tends to increase with A, the resulting estimates of γ_LJ are 1–2 orders of magnitude smaller than the surface tension of water (~100 cal⁻¹ mol Å⁻²) [7, 10, 11, 15, 19, 79, 105, 114]. Even more disturbing, more recent studies have shown that ΔG_LJ decreases with the number of monomers for glycine peptides and extended alanine peptides, and they have produced estimates of γ_LJ for decaalanine (−3 cal⁻¹ mol Å⁻²) and glycine peptides (−74 cal⁻¹ mol Å⁻²) that are less less than 0 [127, 128]. These observations seem to imply that the cavity, i.e. hydrophobic, interactions favor extended rather than collapsed structures in solution.

As argued by WCA and others, these observations can be taken to indicate that the identification of ΔG_hyd as ΔG_LJ is not consistent with the empirical understanding of hydrophobicity outlined above [10, 13, 15, 17, 19, 26, 71, 74, 78, 80, 105–107]. Instead, WCA proposed to divide ΔG_LJ into near-hard-core, ΔG_rep, and attractive, ΔG_att, components, as outlined above. For small organic molecules ΔG_rep increases more rapidly with A than ΔG_LJ, and the slopes (γ_rep) of the least-squares lines of plots of ∂ΔG_rep/∂x_i versus ∂A/∂x_i are positive for decaalanine and glycine peptides [127, 128].

3.1. A near-hard-core definition of the hydrophobic solvation free energy implies that it dominates binding and folding free energies

If we identify ΔG_hyd to be ΔG_rep [26] we recover the idea that ΔG_fold and ΔG_bind are driven by changes in ΔG_hyd. In contrast, identifying GΔ_hyd to be ΔG_LJ leads to the conclusion that ΔG_fold and ΔG_bind are dominated by the formation of direct attractive dispersive interactions in the solute. The reasoning behind this conclusion follows:

First, the net electrostatic contributions to ΔG_fold and ΔG_bind should be small, as can be seen in (31)–(34). The second lines of these equations should be approximately zero because increases in the electrostatic components of the solvation free energies from the formation of additional favorable electrostatic interactions with the solvent should be balanced by corresponding decreases in the solute-solute electrostatic energies because of the loss of corresponding favorable solute-solute electrostatic interactions. Several studies have pointed out that such desolvation and vacuum energies should be of comparable magnitude and opposite sign [6, 22, 129–131].

Now, consider (32) and (34). The first lines of these two equations should be approximately 0 because although ΔG_rep tends to increase with A, ΔG_LJ tends to change relatively little with A because ΔG_att tends to decrease with A and ΔG_LJ = ΔG_rep + ΔG_att. We can therefore conclude that the largest contributions to ΔG_bind and ΔG_att come from the final lines of these two equations, which represent the formation of direct favorable dispersive interactions between the solute atoms. We therefore see that if we define ΔG_hyd to be ΔG_LJ that ΔG_hyd would not dominate ΔG_bind and ΔG_fold, in apparent contradiction to the classic understanding of hydrophobicity.

Now consider (34) and (32). The last lines of these two equations will be approximately 0 because although structures with larger A make more favorable dispersive interactions with the solvent, leading to more negative ΔG_att, this increase in the favorability of ΔG_att is partly counterbalanced by the loss of favorable solute-solute dispersive interactions. We therefore conclude that if we define ΔG_hyd to be ΔG_rep then ΔG_bind and ΔG_fold will be dominated by changes in ΔG_hyd, as expected from the classic understanding of hydrophobicity.

In conclusion, we see that whether ΔG_hyd indeed dominates ΔG_bind and ΔG_fold depends on the way that we partition ΔG_bind and ΔG_fold into different contributions.

3.2. Explanations of anomalously large entropies of folding and binding

If ΔG_hyd is defined to be ΔG_rep, then ΔΔG_bind and ΔΔG_fold can be estimated from (34) and (32). Note that the only terms in these equations that should be primarily entropic are the ΔG_rep terms. Also, note that all of the terms that are primarily enthalpic (ΔG_el, ΔG_att, $U_{\text{att}}^{\text{vac}}$, and $U_{\text{el}}^{\text{vac}}$) in these equations can be combined into terms that are approximately 0, whereas the terms that are primarily entropic (ΔG_rep) are unpaired with any counterbalancing contribution. This observation may explain why ΔΔG_bind and ΔΔG_fold often contain large entropic terms, in agreement with the classical understanding of hydrophobicity.

4. Simple theories fail to provide quantitative predictions of the hydrophobic solvation free energy

Although ΔG_LJ would be the most consistent definition of ΔG_hyd following experiments on small molecule side chain analogs and convenient in implicit-solvent models, the traditional approach to approximating ΔG_LJ, to assume that it is linear in A and V, is not valid [132]. Thus, this definition of ΔG_hyd leads to conclusions that contradict the classical idea that ΔG_bind and ΔG_fold are dominated by changes in ΔG_hyd. Defining ΔG_hyd to be ΔG_rep and computing ΔG_LJ from ΔG_LJ = ΔG_rep + ΔG_att is therefore an attractive strategy. Researchers that have pursued this strategy have assumed that ΔG_rep follows (11) and that ΔG_att can be computed from (12). Recent studies have shown that neither of these assumptions is valid [132, 133]. New theories will be needed to compute G_rep and ΔG_att if quantitative estimates of ΔG_LJ, and therefore ΔG_solv, are to be obtained with implicit-solvent models.

4.1. The near-hard-core component of the nonpolar solvation free energy is not a simple function of simple geometric parameters

Recent studies have shown that ΔG_rep is not a simple linear function of A, so some other theory is needed to compute this quantity. Two alternative simple theories have been proposed that could perhaps address this problem. First, some have proposed that the surface tension, γ_rep, of creating a cavity in water must be corrected for the curvature of the interface between the water and the cavity [3, 6, 7, 13, 14, 18–20, 73, 79, 105, 126]. This idea implies that ΔG_rep should be computed from (14). Second, others have proposed that for sufficiently small cavities ΔG_rep should be linear in V rather than A because ΔG_rep should increase with the number of waters excluded from the cavity for small cavities and that the number of waters excluded by forming the cavity increases roughly linearly in V [9, 12, 15, 17–19, 41, 80, 105, 107, 134]. In such a situation ΔG_rep should be linear in A for large cavities and in some ‘crossover’ regime ΔG_rep should be a function of both A and V. Neither of these ideas is consistent with the results of recent simulation studies [132, 133].

In retrospect, the disagreement between these ideas and simulation results should perhaps not be surprising. As discussed above, 〈∂U_rep(λ)/∂λ〉_λ and 〈∂U_LJ(λ)/∂λ〉_λ typically and have large peaks associated with the drying of the cavity as water is excluded. At such a peak, we would expect perturbative expansions of 〈∂U_rep(λ)/∂λ〉_λ and 〈∂U_LJ(λ)/∂λ〉_λ to require many orders of perturbation theory, and the idea that these complexities will conveniently cancel out to yield a simple dependence on simple geometric quantities, such as A and V, appears to be unrealistic.

4.1.1. Tolman’s equation does not provide better estimates of the near-hard-core component of the nonpolar solvation free energy

The idea of using a curvature correction like that in (14) to predict ΔG_rep was originally advanced to address a particular problem [6, 7, 13, 19]. Some noticed that although both the transfer free energy (ΔG_trans) of a small alkane from a liquid hydrocarbon environment to water and the free energy (ΔG_mac) of creating a macroscopic interface between a liquid hydrocarbon and water increase linearly with A, the slopes (γ_trans) of plots of ΔG_trans versus A were significantly less positive than those (γ_mac) of ΔG_mac versus A. They concluded that these observations imply that γ_rep should be greater for protein molecules than for alkanes because the average radii of curvature of proteins are larger than those of alkanes, and this conclusion would not be affected by noting that the proteins contain regions of negative curvature because such regions would also be associated with a larger γ_rep in this model [6]. However, more recent studies [132, 133, 135] found that γ_rep appears to decrease with A. Reconciling these findings would be difficult. Furthermore, defining the ‘curvature’ for a single molecule is difficult, as it is strongly dependent on how the surface is defined, and no rigorous statistical mechanical theory has been advanced that links ΔG_rep to the detailed curvature of the surface. Indeed, the probability that the statistical mechanical complications around the peak in 〈∂U_rep(λ)/∂λ〉 somehow cancel out to yield a simple dependence on the curvature seems unlikely.

4.1.2. The putative nonpolar solvation free energy crossover from a dependence on volume to a dependence on area

As discussed above, some have proposed that ΔG_rep should be linear in V for small cavities because ΔG_rep should increase with the number of waters expelled to create the cavity, which should increase with V and that for large cavities ΔG_rep should be linear in A, as has been observed for macroscopic surfaces and cavities. Therefore, for cavities in a ‘crossover’ regime between small and large cavities ΔG_rep should be a function of both A and V [9, 11, 12, 17–19, 41, 80, 107]. However, a recent free energy simulation study showed that plotting ΔG_rep versus A produced different estimates of γ_rep than plotting ∂ΔG_rep/∂x_i versus ∂A/∂x_i, where x_i is a coordinate of atom i [132]. Because ∂A/∂x_i was also highly correlated with ∂V/∂x_i for these systems, creating a function of just A and V that could explain this observation seems to be difficult. Furthermore, recent studies on a wide variety of systems have indicated that the slopes of plots of ∂ΔG_rep/∂x_i versus ∂A/∂x_i appear to decrease fairly consistently with A [132, 133]. This finding appears to contradict the idea that there should be a single transition from structures for which ΔG_rep is linear in V to one where it is linear in A. As perturbative theories for 〈∂U_rep(λ)/∂λ〉 have difficulty near the peak, expecting that these complicated contributions to ΔG_rep will cancel to produce simple dependencies on A and V is probably not realistic.

4.2. Single-step perturbation does not give good estimates of the attractive component of the nonpolar solvation free energy

As discussed above, ΔG_el can be computed solely from information on the final water configuration because 〈∂U_el(0)/∂λ〉 ≈ 0. This observation reflects the weak preferential orientation of the dipole moments of the water molecules surrounding an uncharged solute. As the electrostatic field is turned on, there is initially no charge density with which it can interact. In contrast, the water density at the surface of near-hard cavities in solution is significant and correlated before $U_{\text{att}}^{ij}$ is turned on. Therefore 〈∂U_att(0)/∂λ〉₀ ≠0 (figure 2).

Figure 2.

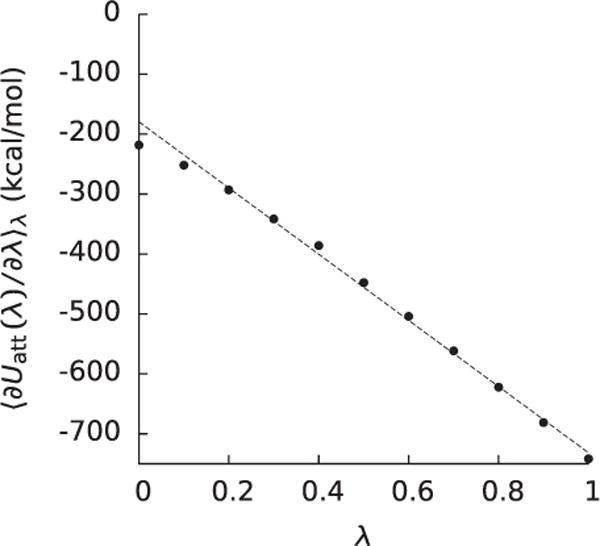
The integrand (〈∂U_att(0)/∂λ〉_λ) of the integral used to compute the attractive component (ΔG_att) of the nonpolar solvation free energy as a function of λ for a barnase-barstar complex taken from a recent study [135].

We among others have pointed out that ΔG_att cannot be reliably computed from a single water distribution for molecules such as decaalanine peptides, decaglycine peptides, and proteins. For example, using either the initial or final water distributions as $\widehat{\rho }(\mathbf{r})$ in (12) would have led to estimates of ΔG_att of −218 kcal mol⁻¹ and −742 kcal mol⁻¹, respectively, as opposed to the answer from FEP,−458 kcal mol⁻¹, for the barnase-barstar complex discussed above. In principle, these estimates could have been improved by using the water distribution from λ = 0.5, but using (12) to predict ΔG_att would only be convenient if $\widehat{\rho }(\mathbf{r})$ can be approximated without running another simulation. One of the approximations advocated for $\widehat{\rho }(\mathbf{r})$ is a step function that is 0 inside the molecule and the bulk concentration outside the molecular surface. Because such a simple approximation of $\widehat{\rho }(\mathbf{r})$

would not be expected to be more accurate than the initial and final structures used above, we could expect such an approximation to yield large errors for proteins, such as the barnase-barstar complex considered here. Such predictions are simply not accurate enough for most biological applications.

5. Conclusions

Several important studies have suggested that the solvation of small nonpolar solutes can help explain the processes of protein folding and protein binding [6, 8–11, 13, 15, 19, 21, 34, 35, 39, 40, 43, 45]. These studies found that ΔG_solv of small nonpolar solutes increases with A [7, 10–13, 15, 19, 26, 27, 30, 32, 35, 37, 39, 43, 45, 53–62, 64–72, 74, 77–80]. If the solubility of an amino acid could be computed by adding the solubility of one unit of backbone to that of a small alkane analog of its side chain, then one should expect that proteins would preferentially bury amino acids with bulkier nonpolar side chains upon folding and binding [6, 11, 15, 22, 30–32, 34–36, 39–41, 43, 45, 46, 54, 82–84]. A large number of researchers have used this idea to create hydrophobicity scales [30–32, 35, 40, 45, 46, 53–55, 85] to predict properties, many of which relate to which amino acids would be preferentially buried upon folding and binding. The predictions of these models have been confirmed by experiment, yet still the order of the amino acids in the scales vary depending on which observations and which criteria were used. Additionally, ΔG_solv is typically dominated by a large entropic component at room temperature [9, 12, 15, 19, 21, 27, 34, 37, 39, 40, 43, 45, 48, 58, 61, 66, 71, 76, 80, 81, 86–94]. Similarly, protein folding and binding often contain large entropic contributions [15, 16, 19, 21, 22, 32, 39, 43, 47, 48, 94, 95]. This parallel has led to the suggestion that protein folding is favorable partly because removing more hydrophobic residues from solution into the protein interior is entropically favorable. Similarly, some have hypothesized that the release of structured water upon binding could be a major driver of protein-protein binding. These observations have led to the following model of protein folding and binding [6, 8–13, 15, 19, 21–28, 30–32, 34–36, 38–41, 43–50, 52, 82–84, 117]: protein folding and binding are driven by the entropically favored release of structured waters upon the burial of hydrophobic side chains.

Some recent experimental and computational results appear to contradict this classic picture. The most convenient definition of ΔG_hyd would be ΔG_LJ, which is closely related to the solvation free energies of small alkanes because the small bond dipoles of these molecules mean that the electrostatic contributions to their solvation free energies are small. With this definition, ΔG_solv could be computed by combining ΔG_el obtained from an implicit-solvent model with some estimate of ΔG_LJ. Many implicit-solvent models have assumed that ΔG_LJ increases linearly with A, in analogy with the free energy required to create macroscopic cavities in solution [6, 15, 57, 79]. However, although it increases with A, the slopes of plots of ΔG_solv versus A for these alkane are orders of magnitude smaller than the observed surface tension of water [10, 13, 15, 19, 79]. Additionally, several studies have found that for small peptides ΔG_LJ sometimes decreases with A, seemingly implying that ΔG_hyd favors extended structures in solution [128, 132]. In short, the surface tensions implied by the slopes of these plots are not constant but vary for different molecular cavities and even different conformations of the same molecule. Finally, as discussed in section 3.1, defining ΔG_hyd to be ΔG_LJ leads to the conclusion that ΔG_fold and ΔG_bind should be dominated by the formation of favorable solute-solute dispersive interactions rather than changes in ΔG_hyd.

As noted, these problems can be partially overcome by defining ΔG_hyd to be ΔG_rep rather than ΔG_LJ. The slopes of plots of ΔG_rep versus A are positive for both alkanes and small peptides, but the slopes are not uniform between molecules or even conformers of a molecule. This definition allows the creation of decompositions of ΔG_bind and ΔG_fold that qualitatively predict that ΔG_hyd drives both protein folding and binding, as expected from the empirical understanding of ΔG_hyd. Finally, these energy decompositions also suggest that ΔΔG_fold and ΔΔG_bind should both contain large entropic components because ΔG_rep is primarily entropic and is not trivially counterbalanced by any other energy term.

Although defining ΔG_hyd to be ΔG_rep reconciles the qualitative understanding of the importance of ΔG_hyd in protein folding and binding with the results of explicit-solvent simulations, the models that have been created to compute ΔG_rep and ΔG_att are not adequate. The results of explicit-solvent simulations indicate that ΔG_rep is not a simple function of simple geometric properties of the cavity, such as A, V [132], and the surface curvature, and ΔG_att cannot be computed from single-step free energy perturbation on an approximate water distribution. Better theories will be required to compute ΔG_rep and ΔG_att if these ideas are to be used to generate quantitatively accurate estimates of ΔΔG_fold and ΔΔG_bind.