Abstract
The idea that a ‘hydrophobic energy’ drives protein folding, aggregation, and binding by favoring the sequestration of bulky residues from water into the protein interior is widespread. The solvation free energies (∆Gsolv) of small nonpolar solutes increase with surface area (A), and the free energies of creating macroscopic cavities in water increase linearly with A. These observations seem to imply that there is a hydrophobic component (∆Ghyd) of ∆Gsolv that increases linearly with A, and this assumption is widely used in implicit solvent models. However, some explicit-solvent molecular dynamics studies appear to contradict these ideas. For example, one definition (ΔGLJ) of ΔGhyd is that it is the free energy of turning on the Lennard–Jones (LJ) interactions between the solute and solvent. However, ΔGLJ decreases with A for alanine and glycine peptides. Here we argue that these apparent contradictions can be reconciled by defining ΔGhyd to be a near hard core insertion energy (ΔGrep), as in the partitioning proposed by Weeks, Chandler, and Andersen. However, recent results have shown that ΔGrep is not a simple function of geometric properties of the molecule, such as A and the molecular volume, and that the free energy of turning on the attractive part of the LJ potential cannot be computed from first-order perturbation theory for proteins. The theories that have been developed from these assumptions to predict ΔGhyd are therefore inadequate for proteins.
Keywords: protein folding, simulation, hydrophobic effect
1. The empirical understanding of hydrophobicity
Oil separates from water, and the free energy cost (ΔGcav) of creating a macroscopic cavity in water is often computed from simple geometric properties of the cavity [1–20]. This free energetic penalty generally increases with both the surface area (A) and volume (V) of the cavity. The proportionality constant between ΔGcav and A defines the surface tension of the water, and the linearity of ΔGcav in V reflects the pressure-volume work of forming the cavity. Because an energy that increases with cavity size would favor aggregation and collapse of molecules as large as proteins in solution, the idea that a hydrophobic cavity-formation energy (ΔGhyd) that increases with A drives these processes is widely discussed [6, 8–13, 15, 19, 21–52]. As we discuss in the following sections, this idea is also supported by the observations of the solvation free energies (ΔGsolv) of small nonpolar solutes. In the Kauzmann–Tanford picture such small, organic compounds are used as molecular analogs of the side chains of the equivalent amino acids [6, 7, 15, 22, 30, 35, 39, 43, 45, 46, 53–57]. Since for these compounds ΔGsolv generally increases with A [7, 10, 11, 13–15, 26, 27, 30, 32, 33, 35, 37, 39, 40, 43, 46, 51, 53, 54, 56–81] we are led to the idea that proteins tend to bury bulkier, nonpolar residues removing them from solvent exposure during folding and binding [6, 11, 15, 22, 30–32, 34–36, 39, 40, 43–46, 50, 54, 56, 82–85]. The ΔGsolv of small nonpolar solutes is dominated by an entropic contribution (ΔSsolv) at room temperature. Both TΔSsolv and the enthalpy (ΔHsolv) of hydration tend to both increase linearly with T, whereas ΔGsolv = ΔHsolv − TΔSsolv tends to be relatively independent of T over the range of biological interest. Additionally, the heat capacity (ΔCp = ∂ΔHsolv/∂T) of non-polar solutes tends to be large [9, 12, 15, 16, 19, 21, 27, 34, 37, 39, 40, 43, 45, 48, 51, 59, 61, 64, 66, 71, 74–76, 78, 86–94]. Similarly, the ΔCp of protein folding and binding free energies are often large [15, 19, 21, 22, 32, 34, 39, 43, 44, 47, 48, 51, 94, 95], suggesting a thermodynamic parallel between these processes and the solvation of small nonpolar solutes.
In this contribution, we consider the theoretical models used in interpreting these fundamental observations. We do not cover all the uses of such implicit solvent effect models but note their common uses in particular areas. Many excellent recent reviews of hydrophobicity exist.(see for instance [96]) Here, we seek to show where theoretical commonalities exist and fundamental problems remain.
1.1. The solvation free energies of small nonpolar solutes
Protein folding and binding in solution are many-body problems. Several common notions are used to simplify the fundamental complexity of the problem. One assumption often made in trying to understand protein folding and binding is that the contributions of each amino acid to ΔGsolv can be divided into a contribution from the protein backbone, which does not vary among most of the amino acids, and a contribution from its side chain [6, 8, 11, 22, 30–32, 35, 39, 43, 45, 46, 51, 53–57, 85]. If this assumption holds, then the relative solubilities of different amino acids can be determined by measuring the solubilities of small-molecule side-chain analogs. For the nonpolar, or, in other words, the least polar residues, the natural side-chain analogs are small alkanes and aromatics.
1.1.1. Solvation versus transfer free energies of side-chain analogs
Several investigators have therefore attempted to measure or compute the relative solubilities of small alkanes [7, 10, 11, 13, 26, 27, 29, 30, 33, 35, 37, 39, 43, 45, 46, 51, 53, 55–67, 69, 73, 74, 77, 78, 80, 88, 97]. Transfer free energies of alkanes from nonpolar solvents into water typically appear to increase linearly with A [7, 12, 13, 15, 26, 27, 30, 32, 35, 37, 39, 43, 45, 46, 51, 53, 54, 57, 61, 64–74, 79, 81, 88], but the slopes of plots of these transfer free energies versus A depend critically on what environment the alkanes were in prior to being transfered into water [6, 7, 10, 15, 30, 35, 39, 43, 45, 46, 51, 57, 71, 79, 88]. Much of this research has been conducted with an eye to a specific definition of ΔGhyd, that it is the free energy of transferring an amino acid from the protein ‘interior’ to its ‘surface.’ [6, 7, 15, 21, 23, 30–32, 34, 35, 39, 40, 43, 46, 51, 53, 54, 71, 79] Such an interpretation requires the reference state to be analogous to the protein ‘interior.’ Typically, some liquid hydrocarbon has been taken as the reference state, and several studies have advocated for several different choices of reference state, each yielding slightly different slopes of plots of ΔGhyd versus A [6, 7, 15, 26, 30, 32, 35, 39, 40, 43, 45, 51, 79].
The approach of using a transfer free energy of peptides and proteins among multicomponent aqueous solutions has been used to complement the studies where transfer was between very different solvents as mentioned above [98–101]. In these studies a component which either stabilizes the solution, such as trimethylamine N-oxide, or destabilizes, such as urea, are used to measure a difference in free energies between solutions which have a direct measurable effect on protein thermodynamics. The change in transfer free energies versus A for each of the amino acids in a variety of proteins show similar trends as the older measurements, until corrected for the solution activities [100]. The effect of solubility changes of the sidechains on folding is nearly indiscernible in the data, however the effect on the back bone becomes strikingly clear. Some issues remain such as a concentration or reference state dependence and even how one models the exposed area changes between the solutions [102, 103]. These effect change the weighting of backbone versus sidechain influences for different applications [104] but the lack of activity corrections in the older literature of compound transfers remains an issue for interpreting the size of the hydrophobic effect on sidechains versus backbones.
This definition of ΔGhyd, although common, is not ideal for comparison to molecular dynamics simulations, partly because the protein’s ‘interior’ and its ‘surface’ do not have single, accepted definitions [6, 15, 32, 34, 39, 40, 43, 45, 71, 88]. These regions are not well defined because they do not trivially follow directly from the system’s Hamiltonian. For simulations and many-body theories, the free energy of turning on the Lennard–Jones interactions between the solute and solvent (ΔGLJ, defined in section 2.1) and its near-hard-core component (ΔGrep, defined in section 2.3) may be more useful definitions of ΔGhyd. If we define ΔGhyd to be ΔGLJ, then the natural reference state is vapor (or near vacuum), and several experimental and computational studies have indeed used this reference state, even though the slopes (γLJ) of plots of ΔGLJ versus A for alkanes (~1 cal−1 mol Å−2) are orders of magnitude smaller than the surface tension of water (~100 cal−1 mol Å−2). This observation can be partly ascribed to the creation of attractive dispersive interactions between the solute and solvent, as discussed in section 2.3 [10, 15, 40, 51, 80, 105–107]. Because in experiment one cannot turn off the dispersive interactions between the solute and solvent, we have no experimentally accessible reference state from which we can obtain ΔGrep. Interestingly, however, because the depth of the Lennard–Jones potentials between a solute and a hydrocarbon liquid is similar to that between the solute and water and because both states are densely packed liquids, the attractive dispersive interactions that the solute loses when being transferred from a liquid hydrocarbon to water may partially cancel against those it gains upon transfer to water. This cancellation may explain why the slopes of plots of the transfer free energies of alkanes from liquid hydrocarbons to water versus A tend to be larger than γLJ [6, 30].
1.1.2. The anomalous entropy of solvation of nonpolar solutes
The original understanding of hydrophobic solvation included the observation that the ΔGsolv of hydrophobic solutes was dominated by a large negative TΔSsolv. This finding was originally interpreted to imply that the water molecules reorganized themselves to make room for the hydrophobic solute in an ice-like or clathrate-like cage, maximizing their enthalpy at the expense of entropy. Many studies have since provided computational and experimental evidence that the water around nonpolar solutes is not as rigid as originally suggested, but the idea that the water undergoes some sort of entropically unfavorable rearrangement around nonpolar solutes is widespread [7, 9, 12, 13, 15–17, 19, 21, 27, 34, 39, 40, 45, 48, 51, 58, 59, 61, 66, 69, 71, 74–76, 80, 81, 86–92, 94, 108–114].
However, some researchers [15, 39, 43, 48, 74, 88, 91–94] pointed out that TΔSsolv is essentially linear for hydrophobic solutes and that ΔGsolv is nearly independent of temperature. Therefore, although ΔGsolv is dominated by a negative TΔSsolv at room temperature, at some higher temperature TΔSsolv is 0 and ΔGsolv is dominated by the enthalpic (ΔHsolv) contribution. These researchers concluded that hydrophobic solvation is defined by two characteristic features: first that the heat capacity (ΔCp) of solvation is large and second that ΔGsolv is nearly independent of T and the sum of two nearly compensating terms, ΔHsolv and −TΔSsolv. As has been pointed out, these two conditions in this case are equivalent [48].
An alternative explanation for the large ΔSsolv of the solvation of nonpolar solutes has been advanced by a number of researchers [8, 9, 12, 15, 19, 40, 71, 74, 80, 81, 87, 89, 91, 111]. These works point out that the energy of inserting a hard cavity into solution can be related directly to the probability of finding an appropriately sized cavity in pure water. Because the probability distribution of cavities in water is roughly Gaussian for small cavities, the energy of inserting a cavity into solution should increase with the size of the cavity. This free energy should also be entropic and arises principally because of the small size of the water molecules, as creating a larger cavity requires the displacement of more water molecules.
These two ideas of the origin of ΔSsolv should be understood as complementary rather than contradictory [9, 12, 19, 40, 41, 51, 76, 87, 89, 111, 115]. Placing a solute into a solvent, such as liquid argon, that interacts with itself only through excluded volume interactions will require an entropy cost to be paid to displace the atoms. This contribution to ΔSsolv does not require the solvent to form strong hydrogen bonds and is analogous to the entropic term discussed by Hummer et al [12, 41, 115]. However, water does form strong hydrogen-bonding networks, and this implicit symmetry breaking will inevitably lead to a loss of solvent entropy, partly compensated for by a gain in solvent enthalpy, upon the solvation of nonpolar solutes, leading to an entropic change analogous to that discussed by Frank and Evans [58]. Determining which of these components of ΔSsolv should be larger for realistic molecules theoretically would be difficult because for cavities larger than the smallest alkanes neither the introduction of an excluded volume or hard core nor the introduction of hydrogen-bonding interactions between the water molecules can be treated as a small perturbation of the system.
1.2. The empirical understanding of the importance of hydrophobicity in protein folding and binding and hydrophobicity scales
Many studying the processes of protein folding and binding have found several apparent parallels between them and the the solvation of nonpolar solutes. Because ΔGsolv increases with solute size for small nonpolar solutes [4, 7, 10, 11, 13–15, 19, 26, 30, 32, 35, 37, 39, 42, 43, 51, 56, 57, 59, 68, 70–72, 74, 77, 79, 80], residues with large nonpolar side chains should be preferentially buried in the protein interior. This expectation has indeed been validated in that amino acids with bulkier side chains do appear to preferentially reside in the protein interior [6, 15, 22, 30–32, 34–36, 39, 40, 43, 45, 46, 56, 82–85]. In addition, many proteins can be denatured either by heating or cooling [11, 16, 19, 34, 40, 42, 45, 116, 117]. That proteins denature upon heating is not surprising, as the chain entropy of the denatured protein is higher than that of the folded state. That proteins denature upon cooling is more interesting, as decreasing the temperature would be expected to decrease entropy, yet by denaturing the protein’s chain, entropy increases. This entropy increase must be more than compensated for by some other decrease in entropy. If the solvating water has to become more ordered upon denaturation at low temperatures to accommodate the exposed nonpolar residues, as would be expected when water becomes more ordered around hydrophobic solutes, then this decrease in entropy could compensate for the increase in entropy from the denaturing of the protein. Finally, the binding free energies (ΔGbind) of many protein-protein complexes are primarily entropic, and the interfaces between the binding partners can contain a number of nonpolar residues.
The idea that the mechanisms driving protein folding and binding are similar to those that govern the solvation of small nonpolar solutes has inspired efforts to rank amino acids quantitatively by their hydrophobicity, either by ranking them by experimental or computational transfer free energies of side-chain analogs from some reference environment into water [7, 30–32, 35, 40, 46, 53–56] or by statistical analyses of the probability that a given residue will be found in the protein interior. Although these different hydrophobicity scales differ on the ranking of a handful of amino acids, they essentially agree that proteins preferentially bury those residues that rank as more hydrophobic during folding [30–32, 34, 35, 39, 40, 45, 46, 54, 56, 82–85] and the interfaces of proteins that form protein-protein complexes tend to be enriched by these more hydrophobic residues [15, 42]. The lack of a single definition for this concept limits its quantitative utility.
From these observations an empirical picture of the importance of hydrophobicity in protein folding and binding has, none the less, been created [21–28, 30–32, 34–36, 38–52, 82–84, 117]: proteins fold in part, because removing the hydrophobic residues from solution into the protein interior is favorable. Proteins bind, in part, because burying hydrophobic residues at the protein interface is favorable. Both of these processes contain large entropic components because of the large water reorganization required to solvate the nonpolar residues when they are on the protein surface.
2. Free energy definitions
Before we can test this empirical understanding of the importance of hydrophobicity in protein folding and binding with explicit-solvent models and explore the consequences of these findings for implicit-solvent models, we have to define the folding free energy (ΔGfold), the binding free energy (ΔGbind), and the hydrophobic component (ΔGhyd) of the solvation free energy in these models. As discussed below, different definitions of ΔGhyd lead to different conclusions about its significance in protein folding and binding. Different partitions of free energy changes into terms that are not state functions, while often convenient, can lead to process-dependent conclusions.
2.1. Decomposing the solvation energy in explicit- and implicit-solvent models
In most classical nonpolarizable force fields, the interaction energy between the solute and solvent is modeled by
| (1) |
where
| (2) |
| (3) |
| (4) |
and are the Lennard–Jones and Coulombic interaction energies between atoms i and j, εij is the depth of the Lennard–Jones potential between atoms i and j, is the distance to this minimum, rij is the distance between atoms i and j, qi and qj are the charges on atoms i and j, ε0 is the vacuum permittivity, and these summations are taken over all atom pairs that contain one solute and one solvent atom.
In such a model ΔGsolv can be defined as the free energy required to go from a state where the solute and solvent do not interact to one where their interaction energy is Uij. Additionally, ΔGsolv can be naturally broken into two components, a nonelectrostatic (ΔGLJ) component that is the free energy required to go from a system where the solute and solvent do not interact to one where their interaction energy is and an electrostatic (ΔGel) component that is the free energy required to go from a system where the solute-solvent interaction energy is to one where it is Uij. From this definition, ΔGsolv = ΔGLJ + ΔGel [6, 44, 79, 107]. This decomposition, it should be noted, depends on defining a process whereby the LJ cavity is created before the charge is introduced. With such a process the decomposition naturally follows terms in the Hamiltonian.
Several implicit-solvent models, such as the Poisson-Boltzmann equation [44, 57, 79, 107, 118–120], the generalized Born model [79], integral equation theories [79], and structured continuum models, have been developed to compute ΔGel.
2.2. The electrostatic component of the solvation free energy, but not the nonpolar component, is amenable to perturbation theory
The success of implicit-solvent models at predicting ΔGel can be partly attributed to the feasibility of computing ΔGel with low-level perturbation theory. If a λ-dependent energy is constructed to link a system where the solute-solvent interaction energy is to one where it is Uij, then ΔGel can be computed from thermodynamic integration (TI),
| (5) |
where 〈…〉λ indicates an averaging over a system where the solvent-solute interaction energy is and where this summation is taken over all solvent-solute atom pairs. In biomolecular systems 〈∂Uel(λ)/∂λ〉λ tends to be linear in λ, and (figure 1). Following (5) ΔGel is the area under this curve, so
| (6) |
Figure 1.
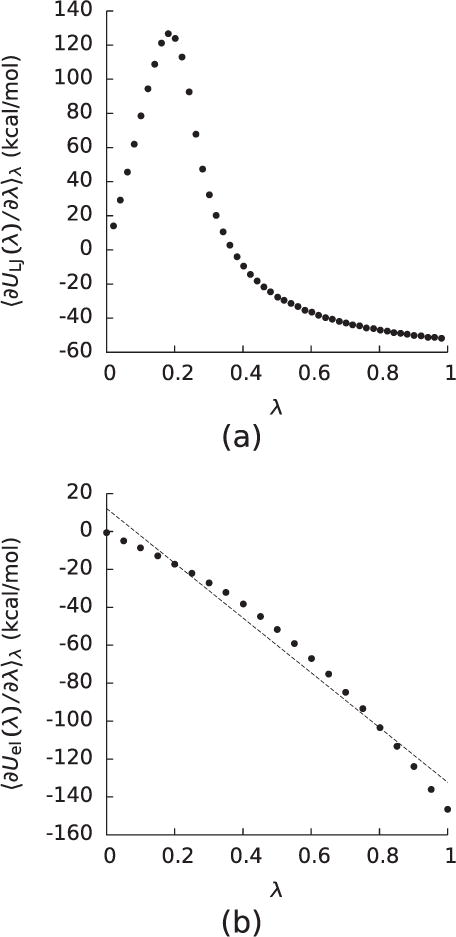
(a)The integrand (〈∂ULJ(λ)/∂λ〉λ) of the integral used to compute the free energy (ΔGLJ) of turning on the Lennard–Jones interactions between the solute and solvent for a decaalanine peptide as a function of λ. (b) The integrand (〈∂Uel(λ)/∂λ〉λ) of the integral used to compute the free energy (ΔGel) of turning on the electrostatic interactions between the solute and solvent once the Lennard–Jones interactions had been turned on for the decaalanine in (a).
Therefore, ΔGel can be accurately estimated solely from information obtained from an ensemble defined by a system where the solute-solvent interaction energy is Uij.
In contrast, computing ΔGLJ is more difficult. In principle a λ-dependent potential can be defined that links a system where the solute and solvent do not interact to one where the solute-solvent interaction energy is , and ΔGLJ can then be computed from TI,
| (7) |
where 〈…〉λ indicates an averaging over a system where the solute-solvent interaction energy is and , where this summation is taken over all solute-solvent atom pairs. However, the obvious choice of a λ-dependent potential that varies linearly with λ leads to a 〈∂ULJ(λ)/∂λ〉λ that diverges at λ = 0. Although this pole is in principle integrable, the computational expense of doing so has led to the development of a number of ‘softcore’ for which 〈∂ULJ(λ)/∂λ〉λ does not diverge at λ = 0. However, although softcore do not generate poles in 〈∂ULJ(λ)/∂λ〉λ, their 〈∂ULJ(λ)/∂λ〉λ still display large peaks associated with the drying of the cavity interior due to excluded volume (figure 1). This observation implies that ΔGLJ cannot be computed from simple perturbative expansions around λ = 0 and λ = 1.
2.3. Empirical models of the nonpolar component of the solvation free energy
Partly because ΔGLJ is not amenable to perturbation theory, many implicit-solvent models have instead assumed that ΔGLJ is linear in A and possibly V [11, 13, 15, 18, 19, 44, 57, 79, 105, 107, 118–121]. For instance
| (8) |
in analogy with the free energy of creating a macroscopic cavity in solution, which increases linearly with A and V. Many other forms of ΔGLJ exist in the literature.
Alternatively, some researchers have argued that the process of going from a system where the solute and solvent do not interact to one where their interaction energy is ULJ is not directly analogous with the creation of a macroscopic cavity because of the attractive 1/r6 tail in used to represent the dispersive interactions between the solute and solvent [10, 13, 15, 17, 19, 71, 74, 80, 105–107, 122]. Instead, they propose to divide into purely repulsive and attractive components. In this study, we will further discuss the decomposition proposed first by Weeks, Chandler, and Andersen (WCA) [14, 26, 27, 80, 105, 107, 123–125],
| (9) |
and
| (10) |
Following the WCA decomposition, we can break ΔGLJ into two components: that (ΔGrep) of going from a system where the solute and solvent do not interact to one where their interaction energy is and that (ΔGatt) of going from a system where the solute-solvent interaction energy is rep to one where it is . Following this definition, ΔGLJ = ΔGrep + ΔGatt. Note that in this definition the repulsive cavity is formed before the attractive interactions are added.
Several researchers have attempted to go further and quantitatively predict ΔGrep and ΔGatt with simple models. Typically, these theories assume that ΔGrep should be linear in A and V, i.e.
| (11) |
where γrep, ρrep, and b are constants to be fit to various small molecules, in analogy with the energy required to create macroscopic cavities in water, and that ΔGatt can be computed from a single-step perturbation expression [17, 71, 74, 105, 107, 125],
| (12) |
around an approximate water distribution , where is the attractive component of the Lennard–Jones interaction energy between solute atom i and a water molecule placed at r.
Alternatively, some researchers, following Tolman, have proposed that either ΔGLJ or ΔGrep should depend not just on A but on the curvature of the molecular surface [3, 6, 7, 13, 14, 18–20, 57, 73, 105, 118, 126]:
| (13) |
or
| (14) |
where γmac is the surface tension of making a macroscopic cavity in solution, where the interface can be considered planar on a molecular scale, R is the radius of curvature of the surface, and δ is here defined as the Tolman length. The quanti ty in parentheses is an expansion in powers of 1/R, which in principle could be extended but in practice is typically truncated at this order [19, 79, 126].
For small cavities scaled particle theory predicts that ΔGrep should increase linearly with V, and so some have supposed that for small molecules [11, 14, 15, 17, 18, 105, 107],
| (15) |
because creating a larger cavity requires the exclusion of more waters and the number of excluded waters should scale roughly as V. Additionally, they claim that for larger cavities ΔGrep should increase linearly with A,
| (16) |
because that is the behavior observed for macroscopic cavities. In between, in a proposed transition region, they then assume that ΔGrep should be a function of both A and V. Some of them have further assumed that ΔGrep should follow (11) in this crossover region.
2.4. Defining the protein binding and folding free energies
In classical force fields we can approximate the free energy (ΔG) required to create a protein in a particular ‘state,’ such as the unfolded state, as
| (17) |
where ΔGsolv(r) is the is the solvation energy of a single configuration taken from that state, the integral is taken over all configurations (r) in the state, ρ(r) is the probability of configuration r, and these summations are taken over all atom pairs in the protein in configuration r. Equation (17) neglects the formation of the internal bonded interactions, but these interactions tend not to change much upon folding and binding.
We can then write an expression for the ΔΔGfold of a protein:
| (18) |
where
| (19) |
| (20) |
| (21) |
| (22) |
〈…〉f and 〈…〉u represent averaging over configurations taken from the folded and unfolded ensembles, and the summations are taken over all atom pairs in the protein in each configuration.
Similarly, for an equilibrium binding event
we can write
| (23) |
where
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
〈…〉c, 〈…〉a, and 〈…〉b represent averaging over configurations, for instance, taken from molecular dynamics simulations of the complex and its two separated components, and the summations are taken over all atom pairs in the protein in each configuration.
Using the breakdowns of ΔGsolv defined above,
| (29) |
or
| (30) |
we can rewrite (18) as
| (31) |
or
| (32) |
Similarly, we can rewrite (23) as
| (33) |
or
| (34) |
3. The value of a near-hard-core definition of the hydrophobic solvation free energy
The most convenient definition of ΔGhyd in implicit-solvent models would be that ΔGhyd was the free energy, ΔGLJ, required to transfer a solute that interacts with the solvent through a Lennard–Jones interaction from vacuum into solvent. If ΔGLJ could be computed from a simple model, such as (8), then ΔGsolv could be computed by combining the resulting estimates of ΔGLJ with estimates of ΔGel from implicit-solvent models. From these ΔGsolv estimates of more interesting free energies, such as ΔGfold and ΔGbind, could then be computed as outlined above.
However, many studies have measured or computed with simulation the ΔGsolv for alkanes [7, 10, 11, 15, 32, 39, 45, 51, 57, 74, 77, 78, 80], and although ΔGsolv tends to increase with A, the resulting estimates of γLJ are 1–2 orders of magnitude smaller than the surface tension of water (~100 cal−1 mol Å−2) [7, 10, 11, 15, 19, 79, 105, 114]. Even more disturbing, more recent studies have shown that ΔGLJ decreases with the number of monomers for glycine peptides and extended alanine peptides, and they have produced estimates of γLJ for decaalanine (−3 cal−1 mol Å−2) and glycine peptides (−74 cal−1 mol Å−2) that are less less than 0 [127, 128]. These observations seem to imply that the cavity, i.e. hydrophobic, interactions favor extended rather than collapsed structures in solution.
As argued by WCA and others, these observations can be taken to indicate that the identification of ΔGhyd as ΔGLJ is not consistent with the empirical understanding of hydrophobicity outlined above [10, 13, 15, 17, 19, 26, 71, 74, 78, 80, 105–107]. Instead, WCA proposed to divide ΔGLJ into near-hard-core, ΔGrep, and attractive, ΔGatt, components, as outlined above. For small organic molecules ΔGrep increases more rapidly with A than ΔGLJ, and the slopes (γrep) of the least-squares lines of plots of ∂ΔGrep/∂xi versus ∂A/∂xi are positive for decaalanine and glycine peptides [127, 128].
3.1. A near-hard-core definition of the hydrophobic solvation free energy implies that it dominates binding and folding free energies
If we identify ΔGhyd to be ΔGrep [26] we recover the idea that ΔGfold and ΔGbind are driven by changes in ΔGhyd. In contrast, identifying GΔhyd to be ΔGLJ leads to the conclusion that ΔGfold and ΔGbind are dominated by the formation of direct attractive dispersive interactions in the solute. The reasoning behind this conclusion follows:
First, the net electrostatic contributions to ΔGfold and ΔGbind should be small, as can be seen in (31)–(34). The second lines of these equations should be approximately zero because increases in the electrostatic components of the solvation free energies from the formation of additional favorable electrostatic interactions with the solvent should be balanced by corresponding decreases in the solute-solute electrostatic energies because of the loss of corresponding favorable solute-solute electrostatic interactions. Several studies have pointed out that such desolvation and vacuum energies should be of comparable magnitude and opposite sign [6, 22, 129–131].
Now, consider (32) and (34). The first lines of these two equations should be approximately 0 because although ΔGrep tends to increase with A, ΔGLJ tends to change relatively little with A because ΔGatt tends to decrease with A and ΔGLJ = ΔGrep + ΔGatt. We can therefore conclude that the largest contributions to ΔGbind and ΔGatt come from the final lines of these two equations, which represent the formation of direct favorable dispersive interactions between the solute atoms. We therefore see that if we define ΔGhyd to be ΔGLJ that ΔGhyd would not dominate ΔGbind and ΔGfold, in apparent contradiction to the classic understanding of hydrophobicity.
Now consider (34) and (32). The last lines of these two equations will be approximately 0 because although structures with larger A make more favorable dispersive interactions with the solvent, leading to more negative ΔGatt, this increase in the favorability of ΔGatt is partly counterbalanced by the loss of favorable solute-solute dispersive interactions. We therefore conclude that if we define ΔGhyd to be ΔGrep then ΔGbind and ΔGfold will be dominated by changes in ΔGhyd, as expected from the classic understanding of hydrophobicity.
In conclusion, we see that whether ΔGhyd indeed dominates ΔGbind and ΔGfold depends on the way that we partition ΔGbind and ΔGfold into different contributions.
3.2. Explanations of anomalously large entropies of folding and binding
If ΔGhyd is defined to be ΔGrep, then ΔΔGbind and ΔΔGfold can be estimated from (34) and (32). Note that the only terms in these equations that should be primarily entropic are the ΔGrep terms. Also, note that all of the terms that are primarily enthalpic (ΔGel, ΔGatt, , and ) in these equations can be combined into terms that are approximately 0, whereas the terms that are primarily entropic (ΔGrep) are unpaired with any counterbalancing contribution. This observation may explain why ΔΔGbind and ΔΔGfold often contain large entropic terms, in agreement with the classical understanding of hydrophobicity.
4. Simple theories fail to provide quantitative predictions of the hydrophobic solvation free energy
Although ΔGLJ would be the most consistent definition of ΔGhyd following experiments on small molecule side chain analogs and convenient in implicit-solvent models, the traditional approach to approximating ΔGLJ, to assume that it is linear in A and V, is not valid [132]. Thus, this definition of ΔGhyd leads to conclusions that contradict the classical idea that ΔGbind and ΔGfold are dominated by changes in ΔGhyd. Defining ΔGhyd to be ΔGrep and computing ΔGLJ from ΔGLJ = ΔGrep + ΔGatt is therefore an attractive strategy. Researchers that have pursued this strategy have assumed that ΔGrep follows (11) and that ΔGatt can be computed from (12). Recent studies have shown that neither of these assumptions is valid [132, 133]. New theories will be needed to compute Grep and ΔGatt if quantitative estimates of ΔGLJ, and therefore ΔGsolv, are to be obtained with implicit-solvent models.
4.1. The near-hard-core component of the nonpolar solvation free energy is not a simple function of simple geometric parameters
Recent studies have shown that ΔGrep is not a simple linear function of A, so some other theory is needed to compute this quantity. Two alternative simple theories have been proposed that could perhaps address this problem. First, some have proposed that the surface tension, γrep, of creating a cavity in water must be corrected for the curvature of the interface between the water and the cavity [3, 6, 7, 13, 14, 18–20, 73, 79, 105, 126]. This idea implies that ΔGrep should be computed from (14). Second, others have proposed that for sufficiently small cavities ΔGrep should be linear in V rather than A because ΔGrep should increase with the number of waters excluded from the cavity for small cavities and that the number of waters excluded by forming the cavity increases roughly linearly in V [9, 12, 15, 17–19, 41, 80, 105, 107, 134]. In such a situation ΔGrep should be linear in A for large cavities and in some ‘crossover’ regime ΔGrep should be a function of both A and V. Neither of these ideas is consistent with the results of recent simulation studies [132, 133].
In retrospect, the disagreement between these ideas and simulation results should perhaps not be surprising. As discussed above, 〈∂Urep(λ)/∂λ〉λ and 〈∂ULJ(λ)/∂λ〉λ typically and have large peaks associated with the drying of the cavity as water is excluded. At such a peak, we would expect perturbative expansions of 〈∂Urep(λ)/∂λ〉λ and 〈∂ULJ(λ)/∂λ〉λ to require many orders of perturbation theory, and the idea that these complexities will conveniently cancel out to yield a simple dependence on simple geometric quantities, such as A and V, appears to be unrealistic.
4.1.1. Tolman’s equation does not provide better estimates of the near-hard-core component of the nonpolar solvation free energy
The idea of using a curvature correction like that in (14) to predict ΔGrep was originally advanced to address a particular problem [6, 7, 13, 19]. Some noticed that although both the transfer free energy (ΔGtrans) of a small alkane from a liquid hydrocarbon environment to water and the free energy (ΔGmac) of creating a macroscopic interface between a liquid hydrocarbon and water increase linearly with A, the slopes (γtrans) of plots of ΔGtrans versus A were significantly less positive than those (γmac) of ΔGmac versus A. They concluded that these observations imply that γrep should be greater for protein molecules than for alkanes because the average radii of curvature of proteins are larger than those of alkanes, and this conclusion would not be affected by noting that the proteins contain regions of negative curvature because such regions would also be associated with a larger γrep in this model [6]. However, more recent studies [132, 133, 135] found that γrep appears to decrease with A. Reconciling these findings would be difficult. Furthermore, defining the ‘curvature’ for a single molecule is difficult, as it is strongly dependent on how the surface is defined, and no rigorous statistical mechanical theory has been advanced that links ΔGrep to the detailed curvature of the surface. Indeed, the probability that the statistical mechanical complications around the peak in 〈∂Urep(λ)/∂λ〉 somehow cancel out to yield a simple dependence on the curvature seems unlikely.
4.1.2. The putative nonpolar solvation free energy crossover from a dependence on volume to a dependence on area
As discussed above, some have proposed that ΔGrep should be linear in V for small cavities because ΔGrep should increase with the number of waters expelled to create the cavity, which should increase with V and that for large cavities ΔGrep should be linear in A, as has been observed for macroscopic surfaces and cavities. Therefore, for cavities in a ‘crossover’ regime between small and large cavities ΔGrep should be a function of both A and V [9, 11, 12, 17–19, 41, 80, 107]. However, a recent free energy simulation study showed that plotting ΔGrep versus A produced different estimates of γrep than plotting ∂ΔGrep/∂xi versus ∂A/∂xi, where xi is a coordinate of atom i [132]. Because ∂A/∂xi was also highly correlated with ∂V/∂xi for these systems, creating a function of just A and V that could explain this observation seems to be difficult. Furthermore, recent studies on a wide variety of systems have indicated that the slopes of plots of ∂ΔGrep/∂xi versus ∂A/∂xi appear to decrease fairly consistently with A [132, 133]. This finding appears to contradict the idea that there should be a single transition from structures for which ΔGrep is linear in V to one where it is linear in A. As perturbative theories for 〈∂Urep(λ)/∂λ〉 have difficulty near the peak, expecting that these complicated contributions to ΔGrep will cancel to produce simple dependencies on A and V is probably not realistic.
4.2. Single-step perturbation does not give good estimates of the attractive component of the nonpolar solvation free energy
As discussed above, ΔGel can be computed solely from information on the final water configuration because 〈∂Uel(0)/∂λ〉 ≈ 0. This observation reflects the weak preferential orientation of the dipole moments of the water molecules surrounding an uncharged solute. As the electrostatic field is turned on, there is initially no charge density with which it can interact. In contrast, the water density at the surface of near-hard cavities in solution is significant and correlated before is turned on. Therefore 〈∂Uatt(0)/∂λ〉0 ≠0 (figure 2).
Figure 2.
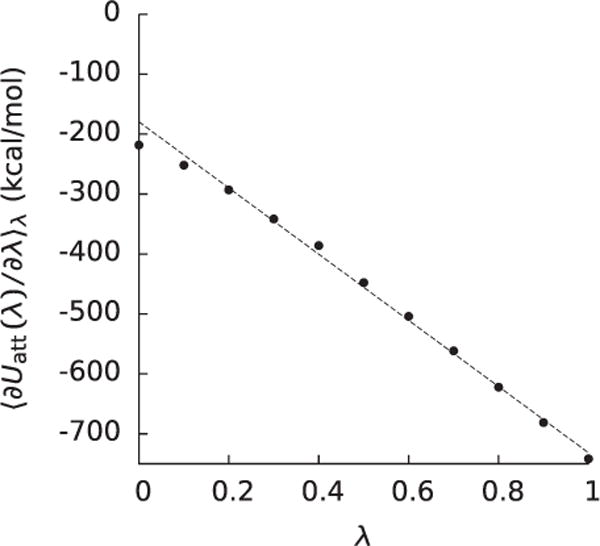
The integrand (〈∂Uatt(0)/∂λ〉λ) of the integral used to compute the attractive component (ΔGatt) of the nonpolar solvation free energy as a function of λ for a barnase-barstar complex taken from a recent study [135].
We among others have pointed out that ΔGatt cannot be reliably computed from a single water distribution for molecules such as decaalanine peptides, decaglycine peptides, and proteins. For example, using either the initial or final water distributions as in (12) would have led to estimates of ΔGatt of −218 kcal mol−1 and −742 kcal mol−1, respectively, as opposed to the answer from FEP,−458 kcal mol−1, for the barnase-barstar complex discussed above. In principle, these estimates could have been improved by using the water distribution from λ = 0.5, but using (12) to predict ΔGatt would only be convenient if can be approximated without running another simulation. One of the approximations advocated for is a step function that is 0 inside the molecule and the bulk concentration outside the molecular surface. Because such a simple approximation of
would not be expected to be more accurate than the initial and final structures used above, we could expect such an approximation to yield large errors for proteins, such as the barnase-barstar complex considered here. Such predictions are simply not accurate enough for most biological applications.
5. Conclusions
Several important studies have suggested that the solvation of small nonpolar solutes can help explain the processes of protein folding and protein binding [6, 8–11, 13, 15, 19, 21, 34, 35, 39, 40, 43, 45]. These studies found that ΔGsolv of small nonpolar solutes increases with A [7, 10–13, 15, 19, 26, 27, 30, 32, 35, 37, 39, 43, 45, 53–62, 64–72, 74, 77–80]. If the solubility of an amino acid could be computed by adding the solubility of one unit of backbone to that of a small alkane analog of its side chain, then one should expect that proteins would preferentially bury amino acids with bulkier nonpolar side chains upon folding and binding [6, 11, 15, 22, 30–32, 34–36, 39–41, 43, 45, 46, 54, 82–84]. A large number of researchers have used this idea to create hydrophobicity scales [30–32, 35, 40, 45, 46, 53–55, 85] to predict properties, many of which relate to which amino acids would be preferentially buried upon folding and binding. The predictions of these models have been confirmed by experiment, yet still the order of the amino acids in the scales vary depending on which observations and which criteria were used. Additionally, ΔGsolv is typically dominated by a large entropic component at room temperature [9, 12, 15, 19, 21, 27, 34, 37, 39, 40, 43, 45, 48, 58, 61, 66, 71, 76, 80, 81, 86–94]. Similarly, protein folding and binding often contain large entropic contributions [15, 16, 19, 21, 22, 32, 39, 43, 47, 48, 94, 95]. This parallel has led to the suggestion that protein folding is favorable partly because removing more hydrophobic residues from solution into the protein interior is entropically favorable. Similarly, some have hypothesized that the release of structured water upon binding could be a major driver of protein-protein binding. These observations have led to the following model of protein folding and binding [6, 8–13, 15, 19, 21–28, 30–32, 34–36, 38–41, 43–50, 52, 82–84, 117]: protein folding and binding are driven by the entropically favored release of structured waters upon the burial of hydrophobic side chains.
Some recent experimental and computational results appear to contradict this classic picture. The most convenient definition of ΔGhyd would be ΔGLJ, which is closely related to the solvation free energies of small alkanes because the small bond dipoles of these molecules mean that the electrostatic contributions to their solvation free energies are small. With this definition, ΔGsolv could be computed by combining ΔGel obtained from an implicit-solvent model with some estimate of ΔGLJ. Many implicit-solvent models have assumed that ΔGLJ increases linearly with A, in analogy with the free energy required to create macroscopic cavities in solution [6, 15, 57, 79]. However, although it increases with A, the slopes of plots of ΔGsolv versus A for these alkane are orders of magnitude smaller than the observed surface tension of water [10, 13, 15, 19, 79]. Additionally, several studies have found that for small peptides ΔGLJ sometimes decreases with A, seemingly implying that ΔGhyd favors extended structures in solution [128, 132]. In short, the surface tensions implied by the slopes of these plots are not constant but vary for different molecular cavities and even different conformations of the same molecule. Finally, as discussed in section 3.1, defining ΔGhyd to be ΔGLJ leads to the conclusion that ΔGfold and ΔGbind should be dominated by the formation of favorable solute-solute dispersive interactions rather than changes in ΔGhyd.
As noted, these problems can be partially overcome by defining ΔGhyd to be ΔGrep rather than ΔGLJ. The slopes of plots of ΔGrep versus A are positive for both alkanes and small peptides, but the slopes are not uniform between molecules or even conformers of a molecule. This definition allows the creation of decompositions of ΔGbind and ΔGfold that qualitatively predict that ΔGhyd drives both protein folding and binding, as expected from the empirical understanding of ΔGhyd. Finally, these energy decompositions also suggest that ΔΔGfold and ΔΔGbind should both contain large entropic components because ΔGrep is primarily entropic and is not trivially counterbalanced by any other energy term.
Although defining ΔGhyd to be ΔGrep reconciles the qualitative understanding of the importance of ΔGhyd in protein folding and binding with the results of explicit-solvent simulations, the models that have been created to compute ΔGrep and ΔGatt are not adequate. The results of explicit-solvent simulations indicate that ΔGrep is not a simple function of simple geometric properties of the cavity, such as A, V [132], and the surface curvature, and ΔGatt cannot be computed from single-step free energy perturbation on an approximate water distribution. Better theories will be required to compute ΔGrep and ΔGatt if these ideas are to be used to generate quantitatively accurate estimates of ΔΔGfold and ΔΔGbind.
Acknowledgments
The Robert A. Welch Foundation (H-0037), the National Science Foundation (CHE-1152876) and the National Institutes of Health (GM-037657) are thanked for partial support of this work.
References
- 1.Young T. An essay on the cohesion of fluids. Phil Trans R Soc. 1805;95:65–87. [Google Scholar]
- 2.Tolman RC. Consideration of the Gibbs theory of surface tension. J Chem Phys. 1948;16:758–74. [Google Scholar]
- 3.Tolman RC. The effect of droplet size on surface tension. J Chem Phys. 1949;17:333–7. [Google Scholar]
- 4.Pierotti RA. A scaled particle theory of aqueous and nonaqueous solutions. Chem Rev. 1976;76:717–26. [Google Scholar]
- 5.Vargaftik NB, Volkov BN, Voljak LD. International tables of the surface tension of water. J Phys Chem Ref Data. 1983;12:817–20. [Google Scholar]
- 6.Nicholls A, Sharp KA, Honig B. Protein folding and association: insights from the interfacial and thermodynamic properties of hydrocarbons. Proteins Struct Funct Bioinf. 1991;11:281–96. doi: 10.1002/prot.340110407. [DOI] [PubMed] [Google Scholar]
- 7.Sharp KA, Nicholls A, Fine RF, Honig B. Reconciling the magnitude of the microscopic and macroscopic hydrophobic effects. Science. 1991;252:106–9. doi: 10.1126/science.2011744. [DOI] [PubMed] [Google Scholar]
- 8.Pratt LR, Pohorille A. Theory of hydrophobicity: transient cavities in molecular liquids. Proc Natl Acad Sci USA. 1992;89:2995–9. doi: 10.1073/pnas.89.7.2995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lum K, Chandler D, Weeks JD. Hydrophobicity at small and large length scales. J Phys Chem B. 1999;103:4570–7. [Google Scholar]
- 10.Ashbaugh HS, Kaler EW, Paulaitis ME. A ‘universal’ surface area correlation for molecular hydrophobic phenomena. J Am Chem Soc. 1999;121:9243–4. [Google Scholar]
- 11.Huang DM, Chandler D. Temperature and length scale dependence of hydrophobic effects and their possible implications for protein folding. Proc Natl Acad Sci USA. 2000;97:8324–7. doi: 10.1073/pnas.120176397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hummer G, Garde S, García AE, Pratt LR. New perspectives on hydrophobic effects. Chem Phys. 2000;258:349–70. [Google Scholar]
- 13.Ashbaugh HS, Paulaitis ME. Effect of solute size and solute–water attractive interactions on hydration water structure around hydrophobic solutes. J Am Chem Soc. 2001;123:10721–8. doi: 10.1021/ja016324k. [DOI] [PubMed] [Google Scholar]
- 14.Huang DM, Geissler PL, Chandler D. Scaling of hydrophobic solvation free energies. J Phys Chem B. 2001;105:6704–9. [Google Scholar]
- 15.Southall NT, Dill KA, Haymet ADJ. A view of the hydrophobic effect. J Phys Chem B. 2002;106:521–33. [Google Scholar]
- 16.Ashbaugh HS, Asthagiri D, Pratt LR, Rempe SB. Hydration of krypton and consideration of clathrate models of hydrophobic effects from the perspective of quasi-chemical theory. Biophys Chem. 2003;105:323–38. doi: 10.1016/s0301-4622(03)00084-x. [DOI] [PubMed] [Google Scholar]
- 17.Chandler D. Interfaces and the driving force of hydrophobic assembly. Nature. 2005;437:640–7. doi: 10.1038/nature04162. [DOI] [PubMed] [Google Scholar]
- 18.Rajamani S, Truskett TM, Garde S. Hydrophobic hydration from small to large lengthscales: understanding and manipulating the crossover. Proc Natl Acad Sci USA. 2005;102:9475–80. doi: 10.1073/pnas.0504089102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ashbaugh HS, Pratt LR. Colloquium: scaled particle theory and the length scales of hydrophobicity. Rev Mod Phys. 2006;78:159–78. [Google Scholar]
- 20.Blokhuis EM, Kuipers J. Thermodynamic expressions for the Tolman length. J Chem Phys. 2006;124:74701–1. doi: 10.1063/1.2167642. [DOI] [PubMed] [Google Scholar]
- 21.Kauzmann W. Some factors in the interpretation of protein denaturation. Adv Protein Chem. 1959;14:1–63. doi: 10.1016/s0065-3233(08)60608-7. [DOI] [PubMed] [Google Scholar]
- 22.Tanford C. Contribution of hydrophobic interactions to the stability of the globular conformation of proteins. J Am Chem Soc. 1962;84:4240–7. [Google Scholar]
- 23.Chothia C. Hydrophobic bonding and accessible surface area in proteins. Nature. 1974;248:338–9. doi: 10.1038/248338a0. [DOI] [PubMed] [Google Scholar]
- 24.Chothia C, Janin J. Principles of protein-protein recognition. Nature. 1975;256:705–8. doi: 10.1038/256705a0. [DOI] [PubMed] [Google Scholar]
- 25.Chothia C. Structural invariants in protein folding. Nature. 1975;254:304–8. doi: 10.1038/254304a0. [DOI] [PubMed] [Google Scholar]
- 26.Pratt LR, Chandler D. Theory of the hydrophobic effect. J Chem Phys. 1977;67:3683–704. [Google Scholar]
- 27.Wilhelm E, Battino R, Wilcock RJ. Low-pressure solubility of gases in liquid water. Chem Rev. 1977;77:219–62. [Google Scholar]
- 28.Tanford C. The hydrophobic effect and the organization of living matter. Science. 1978;200:1012–18. doi: 10.1126/science.653353. [DOI] [PubMed] [Google Scholar]
- 29.Tucker EE, Lane EH, Christian SD. Vapor pressure studies of hydrophobic interactions. Formation of benzene-benzene and cyclohexane-cyclohexanol dimers in dilute aqueous solution. J Solut Chem. 1981;10:1–20. [Google Scholar]
- 30.Kyte J, Doolittle RF. A simple method for displaying the hydropathic character of a protein. J Mol Biol. 1982;157:105–32. doi: 10.1016/0022-2836(82)90515-0. [DOI] [PubMed] [Google Scholar]
- 31.Rose GD, Geselowitz AR, Lesser GJ, Lee RH, Zehfus MH. Hydrophobicity of amino acid residues in globular proteins. Science. 1985;229:834–8. doi: 10.1126/science.4023714. [DOI] [PubMed] [Google Scholar]
- 32.Baldwin RL. Temperature dependence of the hydrophobic interaction in protein folding. Proc Natl Acad Sci USA. 1986;83:8069–72. doi: 10.1073/pnas.83.21.8069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Eisenberg D, McLachlan AD. Solvation energy in protein folding and binding. Nature. 1986;319:199–203. doi: 10.1038/319199a0. [DOI] [PubMed] [Google Scholar]
- 34.Privalov PL, Gill SJ. Stability of protein structure and hydrophobic interaction. Adv Protein Chem. 1988;39:191–234. doi: 10.1016/s0065-3233(08)60377-0. [DOI] [PubMed] [Google Scholar]
- 35.Radzicka A, Wolfenden R. Comparing the polarities of the amino acids: Side-chain distribution coefficients between the vapor phase, cyclohexane, 1-octanol, and neutral aqueous solution. Biochemistry. 1988;27:1664–70. [Google Scholar]
- 36.Spolar RS, Ha J-H, Thomas Record M., Jr Hydrophobic effect in protein folding and other noncovalent processes involving proteins. Proc Natl Acad Sci USA. 1989;86:8382–5. doi: 10.1073/pnas.86.21.8382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Tobias DJ, Brooks CL., III The thermodynamics of solvophobic effects: a molecular-dynamics study of n-butane in carbon tetrachloride and water. J Chem Phys. 1990;92:2582–92. [Google Scholar]
- 38.Eriksson AE, Baase WA, Zhang X-J, Heinz DW, Blaber M, Baldwin EP, Matthews BW. Response of a protein structure to cavity-creating mutations and its relation to the hydrophobic effect. Science. 1992;255:178–83. doi: 10.1126/science.1553543. [DOI] [PubMed] [Google Scholar]
- 39.Privalov PL, Makhatadze GI. Contribution of hydration and non-covalent interactions to the heat capacity effect on protein unfolding. J Mol Biol. 1992;224:715–23. doi: 10.1016/0022-2836(92)90555-x. [DOI] [PubMed] [Google Scholar]
- 40.Blokzijl W, Engberts JBFN. Hydrophobic effects. Opinions and facts. Angew Chem Int Ed Engl. 1993;32:1545–79. [Google Scholar]
- 41.Hummer G, Garde S, García AE, Paulaitis ME, Pratt LR. Hydrophobic effects on a molecular scale. J Phys Chem B. 1998;102:10469–82. [Google Scholar]
- 42.Dill KA. Dominant forces in protein folding. Biochemistry. 1990;29:7133–55. doi: 10.1021/bi00483a001. [DOI] [PubMed] [Google Scholar]
- 43.Makhatadze GI, Privalov PL. Contribution of hydration to protein folding thermodynamics: I. The enthalpy of hydration. J Mol Biol. 1993;232:639–59. doi: 10.1006/jmbi.1993.1416. [DOI] [PubMed] [Google Scholar]
- 44.Honig B, Yang A-S. Free energy balance in protein folding. Adv Protein Chem. 1995;46:27–58. doi: 10.1016/s0065-3233(08)60331-9. [DOI] [PubMed] [Google Scholar]
- 45.Makhatadze GI, Privalov PL. Energetics of protein structure. Adv Protein Chem. 1995;47:307–425. doi: 10.1016/s0065-3233(08)60548-3. [DOI] [PubMed] [Google Scholar]
- 46.Wimley WC, Creamer TP, White SH. Solvation energies of amino acid side chains and backbone in a family of host–guest pentapeptides. Biochemistry. 1996;35:5109–24. doi: 10.1021/bi9600153. [DOI] [PubMed] [Google Scholar]
- 47.Robertson AD, Murphy KP. Protein structure and the energetics of protein stability. Chem Rev. 1997;97:1251–67. doi: 10.1021/cr960383c. [DOI] [PubMed] [Google Scholar]
- 48.Sharp KA, Madan B. Hydrophobic effect, water structure, and heat capacity changes. J Phys Chem B. 1997;101:4343–8. [Google Scholar]
- 49.Tanford C. How protein chemists learned about the hydrophobic factor. Protein Sci. 1997;6:1358–66. doi: 10.1002/pro.5560060627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Pratt LR, Pohorille A. Hydrophobic effects and modeling of biophysical aqueous solution interfaces. Chem Rev. 2002;102:2671–92. doi: 10.1021/cr000692+. [DOI] [PubMed] [Google Scholar]
- 51.Baldwin RL. Energetics of protein folding. J Mol Biol. 2007;371:283–301. doi: 10.1016/j.jmb.2007.05.078. [DOI] [PubMed] [Google Scholar]
- 52.Ball P. Water as an active constituent in cell biology. Chem Rev. 2008;108:74–108. doi: 10.1021/cr068037a. [DOI] [PubMed] [Google Scholar]
- 53.Nozaki Y, Tanford C. The solubility of amino acids and two glycine peptides in aqueous ethanol and dioxane solutions establishment of a hydrophobicity scale. J Biol Chem. 1971;246:2211–7. [PubMed] [Google Scholar]
- 54.Janin J. Surface and inside volumes in globular proteins. Nature. 1979;277:491–2. doi: 10.1038/277491a0. [DOI] [PubMed] [Google Scholar]
- 55.Meirovitch H, Rackovsky S, Scheraga HA. Empirical studies of hydrophobicity. 1. Effect of protein size on the hydrophobic behavior of amino acids. Macromolecules. 1980;13:1398–405. [Google Scholar]
- 56.Wolfenden R, Andersson L, Cullis PM, Southgate CCB. Affinities of amino acid side chains for solvent water. Biochemistry. 1981;20:849–55. doi: 10.1021/bi00507a030. [DOI] [PubMed] [Google Scholar]
- 57.Simonson T, Brünger AT. Solvation free energies estimated from macroscopic continuum theory: an accuracy assessment. J Phys Chem. 1994;98:4683–94. [Google Scholar]
- 58.Frank HS, Evans MW. Free volume and entropy in condensed systems III. Entropy in binary liquid mixtures; partial molal entropy in dilute solutions; structure and thermodynamics in aqueous electrolytes. J Chem Phys. 1945;13:507–32. [Google Scholar]
- 59.Pierotti RA. Aqueous solutions of nonpolar gases. J Phys Chem. 1965;69:281–8. [Google Scholar]
- 60.McAuliffe C. Solubility in water of paraffin, cycloparaffin, olefin, acetylene, cycloolefin, and aromatic hydrocarbons. J Phys Chem. 1966;70:1267–75. [Google Scholar]
- 61.Shinoda K, Fujihira M. The analysis of the solubility of hydrocarbons in water. Bull Chem Soc Japan. 1968;41:2612–5. [Google Scholar]
- 62.Hermann RB. Theory of hydrophobic bonding. II. Correlation of hydrocarbon solubility in water with solvent cavity surface area. J Phys Chem. 1972;76:2754–9. [Google Scholar]
- 63.Reynolds JA, Gilbert DB, Tanford C. Empirical correlation between hydrophobic free energy and aqueous cavity surface area. Proc Natl Acad Sci. 1974;71:2925–7. doi: 10.1073/pnas.71.8.2925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Gill SJ, Nichols NF, Wadsö I. Calorimetric determination of enthalpies of solution of slightly soluble liquids II. Enthalpy of solution of some hydrocarbons in water and their use in establishing the temperature dependence of their solubilities. J Chem Thermodyn. 1976;8:445–52. [Google Scholar]
- 65.Hermann RB. Use of solvent cavity area and number of packed solvent molecules around a solute in regard to hydrocarbon solubilities and hydrophobic interactions. Proc Natl Acad Sci USA. 1977;74:4144–5. doi: 10.1073/pnas.74.10.4144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Shinoda K. ‘iceberg’ formation and solubility. J Phys Chem. 1977;81:1300–2. [Google Scholar]
- 67.Tanford C. Interfacial free energy and the hydrophobic effect. Proc Natl Acad Sci. 1979;76:4175–6. doi: 10.1073/pnas.76.9.4175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Jorgensen WL. Monte carlo simulation of n-butane in water. Conformational evidence for the hydrophobic effect. J Chem Phys. 1982;77:5757–65. [Google Scholar]
- 69.Ben-Naim A, Marcus Y. Solvation thermodynamics of nonionic solutes. J Chem Phys. 1984;81:2016–27. [Google Scholar]
- 70.Jorgensen WL, Gao J, Ravimohan C. Monte Carlo simulations of alkanes in water: hydration numbers and the hydrophobic effect. J Phys Chem. 1985;89:3470–3. [Google Scholar]
- 71.Lee B. The physical origin of the low solubility of nonpolar solutes in water. Biopolymers. 1985;24:813–23. doi: 10.1002/bip.360240507. [DOI] [PubMed] [Google Scholar]
- 72.Jorgensen WL, Kathleen Buckner J. Use of statistical perturbation theory for computing solvent effects on molecular conformation. Butane in water. J Phys Chem. 1987;91:6083–5. [Google Scholar]
- 73.Pohorille A, Pratt LR. Cavities in molecular liquids and the theory of hydrophobic solubilities. J Am Chem Soc. 1990;112:5066–74. doi: 10.1021/ja00169a011. [DOI] [PubMed] [Google Scholar]
- 74.Lee B. Solvent reorganization contribution to the transfer thermodynamics of small nonpolar molecules. Biopolymers. 1991;31:993–1008. doi: 10.1002/bip.360310809. [DOI] [PubMed] [Google Scholar]
- 75.Guillot B, Guissani Y. A computer simulation study of the temperature dependence of the hydrophobic hydration. J Chem Phys. 1993;99:8075–94. [Google Scholar]
- 76.Ashbaugh HS, Paulaitis ME. Entropy of hydrophobic hydration: extension to hydrophobic chains. J Phys Chem. 1996;100:1900–13. [Google Scholar]
- 77.Ashbaugh HS, Kaler EW, Paulaitis ME. Hydration and conformational equilibria of simple hydrophobic and amphiphilic solutes. Biophys J. 1998;75:755–68. doi: 10.1016/S0006-3495(98)77565-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Ashbaugh HS, Garde S, Hummer G, Kaler EW, Paulaitis ME. Conformational equilibria of alkanes in aqueous solution: relationship to water structure near hydrophobic solutes. Biophys J. 1999;77:645–54. doi: 10.1016/S0006-3495(99)76920-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Roux B, Simonson T. Implicit solvent models. Biophys Chem. 1999;78:1–20. doi: 10.1016/s0301-4622(98)00226-9. [DOI] [PubMed] [Google Scholar]
- 80.Gallicchio E, Kubo MM, Levy RM. Enthalpy–entropy and cavity decomposition of alkane hydration free energies: numerical results and implications for theories of hydrophobic solvation. J Phys Chem B. 2000;104:6271–85. [Google Scholar]
- 81.Pratt LR. Molecular theory of hydrophobic effects: she is too mean to have her name repeated. Annu Rev Phys Chem. 2002;53:409–36. doi: 10.1146/annurev.physchem.53.090401.093500. [DOI] [PubMed] [Google Scholar]
- 82.Perutz MF, Kendrew JC, Watson HC. Structure and function of haemoglobin II. Some relations between polypeptide chain configuration and amino acid sequence. J Mol Biol. 1965;13:669–78. [Google Scholar]
- 83.Epstein CJ. Role of the amino-acid ‘code’ and of selection for conformation in the evolution of proteins. Nature. 1966;210:25–8. doi: 10.1038/210025a0. [DOI] [PubMed] [Google Scholar]
- 84.Anfinsen CB. Principles that govern the folding of protein chains. Science. 1973;181:223–30. doi: 10.1126/science.181.4096.223. [DOI] [PubMed] [Google Scholar]
- 85.Meirovitch H, Scheraga HA. Empirical studies of hydrophobicity. 2. Distribution of the hydrophobic, hydrophilic, neutral, and ambivalent amino acids in the interior and exterior layers of native proteins. Macromolecules. 1980;13:1406–14. [Google Scholar]
- 86.Gill SJ, Dec SF, Olofsson G, Wadsö I. Anomalous heat capacity of hydrophobic solvation. J Phys Chem. 1985;89:3758–61. [Google Scholar]
- 87.Lazaridis T, Paulaitis ME. Entropy of hydrophobic hydration: a new statistical mechanical formulation. J Phys Chem. 1992;96:3847–55. [Google Scholar]
- 88.Makhatadze GI, Privalov PL. Energetics of interactions of aromatic hydrocarbons with water. Biophys Chem. 1994;50:285–91. doi: 10.1016/0301-4622(93)e0096-n. [DOI] [PubMed] [Google Scholar]
- 89.Paulaitis ME, Ashbaugh HS, Garde S. The entropy of hydration of simple hydrophobic solutes. Biophys Chem. 1994;51:349–57. [Google Scholar]
- 90.Garde S, Hummer G, Paulaitis ME. Hydrophobic interactions: conformational equilibria and the association of non-polar molecules in water. Faraday Discuss. 1996;103:125–39. [Google Scholar]
- 91.Lazaridis T. Solvent reorganization energy and entropy in hydrophobic hydration. J Phys Chem B. 2000;104:4964–79. [Google Scholar]
- 92.Lazaridis T. Solvent size versus cohesive energy as the origin of hydrophobicity. Acc Chem Res. 2001;34:931–7. doi: 10.1021/ar010058y. [DOI] [PubMed] [Google Scholar]
- 93.Ashbaugh HS, Truskett TM, Debenedetti PG. A simple molecular thermodynamic theory of hydrophobic hydration. J Chem Phys. 2002;116:2907–21. [Google Scholar]
- 94.Graziano G, Lee B. Entropy convergence in hydrophobic hydration: a scaled particle theory analysis. Biophys Chem. 2003;105:241–50. doi: 10.1016/s0301-4622(03)00073-5. [DOI] [PubMed] [Google Scholar]
- 95.Sturtevant JM. Heat capacity and entropy changes in processes involving proteins. Proc Natl Acad Sci USA. 1977;74:2236–40. doi: 10.1073/pnas.74.6.2236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Ben-Amotz D. Water-mediated hydrophobic interactions. Ann Rev Phys Chem. 2016 doi: 10.1146/annurev-physchem-040215-112412. at press. [DOI] [PubMed] [Google Scholar]
- 97.Kaminski G, Duffy EM, Matsui T, Jorgensen WL. Free energies of hydration and pure liquid properties of hydrocarbons from the OPLS all-atom model. J Phys Chem. 1994;98:13077–82. [Google Scholar]
- 98.Santoro MM, Bolen DW. Unfolding free energy changes determined by the linear extrapolation method. 1. unfolding of phenylmethanesulfonyl alpha-chymotrypsin using different denaturants. Biochemistry. 1988;27:8063–8. doi: 10.1021/bi00421a014. (22300/gm/nigms Journal Article Research Support, U.S. Gov’t, P.H.S. United States) [DOI] [PubMed] [Google Scholar]
- 99.Auton M, Bolen DW. Predicting the energetics of osmolyte-induced protein folding/unfolding. Proc Natl Acad Sci USA. 2005;102:15065–8. doi: 10.1073/pnas.0507053102. (NZ Times Cited:130 Cited References Count:30) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Auton M, Holthauzen L, Bolen D. Anatomy of energetic changes accompanying urea-induced protein denaturation. Proc Natl Acad Sci USA. 2007;104:15317–22. doi: 10.1073/pnas.0706251104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Auton M, Bolen DW, Rsgen J. Structural thermodynamics of protein preferential solvation: osmolyte solvation of proteins, aminoacids, and peptides. Proteins. 2008;73:802–13. doi: 10.1002/prot.22103. [DOI] [PubMed] [Google Scholar]
- 102.Auton M, Rosgen J, Sinev M, Holthauzen LM, Bolen DW. Osmolyte effects on protein stability and solubility: a balancing act between backbone and side-chains. Biophys Chem. 2011;159:90–9. doi: 10.1016/j.bpc.2011.05.012. (Matthew Rosgen, Jorg Sinev, Mikhail Holthauzen, Luis Marcelo F Bolen, D Wayne GM049760/GM/NIGMS NIH HHS/United States R01 GM049760-18A1/GM/NIGMS NIH HHS/United States R01 GM049760-19/GM/NIGMS NIH HHS/United States Research Support, N.I.H., Extramural Research Support, U.S. Gov’t, Non-P.H.S. Netherlands Biophysical chemistry Biophys Chem. 2011 Nov;159(1):90-9. Epub 2011 May 19) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Moeser B, Horinek D. Unified description of urea denaturation: backbone and side chains contribute equally in the transfer model. J Phys Chem B. 2014;118:107–14. doi: 10.1021/jp409934q. (Beate Horinek, Dominik eng Research Support, Non-U.S. Gov’t 2013/12/18 06:00 J Phys Chem B. 2014 Jan 9;118(1):107–14) [DOI] [PubMed] [Google Scholar]
- 104.Canchi DR, Garcia AE. Backbone and side-chain contributions in protein denaturation by urea. Biophys J. 2011;100:1526–33. doi: 10.1016/j.bpj.2011.01.028. (Deepak R Garcia, Angel E Research Support, U.S. Gov’t, Non-P.H.S. United States Biophysical journal Biophys J. 2011 Mar 16;100(6):1526–33) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Huang DM, Chandler D. The hydrophobic effect and the influence of solute–solvent attractions. J Phys Chem B. 2002;106:2047–53. [Google Scholar]
- 106.Choudhury N, Pettitt BM. Local density profiles are coupled to solute size and attractive potential for nanoscopic hydrophobic solutes. Mol Simul. 2005;31:457–63. [Google Scholar]
- 107.Wagoner JA, Baker NA. Assessing implicit models for nonpolar mean solvation forces: the importance of dispersion and volume terms. Proc Natl Acad Sci USA. 2006;103:8331–6. doi: 10.1073/pnas.0600118103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Stillinger FH. Structure in aqueous solutions of nonpolar solutes from the standpoint of scaled-particle theory. J Solut Chem. 1973;2:141–58. [Google Scholar]
- 109.Swaminathan S, Harrison SW, Beveridge DL. Monte Carlo studies on the structure of a dilute aqueous solution of methane. J Am Chem Soc. 1978;100:5705–12. [Google Scholar]
- 110.Stillinger FH. Water revisited. Science. 1980;209:451–7. doi: 10.1126/science.209.4455.451. [DOI] [PubMed] [Google Scholar]
- 111.Lazaridis T, Paulaitis ME. Simulation studies of the hydration entropy of simple, hydrophobic solutes. J Phys Chem. 1994;98:635–42. [Google Scholar]
- 112.Matubayasi N, Reed LH, Levy RM. Thermodynamics of the hydration shell. 1. Excess energy of a hydrophobic solute. J Phys Chem. 1994;98:10640–9. [Google Scholar]
- 113.Bowron DT, Filipponi A, Roberts MA, Finney JL. Hydrophobic hydration and the formation of a clathrate hydrate. Phys Rev Lett. 1998;81:4164–7. [Google Scholar]
- 114.Cheng Y-K, Rossky PJ. Surface topography dependence of biomolecular hydrophobic hydration. Nature. 1998;392:696–9. doi: 10.1038/33653. [DOI] [PubMed] [Google Scholar]
- 115.Hummer G, Garde S. Cavity expulsion and weak dewetting of hydrophobic solutes in water. Phys Rev Lett. 1998;80:4193–6. [Google Scholar]
- 116.Brandts JF. The thermodynamics of protein denaturation. I. The denaturation of chymotrypsinogen. J Am Chem Soc. 1964;86:4291–301. doi: 10.1021/ja00995a002. [DOI] [PubMed] [Google Scholar]
- 117.Privalov PL. Stability of proteins small globular proteins. Adv Protein Chem. 1979;33:167–241. doi: 10.1016/s0065-3233(08)60460-x. [DOI] [PubMed] [Google Scholar]
- 118.Sitkoff D, Sharp KA, Honig B. Accurate calculation of hydration free energies using macroscopic solvent models. J Phys Chem. 1994;98:1978–88. [Google Scholar]
- 119.Honig B, Nicholls A. Classical electrostatics in biology and chemistry. Science. 1995;268:1144–9. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 120.Sitkoff D, Ben-Tal N, Honig B. Calculation of alkane to water solvation free energies using continuum solvent models. J Phys Chem. 1996;100:2744–52. [Google Scholar]
- 121.Perkyns J, Pettitt BM. Dependence of hydration free energy on solute size. J Phys Chem. 1996;100:1323–29. [Google Scholar]
- 122.Choudhury N, Pettitt BM. On the mechanism of hydrophobic association of nanoscopic solutes. J Am Chem Soc. 2005;127:3556–67. doi: 10.1021/ja0441817. [DOI] [PubMed] [Google Scholar]
- 123.Lebowitz JL, Waisman EM. Statistical mechanics of simple fluids: beyond van der waals. Phys Today. 1980;33:24–30. [Google Scholar]
- 124.Chandler D, Weeks JD, Andersen HC. Van der Waals picture of liquids, solids, and phase transformations. Science. 1983;220:787–94. doi: 10.1126/science.220.4599.787. [DOI] [PubMed] [Google Scholar]
- 125.Garde S, García AE, Pratt LR, Hummer G. Temperature dependence of the solubility of non-polar gases in water. Biophys Chem. 1999;78:21–32. doi: 10.1016/s0301-4622(99)00018-6. [DOI] [PubMed] [Google Scholar]
- 126.Evans R, Henderson JR, Roth R. Nonanalytic curvature contributions to solvation free energies: influence of drying. J Chem Phys. 2004;121:12074–84. doi: 10.1063/1.1819316. [DOI] [PubMed] [Google Scholar]
- 127.Hu C, Kokubo H, Lynch G, Bolen W, Pettitt BM. Backbone additivity in the transfer model of protein solvation. Protein Sci. 2010;19:1011–22. doi: 10.1002/pro.378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Kokubo H, Harris RC, Asthagiri D, Pettitt BM. Solvation free energies of alanine peptides: the cost of flexibility. J Phys Chem B. 2013;117:16428–35. doi: 10.1021/jp409693p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Hilser VJ, Gómez J, Freire E. The enthalpy change in protein folding and binding: refinement of parameters for structure-based calculations. Proteins Struct Funct Bioinf. 1996;26:123–33. doi: 10.1002/(SICI)1097-0134(199610)26:2<123::AID-PROT2>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- 130.Harris RC, Mackoy T, Fenley MO. A stochastic solver of the generalized Born model. Mol Based Math Biol. 2013;1:63–74. [Google Scholar]
- 131.Harris RC, Mackoy T, Fenley MO. Problems of robustness in Poisson–Boltzmann binding free energies. J Chem Theory Comput. 2015;11:705–12. doi: 10.1021/ct5005017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Harris RC, Pettitt BM. The effects of geometry and chemistry on hydrophobic solvation. Proc Natl Acad Sci USA. 2014;111:14681–6. doi: 10.1073/pnas.1406080111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Harris JDRC, Pettitt BM. Multibody correlations in the hydrophobic solvation of glycine peptides. J Chem Phys. 2014;141:22D525. doi: 10.1063/1.4901886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Hummer G, Garde S, García AE, Pohorille A, Pratt LR. An information theory model of hydrophobic interactions. Proc Natl Acad Sci USA. 1996;93:8951–55. doi: 10.1073/pnas.93.17.8951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Harris RC, Pettitt BM. Examining the assumptions underlying continuum-solvent models. J Chem Theor Comput. 2015;11:4593–600. doi: 10.1021/acs.jctc.5b00684. [DOI] [PMC free article] [PubMed] [Google Scholar]


