Competition between Bending and Internal Pressure Governs the Mechanics of Fluid Nanovesicles

Abstract

Nanovesicles (∼100 nm) are ubiquitous in cell biology and an important vector for drug delivery. Mechanical properties of vesicles are known to influence cellular uptake, but the mechanism by which deformation dynamics affect internalization is poorly understood. This is partly due to the fact that experimental studies of the mechanics of such vesicles remain challenging, particularly at the nanometer scale where appropriate theoretical models have also been lacking. Here, we probe the mechanical properties of nanoscale liposomes using atomic force microscopy (AFM) indentation. The mechanical response of the nanovesicles shows initial linear behavior and subsequent flattening corresponding to inward tether formation. We derive a quantitative model, including the competing effects of internal pressure and membrane bending, that corresponds well to these experimental observations. Our results are consistent with a bending modulus of the lipid bilayer of ∼14k_bT. Surprisingly, we find that vesicle stiffness is pressure dominated for adherent vesicles under physiological conditions. Our experimental method and quantitative theory represents a robust approach to study the mechanics of nanoscale vesicles, which are abundant in biology, as well as being of interest for the rational design of liposomal vectors for drug delivery.

Small unilamellar vesicles (SUVs: ∼0.1 μm) perform multiple vital roles in biology. Prime examples of SUVs in cell biology include synaptic vesicles,¹ viral envelopes,² and extracellular vesicles for cell-to-cell communication.³ In addition, synthetic liposomes of this size are currently used as nanocarriers for drug delivery and developments for further applications continue.^4,5 Mechanical properties of natural and synthetic vesicles and nanoparticles are reported to influence their uptake by cells,⁶⁻¹¹ a phenomenon that is also supported by theoretical models.^12,13 Moreover, the mechanical stability of vesicles is a key limitation of their application for drug delivery.⁴ Consequently, multiple approaches have been developed to stabilize them.^14,15 Therefore, understanding the underlying mechanics of such vesicles is crucial for both understanding biological function and developing effective drug delivery strategies.

Although SUVs are an important class of vesicles, measurement of their mechanical properties is still challenging. The vast majority of previous studies of the mechanical properties of vesicles have been performed on giant unilamellar vesicles (GUVs: ∼10 μm). The techniques used for studying GUVs, e.g., micropipette aspiration and optical imaging of shape fluctuations,^16,17 are developed for these large vesicles and are less suitable for SUVs.^16,17 Instead, for mechanical studies of small vesicles, nanoscale indentations using atomic force microscopy (AFM) have been employed.¹⁸⁻²² However, from these experiments no consistent picture has emerged regarding the underlying mechanical properties. This is partly due to the fact that these nanoindentation studies of SUVs, in contrast to studies of GUVs,^16,17 have generally been interpreted using elasticity models with finite shear moduli, which are inappropriate for fluid bilayers that lack a shear modulus. Moreover, the potential influence of pressure has not been considered.

Here, we present an AFM-based approach to quantify the mechanical properties of small fluid vesicles as well as a model that captures their mechanical response. We performed imaging and nanoindentation measurements on single SUVs of 30–100 nm radius. For accurate measurements of vesicle size and shape we introduced corrections for tip dilation and deformation caused by imaging forces. The mechanical properties were investigated by performing nanoindentations with various AFM tip sizes. In parallel, we developed a model to describe nanoindentation of vesicles, which takes the fluidity of the membrane into account. We then quantitatively compared various aspects of the model with the experimental data, ultimately allowing us to estimate the contributions of bending and pressure to the vesicle stiffness. With the combination of AFM experiments and development of a theoretical model we both deepen the understanding of the mechanics of SUVs and we lay out a framework for more accurate measurements of mechanical properties of SUVs.

Results

Size and Shape Measurement of Nanovesicles

First, we imaged vesicles to determine their geometry (Figure 1a). Vesicles of complex lipid mixture, obtained by extrusion through 200 nm filters, were attached to a 0.001% poly l-lysine coated surface in PBS. Upon adhesion, we observed spreading of the initially spherical vesicles (Figure 1b). The expected resultant shape of an adherent vesicle is a spherical cap,²³ allowing determination of the radius of curvature of vesicles (R_c) by subtracting the tip radius (Figure S1). However, soft samples, such as these vesicles, can be affected by forces applied during AFM imaging. To determine the extent of this effect we imaged many 100 nm extruded vesicles at various force set points and noticed that their apparent height and especially width were underestimated already at low imaging forces (Figure 1c). To avoid underestimation of the height of vesicles we can use the zero force contact point from indentations (H_FDC), which shows that vesicles are 11 ± 1 nm (standard error of the mean (s.e.m.), number of measurements, each of which obtained on a separate vesicle (N) = 46) higher than the apparent height obtained from images for 200 nm vesicles (Figure S1). We used a subsequent correction for the radius of curvature, which is based on geometric arguments (Figure S1) and the experimental data in Figure 1c, to obtain the vesicle geometry and size. This analysis showed that the adhered liposomes adopt approximately hemispherical shapes (H_FDC/R_c ≈ 1) (Figure 1d). Furthermore, these measurements allow calculation of the original vesicle radius before adhesion (R₀), assuming surface area conservation (Figure 1e). We repeated these measurements for 100 nm extruded vesicles and sonicated vesicles, showing that the obtained size distributions correspond well with size distributions acquired with dynamic light scattering (DLS).

Figure 1.

Vesicle size and shape. (a) Topographic images of 200 nm extruded vesicles imaged at ∼100 pN. Dashed lines correspond to the line profiles in b with the same colors. (b) Line profiles through the maximum of 2 vesicles along the slow scanning axes, fitted circular arcs and estimated vesicle shapes after tip deconvolution under assumption that vesicles form spherical caps. (c) Height, fwhm, and radius of curvature determined from images of 100 nm extruded vesicles imaged at various forces. Error bars representing the s.e.m. are present, but are mostly smaller than the marker. For each imaging force >180 particles were analyzed. Linear fits with slope −0.020 (−0.003 to −0.036) (height), −0.056 (−0.069 to −0.045) (fwhm), and −0.053 (−0.063 to −0.042) (R_c) show that apparent fwhm and R_c decrease faster than the height with increasing imaging force (ranges mark 68% confidence intervals). (d) Shape of 200 nm extruded vesicles as characterized by height/R_c (N = 46). Inset shows example shapes corresponding to various ratios. (e) Spherical radius of the vesicles determined by AFM (histogram and Gaussian fits). R₀ = 87 ± 14 nm (standard deviation (st.d.), N = 46), R₀ = 59 ± 16 nm (st.d., N = 87), and R₀ = 31 ± 11 nm (st.d., N = 21) for extruded 200 nm, extruded 100 nm and sonicated vesicles, respectively. Square markers and error bars correspond to vesicle radii obtained with DLS: R₀ = 94 ± 20 nm (st.d.), R₀ = 75 ± 25 nm (st.d.), and R₀ = 39 ± 4 nm (st.d.).

Nanoindentations Reveal Strong Tip Size Dependent Behavior

Next, starting with 200 nm extruded vesicles, we performed nanoindentations by moving the AFM tip to the center of a vesicle and indenting it multiple times using a preset force, creating force distance curves (FDCs).²⁴ A typical FDC is shown in Figure 2a. Before such an indentation we always checked that we were working with a clean tip (Figure S2). As previously observed,^18,19 vesicles can withstand large deformations without permanent damage. This robustness is inferred from the lack of change in contact point after multiple indentations (Figure 2a) and confirmed by imaging afterward (Figure S3). Typically, we first performed a small indentation until 500 pN. The overlap between indentation and retraction suggests that the initial behavior is fully elastic (Figure 2a). In subsequent indentations, we deformed the vesicle until a sudden increase in stiffness (at ∼65 nm indentation in Figure 2a), after which we observed two discontinuities, likely corresponding to the two lipid bilayers being pushed together and penetrated (Figure 2a). The occurrence of only two bilayer penetrations suggests that the vesicles are unilamellar (see Figure S4).

Figure 2.

Force indentation behavior of vesicles. (a) Typical indentation curves obtained on an extruded 200 nm vesicle with a sharp tip (R_t ≈ 18 nm). Various colors represent subsequent indentations. Upper right panel shows the FDC made with the lowest set point, highlighting the overlap between approach (black) and retract (gray). Lower right panel shows a zoom on the dashed box in the main panel, highlighting the bilayer penetration events in the blue curve. (b) FDC made with a 43 nm tip. FDC shows a strong nonlinear response and subsequent discontinuity (Figure S4). Insets show images of a sharp tip (R_t ≈ 18 nm) and a blunt tip (R_t ≈ 43 nm) reconstructed using blind tip reconstruction. Black arrows indicate 50 nm in x,y, and z direction. (c) Average FDCs, constructed from a single FDC per vesicle (each normalized to vesicle radius), for all sharp tips combined, and for individual blunt tips. Legend states tip radius and number of vesicles measured for each condition. Error bars represent 68% confidence intervals of the estimated mean determined by bootstrapping (1000 repetitions). (d) Same data as c, but plotted on logarithmic scale. Force curves show an initial linear regime and subsequent onset of superlinear behavior. Inset shows individual FDCs made with the 43 nm tip.

Previously, both linear and strong superlinear force–distance relationships were reported in vesicle indentation studies.^18−20,22 We reasoned that the origin of this difference could be caused by differences in AFM tip size. To test this hypothesis, we used an approach based on AFM tip wear on high roughness surfaces.²⁵ Such wear leads to increased tip size, while the tip maintains its spherical apex, identical tip material and cantilever properties (Figure 2b, insets and Figure S5). The tip radius (R_t) was estimated using blind tip reconstruction. Next, tips with different radii (R_t = 18, 29, and 43 nm) were used to indent multiple vesicles (Figure 2a,b) and create average FDCs using a single FDC per vesicle (Figure S6). When we used the larger tips, we noticed a strong superlinear response (Figure 2b,c). The initial part of the average FDCs made with the various tips overlaps, but larger tips result in an early (0.05–0.1 R_c) stiffening. The initial response for larger tips is approximately linear and the stiffening leads to an exponent of ∼2, which is also observed in individual FDCs (Figure 2d). Interestingly, previous observations of linear behavior were made with smaller tips (R_t ≈ 15 nm)¹⁹ than observations of superlinear behavior (R_t ≈ 30 nm)^18,20 and with our current results we have a clear explanation for these differences.

High Vesicle Stiffness Is Inconsistent with Bending Alone

A single FDC per vesicle from the data gathered with sharp tips was used to measure the effective stiffness K of vesicles in the regime of linear response (0.02–0.1 R_c), resulting in a value of 0.015 ± 0.001 N/m (s.e.m., N = 46) for 200 nm extruded vesicles (Figure S7). Measurements with extruded 100 nm vesicles (K = 0.021 ± 0.001 N/m (s.e.m., N = 84)) and sonicated vesicles (K = 0.032 ± 0.002 N/m (s.e.m., N = 42)) had similar stiffness. To gain insight in the factors contributing to the vesicle stiffness, we proceeded to describe the mechanical behavior in terms of intrinsic membrane properties, i.e., a bending modulus κ and stretch modulus σ.^16,17,26,27 Since the applied force is perpendicular to the bilayer plane, the contribution of stretching is expected to be negligible. In case of bending energy alone, the vesicle effective stiffness, with units of energy per length squared, should be of order κ/R², where κ is the membrane bending modulus (typically 10–50 k_bT for a fluid bilayer).^28,29 For vesicles much larger than the membrane thickness, the relevant length scale R should be the vesicle radius of curvature R_c. For the typical radii in our experiments (R_c ∼ 100 nm), the stiffness is expected to be of order ∼10^–5 N/m. This strongly suggests that bilayer bending alone cannot account for the 3-orders of magnitude higher stiffness observed experimentally. Therefore, the obtained stiffness is likely dominated by an osmotic pressure difference over the membrane (ΔΠ). Vesicles adhered to the surface are deformed and the lipid bilayer is only able to stretch a few percent.³⁰ Hence, the internal volume of vesicles shrinks and the concentration of membrane impermeable solutes in the lumen goes up, causing an osmotic pressure difference over the membrane. This osmotic pressure in turn will make the vesicle resist indentation and thus increase the stiffness.

Development of an Indentation Model for Fluid Lipid Bilayers

With clean data in place and knowing the potential role of pressure, we set out to generate a quantitative model. Prior nanoindentation experiments of vesicles have been interpreted using the thin elastic shell model.^18,19 Elastic shell theory, however, does not account for membrane fluidity, as it assumes a finite in-plane shear modulus. Therefore, we introduce a model based on the Canham–Helfrich theory for fluid bilayer membranes.^27,31,32 This theory has been widely used for description and characterization of membranes in a variety of experimental studies, mostly at the micrometer scale.^16,17 In our model, we use symmetric bilayers with a bending modulus κ. We model a nanoindentation experiment as compression between two tips, which we do for two reasons. On the one hand, one may expect that deformation occurs mostly near the tip, in which case the deformation of one hemisphere in the symmetric case can be used to approximate the deformation of a hemispherical adherent vesicle. On the other hand, any attempt to model the adhesion more directly, would require knowledge of the adhesion strength, which we lack.

Following Seifert et al.,³² we characterize the (assumed axisymmetric) vesicle by a coordinate S, where 0 ≤ S ≤ S₁, and angle ψ (S), as well as Cartesian coordinates

1

and a similar expression for z (S) with cos ψ replaced by sin ψ. The origin is chosen to be the “South Pole” (Figure 3a). We impose the following conditions for a closed membrane: ψ (0) = 0, ψ (S₁) = π, and x(0) = x(S₁) = 0. In these terms, the free energy associated with bending is

2

where c₀ is the spontaneous curvature. We use zero spontaneous curvature and note that our results are insensitive to a spontaneous curvature on the order of the vesicle radius (Figure S8). Since the applied force is perpendicular to the bilayer plane, the contribution of stretching is expected to be negligible, and we assume the membrane to be laterally incompressible. We impose this constraint by the condition of constant area:

3

Figure 3.

Theoretical force indentation response based on Canham–Helfrich theory. (a) Parametrization of the model. An undeformed (solid black sphere) and deformed shape (dashed line) are shown. Z is the axis of symmetry. S is the length of the arc, which is zero at the “South Pole” and maximum at S₁. The angle ψ(S) is the angle between the contour and the x-axis at point S. (b) Theoretical indentation curve for reduced pressure (ΔΠR_c³κ^–1) 1800, for a parabolic tip with R_t = 0.1 R_c (solid line). In regime I (blue background), the apex of the vesicle flattens and the force response curve is slightly superlinear. In regime II (green) the response softens and a tether is formed. In regime III the response stiffens due to increased contact area between vesicle and tip. Dashed and dotted line show indentation curves with R_t = 0.25 R_c respectively R_t = 0.5 R_c. At the top shapes belonging to the 3 different regimes (indentations 0.2, 0.55, and 0.87 R_c from left to right) are visualized (arrows indicate axes in x,y, and z-direction). Lower right inset shows same curves on logarithmic scale (units same as main panel). (c) Inflection point determination. Upper panel shows a typical force distance curve illustrating the experimental determination of the inflection point for a 200 nm vesicle. FDC with ∼1000 points (in gray); smoothed FDC (in black); numerical derivative of FDC (blue line). Peak of derivative corresponds to the inflection point. Lower panel shows histogram with the localization of inflection point for 200 nm vesicles. Twenty-six out of 34 FDCs (∼76%) that do not show discontinuities before 0.3 R_c were used. Red arrow indicates predicted theoretical value.

Since this constraint reduces to a choice of S₁ for a given geometric shape defined by ψ, we choose to simply define ψ to be a function of σ = S/S₁ ∈ [0,1] (Supporting Information). Using this approach, e.g., for symmetric vesicle shapes, we define ψ (σ) as a sum over various shape modes:

4

We choose to use only the first six shape modes (n = 6) (Supporting Information, Figure S9).

To model an applied indentation force acting at the “North Pole”, we add an additional term to the energy F of the form fz(S₁). This approach corresponds to symmetric, point-like tips indenting the vesicles from both poles if only even shape modes a_n are allowed to be nonzero. We implemented symmetric parabolic tips of curvature R_t by the addition of a potential

5

to the energy, again, provided that only even modes a_n are allowed. There, the strength U₀ of the potential is simply chosen to be large enough to enforce that z > – R_tx²/2, which can only affect the lower hemisphere. However, due to the use of only even modes a_n, this condition is also imposed on the upper hemisphere.

Finally, a pressure difference is included. It is necessary to account for two distinct contributions, the luminal osmotic pressure Π_int and the external osmotic pressures Π_ext, where the former increases with decreasing volume

6

during indentation, while the latter is constant. Given a net pressure difference ΔΠ = Π_int – Π_ext, the change in free energy is given by dF = −ΔΠdV. We assume a dilute solution (ideal gas) form for the internal pressure

7

where (0) refers to prior to indentation.

To solve for the vesicle shape, we minimize the full energy, including bending, pressure, and tip shape, for a given force f, subject to the various constraints, including the area constraint. This yields the various shape amplitudes a_n, as well as the length S₁. From these, we obtain the height z(S₁) and indentation, as functions of the applied force f. Solving the shape for various forces then allowed construction of theoretical FDCs (Figure 3b). By working in reduced coordinates x̂ and ẑ, it becomes natural to express energies in units of 2πκ, lengths in units of πR_c, forces in units of 2κR_c^–1, stiffness in units of 2κR_c, and pressure in units of πκR_c^–3. In this model of a symmetric vesicle, the mechanical response depends only on a single unknown, the bending modulus, along with ΔΠ and the AFM tip radius, which can both be determined separately.

Experimental Observations Agree Well with the Model for Fluid Lipid Bilayers

The indentation response (Figure 3b) based on our model exhibits three regimes: (I) an approximately linear (exponent α ≈ 1.05) increase of force with indentation that corresponds to the flattening of the apex of the vesicle. The stiffness K for small indentations (<0.1 R_c) is ∼28κR_c^–2 (typically ∼10^–4 N/m) for an unpressurized vesicle, indeed much lower than the experimentally observed stiffness in this regime (typically ∼10^–2 N/m) (Figure S8). (II) A flattening of the FDC that is consistent with the onset of formation of an inward membrane tether at 0.35–0.40 R_c. The onset of this appears to be only weakly dependent on ΔΠ (Figure S8). For a point force or very sharp tip, tether formation would result in a force plateau. Extended inward tether formation has been recently observed with GUVs.³³ Moreover, this is in agreement with recent MD-simulations showing flattening of the FDC at similar indentations.⁹ (III) Finally, the finite size of the AFM tip prevents tether extension and leads to a tip dominated stiffening (α ≈ 2) (Figure 3b). Corresponding shapes to the three regimes are shown as insets in Figure 3b. A larger tip results in an earlier onset of the stiffening (Figure 3b) and an extended deformation zone of the vesicle (Figure S10). However, at low pressures no tether forms and, instead, deformation occurs on longer length scales, which results in the tip size dependence becoming apparent only at deeper indentations (Figure S8). Hence, the experimental observation of tip dependence for small indentations (Figure 2d) suggests that the vesicles are strongly pressurized. Furthermore, softening of experimental FDCs occurs at similar indentation as in the model at 0.31 ± 0.03 R_c (s.e.m., N = 26) (Figure 3c). Together, this shows that the model accurately describes the experimental results and that vesicles in our experiments are likely strongly pressurized.

Bending Modulus and Pressure Estimation

Finally, to understand the mechanical response of our vesicles, we need to take pressurization into account. Osmotic pressurization occurs when a vesicle is deformed on the surface in our experiments. However, it is probably a biologically relevant effect, since other interactions, such as adherence of vesicles to a cell surface, likely result in similar pressurization. Experimentally, we estimate the pressure from outward membrane tethers formed during retraction of the AFM tip (Figure 4a, Figure S11). It is well-known that the tether force corresponds to 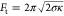, where σ is the tension in the membrane.^34,35 The tension is likely mostly due to the pressure difference over the membrane and hence we can use the Young–LaPlace equation (ΔΠ = 2σR_c^-1) to obtain a direct relationship between tether force and osmotic pressure over the membrane, with the bending modulus as the only unknown:ΔΠ = F_t(4π²R_cκ)⁻¹. Normalized pressure ΔΠR_c³κ^–1 can then be expressed as (R_cF_t)² (2πκ)⁻². Hence, we can now plot our experimental data using normalized units with κ as the only unknown.

Figure 4.

Bending modulus and pressure estimation. (a) Tether force measurements. Left panel shows a typical tether formed during a FDC (approach in gray, retrace in black). Blue lines indicate two fitted regimes; the difference is the tether force. Right panel shows histogram of tether forces measured in the retrace of 200 nm extruded vesicles (N = 46). (b) Dimensionless pressure versus dimensionless stiffness. In red the theoretically predicted curve. Markers show experimental data for 3 preparations of vesicles (200 nm, N = 42, 100 nm, N = 76; sonicated, N = 36). Bending modulus was used as single fitting parameter. (c) Pressure ΔΠ = F_t²(4π²R_cκ)⁻¹ estimated for the 3 combined samples. Median lies at 0.15 ± 0.02 MPa (68% confidence interval obtained by bootstrap).

Next, we obtained theoretical FDCs for various pressures (in units of κR_c^–3) and determined their stiffness (in units of κR_c) numerically (Table S1). Interpolation then allowed us to derive a general relationship, which is independent of κ, between the normalized pressure ΔΠR_c³κ^–1 and normalized stiffness KR_cκ^–1 of a vesicle (Figure 4b). Two regimes are visible in the resulting curve: the response is bending dominated when ΔΠ < ∼ 10 κR_c^–3 and pressure dominated for larger values of ΔΠ. The experimental data of the sonicated, and 100 and 200 nm extruded vesicles, when plotted in these units, collapse for any value of κ, demonstrating the general nature of the model (Figure S12). Moreover, fitting the experimental data to the theoretical curve yields a bending modulus of κ = 14 ± 1k_bT (s.e.m. obtained by bootstrap) (Figure 4b). This is a typical value of kappa for fluid lipid bilayers.^28,29 Finally, having this estimate for κ allows the evaluation of the pressure difference ΔΠ, which is remarkably high at ∼0.15 MPa (Figure 4c, Figure S11).

Discussion

Most recent nanoindentation studies of SUVs using AFM have been interpreted using shell elasticity models.¹⁸⁻²⁰ Such models, however, are for shells with finite shear moduli. It is well-known, e.g., from studies with GUVs,^16,17 that biological membranes have finite bending and stretching moduli but they usually have a vanishing shear modulus.^27,31 Importantly, for a spherical geometry, indentation is not possible without in-plane shear, which would increase shell elastic energy. Thus, previously used shell elasticity models with finite shear modulus are likely not suitable for fluid vesicles such as those studied here. Indeed, multiple aspects of the mechanical behavior observed in our experiments cannot be captured by predictions from such shell elasticity models. For example, we observed strong tip size dependence of the mechanical response, which is not expected in shell theory.³⁶ Also, onset of flattening of the FDC using the appropriate dimensions for a SUV in these theories is predicted to occur much earlier (∼0.05 R_c)¹⁹ than observed in our experiments (∼0.3 R_c). The theory presented here, which takes the fluidity of the lipid bilayer into account, does describe these aspects accurately.

We used our model to understand the mechanical behavior and estimate the bending modulus of 30–200 nm vesicles with membranes of complex lipid mixture. The predicted mechanical behavior and bending modulus estimates remain to be validated for different membrane compositions. However, it is expected that our approach and model will be broadly applicable for other artificial and natural vesicles in the same size range, as long as the membrane is fluid. Moreover, the mechanical behavior identified here, such as the inflection at 0.35–0.40 R_c and the strong tip size dependence, could potentially be useful to test the fluidity of the membrane of nanovesicles, since their occurrence is not expected for membranes with finite shear moduli.^19,36

In this study, we also showed that variation in tip size can have a dramatic effect on observed mechanical behavior probed by nanoindentation. To establish the role of tip size we applied a recently introduced method for broadening tip size without compromising the spherical apex of the tip.²⁵ Additionally, this method does not affect tip chemical properties or cantilever properties. The difference in mechanical response we observed here can be explained by the physical obstruction of lipid tether elongation by the tip leading to a stiffening of the response, which occurs earlier for broader tips. This difference might also explain the large variation in previously reported results of SUV mechanics.¹⁸⁻²² Hence, the approach taken in this study might both help in understanding the mechanical behavior and generating more reproducible AFM results for all kinds of nanoparticles.

AFM has recently gained popularity for performing size measurements on both natural and artificial vesicles.³⁷⁻³⁹ Here, we made several steps in image data analysis that could help in making such size measurements more accurate. First, we used a tip correction for spherical cap shaped vesicles. Tip radius is rarely negligible compared to the radius of SUVs and hence correcting for tip size is essential. A benefit of this correction is that no upfront assumption of degree of vesicle spreading is required. Second, to calculate the original spherical radius of the vesicle from the deformed shape on the surface one typically assumes that the vesicle volume is conserved.⁴⁰ In our study we used the assumption that the surface area is conserved, since the contents of the vesicle might leak, but the membrane is barely able to stretch.³⁰ Indeed, we show that vesicles have likely leaked part of their contents (Figure S11). Finally, we show that small normal imaging forces (∼100 pN) can already strongly deform SUVs, even in absence of lateral forces. These forces affect the obtained height, but affect the fwhm or radius measurements to an even higher extent. Exerting high imaging forces will therefore lead to underestimation of the vesicle size. We used a correction based on combination of imaging and indentation. This approach makes size measurements more time intensive, but these results show that for vesicle size measurements normal forces should at least be minimized. These analysis steps can be broadly applied for accurate measurements of vesicle size and shape.

Finally, our results show that liposomes are strongly stiffened by increased internal osmotic pressure due to deformation by surface adhesion. This finding is important for experimental measurements of vesicle mechanical properties because ignoring the effect of pressure on vesicle stiffness might lead to overestimation of the bending modulus of vesicles. This phenomenon is probably also important for vesicle behavior, such as vesicle uptake by cells. During cellular uptake similar vesicle deformations to those in our experiments are likely to occur, in that case due to adhesion to the cell.^12,41 Strong vesicle deformation is believed to impede full uptake.^12,13 However, pressurization due to deformation would stiffen the vesicle during spreading, which in turn would restrain further deformation and could hence facilitate cellular uptake. Recently, it was suggested that stiffness of nanoparticles can potentially be leveraged to establish specific drug delivery functions, such as cellular uptake.^11,12 For this purpose, it is critical to understand which factors determine the particle stiffness. Therefore, our observation that pressure can strongly affect the mechanical response of SUVs is of immediate interest for the rational design of vesicles for drug delivery.

Conclusions

To summarize, we have presented a thorough AFM nanoindentation based approach for quantification of the mechanics of fluid nanovesicles. In parallel we developed a theoretical model for vesicle indentation, which takes into account the fluidity of the membrane. The experimental data and model agree well and are consistent with a bending modulus of 14 k_bT. Moreover, we have shown the importance of pressure for the mechanics of deformed vesicles under physiological conditions. Our approach will help in the fundamental understanding of the mechanical response of fluid nanovesicles as well as extracting more reliable parameters from experimental data. Therefore, this is an important advance for future nanomechanical studies of natural vesicles, as well as engineered nanocarriers used for drug delivery.

Methods

Liposome Preparation

EggPC (P2772) and cholesterol (C8667) were ordered from Sigma. Brain PS (840032C) was ordered from Avanti Polar lipids. Egg PE and Egg SM were ordered from Lipoid. To make unilamellar liposomes, a protocol was adapted from Li et al.¹⁸ In short: lipid powder was dissolved at 20 mg/mL in a 9:1 chloroform to methanol solution in a round-bottom flask. Molar ratio of mixed lipids was 15% Egg PC, 17% Egg PE, 8% Brain PS, 15% Egg SM, and 45% cholesterol. This complex lipid mixture is designed to mimic the lipid concentrations in the red blood cell⁴² and similarly vesicles excreted by red blood cells.⁴³ For Figure 1c a slightly different composition was used with 4% Brain PS and otherwise similar ratios. The solvent was dried in a rotary evaporator (Buchi), first for 30 min at 400 mbar, and subsequently at least another 30 min at 100 mbar. Dried lipids were resuspended in PBS at 0.075 mg/mL final concentration. After vortexing and sonicating (1 min each), liposomes were frozen at −80 °C and thawed at 37 °C during 5 cycles. Finally, liposomes were extruded 30 times back and forth through two layers of 100 or 200 nm filters. In the case of sonicated vesicles, liposomes were sonicated for 15 min instead.

AFM Experiments

Vesicles were adhered to poly-l-lysine coated glass slides in PBS. Slides were first cleaned in a 96% ethanol, 3% HCl solution for 10 min. Afterward they were coated for 1 h in a 0.001% poly-l-lysine (Sigma) solution and dried overnight at 37 °C. They were stored at 7 °C for maximum 1 month. A 50 μL drop of vesicle solution was incubated on the glass slide. Vesicles were imaged in PeakForce Tapping mode on a Bruker Bioscope catalyst setup. All AFM measurements were performed in fluid (PBS). Force set point during imaging was 100 pN, unless stated otherwise. Nanoindentations were performed by first recording an image of a single particle, then indenting with forces of subsequently 0.5 nN, 2 nN, and 5 nN at 250 nms^–1 and typically making a final image after indentation to check for movement of the vesicle. Importantly, both before and after the vesicle indentation, the tip was checked for adherent lipid bilayers by pushing on the glass surface until a force of 5 nN (Figure S2), or 10 nN in the case of blunt tips. Silicon nitride tips with a nominal tip radius of 15 nm on a 0.1 N/m cantilever were used (Olympus; OMCL-RC800PSA). Individual cantilevers were calibrated using thermal tuning.

AFM Image Analysis

Both images and force curves were processed using home-built MATLAB software. Size and shape were analyzed from line profiles through the maximum of the vesicle along the slow scanning axis. Circular arcs were fit to the part of the vesicle above half of the maximum height to obtain the radius of curvature. For calculation of R₀ a minimum radius of the contact curvature of 5 nm was assumed, since a sharper contact angle is nonphysical.²³ For the data in Figure 1c vesicles with a minimum height and width of respectively 20 and 40 nm were used.

AFM FDC Analysis

Cantilever response was measured on the sample surface and fitted linearly. The resulting fit was subtracted from the measured response when indenting vesicles to obtain FDCs. Contact point was determined by using a change point algorithm,⁴⁴ and occasionally manually adjusted. Before fitting, FDCs were smoothed (moving average with window length of ∼10 points). All parameters (stiffness, inflection point, tether force) were determined using a single FDC per vesicle. This was typically the second FDC on each vesicle, since the first was made until a low force and did always go to deep enough indentations to determine, e.g., the inflection point. Overlap between first and second indentations was very high (Figure 2a,b). Stiffness of the liposomes was found by fitting a straight line in the interval between 0.02–0.1 R_c. This interval was chosen to have one consistent measure, in which the vesicles (including sonicated vesicles) showed no onset of superlinear behavior and no discontinuities. To find the inflection point, FDCs were smoothed further (moving average with window length of ∼40 points and Savitzky–Golay-filter with window length ∼20 point). Then, the derivative was taken numerically and the location of the maximum was obtained. For finding the tether force a home-built step-fitting algorithm based on the change point algorithm was used, which divides the curve into segments with slope 0. Only adhesion events extending beyond the contact point were included. For the fit in Figure 4b, an interpolating function through 13 calculated theoretical value pairs (Table S1) was created in Mathematica. The sum of the squared log Euclidian distance between the resulting curve and experimental values 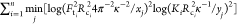, where x_j and y_j are theoretical values pairs for normalized pressure and normalized stiffness, was then minimized by adjusting κ as single parameter. Error bars were estimated by 500 bootstrapping repetitions, for which 154 experimental value combinations were randomly drawn and fitted.

Blind Tip Estimation

Measurements were performed in contact mode on UNCD Aqua 100 surfaces (Advanced Diamond Technologies, Inc.). Blind tip estimation was performed with software from the AFM manufacturer (NanoScope Analaysis). Images were flattened and low pass filtered. Tip estimation was performed using spike rejection (sigma mult 7) and discontinuity rejection (sigma mult 3), which exclude points and lines, respectively, based on a maximum difference in height compared to directly neighboring pixels. End radius (R_t) was estimated by fitting a spherical cap to the resultant tip image from 15 nm below the apex.

Dynamic Light Scattering

DLS measurements were recorded using the Zetasizer Nano S (Malvern Instruments Ltd.). Size measurements are based on intensity.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.6b07302.

• Supporting text with additional details of the model, tip and deformation corrections for AFM images of vesicles, FDCs made on the sample surface before vesicle indentations, vesicles shape before and after indentations, discontinuities in FDCs that likely do not correspond to bilayer penetration, tip reconstruction and wear on a high roughness crystalline diamond surface, density plots of all FDCs used for further analysis, vesicle stiffness, sensitivity of the model to spontaneous curvature and pressure, effect of increasing the number of modes in the model, calculated shapes upon indentation with a large radius tip, pressure estimation, sensitivity to fit parameter, and theoretical normalized pressure vs normalized stiffness values (PDF)

Author Contributions

^# W.H.R. and G.J.L.W. contributed equally.

The authors declare no competing financial interest.