Analysis of algae growth mechanism and water bloom prediction under the effect of multi-affecting factor

Abstract

The formation process of algae is described inaccurately and water blooms are predicted with a low precision by current methods. In this paper, chemical mechanism of algae growth is analyzed, and a correlation analysis of chlorophyll-a and algal density is conducted by chemical measurement. Taking into account the influence of multi-factors on algae growth and water blooms, the comprehensive prediction method combined with multivariate time series and intelligent model is put forward in this paper. Firstly, through the process of photosynthesis, the main factors that affect the reproduction of the algae are analyzed. A compensation prediction method of multivariate time series analysis based on neural network and Support Vector Machine has been put forward which is combined with Kernel Principal Component Analysis to deal with dimension reduction of the influence factors of blooms. Then, Genetic Algorithm is applied to improve the generalization ability of the BP network and Least Squares Support Vector Machine. Experimental results show that this method could better compensate the prediction model of multivariate time series analysis which is an effective way to improve the description accuracy of algae growth and prediction precision of water blooms.

1. Introduction

Algae bloom is a typical manifestation of eutrophication caused by extreme rise in nutrients such as nitrogen and phosphorus in lakes. Under the appropriate conditions of temperature, illumination, climate and hydrology, colored algae floaters are developed caused by explosive breeding in lakes (Yulia and Nadezhda, 2010). Thus, there is no clarity about the critical factors and mechanism of algae blooms, and some effective technologies of prevention and treatment of algae blooms are still lacking in general. It is convenient for relevant departments to adopt countermeasures to reduce the hazards under the condition of predicting the occurrence of blooms accurately.

2. Related work

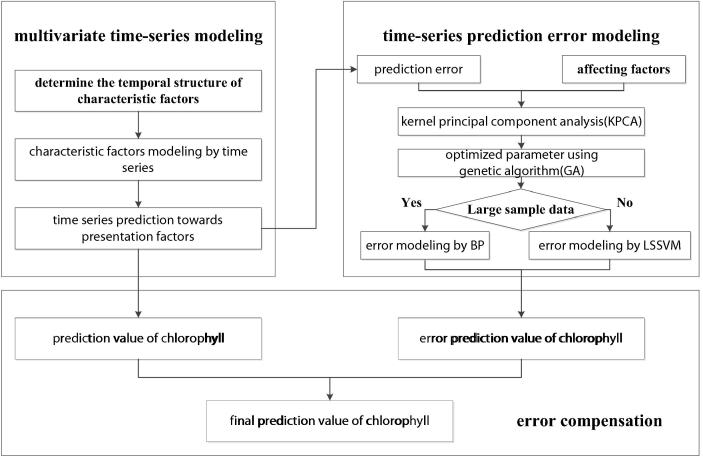
The method of time series analysis is a kind of vital mathematical tool to study stochastic process by means of using historical data to speculate the future trend of development of things (Luo and Wu, 2009, Wang et al., 2013, Wang et al., 2014, Wang et al., 2016, Jin, 2013, Jin et al., 2013a, Jin et al., 2013b). However, a model that is suited for reflecting the relationship between outer affecting factors and data needs to be adopted to make compensation toward the prediction error of time series. To make time series prediction using neutral network is widely paid attention to which has access to success with its good nonlinear properties and distributed storage structure as well as high fault tolerance (Frank et al., 2001, Zhang and Qi, 2003). Li has adopted PNN to make prediction toward blooms which has provided an effective way for forecasting (Li et al., 2011). Zhu has adopted improved BP network to forecast the highest point of nonlinearity about chlorophyll (Zhu et al., 2011). Mulia has developed a hybrid model combined with ANN and GA (Genetic Algorithm) to make real-time forecast as well as mid-long term forecast (Mulia et al., 2013). However, traditional BP(Back Propagation) network and Least Squares Support Vector Machine have some shortcomings such as slow convergence speed and are plunged into local extreme that may lead to low precision unable to accurately describe the strength of the bloom (Xia et al., 2009). For this reason, KPCA (Kernel Principal Component Analysis) is applied to make dimension reduction toward affecting factors while GA is used to make optimization toward random initial weights. Finally, BP network and Least Squares Support Vector Machine are used to make compensation toward the prediction result gotten from time series which is an effective way to improve the accuracy and to realize complementarity between time series and intelligent method.

3. Material and methods

3.1. Biochemical mechanism analysis of algae bloom

Eutrophication is a phenomenon of water pollution caused by excessive nitrogen, phosphorus and other plant nutrients. Aquatic organisms, especially the large number of algae reproduction, change the amount of biomass population and destroy the ecological balance of the water body. The algae are synthesized by photosynthesis using the sunlight and inorganic compounds. The process of eutrophication is as follows.

$$106{\text{CO}}_2+16{\text{NO}}_3^{-}+{\text{HPO}}_4^{2-}+112{\text{H}}_2\text{O}+18{\text{H}}^{+}+\text{energy}+\text{trace element}\to {({\text{CH}}_2\text{O})}_{106}{({\text{NH}}_3)}_{16}({\text{H}}_3{\text{PO}}_4)+138{\text{O}}_2$$

Here ${({\text{CH}}_2\text{O})}_{106}{({\text{NH}}_3)}_{16}({\text{H}}_3{\text{PO}}_4)$ is chemical formula of algae.

The algae cell concentration shows the number of algae in the water and the intensity of the bloom. Before water blooms, algae growth rapidly, the concentration of algal cells increased continuously from tens of thousands to hundreds of millions per liter. Chlorophyll-a is one of the important components of algal cells. All algae contain chlorophyll-a. The content of chlorophyll-a is closely related to the type and quantity of algae in water, it is also related to the quality of water environment. Therefore, through the determination of chlorophyll-a in water, the number of algae in the water and water quality status is reflected.

Fig. 1 is the two-dimensional molecular structure of chlorophyll-a.

Figure 1.

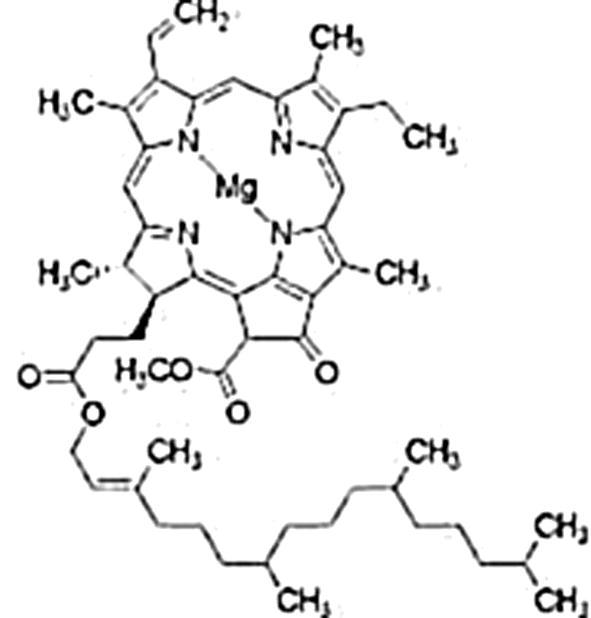
Molecular structure of chlorophyll-a.

Water samples are collected from sampling point using a plastic bucket, and then the collected water samples are loaded into a transparent glass jar and placed in the incubator, cultured under constant temperature of 5000Lx, 26 °C. The algae density and chlorophyll-a of water sample are measured at the same time every day. Algae density is measured by blood cell counting plate microscopy. Chlorophyll-a is measured by the United States YSI company’s 6600 type multi-function water quality monitor (Fig.2).

Figure 2.

Microscopy and experimental incubator.

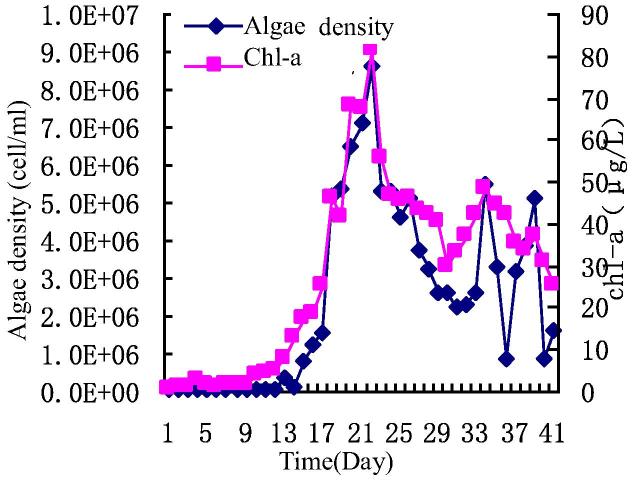
The correlation between algae density and chlorophyll-a is studied. The growth curve was measured by the algae density and chlorophyll-a daily measurement data (Fig. 3).

Figure 3.

Algae growth curve.

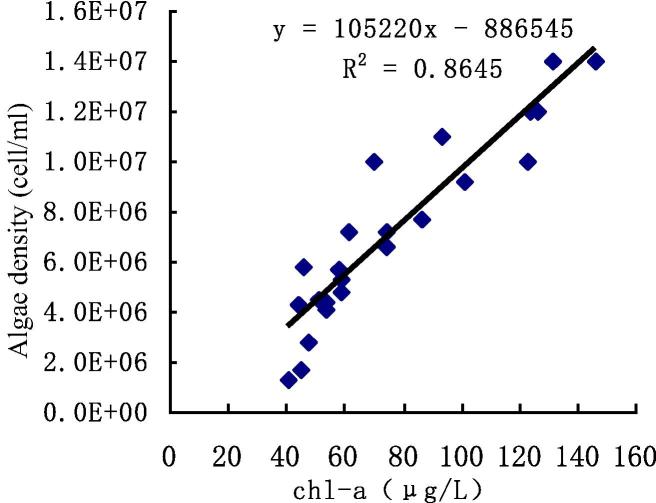
Chlorophyll-a concentration and algal density data are shown as follows (Fig. 4).

Figure 4.

Correlation analysis of algae density and chlorophyll-a.

Through regression analysis of chlorophyll-a and algal density data, the relationship between chlorophyll-a and algal density is linear, and there is a significant correlation between them. Fig. 5 shows the algae cell.

Figure 5.

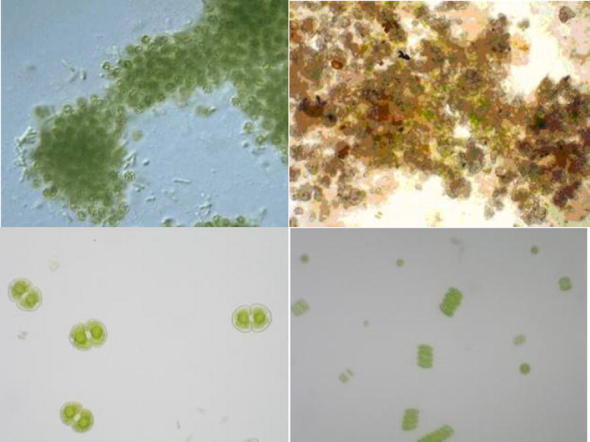
Algae cell.

Through the process of photosynthesis, the main factors that affect the reproduction of the algae can be analyzed, such as the nutrient content of water body, light, water temperature and other physical and chemical factors. Nitrogen is a component of algae, phosphorus is directly involved in the process of photosynthesis, respiration, activation of enzyme system and energy conversion, both of which are essential for the growth of algae and the occurrence of water bloom. Algae bloom generally occurs in the condition of high temperature, small wind and slow lake flow. In addition, PH value in water is mainly affected by the content of carbon dioxide. The PH value changes, mainly due to the photosynthesis process by which algae absorb carbon dioxide and release oxygen, affecting the ion balance. Therefore, in this paper, the selected influence factors on the prediction of chlorophyll-a are as follows: PH value, oxygen consumption (OC), water temperature (T), turbidity, total nitrogen (TN), total phosphorus (TP), dissolved oxygen (DO), and so on.

3.2. The analysis of error compensation

During the growth of algae, influenced by physical and chemical mechanism, seasonal alternation and random disturbance, there may be non-stationary, periodic and random changes in the time series of characteristic factors. Hence, this paper forecasts the chlorophyll concentration by the time series model. However, the formation process of algae bloom is irregular and chaotic, time series model can only describe the linear part of the algae growth process of water bloom. There is a large nonlinear error to simulate and predict the water bloom based on the statistics of the time series model.

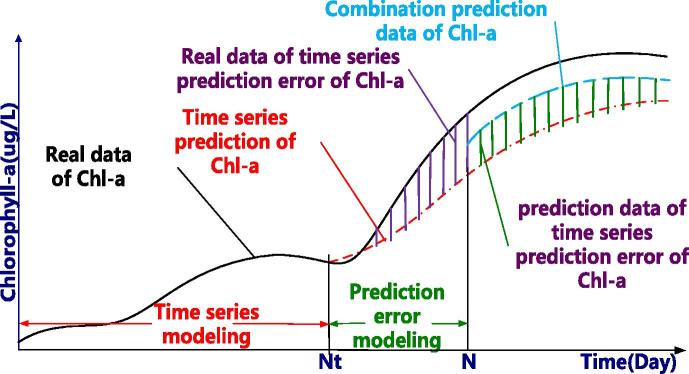
In order to reduce the nonlinear error caused by time series model prediction, the formation process of algae bloom is regarded as a non-stationary random process and the superposition of nonlinear interference in this paper. Nonlinear error prediction model is established using intelligent model. A comprehensive forecasting method of algae bloom was proposed by combining the time series model with the intelligent nonlinear model. The error compensation schematic diagram is shown in Fig. 6.

Figure 6.

Error compensation schematic diagram.

The prediction method toward bloom mentioned in this paper is shown in Fig. 7. Firstly, characteristic factors before the time of N_t(1 < N_t < N) is modeled and the prediction value of chlorophyll-a is obtained at the time of N_t + 1, N_t + 2, …, N, N + 1, N + 2,…. Here N is the total sampling time, N_t is the sampling time for time series modeling. Secondly, correlation of prediction error of chlorophyll-a by time series and affecting factors at the time of N_t + 1, N_t + 2,…, N is analyzed. Thirdly, the factor which has a larger influence on the error of chlorophyll-a is screened out as the input of nonlinear error prediction model. And then prediction error of chlorophyll-a is predicted by the model mentioned above. Finally, the final prediction data of chlorophyll-a is obtained by making linear superposition between chlorophyll error data predicted by error prediction model and chlorophyll-a data predicted by time series model.

Figure 7.

Flow chart of forecasting method of blooms in lakes based on error compensation.

3.3. Multivariate time series bloom predictive modeling

In this paper, time series model is applied to make prediction toward chlorophyll-a and specific steps are as follows.

• (1)
  The characteristic factors vector Y_t is decomposed into superposition of trend term F_t, periodic term C_t and stochastic term R_t.

  $$Y_t=F_t+C_t+R_t$$ (1)
• (2)
  Combining the trend term F_t, periodic term C_t with stochastic term R_t, the multiple cycle non-stationary time series model is acquired namely the multiple regression, hidden periodicity and autoregressive model that is shown as follows.

  $$\begin{array}{cc}\hfill Y_t=& F_t+C_t+R_t\hfill \\ \hfill =& F_t+C(t)+{\displaystyle \sum _{j=1}^p}{H}_j{R}_{t-j}+E_t\hfill \end{array}$$ (2)
• (3)
  According to the best prediction principle (namely the principle of minimum mean square error of prediction), presentation factor is forecasted forward for l(l = 1,2,…)steps at the time of N_t.

  $$Y_{N_t+l}=F_{N_t+l}+C(N_t+l)+{\displaystyle \sum _{j=1}^p}{H}_j{R}_{N_t+l-j}$$ (3)

3.4. The KPCA of error affecting factors

Not only the complexity of model will increase but also the stability will decline if all affecting factors are considered for error modeling. Meanwhile, some affecting factors have less influence than others and there exists nonlinear relationship among them so that KPCA is applied to make analysis whose basic steps are as follows (Wang et al., 2005).

• (1)A group of data composed of affecting factors and prediction error of chlorophyll-are written as X with (N − N_t) × n dimensions.
• (2)
  Nonlinear relationship among them is extracted by KPCA. Assume that ϕ has realized the mapping from input space X to characteristic space F whose covariance matrix is

  $$C=\frac{1}{n}{\displaystyle \sum _{i=1}^n}\varphi (x_i)\varphi {(x_i)}^T$$ (4)

  Here X is data matrix, ϕ(x_i) is the training sample after conversion, C is covariance matrix.
• (3)
  The projection V^k of x in characteristic space F is gotten according to correlation between affecting factors and prediction error of chlorophyll.

  $$V^k\varphi (x)={\displaystyle \sum _{i=1}^n}{a}_i^k\left[\varphi (x_i)\varphi (x)\right]$$ (5)

  Here a_i^k is constant, V^k is principal component in the characteristic space (k = 1,2,…, n).
• (4)
  The final affecting factors of prediction error of chlorophyll can be confirmed according to cumulative contribution rate that is over 85% whose synthesis evaluate function J is

  $$\begin{array}{cc}\hfill & J={\displaystyle \sum _{i=1}^m}{V}^k\varphi (x)={\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=1}^n}{a}_j^k\left[\varphi (x_j)\varphi (x)\right]\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=1}^n}{a}_j^{k}K(x\text{,}{x}_i)\text{,}K(x\text{,}{x}_i)\hfill \\ \hfill & =\exp \left(-\frac{\Vert x-x_i{\Vert }^2}{{\sigma }^2}\right)\text{,}(\sigma >0)\hfill \end{array}$$ (6)

  Here K(x, x_i) is the kernel function and σ is the width parameter.

3.5. The error prediction model of GA-BP

The error prediction of GA-BP neural network is used in the case of large sample data (N − N_t).

• (1)The initial population is generated by prediction error and affecting factors at the time of N_t + 1, N_t + 2,…, N. The optimal GA-BP prediction model is established by optimal solution of initial weights of BP neural network using GA.
• (2)The prediction of chlorophyll error is trained by BP network based on the affecting factors as input of GA-BP model and prediction error of chlorophyll-as output at the time of N + 1, N + 2,….
• (3)The final prediction of chlorophyll error is acquired by trained GA-BP network based on the affecting factors as input and prediction error of chlorophyll-as output at the time of N + 1, N + 2,….

3.6. The error prediction model of GA-LSSVM

The error prediction of GA-LSSVM is used in the case of small sample data (N − N_t).

• (1)The initial population is generated by prediction error and affecting factors at the time of N_t + 1, N_t + 2,…, N. The optimal GA-LSSVM prediction model is established by optimal regularization parameter and kernel function parameter using GA.
• (2)The prediction of chlorophyll error is trained by LSSVM based on the affecting factors as input of GA-LSSVM model and prediction error of chlorophyll-as output at the time of N + 1, N + 2,….
• (3)The final prediction of chlorophyll error is acquired by trained GA-LSSVM based on the affecting factors as input and prediction error of chlorophyll-as output at the time of N + 1, N + 2,….

3.7. Error compensation

The final prediction data of chlorophyll is obtained by adding prediction data of chlorophyll by time series model and chlorophyll error prediction data by error prediction model of GA-BP or GA-LSSVM at the time of N + 1, N + 2,….

4. Results

The method of algae growth analysis and water bloom prediction based on prediction error of chlorophyll-a time series using GA-BP and GA-LSSVM model is adopted in this paper as follows:

• (1)The data mentioned in this paper are provided by lake administration in province of Jiang Su, China that include totally 1050 days and 9 indexes of water quality monitoring data from June 2009 to 2012 which are shown in Table 1. The data sampling period is every four hours and the efficient samples are 8765.

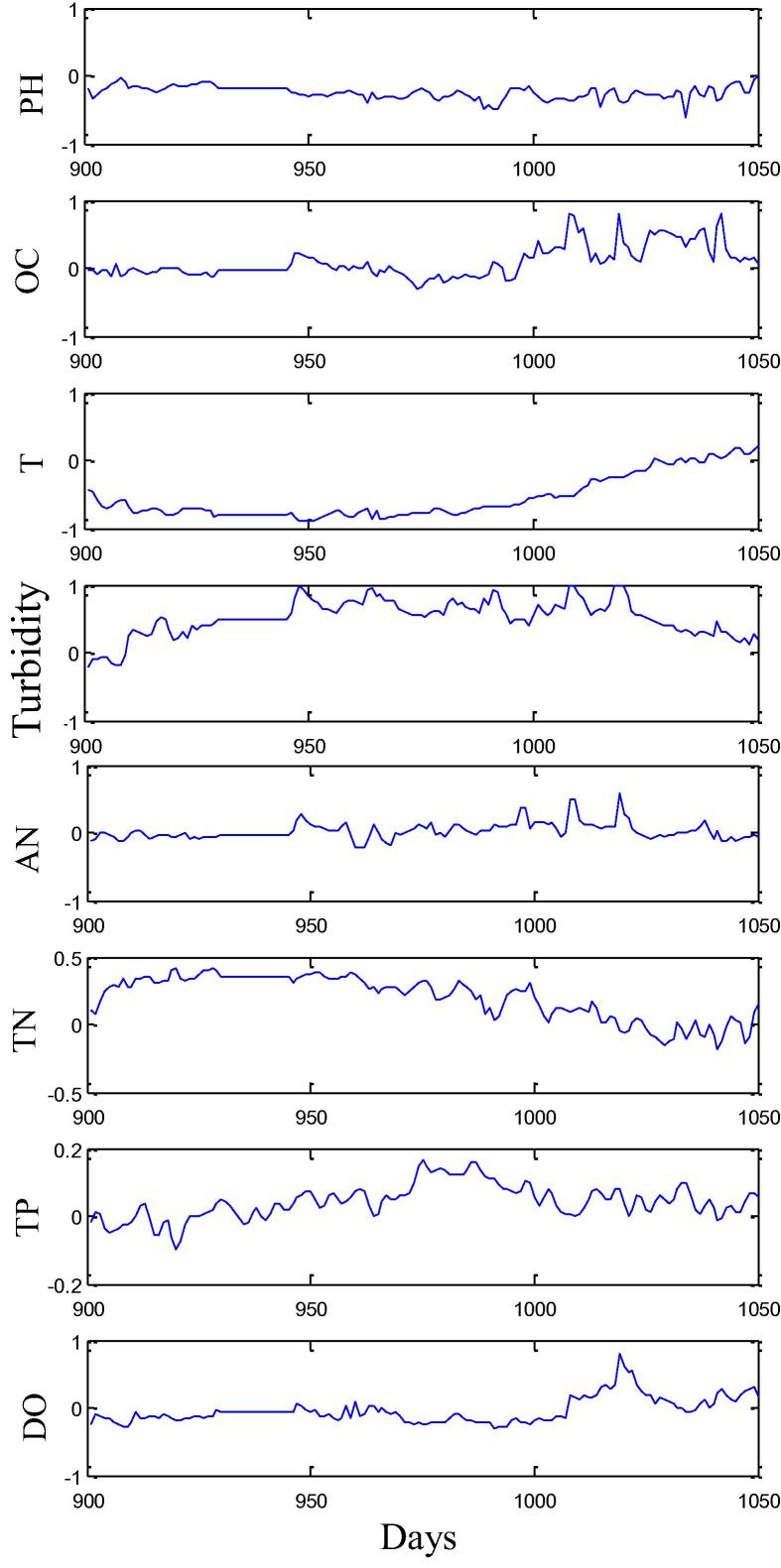
  Chlorophyll-a is the characterization factor of bloom while the remaining factors are influencing factors. The data recorded by monitoring equipment include 1050 days in total. The monitoring data from 1 to 900 days are used for modeling (N_t = 900) while data from 901 to 1050 days are used for predicting (Fig.8).

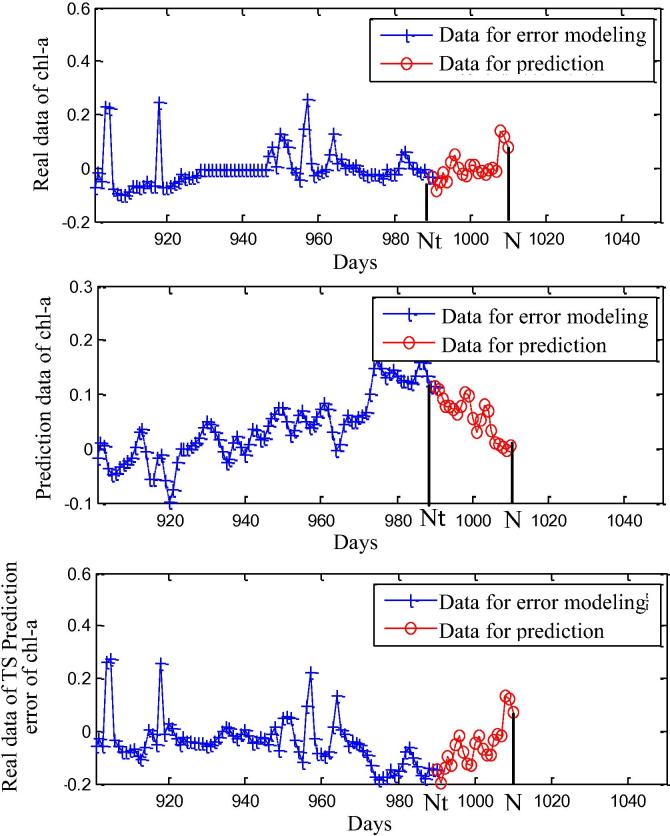
  Real data of chlorophyll-a, time series prediction data of chlorophyll-a and real data of time series prediction error of chlorophyll-a from 901 to 990 days are used as data for error modeling. Real data of chlorophyll-a, time series prediction data of chlorophyll-a and real data of time series prediction error of chlorophyll-a from 991 to 1010 days are used as data for prediction modeling. Then, N = 990, N − N_t = 90 (Fig. 9).

• (2)The result of error affecting factors acquired by KPCA is shown in Table 2.

  According to Table 2, absolute value of DO larger and prediction error is large in the first principal component while absolute value of TP and TN is large in the second one. Therefore, DO, TP, TP are selected as affecting factors of prediction error.

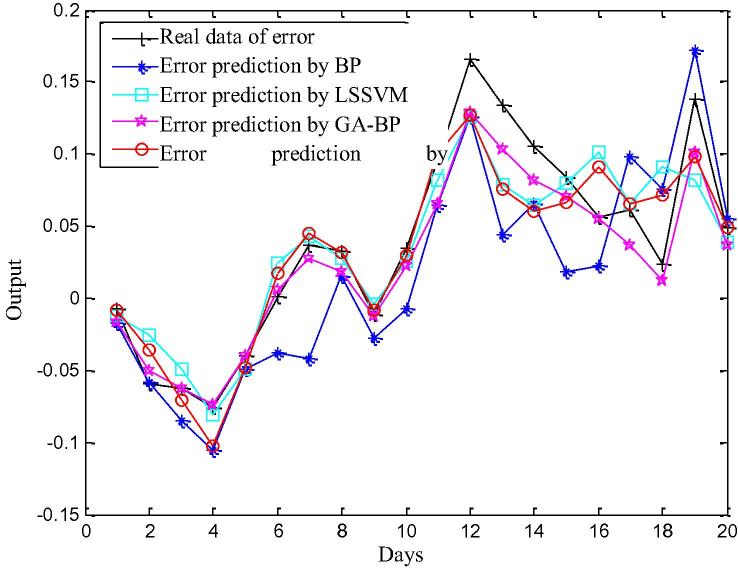
• (3)Affecting factors and prediction data of time series prediction error of chlorophyll-a are modeled by BP, GA-BP, LSSVM and GA-LSSVM. The error prediction data are shown in Fig. 10.
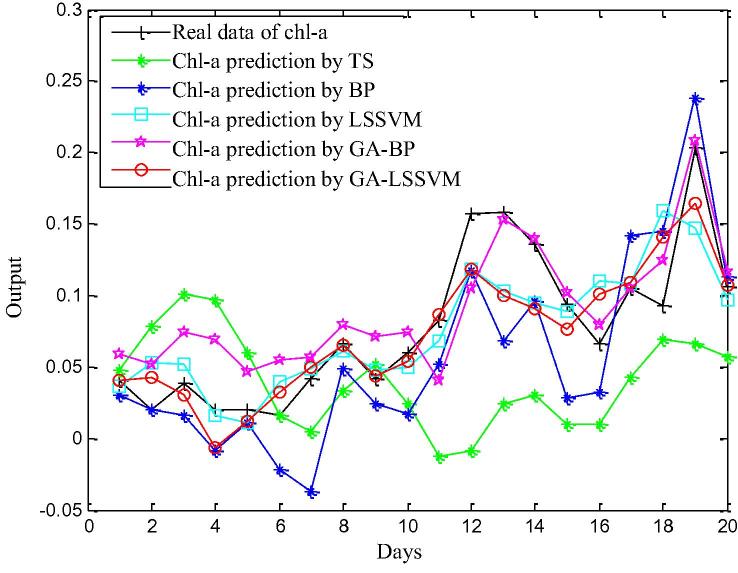
• (4)The final prediction data are acquired by adding time series prediction data of chlorophyll-a and prediction data of time series prediction error of chlorophyll-a by BP GA-BP, LSSVM and GA-LSSVM, which are shown in Fig. 11.

  The ratio between prediction difference value and variance of true value is considered as the relative error to make analysis (Table 3).

Table 1.

The monitoring list of bloom characteristic factors.

Name	PH	OC	T	Turbidity	TN	TP	DO	Chl-a
Unit	Null	mg/L	°C	NTU	mg/L	mg/L	mg/L	mg/L

Figure 8.

Affecting factors monitoring data.

Figure 9.

Chlorophyll-a data for error modeling and prediction.

Table 2.

The Kernel Principal Component Analysis feature vector of error influencing factors.

Principal component	PH	OC	T	Turbidity
1	−0.143	−0.157	0.062	−0.108
2	0.276	0.069	0.245	−0.238
3	−0.147	0.226	0.364	−0.052
Principal component	TN	TP	DO	Prediction error
1	−0.065	0.343	0.311	0.572
2	−0.689	0.685	0.047	−0.421
3	−0.567	0.035	0.093	0.349

Figure 10.

Error prediction.

Figure 11.

Chlorophyll-a prediction.

Table 3.

The error comparison of final prediction with five methods.

	TS	BP	GA-BP	LSSVM	GA-LSSVM
Err (%)	116.9	64.2	40.7	43.4	35.4

The final prediction precision of time series is the lowest of all. The precision of GA-BP model is higher than that of BP model. Meanwhile, the precision of GA-LSSVM is higher than LSSVM. Due to the small sample (N − N_t = 90), the precision of GA-LSSVM is higher than GA-BP, so that the prediction method mentioned in this paper is verified.

5. Conclusions

The prediction method of bloom combined with time series model and intelligent nonlinear model is put forward aiming at the error caused by time series in this paper. Firstly, the correlation between algae density and chlorophyll-a is studied by chemical mechanism analysis. Secondly, chlorophyll-a and multi affecting factors are predicted using time series. KPCA is applied to make dimension reduction toward affecting factors according to prediction error caused by time series which is an effective way to select DO, TP, N as affecting factors of prediction error. Finally, GA-BP and GA-LSSVM models are used for error modeling and error compensation. The result shows that the model mentioned above can better compensate for time series prediction and fix the error timely when outer affecting factors have a large change, which is an effective way to improve prediction accuracy.

In practice, an effective prediction method not only lies in the complexity of algorithm but also in understanding the mechanism of blooms and reliable data. Some single intelligent prediction models do offer a means to make prediction with a limited precision. Therefore, some intelligent model combined with other methods is a good way to make prediction. Meanwhile, some special factors such as weather are not considered into modeling. Thus, the comprehensive model including traditional prediction model and expert system would be taken into account to improve the accuracy in the future.