Toward a Better Compression for DNA Sequences Using Huffman Encoding

Abstract

Due to the significant amount of DNA data that are being generated by next-generation sequencing machines for genomes of lengths ranging from megabases to gigabases, there is an increasing need to compress such data to a less space and a faster transmission. Different implementations of Huffman encoding incorporating the characteristics of DNA sequences prove to better compress DNA data. These implementations center on the concepts of selecting frequent repeats so as to force a skewed Huffman tree, as well as the construction of multiple Huffman trees when encoding. The implementations demonstrate improvements on the compression ratios for five genomes with lengths ranging from 5 to 50 Mbp, compared with the standard Huffman tree algorithm. The research hence suggests an improvement on all such DNA sequence compression algorithms that use the conventional Huffman encoding. The research suggests an improvement on all DNA sequence compression algorithms that use the conventional Huffman encoding. Accompanying software is publicly available (AL-Okaily, 2016).

1. Background

Data compression, in a nutshell, is the process of encoding information using fewer bits than the original representation. The process helps to reduce the consumption of valuable resources such as storage space and transmission bandwidth. Data compression has been an active research topic for long, and a number of algorithms have been proposed for different types of data such as texts, images, videos, audio, and others. In general, there are two types of compression: lossy and lossless. The lossy scenario may exclude some unnecessary data during the compression such as frequencies in audio data that a human will not be able to hear. The lossless algorithms, in contrast, ensure the exact restoration of information and do not allow any loss in data. Several lossless tools for text compression exist in the literature such as the Lempel–Ziv (LZ), Lempel–Ziv–Welch (LZW), gzip (Gailly and Adler, 2003), and bzip2. These tools work well for texts with large alphabet sizes (such as English letters) on the other hand, are not tailored toward compressing biological sequences, which constitute a relatively small alphabet size, and some specific biological characteristics such as repeats.

Taking DNA sequences for example. DNA sequences are composed of just four letters (bases) A, C, G, and T. In addition, there are repeats in different forms within a DNA sequence, which have important biological implications. These repeats, often known as motifs, appear in the sequences with a much higher frequency statistically. DNA sequences can have repeats within chromosomes, the genome itself, or genomes from different species. The number of repetitions in a set of sequences depends on the amount of similarity between the sequences. These repeats usually happen in the noncoding regions of the genomes. They are likely to occur in genomes of individuals of the same species. The genomes of members of the same species are largely similar, that usually reaches 99.5%.

A few algorithms that are specifically designed to compress DNA sequences have recently been proposed. As opposed to general-purposed compression algorithms, these DNA sequence compression algorithms are referred to as special-purpose ones and have been categorized as the Horizontal-mode and the Vertical-mode compression (Grumbach and Tahi, 1994a). Horizontal-mode compresses the DNA sequence using the information in that sequence. Methods falling within this category include those that are substitution-based, statistics-based, two-bit based, and grammar-based. In contrast, Vertical-mode compression compresses a set of DNA sequences using the information from the entire data set, usually by referencing substrings to a different substring from the dataset. In general, Vertical-mode compression performs better for large DNA datasets (Bakr and Sharawi, 2013).

For substitution-based methods, the DNA sequence is compressed by replacing a long DNA string with a smaller one that is mapped back to the original one when decoded. BioCompress is a representative implementation (Grumbach and Tahi, 1994a). A subsequent version, the BioCompress2, further adopts the order-2 arithmetic coding to encode non-repeat regions of DNA sequences (Grumbach and Tahi, 1994b). The reported results indicate a compression ratio of 19.50% by BioCompress and 22.22% by BioCompress2, compared with the 25% by a general-purpose tool (Grumbach and Tahi, 1994a).

Similar to BioCompress, the Cfact uses a two-pass process to look for the longest exact and reverse complement repeats (Rivals et al., 1997). To do that, the algorithm at first builds the suffix tree of the sequence then encodes the sequence using LZ in the second pass. The non-repeat regions are encoded by using two-bits per base. The GenCompress makes the use of approximate repetitions (Chen et al., 2000). In this algorithm, an inexact repeat subsequence is encoded by a pair of integers and a list of edit operations for the mutations in those repeats. The algorithm has two versions: GenCompress-1, which uses the Hamming distance (to substitute) for the repeats, and GenCompress-2, which uses the edit distance which involves the operations of deletion, insertion, and substitution when encoding the repeats. The compression result of GenCompress is within an average of 21.77%, however, it does not perform well when compressing large sequences.

Furthermore, another tool DNACompress further improves the results of GenCompress (Chen et al., 2002). The tool runs in two passes. Firstly, all approximate repeats along with their complementary palindromes are found; this step is carried out by the PatternHunter software (Ma et al., 2002). After that, both of the approximate repeats and the non-repeat regions are encoded by the LZ compression technique. The result of DNACompress indicates a better compression ratio with an average of 21.56%. The tool is able to handle larger sequences in less time, compared to GenCompress.

Algorithms based on statistical methods usually work on replacing the most frequent symbols by a shorter code. The CDNA algorithm is the first to combine statistical compression with approximate repeats (Loewenstern and Yianilos, 1999). Other statistical DNA compressors include the ARM algorithm (Allison et al., 1998) and the XM algorithm (Cao et al., 2007).

Grammar-based compression methods use a context-free grammar to represent the input text. After that, the grammar is transformed into a symbol stream to be finally encoded in binary. An example of a grammar-based compression algorithm is the DNASequitur (Cherniavsky and Ladner, 2004). This algorithm works by inferring a context-free grammar to represent the sequence as an input. The results do not show any better compression ratio compared to the other methods. Algorithms that adopt the two-bit based method, which assigns 2 bit for each base of the four DNA bases before the encoding process, also exist (Saada and Zhang, 2015).

1.1. Approach

New technologies for producing high-definition audio, videos, and images are growing at a fast pace, leading to create a massive amount of data that can exhaust easily storage and transmission bandwidth. To use the available disk and network resources more efficiently, the raw data in those large files are often compressed. The Huffman algorithm is one of the most used algorithms in data compression (Huffman et al., 1952). Huffman encoding is a lossless encoding algorithm that generates variable length codes for symbols that are used to represent information. By encoding high frequency symbols with shorter codes and low frequency symbols with longer codes, the original information is encoded as small as possible. The codes are constructed in such a way that no code is a prefix of any other code, a property that enables unambiguous decoding. While it was proposed half a century ago, the Huffman algorithm and its variants are still actively used in the development of new compression methods (Glassey and Karp, 1976; Parker, 1980; Longo and Galasso, 1982; Ahlswede et al., 2006).

Given the DNA sequence “ACTGAACGATCAGTACAGAAG,” for example, which contains twenty one bases, its bit count is therefore 21 × 8 = 168 bits, assuming each base is stored with an 8-bit ASCII code, where A = 01000001, C = 01000011, G = 01000111, and T = 01010100.

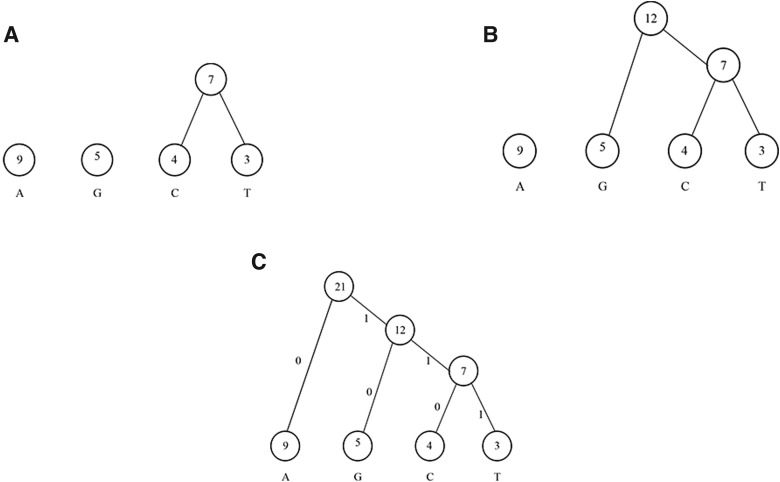
The compression by Huffman method works as follows. The algorithm at first counts the frequency of each base, as described in Table 1. Each base, along with its associated frequency, is to be regarded as a tree node. Mark the four initial nodes as unprocessed. Then, a binary tree is constructed by iterating the following steps. Firstly, search the two unprocessed nodes with the lowest frequencies. Then, construct a parent node whose frequency is the sum of those of the two child nodes. Lastly, return the parent node to the unprocessed list of nodes. The tree construction process ends when all nodes are processed. The construction of the Huffman tree for the given example is illustrated in Fig. 1. Note that, the left link of each internal node is labeled 0, while the right link is labeled 1.

Table 1.

Base Frequency and New Bit Representation

Base	Frequency	The new representation	The old representation
A	9	0	01000001
G	5	10	01000111
C	4	110	01000011
T	3	111	01010100

FIG. 1.

The steps of constructing a Huffman tree.

After building the Huffman tree, each symbol has a new bit representation that can be extracted by traversing the edges and recording the associated bits from the tree's root to the desired symbol (which must be located at the leaf level). For example, the path from the root to base A results in a bit representation of 0, while the path from the root to base T results in 111. The new bit representation for each base is described in Table 1.

The new bit count after encoding is (9 × 1) + (4 × 3) + (5 × 2) + (3 × 3) = 40, with a compression ratio of 40/168 = 23.8%.

Typical algorithms extending from the concept of Huffman encoding when approaching DNA sequence compression include the G-SQZ (Tembe et al., 2010) and the Huffbit (Rajeswari et al., 2010). During the first scan, G-SQZ encoding calculates frequency for each base+quality pair and constructs a Huffman tree to generate pair-specific codes. High-frequency pairs have shorter codes. During a second scan, a header and encoded read-blocks is written to an output binary file. Each read block consists of read identifier fields followed by encoded base-quality data. The Huffbit compresses both repetitive and nonrepetitive regions in a DNA sequence. This algorithm first constructs an extended binary tree and then derives the Huffman codes from the created extended binary tree. The authors claim a compression ratio of 12%, 20%, and 26% in the best, average, and worst-case scenarios, respectively.

Also extended from the Huffman encoding, this research, aims to incorporate the characteristics of DNA sequences when constructing the binary tree, in order to derive bit-codes that allow a better compression ratio than using the conventional Huffman encoding. Hence, this research suggests an improvement for all DNA sequence compression algorithms that employ the conventional Huffman encoding.

2. Compression Algorithm

2.1. The algorithm in general

First of all, the general approach of compression is to find the most repetitive substrings with a length up to a maximum value of k. Note, k is empirically determined. Then encode the resultant substrings using the bit-codes. Specifically, given a set of DNA sequences G and an integer k, construct the set of substrings S, where 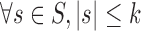, so that encoding all members of S results in the best compression ratio.

The algorithm in general works as follows.

• 1. Perform run-length encoding (RLE) on the genome to encode homopolymers (i.e. sequences of identical bases). In brief, RLE for the sequence DDDDDDD is D7, where 7 is the count for the RLE and D is the base of the homopolymer. Some counts may appear more frequently than others. Therefore, the frequencies of the counts are collected as well. Let R be the set of tuples of the counts and their frequencies.

• 2. Scan G and collect the frequency of each substring of length no more than k. Let A be the set of all collected substrings.

• 3. Find the set of substrings S, so that by encoding this set the best compression ratio is reached. This is the major step of the algorithm. For this, a few different encoding schemes based on the Huffman encoding are designed and discussed in the following subsections.

• 4. Genome files may contain non-DNA bases. These bases need to be encoded into bits too. For this, scan G and collect the frequency of any non-DNA base. Let N be the set of all collected bases. This, along with Step 2, can be merged as a one step.

• 5. Input S, R (collected in Step 1), and N to the Huffman algorithm. The output will be the bit-codes that best represent the members of the three sets.

• 6. Scan G and encode each substring in G with its Huffman code. This will convert the DNA sequence to an (encoded) bit string.

• 7. Convert the bit string into ASCII codes to produce the compressed DNA sequence. This step involves adding headers of the words (members of the three sets) that were encoded and their bit-codes, as well as some other headers. These headers will be used during the decompression process.

2.2. Unbalanced Huffman tree

For Step 3, we propose a new implementation of the Huffman encoding called unbalanced Huffman encoding/tree (UHT). For DNA encoding, forcing the Huffman tree to be unbalanced is a better approach than the standard Huffman tree (SHT), because when the UHT method is applied, three bases can be guaranteed to be encoded using two bits and the fourth using three bits. This, however, can not be done by the SHT method; as encoding for instance the best 20 k-mers (substrings of length no more than k), for instance, will encode each of the four bases with more than 2 bits.

Forcing the Huffman tree to be unbalanced can be performed by the following steps.

• 1. Sort all collected k-mers, where k ≥ 2, based on their frequencies.

• 2. Select the k-mer with the maximum frequency, say f.

• 3. Scan all k-mers with frequencies lower than f in a descending order until a k-mer with a frequency lower than 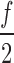is found. Select this k-mer and set f to be equal to the frequency of the selected k-mer. Note that, no selected k-mer is properly contained in another. This allows reducing the overlapping among the selected k-mers; hence, increasing the number of bases to be compressed.

• 4. Repeat steps 2 and 3 until no more k-mers can be selected.

• 5. Finally, input the k-mers (that were selected above) in addition to the four bases, to the Huffman encoding algorithm.

2.3. UHT that prioritizes encoding the k-mers that contain the least frequent base

Using the UHT method, the base with the lowest frequency, x, will be encoded using 3 bits, where the other bases will be encoded using 2 bits each. As a result, encoding the k-mers (k ≥ 2), which contain at least one occurrence of x, will be more feasible. For this, Step 1 is modified to allow only the frequencies of the k-mers, that contain x at least once, to be collected. We denote this method as UHTL (UHT that prioritizes encoding the k-mers that contain the Least frequent base).

2.4. Multiple SHT/UHT/UHTL encoding

Note that, a single SHT, UHT, or UHTL allow to encode few k-mers and they might be insufficient. Moreover, in UHT/UHTL approach, there is no control on the number of k-mers to be encoded as the design is restricted to select k-mers that form an unbalanced Huffman tree, regardless of the number of such k-mers. One way to allow more k-mers to be encoded is to apply multiple encoding. We denote this approach as Multiple SHT/UHT/UHTL encoding MSHT/MUHT/MUHTL, respectively.

To apply multiple Huffman encoding, multiple markers can be identified/implanted in the genome sequences, so that there is a Huffman encoding associated with each marker. The marker can be a pattern or a periodic position, for example the position at every some position x. Then, only the k-mers after such markers are encoded. Clearly, adopting periodic positions as markers is faster than the pattern markers. In fact, instead of computing the periodic positions or pattern markers, one can simply divide the genome sequence into multiple partitions, then encode each partition using an independent set of k-mers (hence an independent bits encoding).

An extra cost is required because of the multiple-partitions, i.e. storing the headers, (k-mers and their bit-codes which will be used during the decompression process) for each partition. However, this will allow to encode the best local k-mers for each partition, which eventually saves more space than storing global k-mers when no partitioning is performed. Moreover, more k-mers are encoded than the single global scheme.

2.5. RLE encoding

Encoding a homopolymer using Run Length Encoding (RLE) encoding is dependent on the base that forms the homopolymer, whether it's a DNA or a non-DNA base, and its length. If the bases of a homopolymer are a DNA base and since each base is expected to ultimately be encoded using at most 3 bits, such homopolymers can be encoded by RLE if its length is greater than 10. Since the RLE count is expected to be encoded using at least 16 bits plus 2–3 bits for the base, this indicates that encoding a homopolymer is feasible when its length is more than 10. For homopolymers of non-DNA bases, the RLE count is required to be greater than 2, because any non-DNA base is expected to be encoded using 8 bits or more.

Moreover, there are different approaches to encode the RLE counts. First of which, is by recording the position of the RLE's encoding along with the count. But since the sizes of the genomes are usually in millions or billions, this will require at least 22 bits (genome size of 5 million) to store the positions plus the needed space for storing RLE counts (i.e. it needs more than 30 bits in total). A second approach is to add a special character before and after the RLE count, then encode the special character and the count. However, this will require at least 8 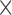2 bits to encode both of the special characters plus encoding the count (at least 24 bits in total). Both approaches are expected to be not feasible compared to the adopted approach as the maximum length of encoding using the adopted approach (Steps 1 and 5 in the general algorithm) is expected to not exceed 24 bits.

3. Experimental Results and Analysis

3.1. Data sets

DNA data sets of five different species have been used in the experiments, including Cholerae, Abscessus, Saccharomyces, Neurospora and Chr22 (NCBI, 2001, 2008, 2011, 2013, 2015), respectively. Additional information about these data sets is presented in Table 2.

Table 2.

Data Sets Used

	Length (in bases), M	File size, MB	Data format
Cholerae	4	4.1	FASTA
Abscessus	5	5.2	FASTA
Saccharomyces cerevisiae	12	12.3	FASTA
Neurospora crassa	38	41.6	FASTA
Chr22	50	51.5	FASTA

The sequence data format that our tool supports is the FASTA (with extensions .fasta and .fna). FASTA is a text-based data format which starts with a description, usually followed by a nucleotide sequence.

As a preprocessing step, we convert the bases from lower-case to upper-case. This preprocessing is needed only for genomes containing lowercase bases within the entire sequence. Among the five genome datasets used in our experiments; two genomes, Saccharomyces and Neurospora, needed a preprocessing step.

3.2. Results of SHT, UHT, UHTL, and MUHTL

We implemented the algorithms that are proposed in section 5.2. Scripts for the SHT, UHT, MUHTL methods, and for decompressing the compressed files have been made available online. Note that the UHTL method becomes a special case of the MUHTL method when the number of partitions is set to one. The programs are available at https://github.com/aalokaily/Unbalanced-Huffman-Tree. The SHT script takes only one parameter, which is the number of k-mers to encode, where the k-mer range is 1–10. The UHT script does not take any parameter, and the k-mer range is 1, 3–10. The reason of exclusion k = 2 is discussed in the following section. The MUHTL script takes one parameter, i.e. the number of partitions. This parameter is left to the users so that the size of each partition can be changed any time. By observing our empirical results, we recommend the partition size to be around 1 Mbp. In addition, the k-mer range for the MUHTL method is 1–10. Lastly, the decompressing script takes no parameter. It simply takes the compressed file as an input. The compressed file can be generated using any of the three scripts, where the file extension is ‘.uht.’ When compared with the other tools, the MUHTL method is used with a partition size of 1 Mbp.

Note that with the SHT approach, the straightforward method for selecting the k-mer set to be encoded is to select the x most frequent k-mers. Clearly, when x is large, more bits are needed to encode each selected k-mer, as described in Table 3. While, there is no control on how many k-mers to be selected using the UHT approach, as the number of k-mers to be encoded is determined by the number of k-mers that are selected so that they form an unbalanced Huffman tree.

Table 3.

Compression Ratios of the Five Genome Files Using Different Huffman Tree Implementations, SHT, UHT, and UHTL

	SHT, %				UHT, %		UHTL, %
Data set	k = 8	k = 16	k = 32	k = 64	k∈[2,10]	k∈[3,10]	k∈[2,10]	k∈[3,10]
Cholerae	29.10	30.12	32.05	31.11	27.12	26.72	26.01	26.33
Abscessus	29.07	29.07	29.58	30.29	26.72	25.33	25.72	25.44
S. cerevisiae	29.95	29.86	30.27	30.99	27.29	25.97	26.09	25.59
N. crassa	30.59	30.27	32.07	31.70	27.15	26.97	26.34	26.69
Chr22	22.47	22.70	23.97	23.13	20.85	20.57	19.75	20.11

In SHT, the selection of the number of the most frequent k-mers is shown, whereas, in UHT and UHTL, the k-mer range is specified. Note that single bases are also encoded, by default.

SHT, ; UHT ; UHTL, .

After analyzing the results of the UHT method using k-mers with k in [2,10] and in [3,10], we noticed that the results of the range [3,10] turn out better, as shown in Table 3. This is likely due to the following fact. With the UHT encoding, there is a base that must be encoded using 3 bits and a 2-mer must be encoded using 4 bits. If the 2-mer does not contain the 3-bit base (in other words, contains any of the other bases that is encoded using 2-bits), encoding this 2-mer becomes unnecessary as it can be encoded using 4 bits, while encoding its bases independently also costs 4 bits. This is not the case when the range is [3,10], since any 3-mer, regardless of its bit-code, will always produce a worthwhile compression. In fact, this reason is the motivation of the UHTL method, as discussed in Section 5.2. A comparison between the UHT and UHTL methods based on the compression ratio is given in Table 3.

We carried out experiments on the MUHTL method using different numbers of partitions (1, 2, 4, 8, 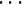, 512). The results are given in Table 4.

Table 4.

Compression Ratios of Different Partitions of MUHTL

Data set	Cholerae	Abscessus	S. cerevisiae	N. crassa	Chr22
	Size, M	Size, M	Size, M	Size, M	Size, M
P	CR, %	CR, %	CR, %	CR, %	CR, %
1	4	5.2	12.3	41.6	51.5
	26.01	25.72	26.09	26.34	19.75
2	2	2.6	6.2	20.8	25.8
	25.96	25.67	26.11	26.36	19.81
4	1	1.3	3.1	10.4	12.9
	25.99	25.59	26.10	26.33	19.74
8	0.5	0.65	1.5	5.2	6.4
	25.91	25.65	26.08	26.33	19.80
16	0.26	0.32	0.77	2.6	3.2
	25.98	25.66	26.10	26.28	19.85
32	0.13	0.16	0.38	1.3	1.6
	26.00	25.63	26.11	26.16	19.88
64	0.06	0.08	0.19	0.65	0.8
	26.05	25.71	26.15	26.16	19.90
128	0.03	0.04	0.09	0.33	0.4
	26.19	25.81	26.19	26.16	19.93
256	0.016	0.02	0.05	0.16	0.2
	26.47	26.03	26.25	26.18	19.97
512	0.008	0.01	0.02	0.8	0.1
	27.05	26.45	26.44	26.23	20.06

P denotes the partition count. Size denotes the partition size.

CR, compression ratio.

After analyzing the compression results of different partitions' sizes, and using the tested datasets in the experiments, we observed that the best compression ratios by the MUHTL method took place when the partition size is around 1 Mbp. Hence, we recommend this size when using the current MUHTL method. The compression results based on this partition size, were used when the MUHTL method was compared with the other tools, as discussed in the following subsections.

3.3. Comparison with tools based on Huffman encoding

Compression tools that are used in our comparison are gzip (Gailly and Adler, 2003), and bzip2. Gzip is a popular compressor that works on different systems and is able to compress various data types including DNA sequences. It is a variation of LZ algorithm, that utilizes Huffman encoding in which duplicated strings are spotted. It employs two Huffman trees; one that compresses the match lengths of a duplicated string and the other for the distance. In most cases, we found that its compression ratio is around 30%.

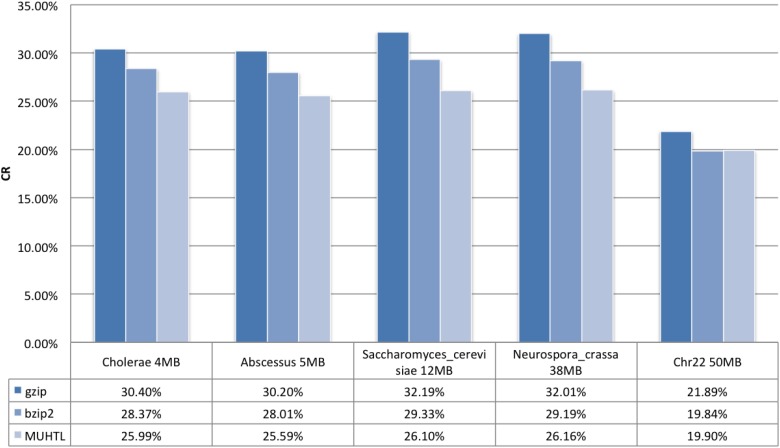
The bzip2 is also widely used, and it outperforms gzip and most of the conventional LZ-based algorithms. In the tested sequences, bzip2 yields a better compression ratio in all of the DNA sequences, as shown in Fig. 2. In the core of this compressor, the Burrows–Wheeler Transform (BWT) and Huffman encoding are utilized.

FIG. 2.

Compression ratio of the MUHTL method and two well-known general purpose compressors, gzip and bzip2. Datasets are in fasta format.

The results of the MUHTL method outperformed gzip in all the tested genomes with a performance gain as high as 23.33%. The compression ratios of Cholerae and Abscessus are 16.9% and 18%, respectively. The sequence length did not appear to play a role in the compression ratios. Instead, we believe the distribution of bases and the selected k-mers play the main role in the compression efficiency. For example, the gzip yields similar compression ratios for Saccharomyces (12 MB) and Neurospora (38 MB) that are 32.19% and 32.01%, respectively, as shown in Fig. 2. The improvement of the MUHTL method over gzip for these datasets is 23.33% and 22.35%, respectively. The dataset of Chr22 relies more on the RLE encoding before the compression process, hence tested all tools show a better compression ratio for Chr22 than the other datasets. As expected, the MUHTL method outperformed gzip by only 10% in this case.

Both bzip2 and the MUHTL method are also compared based on their compression ratios, where the MUHTL method demonstrated almost consistent dominance. For Chr22, bzip2 showed a slight edge over the MUHTL method by just 0.3%. However, the MUHTL method outperformed bzip2 in all the other datasets by 9.15%, 9.45%, 12.37%, and 11.58% for Cholerae, Abscessus, Saccharomyces, and Neurospora, respectively.

Acknowledgment

The authors acknowledge the NSF grant OCI-1156837 for expenses incurred by the publication of this article.

Authors' Contributions

A.A. initiated the research and developed and implemented the algorithms. B.A. and S.A. independently conducted the experimental study and analysis. C.H.H. directed the research. All authors contributed to article preparation and research discussions leading to the completion of this article.

Author Disclosure Statement

No competing financial interests exist.