Task-Based Regularization Design for Detection of Intracranial Hemorrhage in Cone-Beam CT

Abstract

Prompt and reliable detection of acute intracranial hemorrhage (ICH) is critical to treatment of a number of neurological disorders. Cone-beam CT (CBCT) systems are potentially suitable for detecting ICH (contrast 40-80 HU, size down to 1 mm) at the point of care but face major challenges in image quality requirements. Statistical reconstruction demonstrates improved noise-resolution tradeoffs in CBCT head imaging, but its capability in improving image quality with respect to the task of ICH detection remains to be fully investigated. Moreover, statistical reconstruction typically exhibits nonuniform spatial resolution and noise characteristics, leading to spatially varying detectability of ICH for a conventional penalty. In this work, we propose a spatially varying penalty design that maximizes detectability of ICH at each location throughout the image. We leverage theoretical analysis of spatial resolution and noise for a penalized weighted least-squares (PWLS) estimator, and employ a task-based imaging performance descriptor in terms of detectability index using a nonprewhitening observer model. Performance prediction was validated using a 3D anthropomorphic head phantom. The proposed penalty achieved superior detectability throughout the head and improved detectability in regions adjacent to the skull base by ~10% compared to a conventional uniform penalty. PWLS reconstruction with the proposed penalty demonstrated excellent visualization of simulated ICH in different regions of the head and provides further support for development of dedicated CBCT head scanning at the point-of-care in the neuro ICU and OR.

I. Introduction

Intracranial hemorrhage (ICH) is associated with a variety of neurological disorders, including hemorrhagic stroke and traumatic brain injury [1]. Non-contrast-enhanced multi-detector CT (MDCT) is the current front-line modality for diagnosis of acute ICH with high sensitivity but is commonly only available in a dedicated radiology suite or emergency department. Compared to MDCT, cone-beam CT (CBCT) systems typically have smaller footprint, greater portability, and lower cost, and therefore are potentially more suitable for diagnosis of acute ICH at the point of care (e.g., neurological ICU, urgent care, ambulance, and sports and military theatres). However, current CBCT systems face major challenges in image quality required for detecting ICH (blood-to-brain contrast 40-80 HU, size down to 1 mm) [1].

Recent research aims to develop high-quality CBCT for detection of ICH using mobile C-arms or a dedicated head CBCT system designed specifically to provide optimal performance in ICH detection [2]. A high-fidelity artifact correction framework has also been proposed and demonstrates major reduction in artifacts in CBCT of the head, including scatter, beam hardening, and detector lag and glare [3]. Moreover, a statistical reconstruction method has been proposed to compute statistical weights that account for noise in the measurements following artifact corrections, demonstrating improved noise-resolution tradeoffs in CBCT of ICH compared to conventional filtered backprojection [4].

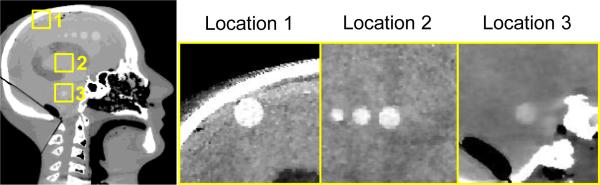
This work addresses two important questions with respect to high-quality CBCT of ICH. First, statistical reconstruction tends to produce nonuniform spatial resolution and noise in the image. For example, Figure 1 shows an image reconstructed using penalized weighted least-squares (PWLS) as in [4], and the conspicuity of the same ICH lesion in various locations of the head is seen to depend strongly on the local spatial resolution and noise characteristics. Various methods have been developed to address this problem by designing a spatially varying penalty that encourages uniform spatial resolution or noise. For example, Fessler et al. designed a penalty that includes a spatially varying certainty term to encourage a uniform point spread function (PSF), providing uniform spatial resolution throughout the image [5]. A second important consideration is that imaging performance should be defined with respect to a specific task [6]. In the case of ICH detection, the task is to discriminate a low-contrast, mid-frequency lesion from a relatively uniform background. One way in which statistical reconstruction can be leveraged to maximize performance is to design a penalty that maximizes detectability index (d′) [7] for a particular task. However, due to nonuniform spatial resolution and noise, a penalty designed to maximize detectability at one location may not necessarily maximize detectability at another. The two considerations described above are therefore intimately connected, and one may design a spatially varying penalty (analogous to the one in [5]) to maximize detectability.

Figure 1.

Illustration of nonuniform spatial resolution and noise in a 3D image reconstructed by PWLS. The anthropomorphic head phantom containing simulated ICH was scanned on a FPD-CBCT test-bench at 24 mGy. Grayscale window: [−10, 110] HU.

In this work, we propose a spatially varying penalty that optimizes detectability for ICH detection at all locations through a CBCT image of the head. Previous related work by Qi et al. optimized directional weights in a penalty to improve detectability for breast lesion detection at an unknown location in 3D PET [8]. Gang et al. optimized a parameter that weights the regularization term in 2D CT to maximize detectability at an unknown location for a few generic detection tasks [9]. This work builds on the method in [9] but differs in two aspects. First, this work introduces a comprehensive and general framework to design a spatially varying penalty for maximal detectability. Second, we extend the design from 2D CT in [9] to 3D CBCT and focus on designing a penalty for a specific task in head imaging. We first validate prediction of spatial resolution and noise characteristics at various locations in 3D, and we then define a 3D detectability index that provides an objective function in penalty design. The performance of the proposed penalty is evaluated on a 3D anthropomorphic head phantom in comparison to a conventional penalty.

II. Methods

A. Penalized Weighted Least-Squares Reconstruction

We choose a PWLS reconstruction method previously developed for CBCT head imaging [4], whose forward model assumes mono-energetic x-rays and independent measurements as:

$$\stackrel{‒}{y}=\mathbf{D}\left\{g\right\}\exp (-\mathbf{A}\mu )$$ (1)

where ȳ denotes the mean measurements, μ is the image estimate, A is the linear projection operator (and A^T is the linear backprojection operator), g are the measurement-dependent gains, and D is an operator that converts a vector into a diagonal matrix.

The PWLS objective can be written as:

$$\begin{array}{c}\hfill \widehat{\mu }=\underset{\mu }{\arg \min }\frac{1}{2}{\Vert \mathbf{A}\mu -l\Vert }_{\mathbf{w}}^2+\beta R\left(\mu \right)\hfill \\ \hfill R\left(\mu \right)=\frac{1}{2}\sum _j\sum _{k\in N_j}{w}_{jk}\psi ({\mu }_j-{\mu }_k)\hfill \end{array}$$ (2)

where l denotes line integrals derived from the measurements y, and W is a diagonal weighting matrix. The statistical weights in W are computed to account for noise in the measurements and noise following artifact corrections (if such corrections are present in the data processing) [4]. The regularization term in Eq. (2) penalizes differences between every voxel μ_j and its neighboring voxel μ_k by a penalty function ψ along with directional weights w_jk, and is weighted by a scalar regularization parameter β. We refer to this penalty below as the “conventional penalty”.

To design a penalty that maximizes detectability, one can modify the regularization parameter, directional weights, and/or penalty function. In this work, we focus on designing a spatially varying β map while keeping the directional weights (w_jk=1 for first-order neighbors) and penalty function (quadratic function) the same throughout the image. Optimization of the directional weights and penalty function for maximal detectability are subjects of future work. The proposed spatially varying penalty can be written as:

$$\begin{array}{c}\hfill \widehat{\mu }=\underset{\mu }{\arg \min }\frac{1}{2}{\Vert \mathbf{A}\mu -l\Vert }_{\mathbf{w}}^2+R^{\prime }\left(\mu \right)\hfill \\ \hfill R^{\prime }\left(\mu \right)=\frac{1}{2}\sum _j{\beta }_j\sum _{k\in N_j}{w}_{jk}\psi ({\mu }_j-{\mu }_k)\hfill \end{array}$$ (3)

where R′ denotes the new regularization term.

As a point of reference, we consider another form of spatially varying penalty derived by Fessler et al. [5] that encourages uniform spatial resolution (referred to below as the “uniform resolution penalty”) and can be written as:

$$R\left(\mu \right)=\frac{1}{2}\sum _j\sum _{k\in N_j}{\kappa }_j{\kappa }_k{w}_{jk}\psi ({\mu }_j-{\mu }_k),{\kappa }_j=\sqrt{\sum _i{a}_{ij}^2{\mathbf{W}}_i/\sum _i{a}_{ij}^2}$$ (4)

where κ_j represents the certainty of all rays that intersect the j^th voxel and a_ij denotes the (i, j)^th element of matrix A.

B. Task-Based Performance Prediction

Previous work [5] shows that if the spatially varying term is spatially smooth, its effects on image quality are essentially local. Thus, while β will be spatially dependent in the resulting penalty, in the design stage, we assume β values at other voxels are the same as the β value at the voxel of interest (i.e., assumes a conventional penalty). One can then derive analytical expressions of the local PSF and local covariance for the PWLS estimator in Eq. (2) using a first-order Taylor expansion and the Implicit Function Theorem as in [5]:

$${\left[PSF\left(\widehat{\mu }\right)\right]}_j={[\mathbf{F}\left(\breve{\mu }\right)+\beta \mathbf{R}]}^{-1}\mathbf{F}\left({\mu }^{true}\right)e_j$$ (5)

$${\left[Cov\left(\widehat{\mu }\right)\right]}_j={[\mathbf{F}\left(\breve{\mu }\right)+\beta \mathbf{R}]}^{-1}\mathbf{F}\left({\mu }^{true}\right){[\mathbf{F}\left(\breve{\mu }\right)+\beta \mathbf{R}]}^{-1}{e}_j$$ (6)

where F is the Fisher information matrix defined as F(μ = A^TD[ȳ(μ)]A, R is the Hessian of R(μ) in the PWLS objective (and is not dependent on the input image when a quadratic penalty function is used), e_j is a unit vector specifying location in the image (with unity j^th element and zero elsewhere). In real data when μ^true (truth image) and $\breve{\mu }$ (PWLS reconstruction of noiseless data) are not available, a “plug-in” method [5] can be used.

Since the local PSF and covariance are evaluated in a relatively uniform region (brain), the matrix of local PSF and covariance can be approximated as circulant in a small region-of-interest (ROI). Their discrete Fourier transform are then the local modulation transfer function (MTF) and noise-power spectrum (NPS) within the ROI:

$$MTF{\left(f\right)}_j=\mid H\left(f\right)\mid ∕H\left(0\right),\text{where}H\left(f\right)=FT\left\{{\left[PSF\left(\widehat{\mu }\right)\right]}_j\right\}$$ (7)

$$NPS{\left(f\right)}_j=\mid FT\left\{{\left[Cov\left(\widehat{\mu }\right)\right]}_j\right\}\mid$$ (8)

With predictions of local MTF and NPS, one may predict the task-based performance of the PWLS estimator in terms of detectability index d′ [7], which relates metrics of MTF and NPS to a spatial-frequency-dependent task function and an observer model. Many observer models can be formulated - in this work, the nonprewhitening (NPW) matched filter observer model. This model does not bias the results according to the characteristics of the observer and has demonstrated reasonable agreement with human observer performance for simple tasks in tomosynthesis and CBCT [10]. The detectability index with a NPW observer model can be written as:

$$d^{\prime 2}=\frac{{[\int \int \int {(MT{F}_j\cdot W_{Task})}^{2}d{f}_{x}d{f}_{y}d{f}_z]}^2}{\int \int \int NP{S}_j{(MT{F}_j\cdot W_{Task})}^{2}d{f}_{x}d{f}_{y}d{f}_z}$$ (9)

The task function W_Task in this work is defined as the difference of two Gaussian functions, representing a low-contrast, mid-frequency task such as ICH detection expressed as follows:

$$W_{\text{Task}}=C[\exp (-{\mid \mathbf{f}\mid }^2∕2{\sigma }_1^2)-\exp (-{\mid \mathbf{f}\mid }^2∕2{\sigma }_2^2)]$$ (10)

where C is the blood-to-brain contrast (0.011 mm⁻¹), σ₁ = 0.35 mm⁻¹, and σ₂ = 0.25 mm⁻¹ corresponding to discrimination of a characteristic feature length of ~2 mm, approximated using the average of four standard deviations of each Gaussian function in the spatial domain.

C. Proposed Regularization Design Framework

While the design goal is to maximize d′ at every location in the image, one may start with maximizing d′ at one location. The optimization problem can be written as:

$${\widehat{\beta }}_j=\underset{{\beta }_j^{\prime }}{\mathrm{argmax}}{d}^{\prime 2}\left({\beta }_j\right)$$ (11)

While directly solving Eq. (11) might be possible, we choose a simple scheme in this work to maximize d′ by evaluating d′ for different β values with regular spacing and choosing the β that yields the maximum d′.

Repeating the optimization at every voxel is computationally impractical for 3D CBCT. We accelerate the design process in two steps. First, we exploit the observation that the optimal β is slowly varying between neighboring voxels and therefore perform the optimization on a 25×25×25 downsampled grid (internal to the cranium) and then interpolate β at intermediate voxels using radial basis functions. Second, since the local PSF reduces toward zero at voxels sufficiently far from the impulse, one may divide the grid into K subgrids, and in each k^th subgrid place N_k unity impulses in the input e_k and predict for N_k locations simultaneously. The prediction accuracy is not affected provided that the impulses are far apart. This applies to the prediction of the local covariance as well. The combination of the downsampled grid and simultaneous prediction reduced the number of calculations needed from the number of voxels (e.g., ~512³ in 3D CBCT) to the number of subgrids. In this work, we placed impulses at 50 voxels apart, which divided the grid into 2³=8 subgrids. A pseudocode outline of the design framework is shown in Algorithm 1.

Algorithm 1.

Spatially varying penalty design for maximum d′

Input precomputed R

for each subgrid k = 1 to K

Construct ek with Nk unity elements (uniform spacing)

Use Eq. (5-6) to predict local PSF and covariance for Nk locations simultaneously

for each voxel j on the kth subgrid

Use Eq. (7-9) to compute MTF, NPS, and d′ at different β

Estimate β that maximizes d′

end for

end for

for each voxel not on the grid

Interpolate β based on the optimal β on the grid

end for

return a β map

III. EXPERIMENTAL RESULTS

We evaluated the proposed penalty in simulation studies using the 3D digital head phantom shown in Fig. 2(a-b). The digital phantom was created by performing a CT scan of a realistic physical head phantom at high dose and setting all soft tissues (including the brain) to a constant value (40 HU). The resulting phantom preserves realistic bone attenuation and exhibits no noise or artifact in soft tissue. A system geometry previously identified for a dedicated CBCT head scanner [2] was used, with a 100 cm source-to-detector distance, 55 cm source-to-axis distance, and 0.556 × 0.556 mm² detector pixel sizes. Projections (N = 720) without noise and with Poisson noise were simulated over 360° using 2×10⁵ photons per detector pixel. Images were reconstructed with 390×485×498 voxels and 0.5×0.5×0.5 mm³ voxel sizes. Artifact corrections were not considered in this work.

Figure 2.

Validation of 3D MTF and NPS prediction. (a-b) 3D head phantom used in this work. Grayscale window: [0, 0.04] mm⁻ (c-d) Predicted and measured 3D local MTF (c) and NPS (d) at location 1-4 denoted in Fig. 2. In each plot, the left half is prediction from Eq. (5-8), and the right half is measurements from PWLS reconstructions. Units are scalar for the 3D MTF and [(mm⁻¹)²(mm)³] for the 3D NPS.

We first validated the prediction of 3D local MTF and NPS, including locations throughout the brain and adjacent to the cranium. Figure 2(c-d) shows the 3D local MTF and NPS at four locations denoted in Fig. 2 with a nominal β value for this dataset (10^6.4). In each plot, the left side shows the prediction from Eq. (5-8), and the right side shows the measurements from PWLS reconstructions. For prediction, we used 100 iterations of the conjugate gradient (CG) algorithm in Eq. (5) for complete convergence of the local PSF, and we applied the CG algorithm twice in Eq. (6) to achieve convergence in the local covariance. For measurements, the local PSF was measured by subtracting two PWLS reconstructions with and without an impulse (no noise added), and local covariance was measured from a large ensemble (n = 100) of PWLS reconstructions with different noise realizations following the method in [9]. 100 iterations of separable quadratic surrogate updates [11] were performed to achieve a nearly converged PWLS image. A ROI size of 21×21×21 voxels was large enough to cover the main extent of the local PSF and covariance and was therefore used in DFT operations. For both MTF and NPS, good overall agreement can be seen between prediction and measurements at all four locations in both x-y plane and z direction. The spatial dependence of MTF and NPS can also be seen. For example, the MTF broadens and is less isotropic near the periphery, whereas the NPS is reduced at certain frequencies according to the magnitude of line integrals from location 1 to 4.

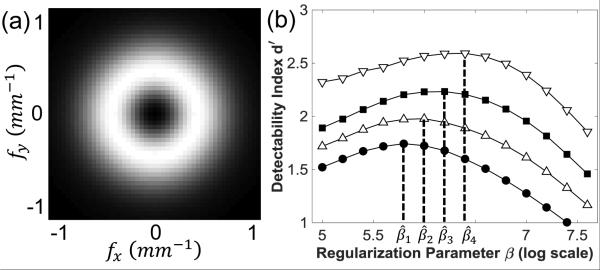
To design a β that maximizes d′ at one location, we predicted the local MTF and NPS at different β values and computed d′ as a function of β. Figure 3(a) shows the 3D task function from Eq. (10). Figure 3(b) shows a calculation of d′ as a function of β at the four locations in Fig. 2. At each location, the function d′(β) exhibited a concave shape and a clear optimum, suggesting the possibility of directly solving for β - for example, using gradient-based optimization. For each location, the d′ reduced at lower β (dominated by high NPS) and higher β (dominated by over-smoothing). The optimal β is also seen to vary over an order of magnitude, suggesting the design of a spatially varying penalty. It is worth mentioning that we observed a lower level of agreement between prediction and measurement in the limit of very low β (~10^5.0), which is attributed to the high conditioning number of the matrices to be inverted in Eq. (5-6) and could potentially be solved by preconditioning. However, such disagreement is not believed to affect the results, since those β values are much smaller than the range of interest about the optimal β value.

Figure 3.

(1) A 3D task function for ICH detection. Grayscale window: [0, 3.3×10⁻⁴] mm⁻¹ (b)Detectability index computed as a function of regularization parameter β at 4 locations denoted in Fig. 2. The optimal β were at ${\widehat{\beta }}_j$ (j = {1,2,3,4}).

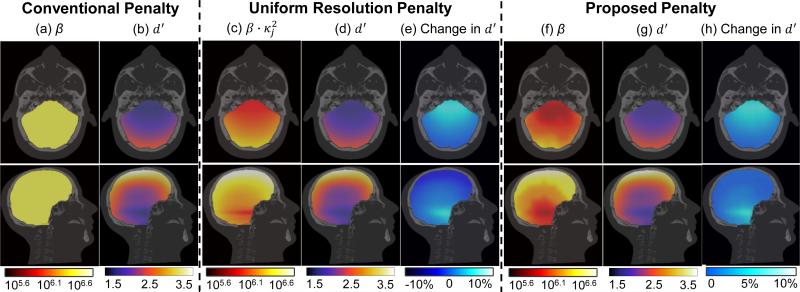
Figure 4 shows the results for the proposed penalty in comparison to the (spatially uniform) conventional penalty and the (spatially varying) uniform resolution penalty. For the conventional penalty, a scalar β value of 10^6.4 was chosen to achieve the highest mean d′ in the head. For the uniform resolution penalty (shown simply as a point of reference as another form of spatially varying penalty), regularization was such as to encourage uniform PSF width of 0.95 mm (FWHM averaged over all radial directions). Fig. 4(f) shows the β map resulting for the proposed d′ optimization penalty, which is seen to follow a similar overall trend as the uniform resolution penalty: penalty strength is lower in regions of high attenuation near the interior skull base and is higher at the periphery near the cranium. Fig. 4 (b), (d), and (g) show the d′ map from each penalty, each exhibiting strong spatial variation in d′ with highest value near the periphery and reduced performance in the interior of the cranial vault. Fig. 4 (e) and (h) show the change in d′ (relative to the conventional penalty) achieved by the two spatially varying penalties. Compared to the conventional penalty, the uniform resolution penalty provides a 10% increase in d′ in the interior of the brain near the skull base but a slight (5%) reduction in d′ at the periphery adjacent to the cranium. This is somewhat expected, since the uniform resolution penalty was designed to achieve uniform spatial resolution (and not maximum detectability). Figure 4(h) shows that the proposed penalty improves d′ up to ~10% and preserves the highest d′ (i.e., does not reduce d′) in comparison to the best conventional penalty.

Figure 4.

Maps of penalty strength and detectability in ICH detection. (a-b) Scalar β and resulting d′ distribution for the conventional PWLS penalty. (c-e) For the uniform resolution penalty: (c) product of certainty (${\kappa }_j^2$) and a scalar β (d) the resulting d′ distribution, and (e) relative change in d′ compared to the conventional penalty (f-h) For the proposed d′-optimization penalty: (f) the β map, (g) the resulting d′ distribution, and (h) relative change in d′ from the “best” conventional penalty.

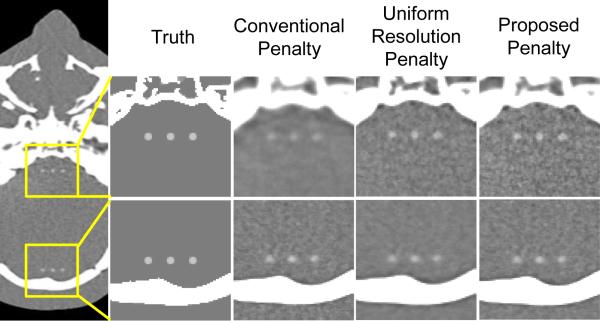
PWLS image reconstructions corresponding to each type of penalty are shown in Fig. 5. Three simulated 3D spherical ICH lesions of 2 mm diameter and 50 HU contrast were added to regions in the deep interior of the brain near the skull base and at the periphery adjacent to the cranium. The best conventional penalty exhibited good visualization of ICH adjacent to the cranium but yielded an over-smoothed image in the deep interior near the skull base. The uniform resolution penalty improved conspicuity of the lesion (particularly near the skull base) and achieved a more uniform appearance of spatial resolution in the image compared to the conventional penalty. The proposed d′-optimization penalty yielded improved visualization of ICH in both regions, particularly in the deep interior region near the skull base.

Figure 5.

Image reconstruction of a 3D spherical ICH lesion of 2 mm diameter and 50 HU contrast. Grayscale: [−50, 130] HU.

IV. CONCLUSION

Image reconstruction in a manner that specifically incorporates a formulation of the imaging task and optimizes penalty design with respect to local, task-based imaging performance presents a promising approach for “task-driven image reconstruction.” For high-quality CBCT imaging of the head, this paper shows that the spatially varying penalty strength could be reliably predicted with respect to an ICH detection task, providing optimal detectability at each location throughout the 3D image. The proposed penalty demonstrated improved or equivalent visualization of ICH in PWLS images compared to a conventional penalty and supports the application of CBCT for ICH detection at the point of care in the ICU and/or operating theater.