Abstract
Taking long-range electrostatic effects into account in classical and hybrid quantum mechanics–molecular mechanics (QM/MM) simulations is necessary for an accurate description of the system under study. We have recently developed a method, termed long-range electrostatic corrections (LREC), for monopolar QM/MM calculations. Here, we present an extension of LREC for multipolar/polarizable QM/MM simulations within the LICHEM software package. Reaction barriers and QM–MM interaction energies converge with a LREC cutoff between 20 and 25 Å, in agreement with our previous results. Additionally, the LREC approach for the QM–MM interactions can be smoothly combined with standard shifting or Ewald summation methods in the MM calculations. We recommend the use of QM(LREC)/MM(PME), where the QM region is treated with LREC and the MM region is treated with particle mesh Ewald (PME) summation. This combination is an excellent compromise between simplicity, speed, and accuracy for large QM/MM simulations.
Keywords: Long-range electrostatics, QM/MM, Polarizable, Multipoles, LREC
1 Introduction
Long-range electrostatic (LRE) interactions are important for the accurate determination of enzyme structures and reaction paths [7, 8, 38, 51]. Unfortunately, directly incorporating LRE interactions in quantum mechanical–molecular mechanical (QM/MM) simulations can be challenging due to the necessity of modifying the Fock matrix elements.
The most straightforward approach for the treatment of electrostatic interactions in QM/MM simulations is to simulate only a small portion of the solvent around a protein or enzyme active site [5] (i.e., embedding a protein in a water droplet). The droplet’s liquid-like environment can be maintained by either freezing the positions of the molecules in the outer edge or applying a stochastic boundary potential [5]. Droplet simulations are efficient due to the small number of atoms, although, the LRE interactions are neglected. However, some of the missing LRE effects can be implicitly included by embedding the droplet in a classical continuum [2–4, 11, 23, 41].
An alternative approach involves using Mulliken charges to approximate the QM charge distribution in periodic images, so that the QM/MM calculation can be carried out using the Ewald summation or smooth particle mesh Ewald (PME) methods [18, 27, 34, 47]. QM/MM calculations with Ewald/PME methods are effective and can readily be improved by replacing Mulliken charges with charges fit from the electrostatic potential. Similar approaches have been developed to extend the Ewald, Wolf, and isotropic periodic sum methods to calculations with semi-empirical, density functional tight binding, Hartree–Fock, and density functional theory [22, 35, 36, 40, 50]. Very recently, Giese and York have reported the ambient-potential composite Ewald method, where no approximations are employed to represent the QM charge density in reciprocal space [20]. Most of these QM/MM LRE methods require modifications to the self-consistent-field (SCF) matrix elements or post-SCF corrections. While these approaches can be quite accurate, modifying SCF routines can limit which QM packages can be used for the QM/MM calculations.
Recently, Fang et al. [14] introduced a cubic smoothing function to include long-range electrostatic corrections (LREC) in QM/MM simulations. The LREC approach uses a combination of a smoothing function and the minimum image convention to scale the electrostatic interactions such that the potential and forces smoothly decrease to zero at a finite cutoff radius. While energy and force shifting approaches also smoothly truncate the potential at a finite radius [16, 28, 29, 35, 36, 44, 49], LREC has an exceptionally simple implementation in the QM/MM Hamiltonian. In the LREC approach, the external MM monopoles are scaled based on their distance from the QM region, which does not require modifications to the matrix elements or post-SCF corrections. The LREC method has been shown to calculate energies and forces that are within 0.2 % of the PME results when using cutoffs of 20–25 Å [14].
The complications of treating LRE interactions of monopoles also affect potentials that include multipole moments and explicit polarization. Truncation, shifting, and smoothing approaches are appealing for multipolar/polarizable QM/MM simulations due to the relative simplicity of introducing these methods into the Hamiltonian [14]. However, each type of shifted multipole–multipole interaction requires a different correction term. As will be shown below, the LREC approach produces a single scale factor for each MM atom, and hence, does not require modifications to the underlying QM software.
In this paper, we extend the LREC approach to atomic multipole moments within the LICHEM software package and implement QM(LREC)/MM(LRE) calculations, where the QM and MM regions are treated with a different LRE approaches. In Sect. 2, we review multipolar/polarizable QM/MM simulations, followed by a discussion of LRE methods in Sect. 3. Our extension of the LREC method to multipolar/polarizable QM/MM simulations is presented in Sect. 4, and we conclude our discussion by examining the performance of multipolar LREC.
2 Multipolar/polarizable QM/MM
2.1 Multipole moments
The electron density and nuclei in a molecule create a continuous, and often, anisotropic electrostatic potential. In classical simulations, interactions due to the diffuse electron density are generally approximated by a set of pair-wise electrostatic potentials. One of the simplest methods for modeling the molecular electrostatic field is to place point-charges (monopoles) on the atomic centers. Atomic monopoles are often inadequate [8, 25], and some models augment the field by adding massless charged dummy atoms to the molecule [24, 33]. However, the dummy atoms can complicate the potential/dynamics during the simulations.
An alternative approach is to add higher-order moments (multipoles) of the electrostatic potential to the model [8, 30, 43, 45]. A multipole expansion is a Taylor series representation of the continuous electrostatic potential (Velst) [45],
| (1) |
where r is the distance from the point of interest (e.g., nucleus, center of mass, etc) and n is the order of the moment. Typically, MM force fields truncate the Taylor series at the second order [8, 30, 43], and the moments can be determined from an analysis of the electron density or electrostatic potential.
The zeroth moment of the electrostatic potential is the monopole, which is equivalent to a point-charge. The first and second moments are referred to as the dipole and quadrupole, respectively. Multipole moments can produce an anisotropic electrostatic potential around individual atoms, as opposed to the spherical potential wells produced by monopoles. Thus, a set of atomic multipole moments, through the quadrupole moment, can reproduce the molecular electrostatic potential with a higher degree of accuracy than monopole moments alone [8, 45]. Atom centered multipolar models provide a reasonable compromise between computational cost and accuracy in the reproduction of the electrostatic potential at medium and long-range.
2.2 QM/MM Hamiltonian
The polarizable QM/MM Hamiltonian may be expressed as
| (2) |
where Hqm is the unperturbed Hamiltonian for the QM subsystem, Vmm is the potential for the MM–MM interactions, Vqmmm is the potential for the QM–MM interactions, and Vpol is the potential due to the polarization of the QM/MM system.
In practice [26], Eq. 2 can be expressed as
| (3) |
where
| (4) |
and
| (5) |
Here adds the MM multipole moments (Vqmmm,mtp) to the QM Hamiltonian, adds the QM–MM bonded (Vqmmm,bnd) and van der Waals (Vqmmm,vdw) interactions to the MM potential, and Vmm,pol is the many-body MM polarization energy. Thus, Eq. 3 divides the QM–MM interactions and polarization between the QM and MM calculations.
The QM/MM Hamiltonian becomes more complicated when the system is periodic. Since the Coulomb interactions have a relatively long range, particles 20 Å or more from the QM region can have non-negligible contributions to the energy and forces [6, 14, 44, 48]. One would expect that monopole–monopole interactions in a neutral system would begin to cancel with interactions of the opposite sign. In fact, Wolf demonstrated [48] that the r−1 dependence of isolated charged particles behaves as a r−5 potential in a homogeneous neutral environment. However, since the pair-wise terms in the electrostatic potential often have relatively large magnitudes beyond 10 Å, the potential cannot simply be truncated [1, 6, 8, 15, 16, 37, 38, 42, 44, 48, 51]. As will be discussed below, many LRE methods can be integrated into the periodic QM/MM Hamiltonian.
2.3 Polarization
Polarizable QM/MM simulations combine quantum polarization (due to many-body electrostatic, exchange, and dispersion interactions) with classical polarization (induced dipoles, Drude oscillators, etc). Within LICHEM, the electron density is polarized by both the QM region and the static MM multipole moments [26]. A separate MM calculation is then performed to determine the response of the MM polarizable sites to the QM and MM electrostatic fields. In this manner, only one QM and two MM calculations ( and Vmm,pol) are required to calculate the relaxed QM/MM total energy and the underlaying QM and MM packages do not need to be modified. Additionally, this approach can easily be implemented for a variety of classical polarizable models.
3 Long-range electrostatics
In this section, some common approaches to calculate long-range electrostatic interactions will be reviewed. While the higher-order moments are neglected in most of this discussion, these long-range methods can readily be extended to include the full multipole–multipole and polarizable interactions [28, 29].
3.1 Shifting
The Coulomb potential produces relatively long-range interactions due to the r−1 distance dependence. The potential is given by
| (6) |
where Vij,cl is Coulomb’s law in atomic units, qi is the monopole on atom i, and rij is the distance between atoms i and j. For periodic systems, the Coulomb potential is often only calculated up to a distance of 9–20 Å to reduce the computational cost [8, 31]. However, due to the length scale of the potential, the residual energy is often non-negligible at the cutoff radius (Rc) [6, 42, 44]. To mitigate some of the truncation artifacts, the potential can be shifted by a constant; such that it is equal to zero at the cutoff [44]. The energy shifted potential, Vij,es, is given by
| (7) |
The force, Fij, due to a general potential, Vij, is given by
| (8) |
where ∇ is the gradient operator, and thus,
| (9) |
and
| (10) |
Since Fij,cl = Fij,es, the use of energy-shifted potential still results in finite forces at the cutoff radius [44]. Thus, energy-shifted potentials produce artifacts in calculations which require forces, e.g., MD simulations or geometry optimizations.
The truncated potential can be further improved by shifting the force in a manner analogous to the shifted potential. The shifted force, Fij,fs, is given by [44]
| (11) |
and the force-shifted potential can be derived by integrating the shifted force [44],
| (12) |
where
| (13) |
The final force-shifted potential is given by
| (14) |
where both the energy and force are now zero at the cutoff.
Truncation and shifting schemes make the calculation of the Coulomb potential tractable for large systems, but they often produce artifacts due to the artificial nature of the finite cutoff. In principle, the shifting procedure could be continued for higher-order derivatives. However, as will be shown in Sects. 3.3 and 4.1, this approach can drastically alter the electrostatic potential. The energy and force shifting derivations given thus far are by no means the only shifting approaches. Polynomial or exponential damping functions are often applied to the Coulomb potential to shift the energy and accelerate the convergence of the LRE interactions. In general, any shifting approach can be rewritten as
| (15) |
where Vij,sm is the smoothed Coulomb potential and S(rij) is a damping function.
3.2 Ewald and PME
The calculation of the total electrostatic potential for an infinite periodic system involves a conditionally convergent sum [48]. However, this issue can be overcome by separating this sum into two absolutely convergent sums, which is the basis of the Ewald method [10]. Ewald summation methods divide the electrostatic potential into a short-range damped Coulomb potential and a long-range Fourier transformed Coulomb potential. The total Coulomb potential, Vtot,cl, may be calculated by [10]
| (16) |
where Vsr is the sum of the damped short-range Coulomb potential, is the Fourier transformed sum of the long-range Coulomb potential, Vself is the self-interaction potential of the multipoles, and εb is a correction term due to the boundary conditions that arises when the unit cell has a finite charge and/or dipole moment [10, 32].
The efficiency of the Ewald method can be improved by employing numerical Fourier transforms. One possibility is by using B-spline functions to interpolate the periodic potential onto a mesh of grid points [9]. This approach, termed (smooth) particle mesh Ewald summation, can be used in conjunction with a fast Fourier transform (FFT) algorithm [13]. The FFT can significantly speed up the calculation of the long-range Coulomb potential and reduces the theoretical computational cost from to .
3.3 LREC
Our approach for treating LRE interactions is to scale the electrostatic potential based on the distance between the atoms [14]. This approach smooths the electrostatic potential and forces, which are zero at the cutoff radius. Conceptually, this is equivalent to the procedure used in shifted or Wolf approaches, except that the LREC smoothing function has been designed to produce energies and forces in good agreement with PME.
The smoothed Coulomb potential used by the LREC method, Vij,lrec, is given by
| (17) |
where
| (18) |
and
| (19) |
Here f is the LREC cubic smoothing function and s is an adjustable integer exponent (see Fig. 1). Unlike most LRE approaches where the damped forces are derived analytically from the damped energy, the LREC force calculations simply use a different exponent in the smoothing function,
| (20) |
The use of different exponents is related to the length scale of the potential and the gradient. Since the forces act over a shorter range than the potential, it is beneficial to move the inflection point of the smoothing function closer to by increasing the exponent (see Figs. 1, 2). Increasing the exponent reduces the damping at short ranges, while increasing the damping in the regions where the forces are small. In general, the LREC exponent and cutoff can be adjusted to control the convergence, cost, and accuracy of the method, similar to adjusting the short-range cutoff and damping parameter in the Ewald, PME, and Wolf methods. As shown by Fang et al. [14], the LREC approach produces energies (s = 2) and forces (s = 3) in good agreement with PME when the cutoff radius is larger than 20 Å.
Fig. 1.
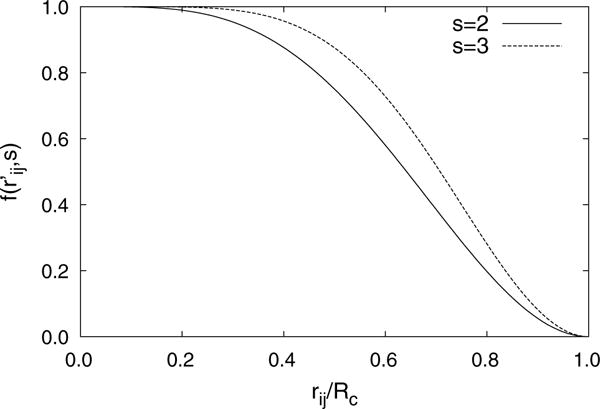
LREC damping function (Eq. 18) with s = 2 and s = 3. Increasing the exponent moves the inflection point of the LREC function closer to the cutoff radius
Fig. 2.
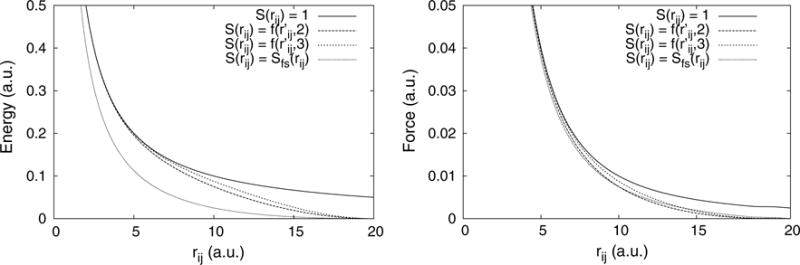
Energy and force for the Coulomb potential with different damping functions, S(rij). At short-range, the LREC smoothing function produces energies and forces nearly identical to those from the true potential, while heavily damping the interactions at longer length scales
4 LREC in QM/MM
4.1 Effective multipole moments
To easily implement any shifting or smoothing function in QM/MM simulations, the MM monopoles can be scaled to a value consistent with the smoothed Coulomb potential,
| (21) |
where is the scaled monopole in the MM region, S is a generalized damping function, and rj is the distance between the MM atom and the QM center of mass. Scaling monopoles based on their distance from the QM region is a simple approach which avoids the need to modify the QM integrals or correct the energies. Since the QM external field contains the damped multipole moments, forces on the QM atoms can be calculated using the QM gradients without further corrections. Additionally, there is no need to modify the forces when is slowly varying, which is the case for iterative QM/MM geometry optimizations [52]. However, one needs to be cautious when performing QM/MM–MD simulations, when there is a small number of QM atoms, or when the cutoff radius is small; since will no longer be slowly varying. Figure 3 reports scale factors calculated for a selection of smoothing and shifting methods. It is clear that the LREC approach faithfully represents the electrostatic potential over a longer length scale than other shifting approaches. At , the LREC approach retains 75 % of the original Coulomb energy, while the force shift potential has been reduced to 25 %.
Fig. 3.
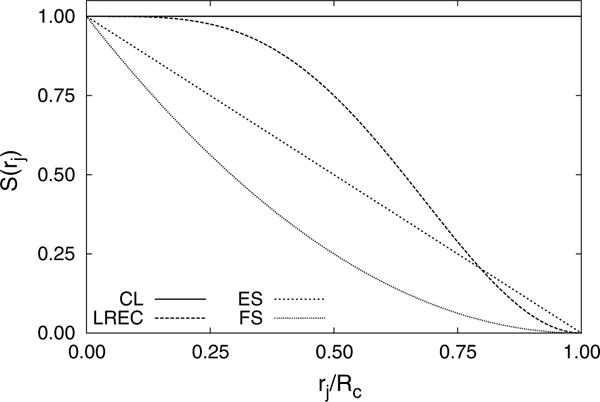
Monopole scaling factors (Eq. 21) from different electrostatic potentials (CL Coulomb’s law, ES energy shifted, FS force shifted, LREC ). LREC faithfully represents the electrostatic field over a larger range than the two shifting approaches
Higher-order multipole moments can be scaled in the same manner as the monopole moments:
| (22) |
and
| (23) |
where Sdpl and Sqpl are the dipole and quadrupole damping functions, respectively. This approach can easily be implemented to produce smoothed multipole expansions. In the LREC approach, Eqs. 22 and 23 reduce to
| (24) |
and
| (25) |
where f and r′ have the same form as in Eqs. 18 and 19. The work Fang et al. [14] and our exploratory calculations (see supporting information) have shown that setting s = 2 is sufficient for QM/MM calculations with only monopoles, while setting s = 3 significantly improves LREC performance for multipolar QM/MM calculations. Within LICHEM, the scaled monopole, dipole, and quadrupole moments can be further approximated as a set of 6 point-charges in an octahedral arrangement [12, 19]. As was shown previously [26], the point-charge approximation is a simple and accurate method for including multipole moments in QM software that can only employ point-charges for the external field.
4.2 Mixed LRE methods
Since QM/MM simulations separate the QM–QM, MM–MM, and QM–MM electrostatic interactions, the long-range electrostatics can be treated with different approximations in each part of Eq. 3. For example, the QM–MM interactions may be treated with the LREC approach while the MM–MM interactions can be calculated with PME. The resulting QM(LREC)/MM(PME) calculations take advantage of the simplicity of the LREC smoothing function in quantum calculations and the speed/accuracy of PME [8, 9, 21] for classical models. It is, perhaps, not intuitively clear why two different LRE approaches can be combined in QM/MM simulations. Separability is key to the validity of smoothly mixing two LRE methods. Two distinct types of separability appear in the QM/MM calculations.
Separation of the optimizations: LICHEM employs the iterative QM/MM optimization algorithm [26, 52] shown in Fig. 4. Since the QM and MM degrees of freedom are optimized independently, only a single LRE method is used to calculate the forces during each optimization procedure. Thus, two different LRE approaches are only used simultaneously while calculating the total energy.
- Separability of the energies: The QM/MM total electrostatic energy, εtot, can be written as
where(26)
and(27)
Here ε represents the electrostatic component of the energies calculated with the QM/MM Hamiltonian (Eq. 3). The QM–MM interaction energies in Eq. 27 are calculated using Gaussian integrals in the QM software, while the electrostatic interactions in Eq. 28 are calculated using the MM force field. Since the QM–MM, MM–MM, and polarization portions of Eq. 26 are already calculated with different algorithms (i.e., Gaussian integrals and force fields), using two sufficiently accurate LRE methods does not significantly affect the total energy. Test calculations with MM(FS)/MM(PME), where the QM region was treated with a force-shifted MM potential, confirmed that there are negligible errors (not reported) compared to full PME calculations.(28)
Fig. 4.
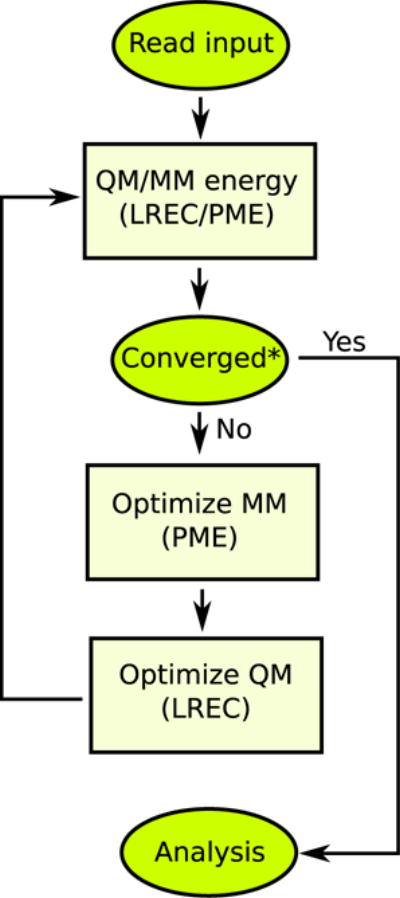
QM/MM optimization procedure (Refs. [26, 52]) implemented in LICHEM. The LRE methods used in each step are shown for QM(LREC)/MM(PME). Based on the change in the atomic positions after optimization; skipped on the first step
QM and polarization calculations are inherently many-body and must include enough of the multipole moments for the calculations to converge. On the other hand, the charges on the QM atoms can simply be neglected in the MM–MM calculations. Since the MM potential is pair-wise additive, calculating the electrostatic interactions without the presence of QM charges generally does not affect the MM–MM interactions.
5 Results
5.1 Computational details
The QM calculations were performed using the 6–31++G(d,p) basis set, and each QM/MM system was solvated using a cubic box of liquid water (32,000 molecules, box length: 98.646 Å). We have tested the LREC method with a variety of cutoff radii up to the maximum cutoff (Rc = 49.323 Å) allowed by the minimum image convention. The QM–MM and MM–MM vdW interactions, on the other hand, were calculated using the default settings of the TINKER software package [39] (polynomial smoothing with Rc = 9 Å). Additionally, we have tested LICHEM’s QM(LREC)/MM(PME) implementation using both the non-polarizable TIP3P [24] and the polarizable AMOEBA [43] potentials.
5.2 QM–MM interactions
To examine the convergence of multipolar LREC calculations, QM/MM calculations were performed on the box of liquid water using the NWChem [46]–TINKER interface in LICHEM. A collection of 5 water molecules in the center of the box were taken as the QM subsystem, and all remaining water molecules were designated as the MM region. The QM–MM interaction energy, Eint, is given by
| (29) |
where Etot is the QM/MM total energy, Eqm is the energy of the QM subsystem in the gas phase, and Emm is the MM energy of the system with the QM atoms removed.
Figure 5 reports the convergence of the QM–MM interaction energy as the electrostatic cutoff is increased. The interaction energies from the long-range corrected QM/MM calculations are in good agreement with the results taken from the AMOEBA force field and, as was shown previously [14], the QM/MM energies converge with a cutoff between 20 and 25 Å. The computational cost of LRE methods is almost entirely determined by the cost of the QM calculations and the LRE cutoff radius. As can be seen in Fig. 6, the computational cost of QM/MM simulations can increase rapidly as the cutoff radius is extended. Since multipolar QM/MM simulations are both more expensive and slower to converge than monopolar QM/MM simulations, it is beneficial to use a higher exponent to accelerate the convergence (see supporting information).
Fig. 5.
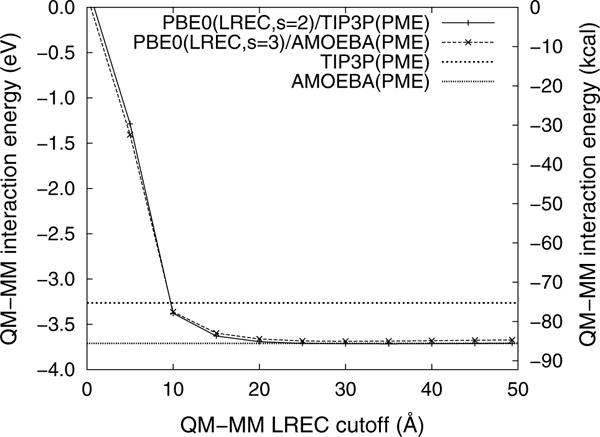
Convergence of the QM–MM interaction energy (Eq. 29) as the LREC cutoff is increased. For comparison, MM(PME) interaction energies are shown for TIP3P and AMOEBA
Fig. 6.
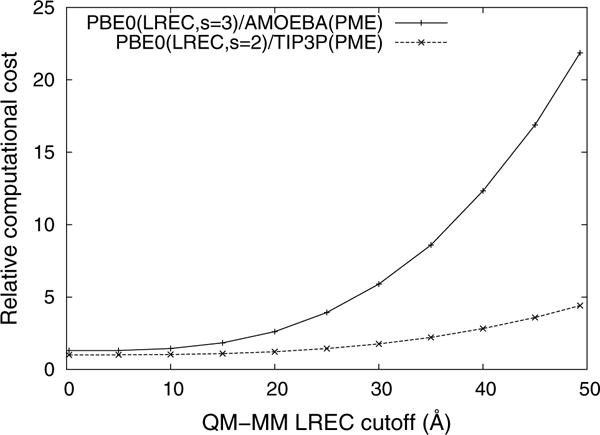
Computational cost of PME0(LREC)/MM(PME) relative to the cost of PBE0(LREC)/TIP3P(PME) with Rc = 0 Å (i.e., the QM region is in the gas phase)
Additionally, PBE0(LREC)/TIP3P(LREC) calculations, using the in-house modified versions of Gaussian and TINKER, confirmed that the QM/MM total energy was within 0.01 % of the PBE0(LREC)/TIP3P(PME) energy. The excellent agreement between the QM(LREC)/MM(LREC), QM(LREC)/MM(PME), and MM(PME) calculations confirms that the LREC method can be smoothly combined with other LRE methods.
5.3 Reaction barriers
Generally, the determination of reaction barriers is one of the main objectives in QM/MM simulations. To test the QM(LREC)/MM(PME) method on chemical reactions, we have chosen to use the aspartic acid dimer double proton transfer reaction from our previous work [14]. The acid dimer reactant, transition state, and product structures were solvated using the water box from Sect. 5.1 and re-optimized at the ωB97xD/AMOEBA (Rc = 25 Å level of theory.
The reaction barriers were calculated using LICHEM’s Gaussian [17]–TINKER interface for single-point energy calculations with Rc = {2, 5, 10,…, 45, 50} Å. The proton transfer barriers reported in Fig. 7 show large fluctuations with small cutoffs before stabilizing with Rc ≥ 20 Å, around 6.06–6.18 kcal/mol. While the barrier continues to increase beyond Rc = 20 Å, the total change induced by further increasing the cutoff from 20 to 50 Å is ∼0.1 kcal/mol. Furthermore, extrapolating to Rc = ∞ yields a barrier of 6.30 kcal/mol. Thus, the approximate error at Rc = 20 Å is only 0.25 kcal/mol, which is well below the so-called chemical accuracy (1 kcal/mol).
Fig. 7.
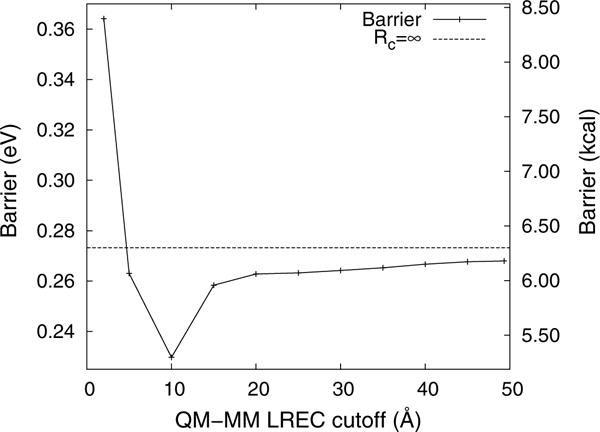
Aspartic acid double proton transfer reaction barriers calculated with s = 3 and different values of the LREC cutoff. Between Rc = 20 and 50 Å, the total change in the barrier height is less than ∼ 0.1 kcal/mol, which is within chemical accuracy
6 Conclusion
We have demonstrated that the LREC approach can be extended to multipolar/polarizable models in a straightforward manner. The interaction energies and reaction barriers from the LREC approach converge as the cutoff radius is increased and, in agreement with our previous results, Rc = 20–25 Å is sufficient to obtain converged QM/MM energies. Using multipolar LREC for QM/MM simulations is an easy-to-implement approach for calculating long-range electrostatic interactions, which does not require modifications to the underlying QM software. Furthermore, the QM(LREC) calculations can readily be combined with efficient and accurate long-range electrostatics methods, such as PME, for the MM calculations.
Supplementary Material
Acknowledgments
Calculations were carried out using computers in the Wayne State University’s high-performance computing grid. This work was supported by the National Institutes of Health Grant No. R01GM108583.
Footnotes
Published as part of the special collection of articles “Festschrift in honour of A. Vela”.
Electronic supplementary material The online version of this article (doi:10.1007/s00214-016-1923-8) contains supplementary material, which is available to authorized users.
References
- 1.Alper HE, Bassolino-Klimas D, Stouch TR. The limiting behavior of water hydrating a phospholipid monolayer: a computer simulation study. J Chem Phys. 1993;99(7):5547–5559. [Google Scholar]
- 2.Bandyopadhyay P, Gordon MS. A combined discrete/continuum solvation model: application to glycine. J Chem Phys. 2000;113(3):1104–1109. [Google Scholar]
- 3.Benighaus T, Thiel W. A general boundary potential for hybrid QM/MM simulations of solvated biomolecular systems. J Chem Theory Comput. 2009;5(11):3114–3128. doi: 10.1021/ct900437b. [DOI] [PubMed] [Google Scholar]
- 4.Benighaus T, Thiel W. Long-range electrostatic effects in QM/MM studies of enzymatic reactions: application of the solvated macromolecule boundary potential. J Chem Theory Comput. 2011;7(1):238–249. doi: 10.1021/ct1005455. [DOI] [PubMed] [Google Scholar]
- 5.Brooks CL, Karplus M. Solvent effects on protein motion and protein effects on solvent motion: dynamics of the active site region of lysozyme. J Mol Biol. 1989;208(1):159–181. doi: 10.1016/0022-2836(89)90093-4. [DOI] [PubMed] [Google Scholar]
- 6.Brooks CL, Pettitt BM, Karplus M. Structural and energetic effects of truncating long ranged interactions in ionic and polar fluid. J Chem Phys. 1985;83(11):5897–5908. [Google Scholar]
- 7.Cheatham TE, Kollman PA. Molecular dynamics simulations highlight the structural differences among DNA:DNA, RNA:RNA, and DNA:RNA hybrid duplexes. J Am Chem Soc. 1997;119(21):4805–4825. [Google Scholar]
- 8.Cisneros GA, Karttunen M, Ren P, Sagui C. Classical electrostatics for biomolecular simulations. Chem Rev. 2014;114(1):779–814. doi: 10.1021/cr300461d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Darden T, York D, Pedersen L. Particle mesh Ewald: an nlog(n) method for Ewald sums in large systems. J Chem Phys. 1993;98(12):10,089–10,092. [Google Scholar]
- 10.Darden TA. Dual bases in crystallographic computing. In: Shmueli U, editor. International tables of chrystallography. B. Kluwer Academic Publishers; Dordrecht: 2007. [Google Scholar]
- 32.de Leeuw SW, Perram JW, Smith ER. Simulation of electrostatic systems in periodic boundary conditions. I. Lattice sums and dielectric constants. Proc R Soc A. 1980;373(1752):27–56. [Google Scholar]
- 12.Devereux M, Raghunathan S, Fedorov DG, Meuwly M. A novel, computationally efficient multipolar model employing distributed charges for molecular dynamics simulations. J Chem Theory Comput. 2014;10(10):4229–4241. doi: 10.1021/ct500511t. [DOI] [PubMed] [Google Scholar]
- 11.De Vries AH, Van Duijnen PT, Juffer AH, Rullmann JAC, Dijkman JP, Merenga H, Thole BT. Implementation of reaction field methods in quantum chemistry computer codes. J Comput Chem. 1995;16(1):37–55. [Google Scholar]
- 13.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A smooth particle mesh Ewald method. J Chem Phys. 1995;103(19):8577–8593. [Google Scholar]
- 14.Fang D, Duke RE, Cisneros GA. A new smoothing function to introduce long-range electrostatic effects in QM/MM calculations. J Chem Phys. 2015;143(4):044,103. doi: 10.1063/1.4926652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Feller SE, Pastor RW, Rojnuckarin A, Bogusz S, Brooks BR. Effect of electrostatic force truncation on interfacial and transport properties of water. J Phys Chem. 1996;100(42):17,011–17,020. [Google Scholar]
- 16.Fennell CJ, Gezelter JD. Is the Ewald summation still necessary? Pairwise alternatives to the accepted standard for long-range electrostatics. J Chem Phys. 2006;124(23):234,104. doi: 10.1063/1.2206581. [DOI] [PubMed] [Google Scholar]
- 17.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery JA, Jr, Peralta JE, Ogliaro F, Bearpark MJ, Heyd J, Brothers EN, Kudin KN, Staroverov VN, Kobayashi R, Normand J, Raghavachari K, Rendell AP, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam NJ, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas, Foresman JB, Ortiz JV, Cioslowski J, Fox DJ. Gaussian 09 rev. d.01 2009 [Google Scholar]
- 18.Gao J, Alhambra C. A hybrid semiempirical quantum mechanical and lattice-sum method for electrostatic interactions in fluid simulations. J Chem Phys. 1997;107(4):1212–1217. [Google Scholar]
- 19.Gao Q, Yokojima S, Fedorov DG, Kitaura K, Sakurai M, Nakamura S. Octahedral point-charge model and its application to fragment molecular orbital calculations of chemical shifts. Chem Phys Lett. 2014;593:165–173. [Google Scholar]
- 20.Giese TJ, York DM. The ambient-potential composite Ewald method for ab initio QM/MM molecular dynamics simulation. J Chem Theory Comput. 2016 doi: 10.1021/acs.jctc.6b00198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Giese TJ, Panteva MT, Chen H, York DM. Multipolar Ewald methods, 1: theory, accuracy, and performance. J Chem Theory Comput. 2015;11(2):436–450. doi: 10.1021/ct5007983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Holden ZC, Richard RM, Herbert JM. Periodic boundary conditions for QM/MM calculations: Ewald summation for extended gaussian basis sets. J Chem Phys. 2013;139(24):244,108. doi: 10.1063/1.4850655. [DOI] [PubMed] [Google Scholar]
- 23.Im W, Bernèche S, Roux B. Generalized solvent boundary potential for computer simulations. J Chem Phys. 2001;114(7):2924–2937. [Google Scholar]
- 24.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79(2):926–935. [Google Scholar]
- 25.Kramer C, Spinn A, Liedl KR. Charge anisotropy: where atomic multipoles matter most. J Chem Theory Comput. 2014;10(10):4488–4496. doi: 10.1021/ct5005565. [DOI] [PubMed] [Google Scholar]
- 26.Kratz EG, Walker AR, Lagardre L, Lipparini F, Piquemal JP, Andrs Cisneros G. Lichem: a QM/MM program for simulations with multipolar and polarizable force fields. J Comput Chem. 2016;37(11):1019–1029. doi: 10.1002/jcc.24295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Laino T, Mohamed F, Laio A, Parrinello M. An efficient linear-scaling electrostatic coupling for treating periodic boundary conditions in QM/MM simulations. J Chem Theory Comput. 2006;2(5):1370–1378. doi: 10.1021/ct6001169. [DOI] [PubMed] [Google Scholar]
- 28.Lamichhane M, Gezelter JD, Newman KE. Real space electrostatics for multipoles. I. Development of methods. J Chem Phys. 2014a;141(13):134,109. doi: 10.1063/1.4896627. [DOI] [PubMed] [Google Scholar]
- 29.Lamichhane M, Newman KE, Gezelter JD. Real space electrostatics for multipoles. II. Comparisons with the Ewald sum. J Chem Phys. 2014b;141(13):134,110. doi: 10.1063/1.4896628. [DOI] [PubMed] [Google Scholar]
- 30.Laury ML, Wang LP, Pande VS, Head-Gordon T, Ponder JW. Revised parameters for the amoeba polarizable atomic multipole water model. J Phys Chem B. 2015;119(29):9423–9437. doi: 10.1021/jp510896n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Leach A. Molecular modelling: principles and applications. 2nd. Prentice Hall; Englewood Cliffs: 2001. [Google Scholar]
- 33.Mahoney MW, Jorgensen WL. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J Chem Phys. 2000;112(20):8910–8922. [Google Scholar]
- 34.Nam K, Gao J, York DM. An efficient linear-scaling Ewald method for long-range electrostatic interactions in combined QM/MM calculations. J Chem Theory Comput. 2005;1(1):2–13. doi: 10.1021/ct049941i. [DOI] [PubMed] [Google Scholar]
- 35.Ojeda-May P, Pu J. Isotropic periodic sum treatment of long-range electrostatic interactions in combined quantum mechanical and molecular mechanical calculations. J Chem Theory Comput. 2014;10(1):134–145. doi: 10.1021/ct400724d. [DOI] [PubMed] [Google Scholar]
- 36.Ojeda-May P, Pu J. Treating electrostatics with wolf summation in combined quantum mechanical and molecular mechanical simulations. J Chem Phys. 2015;143(17):174,111. doi: 10.1063/1.4934880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Patra M, Karttunen M, Hyvönen MT, Falck E, Vattulainen I. Lipid bilayers driven to a wrong lane in molecular dynamics simulations by subtle changes in long-range electrostatic interactions. J Phys Chem B. 2004;108(14):4485–4494. [Google Scholar]
- 38.Peter Tieleman D, Hess B, Sansom MS. Analysis and evaluation of channel models: simulations of alamethicin. Biophys J. 2002;83(5):2393–2407. doi: 10.1016/s0006-3495(02)75253-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ponder JW. Tinker, software tools for molecular design, version 7.0. 2015 doi: 10.1021/acs.jctc.8b00529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Riccardi D, Schaefer P, Cui Q. pka calculations in solution and proteins with QM/MM free energy perturbation simulations: a quantitative test of QM/MM protocols. J Phys Chem B. 2005;109(37):17,715–17,733. doi: 10.1021/jp0517192. [DOI] [PubMed] [Google Scholar]
- 41.Schaefer P, Riccardi D, Cui Q. Reliable treatment of electrostatics in combined QM/MM simulation of macromolecules. J Chem Phys. 2005;123(1):014,905. doi: 10.1063/1.1940047. [DOI] [PubMed] [Google Scholar]
- 42.Schreiber H, Steinhauser O. Cutoff size does strongly influence molecular dynamics results on solvated polypeptides. Biochemistry. 1992;31(25):5856–5860. doi: 10.1021/bi00140a022. [DOI] [PubMed] [Google Scholar]
- 43.Shi Y, Xia Z, Zhang J, Best R, Wu C, Ponder JW, Ren P. Polarizable atomic multipole-based amoeba force field for proteins. J Chem Theory Comput. 2013;9(9):4046–4063. doi: 10.1021/ct4003702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Steinbach PJ, Brooks BR. New spherical-cutoff methods for long-range forces in macromolecular simulation. J Comput Chem. 1994;15(7):667–683. [Google Scholar]
- 45.Stone AJ. The theory of intermolecular forces. Oxford University Press; Oxford: 2013. [Google Scholar]
- 46.Valiev M, Bylaska E, Govind N, Kowalski K, Straatsma T, Van Dam H, Wang D, Nieplocha J, Apra E, Windus T, de Jong W. NWChem: a comprehensive and scalable open-source solution for large scale molecular simulations. Comput Phys Commun. 2010;181(9):1477–1489. [Google Scholar]
- 47.Walker RC, Crowley MF, Case DA. The implementation of a fast and accurate QM/MM potential method in amber. J Comput Chem. 2008;29(7):1019–1031. doi: 10.1002/jcc.20857. [DOI] [PubMed] [Google Scholar]
- 48.Wolf D. Reconstruction of NACl surfaces from a dipolar solution to the madelung problem. Phys Rev Lett. 1992;68(22):3315–3318. doi: 10.1103/PhysRevLett.68.3315. [DOI] [PubMed] [Google Scholar]
- 49.Wolf D, Keblinski P, Phillpot SR, Eggebrecht J. Exact method for the simulation of coulombic systems by spherically truncated, pairwise r−1 summation. J Chem Phys. 1999;110(17):8254–8282. [Google Scholar]
- 50.Wu X, Brooks BR. Isotropic periodic sum: a method for the calculation of long-range interactions. J Chem Phys. 2005;122(044):107. doi: 10.1063/1.1836733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.York DM, Yang W, Lee H, Darden T, Pedersen LG. Toward the accurate modeling of DNA: the importance of long-range electrostatics. J Am Chem Soc. 1995;117(17):5001–5002. [Google Scholar]
- 52.Zhang Y, Liu H, Yang W. Free energy calculation on enzyme reactions with an efficient iterative procedure to determine minimum energy paths on a combined ab initio QM/MM potential energy surface. J Chem Phys. 2000;112(8):3483–3492. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


