Atoms and molecules in cavities, from weak to strong coupling in quantum-electrodynamics (QED) chemistry

Significance

Traditionally, quantum chemistry investigates molecular systems assuming that the photon field, which leads to the interaction of charged particles, is well approximated by the Coulomb interaction. On the other hand, quantum optics describe the photon field in detail while approximating the matter systems via few levels. Recent experiments at the interface between these two areas of research have uncovered situations where both the molecular system and the photon field have to be treated in detail. In this work, we show how theoretical approaches have to be adapted to treat such coupled matter–photon problems and which effects can be anticipated. Our quantum electrodynamics density-functional formalism provides the theoretical framework to open a field of research able to deal with emergent properties of matter.

Abstract

In this work, we provide an overview of how well-established concepts in the fields of quantum chemistry and material sciences have to be adapted when the quantum nature of light becomes important in correlated matter–photon problems. We analyze model systems in optical cavities, where the matter–photon interaction is considered from the weak- to the strong-coupling limit and for individual photon modes as well as for the multimode case. We identify fundamental changes in Born–Oppenheimer surfaces, spectroscopic quantities, conical intersections, and efficiency for quantum control. We conclude by applying our recently developed quantum-electrodynamical density-functional theory to spontaneous emission and show how a straightforward approximation accurately describes the correlated electron–photon dynamics. This work paves the way to describe matter–photon interactions from first principles and addresses the emergence of new states of matter in chemistry and material science.

Novel experimental possibilities have allowed scientists to obtain new insights into how photons interact with matter and how these interactions correlate photonic and particle degrees of freedom. Such experiments show, for example, an increase of the conductivity in organic semiconductors through hybridization with the vacuum field (3), strong shifts of the vibrational frequencies by the coupling of molecular resonators with a microcavity mode (4), nonclassical single photon–phonon correlations (5), the control of spin relaxations using an optical cavity (6), the enhancement of Raman scattering from vibro-polariton states (7, 8), changes of chemical reactivity (9, 10), single-molecule strong coupling (11), sampling of vacuum fluctuations (12), strong exciton–photon coupling of light-harvesting complexes (13), strong long-range atom–atom interactions mediated by photons (14), attractive photonic states (15, 16), or superradiance for atoms in photonic crystals (17). All these results indicate the appearance of new states of matter and subsequently a change in the chemical properties of the matter system (18–21), if the quantum nature of light becomes important. For example, in so-called strong-coupling situations, which are nowadays of central interest in the fields of circuit quantum electrodynamics (circuit QED) (22–24) or cavity QED (25, 26). Whereas the analyses of such experiments are routinely performed with the help of simplified (few-level) models that are able to capture the essential physics, for the (quantitative) prediction of properties of complex multiparticle systems coupled to photons, methods that can treat such coupled boson–fermion situations from first principles seem worthwhile (1, 2, 27–31). On the other hand, the strong coupling to photons can challenge our conventional understanding of electronic structures and allows us to study the influence of the quantum nature of light on chemical processes.

In this work, we want to highlight the possibilities as well as the theoretical challenges that arise at the interface of electronic structure theory and quantum optics. To this end, we discuss three distinct situations where the photon–matter correlation becomes significant and modifies conventional concepts of electronic-structure theory and quantum optics. In Cavity QED—The Molecular Dimer Case we study systems that contain nuclear, electronic, and photonic degrees of freedom explicitly. First, we consider a model dimer molecule that contains two nuclei and two electrons confined to one dimension and is placed in an optical high-Q cavity. We show how the photons change the electronic Born–Oppenheimer (BO) surfaces in a complex way. These changes affect, for example, the bond length and the absorption spectrum of the molecule (32). Additionally, we show how the ground state of the full system obtains an electron–nuclear(vibronic)–photon quasiparticle character, the vibro-polariton. The second model system we study in Cavity QED—The Trimer Case is the 2D Shin–Metiu model (33, 34), which consists of three nuclei and a single electron located in an optical high-Q cavity in resonance to the lowest vibrational excitation. The 2D Shin–Metiu model is a model system for an $H_3^{2+}$ molecule featuring a conical intersection in the BO surfaces, and we show how this intersection can be altered in the case of strong light–matter interactions. In Local Optimal Control we show how the control of electronic systems (35) is modified if we take into account the coupling to a cavity mode. These extra degrees of freedom allow us to achieve a predefined target more efficiently with less external driving, when either the cavity frequency or the electron–photon coupling is chosen. Additionally the external driving of the photonic field by external dipoles allows us to influence the electron transport to gain efficiency. In Quantum-Electrodynamical Density-Functional Theory, we consider single-photon emission and how photon-bound polariton states appear in multimode cavities, if the matter–photon coupling is increased to strong coupling. This limit leads, for example, to the breakdown of the Purcell effect (36). For such a strong-coupling situation we demonstrate the capabilities of the recently developed density-functional theory for cavity-QED systems (1, 2, 28, 37). We show the limitations of a semiclassical treatment and that the first approximate exchange-correlation functional (37) for cavity-QED systems along the line of the optimized-effective potential (OEP) approach (38) allows us to accurately treat such situations.

Cavity QED—The Molecular Dimer Case

Let us start with a model that contains all of the major degrees of freedom of a real system: nuclear, electronic, and photonic. The model we consider is an artificial one-dimensional molecule that consists of two nuclei and two electrons. In a traditional quantum-chemical treatment the photonic degrees of freedom would be neglected because one assumes the multiparticle system to be in free space and the Coulomb interaction* is supposed to describe the major contribution of the interaction due to the photon field. However, if we put the molecule inside an optical cavity, we change the photon modes^† and find situations where the photon degrees of freedom play a crucial role. To investigate this situation, we consider as a first example a molecule inside a cavity where one of the modes is tuned to the first vibrational excitation of the dimer system. This mode is the photon degree of freedom that we will keep in our calculations. We show how this can affect standard concepts of electronic-structure theory, for example, the BO surfaces. Schematically, this electron–nuclear–photon system can be understood as follows.

In Fig. 1, Left the molecule in the cavity is shown. The molecule is exposed to a single cavity mode, which is given by one of the cavity frequencies ${\omega }_{\alpha }$ and the matter–photon coupling strength ${\lambda }_{\alpha }$. In Fig. 1, Right we depict a simplified picture of the hybridization of the system. We show the BO surface depending on the nuclear coordinate $X$ in atomic units (Bohr) and indicate the eigenstates of the molecular system in BO approximation. In the ground state, the electrons are subject to the ground-state BO surface, which is shown in dashed-black lines. The harmonic approximation to this full surface is shown in solid red lines. The individual harmonic excitations of the nuclear (phonon) subsystem are indicated by the quantum number $\nu$. Because the cavity mode is tuned in resonance, we find Rabi splitting (41) of the first vibrational excitation, which is proportional to the matter–photon coupling constant ${\lambda }_{\alpha }$. The first-excited electronic BO surface is shown in gray dashed lines. This surface has no minima, hence featuring the dissociation of the molecule. In the dissociation limit ($X>5$ a.u.), the ground state and the first-excited BO surfaces merge.

Fig. 1.

(Left) Schematic illustration of the dimer in a cavity coupled to a single-mode field polarized along the $x$ axis. (Right) Exact ground-state BO surface in black dashed lines, harmonic ground-state BO surface in solid red lines, and exact first-excited–state BO surface in dashed-dotted gray lines. $\nu$ indicates the phonon excitation, $R_e$ marks the BO equilibrium distance, and $\lambda$ denotes the Rabi splitting by the phonon–photon hybridization and the matter–photon interaction strength. The photon wavevector $k_z$, the magnetic field $B_y$, and the displacement field $D_x$ build a triad (40).

For a detailed investigation in the following, we consider this system in the dipole approximation and in the length gauge. In this setup, the general correlated electron–nuclear–photon Hamiltonian consisting of $n_e$ electrons, $n_n$ nuclei, and $n_p$ photon modes can be written as a sum of the electro-nuclear Hamiltonian ${\widehat{H}}_{en}$ and the photon Hamiltonian ${\widehat{H}}_p$ (2, 28, 37, 42),

$$\widehat{H}={\widehat{H}}_{en}+{\widehat{H}}_p$$ [1]

$${\widehat{H}}_{en}={\widehat{T}}_e+{\widehat{T}}_N+{\widehat{W}}_{ee}+{\widehat{W}}_{NN}+{\widehat{W}}_{eN}$$ [2]

$${\widehat{H}}_p=\frac{1}{2}\sum _{\alpha =1}^{n_p}\left[{\widehat{p}}_{\alpha }^2+{\omega }_{\alpha }^2{\left({\widehat{q}}_{\alpha }+\frac{{𝝀}_{\alpha }}{{\omega }_{\alpha }}\cdot e\mathrm{𝑹}\right)}^2\right]$$ [3]

$$\mathrm{𝑹}=\sum _{I=1}^{N_n}{Z}_I{\text{𝐗}}_I-\sum _{i=1}^{N_e}{\text{𝐱}}_i,$$ [4]

where $Z_I$ specifies the nuclear charges. The kinetic energy is given by $\widehat{T}=-{\sum }_{i=1}{\mathrm{\hslash }}^2{\overrightarrow{\nabla }}_{{\text{𝐱}}_i}^2/2m_i$, for electrons and nuclei with mass $m_i$, respectively. Further, instead of the bare Coulomb interaction, we use a soft Coulomb interaction (43) for $\widehat{W}$ as routinely done for one-dimensional model systems; that is, $\widehat{W}={\sum }_{i,j>i}{Z}_i{Z}_j/4\pi {ϵ}_0\sqrt{{\left({\text{𝐱}}_i-{\text{𝐱}}_j\right)}^2+1}$, with resulting negative (positive) prefactor for the electron–nuclear (electron–electron/nuclear–nuclear) interaction. In the following, for the specific dimer systems, the uppercase variables ${\text{𝐗}}_1$ and ${\text{𝐗}}_2$ denote the nuclear coordinates, whereas the lowercase variables ${\text{𝐱}}_3$ and ${\text{𝐱}}_4$ denote the electronic coordinates, and ${\widehat{q}}_{\alpha }=\sqrt{\frac{\mathrm{\hslash }}{2{\omega }_{\alpha }}}\left({\widehat{a}}_{\alpha }^{†}+{\widehat{a}}_{\alpha }\right)$ defines the photon displacement coordinate, using the photonic creation and annihilation operators (28, 37). The photon displacement operator is connected to the electric displacement field operator ${\widehat{\text{𝐃}}}_{\alpha }={\omega }_{\alpha }{𝝀}_{\alpha }{\widehat{q}}_{\alpha }$, where ${𝝀}_{\alpha }$ is the transversal polarization vector times the dipole-approximation coupling strength ${\lambda }_{\alpha }$. Using $g_{\alpha }=\sqrt{\frac{\mathrm{\hslash }{\omega }_{\alpha }}{2}}{\lambda }_{\alpha }$, we can connect to typical strong-coupling calculations as, for example, in ref. 32. We describe only the two valence electrons explicitly. To this end, we choose for the nuclear masses $M_1=m_p$ and $M_2=m_p$, where $m_p$ is the proton mass and with nuclear charges $Z_1=\mathrm{\hspace{0.17em}1.2}$, and $Z_2=\mathrm{\hspace{0.17em}0.8}$. The electron masses correspond to the electron mass $m_e$; that is, $m_3=m_4=m_e$. In the photon Hamiltonian ${\widehat{H}}_p$, we consider the electron–nuclear–photon coupling in dipole approximation, where $\mathrm{𝑹}$ is the full dipole operator that contains both the electronic and nuclear contributions. The complete many-body problem including two electrons, two nuclei, and one photon mode is a five-dimensional problem. To reduce the computational complexity, we perform a coordinate transformation into a center-of-mass frame such that the center-of-mass motion can be separated and we are left with a four-dimensional problem for the internal degrees of freedom (44). For details on the transformation and the real-space grid used to perform the numerical calculation, we refer the reader to Supporting Information, Relative Jacobi Coordinates for Four-Body Systems. For clarity, we use the original Euclidean coordinates in all formulas throughout this paper with the exception of the nuclear relative coordinate $\text{𝐗}={\text{𝐗}}_1-{\text{𝐗}}_2$. The cavity frequency ${\omega }_{\alpha }$ is chosen to be in resonance to the first vibrionic transition ${\omega }_{12}$; hence ${\omega }_{\alpha }={\omega }_{12}=\mathrm{\hspace{0.17em}0.01216}\text{a.u.}$ The dipole moment of this transition has a value of $d_{12}=\mathrm{\hspace{0.17em}0.01869}\text{a.u.}$

The Hamiltonian in Eq. 1 contains besides the (softened) Coulomb interactions two new interaction terms: the explicit dipolar matter–photon coupling ${\sum }_{\alpha }{\omega }_{\alpha }{\widehat{q}}_{\alpha }\left({𝝀}_{\alpha }\cdot e\mathrm{𝑹}\right)$ and the quadratic dipole self-energy term ${\sum }_{\alpha }{\left({𝝀}_{\alpha }\cdot e\mathrm{𝑹}\right)}^2/2$. The dipole self-energy term is due to the length-gauge transformation (42) that explicitly mixes the electronic and photonic degrees a second time (the first time being the Coulomb gauge condition), such that the electric field ${\widehat{\text{𝐄}}}_{\alpha }$ in Eq. 3 becomes ${\widehat{\text{𝐃}}}_{\alpha }/{ϵ}_0+{𝝀}_{\alpha }{𝝀}_{\alpha }\cdot e\mathrm{𝑹}/{ϵ}_0$. It thus describes how the polarization of the matter system acts back on the photon field. This term is usually neglected and only rarely considered (42, 45–47). It is a clear relevant beyond two-levels effect, because in that case the dipole self-energy term reduces to a constant energy offset in the case of a two-level approximation, such as the Jaynes–Cummings model (37, 41). Additionally, recent experiments have arrived at the same conclusion, that is, the particular importance of such a dipole self-energy term in the strong-coupling regime (48). Furthermore, in an unconfined cavity-free 3D setup, it is usually neglected in the intermolecular region, where it cancels the intermolecular Coulomb interaction (40, 49, 50), or in the limit of dilute atomic gases and infinite quantization volume (42). However, in the intramolecular region in a cavity, which is the focus of the present study, this term has to be taken into account as becomes obvious from Fig. 2.

Fig. 2.

(A) The eigenenergies for different values of the matter–photon interaction strength $\lambda$. (B) The bond length $⟨\text{𝐗}⟩$. In both plots, black circles correspond to the ground-state $|g⟩$, blue squares to the lower polariton state $|LP⟩$, red down-pointing triangles to the upper polariton state $|UP⟩$, green up-pointing triangles to the second lower polariton state $|LP2⟩$, and stars in cyan plots to the second upper polariton state $|UP2⟩$. In B we denote the bond-length values by shaded colored circles without considering the R² term of Eq. 1.

In Fig. 2A we show the exact eigenenergies of the cavity system obtained by exact diagononalization (51) as a function of the matter–photon coupling strength ${\lambda }_{\alpha }$.^‡ The general harmonic trend is given by the self-polarization interaction term. In black, we plot the ground-state energy, in red/blue (cyan/green), we plot the first (second) upper and lower polariton states. The matter–photon coupling induces the Rabi splitting in the energy, as illustrated in Fig. 1. With increasing ${\lambda }_{\alpha }$, we find an increasing Rabi splitting. The bond-length $⟨\text{𝐗}⟩$ of the individual states is plotted in Fig. 2B . For this plot the same color code as in Fig. 2A applies and additionally, we plot the bond-length values in shaded colors of the states, if we neglect the dipole self-energy term in Eq. 1. We find that the full matter–photon coupling of Eq. 1 introduces large changes in the bond length. Here the bond length is reduced from 1.63 a.u. to 1.55 a.u. by around 5% for the ground state. In contrast, if we neglect the dipole self-energy term in Eq 1, we find an increasing bond length with increasing electron–photon coupling and the system is stable (bound) only up to $g_{\alpha }/{\omega }_{\alpha }=\mathrm{\hspace{0.17em}0.9}$. This finding is a clear indication of the importance of the usually neglected dipole self-energy term in the strong-coupling limit and agrees with recent experimental findings (48). Large changes in the chemical landscape of the system under strong light–matter coupling have also been observed experimentally, leading to, for example, the reduction of the chemical reactivity (9, 10).

Next, we show how a spectroscopic quantity of our electron–nuclear–photon model is influenced by strong matter–photon coupling. To this end we determine the ground-state absorption spectrum using a sum-over-states expression (32) explained in Supporting Information, Absorption Spectrum. In Fig. 3 we show spectra for different values of the matter–photon coupling strength ${\lambda }_{\alpha }$. For increasing coupling, we find clear signatures of a strong Rabi-splitting ${\mathrm{\Omega }}_R=(E_3-E_2)/{\omega }_{\alpha }$, where $E_3$ and $E_2$ are the eigenvalues of Eq. 1. In the spectra, we explicitly denote the LP and the UP peak, which become clearly visible in the strong-coupling limit. Additionally, higher lying excitations also show Rabi splitting; for example, the second peak shows a threefold splitting. In Fig. 3, Inset, we show that in the range of the used parameters, the Rabi splitting goes up to $0.3$. For the matter–photon coupling strength, we choose values between $0\le g_{\alpha }\le 1.6{\omega }_{\alpha }$. Recent experiments, as in for example, refs. 4 and 48, report Rabi splittings from $0.1\hspace{0.17em}\text{to}\hspace{0.17em}0.25$ and as seen in Fig. 3, Inset a value of $g_{\alpha }=1.6{\omega }_{\alpha }$ corresponds to a Rabi splitting of around $0.3$.

Fig. 3.

Calculated absorption spectra for the dimer in a cavity of Fig. 1 for different values of the matter–photon coupling strength $g/\omega$. The first two peaks correspond to the lower polariton (LP) peak and the upper polariton (UP) peak. In Inset, we quantify the Rabi splitting ${\mathrm{\Omega }}_R$ as a function of the coupling constant. (See text for details.)

Cavity BO Approximation

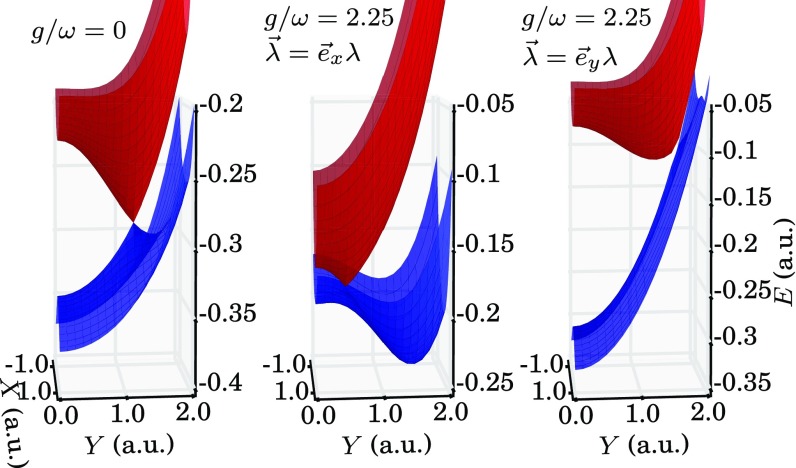
To highlight the effect that the photons can have on quantum-chemical concepts, we compare the exact calculations done with the above Hamiltonian to a BO calculation that takes the photons into account. This cavity-BO (CBO) approximation is introduced in Supporting Information, General CBO for Correlated Electron–Photon Systems and Supporting Information, CBO for Four-Body Systems. In the CBO approximation, the electronic Hamiltonian ${\widehat{H}}_e(\left\{\text{𝐗}\right\},\left\{q_{\alpha }\right\})$ parametrically depends on all nuclear coordinates $\{\text{𝐗}\}$ and photon displacement coordinates $\{q_{\alpha }\}$. This parametrical dependency is inherited to the multidimensional potential energy surfaces (PES) $V_j(\left\{\text{𝐗}\right\},\left\{q_{\alpha }\right\})=E_j(\left\{\text{𝐗}\right\},\left\{q_{\alpha }\right\})+V_{nn}\left(\left\{\text{𝐗}\right\}\right)+1/2{\sum }_{\alpha }{\omega }_{\alpha }^2{q}_{\alpha }^2$, where $E_j$ are the eigenvalues of the electronic CBO Hamiltonian. Such a procedure reduces in the case of ${\lambda }_{\alpha }=0$ to the usual BO approximation (52). For more details, we refer the reader to Supporting Information, General CBO for Correlated Electron–Photon Systems and Supporting Information, CBO for Four-Body Systems. In Fig. 4 we explicitly show different CBO surfaces. These surfaces are 2D surfaces and depend for the dimer system on the nuclear coordinate $𝑿$ and the photon displacement coordinate $q_{\alpha }$. In Fig. 4, Left the surfaces are the ground-state surfaces, whereas in Fig. 4, Right we plot the first-excited–state surfaces. In Fig. 4, Upper row, we plot the surfaces for vanishing matter–photon coupling. Both surfaces show along the x axis the behavior as in Fig. 1, whereas along the y axis we find a harmonic potential that is associated with the photon coordinate. These surfaces show that we can easily distinguish between the photon and nuclear degrees of freedom. In Fig. 4, Lower row we show the surfaces in the strong-coupling limit. Here, we find that new normal coordinates appear that are true polaritonic degrees of freedom. The normal coordinates have now photonic and nuclear degrees of freedom.

Fig. 4.

Upper row shows the ground state and first-excited 2D CBO surface for $g/\omega =\mathrm{\hspace{0.17em}0.0}$. Lower row shows the surfaces in the strong-coupling limit for $g/\omega =\mathrm{\hspace{0.17em}1.56}$. The dashed lines indicate the direction of the normal modes featuring dissociation of the system. The $x$ indicates the equilibrium bond length.

In Fig. 5A we explicitly show different CBO surfaces in a cut along the photon-coordinate $q_{\alpha }=\mathrm{\hspace{0.17em}0}$. In black, we plot the ground-state surfaces and in red the first-excited–state surfaces. We find that for increasing ${\lambda }_{\alpha }$ the polarization term introduces a harmonic (parabolic) barrier, which alters the BO surfaces significantly.

Fig. 5.

(A) The ground-state and first-excited CBO surface for different values of the matter–photon interaction strength $\lambda$. (B) The overlap of the exact states with the CBO states. Black circles correspond to the ground-state $|g⟩$, blue circles to the LP state $|LP⟩$, and red circles to the UP state $|UP⟩$.

The lowest surface in Fig. 5 corresponds to the cavity-free limit. This surface has a flat tail for large $𝑿$. We see that tuning ${\lambda }_{\alpha }$ allows us to shape the BO surfaces harmonically, which has in particular implications on the tail of the surface. In general, changes in the BO surfaces alter the chemistry of the system, with implications on various quantities, for example, the bond length, tunneling barriers, or transition rates. For instance, because the nuclear coordinate $𝑿$ in Fig. 5 is also a measure for the nuclear bond length, we find that increasing the value of ${\lambda }_{\alpha }$ shifts the bond length to smaller values. As in the exact calculation, the opposite trend would be found if we neglected the polarization contribution to the matter–photon coupling. In Fig. 5 in red, we show the first-excited–state surfaces. Whereas these surfaces feature the dissociation of the molecule in the cavity-free case, we find a local minimum of the surfaces for strong matter–photon coupling ${\lambda }_{\alpha }$. We emphasize, however, that along the new normal-coordinate direction indicated in Fig. 4 the system is dissociating, as in the field-free case for $q_{\alpha }=0$. Because in the strong-coupling limit the photonic and nuclear degrees of freedom are highly correlated, the dissociation also corresponds to an excitation in the photonic degree of freedom. Next we assess the quality of the CBO approximation and plot the overlap of the cavity-BO–approximated wave functions with the exact wave functions in Fig. 5B. Whereas for small values of ${\lambda }_{\alpha }$ the CBO approximation has the same quality as the cavity-free electronic BO approximation, we observe lower overlaps for strong matter–photon interaction. The overlap of the CBO UP state with the exact correlated state drops to 0.994% in the strong-coupling limit. Following the usual trend known from the standard BO approximation, the quality of higher-lying states, which here are the UP and the LP states, is lower than the quality of the ground state. However, the high accuracy in the overlaps demonstrates the usefulness of the BO concept also for electron–nuclear–photon problems.

Cavity QED—The Trimer Case

The second system that we analyze is a 2D generalization (34) of the Shin–Metiu model (33). The Shin–Metiu model has been analyzed heavily in the context of correlated electron-nuclear dynamics (53), exact forces in nonadiabatic charge transfer (54), and nonadiabatic effects in quantum reactive scattering (55), to mention a few. The 2D generalization of the Shin–Metiu model consists of three nuclei and a single electron. Two of three nuclei are fixed in space. Therefore, this system serves as a model system for an $H_3^{2+}$ molecule that has been confined to two spatial dimensions. In our case, we furthermore place the system into an optical cavity, where it is coupled to a single electromagnetic mode. As a Hamiltonian for our system we consider the electron-nuclear part as given in ref. 34 and couple to the photon Hamiltonian ${\widehat{H}}_p$ from Eq. 3. The dipole operator that enters the photon Hamiltonian in Eq. 3 is given by $\mathrm{𝑹}={\mathrm{𝑹}}_n-{\text{𝐫}}_e$, where ${\mathrm{𝑹}}_n$ is the nuclear coordinate and ${\text{𝐫}}_e$ the electronic coordinate. For more details, we refer the reader to Supporting Information, Shin–Metiu Model in a Cavity.

Fig. 6 shows the CBO surfaces calculated with $q_{\alpha }=\mathrm{\hspace{0.17em}0}$. In all calculations, we tune the matter–photon coupling strength $\lambda$ from the weak-coupling regime to the strong-coupling regime. In Fig. 6, Left, we choose the value $g_{\alpha }/{\omega }_{\alpha }=\mathrm{\hspace{0.17em}0}$ and in the case of $\lambda =0$, we find a conical intersection between the first-excited–state surface and the second-excited–state surfaces as reported in ref. 34. In Fig. 6, Center, we tune the matter–photon coupling strength to the strong-coupling limit with $g_{\alpha }/{\omega }_{\alpha }=\mathrm{\hspace{0.17em}2.25}$ and the photon polarization in the x direction. The matter–photon coupling alters the PES significantly for $q_{\alpha }=\mathrm{\hspace{0.17em}0}$ and shifts the position of the conical intersection to smaller y values. The opposite trend can be found if the photon field is polarized in the y direction. As shown in Fig. 6, Right, for strong coupling with $g_{\alpha }/{\omega }_{\alpha }=\mathrm{\hspace{0.17em}2.25}$, the conical intersection is shifted to larger y values. These changes of the CBO surfaces have an immediate effect on chemical properties of molecular systems, for example, the nonadiabatic coupling matrix elements (56) that are routinely calculated in nonadiabatic dynamics. These changes in the nonadiabatic coupling terms will affect dramatically the electron-nuclear dynamics and can influence chemical reactions. To conclude the first three sections, we have seen how the photonic degrees of freedom alter chemical properties of molecular model systems. Besides showing the hybrid character of the ground state and the Rabi splitting of the polaritonic states from first principles, we have identified changes in the BO surfaces that explain, for example, photon-mediated changes in bond length or conical intersections.

Fig. 6.

CBO potential energy surfaces for the 2D Shin–Metiu model at $q_{\alpha }=0$. Increasing matter–photon coupling strength shifts the conical intersection, depending on the photon field polarization to larger (smaller) y values for polarization in the y (x) direction. The plots use parameters as in ref. 34.

Local Optimal Control

Whereas in the first part of this article we have shown how the coupling to photons can alter properties of multiparticle systems, in the second part we investigate which consequences the interaction with photons has in the context of quantum control theory. In quantum control theory we are usually interested in finding an external, classical electromagnetical field, for example, a specific laser pulse, that forces an electronic system to behave in a previously specified way. Roughly speaking, such control can be done either by driving the system into a predefined state with side conditions such as a minimal external field, that is, optimal control theory (35, 57, 58), or by prescribing how an observable is supposed to change in time and space, that is, local control theory (59–62). Both approaches can be combined to give local-optimal control theory (62, 63). We use such a hybrid method here. Because quantum control algorithms even for purely electronic systems are numerically very expensive, we further simplify and consider the simplest yet nontrivial model system of an electron coupled to photons, the extended Rabi model (1, 37, 41, 64),

$$\widehat{H}=-t_0{\widehat{\sigma }}_x+\omega {\widehat{a}}^{†}\widehat{a}+\sqrt{\frac{\omega }{2}}\left({\widehat{a}}^{†}+\widehat{a}\right){\widehat{\sigma }}_z+j(t)\left({\widehat{a}}^{†}+\widehat{a}\right)+v(t){\widehat{\sigma }}_z,$$ [5]

where ${\widehat{\sigma }}_x$ and ${\widehat{\sigma }}_z$ denote the corresponding Pauli matrices. The Hamiltonian contains as internal parameters the kinetic energy matrix element $t_0$ that yields an amplitude for the electron to hop between the sites, the photon mode frequency $\omega$ that determines the energy of a single photon in the mode, and the electron–photon coupling strength $\lambda$ that fixes the strength of the interaction. Further, Eq. 5 contains two external variables, which allow us to control the system: the external potential $v(t)$ (corresponding to the usual external laser pulse), which couples to the electron and introduces a potential shift between the sites, and the external dipole $j(t)$, which couples to the photon mode. The external dipole allows us to pump the cavity mode. In our calculations, we choose a resonant setup for the three internal parameters, $t_0=\mathrm{\hspace{0.17em}2.5}$, $\omega =\mathrm{\hspace{0.17em}5}$, and we vary between $\lambda =\mathrm{\hspace{0.17em}0}$ (no coupling) and from the weak- to the strong-coupling limit with $\lambda =(0.25,0.5,1.0)$.

In the following, we use the above model to control charge-transfer processes, which are an important topic in the electronic-structure community and have significant implications for, for example, photovoltaics (65, 66). Similar models have already been used in the same context (67). To see how the coupling to photons changes the charge transfer is motivated also by a recent experiment (3), where the coupling of an organic semiconductor to photon modes has increased the conductivity by an order of magnitude. To model such a charge-transfer reaction, we put most of the charge (why not all will become clear a little later) on one site of our model system and we choose a final time $T=\mathrm{\hspace{0.17em}12.57}$ a.u. at which the charge expectation values are interchanged. In terms of the site-basis functions, this setup amounts to $|\psi (0)⟩=|0.99,0.01⟩\to |\psi (T)⟩=|0.01,0.99⟩$, where the full initial electron–photon wave function is $|{\mathrm{\Psi }}_0⟩=|\psi (0)⟩\otimes |0⟩$; that is, the photon mode is initially in the vacuum state. In terms of the charge differences, this initial state means we go from ${\sigma }_z(0)=\mathrm{\hspace{0.17em}0.98}$ to ${\sigma }_z(T)=-0.98$. As a further condition we want to have a minimal external forcing on the electron, which defines the penalty function $P$ by $P={\int }_0^{T}dtv{(t)}^2$. The setup is, however, different from usual optimal control, because we allow the pair $(v(t),j(t))$ to vary to achieve our goal. Clearly, in the case of no coupling $(\lambda =\mathrm{\hspace{0.17em}0})$ a change in $j(t)$ will not have any influence on the electronic wave function (because the problem decouples) and so we choose $j(t)=\mathrm{\hspace{0.17em}0}$. In this case finding the minimum $v(t)$ can be based on an explicit expression of the local control theory (68). The exact expression provides us with a control field for every prescribed path ${\sigma }_z(t)$ provided the denominator does not go to zero. To avoid such a situation at the initial and the final time we have chosen the initial and final states to be not fully localized. In our approach we use a set of basis functions ${\sigma }_i(t)=C\cos \left((2i-1)\omega t\right)$ consistent with the initial and final state to expand ${\sigma }_z(t)={\sum }_{i=1}^N{c}_i{\sigma }_i(t)$ with ${\sum }_{i=1}^N{c}_i=\mathrm{\hspace{0.17em}1}$, over which the penalty function $P$ is minimized, that is, $\text{min}{}_{\{c_i\}}\int _0^{T}dtv{([{\sigma }_z];t)}^2$. In all calculations we use N = 11. Note that such an expansion is simple only in the case of physical observables such as the charge difference ${\sigma }_z(t)$, whereas in terms of time-dependent wave functions $|\mathrm{\Psi }(t)⟩$ this expansion is extremely demanding. The possibility to restrict to a simple and finite basis of charge paths ${\sigma }_i(t)$ is one advantage of this local optimal control approach. The other advantage is that the charge transfer is guaranteed to be achieved at the final time. The minimization is then performed by the quasi-Newton method (69). Extending the number of basis functions would lead to an even further-optimized value of the penalty function $P$ but does not lead to qualitative differences in the discussion of the obtained results.

In the case of $\lambda \ne \mathrm{\hspace{0.17em}0}$, we do not have a simple analytical expression for $v(t)$ and the electronic part of the wave function will depend also on the choice of external dipole $j(t)$. To find the corresponding $v([{\sigma }_z,j];t)$ for a given density path ${\sigma }_z(t)={\sum }_{i=1}^N{c}_i{\sigma }_i(t)$ and dipole $j(t)={\sum }_{k=1}^M{d}_k{j}_k(t)$, where we choose $j_k(t)=\sin \left(k\omega t\right)$, we use a fixed-point method (1, 2, 27, 61).^§ Now we can vary over a space of electronic $c_i$ and photonic $d_k$ coordinates, that is, $\underset{\{c_i,d_k\}}{\min }{\int }_0^{T}dtv{([{\sigma }_z,j];t)}^2$, where we choose $M=11$. We first briefly review the trivial cases, where no external potentials, that is, $v(t)=j(t)=\mathrm{\hspace{0.17em}0}$, are applied to the system. Table 1 shows the values for ${\sigma }_z(T)$ for all four cases of the electron–photon coupling strength $\lambda$. Whereas ${\sigma }_z(0)$ is given by the initial state and thus equals $0.980$ in all examples, they vary strongly in their free final state ${\sigma }_z(T)$. Analyzing these values already gives us the first hint, how to optimize electron–photon problems to our favor. If there is no electron–photon coupling ($\lambda =0$), the final value for $v(t)=\mathrm{\hspace{0.17em}0}$ is ${\sigma }_z(T)=\mathrm{\hspace{0.17em}0.98}$. In contrast, if we choose the coupling strength of $\lambda =\mathrm{\hspace{0.17em}0.25}$, the free evolution without any external potential already yields a final state very close to the desired value $-0.98$. Thus, we can conclude from this observation that already tuning the electron–photon coupling strength $\lambda$ allows us to use the electron–photon coupling. Additionally, we can suggest that a local control optimization for $\lambda =\mathrm{\hspace{0.17em}0.25}$ coupling strength can be very efficient, because the external potential has to improve the outcome only a little. In contrast, for all other values of $\lambda$ we see that the external potential has to modify the evolution more strongly.

Table 1.

Results of the local control optimization for the extended Rabi model

$g=\sqrt{\frac{\omega }{2}}\lambda$	$0$	$0.25$	$0.5$	$1.0$
$v(t)=j(t)=0:{\sigma }_z(T)$	$0.980$	$-0.979$	$0.975$	$0.969$
$v(t)\ne \mathrm{\hspace{0.17em}0}\text{,}j(t)=0:P$	$0.3015$	$0.0008$	$0.8145$	$3.2473$
$v(t)\ne \mathrm{\hspace{0.17em}0}\text{,}j(t)\ne \mathrm{\hspace{0.17em}0}:P$	—	$0.0008$	$0.8113$	$2.4084$

The resulting external potentials of the local control optimizations with fixed $j(t)=\mathrm{\hspace{0.17em}0}$ are shown in Fig. 7. For the case of $\lambda =\mathrm{\hspace{0.17em}0}$, we find a rather regular oscillation in $v(t)$ and ${\sigma }_z(t)$. The evolution of ${\sigma }_z(t)$ for the case of $\lambda =\mathrm{\hspace{0.17em}0.25}$ is very close to the optimal evolution of $\lambda =0$, but has a very small value of $v(t)$, due to the optimal utilization of the electron–photon interaction. For the cases of $\lambda =\mathrm{\hspace{0.17em}0.5}$ and $\lambda =\mathrm{\hspace{0.17em}1.0}$ the electron–photon interaction is stronger, and thus the system reacts stiffer with respect to the external potential $v(t)$. This strong coupling leads to a higher penalty function as shown in Table 1. For these two examples, we further find a nonsymmetric optimal solution of $v(t)$. This solution can be explained by the fact that requesting a final value of ${\sigma }_z(T)=-0.98$ does not give restrictions on the final photon state. Here, we find excitations of the photonic amplitude. We now turn our focus to the optimization where we lift the restriction on $j(t)$. In Fig. 8, and the last row in Table 1, we show the optimization for the case of $j(t)\ne \mathrm{\hspace{0.17em}0}$. Here we find that the additional degree of freedom allows us to control the system more efficiently. In particular, the example of $\lambda =\mathrm{\hspace{0.17em}1}$ shows the effectiveness of the scheme. Here, we are able to lower the penalty function significantly from $3.2473$ for $j(t)=\mathrm{\hspace{0.17em}0}$ to $2.4084$ for $j(t)\ne \mathrm{\hspace{0.17em}0}$. Our local optimal control results for this simple model show how the coupling to photons can induce charge transfer reactions with only little external forcing on the electron. Although it is not surprising that in a resonant setup the reaction is driven mainly by the coupling to the mode, the optimal-control analysis shows that controlling the photonic part of the electron–photon wave function via $j(t)$ directly allows a reduction of the applied external potential $v(t)$ that acts on the electron. This finding indicates the possibility to optimize charge-transfer reactions in a cavity by specifically populating certain cavity modes via an external dipole or current. Such an approach is different from the usual control approaches where one controls the electronic systems via an external laser only.

Fig. 7.

Results for local optimal control. (A) Density evolution ${\sigma }_z(t)$ for $\lambda =\mathrm{\hspace{0.17em}0}$ in black, $\lambda =\mathrm{\hspace{0.17em}0.25}$ in blue, $\lambda =\mathrm{\hspace{0.17em}0.5}$ in green, and $\lambda =\mathrm{\hspace{0.17em}1.0}$ in red and the corresponding evolution of $v(t)$ in B. Note that $v(t)$ for $\lambda =\mathrm{\hspace{0.17em}0.25}$ has been multiplied by the factor $20$.

Fig. 8.

Results for local optimal control. (A–C) Density evolution of ${\sigma }_z(t)$ (A) for $\lambda =0$ in black, $\lambda =0.25$ in blue, $\lambda =0.5$ in green, and $\lambda =1.0$ in red and the corresponding evolution of $v(t)$ (B) and $j(t)$ (C). Note that $v(t)$ and $j(t)$ for $\lambda =0.25$ have been multiplied by the factor of $20$.

Quantum-Electrodynamical Density-Functional Theory

The last section of this paper is dedicated to quantum-electrodynamical density-functional theory (QEDFT). It allows for numerically feasible ab initio simulations of correlated matter–photon systems. The basic idea is that instead of solving for the (usually infeasible) correlated electron–photon wave function one solves a set of self-consistent (in practice approximate) equations of motion for specific reduced quantities. For details on the method we refer to refs. 1, 2, 27, 28, and 37. All available implementations of QEDFT (1, 2, 37) are based on the electron density as basic variable. However, a consistent treatment of the quantized electric and magnetic field beyond the dipole coupling is possible by using QEDFT based on the charge current and full vector potential of the photon field (1). In this article, we consider the performance of QEDFT for an approximation based on the OEP scheme (37) for the case of single-photon emission and bound electron–photon states. The OEP approximation uses the ground-state Lamb shift as an orbital functional for the DFT scheme. For more details, we refer the reader to ref. 37. We compare the semiclassical (mean-field) and the OEP approximation to the exact numerical treatment beyond the rotating-wave approximation (RWA) (41) for a simple model.

In contrast to the previous models we now consider many photon modes that couple to our particle system. To that end we apply the model Hamiltonian introduced in ref. 70 but go beyond the RWA. We consider electronic two-level systems coupled to $M=\mathrm{\hspace{0.17em}400}$ modes. To be able to treat the photon field consisting of $M$ modes numerically exactly we truncate the Fock space and consider only the vacuum state, the $M$ one-photon states, and the $\left(M^2+M\right)/2$ two-photon states in a (1D) cavity of volume (length) $V$. The Hamiltonian we use is given by (70)

$$\widehat{H}=-t_0{\widehat{\sigma }}_x+\sum _{\alpha }{\omega }_{\alpha }{\widehat{a}}_{\alpha }^{†}{\widehat{a}}_{\alpha }+\sum _{\alpha }{\omega }_{\alpha }{\lambda }_{\alpha }{\widehat{q}}_{\alpha }\left(d_{eg}{\widehat{\sigma }}_z\right),$$ [6]

where ${\widehat{q}}_{\alpha }$ is as in Eq. 3 and the wave vectors $k_{\alpha }={\omega }_{\alpha }/c=\alpha \pi /V$. We fix the position of the two-level subsystems at $x=V/2$ and hence we can deduce the coupling constants from the photon modes ${\lambda }_{\alpha }(x)=\sqrt{\frac{2}{\mathrm{\hslash }{ϵ}_{0}V}}\sin (k_{\alpha }x)$ at this position. At this position the even modes decouple from the system (70) and only the odd modes have to be considered. Hence in the following $\alpha =\{\mathrm{1...200}\}$. The quantized electric field is then given by $\widehat{E}(x)={\sum }_{\alpha }{\omega }_{\alpha }{\lambda }_{\alpha }(x){\widehat{q}}_{\alpha }$, whereas the quantity that is linked more closely to the quantum nature of the light field is the intensity observable (70) that is given by $⟨{\widehat{E}}^2(x,t)⟩={\sum }_{\alpha ,\beta }{\omega }_{\alpha }{\omega }_{\beta }{\lambda }_{\alpha }(x){\lambda }_{\beta }(x)⟨{\widehat{q}}_{\alpha }(t){\widehat{q}}_{\beta }(t)⟩$ and is considered in normal ordering to eliminate the vacuum-state contributions (70). As parameters for the two-level system, we use a one-dimensional hydrogen atom with a soft-Coulomb potential. We consider the first two levels of such a system and use the parameters as in ref. 71. Thus, $t_0=\mathrm{\hspace{0.17em}0.197}$, $d_{eg}=\mathrm{\hspace{0.17em}1.034}$, $V=\mathrm{\hspace{0.17em}12.5}\mu \text{m}$, and ${\lambda }_{\alpha }={(-1)}^{\alpha +1}0.0103$. In the following, we discuss two different initial states. The setup (1) features the initial state $|\mathrm{\Psi }(t_0)⟩=|e⟩\otimes |0⟩$, where $|e⟩=\mathrm{\hspace{0.17em}1}/\sqrt{2}(|s_1⟩-|s_2⟩)$ is the excited state of the bare electronic Hamiltonian of Eq. 6, $|s_1⟩$ and $|s_2⟩$ refer to the individual sites of the two-site model, and $|0⟩$ indicates the photon field in the vacuum state. During time evolution the electronic excitation will decay to the ground state and hereby emit a single photon via spontaneous emission (70). This setup corresponds to the classical textbook case, except that we treat our system beyond the RWA. In the second case (2), the setup to analyze the single-photon emission process consists of a factorizable initial state $|\mathrm{\Psi }(t_0)⟩=\left(\sqrt{\frac{1}{500}}|s_1⟩+\sqrt{\frac{499}{500}}|s_2⟩\right)\otimes |0⟩$. We start by discussing the dipole moment of the system, that is, $⟨{\sigma }_z(t)⟩$. The QEDFT reformulation of Eq. 6 has the basic functional variables $(⟨{\widehat{\sigma }}_z(t)⟩,\{⟨{\widehat{q}}_{\alpha }(t)⟩\})$ (1), which makes this quantity specifically simple to determine. In Fig. 9, Inset, we show the time evolution of $⟨{\sigma }_z(t)⟩$. We find that in the exact propagation the dipole moment ${\sigma }_z(t)=0$; that is, the deexcitation from the excited state to the ground state of the atom is a dipole-free transition. This transition implies that also the electric field observable in this process is zero for all times ($E(x,t)=0$). However, as shown in Fig. 9 and Movie S1, the intensity of the spontaneous emission for this process is nonzero (70). At the initial time, we find two sharp wave fronts appearing, which travel to the boundaries, are reflected at the cavity mirrors, and excite the atom again. The semiclassical approximation and the OEP approximation for this setup correctly reproduce the (trivial) dipole moment and electric field, which are the basic variables. However, simple approximations to the intensity evolution that use the ${\sigma }_z(t)$ and $d_{12}(t)$ of the QEDFT systems for the expression in Supporting Information, Functional Dependency of E²(x,t) fail in correctly describing the intensity evolution. Because ${\sigma }_z(t)$ is equal to zero for all times, the exact functional for the intensity has to provide the correct time evolution of the observable exclusively through the dependence on the initial state. Whereas the semiclassical approximation to the intensity evolution yields a zero intensity evolution, the OEP observable determined from the expression in Supporting Information, Functional Dependency of E²(x,t) via postprocessing of the calculated OEP quantities gives emission with an infinite emission time. This deviation is one of the drawbacks of an implicit functional reformulation of quantum physics, where we do not know the explicit forms of all observables but are often dependent on simple approximations. That these approximations can be useful, though, will become clear in the next case. For this example, the time-dependent evolution of the dipole moment for the two-site model is shown in Fig. 10, Upper. Here, we find an initial exponential decay of the dipole oscillation that is the single-photon emission of the atom. After t = 1,800 a.u., we find the reabsorption of the emitted photon and the dipole moment starts to oscillate again. The exact simulation is shown in black. Our approximate QEDFT propagation based on the OEP approximation, shown in red, is very close to the exact results as can be seen in Fig. 10, Lower. The mean-field approximation also performs qualitatively correctly. It is capable of reproducing the emission process and also the reabsorption of the photon. However, it misses some quantitative features. The emission time is too long, which means that the photon in the exact simulation is emitted faster. The same can be seen for the reabsorption of the photon. Here, the mean-field dipole moment evolution is broader than the exact and the OEP approximation.

Fig. 9.

Time evolution of the spontaneous-photon emission process. Shown is the expectation value of the absolute of the intensity-field operator $⟨{\widehat{E}}^2(t)⟩$ in the exact simulation (gray), the OEP approximation (red), and the semiclassical approximation (green) at time T = 100 a.u., 600 a.u., 1,200 a.u., and 2,200 a.u. Inset shows the dipole moment $⟨{\sigma }_z(t)⟩$. We emphasize that the OEP yields a constant total energy for this setup and the approximate OEP intensity observable is determined via a postprocessing step.

Fig. 10.

Time evolution of the single-photon emission process. (Upper) Expectation value of the dipole-moment operator $⟨{\widehat{\sigma }}_z(t)⟩$ in the exact simulation (black), the OEP approximation (red), and the semiclassical mean-field approximation (green). (Lower) The difference $\mathrm{\Delta }{\sigma }_z(t)$ of OEP approximation (red) and the semiclassical mean-field approximation (green) from the exact propagation for different time intervals of the full evolution.

In Fig. 11 (Movie S2), we plot the absolute value of the expectation value of the electric-field operator. We observe after T = 100 a.u. a wave packet with a sharp front traveling toward the boundaries of the cavity. After T = 1,200 a.u. the wave packets are reflected by the boundary and they travel back to the atom, where they are reabsorbed and then reemitted into the field again. This process generates a second maximum in the wave packet that can be observed in the third column of Fig. 11. The shapes of the wave packet in the OEP approximation, shown in red, nicely agree with the exact shapes, shown in gray. The mean-field approximation is again qualitatively accurate, but in particular the second maximum is too broad due to the wrong decay time of the two-level system.

Fig. 11.

Time evolution of the single-photon emission process. Shown is the expectation value of the absolute of the electric-field operator $⟨\widehat{E}(t)⟩$ in the exact simulation (gray), the OEP approximation (red), and the semiclassical approximation (green) at time T = 100 a.u., 600 a.u., 1,200 a.u., and 2,200 a.u.

In Fig. 12 (Movie S3), we plot the absolute value of $⟨{\widehat{E}}^2(t)⟩$ with the same color coding as before. Here, whereas the OEP develops unphysical oscillations in the wavefront after reflection at the mirrors, it is able to reproduce a remaining photon intensity at the position of the atom. This effect is beyond a semiclassical and a two-photon effect, which is also missed by the RWA (70). Because in the semiclassical approximation the matter system and the photon system completely decouple, no intensity remains at the position of the atom. In the exact and also the OEP approximation, however, the systems are still correlated, leading to the remaining intensity. Indeed, this intensity is due to the hybrid ground state of the correlated electron–photon system and hence corresponds to a bound electron–photon state. This comparison allows us to conclude that we successfully identified important beyond semiclassical effects that can be described by a QEDFT approximation.

Fig. 12.

Time evolution of the single-photon emission process. Shown is the expectation value of the absolute of the intensity-field operator $⟨{\widehat{E}}^2(t)⟩$ in the exact simulation (gray), the OEP approximation (red), and the semiclassical approximation (green) at time T = 100 a.u., 600 a.u., 1,200 a.u., and 2,200 a.u.

Summary and Conclusion

In this paper we have illustrated how long-standing concepts of quantum chemistry have to be adapted if the electron–photon interaction is considered in the quantum limit. We have reported the adapted concept of CBO surfaces that we calculated for a dimer system and the Shin–Metiu model. This concept is accurate for static calculations from the weak- to the strong-coupling limit and can be used to predict chemical quantities such as bond length, nonadiabatic coupling terms, or absorption spectra. In all examples, we compared the approximate solutions to the numerical exact solutions. In a local control scheme, we have shown how we can use the electron–photon interaction to our favor to modify chemical reactions more efficiently. The additional degree of freedom in the photon subsystem offers promising possibilities. In the last section, we have shown how a density-functional approach can be superior to the semiclassical approach for bound polariton states. These states appear in optical cavities and require a correct description of the correlated electron–photon interaction. This work on the interface of quantum optics and material science impacts both research fields and can lead to new applications in chemistry and material science, such as new photonic devices or laser technologies.

Relative Jacobi Coordinates for Four-Body Systems

The Hamiltonian (1–4) can be written explicitly for the studied dimer system as follows:

$$\widehat{H}={\widehat{H}}_{en}+{\widehat{H}}_p$$ [S1]

$$\begin{array}{c}{\widehat{H}}_{en}=-\frac{{\mathrm{\hslash }}^2}{2M_1}{\overrightarrow{\nabla }}_{{\text{𝐗}}_1}^2-\frac{{\mathrm{\hslash }}^2}{2M_2}{\overrightarrow{\nabla }}_{{\text{𝐗}}_2}^2-\frac{{\mathrm{\hslash }}^2}{2m_3}{\overrightarrow{\nabla }}_{{\text{𝐱}}_3}^2-\frac{{\mathrm{\hslash }}^2}{2m_4}{\overrightarrow{\nabla }}_{{\text{𝐱}}_4}^2\\ +\frac{Z_1{Z}_2{e}^2}{4\pi {ϵ}_0\sqrt{{\left({\text{𝐗}}_1-{\text{𝐗}}_2\right)}^2+1}}-\frac{Z_1{e}^2}{4\pi {ϵ}_0\sqrt{{\left({\text{𝐗}}_1-{\text{𝐱}}_3\right)}^2+1}}\\ -\frac{Z_1{e}^2}{4\pi {ϵ}_0\sqrt{{\left({\text{𝐗}}_1-{\text{𝐱}}_4\right)}^2+1}}-\frac{Z_2{e}^2}{4\pi {ϵ}_0\sqrt{{\left({\text{𝐗}}_2-{\text{𝐱}}_3\right)}^2+1}}\\ -\frac{Z_2{e}^2}{4\pi {ϵ}_0\sqrt{{\left({\text{𝐗}}_2-{\text{𝐱}}_4\right)}^2+1}}+\frac{e^2}{4\pi {ϵ}_0\sqrt{{\left({\text{𝐱}}_3-{\text{𝐱}}_4\right)}^2+1}}\end{array}$$ [S2]

$${\widehat{H}}_p=\frac{1}{2}\sum _{\alpha }\left[{\widehat{p}}_{\alpha }^2+{\omega }_{\alpha }^2{\left({\widehat{q}}_{\alpha }+\frac{{𝝀}_{\alpha }}{{\omega }_{\alpha }}\cdot e\text{𝐑}\right)}^2\right]$$ [S3]

$$\text{𝐑}=Z_1{\text{𝐗}}_1+Z_2{\text{𝐗}}_2-{\text{𝐱}}_3-{\text{𝐱}}_4.$$ [S4]

Here, the uppercase variables, ${\text{𝐗}}_1$ and ${\text{𝐗}}_2$, denote the nuclear coordinates, whereas the lowercase variables ${\text{𝐱}}_3$ and ${\text{𝐱}}_4$ denote the electronic coordinates. In the following, we briefly discuss the relative coordinates and the real-space grid used for the numerical calculations of Cavity QED—The Molecular Dimer Case. The coordinates are the electron distance coordinate $\text{𝐱}={\text{𝐱}}_1-{\text{𝐱}}_2$, the nuclear distance coordinate $\text{𝐗}={\text{𝐗}}_1-{\text{𝐗}}_2$, the distance between the electronic and the nuclear center of masses $𝝃$, and the global center of mass ${\text{𝐗}}_{CM2}$ (44). In this coordinate system the Hamiltonians of Eqs. S1–S3 and the dipole moment become

$$\begin{array}{c}{\widehat{H}}_{en}=-{\mathrm{\hslash }}^2\frac{M_1+M_2}{2M_1{M}_2}{\overrightarrow{\nabla }}_{\text{𝐗}}^2-{\mathrm{\hslash }}^2{\overrightarrow{\nabla }}_{\text{𝐱}}^2-{\mathrm{\hslash }}^2\frac{2+M_1+M_2}{4(M_1+M_2)}{\overrightarrow{\nabla }}_{𝝃}^2\\ -\frac{{\mathrm{\hslash }}^2}{2\left(2+M_1+M_2\right)}{\overrightarrow{\nabla }}_{{\text{𝐱}}_{\text{CM}2}}^2+\frac{Z_1{Z}_2{e}^2}{4\pi {ϵ}_0\sqrt{{\text{𝐗}}^2+1}}\\ +\frac{e^2}{4\pi {ϵ}_0}\sqrt{{\text{𝐱}}^2+1}-\frac{Z_1{e}^2}{4\pi {ϵ}_0\sqrt{{\left(𝝃+\frac{\text{𝐱}}{2}+\frac{M_2\text{𝐗}}{M_1+M_2}\right)}^2+1}}\\ -\frac{Z_2{e}^2}{4\pi {ϵ}_0\sqrt{{\left(-𝝃+\frac{\text{𝐱}}{2}+\frac{M_1\text{𝐗}}{M_1+M_2}\right)}^2+1}}\\ -\frac{Z_2{e}^2}{4\pi {ϵ}_0\sqrt{{\left(-𝝃-\frac{\text{𝐱}}{2}+\frac{M_1\text{𝐗}}{M_1+M_2}\right)}^2+1}}\\ -\frac{Z_1{e}^2}{4\pi {ϵ}_0\sqrt{{\left(𝝃-\frac{\text{𝐱}}{2}+\frac{M_2\text{𝐗}}{M_1+M_2}\right)}^2+1}}\end{array}$$ [S5]

$${\widehat{H}}_p=\frac{1}{2}\sum _{\alpha }\left[{\widehat{p}}_{\alpha }^2+{\omega }_{\alpha }^2{\left({\widehat{q}}_{\alpha }+\frac{{𝝀}_{\alpha }}{{\omega }_{\alpha }}\cdot \text{𝐑}\right)}^2\right]$$ [S6]

$$\text{𝐑}=-2𝝃+\frac{\text{𝐗}\left(M_1{Z}_2-M_2{Z}_1\right)}{M_1+M_2}.$$ [S7]

General CBO for Correlated Electron–Photon Systems

The CBO approximation to the Hamiltonians 1–4 in the main text can be constructed as follows: First, solve the electronic Schrödinger equation

$${\widehat{H}}_e(\left\{\text{𝐗}\right\},\{q_{\alpha }\}){\varphi }_j(\left\{\text{𝐗}\right\},\{q_{\alpha }\})=E_j(\left\{\text{𝐗}\right\},\{q_{\alpha }\}){\varphi }_j(\left\{\text{𝐗}\right\},\{q_{\alpha }\})$$ [S8]

with the electronic Hamiltonian

$${\widehat{H}}_e(\left\{\text{𝐗}\right\},\{q_{\alpha }\})={\widehat{T}}_e+{\widehat{W}}_{ee}+{\widehat{W}}_{en}(\left\{\text{𝐗}\right\})+\sum _{\alpha }\frac{1}{2}{\left({𝝀}_{\alpha }\cdot \text{𝐑}\right)}^2+\sum _{\alpha }{\omega }_{\alpha }{q}_{\alpha }{𝝀}_{\alpha }\cdot \text{𝐑}.$$ [S9]

In a second step, we then solve the nuclear-photon problem

$${\widehat{H}}_j(\left\{\text{𝐗}\right\},\{q_{\alpha }\})={\widehat{T}}_n+\sum _{\alpha }\frac{1}{2}{\widehat{p}}_{\alpha }^2+V_j(\left\{\text{𝐗}\right\},\{q_{\alpha }\})$$ [S10]

with the PES determined from the electronic part that are given by

$$V_j(\left\{\text{𝐗}\right\},\{q_{\alpha }\})=E_j(\left\{\text{𝐗}\right\},\{q_{\alpha }\})+{\widehat{W}}_{nn}(\left\{\text{𝐗}\right\})+\sum _{\alpha }\frac{1}{2}{\omega }_{\alpha }^2{q}_{\alpha }^2.$$ [S11]

This procedure allows us to effectively decouple the system into an electronic part and a nuclear-photon part. Using

$${\widehat{H}}_j(\left\{\text{𝐗}\right\},\{q_{\alpha }\}){\chi }_{ij}(\left\{\text{𝐗}\right\},\{q_{\alpha }\})={ϵ}_i(\left\{\text{𝐗}\right\},\{q_{\alpha }\}){\chi }_{ij}(\left\{\text{𝐗}\right\},\{q_{\alpha }\}),$$ [S12]

where ${\chi }_{ij}$ denotes a correlated nuclear-photon wave function, and having all necessary wave functions at hand, we can construct the BO states, that is, for the BO ground state $|{\mathrm{\Psi }}_0⟩=|{\chi }_{00}⟩|{\varphi }_0⟩$.

CBO for Four-Body Systems

To solve the BO problem for the dimer system, we first compute the electronic part that for this system parametrically depends on the position of the nuclei ${\text{𝐗}}_1$ and ${\text{𝐗}}_2$ and on the displacement coordinates of the photon modes $\{q_{\alpha }\}$; that is, we solve the following electronic equation

$${\widehat{H}}_e({\text{𝐗}}_1,{\text{𝐗}}_2,\{q_{\alpha }\}){\varphi }_j({\text{𝐗}}_1,{\text{𝐗}}_2,\{q_{\alpha }\})=E_j({\text{𝐗}}_1,{\text{𝐗}}_2,\{q_{\alpha }\}){\varphi }_j({\text{𝐗}}_1,{\text{𝐗}}_2,\{q_{\alpha }\})$$ [S13]

with the electronic Hamiltonian

$$\begin{array}{c}{\widehat{H}}_e({\text{𝐗}}_1,{\text{𝐗}}_2,\{q_{\alpha }\})\\ =-\frac{{\mathrm{\hslash }}^2}{2m_3}{\overrightarrow{\nabla }}_{{\text{𝐱}}_3}^2-\frac{{\mathrm{\hslash }}^2}{2m_4}{\overrightarrow{\nabla }}_{{\text{𝐱}}_4}^2+\frac{e^2}{4\pi {ϵ}_0\sqrt{{\left({\text{𝐱}}_3-{\text{𝐱}}_4\right)}^2+1}}\\ -\frac{Z_1{e}^2}{4\pi {ϵ}_0\sqrt{{\left({\text{𝐗}}_1-{\text{𝐱}}_3\right)}^2+1}}-\frac{Z_1{e}^2}{4\pi {ϵ}_0\sqrt{{\left({\text{𝐗}}_1-{\text{𝐱}}_4\right)}^2+1}}\\ -\frac{Z_2{e}^2}{4\pi {ϵ}_0\sqrt{{\left({\text{𝐗}}_2-{\text{𝐱}}_3\right)}^2+1}}-\frac{Z_2{e}^2}{4\pi {ϵ}_0\sqrt{{\left({\text{𝐗}}_2-{\text{𝐱}}_4\right)}^2+1}}\\ +\sum _{\alpha }\frac{1}{2}{({𝝀}_{\alpha }\cdot \text{𝐑})}^2+\sum _{\alpha }{\omega }_{\alpha }{q}_{\alpha }{𝝀}_{\alpha }\cdot \text{𝐑}.\end{array}$$ [S14]

In this way, the electronic wavefunctions ${\varphi }_j({\text{𝐗}}_1,{\text{𝐗}}_2,\{q_{\alpha }\})$ have parametrical dependency on the nuclear and photonic coordinates. In a second step we then solve the nuclear-photon problem

$${\widehat{H}}_j({\text{𝐗}}_1,{\text{𝐗}}_2,\{q_{\alpha }\})=-\frac{{\mathrm{\hslash }}^2}{2M_1}{\overrightarrow{\nabla }}_{{\text{𝐗}}_1}^2-\frac{{\mathrm{\hslash }}^2}{2M_2}{\overrightarrow{\nabla }}_{{\text{𝐗}}_2}^2+\sum _{\alpha }\frac{1}{2}{\widehat{p}}_{\alpha }^2+V_j({\text{𝐗}}_1,{\text{𝐗}}_2,\{q_{\alpha }\})$$ [S15]

with the potential-energy surfaces determined from the electronic part that are given by

$$V_j({\text{𝐗}}_1,{\text{𝐗}}_2,\{q_{\alpha }\})=E_j({\text{𝐗}}_1,{\text{𝐗}}_2,\{q_{\alpha }\})+\frac{Z_1{Z}_2{e}^2}{4\pi {ϵ}_0\sqrt{{\left({\text{𝐗}}_1-{\text{𝐗}}_2\right)}^2+1}}+\sum _{\alpha }\frac{1}{2}{\omega }_{\alpha }^2{q}_{\alpha }^2.$$ [S16]

This procedure allows us to effectively decouple the system into an electronic part and a nuclear-photon part. Using

$${\widehat{H}}_j({\text{𝐗}}_1,{\text{𝐗}}_2,\{q_{\alpha }\}){\chi }_{ij}({\text{𝐗}}_1,{\text{𝐗}}_2,\{q_{\alpha }\})={ϵ}_i({\text{𝐗}}_1,{\text{𝐗}}_2,\{q_{\alpha }\}){\chi }_{ij}({\text{𝐗}}_1,{\text{𝐗}}_2,\{q_{\alpha }\}),$$ [S17]

where ${\chi }_{ij}$ denotes a correlated nuclear-photon wave function, we can construct the BO states; that is, for the BO ground state $|{\mathrm{\Psi }}_0⟩=|{\chi }_{00}⟩|{\varphi }_0⟩$. The electronic Hamiltonian that parametrically depends on X and $\{q_{\alpha }\}$ of Eq. S14 becomes

$$\begin{array}{c}{\widehat{H}}_e(\text{𝐗},\{q_{\alpha }\})=-{\mathrm{\hslash }}^2{\overrightarrow{\nabla }}_{\text{𝐱}}^2-\frac{{\mathrm{\hslash }}^2}{4}{\overrightarrow{\nabla }}_{𝝃}^2\\ +\frac{Z_1{Z}_2{e}^2}{4\pi {ϵ}_0\sqrt{{\text{𝐗}}^2+1}}+\frac{e^2}{4\pi {ϵ}_0}\sqrt{{\text{𝐱}}^2+1}\end{array}$$ [S18]

$$\begin{array}{c}-\frac{Z_1{e}^2}{4\pi {ϵ}_0\sqrt{{\left(𝝃+\frac{\text{𝐱}}{2}+\frac{M_2\text{𝐗}}{M_1+M_2}\right)}^2+1}}\\ -\frac{Z_2{e}^2}{4\pi {ϵ}_0\sqrt{{\left(-𝝃+\frac{\text{𝐱}}{2}+\frac{M_1\text{𝐗}}{M_1+M_2}\right)}^2+1}}\\ -\frac{Z_2{e}^2}{4\pi {ϵ}_0\sqrt{{\left(-𝝃-\frac{\text{𝐱}}{2}+\frac{M_1\text{𝐗}}{M_1+M_2}\right)}^2+1}}\\ -\frac{Z_1{e}^2}{4\pi {ϵ}_0\sqrt{{\left(𝝃-\frac{\text{𝐱}}{2}+\frac{M_2\text{𝐗}}{M_1+M_2}\right)}^2+1}}\end{array}$$ [S19]

$$+\sum _{\alpha }\frac{1}{2}{\left({𝝀}_{𝜶}\cdot \text{𝐑}\right)}^2+\sum _{\alpha }{\omega }_{\alpha }{q}_{\alpha }{𝝀}_{𝜶}\cdot \text{𝐑}.$$

The nuclear-photon problem of the CBO approximation Eq. S15 reads as

$$\begin{array}{c}{\widehat{H}}_j=-{\mathrm{\hslash }}^2\frac{M_1+M_2}{2M_1{M}_2}{\overrightarrow{\nabla }}_{\text{𝐗}}^2+V_j(\text{𝐗})+\sum _{\alpha }\frac{1}{2}\left[{\widehat{p}}_{\alpha }^2+{\omega }_{\alpha }^2{\widehat{q}}_{\alpha }^2\right]\\ +{\omega }_{\alpha }{\widehat{q}}_{\alpha }{𝝀}_{\alpha }\cdot \text{𝐑}.\end{array}$$ [S20]

For the numerical calculation we use the following real-space grid: $N_X=\mathrm{\hspace{0.17em}61}$, $dX=\mathrm{\hspace{0.17em}0.08}$, $N_x=\mathrm{\hspace{0.17em}41}$, $dx=\mathrm{\hspace{0.17em}0.5}$, $N_{\xi }=\mathrm{\hspace{0.17em}51}$, $d\xi =\mathrm{\hspace{0.17em}0.2}$, and $N_{pt}=\mathrm{\hspace{0.17em}41}$, where the latter describes the maximum amount of photons in the system.

Absorption Spectrum

We calculate absorption spectra with the following formula (32):

$$\sigma (\omega )=\frac{4\pi \mathrm{\hslash }\omega }{c}\text{Im}\underset{ϵ\to 0}{lim}\sum _k\frac{{\left|⟨{\mathrm{\Psi }}_k|\text{𝐑}|{\mathrm{\Psi }}_0⟩\right|}^2}{\mathrm{\hslash }{\omega }_k-\mathrm{\hslash }{\omega }_0-\mathrm{\hslash }\omega -\mathrm{i}ϵ}.$$ [S21]

Here, $|{\mathrm{\Psi }}_0⟩$ denotes the correlated ground state with energy $\mathrm{\hslash }{\omega }_0$, whereas $|{\mathrm{\Psi }}_k⟩$ are all correlated eigenstates. In the numerical calculations, we apply a broadening of the individual peaks, as presented in ref. (51 for electron–phonon problems.

Shin–Metiu Model in a Cavity

The Hamiltonian of such a system is given by (34)

$$\widehat{H}(\text{𝐫},\text{𝐑})=-\frac{{\mathrm{\hslash }}^2}{2M}{\overrightarrow{\nabla }}_{\text{𝐑}}^2-\frac{{\mathrm{\hslash }}^2}{2m_e}{\overrightarrow{\nabla }}_{\text{𝐫}}^2+V_{en}(\text{𝐫},\text{𝐑})+V_{nn}\left(\text{𝐑}\right)+{\widehat{H}}_p$$ [S22]

with the electron-nuclear potential

$$\begin{array}{c}{V}_{en}(\text{𝐫},\text{𝐑})=V_{en}\left(\left|\text{𝐫}-(\frac{L}{2},0)\right|\right)+V_{en}\left(\left|\text{𝐫}-(-\frac{L}{2},0)\right|\right)\\ +V_{en}\left(\left|\text{𝐫}-\text{𝐑}\right|\right),\end{array}$$ [S23]

and the nuclear–nuclear potential

$$\begin{array}{c}{V}_{nn}\left(\text{𝐑}\right)=V_{nn}\left(\left|\text{𝐑}-(\frac{L}{2},0)\right|\right)+V_{nn}\left(\left|\text{𝐑}-(-\frac{L}{2},0)\right|\right)\\ +V_{nn}\left(L\right)+{\left(R/R_0\right)}^4.\end{array}$$ [S24]

We choose the parameters $a=\mathrm{\hspace{0.17em}0.5}$, $b=\mathrm{\hspace{0.17em}10.0}$, $R_0=\mathrm{\hspace{0.17em}3.5}$, and $L=\mathrm{\hspace{0.17em}4}\sqrt{3}/5$ as in ref. (34 and $V_{en}(x)=-1/\sqrt{a+x^2}$ and $V_{nn}(x)=1/\sqrt{b+x^2}$ with the photon Hamiltonian ${\widehat{H}}_p$ from Eq. S3.

Functional Dependency of E²(x, t)

Here, we give the functional dependence of the electric-field intensity:

$$E^2(x,t)=\frac{1}{4}\sum _{\alpha ,\beta \ne \alpha }{\omega }_{\alpha }{\omega }_{\beta }{\lambda }_{\alpha }(x){\lambda }_{\beta }(x){\lambda }_{\alpha }{\lambda }_{\beta }[-2\underset{t_0}{\overset{t}{\int }}dt\prime \underset{t_0}{\overset{t\prime }{\int }}d{t}^{″}({\sigma }_z(t\prime ){\sigma }_z(t^{″})+d_{12}(t\prime )d_{21}(t^{″}))e^{i{\omega }_{\alpha }\left(t^{″}-t\right)}{e}^{i{\omega }_{\beta }\left(t\prime -t\right)}+\underset{t_0}{\overset{t}{\int }}dt\prime \underset{t_0}{\overset{t}{\int }}d{t}^{″}({\sigma }_z(t^{″}){\sigma }_z(t\prime )+d_{12}(t^{″})d_{21}(t\prime ))e^{i{\omega }_{\alpha }\left(t\prime -t\right)-i{\omega }_{\beta }\left(t^{″}-t\right)}]+c.c.-\frac{1}{2}\sum _{\alpha }{\omega }_{\alpha }^2{\lambda }_{\alpha }^2(x){\lambda }_{\alpha }^2[\underset{t_0}{\overset{t}{\int }}dt\prime \underset{t_0}{\overset{t\prime }{\int }}d{t}^{″}\sigma z(t^{″}){\sigma }_z(t\prime )e^{-i{\omega }_{\alpha }\left(t^{″}+t\prime -2t\right)}+d_{12}(t^{″})d_{21}(t\prime )e^{-i{\omega }_{\alpha }\left(t^{″}+t\prime -2t\right)}]+c.c.+\frac{1}{2}\sum _{\alpha }{\omega }_{\alpha }^2{\lambda }_{\alpha }^2(x){\lambda }_{\alpha }^2[\underset{t_0}{\overset{t}{\int }}dt\prime d_{12}(t\prime )e^{-i{\omega }_{\alpha }\left(t\prime -t\right)}\underset{t_0}{\overset{t}{\int }}dt\prime d_{21}(t\prime )e^{i{\omega }_{\alpha }\left(t\prime -t\right)}+\underset{t_0}{\overset{t}{\int }}dt\prime \sigma z(t\prime )e^{-i{\omega }_{\alpha }\left(t\prime -t\right)}\underset{t_0}{\overset{t}{\int }}dt\prime \sigma z(t\prime )e^{i{\omega }_{\alpha }\left(t\prime -t\right)}].$$ [S25]

With $c.c.$ we denote the complex conjugate of the former term. $d_{12}$ is given by the transition dipole moments $d_{12}=⟨{\mathrm{\Psi }}_1|{\sigma }_z|{\mathrm{\Psi }}_2⟩$ and $d_{21}$ is given analogously. $|{\mathrm{\Psi }}_1⟩$ denotes the occupied electronic state and $|{\mathrm{\Psi }}_2⟩$ the unoccupied electronic state of the two-level system.