Significance
This paper represents a major advance in understanding intrinsic heart beat regulation, because it provides an integrated view of the Frank–Starling law that combines mechanical, structural, and energetic aspects of heart performance. We show that mechanosensing in the myosin filament adjusts the number of myosin motors recruited from the off, ATP hydrolysis-unavailable state to the systolic force. In this way, the energetic cost of the heart beat is tuned to the end systolic pressure–volume relation. These results elucidate a plausible mechanistic link between the mutations that affect the structure of the myosin filament and cause hypercontractility and/or loss of contractile efficiency and dysregulation of the control by the stress-sensing mechanism on the state of the myosin motors.
Keywords: myosin filament mechanosensing, heart regulation, small-angle X-ray diffraction, cardiac muscle, Frank–Starling mechanism
Abstract
The mammalian heart pumps blood through the vessels, maintaining the dynamic equilibrium in a circulatory system driven by two pumps in series. This vital function is based on the fine-tuning of cardiac performance by the Frank–Starling mechanism that relates the pressure exerted by the contracting ventricle (end systolic pressure) to its volume (end systolic volume). At the level of the sarcomere, the structural unit of the cardiac myocytes, the Frank–Starling mechanism consists of the increase in active force with the increase of sarcomere length (length-dependent activation). We combine sarcomere mechanics and micrometer–nanometer-scale X-ray diffraction from synchrotron light in intact ventricular trabeculae from the rat to measure the axial movement of the myosin motors during the diastole–systole cycle under sarcomere length control. We find that the number of myosin motors leaving the off, ATP hydrolysis-unavailable state characteristic of the diastole is adjusted to the sarcomere length-dependent systolic force. This mechanosensing-based regulation of the thick filament makes the energetic cost of the systole rapidly tuned to the mechanical task, revealing a prime aspect of the Frank–Starling mechanism. The regulation is putatively impaired by cardiomyopathy-causing mutations that affect the intramolecular and intermolecular interactions controlling the off state of the motors.
In each sarcomere, the structural unit of the skeletal and cardiac muscles, myosin motors arranged in antiparallel arrays in the two halves of the thick myosin-containing filament work cooperatively, generating force and shortening by cyclic ATP-driven interactions with the interdigitating thin actin-containing filaments. The textbook model for the activation of contraction indicates that the binding to actin of myosin motors from the neighboring thick filament is controlled by a calcium-dependent structural change in the thin filament. However, in these muscles at rest, most of the myosin motors are in the off state and packed into helical tracks with 43-nm periodicity on the surface of the thick filaments (1–4), making them unavailable for binding to the thin filament and ATP hydrolysis (5, 6). Recent X-ray diffraction experiments on single fibers from skeletal muscle showed that, in addition to the canonical thin filament activation system, a thick filament mechanosensing mechanism provides a way for selective unlocking of myosin motors during high load contraction (7). This thick filament-based regulation has not yet been shown in cardiac muscle, in which several regulatory systems are significant. In contrast to skeletal muscle, during heart contraction, the internal concentration of Ca2+ ([Ca2+]i) may not reach the full activation level, and thus, the mechanical response depends on both [Ca2+]i and the sensitivity of the filaments to Ca2+ (8, 9). For a given [Ca2+]i, the maximal force is larger at longer sarcomere lengths [SLs; length-dependent activation (LDA)], which is the cellular basis of the Frank–Starling law of the heart (10, 11). LDA is the result of a chain of yet undefined events relating a mechanosensor of the SL to the number of force-generating motors and consequently the force (12, 13), and moreover, it is modulated by the degree of phosphorylation of contractile (Myosin Regulatory Light Chain), regulatory [Troponin I on the thin filament and myosin-binding protein C (MyBP-C) in the thick filament], and cytoskeletal proteins (14–20). We exploited the nanometer–micrometer-scale X-ray diffraction possible at beamline ID02 of the European Synchrotron Radiation Facility (ESRF) to record the structural changes undergone by the thick filament and the myosin motors during the systole–diastole cycle in intact trabeculae from rat cardiac ventricle under SL control. X-ray signals marking the structure of the thick filament indicate that, in diastole, the myosin motors are in the off state. At the peak of the twitch, the number of motors that have been unlocked from the off state is found to be proportional to the SL-dependent systolic force, indicating that thick filament mechanosensing rapidly tunes the energetic requirements to the mechanical task.
Results
SL–Tension Relation Determined with Ultra-Small-Angle X-Ray Diffraction.
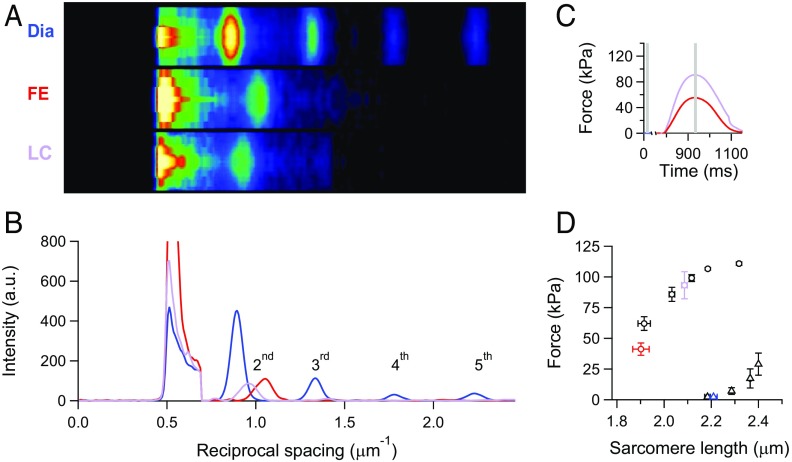
2D X-ray diffraction patterns from an intact trabecula are collected with the detector placed at 30 m from the preparation to record the first orders of the sarcomeric reflections (Fig. 1 A and B). The length of the trabecula between the transducer levers at rest is set, so that the average SL is ∼2.2 µm [Fig. 1 A, Dia (2.23 µm) and B, blue line]. During force development in fixed end (FE) conditions, sarcomeres shorten against the compliance of the attachments, so that, at the peak of force (Tp), SL becomes 1.95 µm (13% shorter) (Fig. 1 A, FE and B, red line). Sarcomere shortening recorded during the force development in an FE twitch is used as a feedforward signal to prevent the sarcomere shortening during the next twitch [length clamp (LC) conditions (13, 21)]. In this case, SL at Tp is 6% shorter (2.1 µm) (Fig. 1 A, LC and B, violet line). Tp is larger in LC (90 kPa) (violet trace in Fig. 1C) than in FE (55 kPa) (red trace in Fig. 1C). In four trabeculae, the SLs are 2.21 ± 0.02 μm (mean ± SE) in diastole (blue triangle in Fig. 1D), 1.90 ± 0.03 μm in FE (red circle in Fig. 1D), and 2.09 ± 0.01 μm in LC (violet circle in Fig. 1D). In agreement with the Tp–SL relation (black circles in Fig. 1D) (13), the corresponding Tp values are 41 ± 4 (red circle in Fig. 1D) and 93 ± 11 kPa (violet circle in Fig. 1D), respectively. As shown by SL recordings with a striation follower during the rise of twitch force (Fig. S1) (13), this protocol allows the development of different systolic forces starting from the same diastolic SL and represents an efficient way to relate the systolic mechanical performance to the loading conditions, independent of diastolic SL.
Fig. 1.
SL measured in a twitching trabecula with ultra-small-angle X-ray diffraction. (A) Meridional slices of 2D diffraction patterns during diastole (Dia) and at the force peak of a systole in either FE or sarcomere LC conditions. Camera length of 30 m; total exposure time of 10 ms for FE and LC and 20 ms for Dia. (B) Meridional intensity profiles from A. Background subtraction starts at ∼0.7 μm−1. Blue, diastole; red, FE twitch; violet, LC twitch. (C) Force of the FE (red) and LC (violet) twitches. Stimulus starts at 775 ms. Gray bars indicate X-ray time windows. (D) Force–SL relations in diastole (triangles) and systole (circles). Black symbols are from ref. 13; blue (Dia), red (FE), and violet (LC) symbols are from four trabeculae used in this work. Graph reprinted with permission from ref. 13.
Fig. S1.
Instantaneous force–SL plots for twitches in FE (red) and LC with the feedforward signal either sufficient (black) or insufficient (violet) to prevent shortening. SL changes are recorded on a horizontally mounted trabecula by the striation follower (46). The feedforward signal is an exponential calibrated on the sarcomere shortening recorded in the FE twitch. Circles are the respective Tp values according to the same color code as the traces. The black dashed line is the force–SL relation interpolated on data from Fig. 1D (13). The shaded areas are two ideal loops followed by contractions that start at SL ∼ 2.2 µm in isometric condition and become isotonic when the force attains the level corresponding to the Tp value identified by the color. In terms of the mechanical parameters of the left ventricle beat, the dashed line is the relation between end systolic pressure and end systolic volume, and the loops are two pressure–volume loops starting from the same preload (i.e., end diastolic volume) and with two different afterloads (i.e., aortic pressures). The correspondence between the stress–strain relation (i.e., tension–SL relation) of a myocyte of the ventricular wall and the pressure–volume relation of the whole ventricle has been extensively discussed in ref. 47.
Changes in the Myosin-Based Reflections with the Force Development.
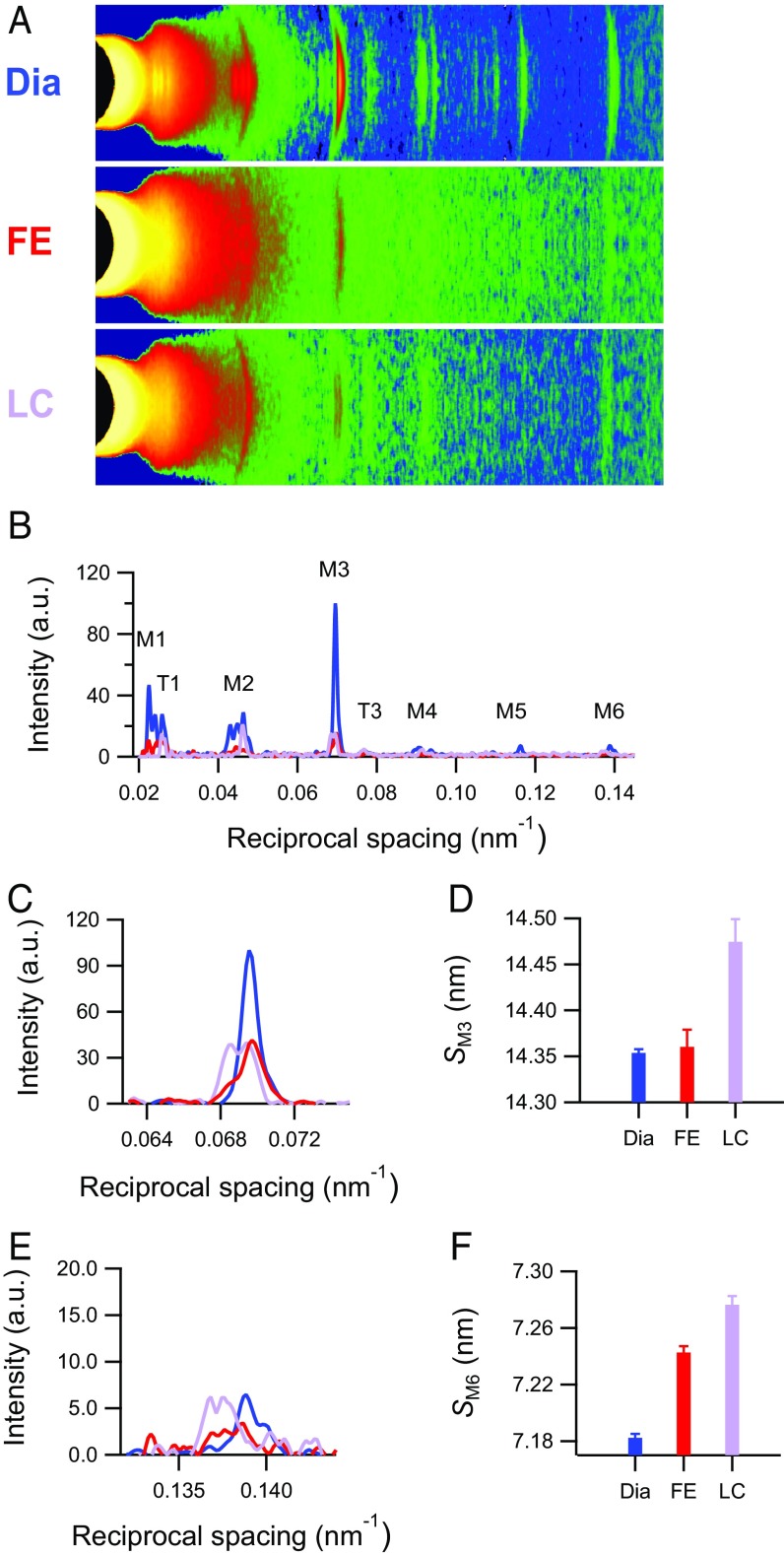
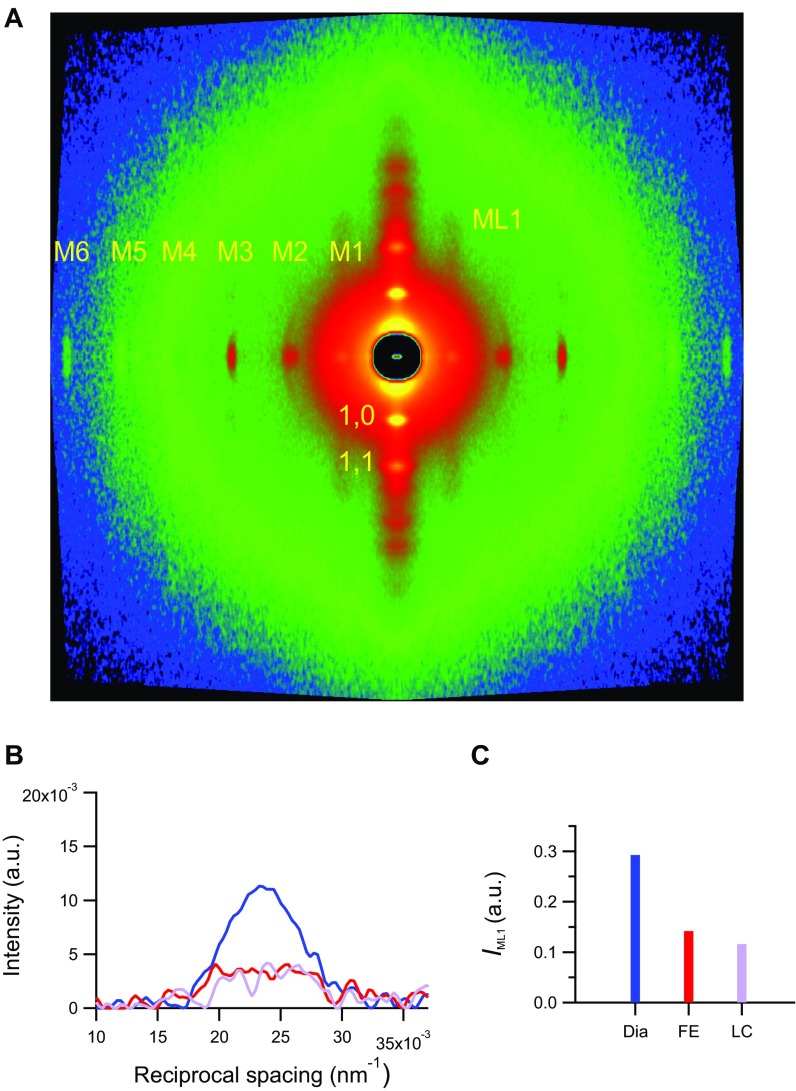
The 2D pattern collected from the trabecula at 1.6 m from the preparation (Fig. 2A and Fig. S2A) shows the first-order layer line reflection (ML1) at an axial spacing of 43 nm and up to the sixth order of the meridional reflections (M1–M6) indexing on the quasihelical three-stranded symmetry with 43-nm periodicity followed by the myosin molecules when they are on the surface of the thick filament in their resting (off) state (2, 4, 7). The spatial resolution achieved along the meridian (parallel to the trabecula axis) with vertically mounted trabeculae is adequate to record the reflection fine structure (Fig. 2) caused by the X-ray interference between the two halves of the thick filament (22) (Fig. S3).
Fig. 2.
X-ray reflections marking the changes in the structure of the myosin filament in a twitching trabecula. (A) Meridional slices and (B) meridional intensity profiles of patterns collected with 1.6-m camera length from four vertically mounted trabeculae. M1–M6 are myosin-based reflections. T1 and T3 indicate troponin-based reflections indexing on a 38-nm axial periodicity. Total exposure times are 150 ms for diastole (Dia), 60 ms for FE, and 90 ms for LC. (C and E) Intensity profiles and (D and F) spacing around the region of M3 and M6 reflections for three conditions as in Fig. 1 (blue, Dia; red, FE; violet, LC).
Fig. S2.
Small angle X-ray diffraction from a horizontally mounted trabecula. (A) 2D pattern collected at 1.6 m from the trabecula in diastole (Dia) showing up to the sixth order of the meridional myosin-based reflections, the first-order myosin layer line (ML1), and the equatorial reflections (1,0 and 1,1). Total exposure time was 70 ms. (B) ML1 intensity along the meridional direction in Dia (blue) and the FE (red) and LC (violet) systole. (C) ML1 integrated intensity (same color code as in B).
Fig. S3.
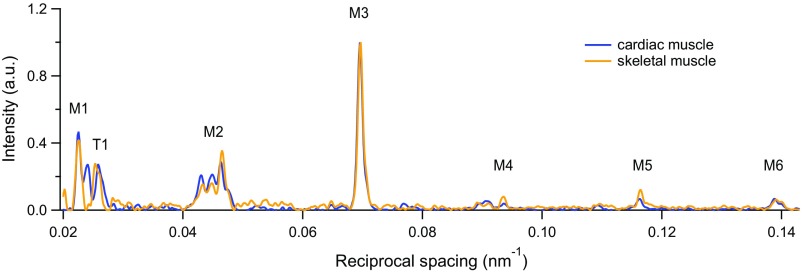
Comparison of the X-ray meridional reflections from the rat trabecula and the intact fiber from frog skeletal muscle. Superimposed meridional intensity profiles from a trabecula in diastole (blue; 27 °C) and a resting muscle fiber from Rana esculenta (orange; 4 °C).
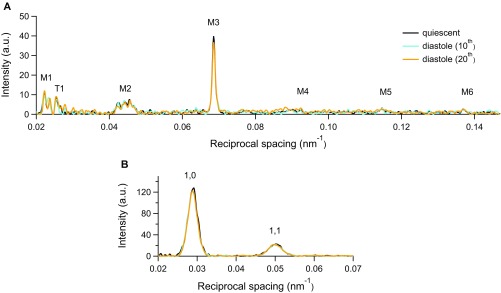
The first-order myosin meridional reflection, M1, has the contribution of the MyBP-C, which is present in the C zone of the thick filament with an ∼43-nm periodicity (3, 23). The second (M2), fourth (M4), and fifth orders (M5) are the so-called forbidden reflections associated with the perturbations of the helical symmetry of the myosin motors in the C-zone of the thick filament (24, 25). The third order (M3), originating from the axial repeat of myosin motors, has a periodicity (SM3) of 14.354 ± 0.004 nm (blue in Fig. 2 C and D), and the sixth order (M6), mainly determined by the mass periodicity in the thick filament backbone, has a periodicity (SM6) of 7.182 ± 0.003 nm (blue in Fig. 2 E and F). The M3 intensity profile shows one main peak with a small satellite on the high-angle side (Fig. 2C, blue line), typical of the off state of the myosin motors (2, 4, 7), and both SM3 (Fig. 2D, blue) and SM6 (Fig. 2F, blue) mark a short backbone periodicity. With the pacing frequency used here (0.5 Hz), these findings are independent of whether the trabecula is quiescent or in diastole (Fig. S4).
Fig. S4.
Comparison of X-ray data in the quiescent trabecula and during diastole. Superimposed intensity profiles along the (A) meridional and (B) equatorial axes from the trabecula in the quiescent state (black) and the diastole of the 10th (cyan) and 20th (orange) cycles during 0.5-Hz pacing.
At the peak of twitch force, the intensities of all of the myosin meridional reflections (Fig. 2B, red and violet lines) and that of the ML1 (Fig. S2 B and C) decrease because of the myosin motors moving away from their helical tracks as the thick filament switches on. The M3 reflection, which remains the most intense, exhibits different fine structure and different increase in spacing depending on whether the contraction occurs in FE or LC mode. In FE (Tp = 41 kPa and SL = 1.9 µm) (Fig. 1D, red), the intensity of M3 (IM3) reduces to 0.58 ± 0.06 that in diastole, and the profile shows a main peak and two satellites on either side, with a prominence of the low-angle satellite (about 1/4 of the main peak) (Fig. 2C, red). SM3 (14.357 ± 0.016 nm) is not significantly different from that at rest (Fig. 2D, red), whereas SM6 increases to 7.243 ± 0.005 nm (0.84%) (Fig. 2F, red). In LC (Tp = 93 kPa and SL = 2.1 µm) (Fig. 1D, violet), IM3 reduces to 0.69 ± 0.07 that in diastole, and the profile is split in two peaks of comparable size (Fig. 2C, violet); SM3 increases to 14.474 ± 0.025 nm (0.84%) (Fig. 2D, violet), and SM6 increases to 7.276 ± 0.006 nm (1.31%) (Fig. 2F, violet). In contrast with the differences of the intensity and fine structure of the M3 reflection between FE and LC twitches, the intensity of ML1 drops to almost the same low level during both contractions, independent of the Tp attained (Fig. S2 B and C). This finding is similar to what already was found in time-resolved X-ray diffraction experiments on skeletal muscle fibers during the development of an isometric contraction (4), in which the half-time of the drop of ML1 intensity is shorter than that of the drop of resting-like head population and the rise of active-disordered population, indicating that the quasihelical symmetry of the myosin motors lying along the thick filament at rest is disrupted with the rise of force somewhat in advance to the axially relevant movements of the motors.
Changes in the State of Myosin Motors During Systole Calculated by Simulation of the M3 Intensity Profile with a Structural Model of the Sarcomere.
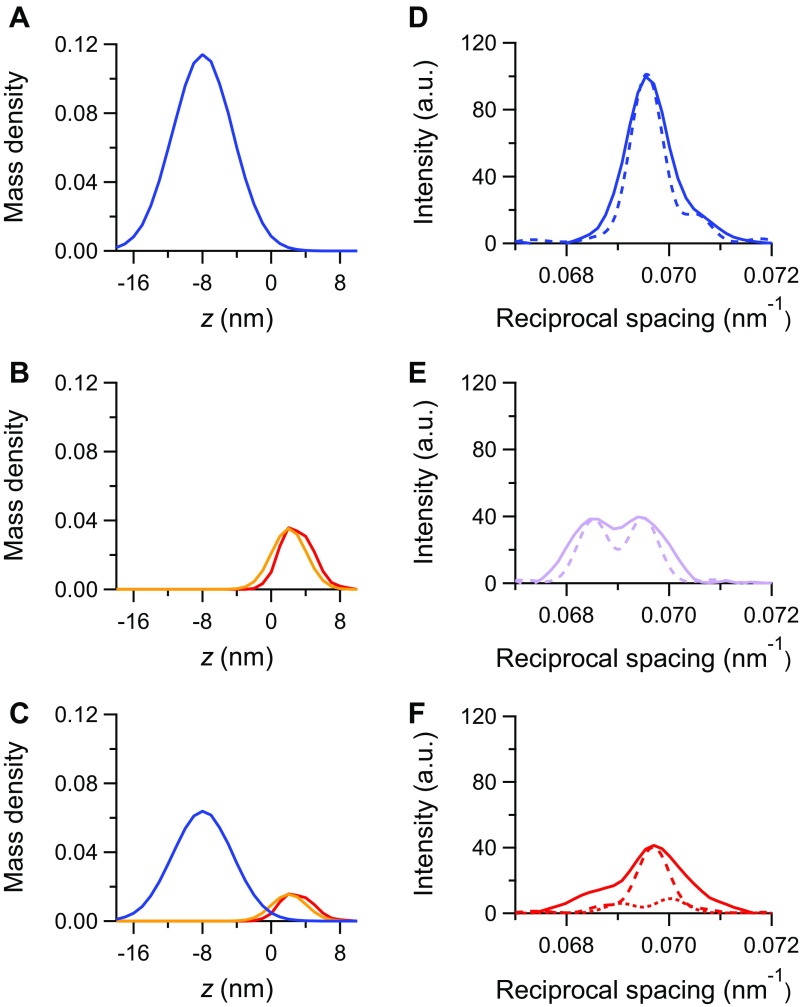
The changes in the intensity and interference fine structure of the M3 reflection are used to calculate the fraction of myosin motors leaving the off state and contributing to force using the same structural model previously used to calculate the movement of the myosin motors during force development in an electrically stimulated skeletal muscle fiber (4) (SI Results). A striking conclusion of the simulation is that, during heart contraction, the fraction of motors leaving the off state is proportional to Tp. Without the contribution of the off motors, the model is able to fit X-ray data of the LC twitch but not those of the FE twitch (Fig. S5).
Fig. S5.
Results of the simulation with model 1. (A–C) Mass density projection of the myosin motors in the different states for (A) the diastole, (B) the LC twitch, and (C) the FE twitch: blue, motors in the off state; red, actin-attached motors; orange, partner motors. (D–F) M3 intensity profiles calculated from the mass projections in A–C in the corresponding rows (dashed lines) superimposed on the observed intensities (continuous lines; same color code as in Fig. 2C). Details are in the text.
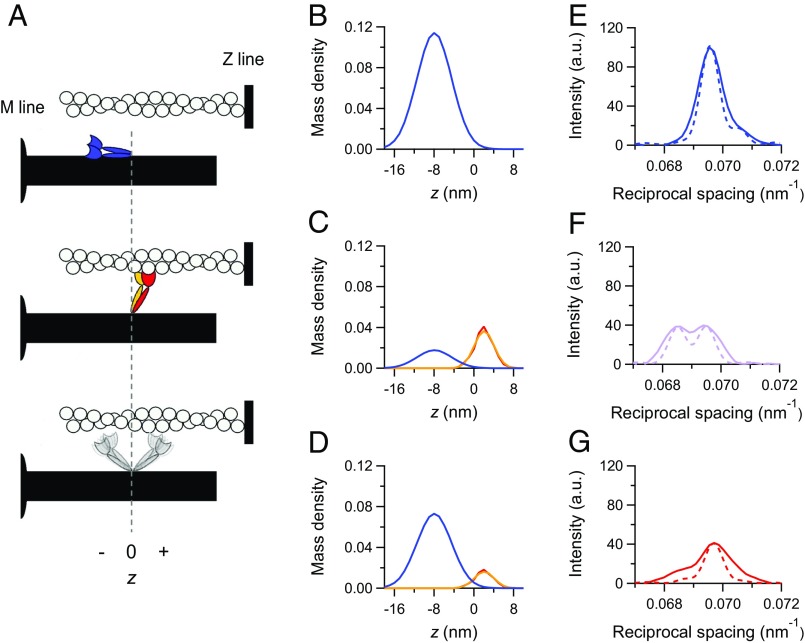
In diastole, the motors are on the surface of the thick filament folded back toward the center of the sarcomere (blue in the cartoon in Fig. 3A), and the backbone has a short periodicity (2, 4, 7). The corresponding axial mass density is represented by a Gaussian with the center at an axial position (z) displaced by −7.97 nm from the head–rod junction (negative direction is toward the center of the thick filament) and σ = 3.5 nm (Fig. 3B, blue) (4). The calculated intensity profile, convoluted with the point spread function of the recording system (beam and detector) (dashed line in Fig. 3E), fits the observed profile (continuous blue line in Fig. 2C) apart a narrower axial width. This difference, even more marked in the intensity profiles at the peak of the twitch (Fig. 3 F and G), is likely caused by the arching of the reflection across the meridional axis (26) because of the orientational dispersion in the multicellular preparation (SI Results).
Fig. 3.
Load-dependent regulation of the state of myosin motors. (A) Schematic of the motor configurations: blue, off state; red, actin-attached motor of a dimer; orange, its detached partner; gray, detached dimer in the on state. The vertical dashed line intercepts the origin of the axial displacement of the center of mass of the motor (z), which corresponds to the position of the head–rod junction; z is negative for displacements toward the center of the thick filament. (B–D) Axial mass density of the myosin motors in the different states identified by the color code as in A and calculated by the simulation for (B) the diastole, (C) the LC twitch, and (D) the FE twitch. (E–G) Superimposed M3 intensity profiles: observed (continuous lines) and calculated from the mass projections in B–D (dashed lines) (same color code as in Fig. 2C). (C, D, F, and G) The simulated data for the LC and FE twitches are obtained with model 2.
The observed intensity and interference fine structure of the M3 reflection at the peak of both twitches can be fit if the mass distribution is given by the contribution of three populations: (i) attached force-generating motors (the structure of which is taken from the cryo-EM model) and (ii) their partners, both tilted away from the center of the sarcomere (25, 27) (red and orange, respectively, in the cartoon in Fig. 3A), as well as (iii) motors in the off state (blue in the cartoon in Fig. 3A), the fraction of which increases with the reduction of force. The detached dimers (gray in the cartoon in Fig. 3A) do not significantly contribute to the M3 intensity (25), likely because of their large conformational dispersion.
At SL of 2.1 µm and external Ca2+ concentration ([Ca2+]o) of 2.5 mM (LC twitch), Tp is 93 kPa, which is 0.85 the force under maximal activation conditions [Tmax = 110 kPa attained at SL 2.25 µm (13, 28)]. The observed intensity profile of the M3 reflection can be simulated with the same degree of precision by either a model in which, as a simplifying assumption, all motors are switched on (model 1) (Fig. S5 B and E) or a model in which the fraction of switched on motors (fON) depends on the force (model 2) (Fig. 3 C and F) as suggested by the FE data simulation. In either case, the free parameters for the simulation of the M3 intensity profile in the LC twitch are the fraction of attached force-generating motors (fA) and the rotation of their light chain domain (LCD) (details are in SI Results). With the simplifying assumption that all motors are in the on state at the peak of the LC twitch, the observed intensity profile (continuous line in Fig. S5E) is best simulated (dashed line in Fig. S5E) when fA is 0.18 (the associated error is in Table 1) and the LCD tilt is 63° to the filament axis, so that the displacement of the center of the mass density profile from the head–rod junction is +3.03 nm (Fig. S5B, red), 1 nm away from the center of the sarcomere with respect to the partner motors (25, 27).
Table 1.
Comparison of the relevant parameters estimated with models 1 and 2
| Parameter | Model 1 | Model 2 |
| fOFF | ||
| LC | 0 | 0.15 ± 0.10 |
| FE | 0.56 ± 0.05 | 0.64 ± 0.08 |
| fA | ||
| LC | 0.180 ± 0.009 | 0.180 ± 0.019 |
| FE | 0.079 ± 0.005 | 0.079 ± 0.010 |
| rc | ||
| LC | 0.180 ± 0.009 | 0.212 ± 0.049 |
| FE | 0.180 ± 0.023 | 0.219 ± 0.075 |
In model 1, fOFF is assumed to be zero at the peak of LC twitch; in model 2, fOFF at the peak of LC twitch is assumed to be 0.15, in agreement with the conclusion from model 1 that fOFF becomes zero when activation is maximal (Tmax = 110 kPa; details are in the text). The errors are calculated as detailed in SI Methods.
In the FE twitch, Tp reduces from 93 to 41 kPa as the corresponding SL reduces from 2.1 to 1.9 µm (Fig. 1D), and, according to the proportionality between Tp and the number of attached motors (13), fA reduces from 0.18 to (0.18 × 41/93 =) 0.08. By simply reducing to this value the contribution of the mass of the attached motors and the partner motors (Fig. S5C, red and orange, respectively), the calculated intensity profile (Fig. S5F, dotted line) is too low, and the size of the low-angle peak relative to that of the high-angle peak is much larger than observed (Fig. S5F, continuous line). The only way to both raise the intensity at the observed spacing (14.36 nm) and recover the observed fine structure is to add the contribution of the mass corresponding to a fraction of motors in the off state (fOFF). The best approximation (Fig. S5F, dashed line) is obtained with fOFF = 0.56 (Fig. S5C, blue line and Table 1) [that is, the fraction of motors available for attachment (fON) is decreased to 0.44 relative to the LC twitch]. Because according to the change in Tp (13), the fraction of motors attached in the FE twitch also decreases to (41/93 =) 0.44 that attached in the LC twitch, the results of the simulation indicate that there is a direct proportionality between the number of attached motors and the number of available motors.
This conclusion on the proportionality between the number of attached motors and available motors is taken into account in the simulation of LC data with model 2. In the LC twitch (SL = 2.1 µm and [Ca2+]o = 2.5 mM), Tp is 0.85 Tmax (110 kPa), suggesting that, according to the conclusions of the simulation of the FE twitch, the calculated M3 intensity profile of the LC twitch must include the contribution to the mass from 15% of the motors in the off state (Fig. 3C, blue line) to be added to the contributions from both the attached motors (Fig. 3C, red line) and their partners (Fig. 3C, orange line) among the 85% of motors in the on state.
In this case, the observed intensity profile (Fig. 3F, continuous line) is fit (Fig. 3F, dashed line) when the attached motors have their LCD tilted by 72° with respect to the filament axis [that is, 9° more tilted toward the end of the working stroke, so that their center of mass is axially displaced by +2.02 nm from the head–rod junction (Fig. 3C, red), almost coinciding with that of the partner motors (Fig. 3C, orange)], and their fraction is 0.18 (Table 1).
Thus, both models 1 and 2 predict the same fA in the LC twitch, independent of the original assumption on fOFF. The new structural constraints from model 2 simulation of the LC twitch and the mechanical constraint of fA = (0.18 × 41/93) 0.08 have been used to simulate again the M3 intensity profile of the FE twitch, leaving fOFF as the only free parameter. The observed intensity profile (Fig. 3G, continuous line) is best simulated (Fig. 3G, dashed line) when fOFF is increased to 0.64 (Table 1). Correspondingly, fON is reduced to 0.36, 42% of the LC value (practically the same reduction as that undergone by the population of attached motors). Thus, both models 1 and 2 (Table 1 shows the comparison) drive to the conclusion that, at Tp, fON (obtained from X-ray data) scales in proportion to fA and force.
In the absence of the thick filament regulation concept, the fraction of motors attached among 294 motors in each half-thick filament (the duty ratio r, which corresponds to fA) seems to depend on the loading conditions and the resulting Tp. In fact, although the different SLs in the LC and FE twitches do not imply any significant change in the number of motors overlapping with the thin filament, r at Tp is 0.18 in the LC twitch and 0.08 in the FE twitch. Considering that, in either case, the condition is isometric, this apparent difference in r contradicts the expectation from the kinetics of a mechanoenzyme-like myosin II that r is uniquely determined by the mechanical condition (29). The contradiction is solved when the thick filament-based regulation of motors in the on state is taken into account: the correct duty ratio rc (the ratio fA/fON) results in fact constant: (0.18/0.85 =) 0.21 ± 0.05 for the LC twitch and (0.08/0.36 =) 0.22 ± 0.07 for the FE twitch. This conclusion is quite robust, because it is independent of the original assumption on the presence of a fraction of motors in the off state in the LC twitch (Table 1). Moreover, as shown in detail in SI Results, the conclusion is also not affected by the possibility, within certain limits, that 110 kPa could represent an underestimate of Tmax (Table S1).
Table S1.
The effect of Tmax (the twitch force for maximal activation) on the relevant parameters simulated with model 2
| Parameter | Tmax = 110 kPa | Tmax = 120 kPa |
| fOFF | ||
| LC | 0.15 | 0.23 |
| FE | 0.64 | 0.68 |
| fA | ||
| LC | 0.18 | 0.19 |
| FE | 0.08 | 0.09 |
| rc | ||
| LC | 0.21 | 0.25 |
| FE | 0.22 | 0.27 |
Tmax is assumed to be 110 kPa (column 2), corresponding to the maximum Tp value attained with [Ca2+] = 2.5 mM at SL = 2.25 µm (Fig. 1D) or ∼10% larger (120 kPa; column 3).
SI Results
Model Simulation.
The number and the axial movement of myosin motors leaving the off state and contributing to the twitch force in the trabecula are calculated by applying the structural model previously used to calculate the movement of the myosin motors during the force development in an electrically stimulated fiber from frog skeletal muscle (4). The only substantial difference, dictated by the evidence that the detached dimers do not significantly contribute to the M3 intensity because of their large conformational dispersion (25, 27), is that the contribution to M3 intensity from the detached motors in the on state is constituted only by the partners of the attached motors. The axial mass density projection of the detached partner motors is represented, as in ref. 4, by a Gaussian centered at a distance z of +2.07 nm from the head–rod junction (positive direction is toward the end of the thick filament) (Fig. 3 A and C and Fig. S5B, orange) and with σ = 2 nm, smaller than that in ref. 4 (3.6 nm) to maintain the contribution to the M3 intensity from the detached population the same as in refs. 25 and 27. With this modification, the model simulation is done as follows. (i) In diastole, the resting structure of the thick filament consists of two arrays of myosin motors in the off state (blue in the cartoon in Fig. 3A) with an axial periodicity of 14.35 nm and separated by a bare zone of 161 nm. The axial mass density profile of the off motors is represented by a Gaussian centered at −7.97 nm from the head–rod junction and σ = 3.5 nm (Fig. 3B and Fig. S5A). This mass distribution is almost identical to that corresponding to the motor conformation observed in isolated thick filaments by EM (2, 3). (ii) At the peak of the twitch force Tp, the bare zone is assumed to extend in agreement with the compliance of the thick filament [17.5 nm/MPa per micrometer (42)], and the axial periodicity of the motors along the filament is adjusted to the observed spacing of the M3 reflection. In the LC twitch, the free parameters for fitting the M3 intensity profile are the fraction of attached force-generating motors (fA) and the rotation of the LCD with respect to the filament axis, with a uniform angular dispersion of ±17° (4, 43, 44) starting from the nucleotide-free (rigor) crystallographic structure of the myosin motor in its actin-attached orientation (45). The calculated intensity profile is then convoluted with the PSF of the recording system (beam and detector; approximated by a Gaussian curve with σs = 2.3 × 10−4 nm−1). In the FE twitch, the LCD tilting of attached motors is constrained by the value obtained from the LC twitch simulation, and fA is constrained by the direct proportionality between Tp and the number of attached motors (13), so that the only free parameter is the fraction of motors in the off state (fOFF).
Although the fine structure of the M3 reflection is well-reproduced by the model simulation, the calculated profiles fail to reproduce the axial dispersion. This failure is attributed to an orientational disorder in the multicellular preparation, responsible for the arching of the reflections across the meridional axis (26), that increases the width of the meridional reflections. Because this kind of disorder is between regions (myocytes) that, in any case, do not diffract coherently, the total intensity of the reflection is not altered. Thus, the relative intensities of the three conditions (diastole, LC, and FE twitch) are satisfactorily reproduced by the model that does not include the disorder between myocytes.
Maximal Activation in the Heart Twitch.
A relevant question in this work is the level of activation of myofilaments in the contractions of the intact trabeculae used for X-ray data recording. The conditions for maximal activation of an intact trabecula have been studied in relation to [Ca2+]o, SL, and various inotropic interventions, like postextrasystolic potentiation, addition of Tetraethylammonium, or a β-receptor agonist such as isoprenaline (28). It was found that, with [Ca2+]o ≥ 2.5 mM and SL ≥ 2.25 µm, the twitch force attained a maximum value Tmax, which was not further increased but in some case, depressed by inotropic agents. This finding suggests that Tmax is determined by the saturation of the sarcomere with Ca2+. Accordingly, in our protocols (Fig. 1D) (13), Tmax (= 110 kPa) is the plateau value attained in the force–SL relation with [Ca2+]o = 2.5 mM.
The possibility that the saturation of the sarcomere occurs at an even higher value of Ca2+ can be considered in relation to the finding that a significant increase above Tmax (∼10% at SL = 2.25 µm) was found when Sr2+ (10 mM) was added to the perfusion solution with 1 mM [Ca2+]o (28). Even if this condition is clearly unphysiological and may affect the mechanical performance of the sarcomere, we calculated the response of the structural simulation in the case that 100% activation of the thick filament is attained with a Tmax = 120 kPa, ∼10% larger than that determined from the relation in Fig. 1D. As shown from the comparison of the responses of model 2 in Table S1, with Tmax = 120 kPa, the fractions of motors in the off state at Tp increase, and to fit the fine structure of the M3 reflection in the LC twitch, the LCD tilting of the attached motors must be further increased by 4° toward the center of the sarcomere. Moreover, although the fraction of attached motors is almost the same as in the case with Tmax = 110 kPa, rc is slightly increased but most importantly, still quite constant independent of Tp.
Discussion
Achievements in Relation to Previous Work.
The Frank–Starling law of the heart represents a fundamental regulatory mechanism that relates the performance of the heart to the ventricular filling. At cell level, the mechanism consists of the increase in contractile force, related to proportional increase in the number of attached motors, with increase in SL (LDA). LDA is generally attributed to the SL modulation of the sensitivity of the thin filament to cytosolic Ca2+ concentration combined with the fact that, during heart contraction, [Ca2+]i undergoes a transient increase that may not reach the full activation level (8, 9, 11). The molecular mechanisms underlying LDA remain largely unknown, although LDA has been shown to be modulated by several factors, such as the degree of phosphorylation of sarcomeric proteins and cardiomyopathy causing mutations in these proteins (14–20, 30).
X-ray diffraction provides a unique tool for in situ investigation of the structural changes undergone by the myofilaments during the cardiac contraction–relaxation cycle. This work, by combining sarcomere-level mechanics with nanometer–micrometer-scale X-ray diffraction in intact trabeculae from the rat cardiac ventricle, describes the changes in the thick filament and the myosin motors after force development in the cardiac twitch and their relation to SL, with the subnanometer precision achieved by using the X-ray interference between the two halves of the thick filament. We find that, in diastole, all of the myosin-based reflections mark the quasihelical three-stranded symmetry followed by the myosin molecules when they are in their off state on the surface of the thick filament with a short periodicity (2, 4, 7). At the peak of twitch force, the intensities of all of the meridional reflections and that of the ML1 decrease because of the myosin motors leaving their helical tracks as the thick filament switches on. The M3 reflection exhibits a different fine structure and different increase in spacing depending on whether the contraction occurs in FE (Tp = 41 kPa) or LC (Tp = 93 kPa) mode. Based on the structural model of the sarcomere defined for the skeletal muscle (4), the results indicate that, during a twitch, only a fraction of motors leaves the off state, and this fraction depends on the level of the force.
By corollary, the motors that attach to actin and contribute to Tp are a constant fraction (rc = 0.21) of the switched on motors, whereas they represent a variable fraction (fA; proportional to the degree of thick filament activation) of 294 motors present in each half-thick filament. From fA, the individual force (F) exerted by the motors contributing to Tp can be calculated following simple lattice geometry considerations, and given the constraint that Tp is accounted for by fA (13), it will be the same for both LC and FE twitches. With a distance of 43.3 nm between myosin filaments in the myofibril (31) and a myofibrillar volume density of 60% (32, 33), the density of myosin filaments can be calculated to be 370 × 1012 filaments m−2, and thus, the density of motors is 1.1 × 1017 m−2. Consequently, F, calculated from the parameters of either the LC (Tp = 93 kPa and fA = 0.18) or the FE twitch (Tp = 41 kPa and fA = 0.08), is 4.7 ± 1.0 pN. This value of F is slightly smaller than that determined in isometric contractions of the fast skeletal muscle of vertebrates in the same range of temperatures (34, 35), a difference that could be explained by the different isoform composition.
Previous work using skinned fiber preparations from mammalian heart provided kinetic (6) (rabbit heart bundles) and structural (36) (rat trabeculae) evidence that (i) in the relaxed cell, only about 50% of motors are in the off state and (ii) the fraction switching on upon Ca2+ activation is rather small. In contrast, our X-ray experiments show that (i) most of motors (apart from a few constitutively on motors) (7) are in the off state in the intact cell at rest and (ii) the proportion of motors switching on during systole rises with the stress on the filament. The reason for the difference of the fraction of the motors in the off state is likely to be caused by the different preparation. In fact, it is well-known from skeletal muscle studies that skinning (causing lattice expansion and loss of soluble proteins) implies, even at the physiological temperature, some loss of the ordered structure of the thick filament, which would imply a reduction in the fraction of motors in the off state. The other discrepancy (the dependence on the force of the fraction of motors switched on during active contraction) can actually be explained, in quantitative terms, considering the low force developed on Ca2+ activation in those skinned preparations: 23 kPa in ref. 6 and 32 kPa (SL = 1.9 µm) and 42 kPa (SL = 2.3 µm) in table S1 of ref. 37. These low forces imply, according to the mechanosensing-based thick filament regulation, a correspondingly low fraction of motors in the on state, a fraction that may be either already present because of the preexisting disorder in the relaxed state or too low to be detected.
The finding that a stress-sensing mechanism in the thick filament recruits motors from the off state in relation to the mechanical task leaves open the question on its molecular basis. The mechanism is likely related to the intramolecular interactions between the two motor domains and between the motor domain and the tail (38) as well as intermolecular interactions of the motor domain with MyBP-C (39) and titin (40). Impairment of the control by the stress-sensing mechanism on the state of the myosin motors is likely the molecular basis of hypertrophic cardiomyopathy (HCM) attributed to mutations that cause hypercontractility. In this respect, it must be noted that the failure of a stabilizing interaction between MyBP-C and the so-called mesa region in the myosin motor has been recently proposed as a possible cause of HCM (30). Mutations in the domains of either protein responsible for the interaction would reduce the affinity of MyBP-C for the myosin and in this way, could blunt the control by the stress-sensing mechanism of the off state of myosin motors, causing the hypercontractility that is thought to lead to HCM.
Aspects of the Frank–Starling Mechanism.
The finding that the changes in the intensity and fine structure of the M3 X-ray reflection of a twitching trabecula can be explained only by introducing the constraint that a variable number of myosin motors, depending on the peak force, remains in the off state provides a different perspective of the Frank–Starling mechanism. The conventional view based on the original experiments of Frank and Starling put the emphasis on the dependence of the end systolic pressure on the ventricular filling at the end of diastole. In this way, the stroke volume could be maintained against an increased aortic pressure. Here, we show that, independent of the diastolic SL, the number of motors recruited from the switched off population scales in proportion to the systolic force. In this respect, the LC and FE twitches approximate the conditions of the left ventricle beating against a high (LC twitch) and a low (FE twitch) aortic pressure (Fig. S1). In turn, the end systolic pressure–volume relation of the left ventricle, defined by the pressure–volume points at which the contracting cardiac cells are neither lengthening nor shortening, is the organ correlate of the active tension–length relation determined at sarcomere level with twitches that, according to our protocol, start from the same SL and experience different loading conditions. In this respect, the finding that the number of myosin motors made available for interaction with actin depends on the loading conditions shows that, independent of the ventricular filling, the thick filament stress-sensing mechanism adapting the number of switched on motors to the actual systolic force must be quite rapid.
This conclusion and the demonstration that almost all motors are in the off state in the diastole provide an integrated view of the Frank–Starling mechanism, which combines mechanical, structural, and energetic aspects: irrespective of the molecular mechanism that relates force to SL, the stress-dependent thick filament regulation optimizes the fraction of motors in the state that prevents ATP splitting in relation to the mechanical output. In this way, independent of the end diastolic SL (end diastolic volume), the energetic cost of the heart beat is tuned to the ventricular end systolic pressure–volume relation.
Methods
All experiments were made on male Rattus norvegicus killed in agreement with Italian regulation on animal experimentation (Authorization 956/2015-PR in compliance with Decreto Legislativo 26/2014). A thin, unbranched, and uniform trabecula was dissected from the right ventricle under a stereomicroscope, transferred into a thermoregulated trough, perfused with oxygenated Krebs–Henseleit solution (27 °C), and attached via titanium double hooks to the lever arms of a strain-gauge force transducer (valve side) and a loudspeaker motor (wall side). The trabecula was precisely oriented with the larger transverse axis orthogonal to the X-ray path by twisting opportunely the double-hook arms. A pair of Mylar windows was positioned close to the trabecula, about 1 mm apart, to minimize the X-ray path in the solution. The trough was sealed to prevent solution leakage, and the trabecula was mounted at the ID02 beamline of the ESRF. Trabeculae were electrically stimulated at 0.5 Hz to produce twitches, and X-ray diffraction patterns were recorded in frames of 5-ms exposure time at the end of the diastole and the peak of FE and sarcomere LC twitches. Details on materials and methods are provided in SI Methods.
SI Methods
Sample Preparation and Experimental Protocol.
Male Rattus norvegicus (Wistar Han weighing 250–350 g; Charles River—Research Models and Services) were housed at the Bio-Medical Facility (ID17) of the ESRF under controlled temperature (20 °C ± 1 °C), humidity (55 ± 10%), and illumination (light on for 12 h daily from 7:00 AM to 7:00 PM). Food and water were provided ad libitum. Rats were chosen at random for each experiment from the available batch and killed in agreement with Italian regulation on animal experimentation (Authorization 956/2015-PR in compliance with Decreto Legislativo 26/2014). Rats were anesthetized with isoflurane [5% (vol/vol)]; the heart was rapidly excised, placed in a dissection dish, retrogradely perfused with a modified Krebs–Henseleit (K-H) solution (composition: NaCl, 115 mM; KCl, 4.7 mM; MgSO4, 1.2 mM; KH2PO4, 1.2 mM; NaHCO3, 25 mM; CaCl2, 0.5 mM; glucose, 10 mM) containing 20 mM 2,3-butanedione monoxime (BDM), and oxygenated with 95% O2 and 5% CO2 (pH 7.4). A thin, unbranched, and uniform trabecula was dissected from the right ventricle under a stereomicroscope. The trabecula was set just taut (length Lt), and the larger and smaller transverse axes (Dl and Ds, respectively) were measured using an eyepiece with a graduate scale. The cross-sectional area (CSA) was calculated as Dl × Ds × π/4. The trabecula was then transferred into a thermoregulated trough perfused (1.2 mL/min) with oxygenated K-H solution (27 °C) and attached via titanium double hooks to the lever arms of a strain-gauge force transducer (valve side) and a loudspeaker motor (wall side). SL was measured with a 40× dry objective and a 25× eyepiece. SL was set at ∼2.2 μm at rest; the corresponding trabecula length (L0) was measured again, and the CSA was corrected for the change in length (L0 − Lt) assuming constant volume behavior. The trabecula was precisely oriented with the larger transverse axis orthogonal to the X-ray path by twisting opportunely the double-hook arms. A pair of Mylar windows was positioned close to the trabecula, about 1 mm apart, to minimize the X-ray path in the solution. The trough was sealed to prevent solution leakage, and the trabecula was mounted at the ID02 beamline of the ESRF. The K-H solution perfusing the trabecula was exchanged with a K-H solution without BDM and containing 2.5 mM CaCl2. Trabeculae were electrically stimulated at 0.5 Hz to produce twitches. Force, motor lever position, and stimulus signals were recorded with a multifunction input/output board (PXIE-6358; National Instruments).
X-Ray Data Collection.
The trabecula was mounted either horizontal or vertical at beamline ID02 of the ESRF (41), which provided up to 2 × 1013 photons per second with 0.1-nm wavelength in a beam of size ∼300 μm (horizontal; FWHM) and ∼50 μm (vertical) at the trabecula. The beam was attenuated for trabecula alignment. To minimize radiation damage, X-ray exposure was limited to the data collection period using a fast electromagnetic shutter (model LS500; nmLaser Products, Inc.), and the trabecula was shifted along its axis by 100–200 μm between exposures. X-ray diffraction patterns were recorded using the FReLoN CCD-based detector with 2,048 × 2,048 pixels (50 × 50-mm2 active area). Pixels were binned by eight in the equatorial direction (perpendicular to the trabecula axis) before the readout to increase the signal to noise (S/N) ratio. Twitches were preliminarily elicited with the X-ray detector at 30 m from the preparation in FE conditions, in which case the sarcomeres shorten during force development against the end compliance. SLs during diastole and at the peak of the twitch (force Tp) were measured by using the second-order sarcomeric reflection (Dia and FE, respectively, in Fig. 1 A and B). In the next series of twitches, shortening was prevented (sarcomere LC condition) by feeding the motor-servo system with a signal based on the changes in SL recorded at the peak of the preceding FE twitch (13), and the actual SL at the peak of the twitch was again recorded using the second-order sarcomeric reflection (LC in Fig. 1 A and B). Because of limits in the range of movement allowed by the motor used at the beamline, the maneuver did not always succeed in completely avoiding sarcomere shortening that, anyway, was drastically reduced. Then, the detector was moved to 1.6 m from the preparation, and patterns were recorded in diastole and at the peak of FE and LC twitches in a random sequence, with 5-ms exposure times. In four vertically mounted trabeculae (each from a different rat) selected for the analysis of the meridional reflections, X-rays were collected from at least 10 twitches in each trabecula with no detectable sign of radiation damage. Two of four trabeculae contributed to both FE (total of three trabeculae) and LC data (total of three trabeculae). ML1 reflection (Fig. S2) was analyzed in two horizontally mounted trabeculae from separate experiments. All of the data discussed in this paper are included in the text and SI Results. Source data are available as Excel files on request.
X-Ray Data Analysis.
X-ray diffraction data were analyzed using Fit2D (A. Hammersley; ESRF), PeakFit (SYSTAT Software, Inc.), and IgorPro (WaveMetrix, Inc.). 2D patterns were centered and aligned using the equatorial 1,0 reflections and then mirrored horizontally and vertically. The number of trabeculae was chosen to measure changes in relative intensities and spacing of the relevant X-ray reflections with adequate S/N ratio and minimize the number of animals to be killed. The number of trabeculae is small because the X-ray signals can be measured with extremely high precision and low biological variability (22, 25, 42). The distribution of diffracted intensity along the meridional axis of the X-ray pattern (parallel to the trabecula axis) was obtained by integrating the 2D pattern from 0.021 nm−1 on either side of the meridian. Given the arching of the reflections (Fig. 2A), these integration limits were not appropriate to accurately determine their spacing; thus, for the spacing, a narrower integration, 0.006 nm−1 on either side of the meridian, was used. The first myosin layer line (ML1) intensity distribution was obtained by integrating the region between 0.064 and 0.037 nm−1 from the meridional axis. Most background intensity distribution was removed using a convex hull algorithm; the small residual background was removed using the intensity from a nearby region of the X-ray pattern containing no reflections. The total intensities of the reflections were then obtained by integrating the axial distribution in the corresponding regions: M3, 0.066–0.073 nm−1; M6, 0.135–0.142 nm−1; and ML1, 0.019–0.023 nm−1. The limits for the ML1 integration were chosen to exclude the contribution of the partially overlapping first-order actin layer line. The intensities were then corrected to account for the different mass of the trabecula crossed by the X-ray beam at the different SLs. M3 and M6 reflections were further corrected for the different cross-meridional widths determined from the radial (parallel to the equatorial axis) intensity distribution in the axial regions specified above using a Gaussian fit in the region ±0.04 nm−1 across the meridian. The combined instrumental point spread function (PSF) was negligible compared with the radial width of the M3 reflection. The interference components of the M3 reflection were determined by fitting multiple Gaussian peaks with the same axial width to the meridional intensity distribution, and the total intensity of the reflection was calculated as the sum of the component peaks. The spacing of the M3 reflection was determined in each individual pattern from the weighted mean of the component peaks and calibrated using an M3 spacing of 14.34 nm in the resting frog skeletal muscle fiber mounted in the same experimental setup at 1.6-m camera length. Because of the much lower S/N ratio, the spacing of the M6 reflection was estimated by determining, in each individual pattern, the centroid of the reflection within the integration limits chosen from the profile obtained from the added patterns.
Error in the Parameters Estimated with the Structural Model Simulation.
The sources of the uncertainties in the results of the model simulation are the errors on the peak force Tp in both LC and FE conditions and the intensities of the M3 reflection in LC and FE conditions relative to the intensity in diastole. It has been taken into account that the errors on Tp values are not independent, because they derive from the uncertainties on the estimates of the CSA, which for a given trabecula, are the same for LC and FE conditions, with a negligible noise on the force traces. The corresponding errors in the relevant parameters of the simulation are reported in Table 1.
Acknowledgments
We thank Corrado Poggesi for insightful comments on the manuscript; the European Synchrotron Radiation Facility (ESRF) for providing beam time and support; Mario Dolfi, Jacques Gorini, and the staff of the mechanical workshop of the Department of Physics and Astronomy, University of Florence for electronic and mechanical engineering support; and the ESRF Biomedical Facility for assistance with animals and preparation. This work was supported by Ente Cassa di Risparmio di Firenze Project 2015.0902 (Italy) and Telethon Project GGP12282 (Italy).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1619484114/-/DCSupplemental.
References
- 1.Huxley HE, Brown W. The low-angle x-ray diagram of vertebrate striated muscle and its behaviour during contraction and rigor. J Mol Biol. 1967;30(2):383–434. doi: 10.1016/s0022-2836(67)80046-9. [DOI] [PubMed] [Google Scholar]
- 2.Zoghbi ME, Woodhead JL, Moss RL, Craig R. Three-dimensional structure of vertebrate cardiac muscle myosin filaments. Proc Natl Acad Sci USA. 2008;105(7):2386–2390. doi: 10.1073/pnas.0708912105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Luther PK, et al. Direct visualization of myosin-binding protein C bridging myosin and actin filaments in intact muscle. Proc Natl Acad Sci USA. 2011;108(28):11423–11428. doi: 10.1073/pnas.1103216108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Reconditi M, et al. Motion of myosin head domains during activation and force development in skeletal muscle. Proc Natl Acad Sci USA. 2011;108(17):7236–7240. doi: 10.1073/pnas.1018330108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Stewart MA, Franks-Skiba K, Chen S, Cooke R. Myosin ATP turnover rate is a mechanism involved in thermogenesis in resting skeletal muscle fibers. Proc Natl Acad Sci USA. 2010;107(1):430–435. doi: 10.1073/pnas.0909468107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hooijman P, Stewart MA, Cooke R. A new state of cardiac myosin with very slow ATP turnover: A potential cardioprotective mechanism in the heart. Biophys J. 2011;100(8):1969–1976. doi: 10.1016/j.bpj.2011.02.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Linari M, et al. Force generation by skeletal muscle is controlled by mechanosensing in myosin filaments. Nature. 2015;528(7581):276–279. doi: 10.1038/nature15727. [DOI] [PubMed] [Google Scholar]
- 8.Allen DG, Kentish JC. The cellular basis of the length-tension relation in cardiac muscle. J Mol Cell Cardiol. 1985;17(9):821–840. doi: 10.1016/s0022-2828(85)80097-3. [DOI] [PubMed] [Google Scholar]
- 9.ter Keurs HE. The interaction of Ca2+ with sarcomeric proteins: Role in function and dysfunction of the heart. Am J Physiol Heart Circ Physiol. 2012;302(1):H38–H50. doi: 10.1152/ajpheart.00219.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sagawa K, Maughan L, Suga H, Sunagawa K. Cardiac Contraction and the Pressure Volume Relationship. Oxford Univ Press; New York: 1988. [Google Scholar]
- 11.de Tombe PP, et al. Myofilament length dependent activation. J Mol Cell Cardiol. 2010;48(5):851–858. doi: 10.1016/j.yjmcc.2009.12.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Spudich JA. Hypertrophic and dilated cardiomyopathy: Four decades of basic research on muscle lead to potential therapeutic approaches to these devastating genetic diseases. Biophys J. 2014;106(6):1236–1249. doi: 10.1016/j.bpj.2014.02.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Caremani M, et al. Size and speed of the working stroke of cardiac myosin in situ. Proc Natl Acad Sci USA. 2016;113(13):3675–3680. doi: 10.1073/pnas.1525057113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Konhilas JP, et al. Troponin I in the murine myocardium: Influence on length-dependent activation and interfilament spacing. J Physiol. 2003;547(Pt 3):951–961. doi: 10.1113/jphysiol.2002.038117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hanft LM, Biesiadecki BJ, McDonald KS. Length dependence of striated muscle force generation is controlled by phosphorylation of cTnI at serines 23/24. J Physiol. 2013;591(18):4535–4547. doi: 10.1113/jphysiol.2013.258400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sequeira V, et al. Perturbed length-dependent activation in human hypertrophic cardiomyopathy with missense sarcomeric gene mutations. Circ Res. 2013;112(11):1491–1505. doi: 10.1161/CIRCRESAHA.111.300436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kumar M, et al. Cardiac myosin-binding protein C and troponin-I phosphorylation independently modulate myofilament length-dependent activation. J Biol Chem. 2015;290(49):29241–29249. doi: 10.1074/jbc.M115.686790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hidalgo C, Granzier H. Tuning the molecular giant titin through phosphorylation: Role in health and disease. Trends Cardiovasc Med. 2013;23(5):165–171. doi: 10.1016/j.tcm.2012.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Methawasin M, et al. Experimentally increasing titin compliance in a novel mouse model attenuates the Frank-Starling mechanism but has a beneficial effect on diastole. Circulation. 2014;129(19):1924–1936. doi: 10.1161/CIRCULATIONAHA.113.005610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ait-Mou Y, et al. Titin strain contributes to the Frank-Starling law of the heart by structural rearrangements of both thin- and thick-filament proteins. Proc Natl Acad Sci USA. 2016;113(8):2306–2311. doi: 10.1073/pnas.1516732113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.ter Keurs HE, Rijnsburger WH, van Heuningen R, Nagelsmit MJ. Tension development and sarcomere length in rat cardiac trabeculae. Evidence of length-dependent activation. Circ Res. 1980;46(5):703–714. doi: 10.1161/01.res.46.5.703. [DOI] [PubMed] [Google Scholar]
- 22.Linari M, et al. Interference fine structure and sarcomere length dependence of the axial x-ray pattern from active single muscle fibers. Proc Natl Acad Sci USA. 2000;97(13):7226–7231. doi: 10.1073/pnas.97.13.7226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rome E, Offer G, Pepe FA. X-ray diffraction of muscle labelled with antibody to C-protein. Nat New Biol. 1973;244(135):152–154. doi: 10.1038/newbio244152a0. [DOI] [PubMed] [Google Scholar]
- 24.Malinchik SB, Lednev VV. Interpretation of the X-ray diffraction pattern from relaxed skeletal muscle and modelling of the thick filament structure. J Muscle Res Cell Motil. 1992;13(4):406–419. doi: 10.1007/BF01738036. [DOI] [PubMed] [Google Scholar]
- 25.Reconditi M, et al. Sarcomere-length dependence of myosin filament structure in skeletal muscle fibres of the frog. J Physiol. 2014;592(5):1119–1137. doi: 10.1113/jphysiol.2013.267849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Juanhuix J, et al. Axial disposition of myosin heads in isometrically contracting muscles. Biophys J. 2001;80(3):1429–1441. doi: 10.1016/S0006-3495(01)76115-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Brunello E, et al. Skeletal muscle resists stretch by rapid binding of the second motor domain of myosin to actin. Proc Natl Acad Sci USA. 2007;104(50):20114–20119. doi: 10.1073/pnas.0707626104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schouten VJ, Bucx JJ, de Tombe PP, ter Keurs HE. Sarcolemma, sarcoplasmic reticulum, and sarcomeres as limiting factors in force production in rat heart. Circ Res. 1990;67(4):913–922. doi: 10.1161/01.res.67.4.913. [DOI] [PubMed] [Google Scholar]
- 29.Fusi L, et al. Minimum number of myosin motors accounting for shortening velocity under zero load in skeletal muscle. J Physiol. 2017;595(4):1127–1142. doi: 10.1113/JP273299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Spudich JA. The myosin mesa and a possible unifying hypothesis for the molecular basis of human hypertrophic cardiomyopathy. Biochem Soc Trans. 2015;43(1):64–72. doi: 10.1042/BST20140324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Matsubara I, Millman BM. X-ray diffraction patterns from mammalian heart muscle. J Mol Biol. 1974;82(4):527–536. doi: 10.1016/0022-2836(74)90246-0. [DOI] [PubMed] [Google Scholar]
- 32.Barth E, Stämmler G, Speiser B, Schaper J. Ultrastructural quantitation of mitochondria and myofilaments in cardiac muscle from 10 different animal species including man. J Mol Cell Cardiol. 1992;24(7):669–681. doi: 10.1016/0022-2828(92)93381-s. [DOI] [PubMed] [Google Scholar]
- 33.Schaper J, Meiser E, Stämmler G. Ultrastructural morphometric analysis of myocardium from dogs, rats, hamsters, mice, and from human hearts. Circ Res. 1985;56(3):377–391. doi: 10.1161/01.res.56.3.377. [DOI] [PubMed] [Google Scholar]
- 34.Decostre V, Bianco P, Lombardi V, Piazzesi G. Effect of temperature on the working stroke of muscle myosin. Proc Natl Acad Sci USA. 2005;102(39):13927–13932. doi: 10.1073/pnas.0506795102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Linari M, Caremani M, Piperio C, Brandt P, Lombardi V. Stiffness and fraction of Myosin motors responsible for active force in permeabilized muscle fibers from rabbit psoas. Biophys J. 2007;92(7):2476–2490. doi: 10.1529/biophysj.106.099549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kampourakis T, Irving M. Phosphorylation of myosin regulatory light chain controls myosin head conformation in cardiac muscle. J Mol Cell Cardiol. 2015;85:199–206. doi: 10.1016/j.yjmcc.2015.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kampourakis T, Sun YB, Irving M. Myosin light chain phosphorylation enhances contraction of heart muscle via structural changes in both thick and thin filaments. Proc Natl Acad Sci USA. 2016;113(21):E3039–E3047. doi: 10.1073/pnas.1602776113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Jung HS, Komatsu S, Ikebe M, Craig R. Head-head and head-tail interaction: A general mechanism for switching off myosin II activity in cells. Mol Biol Cell. 2008;19(8):3234–3242. doi: 10.1091/mbc.E08-02-0206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pfuhl M, Gautel M. Structure, interactions and function of the N-terminus of cardiac myosin binding protein C (MyBP-C): Who does what, with what, and to whom? J Muscle Res Cell Motil. 2012;33(1):83–94. doi: 10.1007/s10974-012-9291-z. [DOI] [PubMed] [Google Scholar]
- 40.Muhle-Goll C, et al. Structural and functional studies of titin’s fn3 modules reveal conserved surface patterns and binding to myosin S1--a possible role in the Frank-Starling mechanism of the heart. J Mol Biol. 2001;313(2):431–447. doi: 10.1006/jmbi.2001.5017. [DOI] [PubMed] [Google Scholar]
- 41.van Vaerenbergh P, et al. An upgrade beamline for combined wide, small and ultra- small-angle x-ray scattering at the ESRF. AIP Conf Proc. 2016;1741:030034. [Google Scholar]
- 42.Brunello E, et al. The contributions of filaments and cross-bridges to sarcomere compliance in skeletal muscle. J Physiol. 2014;592(17):3881–3899. doi: 10.1113/jphysiol.2014.276196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Reconditi M, et al. The myosin motor in muscle generates a smaller and slower working stroke at higher load. Nature. 2004;428(6982):578–581. doi: 10.1038/nature02380. [DOI] [PubMed] [Google Scholar]
- 44.Piazzesi G, et al. Skeletal muscle performance determined by modulation of number of myosin motors rather than motor force or stroke size. Cell. 2007;131(4):784–795. doi: 10.1016/j.cell.2007.09.045. [DOI] [PubMed] [Google Scholar]
- 45.Holmes KC, Angert I, Kull FJ, Jahn W, Schröder RR. Electron cryo-microscopy shows how strong binding of myosin to actin releases nucleotide. Nature. 2003;425(6956):423–427. doi: 10.1038/nature02005. [DOI] [PubMed] [Google Scholar]
- 46.Huxley AF, Lombardi V, Peachey LD. A system for fast recording of longitudinal displacement of a striated muscle fibre. J Physiol. 1981;317:12–13. [Google Scholar]
- 47.Arts T, Bovendeerd PH, Prinzen FW, Reneman RS. Relation between left ventricular cavity pressure and volume and systolic fiber stress and strain in the wall. Biophys J. 1991;59(1):93–102. doi: 10.1016/S0006-3495(91)82201-9. [DOI] [PMC free article] [PubMed] [Google Scholar]