Hunter-gatherer residential mobility and the marginal value of rainforest patches

Significance

Hunter-gatherers are notable for their high levels of mobility, but the ecological and social cues that determine the timing of camp movements (residential mobility) are poorly understood. Using models from foraging theory, we found that, for one population of hunter-gatherers, camp movements coincided with the point at which resource acquisition declined to a critical threshold level, but before local resources were completely depleted. These results suggest that hunter-gatherer residential mobility is constrained in a predictable fashion by rates of local resource depletion.

Abstract

The residential mobility patterns of modern hunter-gatherers broadly reflect local resource availability, but the proximate ecological and social forces that determine the timing of camp movements are poorly known. We tested the hypothesis that the timing of such moves maximizes foraging efficiency as hunter-gatherers move across the landscape. The marginal value theorem predicts when a group should depart a camp and its associated foraging area and move to another based on declining marginal return rates. This influential model has yet to be directly applied in a population of hunter-gatherers, primarily because the shape of gain curves (cumulative resource acquisition through time) and travel times between patches have been difficult to estimate in ethnographic settings. We tested the predictions of the marginal value theorem in the context of hunter-gatherer residential mobility using historical foraging data from nomadic, socially egalitarian Batek hunter-gatherers (n = 93 d across 11 residential camps) living in the tropical rainforests of Peninsular Malaysia. We characterized the gain functions for all resources acquired by the Batek at daily timescales and examined how patterns of individual foraging related to the emergent property of residential movements. Patterns of camp residence times conformed well with the predictions of the marginal value theorem, indicating that communal perceptions of resource depletion are closely linked to collective movement decisions. Despite (and perhaps because of) a protracted process of deliberation and argument about when to depart camps, Batek residential mobility seems to maximize group-level foraging efficiency.

Humans have lived as hunter-gatherers for more than 95% of our species history, moving as individuals and groups in response to variation in the distribution of food in time and space. Food availability is, therefore, central to explaining the logistical and residential (i.e., camp) mobility patterns of hunter-gatherers (1, 2), a relationship that informs prevailing theories of hominin evolution and human uniqueness (3). Given that residential moves are costly, natural selection should minimize these costs within the bounds of local ecological constraints (4). Consistent with this notion, bioenergetic availability dictates the number of residential moves per year and the distance traveled per move, with foragers in warm, high-productivity environments moving shorter distances more frequently compared with foragers in cool, low-productivity environments (1, 4–6).

These group-level macroecological patterns necessarily emerge from the foraging behavior of individuals, but the proximate ecological and social factors that influence these collective movement decisions remain poorly understood (1, 5, 6). One prominent yet untested hypothesis is that selection should optimize the time at which hunter-gatherers abandon camps to maximize foraging efficiency. However, as social central-place foragers who depend on extensive cooperation for survival, hunter-gatherers may face collective action problems when it comes to moving camps, because individuals can have conflicting economic goals. Accordingly, movement decisions are a major source of contention among hunter-gatherers, with arguments sometimes lasting for days or weeks (1).

At the heart of this issue is how individuals and groups perceive and respond to local resource depletion. Ethnographic reports (1) indicate that hunter-gatherers move camp residences in anticipation of the “imminence of diminishing returns” (7). Charnov’s (8) marginal value theorem is a simple yet powerful theoretical model for formalizing these subjective impressions, and support for its predictive capabilities has been found for many species (9, 10). This model predicts that long-term return rate-maximizing foragers should leave a camp or patch (the foraging area associated with a camp) when the instantaneous return rate declines to the environmental average after travel time between patches is taken into account. One important assumption of the marginal value theorem is that the gain curves—describing cumulative resource acquisition across time in a patch—exhibit diminishing marginal returns. In reality, the gain curves may adopt different shapes that reflect the nature, abundance, and distribution of resources in the environment in addition to specific behavioral and technological capabilities of foragers (10).

Several studies of human foragers have found indirect evidence consistent with the marginal value theorem (11–15), but the framework remains underutilized in human behavioral ecology (16), in part because of its “daunting data requirements” (15): travel time between patches must be known, and return rates within patches should be measured at short timescales. Depleting gain functions have been empirically measured in carcass butchery experiments and applied to the ethnoarchaeological record (16–20), but gain functions have proven difficult to quantify in ethnographic settings. It is unknown whether groups of human foragers completely or only partially deplete local resources, because there has been no detailed quantitative assessment of camp-level mobility patterns in relation to foraging returns at short timescales.

Here, we directly test the predictions of the marginal value theorem in the context of hunter-gatherer residential mobility. We used historical data on the foraging economy of the Batek, a population of egalitarian, nomadic hunter-gatherers inhabiting the rainforests of north-central Peninsular Malaysia (21, 22). Using foraging return data collected at high temporal resolution in and around different camps between which travel times are known, we characterized gain functions (cumulative kilocalorie acquisition aggregated across all individuals) for several important resources. We then tested whether the marginal value theorem predicted camp residence times in concordance with empirical observations.

Materials and Methods

Study Site, Subjects, and Data Collection.

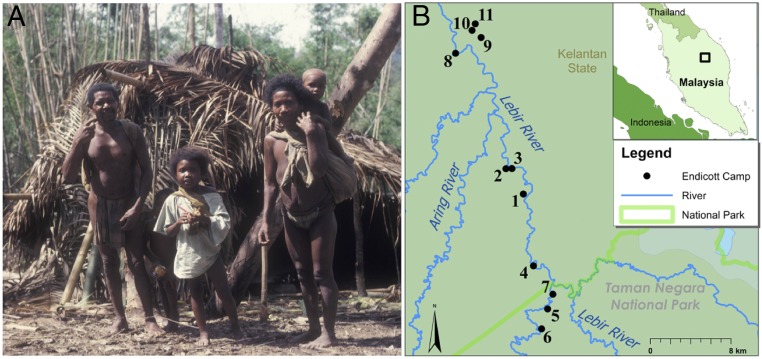
In 1975 and 1976, anthropologists Kirk and Karen Endicott collected data among Batek hunter-gatherer-traders living in the Upper Lebir River watershed in Kelantan, Malaysia (Fig. 1 and Table S1). The environment in that area, which includes the northeastern section of Taman Negara National Park, consisted of tropical lowland dipterocarp rainforest interspersed with a series of rivers and tributaries. Annual rainfall currently averages 2,270 mm, and the temperature is 20 °C to 35 °C (23). Most of the area outside the park has now been logged and converted into oil palm plantations. The population then living in that area numbered about 90 Batek and was usually divided into two to four camps of varying sizes, averaging 34 individuals (20 adults and 14 children). During the period of study, September 16, 1975 to June 11, 1976, the Batek lived most of the time in forest camps, but after late January of 1976, they also participated intermittently in a Department of Aboriginal Affairs-sponsored swidden farming program at Gintah on the bank of the Lebir River.

Fig. 1.

Batek residential mobility from September of 1975 to June of 1976. (A) A Batek nuclear family prepares to move to the next camp. Batek individuals usually carried sleeping mats, digging sticks, blowpipes, and light food during the moves, which typically lasted a few hours. Photograph courtesy of Kirk Endicott and Karen Endicott. (B) The focal group of Batek foragers occupied 11 camps along the Upper Lebir River in the state of Kelantan, Peninsular Malaysia. Map courtesy of Thomas Overly.

Table S1.

Information about Batek camp locations near the Upper Lebir River during the Endicotts’ data collection period in 1975 and 1976

Camp	Dates	Latitude	Longitude	DD (km)	DR (km)
1	September 24–28	4.950947	102.412883	—	—
2	September 29–October 7	4.973600	102.397411	3.1	6.2
3	October 9–11	4.973701	102.402770	0.6	0.6
4	October 12–22	4.886830	102.421915	9.9	14.5
5	October 25–28	4.848432	102.434588	4.5	7.3
6	October 29–November 13	4.830557	102.429197	2.1	7.6
7	November 15–20	4.861484	102.439222	3.6	8.2
8	February 18–20	5.076645	102.352496	NA	NA
9	February 22–26	5.090737	102.375289	3.0	6.1
10	May 5–8	5.097099	102.367166	NA	NA
11	May 9–June 4	5.102913	102.370074	0.7	1.0

DD, linear distance from previous camp; DR, distance from previous camp via river; NA, not available.

The Batek are one of several indigenous groups living in Peninsular Malaysia, collectively termed Orang Asli (“original people” in Malay) (SI Text). The Batek economy revolved around a traditional nomadic hunter-gatherer lifestyle that included hunting, gathering, and fishing (21, 22). Common sources of meat included small game items, such as monkeys, gibbons, squirrels, civets, birds, bamboo rats, and porcupines. Honey and fruit were seasonal, appearing mainly between the months of April and August. The most common tubers available were wild yams in the genus Dioscorea ($\sim$10 species), which provide a stable carbohydrate source throughout the year. The rainforests of Malaysia may be more resource-rich for humans compared with other rainforests around the world (24).

The Batek were highly mobile during the study at both the group and individual levels. In addition to foraging, some Batek visited other camps during the day; individual families and young unmarried adults frequently moved residence from one camp to another, thus changing the size and composition of camps on an almost daily basis. There was a high premium on maintaining social proximity. The Batek did not stay in a camp if the population fell below two or three families out of fear of animal predators and because of a feeling of depression at the sight of empty shelters surrounding them. At some point, the entire group would abandon the location and move elsewhere, either as a group or subgroups, to new locations. Here, we address not individual decisions to leave but instead, how groups abandon patches based on communal perceptions of daily variation in per capita resource acquisition. Ethnographic notes suggest that there was minimal advance planning regarding the timing and destination of moves. Each new campsite was cleared and then, completely abandoned with each move. The Batek moved between camps on foot carrying minimal belongings, and food storage was negligible. Travel times were either recorded or indirectly calculated (Tables S2 and S3). The average duration of camps during the study period was 8.2 d (SD = 6.6; range = 3–24 d).

Table S2.

Estimated travel speeds for different methods of Batek movement

Method of travel	Speed (km/h)
Walking in forest	1.67
Walking near river	2.42
Outboard motor on river	7.26

Data were extracted from the Endicotts’ field notes. Speeds were calculated using known travel times and geographic distances calculated from Google Earth (Materials and Methods).

Table S3.

Estimated travel times between Batek camps

Camp	Method (habitat)	Route	Total travel time (h)
1	NA	NA	4.0
2	Walk (river)	DR	6.1
3	Walk (forest)	DD	4.5
4	Walk	DR	9.5
5	Walk	DR	6.5
6	Walk (forest)	DD	4.8
7	Walk (forest)	DR	5.0
8	NA	NA	5.5
9	Walk (forest)	DD	5.3
10	NA	NA	5.5
11	Walk (forest)	DD	3.9

The speed of travel differs between dense rainforest and along the river. Some travel times are known from the Endicotts’ notes, and the rest are calculated using travel speed estimates and distances between the camps, including information on the exact route taken. Total travel time represents time moving plus 3.5 h for camp breakdown and setup. Travel times for camps 3, 4, and 7 were extracted directly from field notes and used to calculate travel speed so that travel times to other camps could be indirectly calculated. Total travel times were unknown for camps 8 and 10, because the Endicotts were not present during travel to these camps. The value of 5.5 h was calculated as the mean total travel time to the other nine camps. DD, linear distance from previous camp; DR, distance via river from previous camp; NA, not available.

We studied the pattern of acquisition of food and rattan in 11 forest camps. Our analyses focus on those camps in which the Endicotts were present for the establishment and abandonment of the camps (camps 2, 3, 5, 6, 8, 10, and 11). Here, we briefly discuss the exceptions. The Endicotts were not present for the establishment or abandonment of camp 7, and therefore, the gain functions at this camp could not be investigated, but we did include camp 7 in the calculations of the environmental averages. The Endicotts joined two camps (1 and 4) several days after establishment (6 and 13 d, respectively), and they joined camp 8 after an unknown date of establishment. Because the Endicotts departed with the Batek when camps 1, 4, and 8 dissolved, it is still possible to fit gain curves and predict departure times for these camps, despite the shape of the gain functions being uninformative. The return rates for these camps were also used in the calculation of the environmental averages. To summarize, we investigated the shape of the gain functions for resources exploited at camps 2, 3, 5, 6, and 9–11, for which return rate data reflect the camp’s occupation from establishment to abandonment. We tested the predictions of the marginal value theorem using return rate data from camps 1–6 and 8–11.

The Endicotts used spring scales to weigh all items acquired by the Batek on a daily basis (Fig. S1). During the study period, the Batek consumed 60% of total kilocalories from wild foods and 40% of total kilocalories from agricultural products (mainly rice, sugar, and flour) obtained by collecting and trading rattan. We excluded all trade-derived foods from these analyses, because they were not acquired from the rainforest. Caloric values were estimated using standard conversions (Fig. S2).

Fig. S1.

Kirk Endicott uses a spring scale to weigh a bamboo rat (Rhizomys sumatrensis) acquired by the Batek before its processing and consumption. Photograph courtesy of Karen Endicott.

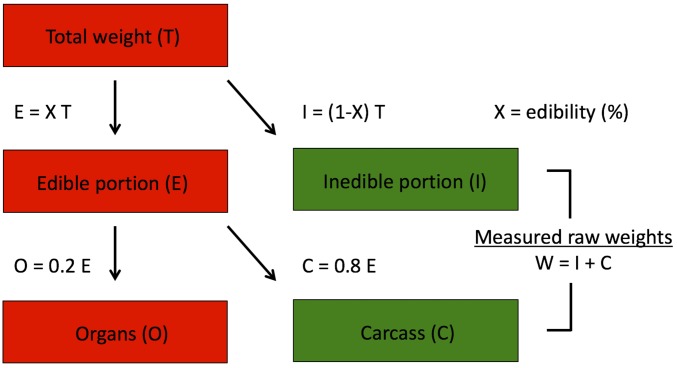
Fig. S2.

Schematic diagram showing how edible organ and carcass weights were derived from the measured raw weights ($W$). The values for organs ($O$) and carcass ($C$) were then converted to kilocalories. Green indicates known variables $I$ and $C$, the sum of which constitutes the measured field weight. Red indicates the calculated quantities $T$, $E$, and $O$.

Rattan is a general term for all climbing palms in the tribe Calameae (Fig. S3). Rattan in the genus Calamus was and is a major component of the Batek economy because of its market value (SI Text). Rattan was either bartered for food or exchanged for cash, which was used immediately to purchase food (21). We, thus, converted rattan proceeds to the kilocalorie units of rice to establish comparability with wild food items. Batek acquisition and trade of rattan focused on two types: species with large diameters (Malay rotan manau) and those with small diameters (Malay rotan barang) (Fig. S3). We examined the energetic returns from five nonexclusive resource sets pursued by the Batek that were likely to impact their movement decisions: (i) meat, (ii) tubers, (iii) rattan, (iv) total wild food, and (v) total wild food and rattan. Total wild food includes meat and tuber returns in addition to vegetables, fruit, honey, and other miscellaneous resources.

Fig. S3.

(A) Two men assembling some small-diameter rattan (rotan barang; foreground) and large-diameter rattan (rotan manau; background) to be picked up by Malay traders. (B) Malay traders assembling a consignment of rattan on bamboo rafts built by Batek. The traders will then pole the raft loads of rattan downstream to their villages. Photographs courtesy of Kirk Endicott and Karen Endicott.

Testing the Predictions of the Marginal Value Theorem.

The fine scale at which foraging returns were collected facilitated the construction of gain curves for each resource set at each of 11 Batek residential camps (patches). These gain curves represent gross gains rather than net gains (SI Text). Because our analysis used naturalistic foraging data rather than experimental data, it is possible that the full extent of the gain curves in each patch was not realized. For the analysis, we operated under the realistic assumption that the tail end of gain functions would follow from the shape of empirically measured data. We fitted a variety of predetermined deterministic models to the data and used information-theoretic model selection to choose the best-performing model. We chose asymptotic and sigmoidal (S-shaped) gain functions commonly used in applications of foraging theory that have several critical properties that satisfy the assumptions of the marginal value theorem (10): (i) net energy gain is zero when time spent in the patch is zero [$f(0)=\mathrm{\hspace{0.17em}0}$], (ii) the function $f(x)$ is at least initially increasing [$f\prime (0)>\mathrm{\hspace{0.17em}0}$], and (iii) the function eventually negatively accelerates [$f^{″}(x)<\mathrm{\hspace{0.17em}0}$]. We opted to fit deterministic models rather than locally weighted regressions, because we assume that Batek foraging behavior can be adequately described by processes similar to those found in other organisms (10).

Deterministic models were generated for 50 camp–resource set combinations. We tested five competing models (two asymptotic, two sigmoidal, and one linear) for each resource set–camp combination.

• i)Asymptotic Michaelis–Menton: $y=ax/(b+x)$, where $a$ and $b$ are constants.
• ii)Asymptotic exponential: $y=a(1-exp(-bx))$, where $a$ and $b$ are constants.
• iii)Sigmoidal: Holling Type III curve: $y=a{x}^2/(b^2+x^2)$, where $a$ and $b$ are constants.
• iv)Sigmoidal: four-parameter logistic function: $y=a+(b-a)/(1+exp((c-x)/d)$), where $a$, $b$, $c$, and $d$ are constants.
• v)Linear: $y=mx+b$, where $m$ and $b$ are constants.

For each resource set–camp combination, we used an information-theoretic criterion [the Akaike Information Criterion corrected for low sample sizes (AICc)] to quantify the strength of evidence for five alternative models.

Environmental average return rates are important quantities in optimal foraging models, because they characterize the quality of the environment “at-large” and represent the decision threshold for patch departure (8). We computed the energy acquired at each campsite for five resource sets and divided by (number of days in the camp + travel time to camp) to calculate foraging efficiency in that camp in the units kilocalories per day. For per capita analyses, we then divided by the mean number of adults (individuals $>$14 y of age) occupying each camp throughout its duration. These 11 values for each resource set were then averaged to generate the environmental average (Table S4). We focused our analysis on the cumulative per capita measure of energy acquisition (kilocalories per person per day), because group size fluctuated between days at each camp.

Table S4.

The environmental average (per capita return rates in units of kilocalories per person per day) after travel time has been taken into account for different resource sets acquired by the Batek

Resource set	Kilocalories per person per day
Meat	253.5
Tubers	963.6
Rattan	2,423.8
Wild food	1,323.3
Wild food and rattan	3,756.1

We selected a single best model for each resource set–camp combination using AICc. For depleting deterministic functions, we used the marginal value theorem to estimate the predicted camp residence time (in days) by calculating when the instantaneous return rate (kilocalories per person per day) of the best-fit theoretical gain curve at each camp declined to the environmental average for that particular resource set. To do so, we took the first derivative of deterministic gain functions with respect to $x$ (days in camp) and solved for the value of $x$ when $f\prime (x)$ was equal to the environmental average for the corresponding resource. We refer to the resulting value as “predicted camp residence time,” which represents the number of days that the marginal value theorem predicts that the Batek will stay in a given camp. We then compared these estimates with the observed camp residence times. For some camps, linear fits performed better than depleting functions, and thus, the marginal value theorem could not be used to generate predicted camp residence times.

As noted above, the Endicotts joined camps 1, 4, and 8 after they were established. Because there were no return rate data for the days before the Endicotts arrived, rather than fitting gain curves to the entire camp duration, we opted to construct curves that started when the Endicotts arrived. For the sake of completeness, we have plotted these gain curves in Fig. 2, but we do not further discuss the functional forms of curves for these camps.

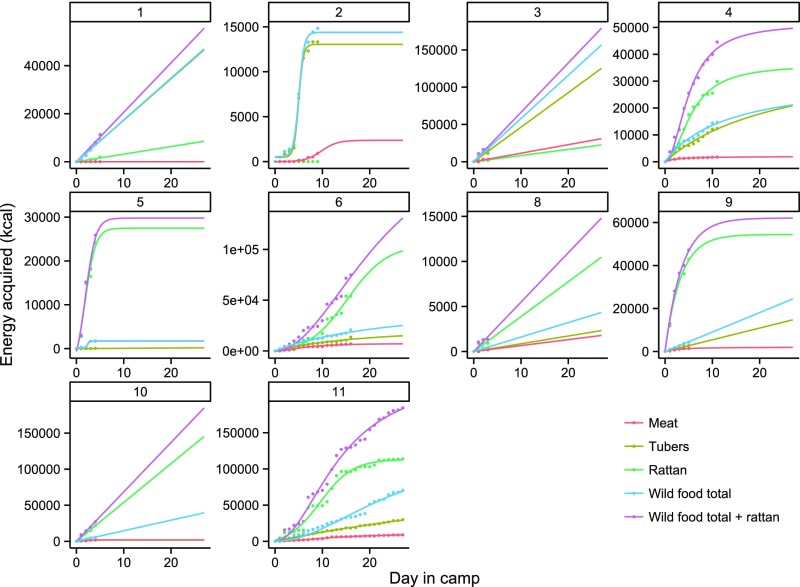
Fig. 2.

The gain functions illustrating energy acquisition at each Batek camp (camps 1–11, excluding camp 7). Data are represented on a standardized 25-d x axis. Colors indicate different resource sets. Ethnographers were not present for the establishment of camps 1, 4, and 8. The gain curves for these camps are shown only for graphical purposes.

All analyses were performed in R (version 3.1.3) (25). The data and associated code for this paper are available at https://github.com/ThomasKraft/HunterGathererMarginalValueTheorem.

Research was conducted with consenting adults under protocols approved by the Research School of Pacific Studies, Australian National University, Canberra, Australia, and the Jabatan Hal Ehwal Orang Asli (formerly Department of Aboriginal Affairs) and Ministry of National Unity, Malaysia (permit nos. VC/60050/70-045847, -581/70, -147485, -4227, and -674/90).

Results

Many resources acquired by the Batek conform to diminishing marginal return curves. Gain functions (n = 34) in this portion of the analysis (with camps 1, 4, 7, and 8 excluded) were depleting in 68% of camp–resource set combinations, whereas linear functions were the best-performing models in 32% of cases. Importantly, 83.3% (five of six) of camps had at least one depleting resource, and “total wild food and rattan” (perhaps the best proxy for overall resource availability) was depleting in 71% of camp–resource combinations. For the depleting functions, the best-fitting curves in these cases evinced either asymptotic (26%) or sigmoidal (74%) shapes. Those camps with primarily linear gain curves were probably abandoned before deceleration in the rate of acquisition, because it is not likely that resources were replenished on the scale of days. For example, one camp with primarily linear gain curves (camp 10) was abandoned because of the danger of tree falls in the vicinity of the camp.

Although our sample sizes make it difficult to identify a characteristic functional form of gain curves for each resource type, the shape of Batek gain curves varied across time, space, and resource sets (Fig. 2 and Table 1). Asymptotic functions—the functional form most commonly assumed to characterize ethnographic and archaeological gain curves—performed poorly relative to sigmoidal functions for Batek foraging. One possibility is that gain curves for human foraging data derived from focal follows typically conform to asymptotic curves (20), whereas aggregated camp-level foraging data reflecting landscape-level bioenergetic constraints may evince more variation in gain curve shapes.

Table 1.

Best-performing model types for deterministic gain functions of 34 camp–resource set combinations listed according to resource type (camps 1, 4, 7, and 8 were excluded from this portion of the analysis)

Resource set	Linear	4PL	H3	M-M	AE	% Depleting
Meat	1	3	2	1	0	86
Tubers	3	2	0	2	0	57
Rattan	2	3	0	0	1	67
Total wild food	3	2	1	1	0	57
Total wild food and rattan	2	2	2	0	1	71

Numbers represent counts of models that fall into each category. Depleting refers to models that are not linear. AE, asymptotic exponential; H3, Holling Type III; M-M, Michaelis–Menton; 4PL, four-parameter logistic.

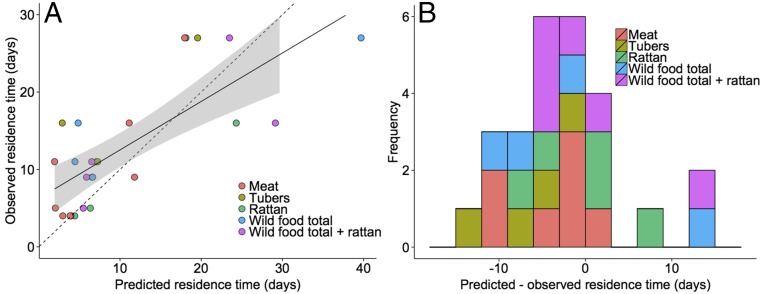
Previous studies of patch residence among foraging societies have implicitly or explicitly assumed diminishing marginal returns and tested an indirect correlate of the marginal value theorem, which states that foragers should occupy more productive patches for longer periods of time (15–19). The fine-grained foraging data available for the Batek enables us to compare indirect tests of the marginal value theorem with direct tests using the gain curves established empirically from foraging data (Fig. 2). If the gain functions for the Batek were unknown, our results would suggest that Batek mobility patterns do not conform with the marginal value theorem, because camp productivity was not correlated with the length of camp occupation (r = − 0.25, P = 0.59, and df = 5 for “total wild food”; r = − 0.49, P = 0.25, and df = 5 for total wild food and rattan). When predictions of the marginal value theorem are generated using the empirical gain curves, however, observed camp occupation times are similar to those predicted by the model (Fig. 3). The data fall close to the 1:1 line (the expected relationship if the marginal value theorem was to perfectly predict camp residence time) plotted in Fig. 3A, which shows predicted vs. observed camp residence times. An ordinary least squares regression has a slope of 0.63 (R² = 0.56, P $<$ 0.001, n = 26).

Fig. 3.

(A) Predicted vs. observed camp residence time for camp–resource set combinations described by depleting functions. The regression line forced through the origin represents the one to one relationship predicted by the marginal value theorem. The marginal value theorem accounts for 56% (adjusted $R^2$) of the variance in Batek camp residence time. Gray shading indicates the 95% confidence interval. (B) Histogram of the differences between empirically observed camp residence times and those predicted based on the marginal value theorem. Each bar represents a camp–resource set combination best-described by a depleting deterministic function.

We also examined which resource sets produced the most accurate predicted camp residence times using the marginal value theorem. The resource set total wild food and rattan produced predicted camp residence times that were, on average, 0.4 d from observed residence times, an effect driven primarily by rattan (Fig. 3 and Table 2). The Batek generally stayed longer in patches than predicted by roughly 2 d (Fig. 3B).

Table 2.

The accuracy of the marginal value theorem for different resource sets relevant to Batek mobility decisions

Resource set	Mean difference (d)	SE
Meat	-3.5	1.7
Tubers	-6.7	2.4
Rattan	-0.5	2.9
Total wild food	-1.8	5.2
Total wild food and rattan	0.4	2.7

Means and SEs for predicted minus observed patch residence times are calculated across all camp–resource set combinations for which a predicted residence time could be generated.

Discussion

Here, we have established the proximate mechanisms that structure variability in the macroecological patterns of hunter-gatherer residential mobility (4, 5). As expected, central-place foraging in hunter-gatherers seems to be associated with diminishing marginal returns. Our results indicate that Batek residential mobility is associated with communal perceptions of declines in resource availability and that marginal rates of return at the times of camp departures were generally similar across patches.

These findings enable us to evaluate alternative hypotheses about the factors that influence collective movement decisions in hunter-gatherers. First, for example, nonsubsistence factors, such as religion or rituals, deaths, or a desire to visit others, are undoubtedly important, but these qualitative models make no a priori predictions about the patterning of camp residence times. Second, the accumulation of waste, which increases exposure to parasites and attracts predators, may also constrain the duration of camp occupation. This hypothesis predicts that the number of people in camp should be negatively associated with camp occupation time. However, these variables were uncorrelated for the Batek (r = 0.3, P = 0.36). Third, the Batek abandoned camps before resources in the surrounding areas were fully depleted. Taken together, our study supports the concept that diminishing marginal return rates are the primary driving factor behind hunter-gatherer residential mobility patterns.

Establishing an empirical connection between individual foraging and residential mobility in hunter-gatherers raises new questions about the social forces that enable group-level foraging efficiency to be maximized. Ethnographic evidence from our case study suggests several contributing factors. First, the Batek promote social norms that result in extensive cooperation and food sharing (21), resulting in common subsistence goals and mutual interdependence. Second, there is public knowledge about the foraging returns of other individuals and shared information about the locations of food sources. Third, collective camp movement decisions were not made by single individuals but instead, were made through a process of informal group discussion that involved most adults (21). We hypothesize that tensions between the economic goals of individuals, pair bonds, and kin groups, mediated through disagreement and eventual consensus, generate a self-correcting mechanism that maximizes group-level foraging efficiency.

Sex Egalitarianism and Hunter-Gatherer Mobility.

Women’s foraging for carbohydrates (often tubers) is thought to dictate hunter-gatherer camp movement decisions (1). Indeed, the Batek claimed that they generally move camps in response to tuber depletion (21). However, camps moved 6–7 d later than expected based on the tuber data (Table 2). These analyses thus reveal a subtle mismatch between what people said and what they did. Rattan performed far better than tubers in predicting camp residence times (Fig. 3B and Table 2). Men collected rattan, which was sold and converted to carbohydrates in the form of rice, thus creating a dynamic in which male carbohydrate contributions replaced those of women (i.e., rice consumption was inversely related to tuber consumption). The Batek case thus illustrates how access to agricultural carbohydrates could introduce elements of gender inequality into hunter-gatherer societies.

Resource Conservation in Small-Scale Societies.

The so-called “ecologically noble savage” debate revolves around whether small-scale societies intentionally practice resource conservation or whether it is an epiphenomenon of other goals, such as maximizing foraging efficiency (26–29). Despite explicit mention of how the marginal value theorem may explain the sustainability (or lack thereof) of harvesting practices, to date there have been few data to bear on the question of whether and how small-scale societies deplete resources.

To show resource conservation, it must be shown that individuals reduce “the level of resource use below what would be fitness-maximizing in the short term in exchange for long-term sustainable benefits in the future” (28) and that there is intent on the part of the actors (27). Our data indicate that the Batek departed patches before completely depleting the resource base (Fig. 2) in a manner consistent with the maximization of foraging efficiency. Although the Batek were fully aware that they could reserve or store resources for future use by leaving a patch before its resources were exhausted, interviews in 1975 and 1976 confirmed that residential moves were primarily motivated by resource depletion: “Eventually, after camp members used up the nearby resources of food and rattan, talk would turn to the possibility of moving on” (21).

These findings strongly suggest that Batek camp movements are inconsistent with resource conservation. However, certain Batek foraging practices and norms may qualify. In 1975, the Batek of the Upper Lebir River deliberately reserved some patches of resources for future use. They avoided exploiting some areas in the headwaters of side streams of the main river with the intention of retreating into them during the annual floods in December and January, which they did. They also harvested particular resources in a sustainable manner. For example, they replanted the growing tip of a yam vine if tubers were too immature to eat and made mental notes about the location, so that they could harvest them at a future time.

If the logic of the marginal value theorem applies broadly to group foraging decisions, it is important to consider how the subsistence behaviors of small-scale societies will respond to habitat degradation under this model. Under conditions of severe habitat degradation, foragers should make decisions based on profitability rather than abundance of prey, and market pressures (i.e., high profits for forest products) may make it optimal to engage in behaviors that conflict with conservation goals (27). The result would be extreme depletion of animal and plant resources that could otherwise be sustainably harvested.

Ethnoarchaeology.

Empirical support for the predictions of the marginal value theorem in an ethnographic context bolsters the explanatory and predictive potential of human behavioral ecology in archaeological reconstructions (30–34). The key constraint identified here—that rapid resource depletion prompts frequent moves (every 1–3 wk) across short distances—has direct implications for archaeological inference. The marginal value theorem fundamentally concerns time allocation, and the time spent at a given location influences activity patterns and thus, the nature and quantity of archaeological remains (35). For example, tropical rainforests are notoriously poor taphonomic environments for preservation (36), but our study also suggests that reduced material accumulation is a direct result of short site occupation in tropical rainforests because of rapidly declining marginal returns.

Conclusion

The marginal value theorem has been influential and widely supported in studies of nonhuman organisms. This study shows that aggregated individual foraging behaviors in a small-scale nomadic society can result in optimized collective action. By investigating the factors affecting residential mobility at a proximate level, our study offers a framework for scaling up fine-scale foraging behavior to broad-scale macroecological mobility patterns.

SI Text

Ethnohistory of the Batek.

The Batek are categorized as Semang, a Malay exonym and subset of Orang Asli with differentiating phenotypic traits, such as short stature, curly hair, and dark skin (37). The Batek are also linguistically distinct, speaking a language in the Aslian branch of the Austroasiatic (Mon-Khmer) language family (38). Available evidence suggests that Semang peoples are united by a deep ancestry, dating to the initial dispersal of modern humans into Peninsular Malaysia $>$50 kya (39–41). Semang peoples have retained a foraging lifeway that has included trade with agricultural peoples for thousands of years (42).

Foraging Theory: Assumptions, Data, and Models.

In this study, we use the framework of optimal foraging theory to analyze Batek mobility patterns. We assume that movement is costly in terms of both time and energy and that natural selection has favored behavioral variants that increase the efficiency of foraging. We treated the surrounding lowland dipterocarp rainforest as the habitat and the 11 campsites as patches that were consecutively occupied. This movement corresponds to residential (vs. logistical) mobility (5, 31). The various food and trade items (resource sets) found within the vicinity of these camps are considered as subpatches that were exploited on logistical forays. To our knowledge, there is no study that quantifies the gain function for a foraging human (or group of humans) to test whether patches are depleted and when patch depression occurs, what shape the function takes (15, 43, 44). The absence of such studies is problematic because tests of the marginal value theorem (MVT) should initially verify that the hypothesized gain function matches empirical reality (10). Our dataset enables us to evaluate how the gain functions of human foragers vary under naturalistic field circumstances. Environmental or other circumstances may create a situation where this is not the case. For the purposes of this study, we assume that Batek foragers have knowledge of the environmental average return rate for the resource sets examined and furthermore, that they know that gain functions within a patch are marginally decreasing.

Studies on humans that are consistent with the MVT include those by Winterhalder (11), Hames (12), and O’Connell and Hawkes (13, 14). Smith (15) writes that the “massive data requirements of the MVT … make direct tests of its predictions so elusive.” Associations between the time spent in patches and the return rates of those patches have been marshalled as support for the MVT. Smith’s (15) study of the Inuit found no evidence for short-term patch depletion. He did find, however, that hunters remained longer in patches with higher profitability (kilocalories per hour). This finding conforms with predictions from the MVT given the following assumptions: (i) alternative patches evince smoothly decelerating return curves, (ii) the return curves run parallel (i.e., they do not cross), and (iii) all patch types are equally “available” (no external constraints that bias against particular patches) (15). Smith (15) acknowledges, however, that this does not make up a rigorous test of the MVT; the gain function was unknown in his case, because the data were “derived from reported rather than observed hunts” (15). Smith (15) further writes that, for a direct test of the MVT, “one would need detailed data on movement patterns, time budgets, and return rates sufficient to estimate both marginal capture rates at specific locales and concurrent average return rates at large.”

Applying the MVT.

When gain functions are not empirically measured, application of the MVT can lead to potential circularities. In particular, there may be a lack of independence between marginal gain rates within patches and the average return for all patches, including travel (10, 15). This problem can emerge when each patch type has characteristic gain functions and/or when the gain functions are assumed rather than empirically measured by the researcher. When patch and environmental averages are calculated from the gain function, the MVT can be tested only implicitly. Our dataset avoids this problem, because there is no necessary relationship between the gain function and the environmental averages. In other words, knowledge of the shape of the gain function does not predict the patch return rate. Camp residence times are predicted from the time at which the derivative of the gain functions (deterministic models fitted to the empirical data) declines to the environmental average.

One critique of the MVT is more specific to human behavioral ecology because of the targeted nature of human foraging. Several workers have noted that naturalistic observations of foraging behavior may result in gain curves that are skewed toward “good days,” because foragers may respond to fluctuations in resource availability by not foraging on a particular day or avoiding particular patch types (15, 43, 44). These considerations have led to the suggestion that “naturalistic observations of foraging behavior will not provide an accurate measure of within patch gain functions” (44). To reduce such bias, ethnographers can ask foragers to alter foraging behavior (45). In the Batek case, we are applying the MVT at the level of the camp over the span of days to weeks, and the vast majority of items in the resource sets acquired by the Batek can hypothetically be exploited on any given day. It is important to note that a zero return on a day could result from failed search or no search at all. In either case, we assume that the resource had low availability on that day. Based on these considerations, we believe that the shape of the gain curves should be essentially unbiased.

Calculating the Energy Content of Foraging Returns.

Endicott and Endicott (21) wrote that “the recorded weights of animals are the whole, unbutchered weights, and the weights of vegetable foods are the raw, unprocessed weights.” To calculate the energetic content of these foods, the raw weights must first be modified to account for the fact that some of the food is inedible and that, for game, tissues vary in energetic content.

For game animals, converting raw weights to calories is somewhat complex and therefore, requires explanation. Fig. S2 presents a visual schematic of these calculations, which roughly follow those in the work by Hill et al. (46). The total weight of the animal is comprised of the inedible and edible portions ($I$ and $E$, respectively). The edibility factor ($X$) varies between animals (e.g., turtles have lower edibility because of the shell). This relationship can be expressed as follows:

$$E=XT$$ [S1]

and

$$I=(1-X)T.$$ [S2]

Some comments on the edibility of animal tissue are warranted. In many hunter-gatherer societies, virtually all of the edible carcass is consumed (47–49), although many modelers have assumed that muscle tissue was the primary animal tissue consumed by preagricultural humans (50–52). Studies have estimated the percentage of edible carcass as between 50 and 75% of the live animal weight (46, 53–55). The field measurements by Hill et al. (46) showed the edible portion of various game items to be between 68.9 and 88.1%, arriving at the value of 75% for their study. Hart (56) calculated the edible portion of Mbuti game items as >80%. Bone is generally inedible, but fat from within the matrix of bone can be extracted by boiling, and indeed, the Batek sometimes boiled bones. In this study, edibility as a percentage of raw weight ($X$) was measured or based on values in the literature. When possible, we used data from the Endicotts’ field study to calculate edibility and the proportional weights of component parts of the raw measured weights. Otherwise we typically referred to the study by Kuchikura (57) of Semaq Beri in Peninsular Malaysia for estimates. Kuchikura’s (57) estimates were either directly measured in the field or derived from published food tables.

After edibility is calculated, it is possible to calculate the corrected weights of the carcass and organs. We follow Hill et al. (46) in assuming that, of the edible portion, 20% is organ, and 80% is carcass:

$$C=0.8E$$ [S3]

and

$$O=0.2E.$$ [S4]

It is crucial to note that the raw weights ($W$) of animals killed by the Batek during the study sometimes did not include organ meat or the tail (in the case of monkeys), which was often removed and consumed in the forest before weighing. As noted by Endicott and Endicott (21), “[i]f hunters made a kill early in the day, they might butcher and cook the animal and eat a bit of the meat before returning to camp with the remaining meat tied up in leaf bundles. Otherwise, they brought the unbutchered animal back to camp.” Thus, the total weight of the animal ($T$) is not equivalent to the raw weight ($W$) measured by the Endicotts. Instead, $W$ is a sum of the boxes highlighted in green in Fig. S1: the inedible portion ($I$) and the carcass ($C$). Thus, $W=I+C$. Given $W$ and $X$, it is possible to use Eqs. S1–S4 to solve for the other variables; in particular, writing $E$ in terms of $W$ yields

$$E=W/(1/X-0.2).$$ [S5]

Nutritional calculations were based on the values for the edible carcass and organs ($C$ and $O$) only. Following the work by Hill et al. (46), the caloric value of internal organs was calculated at 138 kcal/100 g: this value is the mean of brain, heart, intestines, kidneys, liver, lungs, spleen, and tongue from the work by Leung (58). For the edible carcass, caloric values were estimated using several sources, usually Kuchikura (57) and Hill et al. (46) and occasionally, United States Department of Agriculture-based estimates. We generally preferred Kuchikura (57) as a source, because he provided estimates for specific East Asian foods. It seems that the caloric values of game items were approximated with domestic beef values in the works by both Kuchikura (57) and Hill et al. (46), despite the fact that domestic beef clearly differs from wild game in many respects (53). In the absence of data on wild game because of ethical and logistical constraints, however, we use these values and note that these estimates are similar to those of lean beef. Small animals ($<$10 kg) generally have body fat percentages below 5% (59), and therefore, 5% lean beef should be a reasonable approximation. The Batek do not hunt animals with body sizes $>$12 kg (the siamang is the largest). The caloric values of nonmeat food items were calculated in a more simple fashion. For tubers, vegetable items, fruit, fish, and trade-obtained foods, raw weights were corrected for edibility using a single multiplicative factor and subsequently converted to calories. As an example, unprocessed tubers are covered in dirt and may be toxic. Field notes indicate that after processing (cleaning, peeling, and slicing), 92.6% of the raw weight of takop tubers is edible. Similarly, the highly toxic gadong tuber is subject to complex processing, and only 63.8% of the raw weight is edible. For some food, edibility is virtually 100% (e.g., flour, rice, sugar, and oil).

Residential Mobility: Travel Times and the Costs of Search and Travel.

Data on how Batek moved between residential camps were extracted from the Endicotts’ field notes. The moves occurred between the late morning hours and the early afternoon hours. The small thatch-roofed huts were not transported, and only a few belongings were carried, including sleeping mats, personal possessions in back baskets, bush knives, blowpipes and digging sticks, and perhaps, a little food (usually rice or slices of the gadong tuber). Camps were packed in the morning, a process that typically took about a half an hour. On arrival at a new camp, it took $\sim$3 h for a couple to set up their hut and fireplace. People were busy getting organized in the afternoon and evening after a move. Batek looked for signs of animals (e.g., bamboo rats) and edible plants as they walked along, either stopping to forage or making a point to come back and do it later. When they reached a new camp, some of the men might make a point of hunting in the vicinity right away on the theory that there might be game in an undisturbed location, game that would move away over the next few days because of the presence of people. Other men collected the poles and logs needed for the framework and bamboo for the floors of the huts, whereas the women gathered the palm leaves for thatch. Sometimes women immediately dug up any tubers in the vicinity of the new camp.

As noted earlier, the 93-d study by the Endicotts occurred across three seasons: fall, winter, and spring. During this time, the Batek moved camp 11 times, averaging 8.2 d (SD = 6.6) at each campsite (Table S1). The three field seasons were not continuous, because the Endicotts left the field during the rainy season (December and January) and again during the early spring (March). Therefore, the travel times to camps 8 and 10 are not known. We estimated these missing data by computing the mean travel time to the remaining nine camps (5.5 h) and using this value as an estimate for travel time to camps 8 and 10.

We used Google Earth to measure the distances traveled per residential move. We used two methods. First, we measured the linear distance between the camps. Second, we measured the distance by tracing the most efficient path along the river system. We traced the routes manually by assuming that the Batek moved in a straight line to the nearest river and on leaving the river near the new camp, moved in a straight line from the river to the camp. This approach is based on the Endicotts’ field notes on how the Batek traveled to each camp. Most of the moves during the Endicotts’ study consisted of foot travel. Some foot travel occurred along streams, where movement was faster because of more constant elevation and the lack of forest. Tables S2 and S3 summarize the circumstances of Batek movement between camps and the resulting travel times subsequently used in our analyses.

Travel times for the Batek were no more than a few hours. It is possible that the most relevant costs of camp movement may not be primarily with travel per se but may be with camp breakdown and setup and their attendant opportunity cost on foraging. One of the common assumptions of patch models in foraging theory is that searching and traveling are mutually exclusive. However, in the case of the Batek (and we suspect, most human foragers), moving does not entirely halt foraging, but foraging becomes less systematic (see description above).

We can use data from moves for which the distance and travel time are known to arrive at a general picture of travel costs for the Batek. The distance from camp 2 to camp 3 was 0.59 km (the shortest distance moved in the dataset) and took roughly 1 h, giving a travel speed of 1.69 km/h. The distance from camp 3 to camp 4 was 9.89 km in a straight line and 14.53 km via river. The latter is the most accurate quantity for our purposes. Via a trader’s outboard motorboat, this trip took 2 h, resulting in a travel speed of 7.26 km/h. If the Batek walked this same route along the river and took 6 h, their travel speed was 2.42 km/h. If they traveled in a more or less straight line to camp 4, their speed was 1.65 km/h. Estimates for travel speed based on these considerations are presented in Table S2. River travel via a boat with an outboard motor is, therefore, approximately three times more efficient than walking and presumably even more so than travel via river upstream on a bamboo raft.

Using these travel speeds as a guide, it is clear that most residential moves took little time, certainly no more than 6–7 h of travel time itself. From an optimal foraging perspective, for camp occupancies ranging from 3 to 24 d, altering the $x$ intercept by several hours will make little difference to the perceived costs of moving and therefore, the marginal value of returns within a given patch. It may be more realistic to assume that the true cost of travel time is 1 d, regardless of distance, meaning that the Batek lost 1 d of foraging by moving, regardless of how far the move was. Regardless, because we have detailed data at a short timescale, we used the known values for travel time plus 3.5 h for camp breakdown and setup as the true travel times between the eight patches examined here. With these modifications, the resulting median travel time is 0.23 d [$\pm$0.06 d (SD), range = 0.16–0.4 d].

The relative energetic costs of travel and search must also be considered, because they impact the shape of the net gain function. In this paper, we examine the gross gain function rather than the net gain function (i.e., gross gain subtracted by energetic costs of searching and traveling). However, under particular circumstances, the expectations of the MVT converge for the gross and net gain functions. As noted by Stephens and Krebs (10), “if search within a patch (including pursuit and handling) costs the same as travel (e.g., the predator walks both when traveling and searching), then incorporating energy costs does not alter the MVT’s patch residence time predictions.” Here, we assume that the energetic costs of travel and search are the same for the Batek, because both involve walking and few items are carried. As a result, the predictions of the MVT using the gross and net gain curves are identical.