Deactivation kinetics of acid-sensing ion channel 1a are strongly pH-sensitive

Significance

The response from every type of neurotransmitter-gated ion channel (NGIC) decays within a proscribed time when its agonist is removed. NGICs that decay faster are more involved in higher frequency signals, whereas slower channels promote cell excitability and plasticity. Here, we find that certain acid-sensing ion channels have the flexibility to convey either very rapid or quite slow signals, depending on the ambient pH over a very narrow range. This ability may allow these receptors to aid in synaptic plasticity, and hence learning and memory.

Abstract

Acid-sensing ion channels (ASICs) are trimeric cation-selective ion channels activated by protons in the physiological range. Recent reports have revealed that postsynaptically localized ASICs contribute to the excitatory postsynaptic current by responding to the transient acidification of the synaptic cleft that accompanies neurotransmission. In response to such brief acidic transients, both recombinant and native ASICs show extremely rapid deactivation in outside-out patches when jumping from a pH 5 stimulus to a single resting pH of 8. Given that the resting pH of the synaptic cleft is highly dynamic and depends on recent synaptic activity, we explored the kinetics of ASIC1a and 1a/2a heteromers to such brief pH transients over a wider [H⁺] range to approximate neuronal conditions better. Surprisingly, the deactivation of ASICs was steeply dependent on the pH, spanning nearly three orders of magnitude from extremely fast (<1 ms) at pH 8 to very slow (>300 ms) at pH 7. This study provides an example of a ligand-gated ion channel whose deactivation is sensitive to agonist concentrations that do not directly activate the receptor. Kinetic simulations and further mutagenesis provide evidence that ASICs show such steeply agonist-dependent deactivation because of strong cooperativity in proton binding. This capacity to signal across such a large synaptically relevant bandwidth enhances the response to small-amplitude acidifications likely to occur at the cleft and may provide ASICs with the ability to shape activity in response to the recent history of the synapse.

Neurotransmitter levels within the synaptic cleft rise and fall very rapidly, with clearance times generally on the order of a few hundred microseconds to 2 ms (1–3). However, the duration of responses from neurotransmitter-gated ion channels (NGICs) varies widely across several orders of magnitude depending on the receptors involved. For example, in certain regions, glutamatergic excitatory postsynaptic currents (EPSCs) decay with submillisecond time constants (4), but the EPSCs of GluN2D-containing NMDA receptors decay over roughly 200 ms (5, 6). Such differences in the decay or deactivation of NGIC responses can profoundly impact the window of synaptic excitability and integration (4, 7, 8). Control over NGIC kinetics is also a powerful force during development, where slower receptor subtypes tend to be used early on, broadening the window of plasticity during critical periods, and later give way to faster decaying subunits providing greater temporal precision (9–13). This trade-off between the window of integration on the one hand and temporal precision on the other persists in the mature brain. There, synapses host an NGIC compliment kinetically suited to their input patterns (14) but are also capable of dynamically shifting between the priorities of integration and precision (8). Unsurprisingly then, influencing the deactivation kinetics of specific NGIC subtypes using allosteric modulators is a promising therapeutic objective (15–17).

Acid-sensing ion channels (ASICs) have recently been shown to act as NGICs (18, 19). In both the lateral amygdala (18) and the nucleus accumbens (19), the brief acidification of the synaptic cleft accompanying neurotransmission can activate postsynaptic ASICs that contribute to EPSCs. These ASIC EPSCs are carried by ASIC1a homomers and ASIC1a/2a heteromers (18, 19), both of which exhibit submillisecond deactivation kinetics in excised patches (20). The rapid deactivation combined with ASICs’ slow desensitization enables these channels to operate at high stimulus frequencies that desensitize most other NGICs (20). However, the synaptic cleft pH waveform is more complicated than the binary alkaline or acidic stimulation previously used. A pH drop of 0.2–0.6 pH units or greater can accompany single-release events, but the synaptic cleft pH may not return directly back to physiological pH (21–25). Rather, following brief stimulations, synaptic cleft pH “overshoots” the physiological range by 0.2 pH units or more and remains alkaline for several tens or hundreds of milliseconds (18, 26–28). Cleft pH can also remain persistently acidic during prolonged bouts of activity, during stimulation, or during a variety of pathological conditions such as spreading depression or epileptic activity (27, 29, 30). Therefore, the interevent synaptic cleft pH (i.e., the concentration of ASIC agonist) can vary between alkaline, neutral, and acidic depending on prior synaptic activity. Thus, although synaptic structure, proton buffering, and clearance undoubtedly influence ASIC EPSCs (2, 25, 31), characterizing the intrinsic channel response to such brief and variable stimuli is an integral component in understanding neurotransmission through ASICs.

Here, we set out to investigate how ASIC deactivation kinetics may change in response to stimuli that better approximate these dynamics of synaptic pH changes. We find that the kinetics of recombinant ASIC1a can vary over approximately three orders of magnitude depending on the poststimulus pH. This surprising effect is conserved in rat ASIC1a, human ASIC1a (hASIC1a), and chicken ASIC1a (cASIC1a), but is not seen in rat ASIC1a/2a heteromers. From a biophysical perspective, our findings are unexpected because, classically, deactivation kinetics are independent of agonist concentration (32–36). In addition, these findings are physiologically intriguing because they indicate that synaptic ASIC1a could shift between very fast AMPA-like kinetics and slower NMDA-like kinetics depending on the recent history of the synapse.

Results

The Deactivation Kinetics of ASIC1a Are Strongly Dependent on Agonist Concentration.

The deactivation kinetics of ASIC1a to brief applications of acidic solution were recently examined by jumping ASIC1a-containing outside-out patches from a baseline pH of 8.0, followed by a jump to pH 5.0 for 1 ms and then a return to pH 8.0 (20). Under such conditions, ASIC1a deactivation kinetics were surprisingly brief, given their reported single-channel open times (37) and high apparent affinity for protons [pH evoking half the maximal response (pH₅₀) of 6.4–6.6, EC₅₀ of 400–250 nM (38–40)]. However, as mentioned above, during intense neuronal activity or stimulation, the interevent synaptic cleft pH does not toggle between neutral and acidic pH in a binary fashion. Rather, in the milliseconds following stimulation, the synaptic cleft pH shifts toward the alkaline pH of 7.6 or greater for tens or hundreds of milliseconds (18, 26–28, 30). Further, during prolonged activity, the cleft pH can drift into the acidic domain (27, 29, 30). We therefore set out to examine the kinetics of ASIC deactivation to stimuli that might better approximate the dynamics of synaptic cleft pH changes.

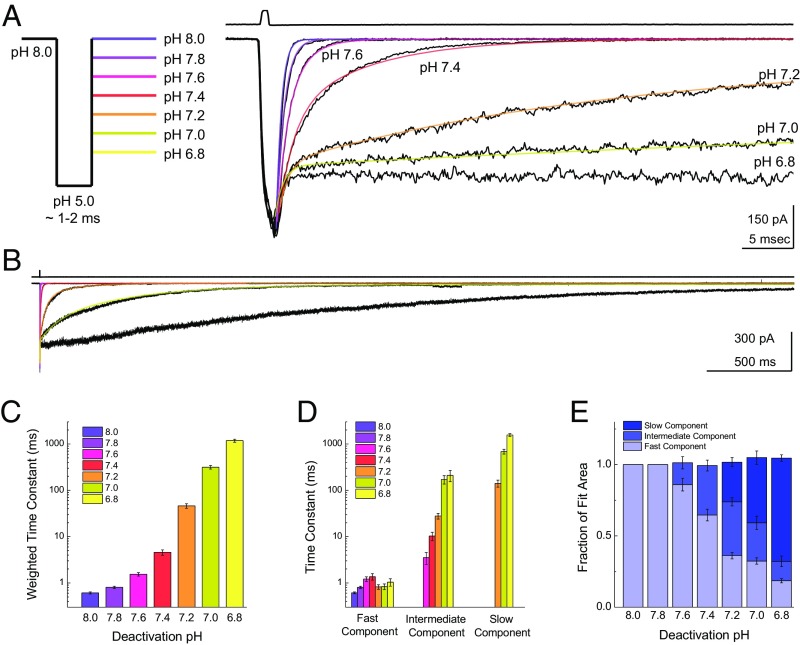
However, probing deactivation kinetics at more acidic pHs is hampered by steady-state inactivation (20, 38). For example, in a standard theta-tube application experiment, a resting pH of 7.2 produces extensive steady-state inactivation, making responses in outside-out patches small and difficult to evaluate. To circumvent this complication, we combined a triple-barrel perfusion tool with a “through-jump” approach (41, 42), where outside-out patches were first exposed to pH 8.0 to populate the apo state and then rapidly jumped through a pH 5.0 solution, residing there for ∼1–2 ms, before arriving at a final pH ranging from 8.0 to 6.8 (Fig. 1A, Left). This approach enables measurements of ASIC kinetics over a much wider range of stimuli without complications arising from steady-state inactivation. At the end of each patch experiment, an open tip current was measured to check the fidelity of solution exchange (Fig. 1A, Right Upper). As expected from previous work, a final or destination pH of 8.0 yielded extremely fast deactivation kinetics and was well fit by a single exponential function (0.61 ± 0.03 ms, n =15; Fig. 1A, purple fit). Interestingly, the deactivation kinetics got notably slower with increasingly acidic pHs of 7.8, 7.6, and 7.4 (pH 7.8: 0.81 ± 0.05 ms, n = 22; pH 7.6: 1.5 ± 0.1 ms, n = 14; pH 7.4: 4.6 ± 0.6 ms, n = 20; Fig. 1A, purple and red fits). Furthermore, a single exponential function was no longer sufficient to describe the data, with double- and even triple-exponential functions becoming necessary (SI Methods). The most striking observations occurred at final pH values of 7.2, 7.0, and 6.8 with deactivation kinetics in the tens or hundreds of milliseconds (pH 7.2: 46 ± 5 ms, n = 19; pH 7.0: 320 ± 30 ms, n = 21; pH 6.8: 1,180 ± 90 ms, n = 13; Fig. 1 A and B, orange and yellow fits). These decays were fit to either double- or triple-exponential functions (Fig. 1 C and D). As a general trend, more acidic pH values caused the time constants of the intermediate and slow components to increase in duration and the areas of these slower components to increase in amplitude (Fig. 1 D and E). Strikingly, the weighted time constants for these deactivation kinetics span roughly three orders of magnitude from 0.61 ± 0.03 ms at pH 8.0 to 320 ± 30 ms at pH 7.0 (Fig. 1C). This observation is noteworthy for two reasons. First, from a physiological perspective, it suggests that synaptic ASIC kinetics may reflect the recent synaptic history as encoded by cleft pH. This mechanism has the potential to exert a powerful influence on neuronal signaling, and is particularly appealing in light of ASIC1a’s involvement in plasticity-related phenotypes (18, 19, 43–45). Second, from an ion channel biophysics perspective, deactivation kinetics are generally assumed to be driven by the channel shut rate, open rate, and ligand-unbinding rates (35, 36, 46–49), as well as the rate of desensitization in some cases (48, 49). None of the above parameters are classically dependent on the agonist concentration, although the deactivation of ASIC1a clearly is.

Fig. 1.

ASIC1a deactivation is strongly pH-dependent. (A, Left) Schematic of the pH application protocol. Patches are first incubated in the pH 8 solution stream for an extended period (>10 s), followed by a rapid jump through the pH 5 solution stream for 1–2 ms, and ending in the final solution stream with a pH between 8 and 6.8. (A, Right) Responses from a patch containing rat ASIC1a to the triple-jump protocol. The deactivation following the pH 5 jump is markedly slower in more acidic pHs. The upper trace is the solution exchange current from this patch, and the solid colored lines denote single-, double-, and triple-exponential fits to the data. (B) Same patch as in A (Right) but on an expanded time scale to show the full decay at more acidic pHs. (C) Summary of weighted deactivation time constants across patches at each pH. (D) Time constants for fast, intermediate, and slow components of the exponential fits across patches at each pH. (E) Summary of the fit area for the slow, intermediate, and fast components across patches at each pH. Each data point is from between 13 and 22 separate patches, and the error bars show SEM.

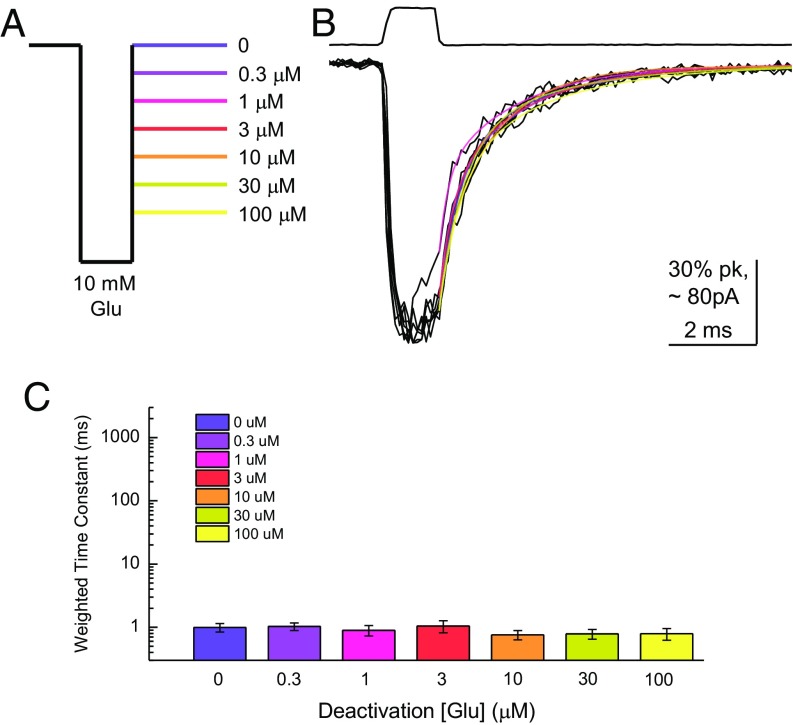
To substantiate this point, we performed an analogous experiment on AMPA receptors using a range of glutamate concentrations in lieu of pH. Patches containing homomeric GluA2(Q) were jumped from glutamate-free saline to 10 mM glutamate for 1–2 ms and then into a third solution containing either no glutamate or subsaturating glutamate from 0.3 to 100 μM (Fig. 2A). As expected of a ligand-gated ion channel, GluA2 deactivation kinetics were completely unaffected by agonist concentrations that are able to either desensitize or, in the case of 100 μM glutamate, directly activate the channel (P = 0.86, no glutamate versus 100 μM glutamate; Fig. 2 B and C). To enable direct comparison of ASIC1a and GluA2 data, as well as subsequent experiments, we calculated the “kinetic span” of these receptors as a ratio of the weighted time constants at the end points of the tested range (SI Methods). For ASIC1a, the kinetics span, or the ratio of deactivation time constants at pH 7 divided by pH 8, was 520 ± 60 (n = 15). However, a similar ratio for GluA2, comparing 0 mM with 100 μM, was 1.1 ± 0.1 (n = 4), which is substantially different from ASIC1a (P = 0.0002). Thus, the deactivation of ASIC1a is steeply dependent on the agonist concentration (i.e., pH). This example is, to our knowledge, the only example of a ligand-gated ion channel with such behavior.

Fig. 2.

AMPA receptor (AMPAR) deactivation is insensitive to agonist concentration. (A) Schematic of the glutamate application protocol. (B) Responses from GluA2 AMPAR to the through-jump applications depicted in A. The upper trace is the solution exchange current from this patch. The colored lines show the double-exponential fits. (C) Deactivation time constants at various glutamate concentrations from four to six separate patches. Error bars show SEM.

Slow Kinetics at Acidic pHs Cannot Be Attributed to Direct Activation.

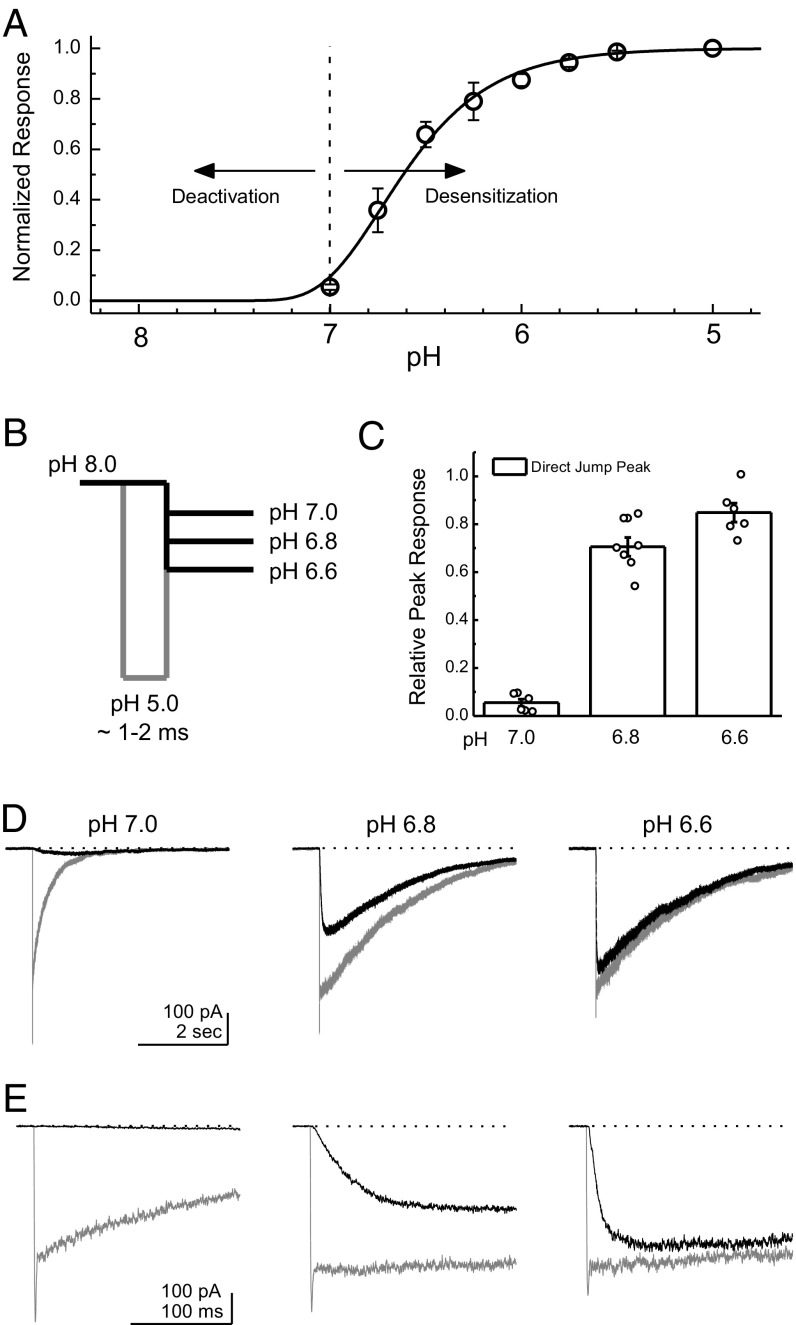
We next addressed whether these kinetics do, in fact, represent deactivation of the receptor and not just direct activation and desensitization. This issue is particularly important because the more acidic “destination” pHs such as pH 7.0 or pH 6.8 may be able to provoke some activation alone (38–40) (Fig. 3A). To test this possibility, we compared the peak response obtained within a single patch with either a through jump with a brief sojourn into pH 5.0 as in Fig. 1 or a direct jump straight from pH 8.0 into the more acidic pH values (Fig. 3B). Note that such a brief pH 5 application produces only a fraction of the total response seen during a prolonged application (56 ± 4% of a 300-ms pH 5 application, n = 22) because of the slower rise time of ASIC1a (10–90% rise time: 14 ± 2 ms, n = 22) (20). As seen in Fig. 3 C–E, a direct jump into pH 7.0 provoked a small and slow response in outside-out patches compared with the through jump passing first through pH 5.0 (6 ± 2% of through-jump peak response, n = 6; Fig. 3 B–E). However, jumps into pH 6.8 or pH 6.6 directly gave robust responses (pH 6.8: 70 ± 4%, n = 7; pH 6.6: 85 ± 4%, n = 6), precluding any attempt to delineate between deactivation and desensitization kinetics unambiguously at these pHs. We therefore confined our analysis to pH values of 7.0 and above. We repeated this check for all mutations and constructs throughout this study and similarly restricted our analysis to pHs that produced ∼6% or less direct activation.

Fig. 3.

Kinetics of deactivation are dissociable from desensitization. (A) pH response curve from ASIC1a illustrating that relaxations from the open state(s) are driven by deactivation at high pH values but are dominated by the desensitization process at lower pH values. Data are from four separate patches. (B) Schematic of the pH application protocol used to probe the deactivation/desensitization cutoff. Patches are first incubated in the pH 8 solution stream for an extended period (>25 s), followed by a triple jump through pH 5 for 1–2 ms to a more acidic pH of 7.0, pH 6.8, or pH 6.6 (gray lines) or a direct jump straight from pH 8 into the more acidic pH values (black lines). (C) Summary of the relative peak responses of the direct jump versus through jump at each pH value. Data are from six or seven separate patches, with individual patches shown as circles. (D) Example responses to a direct jump (black traces) and a triple jump (gray traces) at pH 7 (Left), pH 6.8 (Center), or pH 6.6 (Right) in the same patch. (E) Same data as in D but on an expanded time scale to observe the peak response. Error bars show SEM.

Deactivation Kinetics Can Be Modulated by Calcium.

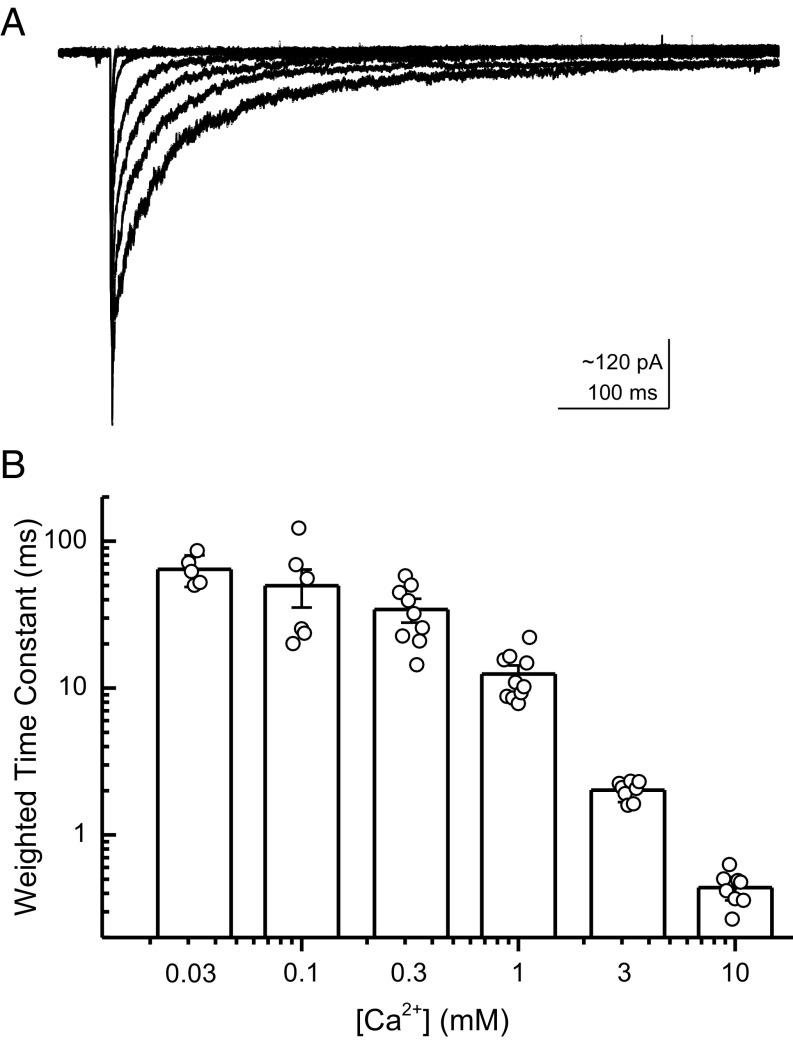
Calcium ions very likely bind to a subset of ASIC’s proton sensors (25), possibly representing the closest thing ASICs have to a true competitive antagonist. Consequently, many aspects of ASIC function are sensitive to external calcium concentration, including the activation and steady-state inhibition curves and peak response amplitude (38). Interestingly, the extracellular Ca²⁺ concentration changes during synaptic activity (38). Plasma membrane Ca²⁺-ATPases may increase the synaptic cleft Ca²⁺ concentration while simultaneously alkalinizing the cleft by exchanging extracellular (synaptic) protons for cytosolic Ca²⁺ (28). Moreover, prolonged synaptic activity increases extracellular lactate, which can promote ASIC responses by chelating Ca²⁺ ions (50). These considerations prompted an investigation of how external Ca²⁺ may modulate proton sensitive deactivation kinetics. To do this investigating, the triple–through-jump protocol was repeated (Fig. 1A), but in lieu of changes in pH in the third solution, pH was held constant at 7.3 and the external calcium concentration was varied from 0.03 to 10 mM (Fig. 4A). As expected, if calcium ions compete with protons for binding sites, increasing calcium concentration accelerated deactivation kinetics and lowering calcium slowed kinetics (Fig. 4 A and B). Specifically, at 10 mM external Ca²⁺, the deactivation time constant was 0.44 ± 0.04 ms (n = 8), but it was slowed considerably to 64 ± 7 ms (n = 5, P = 0.0013) at 0.03 mM external Ca²⁺. Therefore, external Ca²⁺ concentration can also modulate ASIC1a deactivation.

Fig. 4.

External Ca²⁺ accelerates deactivation kinetics. (A) ASIC1a responses jumping from pH 8 to pH 5 (both 1 mM Ca²⁺) to pH 7.3 in various Ca²⁺ concentrations. (B) Summary of deactivation kinetics at various external Ca²⁺ concentrations across five to 11 patches. Error bars show SEM, and circles show individual patch values.

Changes in Deactivation Kinetics Are Not Accompanied by Changes in Selectivity.

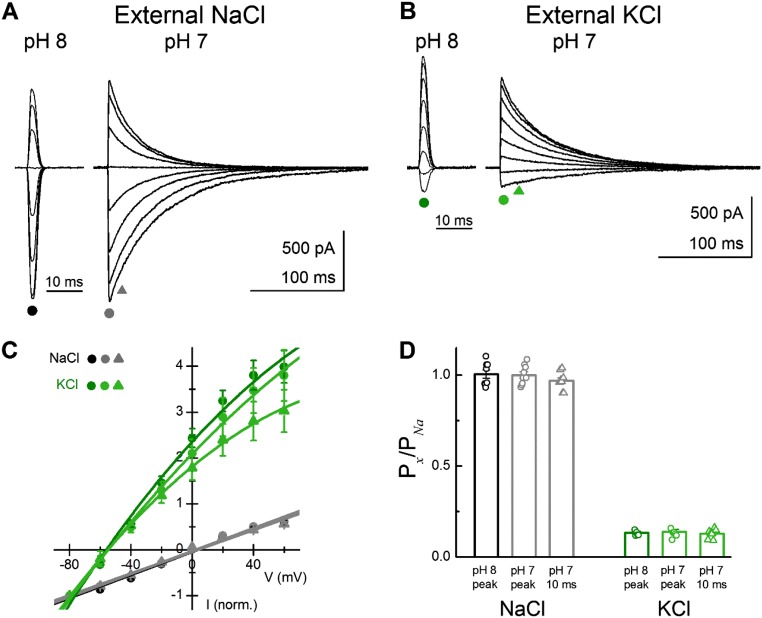
ASIC1a is Na⁺-selective under normal conditions but can populate nonselective open states at neutral pH in the presence of modulatory toxins (51). This observation indicates that ASIC1a has the capacity for multiple open states of differing selectivity. In the previous deactivation experiments, we observed very distinct fast and slow kinetic components (Figs. 1 and 3). Because the lifetime of such states is a direct reflection of their energetic stability, and hence their underlying structure (52), we hypothesized that such different kinetic lifetimes may also be so structurally distinct as to exhibit separate ion selectivities. To test this possibility, we performed bi-ionic reversal potential measurements of deactivation responses at either pH 8 or pH 7 in both external Na⁺ and K⁺ while using intracellular Na⁺. If there was a sizeable change in permeability between the open states underlying the rapid initial decay and the open states underlying the slower deactivation to more acidic pHs, one would expect a time-dependent change in ion selectivity, and therefore a change in reversal potential measured between the peak and a few milliseconds after. To obtain large responses, experiments were performed on cASIC1a, which has more robust peak responses and also displays pH-dependent deactivation (discussed below). However, we did not observe any change in Na⁺ or K⁺ selectivity when using either pH 8 or pH 7 for deactivation. Specifically, K⁺ reversal potentials were −51 ± 1 mV (n = 6), −51 ± 2 mV (n = 7), and −53 ± 2 mV (n = 7) for pH 8 responses, pH 7 peak responses, and the 10-ms postpeak response in pH 7, respectively (P = 0.56 comparing external K⁺ reversal potentials at pH 8 and the 10-ms postpeak response at pH 7; Fig. S1 A–C). The corresponding relative permeabilities of K⁺ compared with Na⁺ (P_K⁺/P_Na⁺) were 0.13 ± 0.01 (n = 6), 0.14 ± 0.01 (n = 7), and 0.13 ± 0.01 (n = 7) for pH 8 peak responses, pH 7 peak responses, and 10-ms post-pH 7 peak responses, respectively (Fig. S1D and SI Methods). Therefore, we detected no change in the selectivity of the open states underlying the rapid or slow deactivation. Thus, the structural differences contributing to the different stability of these open states likely occur above the level of the pore.

Fig. S1.

Cation selectivity is unchanged between fast and slow deactivations. (A) Sample triple-jump response in external Na⁺ at both pH 8 and pH 7. (B) Same patch as in A, but with external K⁺. (C) Summary of normalized current-voltage plot across patches in both external NaCl (black circles, pH 8; gray circles, pH 7; gray triangles, 10 ms after pH 7 peak) or KCl (green circles, pH 8; light green circles, pH 7; light green triangles, 10 ms after pH 7 peak). (D) Summary of calculated relative permeability, compared with internal Na⁺ at various pHs and application times across patches and with individual patches shown as circles or triangles. Na⁺ selectivity is retained in open states populating both fast and slow kinetics. Data were collected from six to nine separate patches. Error bars show SEM.

The pH Sensitive Deactivation Is Unique to ASIC1a.

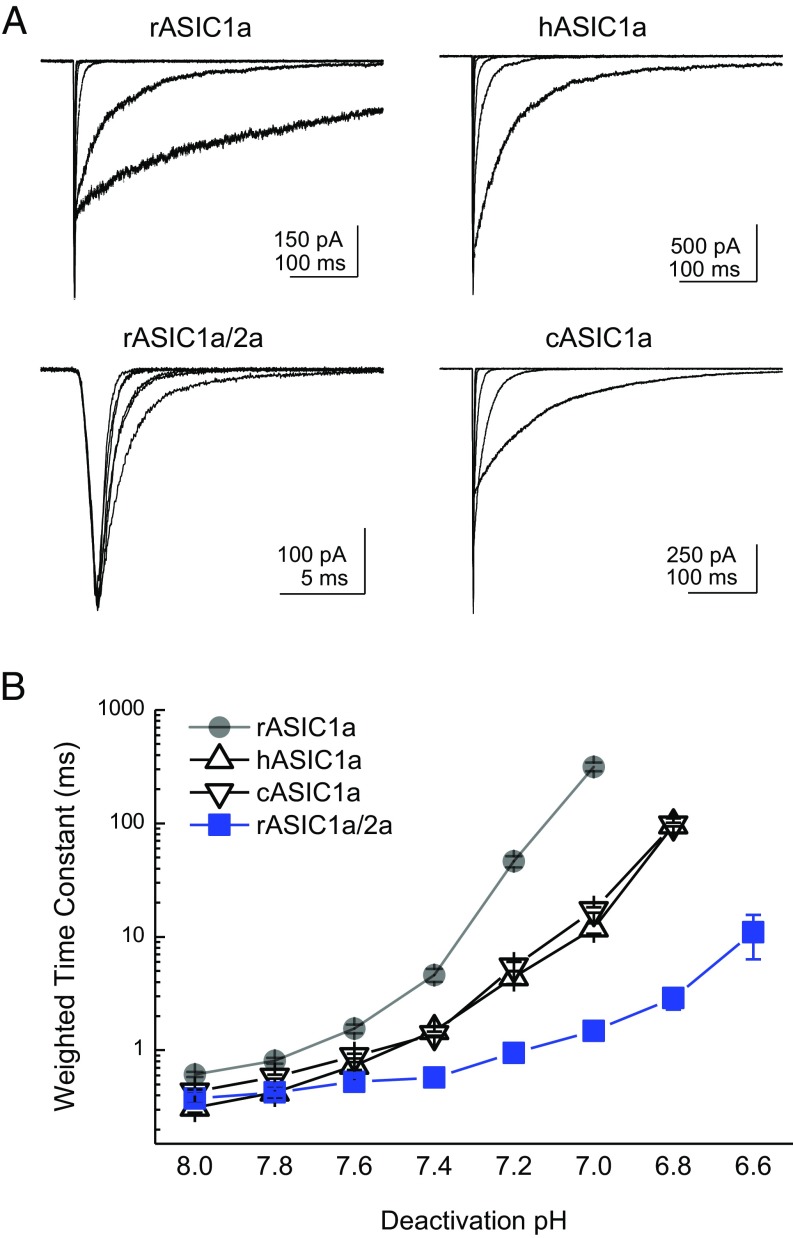
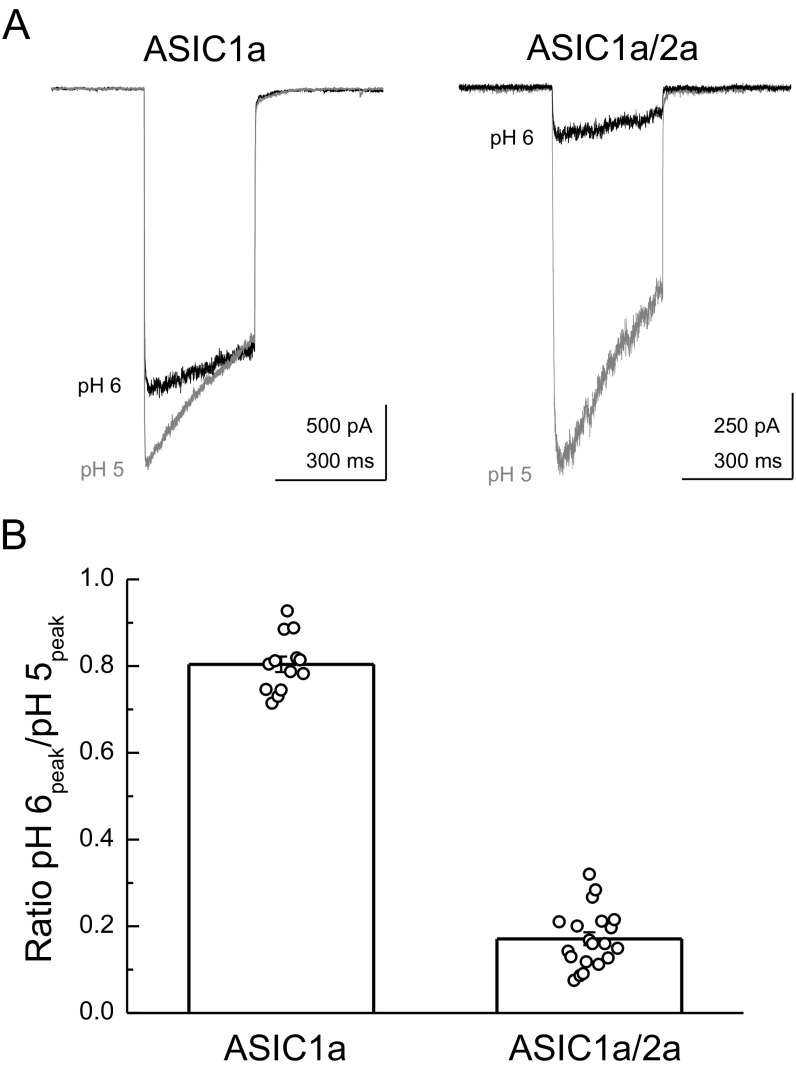
Given the striking magnitude of pH modulation of deactivation, we next addressed if this pH modulation was a general property of other ASICs found to contribute to EPSCs (18, 19). The enormous range of deactivation kinetics was also observed in both hASIC1a and cASIC1a (Fig. 5). Specifically, hASIC1a deactivation kinetics at pH 8.0 were 0.31 ± 0.03 ms (n = 5), but slowed to 100 ± 10 ms (n = 5) at pH 6.8, representing a kinetic span of 240 ± 40 (n = 5). Similarly, cASIC1a deactivation kinetics spanned a range of more than two orders of magnitude, being 0.59 ± 0.02 ms (n = 5) at pH 8.0 and 98 ± 4 ms (n = 5) at pH 6.8 (Fig. 5). As mentioned above, we confirmed that such acidic pHs did not appreciably activate hASIC1a and cASIC1a directly (5 ± 1% through-jump peak at pH 6.8 for hASIC1a, n = 5; 1 ± 1% through-jump peak for cASIC1a, n = 5; Fig. S2 A and B). While investigating deactivation kinetics of rat ASIC1a/2a heteromers, we found deactivation kinetics were not contaminated by desensitization until more acidic pH values (5 ± 1% through-jump peak for pH 6.6, n = 4; Fig. S2C; also Figs. 3 and 5), consistent with ASIC1a/2a possessing a lower apparent affinity for protons. However, in contrast to ASIC1a, rat ASIC1a/2a heteromeric deactivation did not show as strong a dependence on pH over this even greater range. At pH 8.0, the deactivation decays were 0.37 ± 0.04 ms (n = 8), which did slow to 11 ± 5 ms (n = 8) at pH 6.6. Although there was a detectable slowing (P = 0.00013, pH 8 versus pH 6.6), the kinetic range was far smaller than observed with ASIC1a (range of 11 ± 3, n = 6, P < 0.0001 compared with span of rat ASIC1a; Figs. 1 and 5). To assay effective heteromer formation in each patch, we used the ratio of the pH 6 to pH 5 response amplitude as done previously (20). In this dataset, ASIC1a/2a-transfected cells gave a ratio of 0.17 ± 0.02 (n = 20; Fig. S3) which is similar to previous work (20). It should be noted that ASIC1a/2a deactivations were at the limit of our solution exchange (10–90% rise times between 100 and 250 μs). Therefore, we cannot formally exclude the possibility that ASIC1a/2a does show even faster deactivation kinetics at pH 8.0, for example, and hence could span a considerable range because such kinetics would be faster than solution exchange could resolve or, indeed, faster than physiologically relevant. However, with this caveat in mind, ASIC1a is privileged among synaptic ASICs (indeed, among ligand ion channels in general) because its deactivation kinetics encompass nearly a 1,000-fold range of physiologically relevant time scales, depending on the agonist concentration.

Fig. 5.

pH-dependent deactivation is found across ASIC1a but not ASIC1a/2a heteromers. (A) Representative responses to triple-jump protocol from patches expressing rat ASIC1a (Upper Left), hASIC1a (Upper Right), cASIC1a (Lower Right), or rat ASIC1a/2a (Lower Left) heteromers. (B) Summary of weighted deactivation time constants from the constructs in A. Note that time constants for kinetics at more acidic pHs are dictated by the desensitization process, and hence not reported here. Data are from between four and 22 patches. Error bars show SEM.

Fig. S2.

Dissociating deactivation and desensitization in each construct. (A–J, Left) Example traces of triple jumps from resting pH into pH 5 followed by the indicated pH (gray traces) or direct jumps from resting pH into the indicated pH (black traces) in the same patch for the indicated construct. (A–J, Right) Summaries of the peak response to a direct jump compared with the peak response during the triple jump for the indicated construct. The dotted line shows the desensitization cutoff, symbols show the individual patch measurements, bar graphs depict the average, and the error bars show SEM.

Fig. S3.

Cotransfection of ASIC1a/2a resulted in heteromeric channels. (A) ASIC1a (Left) and ASIC1a/2a (Right) responses to pH 5 (gray traces) or pH 6 (black traces) applications. (B) Summary of the pH 6-to-pH 5 ratio across 13–20 patches (bar graph) and for each individual patch (circles). Error bars show SEM.

Agonist-Dependent Deactivation Can Arise from Strong Cooperativity in Binding.

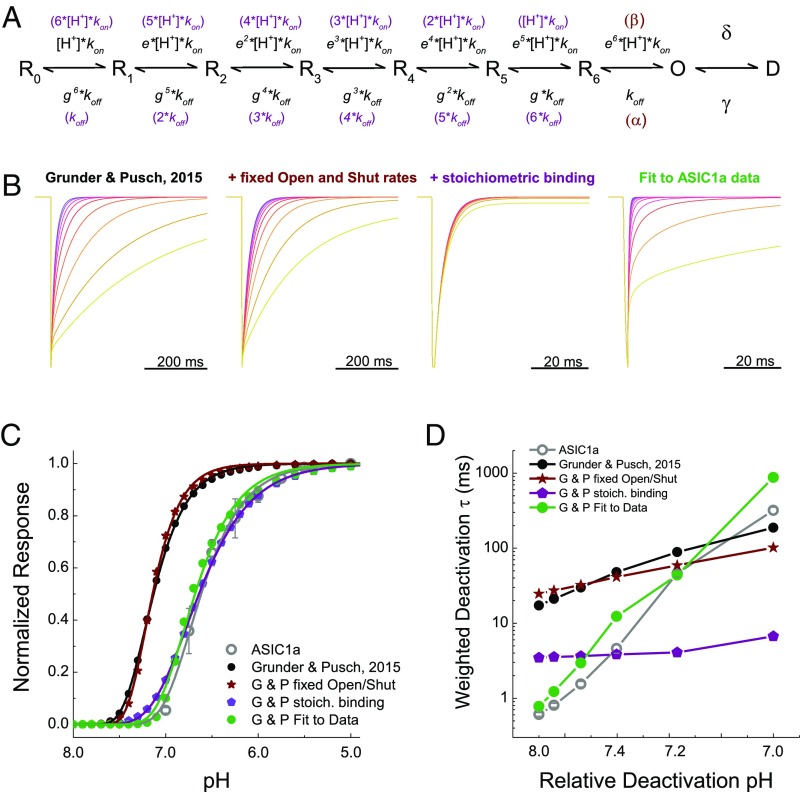
What could be the molecular basis for this strongly pH-sensitive deactivation? To gain insight into this issue, we used kinetic modeling to determine what features would be needed to reproduce agonist-dependent deactivation. We began with the model seen in Fig. 6A, as first put forward by Gründer and Pusch (25). This model is a simple linear reaction scheme with seven proton-binding events and desensitization arising exclusively from the open state (Fig. 6A). It also has two notable features. First, the opening reaction is agonist-dependent. Second, each proton-binding step gets progressively faster, by a factor of e, with increasing occupancy. The unbinding rates are similarly altered by a factor of g. In this way, the steep cooperativity of ASIC steady-state inactivation and activation can be largely reproduced (25). To our surprise, this model also exhibited pH-dependent deactivation kinetics using the same parameters given by Gründer and Pusch (25), albeit over a narrower range of kinetics than in rat ASIC1a. Fig. 6B (Left) illustrates this finding with example responses to a 1-ms through jump into a range of final pHs. The weighted time constants from this model span an 11-fold range from 17 ms at pH 8 to 187 ms at pH 7 (Fig. 6D, black circles). Although the model’s range of kinetics is narrower than ASIC1a’s range (Figs. 1 and 6D, gray circles), agonist-dependent deactivation was still present. We next investigated what feature(s) of the model supported this capacity, focusing on the agonist-dependent open rate and the “cooperativity parameters” e and g. Restricting the open and shut parameters, β and α, respectively, to single values (Table 1) did not prevent pH-dependent deactivation (Fig. 6 B–D, fixed open model, dark red and Table 1), indicating that this feature is not necessary. In contrast, making the agonist-binding and -unbinding events stoichiometric and independent eliminated pH-dependent deactivation (Fig. 6, stoichiometric binding model, purple and Table 1). Thus, in this model, and perhaps in ASIC1a itself, pH-sensitive deactivation arises from strong cooperativity between binding events.

Fig. 6.

Kinetic simulations using a linear gating scheme can broadly reproduce pH-dependent deactivation. (A) Kinetic scheme from Gründer and Pusch (25) used for simulations. (B) Simulated responses to a triple-jump protocol using a range of pHs from the scheme of Gründer and Pusch (25) as published (Left, black subheading), with fixed open and shut rates (Center Left, dark red subheading), with fixed open and shut rates plus stoichiometric binding (Center Right, purple subheading), or fit directly to data (Right, green subheading). (C) pH response curves for each of the models described above, as well as data obtained for rat ASIC1a (gray circles and gray fit line). Data are from four separate patches, and error bars show SEM. G & P, Gründer and Pusch. (D) Weighted deactivation time constants for each of the models tested, as well as data for rat ASIC1a (gray circles and line). To correct for shifts in apparent pH affinity in the models, the activation rheobase was determined (as in Fig. 2) and triple-jump simulations were performed using a pH range between that rheobase and 1 pH unit greater.

Table 1.

Parameters for kinetic models

Rate constant	Gründer and Pusch	Gründer and Pusch fixed open/shut	Gründer and Pusch stoichiometric binding	Gründer and Pusch fit to data
kon	2 × 109	2 × 109	1 × 1010	1.4 × 108
koff	1,000	1,000	1,000	126
e	1.5	1.5	N/A	3.48
g	0.67	0.67	N/A	1.83
α	N/A	7.0 × 105	7.0 × 105	7.0 × 105
β	N/A	4.0 × 105	4.0 × 105	4.0 × 105
δ	2	2	2	2.49
γ	0.02	0.02	0.02	0.02

Rate constants used for simulations in Fig. 6 and Fig. S4. Values for unmodified Gründer and Pusch model (1st column) are taken from ref. 25. N/A, not applicable.

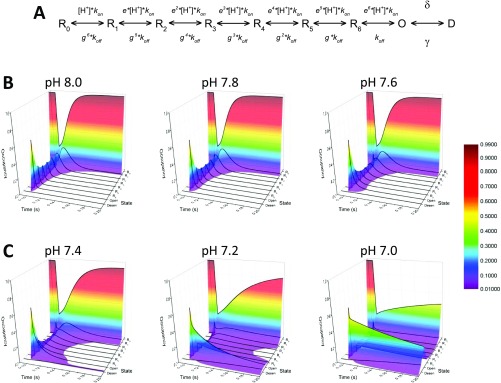
The relative success of this simple model encouraged us to try fitting it directly to experimental data. To constrain such fitting further, pH response curves were constructed [Figs. 3A and 6C, open circles; pH₅₀: 6.59 ± 0.03, slope or Hill coefficient of this relationship (n_H): 2.2 ± 0.1, n = 4] and desensitization decay (τ_{desensitization}) was measured (pH 5 τ_{desensitization}: 1,050 ± 60 ms, n = 12), both in outside-out patches. The fixed open model was then globally fit to the group pH response curves and desensitization decays as well as through-jump deactivation (Fig. 1 A and B) and direct jump activation (Fig. 3 D and E, black traces) traces. The resulting model showed comparable desensitization time constants (τ_{desensitization} = 787 ms), deactivation kinetics (0.77 ms at pH 8, 874 ms at pH 7, kinetic span of 1,135; Fig. 6D), and pH response curves (pH₅₀ = 6.66, n_H = 2.06). Interestingly, this model also showed much higher values of the cooperativity parameters e and g (Table 1). Inspection of a state occupancy versus time plot during a through-jump simulation gives some insight into how pH-dependent deactivation arises in the model (Fig. S4). During a relaxation from pH 5 to pH 8, once the first proton dissociates (open-state to R₆-state transition) the second and subsequent protons follow in short order, and the population rapidly transitions from the open state back to the apo state with minimal delay due to ambient protons rebinding (Fig. S4A). However, when the ambient proton concentration is increased slightly from pH 8 to pH 7.4, that slightly higher proton concentration is able to slow the transition from open to apo (R₀), providing a chance for the channel to reopen and prolonging the deactivation (Fig. S4 A–D). This effect is increased at higher proton concentrations (Fig. S4 E and F), giving rise to the steep and strong pH dependence of deactivation in the model. In essence, the proton dissociation process, a prime determinant of deactivation, is strongly dependent on the number of bound protons, and hence on proton concentration. Although this model is an imperfect and grossly simplified representation of ASIC gating, it does illustrate how, in principle, strong cooperativity in agonist binding could account for and reproduce the experimentally observed agonist-dependent deactivation. We next sought experimental evidence for the role of cooperativity by disrupting proton-binding sites and examining pH-dependent deactivation.

Fig. S4.

Occupancy of linear model states versus time during through jumps at multiple pHs. (A) Linear model of Gründer and Pusch (25). (B) Plots of the occupancy (z axis, colors) of each of nine states of the linear model (y axis, black lines) over time (x axis) for final pH values of 8, 7.8, and 7.6. The pH 5 stimulus is applied for 1.8 ms at time 0.1, followed by a jump into the indicated pH. (C) Same plot as in B, but for pH 7.4, pH 7.2, and pH 7.

Mutations to Putative Proton Sensors Attenuate pH-Dependent Deactivation.

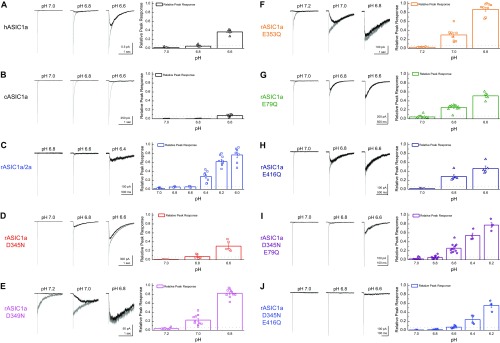
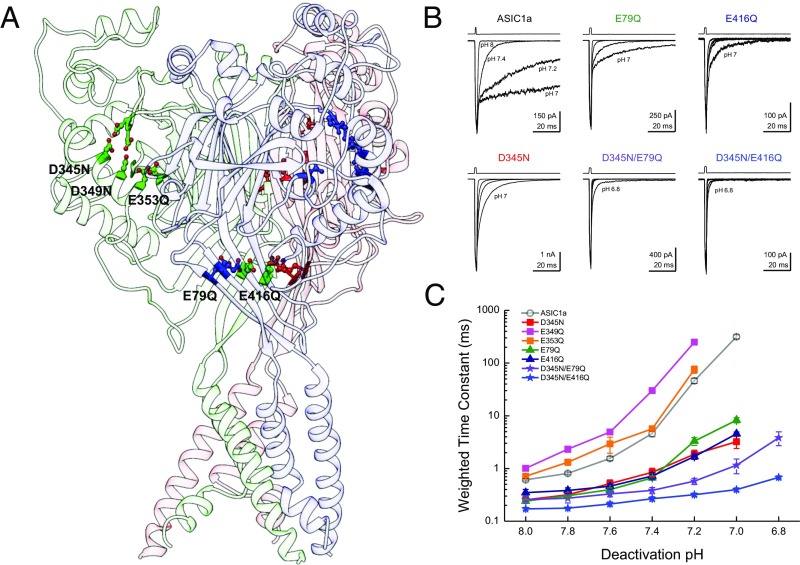
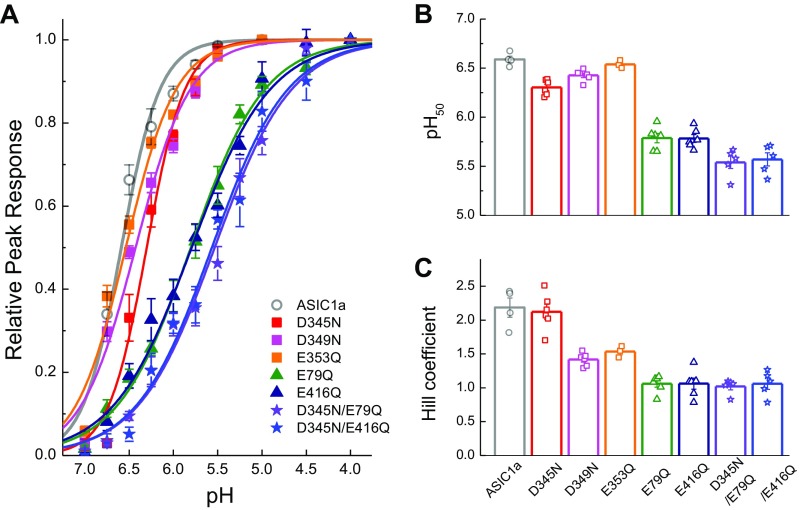
To attenuate cooperativity we set out to remove some of ASICs’ proton sensors. ASICs are known to have at least two distinct regions of acidic residues implicated in gating (53–57): the “acidic pocket” formed at interface between the finger and thumb domains as well as the palm domain (Fig. 7A). In the acidic pocket, three pairs of glutamates and aspartates (D345-D97, D349-D238, and E353-D239) sit in close apposition (51, 53). Protonation of these residues brings the thumb and finger domain close together in a motion correlated with activation/desensitization (55). In the palm domain, protonation of E79 and E416 appears to be important, because neutralizing these positions left shifts dose–response curves and incorporating MTS reagents produces bell-shaped dose–response curves (57). We therefore neutralized each of these positions in turn and examined the effect on the pH dependence of deactivation. Because these mutations may alter apparent proton affinity, we calibrated the deactivation pH range for each construct by examining the responses to direct activation versus triple-jump activation and then restricted our analysis to pH conditions producing no more than 6% direct activation (Fig. S2 D–J). We also examined the pH response curve of each mutant (Fig. S5). Within the acidic pocket, only D345N showed any effect on the range or pH sensitivity of deactivation kinetics, specifically deactivation decays of D345N at pH 8 occurring with a time constant of 0.25 ± 0.03 ms (n = 6) and at a time constant of 3.2 ± 0.8 ms at pH 7 (Fig. 7 B and C). These values correspond to only a 13 ± 3 range, significantly smaller than the 520 ± 60 kinetic span of wild-type (D345N span versus wild-type, P < 0.0001). D345N also showed a slight right shift in the pH response curve (pH₅₀: 6.30 ± 0.03, P = 0.003 versus rASIC1a) with no change in slope (n_H: 2.1 ± 0.1, n = 6, P = 0.74; Fig. S5). Mutations further into the acidic pocket, D349N and E353Q, combined reductions in the pH response curve slope (D349N n_H: 1.42 ± 0.02, n = 6, P = 0.0027; E353Q n_H: 1.54 ± 0.04, n = 3, P = 0.04; Fig. S4) with either a small right shift in pH₅₀ (D349N pH₅₀: 6.42 ± 0.02, n = 6, P = 0.003) or no change (E353Q pH₅₀: 6.54 ± 0.02, n = 3, P = 0.242; Fig. S4). Interestingly, these other acidic pocket mutations showed a minimal effect on deactivation kinetics (D349N: 1.01 ± 0.09 ms at pH 8, 250 ± 25 ms at pH 7.2, n = 5; E353Q: 0.71 ± 0.04 ms at pH 8, 80 ± 10 ms at pH 7.2; n = 5; Fig. 7 B and C). In contrast to this positional selectivity in the acidic pocket, both mutations in the palm domain, E79Q and E416Q, attenuated the span of deactivation kinetics (Fig. 7). Specifically, E79Q exhibited only a 34-fold change in deactivation kinetics from 0.24 ± 0.02 ms at pH 8 to 8.3 ± 0.9 ms at pH 7 (n = 6), whereas E416Q was further constrained to a 14-fold difference, decaying with a 0.35 ± 0.05-ms time constant at pH 8 (n = 7) and 4.5 ± 0.4-ms time constant at pH 7 (n = 6). These values both represent significantly smaller kinetic spans than wild-type ASIC1a (E79Q: span of 37 ± 6, n = 5, P < 0.0001 versus wild-type; E416Q: span of 14 ± 2, n = 6, P < 0.0001). Both of these palm domain mutations right-shifted the pH response curves (E79Q pH₅₀: 5.79 ± 0.05, n = 6, P = 0.004 versus rASIC1a wild type; E416Q pH₅₀: 5.78 ± 0.04, n = 6, P = 0.003; Fig. S5) and reduced their slopes (E79Q n_H: 1.06 ± 0.05, n = 6, P = 0.002 versus rASIC1a wild type; E416Q n_H: 1.06 ± 0.08, n = 6, P = 0.001; Fig. S5). Thus, the palm domain mutations that disrupted pH-dependent deactivation also reduced the pH response curve slope and Hill coefficient (Fig. 7 and Fig. S5), whereas D345N did not alter the slope. One might expect that if cooperativity is involved in both pH-dependent deactivation and the Hill slope, then all mutations affecting cooperativity should affect these two measures as well. This expectation is not necessarily true. The Hill slope depends on agonist-binding events as well as on gating and desensitization events, making it impossible to separate the two effects (58). Furthermore, the Hill slope gives this muddled information only for the narrow range of agonist concentrations that directly activate the receptor without saturating it. However, we explicitly avoided such concentrations so as not to contaminate deactivation kinetics with desensitization (Fig. 3 and Figs. S2 and S5). Thus, the lack of change in D345N’s Hill slope does not undermine the proposed role of agonist cooperativity any more than the reduction in E79Q’s and E416Q’s Hill slopes supports it. Taken together these data reveal that some, but not all, putative proton sensors control the agonist-dependent deactivation kinetics.

Fig. 7.

Neutralizing proton sensors attenuate pH-dependent deactivation. (A) Structure of cASIC1a (Protein Data Bank ID code 4NYK) showing each subunit in a different shade, along with some putative proton sensors in the finger/thumb interface and palm domain. (B) Example responses from through-jump deactivation experiments for the indicated single and double mutants. The pH range displayed was pH 8, pH 7.4, pH 7.2, and pH 7 except for D345N/E79Q and D345N/E416Q, which also include pH 6.8. (C) Summary of weighted time constants of deactivation at various pHs across between four and 10 patches for each mutant tested. Note that kinetics were examined from pH 8 to pH 6.6 for all constructs, and out to pH 6.2 for the double mutants. Error bars show SEM.

Fig. S5.

pH response curves for each ASIC1a construct tested. (A) Summary of pH response curves, where the symbols indicate the mean and SEM and the solid lines are fits of the Hill function to the data. (B and C) pH₅₀ and Hill coefficients from fits of each construct. The bar graph represents the average, with the symbols indicating the values for each patch. Error bars show SEM. Between three and six patches were used for each construct.

To restrict the kinetics of deactivation further, we combined mutations from the acidic pocket and the palm domain. Both double mutants, D345N/E79Q and D345N/E416Q, hugely reduced the span of deactivation kinetics (Fig. 7 B and C). Furthermore, the kinetics of these double mutants could all be well described by single- or double-exponential fits, and not the triple-exponential fits required of wild-type or other mutant data. Specifically, D345N/E79Q deactivation at pH 8 occurred with a time constant of 0.26 ± 0.04 ms (n = 10) and slowed to only 3.8 ± 0.9 ms at pH 6.8 (n = 8), representing a span of 13 ± 2 (n = 7, P < 0.0001 versus wild type). The D345N/E416Q mutations were further delimited, exhibited deactivation kinetics of 0.17 ± 0.01 ms at pH 8 (n = 9), and remained at submillisecond time constants throughout the pH range tested (e.g., 0.68 ± 0.04 at pH 6.8, n = 10). The D345N/E416Q mutation deactivation kinetics only changed by 3.6 ± 0.3 fold (n = 9), which is significantly different from the 520 ± 60-fold span of wild type (P < 0.0001; Fig. 7). We note that, as with ASIC1a/2a kinetics, the deactivations of these double mutants were at the limit of our solution exchange (10–90% rise times between 100 and 250 μs). Thus, they could, in principle, show even faster deactivation kinetics at pH 8.0 if our solution exchange could resolve them, and hence the kinetic span could be greater. However, with this caveat in mind, these constructs may serve as a starting point to design further mutations for synaptic studies.

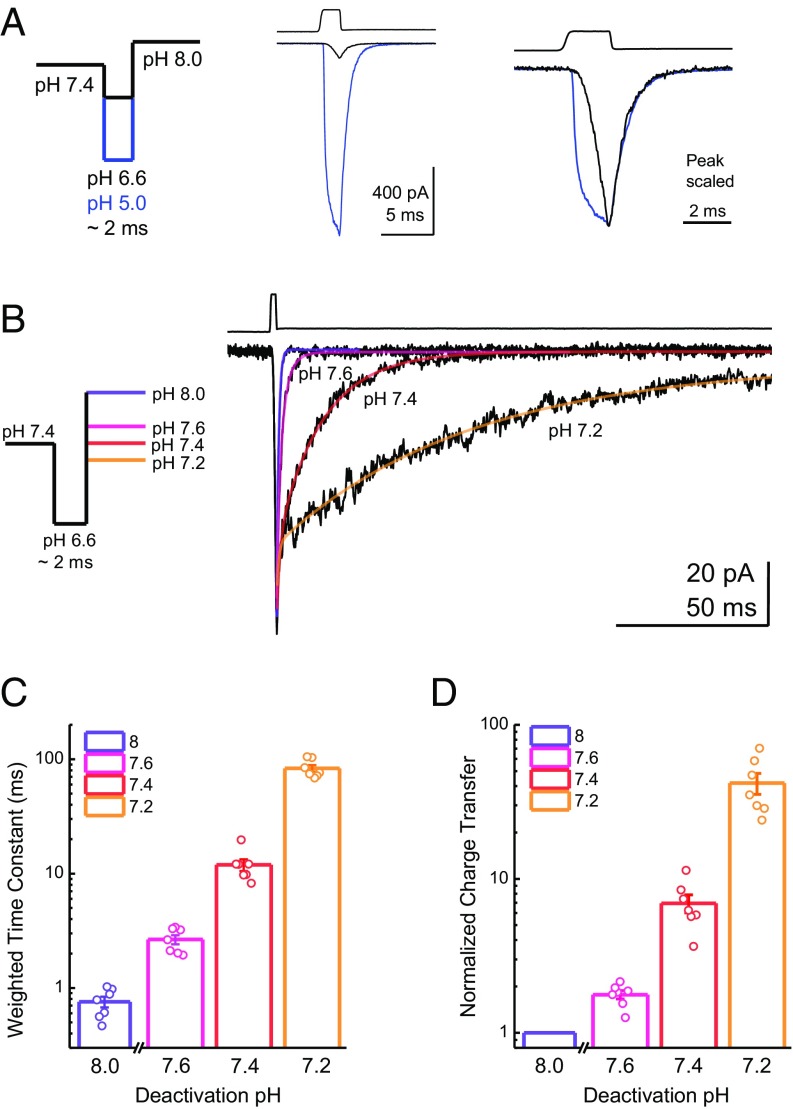
pH-Sensitive Kinetics Enable Subactivation pH to Prolong Channel Activation at Low Agonist Concentrations.

The experimental conditions used above utilize a pH 5 stimulus, with the goal of provoking large responses within the 1- to 2-ms application. However, synaptic cleft pH is unlikely to reach such high concentrations. Estimates of the synaptic cleft pH immediately following a release event range from 7.2 to 6.7 pH units (21–23, 25). Although these results may be underestimations due largely to limitations of measuring pH in such small volumes with high temporal precision, we sought to address how, if at all, pH-sensitive deactivation may impact responses to smaller agonist concentrations. Therefore, we asked if subactivation pH conditions (i.e., >pH 7) can slow the kinetics and enhance the charge transfer of low, more physiologically relevant proton concentrations. To perform this experiment, patches were first incubated at pH 7.4 before jumping to either pH 5 or pH 6.6 for ∼2 ms (Fig. 8A). As expected of a lower agonist concentration, the pH 6.6 stimulus resulted in small, slower activating peak responses within the 2-ms application (11 ± 1% of pH 5 peak, n = 7; Fig. 8A). Interestingly, the deactivation of these smaller responses at pH 8, pH 7.6, pH 7.4, and pH 7.2 was also strongly regulated by pH, with the weighted time constants ranging from very fast at pH 8 (0.76 ± 0.08 ms, n = 7) to progressively slower at pH 7.6 (2.7 ± 0.2 ms, n = 7, P = 0.0006 versus pH 8), pH 7.4 (12 ± 1 ms, n = 7, P = 0.0005 versus pH 8) and pH 7.2 (83 ± 6 ms, n = 7, P = 0.0005 versus pH 8; Fig. 8 B and C). Within this dataset, we also compared the charge transfer in the pH 7.6, pH 7.4, or pH 7.2 conditions, normalized to the charge transfer of pH 8. A pH 6.6 jump followed by pH 7.6 produced a relatively small amount of charge transfer, 1.8 ± 0.1-fold greater than the charge transfer of pH 8 (n = 7, P = 0.0004 versus pH 8; Fig. 8 B and D). However, slight changes to the deactivating pH produced robust enhancements of normalized charge transfer, with 6.9 ± 0.9-fold (n = 7, P = 0.0005 versus pH 8) and 42 ± sevenfold (n = 7, P = 0.0006 versus pH 8) increases, relative to pH 8, at pH 7.4 and pH 7.2, respectively. This finding illustrates that even the relatively small currents elicited by more physiologically plausible pH stimuli can be robustly enhanced by ambient pH to increase charge transfer substantially and, by extension, to impact postsynaptic excitability.

Fig. 8.

pH-sensitive deactivation prolongs responses to weak pH stimuli. (A, Left) Schematic of the pH application protocol used with a brief 2-ms jump into either pH 5 or pH 6.6. (A, Center) Representative response to a 2-ms jump to pH 5 (blue trace) or pH 6.6 (black trace) in the same patch. The upper trace is the solution exchange current from this patch. (A, Right) Same responses but scaled according to peak to compare activation and deactivation kinetics. (B, Left) Schematic of pH application protocol used with a resting pH of 7.4; a brief 2-ms jump to pH 6.6; and a final jump to pH 8, pH 7.6, pH 7.4, or pH 7.2. (B, Right) Responses from ASIC1a to a brief pH jump to 6.6, followed by deactivation with the indicated pH. The upper trace is the solution exchange current from this patch, and the colored lines depict exponential fits to the data. Weighted deactivation time constants (C) and normalized charge transfer (D) from brief pH 6.6 jumps and deactivations as in B to the indicated pH. Error bars show SEM, and values from seven individual patches are shown as circles.

SI Methods

Cell Culture, Mutagenesis, and Transfection.

Chinese hamster vary (CHO) cells were maintained in Ham’s F-12 Nutrient Mix (Invitrogen/Life Technologies), supplemented with 10% FBS (Sigma–Aldrich) and penicillin/streptomycin (Invitrogen/Life Technologies). Cells were passaged upon reaching ∼90% confluency every 2 to 3 d. Mutations were introduced using standard overlap PCR and confirmed by sequencing (Genewiz, Inc.). For transfections, CHO cells were plated in poly-d-lysine–coated 35-mm dishes and transfected 24–48 h later. Cells were transfected with rat ASIC1a, hASIC1a, or cASIC1a and eGFP (GFP_S65T) at a ratio of 8:1 μg of cDNA per 10 mL of media. For heteromeric experiments, rat ASIC1a, rat ASIC2a, and eGFP were transfected at a ratio of 2:6:1 μg of cDNA per 10 mL of media. In GluA2 experiments, a plasmid bearing the Q version of rat GluA2-flip followed by an internal ribosome entry site and eGFP was transfected at a concentration of 7.5 μg of cDNA per 10 mL of media. Transfections were performed using Lipofectamine 2000 (Invitrogen/Life Technologies) or jetPRIME (Polyplus) following the manufacturer’s instructions, with media changed after 6–12 h. Electrophysiology experiments began 48–72 h after the start of transfection.

Electrophysiology.

Outside-out patches were excised from EGFP-expressing CHO cells using fire-polished, thick-walled borosilicate glass pipettes of 3–5 MΩ resistance. The internal solution contained 135 mM CsF, 33 mM CsOH, 11 mM EGTA, 10 mM Hepes, 2 mM MgCl₂, and 1 mM CaCl₂ (pH 7.4). External solutions were composed of 150 mM NaCl, mM 20 Hepes, 1 mM CaCl₂, and 1 mM MgCl₂, with a pH of 8.0 (NaOH) unless otherwise stated. For pH values more acidic than 7.0, Hepes was replaced with MES. All recordings were performed at room temperature with a hold potential of −80 mV using an Axopatch 200B instrument (Molecular Devices). Data were acquired at 50 or 100 kHz and filtered at 10 kHz under the control of Clampex 10.2 or 10.6. Series resistance was routinely compensated by >90% where the amplitude exceeded 100 pA. Rapid application was performed using home-built, triple-barrel application pipettes (Vitrocom), manufactured according to MacLean (42). Translation of application pipettes was achieved using a LZ150M piezo translator (Burleigh Instruments) with voltage commands low-pass-filtered (eight-pole Bessel; Frequency Devices) at 100–200 Hz. The speed of translation over longer distances, compared with two solution theta-tube jumps, made these experiments prone to oscillations and solution exchange artifacts. The fast kinetics at alkaline pH values made such artifacts easy to see and correct online, and solution exchange was routinely measured at the end of each patch recording using open tip currents. The exchange time from open time currents ranged from 100 to 250 μs (10–90% rise time).

Simulations.

All simulations were performed using Kinetic Model Builder (72) in “Eigen Solver” mode. For direct fitting of the Gründer and Pusch model (25), the representative traces from Figs. 1A and 2D, as well as a desensitization decay to pH 5 and a summary dose–response curve (Fig. 2A), were fit. To offset the difference in sample points between experiments (i.e., eight-sample point summary dose–response curves versus 50,000-point electrophysiology traces), the fit cost of fewer point conditions was increased to equal the fit cost of larger data point conditions. All rate constants except β, α, and γ were allowed to vary.

Statistics and Analysis.

Data were analyzed using Origin 8.6 (OriginLab Corp.), MATLAB (MathWorks), and Excel (Microsoft Corp.). Desensitization and deactivation kinetics were fit with single-, double-, or triple-exponential functions in Clampfit 10.6 (Molecular Devices) as judged by eye. Note that the fit areas (Fig. 1D) do not sum to 1 because not all patches were best fit with the same number of components within a pH value (e.g., for pH 7.6, eight patches were better fit with a single exponential, whereas six patches required double exponentials). For simplicity, we report here the weighted time constants (τ_weighted) from these fits calculated with the equation:

$${\tau }_{weighted}=\left(\raisebox{1ex}{$A_{fast}$}\!\left/ \!\raisebox{-1ex}{$A_{total}$}\right.\right)\ast {\tau }_{slow}+\left(\raisebox{1ex}{$A_{inter.}$}\!\left/ \!\raisebox{-1ex}{$A_{total}$}\right.\right)\ast {\tau }_{inter.}+\left(\raisebox{1ex}{$A_{slow}$}\!\left/ \!\raisebox{-1ex}{$A_{total}$}\right.\right)\ast {\tau }_{slow},$$

where A_fast, A_inter., and A_slow are the areas described by the fast, intermediate, and slow time constants τ_fast, τ_inter., and τ_slow, respectively, and A_total is the sum of all three areas. For example traces, one trace was used for desensitization experiments and between three and 10 individual traces from a single patch were averaged for other experiments. To compare the range of deactivation kinetics between constructs in a semiquantitative fashion, a “kinetic span” was calculated with the following equation:

$$kinetic\hspace{0.17em}span=\frac{\left(Deactivation\hspace{0.17em}{\tau }_{max}\right)}{\left(Deactivation\hspace{0.17em}{\tau }_{max+1}\right)},$$

where Deactivation τ_max is the weighted time constant of deactivation at the highest agonist concentration at which deactivation could be measured (i.e., pH 6.8 for hASIC1a; Fig. 5) and Deactivation τ_max+1 is the weighted time constant at one pH unit greater (i.e., pH 7.8 for hASIC1a; Fig. 5) or with no added glutamate in the case of GluA2 (Fig. 2). To give an indication of variance and permit statistical testing, this deactivation span was calculated from the subset of patches that contained both data points (i.e., both pH 7.8 and pH 6.8 in the same hASIC1a patch). The relative permeability of external Na⁺ or K⁺ compared with internal Na⁺ (P_x/P_Na; Fig. S1) was calculated using the equation:

$$\frac{P_X}{P_{Na}}=\left(\frac{\left[N{a}_{internal}\right]}{\left[X_{external}\right]}\right)e^{\left(F\ast V_{rev}\right)/\left(R\ast T\right)},$$

where [Na_internal] and [X_external] are the concentrations of internal Na⁺ and external Na⁺ or K⁺ (millimolar); V_rev is the reversal potential (volts); and F, R, and T have their usual thermodynamic meanings. The pH response curves were collected from outside-out patches using a resting pH of 8 and 300- to 500-ms agonist pH steps to minimize tachyphylaxis. Between one and three different test pH stimuli (pH 7 to pH 4.5) were bookended by maximal pH stimuli to control further for tachyphylaxis. Responses were normalized to the nearest maximal pH stimulus, and individual patches were fit to the logistical equation:

$$Response=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\left(1+{10}^{\left(p{H}_{50}-p{H}_{test}\right)n_H}\right)$}\right.,$$

where Response is the normalized current at pH_test, pH₅₀ is the pH evoking half of the maximal response, and n_H is the slope or Hill coefficient of this relationship. For all statistical tests, n was taken to be a single patch. Nonparametric two-tailed, unpaired randomization tests, implemented in MATLAB, were used to assess statistical significance, with 10⁵ runs each, and P < 0.05 taken to be significant. All summary plots show mean ± SEM.

Discussion

In this study, we use a triple–through-jump approach to probe ASIC kinetics at more acidic pH values while avoiding complications resulting from steady-state inactivation (20, 38). This method provided several insights. First, the kinetics of ASIC deactivation encompass a very broad time scale, from hundreds of microseconds to hundreds of milliseconds, and are precisely tuned over a very narrow pH range (Fig. 1). This effect is not observed in other NGICs (Fig. 2) and cannot be attributed to direct activation by the more acidic pH values (Fig. 3). Furthermore, this dynamic range of deactivation is preserved in rat ASIC1a, hASIC1a, and cASIC1a but is not found in rat ASIC1a/2a heteromers (Fig. 5). Such a range of deactivation kinetics can be explained by a gating mechanism with strong cooperativity in agonist binding (Fig. 6). Consistent with this hypothesis, eliminating certain putative proton sensors is able to limit the range of deactivation kinetics (Fig. 7). Importantly, we also show that the response to relatively short-duration exposures to low agonist concentrations can be prolonged by physiologically relevant pH stimuli (Fig. 8).

Molecular Mechanisms of pH-Dependent Deactivation.

The agonist-dependent deactivation of ASICs is, to our knowledge, the only example of a ligand-gated ion channel whose deactivation is so strongly governed by the concentration of ligand. Classically, the deactivation kinetics are determined by the channels’ open and shut rates as well as by the rate of agonist unbinding and, occasionally, desensitization (32–36, 46, 48, 49), none of which are generally agonist-dependent. Here, we find that the steeply agonist-dependent deactivation of ASIC1a can be explained by strong cooperativity between agonist-binding steps. We cannot exclude other possibilities such as strong cooperativity in agonist-dependent channel opening rates or multiple open states of different duration depending on occupancy or other more complicated arrangements. A detailed investigation at the single-channel level will be needed to discern these issues. However, this observation does solve a question that arose from a previous study, namely, how to reconcile rapid deactivation kinetics at pH 8 (20) with high apparent affinity [pH₅₀ for ASIC1a 6.6 in this study (also refs. 25, 38–40), EC₅₀ of 250–400 nM]. For comparison, GluA2 has identical deactivation kinetics (Fig. 2) but a peak response EC₅₀ of 1–2 mM (59). A possible solution may lie in the unusually high cooperativity in ASIC gating. Hill coefficients for activation range from 2 to 4, with steady-state inactivation curves being even steeper (25, 38). To account for such steepness, Gründer and Pusch (25) advanced a kinetic model of ASIC gating with both proton-binding and -unbinding rates becoming progressively faster as proton occupancy increases (Fig. 6A). Such a model not only accounts for rapid deactivation at pH 8, markedly slower deactivation at pH 7, and the appropriate pH response curve but also harmonizes with existing structural data. Proton activation is thought to proceed from protons binding to pairs of carboxylate residues in the acidic pocket formed by the thumb and finger (53–55). However, contributions may also arise from similar pairs in the palm domain (56, 57) or elsewhere (60, 61). In both regions, carboxylate residues are in close apposition. In the case of the thumb and finger pocket, protonation of carboxylate pairs may bring the thumb and finger domains together in a pinching motion (55). In this view, as one pair of carboxylate residues is protonated, it draws its unprotonated neighbors closer together and thereby increases their proton affinity and their pK_a. Thus, the acidic pocket may close up in a zipper-like motion, as proton-binding primes adjacent pairs for subsequent protonation. The kinetic correlate of this motion is the increase in the binding rate accomplished by the factor e (Fig. 6A). Such a mechanism in reverse may account for the observed rapid deactivation at alkaline pH values. Once proton concentrations drop and the first proton dissociates, the neighboring protonated carboxylate pairs are energetically penalized by two nearby negative charges in close opposition. This electrostatic strain can be relieved by additional protons unbinding, which, in turn, increases the strain for the remaining carboxylate pairs, represented by the factor g (Fig. 6A). At intermediate agonist concentrations, such as pH 7.4, the proton concentration may be sufficient to produce a balance between high-affinity/high-occupancy states (i.e., slow deactivation) and lower affinity/lower occupancy states (i.e., fast deactivation). This hypothesis also explains the effect of D345N compared with the other acidic pocket mutations, D349N and E353Q. The privileged position of D345 at the top of the finger and thumb interface (Fig. 7A) may enable it to act as a latch that, when protonated, exerts a considerable effect on the stability of the fully “pinched” state of the thumb and finger. Molecular dynamics simulations would seem to be an attractive way to explore this hypothesis, but the computational costs of recalculating all relevant amino acid pK_as at each time step are too demanding at present.

Possible Physiological Roles.

Apart from the biophysical question of how ASICs accomplish this unique agonist-dependent deactivation, there is also the physiological question of how this capacity is used, if at all. Measurements of synaptic cleft acidification during transmission range from 7.2 to 6.7 (21–23, 25), which seem too small in amplitude to appreciably activate ASIC1a, which saturates at pH 5, especially considering the brevity of such stimuli. However, one solution to this dilemma, which we demonstrate here, is that agonist-dependent deactivation can be harnessed to prolong the response to brief-duration, small-amplitude acidic stimuli, making ASIC1a a more physiologically relevant mediator of charge transfer (Fig. 8). This role of pH-sensitive deactivation seems quite reasonable. Indeed, it would be surprising if synaptic ASIC1a did not alter their kinetics. Beyond this role, however, the profound slowing of deactivation represents a mechanism that can shape channel activity, and hence synaptic excitability, to a large degree and in response to recent synaptic activity.

In considering possible physiological roles of ASIC EPSCs, however, one is immediately confronted with their relatively small size [∼5–10% EPSC (18, 19)]. In this respect, they are reminiscent of kainate receptor (KAR) EPSCs at the mossy-fiber CA3 synapse (62, 63). KAR EPSCs are also roughly 10% of their grander glutamatergic cousins, and they are also markedly slower, with time constants on the order of 50–100 ms (62, 64). This prolonged decay appears to be important for summation, temporal integration, and, ultimately, induction of potentiation (65–67). Taken together, the studies of KAR EPSCs indicate that the small amplitude of ASIC EPSCs, by itself, is not sufficient to preclude a physiological role. So, how might the pH-sensitive kinetics of ASICs be used? At physiological pH, ASIC1a is expected to decay with a time constant of 3–10 ms (Figs. 1 and 4), in excellent agreement with the kinetics measured of ASIC EPSCs in the lateral amygdala (18). The synaptic alkalization that follows brief stimulus bouts would likely increase the amplitude of subsequent ASIC EPSCs, as well as speeding their decay kinetics and possibly allowing higher frequency signaling (20). However, such conditions also promote the gating of other excitatory NGICs (68–70), potentially masking any contribution from ASICs. More acidic circumstances would prolong the subsequent ASIC EPSC but would also lead to steady-state inactivation, producing a small-amplitude, long-duration inward current lasting several hundred milliseconds. The Na⁺ selectivity of such a current would ensure persistent depolarization, potentially promoting synaptic plasticity and accounting for ASIC1a’s requirement in long-term potentiation in the amygdala (18). Another possibility is that the variable kinetics of ASIC1a might be more important during development than in the adult brain. The slower decay offered by KARs, for example, provides a larger window of excitability than AMPA receptors, and this increased excitability is thought to aid in proper neuronal circuit wiring in the hippocampus and elsewhere (11, 12, 71). ASICs’ agonist-sensitive kinetics may play a similar role in developing regions with variable pH or CO₂ levels. Ultimately, a conditional cell-specific knockout and knock-in strategy will be needed to assess what additional role the ASIC EPSC plays. Such a strategy would also permit knock-in/rescue experiments with ASIC1a constructs showing constrained deactivation, such as the double mutants in Fig. 7, which would allow the role for ASICs’ pH-sensitive deactivation to be investigated also.

Methods

More detailed methods can be found in SI Methods.

Chinese hamster ovary cells were plated into 35-mm dishes and transfected with the indicated cDNA plus eGFP using Lipofectamine 2000 (Invitrogen/Life Technologies) or jetPRIME (Polyplus) following the manufacturer’s instructions. At 48–72 h posttransfection, outside-out patches were excised from eGFP-expressing cells and placed in front of a piezo-driven, triple-barreled, fast-perfusion system manufactured according to MacLean (42). After each experiment, the exchange time from open-time currents was measured and ranged from 100 to 250 μs (10–90% rise time). All simulations were performed using Kinetic Model Builder (72) in “Eigen Solver” mode. For direct fitting of data, all rate constants except β, α, and γ were allowed to vary. Data were analyzed using Origin 8.6 (OriginLab Corp.), MATLAB (MathWorks), and Excel (Microsoft Corp.). For all statistical tests, n was taken to be a single patch. Nonparametric two-tailed, unpaired randomization tests, implemented in MATLAB, were used to assess statistical significance with 10⁵ runs each, and a P value <0.05 was taken to be significant. All summary plots show mean ± SEM.