Significance
We find that there exist fundamental limitations to the joint measurability of time along neighboring space–time trajectories, arising from the interplay between quantum mechanics and general relativity. Because any quantum clock must be in a superposition of energy eigenstates, the mass–energy equivalence leads to a trade-off between the possibilities for an observer to define time intervals at the location of the clock and in its vicinity. This effect is fundamental, in the sense that it does not depend on the particular constitution of the clock, and is a necessary consequence of the superposition principle and the mass–energy equivalence. We show how the notion of time in general relativity emerges from this situation in the classical limit.
Keywords: quantum clocks, entanglement, gravity, classical limit
Abstract
In general relativity, the picture of space–time assigns an ideal clock to each world line. Being ideal, gravitational effects due to these clocks are ignored and the flow of time according to one clock is not affected by the presence of clocks along nearby world lines. However, if time is defined operationally, as a pointer position of a physical clock that obeys the principles of general relativity and quantum mechanics, such a picture is, at most, a convenient fiction. Specifically, we show that the general relativistic mass–energy equivalence implies gravitational interaction between the clocks, whereas the quantum mechanical superposition of energy eigenstates leads to a nonfixed metric background. Based only on the assumption that both principles hold in this situation, we show that the clocks necessarily get entangled through time dilation effect, which eventually leads to a loss of coherence of a single clock. Hence, the time as measured by a single clock is not well defined. However, the general relativistic notion of time is recovered in the classical limit of clocks.
A crucial aspect of any physical theory is to describe the behavior of systems with respect to the passage of time. Operationally, this means establishing a correlation between the system itself and another physical entity, which acts as a clock. In the context of general relativity, time is specified locally in terms of the proper time along world lines. It is believed that clocks along these world lines correlate to the metric field in such a way that their readings coincide with the proper time predicted by the theory—the so-called “clock hypothesis” (1). A common picture of a reference frame uses a latticework of clocks to locate events in space–time (2). An observer, with a particular split of space–time into space and time, places clocks locally, over a region of space. These clocks record the events and label them with the spatial coordinate of the clock nearest to the event and the time read by this clock when the event occurred. The observer then reads out the data recorded by the clocks at his/her location. Importantly, the observer does not need to be sitting next to the clock to do so. We will call an observer who measures time according to a given clock, but not located next to it, a far-away observer.
In the clock latticework picture, it is conventionally considered that the clocks are external objects that do not interact with the rest of the universe. This assumption does not treat clocks and the rest of physical systems on equal footing and therefore is artificial. In the words of Einstein: “One is struck [by the fact] that the theory [of special relativity]… introduces two kinds of physical things, i.e., (1) measuring rods and clocks, (2) all other things, e.g., the electromagnetic field, the material point, etc. This, in a certain sense, is inconsistent…” (3). For the sake of consistency, it is natural to assume that the clocks, being physical, behave according to the principles of our most fundamental physical theories: quantum mechanics and general relativity.
In general, the study of clocks as quantum systems in a relativistic context provides an important framework for investigating the limits of the measurability of space–time intervals (4). Limitations to the measurability of time are also relevant in models of quantum gravity (5, 6). It is an open question how quantum mechanical effects modify our conception of space and time and how the usual conception is obtained in the limit where quantum mechanical effects can be neglected.
In this work, we show that quantum mechanical and gravitational properties of the clocks put fundamental limits to the joint measurability of time as given by clocks along nearby world lines. As a general feature, a quantum clock is a system in a superposition of energy eigenstates. Its precision, understood as the minimal time in which the state evolves into an orthogonal one, is inversely proportional to the energy difference between the eigenstates (7–11). Due to the mass–energy equivalence, gravitational effects arise from the energies corresponding to the state of the clock. These effects become nonnegligible in the limit of high precision of time measurement. In fact, each energy eigenstate of the clock corresponds to a different gravitational field. Because the clock runs in a superposition of energy eigenstates, the gravitational field in its vicinity, and therefore the space–time metric, is in a superposition. We prove that, as a consequence of this fact, the time dilation of clocks evolving along nearby world lines is ill-defined.We show that this effect is already present in the weak gravity and slow velocities limit, in which the number of particles is conserved. Moreover, the effect leads to entanglement between nearby clocks, implying that there are fundamental limitations to the measurability of time as recorded by the clocks.
The limitation, stemming from quantum mechanical and general relativistic considerations, is of a different nature than the ones in which the space–time metric is assumed to be fixed (4). Other works regarding the lack of measurability of time due to the effects the clock itself has on space–time (5, 6) argue that the limitation arises from the creation of black holes. We will show that our effect is independent of this effect, too. Moreover, it is significant in a regime orders of magnitude before a black hole is created. Finally, we recover the classical notion of time measurement in the limit where the clocks are increasingly large quantum systems and the measurement precision is coarse enough not to reveal the quantum features of the system. In this way, we show how the (classical) general relativistic notion of time dilation emerges from our model in terms of the average mass–energy of a gravitating quantum system.
From a methodological point of view, we propose a gedanken experiment where both general relativistic time dilation effects and quantum superpositions of space–times play significant roles. Our intention, as is the case for gedanken experiments, is to take distinctive features from known physical theories (quantum mechanics and general relativity, in this case) and explore their mutual consistency in a particular physical scenario. We believe, based on the role gedanken experiments played in the early days of quantum mechanics and relativity, that such considerations can shed light on regimes for which there is no complete physical theory and can provide useful insights into the physical effects to be expected at regimes that are not within the reach of current experimental capabilities.
Clock Model
Any system that is in a superposition of energy eigenstates can be used as a reference clock with respect to which one defines time evolution. The simplest possible case is that in which the clock is a particle with an internal degree of freedom that forms a two-level system. In the following, we assume the clock to follow a semiclassical trajectory that is approximately static, that is, it has (approximately) zero velocity with respect to the observer who uses the clock to define operationally his/her reference frame, in the sense stated in the Introduction. In this way, special relativistic effects can be ignored. We stress the fact that the observer does not need to be located next to the clock. He/she can perform measurements on it by sending a probe quantum system to interact with the clock and then measuring the probe in his/her location. In the following, we focus only on the clock’s internal degrees of freedom, which are the only ones relevant to our model. The internal Hamiltonian of the particle in its rest reference frame,
| [1] |
generates the evolution of the clock. For convenience, we choose the origin of the energy scale so that , and we define .
An operational meaning of the “passage of a unit of time,” in which, by definition, the system goes through a noticeable change from an initial state to a final state, can be given in terms of the “orthogonalization time” of the clock, that is, the time it takes for the initial state to become orthogonal to itself. For a two-level system, the orthogonalization time is equal to (12). Note that quantifies the precision of the clock, and it is, in this sense, a measure of time uncertainty. The optimal initial state of the clock is one with an equal superposition of energies, which we choose to be
| [2] |
For this state, the optimal measurement to determine the passage of time is given by projectors in the basis. It is important to stress that the relation between orthogonalization time and energy difference is fundamental: Any clock model has a precision limited by the difference of energies involved in the time measuring process. This fact was already noticed in earlier works (4, 10). It is this feature, also shared by more-detailed clock models (13), that plays a fundamental role in this work. The fact that the clock can return periodically to its initial state and therefore give ambiguous time readings can be dealt with by choosing a more elaborate clock model, e.g., a system with more energy levels. This fact is irrelevant for the result of this section, and hence we will treat here only the two-level case. This two-level clock model does not aim to describe all of the features involved in time measurements, like, for example, the reconstruction of the “flow of time” from repetitions of measurements (4, 14). Our intention in this section is to point out the minimal requirements for a system to be a clock, i.e., that the system must be in a superposition of energy eigenstates. It follows from these requirements that the orthogonalization time is inversely proportional to the energy gap of the clock. A more elaborate model of a clock, that addresses the issue of repetitive measurements, will be considered in Clocks in the Classical Limit, when studying how the general relativistic notion of time dilation emerges in the classical limit.
The gravitational effects due to the energies involved are to be expected at a fundamental level. In particular, for a given energy of the clock, there is a time dilation effect in its surroundings, due to the mass–energy equivalence. However, because the mass–energy corresponding to the amplitude of is different than that corresponding to , the time dilation in the vicinity of the clock in the state given by Eq. 2 is uncertain (Fig. 1). Consider a second clock localized at a coordinate distance from the first clock (in the reference frame of the before-mentioned observer). Due to time dilation, this clock would run as in flat space–time for the amplitude corresponding to , and it would run (to second-order approximation in ) as , for the amplitude corresponding to the excited state . Here, denotes the gravitational constant, and can be operationally defined as the proper time of the observer, who is sufficiently far away from the mass-energy distribution so that the effects of the different gravitational fields originating from the two states of the clocks are indistinguishable at his/her location. This observer ensures that the coordinate distance between the first observer and the clocks is kept fixed. In SI Appendix, Analysis of the Coordinate t, we quantify the minimum distance between the observer and the clocks such that he/she cannot operationally distinguish between the different gravitational fields.
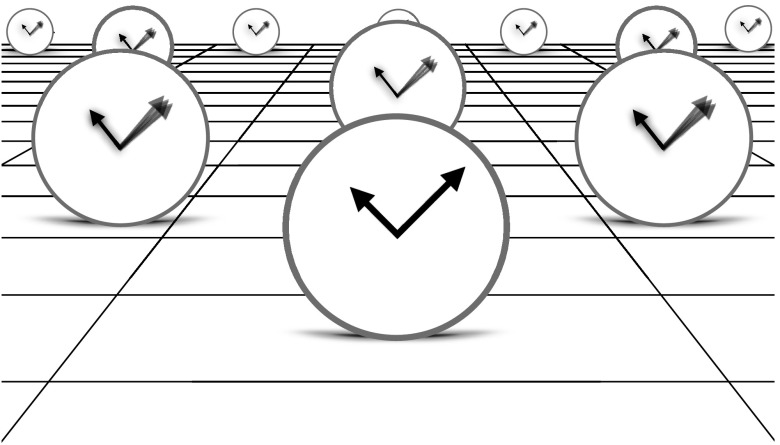
Fig. 1.
Pictorial representation of the fundamental trade-off between uncertainty of time measurement by a given clock and uncertainty of time measurement by nearby clocks. The clock at the frontal plane of the picture has a relatively high accuracy, depicted by its sharply defined hands. The uncertainty of time reading for this clock is inversely proportional to the energy gap of the internal degree of freedom that constitutes the clock (Clock Model). By the mass–energy equivalence, the energy of the clock will produce gravitational time dilation effects on nearby clocks. Because the energy is not well defined but has an uncertainty , nearby clocks will have an uncertainty in their time dilation with respect to the main clock, as depicted by the “fuzzy” hands in a superposition. There exists, therefore, a limitation to the possibility of defining time accurately at nearby points, given by the joint effects of quantum mechanics (superposition principle) and general relativity (gravitational time dilation). This effect is fundamental and independent of the energy gap of the clock, as stated in Eq. 3.
As a consequence of these considerations, there is a fundamental trade-off between the accuracy of measuring time at the location of the clock and the uncertainty of time dilation at nearby points. This trade-off can be succinctly described by the relation
| [3] |
which is an uncertainty relation that arises due to both quantum mechanical and general relativistic effects. It holds independently of the energy gap of the clock or its particular constitution.
So far, our treatment of time dilation in the vicinity of the clock has been classical and nonoperational. In Two Clocks, we explain the above effect in terms of gravitational interaction between quantum clocks.
Two Clocks
Consider two gravitationally interacting clocks, labeled by and , separated by a coordinate distance (in the frame of the far-away observer). To a lowest approximation to the solution of the Einstein equations, the gravitational interaction is described by the Newtonian gravitational energy . In this work, we focus only on the first-order approximation to the solution for the metric. However, post-Newtonian corrections can be analyzed in the same manner. The labels and refer to the masses of particles and , respectively. By these masses, we mean the whole mass–energy contribution to the gravitational field, including both static rest mass and the dynamical mass, corresponding to the energy of the internal degrees of freedom . This notion of dynamical mass is of a purely relativistic nature, and arises from the interaction of the constituents of our composite particle. In fact, from a relativistic point of view, there is conceptually no difference between mass and interaction energy, and their distinction is, effectively, a matter of the energy scale with which the system is probed. The interaction can be described in quantum mechanical terms by promoting the masses of each particle to operators and using the mass–energy equivalence: . For reasons of simplicity, we assume that the static mass is negligibly small compared with the dynamical one and focus only on the effect due to the internal degrees of freedom. Thus, the Hamiltonian for the two-clock system is
| [4] |
A full derivation regarding how the internal degree of freedom of a quantum particle evolves in perturbative general relativity is given in refs. 12 and 15. For a heuristic discussion of Eq. 4 based on the superposition principle and the mass–energy equivalence, see SI Appendix, Heuristic Derivation of the Two-Clock Hamiltonian. The same Hamiltonian can be obtained from a field theory perspective by the restriction to the two-particle sector of the field (16) and the use of the mass–energy equivalence, as we sketch in SI Appendix, Two-Clock Hamiltonian from Quantum Field Theory Approach. Although the methods presented here suffice to describe the entanglement of clocks arising from gravitational interaction, a full description of the physics with no background space–time would require a fundamental quantum theory of gravity. In the works of Rovelli (17) and Isham (18), for example, it is suggested that time itself emerges from the dynamics of more fundamental degrees of freedom.
Let us assume that the energies of both Hamiltonians and are equal and that the initial state of the clocks is uncorrelated: . The state at time according to the far-away observer is
| [5] |
where , and .
We see from Eq. 5 that the clocks get entangled through gravitational interaction: The rate at which time runs in one clock is correlated to the value of the energy of the other clock. The state gets maximally entangled for the time Using dimensionless variables in Planck units, , , and , where is the Planck length, is the Planck time, and is the Planck energy, this time is expressed as , in Planck time units. As we approach , the reduced state of any of the clocks approaches the maximally mixed state and the clock is no longer able to function as a proper clock, because, when we “ask the clock for the time,” we get only random answers. Note that the presence of a static mass in the Hamiltonian would not alter the value of , as it would not enter in any part of the Hamiltonian that contributes to the entanglement between clocks. Specifically, the terms , , and do not create any entanglement between and , and do not change , whereas the term does.
It is important to point out that, for this effect to arise, it is crucial that we consider the internal energy of the clocks as a quantum operator, instead of just taking into account the expectation value of the energy, as is done in semiclassical gravity. To explain this point, let us describe the evolution of clock under the influence of clock , but with replaced by its expectation value. We assume that the initial state of both clocks is . Following refs. 12 and 15, the evolution equation for clock is , where is the derivative of the proper time with respect to . By taking the expectation value of , we have , to first order in . Therefore, the state of at time is . Because the situation is symmetric between and , we can apply the same argument for and obtain, after evolution, a joint state of the form , where has the same form of but with the labels and interchanged. Then we have shown that, in the semiclassical approach, the clocks do not get entangled, and the only result is an overall time dilation of one clock due to the mean energy of the other clock. We will see in Clocks in the Classical Limit that this situation is effectively recovered in the classical limit of clocks.
Note that, after , the purity of the reduced system will increase again. This fact is a consequence of the unitarity of the evolution of the composite system.
The effect presented here has a fundamental influence on the measurement of time that follows only from quantum mechanics and general relativity in the weak-field limit. It is independent of the usual argument concerning limitations of the measurability of space–time intervals due to black hole formation (5, 6). As we will see in N + 1 Clocks, the effect is significant in a parameter regime that occurs long before formation of black holes becomes relevant. To strengthen the effect, we next consider gravitationally interacting clocks, for .
N + 1 Clocks
Now suppose there are clocks contained in a region of space characterized by the coordinate distance . This array of clocks constitutes a reference frame in the sense discussed in the Introduction. We ask the question of how the functioning of a single clock is affected by the presence of the other clocks. To give a lower bound on the effect, we can consider to be the largest coordinate distance between any pair of clocks and write a generalization of the interacting Hamiltonian of Two Clocks,
| [6] |
where the indices and label each of the individual clocks. In this part, we concentrate only on the interacting part of the Hamiltonian, because we wish to analyze the loss of coherence of the reduced state of a single clock. We therefore analyze the evolution in the interaction picture. For an initial state of the form , the reduced state of the zeroth clock is
| [7] |
Interestingly, the time for maximal mixing is independent of and is equal to from the two-clock case. However, coherence can be significantly reduced for times earlier than . To quantify this, we use the visibility , defined by (twice) the absolute value of the nondiagonal element of the density operator.
In our case,
for . From here, we identify a decoherence time that is, back in the initial units,
| [8] |
This characterizes the fundamental limit on the time after which quantum clocks lose their ability to measure time when their gravitational effects are taken into account.
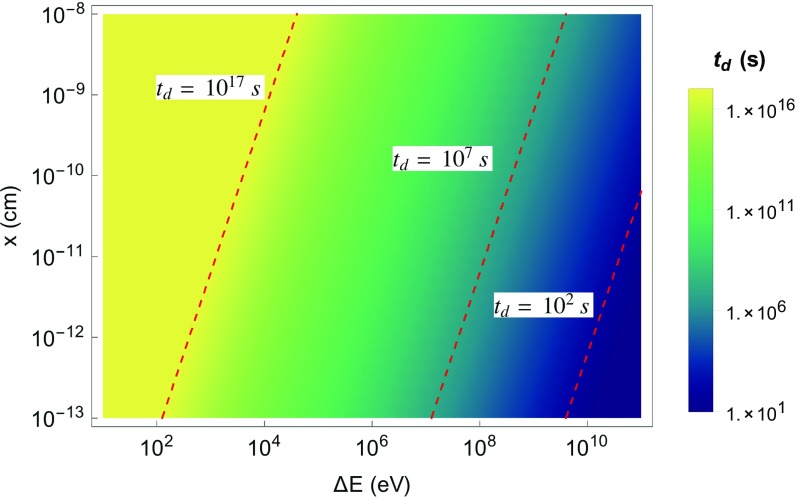
We now give an estimate of the parameter regime where decoherence is significant. The calculations are done ignoring all effects external to our model and should be understood in terms of a gedanken experiment. The intention is to contrast the predictions given by our model with the usual predictions given by quantum gravity models, which do not expect limitations due to the combined effects of quantum mechanics and general relativity before the Planck scale. (For a discussion of the role of the Planck scale in the possibility of defining time, see refs. 5, 19, and 20). Fig. 2 shows the decoherence time as a function of the energy gap and the distance for a macroscopic number of particles . Despite the fact that the effect is very small with respect to the regimes of current atomic clocks, it is important to analyze the order of magnitude of the limitations from a conceptual point of view. For instance, for a distance cm (the order of magnitude of the charge radius of a proton), an energy gap of , which is comparable to, for example, the energy of the nuclear bound state of a particle in 4He (21), and a macroscopic number of particles , we find . The important point is that the regime of these parameters is several orders of magnitude away from the Planck scale. It is also important to note that, for these values of , , the Schwarzschild radius [where and is the total energy] is of the order of m, so that the effect we predict is orders of magnitude away from the regime where a black hole is formed.
Fig. 2.
Clock decoherence time of Eq. 8 as a function of the clocks’ energy gap () and the separation between clocks () for a macroscopic number of particles . The dotted lines show three different decoherence time regimes for different scales of and : s (the order of the age of the universe), s (the order of 1 year), and 100 s. Note that the blue region, showing relatively short decoherence times, corresponds to energies and distances far from the Planck scale regime, suggesting a breakdown of the measurability of time at larger distance and lower energy scales.
To end this section, we note that, despite the fact that this effect is not large enough to be measured with the current experimental capabilities, it might be possible to perform experiments on analog systems to test this effect. Specifically, in ref. 22, the authors consider an atom traversing an oscillating quantum reference frame, and show that the phase of the wave function of the atom has an uncertainty that can be related to the uncertainty in the atom’s elapsed proper time. By the equivalence principle, it is possible to interpret the acceleration that the oscillating reference frame induces on the atom as the gravitational effect that one clock suffers as a consequence of the presence of another nearby clock.
Clocks in the Classical Limit
Given the ill-definedness of time measured by a single clock when it is in the presence of other clocks, how does the classical notion of a clock, including relativistic time dilation effects, arise? In what follows, we answer this question by considering the classical limit of our model. The quantum state that is closest to the classical state of a clock is a spin or atomic coherent state. In general, spin coherent states can be defined as and can be understood in terms of a spin pointing in the direction given by the polar angles and . This picture is convenient because it admits a Bloch sphere representation. We assume that the initial state of the clock is in a spin coherent state:
The Hamiltonian that evolves the state of this clock is the extension to angular momentum of the two-level () Hamiltonian presented above. In terms of the angular momentum operator in the direction, , Eq. 1 is written as . Therefore, for a spin- system, the corresponding Hamiltonian is
| [9] |
where . Note that the spectrum of this Hamiltonian is nonnegative, ensuring the nonnegativity of the mass when considering the mass–energy equivalence.
One of the approaches to the classical limit from within quantum mechanics is based on an experimental resolution that is coarse enough not to reveal the quantum features of the system (23). In our case, we consider coarse-grained time measurements characterized by the experimental resolution . The positive operator-valued measure (POVM) corresponding to these measurements is defined by , with
| [10] |
We can picture this POVM as dividing the Bloch sphere into “bins.” The coherent state evolves by moving along the -direction, in the equator of the sphere. Then, the probability that a measurement yields units, i.e., the probability for a spin coherent state to be in the th bin is , where is the Husimi function, or function, of the density matrix . The characteristic width of this function is proportional to , and, therefore, in the regime where but still , the probability for the pointer of the clock to be found in more than one bin becomes negligible. Consequently, all of the fluctuations due to the quantum nature of the system are not visible in this regime, and the clock behaves effectively classically. Note also that, after a coarse-grained measurement that finds the state of the clock in a particular bin, such a state is effectively nonperturbed, because the part of it that lies outside the bin of size is negligible and, therefore, a projection on the region corresponding to the bin will not alter the state significantly. Therefore, the clock will effectively continue its classical behavior after measurement (24).
Consider now two clocks, labeled by and , each of them being initially in a coherent state and interacting gravitationally with each other. For full generality, we suppose that the () clock is a system with total spin (). The full Hamiltonian is
| [11] |
where () have the form 9. For the initial state , the reduced state for the clock at time is
| [12] |
where . Let us analyze closely this equation. It consists of a sum of coherent states, each of them evolving with a phase , modulated by a binomial distribution. The typical width of these coherent states depends on . The state is measured by the coarse-grained POVM of Eq. 10. When is large and , it is expected that each coherent state is significantly different from zero only inside one bin. This applies also for noninteracting clocks and . However, in the presence of interaction, the coherent states in the mixture of Eq. 12 evolve with different time dilation factors, given by each of the phases .
There are two effects, different in nature, whose relative contributions to the evolution of give us the regime of parameters that defines the classical limit. The situation is depicted in Fig. 3. First, there is the “evolution of the clock as a whole,” that is, the movement of the average phase of the clock . This phase, which corresponds to the pointer with the highest probability for detection, evolves time-dilated due to the average energy of the clock . Second, coherent states tend to spread from each other, leading eventually to a mixing of the reduced state and therefore to ill-definedness of time measurements. To quantify these two effects, we note, on the one hand, that the evolution of the time dilation part of the average phase is proportional to . On the other hand, despite the fact that the angle separation of the coherent states is also proportional to , not all of the terms in 12 contribute significantly to the state, due to the binomial distribution . Indeed, for large , can be approximated by a Gaussian distribution, that is, , which has a characteristic width proportional to . This means that the effective angle separation between coherent states grows with , rather than with ; that is, . Therefore, for times much smaller than a characteristic time
| [13] |
say , where , the angle separation will grow as , but we will have , which grows as for large values of . Therefore, for this scaling with respect to and in the limit where , we reach the regime where the classical limit of clocks holds, because entanglement is negligible at these scales. If, apart from this characteristic time , we have a coarse enough measurement, i.e., , measurements of time will detect time dilation, as classical general relativity predicts, but with no “quantum fluctuations.” Significantly, the time dilation factor corresponds to the average energy of clock , consistent with the semiclassical approximation to gravity in the quantum domain.
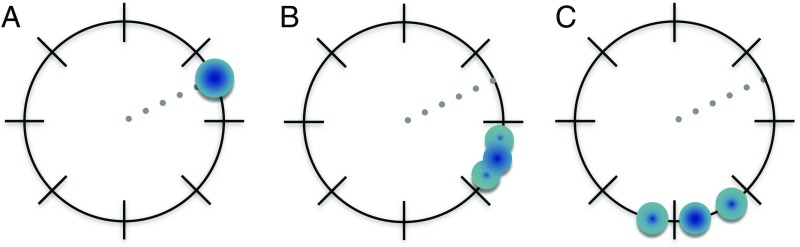
Fig. 3.
Emergence of the classical notion of general relativistic time dilation from the assumption of clocks in coherent states and coarse-grained measurements. Two coherent state clocks with spins and interact gravitationally. The reduced state for the clock is a sum of coherent states modulated by a binomial distribution (Eq. 12). The Husimi function of each coherent state is represented by a blue circle that precesses along the black circumference as it evolves. Each state in the mixture precesses at a different time dilation rate. The darker the color of the circle representing the Husimi function at one location, the higher the probability of finding the clock pointer at that location. We consider a time measurement POVM that gives the probability of finding the clock state in one of the bins that divide the circle. The finite size of the bins represents the finite experimental resolution . There are two effects that contribute to the classical limit: the average motion of the clock and the separation of the different Husimi functions. The average motion of the clock grows as , whereas the effective separation of the coherent states is proportional to (Clocks in the Classical Limit). In A, we depict the initial condition: All of the Husimi functions are centered at the same point. As they evolve, the Husimi functions spread. (B) For and , all of the coherent states lie inside one bin and no “quantum fluctuations” occur when measuring time. The clock is time-dilated according to the average energy of the clock . (C) For , different Husimi functions occupy different bins, and the effects of the quantum entanglement between the clocks emerge despite the coarseness of the measurement.
The evolution of the reduced state can also be studied in terms of its master equation. Following ref. 15, where a full treatment of the master equation for systems of particles evolving in the presence of relativistic time dilation is given, the master equation in this case can be written as
| [14] |
where We note that the first term, corresponding to the unitary part of the evolution, has a time dilation factor that corresponds to the mean energy of the clock. On the other hand, the second term, responsible for decoherence and quadratic in , is proportional to the square of the variance, . We then see that, in a state of clock where the variance of the energy is negligible, clock evolves unitarily with a time-dilation factor given by the average energy of clock , just as expected for a quantum state of matter in the semiclassical limit, where its energy–momentum tensor operator is replaced by its average value. For completeness, we derive Eq. 14 in SI Appendix, Derivation of the Master Equation, following closely ref. 15. We show that the derivation of the master Eq. 14 holds, in general, for any quantum system and any form of the Hamiltonians and . This fact implies that, as long as the initial state of the clocks is not in an energy eigenstate (a condition needed for the system to be a clock), the second term in Eq. 14 will be nonzero, as the variance of the energy will not vanish; implying that, irrespective of the nature of the clocks, they will get entangled.
Finally, in the light of the analysis of the present section, let us now return to Eq. 3, obtained via a heuristic semiclassical argument in Clock Model, and show that it can also be derived from the classical limit of two interacting clocks, connecting the heuristic arguments based on the superposition principle and gravitational time dilation to our treatment of interacting clocks in the classical limit. Consider the two-clock scenario at the beginning of this section with and . We will analyze the limit in which the time dilation of clock due to clock is significant [that is, is nonnegligible], but the time dilation effect on due to can be neglected, i.e., . Let us focus first on clock . Its reduced state after evolution is given by , with , . We now define the operator
| [15] |
Physically, this operator represents the pointer position of clock and has physical dimensions of time. In the limit , spin coherent states are orthonormal, and, therefore, the state becomes an eigenstate of with eigenvalue , for and . Using this fact, it is easy to show that, in this limit, the variance of the operator is given by
| [16] |
On the other hand, the probability of measuring one unit of time on clock is given by the operator . Operationally, the time it takes for the average of to change significantly is given by , where the bars denote absolute value. We can now compute for the reduced state of clock , , with . Because, by assumption, the time dilation effect of clock on clock is negligible, we take into account only the contribution to , yielding the result . Putting the pieces together, we get
| [17] |
which coincides with Eq. 3 up to a factor of .
Discussion
In the (classical) picture of a reference frame given by general relativity, an observer sets an array of clocks over a region of a spacial hypersurface. These clocks trace world lines and tick according to the value of the metric tensor along their trajectory. Here we have shown that, under an operational definition of time, this picture is untenable. The reason does not only lie in the limitation of the accuracy of time measurement by a single clock, coming from the usual quantum gravity argument in which a black hole is formed when the energy density used to probe space–time lies inside the Schwarzschild radius for that energy. Rather, the effect we predict here comes from the interaction between nearby clocks, given by the mass–energy equivalence, the validity of the Einstein equations, and the linearity of quantum theory. We have shown that clocks interacting gravitationally get entangled due to gravitational time dilation: The rate at which a single clock ticks depends on the energy of the surrounding clocks. This interaction produces a mixing of the reduced state of a single clock, with a characteristic decoherence time after which the system is no longer able to work as a clock. Although the regime of energies and distances in which this effect is considerable is still far away from the current experimental capabilities, the effect is significant at energy scales that exist naturally in subatomic particle bound states.
These results suggest that, in the accuracy regime where the gravitational effects of the clocks are relevant, time intervals along nearby world lines cannot be measured with arbitrary precision, even in principle. This conclusion may lead us to question whether the notion of time intervals along nearby world lines is well defined. Because the space–time distance between events, and hence the question as to whether the events are space-like, light-like, or time-like separated, depend on the measurability of time intervals, one can expect that the situations discussed here may lead to physical scenarios with indefinite causal structure (25). The notion of well-defined time measurability is obtained only in the limit of high-dimensional quantum systems subjected to accuracy-limited measurements. Moreover, we have shown that our model reproduces the classical time dilation characteristic of general relativity in the appropriate limit of clocks as spin coherent states. This limit is consistent with the semiclassical limit of gravity in the quantum regime, in which the energy–momentum tensor is replaced by its expectation value, despite the fact that, in general, the effect cannot be understood within this approximation.
The operational approach presented here and the consequences obtained from it suggest that considering clocks as real physical systems instead of idealized objects might lead to new insights concerning the phenomena to be expected at regimes where both quantum mechanical and general relativistic effects are relevant.
Supplementary Material
Acknowledgments
We thank F. Costa, A. Feix, P. Hoehn, W. Wieland, and M. Zych for interesting discussions. We acknowledge support from the John Templeton Foundation, Project 60609, “Quantum Causal Structures,” from the research platform “Testing Quantum and Gravity Interface with Single Photons” (TURIS), and the Austrian Science Fund (FWF) through the special research program “Foundations and Applications of Quantum Science” (FoQuS), the doctoral program “Complex Quantum Systems” (CoQuS) under Project W1210-N25, and Individual Project 24621.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1616427114/-/DCSupplemental.
References
- 1.Brown HR. 2009. The behaviour of rods and clocks in general relativity, and the meaning of the metric field. arXiv:0911.4440.
- 2.Taylor EF, Wheeler JA. Exploring Black Holes: Introduction to General Relativity. Addison Wesley Longman; New York: 2000. [Google Scholar]
- 3.Einstein A. 1979. Albert Einstein: Autobiographical Notes. trans ed Schilpp PA (Open Court, Chicago)
- 4.Salecker H, Wigner EP. Quantum limitations of the measurement of spacetime distances. Phys Rev. 1958;109:571–577. [Google Scholar]
- 5.Amelino-Camelia G. Limits on the measurability of spacetime distances in (the semiclassical approximation of) quantum gravity. Mod Phys Lett A. 1994;9:3415–3422. [Google Scholar]
- 6.Gambini R, Porto RA, Pullin J. Realistic clocks, universal decoherence, and the black hole information paradox. Phys Rev Lett. 2004;93:240401. doi: 10.1103/PhysRevLett.93.240401. [DOI] [PubMed] [Google Scholar]
- 7.Mandelstam L, Tamm I. The uncertainty relation between energy and time in non-relativistic quantum mechanics. J Phys. 1945;9:249–254. [Google Scholar]
- 8.Fleming GN. A unitarity bound on the evolution of nonstationary states. Nuovo Cimento A. 1973;16:232–240. [Google Scholar]
- 9.Margolus N, Levitin LB. The maximum speed of dynamical evolution. Physica D. 1998;120:188–195. [Google Scholar]
- 10.Aharonov Y. Measurement of time of arrival in quantum mechanics. Phys Rev A. 1998;57(6):4130–4139. [Google Scholar]
- 11.Muga G, Sala MR, Egusquiza I, editors. Time in Quantum Mechanics. Vol 1 Springer; New York: 2007. [Google Scholar]
- 12.Zych M, Costa F, Pikovski I, Brukner Č. Quantum interferometric visibility as a witness of general relativistic proper time. Nat Commun. 2011;2:505. doi: 10.1038/ncomms1498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bužek V, Derka R, Massar S. Optimal quantum clocks. Phys Rev Lett. 1999;82(10):2207–2210. [Google Scholar]
- 14.Ranković S, Liang Y-C, Renner R. Quantum clocks and their synchronisation – the alternate ticks game. arXiv:1506.01373. [Google Scholar]
- 15.Pikovski I, Zych M, Costa F, Brukner Č. Universal decoherence due to gravitational time dilation. Nat Phys. 2015;11:668–672. [Google Scholar]
- 16.Anastopoulos C, Hu BL. Problems with the Newton–Schroedinger equations. New J Phys. 2014;16:085007. [Google Scholar]
- 17.Rovelli C. Time in quantum gravity: An hypothesis. Phys Rev D. 1991;43:442–456. doi: 10.1103/physrevd.43.442. [DOI] [PubMed] [Google Scholar]
- 18.Isham CJ. Canonical quantum gravity and the problem of time. In: Ibort LA, Rodrguez MA, editors. Integrable Systems, Quantum Groups, and Quantum Field Theories. Springer; New York: 1993. pp. 157–287. [Google Scholar]
- 19.Ng YJ, Van Dam H. Limit to spacetime measurement. Mod Phys Lett A. 1994;9:335–340. [Google Scholar]
- 20.Padmanabhan T. Limitations on the operational definition of spacetime events and quantum gravity. Class Quantum Grav. 1987;4:L107–L113. [Google Scholar]
- 21.Akaishi Y, Toshimitsu Y. Nuclear K bound states in light nuclei. Phys Rev C. 2002;65:044005. [Google Scholar]
- 22.Katz BN, Blencowe MP, Schwab KC. Mesoscopic mechanical resonators as quantum noninertial reference frames. Phys Rev A. 2015;92:042104. [Google Scholar]
- 23.Kofler J, Brukner Č. Classical world arising out of quantum physics under the restriction of coarse-grained measurements. Phys Rev Lett. 2007;99:180403. doi: 10.1103/PhysRevLett.99.180403. [DOI] [PubMed] [Google Scholar]
- 24.Kofler J, Brukner Č. Conditions for quantum violation of macroscopic realism. Phys Rev Lett. 2008;101:090403. doi: 10.1103/PhysRevLett.101.090403. [DOI] [PubMed] [Google Scholar]
- 25.Oreshkov O, Costa F, Brukner Č. Quantum correlations with no causal order. Nat Commun. 2012;3:1092. doi: 10.1038/ncomms2076. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.