LIGO and the opening of a unique observational window on the universe

Abstract

A unique window on the universe opened on September 14, 2015, with direct detection of gravitational waves by the Advanced Laser Interferometer Gravitational-Wave Observatory (LIGO) detectors. This event culminated a half-century effort around the globe to develop terrestrial detectors of adequate sensitivity to achieve this goal. It also happened appropriately only a few months before the centennial of Einstein’s final paper introducing the general theory of relativity. This detection provided the surprising discovery of a coalescing pair of “heavy” black holes (more massive than $\simeq 25$ M$\mathrm{๏}$) leading to the formation of a spinning $\simeq$62 solar mass black hole. One more binary black-hole detection and a significant candidate event demonstrated that a population of such merging binaries is formed in nature with a broad mass spectrum. This unique observational sample has already provided concrete measurements on the coalescence rates and has allowed us to test the theory of general relativity in the strong-field regime. As this nascent field of gravitational-wave astrophysics is emerging we are looking forward to the detection of binary mergers involving neutron stars and their electromagnetic counterparts, as well as continuous-wave sources, supernovae, a stochastic confusion background of compact-object mergers, known sources detected in unexpected ways, and completely unknown sources.

Historical Context—The Long Road to Detection

On September 14, 2015, the Laser Interferometer Gravitational-Wave Observatory (LIGO) directly detected gravitational waves from the inspiral and final merger (i.e., coalescence) of a pair of “heavy” black holes (1). This observation signals the end of a century-long journey that began in 1915 when Albert Einstein finalized his general theory of relativity (2). Six months later, in the summer of 1916, he published a paper exploring the weak-field approximation to the gravitational field equations and showed that gravitational waves would be generated by a time-varying quadrupole moment of a mass distribution (3, 4). (In this February 1918 paper he expanded the analysis in ref. 3 and corrected errors that had been present in his earlier paper.) Einstein himself doubted that gravitational waves could ever be detected: Upon calculating the rate of energy radiated in the quadrupole approximation, he noted that the leading coefficient was $\approx 2\mathrm{\times }{10}^{-27}$ and concluded that in all conceivable cases the amount of radiation generated would be vanishingly small (3). Moreover, in the decades after his 1916 paper, there was debate whether gravitational waves actually carried away energy from the source or whether they were an artifact of coordinate transformations. [In fact, over the next decade Einstein reversed himself several times on whether gravitational waves existed, prompting Sir Arthur Stanley Eddington in 1922 (ref. 5, p. 269) to quip that apparently “gravitational waves propagate at the speed of thought”.]

It was not until 40 years later, in the late 1950s, that Pirani described the theoretical framework within which one could experimentally determine the (time-dependent) components of the Riemann tensor and thereby detect gravitational waves (6, 7). In early 1957, a conference on the role of gravitation in physics, sponsored by the US Air Force, was held at Chapel Hill, North Carolina (8). At this conference, Pirani, Bondi, Feynman, and others extensively discussed the physical reality of gravitational waves; the attendees left the conference having concluded that not only did these waves carry energy away from the source, but also one could conceive of building a detector that would respond to them, thereby transducing their energy into measurable electrical signals. Saulson notes that Joe Weber attended the conference and participated in these discussions; within several years of the conference Weber was designing the first resonant bar detector for gravitational waves (9).

The invention of the laser in 1960 opened the way for a different way to measure the fluctuations of the space–time metric induced by gravitational waves. Shortly thereafter the notion of using a laser interferometer as a transducer for measuring gravitational wave strain was first considered by Gertsenshtein (10) and then by Gertsenshtein and Pustovo$\stackrel{⌣}{\text{i}}$t (11).

The first prototype gravitational wave interferometer was built by Forward, a former student of Weber, in 1971 (12). In 1972 Rai Weiss at the Massachusetts Institute of Technology (MIT), then unaware of the Gertsenshtein and Pustovo$\stackrel{⌣}{\text{i}}$t paper but aware of Pirani’s earlier work, formulated the phase-sensitive response of a Michelson interferometer to impinging gravitational waves (13). His detailed analysis of the interferometer–gravitational-wave interaction in such an apparatus is a prescient and thorough tour de force, not only addressing the astrophysical aspects of a gravitational wave interferometer, but also identifying and discussing the limiting noise sources that would challenge an implementation of such a detector on Earth. In working out order-of-magnitude numbers, he explicitly assumed that a kilometer-length scale would be required. That unpublished research note may be considered the first rough but essentially complete “blueprint” for LIGO. It is doubtful that those who embarked on this scientific quest would have guessed that it would take another 44 years to finally realize the goal outlined by Weiss in 1972. In parallel with Weiss’s work, the group at the Max Planck Institute for Quantum Optics in Garching, Germany also pursued the detection of gravitational waves, using a prototype suspended interferometer (14–16).

Initial LIGO—The Era of Upper Limits

The discovery of the first binary pulsar system PSR B1913+16 by Hulse and Taylor (17) and subsequent observations of its energy loss by Taylor and Weisberg (18) firmly demonstrated the existence of gravitational waves in nature. By the late 1970s the world of physics was ready for the hunt for gravitational waves. The story of LIGO continued in the 1980s when, after discussions with Weiss, Kip Thorne at California Institute of Technology (Caltech) became convinced that this quest was worth the effort and began a campaign to get Caltech engaged in and committed to building an interferometer capable of detecting gravitational waves. Thorne convinced Ron Drever, who was then at the University of Glasgow, to join him at Caltech to start a research program there. The years 1972–1989 saw the continued conceptual development, improvement, and proof-of-principle experimentation. Much of the work was funded in the United States by the National Science Foundation, which strongly encouraged Caltech and MIT to collaborate on this ambitious program.

During these years the Europeans pursued similar goals in Italy, Germany, France, and the United Kingdom. Alain Brillet from the French CNRS and Adalberto Giazotto from the Italian Istituto Nazionale di Fisica Nucleare (INFN) led an Italian–French effort and created the Virgo Collaboration in the late 1980s to build a 3-km detector near Pisa, Italy (19). About the same time, Jim Hough from the University of Glasgow and Albrecht Rüdiger from the Max Planck Institute for Quantum Optics formed the British/German interferometer collaboration (GEO) and proposed a 3-km interferometer to be built in Germany (20). The reunification of Germany occurred during this epoch and the scope of the GEO detector was ultimately scaled down to 600 m and was constructed outside Hannover, Germany.

In the United States, also in 1989, a joint proposal for LIGO, consisting of two widely separate sites in the United States with 4-km interferometers, was submitted by Caltech and MIT to the National Science Foundation (21, 22). After intense scrutiny and extended peer review, it was funded for construction in 1992. Construction began in earnest in 1994; LIGO was dedicated in the fall of 1999. LIGO consists of two observatories, one [LIGO Hanford Observatory (LHO)] in eastern Washington state, 23 km north of the city of Richland, and the other (LIGO Livingston Observatory) in Louisiana, 33 km east of Baton Rouge (https://www.ligo.caltech.edu). The initial LIGO era witnessed a heroic effort to commission this cutting-edge technology and to achieve the design goals for this first generation of kilometer-scale interferometers (23). The initial LIGO era spanned the period 2002–2010, during which a series of six science runs (S1...S6) with improving sensitivity and increasing duration were carried out by the LIGO Scientific Collaboration (ligo.org). Science run S5 (2005–2007) witnessed LIGO achieving its promised design sensitivity; enhancements beyond the original design were introduced during S6 (2009–2010). During S6 LIGO exceeded by $\mathrm{\sim }$20% its design amplitude sensitivity as measured by the (antenna pattern-averaged and source orientation-averaged) distance to which it could detect with signal-to-noise ratio of $\mathrm{\sim }$8 a pair of binary neutron stars each of mass 1.4 M$\mathrm{๏}$ out to $\simeq 20$ megaparsecs (Mpc).

Observations during the initial-LIGO era led to over 100 publications of observational limits on the strength and frequency of occurrence of gravitational waves from a broad range of putative gravitational wave sources. These sources include (i) compact binary coalescences—neutron star (NS) pairs (BNS or NS+NS), black-hole (BH) neutron systems (BH+NS), and black-hole pairs (BBHs or BH+BH)—having well-understood modeled frequency–time evolution of signal waveforms; (ii) transient burst sources without modeled waveforms [supernovae (SNe) and other short-duration waveforms]; (iii) continuous (essentially monochromatic) signals from rotating neutron stars having nonaxisymmetric deformations—the gravitational-wave counterparts to electromagnetic (EM) pulsars; and (iv) broadband stochastic gravitational-wave background detectable by its cross-power in the strain signals from pairs of detectors [this is the gravitational-wave counterpart to the cosmic microwave background (CMB) or coming from a population of unresolved distant sources falling into one or more of the previous three categories]. The observational upper limits on compact-object coalescence rates were of moderate astrophysical interest, although the upper limits for binary black holes came to within a factor of 2 greater than the most optimistic model predictions (24–26).

Some of the more noteworthy results from initial LIGO include the following: precluding that the progenitor of GRB 070201 could have been a binary neutron star in M31 (the EM error box included a portion of M31) (27); limiting the maximum possible energy loss of the Crab pulsar to less than $\mathrm{\sim }$1% of its observed rotational energy loss and limiting the maximum possible axial asymmetry to $\mathit{\epsilon }\mathrm{\equiv }\left(I_1-I_2\right)/I_3\mathrm{\le }9\mathrm{\times }{10}^{-5}$ (28); and limiting the maximum possible gravitational-wave stochastic energy density (in the LIGO band, around 100 Hz) to ${\mathrm{\Omega }}_{GW}\mathrm{\le }6.9\mathrm{\times }{10}^{-6}$, improving on the indirect bound inferred from Big Bang nucleosynthesis (29).

In the fall of 2010, operation of initial LIGO ceased as preparations to install the Advanced LIGO interferometers commenced.

Advanced LIGO—The Era of Discovery

The design and construction of Advanced LIGO (“aLIGO”) (30, 31) spanned 7 y beginning in 2008. Installation began in 2010 and commissioning began in 2014; by August 2015 both interferometers were operational. Advanced LIGO is an international effort, with in-kind contributions provided by the GEO Collaboration in Europe [funding provided by the Science and Technology Facilities Council (STFC) in the United Kingdom and Max Planck Gesellschaft (MPG) in Germany] and the Australian Consortium for Interferometric Gravitational Astronomy (ACIGA) [funding provided by the Australian Research Council (ARC)]. The key experimental advances included increased laser power, more massive mirrors with better coatings, reduced suspension thermal noise, and a vastly improved seismic isolation system. These improvements led to amplitude sensitivity improvements of factors of 3 or better across the detector frequency range; specifically the latter two improvements improved the sensitivity in the 30- to 200-Hz band by factors of several hundred to about 10. All this resulted to an improvement in volume reach by almost a factor of 30. The aLIGO operations plan (32) called for a sequence of science runs with increasing sensitivity, starting with an initial 3-mo run (O1) in fall 2015 and targeting a NS coalescence distance reach somewhere at 40–80 Mpc (initial LIGO had reached $\simeq$20 Mpc). In reality aLIGO collected $\mathrm{\sim }$47 d of coincident science-quality data for the period of mid-September 2015 to mid-January 2016 with average NS–NS reach of 70–75 Mpc.

On September 14, 2015 at 09:50:45 universal time (UTC), LIGO detected its first event (1). Nature was extraordinarily generous: This first event was clearly evident in minimally processed raw data and cross-correlation, using wavelet transforms with a combined (coherent, two-detector) signal-to-noise ratio (SNR) of $\simeq 24$. In the subsequent analysis, the event turned out to be a greater than 5.1$\sigma$ signal, corresponding to a false alarm probability (FAP) of $\mathrm{\le }2\mathrm{\times }{10}^{-7}$, or once in 203,000 y for the dataset containing the event. The signal came from the coalescence of a binary black-hole system with individual masses $\simeq$36 M$\mathrm{๏}$ and $\simeq$29 M$\mathrm{๏}$ and was consistent with the ringdown signature of the resulting excited black hole of mass $\simeq$62 M$\mathrm{๏}$.

This first signal was actually so strong that no prior assumption of a coalescence signal was needed to discover the signal; the unmodeled wavelet-analysis–based burst search found it at high significance, having a search false alarm rate of less than one event in 22,500 y (33). This first run exceeded all expectations: A second binary black-hole merger was detected with similar high significance greater than 5$\sigma$ on December 26, 2015 at 03:38:53.647 UTC. The individual masses for this second event were $\simeq$14 M$\mathrm{๏}$ and $\simeq$7.5 M$\mathrm{๏}$. Further, a third, less significant signal was detected on October 12, 2015, termed LIGO-Virgo Trigger (LVT)151012. Because the event had lower significance (1.7$\sigma$, false alarm rate of $\mathrm{\sim }$0.37 y⁻¹), it could not be claimed as a detection; however, signal consistency tests show no signs of a noise origin—it is more likely to be of astrophysical origin than not (34).

The First LIGO Discoveries

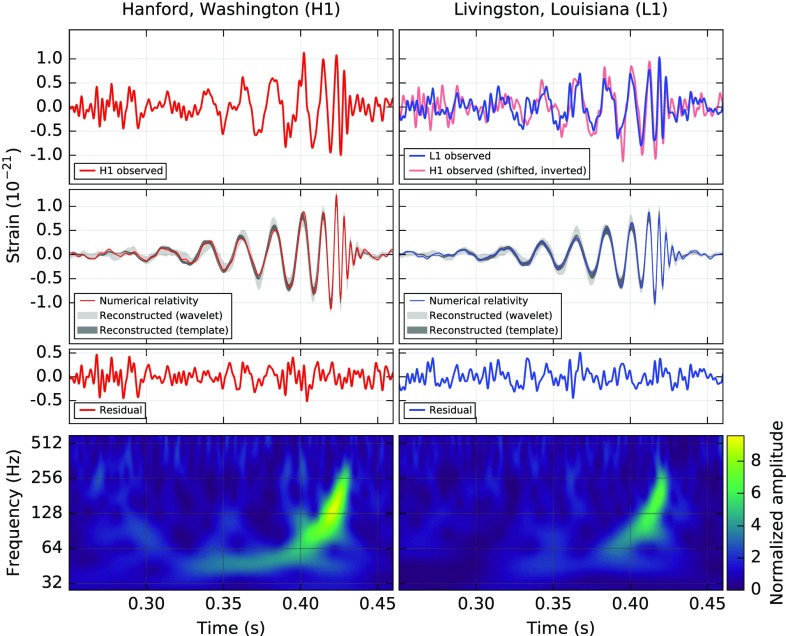
For each event the source properties are estimated assuming that the signal is indeed coming from the coalescence of two compact objects. A Bayesian framework is used with two different sampling methods using many different waveform models calibrated against general relativity (GR); convergence and consistent posterior probability distributions for many parameters are required (35, 36). In the case of the first detection (GW150914), the signal-to-noise ratio is high enough, so that the main mass parameter (chirp mass) of the source can be extracted using a collection of generic wavelets, without having to use coalescence templates. Fig. 1 shows the LIGO data and reconstructed waveforms for GW150914. Even without knowledge of a full coalescence waveform (from post-Newtonian inspiral to merger and ringdown) one can derive basic source properties, just from ($f,\dot{f}$) characteristics of the waveform (37).

Fig. 1.

The first detected gravitational wave event by aLIGO. Shown is the gravitational-wave event GW150914 observed by the LIGO Hanford (H1, Left column) and Livingston (L1, Right column) detectors. Times are shown relative to September 14, 2015 at 09:50:45 UTC. For visualization, all time series are filtered with a 35- to 350-Hz bandpass filter to suppress large fluctuations outside the detectors’ most sensitive frequency band and band-reject filters to remove the strong instrumental spectral lines. Top Left, H1 strain; Top Right, L1 strain. GW150914 arrived first at L1 and ${6.9}_{-0.04}^{+0.05}$ ms later at H1; for a visual comparison, the H1 data are also shown, shifted in time by this amount and inverted (to account for the detectors’ relative orientations). Second row shows gravitational-wave strain projected onto each detector in the 35- to 350-Hz band. Solid lines show a numerical relativity waveform (waveform shown is SXS:BBH:0305 available for download at www.black-holes.org/waveforms) for a system with parameters consistent with those recovered from GW150914 (38, 39) confirmed to 99.9% by an independent calculation based on ref. 40. Shaded areas show 90% credible regions for two independent waveform reconstructions. One (dark gray) models the signal using binary black hole template waveforms (35). The other (light gray) does not use an astrophysical model, but instead calculates the strain signal as a linear combination of sine-Gaussian wavelets (33, 41). These reconstructions have a 94% overlap, as shown in ref. 35. Third row shows residuals after subtracting the filtered numerical relativity waveform from the filtered detector time series. Bottom row shows a time–frequency representation (42) of the strain data, showing the signal frequency increasing over time. Reproduced from ref. 1.

The most important source properties of the ensemble of detections are summarized in Fig. 2.

Fig. 2.

Posterior probability densities of the masses, spins, and distance to the three events GW150914, LVT151012, and GW151226. For the 2D distributions, the contours show $50$% and $90\mathrm{\%}$ credible regions. Top Left shows component masses $m_1^{\text{source}}$ and $m_2^{\text{source}}$ for the three events. The convention is that $m_1^{\text{source}}\mathrm{\ge }{m}_2^{\text{source}}$, which produces the sharp cut in the 2D distribution. For GW151226 and LVT151012, the contours follow lines of constant chirp mass (${\mathcal{M}}^{\text{source}}={8.9}_{-0.3}^{+0.3},\text{M}\mathrm{๏}$ and ${\mathrm{M}}^{\text{source}}={15.1}_{-1.1}^{+1.4},\text{M}\mathrm{๏}$, respectively). In all three cases, both masses are consistent with black holes. Top Right shows the mass and dimensionless spin magnitude of the final black holes. Bottom Left shows the effective spin and mass ratios of the binary components. Bottom Right shows the luminosity distance to the three events. Reproduced from ref. 34.

As Fig. 2 shows, there are important degeneracies that prevent determination of individual properties with high accuracy: (i) The two masses are coupled through the chirp mass, leading to black-hole mass uncertainties of a few solar masses; (ii and iii) spin vectors and mass ratios are correlated (ii), as are distance and inclination (iii); (iv) the two-detector LIGO network could not provide adequate localization (not shown) (figure 6 in ref. 34), which for the sources detected covers extended arcs on the sky of about 200–2,000°². These latter two will improve as additional gravitational wave (GW) detectors join the LIGO network, allowing better constraints on the polarization of the signal; the spins, if magnitudes and tilts are significant, can be better constrained as the number of detections grows and more viewing angles are sampled; however, the binary GW emission pattern favors face-on/-off detections, minimizing precession effects and limiting spin-measurement capabilities.

As Fig. 3 shows, during the 1.6 mo of coincidence data from aLIGO’s first observational run, the population of known stellar-mass black holes was increased by $\mathrm{\sim }$38% beyond the number detected via X-rays during the previous half-century of observations. The masses of the BHs that have been measured to date cover a wide range: from the 5- to 10-M$\mathrm{๏}$ BHs that have been seen mostly in X-ray binaries (XRBs) to the heaviest “stellar-mass” BHs detected so far by LIGO (up to 60–70 M$\mathrm{๏}$). As the detected sample grows, it will be possible to extract the underlying BH mass distribution, correcting for GW observational biases. The high masses already detected point to the need for relativity weak stellar winds and therefore formation environments with subsolar metallicities (43, 44).

Fig. 3.

Measured (red, LIGO) or inferred (blue, X-rays) masses of stellar-mass black holes showing their year of discovery. Letters a and b appended to the LIGO detection labels correspond to the component black holes; the letter f corresponds to the final black hole. In the first observational run with aLIGO (comprising 1.6 mo of coincident data) the number of known black holes in this mass range increased by $\mathrm{\sim }$38% beyond the number of previously known black holes discovered during more than half a century of X-ray observations of accreting systems. Data from ref. 46.

Whereas current conventional astrophysical models of BH–BH coalescences predict that there should be no EM counterparts, given the expected lack of matter, nevertheless, an impressive network of more than 70 observational teams received the LIGO trigger within a couple of days and followed up with observations across the full electromagnetic spectrum. All teams reported upper limits—with the exception of one team with Fermi observations, who reported a potential counterpart (46), a report that spurred significant theoretical speculation as to how matter might still be present during the BH–BH merger (47–55). However, a paper came out questioning the significance of this claim (56), and the space observatories International Gamma-Ray Astrophysics Laboratory (INTEGRAL) and Astrorivelatore Gamma ad Immagini ultra Leggero (AGILE) did not see any evidence of a counterpart (57, 58).

The two detections and the third signal (lower-significance trigger) identified in the O1 data provide the observational data for estimating the rate of BBH coalescences in the nearby universe (out to a redshift $z\mathrm{<}0.5$, the distance to which the most massive of the events could have been detected). Fig. 4 shows the inferred distributions of signal and noise triggers, as well as the combined distribution. The observations are in good agreement with the model (discussed in appendix C of ref. 34). GW150914 stands somewhat above the inferred distribution, as it is an unusually significant event—only 6% of the astrophysical population of sources appearing in the O1 search with a false rate of less than one per century are expected to be more significant than GW150914. It is clear from Fig. 4 that three triggers are more likely to be signal (i.e., astrophysical) than noise (terrestrial). For GW150914 and GW151226, the probability of astrophysical origin is >0.999999, whereas, for LVT151012, it is calculated to be 0.86. The observationally derived probability distribution of BH–BH coalescence rates can be estimated, as shown in Fig. 5. Table 1 lists the posterior median rates and symmetric 90% confidence intervals for the two high-significance events and the lower-significance trigger. The current rate estimates based on a few events are sensitive to assumptions about the underlying mass spectrum of the population: With the growing number of detections it will be possible to constrain the mass distribution and further constrain the rates (59).

Fig. 4.

The cumulative (right to left) distribution of observed triggers in the on-line analysis as a function of the log likelihood. The best-fit signal + noise distribution and the contributions from signal and noise are also shown. The shaded regions show $\mathrm{\pm }1\sigma$ uncertainties. The observations are in good agreement with the model. At low likelihood, the distribution matches the noise model, whereas at high likelihood it follows the signal model. Three triggers are clearly identified as being more likely to be signal than noise. GW150914 stands somewhat above the expected distribution, as it is an unusually significant event—only $6\mathrm{\%}$ of the astrophysical distribution of sources appearing in our search with a false rate of less than one per century will be more significant than GW150914. Reproduced from ref. 34.

Fig. 5.

The posterior density on the rate of BBH mergers. The curves represent the posterior assuming that BBH masses are distributed flat in $\log \left(m_1\right)$ vs. $\log \left(m_2\right)$ (Flat), match the properties of the two detected events and the one less significant event (Event Based), or are distributed as a power law in $m_1$ (Power Law). The posterior median rates and symmetric $90\%$ symmetric credible intervals are given in Table 1. Reproduced from ref. 34.

Table 1.

Rates of BBH mergers based on populations with masses matching the observed events and astrophysically motivated mass distributions

Mass distribution	$R/\left({\text{Gpc}}^{-3}{\text{y}}^{-1}\right)$ combined pipeline results
Event based
GW150914	${3.4}_{-2.8}^{+8.8}$
LVT151012	${9.1}_{-8.5}^{+31.0}$
GW151226	${36}_{-30}^{+95}$
All	${55}_{-41}^{+103}$
Astrophysical
Flat in log mass	${31}_{-21}^{+42}$
Power law ($-2.35$)	${97}_{-67}^{+131}$

Rates inferred by combining the different analyses and median values with 90% credible intervals are shown. Data are from ref. 34.

The full list of derived parameters for the first LIGO detections is shown in Table 2.

Table 2.

Details of the three most significant events detected by LIGO during its first observational run

Event	GW150914	GW151226	LVT151012
Signal-to-noise ratio $\rho$	23.7	13.0	9.7
False alarm rate $\text{FAR}/{\text{y}}^{-1}$	$\mathrm{<}6.0\mathrm{\times }{10}^{-7}$	$\mathrm{<}6.0\mathrm{\times }{10}^{-7}$	0.37
P value	$7.5\mathrm{\times }{10}^{-8}$	$7.5\mathrm{\times }{10}^{-8}$	$0.045$
Significance	$\mathrm{>}5.3\sigma$	$\mathrm{>}5.3\sigma$	$1.7\sigma$
Primary mass $m_1^{\text{source}}/\text{M}\mathrm{๏}$	${36.2}_{-3.8}^{+5.2}$	${14.2}_{-3.7}^{+8.3}$	${23}_{-6}^{+18}$
Secondary mass $m_2^{\text{source}}/\text{M}\mathrm{๏}$	${29.1}_{-4.4}^{+3.7}$	${7.5}_{-2.3}^{+2.3}$	${13}_{-5}^{+4}$
Chirp mass $M^{\text{source}}/\text{M}\mathrm{๏}$	${28.1}_{-1.5}^{+1.8}$	${8.9}_{-0.3}^{+0.3}$	${15.1}_{-1.1}^{+1.4}$
Total mass $M^{\text{source}}/\text{M}\mathrm{๏}$	${21.8}_{-1.6}^{+5.9}$	${21.8}_{-1.6}^{+5.9}$	${37}_{-4}^{+13}$
Effective inspiral spin ${\chi }_{eff}$	$-{0.06}_{-0.14}^{+0.14}$	${0.21}_{-0.10}^{+0.20}$	${0.0}_{-0.2}^{+0.3}$
Final mass $M_f^{\text{source}}/\text{M}\mathrm{๏}$	${62.3}_{-3.1}^{+3.7}$	${20.8}_{-1.7}^{+6.1}$	${35}_{-4}^{+14}$
Final spin $a_f$	${0.68}_{-0.06}^{+0.05}$	${0.74}_{-0.06}^{+0.06}$	${0.66}_{-0.10}^{+0.09}$
Radiated energy $E_{rad}/\left(\text{M}\mathrm{๏}{c}^2\right)$	${3.0}_{-0.4}^{+0.5}$	${1.0}_{-0.2}^{+0.1}$	${1.5}_{-0.4}^{+0.3}$
Peak luminosity $I_{peak}/\left({\text{erg⋅s}}^{-1}\right)$	${3.6}_{-0.4}^{+0.5}\mathrm{\times }{10}^{56}$	${3.3}_{-1.6}^{+0.8}\mathrm{\times }{10}^{56}$	${3.1}_{-1.8}^{+0.8}\mathrm{\times }{10}^{56}$
Luminosity distance $D_L/\text{Mpc}$	${420}_{-180}^{+150}$	${440}_{-190}^{+180}$	${\mathrm{1,000}}_{-500}^{+500}$
Source redshift $z$	${0.09}_{-0.04}^{+0.03}$	${0.09}_{-0.04}^{+0.03}$	${0.20}_{-0.09}^{+0.09}$
Sky localization $\mathrm{\Delta }\mathrm{\Omega }/{\mathrm{deg}}^2$	$230$	$850$	$\mathrm{1,600}$

Source parameters correspond to median values with $90\%$ credible intervals that include statistical errors and systematic errors from averaging the results of different waveform models. The uncertainty for the peak luminosity includes an estimate of additional error from the fitting formula. The sky localization is the $90\%$ credible area. Masses are given in the source frame; to convert to the detector frame multiply by $\left(1+z\right)$. The source redshift assumes standard $\mathrm{\Lambda }\mathrm{C}\mathrm{D}\mathrm{M}$ cosmology (60). Reproduced from ref. 34.

Discovery Implications for General Relativity and for BH–BH Astrophysics

Tests of General Relativity.

The LIGO BBH mergers provide unique strong-field GR tests. The BH velocities cover an astounding range of $\simeq$20–60% the speed of light during the time the signals were in the LIGO band. Never before were relativistic effects observed in this regime—the most relativistic tests with the double-pulsar PSR J0737-3039 involve neutron star velocities $\simeq$0.001 c.

The detected signals allowed the measurement of source parameters; the peak-likelihood parameters were used to produce numerical (general) relativity (NR) waveforms, which have been found to be in excellent agreement with the approximate waveforms and the strain data (34). A number of different quantitative tests were performed and the conclusion was that no deviations from GR can be claimed. Subtracting the best-fit GR coalescence waveform from the data resulted in residuals consistent with the detector noise floor (Fig. 1, Third row). The final BH mass and spin derived from (i) a post-Newtonian analysis of the inspiral part of the signal and (ii) perturbation theory for the ringdown part are both consistent with those derived from the full-waveform analysis that includes the NR dynamical space–time evolution. Alternative theories of gravity can be explored and constraints on their specific parameters can be placed (e.g., ref. 61). However, when the inspiral, merger, and ringdown are expressed as a series of terms with increasing powers in $\frac{v}{c}$, the upper limits on possible deviations of the series coefficients from GR are better than anything that was heretofore possible (62). Finally, by analyzing the time-frequency characteristics of the signals, it was possible to place upper limits on dispersive effects that could be evidence for a finite graviton mass, which is shown in Fig. 6. The dispersion relation follows from the dynamics of a massive graviton. Its propagation speed becomes a function of both mass and energy: $v_g^2/c^2=1-h^2{c}^2/\left({\lambda }_g^2{E}^2\right)$, where its Compton wavelength is given by ${\lambda }_g=h/\left(m_{g}c\right)$. A massive graviton thus propagates at an energy- (and thus frequency)-dependent speed. Further, on general grounds one also expects that the Newtonian potential will be modified by a Yukawa-type correction whose characteristic length scale is determined by ${\lambda }_g$ (see ref. 34 for details).

Fig. 6.

Cumulative posterior probability distribution for ${\lambda }_g$ (black curve) and exclusion regions for the graviton Compton wavelength ${\lambda }_g$ from GW150914. The colored areas show exclusion regions from the double-pulsar observations (turquoise), the static Solar System bound (orange), and the 90% (crimson) region from GW150914. Reproduced with permission from ref. 63, Copyright 2016 by the American Physical Society.

BH–BH Formation Channels.

BH–BH formation has been predicted since the early 1970s, even before the Hulse–Taylor binary pulsar was discovered (63); in fact, BH–BH mergers were proposed as the dominant population among early gravitational-wave detections first by ref. 64. More robustly, BH–BH systems with heavy black holes were predicted because of a number of developments: (i) the downward revision of stellar-wind strengths in recent years (65–67) and (ii) the growing interest in BH–BH formation at stellar environments of lower metallicity compared with the Milky Way (67, 68).

Two qualitatively different BH–BH formation mechanisms have been identified theoretically. The first of these is isolated binary evolution during which interacting binaries composed of massive stars typically undergo common-envelope evolution (for a review see ref. 69). If massive stars are rapid rotators throughout their interiors, then they can undergo a chemically homogeneous evolution: They remain compact, do not interact much, and do not lose much mass before they end up forming heavy black holes (70–72).

The second process is dynamical, whereby BH–BH systems in tight orbits are formed within dense star clusters, such as either the old globulars observable in the present Milky Way and other galaxies or massive young clusters that extend to the superstar-cluster mass scale (for a review see ref. 73). In addition, galactic centers and massive triple systems can also enable BH–BH formation (74–77).

Both formation mechanisms are consistent with the current few LIGO observations (43). The lower-mass systems, GW151226 and LVT151012, need the full range of ages and metallicities present among dense star clusters (44, 78). On the other hand, the chemically homogeneous channel forms only massive systems and so is inconsistent with the two lighter mergers that were observed, but is consistent with GW150914. Additional statistics from more detections will help elucidate and distinguish formation channels. The distribution of chirp/total mass, mass ratios, spin magnitudes, spin tilts, eccentricities, and merger rate as a function of redshift will allow the puzzle to be filled in as more events are observed in the coming years (43).

Prospects for the Future

Advanced LIGO is only at the beginning of its productive lifetime. During the upcoming observational runs planned through the end of 2018, its sensitivity will continue to improve, bringing with it an increase in the event rates that scales as the cube of the instrumental reach: Tens of BH–BH detections are expected, providing an ever-clearer glimpse of the underlying population of these sources (figure 13 in ref. 34). If intermediate-mass black holes exist in merging binary systems with masses of order a few hundreds of solar masses, then LIGO may very well provide secure proof (43). Further, it is apparent from the first detections that the BH–BH population also gives rise to an astrophysical foreground detectable through stochastic background search techniques (79) that are sensitive to mergers far beyond distances to which individual events can be detected. By using both measurements from the stochastic foreground and individual coalescences it may be possible to distinguish among formation mechanisms for binary black holes (80).

In addition, with increased science reach comes the prospect of detecting coalescences of NS–NS and NS–BH binaries involving matter, thereby providing the opportunity for electromagnetic follow-ups to localize and directly determine the distance to the source through redshift measurements. Localization will greatly increase as additional kilometer-scale detectors are added to the global network. The European Advanced Virgo detector (81) is expected to join the two LIGO detectors as a third node in 2017, and the Japanese Kamioke Gravitational Wave Detector (KAGRA) detector (82) is expected to be observing before the end of this decade. The nascent LIGO-India project (83, 84) should bring a third aLIGO detector on line by 2023/2024. As has been shown by a number of studies, adding a third and subsequent nodes to the global detector network will quickly reduce the localization uncertainties from GW detections from many hundreds of square degrees to tens of square degrees or even smaller regions, accessible to electromagnetic observational follow-ups (32, 85). The first observational run did not see any events attributable to mergers containing neutron stars. The published upper limits for mergers involving matter now encroach upon the more optimistic rates deduced from population synthesis models informed by known binary systems containing pulsars detected electromagnetically (ref. 86 and references therein).

Almost a century to the day after the general theory of relativity was published, LIGO detected the weak ripples in the fabric of space–time that Einstein himself doubted could ever be detected. About halfway through since then, radio beacons made it clear gravitational waves are part of nature, but detecting them directly was still very much in doubt. Advanced LIGO’s detection in both amplitude and phase of the dynamic perturbations of the space–time metric itself is unique. We are now poised to explore and discover the gravitational-wave sky, a phrase that many of us have used in describing what we expected once LIGO made its first detection. An analogy may be drawn to where optical astronomy stood after Galileo Galilei first pointed his 37-mm, 20× telescope into the night sky over Padua, Italy in 1609. He immediately perceived previously unsuspected wonders: the craters of the Moon; the miniature “solar system” of the Jovian Galilean moons, which immediately bolstered the Copernican world view; the phases of Venus; and spots on our Sun. And that was just the beginning. True to this analogy, the first detection by LIGO was a surprise. Although binary black-hole systems had been predicted to exist in theoretical arguments, none had been known to exist until LIGO’s first event. Moreover, the pair of black holes were massive. Their merger and disappearance gave rise to a larger spinning black hole: LIGO witnessed this birth—actually “heard” its birth.