Entorhinal–CA3 dual-input control of spike timing in the hippocampus by theta-gamma coupling

SUMMARY

Theta-gamma phase coupling and spike timing within theta oscillations are prominent features of the hippocampus and are often related to navigation and memory. However, the mechanisms that give rise to these relationships are not well understood. Using high spatial resolution electrophysiology, we investigated the influence of CA3 and entorhinal inputs on the timing of CA1 neurons. The theta phase preference and excitatory strength of the afferent CA3 and entorhinal inputs effectively timed the principal neuron activity as well as regulated distinct CA1 interneuron populations in multiple tasks and behavioral states. Feedback potentiation of distal dendritic inhibition by CA1 place cells attenuated the excitatory entorhinal input at place field entry, coupled with feedback depression of proximal dendritic and perisomatic inhibition, allowing the CA3 input to gain control toward the exit. Thus, upstream inputs interact with local mechanisms to determine theta phase timing of hippocampal neurons to support memory and spatial navigation.

eTOC Blurb

Fernandez-Ruiz et al. provide evidence that the phase-precession phenomenon is part of a larger family of spike timing mechanisms and provide a common explanation for all of them. Cooperation of CA3 and entorhinal gamma inputs together with local inhibition determine spike timing.

INTRODUCTION

The entorhinal-hippocampus partnership forms a memory system (Squire, 1992) that relies upon both rate and phase codes (Moser et al., 2008; O’Keefe and Nadel, 1978). Phase codes are related to phase-coupled theta and gamma oscillations and have been examined most often during spatial navigation (Lisman and Jensen, 2013; O’Keefe and Nadel, 1978). Several experiments have described behavior-dependent theta phase changes of various events. First, spike sequences of neurons within theta cycles are temporally compressed representations of the rat’s spatial trajectories (Dragoi and Buzsaki, 2006; Foster and Wilson, 2007; Gupta et al., 2012; Lisman, 2005; Wikenheiser and Redish, 2015; Cei et al., 2014). Second, place cells begin to fire at the peak of the theta cycle when the animal enters a neuron’s place field and spikes move to decending phases when the animal exits the field, a phenomenon known as ‘phase precession’ (Burgess, 2008; Burgess et al., 2007; Dragoi and Buzsaki, 2006; Geisler et al., 2007; Harris et al., 2002; Harvey et al., 2009; Hasselmo et al., 2007; Huxter et al., 2003; Kamondi et al., 1998; Lengyel et al., 2003; Losonczy et al., 2010; Maurer et al., 2006; Maurer et al., 2014; Mehta et al., 2002; O’Keefe and Recce, 1993; Skaggs et al., 1996). Third, encoding and retrieval of memories have been hypothesized to occur on opposite phases of theta oscillations (Hasselmo et al., 2002). Fourth, during REM sleep, a large fraction of CA1 pyramidal neurons shift their preferred phase from the trough to the peak (Mizuseki et al., 2011; Poe et al., 2000), possibly because their upstream entorhinal layer III (EC3) and CA3 neurons increase and decrease their firing rates, respectively, during REM (Mizuseki et al., 2009; Montgomery et al., 2008). Fifth, EC3 and CA3 inputs also play important roles in the generation of theta and gamma rhythms (Bieri et al., 2014; Bragin et al., 1995; Buzsaki et al., 2012; Buzsaki et al., 1983; Cabral et al., 2014; Colgin et al., 2009; Csicsvari et al., 2003; Fernandez-Ruiz et al., 2012; Lasztoczi and Klausberger, 2016; Mizuseki et al., 2009; Montgomery et al., 2008; Schomburg et al., 2014; Zheng et al., 2016). Finally, during exploration in a familiar environment and during memory recall, CA1 pyramidal neurons respond most effectively to CA3 input, which is associated with slow gamma oscillations (gamma_S; 30–80 Hz) in str. radiatum. In contrast, during REM sleep and memory encoding CA1 pyramidal cells preferentially discharge closer to the theta peak in response to EC3 activation, associated with mid-frequency gamma (gamma_M; 60–120 Hz) in str. lacunosum-moleculare, (LM; Figure 1B) (Mizuseki et al., 2009; Schomburg et al., 2014). Therefore, by identifying layer-specific gamma activity, it is possible to determine the distinct afferent contribution that each input provides to the timing and spike-phase coding of CA1 neurons ( Lasztoczi and Klausberger, 2016; Schomburg et al., 2014).

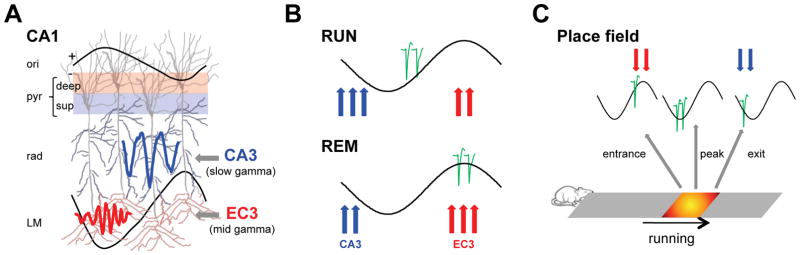
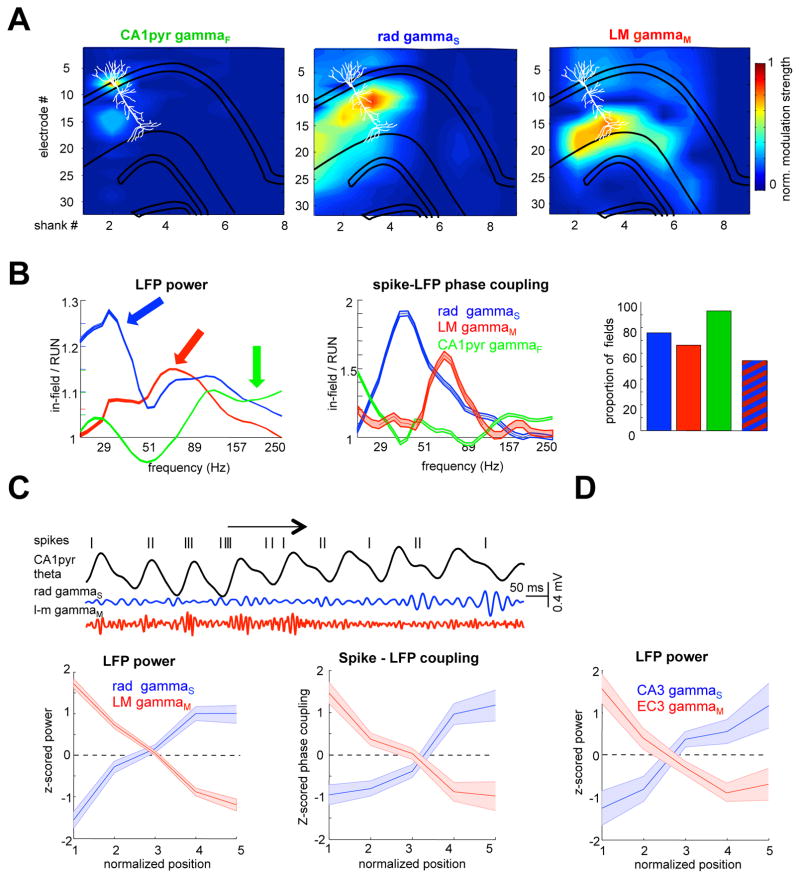
Figure 1. CA3 and entorhinal inputs control CA1 spiking.

(A) Entorhinal layer 3 (EC3) gamma_M input (60–100 Hz) modulates distal dendrites in str. LM at the positive peak of CA1 pyramidal layer theta (CA1_pyr), followed by CA3 gamma_S (30–60 Hz) input in str. radiatum (rad) on the descending theta phase (Schomburg et al., 2014). Deep sublayer CA1 pyramidal cells receive stronger EC3 input than superficial ones. (B) The relative strengths of phase-separated CA3 and EC3 are hypothesized to determine the theta phase of pyramidal cell spikes. During exploration (RUN), CA3 drive is stronger and EC3 is weaker relative to REM. As a result, the preferred phase of spikes moves towards the peak during REM. (C) At the entrance of the place field, place cells fire near the theta peak (EC3 excitation) and the spikes move to earlier phases as the rat transverses the place field due to increasing CA3 drive. Reference theta LFP for (B) and (C) correspond to the CA1 pyramidal layer.

We hypothesized that this wide range of observations can be explained by the same mechanisms. Because EC3 neurons fire maximally at the theta peak, whereas CA3 neurons on the descending phase (Figure 1A) (Kamondi et al., 1998; Mizuseki et al., 2009; Schomburg et al., 2014), we reasoned that timing of CA1 pyramidal cell spikes is tuned by the relative strengths of the cooperating/competing CA3 and entorhinal inputs, and that the strengths of these upstream inputs are reflected by the gamma power and spike-gamma coupling in the appropriate layers (Figure 1). In order to isolate varying spatial-temporal inputs impinging upon individual neurons, we performed high-spatial density recordings in rats. Changes in gamma power across laminae were evaluated in the context of afferent firing activity as well as relative to CA1 pyramidal spike timing. We also examined how the upstream inputs interact with local inhibition. The dual entorhinal-CA3 input control model (Figure 1A–C) predicts that the relative strengths of the entorhinal and CA3 inputs determine (a) the magnitude of gamma power in the target layers, (b) theta power and waveform in different CA1 layers, (c) changes in CA1 spike theta phase preference of hippocampal neurons between waking and REM sleep, (d) theta phase shifts of spikes between early and late trials of exploration, (e) theta phase shifts of spikes between encoding and retrieval of memory trace and (f) properties of theta phase precession of spikes within the place field of neurons in different hippocampal regions and sublayers. Our results support these predictions and demonstrate a general mechanism for temporal coding during navigation and memory.

RESULTS

Local field potentials (LFPs) and spiking activity were recorded in the soma-dendritic layers of the hippocampus and entorhinal cortices during sleep as well as multiple behavioral tasks. Silicon probes with 256 sites on eight shanks were implanted in the dorsal hippocampus (n = 8 rats), spanning the CA1-3 and dentate regions. Additional probes were implanted in the medial EC (n = 2), lateral EC (n = 1) or both (n = 4) (Figure S1 and Table 1). All events are referenced to the theta oscillations recorded in the CA1 pyramidal layer (CA1_pyr).

Gamma oscillations track dual-input control of pyramidal cell spiking

Layer localization of the different gamma currents was determined via current source density analysis (Buzsaki et al., 1986; Mitzdorf, 1985) as well as independent component analysis (ICA) decomposition (Fernandez-Ruiz et al., 2012) of the multi-electrode LFP. Gamma_S (30–60 Hz), gamma_M (60–110 Hz) and fast gamma (gamma_F >100 Hz) were maximal in the str. rad, str. LM and the CA1_pyr, respectively (Figure 2A). Gamma_S power (46 ± 1° Hz peak power, SEM, n = 8 rats; Figure S2) in CA1 str. rad had a maximum on the descending phase of theta waves (125 ± 2°; Figure 2C), whereas gamma _M power (88 ± 2 Hz peak power; Figure S2) near the peak (334 ± 4°; Figure 2C) in str. LM. Gamma _F oscillations (158 ± 4 Hz peak power; Figure S2) in the CA1 pyramidal layer were maximal at the theta through (178 ± 5°).

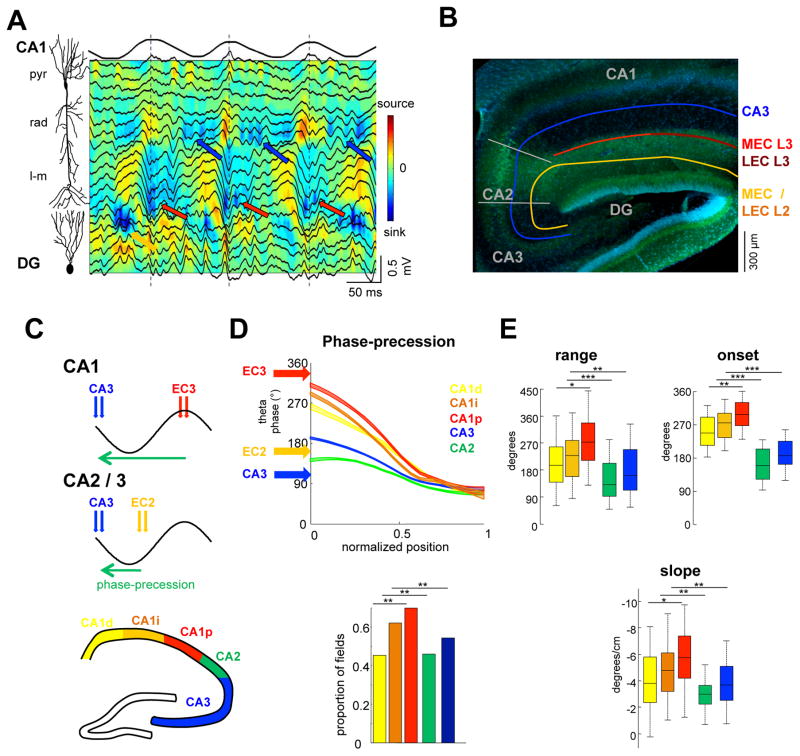
Figure 2. Theta-gamma inputs to hippocampal subregions determines phase-precession magnitude.

(A) Depth profile of theta-nested gamma oscillations. Red arrows indicate gamma_M (60–110 Hz) oscillations in str. LM and local current sinks, coinciding with theta peaks (dashed lines). Blue arrows denote str. rad gamma_S (30–60 Hz) oscillations and local sinks on the descending theta phase. Yellow arrow marks gamma oscillations in the str. moleculare of the dentate gyrus (DG) near theta through. (B) Schema of anatomical pathways. CA3 pyramidal cells send their main axons (blue) to the str. rad of CA3, CA2 and CA1. Medial EC3 (MEC3) and lateral EC3 (LEC3) axons target the proximal CA1 and distal segments, respectively. MEC2 and LEC2 (yellow) innervate CA3, CA2 and DG. (C) Dual-input model predicts that the range of phase-precession depends on the excitatory strength and magnitude of phase separation of theta inputs. (D) Theta phase-precession in different subregions. Mean and 95% confidence intervals are shown at 10% increments of distance from the beginning of the field. Arrows show the preferred theta phases of EC3, EC2 and CA3 driving populations. Only place fields with significant phase precession were considered for these analyses (histogram ;p < 0.05; circular-linear correlation). (E) Range of phase-position correlation, theta phase of spikes at the onset of the place field, , and slope respectively. See also Figure S1–4.

Gamma amplitude-theta phase modulation was also examined in the upstream regions: the medial and lateral entorhinal cortices and CA3 (Figure 2B). Laminar recordings from the medial (n = 4 rats) and lateral (n = 4 rats) EC identified gamma_M (94 ± 3 Hz; Figure S2) in EC3 with maximal power near the peak (345 ± 4°/325 ± 6° ME C/LEC; Figure S2) and gamma_F maximum (148 ± 4 Hz; Figure S2) in EC2 close to the trough (173 ± 4°/159 ± 4° MEC/LEC; Figure S2). The gamma amplitude-theta phase relationship was weaker in the lateral EC compared with the medial EC (p < 0.001 for both EC2 and EC3; t-test; Figure S2). The maximum power of gamma_S in the CA3 pyramidal layer (47 ± 1 Hz; n = 6 rats) occurred on the descending phase of theta (132 ± 3°; Figure S2).

To gain further support for the hypothesis that gamma oscillations in the dendritic regions reflect the activity in their upstream inputs, the interaction between action potentials and LFP was also analyzed. Excitatory EC3 neurons in both medial and lateral EC fired with the highest probability at the peak of CA1 theta (Figure S3). Phase modulation of spikes of medial EC3 neurons to CA1_pyr theta was stronger than for lateral EC3 neurons (Figure S3; p < 0.01, Wilcoxon rank-sum test; n = 113 MEC cells and 182 LEC cells). EC2 excitatory neurons (n = 184 MEC cells and 38 LEC cells) discharged preferentially around the theta trough and spikes of CA3 neurons (n = 211) clustered towards the descending phase (Figure S3), although we were not able to separate stellate neurons from pyramidal cells. Of all upstream regions, medial EC2 neurons showed the strongest theta phase modulation (Figure S3) (Quilichini et al., 2010) and a larger proportion of significantly modulated neurons than in lateral EC (Figure S3; p < 0.001 for both layers; t-test). Therefore, the spike to CA1 theta phase relationship supports the LFP analysis and can explain both the layer specificity and theta phase-locking of gamma_S and gamma_M in the CA1 str. rad and str. LM, respectively. Overall, these findings confirm and expand previous observations that gamma_M in CA1 str. LM is transmitted from medial EC3, whereas gamma_S in CA1 str. rad reflects gamma activity in the upstream CA3 region (Bieri et al., 2014; Csicsvari et al., 2003; Colgin et al., 2009; Schomburg et al., 2014; Lasztoczi and Klausberger, 2016).

Phase segregation of driving inputs determines theta phase-precession

The dual afferent drive model (Figure 1) suggests that pyramidal cells activity is controlled by the strength and phase separation of the upstream drivers. Under this hypothesis, the strong medial EC input initiates the hippocampal neuron’s firing upon entry to its place field. Because the maximal activation of medial EC2 neurons lags (or leads) approximately one-half cycle behind medial EC3, the initiation of firing of CA1 neurons would precede CA2/CA3 place cells, resulting in a significantly larger range of precession (Figure 2C,D). In support of the hypothesis, the range of phase precession was significantly larger for CA1 than for CA2 and CA3 pyramidal neurons (Figure 2D,E; 249 ± 13°/131 ± 21°/162° ± 13° mean ranges for CA1/CA2/CA3, n = 309/90/160 fields; p < 0.001/0.01 for CA1 versus CA2/CA3, rank-sum test). Differences were also found for other parameters of phase-position correlation, including the theta phase onset of the precession, the proportion of ‘precessing’ fields in each region and the slope of phase precession (Figure 2E and S4).

While these data demonstrate differences across hippocampal regions, there is also a unique distribution of excitatory inputs from the medial and lateral EC along the transverse axis of CA1 (Figure 2B; (Oliva et al., 2016; Witter et al., 2000). Therefore, we sought to determine if the physiological differences in lateral and medial EC translate to differences in phase-precession characteristics of CA1 neurons. Proximal CA1 neurons with strong medial EC input (Tamamaki and Nojyo, 1993) showed the largest phase range and the distal CA1 pyramidal cells the smallest (191 ± 27°/235 ± 20°/269 ± 19° mean fo r distal/intermediate/proximal CA1; F(2)=3.75, p < 0.05, n = 92/109/108 fields), with concordant quantitative differences in the other parameters as well (Figure 2E). In all place cells, irrespective of the region in which they resided, spike phase precession ended at the preferred theta phase of the CA3 neurons (Figure 2D,E). At the onset of the field, CA1 place cells fired close to the preferred phase of EC3 input, while CA2 and CA3 cells fired close to phase of EC2 input (Figure 2D). Thus, in accord with the dual input model, the theta phase onset at the place field entry varied across regions and subregions, commensurate with the strength of their driving entorhinal pyramidal neurons (Figure 2D, E).

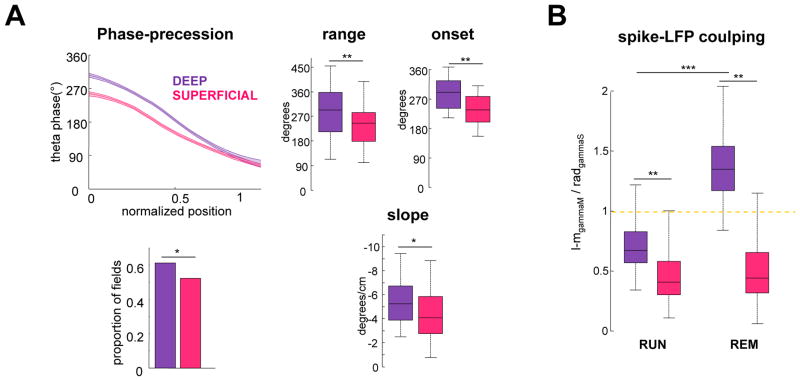
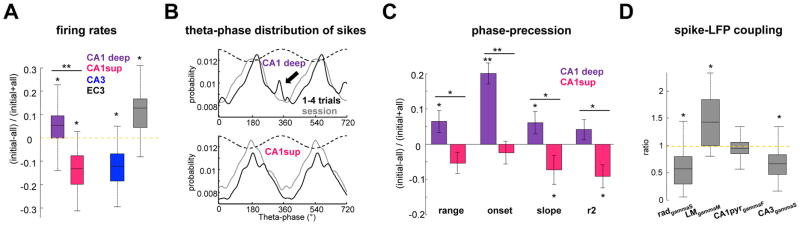
Finally, it has previously been demonstrated that a large fraction of deep layer, but not superficial, CA1 pyramidal neurons shift their preferred theta phase from the trough during RUN to the peak during REM (Figure S3) (Mizuseki et al., 2011). As this shift is potentially due to the increased influence of EC3 input during REM, we sought to determine if the deep versus superficial difference in phase precession characteristics concur with the dual input model. The phase range, theta phase onset at the place field entry, proportion of place fields and the slope of phase-position correlations were significantly larger for deep (n = 159 fields), compared to superficial (n = 150 fields) CA1 place cells (Figure 3A). To relate these changes to the differential driving strengths of the upstream CA3 and EC3 inputs, spike-LFP modulation of CA1 place cells to gamma_M and gamma_S during RUN and REM was also compared (Figure 3B). Spike–gamma_M LFP coupling was significantly stronger for deep layer place cells during both RUN and REM (p < 0.01 for both states, rank-sum test). Moreover, spike–gamma_M phase modulation strength increased significantly during REM in deep (p < 0.001, rank-sum test) but not superficial neurons. Thus, the stronger upstream excitation from EC3 to deep layer CA1 pyramidal neurons can explain their larger phase range and other parameters of phase-position correlation, compared to superficial layer neurons.

Figure 3. Phase-precession and spike-gamma coupling differs for deep and superficial CA1 subpopulations.

(A) Plot illustrates mean theta phase and 95% confidence intervals along the place field for deep and superficial CA1 place cells. Deep CA1 cells have a wider phase range, fire closer to the theta peak at the place field onset. A larger proportion of deep layer cells have place fields significant phase-position correlation and steeper slope, compared to superficial neurons. (B) Ratio of spike-LFP phase modulation in LM gamma_M and rad gamma_S during RUN and REM was calculated for each cell and averaged for superficial (n = 221) and deep (n = 266) layer CA1 place cells. (*/**/*** p < 0.05/0.01/0.001; rank-sum test or one-way Kruskall-Wallis for intra CA1 comparisons). Note that gamma_S spike modulation is stronger than gamma_M for superficial cells during both RUN and REM but for deep neurons gamma_M spike modulation becomes stronger during REM, suggesting an increased control of this subpopulation by EC3 input. See also Figure S2–4.

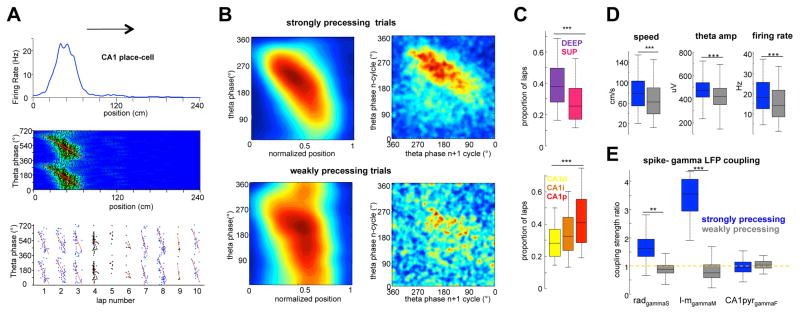
The above findings lend only indirect support for the dual-input model of phase-precession. To more directly test the hypothesis that gradually shifting strengths of the CA3 and entorhinal inputs are responsible for the timing of place cell spikes, we examined spike phase-position correlations on a trial-by-trial basis (Figure 4A). Using linear-circular regression statistics (Kempter et al., 2012), the significance of the spike phase-position slope was tested on each trial. Significant (p < 0.05 and r² > 0.1) and non-significant (p > 0.05) trials are referred to as strongly and weakly precessing trials, or more correctly trials with strong and weak phase-position correlations (Maurer et al., 2014; Figure 4B). In strongly precessing trials, the spike phase in the nth theta wave reliably predicted the spike phase in the n + 1 wave, and this correlation was significantly lower in weakly precessing trials (Figure 4B; p < 0.01; rank-sum test). The fraction of strongly precessing trials was significantly higher in deep compared to superficial CA1 pyramidal neurons (Figure 4C, p < 0.001, rank-sum test), and in proximal versus distal CA1 neurons (F(2)=7.29, p < 0.001). Strongly and weakly precessing trials differed in a number of behavioral and physiological parameters, including within-field firing rate, running speed and theta amplitude (Figure 4D, p < 0.001 for all comparisons, rank-sum test; and Figure S4). Both gamma_M and gamma_S phase-modulation of the CA1 place cells was significantly stronger for strongly, compared to weakly precessing trials (Figure 4E; p < 0.01/0.001 for gamma_S and gamma_M, rank-sum test). Theta phase preference of CA1 place cells was significantly earlier (precessing trials = 295 ± 4^o; non-precessing trials = 270 ± 3^o; P < 0.05; rank-sum test), suggesting a stronger CA3 drive during non-precessing trials. These data support a model in which spatial information is relayed from the medial EC with the strongest phase-position correlation seen in the deep proximal CA1 cells and weakest in the superficial distal neurons, dominated by lateral EC and CA3 inputs.

Figure 4. Place fields with and without phase-precession.

(A) Firing rate plot (upper panel) and theta phase-position spike density map (middle) for an example place cell. Red line represents linear-circular regression. Bottom: Trials with strong (P < 0.05 and r² > 0.1; blue dots) and weak (p > 0.05; black) spike phase-position correlation. (B) Left: Average normalized phase-position correlation density plots for all CA1 place cells (n = 487 cells, 6 rats) constructed separately for trials with strong and weak phase-position correlation. Right: Correlation of spike phase in n versus n + 1 theta waves. (C) Proportion of significantly phase-precessing trials for deep and superficial place cells (top), and for neurons in CA1 subregions (bottom). (D) Running speed, theta amplitude and in-field firing rate during strongly (blue) and weakly (grey) precessing trials. (E) Spike–LFP coupling of place cell spikes for strongly and weakly precessing trials (normalized to the entire session), shown separately for gamma sub-bands. (**/*** p < 0.01/0.001, rank-sum test or one-way Kruskall-Wallis for intra CA1 comparison). See also Figure S5.

Changes in transmembrane current across dendritic segments are also reflected by the afferent-induced LFP near the dendrites (Agarwal et al., 2014). To isolate gamma_M and gamma_S inputs to individual place cells, we calculated the phase-modulation strength of place cell spikes to the layer-specific gamma sub-bands (Figure S5; Methods). As hypothesized, spike-sampled gamma_F, gamma_S and gamma_M were correctly projected onto the somatic location, the mid- and distal apical dendrites of individual place cells reflecting the spatial specificity of underlying synaptic inputs (Figure 5A). A large proportion of place fields had significant spike-gamma phase modulation (Figure 5B and Figure S6). In 75 % of the place fields, place cell spikes were significantly locked to gamma_S (p < 0.01 Rayleigh test; r = 0.34, median resultant vector length), in 66% with gamma_M (r = 0.21) and in 91% with gamma_F (r = 0.42). In addition, 53% of the fields had significant phase modulation by both gamma_S and gamma_M (Figure 5B).

Figure 5. Intra-place field dynamics of layer-specific gamma inputs.

(A) Illustration of the procedure to identify gamma inputs to individual pyramidal cells. Different gamma components were isolated from the LFP by ICA and their specific activities were reconstructed for all 256-electrode sites (Methods). Spike-gamma phase modulation of each neuron was calculated by wavelet spectral decomposition and aligned with the neuron’s putative anatomical location. (B) Instantaneous gamma power (left) and spike-LFP gamma phase modulation strength (middle) for place cell spikes in an example session. Right, proportion of all place fields with significant (P < 0.01 Rayleigh test) spike-gamma oscillations phase-coupling. Striped bar, place fields with significant phase modulation by both gamma_S and gamma_M. Only place fields with significant phase-position correlation (n = 308; P < 0.05, circular-linear correlation) were included. (C) Example trial to illustrate gamma_M and gamma_S change across place field transversal. Spike sampled instantaneous power (bottom left) and spike-phase modulation strength (bottom right) for gamma_S and gamma_M in each of 5 bins of the place field. All place fields (n = 527) from all sessions (n = 16 from 6 rats) were normalized and their spikes pooled together. Only significantly phase precessing place trials were included in these analyses. Note increasing and decreasing spike-LFP modulation strength and power of gamma_M and gamma_S at the beginning and end of the place field, respectively. (D) CA1 place cell spike-sampled gamma power in EC3 (n = 4 rats) and CA3 pyramidal layer (n = 6 rats) in each of 5 bins of the place field. Shaded areas are mean ± SD. See also Figure S6 and S7.

Following verification that place cell spikes were modulated by different upstream gamma oscillations during behavior, we sought to determine how the gamma activity evolves across laminae during single passes through a place field. Place fields were divided into 5 equal bins and place cell spike-sampled str. rad gamma_S and str. LM gamma_M activity was calculated as a function of within-field location. To gain statistical power, all place fields from all sessions were concatenated, mimicking the idealized situation when large numbers of neurons were recorded in a single place field (Figure 5C; n = 487 place cells from 6 rats). For strongly phase-precessing trials, both gamma_M power and spike-gamma_M coupling (Figure 5C) decreased steadily from the beginning to the end of the place field (p < 0.001/0.01 for gamma_M power and phase coupling, respectively; one-way ANOVA followed by Tukey’s post-hoc test), whereas both gamma_S power and spike-gamma_S coupling increased (p < 0.001/0.01 for gamma_S power and phase coupling respectively, Tukey’s post-hoc test). This clear switching dominance of EC3 and CA3 inputs within the place field was largely absent during weakly precessing trials or even showed an opposite trend (Figure S6). In further support of these findings, place cell spike-sampled gamma_S in the CA3 pyramidal layer and spike-sampled gamma_M in EC3 showed similar within-place field increase and decrease, respectively (Figure 5D; p < 0.05 in both cases, Tukey’s post-hoc test). Overall, these findings demonstrate that the EC3 input initiates spiking of place cells but its strength weakens as the rat passes through the place field. Conversely, the CA3 input is initially weak and gains strength gradually. Next, we examined whether and how local circuit mechanisms co-vary with these opposite trends.

Local circuit contribution to spike phase-precession

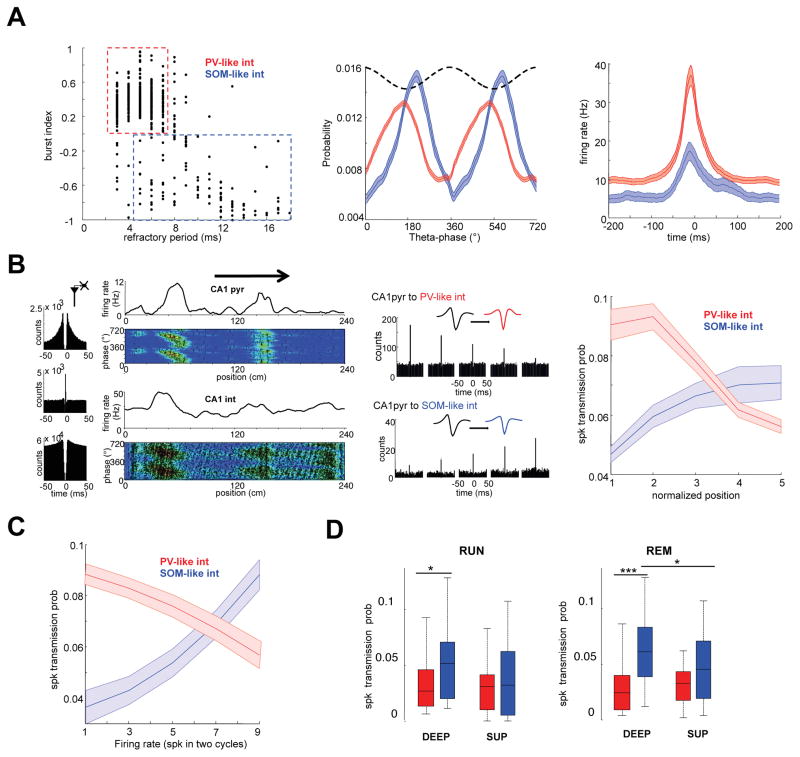
A fraction of hippocampal interneurons are strongly driven by nearby place cells, effectively inheriting the spatial receptive fields of the driver neurons (Geisler et al., 2007; Marshall et al., 2002; Maurer et al., 2006). Using several physiological criteria, which corresponded to parameters of optogenetically classified parvalbumin (PV) and somatostatin (SOM) positive cells in a previous study (Royer et al., 2012), two subgroups of CA1 interneurons were identified. Therefore, we refer to these two subgroups as PV-like and SOM-like. PV-like interneurons were ‘bursty’, had short refractory period, narrow waveform and high firing rate (Figure 7A and S7; n = 618 cells). SOM-like interneurons were non-bursty, had longer refractory period, wider waveform and lower firing rates (Figure 6A and Figure S7; n = 141 cells). PV-like cells were more strongly recruited during sharp wave ripples than SOM-like interneurons (Figure 7A; p < 0.001, rank-sum test) and preferred to fire on the descending theta phase (147 ± 2°), while SOM-like were locked to the ascending theta phase (203 ± 3°; Figure 7A).

Figure 7. Entorhinal input drives CA1 deep layer neurons cells during early exploration of a familiar environment.

(A) Firing rate and theta-phase firing probability distribution (B) changes from early (trials 1–4) to late (mean of entire session) trials. Arrow indicates bump in the firing probability at the theta peak for deep CA1 cells in early trials. (C) Differences in range, onset, slope and strength of phase-position correlation for deep and superficial CA1 place cells. (D) Changes in spike-LFP phase coupling from early to late trials. Spike-gamma phase coupling was quantified for each neuron as a mean vector length ratio of the first 4 trials and the whole session, and averaged across the population. (*/**/*** p < 0.05/0.01/0.001, Wilcoxon signed-rank test for within-group and rank-sum test for across-group comparisons).

Figure 6. Switching somato-dentric inhibition and gamma inputs.

(A) CA1 putative interneurons were divided into PV-like and SOM-like subgroups, according to their proportion of burst spiking and refractory period (Royer et al., 2012: see Methods). Middle: Distribution of theta phase discharge probability for both groups. Right: Peri-ripple firing histogram for both groups. (B) Left panel: Autocorrelogram of pyramidal cell (top), PV-like interneuron (bottom) and their cross-correlogram (middle), indicating that they are monosynaptically connected. Second panel: spike versus theta phase plots of the neuron pair on the track. Note spike phase-precession of both neurons. Third panel: Example cross-correlograms for two representative pyramidal cell-interneuron pairs in the five bins of the place field. Right panel: Spike-transmission probability between CA1 place cells and the two classes of interneurons, shown in five bins of the place field (n = 256 place cell-PV-like pairs; n = 35 place cell-SOM-like pairs). Spike transmission probability between pyramidal cells and PV-like interneurons was high at the entrance of the field and decreased afterward. In contrast, the spike transmission between pyramidal cells and SOM-like interneurons gradually increased as the rat crossed the field. (C) Spike transmission probability as a function of pyramidal cell firing rate in 10 firing rate bins during RUN and REM epochs. Spike transmission probability between pyramidal cells and PV-like interneurons is high at low firing rates and rapidly decreases with rate increase of the driving pyramidal cell, whereas spike transmission to SOM-like interneurons increases with firing rate. Shaded areas mean ± SEM. (D) Spike-transmission probability during RUN and REM shown separately for CA1 deep layer pyramidal cell-interneuron and superficial layer pyramidal cell-interneuron pairs. See also Figure S8.

A subset of both putative interneuron types was monosynaptically driven by their place cells (Maurer et al., 2006), as determined from their short-time cross-correlograms (n = 265 PV-like pairs, 35 % of cells in this group, and 35 SOM-like pairs, 14 % of cells). Figure 6B (first, second and third panels) illustrates ‘inherited place field’ of a PV-like interneuron, monosynaptically driven by its presynaptic place cell, and within-place field spike transmission probability changes between the place cell and its monosynaptically driven PV-like partner. Spike transmission from place cells to PV-like interneurons was high at the entrance of the field and rapidly decayed (Figure 6B, third and last panel; P < 0.01, Tukey’s post-hoc test), while spike transmission to SOM-like cells gradually increased within the place field (Figure 6B, third and last panel; p < 0.05, Tukey’s post-hoc test).

Next, we investigated short-term synaptic plasticity between pyramidal cells and the two types of interneurons, independent of the rat’s spatial position. Spike transmission probability to PV-like interneurons was high at low firing rates and rapidly depressed at higher spike rates of the presynaptic pyramidal cells (Figure 6C; P < 0.05, Tukey’s post-hoc test), while transmission to SOM-like interneurons was facilitated at higher rates (p < 0.05, Tukey’s post-hoc test), similar to in vitro observations (Pouille and Scanziani, 2004).

Finally, we asked whether pyramidal cell – interneuron spike-transmission probability was different for deep and superficial CA1 pyramidal cells. Superficial cells had similar spike transmission probability to both types of interneurons. In contrast, deep layer pyramidal cells more effectively recruited SOM-like interneurons compared to PV-like cells, especially during REM sleep (Figure 7D; p < 0.05, rank-sum test), suggesting that deep layer neurons exert a stronger feedback inhibitory control on dendritic excitation compared to superficial pyramidal cells.

Behavior-dependence of theta phase spiking

In addition to within-field phase precession, theta phase spiking of hippocampal neurons can vary in multiple other behavioral situations. Previous experiments have shown that the firing patterns of CA1 place cells in familiar environments are different during the first few trials of daily sessions compared to subsequent, more stable trials (Feng et al., 2015; Mehta et al., 2002). Therefore, we compared CA1 place cell activity during the initial four trials in the linear track with the whole session. Superficial layer neurons showed slower discharge rates during the early trials (first four) compared to the session mean, whereas deep layer neurons showed the opposite relationship (Figure 7A). CA3 pyramidal cells had lower firing rates during early compared to late trials, while EC3 excitatory cells (MEC and LEC units were pooled together) initially had higher rates (Figure 7A). Another notable difference between early and late trials was that a fraction of deep layer CA1 pyramidal neurons fired preferentially near the theta peak during early trials (Figure 7B), reflecting a higher EC3 input drive. The dual-input model predicts that this increased EC3 drive of deep CA1 place cells should be reflected in a more pronounced phase-position correlation. In support of this hypothesis, the range of phase-precession for deep cells was wider (278° versus 299° median values), their slope steeper (5.2/5.7 degrees/cm) and they fired closer to the theta peak at the field onset (293°/341°) in early-versus-late trials (Figure 6C). Opposite changes were observed for superficial CA1 cells, suggesting that the weaker EC3 input to these neurons is less effective in overcoming the CA3 drive. To address the role of gamma inputs in spike phase changes, we examined spike-LFP coupling of CA1 place cells and found that spike-gamma_M modulation was stronger whereas spike-gamma_S modulation was weaker during early trials (Figure 7D). Overall, these theta phase-spike coupling findings indicate a stronger EC3 influence on CA1 pyramidal cells during early trials, followed by a more dominant effect of the CA3 input in subsequent trials.

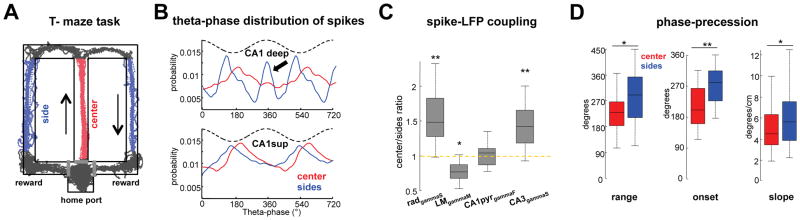
As CA3–CA1 gamma coherence is enhanced during memory recall (Montgomery and Buzsaki, 2007; Schomburg et al., 2014), the dual-input hypothesis suggests that the dominance of CA3 input should reduce the range of phase-precession during memory recall. To test this prediction, we examined phase-precession characteristics in a hippocampal-dependent spatial memory task (Ainge et al., 2007) Rats (n = 6) learned to alternate between the two arms of a figure-8 maze (‘T-maze’) for water reward (Figure 8A). A delay of 15 seconds between trials was introduced to increase memory load and only sessions where the rat performed above 80% of success were analyzed. In support of previous findings, gamma_S coherence between CA3 and CA1 radiatum was higher in the center arm compared to the sides (p < 0.01, rank-sum test), evidencing an increased CA3 gamma input to CA1. The firing rates of CA3 (n = 102) and superficial CA1 pyramidal cells (n = 191) were higher in the central arm than in the side arms (p < 0.01 both, rank-sum test). In contrast, both EC3 (n = 106) and deep layer CA1 pyramidal neurons (n = 139) fired more in the side arms than in the central arm (p < 0.05/0.01 EC3/deep CA1, rank-sum test). A large proportion of deep CA1 cells shifted their maximal discharge probability to the theta peak in the side arms (Figure 7B), likely due to the increased EC3 drive. In support of the differential drive of CA1 neurons in the central and side arms, CA1 place cells were more strongly modulated by str. rad gamma_S and more weakly to str. LM gamma_M in the central compared to the side arms (Figure 8C). Further, phase modulation of CA1 spikes by gamma_S in the upstream CA3 region was elevated in the central arm (Figure 8D). During error trials, no significant differences were observed between place fields in central and side arms in any of the above parameters (p > 0.05, rank-sum test). In light of the dual-input model, the above observations predict reduced extent of phase precession in the central arm. Indeed, the range of phase-position correlation was significantly higher in the side arms compared to the central arm (Figure 8D; p < 0.001/0.05, n = 71/141 fields in central and side arms, rank-sum test). Furthermore, while place cells fired closer to the peak at the onset of their fields in the side arms (279° median), they fired closer to the t hrough in the central arm (209° median). In sum, stronger CA3 excitation of CA1 neurons in the central arm during memory recall results in reduced range of phase-precession.

Figure 8. Task-specific gamma inputs and phase-precession during memory guided navigation.

(A) Delayed alternation task. Black lines, trajectory of the rat in a single session. Highlighted red and blue segments show sampled areas. (B) Theta phase distribution of deep and superficial CA1 pyramidal neurons in central and side arms. Note that many deep neurons fire at theta peak in the side arm (C) Central/side arms ratios for spike-gamma phase coupling. Place cell spikes are more strongly coupled to CA3 gamma_S in the center (memory retrieval) arm while in the side arms they are preferentially entrained by EC3 gamma_M. (D) Range, onset and slope of phase precession for place fields in the center and side arms. Note more limited phase-precession span and earlier theta-phase onset in the central arm, likely due to an increased CA3 input strength. (*/**/*** p < 0.05/0.01/0.001, Wilcoxon signed-rank for within-group and rank-sum test for across-group comparisons).

DISCUSSION

In contrast to the historic view of the hippocampus as a serial, trisynaptic path, contemporary research emphasizes that parallel entorhinal and intrahippocampal drives may interact dynamically in their target effect. Our findings support a dual entorhinal-CA3 input control model of spike timing (Figure 1). In this model, the timing of spikes in the hippocampus is determined by the combined strength and phase differences of the entorhinal and CA3 populations. Place field activity of CA1 neurons is initiated by the EC3 input at the peak of theta and associated with a gamma_M burst in str. LM. As the animal moves across the field, EC3 drive decreases and is supplemented by an increasing CA3 drive, as reflected by increasing power of place-cell sampled gamma_S in str. rad. Feedback potentiation of distal dendritic inhibition by CA1 place cells attenuates the EC3 input. Likewise, depression of proximal dendritic and perisomatic inhibition facilitates the impact of CA3. These combined upstream excitatory and local inhibitory effects result in a monotonic shift of spikes from the late to earlier phases of theta waves as the rat passes through the place field. The shorter extent of theta phase-precession of CA2, CA3 neurons and dentate granule cells can be also explained by the dual-input mechanism. The dual-input model can also explain differences between deep and superficial sublayers of CA1, theta-phase shifts of spikes during memory guided navigation and REM sleep, and the layer-specific amplitude and waveform changes of theta oscillations across brain states.

CA3 and entorhinal inputs time place cell spikes through gamma coupled mechanisms

The combination of phase precession and theta-nested gamma oscillations coupling has been put forward as a potential mechanism of memory encoding (Hasselmo et al., 2002; Jensen and Lisman, 1996; Lisman, 1999). Indeed, several works have examined the relationship between theta-gamma coupling, spatial memory and navigation but the relationship between timing of spikes in the theta cycle and gamma oscillations have remained undisclosed. Previous attempts to clarify such relationship used either single-site recordings from the CA1 pyramidal layer or a single linear electrode in dendritic layers (Bieri et al., 2014; Lasztoczi and Klausberger, 2016; Middleton and McHugh, 2016; Zheng et al., 2016) and did not record simultaneously from upstream regions, nor did they examine spike-theta phase relationship in multiple regions, subregions or sublayers.

Our results, obtained with high spatial resolution recording techniques, enabled us to link several types of results to be explained by a single model. First, previous studies have shown a ~180^o gradual phase-shift of theta oscillations from the CA1 str. oriens to str. LM (Buzsaki, 2002). The phase differences between CA3 and EC3 inputs and their relative strengths contribute to the characteristic depth profile of theta waveforms in different brain states (Figure S2). Second, the relative strengths of these inputs can explain the shift of spike theta phase preference of deep CA1 pyramidal neurons from near the through during wake to the peak during REM (Mizuseki et al., 2011; Poe et al., 2000); that is to the phase where the EC3 output is maximum. In further support of the dominance of the EC3 input during REM, we found that phase modulation of spikes of CA1 deep layer pyramidal neurons by EC3 gamma_M was enhanced during REM (Figure 3). A similar increase of EC3 input strength, potentially driven by environmental inputs (Aghajan et al., 2015), can account for the spike phase difference between early and later trials of exploration in the deep CA1 subpopulation (Figure 4). Furthermore, when CA3 input control is increased during memory recall in the center arm of the T maze (Montgomery and Buzsaki, 2007), the extent and strength of spike phase-position correlation was weaker and shorter than in the side arms (Figure 8). These differences in the preferred theta phase of CA1 pyramidal neuron spikes were echoed by the gamma oscillation power in the respective CA1 dendritic target layers of CA3 and EC3 inputs, supporting the hypothesis that gamma power in the target layers is a reliable indicator of the firing rates of their upstream neurons (Berenyi et al., 2014; Schomburg et al., 2014).

The dual-input model (Figure 1A) can also explain the dynamic phase shifts of spikes within place fields. Theta spike phase at the? place field onset was characteristically different in different regions, subregions and sublayers (Figure 3), whereas at the place field exit, it was always the same and corresponded to the preferred phase of CA3 pyramidal cells. We hypothesize that the phase of spiking at the field onset is determined mainly by the preferred phase and strength of the respective entorhinal inputs. The largest span of phase precession was observed for the proximal and deep divisions of CA1 place cells, most likely because these neurons receive strong spatial input from medial EC. The intermediate and distal CA1 neurons, and possibly superficial neurons, are innervated increasingly more by lateral EC3 input. As expected from the weaker lateral EC input, these CA1 neurons show weaker theta modulation (Henriksen et al., 2010; Oliva et al., 2016) which, according to the dual-input model, may explain the smaller phase span and lower phase position correlation. During circumstances that favor learning, such as the first trials of a day or during encoding phases on an alternating T-maze task, the onset of CA1 place cell spiking was closer to the theta peak, consistent with the strong EC3 drive. Finally, in CA2 and CA3 place cells fire near the theta trough upon place field entry, which is the preferred phase of EC2 neurons (Mizuseki et al., 2009). The limited span of phase precession in CA2, CA3 place cells (Mizuseki et al., 2012; present findings) and dentate granule cells (Skaggs et al., 1996), therefore, can be explained by the relatively small phase separation of the preferred spike phases of their driver EC2 and CA3 neurons (Figure 2).

The spike phase-position correlation of CA1 place cells within the place field was faithfully tracked by both the decreasing power and spike phase modulation by gamma_M in str. LM and increasing power and spike phase modulation by gamma_S in str. rad (Figure 5C). These within-field changes were also tracked by the gamma power in their upstream inputs from EC3 and CA3 (Figure 5D), respectively, supporting our hypothesis that the relative excitatory strength of spike output from the upstream regions is a key factor in determining the theta phase of place cell spikes (Bittner et al., 2015; Chance, 2012; Kamondi et al., 1998; Schlesinger et al., 2014).

Contribution of local inhibitory circuit to spike timing

Our findings also disclosed that upstream excitation of place cells is co-aligned with local feedback inhibitory regulation. We distinguished two subclasses of inhibitory interneurons, which differed in waveform, firing patterns, sharp wave-ripple association and theta phase preference (Figure 6A and S7). Although this is a major simplification of the known variety of interneurons types in the CA1 region (Klausberger and Somogyi, 2008), the chosen physiological properties of the two groups largely correspond to optogenetically-identified PV and SOM-expressing neurons (Royer et al., 2012). Importantly, the spike transmission probability between CA1 place cells and these two groups of interneurons was either depressing or potentiating, and these short-term dynamics were prominently expressed within place fields (Figure 6B,C). Assuming that the potentiating group (SOM-like) contained the O-LM type of interneurons with axonal targets in str. LM, we hypothesize that increased recruitment of distal dendritic inhibition contributes further to the decreasing influence of EC3 input (Katona et al., 1999) from the beginning to the end of the place field. Conversely, decreasing recruitment of putative bistratified and perisomatic PV neurons that innervate the proximal dendrites and somatic region of pyramidal cells (Klausberger and Somogyi, 2008) may progressively increase the impact of the CA3 input on place cell firing as the animal crosses the place field. This hypothesis is also supported by previous findings, showing that optogenetic suppression of PV or SOM-expressing interneurons enhances firing rates of place cells mainly at the beginning and the end of the place field, respectively (Royer et al., 2012).

Comparison with other models of phase-precession

Three classes of theoretical models have been advanced to explain the phase precession phenomenon: oscillatory interference, single neuron mechanisms and cell assembly mechanisms. Based on the observation that hippocampal place cells oscillate faster than the ongoing LFP theta (O’Keefe and Recce, 1993), several investigators suggested that spike phase procession is brought about by phase-interference of the oscillators (Burgess, 2008; Burgess et al., 2007; Geisler et al., 2010 Hasselmo et al., 2007; Kamondi et al., 1998; Lengyel et al., 2003; O’Keefe and Burgess, 2005). Because hippocampal place cells are speed-controlled oscillators (Geisler et al., 2007), the dual oscillator model links the spike timing phenomena to navigation (Burgess, 2008). While the interference model well describes the phenomenology of spike phase precession, it does not explain the mechanisms involved. It predicts a full theta cycle (360^o) within-field phase shift, which is not observed experimentally in single trials (Schmidt et al., 2009; Belluscio et al., 2012). In addition, the phase reset of one of the oscillators in the phase-interference model is expected to interrupt the course of phase precession, a prediction that was not observed experimentally (Zugaro et al., 2005).

Single neuron models assume that perisomatic inhibitory and dendritic excitatory inputs differ in theta frequency or driving force, and spike advancement is induced by either phase interference and/or the magnitude of dendritic depolarization (Harris et al., 2003; Kamondi et al., 1998; Lengyel et al., 2003; Losonczy et al., 2010; Mehta et al., 2003). However, the somato-dendritic interference model cannot explain the experimentally observed slow depolarization ramp within the place field (Harvey et al., 2009) without additional assumptions. Furthermore, intracellular recordings in behaving rats showed that perisomatic inhibition, which is tracked by the somatic membrane potential (Penttonen et al., 1998), is faster than the theta LFP (Harvey et al., 2009). This hypothesis is also supported by the observation that fast firing interneurons often show phase precession, driven monosynaptically by their active place cell partners (Figure 6B) (Geisler et al., 2007; Maurer et al., 2006). An alternative to the single cell model is a cell assembly model, in which the phase-precessing (i.e., faster oscillating) constituent is not a single place cell but a self motion-controlled assembly of neurons, including their transiently ‘enslaved’ interneurons (Geisler et al., 2010). The the evolving phase difference then emerges between the currently active assembly and the large pool of less active pyramidal neurons, which are largely responsible for the generation of LFP theta.

The current dual-input model combines elements of each of the three models of phase precession, integrates them with the role of gamma oscillations (Bieri et al., 2014; Zhang et al., 2016; Lasztoczi and Klausberger, 2016) and demonstrates how upstream excitatory inputs can interact with local inhibitory mechanisms. The dual input model also shares ideas with the computational model of Chance (2012). However, in the Chance model, the CA3 input initiates the field and the EC input is most active at field exit, in contrast to the experimental findings.

Conclusions

These results highlight the power of high-spatial resolution recording methods in circuit analysis. We utilized this approach to demonstrate how two inputs with varying phase offsets and excitatory strengths can affect the timing of their target neurons. The dual-input model accurately predicts several fundamental features of hippocampal network activity, including the phase-shifting depth profile of theta oscillations, brain state- and task-dependent theta phase shift of spikes and the phase precession phenomenon in each hippocampal region and sublayer. Furthermore, it ascribes a functional role for dendritic layer-specific gamma oscillations and feedback dendritic inhibition. Dual-input mechanisms may also explain phase-precession and behavior-dependent theta phase shifts in other regions like the entorhinal cortex or the subiculum.

STAR methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for reagents and resource may be directed to, and will be fulfilled by the lead contact, Dr. György Buzsáki (gyorgy.buzsaki@nyumc.org).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Eleven male rats (Long-Evans, 3–5 months old) were used in this study. Rats were kept in the vivarium on a 12-hour light/dark cycle and were housed 2–3 per cage before surgery and individually after it. All experiments were approved by the Ethical Committee for Human Research at the Albert Szent-Györgyi Medical and Pharmaceutical Center of the University of Szeged and the Institutional Animal Care and Use Committee of New York University Medical Center IACUC.

METHOD DETAILS

Electrode implantation and surgery

Electrode fabrication and implantation surgery were done as described earlier (Berenyi et al., 2014; Mizuseki et al., 2009). Specifically, animals were anesthetized with isoflurane anesthesia and one or several craniotomies were performed under stereotaxic guidance. Different types of silicon probes (NeuroNexus, Ann-Arbor) were implanted in the dorsal hippocampus and in the medial and/or lateral entorhinal cortex (Table 1 and Figure S1). Silicon probes were mounted on custom-made micro-drives to allow their precise vertical movement after implantation. The probes were inserted above the target region and the micro-drives were attached to the skull with dental cement. The craniotomies were sealed with sterile wax. Two stainless steel screws were drilled bilaterally over the cerebellum served as ground and reference for the recordings. Several additional screws were driven into the skull and covered with dental cement to strengthen the implant. In some of the experiments bipolar tungsten stimulating electrodes were implanted in the ipsilateral fornix (−1.4 mm posterior to Bregma, 1.4 lateral and 4.5 depth) and/or the lateral olfactory tract (5.0 mm anterior to Bregma, 2.0 lateral and 7.0 depth). Finally, a copper mesh was attached to the skull with dental cement and connected to the ground screw to act as a Faraday cage preventing the contamination of the recordings by environmental electric noise (see more details in Vandecasteele et al., 2012). After post-surgery recovery, the probes were moved gradually in 75 to 150 μm steps per day until the desired position was reached. The pyramidal layer in the CA1, 2 and 3 regions was identified physiologically by increased unit activity and the occurrence of LFP ripples (Mizuseki et al., 2011; Ylinen et al., 1995). The identification of dendritic sublayers in CA1, DG and CA3 was achieved by the application of CSD and ICA analysis to the LFPs (Fernandez-Ruiz et al., 2012a; Fernandez-Ruiz et al., 2013) and by known physiological markers such as the reversal of sharp-waves (Ylinen et al., 1995) and depth versus amplitude profile of theta oscillations (Buzsaki, 1986; Montgomery et al., 2009). The CA2 region was identified post-hoc from histological sections by the thicker pyramidal layer and wider and sparser cell bodies compared to CA1 (Chevaleyre and Siegelbaum, 2010; Lorente de Nó, 1947) and confirmed by specific immunolabeling (see below; Oliva et al., 2016a). Evoked potentials elicited by brief current pulses (100 μs, 100–500 μA) delivered to the fimbria and/or the lateral olfactory track were used to further guide the identification of entorhinal layers.

Some data included in the present study were also used in previous works (Oliva et al., 2016a,b; Schomburg et al., 2014; Berényi et al., 2014), as listed in Table S1.

Data acquisition and behavior

The operated animals were housed in individual cages and recorded during sleep sessions in their home cage and during different navigational tasks. Neuronal recordings were performed daily for 20–30 days per animal by connecting the probes to a signal multiplexing headstage attached to a thin and light cable pending from the room ceiling on a trolley system that allowed free movement of the animal. The spatial position of the rats during behavioral sessions was monitored using video tracking of two LEDs fixed to the headstage. The wide-band signal was acquired at 20K Sample/s (KJE-1001, Amplipex Ltd, Hungary). The wide-band signal (0.2–10 kHz) was low-pass filtered and downsampled to 1250 Hz to generate LFP, and high-pass filtered (>0.5 kHz) for spike detection.

In the linear track, rats were trained to run back and forth to collect small water rewards. After the first one or two days all animals performed 40–80 trials per day. The linear track was placed one meter above the floor and was 240-cm long and had 20-cm walls.

In the rectangular figure-8 maze (or ‘T-maze’) animals were trained to alternate between right and left arms to collect water rewards. At the beginning of the trial rats were confined in the home port for 15 seconds. After the door of the central arm opened, animals ran through it and chose to turn right or left. If the decision was correct (opposite arm than visited in the previous trial) they would find a water reward after turning the corner of the side arm; if incorrect, the reward port would remain empty. After enough time to consume the reward, or an equivalent time in the case of an error, the door leading to the home port opened and after closing it behind the rat a new trial started. During training, animals were initially trained to alternate without delay and the delay period was progressively increased in later sessions until it reached 15 seconds. After 3 to 4 days of training, animals performed 30–50 trials per day. The maze was placed one meter above the floor and had 160 cm length (for the central and side arms) and 134 cm width (for the lateral connecting arms). All LFP and unit analysis included in the figures were obtained during sessions where animals reached a performance of at least 85% with a 15 seconds’ delay period.

In the dataset obtained from the CRCNS repository (http://crcns.org/hc-3), animals were also recorded during linear track running and delayed T-maze alternation task, with small variations, that have been described in detail elsewhere (Mizuseki et al., 2014; Mizuseki et al., 2012; Mizuseki et al., 2009).

Tissue processing and immunohistochemistry

Following the termination of the experiments, animals were deeply anesthetized and transcardially perfused first with 0.9% saline solution followed by 4% paraformaldehyde solution. Brains were sectioned in 70-μm thick slices (Leica Vibratome) parallel with the plane of the implanted electrodes. Additionally, immunolabeling for the CA2 region specific marker PCP4 (Kohara et al., 2014) and for the layer II of the entorhinal cortex with calbindin (Kitamura et al., 2014) was performed. For the PCP4 slices were washed three times in PBS-Tx 1%, then blocked with 3% bovine serum albumin in PBS-Tx and incubated overnight at room temperature with the primary antibody solution containing rabbit anti-PCP4 (1:300, Sigma HPA005792). After three washes in PBS-Tx, sections were incubated for 2h at room temperature with goat anti-rabbit Alexa Fluor 488 (1:500, Jackson Immunoresearch 115-545-003) (Oliva et al., 2016a; Valero et al., 2015). Sections were then washed and mounted on glass slides with fluorescence medium (Fluoroshield with DAPI - F6057, Sigma, USA). For the calbindin immunostaining sections were washed in PBS-Tx 0.3%, then blocked with 10% normal donkey serum (IHR-8135, ImmunoBioScience) and incubated overnight at room temperature with CB-28k goat anti-calbindin (1:200, Calbindin-Go-Af1040, Frontier Science). Then sections were washed in PBS-Tx 0.3% and incubated for 2h with Alexa Fluor 488-conjugated donkey anti-goat IgG secondary antibody (1:1000, A-11055, Invitrogen). After DAPI staining (1 μg/ml, D8417, Sigma-Aldrich) sections were washed in PBS and mounted on glass slides with Vectashield mounting medium. Immunostained slices were examined and images were acquired with a confocal microscope (LSM880 Carl Zeiss) and/or with an epifluorescence microscope (AxioImager Carl Zeiss).

Spike sorting and unit classification

Neuronal spikes were detected from the digitally high-pass filtered LFP (0.5–5 kHz) by a threshold crossing-based algorithm (Spikedetekt2; https://github.com/klusta-team/spikedetekt2). Detected spikes were automatically sorted using the masked EM algorithm for Gaussians mixtures implemented in KlustaKwik2 (Kadir et al., 2014; https://github.com/klusta-team/klustakwik/), followed by manual adjustment of the clusters using KlustaViewa software (Rossant et al., 2016; https://github.com/klusta-team/klustaviewa/) to obtain well-isolated single units. Multiunit or noise clusters were discarded for the analysis. Cluster isolation quality was estimated by calculating the isolation distance and interspike interval index for each cluster (Schmitzer-Torbert et al., 2005); poor quality clusters were discarded. Putative pyramidal cells and interneurons were separated on the basis of their autocorrelograms and waveform characteristics (Csicsvari et al., 1998; Mizuseki et al., 2009; Stark et al., 2014), assisted by monosynaptic excitatory and inhibitory interactions between simultaneously recorded, well-isolated units (Bartho et al., 2004; Mizuseki et al., 2009). Deep and superficial CA1 pyramidal cells where classified according to the position of their soma (maximal spike amplitude) with respect to the reversal of the slow envelope of ripple power (Mizuseki et al., 2011; Oliva et al., 2016b). Positive ripple envelope corresponded to deep CA1 sublayer and negative envelope to superficial sublayer.

Independent component and current source density analysis of LFP

To address the inverse problem of LFP, that is, to separate the different sources that contribute to the mixed signal, we employed a combination of independent component analysis (ICA) and current source density (CSD) analysis as has been described and validated previously (Fernandez-Ruiz and Herreras, 2013; Fernandez-Ruiz et al., 2012a).

ICA is a blind source-separation technique (Bell and Sejnowski, 1995; Comon, 1994; Hyvarinen et al., 2001) that can isolate spatially segregated stable patterns of activity in a mixed signal recorded with an array of sensors. Applied to linear profiles of LFPs it can separate physiologically meaningful sources that can be attributed to known anatomical pathways, as has been demonstrated for the CA1, CA3 and dentate regions of the rat hippocampus (Benito et al., 2014; Fernandez-Ruiz et al., 2012a; Fernandez-Ruiz et al., 2012b; Fernandez-Ruiz et al., 2013).

Here, we applied ICA to spatially contiguous LFP channels (on one shank at a time). The algorithm takes a time series of data with dimension equal to the number of recording sites, and returns a time series of the same dimensionality, but rotated such at each dimension to represent a different IC. The inverse of the mixing matrix that transforms the LFP data into the ICs gives the channel weight of each component that is captured for each electrode. When plotted according to the anatomical location of the electrodes, this corresponds to the spatial voltage loadings of each IC (Fernandez-Ruiz et al., 2012a). Once ICs have been extracted from the raw LFP traces, they can be analyzed as if they were active independently from activities at other locations. We reconstructed the virtual LFP produced by a single IC, by multiplying the IC time course by its corresponding voltage loading. CSDs for each IC were calculated from their voltage loadings after application of ICA, using standard methods (Mitzdorf, 1985).

The optimization of ICA of LFPs for high-frequency activity has been described in detail elsewhere (Schomburg et al., 2014).

Spectral analysis, cross-frequency coupling and spike - LFP coupling

We estimated the theta-band phase of the LFP recorded in CA1 stratum pyramidale by the linearly interpolated phase between maxima and minima in each theta cycle of the 1–60 Hz bandpass filtered LFP (Belluscio et al., 2012). The intervals in which to detect extrema were determined using zero-crossings of the narrowband-filtered (4–10 Hz) signal. Theta epochs were detected automatically using the ratio of the power in theta band (5–11 Hz) to the power of nearby bands (1–4 Hz, 12–14 Hz) of CA1 LFP, followed by manual adjustment with the aid of visual inspection of whitened power spectra (Sirota et al., 2008). Theta epochs during walking/running were classified as RUN, and those during sleep were classified as REM, with non-REM sleep periods classified as slow-wave sleep (SWS or nonREM; Mizuseki et al., 2009). Theta peaks correspond 0^o and 360^o and troughs at 180^o and 540^o of theta waves recorded in the CA1 pyramidal layer throughout the manuscript. LFP theta phase was estimated from the recording site from which the unit with the maximum spike amplitude was recorded from. Theta modulation indices for each neuron were calculated using the mean resultant length of the phases, and significance was estimated using the Rayleigh test for non-uniformity using the circular statistics toolbox provided by P. Berens (Berens, 2009). The mean angle and mean resultant length of the theta phases for a given neuron’s spikes were taken as the preferred phase and modulation strength of that neuron respectively (Mizuseki et al., 2012).

To analyze high-frequency oscillatory activity in the LFP at a high resolution in time and frequency, the complex wavelet transform (CWT) of the LFP (or ICs) was calculated using complex Morlet wavelets (Torrence and Compo, 1998b). The CWT gives an amplitude and phase measure for each wavelet scale at all time points in the data, obtained by convolving the real and imaginary parts of the wavelets with the data vectors.

The phase-amplitude cross-frequency coupling during theta oscillations for a given LFP recording was assessed using the modulation index (MI) introduced by (Tort et al., 2008).

Wavelet phase was calculated at 73 levels from 2–20 Hz, and the amplitude at 136 levels from 30–300 Hz. Phase time-series were binned into phase intervals and the mean wavelet amplitude was calculated for each of them. The MI was obtained by measuring the divergence of the observed amplitude distribution from the uniform distribution. The statistical significance of the MI values (p-value) was assessed by a surrogate analysis (n=500 surrogates) with random shifts between the phase and amplitude time series (Canolty et al., 2006).

The phase-locking of spikes to LFP features at each frequency was measured for individual units using the wavelet phase from 30–250 Hz (28 logarithmically spaced wavelet scales) at the time of each spike. Modulation indices were calculated using the mean resultant length of the phases, and significance was estimated using the Rayleigh test for non-uniformity using the circular statistics toolbox provided by P. Berens (Berens, 2009).

All LFP analysis was performed with custom-made MATLAB (The MathWorks, Inc., Natick, MA); scripts available upon request.

Place cell identification

Positions of the linear track were projected onto the track axis. The position and spiking data were binned into 5-cm wide segments, generating the raw maps of spike number and occupancy probability. Rate map, number of place fields, spatial information (Skaggs et al., 1993), selectivity and sparsity (Skaggs et al., 1996) were calculated for each direction separately. A Gaussian kernel (SD = 5 cm) was applied to both raw maps of spike and occupancy, and a smoothed rate map was constructed by dividing the smoothed spike map by the smoothed occupancy map. A place field was defined as a continuous region, of at least 15 cm (3 pixels), where the firing rate was above 10% of the peak rate in the maze, the peak firing rate was > 2 Hz and the spatial coherence was > 0.7. Place fields with fewer than 50 spikes, those that included the turning position of the track and truncated or overlapping fields were discarded. Place fields in both running directions in the linear track and the different arms of the T-maze were treated independently. Only fields that fulfill all the above criteria were considered for phase-precession and gamma LFP analyses.

Phase-precession analysis

To visualize the theta phase advancement of spikes along the field traversal (phase-precession), the instantaneous theta phases (from the filtered CA1 pyramidal layer LFP) of spikes were plotted against the linearized positions in the track for each place field. Circular-linear regression between position and theta phase was applied to calculate the phase-precession slope and correlation strength (Kempter et al., 2012). This was performed by first fitting a linear regression model to circular-linear data by minimizing the circular error between measured and predicted angles. The slope of the resulting regression line was used to scale the linear variable (position) and to transform it into a circular one. Finally, a correlation coefficient, similar to the Pearson’s correlation, was obtained. For further analyses, only fields displaying significant phase-position correlation (p < 0.05) were considered. The slope and correlation strength (r²) of phase precession were derived from this circular-linear regression analysis. The phase range was obtained by multiplying the slope by the place field length or single lap spatial range (see below). For the estimation of the range, slopes were limited to the [−4π,4π] interval. The phase onset was estimated as the phase value of the regression line relative position zero (beginning of the field). The statistical method of (Kempter et al., 2012) allowed us to reliably asses phase-precession parameters of single trials (Schmidt et al., 2009). For single trials the place field length or spatial range was defined as the difference in the relative position in the field of the first and last spike in the trial. Only trials in which the putative place cell emitted at least 5 spikes and the running speed was larger than 10 cm/s were considered.

Place cell and phase-precession analysis were performed with custom made Matlab scripts and routines from the publically available FMA toolbox (http://fmatoolbox.sourceforge.net).

Intra place field analysis of spike sampled LFPs

To analyze within-place field dynamics, we first normalized each place field and divided it into five consecutive spatial bins. Place field bins were determined for each place cell and the total number of spikes was the same in each spatial bin. Spikes in each bin, for all included fields, were pooled together for population analysis. Instantaneous phase and amplitude of the LFP (or IC) at spikes times was calculated from either the theta interpolated phase vector or phase and amplitude wavelet time series for each gamma frequency. Modulation strength and preferred phase of spikes in each place field bin were quantified using circular statistics as explained above for single cells. For better comparison, in the final plots, results were expressed as z-scored magnitudes relative to the mean of the whole place field.

The procedure to isolate gamma inputs to individual place cells is illustrated in Figure S5. First, LFPs recorded from all 256 electrodes were filtered (30–250 Hz) and decomposed applying ICA on a shank-by-shank basis, as described above. The spatial distribution of voltage and currents (obtained by CSD analysis) of each component allowed the identification of CA1pyr, radiatum and LM ICs (Fernández-Ruiz et al., 2012; Schomburg et al., 2014). Second, ICs isolated from every shank were decomposed by complex wavelet transform and modulation of their amplitude at all frequencies (30–250 Hz) by the theta phase was evaluated using the modulation index. A surrogate test was used for obtaining P values of significance. Theta phase was obtained by peak-trough interpolation of the LFP taken form the middle of the CA1 pyramidal layer, separately at every shank. This procedure allowed the verification of layer-specific gamma oscillations, i.e. gamma_F in pyramidal layer, gamma_S in str. radiatum and gamma_M in str. lacunosum-moleculare. Third, for each neuron, spike-LFP phase-coupling was calculated with all wavelet scales from the IC-specific activity at all recordings sites. Fourth, the mean resultant length of the phases for all wavelet scales corresponding to the gamma_S (30–60 Hz), gamma_M (60–110 Hz) and gamma_F (120–180 Hz) sub-bands was averaged to obtain a single phase-modulation value for each cell with each gamma component at every recording location. Finally, the sites with highest phase-modulation values in each gamma sub-band for the specific IC were selected as reference sites for further analysis. This procedure resulted in different reference signals (ICs time courses) for radiatum gamma_S, LM gamma_M and CA1pyr gamma_F inputs to each place cell.

The significance of intra place field spike-LFP coupling for each gamma sub-band was estimated for each individual cell using the Rayleigh test and considering only spikes emitted inside the place field. For the analysis of within-place field variations of gamma inputs, the instantaneous wavelet phase and amplitude were sampled by the spikes of individual place cells in each spatial bin. To increase statistical power, the phase and amplitude values from all place cells were pooled together. This approach mimics the idealized situation.

Physiological classification of interneurons

After separating excitatory and inhibitory cells, CA1 interneurons were further classified into two groups according to auto-correlogram and waveform characteristics (Royer et al., 2012).

From the auto-correlogram (1 ms time bin) of each cell, a burst index was defined as the amplitude of the peak measured between 0 and 10 ms minus the baseline value (mean between 40 and 50 ms). This measure reflects the probability of burst discharges. To calculate the refractory period, first the instantaneous derivative from 0 ms to the time of the peak of the auto-correlogram was calculated and the s.d. of the derivative values was estimated. The refractory period was defined as the first time bin for which the instantaneous derivative exceeded one s.d.

Two parameters were used to quantify spike waveforms. Spike duration (from the negative maxima to the following positive maxima) and spike asymmetry (height of the first positive peak minus height of the second divided by their sum).

Interneurons with a positive burst index and a refractory period shorter than 7 ms were initially classified as putative PV-like cells while those with negative burst index and refractory periods larger than 4 ms were classified as putative SOM-like cells. This classification was further refined by examining waveform characteristics. PV-like cells had shorter and less asymmetric waveforms than SOM-like cells. These classification criteria were chosen following what was previously described for optogenetically identified PV and SOM interneurons (Royer et al., 2012; Stark et al., 2014).

Physiological correlates of both subtypes of putative interneurons were further evaluated by assessing their theta-phase discharge probability (described above) and ripple modulation (Oliva et al., 2016a).

Cross-correlogram analysis of single units

Cross-correlation (CCG) analysis has been applied to detect putative monosynaptic connections (Bartho et al., 2004; Csicsvari et al., 1998; Fujisawa et al., 2008). CCG was calculated as the time resolved distribution of spike transmission probability between a reference spike train and a temporally shifting target spike train. A window interval of [−5, +5] ms with a 1-ms bin size was used for detecting sharp peaks or troughs, as identifiers of putative monosynaptic connections. Significantly correlated cell pairs were identified using the jittering method (Amarasingham et al., 2012). For each cell pair, surrogate data sets were constructed by randomly and independently jittering each spike’s timestamp with a uniformly distributed value in the range of [−5, 5] ms, 1000 times. 99% acceptance bands were calculated from the surrogate data set CCGs for each bin, multiple comparison error was corrected by introducing ‘global significance bands’ (Fujisawa et al., 2008). The reference cell of a pair was considered to have an excitatory monosynaptic connection with the refereed neuron, if any of its CCG bins reached above these global bands within the considered time window.

QUANTIFICATION AND STATISTICAL ANALYSIS

All statistical analyses were performed with standard Matlab functions. No specific analysis to estimate minimal population sample were used, but the number of animal, trials and recorded cells were larger or similar to those employed in previous works (Bieri et al., 2014; Lasztoczi and Klausberger, 2016; Middleton and McHugh, 2016; Zheng et al., 2016). Unless otherwise noted, for all tests, non-parametric two-tailed Wilcoxon rank-sum (equivalent to Mann-Whitney U-test), Wilcoxon signed-rank or Kruskal-Wallis one-way analysis of variance were used. For multiple comparisons, Tukey’s honesty post-hoc test was employed. Box-plots represent median and 25^th 75^th percentiles and their whiskers the data range. In some of the plots outlier values were not represented but they were always included in the statistical analysis.

DATA AND SOFTWARE AVAILABILITY

Part of the data included in this article is already available in the CRCNS.org database. The rest is currently under preparation to be deposited in the same database but will be immediately available upon request.

The software used for data acquisition and analysis is freely available for download (see Methods text and Key Resources Table).

Highlights.

• Cooperation of entorhinal and CA3 inputs control spike timing of hippocampal neurons

• Phase precession is under dual entorhinal and CA3 control

• Spike timing in REM and learning depends on the strengths of upstream gamma inputs

• Feedback inhibition is layer specific and varies within place fields