Dopamine reward prediction errors reflect hidden state inference across time

Abstract

Midbrain dopamine neurons signal reward prediction error (RPE), or actual minus expected reward. The temporal difference (TD) learning model has been a cornerstone in understanding how dopamine RPEs could drive associative learning. Classically, TD learning imparts value to features that serially track elapsed time relative to observable stimuli. In the real world, however, sensory stimuli provide ambiguous information about the hidden state of the environment, leading to the proposal that TD learning might instead compute a value signal based on an inferred distribution of hidden states (a ‘belief state’). In this work, we asked whether dopaminergic signaling supports a TD learning framework that operates over hidden states. We found that dopamine signaling exhibited a striking difference between two tasks that differed only with respect to whether reward was delivered deterministically. Our results favor an associative learning rule that combines cached values with hidden state inference.

Introduction

Midbrain dopamine neurons are thought to drive associative learning by signaling the difference between actual and expected reward, termed reward prediction error (RPE)^1-4. In particular, dopaminergic responses bear a striking resemblance to the error signal in a simple machine learning algorithm known as temporal difference (TD) learning^1,5. Several observations support this hypothesis^1-3. Unexpected reward delivery elicits a large phasic burst of spikes from dopamine neurons. After an animal learns that a sensory cue predicts reward, dopamine neurons burst following the reward-predictive cue and their phasic response is reduced following reward delivery. If a predicted reward is omitted, dopamine neurons pause at the time when the animal usually receives reward.

Some of the theoretical assumptions in the original TD model are not realistic. For one, the TD learning model assumes that the agent assigns values to “states”—representations of environmental conditions at any given time, which are classically specified in terms of observable stimuli. However, in the real world, stimuli often provide ambiguous information about states; the true underlying states are “hidden” and must therefore be inferred^6,7. For example, a lion crouching in the savannah might be indistinguishable from the tall grass, but these two objects carry very different consequences for an antelope. A principled way to incorporate hidden states into the TD learning framework is to replace the traditional stimulus representation with a “belief state”, which tracks the probability of being in each state given the trial history. This revised TD framework generates a value prediction that is computed on an inferred belief state. While this idea has been explored theoretically^8,9, the empirical evidence remains sparse.

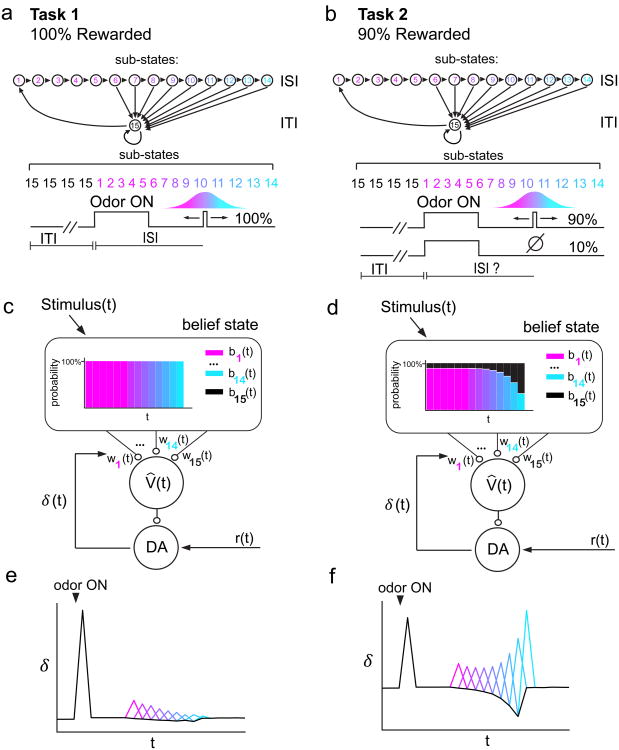
In the present study, we designed two tasks to test whether dopaminergic RPEs provide evidence for a value prediction computed on a belief state. In both tasks, the cue-reward interval (ISI) was varied across trials. In the first task, reward was delivered deterministically (100% rewarded). Our first task resembles other studies that examined dopamine signaling in tasks with variable ISIs^10-12. This previous work, particularly Fiorillo et al, 2008, described a mathematical framework for how temporal expectation influences dopamine RPEs. This work demonstrated that a hazard function, or a temporally blurred ‘subjective’ hazard function, describes temporal expectancy in the case of 100% reward delivery. Expanding upon this previous work, we also included a second task in which reward was occasionally omitted (90% rewarded). In the second task, the animal cannot initially be sure whether the absence of reward means that it was delayed or omitted entirely. As time elapses following cue onset, the animal's belief that reward will arrive gradually yields to the belief that an omission trial occurred. Our results showed striking differences in dopamine signaling between these two tasks, which can be accounted for by incorporating hidden state inference into the value prediction generated by the TD model. These results provide novel evidence that dopaminergic RPEs are shaped by state uncertainty.

Results

Behavioral task and electrophysiology

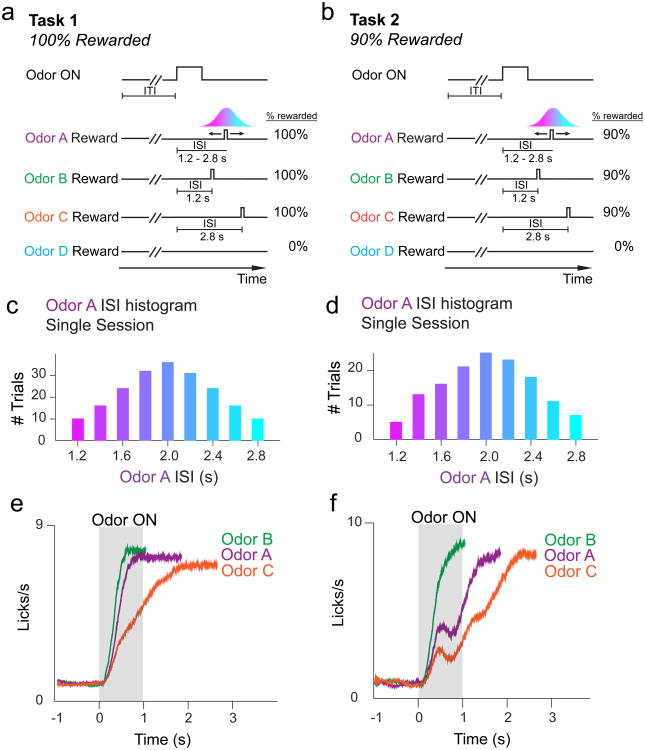
We trained mice on either of two tasks (Fig. 1a,b) (separate sets of 3 and 4 mice in Task 1 and 2, respectively). In Task 1, reward-predicting odors A-C forecasted reward delivery in 100% of trials. In Task 2, odors A-C forecasted reward delivery in 90% of trials. In both tasks, the ISI following odor A was drawn from a discretized Gaussian distribution (mean: 2s, S.D.: 0.5s) defined over 9 timepoints ranging from 1.2s to 2.8s (Fig 1c,d). Odor B and C trials had constant ISIs of 1.2s and 2.8s, respectively. We included odors B and C to examine the effect of temporal delay on dopamine RPEs. On odor D trials, reward was never delivered. In a subset of mice trained on Task 2 (Supplementary Fig. 1a, ‘Task 2b’), we included an odor followed 2s later by reward in order to compare dopamine RPEs in omission trials for constant versus variable ISIs. Mice learned to lick in anticipation of water reward following reward-predicting odors in Tasks 1 and 2 (anticipatory licking in odor A-C ≠ baseline; F_1,50 > 150, P < 6 × 10^-17 for odors A-C in Task 1, 1-way ANOVA; F_1,16 > 60, P < 1 × 10^-6 for odors A-C in Task 2, 1-way ANOVA; F_1,42 > 100, P < 5 × 10^-13 for odors A-C in Task 2b, 1-way ANOVA; Supplementary Fig. 2a-c). Mice ramped up their licking rates sooner and more steeply for odor B (ISI = 1.2s) overodor C (ISI = 2.8s) (Fig 1e,f), and for 100% rewarded odors over 90% rewarded odors (Fig 1e,f, Supplementary Figs. 2d-e, 3). In both Tasks 1 and 2, licking patterns for odor A trials (average ISI = 2.0s) fell in between licking patterns for odor B and odor C. Lick rates following odor D, which never predicted reward, did not change significantly from baseline (F < 2.5, P > 0.10 for both tasks, 1-way ANOVA), demonstrating that mice learned the odor-outcome association.

Figure 1. Task design.

a, In Task 1, rewarded odors forecasted a 100% chance of reward delivery. Odors B and C trials had constant ISIs, while odor A trials had a variable ISI drawn from a discretized Gaussian distribution defined over 9 timepoints. b, In Task 2, rewarded odors forecasted a 90% chance of reward delivery. ISIs for each odor were identical to Task 1. c, Histogram of ISIs for odor A trials during an example Task 1 recording session, showing 9 possible reward delivery times. d, Histogram of ISIs for odor A trials during an example Task 2 recording session. e-f, Averaged non-normalized PSTH for licking behavior across all Task 1 (e) and Task 2 (f) recording sessions. Animals lick sooner for Odor B (ISI = 1.2s) than for Odor C (ISI = 2.8s) trials. Licking patterns for Odor A (variable ISI centered around 2.0s) fall in between licking patterns for Odor B and Odor C.

We recorded the spiking activity of neurons in the VTA (387 neurons in 7 animals, see Supplementary Fig. 4 for recording sites) while animals performed Task 1 or 2. To unambiguously identify dopamine neurons, we expressed the light-gated cation channel channelrhodopsin-2 (ChR2) in dopamine neurons. We delivered pulses of blue light through an optic fiber positioned near our electrodes, and classified units as dopaminergic when they responded to light reliably with short latency (Supplementary Fig. 5; see Methods)^3,4,13.

Dopamine RPEs show opposing patterns of modulation across time in Tasks 1 and 2

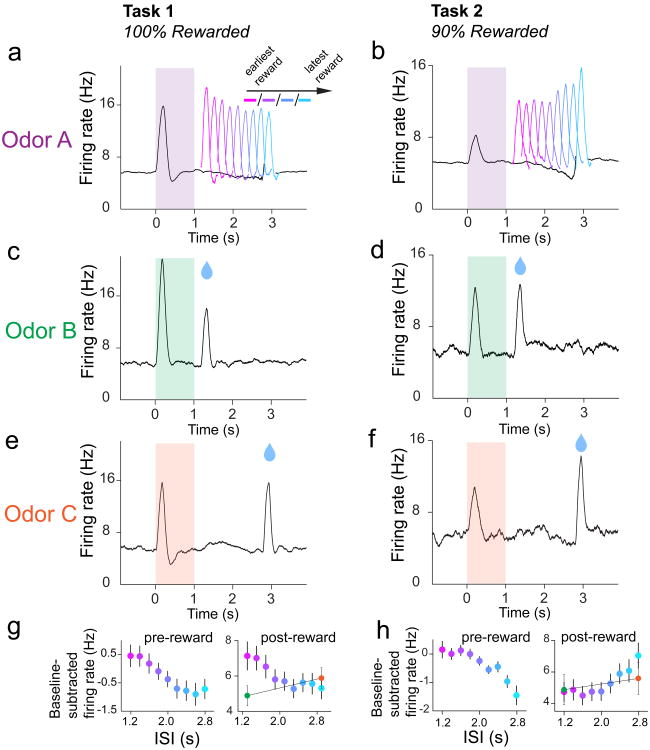
We recorded optogenetically-identified dopamine neurons in Tasks 1 and 2 (Fig. 2). In Task 1 (100% reward probability), reward delivery elicited a phasic burst in dopamine firing (‘post-reward firing’) that was significantly modulated by ISI length (n = 30 neurons; F_8,232 = 5.56, P = 1.9 × 10^-6, 2-way ANOVA; factors: ISI, neuron). Post-reward firing was greatest for the shortest ISI and smallest for longer ISIs (Fig. 2a). We quantified post-reward as the firing rate between 50-300ms following water-valve opening, minus the firing rate 1000-0ms prior to odor onset. We quantified post-reward firing beginning at 50ms post-water valve opening to distinguish between temporal modulation of pre-reward firing and post-reward firing, because the dopaminergic phasic response began 50ms after valve-opening (Supplementary Fig. 6). Furthermore, a recent study showed that intra-trial changes in dopamine firing may signal information distinct from pure RPEs, prompting us to choose a single pre-cue baseline rather than an intra-trial baseline¹⁴. Our quantification of post-reward firing revealed that, on average, post-reward firing was modulated negatively by time (Fig. 2g). In addition to post-reward firing, we also found that the firing rate just prior to reward delivery (‘pre-reward firing’) was modulated over time (F_8,232 =4.76, P = 2.0 × 10^-5, 2-way ANOVA; factors: ISI, neuron). We computed pre-reward firing as the firing rate 400-0ms prior to reward onset, minus the firing rate 1000-0ms prior to odor onset. We found that pre-reward firing mirrored the post-reward pattern of negative modulation by time (Fig. 2a,g). Therefore, in the case of 100% reward probability, both pre- and post-reward dopamine firing decreased as a function of time. This result is consistent with other studies that have examined the effect of variable ISI length on dopaminergic RPEs in the case of 100% reward delivery (or reward-predicting event occurrence)^10-12.

Figure 2. Averaged dopamine activity in Tasks 1 and 2 shows different patterns of modulation over variable ISI interval.

a, Average non-normalized PSTH for all 30 dopamine neurons recorded during Odor A trials in Task 1. Average pre- and post-reward dopamine RPE's were negatively modulated by time (post-reward firing: F_8,232 = 5.56, P = 1.9 × 10^-6, 2-way ANOVA; factors: ISI, neuron; pre-reward firing: F_8,232=4.76, P = 2.0 × 10^-5, 2-way ANOVA; factors: ISI, neuron). b, Average PSTH for all 43 dopamine neurons recorded during Odor A trials in Task 2 (includes neurons from Task 2b). Pre-reward dopamine RPE's (400-0ms prior to reward onset) tended to be negatively modulated by time, while post-reward RPE's (50-300ms following reward onset) tended to be positively modulated by time (post-reward firing: F_8,336 = 8.23, P = 3.48 × 10^-10, 2-way ANOVA; factors: ISI, neuron; pre-reward firing: F_8,336 = 7.86, P = 1.0 × 10^-9, 2-way ANOVA; factors: ISI, neuron). c-f, Average PSTHs for odor B and C trials in Tasks 1 and 2. g-h, Summary plots for average pre- and post-reward firing (mean ± s.e.m.).

We next explored how manipulating the certainty of reward delivery would alter the pattern of RPE modulation across time. In Task 2, odor A's ISI was drawn out of the same Gaussian distribution as before, but reward was given in only 90% of trials. Pre- and post-reward firing in Task 2 was calculated as described above for Task 1. We found that post-reward firing was significantly modulated by ISI length (n = 43 neurons, F_8,336 = 8.23, P = 3.48 × 10^-10, 2-way ANOVA; factors: ISI, neuron). Strikingly, we observed the opposite trend of modulation over time, compared to Task 1. On average, reward delivery elicited a phasic response that was smallest for shorter ISIs and greatest for the longest ISI (Fig. 2b,h). Pre-reward firing in Task 2 was also significantly modulated by ISI length (F_8,336 = 7.86, P = 1.0 × 10^-9, 2-way ANOVA; factors: ISI, neuron), and tended to decrease throughout the variable ISI interval (Fig 2b,h). In sum, in the case of 90% reward probability, pre-reward firing decreased as a function of time, and post-reward firing increased as a function of time.

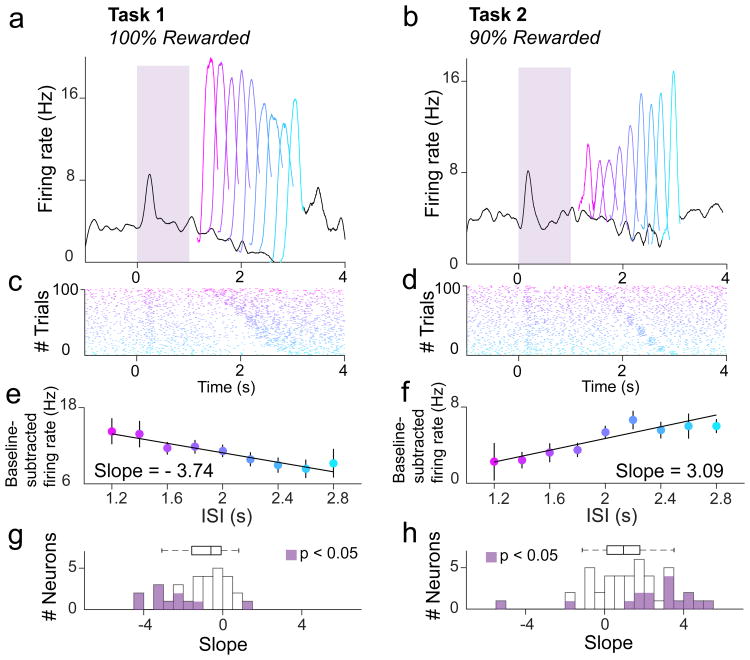
We asked whether these trends of temporal modulation could be seen at the level of individual neurons. In each Task, and for each neuron, we plotted the post-reward firing rate versus ISI on every trial and drew a best-fit line through the data (Fig. 3a-f). Based on the slopes of these best-fit lines, we found that 23/30 neurons tended towards negative modulation by time in Task 1 (95% CI < 0 for 11/30 neurons; Fig. 3g). In Task 2, we found that post-reward RPEs for 33/43 neurons tended to be positively modulated by time (95% CI > 0 for 14/43 neurons; Fig. 3h). We repeated the same analysis for pre-reward firing in both Tasks. In Task 1, pre-reward firing for 19/30 individual neurons tended towards negative modulation by time (95% CI < 0 for 14/30 neurons). In Task 2, pre-reward firing for 32/43 neurons tended towards negative modulation by time (95% CI < 0 for 9/43 neurons). Therefore, individual neurons recorded in each Task tended to reflect the trends of temporal modulation described above.

Figure 3. Individual dopamine neurons show opposing patterns of post-reward firing in Tasks 1 and 2.

a,b,PSTH for two example dopamine neurons during odor A trials of a single recording session in Task 1 (a) or Task 2 (b), respectively. c,d, Raster plots for the first 100 odor A trials of a single recording session in Task 1 (c) or Task 2 (d). e,f, Examples of single-unit analysis. A best-fit line was drawn through a plot relating the ISI to the post-reward firing rate (50-300ms following reward onset) for each odor A trial in Task 1 (e) or Task 2 (f). g,h, Slopes of best-fit lines in Task 1 (g) or Task 2 (h), as shown in (e) and (f), for all dopamine neurons recorded. Purple shading indicates P < 0.05, or a 95% confidence interval for the slope coefficient that does overlap with 0.

To summarize, in Tasks 1 and 2, we found that dopaminergic RPEs were modulated over time for various ISI lengths. Pre-reward firing in both tasks tended to decline throughout the variable ISI interval. However, post-reward firing showed opposite trends of temporal modulation in these two tasks. In Task 1, post-reward firing showed negative temporal modulation, and in Task 2, post-reward firing showed positive temporal modulation.

Dopaminergic RPEs in Task 2 cannot be explained by ISI length

Previous studies have demonstrated that phasic dopamine RPEs are sensitive to ISI length^10,15,16. Specifically, post-reward firing is greater for longer ISIs, suggesting that growing temporal uncertainty increases the dopamine reward response. We asked whether the positive temporal modulation of post-reward firing in Task 2 could be attributed to ISI length alone. If this were true, we would expect the difference between post-reward firing for odor B trials (ISI = 1.2s) and odor C trials (ISI = 2.8s) to account for the difference between post-reward firing for the earliest and latest rewards for odor A trials (ISI = 1.2s and 2.8s, respectively; Fig. 2h). In Task 2, we found that the average post-reward firing rate for odor C was about 1Hz higher than for odor B. This modest difference was not significant (n = 14 neurons; F_1,13 = 0.85, P = 0.37, 2-way ANOVA; factors: odor, neuron). Moreover, the latest possible reward delivery following odor A (ISI = 2.8s) elicited post-reward firing significantly higher than odor C post-reward firing (n = 14 neurons; F_1,13 = 7.15, P = 2 × 10^-2, 2-way ANOVA; factors: odor, neuron). These results indicate that the positive temporal modulation of post-reward firing observed in Task 2 cannot be attributed to ISI length alone.

TD learning with a complete serial compound representation cannot explain dopamine RPEs in Tasks 1 and 2

Dopaminergic RPEs are believed to signal the error term in TD learning models¹. We therefore examined whether previously proposed TD learning models can account for the dopamine signals observed in Tasks 1 and 2.

In reinforcement learning models, including TD learning models, value is typically defined as the expected discounted cumulative future reward¹⁷:

$$V(t)=E[\sum _{\tau =t}^{\infty }{\gamma }^{\tau -t}r(\tau )]$$ (1)

where E[·] denotes an average over randomness in reward delivery, and γ is a discount factor that down-weights future rewards. The goal of reinforcement learning models is to learn correct value estimates so as to maximize future rewards.

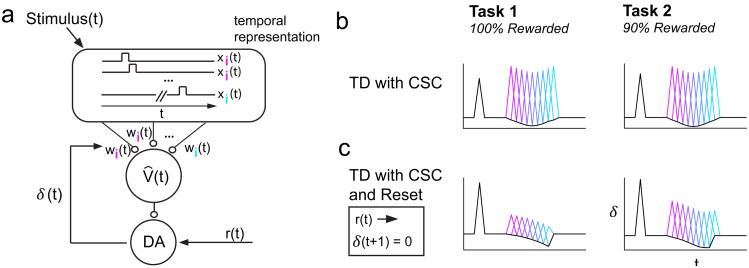
The original application of TD learning to the dopamine system¹ assumed a “complete serial compound” (CSC) representation x(t) = {x₁(t), x₂(t), …} as stimulus features for value computation (Fig. 4a). The onset of a reward-predictive stimulus initiates a ballistic sequence of sub-states marking small post-stimulus time-steps. At a given time after the stimulus, only one of the sub-states x_i(t) becomes active. In other words, x_i(t) = 1 exactly i time-steps following stimulus onset and x_i(t) = 0 in other time steps. The value function estimate is modeled as a linear combination of stimulus features:

Figure 4. TD with CSC model, with or without Reset, is inconsistent with our data.

a, Schematic adapted from¹. The CSC temporal representation comprises features x(t) = {x₁(t), x₂(t), …} that are weighted to produce an estimated value signal V̂(t). δ(t) reports a mismatch between value predictions, and is used to update the weights of corresponding features. b, TD with CSC produces a pattern of RPEs that resembles a flipped probability distribution, for both Tasks 1 and 2. c, TD with CSC and Reset produces a pattern of RPEs that decreases over time, for both Tasks 1 and 2.

$$\widehat{V}(t)=\sum _i{w}_i{x}_i\left(t\right)$$ (2)

where w_i is a predictive weight associated with feature i. The weights are updated according to the following learning rule:

$$\Delta w_i=\alpha x_i(t)\delta (t)$$ (3)

where α is a learning rate and δ(t) is the RPE, computed according to:

$$\delta (t)=r(t)+\gamma \widehat{V}(t+1)-\widehat{V}(t)$$ (4)

We first tested whether TD learning with the CSC can explain our experimental results.

For both Tasks 1 and 2 we found that TD learning with the CSC produced RPEs that were most suppressed for rewards delivered at the center of the Gaussian ISI distribution, and least suppressed for rewards delivered at the tails of the distribution (Fig. 4b). The pattern of RPEs across different ISIs resembled a flipped distribution of experienced ISIs. Moreover, the modulation of RPEs across ISIs was identical between Tasks 1 and 2, indicating that this model cannot explain our data.

We next asked whether a simple modification of the original model could better account for our results: a ‘reset’ feature that sets the RPE to zero after reward arrives^18-19. This model rectifies one key inconsistency between data and a simple CSC TD model: when a reward is delivered unexpectedly early, the ‘pause’ predicted by the CSC TD model at the usual time of reward does not occur²⁰. When we trained a TD model with the CSC and reset on our tasks, the model produced a pattern of RPEs suggestive of a hazard function, that is, reward expectation that grows over time, increasingly suppressing excitation towards the end of the variable ISI interval (Fig. 4c). A pattern of decreasing RPEs over time matches our Task 1 data. However, in Task 2, this model also produced RPEs that generally decreased throughout the variable ISI interval, deviating from the trend of our data. Therefore, this proposed modification to the original model cannot explain our results. Our data do not completely rule out other reset devices, such as resetting the stimulus trace following reward²¹. However, as pointed out by Daw and colleagues⁹, such a reset device assumes an inferred state change, and may not generalize gracefully to more complex scenarios with multiple rewards.

TD learning with belief states explains dopaminergic RPEs in Tasks 1 and 2

Another way to approach these data is to reconsider the computational problem being solved by the animal. One potentially important problem for the animal in the above tasks is knowing whether it is in one of the two states: the ISI state during which the animal expects reward, and the ITI state during which no reward is expected. In Task 1, these two states are fully observable, since cue onset unambiguously signals a transition to the ISI state, and reward onset unambiguously signals a transition to the ITI state; no transitions occur without one of these events (Supplementary Fig. 7a). Thus, the states are fully observable, and the only computational problem is predicting reward. In Task 2, omission trials cause the ITI state to self-transition (while still emitting a cue). This means that both ITI-to-ISI and ITI-to-ITI generate the same observation, rendering the states partially observable or “hidden” (Supplementary Fig. 7b). Thus, Task 2 introduces an additional computational problem: hidden state inference.

In this framework, a critical computation is to assign a probability of being in ITI or ISI at a given moment. To incorporate this process in our model, here we assume that the ISI and ITI comprise temporal “sub-states” with the analogy to the CSC model (Fig. 5a,b). The normative solution to the hidden state inference problem is given by Bayes' rule, which stipulates how an animal's probabilistic beliefs about states should be updated over time:

Figure 5. Belief state model is consistent with our data.

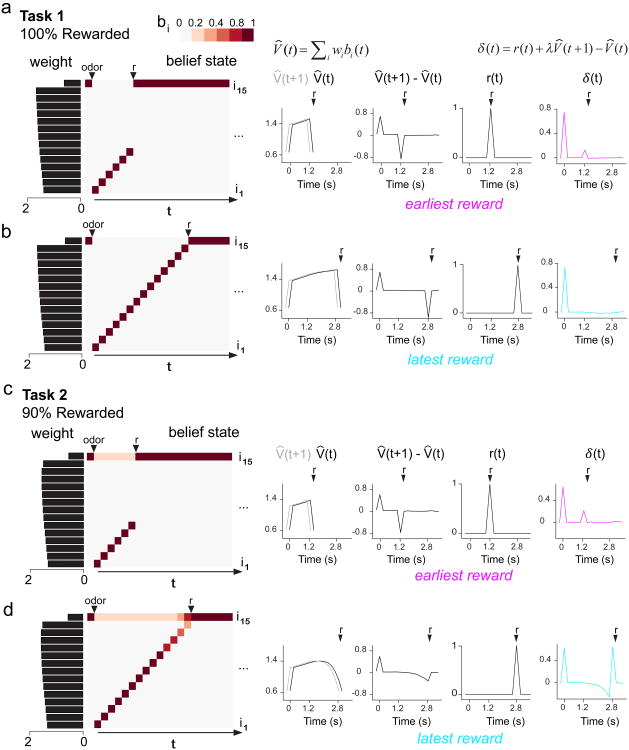
a,b, In our model, the ISI and ITI states comprise sub-states 1-15 c,d, The CSC temporal representation is swapped for a belief state. Expected value is the linear sum of both weight and belief state V̂(t) = Σ_iw_ib_i(t). In Task 1 (c), the belief state sequentially assigns 100% probability to each ISI sub-state as time elapses after odor onset. In Task 2 (d), the belief state gradually shifts in favor of the ITI as time elapses and reward fails to arrive. e,f, Belief state model captures the opposing post-reward firing patterns between Task 1 (e) and Task 2 (f) (see Supplementary Fig. 8 for quantification). This model also captures negative temporal modulation of pre-reward firing in both Tasks.

$$b_i(t+1)\propto p(o(t)|i)\sum _{j}p(i|j)b_j(t-1)$$ (5)

where b_i(t) is the posterior probability that the animal is in sub-state i at time t, p(o(t)|i) is the likelihood of the observation o(t) ∈ {cue, reward, null} under hypothetical sub-state i, and p(i|j) is the probability of transitioning from sub-state j to sub-state i (Supplementary Fig. 7c-f).

The vector b(t) functions as a “belief state” that can substitute for the CSC in learning equations (2) and (3) shown above (Fig. 5c,d). In Task 1, where the observations are unambiguous, the belief state is identical to the CSC. In Task 2, the belief state departs from the CSC by representing subjective uncertainty about the current sub-state (the posterior probability of being in the ISI or ITI state can be computed from this representation by summing the belief state vector over all sub-states within a particular state).

While we have formulated the model in terms of probabilities over sub-states, the model could have alternatively been formulated in continuous time using semi-Markov dynamics⁹, where sub-states are replaced by dwell-time distributions in each state. These models are mathematically equivalent; we chose the sub-state formulation in order to draw clearer connections to other models (a point to which we return in the Discussion).

A belief state TD model produced error signals that resembled dopamine RPEs in our Tasks (Fig. 5e,f). In Task 1, the states are fully observable and thus the belief state is uniform throughout the variable ISI interval (Fig. 5c, Fig. 6a,b): as soon as the cue comes on, the belief state encodes a 100% probability of being in one of the ISI sub-states, and a 0% probability of being in the ITI sub-state. Because the momentary probability of receiving reward is greater at later ISIs than at sooner ISIs, later sub-states accrue higher weights than earlier sub-states, producing a ramping value signal (Fig. 6a,b). This ramping value signal results in RPEs that are increasingly suppressed towards the end of the variable ISI interval (Fig. 5e, Fig. 6a,b; see Supplementary Fig. 8a,c for quantification), producing a pattern of negative modulation by time similar to our Task 1 data.

Figure 6. Belief state model shapes value signals that differ between Tasks 1 and 2, leading to opposite patterns of post-reward modulation over time.

a,b, As time elapses following odor onset in Task 1, the belief state proceeds through ISI sub-states (i₁-i₁₄) by sequentially assigning a probability of 100% to each sub-state. Later ISI sub-states accrue greater weights. Estimated value is approximated as the dot product of belief state and weight, producing a ramping value signal that increasingly suppresses δ(t) for longer ISIs. c,d, As time elapses following odor onset in Task 2, the belief state comprises a probability distribution that gradually decreases for ISI sub-states (i₁-i₁₄) and gradually increases for the ITI sub-state (i₁₅). This produces a value signal that declines for longer ISIs, resulting in the least suppression of δ(t) for the latest ISI.

In Task 2, the belief state takes into account the possibility of an unobservable state transition. Therefore, unlike in Task 1, the belief state was not uniform throughout the variable ISI interval. As time elapses and reward fails to arrive, the belief state progressively shifts in favor of the ITI over the ISI (Fig. 5d, Fig. 6d). Rewards sometimes arrive at the latest ISIs, increasing the weights for the corresponding sub-states. However, the belief state for these late timepoints is so skewed towards the ITI that the value signal actually decreases relative to earlier timepoints (Fig. 6c,d). This decreasing value signal results in pre-reward RPEs that are most suppressed, and post-reward RPEs that are least suppressed, at the end of the variable ISI interval (Fig. 5f, Fig. 6c,d; see Supplementary Fig. 8b,d for quantification). Post-reward RPEs towards the end of the interval were nearly as large as unpredicted rewards, both in our model results (Supplementary Fig. 8d) and our data (Supplementary Fig. 9). Therefore, our model captures the pattern of pre- and post-reward RPEs in our Task 2 data. Importantly, the belief state model captures the striking opposing trends of temporal modulation for post-reward dopamine RPEs in Tasks 1 and 2.

One additional empirical result that we compared with our belief state TD model was Task 2b reward omission responses. For Odor A omission trials (2s variable ISI), we found that the trough of the dip in dopamine firing occurred slightly later than the trough for Odor B trials (2s constant ISI). This shift in the trough of the omission response was also reproduced by our belief state TD model (Supplementary Fig. 1b,c).

One assumption of our model was that animals had perfectly learned the Gaussian distribution of ISIs. We lacked any behavioral indication that the animals had truly learned the probability distribution, so we tried relaxing this assumption of our model by instead training it on a uniform distribution of ISIs. We found that our model produced the same ‘flip’ in the temporal modulation of post-reward RPEs between Tasks 1 and 2, when trained on a uniform distribution (Supplementary Fig. 10). Therefore, our modeling result is relatively agnostic to the precise shape of the learned ISI distribution.

Finally, while our model captures the trends of pre- and post-reward temporal modulation in both Tasks 1 and 2, the overall dopamine firing in Task 1 is much larger than predicted by our model. What could cause the discrepancy in post-reward RPE magnitude between our Task 1 data and model? Because our mice are trained on an odor-outcome association, the exact time when the animals sniff and detect ‘odor ON’ is jittered from trial to trial. This temporal jitter limits how precisely the animal can anticipate reward timing. Therefore, because our model does not incorporate this trial-by-trial jitter, it suppresses RPEs more effectively, particularly in Task 1 conditions that allow reward timing to be predicted perfectly by the end of the interval. Furthermore, our mice are trained for a relatively short length of time (∼1-2 weeks) prior to recording, potentially limiting the extent to which RPEs can be suppressed. Indeed, training our model on fewer trials increases the magnitude of post-reward RPE's.

Previous accounts of ‘hazard-like’ expectation signals cannot explain our data

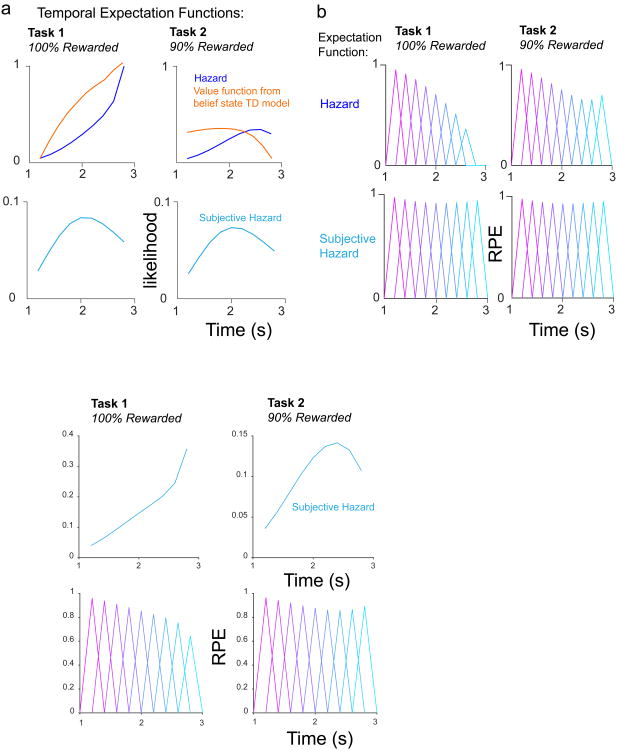
Previous work has described ‘hazard-like’ expectation signals that shape neural firing and animal behavior^22-25. A hazard function is defined as the probability function divided by the survival function, or in other words, the likelihood that an event will occur, given that it has not yet occurred. In other studies that analyzed dopaminergic RPEs in tasks with variable ISIs^10-12, the variably timed event always occurred (100% event probability) and the ISI was drawn from a uniform distribution. With respect to both pre- and post-reward dopamine firing, all of these studies found a pattern of decreasing excitation over elapsed time, thought to correspond to a rising hazard function that increasingly suppressed later RPEs. Furthermore, a functional magnetic resonance study provided evidence that blood-oxygen-level dependent (BOLD) signals in VTA track hazard signals in humans²⁶. However, one aspect of previous work could not be explained using a hazard function: when animals were trained on an exponential distribution of ISIs, post-reward RPE's were still negatively modulated over time despite the flat hazard function of the ISI distribution¹⁰. Intriguingly, when we trained our belief state TD model on an exponential distribution similar to this previous work, our model was able to reproduce the negative temporal modulation of post-reward RPEs (Supplementary Fig. 11d,e).

Our data in Task 1, which utilized a Gaussian ISI distribution and 100% reward probability, also revealed a pattern of decreasing pre- and post-reward dopamine firing, which matches the proposal that a hazard function may describe the trend of temporal expectancy reflected by dopamine RPEs (Fig. 7). However, our data in Task 2 cannot be explained by a hazard function, nor can they be explained by a temporally-blurred subjective hazard function, computed by blurring the probability distribution function with a Gaussian whose standard deviation scales with elapsed time (see ^23,24, Methods) (Fig. 7). Plotting the hazard function and subjective hazard functions for Task 2 reveals that both of these functions find a minimum for the earliest rewards. However, our data indicates that temporal expectation is at its maximum for the earliest rewards, because the earliest post-reward RPE's are most suppressed (Fig. 2b). We illustrated this contrast by plotting the value function from our belief state TD model alongside the hazard function for Task 2 (Fig. 7a). In sum, a hazard function may describe temporal expectancy for 100% rewarded conditions. However, temporal expectancy is dramatically altered in conditions involving uncertainty about whether the event will occur at all.

Figure 7. Hazard and subjective hazard functions cannot explain the trend of our data.

a, Hazard and subjective hazard functions deviate substantially from the trend of value expectation over time in our belief state TD model, particularly in Task 2. Note the value functions are scaled versions of those shown in Fig. 6b,d to aid visual comparison of trends over time. b, Illustration of how RPEs would appear in our data, if the reward expectation signal corresponded to hazard or subjective hazard functions.

Discussion

In this work, we examined how dopaminergic RPE signals change with respect to reward timing and probability. Our experimental results showed that, depending on whether or not reward is delivered deterministically, dopaminergic RPEs exhibited opposite patterns of temporal modulation. Furthermore, our modeling result showed that these data are well explained by a TD model incorporating hidden state inference⁹. Because dopaminergic RPEs are proposed to signal the error term in TD learning, these findings deepen our understanding of how TD learning may be implemented in the brain. TD learning uses RPEs to update the weights of task-related features, which were classically represented as a cascade of sub-states (the “complete serial compound” or CSC) that track elapsed time following stimulus onset^1,5. Our findings support an alternative “belief state” model that tracks a posterior distribution over sub-states.

A long-standing idea in modern neuroscience is that the brain computes inferences about the outside world rather than passively observing its environment^27,28. This is accomplished through the inversion of a generative model that maps hidden states to sensory observations. For example, the hidden state of a lion crouching in the grass could be mapped to sensory cues such as a faint rustling or a nearby pawprint. By conditioning its belief state on observations of its environment, the antelope may predict the lion's presence. Following earlier theoretical work^8,9,29, we argue that this inferential process is at play in the dopamine system. In particular, inferences about hidden states furnish the inputs into the reward prediction machinery of the basal ganglia, with dopamine signaling errors in these reward predictions.

This work follows two recent empirical studies that explored a state-based framework in the striatum and the VTA^30,31. In the first of these studies, the authors found that individual striatal cholinergic interneurons preferentially fire for certain ‘states’, which mapped onto different blocks of a behavioral task³⁰. In the second of these studies, a state-based model was used to capture the effect of a striatal lesion, which selectively impacted the temporal specificity of dopaminergic prediction errors but spared value-related prediction errors³¹. These two studies support our claim that a belief state representation may be at play in the basal ganglia reward-processing circuitry.

Previous studies have shown a pattern of decreasing RPE's over time during tasks in which ISIs are drawn from a uniform probability distribution^10-12. Can our model account for the temporal modulation of dopamine RPEs in these previous studies? Upon training the belief state TD model on a uniform distribution of reward timings, our model elicited negative temporal modulation of RPE signals (Supplementary Fig. 11a-b), indicating that our model is compatible with the data in these studies. However, we found that the belief state TD model was not the only model that produced decreasing RPE's over time. TD learning using the complete serial compound and reset also produced a pattern of decreasing excitation over time when trained on a flat probability distribution (Supplementary Fig. 11c). Because a 100% rewarded condition fails to distinguish between these two models, it was critical that our experiments included both ‘100% Rewarded’ and ‘90% Rewarded’ tasks for comparison. Comparing RPEs in both of these task conditions allowed us to distinguish between the predictions of various associative learning models, thereby expanding upon these previous studies.

The belief state model provides a framework that is separate from, and entirely compatible with, previous work that examined the effect of temporal delay on dopamine RPEs^10,15,16. These works showed that dopamine RPEs are less suppressed for lengthier ISIs, likely due to scalar timing uncertainty. For simplicity, our belief state model omitted the effect of temporal uncertainty in order to clearly demonstrate the effect of belief state inference on the value function and dopamine RPEs. However, we can incorporate scalar temporal uncertainty into our model by blurring the belief state distribution with a Gaussian kernel whose standard deviation is proportional to elapsed time³¹ (see Supplementary Fig. 12). To create this ‘blurred’ belief state model, we fit a scalar timing noise parameter to account for post-reward RPE's for 1.2s and 2.8s constant delays (Odors B and C). This temporally blurred belief state model still captured our data well in Tasks 1 and 2.

Although we have focused on the belief state TD model, another prominent account replaces the CSC with “microstimulus” features—temporally diffuse versions of the discrete time markers in the CSC³². The microstimulus model incorporates neural timing noise that accrues for longer intervals by representing each sub-state's temporal receptive field as a Gaussian function whose standard deviation increases and amplitude decreases with the post-stimulus interval. Although the microstimulus and belief state models are typically thought of as alternatives [see³³ for a review], they can be conceived as realizations of the same idea at different levels of analysis.

Examining the belief state over time, we can see that the posterior over each sub-state peaks at a specific moment during the trial (Fig. 6). In Task 2, the peaks become progressively lower as a function of time, due to the increased probability of a state transition. This decrease in amplitude mirrors the decrease in amplitude of microstimuli as a function of time. If we take into account noise and autocorrelation in neural signaling, then we expect these functions to become more temporally dispersed, further increasing the resemblance to microstimuli. This suggests that microstimuli might be viewed as a neural realization of the abstract state representation implied by the belief state model.

The key difference between microstimuli and belief states is that the shape of belief states is sensitive to task structure (e.g., the omission probability), whereas microstimuli have been traditionally viewed as fixed. However, if we view microstimuli as being derived from belief states, then we expect the microstimulus shape to change accordingly. Indeed, evidence suggests that microstimulus-like representations adapt to the distribution of ISIs, ‘stretching’ to accommodate distributions with a wider range of ISIs³⁴. This is precisely what we would expect to see if the transition function in the belief state model is adapted to the ISI distribution.

In summary, our data provide support for a TD learning model that operates over belief states, consistent with the general idea that the cortex computes probability distributions over hidden states that get fed into the dopamine system. While belief states are cognitive abstractions, they could be realized in the brain by neurons with temporal receptive field structure resembling microstimuli.

Methods

Animals

We used 7 adult male mice, hetereozygous for Cre recombinase under the control of the DAT promoter (B6.SJL-Slc6a3^{tm1.1(cre)Bkmm}/J, The Jackson Laboratory) and backcrossed for >5 generations with C57/BL6J mice³⁶. 3 animals were used in Task 1 (Fig. 1a), 1 animal was used in Task 2 (Fig. 1b), and 3 animals were used in Task 2b (Supplementary Fig. 1). Animals were housed on a 12-h dark/12-h light cycle (dark from 7AM to 7PM). We trained animals on the behavioral task at approximately the same time each day. All experiments were performed in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and approved by the Harvard Institutional Animal Care and Use Committee.

Surgery and viral injections

We performed all surgeries under aseptic conditions with animals under isoflurane (1-2% at 0.5-1.0L/min) anesthesia. Analgesia (buprenorphine, 0.1mg/kg, intraperitoneal) was administered pre-operatively and at 12-h checkpoints post-operatively. We performed two surgeries, both stereotactically targeting the left VTA (from bregma: 3.1mm posterior, 0.6mm lateral, 4.2mm ventral). In the first surgery, we injected 500nL of adeno-associated virus (AAV, serotype 5) carrying an inverted ChR2 (H134R) fused to the fluorescent reporter eYFP and flanked by double loxP sites^3,37. We previously showed that the expression of this virus is highly selective and efficient in dopamine neurons³. After 2 weeks, we performed the second surgery to implant a head plate and custom-built microdrive containing 6-8 tetrodes and an optical fiber.

Behavioral paradigm

After 1 week of post-surgical recovery, we water-restricted mice in their cages. Weight was maintained above 85% of pre-restriction body weight. We habituated and briefly head-retrained mice for 2-3 days before training. Odors were delivered to animals with a custom-made olfactometer³⁸. Each odor was dissolved in mineral oil at 1/10 dilution. 30uL of diluted odor was placed into glass fiber filter-paper, and then diluted with filtered air 1:20 to produce a total 1L/min flow rate. Odors included isoamyl acetate, (+)-carvone, 1-hexanol, p-cymene, ethyl butyrate, 1-butanol, limonene, dimethoxybenzene, caproic acid, 4-heptanone, and eugenol. The combination of these odors differed for different animals. We automatically detected licks by measuring breaks of an infrared beam placed in front of the water spout.

For both tasks, rewarded odor A trials consisted of 1s odor presentation followed by a delay chosen from a Gaussian distribution defined over 9 points ([1.2s 1.4s 1.6s 1.8s 2.0s 2.2s 2.4s 2.6s 2.8s]; mean = 2s; SD = 0.5s), prior to reward delivery. For both Tasks 1 and 2, rewarded odor B and odor C trials consisted of 1s odor presentation followed by either 1.2s or 2.8s delay from odor onset, respectively, prior to reward delivery (Fig. 1a,b). In Task 2b, rewarded odor B trials consisted of 1s odor presentation followed by 2s delay from odor onset; odor C was not given (Supp. Fig. 1). In all tasks, odor D trials were unrewarded. In Task 1, reward was given in 100% of trials. In Tasks 2 and 2b, reward was given in 90% of trials. For all tasks, reward size was kept constant at 3uL. Trial type was drawn pseudorandomly from a scrambled array of trial types, in order to keep the proportion of trial types constant between sessions. The ITI between trials was drawn from an exponential distribution (mean = 12-14s) in order to ensure a flat hazard function. Animals performed between 150-300 trials per session.

Electrophysiology

We based recording techniques on previous studies^3,4,13. We recorded extracellularly from the VTA using a custom-built, screw-driven Microdrive (Sandvik, Palm Coast, Florida) containing 8 tetrodes glued to a 200μm optic fiber (ThorLabs). Tetrodes were glued to the fiber and clipped so that their tips extended 200-500μm from the end of the fiber. We recorded neural signals with a DigiLynx recording system (Neuralynx) and data acquisition device (PCIe-6351, National Instruments). Broadband signals from each wire were filtered between 0.1 and 9000 Hz and recorded continuously at 32kHz. To extract spike timing, signals were band-pass-filtered between 300 and 6000Hz and sorted offline using MClust-3.5 (A.D. Redish). At the end of each session, the fiber and tetrodes were lowered by 75um to record new units the next day. To be included in the dataset, a neuron had to be well-isolated (L-ratio < 0.05)³⁹ and recorded within 300um of a light-identified dopamine neuron (see below) to ensure that it was recorded in the VTA. We also histologically verified recording sites by creating electrolytic lesions using 10-15s of 30μA direct current.

To unambiguously identify dopamine neurons, we used ChR2 to observe laser-triggered spikes^3,40,41. The optical fiber was coupled with a diode-pumped solid-state laser with analog amplitude modulation (Laserglow Technologies). At the beginning and end of each recording session, we delivered trains of 10 473nm light pulses, each 5ms long, at 1, 5, 10, 20, and 50Hz, with an intensity of 5-20mW/mm² at the tip of the fiber. Spike shape was measured using a broadband signal (0.1-9,000Hz) sampled at 32kHz. To be included in our dataset, neurons had to fulfill 3 criteria^3,4,13:

1) Neurons' spike timing must be significantly modulated by light pulses. We tested this by using the Stimulus-Associated spike Latency Test (SALT)⁴¹. We used a significance value of P < 0.05, and a time window of 10ms after laser onset.

2) Laser-evoked spikes must be near-identical to spontaneous spikes. This ensured that light-evoked spikes reflect actual spikes instead of photochemical artifacts. All light-identified dopamine neurons had correlation coefficients > 0.9 (Supplementary Fig 3b,g).

3) Neurons must have a short latency to spike following laser pulses, and little jitter in spike latency (Supplementary Fig. 3c,e,f). While others have used a latency criteria of 5ms or less (‘short latency’)^3,4,13, we found that the high laser intensity required to elicit this short latency spike sometimes created a mismatched waveform, due to 2 neurons near the same tetrode being simultaneously activated. For this reason, we often decreased the laser intensity and elicited a spike 5-10ms (‘longer latency’) after laser onset. We separately analyzed neurons in both the ‘short latency’ and ‘longer latency’ categories, and found qualitatively similar results in each group. Therefore, we pooled all dopamine neurons with latencies below 10ms in our analyses.

Data analysis

We focused our analysis on light-identified dopamine neurons (n = 30 for Task 1; n = 43 for Task 2). To measure firing rates, PSTHs were constructed using 1ms bins. Averaged PSTHs shown in figures were smoothed with a box filter of 100-150ms. Average pre-reward firing rates were calculated by counting the number of spikes 0-400ms prior to reward onset. We also attempted using window sizes ranging from 200-500ms, and these produced similar results. Average post-reward firing rates were calculated by counting the number of spikes 50-300ms after reward onset in both Tasks 1 and 2. Both pre- and post-reward responses were baseline-subtracted, with baseline taken 0-1s prior to odor onset.

We further examined the licking behavior on each day of recording. We fit a logistic function to each day's data, for each animal, which takes the following form:

$$f\left(t\right)=\frac{L}{1+{\mathrm{e}}^{-k(t=-t0)}}$$

Where t is time relative to odor onset, L is the curve's maximum value, k is the steepness of the curve, and t₀ is the time of the sigmoid's midpoint.

We plotted a subjective hazard rate by blurring the probability distribution function p(t) by a normal distribution whose standard deviation scales with elapsed time. Similar to previous work^23-24, we used a Weber fraction ϕ = 0.25:

$$\stackrel{\sim }{p}(t)=\frac{1}{\varphi t\sqrt{2\pi }}{\int }_{-\infty }^{\infty }f(\tau )e^{-{(\tau -t)}^2(/2{\varphi }^2{t}^2})d\tau$$

Statistics

No statistical methods were used to pre-determine sample sizes but our sample sizes are similar to those reported in previous publications^3,4,13. Data collection and analysis were not performed blind to the conditions of the experiments. Animals were chosen at random for Tasks 1 or 2. All trial types were randomly interleaved within a single recording session. We verified that all groups of data (including both electrophysiology and behavior) compared using ANOVAs did not deviate significantly from a normal distribution, using a chi-square goodness of fit test. To test whether dopamine RPEs were modulated by ISI length, we used a 2-factor ANOVA, with neuron and ISI as factor. To test whether licking was modulated by odor identity, we used a 1-factor ANOVA, with Odor identity as a factor. To test whether individual neurons' RPEs were modulated by factors such as ISI length or lick rates, we fit a line to the data (dopamine RPEs versus ISI) and reported the slope. We also displayed the 95% confidence interval of the slope (Supplementary Fig. 3) or a summary of whether or not the 95% confidence interval included 0 (shaded in Fig. 3g,h).

Code Availability

Code used to implement the computational modeling in this manuscript can be found in a Supplementary Software section and at this GitHub link: https://github.com/cstarkweather

Immunohistochemistry

After 4-8 weeks of recording, we injected mice with an overdose of ketamine/medetomidine. Mice were exsanguinated with saline and perfused with 4% paraformaldehyde. We cut brains in 100um coronal sections on a vibrotome and immunostained with antibodies to tyrosine hydroxylase (AB152, 1:1000, Millipore) in order to visualize dopamine neurons. We additionally stained brain slices with 49,6-diamidino-2-phenylindole (DAPI, Vectashield) to visualize nuclei. We confirmed AAV expression with eYFP fluorescence. We examined slides to verify that the optic fiber track and electrolytic lesions were located in a region with VTA dopamine neurons and in a region expressing AAV (see Supplementary Fig. 7)

Computational modeling

Temporal difference (TD) Model

We first simulated TD error signaling in our Tasks by using Temporal Difference learning with a complete serial compound representation, identical to the algorithm presented by Schultz and colleagues¹. We set stimulus onset at t = 20, and set 9 possible reward times at t = 26, 27, 28, 29, 30, 31, 32, 33, 34. In our Task 1 simulation, reward was always delivered. In our Task 2 simulation, reward was delivered in 90% of trials. The results presented in the text were obtained by running 10× simulations of each task, with 5000 trials per simulation. The ‘TD with reset’ variant was simulated by setting the error term to 0 at any timesteps after reward was delivered.

Belief state TD Model

We next simulated TD error signaling in our Tasks by using a belief state TD model, similar to that proposed by Daw and colleagues, as well as Rao^8,9. To capture the discrete dwell times in our Tasks (1s odor presentation, followed by nine discrete possible reward delivery timings at 1.2, 1.4, 1.6, 1.8, 2.0, 2.2, 2.4, 2.6, and 2.8s after odor onset), we coded a Markov equivalent of a Semi-Markov model (see ⁹). This Markov equivalent contained 15 total hidden sub-states (see Supplementary Fig. 7a,b). Sub-states 1-5 corresponded to the passage of time during the 1s odor presentation; sub-states 6-14 corresponded to the passage of time preceding the 9 possible reward delivery time. Sub-state 15 corresponded to the ITI. If reward was received at the earliest possible time (1.2s), this would correspond to the model proceeding through sub-states 1-6, and then transitioning to sub-state 15. If reward was received at the latest possible time (2.8s), this would correspond to the model proceeding through sub-states 1-14, and then transitioning to sub-state 15.

In the belief state TD model, it is assumed that the animal has learned a state transition distribution, encoded by matrix T. We captured the dwell-time distribution in the ISI state by setting elements of T to match either the hazard function or the inverse hazard function of receiving reward at any of the 9 discrete timepoints. For example, the hazard rate of receiving reward at 1.2s would correspond to T(6,15), or the probability of transitioning from sub-state 6→15. 1 minus the hazard rate of receiving reward at 1.2s would correspond to T(6,7), or the probability of transitioning from sub-state 6→7. We captured the exponential distribution of dwell-times in the ITI state by setting T(15,15) to 64/65, and T(15,1) = 1/65. An exponential distribution with a hazard rate (ITI_hazard) of 1/65 has an average dwell time of 65. This average ITI dwell time was proportionally matched to the average ISI dwell time to be comparable to our task parameters. The only difference in T between Task 1 and Task 2 was as follows:

• Task 1:

  • T(15,15) = 1 - ITI_hazard

  • T(15,1) = ITI_hazard

• Task 2:

  • T(15,15) = 1 - ITI_hazard * 0.9

  • T(15,1) = ITI_hazard * 0.9

This difference in T between Task 1 and 2 captured the probability of undergoing a hidden state transition from ITI back to the ITI, in the case of 10% omission trials. In the belief state TD model, it is also assumed that the animal has learned a probability distribution over observations given the current state, encoded by observation matrix O. There were 3 possible observations: null, cue, and reward. The likelihood of a particular observation given that the hidden state underwent a transition from i→j, was captured as follows:

• O(i,j,1) = likelihood of observation of ‘null’, given i→j transition

• O(i,j,2) = likelihood of observation of ‘cue’, given i→j transition

• O(i,j,3) = likelihood of observation of ‘reward’, given i→j transition

In order to switch from sub-state 15 (ITI) to sub-state 1 (first state of ISI), the animal must have an observation of the cue: O(15,1,2) = 1. In order to switch from sub-state 10 (middle of ISI) to sub-state 15 (ITI), the animal must have an observation of reward: O(10,15,3) = 1 The only difference in O between Task 1 and Task 2 was as follows:

• Task 1:

  • O(15,15,1) = 1 (null observation)

• Task 2:

• O(15,15,1) = 1-ITI_hazard*0.1 (null observation)

• O(15,15,2) = ITI_hazard*0.1 (cue in a small percentage of cases)

This difference in O between Task 1 and 2 captures the fact that in 10% omission trials the animal will observe a cue, but in fact be in the hidden ITI state rather than a hidden ISI state.

The results presented in the text were produced by training the belief state TD model on either Task 1 (100% rewarded) or Task 2 (90% rewarded), for 5000 trials each. We found that the model yielded asymptotic results after about 1000 trials. For this reason, the results shown in the text are taken from trials 2000-5000. In all simulations, we used a learning rate of α = 0.1 and a discount factor of γ = 0.98.

Supplementary Material

1

Supplementary Figure 1. Task 2b. a, Task 2b was identical to Task 2, except for the constant ISI trial type. Odor B trials had a constant ISI of 2.0 s. b, The trough of the dopamine omission ‘dip’ was slightly later for 2s variable ISI omission trials than for 2s constant ISI omission trials, as indicated by the arrows. c, This slightly later omission dip is consistent with our belief state TD model. If our belief state TD model was adjusted to incorporate timing uncertainty (see Supplementary Fig. 12), the ‘dip’ for reward omission would be more blurred in time, particularly for the 2s constant ISI omission response.

Supplementary Figure 2. Mice learn to lick in anticipation of rewarded odors. a-c, Anticipatory lick rate increased above baseline for all rewarded trial types (n = 26 sessions, F_1,50 > 150, P < 6 × 10^-17 for odors A-C in Task 1, 1-way ANOVA; n = 9 sessions, F_1,16 > 60, P < 1 × 10^-6 for odors A-C in Task 2, 1-way ANOVA; n = 22 sessions, F_1,42 > 100, P < 5 × 10^-13 for odors A-C in Task 2b, 1-way ANOVA). Anticipatory lick rate did not increase above baseline for odor D trials (P > 0.10 for all Tasks, odor D, 1-way ANOVA). d, Average licking PSTH for all sessions across all animals trained on Task 1. e, Average licking PSTH for all sessions across all animals trained on Task 2 (including Task 2b).

Supplementary Figure 3. Are any aspects of licking behavior correlated with temporal modulation of dopamine RPEs? Because the trends of licking behavior across time appeared to be different between Tasks 1 and 2 (see Supplementary Figure 2d,e), we asked whether licking patterns during each session were at all predictive of temporal modulation of dopamine RPEs recorded during that session. a,c, Example fits of logistic function to lick data during individual sessions (see Methods). b,d, Correlations between various parameters of these logistic functions and the slope of phasic dopamine RPEs across time in Task 1 (b) and Task 2 (d). e, Correlations between the slope k of the logistic function and the slope of phasic dopamine RPEs across time as an aggregate in both Task 1 and Task 2 cohorts. f, Correlations between the slope of licking behavior across time just prior to reward delivery (200ms-0ms) and the slope of phasic dopamine RPEs across time. Our analysis revealed a relationship between the steepness, k, of the logistic licking function and negative modulation over time for post-reward firing in Task 1 (b), and in an aggregate analysis of both Task 1 and Task 2 cohorts (e). However, the steepness of the logistic function in Task 1 is determined in the time prior to reward delivery (see a). None of these analyses revealed a behavior correlate of shifting temporal expectation during the interval in which rewards could be delivered.

Supplementary Figure 4. Recording sites. a,b, Schematic of recording sites for animals used in Task 1(a) and Task 2 (b)

Supplementary Figure 5. Optogenetic identification of dopamine neurons. a, Raw trace for single example neuron, demonstrating laser pulses and laser-evoked spikes. b, Near-identical match between waveform of average laser-evoked spike (blue) and average spontaneous spike (black) for same example neuron. c, Histogram of latencies to spike for same example neuron. d, Light-evoked spikes for 10Hz and 50Hz pulses, for same example neuron. e,f, Mean latency and standard deviation of light-evoked spikes, for all identified dopamine neurons. g, Waveform correlation between laser-evoked and spontaneous spikes, for all identified dopamine neurons.

Supplementary Figure 6. Onset of phasic post-reward RPEs begin 50ms following water valve opening. Non-normalized PSTH for Tasks 1 (a) and 2 (b) aligned to the time of reward with only a 20ms box used for smoothing. Although water valve opens at 0ms, phasic dopaminergic response does not begin until 50ms following water valve opening.

Supplementary Figure 7. Visualization of belief state model parameters (see Computational Methods for details). a,b, Schematic of the difference between modeling Task 1 and 2. Whereas cue can never lead back to the ITI sub-state in Task 1, this ‘hidden’ transition occurs in 10% of trials (omission trials) in Task 2. c,d, Observation matrices for Task 1 and 2. In a tiny percentage of cases in Task 2 (see Computational Methods), the animal observes ‘cue’ when in fact it transitions from the ITI back to the ITI during an omission trial. This occurs in such a small proportion of sub-state 15→15 transitions that it cannot be visualized in this map, so we have indicated values that differ between Tasks directly below the matrices. See Methods for how these values were computed. e,f, Transition matrices for Task 1 and 2. The probability of transitioning from the sub-state 15 back to the sub-state 15 is slightly higher in Task 2 (see Computational Methods), due to the presence of omission trials. The baseline probability of transitioning out of the ITI in either task is so small that it cannot be visualized here, so we have indicated values that differ between Tasks directly below the matrices. See Methods for how these values were computed.

Supplementary Figure 8. Belief state model reproduces modulation of pre- and post-reward RPEs over variable ISI interval. a,c, Pre-reward (a) and post-reward (c) RPEs generated by belief state model for different ISIs in Task 1. b,d, Pre-reward (b) and post-reward (d) RPEs generated by belief state model across different ISIs in Task 2.

Supplementary Figure 9. Post-reward RPEs normalized to free water response. In order to compare the magnitude of dopamine RPEs across different populations of neurons, post-reward RPEs must be normalized to the free water response (see ³⁵). a, Post-reward RPEs in Task 1 are suppressed to about 60% of the free water response at the beginning of the interval (1.2s), and are suppressed to about 40% of the free water response at the end of the interval (2.8s). RPEs plotted are from the 29 neurons for which we included 2-5 free water deliveries during recording. b, Post-reward RPEs in Task 2 are suppressed to about 60% of the free water response at the beginning of the interval (1.2s), and are suppressed to about 90% of the free water response at the end of the interval (2.8s). RPEs plotted are from the 34 neurons for which we included 2-5 free water deliveries during recording. c, Schematic of data in (a) and (b), highlighting that the opposing trends of temporal modulation in Tasks 1 and 2 arise mostly from diverging patterns towards the end of the interval.

Supplementary Figure 10. Belief state model result is agnostic to precise shape of trained distribution. When we trained our belief state TD model on a uniform distribution, the model produced negative modulation of post-reward RPEs over time in the 100% rewarded condition, and positive modulation of post-reward RPEs over time in the 90% rewarded condition. Therefore, while an assumption of our model is that mice perfectly learned the Gaussian distribution of reward timings, relaxing this assumption produces the same qualitative result.

Supplementary Figure 11. Testing belief state TD model and TD with CSC and Reset model on other studies' data. a, Other studies trained animals to anticipate rewarding or reward-predicting events during a variable ISI interval in which the ISI was drawn from a flat probability distribution^10-12. In these studies, reward was delivered in 100% of trials. b,c, Both the belief state model (b) and TD with CSC and Reset model (c) produce negative modulation of RPEs over time. d, Exponential distribution of ISIs, similar to Fiorillo et al, 2008 Figure 5d, on which we trained our belief state TD model. e, Post-reward RPEs decreased over time for belief state model trained on exponential distribution of ISIs, similar to data in Fiorillo et al, 2008 Figure 5e.

Supplementary Figure 12. Belief state model can be adapted to incorporate temporal uncertainty. a, Belief state at time t was blurred by a Gaussian distribution with standard deviation proportional to t, in order to capture temporal uncertainty. b,c, Belief state model with temporal uncertainty captures our data well. Post-reward RPEs are less suppressed for Odor C than for Odor B in both tasks, due to temporal uncertainty that grows with elapsed time.