Differential roles of two delayed rectifier potassium currents in regulation of ventricular action potential duration and arrhythmia susceptibility

Abstract

Key points

• Arrhythmias result from disruptions to cardiac electrical activity, although the factors that control cellular action potentials are incompletely understood.

• We combined mathematical modelling with experiments in heart cells from guinea pigs to determine how cellular electrical activity is regulated.

• A mismatch between modelling predictions and the experimental results allowed us to construct an improved, more predictive mathematical model.

• The balance between two particular potassium currents dictates how heart cells respond to perturbations and their susceptibility to arrhythmias.

Abstract

Imbalances of ionic currents can destabilize the cardiac action potential and potentially trigger lethal cardiac arrhythmias. In the present study, we combined mathematical modelling with information‐rich dynamic clamp experiments to determine the regulation of action potential morphology in guinea pig ventricular myocytes. Parameter sensitivity analysis was used to predict how changes in ionic currents alter action potential duration, and these were tested experimentally using dynamic clamp, a technique that allows for multiple perturbations to be tested in each cell. Surprisingly, we found that a leading mathematical model, developed with traditional approaches, systematically underestimated experimental responses to dynamic clamp perturbations. We then re‐parameterized the model using a genetic algorithm, which allowed us to estimate ionic current levels in each of the cells studied. This unbiased model adjustment consistently predicted an increase in the rapid delayed rectifier K⁺ current and a drastic decrease in the slow delayed rectifier K⁺ current, and this prediction was validated experimentally. Subsequent simulations with the adjusted model generated the clinically relevant prediction that the slow delayed rectifier is better able to stabilize the action potential and suppress pro‐arrhythmic events than the rapid delayed rectifier. In summary, iterative coupling of simulations and experiments enabled novel insight into how the balance between cardiac K⁺ currents influences ventricular arrhythmia susceptibility.

Key points

• Arrhythmias result from disruptions to cardiac electrical activity, although the factors that control cellular action potentials are incompletely understood.

• We combined mathematical modelling with experiments in heart cells from guinea pigs to determine how cellular electrical activity is regulated.

• A mismatch between modelling predictions and the experimental results allowed us to construct an improved, more predictive mathematical model.

• The balance between two particular potassium currents dictates how heart cells respond to perturbations and their susceptibility to arrhythmias.

Abbreviations

AP

action potential

APD

action potential duration

EAD

early afterdepolarization

GA

genetic algorithm

I_CaL

L‐type Ca²⁺ current

I_Kr

rapid delayed rectifier K⁺ current

I_Ks

slow delayed rectifier K⁺ current

LivR

mathematical model published by Livshitz and Rudy

LQTS

long QT syndrome

V_m

membrane voltage

Introduction

The action potential (AP) of ventricular cardiomyocytes plays a fundamental role in both normal cardiac physiology and the development of potentially fatal ventricular arrhythmias (Qu et al. 2013; Dutta et al. 2016). AP duration (APD) is central to this because both excessively short and excessively long action potentials can predispose the heart to arrhythmias (Weiss et al. 2015) via mechanisms such as early‐afterdepolarizations (EADs) (January & Moscucci, 1992; Sato et al. 2009; Weiss et al. 2010) and facilitation of re‐entry (Karma, 1994; Qu et al. 2000; ten Tusscher & Panfilov, 2006). Although many studies over decades have allowed for a good qualitative understanding of the AP and detailed electrophysiological characterizations of the key currents involved, our quantitative understanding of emergent AP dynamics is much weaker. Quantitatively untangling the web of non‐linear interactions between the membrane potential, ionic concentrations and the many distinct ionic currents remains a challenging goal.

The complexity and importance of the cardiac AP make mathematical modelling a crucial tool for understanding the system. However, as models become increasingly detailed aiming to better represent our ever‐deepening physiological knowledge, the resulting complexity makes it more difficult to comprehensively understand the determinants of emergent model behaviours (such as APD). Parameter sensitivity analysis allows for global and readily interpretable quantification of how these behaviours are influenced by many different model parameters, such as the levels of all ion channels, transporters and pumps. These techniques have been used to quantify the determinants of a variety of crucial aspects of cardiomyocyte physiology, such as Ca²⁺ handling (Lee et al. 2013; Devenyi & Sobie, 2016), AP morphology (Tondel et al. 2011; Mann et al. 2012; Britton et al. 2013; Heijman et al. 2013), arrhythmogenic dynamics (Sarkar & Sobie, 2011; Sadrieh et al. 2013; Chang et al. 2014; Cummins et al. 2014; Sadrieh et al. 2014; Zhou et al. 2016) and pacemaking in the sinoatrial node (Cummins et al. 2013; Maltsev & Lakatta, 2013).

As essential as mathematical modelling studies are, it is necessary to keep model analysis physiologically grounded. Although a number of population‐based modelling studies have constrained their analysis based on experimental data (Britton et al. 2013; Muszkiewicz et al. 2016; Zhou et al. 2016), only a few studies in cardiomyocytes have directly experimentally tested the key predictions of parameter sensitivity analysis (Lee et al. 2013; Devenyi & Sobie, 2016). Experimentally testing a large number of predictions using traditional methods, such as pharmacological inhibition, is difficult and labour intensive. In the present study, we leverage dynamic clamp (Berecki et al. 2005; Berecki et al. 2006; Wilders, 2006; Ahrens‐Nicklas & Christini, 2009; Bot et al. 2012; Nguyen et al. 2012; Bett et al. 2013; Nguyen et al. 2015), a technology used to inject currents calculated in real‐time to mimic specific endogenous cellular currents. This allows the application of many perturbations in a single cell, making it ideally suited for testing comprehensive sets of predictions.

In the present study, we combined parameter sensitivity analysis with dynamic clamp experiments to systematically analyse the determinants of APD in guinea pig left ventricular cardiomyocytes. After quantifying the impact of acute changes in all ionic currents in a cardiomyocyte mathematical model (Livshitz & Rudy, 2009), dynamic clamp was used to systematically test these predictions. When we observed a striking discrepancy between model predictions and experimental results, we used a global optimization technique to adjust ionic currents in the model for better agreement with the experimental results. This adjustment process predicted much lower levels (relative to the original model) of the slow delayed rectifier K⁺ current (I _Ks), a prediction that we then confirmed experimentally. Importantly, further simulations with the adjusted model allowed us to demonstrate that the balance between I _Ks and the rapid delayed rectifier K⁺ current (I _Kr) controls the stability of APD and susceptibility to arrhythmogenic membrane dynamics (early after depolarizations, EADs). Overall, the present study demonstrates how closing the loop between simulations and experiments can enable both improved mathematical models and novel insight into pathophysiological cellular dynamics.

Methods

Ethical approval

This investigation conforms with the Guide for the Care and Use of Laboratory Animals by the US National Institutes of Health (NIH Publication No. 85‐23, revised 1996). All experimental protocols were approved by the Institutional Animal Care and Use Committees of Weill Cornell Medical College (protocol number 0701‐571A) and the Icahn School of Medicine at Mount Sinai (protocol number LA12‐00295).

Isolation of ventricular myocytes

In total, seven guinea pigs were used for the present study. To isolate cells, guinea pigs were anaesthetized using a lethal i.p. injection of Euthasol (Virbac Corporation, Fort Worth, TX, USA), 550 mg kg^–1. Hearts were removed from the animals, retrograde perfused with a Langendorff apparatus and myocytes were isolated from the base (top third) of the left ventricle by enzymatic digestion. Myocytes were stored in Dulbecco's modified Eagle's medium with 5% fetal bovine serum.

Parameter sensitivity analysis

We performed population‐based parameter sensitivity analysis (Sobie, 2009) of the Livshitz‐Rudy (LivR) model of the guinea pig left ventricular cardiomyocyte (Livshitz & Rudy, 2009). The analysis was performed both with the model as originally published (the ‘original model’) and with model parameters adjusted by an optimization procedure (the ‘adjusted model’). In each case, model variants were generated by randomly scaling 13 parameters representing the activity levels of ion channels, pumps and transporters (Table 1). Each parameter was simultaneously and independently varied about its baseline value with a log normal distribution to create a population of 500 model variants. The standard deviation (σ) of the log‐transformed scale factors was equal to 0.4. Each model variant was stimulated 20 times at 2 Hz to assess the effect of acute parameter changes on model behaviour. The initial state variables for each model variant were those obtained after pacing the corresponding baseline model (either the original or adjusted model) to a steady‐state (1000 stimuli at 2 Hz).

Table 1.

Model parameters and corresponding cell currents in the model of the guinea pig left ventricular cardiomyocyte, as well as the perturbation factors used in the dynamic clamp experiments

Parameter	Current	Dynamic clamp scaling
G Kr	Rapid delayed rectifier K+ current (I Kr)	–40%
G Ks	Slow delayed rectifier K+ current (I Ks)	+40%
G K1	Inward rectifier K+ current (I K1)	–40%
G CaL	L‐type Ca2+ current (I CaL)	+40%
G CaT	T‐type Ca2+ current (I CaT)	–40%
G NaK	Na+/K+ ATPase current (I NaK)	+40%
G NCX	Na+/Ca2+ exchanger current (I NCX)	–40%
G Na	Fast Na+ current (I Na)
G Nab	Background Na+ current (I Nab)
G Cab	Background Ca2+ current (I Cab)
G Kp	Plateau K+ current (I Kp)
G pCa	Plasma Ca2+ ATPase current (I pCa)
v SERCA	Sarco/endoplasmic reticulum Ca2+ ATPase

AP duration at 90% repolarization (APD) was measured for each model variant, and multivariate regression (non‐iterative partial least squares method) was used to relate model APD to the 13 model parameters (after log‐transformation of each). This yields regression‐based sensitivity coefficients that together represent comprehensive, quantitative predictions about how acute changes in these 13 parameters affect APD.

Dynamic clamp experiments

After isolation, cells were plated on coverslips previously coated with 0.1% poly‐l‐lysine solution for 15 min and perfused at 35°C with a solution containing (in mm) 137 NaCl, 5.4 KCl, 2 CaCl₂, 1 MgSO₄, 10 HEPES and 10 glucose, with pH 7.35 (NaOH), and osmolality 310 ± 3 mmol kg^–1. The cells were patch clamped, with whole‐cell access gained by 480 μg/mL amphotericin B in the pipette solution, which also contained (in mm) 136 KCl, 10 NaCl, 0.01 CaCl₂, 5.5 glucose, 0.5 MgCl₂, 11 KOH, 10 HEPES, with pH 7.1 (HCl) and osmolality 295 ± 3 mmol kg^–1. Adequate access was defined by access resistance below 15 MΩ, and total membrane capacitance (204.6 ± 68.3 pF; n = 12) was measured by integrating the area under the capacitance current transients during the average of 50 voltage pulses (20 mV/20 ms) at –80 mV.

Dynamic clamp experiments were carried out using RTXI software (Christini et al. 1999; Dorval et al. 2001; Ortega et al. 2014). Cells were stimulated to a steady state (500–1000 stimulations) with 1 ms suprathreshold inward current pulses at 2 Hz. The LivR model was simulated in real‐time using Euler's method (0.01 ms time step) with the experimentally‐recorded (at 10 kHz) voltage used as a voltage‐clamp input. During the dynamic clamp protocol, 20 action potentials with dynamic clamp current injection were alternated with 20 unperturbed action potentials. For each dynamic clamp perturbation, a specific current calculated from the LivR model was scaled by total membrane capacitance, multiplied by +0.4 (+40% scaling) or –0.4 (–40% scaling), and injected at 10 KHz, in the following order: –40% I _Kr, +40% I _Ks, –40% I _K1, +40% I _CaL, –40% I _CaT, +40% I _NaK and –40% I _{NCX .} One cell was excluded from analysis as a result of its inability to tolerate the +40% I _CaL perturbation.

Simulating dynamic clamp in silico

To simulate dynamic clamp experiments, two cells were simulated in parallel: the ‘target’ cell, which represents the experimental cell, and the ‘source’ cell, which represents the model simulated by the computer during the dynamic clamp experiments. The source cell voltage is clamped to that of the target cell, and a scaled current based on calculations in the source cell is injected into the target cell. This injected dynamic clamp current lacks the ionic selectivity of the endogenous current, and instead passes a generic K⁺ current (as does the 1 ms, –40 A/F current that stimulates each AP). In keeping with the experiments, which use the original LivR model to calculate all currents injected via dynamic clamp, the ‘source’ cell always used the parameters from the original LivR model, even when the ‘target’ cell used adjusted parameters. With this configuration, the voltage from the source cell will be clamped to that of the target cell, although other state variables required to calculate currents (such as ionic concentrations) will be simulated independently between the two cells. This is a way to account for the fact that, in the experiments, variables such as intracellular [Ca²⁺] will be unknown.

Global optimization procedure to re‐parameterize the models

A genetic algorithm (GA) was used to adjust the values of the same 13 parameters that were varied in the sensitivity analysis (Table 1) to match experimental data from each of 12 cells, with the GA being run separately for each cell to create a cell‐specific fit. The algorithm of Sastry (2007) was utilized, as implemented in Groenendaal et al. (2015).

For each cell‐specific GA run, an initial population of 500 models was generated by randomly scaling the 13 parameters (Table 1) from 0.1% to 300% of their original value with a uniform distribution. Each was run to steady state (1000 stimuli) at 2 Hz followed by application of the dynamic clamp protocol used experimentally. It is important to note that the experimental dynamic clamp protocol scaled ionic currents by +40% or –40% based on the conductances in the original LivR model. During the GA adjustment process, we injected into each simulated cell exactly the same current waveforms that were applied experimentally. In this way, we account for the fact that the actual percentage scaling will be different in each cell.

The final APs from steady‐state baseline pacing and each dynamic clamp perturbation were extracted from each simulation in the population, and the total absolute value difference in the membrane voltage (V _m) time course was calculated (between simulated and experimental APs). The GA objective function was to minimize this difference between model and experiment, with each of the eight conditions (baseline and the seven dynamic clamp perturbations) weighted equally.

In each generation, the 500 individuals were randomly paired, and the individual from each pair with the better fit was kept (tournament selection). This process was performed twice each generation to create a new population of 500 individuals that contained 0, 1, or 2 copies of each individual from the previous generation. This new set of 500 individuals was again randomly paired, and each pair had a 90% probability of undergoing ‘cross‐over’, where the two parameter sets were randomly intermixed, whereas the other 10% remained unchanged. Each parameter value in the population then had a 10% chance of undergoing ‘mutation’, where it was multiplied by a random scale factor selected from a bounded, asymmetric multinomial distribution (Deb & Deb, 2014). Finally, an ‘elitism’ strategy was used, with the top 10% of individuals from the previous generation directly replacing the bottom 10% of individuals.

The GA was performed in two stages (Hobbs & Hooper, 2008; Groenendaal et al. 2015). An initial run sampling the full parameter space (0.1% to 300%) was run for 100 generations, and the best five individuals from the final generation were extracted. The range of each of the 13 parameters from these five individuals was used as new bounds for each parameter in a subsequent round of the GA, which also contained 500 individuals and was run for 100 generations. The parameters from the best individual fit from the final generation of each cell‐specific fit are reported in Fig. 3 C and utilized subsequently.

Figure 3. Genetic algorithm (GA) improves model agreement with experiment.

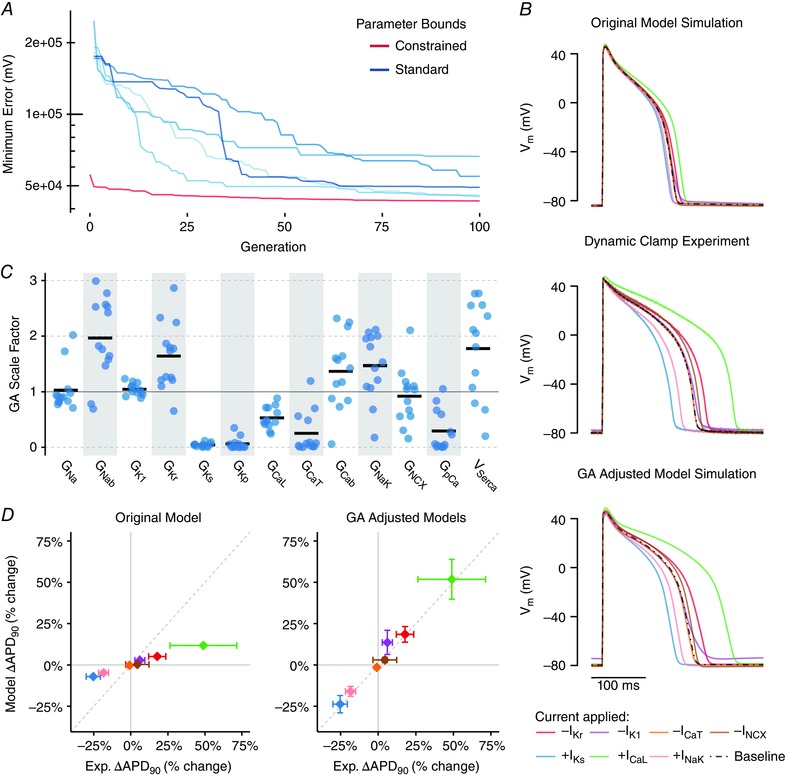
A, best individual model‐experiment discrepancy decreases over successive generations (typical cell). For each cell, five independent runs with standard parameter bounds (0.01 to 3) were performed (blue). The range of each of the 13 parameters across the five runs was used to create new constrained parameter bounds for an additional run (red), and the best individual at the end of this constrained run is taken as the best solution. B, comparison of simulation of the dynamic clamp protocol in original model (top), experimental recordings (middle) and simulation of the dynamic clamp protocol in the model with the GA‐adjusted parameters (bottom). Top and middle traces are the same as in Fig. 2 and are re‐plotted here to allow for comparison. C, scale factors resulting from GA process (n = 12 cells, black bar indicates mean). D, change in APD with each of the dynamic clamp perturbations (indicated by the same colours as the traces in B) in the GA‐adjusted models (right) show much better agreement with experimental results than the original model (left). Data are the mean ± SD for each effect (n = 12).

Chromanol 293B experiments

Cells were stimulated in current‐clamp mode to a steady state at 2 Hz (500–1000 beats), followed by the application of the ‘stochastic pacing’ protocol used in Groenendaal et al. (2015), wherein the cell was stimulated 11 times over 5 s with a predefined aperiodic stimulation pattern. APD was measured from only the first beat of this protocol, which occurred 716.48 ms after the final steady‐state beat. This protocol was repeated for each cell (n = 4) under control conditions and in the presence of 10 μm chromanol 293B, an inhibitor of the slow delayed rectifier current (I _Ks). In the model, this was simulated by comparing the APD during a comparable pacing protocol (for both the original and adjusted models) with and without an 80% reduction in G _Ks, the degree of I _Ks block that 10 μm chromanol 293B is estimated to provide based on previously published data (Bosch et al. 1998; Fujisawa et al. 2000; Lu et al. 2001).

Simulation implementation

Parameter sensitivity analysis simulations were run in MATLAB (MathWorks, Natick, MA, USA) using the ode15s solver, with absolute tolerance of 10⁻³ and relative tolerance of 10⁻⁶ for each state variable. Experimental dynamic clamp simulations were run in C++ using Euler's method and a 0.01 ms time step. Genetic algorithm simulations were run in C++ using Euler's method with an adaptive time step between 0.001 and 0.1 ms, determined by the change in membrane voltage of the previous time step.

Results

Simulated APD is most sensitive to L‐type Ca²⁺ and delayed rectifier K⁺ currents

We performed a population‐based sensitivity analysis (Sobie, 2009) to quantify the influence of the levels of ion channels and transporters on APD in the guinea pig model (Livshitz & Rudy, 2009) (Fig. 1 A). A population of models was generated by randomly scaling the maximal activities of 13 ion channels, pumps and transporters (Table 1), and the effect of acute changes in these currents was assessed by quantifying APD after pacing 20 times at 2 Hz. Multivariate regression was applied to derive parameter sensitivities that represent quantitative predictions of how APD responds to changes in each parameter (Fig. 1 A). We also validated these results by performing the simpler test of acutely perturbing each of seven currents individually and quantifying the effects on APD (Fig. 1 B and C).

Figure 1. Effects of acute changes in ionic currents on APD.

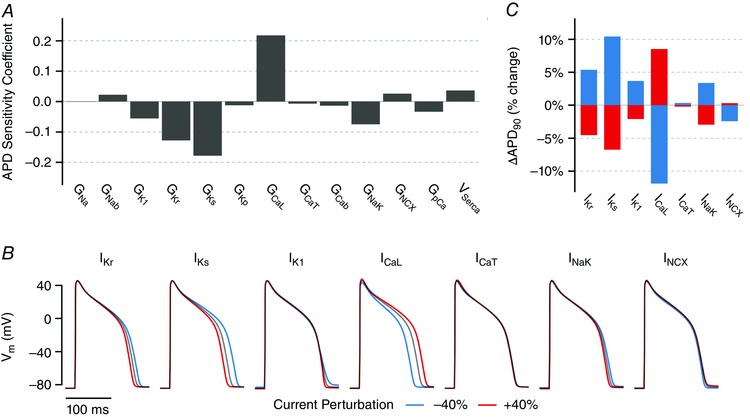
A, population‐based parameter sensitivity coefficients for the sensitivity of APD to variation in 13 parameters, representing maximal ionic current densities, in the guinea pig cardiomyocyte model. Each bar quantifies how an acute change in that current influences APD. B, baseline APs at steady‐state 2 Hz pacing (black) superimposed with APs resulting from a 40% increase (red) and decrease (blue) in each current for 20 stimuli. C, quantification of change in APD for results shown in (B).

Together, these results demonstrate that changes in I _CaL and I _Ks have the largest impact on APD, followed by I_Kr (Fig. 1). Acute changes in I _K1 and I _NaK produce smaller (but clear) changes in APD, while I _NCX and I _CaT have minimal impact. Importantly, these simulations yield testable predictions of how APD will be affected by acute changes in the levels of each of these currents, such as by partial pharmacological inhibition.

Dynamic clamp experiments find larger effects of current perturbations than predicted by the original model

We subsequently tested these quantitative predictions using dynamic clamp, a closed‐loop system in which V _m is recorded from cells while synthetic currents are simultaneously calculated and injected in real‐time (Fig. 2 A). This allowed us to quickly test the effect of acute changes in the levels of seven currents in a single cell, yielding in‐depth data from each. Currents were scaled by  ±40% and injected into the cell via the perforated patch to mimic a change in the level of that particular current.

Figure 2. Dynamic clamp results testing the effect of seven ionic current perturbations on APD.

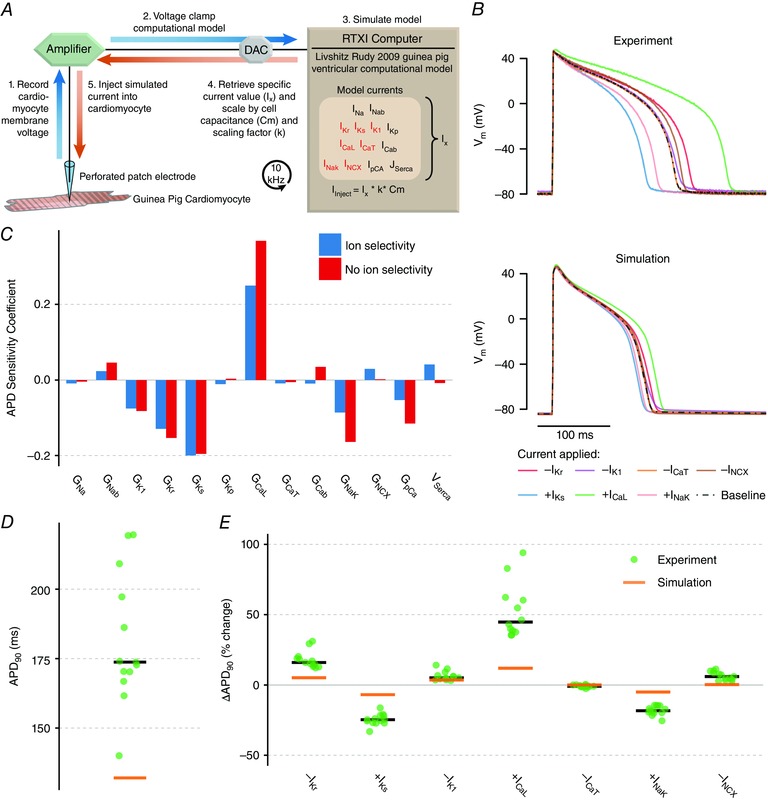
A, dynamic clamp schematic. Using whole‐cell patch clamp, recorded voltage is used to calculate a current based on the model, and this current is scaled and injected into the cell in real‐time. B, dynamic clamp results in experiment (top) and simulation (bottom). Currents were calculated in the model based on recorded voltage and were scaled for 20 stimuli each as either +0.4·I (+I _Ks, +I _CaL, +I _NaK) to simulate a 40% increase in that current or –0.4·I to simulate a 40% decrease (–I _Kr, –I _K1, –I _CaT, –I _NCX). Simulation accounted for limitations of the dynamic clamp method to enable direct comparison with experiment. C, parameter sensitivity analysis of acute parameter changes where changes include ionic selectivity (blue; as in Fig. 1 C) and where they do not (red). D, comparison of experimentally recorded baseline APD (green dots, black bar shows median) compared to simulation (orange bar). E, comparison of changes in APD with each perturbation in experiments and simulation. Experimental results from 12 cells from three animals.

We tested the following dynamic clamp perturbations in each of 12 cells: –40% I _Kr, +40% I _Ks, –40% I _K1, +40% I _CaL, –40% I _CaT, +40% I _NaK and –40% I _NCX, scaled according to the maximal conductance in the published model. Traces from a typical cell are shown in Fig. 2 B (top). I _CaL scaling had the largest impact on APD, followed by I _Ks scaling and then I _NaK and I _Kr scaling.

We simulated the dynamic clamp experiments by adapting the model to the limitations of dynamic clamp. An important limitation is that the synthetic current lacks the ionic selectivity of endogenous cellular currents. In Fig. 2 C, we show how accounting for this limitation affects model predictions. In general, the sensitivity of APD to dynamic clamp currents was similar to the sensitivity to real currents, with the exception that APD is more sensitive to changes in I _CaL and I _NaK without ionic selectivity. An additional limitation is that intracellular ionic concentrations such as Ca²⁺ are not measured directly in this experiment, and current calculations must rely on concentration estimates from the model. We accounted for this limitation by simulating current injection from a ‘source’ cell to a ‘target’ cell, as described in the Methods.

When we simulated the dynamic clamp protocol in the model (Fig. 2 B, bottom), we found that, as in the experiments, changes in the magnitude of I _CaL had the largest effect on APD, followed by I _Ks, I _Kr and I _NaK. However, despite this qualitative agreement in the relative effect sizes of each perturbation, there was a drastic quantitative difference between simulations and experiments. Compared to simulations, experimental results showed significantly larger percentage changes in APD in response to all dynamic clamp scalings, except I _CaT (∆APD, one‐way t test, P = 0.072 for effect of –40% I _CaT, P < 0.001 for all others) (Fig. 2 E), as well as significantly longer baseline APD (P < 0.001) (Fig. 2 D).

A GA tunes current levels to improve consistency with experimental data

Given this mismatch between simulation results and experimental data, we turned to a GA to re‐parameterize the model to better match the experimental results. We initially varied 13 parameters (Table 1) from 0.01% to 300% of the values in the previously published model, and selected for individuals over two rounds of 100 generations based on agreement with experimental voltage traces. The results from each of the 12 experimental cells were used to generate cell‐specific fits. In each simulation, the model was run to a steady state at baseline (1000 stimuli at 2 Hz), followed by injection of the experimentally applied dynamic clamp current for that particular cell. The objective function for the GA was to minimize the total absolute value discrepancy in the AP time course at baseline, as well as with each of the seven current perturbations.

The large error seen in the initial population was greatly reduced as a result of the GA (Fig. 3 A), ultimately producing excellent agreement between experiments and simulations. As shown for a typical cell (Fig. 3 B), the behaviour of the model run with the cell‐specific GA‐adjusted parameter set shows vastly superior agreement, compared to the original model, with the experimental traces obtained in that cell. Quantifying the effects of dynamic clamp perturbations (Fig. 3 D) showed similarly improved agreement across all 12 cells.

The relative ionic current magnitudes resulting from the GA process are shown in Fig. 3 C. Although some parameters, such as G _Na and G _K1, show tight spread and agreement with the original model, the GA strongly selects for many parameter values that are different from the original model. For example, the algorithm selects for greatly decreased G _Kp (the plateau K⁺ current), somewhat decreased G _CaL and increased G _NaK. Most notably, the algorithm selects for an apparent ‘trade‐off’ in the two delayed rectifier currents, with I _Kr levels being increased and I _Ks greatly decreased. These currents are partially redundant in that they both repolarize the membrane and shorten APD, although clearly other functional differences between these currents cause the GA to select one instead of the other.

We used these parameter sets to develop a consensus ‘adjusted model’ (Table 2) by taking the mean value for each scaled parameter from 10 of the cell‐specific parameter sets (the parameter sets from two cells were excluded from this average because they showed excessive [Na⁺]_i and [Ca²⁺]_i overload).

Table 2.

Parameter scaling in the adjusted model

Parameter	Adjusted value (% of baseline)
G Kr	178.2%
G Ks	4.2%
G K1	107.3%
G CaL	52.5%
G CaT	32.2%
G NaK	164.5%
G NCX	109.6%
G Na	96.7%
G Nab	199.1%
G Cab	155.9%
G Kp	5.9%
G pCa	27.0%
v SERCA	214.0%

Model adjustments lead to altered current dynamics and sensitivity of APD to perturbations

Simulations with the original and adjusted models after pacing at 2 Hz are compared in Fig. 4 A and B, demonstrating the different time course of the membrane voltage and several important currents during a steady‐state action potential (2 Hz). The adjusted model shows a significantly longer APD, increased I _Kr, decreased I _CaL and greatly decreased I _Ks, in keeping with the parameter adjustments. Although the decrease in I _CaL and increase in I _Kr favour a shorter APD, the dramatic decrease in I _Ks overwhelms these effects, leading to a longer APD in the end.

Figure 4. Behaviours in GA‐adjusted model compared to original model at 2 Hz.

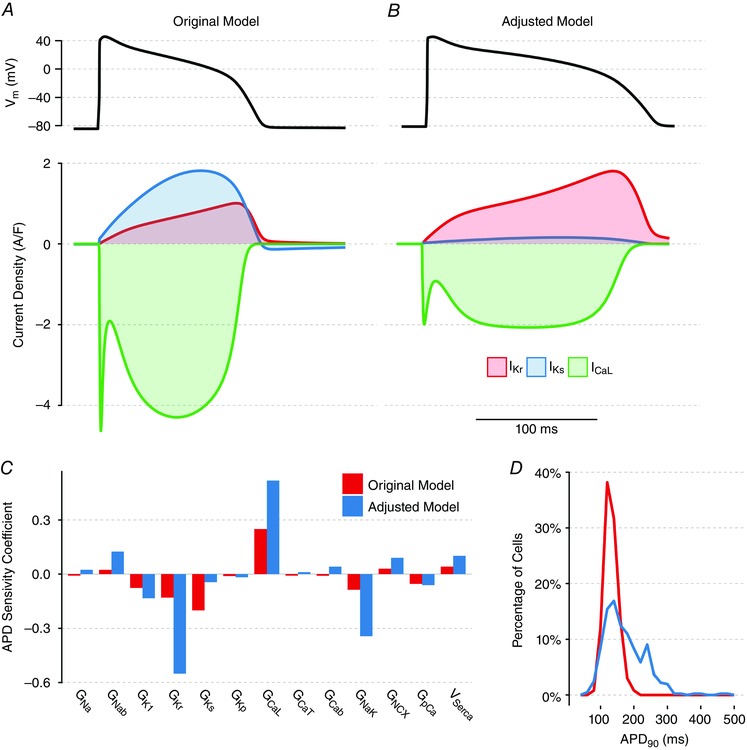
The parameters in the adjusted model are the mean parameters from 10 of the cell‐specific GA fits that passed quality control. The adjusted model (B) exhibits both longer APD (top) and very different current balance (bottom) compared to the original model (A). C, parameter sensitivity coefficients quantifying sensitivity of APD to acute changes in the levels of 13 currents in the original model and the adjusted model, under the same conditions as in Fig. 1 C. D, distribution of APD in the populations of models used to generate (C), demonstrating greater variability in APD in the adjusted model.

We repeated our population‐based parameter sensitivity analysis on the adjusted model to quantify how the same 13 model parameters influence APD (Fig. 4 C). The adjusted model has an APD that is much more sensitive to changes in I _Kr but less sensitive to changes in I _Ks, which follows intuitively from the changes in the abundance in these two currents between the original and adjusted model. However, the adjusted model also shows greater sensitivity to changes in many other currents, such as I _NaK and I _CaL, despite the fact that I _CaL abundance is decreased in the GA‐adjusted model. This reflects an overall increase in APD heterogeneity across the adjusted model population despite identical levels of parameter variability (Fig. 4 D).

Predicted changes in I _Ks levels are experimentally validated

Once we had obtained an adjusted model based on GA analysis of the dynamic clamp data, we aimed to address two additional questions. First, does the adjusted model generate more accurate predictions? Second, can a comparison of the original and adjusted models provide new insight into AP stability and arrhythmia dynamics?

Because the GA parameter adjustments predicted much smaller I _Ks current in these cells, APD in the adjusted model is much less sensitive than the original model to perturbations in I _Ks (Fig. 4 C). This is demonstrated in Fig. 5, where 80% I _Ks block (i.e. an 80% reduction in G _Ks) leads to a 40.5% prolongation of APD in the original model (Fig. 5 A and D) but only a 10.0% prolongation in the adjusted model (Fig. 5 B and D).

Figure 5. Experimental confirmation of greatly reduced I _Ks predicted by model adjustments.

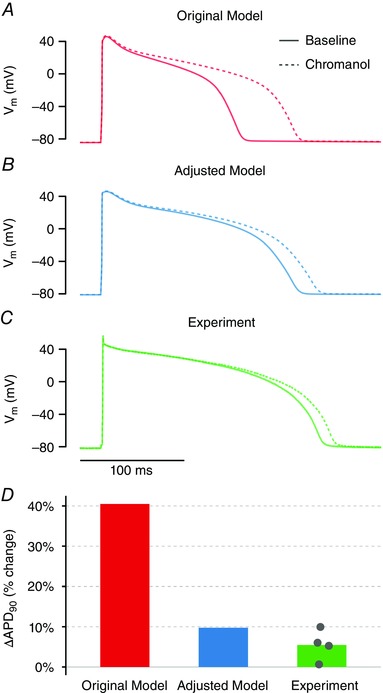
A, in the original model, 80% reduction in G _Ks dramatically prolongs APD. B, the adjusted model shows only a small (10%) prolongation in APD with 80% reduction in G_Ks. C, in experimental measurements (n = 4), 10 μm chromanol 293B (which should block I _Ks by approximately 80%) caused minimal APD prolongation. D, quantification of percentage change in APD with 10 μm chromanol 293B for each condition shows better agreement between adjusted model and experiment.

We then experimentally tested which model was better able to predict the effect of I _Ks block. We measured the effect on APD of 10 μm chromanol 293B, a selective I _Ks blocker that should reduce the current by ∼80% at this concentration (Bosch et al. 1998; Fujisawa et al. 2000; Lu et al. 2001). The results of treatment of four cells with 293B (Fig. 5 C and D) showed only a small prolongation of APD (mean 5.5%), which is consistent with the behaviour of our adjusted model (Fig. 5 D) and confirms the prediction of greatly reduced G _Ks.

I _Ks stabilizes APD and prevents EADs more effectively than I _Kr does

Compared to the original model, the adjusted model shows greater changes in APD in response to the same dynamic clamp perturbations, in agreement with experimental results (Fig. 3 B and D). We hypothesized that this reduced stability may predispose cells to potentially arrhythmogenic dynamics. To investigate this possibility, we stressed the two models by applying additional L‐type Ca²⁺current. This stressor will prolong the APD in both models (Fig. 4 C) and can lead to potentially arrhythmogenic EADs, defined as secondary upstrokes that occur prior to repolarization. To allow for a direct comparison, we applied the same absolute magnitude of I _CaL to both models and expressed this relative to I _CaL in the original model, which we call the ‘I _CaL perturbation factor’. For example, applying an additional I _CaL that is 10% of the value in the original model corresponds to an I _CaL perturbation factor of 0.1.

The GA consensus model was less stable in the face of this perturbation, in terms of both APD stability and EAD susceptibility. Although an I _CaL perturbation factor of 0.84 only moderately prolonged APD in the original model (Fig. 6 A, orange traces), this same perturbation caused arrhythmogenic EADs and failure of repolarization in the adjusted model (Fig. 6 A, blue traces). As shown in Fig. 6 C, increasing levels of I _CaL perturbation led to greatly prolonged APD in the GA consensus model (blue) and ultimately caused EADs with I _CaL perturbation factors above 0.8. By contrast, the original model (orange) was able to sustain I _CaL perturbation factors as large as 2 without displaying EADs.

Figure 6. I _Ks/I _Kr balance determines susceptibility to APD prolongation and early afterdepolarizations (EADs) in response to depolarizing perturbations.

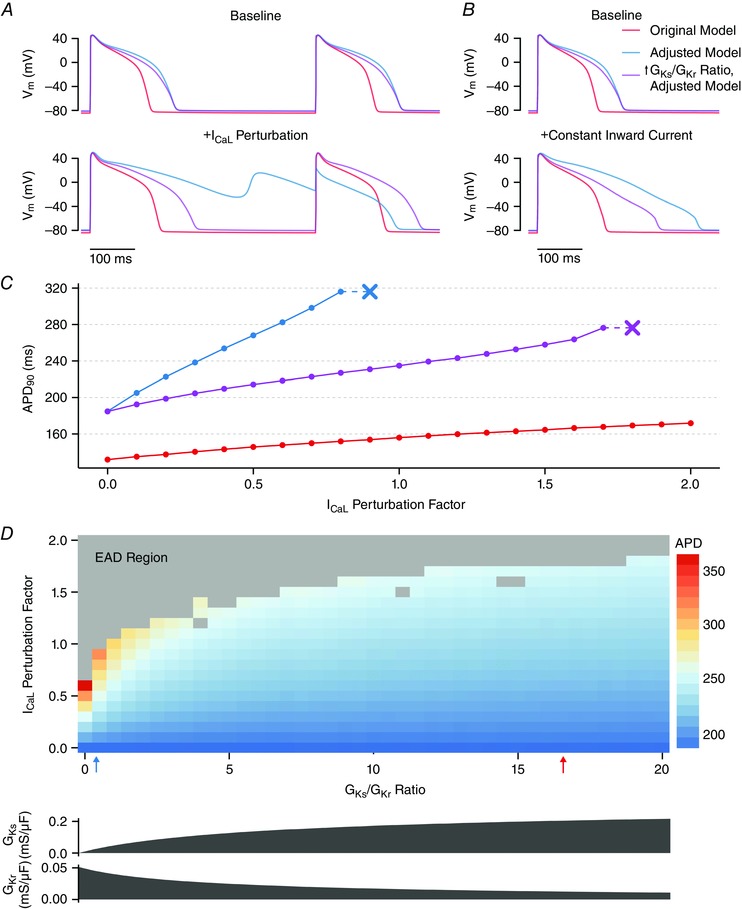
A–C, results from the original model, the adjusted model, and a third model (the ‘altered ratio’ model) with APD identical to the adjusted model, but only G _Ks/G _Kr altered. A, increasing I _CaL by a constant absolute magnitude (+84% relative to the original model) prolonged APD mildly in the original model (red), prolonged APD to a greater extent in the adjusted ratio model and resulted in EADs with 2:1 block in the adjusted model. B, applying a constant inward current of 0.9 A/F during the AP (when depolarized above –60 mV) prolonged the APD in all three models, but with a much larger effect in the adjusted model (blue). C, relationship between I _CaL perturbation factor and APD and EAD threshold (indicated by the ‘x’) in the three models. D, relationship between the G _Ks/G _Kr ratio and I _CaL perturbation factor on APD and EAD generation. In all models, only G _Ks and G _Kr are altered (as shown) to produce a model with the same baseline APD as the adjusted model but with a given G _Ks/G _Kr ratio. The G _Ks/G _Kr ratios for the original (red) and adjusted (blue) model are indicated by the arrows.

Many parameters differed between these two models, and so it was not immediately clear which changes accounted for the dramatic difference in AP stability. Given that a decrease in I _Ks was accompanied by an increase in I _Kr in the model adjustments, we hypothesized that the balance between these two repolarizing currents determines how cells respond to perturbations. To test this, we began with the adjusted model and increased the G _Ks/G _Kr ratio while maintaining the same baseline APD. This alteration (termed the ‘altered ratio’ model) led to a smaller change in APD in response to a given I _CaL perturbation and allowed the cell to withstand much higher I _CaL perturbation factors without displaying EADs (Fig. 6 A and C, magenta).

To confirm that the observed difference in stability was not specific to the I _CaL stressor applied, we also subjected cells to a constant current injection, as in previous studies (Banyasz et al. 2009; Zaza, 2010). This stressor (0.9 A/F; injected only when V _m ≥ –60 mV) also prolonged APD much more in the adjusted model than in either the original model or the altered ratio model (Fig. 6 B). Furthermore, simulation of a heterogeneous cell population (Fig. 4 C) led to the greatest APD variability in the adjusted model (coefficient of variation = 0.33) compared to either the altered ratio model (coefficient of variation = 0.22) or the original model (coefficient of variation = 0.15). These results further confirm that the G _Ks/G _Kr ratio, and not solely the baseline APD, determines how ventricular myocytes respond to perturbations.

When a wide variety of G _Ks/G _Kr ratios were tested (while maintaining a constant baseline APD), a clear relationship was seen between the balance of these two currents and the amount of applied I _CaL needed to produce an EAD (Fig. 6 D). An increase in G _Ks/G _Kr meant that the same I _CaL perturbations led to smaller changes in APD, and the AP was able to withstand greater I _CaL perturbation without EADs. Therefore, I _Ks is much better than I _Kr at resisting perturbations and preventing EADs.

Discussion

Closing the simulation‐experiment loop facilitates insight into APD and EADs

Interplay between mathematical models and experiments has been an integral component of quantitative cardiomyocyte physiology for decades. In the present study, we cycled repeatedly between mathematical modelling and experimental tests, refining and extending insights in each iteration, which ultimately allowed us to both improve the model and gain new insight into the determinants of APD and mechanisms of pro‐arrhythmic cellular behaviour (EADs).

After an initial test of experimental predictions using dynamic clamp (Figs. 1 and 2), we returned to the model, using a GA to improve model agreement with our new experimental data (Fig. 3). This led to the secondary prediction about the reduced level of I _Ks compared to the original model, which was experimentally validated (Fig. 5), demonstrating the greater predictive power of the new model. This allowed us to confidently make a new round of predictions (Figs. 4 and 6), which led to the novel insight into how interplay between different K⁺ currents controls AP stability and the propensity of cells to develop pro‐arrhythmic behaviours. This insight would have been more difficult to obtain with either a purely experimental or a purely computational study.

Comprehensive quantification of how APD is influenced by different currents

In the present study, we took a comprehensive approach to both modelling and experimental work, aiming to gain a more holistic understanding of AP dynamics. Our initial sensitivity analysis (Fig. 1) quantified the contributions of 13 ion channels, pumps and transporters to APD in the guinea pig cardiomyocyte model. Experimental tests (Fig. 2) then used dynamic clamp to study the effects of changes in seven currents on APD within a single cell. This gave us sufficient depth of cell‐specific information to use the GA to tune many parameters in the model at once to better match our experimental results (Fig. 3). Therefore, we were able to perform a closed‐loop of model analysis, testing and adjustment thoroughly at each step.

This comprehensive strategy also allowed us to compare the impact on APD of 13 ionic currents between the original and adjusted models. This comparison (Fig. 4 C) indicated that G _CaL and G _Ks have the greatest impact on APD in the original model, whereas G _CaL and G _Kr have the greatest impact in the adjusted model. The shift in importance from I _Ks to I _Kr is not surprising giving the corresponding alterations in current density (Fig. 3 C). A more interesting observation, however, was the greater sensitivity of the adjusted model APD to a variety of perturbations, including changes in G _CaL, a current that decreased in magnitude during the adjustment process. This is also reflected in a more heterogeneous APD in populations derived from the adjusted model compared to the original model (Fig. 4 D). Although longer APs intrinsically show greater changes in APD in response to perturbations (Banyasz et al. 2009; Zaza, 2010), the I _Ks/I _Kr ratio independently influences the response to perturbations even when the two are adjusted so that the baseline APD is held equal (Fig. 6). These observations, enabled by our comprehensive approach, allowed us to develop the novel hypothesis that the I _Ks/I _Ks ratio determines AP stability.

High‐content experiments allow for unbiased model adjustment with a GA

A GA is a powerful tool for adjusting models in an unbiased manner. However, when a large number of parameters need to be constrained, a sufficiently large set of independent information is required. Because many parameter combinations can produce virtually indistinguishable electrophysiological behaviours (Golowasch et al. 2002; Dokos & Lovell, 2004; Prinz et al. 2004; Achard & De Schutter, 2006; Sarkar & Sobie, 2010; Zaniboni et al. 2010; Marder, 2011; Weiss et al. 2012), whole‐cell model parameters cannot be adequately re‐parameterized using only a baseline experimental AP trace. Therefore, ‘high content’ experimental studies that yield a greater amount of independent information are needed to properly constrain parameter values (Krogh‐Madsen et al. 2016). Recordings from multiple pacing rates or other electrophysiological data can provide additional information to allow for improved GA‐driven fits (Syed et al. 2005; Kaur et al. 2014; Groenendaal et al. 2015).

In the present study, we used dynamic clamp to measure the AP not only under baseline conditions, but also in response to seven different perturbations, each of which was designed to resemble a change in an endogenous current, giving us a data set with high information content. These experiments were designed to extract maximal information from each cell, and are similar in strategy to other recent approaches such as combining stochastic pacing with voltage clamp recordings (Groenendaal et al. 2015) and measuring sequential current dissection using AP clamp (Banyasz et al. 2011; Chen‐Izu et al. 2012).

Although it is well appreciated that cells with different ionic currents can exhibit the same baseline APD, we have a weaker understanding of why cells with the same baseline APD can show different responses to perturbations (Fig. 6). In our particular case, this occurs because I _Kr and I _Ks are somewhat redundant with regard to APD but differ in how they affect the response to perturbation. Therefore, the perturbation data were essential to adjusting the G _Ks/G _Kr ratio, and the high‐content experiments were able to set the stage for robust model adjustments later on.

Careful simulation of dynamic clamp limitations allows for apt comparisons between model and experiment

As we have illustrated, dynamic clamp is a powerful technique that allows the user to test the effect of many current changes within a single cell, without any need for drug washout or the risk of off‐target drug effects (Wilders, 2006; Madhvani et al. 2011; Madhvani et al. 2015). However, the limitations of this technique must be taken into account to properly interpret experimental results and compare them with simulations. Most prominent among these limitations is a lack of ionic selectivity, such that dynamic clamp currents influence membrane potential but do not alter intracellular concentrations the way that endogenous currents would.

For most currents, the acute effects of changing the level of a current are virtually identical with and without ionic selectivity (Fig. 2 C) because it is the direct effect on voltage that alters the APD. The most notable exception is the effect of changing I _CaL. Because I _CaL is inactivated by Ca²⁺ itself, a physiological increase in I _CaL will lead to greater current inactivation, thereby attenuating the AP‐prolonging effects. By contrast, this feedback will not be present when increased I _CaL is injected via dynamic clamp. However, although we cannot overcome this limitation experimentally, if we appropriately simulate this lack of ionic selectivity when comparing experimental results to simulations, we can ensure that we correctly interpret the data we do have.

Comparison of these new I _Ks results with those from previous experiments and simulations

Perhaps the most notable parameter adjustment made by the GA was a significant reduction in the I _Ks maximal conductance (G _Ks) to an average of only 4.2% of the value in the original model, with G _Ks being universally reduced in all of our cell‐specific fits. Because this adjustment was dramatic and surprising, we performed the independent experimental test of blocking I _Ks with chromanol 293B. The consistency with the adjusted model predictions (Fig. 5) suggests that this adjustment was correct. What can account for this discrepancy in I _Ks levels?

The literature contains substantial discrepancies about the levels I _Ks in guinea pig. For example, Lu et al. (2001) recorded robust I _Ks currents in guinea pig ventricular cardiomyocytes and showed dramatic APD prolongation across a range of pacing rates after blocking I _Ks with 10 μm chromanol 293B, in contrast to the slight (5%) APD prolongation that we observed (Fig. 5). However, Banyasz et al. (2014) and Rocchetti et al. (2001; 2006) observed only minimal I _Ks during AP clamp in guinea pig ventricular cardiomyocytes under baseline conditions, in agreement with our results.

A prosaic explanation is that the differences are a result of experimental artefact in the studies suggesting minimal I _Ks. I _Ks is prone to current ‘rundown’ during traditional whole‐cell patch clamp protocols because of dialysis of the cytosol (Harvey & Hume, 1989). However, the use of perforated patch in the present study will largely preserve the intracellular milieu and should minimize this effect. Furthermore, one would expect dramatic I _Ks rundown to lead to APD prolongation over time, and this was not seen over our 10 min pacing protocol. However, we cannot exclude a decrease in I _Ks as an artefact of cardiomyocyte isolation or another aspect of the experimental protocol.

A more interesting possibility is suggested by the results of Banyasz et al. (2014), who found that, although I _Ks was minimal at baseline (0.152 A/F, comparable to our adjusted model), it was rapidly and dramatically enhanced over 13‐fold by β‐adrenergic stimulation (to 2.067 A/F). When run under the same conditions, I _Ks in our adjusted model shows good agreement with their baseline data (0.108 A/F), whereas I _Ks in the original model (1.883 A/F). approximates data with β‐adrenergic stimulation. This strongly suggests that the low I _Ks that they (and we) measure is not a result of current rundown or digestion artefact.

Perhaps, then, this difference in I _Ks between reports occurs because the cells experimented on by Lu et al. (2001) (and others finding similarly high I _Ks) were in a different regulatory state compared to our cells and those examined by Banyasz et al. (2014). More specifically, we hypothesize that cells in some studies may exhibit significant basal PKA‐dependent phosphorylation of the I _Ks channel, increasing the importance of I _Ks in those cells. Therefore, although I _Ks has minimal impact on APD in our cells at baseline, the importance of I _Ks in influencing APD is almost certainly highly dependent on cell state.

Coupling simulations and experiments reveals I _Kr and I _Ks have different roles in influencing APD

Initially, the two delayed rectifier currents I _Kr and I _Ks may appear redundant, with each one able to compensate perfectly for the other. Indeed, many different combinations of I _Kr and I _Ks can produce almost identical APD, as our simulations show and as previous modelling studies (Grandi et al. 2010; Sarkar & Sobie, 2010) have suggested. Our analysis, however, uncovered the more subtle result that I_Ks is much better than I _Kr at stabilizing APD in the face of perturbations. How can two similar currents play such different roles?

The slow activation and de‐activation kinetics of I _Ks (Tohse, 1990; Lu et al. 2001) mean that there is greater I _Ks activation with a longer AP plateau (allowing more time for current activation) and a shorter diastolic interval (allowing less time for current de‐activation). It follows from this that a depolarizing, AP‐prolonging perturbation will lead to increased I _Ks activation, and this stronger repolarizing drive will counteract the initial depolarizing perturbation. No such feedback exists for I _Kr, which activates sufficiently quickly that it is not limited by AP duration but, instead, is dependent on AP shape as a result of its rapid inactivation at highly positive potentials.

This conclusion is in agreement with the results of Rochetti et al. (2001), who found that the amplitude of I _Ks was increased at faster pacing rates as a result of a greater fraction of time spent in the AP plateau, allowing for accumulation of channels in a partially activated state. They postulated that, following partial I _Ks block, the initial APD prolongation and resultant increased I _Ks activation could provide negative feedback that partially compensates for the effects of block. Our results suggest that this stabilizing role of I _Ks feedback appears to extend to a variety of perturbations that alter the APD.

I _Ks may help suppress pro‐arrhythmic EADs under β‐adrenergic stimulation

We confirmed these differential roles of I _Kr and I _Ks by measuring APD stability in the face of an increasing I _CaL perturbation at the same time as varying the G _Ks/G _Kr ratio but holding baseline APD constant. This revealed that not only is I _Ks better able to resist perturbation‐induced changes in APD, but also it is better able to suppress potentially pro‐arrhythmic EADs. We hypothesize that upregulation of I _Ks, such as that which results from β‐adrenergic stimulation, therefore probably not only shortens the AP, but also directly helps prevent EADs.

Although the evidence suggests that the guinea pig left ventricular cardiomyocytes used in the present study display minimal I _Ks, this is clearly not true in all situations because this current is upregulated by a variety of cell signalling processes. Indeed, Banyasz et al. (2014) show that the ratio of I _Ks/I _Kr increased from 0.074 at baseline to 1.707 with β‐adrenergic stimulation with 30 nm isoproterenol (when both currents are recorded at –20 mV). This is comparable to the difference between our adjusted model (0.045) and the original model (1.416) when run under the same conditions. Our data suggest that such an upregulation of I _Ks will not only shorten the action potential, but also stabilize it in the face of perturbations, thus having a potentially strong anti‐arrhythmic effect. We speculate that part of the function of β‐adrenergic I _Ks activation may be to maintain a short, stable AP under the physiologically stressful conditions of sympathetic stimulation.

Mutations in the genes encoding the pore‐forming subunits for I _Ks (KCNQ1) and I _Kr (KCNH2, also known as hERG) are the most common causes of congenital long‐QT syndrome (LQTS) (Napolitano et al. 2005), which is characterized by excessively long APD and elevated arrhythmic risk (Modell & Lehmann, 2006). Given the larger magnitude of I _Kr compared to I _Ks in our adjusted model, which is consistent with data obtained in human ventricular myocytes (Jost et al. 2005), it has long seemed paradoxical that mutations in the gene encoding I _Ks cause congenital LQTS with a greater frequency than mutations in the gene encoding I _Kr (Napolitano et al. 2005). The results that we have obtained, if they extend to human myocytes, may offer novel insight into this question. Despite its smaller magnitude, I _Ks may have an outsize role in preventing arrhythmias in LQTS patients because I _Ks has a superior ability to suppress EADs compared to I _Kr. A mutation‐induced reduction in I _Ks will lead to loss of its stabilizing effect on APD and therefore increase the potential for long APDs and arrhythmias.

Conclusions

The present study represents a novel approach to combining systematic model analysis with high‐content experiments that measure both baseline behaviour and the response to many perturbations, a rich data set that allowed us to systematically constrain parameters to improve the model. We repeatedly ‘closed the loop’ by experimentally testing model predictions, systematically improving the model, experimentally testing a key change (a decrease in I _Ks), and using the adjusted model to gain new insight into important biology. This not only produces better agreement with the data used to constrain the model, but also better agreement with new experiments. The adjusted model yields an improved understanding of the quantitative effects of each current on action potential duration. A key insight resulting from this approach is that two superficially similar currents (I _Kr and I _Ks) may play very different roles in the genesis of pro‐arrhythmic early afterdepolarizations. This may have important clinical implications for the understanding of long QT syndromes, as well as the dynamics of ventricular arrhythmias in general.

Additional information

Competing interests

The authors declare that they have no competing interests.

Author contributions

RAD, FAO, TKM, DJC and EAS conceived and designed the experiments and simulations. RAD, FAO and WG performed the experiments and simulations. RAD, FAO, TKM, DJC and EAS analysed and interpreted the results. RAD, FAO, TKM, DJC and EAS wrote the manuscript. All authors approve submission of the manuscript, and all qualify for authorship.

Funding

This work is supported by grants from the National Institutes of Health to EAS [P50 GM071558] and DJC [R01 EB016407]. Ryan Devenyi was supported by a training grant from the National Institute of General Medical Sciences [T32 GM062754].