Quantitative analysis of the Ca²⁺‐dependent regulation of delayed rectifier K⁺ current I _Ks in rabbit ventricular myocytes

Abstract

Key points

• [Ca²⁺]_i enhanced rabbit ventricular slowly activating delayed rectifier K⁺ current (I _Ks) by negatively shifting the voltage dependence of activation and slowing deactivation, similar to perfusion of isoproterenol.

• Rabbit ventricular rapidly activating delayed rectifier K⁺ current (I _Kr) amplitude and voltage dependence were unaffected by high [Ca²⁺]_i.

• When measuring or simulating I _Ks during an action potential, I _Ks was not different during a physiological Ca²⁺ transient or when [Ca²⁺]_i was buffered to 500 nm.

Abstract

The slowly activating delayed rectifier K⁺ current (I _Ks) contributes to repolarization of the cardiac action potential (AP). Intracellular Ca²⁺ ([Ca²⁺]_i) and β‐adrenergic receptor (β‐AR) stimulation modulate I _Ks amplitude and kinetics, but details of these important I _Ks regulators and their interaction are limited. We assessed the [Ca²⁺]_i dependence of I _Ks in steady‐state conditions and with dynamically changing membrane potential and [Ca²⁺]_i during an AP. I _Ks was recorded from freshly isolated rabbit ventricular myocytes using whole‐cell patch clamp. With intracellular pipette solutions that controlled free [Ca²⁺]_i, we found that raising [Ca²⁺]_i from 100 to 600 nm produced similar increases in I _Ks as did β‐AR activation, and the effects appeared additive. Both β‐AR activation and high [Ca²⁺]_i increased maximally activated tail I _Ks, negatively shifted the voltage dependence of activation, and slowed deactivation kinetics. These data informed changes in our well‐established mathematical model of the rabbit myocyte. In both AP‐clamp experiments and simulations, I _Ks recorded during a normal physiological Ca²⁺ transient was similar to I _Ks measured with [Ca²⁺]_i clamped at 500–600 nm. Thus, our study provides novel quantitative data as to how physiological [Ca²⁺]_i regulates I _Ks amplitude and kinetics during the normal rabbit AP. Our results suggest that micromolar [Ca²⁺]_i, in the submembrane or junctional cleft space, is not required to maximize [Ca²⁺]_i‐dependent I _Ks activation during normal Ca²⁺ transients.

Abbreviations

AP

action potential

β‐AR

β‐adrenergic receptor

CaM

calmodulin

[Ca²⁺]_i

intracellular calcium

CaT

Ca²⁺ transient

k

slope‐factor for the V _m dependence of activation

I_CaL

L‐type Ca²⁺ current

I_CFTR

cystic fibrosis transmembrane conductance regulator Cl⁻ current

I_Cl,Ca

Ca²⁺‐activated Cl⁻ current

I_Ks

slowly activating delayed rectifier K⁺ current

I_Kr

rapidly activating delayed rectifier K⁺ current

ISO

isoproterenol

I_MAX

maximally activated current

I–V

current–voltage

PKA

protein kinase A

PKC

protein kinase C

PLM

phospholemman

τ_act

time course of activation

τ_deact

time course of deactivation

V_1/2

half‐maximal activation potential

V_m

membrane potential

Introduction

In the heart, the repolarizing delayed rectifier potassium current (I _K) consists of a slowly activating component (I _Ks) and a rapidly activating component (I _Kr) that differ in drug sensitivity, and voltage‐ or time‐dependent properties (Sanguinetti & Jurkiewicz, 1990; Selnick et al. 1997). These outward currents are required during phase 2 and phase 3 of the ventricular action potential (AP) for cardiac repolarization (Nerbonne & Kass, 2005). Under normal physiological conditions and in the absence of β‐adrenergic stimulation, I _Kr plays a primary role in repolarization in large mammals (such as rabbit, dog and human). I _Ks density has typically been measured to be much lower than I _Kr in these animals under basal conditions, but these studies were performed in situations where intracellular Ca²⁺ ([Ca²⁺]_i) was highly buffered (Jost et al. 2007). Additionally, most studies of I _Ks in native systems are performed in guinea pig, where I _Ks density is very large, and activation and deactivation kinetics are significantly slower than human I _Ks. Rabbit and dog I _Ks more closely resemble human I _Ks, thus making these species more suitable to use when studying I _Ks function and regulation (Liu & Antzelevitch, 1995; Heath & Terrar, 1996; Li et al. 1996; Salata et al. 1996). Furthermore, because repolarization depends on a fine balance between inward (mainly Ca²⁺‐selective) and outward (K⁺‐selective) currents, I _Ks might play an important role when normal repolarization reserve is impaired (Jost et al. 2005; Grandi et al. 2010).

The I _Ks macromolecular channel complex minimally consists of the Kv7.1 pore‐forming α‐subunit and the ancillary MinK1 β‐subunit (Barhanin et al. 1996; Sanguinetti et al. 1996). ‘Loss‐of‐function’ mutations within the genes encoding Kv7.1 (KCNQ1) or MinK1 (KCNE1) typically cause a decrease in I _Ks and are linked to congenital arrhythmia syndromes, type 1 and type 5 long QT syndromes (LQT1 and LQT5), respectively (Wang et al. 1996; Splawski et al. 1997). The dysfunctional I _Ks may lead to prolongation of the QT interval on a patient's electrocardiogram (ECG) and increases the risk for the phenotypic polymorphic ventricular tachycardia, torsades de pointes (El‐Sherif et al. 1997; Shah et al. 2005). Interestingly, the onset of torsades de pointes in LQT1 patients is typically triggered by adrenergic stress, highlighting the physiological importance of β‐adrenergic regulation in mediating the cardiac AP and specifically I _Ks (Schwartz et al. 2001; Goldenberg et al. 2012). During β‐adrenergic stimulation, Kv7.1 is phosphorylated by protein kinase A (PKA) on the amino terminus and causes an increase of I _Ks that is important for normal AP shortening (Walsh & Kass, 1988; Marx et al. 2002). Mutations that disrupt the β‐adrenergic upregulation of I _Ks are also linked to LQT1, further emphasizing the importance of this process (Heijman et al. 2012; Bartos et al. 2014). Interestingly, [Ca²⁺]_i can also influence I _K (sum of I _Kr and I _Ks), and β‐adrenergic stimulation increases Ca²⁺ transients (CaTs) in myocytes (Tohse, 1990; Bers, 2002). Dynamic clamp experiments in guinea pig myocytes demonstrated that I _Ks was larger than I _Kr subsequent to β‐adrenergic stimulation (Banyasz et al. 2014). This is an important finding because these recordings are in conditions where [Ca²⁺]_i is not buffered and physiological membrane and Ca²⁺ dynamics are maintained (Banyasz et al. 2011).

Several studies have reported on the regulation of I _K by [Ca²⁺]_i by using the whole‐cell and inside‐out patch clamp methods. The results suggested that increasing [Ca²⁺]_i (similar to the rise in [Ca²⁺]_i during each cycle of contraction and relaxation from ∼0.1 to 1 μm) in guinea pig ventricular myocytes increases I _K, most likely by increasing the open probability (P _O) or number of channels at the cell surface (Tohse, 1990). A later study determined calmodulin (CaM) is required for Ca²⁺‐sensitive increases of I _K, and this process was PKA and protein kinase C (PKC) independent (Nitta et al. 1994). Because Ca²⁺–CaM interaction with nitric oxide synthase (NOS) is an important determinant for NOS activation and NO release (Bai et al. 2004, 2005), the same group also showed that NO enhancement of I _Ks is critical for regulating AP duration, Ca²⁺ sensitivity of I _Ks itself, and intracellular Ca²⁺ cycling (Bai et al. 2005). More recently, two studies reported that CaM binds to IQ motifs on the C‐terminus of Kv7.1, and CaM interaction with the I _Ks channel complex is required for proper channel assembly, Ca²⁺ sensitivity and cell surface expression (Ghosh et al. 2006; Shamgar et al. 2006). Additionally, LQT1‐linked mutations can disrupt the CaM–Kv7.1 interaction, uncover inactivation of I _Ks and decrease I _Ks similar to other defined loss‐of‐function mutations (Ghosh et al. 2006; Shamgar et al. 2006).

While previous studies have suggested the importance of [Ca²⁺]_i regulation of I _Ks, quantitative information as to how Ca²⁺ sensitivity of I _Ks may affect cardiac repolarization in a more physiologically relevant environment is lacking. We sought to fill this gap in knowledge here.

Methods

Ethical approval

All animal care and procedures were approved by the University of California, Davis Institutional Animal Care and Use Committee and are in accordance with National Institutes of Health guidelines.

Rabbit euthanasia and ventricular myocyte isolation

Adult male New Zealand White rabbits (source, Western Oregon Rabbit Company) were housed at the University of California, Davis vivarium with access to normal food and water ad libitum. Rabbit ventricular myocytes were isolated with techniques modified from Pogwizd et al. (1999, 2001) and used acutely. Rabbits were administered Heparin, at 400 units kg^–1 subcutaneously, 15–30 min before surgery. Animals were then placed in a conventional restraint cage and given propofol at 0.5–2 mg kg^–1 or to effect. Once sedated, rabbits were gently but quickly removed from the restrainer and masked for isoflurane inhalation while being placed supine for surgery. Isoflurane was delivered with 100% oxygen through a facemask via a regularly calibrated veterinary vaporizer at a flow rate of 3–4 l min^–1, initially at 3–4.5% but reduced as appropriate as long as full areflexia was assured. Once very deep anaesthesia was verified, the heart was rapidly excised. Therefore, the animals only experienced brief restraint and minor discomfort of the injection.

Excised hearts were quickly washed in Ca²⁺‐free normal Tyrode solution at 4°C. They were then cannulated via the aorta for retrograde Langendorff perfusion. Oxygenated Hepes‐buffered Ca²⁺‐free Tyrode solution at 37°C was perfused long enough to ensure clearing of blood and Ca²⁺, resulting in arrest and relaxation. Pressure was ∼60–80 mmHg and flow rate was ∼20–30 ml min^–1. Perfusion was then switched to the same Tyrode solution containing either a crude collagenase (∼1 mg ml^–1) and protease (∼0.05 mg ml^–1) mixture or a defined enzyme product such as Roche Liberase (collagenase/thermolysin) at an equivalent concentration, with [Ca²⁺] adjusted to 20–25 μm. The tissue softened within 20–30 min, at which time the heart was removed and minced into 1–2 mm pieces in Tyrode solution containing 1% BSA. The pieces were gently agitated or triturated and passed through a nylon mesh of 200–250 μm pitch, resulting in liberation of individual cells, which were washed free of BSA and maintained at room temperature in Tyrode solution containing 50 μm Ca²⁺ until the time of the experiments.

Electrophysiology

Cardiac myocytes were plated on laminin‐coated glass coverslips at room temperature and transferred to an inverted microscope (Leica DMI3000B; Leica Microsystems; Buffalo Grove, IL, USA). Patch pipettes were fabricated from thin‐walled, filamented borosilicate glass and fire polished (World Precision Instruments; Sarasota, FL, USA). Uncompensated pipette resistances were ∼1–1.8 MΩ. Only cells with seal resistances  > 1 GΩ were used for recordings and series resistance was compensated up to 80%. pCLAMP 10.4 (Molecular Devices; Sunnyvale, CA, USA) was used to generate the voltage clamp protocols, acquire current signals, and initiate data analyses. An Axopatch‐200A patch clamp amplifier (Axon Instruments/Molecular Devices) was used to measure membrane current and cell capacitance. The giga seal was obtained in normal Tyrode solution containing (in mm): 135 NaCl, 0.33 NaH₂PO₄, 5.4 KCl, 2 CaCl₂, 0.53 MgCl₂, 5.5 glucose and 5 Hepes (pH adjusted to 7.4 with NaOH). Once the cell membrane was ruptured and the whole‐cell configuration was obtained, the external solution was switched to and continuously superfused at room temperature for experiments using square pulses as the voltage (V _m) command, or at 37°C for experiments implementing an AP waveform as the V _m command, with the I _Ks recording solution containing (in mm): 132 NaCl, 4 KCl, 1.8 CaCl₂, 1.2 MgCl₂, 0.2 BaCl₂, 10 glucose, 10 Hepes, 5 4‐aminopyridine (4‐AP), 0.01 nifedipine, and 0.003 dofetilide (pH adjusted to 7.4 with NaOH). 4‐AP, nifedipine, and dofetilide were obtained from Sigma‐Aldrich (St Louis, MO, USA). For I _Kr recordings, dofetilide was replaced with the I _Ks‐selective inhibitor HMR‐1556 (0.001 mm, Tocris Bioscience; Bristol, UK) to block I _Ks. To obtain [Ca²⁺]_i signals, Fluo‐4 K⁺‐salt (0.05 mm) was included in the intracellular pipette solution (described below). For most experiments [Ca²⁺]_i was buffered using a combination of 5 mm BAPTA (K _d ∼190 nm) plus 1 mm dibromo‐BAPTA 4K (K _d ∼1.8 μm) in the pipette solution. Total [Ca²⁺]_i was adjusted to achieve free [Ca²⁺]_i of 0, 100, 300, 500 and 600 nm, using the MaxChelator program (http://www.stanford.edu/~cpatton/maxc.html). In some experiments we let the myocyte control free [Ca²⁺]_i, in which case millimolar BAPTA + dibromo‐BAPTA were replaced with 0.05 mm EGTA. In addition, the intracellular pipette solution contained (in mm): 120 KOH, 20 KCl, 2 MgCl₂, 5 Mg‐ATP, 10 Hepes, 0.003 CaM and 100 aspartic acid (pH adjusted to 7.2 with KOH). I _Ks was recorded initially within 2–4 min once the Ca²⁺‐signal and I _Ks amplitude reached steady‐state. Depolarizing square‐pulses every 15 s allowed monitoring of both I _Ks and Ca²⁺ signals. For experiments involving β‐adrenergic stimulation, 50 nm isoproterenol (ISO) was perfused in the extracellular solution after an initial current‐voltage (I‐V) protocol was recorded, and after 5 min an additional I–V was measured.

For measuring I _Ks during an AP waveform, a rabbit ventricular AP waveform previously recorded at 1 Hz was implemented as the V _m command, also at 1 Hz. No drugs were used for initial recordings. The first 50 sweeps were averaged as the control current activated during the AP waveform. Then, 1 μm HMR‐1556 was added to the extracellular solution, and 50 more sweeps were recorded and averaged, then subtracted in order to define the HMR‐sensitive I _Ks. All AP‐clamp current recordings were performed at 35–37°C using an in‐line and bath temperature control system (Warner Instruments; Hamden, CT, USA).

Standard epifluorescence microscopy

Changes in [Ca²⁺]_i were monitored using wide‐field epifluorescence microscopy. The intracellular pipette solution was modified to contain 0.05 mm Fluo‐4 pentapotassium salt (Thermo Fisher Scientific; New York, NY, USA) for experiments using the whole‐cell patch clamp technique. Cells were preloaded with cell permeable Fluo‐4 AM (Thermo Fisher Scientific) for 28 min in a Ca²⁺‐free Tyrode solution containing 10 μm Fluo‐4 AM (K _d for Ca²⁺ of ∼335 nm). Fluo‐4 was excited by light of 488 nm wavelength, and emission was detected using a 514 nm long‐pass filter. The wavelength of excitation was controlled by an Optoscan monochromator (Cairn Research; Faversham, UK), and the emission signal was detected by a photomultiplier tube.

Mathematical modelling and simulation

We modified the Hodgkin–Huxley type formulation of I _Ks in our rabbit ventricular model (Shannon et al. 2004; Negroni et al. 2015) to fit the experimentally observed Ca²⁺‐ and ISO‐dependent regulation of maximal current, activation V _1/2, and deactivation kinetics. Experimental data were scaled to 37°C using a Q ₁₀ of 2.5 for both maximal conductance and time constants of activation and deactivation.

I _Ks channels are assumed to be uniformly distributed on the sarcolemma. This means that 11% are in junctional clefts with the SR (I _Ks‐junc vs. 89% in the external sarcolemma, I _Ks‐sl), corresponding with the fraction of rabbit ventricular myocyte sarcolemma involved in such junctions (21% of T‐tubular membrane plus 4.6% of surface sarcolemma; Shannon et al. 2004). This accounts for local differences in [Ca²⁺]_i that occur at the cleft and subsarcolemmal space. Total current is defined by the following equation:

$$I_{\mathrm{Ks}}=I_{\mathrm{Ks}-\mathrm{junc}}+I_{\mathrm{Ks}-\mathrm{sl}}$$

Each component is calculated using the following formulation:

$$\begin{array}{ccc}\hfill I_{\mathrm{Ks}-c}& =& F_{\mathrm{Ks}-c}{G}_{\mathrm{Ks}-c}{x}_{\mathrm{s}}^2\left(E_{\mathrm{m}}-E_{\mathrm{Ks}-c}\right)\hfill \\ \hfill E_{\mathrm{Ks}-c}& =& \frac{\mathit{RT}}{F}ln\frac{{\left[\mathrm{K}\right]}_{\mathrm{o}}+p_{\mathrm{NaK}}{\left[\mathrm{Na}\right]}_{\mathrm{o}}}{{\left[\mathrm{K}\right]}_{\mathrm{c}}+p_{\mathrm{NaK}}{\left[\mathrm{Na}\right]}_c}\hfill \\ \hfill \frac{\mathrm{d}{x}_{\mathrm{s}}}{\mathrm{d}t}& =& \frac{x_{\mathrm{s},\infty }-x_{\mathrm{s}}}{{\tau }_{x\mathrm{s}}}\hfill \\ \hfill x_{\mathrm{s},\infty }& =& 1/\left(1+{\mathrm{e}}^{-(E_{\mathrm{m}}-V_{{}_{1/2}})/25}\right)\hfill \\ \hfill {\tau }_{x\mathrm{s}}& =& 100+\frac{100+700{\mathrm{e}}^{-\frac{{\left(E_{\mathrm{m}}+30\right)}^2}{4000}}}{1+{\mathrm{e}}^{-\frac{(E_{\mathrm{m}}+{V_{\tau }}_{1/2})}{10}}}\hfill \end{array}$$

where c represents either the junctional (F _Ks‐junc  = 0.11) or subsarcolemmal (F _Ks‐sl  = 0.89) compartment, and the Na⁺:K⁺ permeability ratio (p _NaK) of the channel is 0.01833. Note that each compartment senses different Ca²⁺ and Na⁺ concentrations ([Ca]_c and [Na]_c in this formulation). However, as opposed to Ca²⁺, significant [Na⁺] gradients are not seen in the model during excitation contraction coupling.

PKA‐ and Ca²⁺‐dependent modulation of I _Ks is modelled as follows:

$$\begin{array}{ccc}\hfill G_{\mathrm{Ks}-c}& =& G_{\mathrm{Ks}0}+\frac{\mathrm{\Delta }{G}_{\mathrm{Ks}}}{1+{\left(150{\mathrm{e}}^{-6}/{\left[\mathrm{Ca}\right]}_c\right)}^{1.3}}\hfill \\ \hfill V_{1/2-c}& =& V_{\mathrm{h}0}+\frac{\mathrm{\Delta }{V}_{\mathrm{h}}}{1+{\left(350{\mathrm{e}}^{-6}/{\left[\mathrm{Ca}\right]}_c\right)}^4}\hfill \\ \hfill {V_{\tau }}_{1/2-c}& =& V_{\tau 0}+\frac{\mathrm{\Delta }{V}_{\tau }}{1+{\left(150{\mathrm{e}}^{-6}/{\left[\mathrm{Ca}\right]}_c\right)}^3}\hfill \\ \hfill G_{\mathrm{Ks}0}& =& 0.010+0.010k_{\mathrm{PKA}}[\mathrm{mS}\mu {\mathrm{F}}^{-1}]\hfill \\ \hfill \mathrm{\Delta }{G}_{\mathrm{Ks}}& =& 0.030+0.015k_{\mathrm{PKA}}[\mathrm{mS}\mu {\mathrm{F}}^{-1}]\hfill \\ \hfill V_{\mathrm{h}0}& =& -1-10k_{\mathrm{PKA}}\left[\mathrm{mV}\right]\hfill \\ \hfill \mathrm{\Delta }{V}_{\mathrm{h}}& =& -11+1k_{\mathrm{PKA}}\hfill \\ \hfill V_{\tau 0}& =& 26+9k_{\mathrm{PKA}}\left[\mathrm{mV}\right]\hfill \\ \hfill \mathrm{\Delta }{V}_{\tau }& =& 14-5k_{\mathrm{PKA}}\left[\mathrm{mV}\right]\hfill \end{array}$$

where the parameters G _Ks0, ∆G _Ks0, V _h0, ∆V _h, V _τ0 and ∆V _τ are fitted to the experimentally observed changes in G _Ks, V _1/2, and V _τ1/2 with ISO. These parameters are modulated by the scale factor, k _PKA (varying between 0 and 1) given by:

$$k_{\mathrm{PKA}}=\frac{\mathrm{PK}{\mathrm{A}}_{\mathrm{p}}-0.1098}{0.7282}$$

where PKA_p is the fraction of I _Ks phosphorylated by PKA (I _Ksp) over total I _Ks (I _Kstot), calculated as in (Negroni et al. 2015):

$$\mathrm{PK}{\mathrm{A}}_{\mathrm{p}}=\frac{I_{\mathrm{Ksp}}}{I_{\mathrm{Kstot}}}$$

and 0.1098 is basal PKA_p (in the absence of ISO) and 0.7282 is the difference between PKA_p at ISO = 100 nm (corresponding to ‘maximal activation’) and basal PKA_p.

AP and current‐clamp simulations were performed incorporating the new I _Ks model within our well‐established rabbit ventricular model (as last updated in Negroni et al. 2015). The same AP waveform used for experiments was given as a V _m command in AP‐clamp simulations (1 Hz). APs were simulated at 3 Hz in the absence or presence of 20 and 50 nm [ISO]. In addition to I _Ks, PKA targets were: L‐type Ca²⁺ current (I _CaL), ryanodine receptor, phospholamban, phospholemman (PLM), I _Kr, cystic fibrosis transmembrane conductance regulator Cl⁻ current (I _CFTR), Ca²⁺‐activated Cl⁻ current (I _Cl,Ca), troponin I, titin and myosin binding protein C. Model differential equations were implemented in Matlab (The Mathworks Inc., Natick, MA, USA) and solved numerically using a variable order solver (ode15s). The code is available for download at: https://somapp.ucdmc.ucdavis.edu/Pharmacology/bers/

Analysis and statistics

I–V relations were plotted for the peak I _Ks (normalized to capacitance, pA pF^–1) measured at the end of the step pulse or at the initiation of the tail pulse. Origin 7.0 (OriginLab Corp.; Northhampton, MA, USA) was used for performing Boltzmann fitting and plotting I–V graphs. The following Boltzmann equation was used to describe the I–V relations:

$$I=I_{\mathrm{MIN}}+\left(I_{\mathrm{MAX}}-I_{\mathrm{MIN}}\right)/(1+{\mathrm{e}}^{\left(V_{1/2}-V\right)/k})$$

where I _MIN is the minimally activated I _Ks, I _MAX is the maximally activated I _Ks (pA pF^–1), V _1/2 is the midpoint potential for half‐maximal activation of I _Ks (mV), and k is the slope factor (mV per e‐fold change). The time course of activation and deactivation (τ_act and τ_deact, respectively) were determined by fitting a single exponential equation using pCLAMP 10.4 software. Data were reported as the mean ± standard error of the mean (SEM). Student's paired or unpaired t test was performed when appropriate to determine if values were different from one another. For comparison of three or more groups, a one‐way ANOVA was performed with Tukey's post hoc analysis. Significance was determined when P < 0.05.

Results

Distinguishing the delayed rectifier K⁺ currents, I _Ks and I _Kr

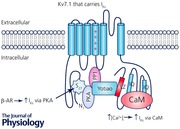
Figure 1 shows control experiments to demonstrate how we distinguished between rabbit I _Ks and I _Kr. To isolate total I _K (sum of I _Ks and I _Kr), we blocked I _K1, I _to and I _CaL by using Ba²⁺, 4‐AP and nifedipine, respectively (Fig. 1 A; with I–V protocol in inset). Figure 1 A shows total delayed rectifier I _K (i.e. I _Kr + I _Ks) with the expected slow I _Ks activation during depolarized V _m and the large tail current upon repolarization as expected for I _Kr. When recording I _Kr, HMR‐1556 was added to block I _Ks (Fig. 1 B; note the typical I _Kr tail currents that exceed I _Kr during the ‘step’ pulse). To isolate I _Ks, we used 3 μm dofetilide (instead of HMR) to block I _Kr (Fig. 1 C). The remaining time‐dependent currents were then completely abolished by 1 μm of the I _Ks selective inhibitor HMR‐1556 (Fig. 1 D), leaving only a small linear leak current.

Figure 1. Distinction between I _Ks and I _Kr .

A–C, representative traces of whole‐cell total I _K (A), I _Kr (B) and I _Ks (C) measured from isolated rabbit ventricular myocytes. Currents were recorded by applying step‐like pulses (inset) from −40 to 50 mV in 10 mV increments for 3 s, followed by a ‘tail’ pulse to −50 mV for 3 s. The inter‐pulse interval was 15 s. D, representative traces of whole‐cell currents recorded with high pipette [Ca²⁺] from the same cell as in C after perfusion of 1 μm HMR to show selective I _Ks block. E, an exemplar time course of tail I _Ks monitored before (black) and after (red) perfusion of ISO when pipette [Ca²⁺] was high.

Preliminary experiments showed that blockade of I _Cl,Ca using 30 μm niflumic acid did not alter I _Ks when [Ca²⁺]_i was low or high, so niflumic acid was not included in the extracellular bath. I _Ks currents are small and subject to rundown, and an exemplar time course of our protocol before and after perfusion of ISO (with high pipette [Ca²⁺]) is shown in Fig. 1 E. There was typically some initial rundown immediately after membrane rupture (and we monitored I _Ks single square pulses every 15 s). I _Ks usually stabilized within 2–4 min, at which time we performed a full I–V set. ISO was added immediately after the I–V protocol. Once I _Ks stabilized with ISO (within 2–4 min), a subsequent I–V was recorded. A small number of cells did not respond significantly to ISO, but were still included in the analysis (2 out of 22 total cells).

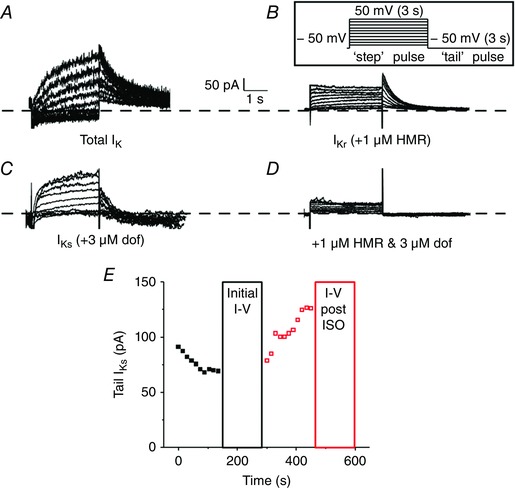
Elevated [Ca²⁺]_i enhances I _Ks amplitude and negatively shifts voltage dependence of activation in rabbit ventricular myocytes

To determine if steady‐state increases in [Ca²⁺]_i regulate rabbit I _K, we recorded I _Ks and I _Kr from freshly isolated rabbit ventricular myocytes with intracellular pipette solutions that buffered free [Ca²⁺]_i to 0, 100, 300, 500, or 600 nm. From a holding potential of −50 mV, I _Ks was recorded by step‐like square pulses from −40 to 50 mV in 10 mV increments for 3 s, followed by a tail‐pulse to −50 mV for 3 s (Fig. 2 A inset). The voltage dependence of I _Ks amplitude at the end of the 3 s pulse (minus a baseline that was leak‐corrected for each voltage step) is shown in Fig. 2 B (Step I _Ks). The I–V relations for tail I _Ks upon repolarization to −50 mV (measured as the amplitude of the decaying tail current exponential fit) are shown in Fig. 2 C. I _Ks amplitudes at +50 mV (I _MAX) were fitted by a Hill equation (I = I _MAX/(1 + (K _m/[Ca²⁺]_i)N _H)) as a function of [Ca²⁺]_i, yielding an apparent K _m of 253 nm and Hill coefficient (N _H = 2.4), indicative of cooperative activation typical of CaM‐dependent mechanisms (Fig. 2 D). Boltzmann equation fits shown in Fig. 2 C yielded the V _m for half‐maximal activation (V _1/2, Fig. 2 E) and activation slope factor (k, Fig. 2 F).

Figure 2. Assessment of steady‐state Ca²⁺ dependence of I _Ks .

A, representative traces of whole‐cell I _Ks measured from isolated rabbit ventricular myocytes. I _Ks was recorded by applying the same V _m protocol as Fig. 1 (inset). B and C, the mean peak ‘step’ (B) and ‘tail’ (C) I _Ks are plotted as a function of the step voltage for cells recorded using a pipette solution containing free [Ca²⁺]_i of 0, 100, 300, 500, and 600 nm. D–F, the tail I–V relations were described using a Boltzmann equation (grey line, C) to determine I _MAX (D), V _1/2 (E) and k (F). For all figures, number of cells (n) and significance tests are indicated in boxed insets where appropriate.

When [Ca²⁺]_i was increased from 0 to 300 nm, mean I _MAX was more than doubled (0.60 vs. 0.23 pA pF^–1). Importantly, raising the pipette [Ca²⁺]_i from 500 to 600 nm [Ca²⁺]_i further increased I _MAX (0.78 or 0.82 pA pF^–1, respectively), and the plateau suggested an approach to saturation (Fig. 1 C and D). V _1/2 was negatively shifted by ∼10 mV when I _Ks was recorded with high [Ca²⁺]_i of 500 and 600 nm (Fig. 2 E), with the steepest decline consistent with the [Ca²⁺]_i dependence of I _MAX. The slope factor, k, was not significantly changed by [Ca²⁺]_i (Fig. 2 E). I _Ks could not be measured using steady‐state [Ca²⁺]_i > 600 nm due to progressive cellular contracture and cell death. These data suggest that high [Ca²⁺]_i alters I _Ks by increasing I _MAX and shifting the V _m dependence of channel activation to more negative potentials.

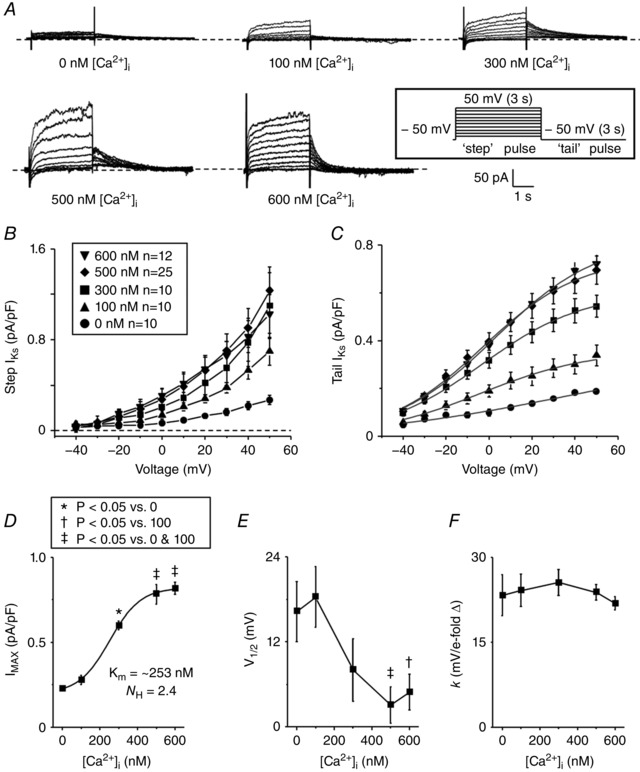
To ensure that the free‐Ca²⁺ of the pipette solutions were calculated correctly, [Ca²⁺]_i was monitored during electrophysiological recordings by preloading myocytes with Fluo 4‐AM and including 50 μm Fluo 4‐K⁺ salt in the pipette solution (Fig. 3 A). The fluorescence signal was background subtracted and fitted to a single site binding equation to determine an apparent K _d of 546 nm (Fig. 3 B). While higher than the published K _d of Fluo‐4 in aqueous solutions (335 nm), it is consistent with ∼2‐fold higher K _d values for this class of Ca²⁺ indicators when directly measured in myoplasm (Harkins et al. 1993; Bassani et al. 1995). These data showed that the actual [Ca²⁺]_i in the myocytes used to measure K⁺‐currents were close to the predicted free [Ca²⁺] of the pipette solutions.

Figure 3. Representative traces of Ca²⁺‐fluorescence signal recordings during simultaneous whole‐cell patch clamp measurements.

A, isolated rabbit ventricular myocytes were preloaded with Fluo‐4 AM and the patch pipette solution was loaded with Fluo‐4 K⁺ salt. The Ca²⁺ signal was recorded for 0, 100, 300, 500 and 600 nm [Ca²⁺]_i using the same V _m protocol as in Fig. 1. B, the fluorescence signal was background subtracted and fitted to a single site binding equation. C, representative traces of I _Ks recorded with pipette [Ca²⁺] 500 nm before (black) and after (red) perfusion of 50 μm W7. I _Ks was recorded by applying a step pulse from −50 to 40 mV for 3 s, followed by a tail pulse to −50 mV for 3 s (inset). D, the bar graph represents the mean peak tail I _Ks recorded before or after W7 perfusion (n = 5, P < 0.05).

To confirm that CaM is involved in the [Ca²⁺]_i dependence of I _Ks, as is expected, we measured I _Ks in the absence and presence of 50 μm W7, a widely used CaM inhibitor. Figure 3 C and D shows that W7 inhibited I _Ks measured at 500 nm [Ca²⁺]_i by approximately 50%, consistent with CaM being the mediator of the Ca²⁺‐dependent increase in I _Ks in Fig. 2.

Since previous studies in mammalian myocytes had only assessed [Ca²⁺]_i dependence of total I _K, rather than I _Ks vs. I _Kr (Tohse, 1990; Nitta et al. 1994), we also repeated our protocols measuring I _Kr to test whether rabbit ventricular I _Kr is sensitive to high physiological [Ca²⁺]_i (Fig. 4 A). The I–V relations of tail I _Kr were described using a Boltzmann equation to determine I _MAX, V _1/2 and k (Fig. 4 B–E). We concluded that rabbit I _Kr is not sensitive to steady‐state changes in [Ca²⁺]_i because no parameters were significantly altered when I _Kr was recorded with [Ca²⁺]_i of 0, 100, 300, or 600 nm.

Figure 4. Assessment of steady‐state Ca²⁺ dependence of I _Kr .

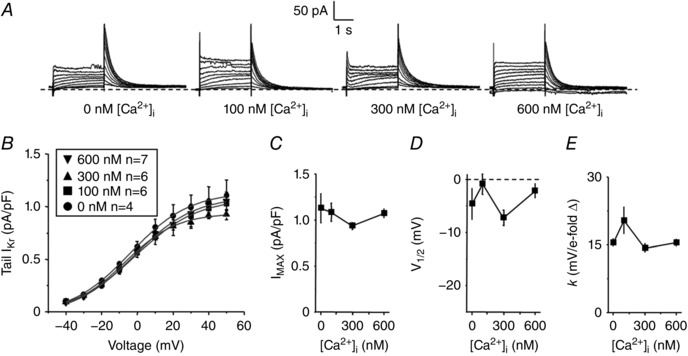
A, representative traces of whole‐cell I _Kr measured from isolated rabbit ventricular myocytes. The same V _m protocol was used as in Fig. 1. B, the mean peak tail I _Kr are plotted as a function of the step voltage for cells recorded using a pipette solution containing free [Ca²⁺]_i of 0, 100, 300 and 600 nm. C–E, the tail I–V relations were described using a Boltzmann equation (grey line, Fig. 4 B) to determine I _MAX (C), V _1/2 (D) and k (E).

Next, since β‐adrenergic stimulation plays an important role in regulating I _Ks, we measured differences in steady‐state [Ca²⁺]_i sensitivity of I _Ks induced by 50 nm ISO perfusion (Fig. 5). Tail I–V relations of I _Ks were plotted as a function of the step‐pulse potential before and after perfusion of 50 nm ISO and described with a Boltzmann equation (Fig. 5 B and C). ISO perfusion increased I _MAX even at zero [Ca²⁺]_i, but in the presence of ISO raising [Ca²⁺]_i further increased I _MAX, roughly parallel to that seen in the control (CNT in Fig. 5 D). In this series, the Ca²⁺ dependence was less sigmoidal, but the apparent half‐point for Ca²⁺‐dependent I _MAX increase was similar plus or minus ISO (225 and 235 nm, respectively), and consistent with the K _m estimate in Fig. 2 D. ISO perfusion also caused a negative shift in the V _1/2 for all [Ca²⁺]_i tested, but retained a roughly parallel [Ca²⁺]_i dependence (Fig. 5 E). Neither ISO nor [Ca²⁺]_i altered k significantly (Fig. 5 F). Thus, ISO does not appreciably alter the [Ca²⁺]_i dependence of I _Ks.

Figure 5. ISO and [Ca²⁺]_i increase I _MAX of I _Ks .

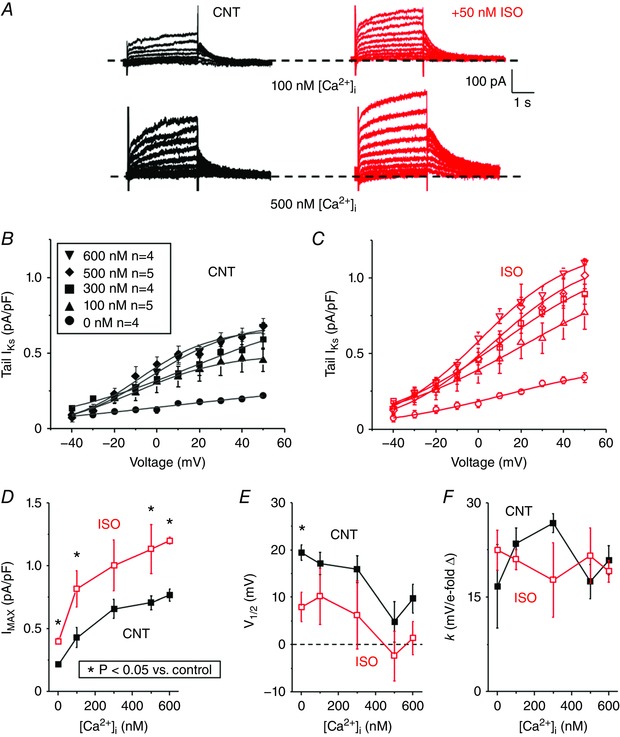
A, representative traces of I _Ks measured from isolated rabbit ventricular myocytes at room temperature before (black) and after (red) 50 nm [ISO] perfusion for pipette solutions containing [Ca²⁺]_i of 100 and 500 nm. The same V _m protocol was used as in Fig. 1. B and C, the mean peak tail I _Ks before (B) and after (C) ISO are plotted as a function of step voltage for cells recorded with a pipette solution containing free [Ca²⁺]_i of 0, 100, 300, 500, or 600 nm. D–F, the tail I–V relations were described using a Boltzmann equation (grey line, Fig. 5 B and C) to determine I _MAX (D), V _1/2 (E) and k (F).

Additionally, activation kinetics, τ_act, were fitted to a single exponential during the 40 mV test pulse and were unchanged by ISO (Fig. 6 A and B). The tail current at −50 mV following a 40 mV test pulse was fitted to a single exponential to determine τ_deact. Both ISO and [Ca²⁺]_i slowed deactivation kinetics of tail I _Ks, and appeared additive, based on the similar shapes of the curves (Fig. 6 C). These results indicate that in rabbit both elevated [Ca²⁺]_i and β‐adrenergic stimulation increase I _Ks amplitude, negatively shift V _1/2 and slow deactivation kinetics. And the effects of [Ca²⁺]_i and ISO are phenotypically similar, but appear additive. That is, even at a [Ca²⁺]_i that seems maximal with respect to [Ca²⁺]_i, ISO still causes a further change in I _MAX, V _1/2 and deactivation.

Figure 6. [Ca²⁺]_i slows deactivation of I _Ks .

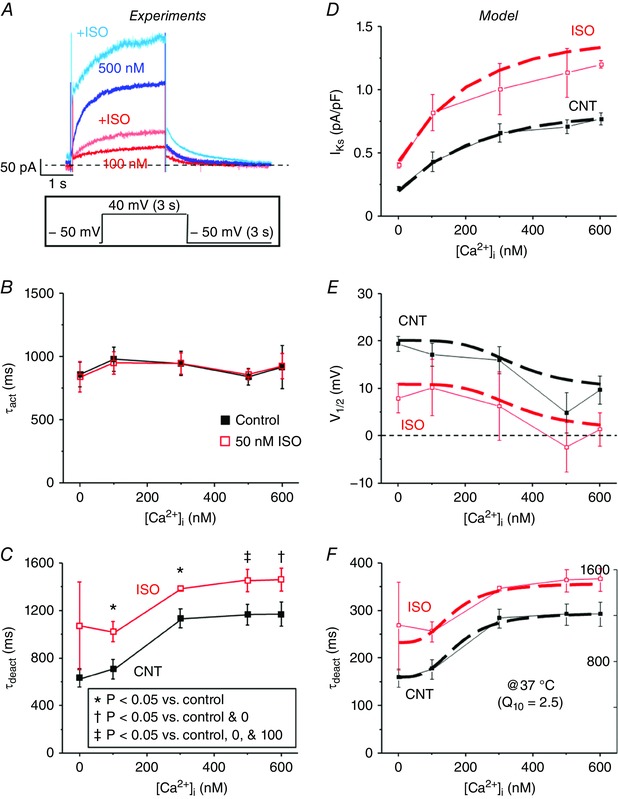
A, representative traces of I _Ks recorded using pipette solutions with free [Ca²⁺]_i of 100 and 500 nm before (100 nm, red; 500 nm, blue) and after (100 nm, light red; 500 nm, light blue) ISO are overlaid. I _Ks was recorded using the same V _m protocol as in Fig. 3 C by applying a step pulse from −50 to 40 mV for 3 s, followed by a tail pulse to −50 mV for 3 s. B, τ_act of I _Ks was fitted to a single exponential during the step pulse to 40 mV and is plotted as a function of free [Ca²⁺]_i in the pipette solution before (black) and after (red) ISO perfusion for 0, 100, 300, 500, and 600 nm [Ca²⁺]_i. C, the decay in tail I _Ks following the 40 mV step‐pulse was fitted to a single exponential to determine  τ_deact and is plotted as a function of free [Ca²⁺]_i in the pipette solution before and after ISO perfusion for 0, 100, 300, 500, and 600 nm [Ca²⁺]_i. The n values for each situation are the same as in Fig. 5. The [Ca²⁺]_i dependence and ISO effects (50 nm) on I _Ks (D), V _1/2, (E) and τ_deact (F) were incorporated into a model of I _Ks based on the experimental data and was scaled to 37 °C. Simulated I _Ks (dashed lines) are shown overlaid with experimental results (solid lines).

I _Ks increases during an AP with high buffered [Ca²⁺]_i and during physiological Ca²⁺ transients

Figure 6 D–F shows how our updated I _Ks model recapitulates our experimental results, with respect to the Ca²⁺ and ISO dependence of current amplitude, voltage dependence, and deactivation kinetics. During AP‐clamp simulations at 1 Hz we further tested how normal CaTs vs. [Ca²⁺]_i clamping affected I _Ks (Fig. 7 A–C). When [Ca²⁺]_i was clamped at 100 nm, I _Ks was small, but I _Ks was ∼3‐fold larger when [Ca²⁺]_i was clamped at 500 nm. When [Ca²⁺]_i was unbuffered, which allowed normal dynamic CaTs, I _Ks was nearly identical to the 500 nm simulations (Fig. 7 B). This seemed somewhat surprising, because the peak submembrane and cleft [Ca²⁺]_i where the potassium channels reside rises much higher (∼12 and 220 μm, respectively, in the model), far exceeding the [Ca²⁺]_i used in the [Ca²⁺]_i‐clamp experiments. This would suggest that in myocytes I _Ks is typically maximally Ca²⁺‐activated at [Ca²⁺]_i  > 600 nm, which would virtually always occur during the AP in the submembrane and cleft domains. The only noticeable difference in the unbuffered and 500 nm curves in Fig. 7 B is that I _Ks declines slightly faster in the unbuffered case, consistent with the declining CaT at that time (between the 100 and 500 nm clamp curves in Fig. 7 C).

Figure 7. Ca²⁺ dependence of HMR‐sensitive I _Ks activated during AP waveform.

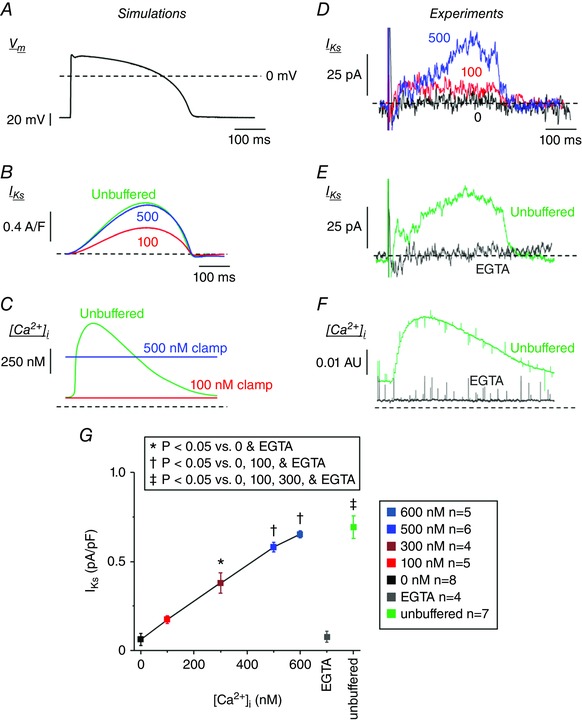
A, rabbit ventricular AP waveform used for AP simulations and to record HMR‐1556‐sensitive I _Ks at 35–37°C. B and C, time courses of I _Ks (B) and CaT (C) during 1 Hz computational simulations using the AP waveform as in Fig. 7 A are shown with [Ca²⁺]_i clamped at 100 (red) and 500 nm (blue), or unbuffered (Free CaT, green). D, representative whole‐cell current subtracted HMR‐sensitive (1 μm) I _Ks traces are overlaid for cells recorded with free [Ca²⁺]_i of 0 (black), 100 (red) and 500 nm (blue). E, representative whole‐cell current subtracted HMR‐sensitive (1 μm) I _Ks traces are overlaid for cells recorded (using the AP waveform in Fig. 7 A as the V _m command) with [Ca²⁺]_i heavily buffered by 10 mm EGTA (grey) or unbuffered (green). F, the corresponding Ca²⁺ signal is shown. Note that free [Ca²⁺]_i is reduced at baseline and during the AP when buffered, and a normal CaT is present when unbuffered. G, the peak I _Ks during ventricular AP waveform recordings are plotted for cells recorded using a pipette solution containing free [Ca²⁺]_i of 0, 100, 300, 500, or 600 nm, and buffered with EGTA or unbuffered.

To explore these in silico inferences experimentally, we measured I _Ks during AP‐clamp conditions (Fig. 7 D–G) using a typical rabbit ventricular AP waveform recorded from freshly isolated rabbit ventricular myocytes at 35–37°C. HMR‐1556 (1 μm) was used to isolate I _Ks as the HMR‐sensitive current activated during the AP. We again used pipette solutions with free [Ca²⁺]_i clamped at 0, 100, 300, 500 and 600 nm (now at physiological temperature; Fig. 7 D and G). Similar to the room temperature experiments (Figs 1, 2, 3, 4, 5, 6), the HMR‐sensitive I _Ks increased in a [Ca²⁺]‐dependent manner (Fig. 7 G). The Ca²⁺ dependence was less obviously saturating at 600 nm (vs. Figs 2 D and 5 D), but the I _Ks at 300 nm was ∼60% of that at 600 nm [Ca²⁺]_i.

In this experimental series we also used pipette solutions that were either unbuffered (no BAPTA or dibromo‐BAPTA), which allows normal CaTs to occur, or heavily buffered with 10 mm EGTA, i.e. similar to the 0 nm [Ca²⁺]_i BAPTA‐based solution (Fig. 7 E). [Ca²⁺]_i was monitored again using Fluo 4‐AM and 50 μm Fluo 4‐K⁺ salt in the pipette to detect either a normal CaT during the AP (unbuffered) or a flat Ca²⁺ signal with 10 mm EGTA (Fig. 7 F). Figure 7 G shows that the peak I _Ks during the AP in the unbuffered case was similar to that in the 600 nm [Ca²⁺]_i‐clamp case. These data are consistent with the model prediction and suggest that I _Ks is maximally activated when [Ca²⁺]_i reaches > 500 nm, and that that condition is met during the normal CaT. We examined for, but could not detect any kinetic differences (e.g. I _Ks in the unbuffered case being higher early and lower late), which is likely to be because noise levels and cell–cell variations in these small difference‐currents limited resolution of such kinetic differences.

Functional consequences of Ca²⁺ and ISO dependence of I _Ks

To assess the impact and potential synergy of Ca²⁺ and ISO dependence of I _Ks on AP repolarization, Fig. 8 shows simulations at a fast rate (3 Hz) in the absence of ISO and in the presence of either 20 nm ISO (submaximal) or 50 nm (near‐maximal and as used in experiments). During β‐adrenergic activation, the increase in I _Ks is mostly a consequence of PKA phosphorylation, because the effect of [Ca²⁺]_i augmentation on I _Ks is already near maximal in control. That is, the higher CaT amplitude with ISO does not further increase I _Ks. Importantly, our results show evident I _Ks enhancement at this fast rate, and particularly, the slowed deactivation kinetics enhance instantaneous I _Ks at the start of the subsequent AP. This factor gives I _Ks a head‐start during the AP, ensuring that at high heart rates and shorter AP duration, I _Ks can limit AP prolongation (together with PKA effects at other targets, e.g. I _CaL and PLM; Negroni et al. 2015).

Figure 8. Ca²⁺ and ISO dependence of I _Ks contribute to rabbit ventricular AP shortening during β‐AR stimulation.

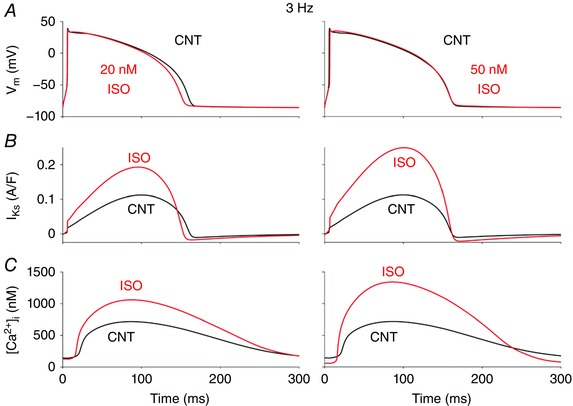
Simulated time courses of membrane potential, V _m (A), I _Ks (B) and CaT (C) during steady‐state 3 Hz pacing are shown before (black) and after (red) ISO (20 nm, left; and 50 nm, right).

Discussion

Many studies over the past several decades have shown how Ca²⁺ can directly or indirectly influence ion channel function in the heart, neurons, epithelial tissue and other important regions of the body. In contractile cells, such as cardiomyocytes, studying these mechanisms is technically difficult, because high levels of [Ca²⁺]_i lead to contraction or cell death during recordings, and thus data acquisition is challenging. This is the first study to dissect the Ca²⁺ dependence of both I _Ks and I _Kr in rabbit ventricular myocytes and to provide direct evidence that [Ca²⁺]_i is critical for I _Ks function during a rabbit ventricular AP.

Key novel findings here are the following: (1) [Ca²⁺]_i in the physiological range (K _m ∼250 nm) dynamically regulates I _Ks (and not I _Kr). (2) The [Ca²⁺]_i‐dependent effects are quite similar to those of ISO, in the extent to which they increase I _Ks amplitude, negatively shift V _1/2 of activation, and slow deactivation. Likewise, neither an increase in [Ca²⁺]_i nor β‐AR activation alter the slope of V _m dependence activation (k) or τ_act. (3) The effects of increased [Ca²⁺]_i and ISO are additive and both contribute to increase I _Ks during β‐AR activation. (4) During the physiological AP and CaT, Ca²⁺‐dependent activation of I _Ks is nearly maximal, even in the absence of ISO. These observations from experimental data were recapitulated in silico, and together suggest that although Ca²⁺ is critical for normal I _Ks function, I _Ks reaches a maximal amplitude at [Ca²⁺]_i of ∼600 nm. Importantly, our experimental and simulated results suggest that I _Ks kinetics are quite similar when [Ca²⁺]_i is buffered at high concentrations or when [Ca²⁺]_i is cycling in the cell during a CaT.

It has been estimated that ion channels at the sarcolemma ‘sense’ [Ca²⁺]_i in the micromolar range during the initial milliseconds of a normal CaT during myocyte contraction, and in our simulations the [Ca²⁺] in the submembrane space reaches > 10 μm (Weber et al. 2002; Negroni et al. 2015). Our results suggest that Ca²⁺ regulates I _Ks with sufficiently high affinity that this regulation is saturated at all submembrane [Ca²⁺]_i levels that are likely to occur physiologically during each beat. We had hoped to assess the kinetics of Ca²⁺‐dependent activation during the physiological CaTs, where some cells showed rapid I _Ks activation (as in the exemplar in Fig. 7 E). However, cell‐to‐cell variability and the small current size prevented unequivocal distinction with respect to the early phase of I _Ks with SR Ca²⁺ release vs. [Ca²⁺]_i clamp at 500 nm. The modelling simulations in Fig. 7 B illustrate that the theoretical difference is expected to be quite small.

Comparison with previous studies

Previous studies have assessed the Ca²⁺ dependence of I _K in guinea pig ventricular myocytes by whole‐cell and excised patches (Tohse, 1990; Nitta et al. 1994). Both studies showed that I _K increased in a concentration‐dependent manner with increasing [Ca²⁺]_i with slightly higher affinity than our results (K _m ∼38 nm, N _H = 1.4 in Nitta et al. 1994 vs 253 nm, N _H = 2.4). Note, that Tohse (1990) tested only up to 100 nm [Ca²⁺]_i. Most modern AP models have used a K _m for I _Ks [Ca²⁺]_i dependence of either 38 or 63 nm (Zeng et al. 1995; Negroni et al. 2015). We have now updated the I _Ks model within Negroni et al. (2015) to fit our present data. Nitta et al. (1994) found a negative shift in the V _1/2 of I _K activation while Tohse (1990) did not. These studies provide evidence that I _K could limit Ca²⁺ entry by accelerating repolarization and subsequently promoting Ca²⁺ extrusion from the cytosol. However, the Ca²⁺ sensitivity was never distinguished between I _Kr and I _Ks, and I _Ks amplitude and kinetics in guinea pig differ greatly from larger mammals such as rabbit, dog and human (Jost et al. 2007; Bartos et al. 2015). Our results clearly distinguish that rabbit I _Ks is highly Ca²⁺ sensitive, but I _Kr is not. We also show that the voltage dependence of I _Ks was negatively shifted and deactivation kinetics were slowed by high [Ca²⁺]_i, consistent with previous findings.

I _Ks increases in a Ca²⁺‐dependent manner, but I _Kr is larger at all [Ca²⁺]_i tested here and is the key outward current during normal rabbit ventricular repolarization. However, I _Ks reaches an amplitude similar to I _Kr subsequent to ISO perfusion when recorded with high [Ca²⁺]_i, thus highlighting the importance of β‐adrenergic regulation of I _Ks. These observations align with dynamic clamp recordings in guinea pig myocytes made while maintaining physiological [Ca²⁺]_i cycling, whereby I _Ks is larger than I _Kr subsequent to β‐adrenergic stimulation (Banyasz et al. 2014). Regardless of ISO perfusion, rabbit I _Ks increases ∼3.5‐fold when [Ca²⁺]_i is increased from 0 to 500–600 nm. Importantly, at all Ca²⁺ concentrations ISO perfusion still led to an increase of I _Ks by ∼2× (Fig. 9). These results resemble the original I _K observations in guinea pig ventricular myocytes, where even with PKA or PKC activity inhibited, I _K remained augmented at elevated [Ca²⁺] (Nitta et al. 1994). We conclude that β‐adrenergic activation is able to stimulate I _Ks in a manner independent of [Ca²⁺]_i; however, the similar (and additive) effects might imply a common molecular shift. Specifically, several studies showed how PKA phosphorylation at S27 on the N‐terminus of Kv7.1 leads to a reduction in drug sensitivity suggesting that PKA phosphorylation restricts allosteric drug binding because of changes in the molecular conformation of Kv7.1 (Yang et al. 2009, 2013; Bartos et al. 2014). The ISO‐ and Ca²⁺‐dependent changes in I _Ks biophysical properties are similar, and these effects may influence the voltage‐sensing and pore domains in a comparable fashion. However, the ISO‐dependent process may originate in the N‐terminus and the Ca²⁺ dependency may act via direct binding to CaM on the C‐terminus of Kv7.1.

Figure 9. Effects of Ca²⁺ and ISO dependence of rabbit I _Ks .

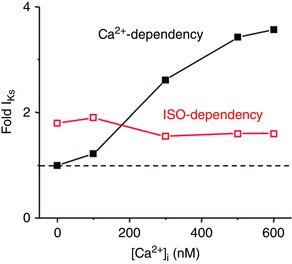
Dashed line represents I _Ks amplitude under control conditions when [Ca²⁺]_i is highly buffered essentially to 0 in the pipette solution (based on data in Fig. 5 D).

When using high [Ca²⁺]_i, it is noteworthy that both main ventricular myocyte isoforms of adenylyl cyclase (AC; AC5 in adult and AC6 in neonate) are partially inhibited by high [Ca²⁺]_i, in part by competing with Mg²⁺‐dependent activation (Hu et al. 2002). Over the physiological range of [Ca²⁺]_i and [Mg²⁺]_i, this may limit, but not prevent, AC activation by β‐adrenergic agonists. Indeed, there is little question that β₁‐adrenergic activation strongly activates both cAMP production and PKA activity in cardiac myocytes despite a concurrent rise in [Ca²⁺]_i that might temper AC5 activation. Furthermore, the fact that the curves in Fig. 5 D are relatively parallel demonstrates that the high [Ca²⁺]_i is not preventing β‐adrenergic‐dependent increase in I _Ks at that [Ca²⁺]_i. This tells us that the physiologically resulting effect of these two activating effects predominate over Ca²⁺‐dependent AC inhibition. It is conceivable that the apparent slight decrease in percentage increase of I _Ks by ISO at higher [Ca²⁺]_i (Fig. 9, red curve) might reflect this AC effect, but that is only speculation.

Ca²⁺ regulation of I _Ks involves proper binding of CaM to the Kv7.1 macromolecular complex

Reports of LQT1 mutants in IQ motifs of Kv7.1 and structural modelling insight suggest that CaM is required for proper I _Ks function in native and heterologous systems (Nitta et al. 1994; Bai et al. 2005; Ghosh et al. 2006; Shamgar et al. 2006; Sachyani et al. 2014). Mutants that disrupt the IQ motifs critical for CaM binding to the C‐terminus of Kv7.1 or engineered mutations that disrupt the EF hand on the N‐lobe of CaM (rendering the N‐lobe of CaM Ca²⁺‐insensitive) suggest that CaM is constitutively bound to Kv7.1 and Ca²⁺ dependency of I _Ks is a CaM‐dependent process (Ghosh et al. 2006; Shamgar et al. 2006; Sachyani et al. 2014). When Kv7.1–CaM interactions are disrupted, I _Ks is largely reduced and the voltage dependence of activation is positively shifted. Furthermore, we found that rabbit I _Ks recorded with high [Ca²⁺]_i (500 nm) was inhibited by 50% following perfusion of W7, a CaM antagonist (Figure 3 C). These studies and our results suggest that Ca²⁺ sensitivity of I _Ks is a CaM‐mediated process, with an apparent K _m in the physiological [Ca²⁺]_i range.

Physiological impact of the Ca²⁺ dependence of I _Ks

It is likely that the negative shift in voltage dependence of activation and postponed deactivation of rabbit I _Ks contribute to the increase in current amplitude subsequent to a rise in [Ca²⁺]_i, as replicated by our mathematical model. Recent studies have showed that an elevation in [Ca²⁺]_i or cellular stress leads to higher co‐localization of Kv7.1 with KCNE1 at the sarcolemma of guinea pig ventricular myocytes, which one would expect to result in increased I _Ks (Wang et al. 2013). Alterations in Kv7.1 protein expression at the cell surface were not assessed in our study, but rapid increases in surface expression could conceivably contribute to the overall Ca²⁺‐induced increase in rabbit I _Ks density.

Our simulation results suggest that during β‐adrenergic activation both Ca²⁺ increase and PKA‐dependent phosphorylation contribute to I _Ks enhancement that tends to abbreviate the cardiac AP. Although speculative, our data and other studies support the concept that Ca²⁺ sensitivity of I _Ks is crucial for the repolarization reserve during situations when cells are overloaded with Ca²⁺, for example during heart failure.

Clinical significance

In heart failure, impaired [Ca²⁺]_i dynamics (elevated diastolic [Ca²⁺]_i and attenuated CaT) and AP prolongation are a common observation in cellular pathophysiology. Here, we show that normal CaTs are necessary for normal I _Ks function, and suppression of [Ca²⁺]_i leads to reduced I _Ks. This may suggest that pathological AP prolongation and Ca²⁺‐loading favours the role of I _Ks during repolarization. Therapeutic strategies designed to restore normal [Ca²⁺]_i dynamics and regulation of ion channel function, specifically Ca²⁺‐dependent channels like I _Ks, may prevent the occurrence of lethal arrhythmias and lead to a retention of the repolarization reserve in patients with heart failure.

Conclusions

We have shown that increasing [Ca²⁺]_i from 0 to 600 nm in rabbit ventricular myocytes increased maximally activated I _Ks, negatively shifted I _Ks voltage dependence of activation, and slowed deactivation kinetics, similar to β‐adrenergic stimulation, without affecting I _Kr properties. During a physiological AP and CaT, measured and simulated I _Ks were comparable to that measured or simulated when [Ca²⁺]_i was buffered at 500–600 nm, suggesting that Ca²⁺ regulation of I _Ks is saturated at high submembrane [Ca²⁺]_i that occurs normally during the CaT. For the first time, this study distinguishes the Ca²⁺ dependence of I _Ks and I _Kr and provides direct measurement of the role of [Ca²⁺]_i in shaping I _Ks function during a rabbit ventricular AP.

Additional information

Competing interests

No competing interests exist.

Author contributions

Conceived and designed the experiments and simulations: D.C.B, S.M., K.S.G., E.G. and D.M.B. Performed the experiments and simulations: D.C.B, S.M. Analysed and interpreted the results: D.C.B, S.M., K.S.G., E.G. and D.M.B. Wrote the manuscript: D.C.B, S.M., E.G. and D.M.B. All authors approved the final version of the manuscript and all persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

This work was supported by the National Institutes of Health NRSA postdoctoral award F32 HL126331 (D.C.B.), R01 grants HL131517 (E.G.) and HL030077 and P01‐HL080101 (D.M.B.), the American Heart Association Scientist Development Grant 15SDG24910015 (E.G.) and postdoctoral fellowship 2014POST18380011 (S.M.), and the Heart Rhythm Society postdoctoral fellowship 16OA9HRS (S.M.).