Minimum toe clearance adaptations to floor surface irregularity and gait speed

Abstract

Toe speed during gait generally nears its maximum while its height reaches a local minima approximately halfway through swing phase. Trips are thought to frequently occur at these local minima (minimum toe clearance or MTC events) and trip risk has been quantified using the minimum distance between the toe and ground here (MTC). This study investigated MTC on floor surfaces with and without multiple small obstacles. After shoes and floor surfaces were digitized, 14 unimpaired subjects (half women) each traversed a 4.88m walkway 4 times at slow, preferred, and fast speeds across surfaces with no obstacles, visible obstacles, and hidden obstacles. Both surfaces with obstacles had the same random obstacle configuration. Shoe and body segment motions were tracked using passive markers and MTC and joint kinematics calculated. All MTC and kinematic variables tested significantly increased with faster instructed gait speed except the likelihood of MTC event occurrence (local minima in minimum toe clearance trajectory when foot is in upper quartile of speed). MTC events were less frequent for swing phases on surfaces with obstacles (80% vs. 98% for no obstacles). MTC values, when present, were doubled by the presence of visible obstacles (22.2±7.3mm vs. 11.1±5.7mm) and further increased to 26.8±7.1mm when these obstacles were hidden from view (all comparisons p≤0.0003). These substantial floor surface-related changes in MTC event occurrences and values resulted from alterations in toe- and heel-clearance trajectories caused by subtle but significant changes in joint kinematics that did not exceed 10% each joint’s swing phase range of motion.

1. Introduction

Falls are responsible for nearly half (47.9%) of all injury-related deaths in persons over the age of 65. This is nearly triple the number of injury-related deaths due to motor vehicle accidents (17.3%), the next most frequent cause of lethal injury in this age group (CDC, 2010). Non-fatal injuries due to falls are nearly twice (1.9×) as frequent as injuries from all other causes combined in older adults (NCIPC, 2010). Fifty-three percent of falls in healthy older adults are estimated to be due to tripping while walking (Blake et al., 1988) and the minimum toe clearance (MTC) is the local minimum distance between the shoe and ground during the swing phase of gait where these trips are likely to occur (Winter, 1992). MTC occurs at a critical instant where the toe is at a local minima in proximity to the ground, but the speed of the foot and toe is also at or near its maximum and the body center of mass is located anterior to the stance foot and outside of the base of support in the direction of progression (Winter, 1992). If a trip occurs at or near the point of MTC, stability cannot be regained without a rapid and safe placement of the swing foot (Eng et al., 1994; Winter, 1992; Pijnappels et al., 2004). Thus, a lower or more variable MTC in a specific population or during a specific concurrent task performed during gait would presumably indicate an increased risk of trip-related falls.

MTC has often been evaluated on a treadmill (Mills et al., 2008; Begg et al., 2007; Khandoker et al., 2008; Miller et al., 2009), which enables the rapid collection of a large number of consistent steps, but cannot account for ground height variations (e.g. changes in slope, level, or flatness), obstacles, and speed or direction changes of overground gait in real-world conditions. Recording MTC overground circumvents the restrictions of treadmills but introduces the requirement of accounting for variations in ground height. Considering that MTC values can be less than 10mm and a concrete slab floor can vary in height by approximately 9mm for a walkway less than 4m long (Schulz et al., 2010), these variations in flooring should be accounted for in order to accurately calculate overground MTC.

This purpose of this study was to determine how ground height variations and their visibility alter MTC. We hypothesized that overground MTC would be greater across flooring surfaces 1) covered with multiple small obstacles than on surfaces without obstacles and 2) on surfaces where these obstacles were obscured from view (hidden) than on surfaces where the obstacles were clearly visible. Since gait speed is known to affect many gait parameters (Bejek et al., 2006), gait at slow, preferred, and fast speed was tested on each surface. As any changes in MTC are ultimately the result of changes in lower limb kinematics; ankle, knee, and hip joint angles were calculated to determine which joint or joints were responsible for the changes.

2. Methods

2.1. Subjects and instrumentation

A convenience sample of seven unimpaired men and seven unimpaired women were recruited, ranging in age from 20–35 years (mean±standard deviation of 27±5 years). These subjects had no major health problems, 20/20 corrected vision, and good balance as defined by one-legged stance times of over 30 seconds on each foot. After completing the informed consent process, each subject was given instrumented shoes in their own size (model 811, New Balance Athletic Shoe, Inc., Boston, MA, USA).

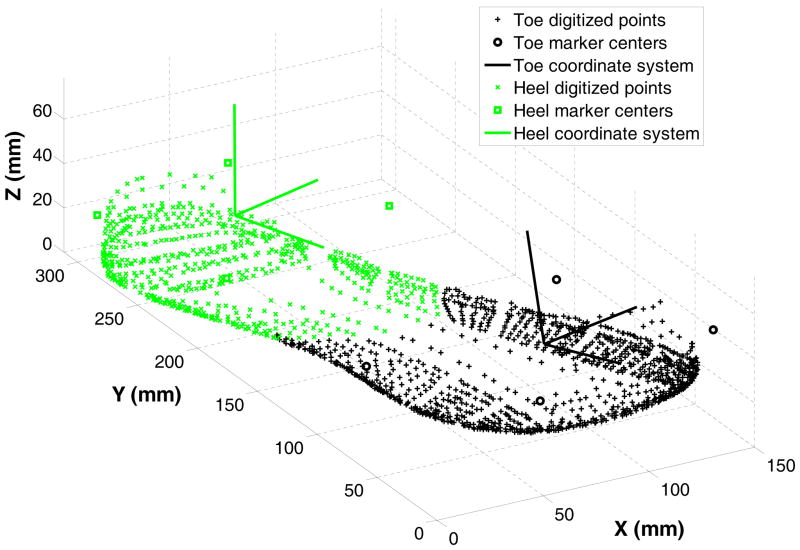
Each of these experimental shoes had eight 9.5mm retroreflective markers mounted on 3cm long M4-0.7 threaded rods partially embedded in the outsole, with four affixed to the toe and four to the heel (Figure 1a). The addition of these rods and markers did not perceptibly alter the sole stiffness, comfort, or use of these shoes in any way. Prior to subject testing, each shoe was mounted on a jig to immobilize it during digitization with a MicroScribe-3DX stylus digitizer (Immersion Corp., San Jose, CA, USA, see Figure 1b). At least 25 points on each marker, 260 points on the toe area of the sole, and 174 points on the heel area of the sole were captured (Figure 2). These were the numbers of digitized points for one of the smallest women’s shoes (size 6). In comparison, one of the largest shoes used (men’s size 13) had 817 digitized points on the toe and 601 on the heel.

Figure 1.

Representative experimental shoe (a) and shoe mounted on custom jig being digitized (b).

Figure 2.

Representative data of digitized shoe sole and embedded markers.

The floor surfaces were also digitized prior to subject testing using a custom rolling digitizing wand. This wand was created by replacing the points on the ends of a CalTester (Holden et al., 2003) with a knife-edge wheel and handle (Figure 3) and used to trace a grid pattern on each piece of plywood that comprised the floor surface (Figure 4a and b). A 13-camera Vicon MX40 system using Workstation v5.2.9 was used to collect all data at 120Hz (Vicon, Centennial, CO, USA).

Figure 3.

Custom rolling digitizing wand based on CalTester.

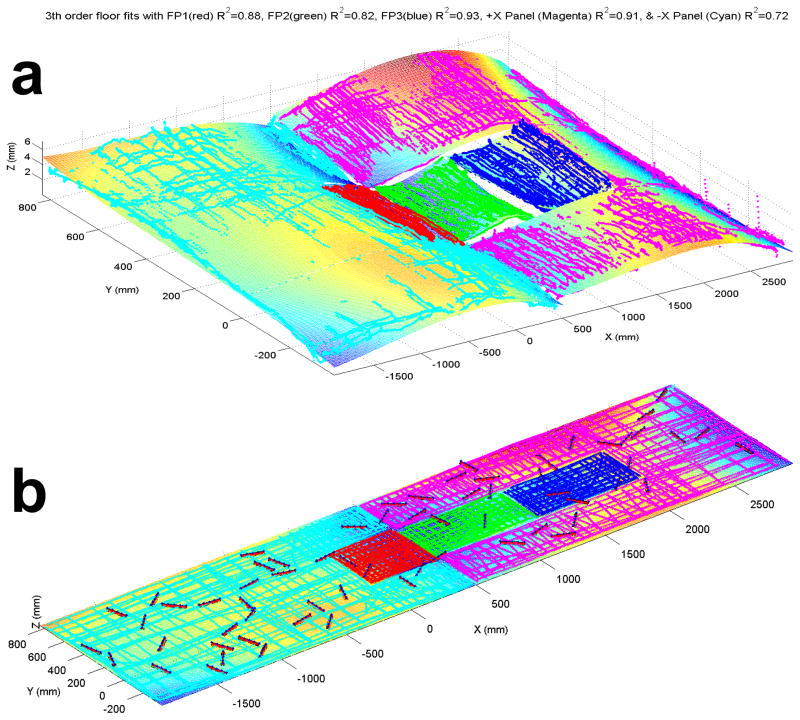
Figure 4.

Unequal-axis plot of piecewise 3rd-order polynomial fit for floor surface segments without obstacles (a) and equal-axis plot of floor surface segments with obstacles (b). Note that the shape and alignment of these polynomial surfaces reflects the unevenness, inconsistencies, and slopes of flooring surface sections affixed to the laboratory floor.

Subjects were additionally instrumented with rigid four-marker clusters affixed to the thighs and shanks using double-sided tape and SuperWrap (Fabrifoam, Exton, PA, USA). Four pelvis markers were affixed to the iliac crests and posterior-superior iliac spines and foot markers were attached to the calcaneus and 2nd metatarsophalangeal joint via short wands. The bases of these wands were adhered to the skin of the foot and the wands attached to the bases through holes punched in the shoes and socks worn.

2.2. Data collection

Each subject performed four gait passes at three speeds across three 1.22m (4 foot) wide x 4.88m (16 foot) long surfaces. The instructed speeds were “preferred”, “slower than preferred”, and “as fast as safely possible”. These speed instructions were selected to allow actual gait speed to change with surface condition if this were one of the compensatory mechanisms utilized. Surface conditions were presented in randomized order and speed conditions were randomized within each surface condition. A safety harness was worn at all times to minimize the chance of fall-related injuries. The floor surfaces traversed were “no obstacles” (flat, smooth, level surface), “visible obstacles” (white obstacles on black surface), and “hidden obstacles” (black obstacles on black surface). All trials were conducted under identical low lighting conditions designed to minimize visual feedback of obstacle location for the hidden obstacles surface condition (see details below). Subjects were not allowed to see the hidden obstacles surface under normal lighting conditions and were instructed that the obstacles on this surface were identical to the visible obstacles in size, shape, and number, but that their layout was only “similar” while in fact their layout was identical. Subjects were instructed that they may look at the floor during the visible obstacles condition, but that they should keep their eyes focused on the end of the walkway for the hidden obstacles condition. These differing instructions were adopted as a countermeasure to subject attempts to see the hidden obstacles (by leaning forward and looking downward) and were intended to maintain consistent posture throughout all surface conditions. Head and torso inclination angles were not substantially different between conditions (supplementary figure 1).

The obstacles used were 10cm lengths cut from roughly triangular wood stock (locally sold as “cove molding”). The cross section of this stock is roughly a right triangle that resulted in ~13mm high obstacles when attached to the floor by the larger “hypotenuse” face with the 90° angle edge facing upwards. These obstacles were affixed with a density of 10.8/m² (1/ft²) to the experimental surfaces (18.26mm thick plywood sheets) such that each floor surface had 64 obstacles affixed in the same random configuration (random placement created via custom MATLAB code). The experimental floor surfaces were attached to the floor of the laboratory in the same repeatable positions via a combination of locating pins, alignment rails, hold down pins, and high-strength neodymium magnets that pulled the plywood floor surface sections tightly against the steel-panel raised flooring system that comprised the laboratory floor.

Floor surface conditions have previously been masked using goggles with the lower portion blacked out (Rhea et al., 2007; Graci et al., 2010; Pijnappels et al., 2001), but this method blocks all vision of the floor surface and lower limbs rather than just the obstacles. As this reduction in visual exproprioceptive information (relation of body segments to the environment) has been shown to increase MTC and MTC variability and this information is used on-line to “fine-tune” gait during obstacle avoidance (Rhea et al., 2007; Graci et al., 2010), an alternative method of obstacle masking was developed and employed. Noting that low lighting conditions have previously been shown to not significantly alter many gait parameters (Thies et al., 2005) and are representative of challenging, real-world gait conditions, laboratory lighting conditions were manipulated to minimize visibility of the hidden obstacles (low-contrast black obstacles on black surface) while retaining visibility of the rest of the laboratory, subject, and visible obstacles (high-contrast white obstacles on black surface). This was accomplished by only illuminating the laboratory with two lengths of rope lights on the floor along the walkway edges - similar to a walkway in a darkened movie theater. However, these rope lights were mounted just below the height of the walkway surface such that the obstacles and walkway surface were shaded (<1 lux) while the rest of the room was more illuminated (~2 lux). This lighting configuration resulted in a mild disability glare, a reduction in visual performance caused by veiling luminance on the retina (van Rijn et al., 2005), such that all subjects reported that the high-contrast white-on-black obstacles were easily visible and the low-contrast black-on-black hidden obstacles were difficult or impossible to see under the experimental lighting conditions.

2.3. Data processing

All data were collected and labelled using Vicon Workstation, then processed using Visual3D (C-Motion, Inc., Germantown, MD, USA) and custom MATLAB code (The MathWorks, Natick, MA, USA). Motion capture data were low-pass filtered using a zero-lag 4th order Butterworth filter at 10Hz for shoe marker data and 6Hz for segment marker data. These frequencies were determined from prior work and spectral analysis of pilot data that showed the higher velocities and accelerations of the shoe marker to require a higher cut-off frequency to avoid overfitting. Joint centers were determined functionally (Schwartz et al., 2005) and ankle, knee, and hip flexion-extension angles calculated using a recently-described shanks-only marker set (Schulz Kimmel, 2010). Foot segment angle was defined as the angle between a vector parallel to the floor in the direction of progression and the vector from each ankle joint center to the midpoint of the two toe tip markers (i.e. toe-down is negative and toe-up is positive).

The shoe data were processed as per previously-described methods (Schulz et al., 2010). In summary, a sphere-fitting algorithm was first applied to the MicroScribe-digitized data to calculate marker centroid positions that were used to define local coordinate systems for the toe and heel shoe segments (Figure 2). The motion capture data of these shoe maker centroids were then used to translate and rotate the positions of the digitized points on the shoe sole segments into the global coordinate system for every frame of every trial.

The floor surfaces were fit to the traced grids of digitized points on the floor using 3rd order polynomial surface sections- one for each plywood section (Figure 4a and b). No filtering was applied to the motion capture data of markers on the floor digitizing wand because the polynomial floor fit attenuated noise in the marker data and filtering these data prior to fitting can exacerbate errors. The shoe-floor clearance for these methods during 24 validation trials of empty shoes placed along the walkway was −0.35±0.89mm.

The obstacle positions were digitized using a custom three-marker “saddle” placed on each obstacle that captured five equidistant points along the upper edge of each obstacle. These obstacle points were overlaid on the interpolated floor surface for the visible and hidden obstacles conditions. The minimum toe and heel clearances were then calculated as the time series of the minimum distance between all digitized points on the toe and heel shoe segments and the interpolated floor surface (floor or, if present, obstacle) beneath each point for every frame of data. Note that minimum heel clearance was only used to determine ground contacts and define MTC events. The foot was defined to be in contact with the ground when the minimum speed of any digitized point on the shoe (toe or heel segment) was below 0.1 m/s.

MTC events were defined to occur at a point in the swing phase where the following three criteria were met: 1) The minimum toe clearance was at a local minima (value is less than that for preceding or following two frames), 2) Toe segment centroid speed (mean speed of the four toe markers) was within the upper quartile for that step, and 3) The minimum toe clearance was lower than the minimum heel clearance. Note that these MTC values are the minimum (by gait cycle) of the minimum (by all of the digitized points on the toe segment) toe clearance (i.e., the minimum of a time history of minimums). If these criteria were met by more than one point per gait cycle (more common on surfaces with obstacles), then the point with the smaller MTC value was used.

2.4. Statistical analysis

Values for all valid swing phases (all data exist from foot-off to initial contact) for each combination of the three speeds and three surfaces were compiled as eight mean values for actual gait speed, number of MTC events possible, number of actual MTC events, MTC; and foot, ankle, knee, and hip angle at MTC for each subject. The mean of the right and left swing-leg values were analyzed and reported. Repeated-measures linear mixed models were used to simultaneously test the effects of floor surface (no obstacles, visible obstacles, or hidden obstacles) and instructed gait speed (slow, preferred, or fast) on these eight dependent variables. Uncorrected p-values were reported but all thresholds of significance were corrected as per Bonferroni. Main effects were considered significant at p<0.0007 (0.05/8 dependent variables tested×3 speeds×3 surfaces). If main effects were determined to be significant, post-hoc multiple comparisons were conducted and considered significant at p<0.017 (0.05/3 speeds or surfaces). The frequency of occurrence of MTC events was calculated from these data by dividing the number of MTC events by the number of valid swing phases. The distribution of this calculated variable was highly skewed (skewness = −2.11, Shapiro-Wilks p<0.001), so the Kruskall-Wallis one-way analysis of variance by ranks was used to independently test for the effects of instructed speed and surface on the frequency of occurrence of MTC events. No gender or (speed*surface) interaction effects reached significance, so these factors were not included in the analyses presented here. SAS (SAS Institute Inc., Carey, NC, USA) was used for all statistical analyses.

3. Results

3.1. Effects of instructed gait speed

Instructed gait speed (slow, preferred, or fast) had significant effects on every variable measured except the percentage of valid swing phases that exhibited MTC events (Table 1). Fewer valid swing phases and fewer MTC events were detected with increasing instructed gait speed (Table 1, p<0.0001). Actual gait speed and MTC values significantly increased with instructed gait speed (Table 1, p<0.0001). All post-hoc multiple comparison effects of instructed gait speed on actual gait speed and MTC were significant (p≤0.001) except the difference in MTC between slow and preferred instructed gait speeds. Knee and hip flexion at MTC significantly increased with instructed gait speed (Table 1, p<0.0001) while foot segment angle significantly decreased (shoe sole closer to vertical, p<0.0001). Ankle dorsiflexion angle at MTC was also significantly affected by gait speed (p=0.0006), but post-hoc multiple comparisons indicated that dorsiflexion angles at slow (5.3±3.5°) and fast (5.8±2.9°) instructed speeds were not significantly different while dorsiflexion angles were significantly reduced at preferred speeds (4.3±2.8°, p=0.005 for the difference between slow and preferred speeds and p=0.0002 for the difference between preferred and fast speeds).

Table 1.

Mean (SD) of all dependent variables tested using repeated-measures linear mixed models (PROC MIXED in SAS) by floor surface and instructed gait speed.

Dependent Variable	No Obstacles Floor Surface			Visible Obstacles Floor Surface			Hidden Obstacles Floor Surface
	Slow Speed	Preferred Speed	Fast Speed	Slow Speed	Preferred Speed	Fast Speed	Slow Speed	Preferred Speed	Fast Speed
Actual gait speed (% Leg Length/s)*	1.02 (0.23)	1.5 (0.26)	2.56 (0.49)	1.02 (0.28)	1.44 (0.23)	2.41 (0.42)	1.06 (0.24)	1.47 (0.23)	2.31 (0.39)
Number of valid swing phases *	24.6 (4.7)	19.4 (3.3)	13.4 (3.5)	23.4 (7.2)	18.2 (5.3)	12.6 (3.6)	24.4 (8.4)	18.4 (4.4)	13.1 (3.5)
Number of MTC events * †	23.9 (5.0)	19.0 (3.0)	13.0 (3.7)	18.4 (6.1)	15.4 (4.7)	11.2 (2.8)	16.8 (6.2)	14.0 (4.9)	10.8 (3.7)
Percent of swing phases with MTC events †	97.2 %	98.6 %	97.3 %	81.2 %	87.3 %	89.8 %	74.0 %	79.7 %	85.1 %
MTC to flooring surface (mm)* †	8.5 (5.0)	10.2 (4.5)	14.6 (6.0)	18.5 (5.1)	22.2 (5.5)	25.9 (9.2)	23.5 (5.1)	26.4 (5.8)	30.4 (8.5)
Foot segment angle at MTC (deg)*	−39.2 (7.2)	−41.8 (7.2)	−47.5 (5.5)	−39.7 (6.2)	−41.9 (5.7)	−45.5 (7.6)	−39.0 (7.5)	−44.1 (6.8)	−46.3 (6.6)
Ankle dorsiflexion at MTC (deg)* †	3.7 (3.0)	2.4 (2.5)	4.9 (3.1)	6.0 (3.1)	4.7 (2.5)	5.9 (2.8)	6.2 (4.1)	5.7 (2.6)	6.6 (2.6)
Knee flexion at MTC (deg)* †	48.7 (8.8)	52.1 (8.6)	60.0 (6.3)	54.8 (9.1)	57.7 (6.3)	63.3 (7.4)	55.8 (10.0)	61.1 (8.8)	65.5 (7.7)
Hip flexion at MTC (deg)* †	41.4 (9.9)	44.5 (10.3)	47.5 (10.5)	45.0 (10.4)	48.0 (12.1)	51.5 (11.4)	45.2 (9.6)	47.2 (10.3)	51.3 (11.3)

Note: No foot, gender, or interaction effects were significant. Please refer to the text for effects of post-hoc multiple comparisons.

^*Indicates significant main effect of instructed gait speed (p<0.0006).

^†Indicates significant main effect of floor surface (p<0.000).

3.2. Effects of flooring surface

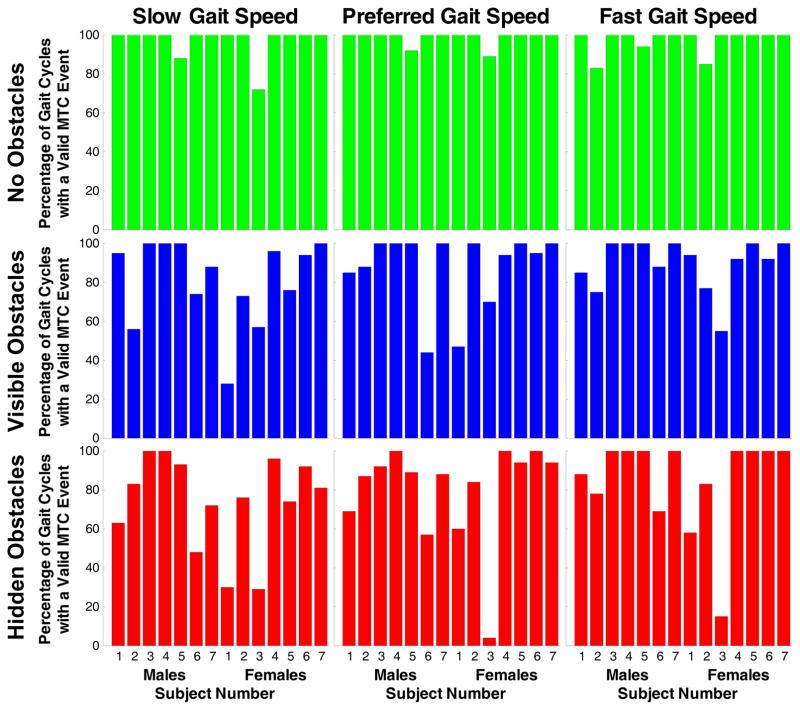
Fewer MTC events were detected for surfaces with obstacles (Table 1, p≤0.0001 for main effect of flooring surface and post-hoc multiple comparisons between no obstacles and both hidden and visible obstacles). When the number of detected events was normalized to the number of valid swing phases, the percentage of swing phases exhibiting MTC events decreased only with increasing flooring surface challenge (Table 1, p<0.0001 by Kruskall-Wallis) and was unaffected by instructed gait speed. However, these effects were not consistent across all subjects (Figure 5).

Figure 5.

Bar plots of percentage of valid gait cycles with an MTC event for each subject. Data are plotted by instructed gait speed (slow = left column row, preferred = middle column, fast = right column) and by flooring surface condition (no obstacles = top row, visible obstacles = middle row, hidden obstacles = bottom row).

MTC on the visible obstacles surface was 2× greater and MTC on the hidden obstacles surface was 2.5× greater than MTC on the no obstacles surface with little change in variability (Table 1 and Figure 4). Multiple comparisons indicated that MTC on all surfaces were significantly different from each other (p≤0.0003), but the difference between MTC on the no obstacles and visible obstacles surfaces (11.1mm) was more than double that between MTC on visible and hidden obstacles surfaces (4.6mm).

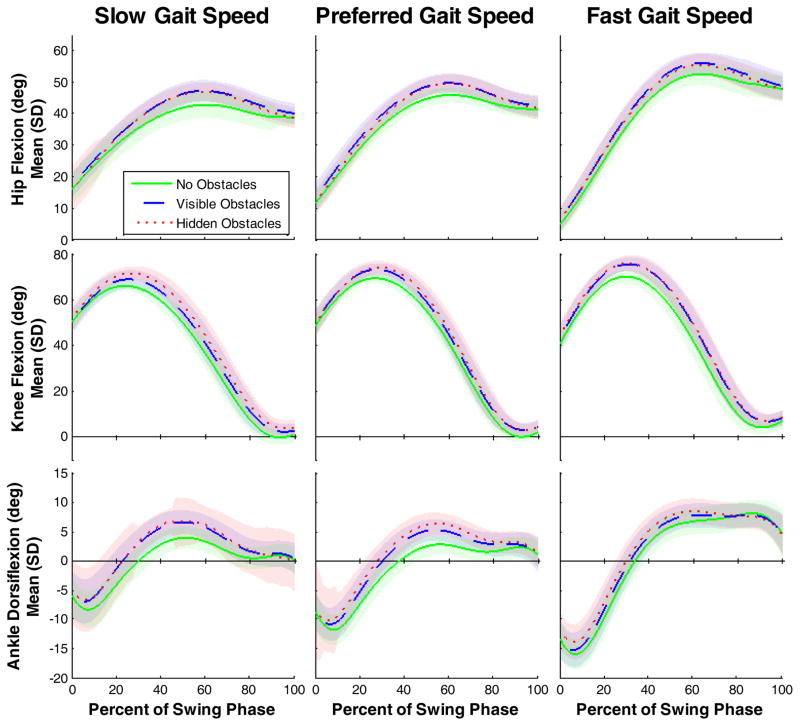
Ankle dorsiflexion and knee and hip flexion angles at MTC all significantly increased (p<0.0001) with flooring surfaces challenge. Multiple comparisons indicated that these joint angles were only significantly increased by the presence of obstacles (Table 1 and Figure 5, p<0.0001)- the differences between visible and hidden obstacle surfaces were not significant. Foot segment angles were not affected by flooring surface.

4. Discussion

Prior MTC results using the same experimental shoes and methods for different subjects on a different flooring surface for gait at preferred speed (10.3±3.2mm for 10 gait passes (Schulz et al., 2010)) were similar to results reported here (10.2±4.5mm for 4 gait passes). Overground MTC significantly increased with gait speed for all surfaces (p<0.0001, +4.0mm/(m/s) for no obstacles surface). This finding is reasonable in that it indicates an adaptation to reduce trip risk during more hazardous gait conditions, but it contradicts the only other significant previous findings for MTC changes due to gait speed (−4.3mm/(m/s), p<0.01)(Miller et al., 2009). This discrepancy was most likely due to differences in methodology (treadmill gait using single virtual toe marker vs. overground gait using hundreds of virtual toe markers) and task (concurrent dynamic visual acuity task vs. no concurrent task).

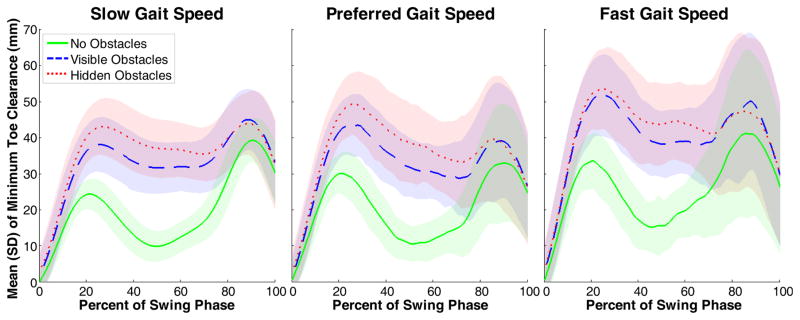
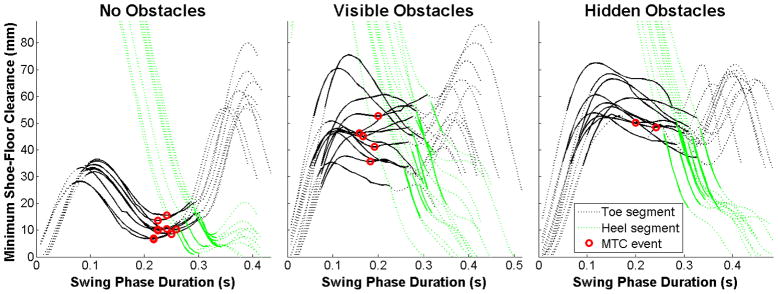
Fewer valid swing phases were detected for faster instructed gait speeds due to the longer steps taken resulting in fewer steps within the capture volume. This speed effect was passed on to the number of MTC events detected, but an effect of floor surface was also detected. Normalizing the number of MTC events to the number of valid swing phases effectively removed the speed effect and left only the effect of flooring surface. This reduction in MTC event occurrence resulted from changes in the minimum toe and heel clearances when traversing surfaces with obstacles. These adaptations to surface conditions caused the local minima in the minimum toe clearance near mid-swing, if present, to be higher, flattened, and less distinct (Figures 6 and 8). Occasionally, these adaptations caused the point of minimum foot-floor clearance to transition from the toe to heel segments when the minimum heel clearance dropped below the minimum toe clearance prior to the occurrence of a local minima (i.e. MTC) in the minimum toe clearance (Figure 6).

Figure 6.

Ensemble means (±1SD envelope) of minimum distances from toe to floor surface across the swing phase of gait plotted by instructed gait speed (slow = left, preferred = middle, fast = right) and flooring surface condition.

Figure 8.

Traces of minimum distances from toe (blue) and heel (green) shoe segments to floor surface across the swing phase of gait on surfaces with no obstacles (left), visible obstacles (center), and hidden obstacles (right) for all viable gait cycles of the left foot of a single subject walking at preferred speed. Note that at the local minimum in minimum heel clearance just prior to ground contact, the swing foot is no longer moving near its maximum speed and the walker’s center of mass is no longer in front of the base of support if the swing foot motion is arrested. Thus, if the heel contacts the ground at this point it merely “skips” or skids on the ground without substantially interrupting the gait pattern. This subject (Female #3) exhibited the strongest reduction in MTC event frequency on more challenging surfaces and is the best example of these adaptations to more challenging surface conditions. Solid lines indicate the trace that is closest to the floor surface (including obstacles if present) during the upper quartile of toe centroid speed. Minimum toe clearance (MTC) events circled in red. Y-axis range limited to better display region of interest; peaks in truncated minimum heel clearance traces reach approximately 160mm around 0.1s into swing phase.

Despite the significant and substantial effects of instructed gait speed on all parameters measured, alterations in floor surface resulted in significant effects on minimum toe clearances and joint kinematics that were independent of gait speed. To adapt to the visible obstacles condition, subjects adopted more conservative swing foot trajectories by utilizing 1.9° (~9%) additional ankle dorsiflexion, 5.0° (~7%) additional knee flexion, and 3.7° (~10%) additional hip flexion to double MTC (from 11.1 to 22.2mm) without changing the angle of the shoe sole in relation to the ground. Further compensations for the hidden obstacle condition included 0.7° (~3%) additional ankle dorsiflexion, 2.3° (~3%) additional knee flexion, and 0.2° (~0.6%) less hip flexion and increased MTC by 4.6mm (from 22.2 to 26.8mm). These results not only reinforce earlier findings that subtle changes in joint kinematics can result in substantial changes in endpoint trajectories (i.e. minimum toe clearance) (Winter, 1992; Moosabhoy et al., 2006), but also demonstrate when and how these changes are modulated by gait speed and perceived threat of flooring surface. It is noteworthy that the subjects were informed of the presence of the obstacles, even if they could not be seen, as the ~11mm mean MTC recorded on the no obstacles surface was insufficient to completely clear any 13mm obstacles if encountered. None of the subjects reported here stumbled or tripped on any trial, but it is not known if or how frequently this small overlap would have resulted in a stumble or trip if encountered under naïve conditions. While mean and median MTC have been shown to be unaffected by age (Mills et al., 2008; Begg et al., 2007), the effects of age and physical and cognitive impairment on MTC adaptations to challenging flooring surfaces and concurrent tasks should be explored, as they may help to explain the high rates of trip-related falls in these populations (Blake et al., 1988).

Figure 7.

Ensemble means (±1SD envelope) of hip flexion (top row), knee flexion (middle row), and ankle dorsiflexion (bottom row) angles across the swing phase of gait plotted by instructed gait speed (slow = left, preferred = middle, fast = right) and flooring surface condition.