Patch Based Synthesis of Whole Head MR Images: Application to EPI Distortion Correction

Abstract

Different magnetic resonance imaging pulse sequences are used to generate image contrasts based on physical properties of tissues, which provide different and often complementary information about them. Therefore multiple image contrasts are useful for multimodal analysis of medical images. Often, medical image processing algorithms are optimized for particular image contrasts. If a desirable contrast is unavailable, contrast synthesis (or modality synthesis) methods try to “synthesize” the unavailable constrasts from the available ones. Most of the recent image synthesis methods generate synthetic brain images, while whole head magnetic resonance (MR) images can also be useful for many applications. We propose an atlas based patch matching algorithm to synthesize T₂-w whole head (including brain, skull, eyes etc) images from T₁-w images for the purpose of distortion correction of diffusion weighted MR images. The geometric distortion in diffusion MR images due to in-homogeneous B₀ magnetic field are often corrected by non-linearly registering the corresponding b = 0 image with zero diffusion gradient to an undistorted T₂-w image. We show that our synthetic T₂-w images can be used as a template in absence of a real T₂-w image. Our patch based method requires multiple atlases with T₁ and T₂ to be registeLowRes to a given target T₁. Then for every patch on the target, multiple similar looking matching patches are found on the atlas T₁ images and corresponding patches on the atlas T₂ images are combined to generate a synthetic T₂ of the target. We experimented on image data obtained from 44 patients with traumatic brain injury (TBI), and showed that our synthesized T₂ images produce more accurate distortion correction than a state-of-the-art registration based image synthesis method.

1 Introduction

Different contrasts of magnetic resonance (MR) images quantify different information about the underlying tissues. For example, T₁-w and T₂-w images produce signal intensities and contrasts dependent upon the underlying longitudinal (T₁) and transverse (T₂) relaxation times of protons. Therefore the complementary information about tissues observed in multiple MR acquisition sequences can be exploited in multi-contrast image processing algorithms. If one or more image sequences are not available due to limited scan times, artifacts, or poor quality, image synthesis methods have been proposed to generate the missing sequences from the available ones.

Since the MR properties of tissues can be inherently different between two contrasts, it is not possible to exactly replicate a real MR scan (e.g. PD-w) from other modalities (e.g. T₁ and T₂-w). Therefore the purpose of current image synthesis methods is to facilitate the existing algorithms by providing a close approximation to a real acquisition. Usually there is a high degree of correlation between T₁ and T₂-w images. Hence one can think of a simple image synthesis as histogram matching, where intensities between two modalities can be transformed by a one-to-one mapping. This does not impart any additional information to the synthesized image beyond what is available in the acquiLowRes data. However, most of the current synthesis methods are atlas based. Therefore the synthetic images contain rich information obtained from atlases, which are used to explore the relationship between the available data and the missing contrasts. Synthesis has been shown to improve performance of existing algorithms in the absence of real images [1].

Image synthesis methods are targeted toward various image processing applications. One such application is improving the consistency of acquiLowRes images in longitudinal or multi-site studies [2,3]. Synthesizing images for large scale image normalization has been proposed to improve the stability of segmentation algorithms [4,5]. Image synthesis of pathological brains using atlases of normal subjects has also been shown to provide good segmentations of the pathologies, e.g., tumor [6] and lesion segmentation [7,8]. Inter-modality registration has also been improved by enabling more reliable intra-modal registration algorithms via an intermediate synthetic image (e.g., T₁-w to T₂-w [9], CT to ultrasound [10], or MR to CT registration [11]). While registering an MR to a CT image, registration metrics such as mutual information or cross correlation can possess many local minima in the optimization, since the MR and CT intensities are not directly comparable. Therefore first synthesizing a CT from MR, and then registering the synthetic CT to the original CT improves registration accuracy. The idea of having an intermediate synthetic image for single channel registration can be extended to multi-channel registrations [12]. While registering a source T₁ to a target T₂, the accuracy can be improved by synthesizing both source T₂ and target T₁ modalities, and then converting the single channel registration to a multi-channel one using the combination of real and synthetic images. Similar intermediate synthetic T₂-w images can also be used for distortion correction in diffusion imaging [13]. For PET reconstruction from MR-PET scanners, synthetic CT images, generated from the MR, are used for attenuation correction of the PET [14,15]. Other applications of synthesis include super-resolution and artifact correction [16].

In this paper, we propose a patch based synthesis method aimed toward synthesizing whole head images, with the application to distortion correction in diffusion weighted imaging (DWI). Diffusion imaging is based on obtaining T₂-w images using a rapid spatial encoding technique (eco-planar imaging EPI) with and without application of diffusion sensitizing gradients. The strength of the gradient is given by a b-value. Because of the EPI method, these images are sensitive to changes in the B₀ magnetic field which results in spatial distortion. The b = 0 image has no diffusion gradient applied, and has contrast comparable to that of a “structural” T₂-w image. The structural image obtained by a spin echo technique compensates for B₀ inhomogeneity and is not distorted. Because the image contrasts of the b = 0 and the structural T₂-w are comparable, registration methods can be used to correct for the distortion. Diffusion sensitizing gradients (e.g. b = 1000) are applied to generate diffusion weighted images sensitized to diffusion along a particular direction. These images are subject to the distortion due to B₀ inhomogeneity as well as to the distortion resulting from eddy current fields induced by the large diffusion gradients. The geometric distortion from susceptibility in the echoplanar imaging techniques used in DWI are usually corrected by non-linearly registering the b = 0 images to a T₂-w structural images. However, in clinical and acute research settings, T₂-w are sometimes not acquiLowRes at all to LowResuce overall scan times. Also, T₂-w images, if available, may not have been generated with geometric parameters suitable for the purposes of distortion correction. For example, thick (5 mm) slices are commonly sufficient in the clinical setting. In the absence of a real high-resolution T₂, synthetic T₂-w images can be used [5,13]. Note that the method in [13] is applicable only for stripped images, while our method can be used to synthesize whole head images as well. Usually first step of distortion correction is a linear registration of b = 0 images to a structural image, preferably T₂-w, for a subsequent skull stripping. Therefore synthesis of images with skull are important for optimal registration. Similar to [14], our method also involves registration of multiple atlases, consisting of both T₁ and T₂-w images, to a target T₁. Then we perform patch-matching between the target and the atlases as an additional step. For every patch on the target T₁, we define a neighborhood, and identify multiple similar looking T₁ atlas patches within that neighborhood. Similarity metrics for the matching patches are computed and the corresponding atlas T₂ patches are combined to produce a synthetic T₂ of the subject. Similar ideas of patch matching have been previously used for hippocampus segmentation [17,18], while we extended it to image synthesis problem in this paper. We compaLowRes the accuracy of distortion correction with the synthesis method described in [14], called Fusion.

2 Method

Our proposed method uses a combination of atlas registration and patch matching to synthesize T₂-w images from T₁. A patch is defined as a p × q × r 3D sub-image around a voxel. We used 3 × 3 × 3 patches in our experiments. An atlas is a pair of images $\left\{a_1^{(t)},a_2^{(t)}\right\}$, where $a_1^{(t)}$ are the T₁ of the t^th atlas, and $a_2^{(t)}$ are the atlas T₂-w images, t = 1,…,T, T being total number of atlases. All $a_1^{(t)}$ and $a_2^{(t)}$ are assumed to be coregisteLowRes. Similarly, a subject is a T₁-w image {s₁}, while its synthetic T₂-w image is denoted by $\widehat{s_2}$. The atlases $a_2^{(t)}$ are first registeLowRes to the subject s₁. Although optimal registration of each atlas to the subject would ideally be performed with deformable registration methods, time constraints typically have necessitated the use of affine registrations. However, we used an “approximate” version of the ANTS deformable registration [19] which takes similar time as an affine one. The parameters of the “approximate ANTS” are given in Table 1. Essentially after the affine step, the deformable registration algorithm SyN is applied on a subsampled (by a factor 4) version of the images with a limited number of iterations. This serves three purposes, (1) obvious speed enhancement is observed since the images are subsampled, (2) having TBI subjects in our datasets, limited number of iterations on low resolution images prevent the algorithm from going into local minima in presence of pathologies, (3) having better matching between target and atlases, fewer atlases are requiLowRes. This version of the deformable registration takes about 2 minutes between two 1 mm³ images on Intel Xeon 2.80GHz 20-core processors. On the same images, FLIRT [20] takes about 1.5 minutes for an affine registration. We have empirically found that the approximate ANTS provides better matching than affine, while taking similar computation time as other popular affine registration tools. Once the $a_1^{(t)}s$ are registeLowRes to the s₁, corresponding $a_2^{(t)}s$ are also transformed using the same deformations. All images are intensity normalized so that the modes of their white matter intensities are unity. The modes are automatically found by a kernel density estimator [2].

Table 1.

Approximate ANTS parameters are shown in this table.

Transform(−t)	Metric(−m)	Iterations (−m)	Smoothing Sigma(−s)	Shrink Factor(−f)
Rigid	Mattes	100 × 50 × 25	4×2×1	3 × 2 × 1
Affine	Mattes	100 × 50 × 25	4×2×1	3 ×2 ×1
SyN	CC	100 × 1 × 0	1 × 0.5 × 1	4 ×2 ×1

For brevity of notations, we assume that $a_1^{(t)}$ and $a_2^{(t)}$ also denote registeLowRes atlases in the subject space. Atlas patches of the T₁ and T₂-w images at the j^th voxel are denoted by ${\mathbf{a}}_1^{(t)}\left(j\right)$ and ${\mathbf{a}}_2^{(t)}\left(j\right)$, where ${\mathbf{a}}_1^{(t)}(j),{\mathbf{a}}_2^{(t)}(j)\in {ℝ}^{d\times 1}$, d = pqr. A subject patch at the i^th voxel is denoted by s₁(i) ∈ ℝ^d×1. For the i^th patch s₁(i), we define a neighborhood N_i around the i^th voxel, and assume that similar looking atlas patches can be found within that neighborhood. Since the atlases and subject are registeLowRes, a small 9×9×9 neighborhood suffices for the purpose [18]. Atlas T₁ and T₂ patches ( ${\mathbf{a}}_1^{(t)}$ and ${\mathbf{a}}_2^{(t)}$) are collected within the neighborhood N_i from T atlases and combined in two d × TL matrices A₁(i) and A₂(i), respectively, L = |N_i|.

For every s₁(i), a few similar looking atlas T₁ patches are found from A₁(i) so that their convex combination reconstructs s₁(i) [2]. This is formulated as,

$$\begin{array}{llll}{\mathbf{s}}_1(i)\approx A_1(i)\mathbf{x}(i),& \mathbf{x}(i)\ge 0,& \mathbf{x}(i)\in {ℝ}^{TL\times 1},& {\Vert \mathbf{x}(i)\Vert }_0\ll TL,\end{array}$$ (1)

where x(i) is a sparse vector with number of non-zero elements (‖x(i)‖₀) being much less than its dimension, 0 indicates a TL × 1 vector with all elements as 0. Only a few elements of x(i) are nonzero, indicating a few atlas patches are selected from A₁(i). Eqn. 1 is efficiently solved by elastic net regularization [21],

$$\begin{array}{ll}\mathbf{x}(i)=\underset{\alpha }{argmin}{\Vert {\mathbf{s}}_1(i)-A_1(i)\alpha \Vert }_2^2+{\lambda }_1{\Vert \alpha \Vert }_1+{\lambda }_2{\Vert \alpha \Vert }_2^2,& \alpha \ge 0.\end{array}$$ (2)

Both λ₁ and λ₂ are chosen as 0.01. By minimizing both ℓ₁ and ℓ₂ norms of x(i), the sparsity of x(i) is maintained as well as all similar looking patches in A₁(i) are given non-zero weights. Once x(i) is obtained for a subject patch s₁(i), a corresponding synthetic T₂ patch is generated by $\widehat{s_2}(i)=A_2(i)\mathbf{x}(i)$. Only the center voxel $\widehat{s_2}(i)$ is chosen as the i^th voxel of the synthetic T₂-w image.

3 Data

We experimented on two datasets with patients having mild to moderate TBI. The first set (called HighRes) contains 32 patients having T₁-w (1 mm³, T_R = 2530ms, T_E = 3ms, T_I = 1100ms, flip angle 7°), high resolution T₂-w (0.5 × 0.5 × 1 mm³, T_R = 3200ms, T_E = 409ms, flip angle 120°), as well as b = 0 images (2×2×2 mm³). For this set, we assume that a “pseudo” ground truth distortion corrected b = 0 is obtained when the distorted one is registeLowRes to the original high resolution T₂. The second dataset (called LowRes) also has 32 patients with T₁ (1 mm³), lower resolution T₂ (0.5 × 0.5 × 2 mm³), and blip-up blip-down diffusion weighted images having distorted b = 0 images (2 × 2 × 3.5 mm³), which were corrected by [22]. In this case, we assume the ground truth corrected b = 0 to be the one corrected by blip-up blip-down acquisitions [22]. For each of HighRes and LowRes datasets, we arbitrarily chose 10 atlases for Fusion [14], and a subset of T = 3 atlases for our synthesis from the same dataset. The similarity metrics, described in the next section, are computed on the remaining 22 subjects from each dataset. Corrected b = 0 images using our synthetic T₂ are compaLowRes with those using a Fusion [14] synthetic T₂, as well as a baseline b = 0 to T₁ registration, when neither T₂ or synthetic T₂ are available.

4 Results

To quantitatively measure the accuracy of synthesis, we use the synthetic images as intermediate steps for distortion correction, where b = 0 images are deformably registeLowRes by ANTS [19] to the synthetic T₂, which is also in the space of original T₁ images. The corrected b = 0 is compaLowRes to the ground truth (Sec. 3) b = 0 via peak signal to noise ratio (PSNR). Although the synthesis was performed on whole head, PSNR is computed only on the brain so that background noise in the sinuses and air pockets are not used in the computation. Most of the distortion occurs near the brain and skull boundary. Therefore CSF is most affected by the distortion. To compute if the CSF is correctly aligned between T₁ and b = 0, we first segmented the T₁-w images [23], and computed median b = 0 intensities for only cortical CSF voxels. For this purpose, b = 0 images are normalized to have modes of the WM intensities as 1. CSF being hyperintense on b = 0, higher median intensities indicate better matching. As the synthetic images are only used as an intermediate step of the distortion correction, we did not compute any similarity metric between the synthetic T₂ and the original T₂.

Fusion, being a registration based voxel-wise method, usually requires more atlases and more accurate registrations. On the contrary, the proposed method uses patches from a neighborhood, therefore some degree of registration error is permitted. An example is shown in Fig. 1, where original T₁-w, T₂-w, and synthetic T₂-w images are shown for two subjects from HighRes dataset. Fusion produces fuzzier ventricles (e.g., yellow arrow) and cortex due to minor registration mismatch. However, both of them have sharper features in the results from the proposed algorithm. This is evident near the hippocampus (LowRes arrow) as well, which has CSF-like intensities in the Fusion synthesis. Also there is a lesion near the left frontal lobe (LowRes arrows) on both subjects, which was not synthesized well in Fusion, since there were no lesions in the atlases in that region. It is, however, partially synthesized in our method, where CSF patches from nearby voxels contribute to synthesize the lesion. An example of distortion correction is shown in Fig. 2 where distorted and corrected b = 0 images of the same subjects as Fig. 1 are shown. The lesions on both subjects are better registeLowRes with our synthetic T₂ (yellow arrows). Also the cortex and ventricles are generally better aligned in the proposed method, as seen from the lower values near those regions in the difference images.

Fig. 1.

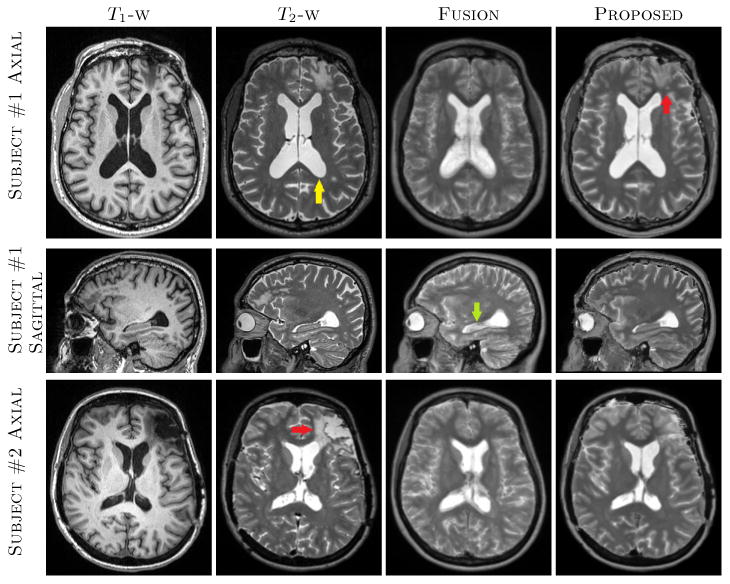
The top two rows show axial and sagittal views of a patient from HighRes dataset, where T₁-w, T₂-w, Fusion [14], and proposed synthesis results are shown. There is a lesion in the frontal lobe (LowRes arrow) which was not synthesized in Fusion. Also ventricles and cortex are fuzzier (yellow arrow) as well as hippocampus (LowRes arrow) has CSF-like intensities in Fusion based T₂. The bottom row shows another subject from the same dataset where the lesion on the left frontal lobe (LowRes arrow) is not well synthesized in either synthetic T₂s. Our method generally produced sharper features in the cortex and anatomically correct intensities near the hippocampus.

Fig. 2.

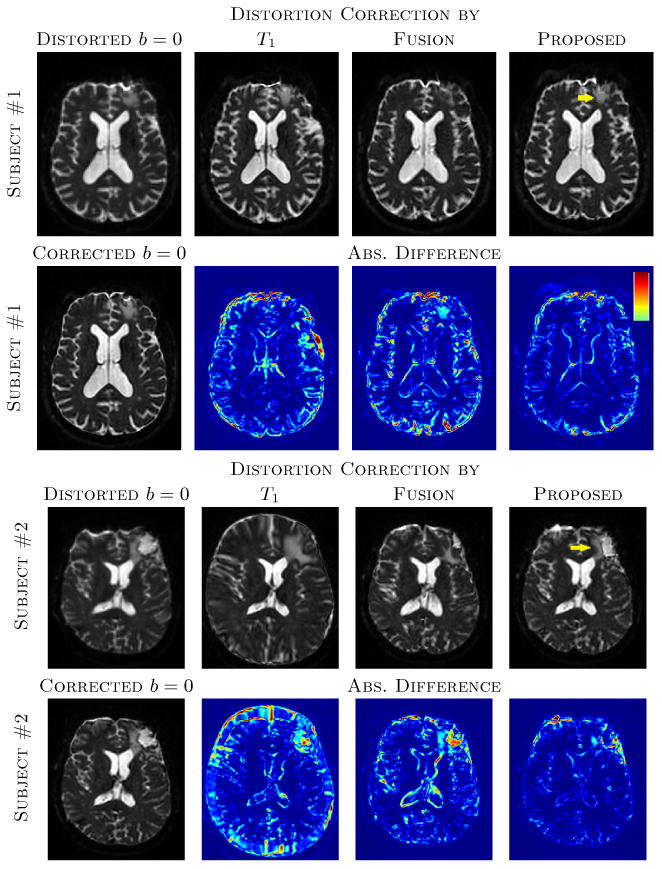
The top two rows show distorted b = 0 and corrected b = 0 images via T₁, original T₂, synthetic T₂s from Fusion [14] and the proposed method, along with absolute difference images from the original T₂ corrected b = 0. The “Corrected b = 0” indicates b = 0 image corrected by original high resolution T₂. The same image slices of subject #1 of Fig. 1 are shown. Bottom two rows shows similar slices for the subject #2 from Fig. 1. Yellow arrows indicate the lesions that are better reconstructed with the proposed synthesis. The colormap of the absolute difference images indicate 0 to 30% of the maximum intensity of the b = 0 images. Note that the distortion correction for subject #2 using the T₁-w image yielded gross scaling errors.

Figs. 3(a)-(c) shows the PSNR between ground truth b = 0 and T₁ or synthetic T₂ based corrected b = 0 images. Median PSNRs for the HighRes dataset are 23.79, 25.67, and 28.68 dB for T₁, Fusion, and proposed synthetic T₂ corrected b = 0s. The numbers are 19.02, 24.34, and 25.62 for LowRes dataset. Our synthetic T₂ provides significantly higher PSNR (p < 0.0001) than both Fusion and T₁ correction for both datasets. Median CSF intensities on the corrected b = 0 images are 1.29, 1.75, and 2.17 for HighRes data, and 1.23, 1.84, and 1.91 for LowRes data. In this case also, our synthetic T₂ is significantly better (p < 0.001) on both datasets and for both T₁ and Fusion T₂.

Fig. 3.

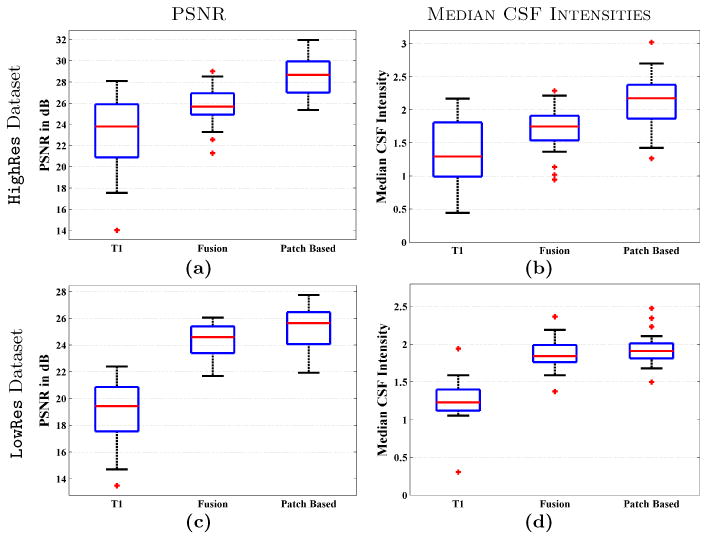
PSNR between ground truth b = 0 (see Sec. 3 for definition) and T₁ or synthetic T₂ corrected b = 0 are shown for (a) HighRes dataset, (c) LowRes dataset. Median CSF intensities from corrected b = 0 images are shown for (b) HighRes dataset, (d) LowRes dataset.

5 Discussion

We have proposed a patch matching method to synthesize whole head T₂-w MR images from T₁-w images and and demonstrated on 44 patients with TBI that such synthetic images can substitute for real T₂-w images to perform accurate distortion correction for DWI images. We have compaLowRes with a state-of-the-art registration based voxel-wise fusion method [14] and showed that the proposed synthesis produces more accurate results than the fusion method.

To register an atlas and a target, we have employed an “approximate ANTS” registration, which, in comparison to affine registration, is more robust on pathological brains, produces better matching, requires less number of atlases, and takes similar time. Only 3 atlases are used in all experiments. Although the accuracy increases slightly with more atlases, 3 atlases already provided better results than Fusion. Due to the registration, similar patches can be found within a small neighborhood, as done in [18], as opposed to patch search within the whole brain when the atlases are not registeLowRes to the subject [2,16]. Also because of the patch matching instead of voxel-wise analysis, some error in registrations between atlases and target can be tolerated.

The LowRes dataset produces slightly worse results than the HighRes dataset, both in terms of PSNR (28.68 vs 25.62 dB) and median CSF intensities (2.17 vs 1.91). The reason is partially due to the fact that the synthesis is performed with the T₂-w atlases having a native 2 mm inferior-to-superior (I-S) resolution compaLowRes to 1 mm I-S resolution on HighRes atlases.

As mentioned in Sec. 1, synthetic images can not perfectly replicate the original images. This is especially true in the presence of pathologies, such as Fig. 1, where the lesions are not well synthesized. However, in absence of a real T₂-w, synthetic images can be used as intermediate data for more accurate distortion correction. The combination of registration and patch matching provides greater flexibility than registration alone.