Suppressing Membrane Height Fluctuations Leads to a Membrane–Mediated Interaction Among Proteins

Abstract

Membrane-induced interactions can play a significant role in the spatial distribution of membrane-bound proteins. We develop a model that combines a continuum description of lipid bilayers with a discrete particle model of proteins to probe the emerging structure of the combined membrane-protein system. Our model takes into account the membrane’s elastic behavior, the steric repulsion between proteins, and the quenching of membrane shape fluctuations due to the presence of the proteins. We employ coupled Langevin equations to describe the dynamics of the system. We show that coupling to the membrane induces an attractive interaction among proteins, which may contribute to the clustering of proteins in biological membranes. We investigate the lateral protein diffusion and find that it is reduced due to transient fluctuations in membrane shape.

I. INTRODUCTION

Cellular membranes, such as the plasma membrane, play a critical role for the stability of a cell and the multitude of biochemical processes that occur therein. Their principal structure is a bilayer of phospholipid and sterol molecules that hosts a large variety of integral and peripheral membrane proteins. The spatial organization of these membranes has been a topic of great interest because it determines which proteins are in sufficiently close proximity to interact with one another, which in turn is a prerequisite for cellular processes such as signaling.

The structure of a membrane is determined by the interactions between proteins and the lipid bilayer. While the specifics of this interaction depend on molecular-level details of the involved molecules, the principal effects of a broad range of proteins on membrane organization can be understood by considering how binding to a membrane affects its shape and shape fluctuations. For example, earlier experimental work shows protein crowding can lead to membrane bending [1, 2]. It has also been shown both in experiment [3–6] and theory [7–10] that scaffolding proteins, which induce and/or sense local membrane curvature, can cause large-scale membrane deformations with concomitant lateral organization of the proteins. Similarly, actin filaments that exert a force on the membrane due to polymerization can cause membrane deformations, which in turn induce a compressive force on the filaments that can lead to their bundling [20]. The dominant physical features of these illustrative examples are due to a coupling between protein degrees of freedom and the local membrane shape in the vicinity of the proteins.

The nature of this coupling depends on the type of protein under consideration. Important earlier work has focused on modeling transmembrane proteins as disk-shaped inclusions in elastic membranes, which impose geometric boundary conditions at the protein–membrane interface or that locally alter the membrane’s elastic constants. These couplings result in an effective interaction between proteins that scales as 1/r⁴ where r is the distance between two such inclusions [21–23]. Others have considered adhesion sites that pin a membrane to a surface [24], and found a pair-wise interaction that depends logarithmically on the separation between adhesion sites. Typically these are many-body interactiones, i.e., they cannot be decomposed into a sum of pairwise contributions [25].

In this work we consider proteins that impose local constraints on the position of the membrane. This scenario arises, for example, when the membrane is coupled to other components of the cellular environment. For example, actin filaments that are anchored in the cytosolic actin network and whose tips are in contact with the membrane effectively suppress shape fluctuations of the membrane. In related work, Speck and coworkers considered the effect of membrane pinning to a solid substrate, and showed that the quenching of membrane fluctuations gives rise to an attractive interaction between adhesion sites [26, 27].

Spatial organization of the combined membrane/protein system can occur over length scales of hundreds of nanometers to several micrometers. This makes modeling such processes at atomistic resolution unfeasible, and therefore many coarse-grained approaches have been suggested in the literature, see for example Refs. 8–19. Our approach combines a continuum description of the membrane and a discrete particle model for the proteins. The former is based on the classic description of membrane elasticity due to Canham and Helfrich [28, 29], which we simulate using the Fourier Space Brownian Dynamics method developed by Brown and coworkers [30–32]. Proteins are treated as spherical objects with non-specific repulsive interactions. The coupling between both subsystems is a simple harmonic potential that centers the membrane position to a constant value at the position of the proteins. The model is described in detail in the following section. We simulate the dynamics of our model, which is governed by a set of coupled Langevin equations. In Section III we present our findings for membrane fluctuation spectra, protein-protein correlation functions, and protein diffusion constants. We show that our model predicts the emergence of a fluctuation-induced, membrane-mediated attraction between proteins that influences the spatial organization of the membrane–protein system.

II. THE MODEL

We construct our model by considering the effects of membrane elasticity, protein–protein interactions, and membrane-protein coupling. The total energy E of the system for a given configuration is the sum of these three contributions.

A. Membrane Elasticity

We use the elastic model developed by Canham and Helfrich to capture the effect of membrane shape deformations [28, 29, 33]. This model views the membrane as a two-dimensional surface whose energetics are determined by its elastic material constants. We limit ourselves to membrane shapes that can be parametrized by a single scalar function h(r) that represents the height deviation of the membrane from a flat reference plane. The membrane is located at the positions (r, h(r)), where r = (x, y) ∈ [0, L]², and L is the side length of the simulation box. If membrane deformations are small one can expand the Canham-Helfrich energy to quadratic order in h and its derivatives, and obtains

$$E_{\mathrm{m}}[h(\mathit{r})]={\int }_{L^2}\mathrm{d}\mathit{r}\left[\frac{\sigma }{2}{(\mathbf{\nabla }h(\mathit{r}))}^2+\frac{\kappa }{2}{({\mathbf{\nabla }}^{2}h(\mathit{r}))}^2\right]$$ (1)

as the energy functional of a free membrane. The parameters describing the elastic properties are the surface tension σ and the bending rigidity κ. We assume that the membrane is symmetric so that there is no spontaneous curvature. We have omitted the contribution of Gaussian curvature to the energy, which is a constant offset if the membrane topology is closed and fixed, as is the case for our model.

Equation (1) can be simplified by expanding h(r) in a plane wave basis, h(r) = L⁻²Σ_kh̃_ke^ik·r. The coefficients h̃_k = ∫∫_L² dr h(r)e^−ik·r are the Fourier transform of h(r), and the wavevector is of the form k = (p 2π/L, q 2π/L) with p, q ∈ ℤ. With these definitions we can express the membrane energy as

$$E_{\mathrm{m}}\left(\left\{{\stackrel{\sim }{h}}_{\mathit{k}}\right\}\right)=\frac{1}{L^2}\sum _{\mathit{k}}\left(\frac{\sigma }{2}{k}^2+\frac{\kappa }{2}{k}^4\right){\mid {\stackrel{\sim }{h}}_{\mathit{k}}\mid }^2.$$ (2)

The advantage of this representation is that different Fourier modes are uncoupled, which allows us to derive several useful results analytically.

In our simulations we treat the real and imaginary parts of the Fourier coefficients h̃_k as the dynamical variables that evolve in time. To do that we have to consider two modifications to this equation [34]. First, we must limit ourselves to a finite basis set, which we do by considering only wavevectors k with |p| ≤ P and |q| ≤ Q. The numbers P and Q determine the magnitude of the largest wavevector (or the smallest lengthscale) that our model can resolve. Second, due to the symmetry relationship ${\stackrel{\sim }{h}}_{\mathit{k}}={\stackrel{\sim }{h}}_{-\mathit{k}}^{\ast }$ only half of those Fourier coefficients are independent. Ignoring the k = (0, 0) mode, we choose the Fourier coefficients with wavevectors {(p2π/L, q2π/L) : (1 ≤ p ≤ P, q = 0)or(−P ≤ p ≤ P, 1 ≤ q ≤ Q)} as independent degrees of freedom, and refer to this set as k > 0. Expressed in terms of these modes, the membrane energy (2) becomes

$$E_{\mathrm{m}}\left(\left\{{\stackrel{\sim }{h}}_{\mathit{k}}\right\}\right)=\frac{1}{L^2}\sum _{\mathit{k}>0}(\sigma k^2+\kappa k^4){\mid {\stackrel{\sim }{h}}_{\mathit{k}}\mid }^2.$$ (3)

Unlike some previous work [30, 31, 35, 36], our approach does allow the imaginary part of the Fourier coefficients at the Nyquist modes to be non-zero, thereby preserving translational invariance even for those high-wavevector modes [34].

B. Protein-Protein Interactions

The interaction among multiple proteins is a complicated function that in principle depends on the type, molecular structure, orientation, and conformation of the biomolecules. Here we neglect nearly all this detail in order to construct a simple model that captures the basic physical feature that is independent of the specific nature of the proteins, which is the steric repulsion that prevents multiple proteins from occupying the same region in space. We consider a collection of N proteins, each of which is completely defined by its position r_i in the xy-plane (1 ≤ i ≤ N). The potential energy E_pp of their interaction is pairwise additive,

$$E_{\text{pp}}(\{{\mathit{r}}_i\})=\sum _{1\le i<j\le N}V(\mid {\mathit{r}}_i-{\mathit{r}}_j\mid ),$$ (4)

and we choose the purely repulsive Weeks-Chandler-Andersen (WCA) potential [37]

$$V(r)=\{\begin{array}{ll}4{\epsilon }_{\mathrm{p}}\left[{(\frac{{\sigma }_{\mathrm{p}}}{r})}^{12}-{\left(\frac{{\sigma }_{\mathrm{p}}}{r}\right)}^6\right]+{\epsilon }_{\mathrm{p}}\hfill & \text{if}r<2^{1/6}{\sigma }_{\mathrm{p}}\hfill \\ 0\hfill & \text{if}r\ge 2^{1/6}{\sigma }_{\mathrm{p}}\hfill \end{array}$$ (5)

as the pair interaction. The parameters ε_p and σ_p denote the energy and length scales of this interaction, the latter being approximately the diameter of the proteins.

C. Membrane-Protein Interactions

There are multiple ways in which proteins can interact with cellular membranes. Here we consider a potential energy term that couples the protein position and the height field of the membrane:

$$E_{\text{mp}}\left(\{{\stackrel{\sim }{h}}_{\mathit{k}}\},\{{\mathit{r}}_i\}\right)=\frac{\epsilon }{2}\sum _i{(h({\mathit{r}}_i)-l)}^2.$$ (6)

The physical meaning of this interaction is that the position of the membrane above or below the proteins has to be close to the constant value l relative to the z = 0 reference plane. The parameter ε described the strength of this constraint. If it is large, then the proteins effectively pin the membrane to the specific height l.

It is instructive to rewrite this interaction in terms of a potential energy surface in which the proteins diffuse: defining

$$\varphi (\mathit{r})=\frac{\epsilon }{2}{(h(\mathit{r})-l)}^2,$$ (7)

equation (6) becomes

$$E_{\text{mp}}(\{{\mathit{r}}_i\})=\sum _i\varphi ({\mathit{r}}_i),$$ (8)

where the potential ϕ depends on the membrane configuration and is therefore time-dependent.

D. Dynamics

Our goal is to study both dynamical and static equilibrium properties of the model. To this end we introduce coupled Langevin equations for both membrane and protein degrees of freedom that describe the time evolution of the system, and that generate an ensemble of configurations according to the canonical Boltzmann distribution.

The Langevin equation for the membrane Fourier modes h̃_k is based on the Fourier Space Brownian Dynamics model [30–32]:

$$\frac{\mathrm{d}{\stackrel{\sim }{h}}_{\mathit{k}}}{\mathrm{d}t}=-{\stackrel{\sim }{\mathrm{\Lambda }}}_{\mathit{k}}{\left\{\frac{\delta E}{\delta h(\mathit{r})}\right\}}_{\mathit{k}}+{\stackrel{\sim }{\xi }}_{\mathit{k}}(t)$$ (9)

$$=-{\stackrel{\sim }{\mathrm{\Lambda }}}_{\mathit{k}}\left[(\sigma k^2+\kappa k^4){\stackrel{\sim }{h}}_{\mathit{k}}+\epsilon \sum _i{\mathrm{e}}^{-i\mathit{k}·{\mathit{r}}_i}(h({\mathit{r}}_i)-l)\right]+{\stackrel{\sim }{\xi }}_{\mathit{k}}(t).$$ (10)

Here, E = E_m + E_pp + E_mp is the total energy of the system, δE/δh(r) is its functional derivative with respect to a membrane height change at position r, and {.}_k denotes the Fourier transform. The mobility factor Λ̃_k is the Oseen tensor [32], Λ̃

$${\stackrel{\sim }{\mathrm{\Lambda }}}_{\mathit{k}}=\frac{1}{4\eta k},$$ (11)

which accounts for the hydrodynamic behavior of the aqueous solvent with viscosity η. The last part of (10) is a stochastic noise term. Its real and imaginary parts have mean zero and satisfy the Fluctuation-Dissipation relationships [34]

$$\langle Re\left({\stackrel{\sim }{\xi }}_{\mathit{k}}(t)\right)Re\left({\stackrel{\sim }{\xi }}_{{\mathit{k}}^{\prime }}(t^{\prime })\right)\rangle ={\stackrel{\sim }{\mathrm{\Lambda }}}_{\mathit{k}}{k}_{\mathrm{B}}T{L}^2\delta (t-t^{\prime })({\delta }_{\mathit{k},{\mathit{k}}^{\prime }}+{\delta }_{-\mathit{k},{\mathit{k}}^{\prime }})$$ (12)

$$\langle Im\left({\stackrel{\sim }{\xi }}_{\mathit{k}}(t)\right)Im\left({\stackrel{\sim }{\xi }}_{{\mathit{k}}^{\prime }}(t^{\prime })\right)\rangle ={\stackrel{\sim }{\mathrm{\Lambda }}}_{\mathit{k}}{k}_{\mathrm{B}}T{L}^2\delta (t-t^{\prime })({\delta }_{\mathit{k},{\mathit{k}}^{\prime }}-{\delta }_{-\mathit{k},{\mathit{k}}^{\prime }})$$ (13)

$$\langle Re\left({\stackrel{\sim }{\xi }}_{\mathit{k}}(t)\right)Im\left({\stackrel{\sim }{\xi }}_{{\mathit{k}}^{\prime }}(t^{\prime })\right)\rangle =0$$ (14)

which guarantee convergence to the correct equilibrium distribution.

The Langevin equation for the position of the i-th protein in the (x, y) plane, r_i, is

$$\frac{\mathrm{d}{\mathit{r}}_i}{\mathrm{d}t}=-{\gamma }_{\mathrm{p}}{\mathbf{\nabla }}_{i}E+{\mathit{\zeta }}_i$$ (15)

$$=-{\gamma }_{\mathrm{p}}\left[\epsilon \sum _i(h({\mathit{r}}_i)-l)\mathbf{\nabla }h({\mathit{r}}_i)+{\mathbf{\nabla }}_i{E}_{\text{pp}}(\{{\mathit{r}}_i\})\right]+{\mathit{\zeta }}_i(t)$$ (16)

where ∇_i is the gradient with respect to r_i, γ_p is the mobility of the protein, and the stochastic term ζ_i(t) has mean zero and variance

$$\langle {\mathit{\zeta }}_{i,\alpha }(t){\mathit{\zeta }}_{j,\beta }(t^{\prime })\rangle =2{\gamma }_{\mathrm{p}}{k}_{\mathrm{B}}T{\delta }_{ij}{\delta }_{\alpha \beta }\delta (t-t^{\prime })$$ (17)

where the subscripts α and β represent the Cartesian components of the two-dimensional vector ζ_i. As before, this choice of the stochastic term ensures proper equilibration of the system. For a free protein that does not interact with the membrane (i.e., ε = 0), equation (15) generates a two-dimensional Brownian motion with diffusion coefficient D₀ = k_BTγ_p.

E. Simulation Scheme

Solving the coupled Langevin equations for membrane and protein degrees of freedom allows us to study the equilibrium behavior of our model system. We use the Euler-Maruyama method to solve these equations numerically for small time increments Δt. In this discrete representations, equations (10) and (16) become

$${\stackrel{\sim }{h}}_{\mathit{k}}(t+\mathrm{\Delta }t)={\stackrel{\sim }{h}}_{\mathit{k}}(t)-\mathrm{\Delta }t{\stackrel{\sim }{\mathrm{\Lambda }}}_{\mathit{k}}\left[(\sigma k^2+\kappa k^4){\stackrel{\sim }{h}}_{\mathit{k}}(t)+{\epsilon }_{\mathrm{p}}\sum _i(h({\mathit{r}}_i)-l){\mathrm{e}}^{-i\mathit{k}·{\mathit{r}}_i}\right]+\sqrt{2k_{\mathrm{B}}T{L}^2\mathrm{\Delta }t{\stackrel{\sim }{\mathrm{\Lambda }}}_{\mathit{k}}}r$$ (18)

$${\mathit{r}}_i(t+\mathrm{\Delta }t)={\mathit{r}}_i(t)-\mathrm{\Delta }t{\gamma }_{\mathrm{p}}\left[{\epsilon }_{\mathrm{p}}\sum _i(h({\mathit{r}}_i)-l)\mathbf{\nabla }h({\mathit{r}}_i)+{\mathbf{\nabla }}_i{E}_{\text{pp}}(\{{\mathit{r}}_i\})\right]+\sqrt{2k_{\mathrm{B}}T\mathrm{\Delta }t{\gamma }_{\mathrm{p}}}r$$ (19)

where r stands for independent, normally distributed random numbers with zero mean and unit variance for both real and imaginary parts of the membrane Fourier modes h̃_k for k > 0 (equation (18)) and for each Cartesian component of the position r_i of each protein (equation (19)).

The choice of the timestep Δt is determined by the requirement that it must be smaller than all relevant dynamical processes in the system so that they can be resolved by the numerical integration. Several such processes exist in our model. The first is the dynamics of the membrane. In absence of any proteins, each membrane mode relaxes on the wavevector-dependent timescale [35]

$${\tau }_{\mathrm{m}}=\frac{1}{{\stackrel{\sim }{\mathrm{\Lambda }}}_{\mathit{k}}(\sigma k^2+\kappa k^4)}$$ (20)

which together with (11) implies that

$$\mathrm{\Delta }t\ll \frac{4\eta }{\sigma k_{max}+\kappa k_{max}^3}.$$ (21)

where $k_{max}=2\pi \sqrt{P^2+Q^2}/L$ is the largest wavevector in the system. Using a large number of wavevectors therefore necessitates a very small timestep if one wants to simulate the membrane dynamics accurately. The equilibrium properties, however, are independent of the choice of the mobility factor Λ̃_k, as long as the stochastic noise terms satisfy the Fluctuation-Dissipation relationships (12)–(14). For our equilibrium studies we choose

$${\stackrel{\sim }{\mathrm{\Lambda }}}_{\mathit{k}}=\frac{{\tau }^{-1}}{\sigma k^2+\kappa k^4}$$ (22)

which makes the membrane relaxation times (20) wavevector independent. The constant τ has dimensions of time and sets the timescale for membrane dynamics. Its value does not affect the equilibrium properties of the system, and we set it to one second for convenience. In simulations that aim to study dynamical properties, such as the diffusion of proteins discussed in Section III C, we use the physical expression (11) for the Oseen tensor.

The second constraint on Δt limits protein motions to distances less than their diameter per time-step, $\mathrm{\Delta }t\ll {\sigma }_{\mathrm{p}}^2/4D_0$. This condition ensures proper sampling of protein-protein interactions. Finally, we impose that the typical protein displacement in a single time-step is small compared to the shortest wavelength of the membrane, $\mathrm{\Delta }t\ll {\pi }^2/D_0{k}_{max}^2$.

F. Simulation Parameters

Our model has a considerable number of parameters. Here we limit ourselves to systems where both the membrane surface tension σ and the preferred membrane height l are chosen to be zero. The strength ε of the protein-membrane interaction is set to $100k_{\mathrm{B}}T/{\sigma }_{\mathrm{P}}^2$, where k_B is Boltzmann’s constant and T is the temperature. The energy scale ε_p of the protein–protein interactions is set equal to k_BT. The linear dimension L of the simulation box is 50 times the diameter σ_P of the proteins. When studying the equilibrium behavior of our model we use a grid of P = Q = 32 Fourier modes together with expression (22) for the mobility factor Λ̃_k. As discussed previously, studying the diffusive behavior of the proteins requires the use of (11) for the Oseen tensor, which leads to dramatically different relaxation timescales for membrane modes with different wavevector magnitudes. We therefore used a significantly reduced model system with (P,Q) = (1, 0) or (P,Q) = (1, 1) wavevectors for those simulations. The timestep Δt is set to ${10}^{-3}{\pi }^2/D_0{k}_{max}^2$ for simulations with N = 2 proteins, as well as for N = 100 proteins with bending rigidities βκ equal to 10 or 100 where β = 1/k_BT. Simulations with N = 100, βκ = 1 and N = 500, βκ ∈ {10, 100} needed a 5 times smaller timestep, while those with N = 500, βκ = 1 required another tenfold reduction in Δt to reach proper equilibrium behavior.

III. RESULTS

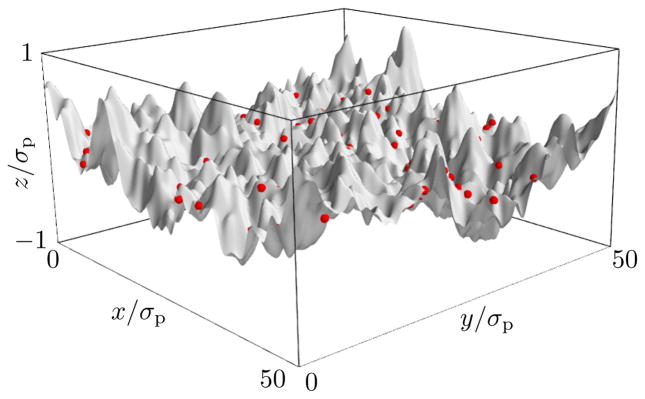
A typical snapshot of our simulations is shown in Figure 1. The membrane exhibits undulations that are driven by thermal fluctuations. Proteins diffuse in the (x, y)-plane, effectively pinning the membrane to the height l = 0 at their positions.

FIG. 1.

Snapshot of a simulation of the combined membrane/protein system. The gray surface shows the current membrane configuration; red dots illustrate protein positions. Simulation parameters are P = Q = 32, σ = 0, βκ = 10, $\epsilon =100k_{\mathrm{B}}T/{\sigma }_{\mathrm{p}}^2$, N = 100.

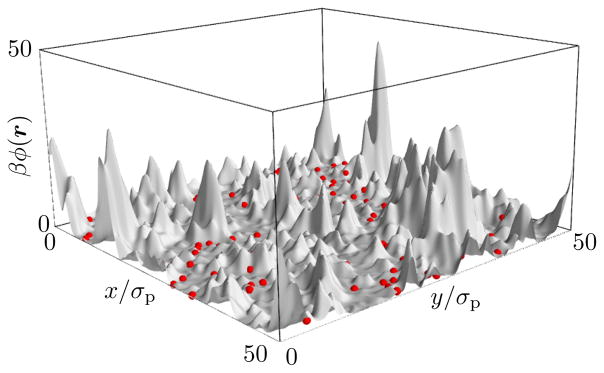
Figure 2 shows the effective potential energy surface ϕ(r) in which the proteins diffuse. In this representation it becomes apparent that there are regions of high potential that are effectively inaccessible to the proteins. These regions are caused by fluctuations that move the membrane away from the protein’s preferred height l. A protein entering such a region would require either a rare fluctuation to overcome this potential or waiting until the membrane has relaxed back to its ground state. This exclusion of proteins from parts of the membrane area leads to motion akin to diffusion in a dynamically crowded environment.

FIG. 2.

Same snapshot as in Fig. 1, but showing in gray the potential energy surface ϕ(r) instead of the membrane conformation. Proteins remain in the low-energy regions of this potential, whereas the membrane is free to fluctuate in protein-free regions.

We will study protein diffusion in detail in Section IIIC. First we will focus on the equilibrium properties of the membrane and protein subsystems. To this end we define the probability distribution of a microstate, uniquely specified by the protein positions {r_i} and Fourier components {h̃_k}, which is the Boltzmann distribution

$$P(\{{\mathit{r}}_i\},\{{\stackrel{\sim }{h}}_{\mathit{k}}\})=\frac{1}{Q}{\mathrm{e}}^{-\beta E(\{{\mathit{r}}_i\},\{{\stackrel{\sim }{h}}_{\mathit{k}}\})}$$ (23)

where

$$Q={\int }_{L^2}\mathrm{d}\{{\mathit{r}}_i\}{\int }_{ℂ}\mathrm{d}\{{\stackrel{\sim }{h}}_{\mathit{k}}\}{\mathrm{e}}^{-\beta E(\{{\mathit{r}}_i\},\{{\stackrel{\sim }{h}}_{\mathit{k}}\})}$$ (24)

is the partition function. Here the first integral is taken over all possible positions of each protein in the square [0, L]². The second integral is over all possible complex values for every Fourier coefficient h̃_k with k > 0.

A. Membrane Fluctuations

The interaction between protein and membrane degrees of freedom has a significant effect on the membrane fluctuation spectrum. In the absence of proteins (N = 0) or if the coupling strength ε is zero, the spectrum can be readily computed from the equipartition theorem to be

$${\langle {\mid {\stackrel{\sim }{h}}_{\mathit{k}}\mid }^2\rangle }_0=\frac{k_{\mathrm{B}}T{L}^2}{\sigma k^2+\kappa k^4},$$ (25)

If proteins at static positions ({r_i}) interact with the membrane, the variance of the Fourier modes changes to

$${\langle {\mid {\stackrel{\sim }{h}}_{\mathit{k}}\mid }^2\rangle }_{(\{{\mathit{r}}_i\})}=\frac{{\int }_{ℂ}\mathrm{d}\{{\stackrel{\sim }{h}}_{\mathit{k}}\}{\mid {\stackrel{\sim }{h}}_{\mathit{k}}\mid }^2{\mathrm{e}}^{-\beta [E_{\mathrm{m}}+E_{\text{mp}}]}}{{\int }_{ℂ}\mathrm{d}\{{\stackrel{\sim }{h}}_{\mathit{k}}\}{\mathrm{e}}^{-\beta [E_{\mathrm{m}}+E_{\text{mp}}]}}$$ (26)

Because the coupling term (6) is quadratic in the membrane height, this expression is the variance of a multivariate Gaussian probability distribution, which we compute numerically using matrix inversion (see Appendix A for details).

Finally, if the proteins are mobile, the variance of a membrane Fourier amplitude h̃_k is

$$\langle {\mid {\stackrel{\sim }{h}}_{\mathit{k}}\mid }^2\rangle ={\int }_{L^2}\mathrm{d}\{{\mathit{r}}_i\}{\int }_{ℂ}\mathrm{d}\{{\stackrel{\sim }{h}}_{\mathit{k}}\}{\mid {\stackrel{\sim }{h}}_{\mathit{k}}\mid }^{2}P(\{{\mathit{r}}_i\},\{{\stackrel{\sim }{h}}_{\mathit{k}}\}),$$ (27)

and we compute this quantity as the time-average of trajectories generated by the Langevin equations (18, 19).

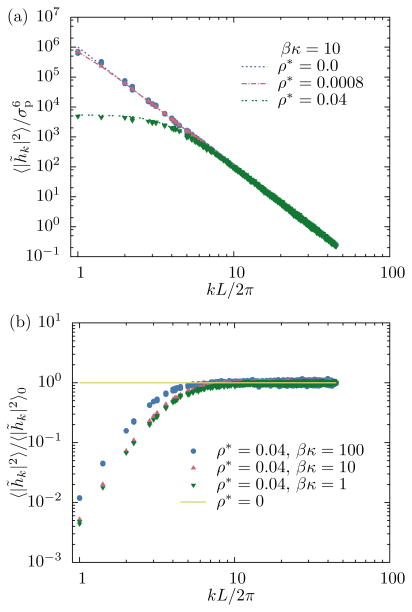
Results for calculated membrane fluctuation spectra are shown in Fig. 3. The top panel shows the effect of protein density, specified by the dimensionless quantity ${\rho }^{\ast }=N{\sigma }_{\mathrm{p}}^2/L^2$. As expected, both the numerical calculation (26) and the simulation result yield the analytical free membrane result (25) if no proteins are present (ρ^* = 0), which serves as a useful test to validate the respective computer codes. As the protein density increases, the variance of membrane Fourier modes with small wavevectors, corresponding to large length scales, is significantly suppressed, while modes with high wavevectors are not affected by the interaction with the proteins. Membrane spectra computed with static proteins at randomly chosen positions are indistinguishable from those obtained from simulations in which proteins were freely diffusing.

FIG. 3.

(a) Dependence of membrane fluctuations on protein density. If no proteins are present the spectra are given by the free membrane result (25). As the protein density increases, the variance of membrane modes with small wavevectors is significantly reduced. Dashed lines represent numerical solutions of (26); points were obtained from simulations. (b) Dependence of membrane fluctuations on bending rigidity. The reduction of membrane fluctuations (relative to the free membrane result) is largest for flexible membranes that have low bending rigidity.

The bottom panel of Fig. 3 illustrates how bending rigidity affects membrane spectra at fixed protein density. The relative reduction in variance of Fourier amplitude at small wavevectors is largest for flexible membranes with low bending rigidities. A natural interpretation of this result is that membranes with high bending rigidities already have smaller fluctuations, and are therefore less affected by the additional pinning to a specific height imposed by the proteins.

B. Membrane-Induced Protein Interactions

From the proteins’ perspective the membrane acts like a time-dependent external potential ϕ(r, t). Because all proteins are embedded in the same membrane, its elastic behavior mediates an effective interaction among the proteins. To quantify this coupling, we compute the free energy for a configuration with proteins at positions r₁, . . . , r_N by performing a partial trace over membrane degrees of freedom:

$$F(\{{\mathit{r}}_i\})=-k_{\mathrm{B}}Tlog{\int }_{ℂ}\mathrm{d}\{{\stackrel{\sim }{h}}_{\mathit{k}}\}{\mathrm{e}}^{-\beta E(\{{\mathit{r}}_i\},\{{\stackrel{\sim }{h}}_{\mathit{k}}\})}$$ (28)

$$=E_{\text{pp}}(\{{\mathit{r}}_i\})+F_{\text{mm}}(\{{\mathit{r}}_i\})$$ (29)

where

$$F_{\text{mm}}(\{{\mathit{r}}_i\})=-k_{\mathrm{B}}Tlog{\int }_{ℂ}\mathrm{d}\{{\stackrel{\sim }{h}}_{\mathit{k}}\}{\mathrm{e}}^{-\beta (E_{\mathrm{m}}+E_{\text{mp}})}$$ (30)

is the membrane-mediated interaction between the proteins. It is in general a complicated function of the protein positions that is not pairwise additive. However, due to the Gaussian nature of the protein-membrane coupling it can be easily computed numerically (see Appendix B for details).

From our simulations we obtain the radial distribution function (RDF) [38]

$$g(\mathit{r})=\frac{L^2}{N^2}\sum _{i\ne j}\langle \delta (\mathit{r}-({\mathit{r}}_j-{\mathit{r}}_i))\rangle .$$ (31)

This function is a measure for density correlations between two points in space that are separated by the distance vector r.

If there are only two proteins in the system, then the RDF is related to the effective free energy of the protein subsystem as

$$g(\mathit{r})\propto {\mathrm{e}}^{-\beta F({\mathit{r}}_1,{\mathit{r}}_2)}$$ (32)

where r = r₂–r₁ is the separation of the proteins. Even though our model is not fully isotropic due to the square shape of the reference domain, we typically consider rotationally averaged quantities g(r) and F(r).

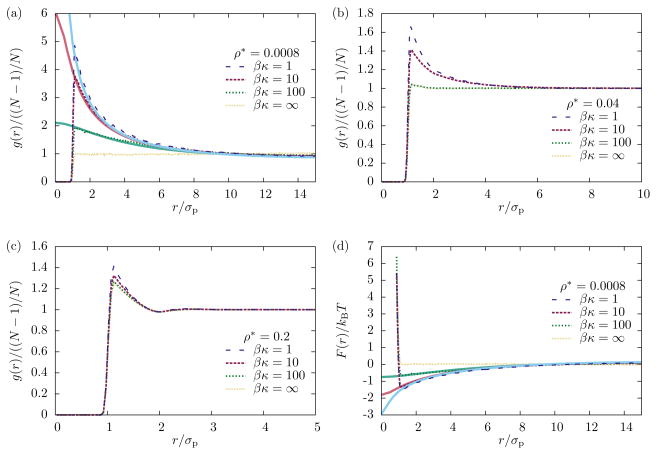
Protein density correlation functions obtained from simulations are shown in Fig. 4 for different values of membrane bending rigidities and protein densities. If the membrane is completely rigid (κ = ∞) proteins behave like a two-dimensional WCA fluid: the pair correlation function is equal to one at distances larger than the protein diameter if the density is low (Fig. 4a). Softening the membrane (i.e., reducing the value of κ) has a large effect on the RDF in this case: a significant peak forms right at the constact distance σ_p with a broad shoulder that extends to distances about five times the protein diameter (Fig. 4a). This emergence of protein density correlations is a consequence of their coupling to the membrane, which mediates an attractive interaction. The magnitude of this effect decreases with increasing protein density (Fig. 4b,c). In this case we observe a peak in g(r) even for rigid membranes, which is due to the steric repulsion between proteins and their resulting packing structure. Decreasing κ enhances this peak to a lesser extent than in the case of low protein density.

FIG. 4.

Effect of membrane rigidity on protein pair correlation functions at different densities. (a) At low densities (N = 2) the RDF is essentially flat outside the protein diameter if the membrane is rigid, and develops a significant peak as the bending rigidity is reduced. (b) At intermediate densities (N = 100) this effect is less pronounces. (c) At high densities (N = 500) there is a peak in the pair correlation function, but it is due to packing and nearly independent of the membrane bending rigidity. (d) Free energy of the protein–protein interaction, eq. (32), and membrane-mediated interaction, eq. (30). Dashed lines are obtained from simulations; solid lines in panels (a) and (d) are obtained numerically as described in Appendix B.

In the low-density limit the RDF is directly related to the free energy of the protein subsystem, eq. (32). In Fig. 4d we show the free energy surface F(r) as obtained from the simulations of N = 2 proteins, together with numerical calculations of the membrane-mediated interaction F_mm(r). We find that for physically relevant membrane bending energies (βκ ≈ 10) the membrane-mediated attraction contributes approximately 1.3 k_BT, or 3 kJ/mol, to the protein-protein interaction at contact.

C. Protein Diffusion

The diffusion constant D of proteins moving in the (x, y)-plane is a quantity of great interest [35, 39–43]. Due to the coupling between protein and membrane degrees of freedom this constant can differ from the bare diffusion constant D₀ that the Langevin equation (16) would generate if no such coupling existed, or if the membrane was infinitely rigid.

In this section we report simulation results that were obtained using a single protein. This allows us to isolate the effect of membrane fluctuations on the diffusion constant from that due to protein crowding. For the reasons stated in Section II F we chose an artificially small number of wavevectors, (P,Q) = (1, 0) or (P,Q) = (1, 1). In the former case we only study the protein motion along the x-axis (d = 1), while in the latter we consider both the x- and the y-direction (d = 2).

The diffusion constant can be obtained from the mean-squared displacement (MSD) at sufficiently long times through the relationship

$$D=\frac{\langle {(\mathrm{\Delta }\mathit{r}(\tau ))}^2\rangle }{2d\tau }$$ (33)

where the numerator is the variance of the protein displacement over a time period τ.

If there are no interactions, the discretized Langevin equation (19) generates a stochastic process that has the diffusion constant D₀ independent of the chosen values for the lag time τ or the timestep Δt. This is no longer the case if the diffusing protein interacts with the membrane, as illustrated in Fig. 5. First, we find that one must use a very small timestep to obtain MSDs that are independent of Δt, and that therefore correspond to the continuum limit Δt → 0. Second, even with a properly chosen timestep the apparent diffusion constant depends on the lag time if the latter is not sufficiently large. The likely cause for this behavior is the finite relaxation time of the membrane whose dynamics affects the motion of the proteins. This problem can be avoided by making τ larger than the timescale of all other dynamical processes in the system. This approach, however, has the disadvantage that for a fixed trajectory length one has fewer independent data points to estimate the MSD if τ is large. This leads to large uncertainties in the estimate of 〈(Δr(τ ))²〉, and therefore of D. To quantify the uncertainty in our estimate of the MSD we use the fact that the variance estimator for an underlying Gaussian process follows the chi-squared distribution, and compute the confidence interval

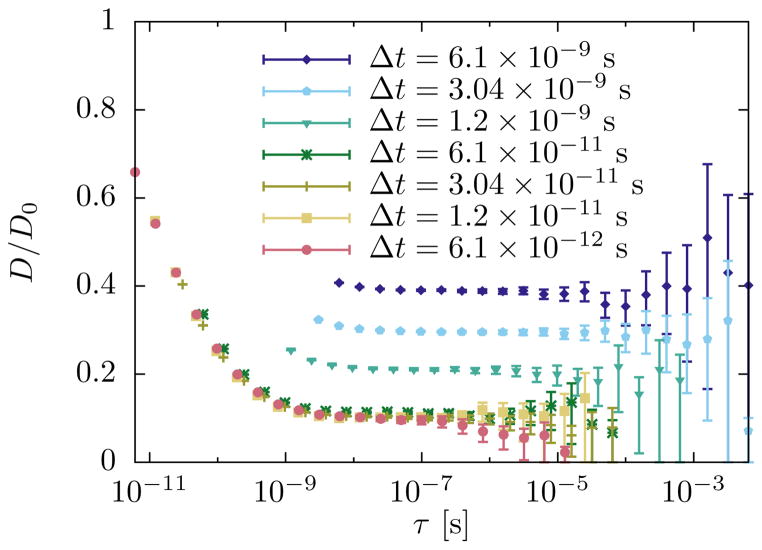
FIG. 5.

Determination of the diffusion constant from mean squared displacements. The timestep Δt must be chosen sufficiently small so that observed MSDs do not depend on its value. The lag time τ must be large enough so that the dynamics reaches the diffusive regime, indicated by a constant value of D as computed by (33). Uncertainties increase significantly with τ if the total length of the simulation data is fixed. Simulation parameters: L = 250 nm, P = 1, Q = 0, N = 1, D₀ = 5 × 10⁹ nm²/s, βκ = 10, σ = 0, η = 10⁻²⁹ Js/nm³, $\epsilon =100k_{\mathrm{B}}T/{\sigma }_{\mathrm{P}}^2$.

$$\left[\frac{(n-1)S^2}{{\chi }_{\alpha /2}^2},\frac{(n-1)S^2}{{\chi }_{1-\alpha /2}^2}\right].$$ (34)

Here S² is the sample variance, which is an unbiased estimate for the population variance 〈(Δr(τ ))²〉, n is the number of independent observations of displacements with lag time τ, and the parameter α is set to 0.05, which corresponds to a 95% confidence level. This interval is typically not symmetric around the estimated MSD.

Figure 5 illustrates how we calculate the diffusion constant for a typical choice of system parameters. First, we successively decrease the timestep Δt in our simulations until the observed MSD, and therefore the apparent diffusion constant (33), becomes independent of the timestep. We then identify the lag time τ at which the estimate for D is within the confidence intervals of all subsequent estimates using longer lag times. This estimate of the diffusion constant, together with its uncertainties, is then used in further analysis.

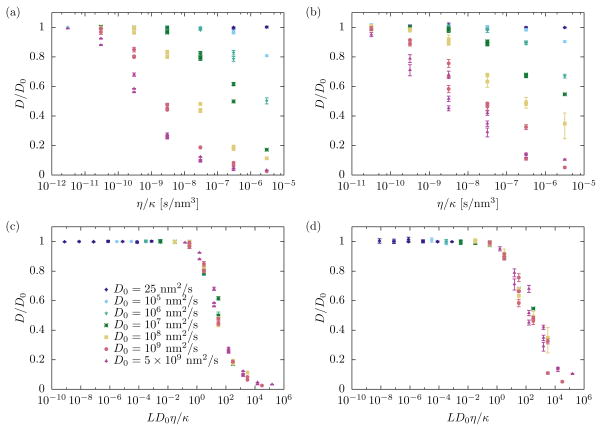
The ratio of the actual diffusion constant D and the bare diffusion constant D₀ in principle depends on all parameters in the model, in particular the solvent viscosity η, the membrane bending rigidity κ, and D₀ itself. This behavior can be seen in Figure 6, which shows results for D/D₀ obtained from simulations using P = 1,Q = 0 (a) and P = 1,Q = 1 (b) Fourier modes and a wide range of parameter values. We find that in general the relative diffusion constant decreases with increasing solvent viscosity, decreasing membrane rigidity, or increasing D₀. In no case did we observe an increase of the diffusion constant above the bare value D₀.

FIG. 6.

Renormalization of protein diffusion as a function of membrane bending rigidity κ and solvent viscosity η. The ratio of actual to bare diffusion constant, D/D₀, varies strongly with system parameters both in the one-dimensional case (P = 1,Q = 0, panel (a)) and the most basic two-dimensional case (P = 1,Q = 1, panel (b)). When plotted as a function of D₀η/κ the data points collapse onto single curve in both cases (panels (c) and (d), respectively).

The interaction between the proteins and the membrane couples the diffusive dynamics of the former to the relaxation dynamics of the latter. Protein diffusion throughout the system occurs on a time scale τ_diff ∝ L²/D₀. According to (21) the membrane relaxation time is τ_m ∝ ηL³/κ for the longest wavevector mode if the surface tension vanishes. Plotting the effective diffusion constant D/D₀ as a function of the ratio τ_m/τ_diff of these two timescales, we find that all data points collapse onto a single curve (Figures 6c,d). This fact illustrates that the competition between planar diffusion and membrane relaxation determines the actual diffusion constant of the proteins. For biologically realistic values of the parameters involved (D₀ = 10⁻¹³ m²/s, η = 10⁻³ Js/m³, κ = 10k_BT, T = 310 K) the ratio LD₀η/κ is approximately 6 × 10⁻⁴, at which D/D₀ ≈ 1. In this case the coupling between the membrane and the proteins therefore does not have a significant effect on the effective protein diffusion constant.

IV. DISCUSSION

Our model is based on a continuum description of a cellular membrane and a simple particle representation of peripheral proteins. Both components interact through a harmonic interaction that suppresses membrane height fluctuations at the protein locations. Our results show that this interaction gives rise to multiple observable changes in the behavior of both subsystems. First, membrane fluctuations over long length scales are depressed; the extent of which increases with protein density and decreasing membrane rigidity. Second, the coupling to the membrane induces an effective attraction between proteins. Third, the apparent diffusion constant of the proteins decreases if the bending rigidity is low. This effect, however, is likely negligible for typical biological membranes.

The emergence of a membrane-mediated interaction between proteins has been previously established for different types of couplings between the two subsystems. Early work in this field established an effective interaction that scales with 1/r⁴ for membrane inclusion [21–23]. The same dependence has been calculated for the interaction between rods absorbed to membranes [44, 45]. Theoretical studies of the distance-dependent free energy of membrane adhesion sites have different functional forms [24, 26, 27]. In all cases the interaction is induced by the thermal fluctuations of the membrane, and therefore entropic in origin.

We find that the induced attraction contributes on the order of 3 kJ/mol to the interaction energy between two proteins for biologically relevant values of the involved parameters. This contribution decreases at higher protein densities. In particular, in no case did we observe a condensation of proteins into a high-density droplet, as one observes in systems with sufficiently attractive pairwise interactions that exhibit a liquid-vapor transition.

In this work we focused on a specific coupling between the membrane and the proteins, namely a quadratic interaction the depends on the membrane height at the positions of the proteins. This model is appropriate for proteins that suppress membrane height fluctuations. There are other classes of proteins that couple differently to the membrane. For example, some membrane scaffolding proteins sense and induce local curvature upon membrane binding [46–48]. To study these systems our model can be modified by replacing the coupling to the membrane height h(r_i) in eq. (6) by one to the local mean curvature ∇²h(r_i)/2. Related models have been proposed in the literature [8, 40, 42, 43, 49, 50]. Higher resolution models that take into account the non-isotropic shape of specific proteins have shown that the combination of membrane-mediated and direct protein–protein interactions can give rise to orientationally ordered aggregates [10, 51–53]. Together, these studies highlight the variety and complexity of structures that can emerge from seemingly simple membrane–protein interactions.

Appendix A: Calculation of Membrane Fluctuation Spectra

In Section IIIA we derived equation (26) for the membrane fluctuation spectrum in the presence of N static proteins at positions r₁, . . . , r_N. This expression is the variance of a multivariate Gaussian probability distribution. Here we explain in detail how we computed this variance numerically.

We begin by enumerating the independent real-valued degrees of freedom [34]. We do so by choosing the following ordering of the real and imaginary parts of the membrane Fourier modes: Reh̃_1,0, Imh̃_1,0, . . ., Reh̃_P,0, Imh̃_P,0, Reh̃ _−P,1, Imh̃ _−P,1, . . ., Reh̃_P,1, Imh̃_P,1, . . . , Reh̃ _−P,Q, Imh̃ _−P,Q, . . ., Reh̃_P,Q, Imh̃_P,Q. The total number of real-valued degrees of freedom is M = 2P + 2Q + 4PQ. For notational convenience we relabel this sequence as d₁, . . . , d_M such that

$$Re{\stackrel{\sim }{h}}_{p,q}=d_{2(p+q(2P+1))}$$ (A1)

$$Im{\stackrel{\sim }{h}}_{p,q}=d_{2(p+q(2P+1)+1)}$$ (A2)

This allows us to rewrite the exponent in (26) as

$$-\beta [E_{\mathrm{m}}(\{{\mathit{r}}_i\})+E_{\text{mp}}(\{{\mathit{r}}_i\})]=-\frac{1}{2}{\mathit{d}}^{\mathbf{\top }}\mathit{Xd},$$ (A3)

where d is the M-dimensional column vector containing the variables d_i, d^⊤ is its transpose, and the coupling matrix X is of the form

$$\mathit{X}=\left[\begin{array}{ccc}{\mathit{C}}_{1,1}& \cdots & {\mathit{C}}_{1,M/2}\\ ⋮& \ddots & ⋮\\ {\mathit{C}}_{M/2,1}& \cdots & {\mathit{C}}_{M/2,M/2}\end{array}\right].$$ (A4)

Here C_n,m is a 2×2 submatrix that couples the real and imaginary part of a single Fourier mode h̃_k. Its components are

$${({\mathit{C}}_{n,m})}_{0,0}=\frac{2\beta }{L^2}(\sigma {\mathit{k}}_n^2+\kappa {\mathit{k}}_n^4){\delta }_{n,m}+\frac{4\epsilon \beta }{L^4}\sum _{i=1}^{N}cos({\mathit{k}}_n·{\mathit{r}}_i)cos({\mathit{k}}_m·{\mathit{r}}_i)$$ (A5)

$${({\mathit{C}}_{n,m})}_{1,0}=\frac{4\epsilon \beta }{L^4}\sum _{i=1}^{N}cos({\mathit{k}}_n·{\mathit{r}}_i)sin({\mathit{k}}_m·{\mathit{r}}_i)$$ (A6)

$${({\mathit{C}}_{n,m})}_{0,1}=-\frac{4\epsilon \beta }{L^4}\sum _{i=1}^{N}sin({\mathit{k}}_m·{\mathit{r}}_i)cos({\mathit{k}}_n·{\mathit{r}}_i)$$ (A7)

$${({\mathit{C}}_{n,m})}_{1,1}=\frac{2\beta }{L^2}(\sigma {\mathit{k}}_n^2+\kappa {\mathit{k}}_n^4){\delta }_{n,m}+\frac{4\epsilon \beta }{L^4}\sum _{i=1}^{N}sin({\mathit{k}}_n·{\mathit{r}}_i)sin({\mathit{k}}_m·{\mathit{r}}_i)$$ (A8)

The coefficients (p, q) of the wavevector k_n are p = (n – P –1) mod (2P +1)–P, q = (n–P –1)/(2P +1)⌋ +1.

With the exponent written in the form (A3) we can compute the covariances as elements of the inverse of X,

$$\langle d_j{d}_{j^{\prime }}\rangle ={[{\mathbf{X}}^{-1}]}_{j{j}^{\prime }},$$ (A9)

with 1 ≤ j, j′ ≤ M.

The variance of a single membrane mode can then be computed as the sum of the variances of its real and imaginary parts,

$$\langle {\mid {\stackrel{\sim }{h}}_{p,q}\mid }^2\rangle =\langle {(Re{\stackrel{\sim }{h}}_{pq})}^2\rangle +\langle {(Im{\stackrel{\sim }{h}}_{pq})}^2\rangle$$ (A10)

$$=\langle d_{2(p+q(2P+1))}^2\rangle +\langle d_{2(p+q(2P+1)+1)}^2\rangle .$$ (A11)

Appendix B: Calculation of Protein Density Correlation Functions

To calculate the membrane-mediated interaction F_mm for a static collection of proteins at positions ({r_i}) we proceed as in Appendix A and rewrite the Boltzmann factor in the form (A3). The integration in eq. (30) can then be performed analytically and yields

$$F_{\text{mm}}(\{{\mathit{r}}_i\})=\frac{1}{2}{k}_{\mathrm{B}}\mathit{T}logdet\mathit{X}.$$ (B1)

Here we have suppressed constants independent of the protein positions that cause an overall shift in the free energy. Instead, we normalize the free energy such that it is zero at the largest possible distance within our simulation box.

In the special case of only N = 2 proteins we can then directly calculate the pair correlation function from this energy using eq. (32).