ENDOR with band-selective shaped inversion pulses

Abstract

Electron Nuclear DOuble Resonance (ENDOR) is based on the measurement of nuclear transition frequencies through detection of changes in the polarization of electron transitions. In Davies ENDOR, the initial polarization is generated by a selective microwave inversion pulse. The rectangular inversion pulses typically used are characterized by a relatively low selectivity, with full inversion achieved only for a limited number of spin packets with small resonance offsets. With the introduction of pulse shaping to EPR, the rectangular inversion pulses can be replaced with shaped pulses with increased selectivity. Band-selective inversion pulses are characterized by almost rectangular inversion profiles, leading to full inversion for spin packets with resonance offsets within the pulse excitation bandwidth and leaving spin packets outside the excitation bandwidth largely unaffected. Here, we explore the consequences of using different band-selective amplitude-modulated pulses designed for NMR as the inversion pulse in ENDOR. We find an increased sensitivity for small hyperfine couplings compared to rectangular pulses of the same bandwidth. In echo-detected Davies-type ENDOR, finite Fourier series inversion pulses combine the advantages of increased absolute ENDOR sensitivity of short rectangular inversion pulses and increased sensitivity for small hyperfine couplings of long rectangular inversion pulses. The use of pulses with an almost rectangular frequency-domain profile also allows for increased control of the hyperfine contrast selectivity. At X-band, acquisition of echo transients as a function of radiofrequency and appropriate selection of integration windows during data processing allows efficient separation of contributions from weakly and strongly coupled nuclei in overlapping ENDOR spectra within a single experiment.

Graphical Abstract

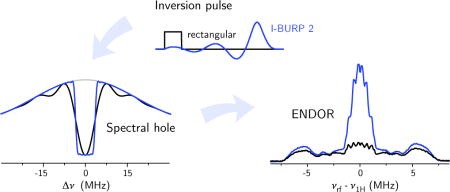
1. Introduction

Electron Nuclear DOuble Resonance (ENDOR) spectroscopy is widely used for the investigation of electron-nuclear hyperfine couplings in paramagnetic systems. ENDOR techniques are based on the detection of nuclear transition frequencies through changes in the polarization of EPR transitions. In Davies ENDOR [1], the initial polarization is created by a selective microwave π pulse (Figure 1), which inverts spin packets over a bandwidth defined by the length of the pulse, burning a hole into the EPR line. The shape of the hole is determined by the inversion profile of the pulse. A radiofrequency π pulse on resonance with a nuclear transition causes a polarization transfer leading to reduction of the intensity of the hole and creation of two side holes of the same shape shifted by the hyperfine coupling A with respect to the central hole. The changes in the hole pattern as a function of radiofrequency are measured with a free-induction decay (FID) or two-pulse echo detection sequence. Compared to the Mims ENDOR experiment [2], where the initial polarization is created by a sequence of two non-selective microwave $\frac{\pi }{2}$ pulses, Davies ENDOR is characterized by a lower intrinsic sensitivity due to the use of selective excitation. Nevertheless, the higher sensitivity for large hyperfine couplings makes it the technique of choice for the measurement of hyperfine couplings A > 6 MHz [3].

Figure 1.

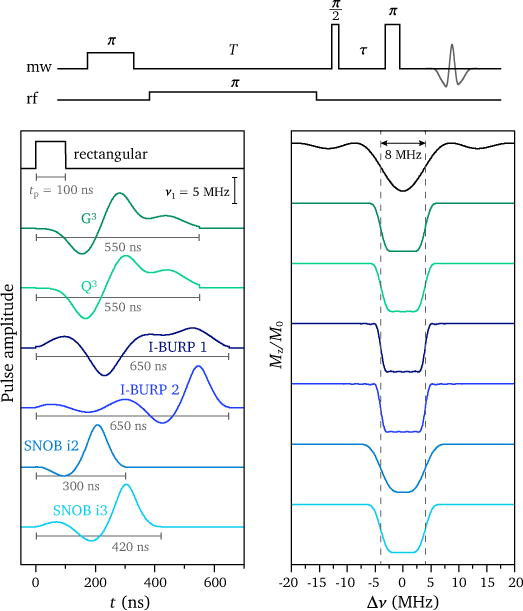
Echo-detected Davies ENDOR pulse sequence with non-selective detection (top) and pulse shapes and inversion profiles for band-selective shaped inversion pulses compared to a rectangular pulse with the same bandwidth (defined as FWHM of the inversion profile) (bottom).

The sensitivity for different hyperfine couplings in Davies ENDOR is determined by the inversion profile of the initial selective microwave π pulse, P_π, and by the properties of the sequence used for detection, i.e. a detection profile, D, depending both on the properties of the microwave pulses and the choice of integration window [4, 5]. In the limit of non-selective detection pulses and full integration of the FID or echo, the ENDOR sensitivity is almost exclusively determined by the properties of the inversion pulse. The inversion profile of a rectangular microwave π pulse, and therefore the shape of the hole burnt into the EPR line by the selective π pulse in the Davies ENDOR sequence, is given by

$$P_{\pi ,\mathrm{rect}}\left(\mathrm{\Delta }v\right)={\left(\frac{M_z\left(\mathrm{\Delta }v\right)}{M_0}\right)}_{\pi ,\mathrm{rect}}=\frac{\mathrm{\Delta }{v}^2+v_1^2\cos (2\pi v_{\mathrm{eff}}{t}_p)}{v_{\mathrm{eff}}^2}$$ (1)

where M_z is the magnetization along the z axis, M₀ is the equilibrium magnetization, $v_{\mathrm{eff}}=\sqrt{\mathrm{\Delta }{v}^2+v_1^2},\mathrm{\Delta }v$ is the resonance frequency offset, ν₁ is the pulse amplitude and t_p is the pulse length. Spectral diffusion during the pulse and the following time delay can affect the shape of the hole, which is therefore often approximated by a Lorentzian [4, 5].

The highest ENDOR sensitivity is achieved for hyperfine couplings exceeding the width of the spectral hole. A reduction of the ENDOR effect is observed for smaller hyperfine couplings, where both electron transitions lie within the excitation bandwidth of the pulse. The sensitivity for small or large hyperfine couplings can be tuned by changing the inversion pulse bandwidth, via the pulse length, with longer pulses providing increased sensitivity for small hyperfine couplings. However, the pulse bandwidth of the selective inversion pulse also determines the number of spin packets contributing to the ENDOR signal, hence increased pulse lengths, i.e. decreased pulse bandwidths, decrease the overall sensitivity of the experiment.

The hyperfine contrast selectivity determined by the inversion pulse in Davies ENDOR can be exploited for the analysis of overlapping spectra of nuclei with significantly different hyperfine couplings. At X-band, the ENDOR spectra of strongly coupled heteronuclei, such as ¹⁴N, ¹⁵N, ⁵⁷Fe, ¹³C and ³³S, can overlap with the ¹H ENDOR spectra centred at the proton Larmor frequency. By choosing a pulse bandwidth $A_{1_{\mathrm{H}}}\ll \mathit{BW}<A_{\mathrm{heteronucleus}}$, the proton signals can be suppressed. Comparison of ENDOR spectra recorded with different lengths of the inversion pulse and therefore different relative intensities of small and large hyperfine couplings can allow assignment of the different ENDOR peaks to different types of nuclei. The optimum inversion pulse bandwidth for suppression of proton hyperfine couplings was found to also maximize the ENDOR signal for larger heteronuclear hyperfine couplings and led to the proposal of the POSHE (PrOton Suppression and Heteronuclear Enhancement) ENDOR technique for selectively recording heteronuclear ENDOR spectra [6, 7].

The introduction of pulse shaping in EPR [8–11] provides the opportunity to improve the selectivity of the initial inversion pulse in Davies ENDOR by replacing rectangular pulses with pulses designed to selectively invert spins over a well-defined window in the frequency domain, while leaving spins with resonance frequencies outside this window unperturbed. Improved inversion selectivity compared to rectangular pulses was first achieved with Gaussian pulses [12, 13], which generate Gaussian-shaped spectral holes instead of the sinc-function-shaped holes of rectangular pulses and therefore limit off-resonance excitation. The differences in inversion profiles are however small, leading to an ENDOR sensitivity and hyperfine contrast selectivity similar to rectangular pulses. Inversion selectivity can be improved further by designing shaped pulses with almost rectangular excitation profiles. A variety of such narrowband-selective pulses has been developed for selective inversion, excitation and universal rotation in NMR [14–20]. Purely amplitude-modulated pulses were designed based on analytical functions and optimized to produce a desired target profile by numerical minimization in the multidimensional space defined by the pulse parameters. Two main classes of these pulses exist:

• -Gaussian pulse cascades, consisting of a superposition of Gaussians and described by the amplitude function [14, 16]

$$A\left(t\right)={\displaystyle \sum _{n=1}^N{A}_n\exp \left[-\frac{4\ln 2}{{(\mathrm{\Delta }{x}_{1/2n}{t}_p)}^2}{(t-x_n{t}_p)}^2\right]}$$ (2)

where A_n are the amplitudes, x_nt_p the positions and Δx_1/2nt_p the full width at half maximum (FWHM) of the Gaussians.

• -finite Fourier series pulses, described by the amplitude function [15, 17–19]

$$A\left(t\right)=A_0+{\displaystyle \sum _{n=1}^N\left[A_n\cos \left(n\omega t\right)+B_n\sin \left(n\omega t\right)\right]}$$ (3)

where ω = 2π /t_p and t_p is the pulse length.

Examples of inversion pulses belonging to the class of Gaussian pulse cascades are the G³ and Q³ pulses based on three Gaussians and therefore with amplitude envelopes defined by nine parameters [14, 16]. Examples of members of the class of finite Fourier series pulses are the BURP (Band-selective, Uniform Response, Pure phase) [15], the SLURP (Silhouette Largely Unaffected by Relaxation Processes) [17] and SNOB (Selective excitatioN fOr Biochemical applications) [18] pulses, where the number of Fourier coefficients defining the pulse shape varies from 17 to 25. The pulse lengths are set to achieve the desired excitation bandwidth, and the overall amplitude is adjusted for a flip angle of π. For purely amplitude-modulated pulses, the flip angle is given by the integral over the pulse shape function.

The pulse shapes and inversion profiles of a series of band-selective inversion pulses are compared to a rectangular pulse with the same bandwidth, defined as the FWHM of the inversion profile, in Figure 1. All of the shown band-selective inversion pulses yield approximately rectangular inversion profiles. In all cases, the pulse lengths for a given bandwidth exceed the length of a rectangular pulse with a comparable bandwidth. The class of SNOB pulses has been specifically designed to achieve selective inversion within a short pulse duration. The corresponding inversion profiles are characterized by an increased width of the transition region between the resonance frequencies of inverted and non-inverted spins, and therefore by a lower selectivity, compared to the related BURP pulses.

In this paper, we investigate the consequences of replacing the initial rectangular inversion pulse in Davies ENDOR with an amplitude-modulated band-selective pulse. First, we analyse the performance of both Gaussian pulse cascades and finite Fourier series pulses for selective inversion in EPR by hole-burning experiments and compare the experimental results to theoretical predictions. We then go on to compare the results of ENDOR experiments with rectangular and shaped band-selective inversion pulses.

The FID and echo signals observed in ENDOR with band-selective pulses exhibit oscillations determined by the rectangular inversion profile of the pulses and standard integration leads to cancellation of the positive and negative contributions to the echo signal. Therefore, we use acquisition of the complete echo transients as a function of radiofrequency and subsequent analysis of the 2D data set to take advantage of the benefits of the band-selective pulses. We investigate the differences in ENDOR intensity and signal-to-noise ratio as a function of hyperfine coupling for different inversion pulses on a copper histidine complex in frozen solution at X- and Q-band. At X-band, we also demonstrate the capability of separating overlapping ENDOR spectra due to protons and strongly coupled nitrogen nuclei in a single experiment with a band-selective inversion pulse instead of two experiments with rectangular inversion pulses of different lengths.

2. Experimental details

2.1. Sample preparation

The Cu(II)-histidine complex was prepared according to the procedure reported in [21, 22]. A solution of CuSO₄ 5H₂O (Mallinckrodt) and L-histidine (Sigma Aldrich) in a molar ratio of 1:5 was prepared in H₂O and stirred at room temperature for 1 h. The pH of the solution was adjusted to 7.3 with a 0.1 M solution of NaOH. Glycerol was added to the aqueous solution (1:1/v:v) to form a good glass. The final concentration of the Cu complex was 2 mM. Cu-doped L-histidine crystals were prepared according to the procedure described in [23]. 0.5% mol CuSO₄·5H₂O was added to a solution of L-histidine in D₂O and crystals were grown by slow evaporation at room temperature over a period of two weeks.

2.2. EPR measurements

A Bruker Elexsys E580 X/Q-band spectrometer extended by a custom-made pulse shaping unit based on a Keysight 81180B Arbitrary Waveform Generator (4.6 GSa/s) as described in [24] was used for the pulse EPR measurements. X-band measurements were performed with a Bruker EN 4118X-MD4 dielectric resonator at 10 K and Q-band measurements with a Bruker EN 5107D2 dielectric resonator at 13 K using a cryogen-free cooling system (Bruker ER 4118HV-CF58). The samples were characterized by measurement of echo-detected field sweeps and the relaxation times were determined by measurement of the two-pulse echo decay and inversion recovery experiments. The determined relaxation times under the experimental conditions used were T₁ ≈ 1 ms and T_m ≈ 3 μs.

FID- and echo-detected hole-burning experiments were performed with the sequences $\pi -T-\frac{\pi }{2}$ and $\pi -T-\frac{\pi }{2}-\tau -\pi$, respectively, with T = 5 μs, τ = 0.8–1.0 μs and with pulse lengths t_π/2 = 10 ns at X-band and t_π/2 = 32 ns at Q-band. The inversion pulse was a rectangular or shaped band-selective pulse (G³, Q³, I-BURP 1, I-BURP 2, SNOB i2, SNOB i3, see Section 1 in the SI for details on the parameters used to define the pulse shapes) of varying length (see details in the text). A two-step phase cycle on the detection $\frac{\pi }{2}$ pulse was used. In order to adjust the amplitude of the inversion pulses, signals were detected as a function of the pulse amplitude programmed on the AWG (varying from 0 to 100% in 1% steps). The final pulse amplitude was chosen based on the relative calculated amplitude with respect to a rectangular π pulse of the same bandwidth (see Section 1) and on inspection of the echo intensities and Fourier transforms of the echo signal (see details in Section 1.4 of the SI).

Davies-type ENDOR experiments were performed with the sequence $\pi -T-\frac{\pi }{2}-\tau -\pi$. A radiofrequency pulse was applied during the time delay T with a length of 12 μs at X-band and 20 μs at Q-band; the length was adjusted for ¹H based on the results of Rabi nutation experiments. The first microwave π pulse was a rectangular or shaped band-selective inversion pulse programmed on the AWG. The detection pulses were programmed on the main pulse channels of the spectrometer with lengths of t_π/2 = 10 ns, t_π = 20 ns at X-band and t_π/2 = 32 ns, t_π = 64 ns at Q-band. Additional experiments with selective detection pulses were performed and are compared to non-selective detection in Section 2 of the SI. A two-step phase cycle on the detection $\frac{\pi }{2}$ pulse was used. FID and echo transients were recorded with a single shot per point and shot repetition times of 5–7 ms. All ENDOR measurements were performed at the g_⊥ field position of the copper EPR spectrum. The same number of averages was recorded for ENDOR experiments with different types of inversion pulses.

For all experiments, echo transients were recorded with a two-channel external digitizer (Agilent U1084) triggered by the spectrometer’s pulse programmer (PatternJet) and operated at 1 GSa/s. The time-jitter (up to 5 ns) between subsequently recorded echo transients was corrected before averaging by shifting the time axis based on the position of the maximum of the two-pulse echo estimated by Gaussian fitting. In order to be able to assign the acquired echoes to the radiofrequencies in the ENDOR experiments, the radiofrequency was swept linearly.

2.3. Data analysis and simulations

Pulse inversion profiles were calculated from the data of the FID-detected hole burning experiments by dead-time reconstruction, zero-filling and Fourier transform. Dead-time reconstruction was performed by least-squares fitting of the experimental FID with the FT of the computed inversion profile for varying pulse flip angles. The theoretical pulse inversion profiles were calculated using two-level density matrix dynamics starting from thermal equilibrium. The corresponding calculated FID was shifted and scaled to match the initial part of the experimental FID and used to define the signal during the experimental dead-time (ca. 80 ns). The results were compared to simulations performed for ideal π pulses and scaled to match the experimental data. The effect of B₁ inhomogeneity was investigated by simulating inversion profiles for a Gaussian distribution of flip angles.

The echo signals recorded in the echo-detected hole-burning experiments and the corresponding Fourier transforms were compared to simulations performed using density matrix dynamics in the absence of relaxation. The simulated signals were scaled individually to match the experimental data.

The 2D data set obtained from detection of the echo transients in the ENDOR experiments was background-corrected along the time domain using the last 100 points of the transient and in the radiofrequency domain by using the off-resonance echo signals. The real part of the signal or its absolute value were summed to give the overall ENDOR spectra. The selection of the integration windows was guided by the signal-to-noise ratio of the spectra. The signal-to-noise ratios were computed by dividing the ENDOR signal by the standard deviation of the baseline. For better comparison, similar integration windows were used for band-selective pulses with the same excitation bandwidth. For the X-band ENDOR data, integration was performed between the second zero-crossings of the broad inverted echo on both sides with respect to the echo centre and for the Q-band ENDOR data, characterized by a better overall signal-to-noise ratio, the integration window was extended to just before the fourth zero-crossings. Due to strong nitrogen ESEEM modulations for the investigated Cu(His)₂ complex, it was more advantageous to choose a long τ delay between the two pulses of the detection sequence, which allowed symmetric integration with respect to the echo maximum even for relatively long shaped pulses.

Calculations of the theoretical dependence of the ENDOR amplitude on the strength of the hyperfine coupling for different types of preparation and detection sequences were performed using a density matrix calculation of the ENDOR experiment for a $S=\frac{1}{2}$, $I=\frac{1}{2}$ system in Hilbert space.

3. Results and discussion

3.1. Hole burning

To evaluate the performance of different amplitude-modulated band-selective inversion pulses designed for NMR, we performed FID- and echo-detected hole-burning experiments. Figure 2 shows the FID and echo transients recorded with a non-selective detection pulse (left) and a non-selective two-pulse detection sequence (right).

Figure 2.

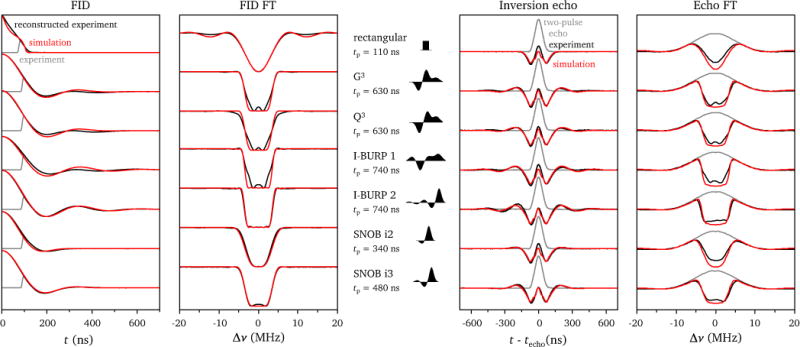
FID- and echo-detected hole-burning experiments: Experimental FID (left) and echo transients (right) and corresponding Fourier transforms for a series of different selective inversion pulses with an inversion bandwidth (FWHM) of 7 MHz. The experimental data is shown in black and grey and was recorded at Q-band (ν_mw = 33.885 GHz) at 13 K at the g_⊥ field position (1178.9 mT) on a Cu(His)₂ complex in H₂O:glycerol. The inversion pulse lengths and shapes are indicated in the figure, rectangular pulses with lengths t_π/2 = 32 ns and tπ = 64 ns were used for the detection (further details in Section 2). For the FID-detected experiments, the signal during the initial dead-time was reconstructed as described in Section 2.3 and the resulting signal (shown in black) was used for Fourier transformation. The experimental Fourier transforms and calculated inversion profiles were normalized for comparison. For the echo-detected experiments, the echo in the absence of the inversion pulse is shown as a reference in grey. The experimental results are compared to simulations shown in red.

The FID-detected experiments allow measurement of the experimental inversion profiles and comparison with theoretical predictions. The FID represents the part of the EPR spectrum within the excitation bandwidth of the detection pulse with a spectral hole determined by the properties of the inversion pulse. However, only parts of the FID representing narrow spectral features exceed the instrumental dead-time and therefore the Fourier transform of this part of the signal yields the pulse inversion profile, i.e. the spectral hole, while information on the broad excited EPR line is lost in the dead-time.

The almost rectangular inversion profile of the band-selective inversion pulses leads to oscillating FIDs with zero-crossing points spaced by the inverse of the pulse bandwidth (defined as the FWHM of the inversion profile). In all cases, we observe that the length of the FID is equal or smaller than the length of the inversion pulse, as expected for a broad inhomogeneous line based on the Schenzle-Wong-Brewer theorem [25, 26]. The amplitude of the oscillations is determined by the steepness of the transition region of the inversion profile; for the I-BURP 2 pulse it most closely approaches a rectangle and the corresponding FID shows the most pronounced oscillations.

The experimental results agree reasonably well with simulations for the finite Fourier series pulses I-BURP 2, SNOB i2 and SNOB i3. However, for the Gaussian pulse cascades, G³ and Q³, and the I-BURP 1 pulse, the inversion profiles calculated based on the experimental data are characterized by larger transition regions and incomplete inversion for spin packets with resonance offsets close to zero. Although both groups of pulses lead to inversion of intra-bandwidth spin packets at the end of the pulse, they differ in the nature of the spin trajectories during the pulse (see Figure S2 in the SI). For the I-BURP 2 and SNOB pulses, with shapes characterized by significant pulse amplitudes only towards the end of the pulse, the spin vectors remain close to the equilibrium position for most of the pulse duration and therefore these pulses are less affected by relaxation and diffusion processes.

The discrepancies between the experimental results and theoretical predictions could be attributed to B₁ inhomogeneity in the resonator, leading to different flip angles for spins at different positions in the resonator. Simulations performed for a distribution of flip angles show excellent agreement with the experimental FID signals and inversion profiles (see Figure S4 in the SI). In addition to B₁ inhomogeneity, relaxation and flip angle miscalibration can also lead to deviations from the ideal inversion behaviour [15], but were found not to have a significant influence on the inversion profiles observed here (see Section 1.4 in the SI for details).

In the echo-detected experiments (see Figure 2), the observed echo shape is a combination of a narrow positive signal representing the excited broad EPR line and a much broader inverted signal representing the narrow spectral hole created by the selective inversion pulse. The inverted component of the echo is significantly broader for the band-selective inversion pulses compared to the rectangular pulse with the same bandwidth, and, as already observed for the FID signals, is characterized by oscillations. Since the whole signal can be detected in this case, Fourier transformation gives the part of the EPR line within the detection bandwidth as well as the spectral hole created by the inversion π pulse. Comparison of the experimental results with simulations, also shown in Figure 2, leads to the same conclusions as for the FID-detected experiments: The I-BURP 2 and SNOB pulses create approximately rectangular spectral holes in agreement with theoretical predictions, while more significant deviations are observed for the Gaussian pulse cascades and the I-BURP 1 pulse and can be attributed to B₁ inhomogeneity. Additional deviations in the relative intensities of the broad and narrow contributions to the echo and the incomplete inversion observed in the corresponding Fourier transforms for all of the pulses are mostly due to relaxation and spectral diffusion, which have not been taken into account in the simulations.

Experiments with inversion pulses with bandwidths ranging from 4 MHz to 20 MHz show similar results to those described above. Increased deviations from the predicted behaviour are observed for increasing pulse lengths (decreasing pulse bandwidths). Increased pulse bandwidths lead to increased transition regions in the inversion profile and therefore decreased selectivity for the pulses analysed here. Broadband selective inversion is more efficiently achieved by frequency-swept pulses, such as the hyperbolic secant pulse [9, 10, 27]. In contrast to these amplitude- and phase-modulated pulses, the band-selective inversion pulses described here invert all of the spins with resonance offsets within the pulse bandwidth at the same time.

3.2. ENDOR with shaped inversion pulses

In order to investigate the potential advantages of the use of shaped band-selective inversion pulses in ENDOR, we performed experiments on Cu(His)₂ in frozen solution. This complex is characterized by ¹H hyperfine couplings ranging from <1 to 14 MHz and nitrogen hyperfine couplings of about 30 to 40 MHz [22].

The echo signals recorded in Q-band ENDOR experiments with an I-BURP 2 inversion pulse and rectangular inversion pulses of the same bandwidth or length are depicted in Figure 3 and the range of changes for different radiofrequencies is highlighted. Due to the oscillatory behaviour of the echo obtained for the almost rectangular spectral holes of band-selective inversion pulses, the standard echo integration procedure used in ENDOR would lead to cancellation of part of the signal and a significant decrease in signal-to-noise ratio. Therefore, full transients were recorded and the ENDOR intensity was calculated by subtraction of the echo signal for an off-resonance radiofrequency pulse from the two-dimensional dataset:

$$I_{\mathrm{ENDOR}}\left(v_{\mathrm{rf}},t\right)=I_{\mathrm{echo}}\left(v_{\mathrm{rf}},t\right)-I_{\mathrm{echo}}\left(v_{\mathrm{rf}}=\mathrm{off}-\mathrm{resonance},t\right)$$ (4)

The resulting ENDOR intensity is plotted as a function of both radiofrequency and time with respect to the echo centre on the bottom in Figure 3. The overall ENDOR spectrum is obtained by absolute integration of the two-dimensional ENDOR intensity along the time axis.

Figure 3.

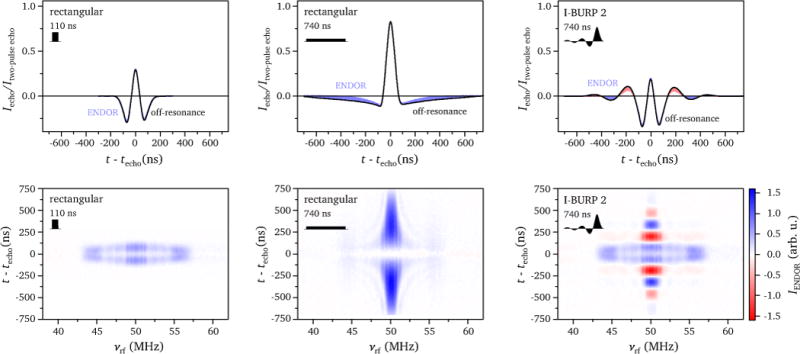
ENDOR echo signals and ENDOR intensities: (top) off-resonance echo transients (black) and range of changes in the echo shape for different radiofrequencies in ENDOR experiments performed using rectangular inversion pulses with lengths of 110 ns and 740 ns and an I-BURP 2 inversion pulse with a length of 740 ns; (bottom) ENDOR intensity as a function of radiofrequency and time with respect to the echo maximum calculated from the echo transients according to Eq. (4). The experiments were performed on a frozen solution of Cu(His)₂ at 13 K at the g_⊥ field position of the copper spectrum at Q-band (1178.9 mT).

A comparison of the results for an I-BURP 2 and a rectangular pulse with the same bandwidth of 7 MHz (Figure 3 left and right) shows that the central region of the echo, delimited by the positions of the first zero-crossings in the broad inverted echo (at about ±140 ns), and the ENDOR intensities in the corresponding region of the contour plot are essentially identical. Integration over this region would give the same result for both types of inversion pulses. The signal intensities beyond the first zero-crossings in the echo obtained with the I-BURP 2 pulse vary significantly for radiofrequencies on resonance with nuclear spins characterized by small hyperfine couplings and lead to additional alternately positive and negative ENDOR intensities. Absolute integration of the ENDOR intensity measured over the whole echo for the I-BURP 2 pulse therefore yields increased intensities in the small-hyperfine coupling region. The maximum peak amplitudes and the maximum ENDOR intensities in the oscillating echo wings correspond to those observed for a rectangular pulse of the same length at the same positions in the echo (Figure 3 center). Due to the oscillatory behaviour of the signal for the I-BURP 2 pulse, the overall ENDOR intensity in the small-hyperfine coupling region is however lower (see Figure S6 in the SI). The similarities in ENDOR sensitivity for small hyperfine couplings between the I-BURP 2 pulse and the long rectangular inversion pulse can be attributed to the similar width of the transition regions in the corresponding inversion profiles (see discussion below).

X- and Q-band ENDOR spectra recorded with different band-selective inversion pulses and different inversion bandwidths are compared in Figure 4. At X-band, the ¹⁴N and ¹H ENDOR signals partially overlap. The ENDOR spectra were obtained by absolute integration and, for better comparison, similar integration window lengths were used for pulses with the same bandwidth. The ENDOR spectra recorded with the band-selective inversion pulses are similar to the spectra recorded with a rectangular pulse of the same bandwidth for large hyperfine couplings, but show significantly increased signal intensities in the small-hyperfine coupling region. For the Q-band data shown here, increases in signal-to-noise ratio of up to a factor of four were obtained for small hyperfine couplings (< ca. 2 MHz). The resulting ENDOR spectra resemble Mims ENDOR spectra regarding the relative signal intensities for ENDOR peaks corresponding to large and small hyperfine couplings, but are not affected by blind spots. Due to the non-selective excitation in Mims ENDOR, the absolute ENDOR intensities for small hyperfine couplings in the Davies-type ENDOR experiment with band-selective inversion pulses are however smaller.

Figure 4.

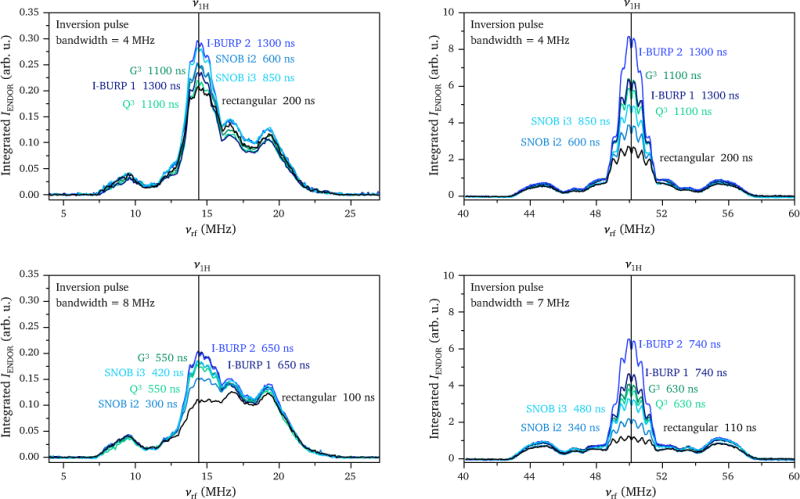
X-band (left) and Q-band (right) echo-detected ENDOR spectra of Cu(His)₂ in a frozen aqueous solution recorded with different inversion pulses. The inversion pulse lengths were adjusted to give an inversion bandwidth (defined as FWHM) of 4 MHz and 7 or 8 MHz as indicated in the corresponding graphs. The experiments were performed at the g_⊥ field positions of the copper spectrum, corresponding to 338 mT at X-band and 1178.9 mT at Q-band. Further experimental details can be found in Section 2. The results of ENDOR experiments with band-selective inversion pulses are compared to the results obtained for a rectangular inversion pulse of the same bandwidth (black line). The integration windows were chosen to extend to the edges of the echo for the rectangular pulse and up to just before the second or fourth zero-crossing of the broad inverted echo on both sides of the echo maximum for band-selective pulses at X- and Q-band, respectively (these integration windows were found to give optimal signal-to-noise ratios in most cases).

The increase in signal intensity in the small-hyperfine coupling region differs significantly for different band-selective inversion pulses. As can be seen in Figure 4, the best results are obtained for longer pulses with inversion profiles exhibiting steeper transition regions, corresponding to the echo signals with the largest oscillation amplitudes. Despite the deviations observed from the predicted inversion behaviour for the Gaussian pulse cascades and the I-BURP 1 pulse in Section 3.1, the performance of these pulses in the ENDOR experiments is not significantly reduced with respect to the other pulses. Nevertheless, even though the I-BURP 1 and I-BURP 2 pulses are predicted to give the same inversion profile and therefore the same behaviour in the ENDOR experiments, the I-BURP 2 pulse consistently outperforms the I-BURP 1 pulse. Combined with the increased robustness of this pulse with respect to relaxation effects and flip angle miscalibration, it seems the most suited for band-selective inversion in systems with sufficiently long phase memory times so as not to significantly affect spin evolution during the pulse or the detected FID or echo signal. The results shown in Figure 4 were obtained with pulse excitation bandwidths of 4–8 MHz (corresponding to t_p = 100–200 ns for a rectangular pulse). For much larger pulse bandwidths (and therefore shorter pulses), the increase in ENDOR intensity for small hyperfine couplings is reduced and the performance of the band-selective pulses becomes similar to that of equivalent rectangular pulses.

The increase in ENDOR intensity for small hyperfine couplings observed for the band-selective inversion pulses can be qualitatively understood by considering the shape of the spectral hole created by the selective inversion pulse and the changes induced by the excitation of nuclear transitions. A resonant radiofrequency pulse induces a polarization transfer from the initial hole to side holes of the same shape, shifted with respect to the centre by the magnitude of the hyperfine coupling. The ENDOR sensitivity is determined by the degree of the resulting change in shape and intensity of the spectral hole.

The dependence of the ENDOR sensitivity for different hyperfine couplings on the nature of the inversion profile of the first pulse is illustrated in Figure 5. In the case of inversion profiles with wide transition regions, such as for short rectangular, Gaussian or truncated sinc pulses, the changes induced in the spectral hole for small hyperfine couplings are limited, amounting only to a slight broadening and a reduction in intensity. As a consequence, the echo intensity also does not vary significantly, leading to low sensitivity for small hyperfine couplings. The degree of suppression of small hyperfine couplings is described by an ENDOR sensitivity envelope determined by the inversion pulse profile, the excitation profile of the detection sequence and the integration window [4, 5]. For non-selective detection pulses, the overall ENDOR sensitivity envelope is given by the convolution of the pulse inversion profile with the Fourier transform of the integration window. For full standard echo integration, it can be approximated to the pulse inversion profile, i.e. Eq. (1) with Δν = A/2 in the weak coupling limit, as shown in the top panel of Figure 5.

Figure 5.

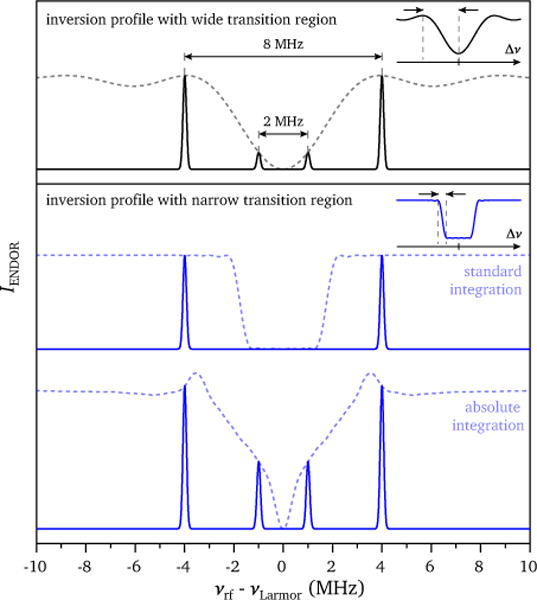
Calculated ENDOR sensitivity envelopes for a pulse with an inversion profile with wide transition regions (top panel, 110 ns rectangular pulse) and a band-selective pulse with narrow transition regions (bottom panel,740 ns I-BURP 2 pulse) and schematic representation of the relative intensity of ENDOR lines due to hyperfine couplings of 2 MHz and 8 MHz (weak coupling limit). The inversion profiles of the pulses are shown in the insets and the width of the transition region is highlighted. Further details on the calculations can be found in Section 2.3 and Section 3 in the SI.

The shaped band-selective inversion pulses have inversion profiles with narrow transition regions and, in this case, the transfer of polarization for small hyperfine couplings from inside the inverted region to just outside the spectral hole leads to significant changes in the edge steepness of the spectral hole. Since this is what determines the amplitude of the oscillations in the wings of the echo signal, the outer region of the echo provides increased sensitivity for small hyperfine couplings. For standard echo integration, the ENDOR sensitivity envelope is again given by the pulse inversion profile, which in this case is almost rectangular and leads to complete suppression of hyperfine couplings within the pulse excitation bandwidth (see the bottom panel of Figure 5). In order to take advantage of the increased sensitivity for small hyperfine couplings, absolute integration as described at the beginning of this section is necessary. Since this is equivalent to the use of an integration window given by the sign function of the echo signal, the ENDOR sensitivity envelope can be calculated as the convolution of the Fourier transform of this function with the pulse inversion profile. The resulting curve is shown for an I-BURP 2 pulse on the bottom of Figure 5 and predicts an overall higher ENDOR intensity as well as increased relative intensity for small hyperfine couplings, in agreement with experimental observations.

The extent of the increase in ENDOR intensity in the small-hyperfine coupling region depends on the width of the transition regions in the inversion profile and the length of the integration window. For the band-selective pulses, the width of the transition regions is determined by both the bandwidth and the type of pulse. The I-BURP 2 pulse provides the narrowest transition regions for a given bandwidth, explaining the observation of the largest increase in ENDOR intensity in the small-hyperfine coupling region for this inversion pulse. Since the signal-to-noise ratio of the recorded echo signals limits the width of the optimal integration window and therefore the increase in ENDOR intensity, ENDOR with shaped band-selective inversion pulses is particularly advantageous in cases where a good signal-to-noise of the echo transients can be obtained. This is reflected in the more significant changes in ENDOR intensity observed at Q-band, where the better signal-to-noise ratio allowed the use of longer integration windows (Figure 4).

3.3. Hyperfine contrast selectivity

The hyperfine contrast selectivity provided by the properties of the inversion pulse can be exploited for the assignment of ENDOR peaks to weakly or strongly coupled nuclei in X-band spectra where overlap of ENDOR signals due to strongly coupled heteronuclei and weakly coupled protons occurs [6, 7, 26]. We explored the hyperfine contrast selectivity provided by shaped band-selective inversion pulses and found that overlapping ENDOR spectra could be separated more efficiently compared to experiments with rectangular pulses.

Generally, in order to separate ENDOR spectra of protons and strongly coupled nuclei, Davies ENDOR experiments are performed with a short rectangular inversion pulse, with an excitation bandwidth adjusted so that $A_{1_{\mathrm{H}}}\ll \mathit{BW}<A_{\mathrm{heteronucleus}}$ [6], and with a long rectangular inversion pulse. Comparison of the ENDOR intensities of different lines in the two spectra then allows their assignment to the different nuclei. This is exemplified in Figure 6 for X-band ENDOR of a Cu(II)-doped L-histidine crystal, where proton hyperfine couplings overlap with nitrogen signals. The ENDOR intensities as a function of radiofrequency and time with respect to the echo centre are shown on top and the two ENDOR spectra are compared on the bottom left.

Figure 6.

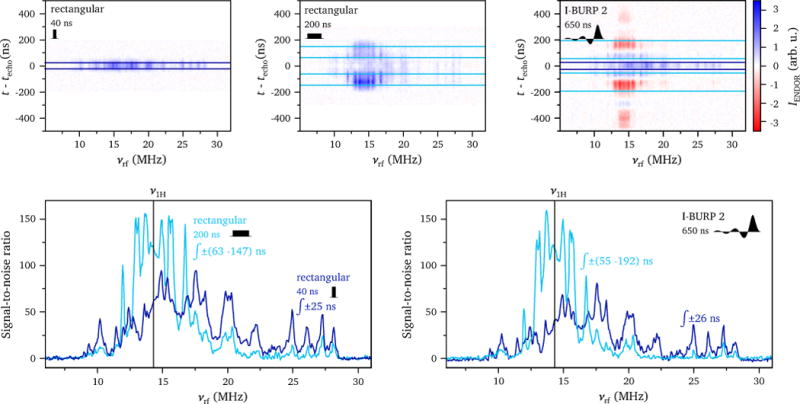
(top) ENDOR intensity as a function of radiofrequency and time with respect to the echo maximum for rectangular inversion pulses with lengths of 40 ns and 200 ns and an I-BURP 2 pulse with a length of 650 ns. (bottom) X-band ENDOR spectra of a Cu-doped histidine crystal obtained using different inversion pulses and integration windows as indicated in the graphs. The experiments were performed at X-band on a Cu-doped histidine crystal at 10 K and a field position corresponding to g_⊥ (337 mT). The detection sequence was $\frac{\pi }{2}-\tau -\pi$ with $t_{\frac{\pi }{2}}=10\mathrm{ns},$ t_π = 20 ns and τ = 600 ns. The horizontal lines in the contour plots indicate the integration windows used to obtain the ENDOR spectra and were selected based on the optimal mean signal-to-noise ratio in the region containing the ENDOR peaks of interest.

A similar separation of the ¹H and ¹⁴N ENDOR signals can be achieved in a single experiment using a shaped band-selective pulse and echo transient acquisition. As shown in Section 3.2, for shaped band-selective inversion pulses, the ENDOR intensities of nuclei with different hyperfine coupling strengths reach their maxima at different times with respect to the echo centre. Furthermore, the ENDOR intensities for large hyperfine couplings are similar to those obtained for rectangular pulses of the same bandwidth, while ENDOR intensities for small hyperfine couplings approach those obtained with rectangular pulses of the same length. Therefore, integration over different regions of the echo signal, specifically in the region of the narrow echo contribution due to the two-pulse detection sequence and the outer regions of the broad inverted signal, yields ENDOR spectra containing mostly signals of strongly coupled nuclei and weakly coupled nuclei, respectively. This is illustrated on the bottom right in Figure 6 for an I-BURP 2 pulse with an excitation bandwidth of 8 MHz. The signal-to-noise ratios of the two types of ENDOR spectra obtained with different integration windows are the same as those obtained in the ENDOR experiments with a short and a long rectangular inversion pulse. Since the same number of transients was acquired in all three experiments, the use of the I-BURP 2 pulse to separate spectra due to hyperfine couplings of different strengths reduces the experimental measurement time by a factor of two. In addition to this, comparison of the two pairs of ENDOR spectra in Figure 6 shows that a more efficient separation of the two sets of ENDOR peaks is achieved with the I-BURP 2 pulse.

4. Conclusions

We investigated the use of purely amplitude-modulated band-selective inversion pulses in Davies-type ENDOR experiments. We applied the Gaussian pulse cascades and finite Fourier series pulses designed for narrowband selective inversion in NMR experiments to EPR and verified their increased inversion selectivity compared to rectangular inversion pulses. An almost rectangular inversion profile can be achieved with a variety of different pulse shapes. The pulses tested here only constitute a subset of the solutions to the pulse optimization problem [19]. Hole-burning experiments have shown that finite Fourier series pulses with similar overall pulse envelopes characterized by large pulse amplitudes at the end of the pulse (I-BURP 2, SNOB i2 and SNOB i3) yield experimental inversion profiles in excellent agreement with theoretical predictions. However, pulses characterized by pulse envelopes reaching significant amplitudes at earlier times (G³, Q³ and I-BURP 1) show deviations from the predicted behaviour. The I-BURP 2, and the related SNOB pulses, are known from NMR to be more robust to relaxation effects, flip angle miscalibration and B₁ inhomogeneity [15], which explains their improved performance in the hole-burning EPR experiments performed here.

In Davies-type ENDOR experiments, we found that the use of band-selective inversion pulses combines the advantages of increased absolute ENDOR intensity of short rectangular inversion pulses and increased sensitivity for small hyperfine couplings of longer rectangular pulses. Given the interdependence of hyperfine selectivity and sensitivity in ENDOR, shaped band-selective inversion pulses thus maximize the capabilities of this type of experiment. ENDOR with shaped band-selective inversion pulses can therefore be of advantage compared to standard Davies ENDOR with rectangular inversion pulses or Mims ENDOR for the investigation of hyperfine interactions in systems with multiple nuclei of significantly different coupling strengths. In order to exploit these benefits, the acquisition of the full echo transients as a function of radiofrequency is required. The ENDOR spectra are obtained by subtraction of the off-resonance echo signal from the two-dimensional data set and absolute integration over the echo signal. ENDOR spectra recorded for a Cu(His)₂ complex with band-selective inversion pulses show similar intensities compared to a rectangular pulse of the same bandwidth for large hyperfine couplings and increased intensities for small hyperfine couplings. An increase of the signal-to-noise ratio in the small coupling region of up to a factor of four was observed for ¹H ENDOR at Q-band.

The high sensitivity for both large and small hyperfine couplings obtained using shaped inversion pulses combined with the acquisition of the echo transients further provides an improved method for the separation of ENDOR spectra of nuclei with different hyperfine coupling strengths by exploiting hyperfine contrast selectivity. As demonstrated for a Cu-doped histidine crystal at X-band, integration over regions of the echo signal sensitive to either large or small hyperfine couplings can be used for the assignment of ENDOR peaks to weakly coupled protons or strongly coupled nitrogen nuclei. The signal-to-noise ratio of the ENDOR spectra resulting from different integration windows matches the signal-to-noise ratio of corresponding ENDOR spectra recorded with either a short or a long rectangular pulse, reducing the overall required measurement time for the separation of overlapping signals by a factor of two.

In the experiments described in this paper, the I-BURP 2 pulse was found to provide the best results, both in the hole-burning experiments and in ENDOR. Amongst the pulses investigated here, this type of pulse has the longest pulse duration for a given bandwidth and requires larger pulse amplitudes to achieve inversion over a specified bandwidth. In the presence of significant relaxation, the advantages of this pulse compared to the shorter SNOB pulses will likely be reduced.

To account for the differences in sample properties and instrumental capabilities, real-time optimization of the coefficients of finite Fourier series inversion pulses to give efficient inversion and a target excitation profile under specific experimental conditions could be envisioned. Since the importance of the Fourier coefficients decreases with their order [15], the series can be truncated after a small number of terms, decreasing the dimensions of the optimization problem and making it more manageable compared to standard optimal control approaches.

Highlights.

• -Selective narrowband inversion by amplitude-modulated pulses is shown for EPR.
• -Fourier series pulses in ENDOR increase sensitivity for small hyperfine couplings.
• -Improved separation of spectra of weakly and strongly coupled nuclei is achieved.