We show that whereas motor cortex spiking rates and beta (~20 Hz) spiking rhythmicity remain sustained during steady-state movement preparation periods, β-local field potential (β-LFP) oscillations emerge, in contrast, as transient events. Furthermore, the β-LFP phase at which neurons spike drifts: phase coupling is typically weak or absent. This dissociation points to two sources of variation in the level of motor cortex beta: one that impacts single-neuron spiking and another related to the generation of measured mesoscopic β-LFPs.
Keywords: beta oscillations, collective dynamics, motor cortex, neural dynamics, spike-field coupling
Abstract
Determining the relationship between single-neuron spiking and transient (20 Hz) β-local field potential (β-LFP) oscillations is an important step for understanding the role of these oscillations in motor cortex. We show that whereas motor cortex firing rates and beta spiking rhythmicity remain sustained during steady-state movement preparation periods, β-LFP oscillations emerge, in contrast, as short transient events. Single-neuron mean firing rates within and outside transient β-LFP events showed no differences, and no consistent correlation was found between the beta oscillation amplitude and firing rates, as was the case for movement- and visual cue-related β-LFP suppression. Importantly, well-isolated single units featuring beta-rhythmic spiking (43%, 125/292) showed no apparent or only weak phase coupling with the transient β-LFP oscillations. Similar results were obtained for the population spiking. These findings were common in triple microelectrode array recordings from primary motor (M1), ventral (PMv), and dorsal premotor (PMd) cortices in nonhuman primates during movement preparation. Although beta spiking rhythmicity indicates strong membrane potential fluctuations in the beta band, it does not imply strong phase coupling with β-LFP oscillations. The observed dissociation points to two different sources of variation in motor cortex β-LFPs: one that impacts single-neuron spiking dynamics and another related to the generation of mesoscopic β-LFP signals. Furthermore, our findings indicate that rhythmic spiking and diverse neuronal firing rates, which encode planned actions during movement preparation, may naturally limit the ability of different neuronal populations to strongly phase-couple to a single dominant oscillation frequency, leading to the observed spiking and β-LFP dissociation.
NEW & NOTEWORTHY We show that whereas motor cortex spiking rates and beta (~20 Hz) spiking rhythmicity remain sustained during steady-state movement preparation periods, β-local field potential (β-LFP) oscillations emerge, in contrast, as transient events. Furthermore, the β-LFP phase at which neurons spike drifts: phase coupling is typically weak or absent. This dissociation points to two sources of variation in the level of motor cortex beta: one that impacts single-neuron spiking and another related to the generation of measured mesoscopic β-LFPs.
sensorimotor cortex β-local field potential (β-LFP) oscillations result from coherent activity and reflect in part the collective dynamics of neuronal populations embedded in local and large-scale brain networks. In the specific case of motor cortex, β-LFP oscillations are especially evident during movement preparation and planning, and also during the execution of isometric force grip tasks (Baker et al. 1997; Baker et al. 2001; Baker et al. 2003; Jackson et al. 2003; Murthy and Fetz 1992; Murthy and Fetz 1996a; Murthy and Fetz 1996b; Sanes and Donoghue 1993). The relationship between single-neuron spiking and β-LFP oscillations remains an important issue toward revealing the origin and function of these oscillations in the primate motor cortex. Addressing this issue may be critical for the development of new therapies for movement disorders, such as Parkinson’s disease (Beuter et al. 2014; Gale et al. 2008; Yang et al. 2014), and for the development of brain-machine interfaces for people with paralysis. More generally, the relationship between single-neuron activity and collective activity is important for understanding the neural dynamics of motor steady states.
Most previous studies have examined the relationship between neuronal spiking and ongoing β-LFPs by using spike-triggered averages (STAs). Based on this approach, several studies have shown some level of phase coupling between spikes and LFP (e.g., Murthy and Fetz 1996b). However, assessing the coupling strength on the basis of STAs is difficult because STAs are expressed in field potential units rather than a direct measure of phase coupling. To address this issue, several other studies have used spike-field coherence and related measures (e.g., Baker et al. 2003) during the execution of isometric force precision grip tasks. However, it remains unclear how neuronal firing rates and rhythmic spiking activity relate to transient β-LFP oscillations during controlled steady-state movement preparation periods, i.e., periods unperturbed by the strong influence of motor or sensory stimulus-driven transients in neural activity. In particular, how firing rates, beta-rhythmic spiking, and the phase coupling between spiking and β-LFPs behave within and outside transient β-LFP events has not been examined in detail. Clarifying these issues is an important step for understanding the function and mechanisms of beta oscillations in motor cortex.
We address these issues in the context of a visually cued reaching and grasping task with instructed delays. Single units were simultaneously recorded via multiple microelectrode arrays implanted in primary motor (M1), ventral premotor (PMv), and dorsal premotor (PMd) areas while nonhuman primate subjects performed reach and grasp actions in a three-dimensional (3-D) workspace. We focused on examining the relationship between well-isolated single units and β-LFP activity during steady-state movement preparation stages of this task, which may potentially differ from synchronization dynamics previously studied in association with isometric force during precision grip, as described above. Overall, we found a striking phenomenon that has been overlooked in previous studies. Whereas β-LFP oscillations tended to appear as short transients, even during steady-state movement preparation periods, neuronal firing rates and beta spiking rhythmicity, evident in the interspike time interval (ISI) distributions and autocorrelation functions, were sustained. Furthermore, different spike-LFP phase-coupling measures revealed that single-neuron beta-rhythmic spiking was at most weakly coupled to the β-LFP oscillations, even when the analysis was restricted to transient periods of high β-LFP power. We observed this phenomenon in many single units from the three recorded motor cortical areas. In addition, although single units clustered into two groups (narrow and wide extracellular action potentials) that showed differences in firing statistics between groups, no consistent differences in the strength of their phase coupling to β-LFP oscillations were detected, indicating that the dissociation between spiking and β-LFP activity is present in different neuronal populations.
METHODS
The cued grasp with instructed delay task.
The cued grasp with instructed delay (CGID) task investigates neural activity in motor cortex associated with sensory integration, working memory across instructed delays, and planning of upcoming reach and grasp actions (see Vargas-Irwin et al. 2015 for additional details). All experimental procedures were conducted as approved by the local Institutional Animal Care and Use Committee. The task requires a subject (macaque monkey) to reach out and grasp one of two objects by using one of two possible grips. A sequence of visual cues instructs the subject which object to grasp and which grip to use. When the task begins, the lights in the room are turned off, and one of the two objects is rotated into place. One second later, said object is illuminated. The subject now knows which object to grasp, but not which grasp to perform. One second after object presentation, a cue light (red or yellow, left or right position) is illuminated, specifying the grip. If the light is red, the subject is to perform a power grip. If the light is yellow, the subject is to perform a precision grip or a key grip, depending on the object. Two seconds after the “grip” cue, a “go” cue (green light, middle position) is given. The subject may then reach out and grasp the object. If the subject moves before the go cue or uses the incorrect grip on the object, the trial is voided. If the subject uses the correct grip, a juice reward is received.
In this article, we refer to the task epochs preceding the go cue as the planning and preparatory period. Movement periods were defined as the time from when the subject lifts the hand from the holding position to the time when the subject contacts the object, as detected by capacitive touch sensors. We focus on two steady-state periods. The first period is the 1-s period between the start of the trial and when the object is presented, during which the subject is waiting attentively and has not yet received the information needed to plan or prepare for movement. The second period is the 1-s period preceding the go cue. In this period, the subject has been cued with the information needed to plan the reaching and grasping action, and the transient neural activity associated with the visual cues has passed. It is important to note that the visual cue lights were present until the go cue, so this second steady-state epoch represents a motor preparatory state and not a state that explicitly requires working memory.
Neural recordings.
Data were recorded from triple microelectrode arrays (Blackrock Microsystems, Salt Lake City, UT), with an electrode depth of 1.5 mm targeting layers II/III–V of motor cortex. Neuronal spiking and LFP data were recorded on 10 × 10 (PMv) and two 6 × 8 (PMd and M1) arrays with 0.4-mm electrode spacing. Data from two subjects (R and S) were analyzed (see Vargas-Irwin et al. 2015 for additional details). Broadband LFPs (0.3 Hz to 7.5 kHz) recorded at 30 kilosamples/s were downsampled (zero-phase 4th-order Butterworth, less than or equal to ~250-Hz MATLAB filtfilt) to 1 kilosample/s for analysis.
Spike sorting.
For each electrode, candidate spikes (extracellular action potentials) were identified online via threshold crossing in the amplitude of the high-pass filtered signal (250-Hz 4th-order high-pass Butterworth filter; Cerebus data acquisition system; Blackrock). Preliminary spike sorting was performed by a custom automated spike sorter (Vargas-Irwin and Donoghue 2007) and verified using the commercial Plexon Offline Sorter (Plexon). Candidate units included in the analysis had a minimum signal-to-noise ratio (SNR) of 3.0, defined as one-half the average sorted spike waveform peak-to-valley height, divided by the standard deviation of the >250-Hz high-pass filtered LFP on the same channel (Vargas-Irwin and Donoghue 2007). Additionally, we required 1) that the interspike interval (ISI) histogram display a clear refractory period to exclude multiunit clusters; 2) that the units exhibit at least 100 ISI events during the 1-s steady-state periods of the CGID task within each session, to provide for accurate estimation of ISI distributions; and 3) that units be clearly separated into different clusters in the waveform principal components analysis feature space. Electrodes exhibiting cross talk or excess noise were excluded from analysis.
ISI histogram statistics.
Isolated single units showed diverse firing characteristics as assessed by the ISI distribution and related statistics, both across time and across units. For a given unit, these statistics were computed from the ISI distribution from all ISIs pooled over all trials for a given 1-s epoch of the CGID task. We computed mean firing rates, the ISI mode, and the coefficient of variation (CV; i.e., the standard deviation of the ISI distribution divided by the corresponding mean). We quantified the tendency of units to fire bursts as the percentage of ISIs shorter than 10 ms.
We summarized a single unit’s preferred firing frequency (in Hz) by computing the inverse of the ISI mode, henceforth referred to as mode firing frequency. The mode firing frequency was identified for unimodal and bimodal ISI histograms using kernel density estimation (Python scipy.stats.gaussian_kde). Because some units exhibited an ISI distribution with an additional mode corresponding to bursts, and since we were interested in slower “rhythmicities,” we considered only ISI events longer than 10 ms when estimating the mode firing frequency. Because ISI distributions were right-skewed, we applied kernel density estimation to the transformed variable log(5 ms + ISI). The shift of 5 ms improved numerical stability close to zero, which was an issue in the subset of units that fired bursts of spikes.
Unit categorization.
Units were categorized on the basis of the features of their ISI distributions during the movement preparation steady-state periods of the CGID task. Units exhibiting a clear mode in the ISI distribution between 10 and 100 ms were classified as unimodal. Units that showed an additional peak below 10 ms in the ISI histogram were further classified as bimodal (bursting/rhythmic) cells. All ISI events were included when categorizing unimodal vs. bursting neurons, in contrast to the calculation for mode frequency, for which bursts were excluded. Units exhibiting exponential ISI distributions (allowing for refractoriness) were classified as Poisson-like. Units displaying a mixture of these features, e.g., some amount of bursting, with an exponential ISI distribution exhibiting a long recovery period, were classed as “intermediate.” We restricted spike-field phase-coupling analysis to well-isolated single units classified as unimodal or bimodal (bursting/rhythmic) that also displayed an ISI mode frequency between 10 and 45 Hz in at least one of the steady-state movement preparation epochs and a mean rate at least one-fifth of the mode firing frequency. Allowing low firing rates permitted analysis of single units whose spiking was coupled to the beta phase but did not fire in every beta cycle. The distribution of mean firing rates across units during these epochs was concentrated below 30 Hz.
Units were further classified as narrow- and broad-spike cells on the basis of their mean extracellular action potential waveform. To precisely align spikes, we upsampled waveforms using sinc interpolation. To minimize edge effects during upsampling, the linear trend in the waveform was removed, the detrended waveforms were upsampled with reflected boundary conditions, and the linear trend was restored. We extracted mean waveforms by averaging peak-aligned upsampled waveforms. Waveforms were clustered on the basis of the voltage of the mean waveform 300 μs after the spike peak. This feature led to better cluster separation than the use of the waveform width, since by this time narrow spike cells have recovered (and may exhibit afterhyperpolarization), whereas broad-spike cells remain depolarized. Average waveforms from all areas, sessions, and subjects were combined for clustering. Clustering was performed by using a 1-D Gaussian mixture model, and units were assigned as either narrow- or broad-spike cells on the basis of likelihood ratio.
Beta-phase extraction and transient identification.
For analysis, raw LFP traces (30 kilosamples/s) were low-pass filtered at 250 Hz with a zero-phase, fourth-order Butterworth, MATLAB filtfilt and then downsampled to 1 kHz (MATLAB decimate). In the generalized linear model (GLM; Truccolo et al. 2005) assessment of spike-LFP phase coupling, the beta band was identified separately for each session and channel, and separately for the two different steady-state movement preparation periods. Beta was selected as the 5-Hz band surrounding the highest peak between 15 and 30 Hz in the LFP power spectrum. We estimated the power spectra for each 1-s epoch using multitaper spectral estimation (Mitra and Pesaran 1999; Percival and Walden 1993). We chose a 2.5-Hz half-bandwidth parameter, which resulted in 5 tapers. Tapers were computed by the dpss function in the Python package “spectrum.” Spectral estimates were computed separately for each trial for a given epoch and then averaged over all trials.
Once the beta peak was identified, the β-LFP was extracted in the time domain using a 4th-order Butterworth bandpass filter (centered at the highest peak in beta) applied forward and backward. Beta phase was extracted using the Hilbert transform (SciPy hilbert; Oliphant 2007), which generates a beta analytic signal z(t) consisting of a real component (the filtered beta signal) and an imaginary component, which is a π/2 phase-shifted copy of the filtered beta signal. The instantaneous phase φ(t) and amplitude |z(t)| can be extracted from the analytic signal z(t) = |z(t)| · exp[iφ(t)]. We extracted transient periods of elevated beta power by examining the amplitude envelope of the beta analytic signal. First, the amplitude envelop |z| was smoothed with a 50-ms boxcar filter. Events for which this smoothed amplitude signal exceeded 1.5 times the standard deviation of the filtered beta signal for at least 40 ms (~1 beta cycle) were designated as high-beta events. We visualize (see Figs. 1 and 7) single-trial LFP activity using a Morlet continuous wavelet transform with a time-bandwidth ratio of 5, which enabled good time resolution for higher frequencies while maintaining good frequency resolution at low frequencies; wavelets were normalized by the integral of their absolute magnitude (Torrence and Compo 1998).
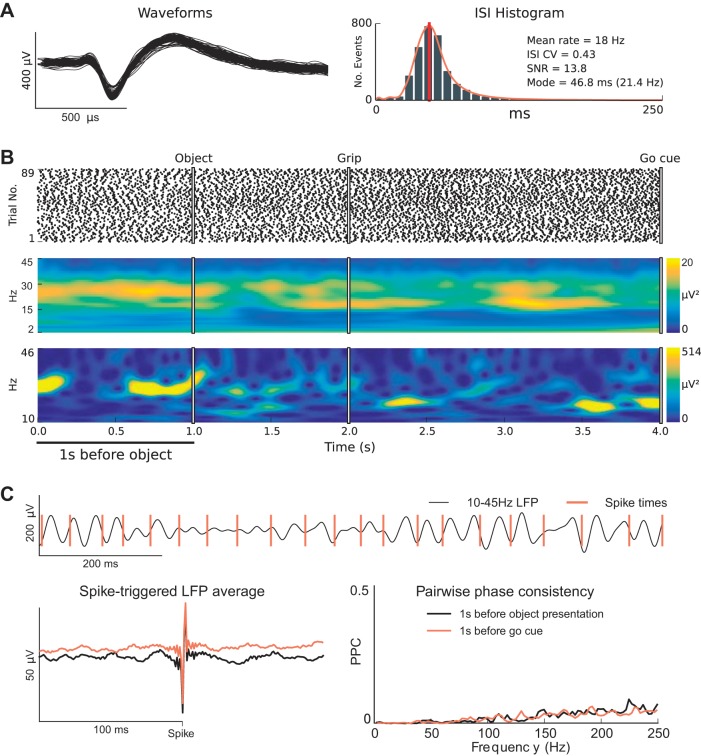
Fig. 1.
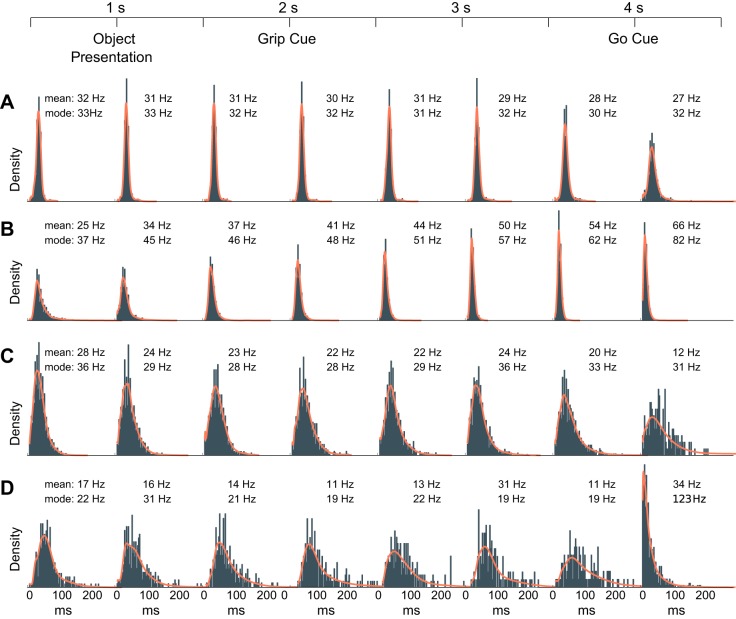
Single units exhibit sustained firing rates and beta rhythmicity that appear dissociated from the phase of transient β-LFP oscillations. A: example of a well-isolated unit recorded from motor cortex that displayed sustained firing rates and rhythmic spiking at beta frequency (~20 Hz) during the steady-state movement preparation periods of the CGID task. B: spike raster plot shows reliable and steady firing during the steady-state movement preparation periods (top). Likewise, a trial-averaged spectrogram shows elevated β-LFP power during the steady-state delay periods of the task (middle). In contrast, the example single-trial β-LFP spectrogram plot shows transient high-power β-LFP events (bottom). The observed trial-averaged β-LFP was much lower because high-power β-LFP transients occurred randomly throughout the steady-state periods. C: an inspection of neuronal spiking and β-LFP oscillations during the first second of this trial reveals that the phase at which single units fired relative to the β-LFP oscillations drifted and that beta-rhythmic spiking remained steady whereas β-LFP power fluctuated. The spike-triggered LFP average (STA) plot shows primarily an artifact from spike contamination (see methods) and reveals some weak beta phase coupling during both the first second of the task and the 1 s before the go cue. Note that it is difficult to assess the overall magnitude of spike-LFP phase coupling from the STA plot alone. Pairwise phase consistency plots corroborated this finding, showing mainly a broadband increase in high-frequency phase coupling associated with contamination of the LFPs by extracellular action potentials (see methods). This example is from isolated unit 26, area PMd, subject R, session 2.
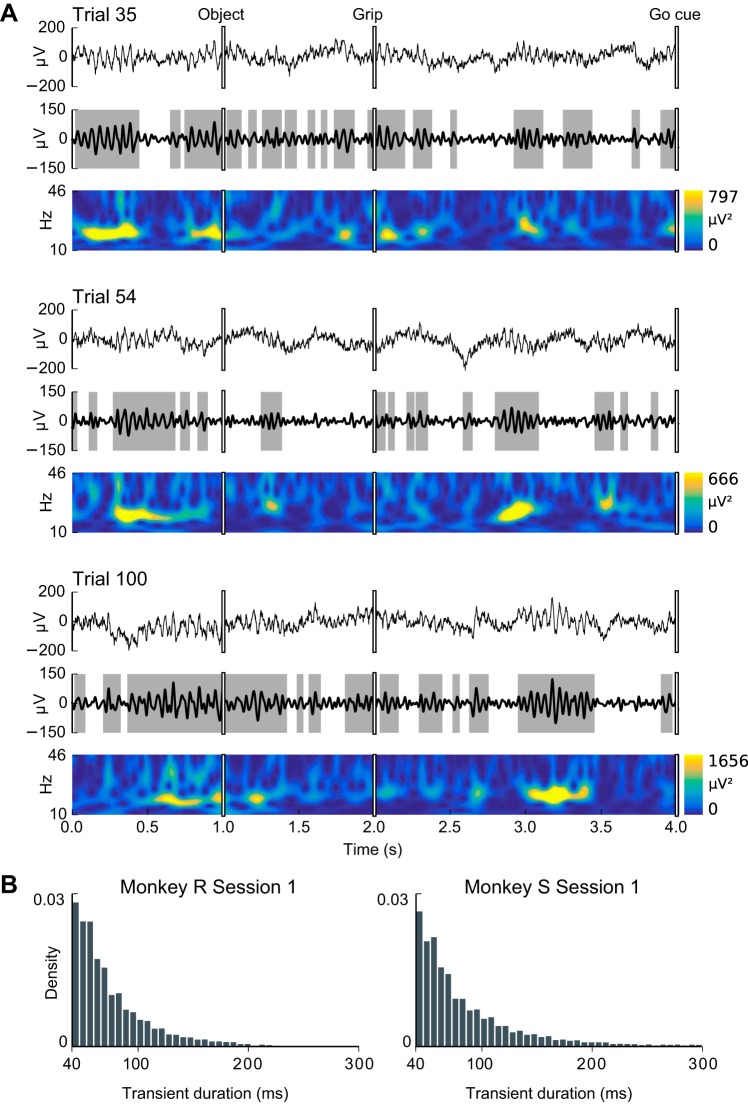
Fig. 7.
β-LFP oscillations occur in transients and exhibit high trial-to-trial variability. A: shown are 3 representative example trials from a single session (subject S, areas M1, session 1). In each example, the top plot shows the “raw” LFP, the middle plot shows the bandpass-filtered β-LFP, and the bottom plot shows the spectrogram. Transient beta events were defined as periods for which β-LFP amplitude was elevated (~1:5 SD, shaded in gray). Inspection of β-LFP activity in single trials revealed that beta oscillations were rarely sustained, occurring as transients lasting commonly a few oscillation cycles. B: however, as evidenced by the absence of modes in the histograms of the durations of high-beta transients, there was no characteristic duration for these transients, and periods of sustained beta oscillations lasting up to 8 or more beta cycles (e.g., <200 ms) were also observed in many trials.
Spike-triggered LFP averages.
We estimated the STAs between spikes and the 250-Hz low-pass filtered (4th-order Butterworth, forward-backward, MATLAB filtfilt) LFP sampled at 1 kilosample on the same electrode. This approach does not remove the spiking contribution to the LFP. (Spike contamination below addresses this concern.) Stable phase coupling of neuronal spiking to LFP oscillations appears as oscillatory components in the STAs. However, estimation of spike-LFP phase coupling is susceptible to several biases. These biases are exacerbated if both the spike trains and the LFP signals exhibit autocorrelations at similar timescales. For example, if a rhythmic spike train (~20 Hz) co-occurs with a burst of 20-Hz LFP oscillations, it might appear that the single unit is phase coupled to the LFP even if there is no relationship. Additional biases may emerge if changes in firing rates are correlated with changes in LFP power. In addition, the STA does not offer a direct assessment of the phase-coupling magnitude, because it reflects both phase-coupling and amplitude effects, and poorly visualizes variability around the mean trend. Because of the biases inherent in the STA, we used two complementary approaches to get unbiased estimates of spike-LFP phase coupling: pairwise phase consistency (PPC) and GLM point process models for assessment of phase coupling.
Pairwise phase consistency.
PPC (Vinck et al. 2010) is an estimate of spike-LFP phase coupling that is not biased by the firing rate or correlated modulations in LFP power and firing rate. Vinck et al. (2010) define PPC as the average dot product between all pairs of spike-triggered phase measurements. We computed PPC using the equivalent expression (Aydore et al. 2013; Eq. 11):
| (1) |
where is the magnitude of the average over spike-triggered β-LFP phase vectors , φk represents the phase measurement at a given spike time, and k indexes over spikes. To compute PPC, we extracted instantaneous LFP phase estimates for a range of frequencies by taking the Fourier transform of the LFP in an ~100-ms window surrounding each spike. Each LFP segment was mean-subtracted and multiplied by a Hanning window to reduce boundary effects. To attenuate temporal dependencies among samples, spikes that occurred within 200 ms after a previous spike were excluded. We report the PPC value at the peak beta frequency, identified separately for each subject, session, channel, and task epoch. The PPC bias correction requires that successive samples be independent. Although we reduced temporal correlations between successive samples by removing events for which the spike-triggered LFP segments would overlap, residual correlations may remain in both the spike trains and LFP. Therefore, we estimated the chance level empirically by phase randomizing LFP segments (Mammen et al. 2009), preserving the autocorrelation structure of the LFP.
Point process GLM-CIF models for spike-LFP phase coupling.
We used a discrete-time point process GLM framework (Truccolo et al. 2005) to detect spike-LFP phase coupling. Time was discretized to 1-ms time bins. This is similar to the approach used by Lepage et al. (2013), Zhou et al. (2015), and Rule et al. (2015). GLM point process-based estimators explicitly model the conditional intensity function (CIF) λ(t) and include an offset parameter μ as a separate regression term, therefore providing an estimate of spike-LFP phase coupling that is less susceptible to variations in firing rate. We considered GLM point process models of the form
| (2) |
where μ is a mean-rate parameter, φ0 is the preferred phase of firing relative to the (bandpass filtered) beta LFP, φLFP(t) is the time-varying instantaneous Hilbert phase of the LFP signal, and α is the strength of phase coupling. In this study we assess the predictive power of the model using receiver operating characteristic (ROC) curve analysis (Fawcett 2006; Rule et al. 2015; Truccolo et al. 2010). The area under the ROC curve (AUC) summarizes the accuracy of spike times predicted by the model and ranges from 0.5 (chance level) to 1.0 (perfect prediction). We report predictive power (PP) as normalized AUC values such that 0 is chance level and 1 is perfect prediction. Chance level was estimated by using phase-randomized LFP (Mammen et al. 2009) and by shuffling the LFP trial blocks relative to the spike trains.
Point process GLM-CIF models for relating single-neuron spiking to population spiking activity.
We also used CIF models to relate single units to the population spiking activity A(t), defined as the total number of spikes across all of the recorded single units (except the predicted neuron) in a given motor area within 1-ms time bins, followed by a 25-ms boxcar filter. The CIF model consisted of
| (3) |
where μ is a mean rate parameter, β reflects the coupling of the single unit to the population spiking activity A(t), and λ[t|A(t)] is the point process intensity function conditioned on the population spiking activity. As a second measure of population activity, we also considered multiunit activity (MUA) recorded in the same electrode as the single unit. MUA was defined as the amplitude envelope of >250-Hz LFP bandpass filtered in the 5-Hz band surrounding the peak beta frequency.
Assessing coupling between population spiking activity and ongoing β-LFP.
We assessed the relationship between the population spiking activity and the ongoing β-LFP activity by computing their cross-correlation functions. Population spiking activity was defined as above, except that in this case, all well-isolated single units were included (for the spiking population history model, the unit being predicted was excluded from the population rate). Statistical tests were applied to the peak of the cross-correlation functions computed for time lags ranging over one beta cycle (±25 ms).
Spike contamination.
In this study, we examined statistical relationships between neuronal spiking activity and LFPs recorded on the same electrode. In this case, the spikes themselves can contribute to LFP power, even at frequencies as low as the ~20-Hz beta band investigated (Waldert et al. 2013). Waldert et al. (2013) found that the spiking contribution to low-frequency LFPs can arise from both low-frequency components of the spike waveform, including slow afterhyperpolarization potentials (AHPs), and spike-train rhythmicity at low frequencies. We elected not to use spike removal procedures like those of Zanos et al. (2011) for several reasons. We are primarily interested in the observed phenomenon of weak spike-field phase coupling demonstrated in results. Contributions of neuronal spikes to the overall LFP signal can only inflate our estimated phase coupling, thus making these estimates more conservative with respect to the main point being made in this article. It is possible that there is ambiguity between spike-locked local network oscillations and low-frequency components of the extracellular spike waveform (e.g., slow AHPs). Since it is possible that low-frequency components of the spike waveform relate to the origins of LFP, we want to avoid erroneously removing a true contributor to β-LFP. Nevertheless, we can distinguish between action potential contamination and other spike-LFP phase interactions by inspecting the PPC spectrum. True spike-LFP phase coupling leads to a PPC peak at the beta band, whereas spiking contamination leads to a broadband monotonically increasing PPC spectrum.
RESULTS
We analyzed three CGID task sessions each from two subjects (R, S) with simultaneous microelectrode array (MEA) implants in three motor areas (M1, PMv, PMd) (see The cued grasp with instructed delay task). Each session yielded between 46 and 114 correctly executed 7-s CGID trials, collected over 20 min to 1 h. For each session, each MEA yielded between 7 and 48 well-isolated and high-SNR single units, for a total of 699 unit recordings. Of these, 292 exhibited sufficient firing rates during the steady-state movement preparation periods of the task to permit further analysis. Steady-state periods corresponded to an attentive waiting period in the first second before object presentation and a movement preparation period 1 s before the go cue (see methods).
Sustained neuronal firing rates and beta-rhythmic spiking can be dissociated from β-LFP oscillations during steady-state movement preparation periods.
We observed isolated single units that exhibited sustained rhythmic firing at beta frequencies during the steady-state movement preparation periods of the CGID task (e.g., Figs. 1 and 4). Concurrently, β-LFP power was elevated during steady-state movement preparation periods of the CGID task, including the first second of the task before object presentation (pre-object period) and the 1 s leading up to the go cue (pre-go period). The phase of the β-LFP at which example single units spiked appeared to drift over various short β-LFP transients (e.g., Fig. 1C). Inspection of STAs revealed little reliable phase relationship, and examples, shown in Fig. 1C, confirmed these initial observations, showing only a spiking artifact, i.e., a residual of the extracellularly recorded action potential in the low-pass filtered LFP data. We explore in depth this apparent decoupling of highly rhythmic single neurons from the population oscillation evidenced on the LFP in the following sections.
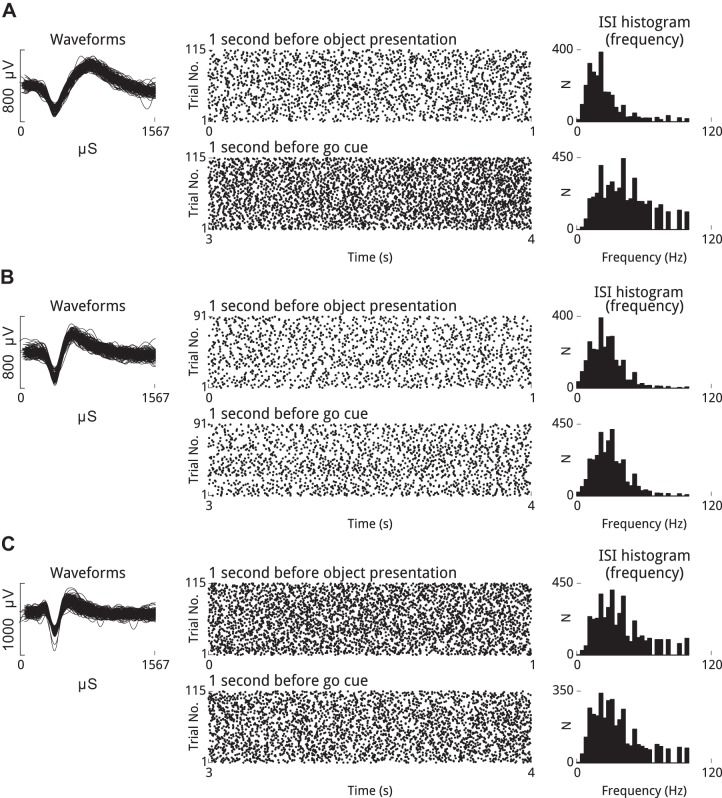
Fig. 4.
Well-isolated single units can fire rhythmically at beta frequency, and firing rates are stable across trials during movement preparation periods. Shown are 3 well-isolated units that exhibited beta-rhythmicity during the steady-state movement preparation periods of the CGID task (left). Spike rasters (middle), which show trial number on the vertical axis and task time on the horizontal axis for the 2 steady-state epochs, reveal that these units fired in a rhythmic manner that was reliable over trials and sustained across the steady-state periods. The modes of the ISI distributions for these units, expressed in terms of frequency, show that these units fired with a preferred frequency in the beta range (right). In several cases the mode frequency differed between the steady-state period at the beginning of the trial, before visual cues had been provided, and the 1-s period preceding the go cue. A: unit 43 from area PMd, subject S, session 3. B: unit 49 from area PMd, subject S, session 2. C: unit 20 from area M1, subject S, session 3.
To investigate systematically the relationship between neurons that fire rhythmically at beta frequencies with the β-LFP, we developed criteria to identify beta-rhythmic neurons within the population. We categorized units on the basis of features of their ISI distributions (see ISI histogram statistics) during the steady-state movement preparation periods (Fig. 2, A and B). A total of 699 units exhibited well-isolated spiking. Of those, 71% (499/699) met the minimum SNR cutoff of 3.0 for inclusion in the analysis, 54% (377/699) exhibited at least 100 ISI events during the task steady-state epochs, and 42% (292/699) met both conditions and were suitable for analysis. (See methods for more details on the inclusion criteria.) Of these 292 well-isolated single units that satisfied the inclusion criteria, 66% (192/292) showed a unimodal peak in ISI events longer than 10 ms during the two steady-state movement preparation periods. A subset of units (25%, 72/292) exhibited bursting as evidenced by bimodal ISI distributions with a second peak in short-latency (<10 ms) ISI events while also exhibiting an overall slower rhythmicity. A minority of units (7%, 21/292) showed low firing rates and irregular Poisson-like spiking or had an ISI distribution that could not be clearly categorized (2%, 7/292).
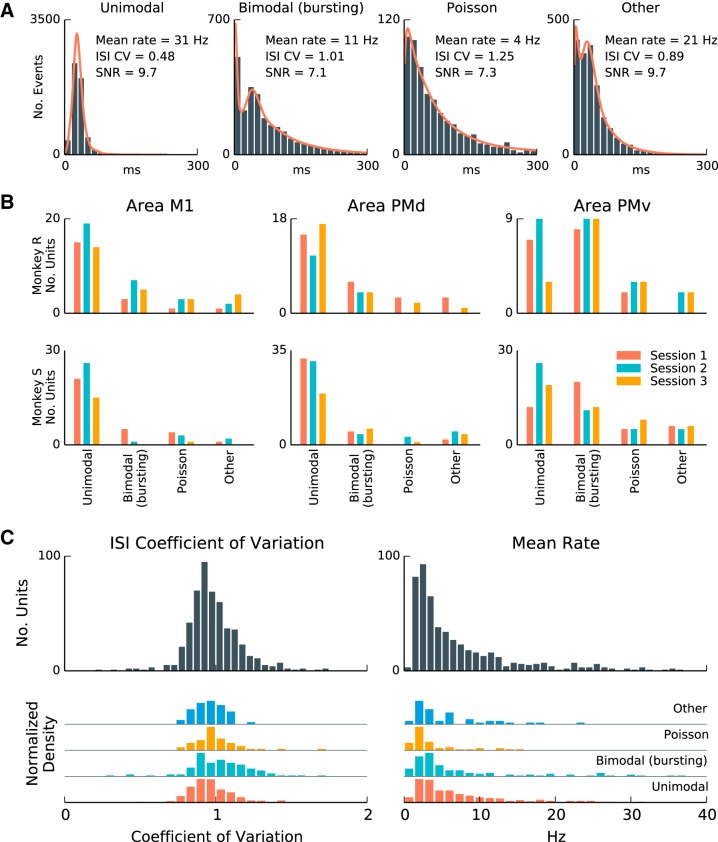
Fig. 2.
A subset of units fire rhythmically during steady-state movement preparation periods of the CGID task. A: interspike interval (ISI) distributions from selected well-isolated units during the steady-state periods of the CGID task. In each plot, from left to right, we see rhythmically firing units, units that exhibit both bursting and rhythmicity, units that exhibit Poisson-like firing, and units that exhibit intermediate ISI distributions. The ISI coefficient of variation (CV) reflects the dispersion of the ISI distribution, with low CV correlating with rhythmicity. SNR is the signal-to-noise ratio for unit waveform. B: single units were categorized on the basis of ISI features (see methods) as unimodal (rhythmic), bimodal (bursting and rhythmic), Poisson process-like (i.e., exponential with refractory period), or intermediate ISI distributions (other). In both subjects and all areas, single units with unimodal and bimodal ISIs were most prevalent. C: a summary of ISI mean and CV statistics for the same units. Statistics of ISI distributions varied continuously and did not form discrete clusters. Mean rate was variable, with 25% of units exhibiting mean rates higher than 10 Hz. Because some rhythmic units start and stop firing during the steady-state epochs, and because the rhythmic frequency may change over time and across trials, the effective CVs were larger than expected for sustained rhythmic firing at a single narrowband frequency.
We considered identifying the above three classes, (refractory) Poisson-like spiking, bimodal (bursting/rhythmic), and unimodal (rhythmic) units with the three neuron types I, II, and III described by Chen and Fetz (2005), each of which exhibits different characteristic spike waveforms. However, Baranyi et al. (1993a; 1993b) described a larger number of neuronal subtypes in motor cortex, with overlapping firing statistics and spike waveform shapes, and we found that 63% (185/292) of units exhibited ISIs that could not be clearly identified with any of the categories in Chen and Fetz (2005). We tentatively identified 38% (21/55) irregular Poisson-spiking units with type I, 31% (22/72) bursting units with type II, and 33% (64/192) units exhibiting fast regular spiking with type III.
The overlap between the distributions of firing statistics for each neuronal subtype in our data was too large to allow classification. Previous work has highlighted that intrinsic neural properties can be heterogeneous (Battaglia et al. 2013). Because of these ambiguities in identifying neuronal subtypes on the basis of spike train statistics, we focused on units that exhibited a clear mode in the ISI between 20 and 100 ms, which may potentially exhibit rhythmicity at the same frequencies as β-LFP. Two summary statistics, the ISI coefficient of variation (CV) and mean firing rate, are shown in Fig. 2C.
We also note that several of the single units that exhibited rhythmic firing during the movement preparation periods dramatically changed their firing statistics during the movement execution period (Fig. 3). Following the go cue, many units increased or decreased their firing rates (e.g., Fig. 3, A, C, and D) as expected. Some units did not show abrupt changes following the go cue, but rather a gradual shift over the course of the preparatory period (e.g., Fig. 3B). In this task, the cue times were predictable, and these gradual shifts may have reflected ramping in anticipation of the cue. More importantly, some units that exhibited unimodal/bimodal ISI distributions (a potential signature of rhythmic firing) during the preparatory period shifted to more Poisson-like spiking following the go cue (Fig. 3D). This finding suggests that rhythmic spiking need not be a fixed subthreshold resonance property of these neurons, and instead likely reflects the network state during the preparatory and delay periods.
Fig. 3.
Single-unit ISI statistics change across different stages of the task. Shown are 4 examples of how the ISI distributions change for well-isolated units over the course of the CGID task. Insets specify the mean rate μ and the mode frequency derived from the mode of the ISI distribution. Each ISI histogram was computed on the basis of nonoverlapping 0.5-s time windows of the CGID task. All trials within a session were combined. Examples illustrate a highly rhythmic unit (subject R, session 2, unit 101) that decreased its mean firing rate during the movement epoch (0.5 s after go cue) without changing its mode (A); a highly rhythmic unit (subject S, session 1, unit 74) that steadily increased both its ISI mode frequency and mean firing rate, transitioning gradually over the task from μ = 25 Hz at the trial outset to μ = 66 Hz during the movement epoch (B); a unit (subject R, session 3, unit 92) whose firing became more variable, with a slight decrease in mode frequency, only during the movement epoch (C); and a unit (subject R, session 1, unit 88) that switched from rhythmic firing at beta frequency ~11–17 Hz to Poisson-like firing at a much higher rate of 123 Hz (D). These examples emphasize that the rhythmicity observed in a subset of units during the steady-state movement preparation periods of the CGID task was unlikely to arise exclusively from intrinsic neuronal properties (e.g., subthreshold resonance). Instead, this rhythmicity likely reflected and was modulated by the collective network state. The colored traces represent the transformed kernel density estimation (KDE) of the distributions used to determine the ISI mode and is shown to confirm that the mode estimation procedure approximates well the location of the ISI mode firing frequency (see ISI histogram statistics).
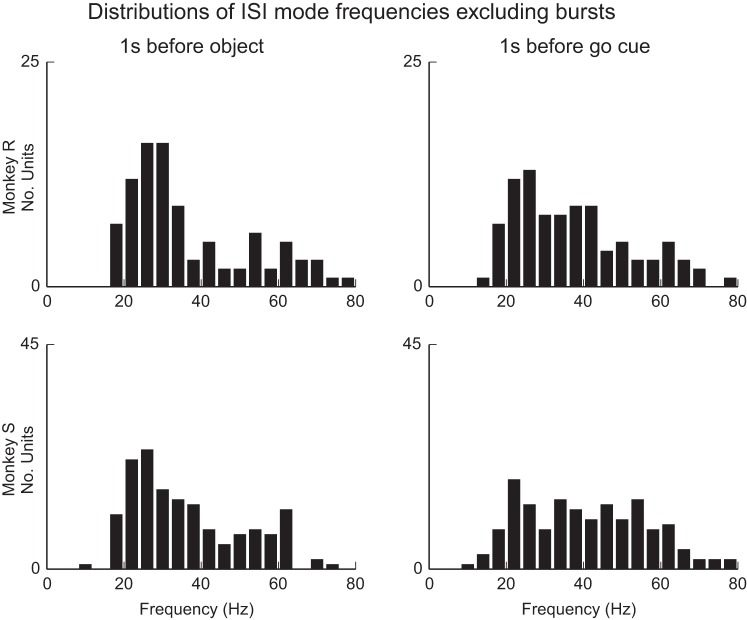
We observed that most rhythmically firing units tended to fire in a sustained manner during the examined steady-state periods, with high reproducibility across trials in terms of mean firing rates and ISIs (e.g., Fig. 4). Inspection of the firing mode frequency for rhythmic units (Fig. 5) revealed that the preferred firing frequencies were concentrated between 10 and 45 Hz, overlapping the beta range. In the first steady-state epoch preceding the visual cues, 76% (78/103) of units showed an ISI mode frequency between 10 and 45 Hz for subject R and 74% (119/161) for subject S. In the second steady-state epoch following the visual cues and preceding the go cue, 73% (75/103) of units in subject R and 60% (96/161) of units in subject S fell between 10 and 45 Hz. Mode frequencies increased to some extent between the pre-and post-cued movement preparation periods (e.g., Fig. 4A), with the median mode frequency shifting from 30 to 34 Hz for subject R and from 32 to 39 Hz for subject S. This increase was statistically significant (P < 0.05) in 5/6 sessions after a Benjamini-Hochberg false discovery correction for multiple comparisons (Benjamini and Hochberg 1995).
Fig. 5.
The preferred mode firing frequency of rhythmic units varies but tends to fall within the beta band. Shown are summary distributions, pooled over all sessions and areas, for both subjects during the 2 steady-state movement preparation epochs for units that showed unimodal and bimodal ISI distributions. Mode firing frequency for isolated single units ranged between 10 and 80 Hz, but for each monkey and epoch, between 60% and 75% of units fell within the range 10–45 Hz. Firing rates were higher in the pre-go delay period that followed visual cue presentation. (Wilcoxon signed-rank test, P < 0.05; 5/6 sessions significant with Benjamini-Hochberg correction for an FDR of 0.05.)
Dissociation between beta-rhythmic spiking and β-LFP during steady-state movement preparation periods: summary over population.
Given that a majority of isolated single units exhibited sustained rhythmicity close to beta frequencies during the steady-state movement preparation periods of the CGID task, we investigated the extent to which this beta rhythmicity was evident in LFP oscillations. In both subjects, the LFP showed task-related changes in its power spectrum, especially in the beta band. Consistent with previous studies, the movement period was associated with suppression of β-LFP power. Importantly, beta was also transiently suppressed following the visual cues. In contrast, beta was elevated during steady-state movement preparation periods of the CGID task, including the first second of the task before object presentation and the 1 s leading up to the go cue.
For subject S, the beta peak was identified between 22 and 25 Hz for all areas and sessions. Subject R exhibited two beta-frequency peaks, 16–19 Hz and 23–36 Hz. These two different beta frequencies may potentially correspond to the “beta1” (~15 Hz) and “beta2” (~25 Hz) oscillations previously examined in experimental and computational studies (Kopell et al. 2011; Roopun et al. 2006; Roopun et al. 2008). Roopun et al. (2008) suggest that beta1 emerges as a result of a concatenation of one period of beta2 with one period of a (~40 Hz) gamma oscillation. Whether the dual bands observed in subject R are related to this concatenation phenomenon remains an open question. Because the second beta peak in subject R was much broader, we focused the present analyses on the beta activity at 16–19 Hz for this subject and on that at 22–25 Hz for subject S.
To comprehensively quantify the relationship between single-unit firing and the phase of ongoing β-LFP oscillations, we used two measures of spike-field coupling that are designed to avoid the biases inherent to STA and spike-field coherence approaches: the pairwise phase consistency (PPC; Vinck et al. 2010; see Pairwise phase consistency) and point process generalized linear models (GLMs), which expressed the conditional intensity (instantaneous spiking rate) as a function of the phase of the ongoing β-LFP oscillations (see Point process GLM-CIF models for spike-LFP phase coupling). PPC assesses the tendency of a neuron to fire at the same phase of the ongoing β-LFP oscillation. It ranges from 0 for no phase coupling to 1 for perfect phase coupling.
For assessing spike-LFP phase coupling, we analyzed single units that showed unimodal or bimodal ISI distributions and exhibited a preferred firing frequency (ISI mode frequency) between 10 and 45 Hz. We observed that mean firing rates were typically lower than 10 Hz and on inspection found that rhythmic single units could skip some beta cycles. For this reason, we also required that units exhibit mean rates of at least 20% their mode frequency. Overall, 47% (125/264) of units were selected as exhibiting beta rhythmicity under these criteria. Of those selected, 23% (29/125) exhibited bimodal (bursting/rhythmic) ISIs and 77% (96/125) had unimodal ISIs. Both of these groups were analyzed for spike-LFP phase coupling. Of the units with unimodal ISIs, 40% (38/96) exhibited oscillations in their autocorrelation functions, 40% (38/96) exhibited a nonoscillatory postrecovery rebound, and 21% (20/96) exhibited irregular Poisson-like spiking with a long recovery period that placed their mode frequency in the beta range.
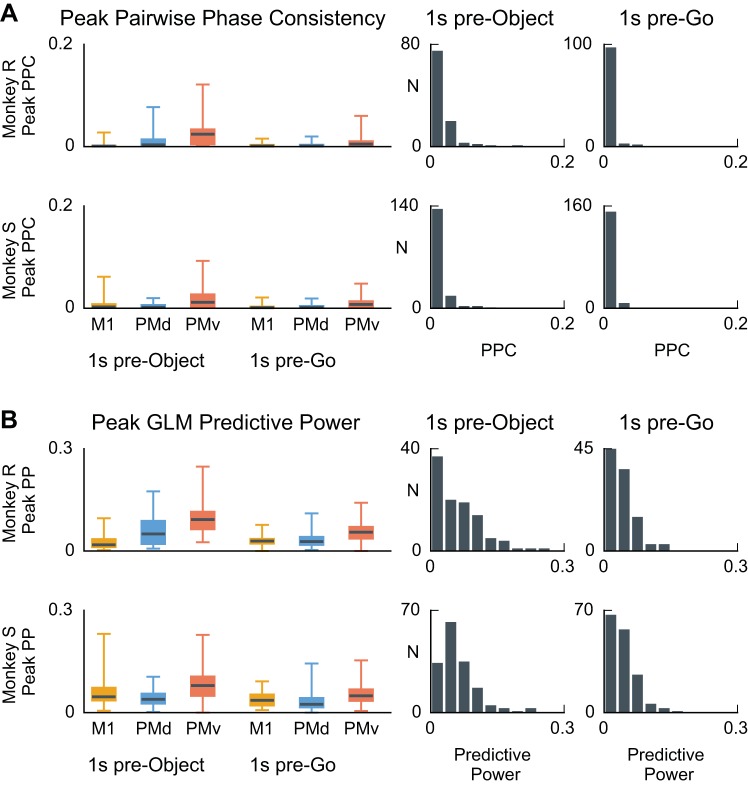
We found that PPC values during the 1-s steady-state epochs were typically close to 0 (Fig. 6A), with the median PPC for each session, area, and task epoch within the 0 to 0.12 range. Overall, 95% (118/125) of 382 units had a PPC value smaller than 0.03 during the pre-object period and less than 0.01 during the pre-go period. No unit had a PPC value that exceeded the 95% confidence interval for the null hypothesis PPC distribution, assessed by computing PPC between spikes and trial-shuffled LFPs. PPC values were surprisingly weak, given that one might expect the β-LFP and the beta-rhythmic spiking to relate to the same ongoing network phenomenon and thus be more strongly phase coupled. We also found similar qualitative results for the phase coupling if the analysis was restricted to the 200 ms immediately preceding the grip and go cues, indicating that phase coupling was not noticeably enhanced in anticipation of the task cues.
Fig. 6.
Spike-LFP phase coupling at the peak beta frequency is typically small during the steady-state movement preparation periods. A, left: box plots summarize the magnitude of the pairwise phase consistency (PPC) value at the beta peak (see methods, Pairwise phase consistency). Whiskers extend to the minimum and maximum values. Each area is summarized separately for each subject and for 2 steady-state periods: the first second of the task before object presentation (pre-object) and the 1 s before the go cue (pre-go). Right, histograms representing the distribution of PPC values for each subject in the 2 task epochs. All sessions and areas are combined. Despite the spiking rhythmicity at beta and elevated β-LFP power, PPC values between spikes and LFP were typically negligible, with 95% of units showing PPC values below 0.04 for any given session or area. No units showed PPC above the 95% chance level as assessed by phase randomization of the LFP signals. B: spike-LFP phase coupling assessed by the predictive power of point process GLMs based on the phase of the ongoing beta oscillations (see methods, Point process GLM-CIF models for spike-LFP phase coupling) was also marginally close to zero. Although select units displayed predictive power as high as 0.24, predictive power was less than 0.1 for 95% (118/125) of units during both epochs. During the first steady-state period (pre-object), the predictive power exceeded the 95% chance level confidence interval for 39% (49/125) of the units. During the second steady-state period (1 s pre-go), the predictive power exceeded the 95% chance level confidence interval for 19% (24/total) of the units. We report these numbers without correcting for multiple comparisons, so 5% of units are expected to be above the 95% chance level. Point process GLMs based on the beta phase were able to detect weak phase coupling that the PPC did not.
As a complementary approach, we summarized phase coupling between single-neuron spiking and β-LFP oscillations by assessing the conditional intensity function (CIF) phase model’s ability to predict the timing of spikes (see methods). We report a measure of model performance “predictive power” (PP), which ranges from 0 for no prediction to 1 for perfect prediction (see Point process GLM-CIF models for spike-LFP phase coupling). In terms of phase coupling, a PP of 0 implies no coupling, and a PP of 1 implies perfect phase coupling. During the steady-state epoch preceding object presentation, 39% (49/125) units exceeded the 95% confidence interval for the null PP distribution, and during the steady-state epoch preceding the go cue, 19% (24/125) of units exceeded their 95% chance level. This suggests that true phase coupling is present. Although the predictive power was sometimes statistically significant (in one case as high as 0.24), it remained extremely low for the vast majority of units, with 94% (118/125) of units exhibiting a GLM phase model predictive power less than 0.1. Thus, consistent with the PPC results, the CIF phase model found relatively little stable phase coupling of spikes to β-LFP oscillations (Fig. 6).
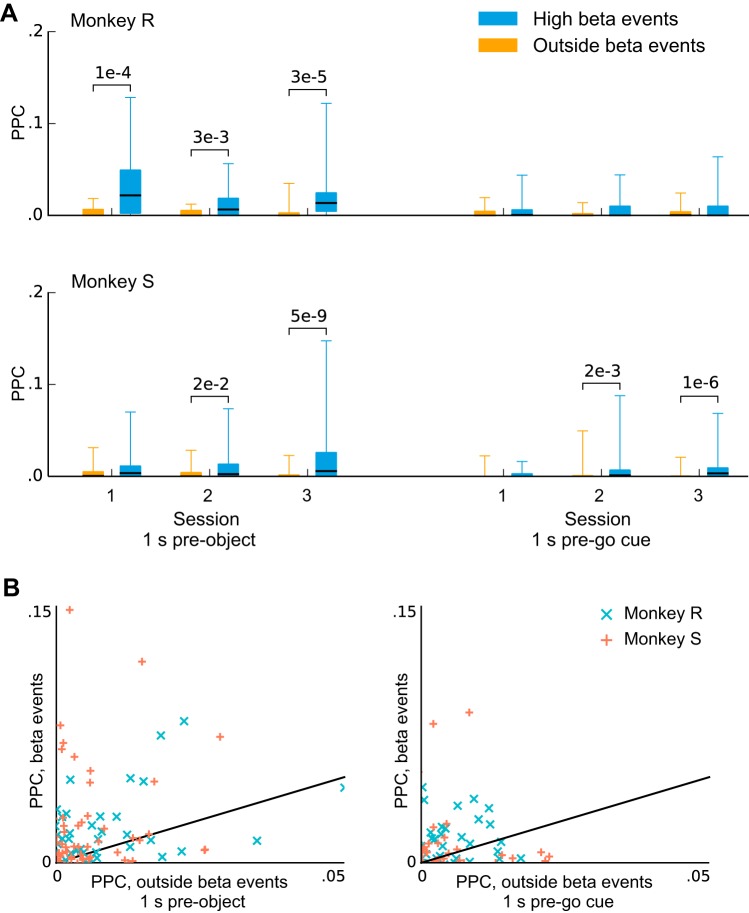
We considered the possibility that trial-to-trial variability in β-LFP dynamics affected our ability to detect β-LFP phase coupling. β-LFP power was rarely sustained across the entire steady-state task epoch, but rather occurred as short transient bursts (Fig. 7A). The timing of these transients varied, and they did not exhibit a characteristic duration that might indicate, for example, a stereotyped event or input into motor cortex (Fig. 7B). We tested the hypothesis that β-LFP phase coupling might be weak overall, but strong during these high-power transients due to increased collective β-LFP activity. We found that PPC values remained very small when the analysis was restricted to these transient high-beta LFP events (Fig. 8A). Nevertheless, such events were associated with an increase in phase coupling that was statistically significant in 7 of 12 session/epochs, indicating that the β-LFP power transients correlate with changes in spike-LFP phase coupling and synchronization [corrected for multiple comparisons using Benjamini-Hochberg procedure for 12 comparisons and a false discovery rate (FDR) of 0.05; Benjamini and Hochberg (1995)].
Fig. 8.
Pairwise phase consistency (PPC) increases marginally for some units when the analysis is restricted to high-beta transient events. A: box plots show PPC values at the peak beta frequency computed only during (transient) beta events with high power. Whiskers extend to the minimum and maximum values. Beta events were associated with a small but statistically significant increase in phase coupling in 7 of the 12 sessions/conditions. (P values were computed using the Wilcoxon signed-rank test for difference of medians and corrected with the Benjamini-Hochberg procedure for 12 comparisons with an FDR of 0.05.) B: the number of spikes used to compute PPC was matched between the high- and low-beta conditions by randomly thinning the group with more spikes. This analysis confirms that spike-LFP coupling remained weak even during high-beta events but also suggests that such events may also be associated with a modest increase in coupling.
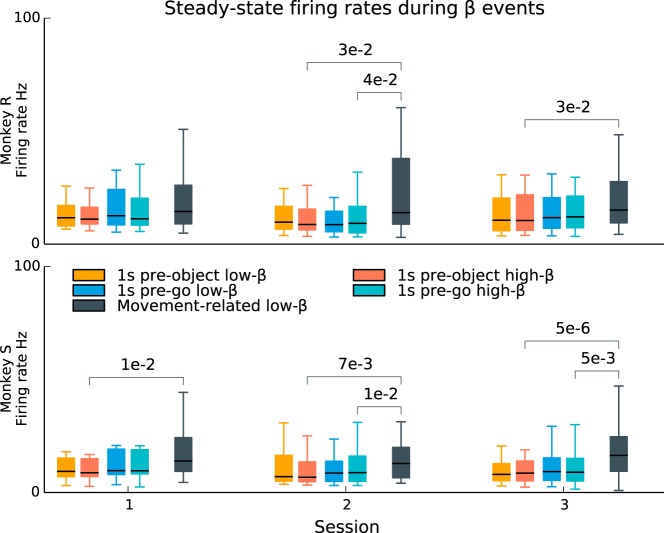
In addition, we found that there was relatively little difference in firing rate statistics during beta transients compared with periods outside beta transients (Fig. 9). In contrast, firing rates were significantly higher during movement-related beta suppression, showing statistically significant increases between the pre-object and movement periods in 5 of 6 sessions and between the pre-go and movement periods in 3 of 6 sessions. (Wilcoxon signed-rank tests for difference in the median, corrected for 24 multiple comparisons using the Benjamini-Hochberg procedure for a FDR of 0.05.) This finding indicates that the modulations in β-LFP power during steady-state movement preparation periods were dissociated from changes in the firing rates of the underlying neuronal population, as was the case during the movement execution- and visual cue-related beta suppression.
Fig. 9.
Single-unit firing rates during steady-state movement preparation periods are not affected by beta transients. During the steady-state movement preparation periods of the CGID task, β-LFP oscillations occurred as transient events. However, single-unit firing rates did not change between high-beta (Hilbert amplitude > 1:5σ) and low-beta time periods during these steady-state periods (box plots; whiskers extend to the minimum and maximum values). In contrast, beta suppression related to movement execution (after the go cue) was associated with increased firing. (P values were computed using the Wilcoxon signed-rank test for difference in medians and corrected for 24 multiple comparisons; 4 comparisons per session: high-low beta within each steady-state epoch and high beta in each epoch to movement-related low-beta; Benjamini-Hochberg procedure for an FDR of 0.05.) This result suggests that the transient beta power fluctuations during steady-state movement preparation periods may arise from a different mechanism than the power fluctuations (beta suppression) associated with movement execution.
Previous studies from our group, some using the same data sets analyzed in the present study, have shown that object and grip type can be decoded from spiking activity in the neuronal population during the movement preparation (Vargas-Irwin et al. 2010; Vargas-Irwin et al. 2015). Despite the observed weak coupling between spiking and β-LFPs, we examined whether β-LFPs also carried information about object and grip type during these steady-state movement preparation periods. We performed a decoding analysis by classifying object (2-class) and grip (3-class) on the basis of discriminative features consisting of single-channel beta power in either the 200 or 400 ms preceding the grip cue or go cue, respectively. The beta power was computed on the ~5-Hz band around the β-LFP peak (multitaper power spectral density, 10-Hz bandwidth). We used linear discriminant analysis (LDA) with leave-one-out trial cross-validation. Chance levels and P values were determined by sampling from a null hypothesis distribution generated by randomly permuting the grip and object labels for each trial. We have found no statistically significant classification (P > 0.05) of the object or upcoming grip movement from β-LFP power during the examined steady-state movement preparation periods.
Population spiking activity also shows only weak coupling to transient β-LFP oscillations.
We examined the possibility that the phase coupling between spiking and the transient β-LFP oscillations could be too weak to be detected, but much stronger if assessed at the level of the population spiking activity. Population spiking activity was defined as the total number of spikes (1-ms time bins) summed across the well-isolated single units within a given motor area, smoothed by a 25-ms boxcar filter (see methods). For each motor area we computed the cross-correlation function between the population spiking activity and the β-LFP averaged across the channels in the area. Cross-correlation functions were computed for time lags ranging over one beta cycle (± 25 ms). A cross-correlation function was computed for each area, epoch, session, and subject.
The extrema of the cross-correlation functions between population spiking activity and the mean β-LFP were also very small, ranging from 0.0039 to 0.042. After correction for 36 (subject, session, area, epoch) comparisons using the Benjamini-Hochberg procedure with an FDR of 0.05 (Benjamini and Hochberg 1995), three correlations were statistically significant, all in subject S. Subject S area PMv showed significant correlations of 0.036 and 0.033 for sessions 1 and 3, and subject S area M1 showed a significant correlation of 0.042 for session 3. P values were obtained from a chance level distribution: cross-correlation function peaks were computed from resampled data generated by shuffling the LFP trials (2,000 resamples).
Single units show weak coupling to measures of population activity.
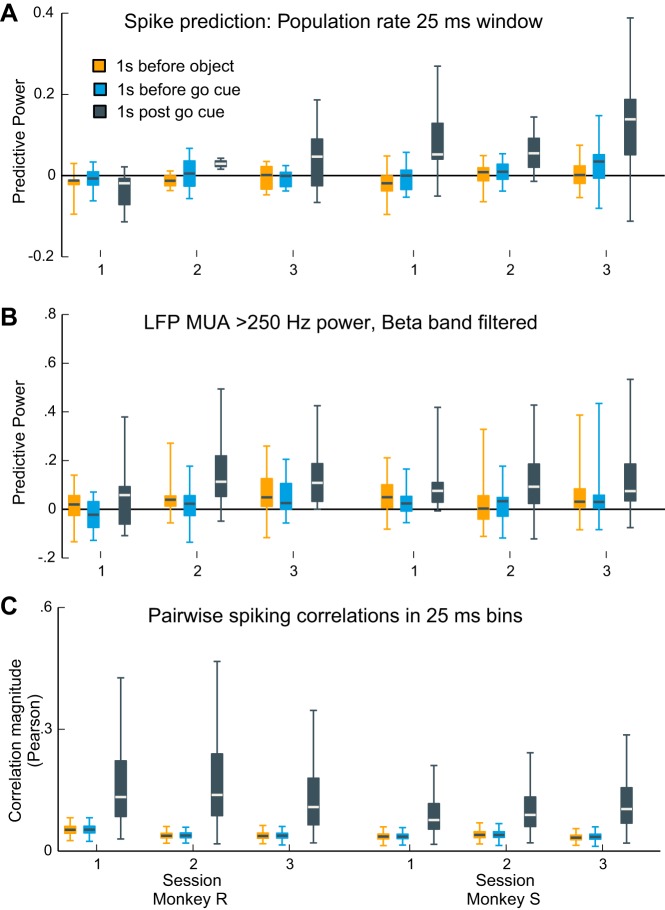
Previous studies in sensorimotor cortex have demonstrated strong coupling of single-neuron spiking to both the population spiking activity (Aghagolzadeh and Truccolo 2014; Aghagolzadeh and Truccolo 2016; Okun et al. 2015) and ensemble spiking histories (2010) during sensory stimulation and movement execution. In particular, Aghagolzadeh and Truccolo (2014; 2016) show that, in the same data sets examined in the present study, single-neuron spiking is strongly coupled to low-dimensional representations of the neuronal ensemble activity during the movement execution phase of the CGID task. For completeness, we thus also considered the possibility that spiking could be only weakly coupled to the transient β-LFP, but at the same time show strong coupling to other measures of the population activity during the movement preparation epochs. Using point process GLM analysis (see Point process GLM-CIF models for relating single-neuron spiking), we found that single-neuron spiking was only weakly related to the population spiking activity during the steady-state movement preparation periods (Fig. 10A). In contrast, and consistent with previous work (Rule et al. 2015), predictive power was higher during the 1-s movement period following the go cue.
Fig. 10.
Contrasting collective neural dynamics between steady-state movement preparation and movement execution periods. A and B: predictive power of point process GLM models for beta-rhythmic single-neuron spiking based on the population spiking activity (see methods). A: spiking prediction based on the population spiking activity measured on the same MEA (excluding the unit being predicted). Each box plot summarizes the distribution of predictive power values for 1 session and epoch (whiskers extend to the minimum and maximum values). Predictive power during steady-state movement preparation periods (colored bars) was typically distributed around chance level. In contrast, population spiking activity predicted single-unit spiking above chance levels during movement execution (black bars). B: single-neuron spiking prediction based on MUA using the same point process GLM approach as in A. MUA was defined as the >250-Hz LFP rectified amplitude envelope bandpass filtered in the 5-Hz band surrounding the peak beta frequency. Predictive power trends are similar to those obtained in A for the population spiking activity. C: box plots summarize the distribution of peak absolute pairwise (Pearson) correlation coefficients of 25-ms binned spike counts. Pairwise correlations were weaker during steady-state movement preparation periods compared with the movement execution period.
Qualitatively similar results were obtained with the use of another measure of population activity consisting of multiunit activity (MUA), defined as >250-Hz LFP rectified amplitude fluctuations (Fig. 10B) bandpass filtered in the 5-Hz band surrounding the peak beta frequency (see methods). Specifically, median PP values during the two movement preparation epochs (pooled across motor areas) were distributed around chance level, ranging from 0 to 0.05 (pre-object period), and pre-go period median PP ranged from 0 to 0.03 (pre-go cue period). During the movement period, median PP values ranged from 0.06 to 0.11. PP values during movement were statistically significantly higher than those in the pre-object period in two sessions for subject S and were higher than those in the pre-go period in one session in subject R and all sessions in subject S (Wilcoxon signed-rank test with Benjamini-Hochberg correction for an FDR of 0.05 for 12 comparisons). This analysis confirmed that measures of population activity in the CGID task could predict single-unit spiking but showed that this predictive information was much weaker during the steady-state movement preparation periods. Corroborating the increased coupling of single units to populating activity, we observed that the peak cross-correlation values (25-ms bins) between pairs of neurons were substantially higher during the movement period (Fig. 10C).
Finally, we investigated whether MUA might show more substantial phase coupling to β-LFP. We examined two measures of MUA: 1) all threshold crossings (unsorted spikes) occurring on the same channel as the β-LFP and the four nearest neighbor channels (spiking-MUA), summed in 1-ms bins, and 2) the amplitude envelope in >250-Hz filtered LFP as described previously (LFP-MUA). Beta coherence between these measures of MUA and the β-LFP on the same channel were weak: we found a statistically significant coherence peak between β-LFP and LFP-MUA in 4% of channels and between β-LFP and spiking-MUA in 8% of channels. A strong coherence peak between spiking-LFP and MUA-LFP was also rare, with only 9% of channels exhibiting a significant beta peak. All coherence results are reported at the P < 0.05 level, corrected for an FDR of 0.05 using the Benjamini-Hochberg correction. The β-LFP peak was identified as the largest local maximum within 10–45 Hz. All P values were computed as in Jarvis and Mitra (2001) and Pesaran et al. (2008).
Overall, the above results show a stark contrast between collective dynamics during the steady-state movement preparation periods in the CGID task, where spiking activity appears to be much more asynchronous, and collective dynamics during movement execution, where both the ability of population activity to predict single-neuron spiking and pairwise correlations are much higher.
Narrow- and broad-spike waveform neurons show similar weak phase coupling to β-LFP oscillations during preparatory steady states.
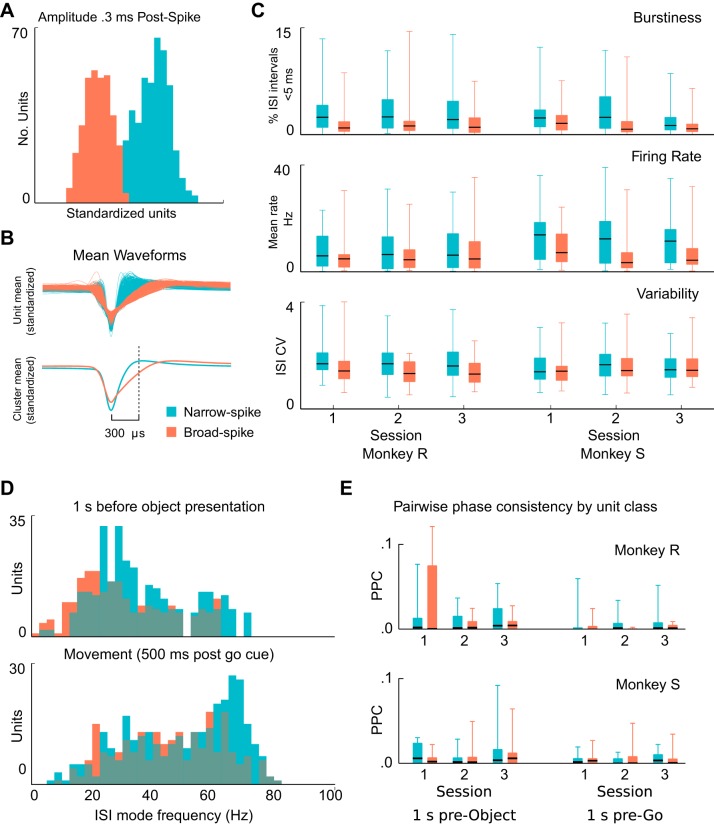
Waveform features of recorded extracellular action potentials can correlate with neuronal types. We further examined whether the examined single neurons showed waveforms that clustered into different groups and whether these groups showed distinct properties in the terms of spike and β-LFP phase coupling. Recorded extracellular action potential waveforms tended to cluster into “narrow” (42%, 124/292) and “broad” (58%, 168/292) classes (Fig. 11, A and B; see Unit categorization). We observed a partial agreement between ISI features and the extracellular waveform categorizations consistent with Chen and Fetz (2005): 62% (13/21) of putative type I neurons exhibited broad spikes, and 86% (19/22) of type II (bursting) neurons and 72% (46/64) of putative type III (fast rhythmic) neurons exhibited narrow spikes. We note that Chen and Fetz (2005) suggested that the rhythmic firing observed in the bursting neurons in their study was likely to arise from network interactions and not intrinsic neuronal properties, as is the case for the type III neurons.
Fig. 11.
Single units cluster into narrow- and broad-spike waveform groups, but these groups show no consistent differences in PPC values. Spike waveforms recorded in motor cortex exhibited a diversity of spike widths that clustered into 2 main groups. A: histograms show the clustering of well-isolated units according to spike widths, including all sessions, areas, and subjects. Clustering based on the amplitude of the normalized waveform 300 μs after the spike peak provided better separation than the traditional approach of estimating the spike width at half maximum. Narrow-spike units are denoted in blue and broad-spike units in red. B: traces of the mean waveform for narrow-spike and broad spike units illustrate the differences between the unit classes. C: narrow- and broad-spike units showed consistent differences in firing statistics. On average, narrow-spike units fired more bursts (top), fired at higher mean rates (middle), and exhibited higher coefficients of variation (bottom). However, none of these apparent differences were statistically significant (Mann-Whitney U-test with Benjamini-Hochberg correction for an FDR of 0.05 for dependent samples and 18 comparisons.) Box plot whiskers extend to the minimum and maximum values. D: preferred spiking frequency (ISI mode) of narrow-spike and broad-spike units changed with different CGID task stages. Units for all sessions, subjects, and areas were combined in these summary histograms. During the first second of the task, both narrow- and broad-spike units fired rhythmically around beta frequency. During movement execution, firing rates increased on average, but the increase was most notable for narrow-spike units. E: beta-peak PPC values showed no consistent trend in the differences for narrow- vs. broad-spike units. Furthermore, none of the differences were statistically significant (Mann-Whitney U-test with Benjamini-Hochberg correction for an FDR of 0.05 for dependent samples and 18 comparisons).
These two classes appeared to exhibit differences in firing statistics. Overall, narrow-spike neurons exhibited more short-ISI events (<10 ms), indicative of bursting, fired at higher rates, and had greater CVs (Fig. 11C). The ISI mode frequency of narrow-spike units appeared typically slightly higher during the steady-state movement preparation periods. In addition, narrow-spike units appeared to show a greater increase in their mode firing frequency during movement compared with broad-spike neurons (Fig. 11D). These apparent differences between the two classes, even though consistent across subjects and sessions, were not statistically significant (Mann-Whitney U-test with Benjamini-Hochberg correction for multiple comparisons for positively dependent samples and an FDR of 0.05). Additionally, no consistent differences were found between narrow and broad spike units with respect to spike and β-LFP phase coupling (Fig. 11E).
DISCUSSION
In this study, we have characterized a strong dissociation between sustained neuronal firing rates and beta-rhythmic spiking and transient β-LFP oscillations in primate motor cortex during steady-state movement preparation periods of a visually cued reaching and grasping task. We observed that firing during steady states was rhythmic and sustained for many of the recorded single neurons. In contrast, β-LFP oscillations emerged as short transients that exhibited high trial-to-trial variability during the same movement preparation periods. The fact that single-neuron firing rates were neither affected by the occurrence of transient β-LFP events nor correlated with β-LFP amplitude suggests that the modulations in β-LFP power during these steady-state periods did not result from changes in the level of beta rhythmicity in the underlying neuronal population activity reflected in the recorded β-LFP signals, as is the case for movement- and visual cue-related beta suppression. Furthermore, two complementary measures of spike-LFP phase coupling (pairwise phase consistency and predictive power of point process GLMs) showed that the coupling was at chance level for the majority of the neurons. This dissociation between steady rhythmic spiking and β-LFP oscillations has implications for understanding the multiscale (single neuron and ensembles) dynamics underlying the generation of the measured mesoscopic β-LFP signals and for understanding the functional role of beta oscillations in motor cortex, including putative roles for beta in modulating communication among cortical areas and phase coding. Our findings also contribute to the characterization of the statistical properties of neocortical electrical signals recorded via MEAs.
Precedence for dissociation between single-neuron spiking activity and narrowband LFP oscillations in neural systems.
Among various components, LFPs are thought to reflect to a large extent synaptic activity, i.e., inputs to neurons (e.g., Buzsáki et al. 2012). The intuition that spiking outputs reflect synaptic inputs suggests that strong LFP oscillations might imply strong spike-LFP phase coupling. Our findings of weak phase coupling, then, might seem to challenge this intuition. However, LFP reflects spatial averages of synaptic activity over relatively large ensembles of neurons. How strongly correlated LFPs are to synaptic activity in single neurons remains an open question and is likely to depend on neural state and cortical area. Several previous experimental and theoretical studies (Ardid et al. 2010; Baker et al. 2003; Brunel and Wang 2003; Geisler et al. 2005; Harvey et al. 2009; Hoseini and Wessel 2016; Truccolo et al. 2011; Truccolo et al. 2014) have shown that narrowband LFP oscillations can coexist with weakly coupled single-neuron spiking activity, from which a population oscillation can nevertheless emerge as a collective mean field effect of the neuronal ensemble dynamics.
In particular, a precedent for the dissociation between single-unit rhythmicity and ongoing LFP oscillations has been studied in rodents for many years as the hippocampal “theta phase precession” (e.g., Harvey et al. 2009). During spatial navigation, the phase at which place cells fire relative to theta LFP depends on the animal’s past, present, and planned location. As a result, the phase at which neurons spikes relatively to the ongoing theta LFP drifts. Because of this, units show weak phase coupling to LFP if averaged even over short time periods (i.e., a few cycles). Despite this weak coupling, Harvey et al. (2009) find that place cell spiking is nevertheless strongly phase coupled to theta oscillations in the intracellular membrane potential. Their finding indicates that the “local” synaptic oscillation that impinges on single-unit spiking can appear dissociated from the population oscillation reflected in the LFP. It illustrates that LFP oscillations need not be a good proxy for the synaptic input and membrane potentials driving the spiking of specific single neurons. As Harvey et al. (2009) discuss, several alternative computational models have been put forward to explain the drift leading to phase precession and the resulting weak coupling. It remains to be clarified whether neurons in motor cortex also exhibit a similar phase drift phenomenon, and if so, whether phase drifts are explained by a more complex relationship (e.g., phase precession) or have any functional significance.
In the visual cortex, recent work by Haider et al. (2016) show that LFPs can predict excitatory and inhibitory postsynaptic potentials (EPSPs and IPSPs, respectively). However, the explained variance was relatively small for both EPSPs and IPSPs, with the latter being better predicted during stimulation. Furthermore, Haider et al. (2016) note that their finding is not inconsistent with previous studies showing weakly correlated spiking activity in neuronal pairs in V1 and the significant decorrelation between single-neuron spiking and nearby LFPs during visual stimulation (Nauhaus et al. 2009; Ray and Maunsell 2011). In fact, they argue that because inhibition may enhance processing by decorrelating spiking activity in a neuronal population, and because LFPs in V1 tend to be more correlated with IPSPs during stimulation, one should observe a decorrelation between single-neuron spiking and the population signal reflected in LFP oscillations.
In the case of narrowband gamma oscillations, Brunel and Wang (2003) have demonstrated with computational analyses how the previously observed coexistence of narrowband gamma and highly irregular spiking (and therefore weak phase coupling) can emerge in neocortical activity. Recent experimental results by our own group based on spike-LFP PPC analyses have shown weak coupling (PPC values <0.1) between single-unit spiking and narrowband (~50 Hz) gamma LFP oscillations induced by optogenetic stimulation in nonhuman primate motor cortex during awake and behavioral states (Lu et al. 2015). More recently, Ni et al. (2016), using a similar optogenetic stimulation protocol in cat area 21a (homologous to V4), find even weaker coupling between multiunit and narrowband gamma LFP (mean peak PPC values of ~0.003 and ~0.014 in 2 cats, respectively). Jia et al. (2013; see e.g., their Fig. 1B), using spike-field coherence instead of PPC, also find low mean coherence values in V1-V1 pairs (mean values <0.1, computed across all pairs), based on both multiunit and single-unit data during visual evoked responses.
In the particular case of motor cortex β-LFPs, other studies have examined the issue of spike-LFP coupling. Witham and Baker (2007) find that the level of β-LFP power in a given area need not correlate with the corresponding single-unit rhythmicity in the same area, and Baker et al. (2003) observe relatively weak spike-field coherence in beta during the execution of an isometric force precision grip task. We emphasize that our work goes beyond these studies by examining neural activity during steady-state movement preparation and instructed delay periods, as opposed to execution of isometric force precision grip tasks. In addition, we note that in contrast to spike-field coherence, the phase-coupling measures adopted in the present study can correctly quantify strong phase coupling even if single-neuron spiking, though phase-locked to a LFP oscillation, skips most cycles of the oscillation. Beyond these studies based on isometric force tasks, we have shown that phase coupling remains weak even when the short transient nature of β-LFP events is taken into account, i.e., by restricting the analysis to transient periods of elevated beta activity. More recently, analyses by Denker et al. (2007) have indicated that phase coupling may occur primarily during beta transients during movement preparation periods. Our work extends the characterization of preparatory beta oscillation by explicitly examining the relationship between transient β-LFP and single-unit firing rates and rhythmicity. Given our focus on neurons showing β-rhythmic spiking during β-LFPs, we also note that the phenomenon reported presently differs from the scenario examined by Brunel and Wang (2003), where spiking remained highly irregular despite narrowband LFP oscillations. The coexistence of sustained beta-rhythmic spiking with β-LFP transients, as well as the relatively weak phase coupling of single units to the β-LFP and mean population activity, are important features that should be recapitulated in computational models of motor cortex.
Statistical considerations.
When both LFP and spikes exhibit autocorrelations in the form of narrowband oscillations, there is risk of detecting apparent phase coupling by chance. This is true even for estimators that correct for spike-rate biases, such as the PPC. We addressed this problem by obtaining empirical chance level distributions through phase randomization and shuffling of trials. Nevertheless, any potential spurious contributions of these temporal correlations to inflated phase coupling assessments would only reinforce the points being made in this article. As stated above, both the PPC and point process GLM phase coupling assessments are capable of detecting a preferred phase of firing relative to the β-LFP even when cells do not spike on every cycle. This is because the PPC relies primarily on the distribution of spike-triggered LFP phases (as does the point process GLM, albeit indirectly), and a phase-locked unit that fires only occasionally still exhibits a concentrated spike-triggered distribution of LFP phase.
Localization of β-LFP activity.
A natural question is whether the dissociation between spiking and β-LFP oscillations results from LFPs not being as local as commonly thought (Kajikawa and Schroeder 2011). We observed that adjacent electrodes often exhibited very different β-LFP phases, indicating that localization on the order of the electrode spacing (400 μm or smaller) is possible. As a cautionary note, however, this does not exclude the possibility that local beta oscillations may mix with remote sources during transient globally synchronous states. Nevertheless, a recent study in primate visual cortex (Dubey and Ray 2016) using the same type of MEA as in our recordings also suggested a localization on the order of ~400 μm. Another possibility is that the single units and the sources of the LFP signal were located in different cortical layers. Identifying the laminar origin of β-LFP is not possible with the MEA recording setup used in our present study because LFP can conduct between layers. Previous studies have shown that β-LFP power is highest in layer V of motor cortex (Murthy and Fetz 1996a; Witham and Baker 2007) and that pyramidal tract layer V neurons can fire rhythmically in the beta frequency (Wetmore and Baker 2004). Given the uncertainty about the depth of the MEA implant, it is possible that the single units we recorded were from layer II-III and that single-unit spiking activity could then be dissociated from β-LFP arising in layer V. If so, the existence of rhythmic layer II/III spiking and its dissociation from β-LFP in deep layers would raise important questions about the role of different cortical layers in beta oscillations, as well as the interpretation of spiking activity and LFPs recorded from MEAs.
Origins of single-neuron spiking beta rhythmicity and β-LFP transients.
The origin of sustained beta-rhythmic spiking and its weak coupling to β-LFP transients across movement preparation remains puzzling. One possibility is that very specific subsets of neuronal types (e.g., inhibitory interneurons, etc.) might show a stronger coupling with the ongoing β-LFP oscillations. Recorded single units clustered into two classes of narrow and broad spikes, suggesting different types of neurons. These two classes are commonly associated with putative inhibitory interneurons and principal cells, respectively (Barthó et al. 2004; McCormick et al. 1985). However, the unique features of pyramidal tract neurons (PTNs) makes identifying putative inhibitory interneurons vs. excitatory pyramidal cells from extracellular spike width and firing properties challenging. Some PTNs show higher firing rates and narrow-spike waveforms and can be mistaken for fast-spiking interneurons (Vigneswaran et al. 2011). More advanced approaches that identify or manipulate specific neuronal subtypes will be needed to clarify the relation between single-unit beta-rhythmic spiking and β-LFP. Previous computational and experimental studies on the origin of beta oscillations have emphasized a variety of mechanisms ranging from the role of thalamic inputs (Jones et al. 2009) to more local or intrinsic features of cortical dynamics (Kopell et al. 2011; Roopun et al. 2006). Regarding the latter, Kopell et al. (2011) proposed that the “beta1” rhythm (~15 Hz) in rat association cortex arises as a consequence of rebound from inhibition and can be maintained without strong collective activity. Roopun et al. (2006) also found in in vitro neocortical slices from rats a 20- to 30-Hz rhythm in layer V pyramidal tract neurons that depends on intrinsic currents and is synchronized by gap junctions. Thus beta rhythmicity may be supported by the subthreshold dynamics of single units, possibly related to the slow afterhyperpolarizations identified by Chen and Fetz (2005) in type III rhythmic neurons. Conversely, beta oscillations could be mediated by collective network reverberations in small-scale networks inaccessible in LFPs as recorded by the MEAs used.
Previous studies have examined the transient nature of β-LFP oscillations (e.g., Denker et al. 2007; Feingold et al. 2015). Our data highlight this transiency in motor cortex: β-LFP power fluctuates during steady-state movement preparation periods in our task, even while the firing rates of beta-rhythmic single neurons remain constant. We conjecture that the observed fluctuations in β-LFP power during movement preparation could arise from changes in the synchronization among more local sources of beta-rhythmic network activity. It is possible that β-LFP power fluctuations represent transient synchronization of a large population of weakly coupled single units such that although the macroscopic LFP power exhibits a transient amplitude increase, individual spike-LFP phase coupling remains weak. These transient changes in the level of synchrony and spatial coherence might result from the locally evolving dynamics in the neocortical patches or from the interaction with transient inputs originating in other cortical and subcortical areas. In the more general scenario of weakly coupled oscillators, Popovych and Tass (2011) find that when oscillators with slightly heterogeneous frequencies are driven by a common oscillatory input, transient power fluctuations are expected to result from momentary synchronization between oscillators, in a mechanism akin to the beats heard from two notes slightly out of tune.
The above scenarios are to be contrasted with the attenuation of β-LFP power during movement execution. During movement execution, the majority of units exhibit large excursions in firing rate, and many rhythmic single units shift their firing frequencies up and out of the beta-frequency band, whereas other units switch from rhythmic to irregular firing. Therefore, it is likely that movement-related beta suppression relates to a reduction of total beta-rhythmic network activity. This points to two processes governing variability of β-LFP power in motor cortex: an overall modulation of the level of beta rhythmicity that is evidenced by changes in single-unit firing properties during movement preparation and execution, and an additional source of variability that gives rise to the transient fluctuations in β-LFP power despite sustained firing rates and β-rhythmicity at the level of single-neuron spiking during movement preparation steady states.
Implication for encoding and motor steady states.
Previous decoding analyses from our group (Bansal et al. 2012; Zhuang et al. 2010) show that β-LFP power improves, although by a small amount, the decoding performance of reach/grasp kinematics during movement execution. In these two studies, beta tends to show the lowest decoding performances compared with other lower and higher frequency bands. In contrast, during steady-state movement preparation periods, our decoding analysis showed no significant classification performance of object and grip type based on β-LFP activity. Our conjecture is that the contribution of β-LFP activity found during movement execution relates more to discriminating moving vs. not moving, rather than carrying specific information about movement kinematics per se, e.g., time-varying 3-D positions/trajectories and velocities of the hand/arm during reach and grasp actions. We also note that Rule et al. (2015) examined the contribution of several LFP features to spiking variability during execution of reach and grasp movements, including β-LFP power, and did find some contribution. Importantly, however, a similar analysis performed during the steady-state movement preparation periods (Fig. 9) found no such relationship during movement preparation.
Mode firing frequencies of single neurons were not identical, but rather varied within the beta band. This diversity in mode frequencies and firing rates increased following visual cue presentation, after which the subjects had presumably prepared for a specific reach and grasp action plan. Indeed, Vargas-Irwin et al. (2015), examining the same data sets considered in the present study from the perspective of neural decoding, demonstrate that planned upcoming movements (object and grip type) can be decoded from the spike patterns in the recorded neuronal ensemble during the preparation period. The information about object and grip type was sustained across the instructed delay period. It may be that both diverse rates and rhythmic firing are instrumental to the maintenance of preparatory states in motor cortex. If so, this would naturally limit the ability of single neurons and different neuronal populations to strongly phase couple to a single dominant β-LFP oscillation, resulting in the observed spike-LFP weak coupling.
Future work.
Beta oscillations in the brain remain an intriguing and heterogeneous phenomenon, and further work is needed to clarify their origin and function. The present work raises interesting questions about the nature of motor steady states during attentive waiting and movement preparation. It will be important to examine the coupling between single-neuron activity and β-LFP oscillations in instructed delay tasks that test working memory, something not required in the task examined in the present study. This additional instructed delay condition might elucidate which features of beta activity relate to the active maintenance of the preparatory state vs. simply the hold condition before movement execution. The extent to which motor cortex beta-rhythmic spiking arises from nonlocal oscillatory network inputs, local recurrent dynamics, or the intrinsic electrical properties of single neurons remains unclear. Combined extracellular and intracellular in vivo recordings akin to those performed by Harvey et al. (2009) may be illuminating. We have also identified several features of beta oscillations that should inform future modeling work, with relevance to a theoretical understanding of maintenance of neural states over long timescales with oscillatory dynamics.
In summary, the dissociation of single-unit spiking and β-LFP reported presently, in terms of both power modulation and phase coupling, is an important finding that has not been thoroughly investigated before. It is possible that the nature of the beta states revealed allows multiple cell assemblies, each resonant at slightly different frequencies, to coexist with relatively little interference or competition. Future work is needed to evaluate the functional importance of beta phase and frequency diversity during preparatory steady states in motor cortex, especially with respect to evaluating potential roles for this diversity in encoding, attentional processes, gating communication, and assisting the binding together of functional assemblies of neurons (e.g., Maris et al. 2016).
GRANTS
This research is supported by National Institutes of Neurological Disorders and Stroke (NINDS) Grants R01 NS25074 (to J. P. Donoghue) and K01 Career Award NS057389 (to W. Truccolo), Defense Advanced Research Projects Agency (DARPA) REPAIR Grant N66001-10-C-2010 (to J. P. Donoghue and W. Truccolo), a National Science Foundation predoctoral fellowship (to M. E. Rule), and the Pablo J. Salame ’88 Goldman Sachs Endowed Assistant Professorship of Computational Neuroscience (to W. Truccolo).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
M.E.R. and W.T. conceived and designed research; M.E.R. analyzed data; M.E.R. and W.T. interpreted results of experiments; M.E.R. prepared figures; M.E.R. and W.T. drafted manuscript; M.E.R., C.E.V.-I., J.P.D., and W.T. edited and revised manuscript; M.E.R., C.E.V.-I., J.P.D., and W.T. approved final version of manuscript; C.E.V.-I. performed experiments.
REFERENCES
- Aghagolzadeh M, Truccolo W. Latent state-space models for neural decoding. In: 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC 2014) Chicago, IL: IEEE, 2014, p. 3033–3036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aghagolzadeh M, Truccolo W. Inference and decoding of motor cortex low-dimensional dynamics via latent state-space models. IEEE Trans Neural Syst Rehabil Eng 24: 272–282, 2016. doi: 10.1109/TNSRE.2015.2470527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ardid S, Wang X-J, Gomez-Cabrero D, Compte A. Reconciling coherent oscillation with modulation of irregular spiking activity in selective attention: gamma-range synchronization between sensory and executive cortical areas. J Neurosci 30: 2856–2870, 2010. doi: 10.1523/JNEUROSCI.4222-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aydore S, Pantazis D, Leahy RM. A note on the phase locking value and its properties. Neuroimage 74: 231–244, 2013. doi: 10.1016/j.neuroimage.2013.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker SN, Olivier E, Lemon RN. Coherent oscillations in monkey motor cortex and hand muscle EMG show task-dependent modulation. J Physiol 501: 225–241, 1997. doi: 10.1111/j.1469-7793.1997.225bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker SN, Pinches EM, Lemon RN. Synchronization in monkey motor cortex during a precision grip task. II. effect of oscillatory activity on corticospinal output. J Neurophysiol 89: 1941–1953, 2003. doi: 10.1152/jn.00832.2002. [DOI] [PubMed] [Google Scholar]
- Baker SN, Spinks R, Jackson A, Lemon RN. Synchronization in monkey motor cortex during a precision grip task. I. Task-dependent modulation in single-unit synchrony. J Neurophysiol 85: 869–885, 2001. [DOI] [PubMed] [Google Scholar]
- Bansal AK, Truccolo W, Vargas-Irwin CE, Donoghue JP. Decoding 3D reach and grasp from hybrid signals in motor and premotor cortices: spikes, multiunit activity, and local field potentials. J Neurophysiol 107: 1337–1355, 2012. doi: 10.1152/jn.00781.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baranyi A, Szente MB, Woody CD. Electrophysiological characterization of different types of neurons recorded in vivo in the motor cortex of the cat. I. Patterns of firing activity and synaptic responses. J Neurophysiol 69: 1850–1864, 1993a. [DOI] [PubMed] [Google Scholar]
- Baranyi A, Szente MB, Woody CD. Electrophysiological characterization of different types of neurons recorded in vivo in the motor cortex of the cat. II. Membrane parameters, action potentials, current-induced voltage responses and electrotonic structures. J Neurophysiol 69: 1865–1879, 1993b. [DOI] [PubMed] [Google Scholar]
- Barthó P, Hirase H, Monconduit L, Zugaro M, Harris KD, Buzsáki G. Characterization of neocortical principal cells and interneurons by network interactions and extracellular features. J Neurophysiol 92: 600–608, 2004. doi: 10.1152/jn.01170.2003. [DOI] [PubMed] [Google Scholar]
- Battaglia D, Karagiannis A, Gallopin T, Gutch HW, Cauli B. Beyond the frontiers of neuronal types. Front Neural Circuits 7: 13, 2013. doi: 10.3389/fncir.2013.00013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc Series B Methodol 57: 289–300, 1995. [Google Scholar]
- Beuter A, Lefaucheur J-P, Modolo J. Closed-loop cortical neuromodulation in Parkinson’s disease: An alternative to deep brain stimulation? Clin Neurophysiol 125: 874–885, 2014. doi: 10.1016/j.clinph.2014.01.006. [DOI] [PubMed] [Google Scholar]
- Brunel N, Wang X-J. What determines the frequency of fast network oscillations with irregular neural discharges? I. Synaptic dynamics and excitation-inhibition balance. J Neurophysiol 90: 415–430, 2003. doi: 10.1152/jn.01095.2002. [DOI] [PubMed] [Google Scholar]
- Buzsáki G, Anastassiou CA, Koch C. The origin of extracellular fields and currents–EEG, ECoG, LFP and spikes. Nat Rev Neurosci 13: 407–420, 2012. doi: 10.1038/nrn3241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen D, Fetz EE. Characteristic membrane potential trajectories in primate sensorimotor cortex neurons recorded in vivo. J Neurophysiol 94: 2713–2725, 2005. doi: 10.1152/jn.00024.2005. [DOI] [PubMed] [Google Scholar]
- Denker M, Roux S, Timme M, Riehle A, Grün S. Phase synchronization between LFP and spiking activity in motor cortex during movement preparation. Neurocomputing 70: 2096–2101, 2007. doi: 10.1016/j.neucom.2006.10.088. [DOI] [Google Scholar]
- Dubey A, Ray S. Spatial spread of local field potential is band-pass in the primary visual cortex. J Neurophysiol 116: 1986–1999, 2016. doi: 10.1152/jn.00443.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fawcett T. An introduction to ROC analysis. Pattern Recognit Lett 27: 861–874, 2006. doi: 10.1016/j.patrec.2005.10.010. [DOI] [Google Scholar]
- Feingold J, Gibson DJ, DePasquale B, Graybiel AM. Bursts of beta oscillation differentiate postperformance activity in the striatum and motor cortex of monkeys performing movement tasks. Proc Natl Acad Sci USA 112: 13687–13692, 2015. doi: 10.1073/pnas.1517629112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gale JT, Amirnovin R, Williams ZM, Flaherty AW, Eskandar EN. From symphony to cacophony: pathophysiology of the human basal ganglia in Parkinson disease. Neurosci Biobehav Rev 32: 378–387, 2008. doi: 10.1016/j.neubiorev.2006.11.005. [DOI] [PubMed] [Google Scholar]
- Geisler C, Brunel N, Wang X-J. Contributions of intrinsic membrane dynamics to fast network oscillations with irregular neuronal discharges. J Neurophysiol 94: 4344–4361, 2005. doi: 10.1152/jn.00510.2004. [DOI] [PubMed] [Google Scholar]
- Haider B, Schulz DP, Häusser M, Carandini M. Millisecond coupling of local field potentials to synaptic currents in the awake visual cortex. Neuron 90: 35–42, 2016. doi: 10.1016/j.neuron.2016.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey CD, Collman F, Dombeck DA, Tank DW. Intracellular dynamics of hippocampal place cells during virtual navigation. Nature 461: 941–946, 2009. doi: 10.1038/nature08499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoseini MS, Wessel R. Coherent and intermittent ensemble oscillations emerge from networks of irregular spiking neurons. J Neurophysiol 115: 457–469, 2016. doi: 10.1152/jn.00578.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson A, Gee VJ, Baker SN, Lemon RN. Synchrony between neurons with similar muscle fields in monkey motor cortex. Neuron 38: 115–125, 2003. doi: 10.1016/S0896-6273(03)00162-4. [DOI] [PubMed] [Google Scholar]
- Jarvis MR, Mitra PP. Sampling properties of the spectrum and coherency of sequences of action potentials. Neural Comput 13: 717–749, 2001. doi: 10.1162/089976601300014312. [DOI] [PubMed] [Google Scholar]
- Jia X, Tanabe S, Kohn A. Gamma and the coordination of spiking activity in early visual cortex. Neuron 77: 762–774, 2013. doi: 10.1016/j.neuron.2012.12.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones SR, Pritchett DL, Sikora MA, Stufflebeam SM, Hämäläinen M, Moore CI. Quantitative analysis and biophysically realistic neural modeling of the MEG mu rhythm: rhythmogenesis and modulation of sensory-evoked responses. J Neurophysiol 102: 3554–3572, 2009. doi: 10.1152/jn.00535.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kajikawa Y, Schroeder CE. How local is the local field potential? Neuron 72: 847–858, 2011. doi: 10.1016/j.neuron.2011.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopell N, Whittington MA, Kramer MA. Neuronal assembly dynamics in the beta1 frequency range permits short-term memory. Proc Natl Acad Sci USA 108: 3779–3784, 2011. doi: 10.1073/pnas.1019676108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lepage KQ, Gregoriou GG, Kramer MA, Aoi M, Gotts SJ, Eden UT, Desimone R. A procedure for testing across-condition rhythmic spike-field association change. J Neurosci Methods 213: 43–62, 2013. doi: 10.1016/j.jneumeth.2012.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Y, Truccolo W, Wagner FB, Vargas-Irwin CE, Ozden I, Zimmermann JB, May T, Agha NS, Wang J, Nurmikko AV. Optogenetically induced spatiotemporal gamma oscillations and neuronal spiking activity in primate motor cortex. J Neurophysiol 113: 3574–3587, 2015. doi: 10.1152/jn.00792.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mammen E, Nandi S, Maiwald T, Timmer J. Effect of jump discontinuity for phase-randomized surrogate data testing. Int J Bifurcat Chaos 19: 403–408, 2009. doi: 10.1142/S0218127409022968. [DOI] [Google Scholar]
- Maris E, Fries P, van Ede F. Diverse phase relations among neuronal rhythms and their potential function. Trends Neurosci 39: 86–99, 2016. doi: 10.1016/j.tins.2015.12.004. [DOI] [PubMed] [Google Scholar]
- McCormick DA, Connors BW, Lighthall JW, Prince DA. Comparative electrophysiology of pyramidal and sparsely spiny stellate neurons of the neocortex. J Neurophysiol 54: 782–806, 1985. [DOI] [PubMed] [Google Scholar]
- Mitra PP, Pesaran B. Analysis of dynamic brain imaging data. Biophys J 76: 691–708, 1999. doi: 10.1016/S0006-3495(99)77236-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE. Coherent 25- to 35-Hz oscillations in the sensorimotor cortex of awake behaving monkeys. Proc Natl Acad Sci USA 89: 5670–5674, 1992. doi: 10.1073/pnas.89.12.5670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE. Oscillatory activity in sensorimotor cortex of awake monkeys: synchronization of local field potentials and relation to behavior. J Neurophysiol 76: 3949–3967, 1996a. [DOI] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE. Synchronization of neurons during local field potential oscillations in sensorimotor cortex of awake monkeys. J Neurophysiol 76: 3968–3982, 1996b. [DOI] [PubMed] [Google Scholar]
- Nauhaus I, Busse L, Carandini M, Ringach DL. Stimulus contrast modulates functional connectivity in visual cortex. Nat Neurosci 12: 70–76, 2009. doi: 10.1038/nn.2232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ni J, Wunderle T, Lewis CM, Desimone R, Diester I, Fries P. Gamma-rhythmic gain modulation. Neuron 92: 240–251, 2016. doi: 10.1016/j.neuron.2016.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okun M, Steinmetz NA, Cossell L, Iacaruso MF, Ko H, Barthó P, Moore T, Hofer SB, Mrsic-Flogel TD, Carandini M, Harris KD. Diverse coupling of neurons to populations in sensory cortex. Nature 521: 511–515, 2015. doi: 10.1038/nature14273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliphant TE. Python for scientific computing. Comput Sci Eng 9: 10–20, 2007. doi: 10.1109/MCSE.2007.58. [DOI] [Google Scholar]
- Percival DB, Walden AT. Spectral analysis for physical applications. Cambridge, UK: Cambridge University Press, 1993. doi: 10.1017/CBO9780511622762. [DOI] [Google Scholar]
- Pesaran B, Nelson MJ, Andersen RA. Free choice activates a decision circuit between frontal and parietal cortex. Nature 453: 406–409, 2008. doi: 10.1038/nature06849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popovych OV, Tass PA. Macroscopic entrainment of periodically forced oscillatory ensembles. Prog Biophys Mol Biol 105: 98–108, 2011. doi: 10.1016/j.pbiomolbio.2010.09.018. [DOI] [PubMed] [Google Scholar]
- Ray S, Maunsell JH. Network rhythms influence the relationship between spike-triggered local field potential and functional connectivity. J Neurosci 31: 12674–12682, 2011. doi: 10.1523/JNEUROSCI.1856-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roopun AK, Kramer MA, Carracedo LM, Kaiser M, Davies CH, Traub RD, Kopell NJ, Whittington MA. Period concatenation underlies interactions between gamma and beta rhythms in neocortex. Front Cell Neurosci 2: 1, 2008. doi: 10.3389/neuro.03.001.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roopun AK, Middleton SJ, Cunningham MO, LeBeau FE, Bibbig A, Whittington MA, Traub RD. A beta2-frequency (20-30 Hz) oscillation in nonsynaptic networks of somatosensory cortex. Proc Natl Acad Sci USA 103: 15646–15650, 2006. doi: 10.1073/pnas.0607443103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rule ME, Vargas-Irwin C, Donoghue JP, Truccolo W. Contribution of LFP dynamics to single-neuron spiking variability in motor cortex during movement execution. Front Syst Neurosci 9: 89, 2015. doi: 10.3389/fnsys.2015.00089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanes JN, Donoghue JP. Oscillations in local field potentials of the primate motor cortex during voluntary movement. Proc Natl Acad Sci U S A 90: 4470–4474, 1993. doi: 10.1073/pnas.90.10.4470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torrence C, Compo GP. A practical guide to wavelet analysis. Bull Am Meteorol Soc 79: 61–78, 1998. doi:. [DOI] [Google Scholar]
- Truccolo W, Ahmed OJ, Harrison MT, Eskandar EN, Cosgrove GR, Madsen JR, Blum AS, Potter NS, Hochberg LR, Cash SS. Neuronal ensemble synchrony during human focal seizures. J Neurosci 34: 9927–9944, 2014. doi: 10.1523/JNEUROSCI.4567-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Truccolo W, Donoghue JA, Hochberg LR, Eskandar EN, Madsen JR, Anderson WS, Brown EN, Halgren E, Cash SS. Single-neuron dynamics in human focal epilepsy. Nat Neurosci 14: 635–641, 2011. doi: 10.1038/nn.2782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Truccolo W, Eden UT, Fellows MR, Donoghue JP, Brown EN. A point process framework for relating neural spiking activity to spiking history, neural ensemble, and extrinsic covariate effects. J Neurophysiol 93: 1074–1089, 2005. doi: 10.1152/jn.00697.2004. [DOI] [PubMed] [Google Scholar]
- Truccolo W, Hochberg LR, Donoghue JP. Collective dynamics in human and monkey sensorimotor cortex: predicting single neuron spikes. Nat Neurosci 13: 105–111, 2010. doi: 10.1038/nn.2455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vargas-Irwin C, Donoghue JP. Automated spike sorting using density grid contour clustering and subtractive waveform decomposition. J Neurosci Methods 164: 1–18, 2007. doi: 10.1016/j.jneumeth.2007.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vargas-Irwin CE, Franquemont L, Black MJ, Donoghue JP. Linking objects to actions: Encoding of target object and grasping strategy in primate ventral premotor cortex. J Neurosci 35: 10888–10897, 2015. 10.1523/JNEUROSCI.1574-15.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vargas-Irwin CE, Shakhnarovich G, Yadollahpour P, Mislow JM, Black MJ, Donoghue JP. Decoding complete reach and grasp actions from local primary motor cortex populations. J Neurosci 30: 9659–9669, 2010. doi: 10.1523/JNEUROSCI.5443-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vigneswaran G, Kraskov A, Lemon RN. Large identified pyramidal cells in macaque motor and premotor cortex exhibit “thin spikes”: implications for cell type classification. J Neurosci 31: 14235–14242, 2011. doi: 10.1523/JNEUROSCI.3142-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinck M, van Wingerden M, Womelsdorf T, Fries P, Pennartz CM. The pairwise phase consistency: a bias-free measure of rhythmic neuronal synchronization. Neuroimage 51: 112–122, 2010. doi: 10.1016/j.neuroimage.2010.01.073. [DOI] [PubMed] [Google Scholar]
- Waldert S, Lemon RN, Kraskov A. Influence of spiking activity on cortical local field potentials. J Physiol 591: 5291–5303, 2013. doi: 10.1113/jphysiol.2013.258228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wetmore DZ, Baker SN. Post-spike distance-to-threshold trajectories of neurones in monkey motor cortex. J Physiol 555: 831–850, 2004. doi: 10.1113/jphysiol.2003.048918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witham CL, Baker SN. Network oscillations and intrinsic spiking rhythmicity do not covary in monkey sensorimotor areas. J Physiol 580: 801–814, 2007. doi: 10.1113/jphysiol.2006.124503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang AI, Vanegas N, Lungu C, Zaghloul KA. Beta-coupled high-frequency activity and beta-locked neuronal spiking in the subthalamic nucleus of Parkinson’s disease. J Neurosci 34: 12816–12827, 2014. doi: 10.1523/JNEUROSCI.1895-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanos TP, Mineault PJ, Pack CC. Removal of spurious correlations between spikes and local field potentials. J Neurophysiol 105: 474–486, 2011. doi: 10.1152/jn.00642.2010. [DOI] [PubMed] [Google Scholar]
- Zhou P, Burton SD, Snyder AC, Smith MA, Urban NN, Kass RE. Establishing a statistical link between network oscillations and neural synchrony. PLoS Comput Biol 11: e1004549, 2015. doi: 10.1371/journal.pcbi.1004549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhuang J, Truccolo W, Vargas-Irwin C, Donoghue JP. Decoding 3-D reach and grasp kinematics from high-frequency local field potentials in primate primary motor cortex. IEEE Trans Biomed Eng 57: 1774–1784, 2010. doi: 10.1109/TBME.2010.2047015. [DOI] [PMC free article] [PubMed] [Google Scholar]