Spontaneous dynamics of neural networks in deep layers of prefrontal cortex

Using calcium imaging and a novel analytic framework, we characterized the spontaneous and NMDA-evoked activity of layer 5 prefrontal cortex at a largely unexplored spatiotemporal scale. Our results suggest that the mPFC microcircuitry is capable of intrinsically generating delta oscillations and sustaining synchronized network activity that is potentially relevant for understanding its contribution to cognitive processes.

Abstract

Cortical systems maintain and process information through the sustained activation of recurrent local networks of neurons. Layer 5 is known to have a major role in generating the recurrent activation associated with these functions, but relatively little is known about its intrinsic dynamics at the mesoscopic level of large numbers of neighboring neurons. Using calcium imaging, we measured the spontaneous activity of networks of deep-layer medial prefrontal cortical neurons in an acute slice model. Inferring the simultaneous activity of tens of neighboring neurons, we found that while the majority showed only sporadic activity, a subset of neurons engaged in sustained delta frequency rhythmic activity. Spontaneous activity under baseline conditions was weakly correlated between pairs of neurons, and rhythmic neurons showed little coherence in their oscillations. However, we consistently observed brief bouts of highly synchronous activity that must be attributed to network activity. NMDA-mediated stimulation enhanced rhythmicity, synchrony, and correlation within these local networks. These results characterize spontaneous prefrontal activity at a previously unexplored spatiotemporal scale and suggest that medial prefrontal cortex can act as an intrinsic generator of delta oscillations.

NEW & NOTEWORTHY Using calcium imaging and a novel analytic framework, we characterized the spontaneous and NMDA-evoked activity of layer 5 prefrontal cortex at a largely unexplored spatiotemporal scale. Our results suggest that the mPFC microcircuitry is capable of intrinsically generating delta oscillations and sustaining synchronized network activity that is potentially relevant for understanding its contribution to cognitive processes.

the prefrontal cortex (PFC) plays a critical role in converting sensory inputs, memories, emotional states, and learned associations into behavioral outputs. The details of this process are dependent on the interaction between diverse inputs from distant brain regions with the fixed features of the local cortical networks that receive these inputs. Intrinsic properties of prefrontal microcircuits, such as the organization of synaptic connectivity and the frequency tuning profiles of its constituent neurons, likely play a major role in determining how the PFC couples to other brain regions. Furthermore, differences in these intrinsic properties between cortical subregions may explain how PFC uniquely sustains working memory (Goldman-Rakic 1995). PFC activity has been intensively studied macroscopically by using techniques such as EEG (Gevins et al. 1997; Tallon-Baudry et al. 1998; van Aerde et al. 2009; Benchenane et al. 2011) and at the level of individual neurons recorded by microelectrodes (Yang et al. 1996; Jung et al. 1998). Recently, calcium imaging has enabled the interrogation of these networks in vitro (Luongo et al. 2016a, 2016b) and in vivo (Pinto and Dan 2015) with cellular resolution. However, relatively little is known about the intrinsic dynamics of the local prefrontal microcircuits that mediate cognitive and executive functions. Activity within layer 5 is of particular interest, as pyramidal neurons in this layer are known to play a critical role in instigating and sustaining recurrent network activity (Sanchez-Vives and McCormick 2000; Beltramo et al. 2013; Neske 2016).

In the absence of external excitation, cortical networks engage in internally driven spontaneous activity that reflects the interactions of cortical neurons alone, and often resembles the dynamics observed during externally evoked activity (Luczak and MacLean 2012). Thus the study of the spontaneous dynamics of the PFC microcircuits represents an interesting and necessary starting point for disentangling intrinsic and extrinsic contributions to cortical information storage and processing. Here, we used calcium imaging to infer the patterns of spontaneous activity within local networks of layer 5 prefrontal neurons. While the majority of neurons studied engaged in only sporadic firing, a subset of neurons showed a tendency to oscillate within the delta frequency band (0.5–4 Hz). Furthermore, we observed that while functional connections between neighboring neurons were mostly weak, the network still supported occasional synchronized recurrent activity. Consistent with the known role of N-methyl-d-aspartate (NMDA) receptors in the establishment of sustained recurrent network activity (Sanchez-Vives and McCormick 2000; Wang et al. 2013), stimulation of the microcircuitry with modest concentrations of NMDA strengthened coupling between neurons, enhanced the prevalence and coherence of delta oscillations, and increased the frequency of synchronized activity. These results serve to characterize the structure and intrinsic dynamics of deep-layer prefrontal microcircuitry and suggest its involvement in delta frequency rhythmogenesis.

MATERIALS AND METHODS

Animals and GCaMP Expression

All procedures were approved by the Brown University Institutional Animal Care and Use Committee. ICR mice were obtained from Charles River Laboratories. Expression of GCaMP6f was achieved through stereotaxic injection of a viral vector (AAV1.Syn.GCaMP6f.WPRE.SV40, 3.58 × 10¹³ genome copies/ml, obtained from University of Pennsylvania Vector Core) at 0.6 mm lateral from midline, 2.2 mm anterior of bregma, and 2.0 mm below the pial surface. All injections were performed at postnatal day 12, and each mouse received ~1 μl of virus. Subjects were allowed at least 4 days for recovery and gene expression before experimentation.

Slice Preparation and Solutions

Acute slices were prepared from mice aged P16-22 (median age of P18). During the slicing procedure two distinct artificial cerebral spinal fluid (ACSF) recipes (“cutting” and “recovery” ACSF) were used. Our cutting recipe, based on the recommendations of Hájos and Mody (2009), contained, in mM: 125 NaCl, 2.7 KCl, 25 NaHCO₃, 1.2 NaH₂PO₄, 10 d-glucose, 2 CaCl₂, 2 MgSO₄, 1 ascorbic acid, 2 thiourea, 3 sodium pyruvate, 2 taurine. Our recovery recipe, modified from Peça et al. (2011), contained: 92 NMDG, 92 HCl, 2.5 KCl, 30 NaHCO₃, 1.2 NaH₂PO₄, 25 D-glucose, 0.5 CaCl₂,10 MgSO₄, 1 ascorbic acid, 2 thiourea, 3 sodium pyruvate, 2 taurine. Experiments were performed in a “recording ACSF” identical to the cutting ACSF except that CaCl₂ and MgSO₄ were reduced to 1 mM and taurine was omitted. In some experiments, a second bottle of recording ACSF was prepared containing 3 μM (n = 5 slices), 8 μM (n = 6), 12 μM (n = 1), or 16 μM (n = 1) NMDA.

Each mouse was deeply anesthetized by intraperitoneal injection of ketamine and xylazine dissolved in sterile saline. The brain was quickly extracted, kept in ice-cold cutting ACSF, and sectioned into 300-μm-thick coronal slices by using a vibratome. As each slice detached from the brain, it was placed into a bath of warm (32 °C) recovery ACSF for 5 min. Subsequently, each slice was transferred into a second chamber of warm cutting solution. After 30 min at 32 °C, this chamber was removed from the bath and allowed to reach room temperature. Both chambers were gently and continuously bubbled with 95% O₂-5% CO₂ (carbogen). All slices were allowed to recover for at least 1 h after slicing before experimentation.

Selection of Neuronal Populations

Individual slices were transferred into a slice chamber underneath an upright microscope. Each slice was placed onto a glass slide coated in poly-l-lysine, which prevented the slice from drifting substantially throughout the duration of the recording. Carbogenated ACSF flowed continuously through the slice chamber at a rate of 2–3 ml/min. mPFC was inspected at low magnification in both differential interference contrast and epifluorescence modes and judged on criteria of anatomy, visible fluorescence, and tissue health. If a suitable area was found within the infralimbic or prelimbic cortical subregions, the microscope objective was switched to high magnification (×40) and the area was examined in detail. By adjusting the x-y position of the objective, as well as the focal plane, many candidate neighborhoods of neurons were considered. Data was only collected from areas that contained many healthy-looking cells, as judged by cell morphology, size, and calcium fluorescence. All imaged populations were located at depths of 10–50 μm below the slice surface.

Electrophysiology

Pipettes for patch-clamp recordings were made in-house with a Sutter P-97 Flaming/Brown Micropipette Puller. We used pipettes with a series resistance of 1–5 MΩ and tip diameter of 1–1.5 μm. Just before each experiment, a pipette was backfilled with internal solution composed of (in mM) the following: 130 K-gluconate, 4 KCl, 2 NaCl, 10 HEPES, 0.2 EGTA, 4 ATP-Mg, 0.3 GTP-Tris, and 14 phosphocreatine-Tris. Electrophysiological recordings were obtained with an Axoclamp 2B amplifier in current-clamp mode and the HS-2A model headstage. Signals were sampled at 50 kHz with a Digidata 1440 digitizer and recorded with the pClamp software package. Further postprocessing (filtering and spike detection) of these electrophysiological signals was conducted offline in MATLAB using custom-written functions.

Calcium Imaging

Neuronal populations expressing GCaMP6f were imaged under a Nikon Eclipse E600FN upright microscope in epifluorescence mode by using a Nikon ×40 magnification, water-immersion objective (NA = 0.8). A Polychrome V light source provided 490-nm excitation illumination at 1-mW average power. A band-pass (505–540 nm) filter in front of the camera separated the blue excitation light from the green fluorescence. Images were acquired with an Andor iXon 887 EMCCD camera (gain = 1) cooled to −60 °C, with 10- to 30-ms exposure time per frame (depending on what was needed to achieve sufficient image quality), 256 × 256 pixel resolution, and 16-bit depth by using MetaFluor software. The final movies ranged from 20- to 60-Hz frame rate, with ~30 Hz being the most common. For each neuronal population, 10–30 movies (typically around 3 min per movie) were recorded across various experimental conditions. When necessary, small adjustments of focus or x-y position were made between movies to ensure that the same focal plane and cell population were maintained throughout the experiment. In experiments involving NMDA application, neuronal populations were imaged under the baseline condition for at least 10 min before wash-in.

Data Analysis

First-pass image segmentation.

Image segmentation was achieved by using an iterative, two-step procedure. In the first step, each movie was carefully inspected visually. Neuronal somata were identified by eye on the basis of morphology and fluorescence. For each identified neuron, an elliptical or rectangular region of interest (ROI) was drawn around the soma by using MetaFluor software. These ROIs were intentionally drawn somewhat larger than the apparent sizes of the somata to allow for slight (<5 pixel) translational drift within or between movies. A background ROI was also defined as all pixels not included in any first-pass neuronal ROI.

Time-series analysis.

After initial segmentation, all further analysis was conducted in MATLAB. Time series representing the average fluorescence of the i^th neuron, F_i(t), were constructed as the arithmetic mean of the values of all pixels within the i^th ROI for each frame. A background series, F_back(t), was constructed in the same way. F_back(t) was subtracted from each F_i(t) for each movie. To suppress shot noise, the background-subtracted traces were then digitally filtered, forward and backward, with a third-order low-pass Bessel filter with a cutoff frequency of 10 Hz.

Statistical noise for a given data set, σ, was estimated by using a two-step process. First, each filtered, background-subtracted fluorescence trace, F_i,k (i^th neuron, k^th movie), was SD-filtered by using a 20-s sliding window. In the second step, the minimum of each SD-filtered trace was then taken as an estimate of the statistical noise. All such minima were then pooled, and a final, overall noise estimate was obtained by taking the median value of this pool.

Slice motion estimation.

We observed slight translation in the xy-plane in some data sets. We quantified this motion by using image registration functions from the MATLAB Image Processing toolbox. For each movie, we generated a normalized mean projection image. By registering each projection image to that of the previous movie, we estimated the trajectory of the slice throughout the data set. Data sets in which the slice moved more than five pixels (~4 μm) from its starting position were not used for further analysis.

First-pass event detection and subevents.

Detection of fluorescent events was achieved through an iterative algorithm optimized for the characteristics of GCaMP6f, as determined in simultaneous patch-clamp/imaging experiments. For each fluorescence trace, F_i(t), the algorithm first identified any sequences of frames in which fluorescence increased consecutively, dubbed “rises.” For each rise, a local baseline value, F₀, was defined as the value of F_i(t) during the first frame of the rise. Only rises whose height, ΔF = F_peak – F₀, exceeded a threshold value of 2.5σ were retained. Each surviving rise was then matched with a falling phase, extending from the peak of the rise to the next local minimum below the threshold value. The series of frames from the beginning of each rise until the end of the falling phase was defined as an event.

To approximate the timing of the underlying spiking within a given event, each event was further divided into subevents, defined as all the rising phases (selected by the same criteria as events) contained within the event. The duration of each subevent was defined as the time interval from the first frame of the subevent to its peak. The relative magnitude of each subevent was defined as ΔF/F₀. Relative magnitude is expressed in terms of percent (i.e., multiplied by 100) throughout this study.

Second-pass image segmentation.

We used a second-stage segmentation step to semiautomatically draw ROIs tailored to each neuron’s morphology. Having discovered the brightest events from each neuron during first-pass event detection, we generated sets of summary images for each event by taking the mean and SD, over the event’s frames, for each pixel within a rectangular neighborhood defined by the length and width of the first-pass ROIs. We also generated mean and SD summary images of each neuron by using all frames from each movie. All summary images were then median filtered (2 × 2 pixel kernel) and thresholded at the 90th percentile, generating sets of binary images that approximated the putative cellular morphology. These binary images were then presented one-by-one to the user, who visually compared the binary images with the corresponding summary image and identified the binary images that captured the morphology of the neuron. If no good binary images were identified for a neuron, that neuron was excluded from any further analysis.

The selected binary images were then padded to account for slice drift and then merged to make one final composite binary image for each neuron. Merging was accomplished by setting each pixel that was set to 1 in any selected binary image to 1 in the composite image. This composite image was smoothed by taking the convex hull around all pixels set to 1. Finally, any pixel that was shared by two or more composite images was assigned to whichever image it was closest to the centroid of. Thus we obtained final ROIs that captured the morphology of each neuron with minimal background pixels and allowed for minor (<5 pixels) slice motion.

Subevent validation.

To ensure that each detected subevent could be attributed to the activity of the underlying neuron, and not to neuropil contamination or fluorescence from neighboring neurons leaking into the ROI, a validation step was implemented. Validation was based on the assumption that during spiking, ionic calcium concentration should rise throughout the soma, not just in one compartment. Therefore, we expected that during each real subevent, there should be strong correlation between the time series of individual pixels in the ROI and the mean fluorescence trace, F_i(t), from which the subevent was derived.

For each ROI, a local neighborhood was defined including the ROI itself and all pixels within 20 μm of the ROI. For each subevent, a local correlation map, ρ(x,y), was formed by calculating the Pearson correlation coefficient between F_i(t), the mean fluorescence time series for the i^th ROI, and G_i(x,y,t), the fluorescence time series of pixel (x,y) within the neighborhood of the i^th ROI over the frames of the subevent. Thresholding ρ above the 90th percentile and retaining only sets of 10 or more contiguous pixels (“blobs”) yielded an estimate of the spatial distribution of the source(s) of each subevent. Blobs whose centroid and maximum fell outside the ROI were discarded. A subevent was rejected if less than 75 blob pixels overlapped with the ROI or if less than 40% of the blob pixels overlapped with the ROI. These parameters were determined by examination of the fluorescence response to spiking in patched neurons.

Binarization.

The final representation of neural activity was generated by converting each fluorescence time series, F_i(t), to a binary vector B_i. B_i(t) was set to 1 if the t^th frame was included in a subevent from the i^th neuron or set to 0 otherwise. Overall population level activity, A, was quantified as the vector sum of all B_i. The activity rate was calculated by binning A into 10-s bins, summing A(t) over the duration of each bin, and dividing the result by the bin width multiplied by the number of neurons analyzed.

Measures of synchrony.

Similarity between pairs of binary vectors, B_i and B_j, was calculated by using the Jaccard similarity index, J. For pairs of binary vectors, this index is given by

$$J=M_{11}/(M_{10}+M_{01}+M_{11}),$$

where M_xy represents the number of frames where $B_i\left(t\right)=x$ and $B_j\left(t\right)=y$.

The Jaccard index is suitable for measuring pairwise correlation between neurons, but is not easily generalized to higher-order correlations. To examine synchrony between larger numbers of neurons, we used a complementary measure: synchronous events (not to be confused with the fluorescence events described above). This measure is based on the notion that network activity will induce multiple neurons to fire nearly simultaneously, resulting in strongly time-locked subevents from multiple neurons. To detect these times, we first read off the frames corresponding to the peaks of the time derivatives (dF/dt) of each subevent. We then constructed a vector wherein each element contained the number of such peaks, across all neurons, which occurred within ±50 ms of each frame. Finally, we found all local maxima of this vector greater than 1, and read off the identities of the neurons involved in the corresponding synchronous event, along with various other properties such as the distances between the participant neurons and the relative magnitudes and durations of the constituent subevents.

Surrogate data sets.

For many observations in our data, it is important to answer the question, “How probable is this observation under the null hypothesis of independent activity?” This is a difficult question to fully address, because the probability distribution under the null hypothesis is unknown. Under these conditions, one common approach is to generate, via Monte Carlo methods, surrogate data sets from the observed data that preserve some relevant properties (such as the overall activity rate) but scramble other details (such as the relative timing of events) (Sasaki et al. 2007; Lopes-dos-Santos et al. 2013). This method sets up the permutation test, a model-free test of statistical significance. By generating N surrogate data sets, one can estimate an upper limit on the P value of a given test statistic, S, as:

$$P\le \left(n+1\right)/\left(N+1\right)$$

where n is the number of surrogates data sets where S is more extreme than the measured S in the actual data (Phipson and Smyth 2010). Alternatively, one can obtain confidence intervals on S from its distribution in the surrogate data and then compare the measurement with these intervals to test against the null hypothesis.

We generated 1,000 surrogates for each data set. For analysis of the significance of observed values of correlation and synchrony, we used circular shifts to generate surrogate data. Each binary time series B_i,k(t), corresponding to the activity of the i^th neuron in the k^th movie, was circularly shifted by a pseudorandom number of frames, Δt, drawn from a uniform distribution on the interval [0, N_frame-1], where N_frame is the number of frames within the movie:

$$B_{i,k}\left(t\right)\to B_{i,k}\left(t+\Delta t\right)\mathrm{.}$$

In this way, the surrogate data sets preserved the overall activity rate, the distribution of activity among neurons, and the sequence of activity (up to a circular shift) but scrambled the timing of activity relative to other neurons.

Multitaper spectral analysis.

To estimate the Fourier power spectra of each binarized time series, we used the multitaper method for point-binned processes, as implemented by the Chronux Toolbox (Bokil et al. 2010) for MATLAB. For each movie, the number of tapers used, K, was determined by

$$K=2TW-1$$

where T is the total length of the movie and W is the desired spectral resolution. W was always set to 0.2 Hz.

We also used the Chronux Toolbox to test for coherence between oscillatory neurons. After obtaining the Fourier power spectra of all traces, we checked each movie for pairs of neurons whose spectra peaked at frequencies above 0.2 Hz (our spectral resolution). For each pair of neurons that met this criterion, we calculated the spectral coherence and calculated a confidence level, C_conf, on |C_ij(f)| by using jackknife resampling, such that the probability of observing |C_ij(f)| > C_conf under the null hypothesis was 0.01. We checked |C_ij(f)| for peaks greater than C_conf within a frequency range defined as [f_low – W, f_high + W], where f_low is the lower of the two neuronal peak frequencies and f_high is the higher frequency. Pairs of neurons that met these criteria were considered coherent and we extracted the magnitude, phase, and frequency of peak coherence.

Identification of epochs of rhythmic activity.

To identify rhythmic activity, we searched each trace for sequences of subevents in which both the timing and duration of subevents were predictable. For each subevent in a trace, the timings of the nearest neighbor subevent, before and after the subevent under consideration, were predicted by assuming that the two intersubevent intervals would be equal:

$$t_{i+1}=T_i+\left(T_i-T_{i-1}\right)=2T_i–T_{i-1}$$

$$t_{i-1}=T_i-\left(T_{i+1}-T_i\right)=2T_i–T_{i+1}$$

where T_i denotes the observed timing of the peak of the i^th subevent and t_i is the predicted timing of the i^th subevent. The accuracy of each prediction was evaluated by the relative error (RE):

$$\text{RE}=\left(t–T\right)/T\mathrm{.}$$

Similarly, the duration of each nearest neighbor subevent was predicted to be equal to the duration of the subevent under consideration, and RE was again used to evaluate the predictions. The first and last subevents in each trace had only one nearest neighbor, and hence only one prediction was made. Sequences of five or more consecutive subevents in which all predictions had RE < 0.5 were considered as epochs of rhythmic activity.

We characterized each epoch in terms of a number of basic properties. Duration was defined as the difference between the timing of the end of the last constituent subevent and the start of the first. Frequency was estimated as the arithmetic mean of the inverse of all intersubevent intervals within the epoch. We calculated the duty cycle for each epoch as the ratio of the mean duration of all constituent subevents to the mean intersubevent interval.

Statistics.

All statistical analysis was performed in MATLAB. Mean ± standard error (SE) is reported, except when specified otherwise. Distributions of test statistics of interest often violated the assumption of normality, and hence nonparametric hypothesis tests were used. Significance bars presented in figures follow the following convention: *P < 0.05; **P < 0.01; ***P < 0.001. In some cases, distributions are presented as box plots. For these figures, box edges represent 25th and 75th percentiles, red lines represent median values, red plus signs represent outlier data points, and whiskers extend to the most extreme nonoutlier data points.

Statistical analysis of drug effects were made by using hypothesis tests appropriate for dependent samples, usually the Wilcoxon signed-rank test. Effect sizes and confidence intervals were calculated by using the Measure of Effect Size Toolbox (Hentschke and Stüttgen 2011), and interpretation of effect sizes followed the guidelines of the toolbox’s documentation. For nonparametric statistical tests, we used Cohen’s U3 as a measure of effect size. For two samples, X and Y, with medians x and y:

$$U3=\frac{N\left(X<y\right)+0.5N\left(X=y\right)}{N\left(X\right)}$$

where N(…) gives the number of elements of X that satisfy the logical criteria contained within the argument.

RESULTS

GCaMP6f Expression and Characterization in mPFC

Stereotaxic injection of adeno-associated virus (AAV)-based viral vector consistently produced widespread, dense expression of GCaMP6f throughout the mPFC (Fig. 1A). At the level of cell populations selected for imaging at high magnification, 44 ± 8 somata per slice (mean ± SD, 25 slices from 11 mice) were identified by eye for initial analysis, and acceptable regions of interest (see materials and methods) were attained for 93 ± 1% of these neurons. A large majority (90 ± 3%) of these cells emitted at least one fluorescence subevent, demonstrating that the vast majority of the imaged neurons were alive.

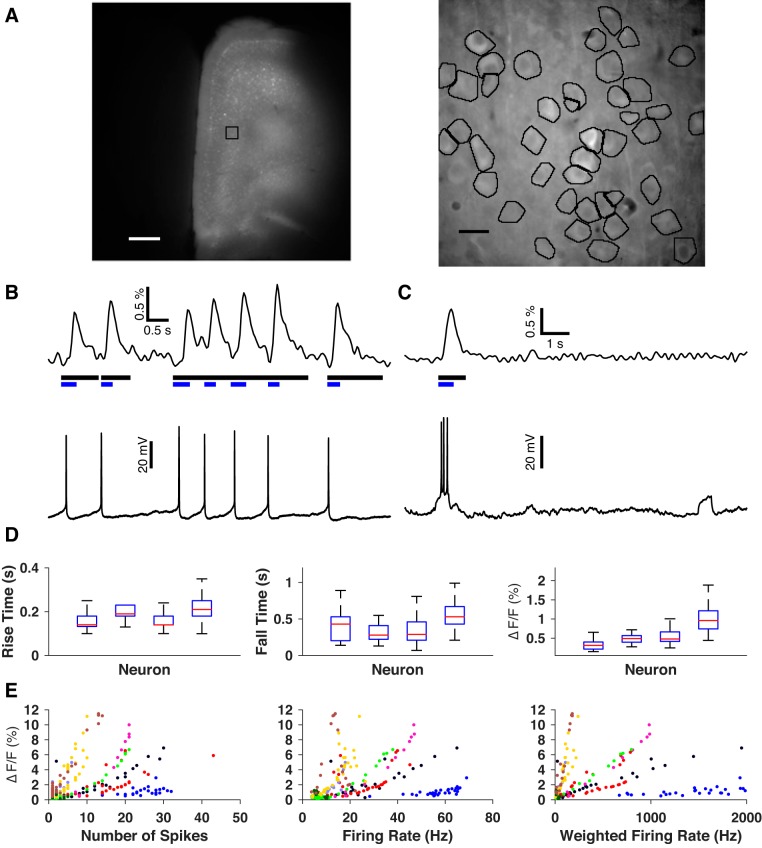
Fig. 1.

Expression and characterization of GCaMP6f in mPFC neurons. A: GCaMP6f fluorescence in mPFC imaged at low (left) and high (right) magnification. The black square on the low-magnification image indicates the approximate area imaged at high magnification. The high-magnification image is a mean projection of one movie. Black outlines indicate final regions of interest around neuronal somata. Scale bars: 0.5 mm, 10 μm, respectively. B and C: representative examples of the correspondence between neuronal firing and GCaMP6f fluorescence response. Black bars signify the durations of detected events. Blue bars represent durations of subevents detected within these events. B: subevents generated from single action potentials. C: a different neuron’s fluorescence response to a spike train and non-response to a subthreshold depolarization. D: neuron-to-neuron comparisons of GCaMP6f response to single action potentials in terms of rising time constant (left), falling time constant (middle) and relative magnitude (right). E: calibration of relative magnitude of fluorescence response to spike trains as a function of number of spikes (left), mean firing rate (middle) and spike-weighted firing rate (right). Each marker’s color/shape combination identifies a distinct neuron.

We used the synapsin promoter to drive neuron-specific expression (Kügler et al. 2003) of GCaMP6f. Virus injection induced expression in both pyramidal cells and interneurons. Pyramidal cells are the predominant class of neurons in neocortex, hence numerically they constitute the bulk of the neurons that we imaged. Interneurons are also known to have relatively weaker calcium fluorescence signals (Kerlin et al. 2010), and in pilot experiments we confirmed that fast-spiking interneurons were nearly silent in baseline conditions and emitted detectable fluorescence responses only during sustained high-frequency spiking (data not shown). Therefore, the activity we detected primarily represents the spiking of pyramidal neurons.

GCaMP6f has been functionally characterized in pyramidal cells of layer 2/3 visual cortex, and is reported to be sensitive to individual action potentials (Chen et al. 2013). However, the relationship between spiking and fluorescence response of GCaMP6f-expressing pyramidal neurons in deep-layer prefrontal cortex remains unknown. We therefore sought to determine if individual action potentials were detectable in our preparation and, more generally, to characterize the relationship between spiking and fluorescence response. We conducted simultaneous imaging and electrophysiological recordings and measured fluorescence response to both spontaneous and evoked action potentials. Fluorescence response was quantified by first identifying periods of time during which a cell’s fluorescence was significantly brighter than its baseline (events) and then identifying specific periods of time within each event during which fluorescence rose substantially (subevents). For each patched neuron, we matched each subevent to any spikes within a time window from 100 ms before the onset of the subevent until its peak (Fig. 1, B and C). Of nine GCaMP6f-expressing neurons patched, eight had at least two subevents matched to single spikes. We never observed subevents associated with subthreshold depolarizations. These results demonstrate that our imaging detected neuronal spiking only and was capable of detecting single action potentials in some neurons. The inability to reliably detect individual spikes in some cells suggests that there was some level of low-frequency spiking in the imaged populations that went undetected and that the activity detected here represents a lower bound on the true network activity.

To better understand the relationship between spikes and fluorescence transients, we focused on four neurons that had 10 or more isolated subevents (an event containing only one subevent) matched to single spikes (n = 83 ± 36 matches/cell). We examined fluorescence response to individual spikes in terms of three parameters: durations of the rising phase (t_rise) and falling phase (t_fall) and relative magnitude (ΔF/F₀). Single action potentials evoked fluorescence responses that lasted 0.54 ± 0.33 s (mean ± SD, N = 2,583 subevents) and had a relative magnitude of 2.03 ± 1.67%. However, the ranges of these parameters varied considerably from neuron to neuron (Fig. 1D), making it difficult to infer whether an observed subevent could be attributed to a single spike without the benefit of an electrophysiological ground truth.

Although GCaMP6f was capable of reporting individual spikes in some neurons, the time scale of this signal was on the order of hundreds of milliseconds. Spike trains with interspike intervals shorter than this would therefore be expected to appear as single subevents (see Fig. 1C), with greater relative magnitude reflecting increased calcium entry. To study this case, we searched our data for isolated subevents that matched with multiple spikes. We quantified these spike trains in terms of three parameters: number of spikes during the subevent time window (N_spike), mean firing rate (R_spike), and mean firing rate weighted by the number of spikes in the train (N_spike × R_spike). Figure 1E displays the relative magnitude of all isolated subevents that matched with multiple spikes in terms of these parameters. The highest correlation was obtained for the weighted spike rate (ρ = 0.66 ± 0.15, N = 9 neurons). The variability of fluorescence response from neuron to neuron likely reflects the variability in the expression of GCaMP6f, possibly due to the relatively short latency (~4 days) between viral transduction and imaging. Thus GCaMP6f reported neuronal activity over a wide range of spiking conditions, but the precise inference of underlying spiking patterns was not possible. In light of this finding, we interpreted subevents strictly as a readout of the approximate times at which neurons are known to be active, while remaining agnostic about the details of that spiking.

Basic Properties of Spontaneous Activity

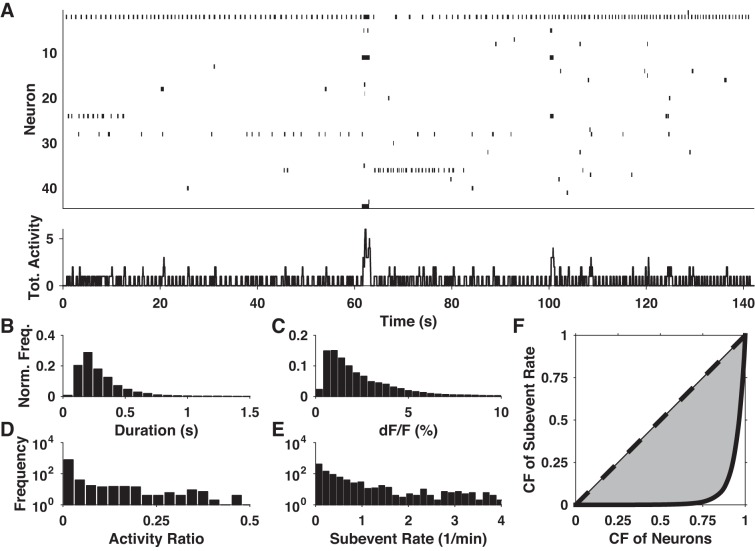
We imaged spontaneous activity in 25 slices from 11 mice expressing GCaMP6f in baseline ACSF for a total of 1,092 neurons. We observed diverse patterns of spontaneous activity in all slices, with some neurons engaging in sporadic or rhythmic firing while many neurons remained nearly silent (Fig. 2A). At a gross level, we observed subevent rates of 4.57 ± 1.02 subevents·min⁻¹·neuron⁻¹ (N = 25 slices). Neuronal activity ratios (total subevent duration/total recording length) were typically low (<10%), with no neuron reaching 50% (Fig. 2D). At the level of individual data sets, the distribution of subevent rates among neurons was always highly positively skewed (skewness = 3.58 ± 0.33, N = 25), suggesting that the spontaneous activity within each slice was dominated by a few highly active neurons, while the majority of neurons showed little or no activity (Fig. 2E). We quantified the inequality of these distributions by using the Gini coefficient, which measures the distance of a distribution from perfect equality. Pooling all neurons, the Gini coefficient was 0.89, close to the theoretical limit of 1 for a maximally unequal distribution (Fig. 2F).

Fig. 2.

Basic properties of spontaneous activity. A: panel at top shows an example raster plot of spontaneous activity: each row represents a neuron, and black dashes signify subevents. Panel at bottom shows total (sum) activity of all neurons shown in the panel at top. B and C: normalized histograms of subevent duration and relative magnitude pooled from all data sets. D and E: histograms of activity ratio and subevent rate of all analyzed neurons. F: Lorenz curves of subevent rate observed across all neurons (solid black curve) and for a perfectly uniform distribution (dashed line). The shaded area between these curves is used to calculate the Gini coefficient. CF, cumulative fraction.

We examined two basic subevent properties: duration and relative magnitude (ΔF/F₀). Pooling all data sets, the distributions of both variables were highly positively skewed and resembled lognormal distributions (Fig. 2, B and C). As such, we characterized their location and scale in terms of their geometric mean and median absolute deviation. Median subevent duration was 0.25 s, with a median absolute deviation of 0.08 s, indicating that baseline activity was dominated by brief packets of action potentials. Median relative magnitude was 1.83% with a median absolute deviation of 0.96%. These numbers are comparable with the relative magnitude of fluorescence responses to individual action potentials (Fig. 1D), although variability in the spike-fluorescence relationship precluded a precise inference of the spike patterns underlying each subevent.

Rhythmic Firing

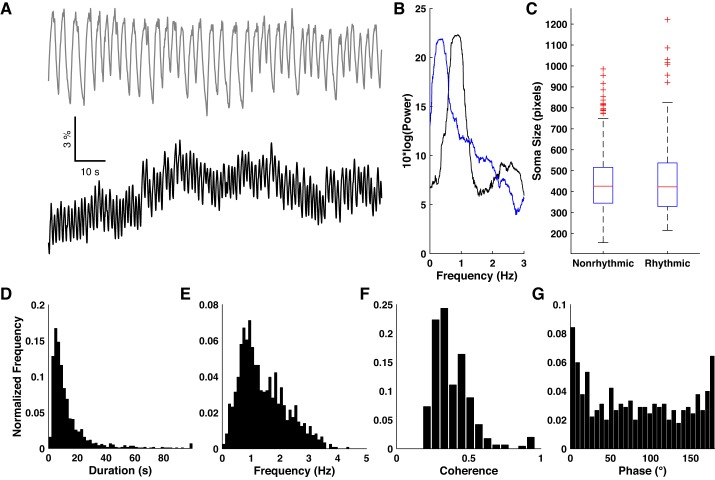
We noticed that a subset of imaged neurons tended to spontaneously oscillate between periods of activity and inactivity (Fig. 3A). Fourier analysis of the binarized traces revealed prominent peaks in the delta frequency band (Fig. 3B). In some cases, neurons exhibited oscillatory epochs interspersed with silence or sporadic activity. To identify rhythmic firing, we searched each trace for sequences of five or more subevents in which both the timing and duration of subevents were predictable to within 50% RE (see materials and methods). Under baseline conditions 14.6 ± 2.8% of neurons showed at least one rhythmic epoch (N = 25 slices). The probability of observing two or more such epochs, given that one had been observed, was 65.5 ± 6.2%. Duration of epochs varied widely, ranging from a few seconds to longer than 1 min (Fig. 3D). Neurons were found to oscillate at frequencies spanning the entire delta frequency band, but showed a preference for the 0.5–2 Hz range (Fig. 3E). These results demonstrate that a minority of rhythmically active neurons provided a major component of the overall spontaneous activity under baseline conditions.

Fig. 3.

Spontaneous rhythmic activity. A: representative example of two neurons showing highly rhythmic activity in baseline ACSF. B: Fourier power spectra of the binarized traces derived from the two traces in A. C: comparison of soma size between nonrhythmic and rhythmic cells. D and E: normalized histograms of basic properties of rhythmic epochs under baseline conditions. F and G: normalized histograms of coherence magnitude and phase angle for all pairs of neurons exhibiting statistically significant coherence.

Rhythmic activity could potentially be explained as unhealthy neurons being unable to maintain a hyperpolarized resting potential, hence we looked for evidence of poor cell health. Maintenance of intracellular calcium concentration is often compromised in dying neurons (Hyrc et al. 1997), hence we compared the baseline GCaMP fluorescence levels (see materials and methods) of rhythmic neurons (neurons with showing 2 or more rhythmic epochs) with their nonrhythmic counterparts within each slice. Of the 25 slices, rhythmic neurons were significantly brighter (P < 0.01, two-sample Kolomogorov-Smirnov test) than low-activity neurons in only one slice. Similarly, unhealthy neurons often swell and then shrink below their normal size. We compared the size of regions of interest of rhythmic and nonrhythmic neurons but found no significant difference (Fig. 3C). Overall, we found no evidence to support the possibility that rhythmic neurons were unhealthy.

We investigated possible interactions between pairs of rhythmic neurons by using coherence analysis. Coherence is a complex-valued measure of interaction between two oscillators as a function of frequency: its magnitude indicates the strength of interaction, and its phase gives the relative delay between oscillations. The sign of the phase angle depends on which oscillator is considered the reference and is not of interest for this analysis, hence we present its absolute value instead. We found 1.6 ± 0.7% (N = 25 slices) of all pairs of neurons within a slice showed statistically significant coherence. The magnitude of significant coherence was typically low (0.384 ± 0.005, N = 522 pairs; Fig. 3F) relative to the theoretical maximum of 1. The distribution of phase delay among coherent pairs (Fig. 3G) was inconsistent with a uniform angular distribution (P < 0.01, Rayleigh test) and peaked around 0°, indicating a preference for in-phase interaction. For each slice we compared the distribution of distances between coherent pairs with the distances between all possible pairs by using the two-sample Kolmogorov-Smirnov test. We found no significant differences and therefore no evidence of any spatial clustering among coherent neurons. Taken together, these results suggest that the rhythmic activity we observed represents the output of many independent or weakly coupled oscillators.

Pairwise Similarity and Synchrony

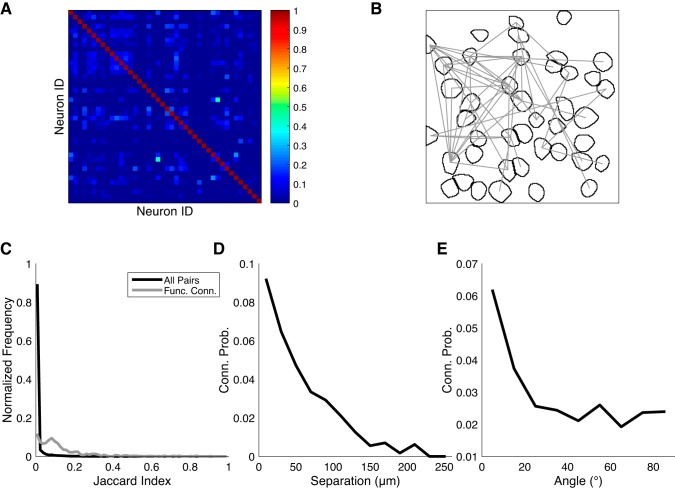
To study network topology, we examined the pairwise similarity between neurons’ activity patterns. Whereas coherence measures the synchrony of pairs of oscillators, pairwise similarity makes no assumptions about the periodicity of the neurons’ activity and simply summarizes their overall coactivity. Although calcium imaging cannot definitively reveal the synaptic connections between neurons, functional connections can be inferred by searching for pairs of neurons whose degree of coactivity is much greater than chance (Feldt et al. 2011). Under baseline conditions, Jaccard similarity indices (see materials and methods) were almost always low, with most pairs having no overlap at all (Fig. 4, A and C). Even if cortical neurons were completely decoupled, given sufficient activity one would expect to see some level of coincidental overlap that would result in some nonzero values. To account for this, we estimated P values on each pair’s similarity by using surrogate data sets in which any latent temporal structure between traces was destroyed (see materials and methods). Here, we considered pairs of neurons with nonzero similarity and P values < 0.01 to be functionally connected (Fig. 4B). Under these criteria, 2.41 ± 0.39% of pairs (N = 25 slices) were identified. Even among functionally connected pairs, Jaccard indices were generally low in an absolute sense, although a nonnegligible fraction (~3%) reached values of 0.5 or greater. The distribution of functionally connected J values was significantly higher (P < 0.01, two-sample Kolmogorov-Smirnov test, U3 = 0.96) than the overall distribution (Fig. 4C). These results are consistent with a local network architecture characterized by sparse, predominantly weak connections between neurons.

Fig. 4.

Pairwise correlation of spontaneously active neurons. A: example Jaccard similarity matrix obtained from one slice in baseline ACSF. B: example map of functional connections (gray lines) between neurons in the same data set as A. C: distributions of Jaccard indices under baseline conditions, pooling all pairs (black curve), or functionally connected pairs (gray) of active neurons from all slices. D and E: conditional probability of functional connection, as a function of neuronal separation distance and the angle between the line segment connecting the pair of neurons and the medial-lateral axis.

We looked for possible spatial organization among functionally connected pairs. We estimated the conditional probability of functional connectivity as a function of separation (20-μm bins) and found a strong preference for connectivity among proximal neurons (Fig. 4D). Fifty percent of functionally connected neurons fell within 60 μm of each other, and 95% within 140 μm. We performed a similar analysis on the orientation (10° bins) of functionally connected pairs relative to the medial-lateral axis and observed a preference for alignment along this axis over the dorsal-ventral axis (Fig. 4E).

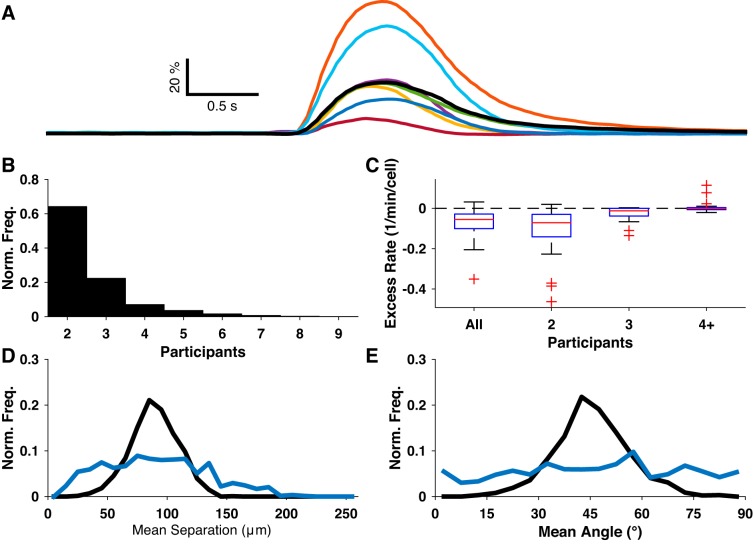
We occasionally observed brief periods during which multiple neurons nearly simultaneously became active, possibly indicating some underlying network activity (for example, Fig. 2A and Fig. 5A). To study this phenomenon in detail, we identified synchronous events by searching for frames in which multiple neurons emitted subevents whose time derivatives peaked within 50 ms of the frame. The majority of synchronous events consisted of only two participant neurons (Fig. 5B). The overall rate of synchronous events in baseline conditions varied over several orders of magnitude and was very strongly correlated with the overall subevent rate (R = 0.97, P < 0.01, N = 25 slices). Since some degree of synchrony would be expected to arise by chance, we quantified the excess synchrony rate as the difference between the observed synchronous event rate and the upper 99% confidence level (i.e., any positive rate corresponds to a statistically significant excess). Only 1 slice of 25 had a synchronous event rate that exceeded the 99% confidence interval derived from surrogate data sets (Fig. 5C), seemingly suggesting that most or all of the synchrony we observed could be explained by coincidence. However, we consistently observed bright synchronous events involving many neurons, and it was implausible that these synchronous events could be explained by coincidence. For uncorrelated activity, the probability of multiple neurons synchronizing should scale as the product of the neurons’ individual activation probabilities. For correlated activity, the activation of multiple neurons enhances the probability of recruiting even more neurons, and thus we would expect to see an excess of high-synchrony events. To reconcile these observations, we examined the rates of synchronous events with exactly two, exactly three, or four-plus participant neurons separately. For each bin, only one slice exceeded its expected two-participant rate, two slices had positive excesses of three-participant events, and seven slices exceeded their four-plus expectation (Fig. 5C). On the basis of this observation, we hypothesized that the four-plus participant synchronous events were due to functional connectivity among neurons and not simple chance. To assess the spatial profile of these synchronous events, we redivided the data into low-synchrony (2 or 3 participants) and high-synchrony (4+ participants) groups and compared the distributions of the mean separation between all participants (Fig. 5D) and mean angle between participants (Fig. 5E). In each case, the distributions were significantly different (P < 0.01, two-sample Kolmogorov-Smirnov test). Thus the high-synchrony events appear to represent a distinct form of network activity.

Fig. 5.

Spontaneous synchrony. A: fluorescence traces from eight neurons identified as participants in a synchronous event. B: distribution of number of neuronal participants for all synchronous events. C: excess rate of synchronous events, binned by number of participants. D and E: distributions of mean separation and mean angle of participant subevents/neurons for low-synchrony (blue) and high-synchrony (black) synchronous events.

Effects of NMDA on Individual Neuronal Activity

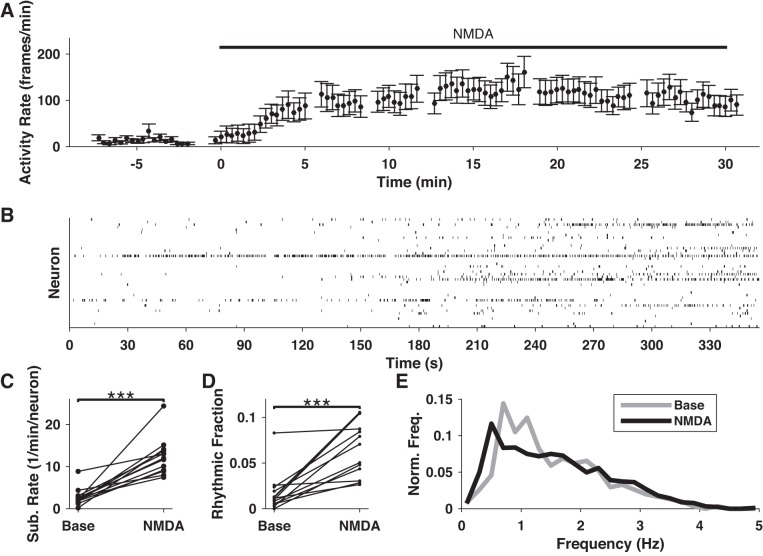
Application of moderate concentrations of NMDA is known to activate neural microcircuits (Carrillo-Reid et al. 2008). To gain further information about PFC network activity and structure, we imaged 519 neurons across 13 slices before (92 min total) and after (154 min total) wash-in of NMDA. NMDA application coincided with dramatic upticks in overall activity after a 2–5 min delay (Fig. 6A). This delay represented the time required for NMDA ACSF to flow into the slice chamber and replace the baseline ACSF. Data from this transition period was excluded from our analysis. We found a significant increase in the mean subevent rates of slices under NMDA ACSF (P < 0.01, Wilcoxon signed-rank test, N = 13 slices; Fig. 6B) with a Cohen’s U3 effect size of 1, the theoretical maximum for this metric. Thus we found very strong evidence that NMDA increased overall neural activity.

Fig. 6.

Effects of NMDA on spontaneous neuronal activity. A: representative example of the activity rate (total subevent frames per neuron per 30-s bin) in response to wash-in of NMDA. B: example raster plot showing the effect of NMDA on rhythmic activity. Activity increases roughly 3 min after beginning of wash-in (180 s). Rhythmic activity in particular increases under NMDA stimulation, as evidenced by the appearance of several neurons showing repetitive activations of self-similar duration and frequency. C: comparison of overall subevent rates before and after NMDA application for all NMDA data sets. D: the fraction of neurons exhibiting rhythmic activity increases under NMDA stimulation. E: frequency spectra of rhythmic epochs under baseline (gray) and NMDA (black) conditions. ***P < 0.001.

We noticed that rhythmic activity often increased following application of NMDA (for example, Fig. 6C). For each slice, we compared the fraction of recording time neurons spent oscillating before and after NMDA application, and found significant increases (P < 0.01, Wilcoxon signed-rank test) in 11 of 13 slices (Fig. 6D). Effect sizes were very strong (Cohen’s U3 = 0.93 ± 0.04) for those 11 slices. In all slices that received NMDA, a substantial fraction of neurons (50 ± 3%, N = 13 slices) were found to switch from nonrhythmic (0 epochs) to rhythmic (≥1 epoch) after NMDA application. Thus NMDA acted as a powerful driver of rhythmic activity.

To detect any possible effect on the frequency of oscillation, we looked at neurons that showed rhythmic activity before and during NMDA application. In some cases, neurons exhibited multiple epochs with distinct frequency ranges within one condition, making it difficult to assign one meaningful summary frequency per neuron. Instead, we compared frequency distributions by pooling the intersubevent intervals from all epochs within each condition for each neuron. We tested for significant differences between these samples by using the two-sample Kolmogorov-Smirnov test. Effect sizes were assessed by using Cohen’s U3, with U3 > 0.5 signifying an overall increase in frequency, and U3 < 0.5 signifying a decrease. We found significant differences (P < 0.01) in 23 of 41 neurons through this analysis, 15 of which showed decreases (U3 = 0.08 ± 0.02), and 8 of which showed increases (U3 = 0.97 ± 0.02). The overall spectrum of rhythmic activity under NMDA shifted toward lower frequencies (<1 Hz) relative to baseline (Fig. 6E).

Effects of NMDA on Network Activity

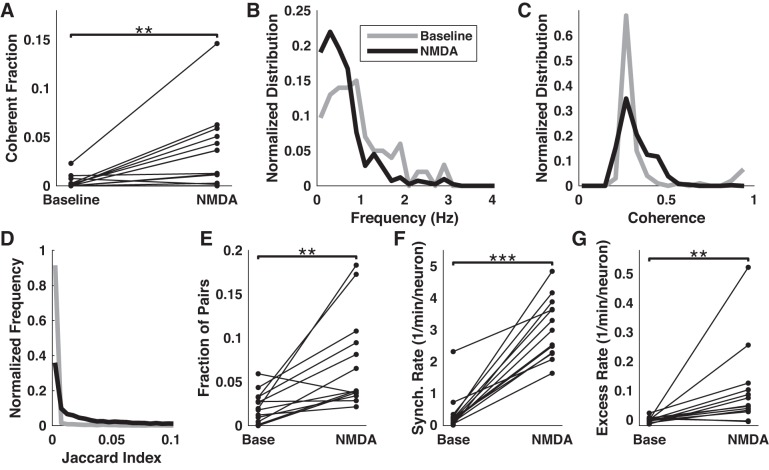
NMDA increased the overall number of pairs of rhythmically active neurons that showed significant coherence (Fig. 7A). Mirroring the overall tendency toward lower frequency oscillations under NMDA, coherence tended to peak at lower frequencies (Fig. 7B), with almost all coherent pairs peaking below 1 Hz. We also found a moderate increase in the magnitude of coherence (Fig. 7C). As in the baseline condition, the phase delay of coherence was widely distributed but showed a distinct preference for low delays. Taken together, these results suggest that NMDA strengthened the coupling between oscillating neurons.

Fig. 7.

Effects of NMDA on network activity. A Comparison of the fraction of pairs of neurons showing statistically significant coherence before and during application of NMDA. B and C: distributions of frequencies of peak coherence and magnitude of coherence before and during NMDA stimulation. D: normalized histograms of Jaccard indices pooled from all pairs of neurons under baseline (gray) or NMDA (black) condition. E: fraction of pairs of neurons that were identified as functionally connected under each condition. F: the overall rate of synchronous events increased during NMDA application. G: excess rate of 4+ neuron-synchronous events (relative to upper 99% confidence interval) increased during NMDA application. **P < 0.01 and ***P < 0.001.

As in the baseline condition, pairwise similarity between neuronal activity traces was very low compared with the theoretical maximum of 1 and typically fell below 0.1 (98% of all pairs in wash condition, 92% in NMDA, Fig. 7D). However, the fraction of functionally connected pairs increased under NMDA in 12 of 13 slices (Fig. 7E), and the overall effect was significant (P < 0.01, Wilcoxon signed-rank test) and strong (Cohen’s U3 = 0.83). A minority (12.7 ± 3.8%) of the pairs that were identified as significantly correlated during the baseline period were also identified under NMDA stimulation. We wondered whether NMDA affected the distance between correlated neurons. Comparison of the distributions of distances for these pairs of neurons, between baseline and NMDA, failed to find significant differences for any slice (P > 0.01, two-sample Kolmogorov-Smirnov test).

We compared the overall rates of synchronous activity in baseline and NMDA conditions. NMDA significantly increased the rate of synchronous events (P < 0.01, Wilcoxon signed-rank test, N = 13 slices, Cohen’s U3 = 1; Fig. 7F). However, the rates of synchrony under both conditions were very strongly correlated with the corresponding overall subevent rates (R = 0.94 in baseline, 0.90 in NMDA, P < 0.01), suggesting that the observed synchrony might be explained primarily, if not entirely, by the sheer volume of ongoing activity. Indeed, comparing the confidence intervals on overall synchrony rates (obtained from surrogate data sets) to the observed values, we found that 11 of 13 slices fell within the 99% confidence range (for example, Fig. 7G), 1 slice fell below this range, and 1 above. Under NMDA ACSF, 8 of 13 slices fell within this range, and 5 fell below it. Thus the overall synchrony rates were generally consistent with the null hypothesis of independent neurons or, in several cases, underperformed this prediction.

We again looked at the rates of synchronous events as a function of the number of participants in each synchronous event. As in our analysis of baseline synchrony, we looked at the rates of synchronous events with two, three, or four-plus neuronal participants. Results for the 2 and 3-participant rates were mixed, with slices generally falling within the 99% confidence intervals both in the baseline and NMDA conditions. However, we consistently found excess rates of synchronous events involving four or more neurons. We quantified the excess as the difference between the observed rate and the upper 99% confidence level for each slice and condition, and compared the excesses between conditions. NMDA’s effect on the rate of four-plus neuron-synchronous events was statistically significant (P < 0.01, Wilcoxon signed-rank test, N = 13 slices) and strong (U3 = 1; Fig. 7G), indicating that NMDA served as a potent driver of network activity.

DISCUSSION

It has long been known that the prefrontal cortex is deeply involved in various higher cognitive functions. Layer 5 pyramidal cells are strongly implicated in the initiation and maintenance of the network activity states associated with cognition, and we therefore used calcium imaging to study its local neuronal network dynamics. By imaging deep-layer neurons in an acute slice preparation and developing an appropriate analysis framework, we were able to approximate the simultaneous activity of populations of tens of neurons with micrometer-scale spatial resolution, temporal resolution on the order of hundreds of milliseconds, and, for some neurons, single action potential sensitivity. We observed several motifs that strongly resemble the activity states associated with various cognitive functions. We also used this ongoing activity to map network functional connectivity at this spatiotemporal scale. Further experimentation using this paradigm will therefore aid in determining the neuronal origins of cognition and mental disease, and in assessing potential therapies.

Our most basic finding was that many statistics characterizing spontaneous activity were highly unequally distributed. A relative few neurons contributed the vast majority of the activity we observed, and the functional connectivity among neurons was also highly skewed. These results are consistent with a broader theme in neuroscience, wherein neocortical microcircuits comprise a set of sparsely firing neurons with a few strong connections embedded on background of weak or negligible connections (Song et al. 2005; Barth and Poulet 2012; Buzsáki and Mizuseki 2014). Whereas these properties have been established primarily in sensory and parahippocampal cortices, our results appear to extend those findings to deep-layer medial prefrontal cortex.

Perhaps the most consistent and striking phenomenon we observed was the existence of a population of neurons oscillating, at delta-band frequencies, between periods of silence and spiking. Whereas delta rhythms in the intact neocortex are primarily attributed to thalamocortical interactions (Steriade et al. 1993a; Crunelli et al. 2015), the results of this study were obtained in coronal slices where all thalamocortical and neuromodulatory afferents were severed. The rhythmic activity we observed must therefore be attributed to intrinsic neuronal activity in the mPFC alone. Several lines of evidence corroborate the putative role of deep mPFC neurons in delta-band rhythmogenesis. Disruption of thalamocortical connectivity has been associated with enhanced cortical delta oscillations (Amzica and Steriade 1998). Similarly, a source of delta rhythms has been identified in the medial frontal cortex through EEG analysis (Michel et al. 1992; Alper et al. 2006). Given layer 5’s role as an instigator of local, recurrent network activity, our identification of a subpopulation of spontaneously delta-oscillating neurons there offers a parsimonious explanation for these observations. This result also comports with the recent discovery of a class of network-activating, intrinsically bursting layer 5 neurons oscillating at delta frequencies (Lőrincz et al. 2015). Thus local intracortical rhythmogenesis may represent a major component of the greater thalamocortical delta generation mechanism in general, and for the prefrontal cortex in particular.

The oscillations we observed could originate from intrinsic properties of the neurons themselves or as a response to rhythmic input from elsewhere in the slice. Although calcium imaging cannot definitively answer this question, several details of the rhythmic activity imply that they are predominantly intrinsically generated. If the oscillating neurons were responding to some common extrinsic rhythm, they would be expected to exhibit strong coherence with low phase delay, as they would fire most strongly during the peak of that rhythm. The relative rarity of significant coherence between neurons, the weakness of coherence between those neurons, the wide distribution of phase delays and frequencies, and the relatively weak correlations between neurons all argue against the common input explanation. Furthermore, the finding that a minority of neurons showed any oscillations, but oscillations tended to recur in those neurons that did show one such epoch, supports the proposition that cell-intrinsic properties are critical. The existence of a known subpopulation of repetitive oscillatory bursting pyramidal cells in murine mPFC (Yang et al. 1996) matches well with our observations. It is therefore more plausible that the rhythmic activity we observed primarily reflects the intrinsic properties of the individual neurons. Further studies are needed to fully characterize the physiological mechanisms underlying these oscillations and to elucidate their potential roles in cognition.

Spontaneous activity was dominated by a few highly active neurons, while the larger networks remained mostly silent. Since NMDA receptors (NMDARs) are strongly implicated in maintaining recurrent network activity, we used NMDA to provide unstructured stimulation of the wider networks. NMDARs are expressed broadly throughout the central nervous system (Wenzel, et al. 1995) and hence a precise interpretation of the effects of bath application is not possible, but the overall effect was clearly excitatory. NMDA stimulation strongly promoted the emission of delta-band oscillations in particular and was accompanied by a modest strengthening of the coherence among these neurons, possibly reflecting strengthened synaptic coupling between these neurons. The existence of an NMDA-sensitive population of layer 5 neurons with an intrinsic proclivity for delta frequency oscillations parallels the recent discovery of intrinsic delta generation in layer 5 somatosensory cortex (Carracedo et al. 2013) and comports with the broader notion that local delta generation is a general property of cortical systems (Krueger et al. 2008; Mormann et al. 2008). However, further work is needed to definitively establish a causal role of the observed neuronal oscillations in the field potential delta waves familiar to electrophysiologists.

The sparse, ongoing spontaneous activity we observed was occasionally punctuated by brief bouts of activity synchronized across multiple neurons. By comparing the frequency of these synchronous events in our data to the predicted rate due to pure coincidence, we showed that some of this synchrony (particularly that involving four or more neurons) must be attributed to the underlying network structure. We were able to map the functional connectivity of these networks statistically and found that relatively few (~2–3%) pairs could be considered more correlated than chance. Connection probabilities among pyramidal cells in neocortex are generally reported to be around 0.1 within 100 μm of separation (Morishima and Kawaguchi 2006; Wang et al. 2006) and fall to around 0.01 by 200 μm, in good agreement with our results (Fig. 4D). In a recent study, Luongo et al. (2016b) determined that PFC networks exhibit a “small world” organization, in which connections exist primarily within clusters of neurons and just a small fraction of connections links these clusters. In that study, a similarly sharp decline in correlation was observed over the first 200 μm of separation. Those results combined with our own strongly suggest that the small worlds within deep layers of murine PFC have a characteristic radius of around 150 μm. Another study indicated that layer 5 neurons preferentially connect to nearby columnar partners over neighboring neurons located on the same horizontal plane (Thomson and Deuchars 1997). We looked for anisotropy in the microcircuits we mapped and also found a preference for connectivity among pairs of neurons oriented along the columnar (medial-lateral) axis over connections in the horizontal (dorsal-ventral) axis. The excellent agreement between our measures of local network architecture and those established directly by paired whole cell recordings validates our imaging-based approach, providing a powerful and efficient complement to electrophysiology for future studies. It is important to note that since these experiments were performed in slices obtained from juvenile mice, the underlying microcircuitry itself is not fully mature. Applying this experimental and analytical approach to mice at multiple age groupings could potentially enable the characterization of the development of cortical microcircuitry and provide insights into the effects of natural aging on cognitive function.

The phenomenology of high-synchrony events is strongly reminiscent of the cortical UP-state, in which spiking among many local, recurrent networks of neurons induces a brief period of increased excitability and spiking. UP-DOWN states have been observed in diverse cortical models in vivo (Steriade et al 1993b) and in vitro (Sanchez-Vives and McCormick 2000; Fanselow and Connors 2010; Neske et al. 2015), but it has previously been reported that they are rare in murine prefrontal slices (Tahvildari et al. 2012), consistent with our finding that many-neuron synchronous events were infrequent under baseline conditions. NMDARs are critical for UP states (Sanchez-Vives and McCormick 2000; Seamans et al. 2003), and hence the finding that application of NMDA increased the frequency of high-synchrony events offers further evidence that some of the highly synchronous events we observed are likely cortical UP states. Although an explicit connection between behavior and neural activity cannot be made in a slice-based experiment, our results demonstrate that detailed spatiotemporal information about PFC network dynamics resembling those associated with cognition can be obtained through calcium imaging of acute slices. Future studies may employ this approach to detect differences between diseased and healthy brains, to track local network activity and connectivity through development, or to test potential PFC-targeted therapies.

GRANTS

This work was supported by Defense Advanced Research Projects Agency (DARPA) Grant REPAIR N66001-10-C-2010 (to A. Nurmikko) and National Science Foundation (NSF/EFRI) Grant 0937848 (to A. Nurmikko).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.S.B. conceived and designed research; A.S.B. performed experiments; A.S.B. analyzed data; A.S.B., B.W.C., and A.V.N. interpreted results of experiments; A.S.B. prepared figures; A.S.B. drafted manuscript; A.S.B., B.W.C., and A.V.N. edited and revised manuscript; A.S.B., B.W.C., and A.V.N. approved final version of manuscript.