Interfacing whispering-gallery microresonators and free space light with cavity enhanced Rayleigh scattering

Abstract

Whispering gallery mode resonators (WGMRs) take advantage of strong light confinement and long photon lifetime for applications in sensing, optomechanics, microlasers and quantum optics. However, their rotational symmetry and low radiation loss impede energy exchange between WGMs and the surrounding. As a result, free-space coupling of light into and from WGMRs is very challenging. In previous schemes, resonators are intentionally deformed to break circular symmetry to enable free-space coupling of carefully aligned focused light, which comes with bulky size and alignment issues that hinder the realization of compact WGMR applications. Here, we report a new class of nanocouplers based on cavity enhanced Rayleigh scattering from nano-scatterer(s) on resonator surface, and demonstrate whispering gallery microlaser by free-space optical pumping of an Ytterbium doped silica microtoroid via the scatterers. This new scheme will not only expand the range of applications enabled by WGMRs, but also provide a possible route to integrate them into solar powered green photonics.

The last two decades have witnessed a revolution in photonic technologies pioneered on one hand by new concepts in materials and devices such as photonic crystals and metamaterials, and, on the other hand, by the realization and testing of century-old well-known theories such as quantum theory, plasmonics and whispering galleries which have been enjoying many benefits of recent developments in enabling technologies and fabrication techniques¹,²,³,⁴,⁵. Since its first explanation in acoustic regime by Lord Rayleigh in London's St Paul's Cathedral, WGM phenomenon has been explored in various optical structures for a variety of applications⁶,⁷,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴, opening unprecedented and unforeseen directions in optical sciences. Recent advances in fabrication techniques and material sciences have helped to achieve WGMRs with high-quality (Q) factors and nano/micro-scale mode volumes(V). Novel applications and devices using WGMRs have been demonstrated, such as ultra-low threshold on-chip microlasers⁷,⁸,¹⁵,¹⁶, narrowband filters and modulators for optical communication⁹,¹⁰,¹⁷, high performance optical sensors achieving label-free detection at single-particle resolution¹,⁴,⁵,¹¹,¹², cavity opto-mechanics²,¹⁸,¹⁹, quantum electrodynamics³,¹³, and nonreciprocal optical devices utilizing the concepts of parity-time symmetry²⁰.

Despite their great promises for photonic technologies, coupling light into and from WGMRs is intrinsically hindered by their unique feature of rotational symmetry. The circular geometry is also responsible for the deviation from total internal reflection condition, and introduces radiation losses in particular when the wavelength of the light is comparable to the radius of curvature. Thus, an evanescent field channel exists for extracting light from WGMs, and for coupling light into WGMs using prisms, tapered fibers or waveguides²¹,²²,²³,²⁴,²⁵. Coupling efficiency with tapered fibers can reach values as high as 99%. However, achieving this coupling and maintaining it for long durations require active stabilization and precise alignment with nano positioning systems, because coupling conditions are prone to environmental perturbations (e.g., air flow and mechanical vibrations). This significantly limits the practical use of fiber-taper-coupled WGMRs. Prism and on-chip waveguide couplers are more stable, but their applications are limited by the bulkiness of prism system, or the requirement of additional optics to couple light into the on-chip waveguide. Alternative to evanescent coupling techniques is free space coupling (edge coupling) to asymmetric WGMRs such as spiral, ellipsoid, quadrupole and limaco, where circular symmetry is lifted by introducing controlled deformations either after the WGMRs are fabricated or during lithographic patterning²⁶,²⁷,²⁸,²⁹,³⁰,³¹,³². Free-space coupling into and directional emission from deformed/asymmetric resonators are possible due to the dynamic tunneling between the co-existing chaotic and regular WGM modes, which help the light to escape from or couple into the resonator along the direction of deformation. Coupling of free space light into such resonators still remains as a challenge, mostly because it relies significantly on precise alignment of the focused free-space light on the cavity edge along the direction of deformation, which requires optical and mechanical systems with high angular and translational resolution. These unavoidably make the system bulky and difficult to move out of the lab environment. Moreover, with the exception of a few studies, such cavities suffer from significant Q-degradation as the degree of deformation is increased. Here we introduce a new interface between the free space light and the WGMs of circular resonators. This interface is formed by directly depositing nano-scatterers or nanoparticles onto the circular WGMR. We show that each of the nanoparticle deposited on the resonator surface effectively acts as a nanocoupler to couple free space light into WGMs without additional bulk optical components and precise alignment processes. Further, we demonstrate lasing in an Ytterbium (Yb³⁺) doped silica microtoroid. Cavity-enhanced Rayleigh scattering lies at the heart of our nano-scale interface between the micro-scale WGMR and the free-space light field³³. The hybrid microresonator-nanoparticle system here enables the collection of a large fraction of the scattered light into the cavity mode via Purcell enhancement, and has the ability to harvest even weak light fields. This nanocoupler scheme brings together and relies on four fundamental observations. First, coupling of an emitter to a cavity mode enhances its spontaneous emission rate by increasing the local density of modes, implying that the emitter will emit mostly into the cavity modes and with much faster rate than in vacuum. This enhancement is proportional to Q/V and is known as Purcell enhancement factor. Second, a sub-wavelength particle (i.e., the nanocoupler) can be treated as an oscillating dipole, with the dipole moment induced by the electric field of the incident light, radiating into the surrounding (i.e., Rayleigh scattering). For the resonator, there is no difference between the light coming from an emitter placed its proximity and the light coming via scattering from a nanoparticle illuminated by a free-space incident light. Thus, Purcell enhancement should take place leading to collection of the weak scattered-light into the cavity WGM. Third, when a nanoparticle is placed close to a resonator and interact with the evanescent field of the resonator, light scattering back into the WGM and also to the free-space reservoir modes takes place. Here, Purcell effect manifests itself again by enhancing the coupling of the scattered light back into the degenerate WGMs (i.e., over 95% of the scattered light is coupled back³⁴,³⁵). Fourth, nanoscatterers on the resonator break its rotational symmetry thus open a channel for coupling light in and out of WGMs³⁶,³⁷. Therefore, the proposed nanocoupler should provide an efficient route for free-space coupling of light to and from WGMs. An illustration of the concept is given in Fig. 1.

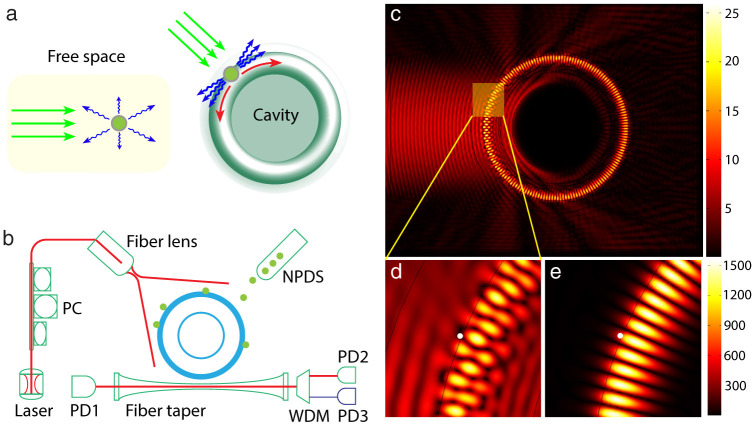
Figure 1. Coupling of free space light into whispering gallery modes via nano-scatterers.

(a), Cavity enhanced light collection. A nanoscale structure usually scatters light in all directions; when a nano-scatterer is placed close to a cavity, most of the scattered light is collected into the cavity mode due to Purcell enhancement. (b), Simplified scheme used for characterizing the performance of the nanocoupler. Light from a tunable laser is sent through a fiber lens and incident onto the resonator. The distance between the fiber lens and cavity is tunable. A fiber taper is used to monitor the light field inside the cavity. PC: polarization controller. WDM: wavelength division multiplexer. NPDS: nanoparticle delivery system. (c), Finite element simulation shows free space light cannot couple into a WGM resonator by direct illumination. (d), Magnified view of the WGM area in (c). (e), With a nanoparticle on the surface of resonator, WGM is efficiently excited from free space. In (d) and (e), the location of nanoparticle was marked with white dot.

We have developed a theoretical model (Supplementary Note 1) and performed extensive numerical simulations (Supplementary Note 2) to quantify the interaction between free-space light and a WGMR with and without perturbing nanoparticles of spherical shape. Figure 1c clearly shows that in the absence of nanoparticles, free-space light does not couple into WGMs while the presence of a single nanoparticle opens up a channel, which interfaces the WGMs inside the resonator with the outside optical modes, including the free-space incident light and the reservoir modes into which the WGMs dissipate.

Results

The setup used in the experiments is depicted in Fig. 1b. It consists of a tunable external cavity laser and a fiber lens as the free-space light source, a fiber-taper coupler to extract the light, which is coupled into the microtoroid from free-space via the nanocouplers, out from the WGM, and a nanoparticle delivery system to deposit the nanoparticles onto the resonator (see Supplementary Fig. 1 and Method 1 for details). The light extracted from the WGM through the fiber-coupler is evaluated using optical spectrum analyzer (OSA) and photodiodes. Fiber-taper coupler enables efficient and tunable out-coupling of the light from the microtoroid for accurate evaluation of the proposed nanocoupler. To evaluate the performance of the nanocoupler, we performed three sets of experiments using this scheme.

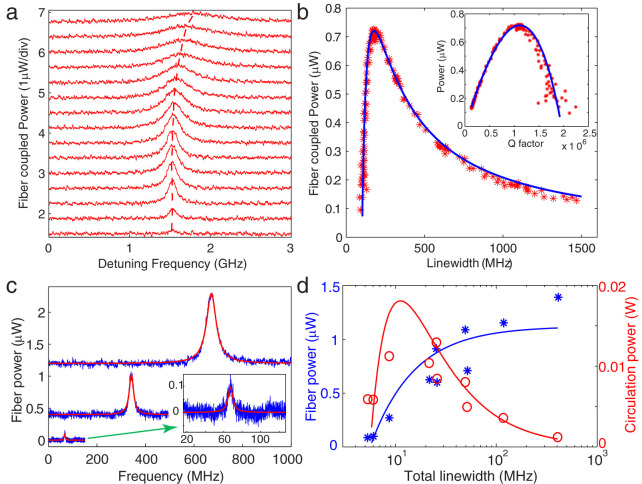
In the first set of experiments, we investigated the effect of nanocoupler-resonator and resonator-taper coupling strengths, quantified by 2Γ and κ₁, respectively (see Supplementary Note 1), on the intracavity power using a free space light whose spot size was larger than the area of the resonator so that all the nanocouplers were illuminated from the top at an angle of about 45-degrees. In this way, we avoided edge coupling and investigated the collective response of all possible coupling channels (nanocouplers). Before depositing any nanoparticles, we tested whether any WGM is excited with this illumination configuration. The result was that no WGM was excited confirming that this configuration of illumination avoids edge-coupling of free-space light into WGMs. Then we monitored the fiber-taper output as the nanoparticles were deposited. We continued nanoparticle deposition until enough power was transmitted from free space into the resonator through the coupling channels made available by the nanoparticles. We specifically chose a large resonator having a large mode volume to prevent or reduce the possibility of observable mode splitting (i.e., amount of mode splitting scales inversely with V). Using a nano positioning system, we changed κ₁ by tuning the taper-resonator distance and monitored the out-coupled light from fiber taper as the wavelength of the free-space light is scanned (Fig. 2a). Since the WGM resonator supports two counter-propagating modes (clockwise, CW and counterclockwise, CCW) at the same resonance frequency, the free space light is coupled into both CW and CCW modes. We observed clear resonance peaks in both the forward (PD1) and the backward (PD2) directions implying the coupling of free-space light into WGM via the nanoparticle based interface (nanocoupler). The extracted light intensity changed as the distance between the resonator and the fiber taper (i.e., air gap) was changed (Fig. 2a,b). As shown in Fig. 2a, in the deep-under-coupling regime (κ₁ ≪ κ₀ + 2Γ), the sum of the intrinsic resonator loss κ₀ and the loss induced by the nanocouplers 2Γ dominated the fiber-coupling loss κ₁; thus, only a small amount of light was extracted from WGM. Decreasing the air gap brought the system closer to the critical coupling (κ₁ = κ₀ + 2Γ), which was accompanied by an increase in the extracted light power at the resonance wavelength; the extracted power reached its maximum value at the critical coupling condition. Further decrease of the air gap moved the system to over-coupling regime (i.e., fiber-coupling loss dominates other losses κ₁ ≫ κ₀ + 2Γ) and led to reduction in the extracted peak power and to an increase in the linewidth of the resonance peak due to increased loss. We estimated the Q as 10⁶ at the critical coupling point, and ~2 × 10⁶ at the deep-under-coupling regime, which is consistent with the definition of critical coupling condition (Fig. 2b). There is a slight difference between the data obtained in our experiments and the theory based on an ideal coupling model²²,³⁸. This difference is the result of the deviation of the fiber-taper coupler from ideality, which introduces additional losses that becomes prominent when the fiber-taper is very close to the resonator. Since the theoretical model assumes an ideal fiber-taper coupler, such losses are not accounted for. This effect is also seen in Fig. 2a, which shows a small resonance shift in the over-coupling regime. In Fig. 2b, the fitting curve is obtained using the model based on the ideal taper-coupler, and by considering an extra cavity loss factor proportional to κ₁ as the free parameter.

Figure 2. Loading curves of nanocoupler-resonator-taper system.

(a), Spectra of a WGMR, with input light coupled from free space into the resonator via nanocouplers, obtained at different fiber-taper coupling strength quantified by κ₁. The upper two spectra are vertically shifted up by 0.375 and 0.75 from the lower one for clarity. From bottom to top: the air gap between the fiber taper and the resonator decreases (κ₁ increases). (b), Power coupled out from the WGMR by the fiber taper versus the total linewidth of the nanocoupler-resonator-taper system when κ₁ is increased. Inset shows the power out-coupled using the fiber taper versus total Q factor. The blue fitting curve is obtained using theoretical model described in Supplementary Note 1, and considering a cavity loss factor proportional to κ₁ induced by the non-ideal fiber taper. (c), Mode spectra with increasing number of particles deposited on the microtoroid (increasing 2Γ). Spectra are vertically shifted for clarity. From bottom to top: particle number increases. For each spectrum, fiber taper coupling is optimized to obtain the maximum on-resonance power (κ₁ = κ₀ + 2Γ). The inset shows a magnified view of the spectrum with lowest peak power. (d), Blue asterix: power coupled from WGM using the fiber taper versus total linewidth of the system when more particles are deposited. Red circles: Calculated intra-cavity power versus total linewidth. Solid curves are fitting functions obtained from the theoretical model. For these experiments, the input power of free space laser beam is about 2 mW, and wavelength is in 1550 nm band.

Increasing the number of nanoparticles (channels, nanocouplers) increased the number of coupling channels between the WGM and its environment (i.e., increasing 2Γ) and thus led to broader resonance linewidth (i.e., 2Γ + κ₀ + κ₁) and to more light coupled from free space to WGMs at resonance (Fig. 2c,d). For each measurement depicted in Fig. 2c,d, we fixed the number of nanoparticles and optimized κ₁ such that κ₁ = κ₀ + 2Γ was satisfied. Thus, power extracted from the WGM via the taper was maximized. In this case, the maximum intracavity power was achieved at the critical coupling of nanocoupler-resonator system quantified by 2Γ = κ₀ (Fig. 2d). Further increase of the number of nanocouplers (larger 2Γ) shifted the system beyond this critical point and lowered the intracavity power by increased particle-induced dissipation. Because of the random placement of nanoparticles, there is deviation of this specific set of experiments from the theoretical curve. However, averaged results of a large number of simulations follow closely the trend indicated by Eq. S13 and S14 (Supplementary Note 3). These results (Fig. 2) are similar to what has been observed for an add-drop filter configuration where a resonator is coupled to two fiber taper couplers simultaneously³⁹. The experimentally observed dependence of extracted power and the intracavity power on κ₁, κ₀ and 2Γ agrees well with theoretical model (see Supplementary Note 1).

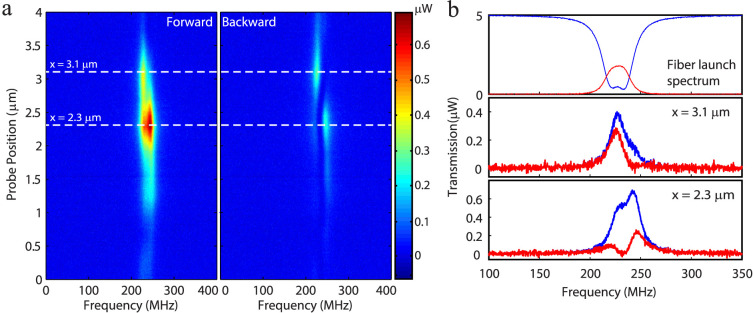
In the second set of experiments, we started with a resonator-nanocouplers system with observable mode splitting in the transmission spectra (Fig. 3b) and investigated the response of local channels (nanocouplers) by changing the position of a tightly focused free-space beam spot along the equator of a microtoroid. One of the reasons we used a smaller beam spot is to avoid the area where edge coupling is allowed. We can specifically work in the area where nanoparticles are deposited and study nano-scatterer coupling scheme. In this way, we opened only the local channels within the small beam spot size for coupling free space light into WGMs, and recorded the extracted light in both forward (PD1) and backward (PD2) directions as a function of the beam spot position. In such a case when mode splitting exists, the light inside the resonator is expressed as two orthogonal standing wave modes formed by the superposition of the CW and CCW modes³⁶,³⁷,⁴⁰; the first standing wave mode SWM1 is expressed as 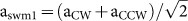and the second standing wave mode SWM2 is expressed as 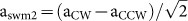. The spatial distribution of these modes are π/2-phase shifted from each other with the phase describing the spatial distance between the nodes of the SWMs, and the distance between two adjacent nodes of a SWM corresponding to π. As we scanned the beam spot along the resonator surface, we observed distinct spectra at different positions due to the fact that at each position different sets of local nanocouplers were excited and consequently different local channels were opened. Mode splitting was observed in both the forward and the backward transmission spectra. While some sets of local channels coupled light strongly into the SWM1, the other sets of local channels coupled light strongly into the SWM2. This reveals that the nanocouplers channel more free space light into the mode that has stronger spatial overlap with the nanocouplers. If the excited couplers are closer to the node of a mode, either no light or only a small amount of light can be coupled to that mode. These features are clearly seen in Fig. 3b, where split modes show different heights at different probe positions. The discrepancy in the intensity of the two modes is attributed to the different coupling channels and the variation (phase and amplitude) in the light coupled to each of these channels. We also observed that the intensities of the light coupled out in the forward and backward directions were not the same (Fig. 3). This is because the placement of nanoparticles was not symmetric with respect to forward and backward directions, which gave different phase for the forward and backward light. In this case the CW and CCW light inside the resonator were no longer the same.

Figure 3. Mode spectra of a WGMR with incident beam spot at different positions.

(a), Spectrograms of light coupled out of the WGMR by a fiber taper in the forward and backward directions when a tightly focused free-space beam spot was scanned along the equator of the microtorid with nanocouplers. The size of beam spot was about 5 μm. The input power of free space laser beam was about 5 mW, and wavelength is in 1550 nm band. (b), Light coupled out from the microtoroid via a fiber taper when the same fiber taper was used to couple light into the microtoroid(top panel) and when free-space light is coupled into the microtoroid via the nanocouplers within the beam spot size (middle and bottom panels). The transmission spectra in the middle and bottom panels correspond to the probe positions of 3.1 μm and 2.3 μm in (a). Different probe positions yield distinctively different spectra. Blue and red curves denote the transmission spectra in the forward and backward directions, respectively.

In the third set of experiments, we demonstrated that the free-space-to-WGM coupling efficiency of the proposed nanocoupler scheme was sufficient to obtain WGM microlasers (Fig. 4). Using free-space light from a tunable laser in the 980 nm band, we observed WGM lasing in the 1050 nm band from an Yb³⁺-doped silica microtoroid⁴¹,⁴². Lasing started when sufficiently high pump power was built-up in the microcavity (Fig. 4c). The lasing threshold depends on the spatial overlap between the lasing and the pump mode as well as the spectral overlap between WGMs and the absorption and emission bands of Yb³⁺ ions. In the experiments whose results are depicted in Fig. 4c, we used a fiber-taper with thickness optimized to achieve phase matching for the pump mode. The taper-resonator system was then set at under-coupling condition so that only a small amount of intracavity pump power could be coupled out without causing a significant disturbance to the intracavity pump power. This out-coupled light allowed us to estimate the intracavity pump power but since it also reduces the intracavity pump power it leads an effective increase in the lasing threshold power. At the under-coupling condition, the out-coupled power is less than 1/3 of that at the optimal (critical) coupling. In our experiment, the intracavity pump power (estimated as ~37.5 mW at threshold level) is much higher than the total free space pump power (485 μW at threshold) due to the cavity enhancement. As a result the gain provided by direction illumination of Yb³⁺ ions with the free-space light can be ignored, and we can safely conclude that the optical gain is due to resonantly enhanced circulating pump power. We observed not only single mode lasing but also multimode lasing within the emission band of Yb³⁺ ions (Fig. 4b). In multimode lasing, mode competition among many modes in the WGMRs may affect the lasing threshold.

Figure 4. Whispering gallery mode microlasers by free space excitation via nanocouplers on a microtoroid resonator.

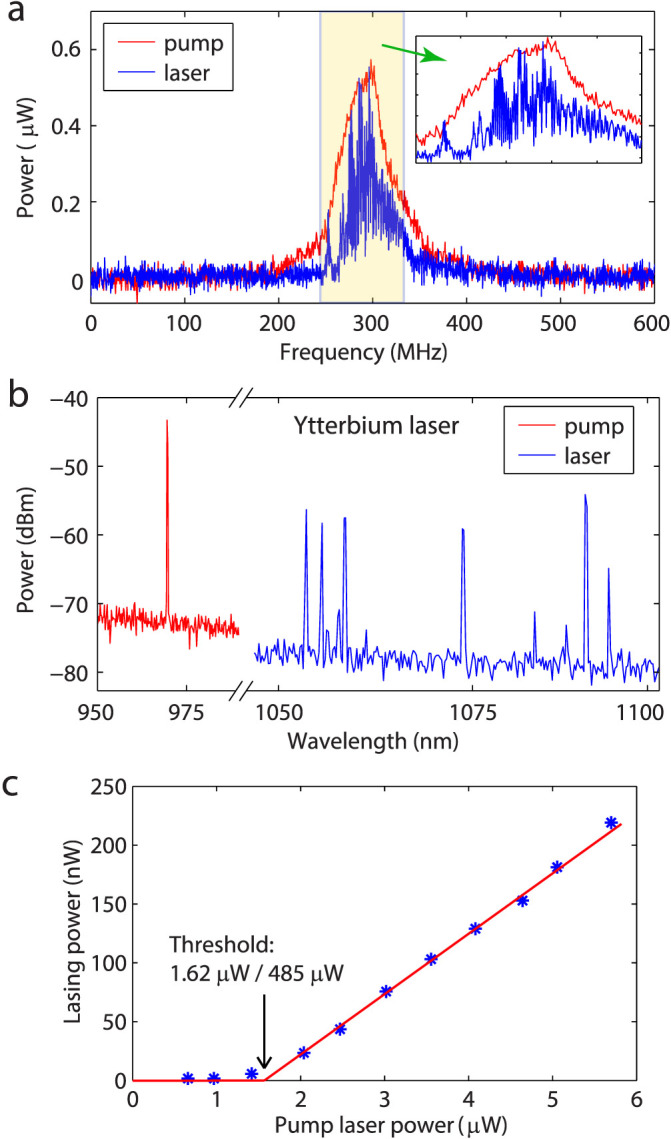
(a), Lasing from an Ytterbium doped silica microtoroid achieved by free space excitation. The frequency of the free space pump at 975 nm band was scanned across 600 MHz range around a resonance. The red and blue spectra were obtained by out-coupling the field in the microtoroid using a fiber-taper coupler, and they respectively correspond to the pump in the 975 nm band and the generated ytterbium lasing in the 1050 nm band. The diameter of the fiber taper coupler was optimized for maximal out-coupling of 1050 nm band light from the microtoroid. (b), Pump and lasing spectrum of the Ytterbium laser shown in (a). (c), Relationship between lasing power and pump power of a Ytterbium laser. The threshold pump power for the lasing was measured at two different points, and was found to be 1.62 μW when the power was measured at the output of the fiber taper and 485 μW when it was measured at the input end of the fiber lens. The thickness of the fiber taper coupler was optimized for out-coupling of pump light from the microtoroid, but it was kept at under-coupling regime to reduce extraction of pump power.

Discussion

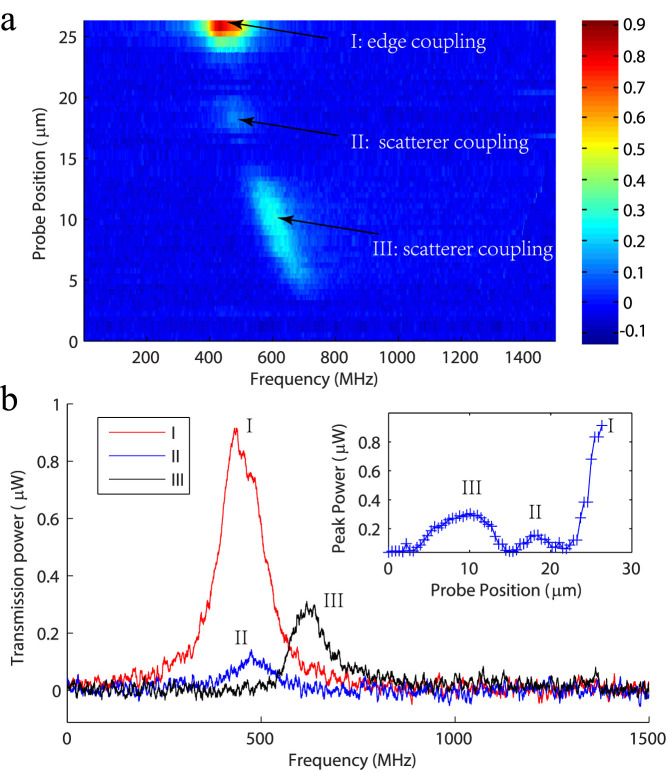
To compare the nanoscatterer-based coupling of free space light into the WGM with coupling via focusing the free-space light to the edge of the resonator (i.e., tangential to the circular rim) which we call as edge coupling, we conducted an experiment that involved scanning the free space beam from the center to the equatorial edge of a microsphere. When the beam was aligned at the edge of the microsphere, light was coupled directly into the WGM, as shown by the mode in Fig. 5, at position I. When the beam was moved (in the equatorial plane) away from the edge in the azimuthal direction, edge coupling efficiency decreased rapidly. However, when the beam spot overlapped with scattering centers on the microsphere, we saw the excitation of WGMs again, as shown in Fig. 5, at position II and III, which clearly shows scatterer-based coupling scheme works at different regimes than edge coupling.

Figure 5. Coupling of free-space light into a WGM resonator when the free space light beam was moved from the center to the edge of a microcavity.

Edge coupling is clearly seen at position I, and nano-scatterer coupling is seen at positions II and III. (a). Spectrogram of fiber taper collected transmission from the cavity. Light is coupled into the sphere from a free space laser beam in 1550 nm band. The shift of the resonance frequency may be attributed to the changes in the phase of input light incident on different scatterers as the probe position changes, and also to thermal drift. (b). Transmission spectra at different probe positions. Inset shows the peak power of the transmission mode at different probe positions.

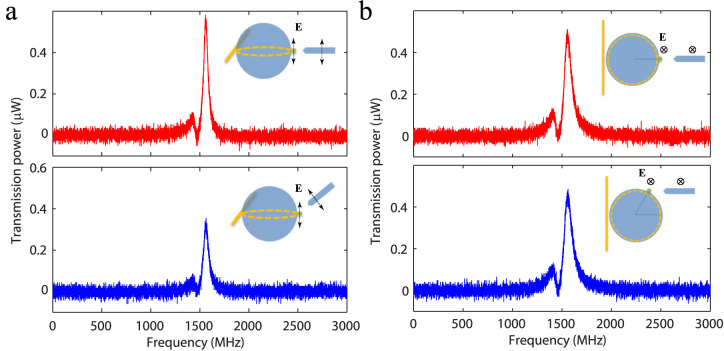
In our nanoscatterer-based coupling scheme, it is, in principle, possible to couple light at any incidence angle of the free-space light onto the resonator provided that the dipole moment induced by the free space light is not orthogonal to the electric field of the cavity mode³³. Here we show experimentally-obtained transmission spectra at different illumination configurations where the free space light was focused on the scattering center at different polar (Fig. 6a) and azimuthal angles (Fig. 6b). In theory, both TE and TM modes are sensitive to the changes in the polar angle. At zero-degree polar angle the coupling to TE mode is maximized. TM modes in theory cannot be coupled at zero-degree polar angle, but it can be coupled from 90-degree polar angle. Different polar angles change the alignment between the induced dipole and E field of WGM. In Fig. 6a, despite the presence of mode splitting, it is clear that the WGM excited by the free-space light is a TE mode because free-space light is coupled into this mode efficiently at zero-degree polar angle. Any deviation from the zero-degree polar position decreases the coupling efficiency. The same TE mode is not sensitive to the changes in the azimuthal angle (Fig. 6b), because the induced dipole (in the direction of in/out of the plane) is always aligned with the electrical field of the WGM.

Figure 6. Angle dependence of free space coupling using nano-scatterers.

(a). Free space coupled transmission when the polar angle of the free space beam changed from 0 degrees to 45 degrees. (b). Free space coupled transmission when the azimuthal angle of the free space beam changed from zero to 60 degrees. The directions of electrical field of the WGM and free space light is marked in all figures. It is evident that this mode is a TE mode because in theory light cannot be coupled into TM mode at a polar angle of zero-degree. The green dots in the inset figures are the nano-scatterers.

In summary, we have introduced a simple yet elegant and nanocoupler scheme to couple free-space light into WGMRs. The nanocoupler is based on nano-scatterers deposited onto the WGMR. We have observed enhanced light coupling into the WGM through the channels opened by this nanocoupler scheme, and demonstrated WGM lasers using free-space pumping of the resonator via this nanocoupler. With a single nanoparticle, the coupling rate is small (less than 1% of total free space input power) due to the extremely small optical scattering cross-section of a nanoparticle. However, the intracavity power reaches values 100-fold larger than the total input free space power due to resonance enhancement (see Supplementary Note 3). Even with 1% coupling efficiency, the intracavity field intensity is high enough to generate lasing and to perform WGM-based sensing. One could further enhance the coupling efficiency by placing the nanoscatterers in well-defined locations on the resonator with equal distances between them to facilitate constructive interference. The nanoscatterers used to couple light into the cavity can also be used for out-coupling of light. This is possible because the nanoscatterers also open out-coupling channels for the laser generated inside the cavity by scattering it to the surrounding. The scattered laser light then can be detected by photodetectors or an imaging system placed near the resonator. We believe that this study lays the foundation for future on-chip solar/non-coherent light pumped microlasers, and will greatly facilitate miniaturized WGM resonator applications without complicated coupling optics, and free from chaotic behavior often observed in deformed cavities. Also significant is the inherent local enhancement near the nanoparticles (i.e., optical hot spots due to increased refractive index or plasmon effect) which can dually serve for considerably enhancing sensing¹².

Supplementary Material

Supplementary Information

Supplementary Information